Abstract
Tower cranes find wide use in construction works, in ports and in several loading and unloading procedures met in industry. A nonlinear optimal control approach is proposed for the dynamic model of the 4-DOF underactuated tower crane. The dynamic model of the robotic crane undergoes approximate linearization around a temporary operating point that is recomputed at each time-step of the control method. The linearization relies on Taylor series expansion and on the associated Jacobian matrices. For the linearized state-space model of the system a stabilizing optimal (H-infinity) feedback controller is designed. To compute the controller’s feedback gains an algebraic Riccati equation is repetitively solved at each iteration of the control algorithm. The stability properties of the control method are proven through Lyapunov analysis. The proposed control approach is advantageous because: (i) unlike the popular computed torque method for robotic manipulators, the new control approach is characterized by optimality and is also applicable when the number of control inputs is not equal to the robot’s number of DOFs, (ii) it achieves fast and accurate tracking of reference setpoints under minimal energy consumption by the robot’s actuators, (iii) unlike the popular Nonlinear Model Predictive Control method, the article’s nonlinear optimal control scheme is of proven global stability and convergence to the optimum.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tower-cranes are complicated mechatronic systems which are widely used for the transportation of payloads in a large workspace and at large height [1–3]. Tower cranes can accomplish accurate transport and positioning of heavy items in construction sites, in multi-storey building erection,in loading and unloading of cargos in ports and in storage tasks for the logistics industry [4–6]. Tower cranes exhibit the advantages of simple structure, convenient installation, low cost, high payload capacity and low energy consumption [7–9]. Tower cranes usually consist of an actuated jib arm, an actuated translational trolley and an unactuated payload below the trolley [3, 10, 11]. Tower cranes have a complicated and strongly nonlinear dynamics and are also subject to underactuation [12–14]. Major issues in the precise and safe operation of tower cranes are the accurate trajectory tracking about the cranes’ moving parts, as well as the suppression of the swinging and sway motion of the payload which can emerge when large and fast manoeuvres take place [15–17]. Under such operating conditions tower cranes are also exposed to bending and torsional deformations therefore their operation is a demanding and delicate task [18, 19]. Even nowadays most cranes are manually operated by skilled personnel. However, for human operators it is often difficult to achieve precise positioning and suppression of swinging and swaying phenomena [20, 21]. Operational mistakes occur frequently when pursuing highly repetitive tasks under time-pressure. To avoid the deficiencies of the human operation of cranes, automation of such systems has become a pre-requisite and to this end elaborated nonlinear control methods have been developed [22, 23].
The use of robotic tower cranes is rapidly deploying in several construction, industrial and supply-chain applications and the treatment of the associated nonlinear control problems has become a necessity. To this end new results have been recently developed. In [24] a neural adaptive control method is introducted for 4-DOF tower cranes. In [25] a 2-DOF overhead and a 4-DOF rotary crane are controlled through a neural adaptive control scheme. In [26] a control method is presented about vibrations suppression in a 4-DOF tower crane with a flexible jib. In [27] a neural adaptive control scheme is developed for a double-pendulum tower crane. In [27] a 4-DOF tower crane is controlled by a nonlinear controller that consists of a PD control part and a sliding-mode control part. In [28] an input-shaping control technique is applied to suppress oscillations in the 4-DOF underactuated robotic crane. Finally, in [29] an adaptive control scheme is proposed for an underactuated 2-DOF overhead crane.
In the present article, a nonlinear optimal control method is proposed for the 4-DOF nonlinear and underactuated model of tower cranes [30, 31]. The dynamic model of the 4-DOF underactuated tower crane undergoes first approximate linearization around a temporary operating point which is updated at each sampling instance. This operating point is defined by the present value of the crane’s state vector and by the last sampled value of the control inputs vector. The linearization process relies on first-order Taylor series expansion and on the computation of the associated Jacobian matrices [32–34]. The modelling error which is due to the truncation of higher-order terms in the Taylor series expansion, is proven to be small and is asymptotically compensated by the robustness of the control algorithm. For the approximately linearized state-space description of the system a stabilizing H-infinity feedback controller is defined.
The proposed H-infinity controller achieves the solution of the optimal control problem for the tower crane under model uncertainty and external perturbations [16]. Actually, it represents a min-max differential game which takes place between the control inputs of the system that try to minimize a cost function comprising a quadratic term of the state vector’s tracking error and the model uncertainty or exogenous perturbation terms which try to maximize this cost function. To compute the stabilizing feedback gains of this controller an algebraic Riccati equation has to be also solved at each time-step of the control method [35–37]. The global stability properties of the control scheme are proven through Lyapunov analysis. First, it is proven that the control loop satisfies the H-infinity tracking performance criterion [16, 38]. Next, it is proven that under moderate conditions, global asymptotic stability of the control loop is ensured. To implement state estimation-based control without need to measure the entire state vector of the system the H-infinity Kalman Filter is used as a robust state estimator. The nonlinear optimal control method retains the advantages of linear optimal control, that is fast and accurate tracking of reference setpoints under moderate variations of the control inputs [16].
The article has also a meaningful contribution to the area of nonlinear control. One can point out the advantages of the nonlinear optimal control method against Nonlinear Model Predictive Control (NMPC) [16]. In NMPC the stability properties of the control scheme remain unproven and the convergence of the iterative search for an optimum often depends on initialization and parameter values’ selection. It is also noteworthy that the nonlinear optimal control method is applicable to a wider class of dynamical systems than approaches based on the solution of State Dependent Riccati Equations (SDRE). The SDRE approaches can be applied only to dynamical systems which can be transformed to the Linear Parameter Varying (LPV) form. Besides, the nonlinear optimal control method performs better than nonlinear optimal control schemes which use approximation of the solution of the Hamilton–Jacobi–Bellman equation by Galerkin series expansions. The stability properties of the Galerkin series expansion-based optimal control are still unproven.
The structure of the paper is as follows: In Sect. 2 the dynamic model of the tower crane is given and the associated state-space model is formulated in the affine-in-the-input nonlinear state-space form. In Sect. 3 the dynamic model of the robotic crane undergoes approximate linearization through Taylor series expansion and with the computation of the associated Jacobian matrices. In Sect. 4 the H-infinity optimal control problem for the dynamic model of the tower crane is analyzed. In Sect. 5 the global stability properties of the H-infinity control scheme are proven through Lyapunov analysis. Besides, the H-infinity Kalman Filter is introduced as a robust state estimator. In Sect. 6 the accuracy of setpoints tracking by the state variables of the robotic crane, under the nonlinear optimal control method, is further confirmed through Simulation experiments. Finally, in Sect. 7 concluding remarks are stated.
2 Dynamic model of the robotic tower crane
2.1 State-of-the-art in the control of underactuated robotic cranes
As noted, robotic cranes can find use in construction works, in buildings erection, in loading and unloading of cargo-ships in ports, in heavy material lifting for several industrial tasks and in heavy items pick-and-place tasks in logistics. The solution of the nonlinear optimal control problem for underactuated robotic cranes is important for ensuring the reliable performance of robotic cranes in such applications. In the following, the state-of-the-art in the control of underactuated robotic cranes is outlined. To this end, indicative results are overviewed about (a) the use of established model-based and model-free control approaches in robotics, (b) the use of the proposed nonlinear optimal control methods in specific types of autonomous cranes.
There exist several recent results showing the performance of advanced nonlinear control techniques to the stabilization and trajectory tracking problem of robotic cranes. In [39] Lyapunov stability analysis is used to select the gains of a PID-type conntroller so as to ensure global stability for an overhead robotic crane. In [27] a feedback controller which comprises a PID-type control part and an SMC-type control part is proposed for a 4-DOF robotic tower crane. Lyapunov stability analysis is used to select the feedback gains of the controller and to ensure global stability of the control loop. In [40] an adaptive fuzzy controller jointly with a disturbances estimator are used to stabilize an offshore boom crane. The controller’s feedback gains are chosen through Lyapunov stability analysis so as to ensure global stability for the control loop. In [41] an adaptive PID-type controller is developed for dual rotary cranes. The selection of the controller’s gains is performed through the system’s Lyapunov analysis. Global stability is proven through the Lyapunov technique and LaSalle’s invariance principle. In [42] adaptive output feedback control is proposed for a double-pendulum ship-mounted crane while also considering uncertainty about the cargo’s mass. The controller’s gains and the adaptation law which are used for compensating for the model’s uncertainty are chosen through Lyapunov analysis. In [29] a state-variables transformation and the backstepping control technique are used for treating the stabilization of a 2-DOF crane. The stability properties of the control method are proven through Lyapunov analysis. In [43] an energy-based control method is proposed for the dynamic model of a large gantry crane which comprises also elements that are subjected to elastic deformation. Stability properties are demonstrated with the use of Lyapunov analysis. In [44] a knuckle boom crane is controlled by a cascade controller where the inner control loop is designed to damp out the pendulum oscillation, and the crane tip is controlled by the outer loop. An extended Kalman filter is used for the estimation of payload angles and angular velocity. In [45] modified tracking error variables and Lyapunov stability analysis are used to define a feedback controller that finally stabilizes a 4-DOF overhead crane. The global stability proof makes use of LaSalle’s invariance principle. Moreover, in [46] the dynamic model of a knuckle boom crane is considered and a stabilizing feedback controller is designed about it using the Nonlinear Model Predictive Control concept and a Lyapunov analysis-based auxiliary controller.
In particular, the proposed nonlinear optimal control method is suitable for use in a variety of autonomous robotic cranes and several related results have been obtained [1, 16, 17]. Thus, one can note nonlinear optimal control for (i) the 4-DOF overhead crane, (ii) offshore boom cranes, (iii) the double-pendulum overhead crane, (iv) the 4-DOF tower crane and (v) quay-side cranes. The use of the nonlinear optimal control method in robotic systems is not limited into specific state-space forms (e.g., canonical forms, strict feedback or pure feedback forms). The computational complexity of the nonlinear optimal control method remains also moderate because (a) it does not require complicated changes of state variables and transformations of the cranes’ state-space representation, (b) it does not rely on matrices for computing the robots’ control inputs and consequently it avoids the risk of singularities, (c) it performs linearization around one single operating point which is easy to define, (d) it does not require the solution of multiple Riccati equations or LMIs, (e) it avoids the deadlocks of pole-placement techniques which arise in the case of underactuation.
2.2 State-space model of the tower crane
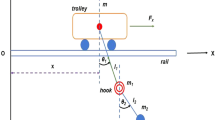
The diagram of the 4-DOF robotic tower crane in depicted in Fig. 1. The tower crane consists of an actuated jib arm, an actuated translational trolley and an unactuated payload below the trolley. The trolley of mass M can perform an one-dimensional motion along the jib. The load mass m is suspended from the vehicle with a rope of length L. The jib can rotate around the vertical axis. The state variables of the tower-crane are defined as follows: (i) ϕ is the turn angle of the crane, (ii) ϕ̇ is the rate of change of the turn angle of the crane, (iii) η is the displacement of the trolley along the jib, (iv) η̇ is the velocity of the jib, (v) \(\delta _{1}\) is the primary projection angle of the link that connects the trolley with the suspended load (swinging angle), (vi) \(\dot{\delta}_{1}\) is the rate of change of the primary projection angle, (vii) \(\delta _{2}\) is the secondary projection angle of the link that connects the trolley with the suspended load (sway angle), (viii) \(\dot{\delta}_{2}\) is the rate of change of the secondary projection angle [2, 3].
The vector of the main variables of the robotic tower crane is defined as \(q=[\phi,\eta,\delta _{1},\delta _{2}]^{T}\). The dynamic model of the crane is given by [1, 2, 16]
The inertia matrix of the crane \(M(q)\) is symmetric and positive definite and is defined as [2, 3]
where \(m_{11}=m(\sin^{2}(\delta _{1})\cos^{2}(\delta _{2})+\sin^{2}(\delta _{2})){L^{2}}+2mL{ \eta}\times \cos(\delta _{2})\sin(\delta _{2})+(m+M){\eta ^{2}}+J\), \(m_{12}=m_{21}=-mL\sin(\delta _{2})\), \(m_{13}=m_{31}=-m{L^{2}}\cos(\delta _{2})\cos(\delta _{2})\sin(\delta _{2})\), \(m_{14}=m_{41}= mL({\eta}\cos(\delta _{2})+L\sin(\delta _{2}))\), \(m_{22}=m+M\), \(m_{23}=m_{32}=mL\times \cos(\delta _{1})\cos(\delta _{2})\), \(m_{24}=m_{42}=-mL\sin(\delta _{1})\sin(\delta _{2})\), \(m_{33}= m{L^{2}}\cos(\delta _{2})\), \(m_{34}=m_{43}=-mL\sin(\delta _{1})\sin(\delta _{2})\), \(m_{44}=m{L^{2}}\).
The Coriolis and centrifugal forces matrix of the crane is [2, 3]
where
The gravitational vector of the robotic crane is defined as [2, 3]
The disturbances and friction vector of the robotic crane is defined as
The complexity of the dynamics of the model of the tower-crane can be partially alleviated by considering moderate (small angle) swinging or sway motion for the load. In such a case the associated sinusoidal and cosinusoidal variables \(\sin(\delta _{i})\) and \(\cos(\delta _{i})\), \(i=1,2\) can be substituted by the first terms of the related Taylor series expansions. Next, the inverse of the inertia matrix M is defined as
where the above noted subdeterminants \(M_{ij}\) for \(i=1,2,3,4\) and \(j=1,2,3,4\) are defined as
The determinant of matrix M is
For the dynamic model of the robotic crane that was initially written in the form
It holds that
or equivalently
Consequently, the dynamic model of the robot can be written as
Next, the dynamic model of the robotic crane is written as
Equivalently, the dynamic model of the robotic crane is written as
The state vector of the robotic crane is
Moreover, the following functions are defined
Thus, the state-space model of the tower-crane is written as
or in concise form one has the affine-in-the-input nonlinear state-space model
where \(x\in R^{8{\times}1}\), \(f(x)\in R^{8{\times}1}\), \(g(x)\in R^{8{\times}2}\), and \(u\in R^{2{\times}1}\). It is noted that the underactuated tower crane is not a 0-flat system. To be brought to a differentially flat form the dynamic extension approach has to be applied [36].
3 Approximate linearization of the dynamic model of the robotic crane
3.1 Approximate linearization with Taylor series expansion
The dynamic model of the tower crane being initially expressed in the state-space form
undergoes approximate linearization at each sampling instance around the temporary operating point \((x^{*},u^{*})\), where \(x^{*}\) is the present value of the system’s state vector and \(u^{*}\) is the last sampled value of the control inputs vector. The linearization process is based on Taylor series expansion and gives
where d̃ is the cumulative disturbances vector which may be due to truncation of higher-order terms from the Taylor series expansion, exogenous perturbations, and sensor measurements noise of any distribution. Matrices A and B are Jacobian matrices of the Taylor series expansion which are defined as:
This linearization approach which has been followed for implementing the nonlinear optimal control scheme results into a quite accurate model of the system’s dynamics. Consider for instance the following affine-in-the-input state-space model
where \(\tilde{d}_{1}\) is the modelling error due to truncation of higher order terms in the Taylor series expansion of \(f(x)\) and \(g(x)\). Next, by defining \(A=[{\nabla _{x}}f(x)|_{x^{*}}+{\nabla _{x}}g(x)|_{x^{*}}u^{*}]\), \(B=g(x^{*})\) one obtains
Moreover by denoting \(\tilde{d}=-Ax^{*}+f(x^{*})+g(x^{*})u^{*}+\tilde{d}_{1}\) about the cumulative modelling error term in the Taylor series expansion procedure one has
which is the approximately linearized model of the dynamics of the system of Eq. (17). The term \(f(x^{*})+g(x^{*})u^{*}\) is the derivative of the state vector at \((x^{*},u^{*})\) which is almost annihilated by \(-Ax^{*}\).
3.2 Computation of Jacobian matrices
The computation of the Jacobian matrices A and B proceeds as follows:
Computation of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\).
First row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}f_{1}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}f_{1}}{{\partial}x_{2}}}=1\), \({\frac{{\partial}f_{1}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}f_{1}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}f_{1}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}f_{1}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}f_{1}}{{\partial}x_{7}}}=0\) and \({\frac{{\partial}f_{1}}{{\partial}x_{8}}}=0\).
Second row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): It holds that \(f_{2}(x)={\frac{f_{2,\mathrm{num}}}{f_{2,\mathrm{den}}}}\) with \(f_{2,\mathrm{num}}=-M_{11}(c_{1}+g_{1}+d+1)+M_{21}(c_{2}+g_{2}+d_{2})-M_{31}(c_{3}+g_{3}+d_{3})+M_{41}(c_{4}+g_{4}+d_{4})\) and \(f_{2,\mathrm{den}}=\det M\). Thus, for \(i=1,2,\ldots,8\) one has
and also
and finally
Third row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}f_{3}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}f_{3}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}f_{3}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}f_{3}}{{\partial}x_{4}}}=1\), \({\frac{{\partial}f_{3}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}f_{3}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}f_{3}}{{\partial}x_{7}}}=0\) and \({\frac{{\partial}f_{3}}{{\partial}x_{8}}}=0\).
Fourth row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): It holds that \(f_{4}(x)={\frac{f_{4,\mathrm{num}}}{f_{4,\mathrm{den}}}}\) with \(f_{4,\mathrm{num}}=M_{12}(c_{1}+g_{1}+d+1)-M_{22}(c_{2}+g_{2}+d_{2})+M_{32}(c_{3}+g_{3}+d_{3})-M_{42}(c_{4}+g_{4}+d_{4})\) and \(f_{4,\mathrm{den}}=\det M\). Thus, for \(i=1,2,\ldots,8\) one has
and also
and finally
Fifth row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}f_{5}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}f_{5}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}f_{5}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}f_{5}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}f_{5}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}f_{5}}{{\partial}x_{6}}}=1\), \({\frac{{\partial}f_{5}}{{\partial}x_{7}}}=0\) and \({\frac{{\partial}f_{5}}{{\partial}x_{8}}}=0\).
Sixth row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): It holds that \(f_{6}(x)={\frac{f_{6,\mathrm{num}}}{f_{6,\mathrm{den}}}}\) with \(f_{6,\mathrm{num}}=-M_{13}(c_{1}+g_{1}+d+1)+M_{23}(c_{2}+g_{2}+d_{2})-M_{33}(c_{3}+g_{3}+d_{3})+M_{43}(c_{4}+g_{4}+d_{4})\) and \(f_{6,\mathrm{den}}=\det M\). Thus, for \(i=1,2,\ldots,8\) one has
and also
and finally
Seventh row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}f_{7}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}f_{7}}{{\partial}x_{7}}}=0\) and \({\frac{{\partial}f_{7}}{{\partial}x_{8}}}=0\).
Eighth row of the Jacobian matrix \({\nabla _{x}}f(x)|_{(x^{*},u^{*})}\): It holds that \(f_{4}(x)={\frac{f_{8,\mathrm{num}}}{f_{8,\mathrm{den}}}}\) with \(f_{8,\mathrm{num}}=M_{14}(c_{1}+g_{1}+d+1)-M_{24}(c_{2}+g_{2}+d_{2})+M_{34}(c_{3}+g_{3}+d_{3})-M_{44}(c_{4}+g_{4}+d_{4})\) and \(f_{8,\mathrm{den}}=\det M\). Thus, for \(i=1,2,\ldots,8\) one has
and also
and finally
Computation of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\).
First row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{11}(x)}{{\partial}x_{1}}}=0\) for \(i=1,2,\ldots,8\).
Second row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{21}(x)}{{\partial}x_{i}}}={ \frac{{{\frac{{\partial}M_{11}}{{\partial}x_{i}}}\det M-M_{11}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Third row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{31}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Fourth row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{41}(x)}{{\partial}x_{i}}}={ \frac{{-{\frac{{\partial}M_{12}}{{\partial}x_{i}}}\det M+M_{12}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Fifth row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{51}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Sixth row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{61}(x)}{{\partial}x_{i}}}={ \frac{{{\frac{{\partial}M_{13}}{{\partial}x_{i}}}\det M-M_{13}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Seventh row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{71}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Eighth row of the Jacobian matrix \({\nabla _{x}}g_{1}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{81}(x)}{{\partial}x_{i}}}={ \frac{{-{\frac{{\partial}M_{14}}{{\partial}x_{i}}}\det M+M_{14}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Computation of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\).
First row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{12}(x)}{{\partial}x_{1}}}=0\) for \(i=1,2,\ldots,8\).
Second row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{22}(x)}{{\partial}x_{i}}}={ \frac{{-{\frac{{\partial}M_{21}}{{\partial}x_{i}}}\det M+M_{21}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Third row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{32}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Fourth row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{42}(x)}{{\partial}x_{i}}}={ \frac{{{\frac{{\partial}M_{22}}{{\partial}x_{i}}}\det M-M_{22}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Fifth row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{52}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Sixth row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{62}(x)}{{\partial}x_{i}}}={ \frac{{-{\frac{{\partial}M_{23}}{{\partial}x_{i}}}\det M+M_{23}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Seventh row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{72}(x)}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Eighth row of the Jacobian matrix \({\nabla _{x}}g_{2}(x)|_{(x^{*},u^{*})}\): \({\frac{{\partial}g_{82}(x)}{{\partial}x_{i}}}={ \frac{{{\frac{{\partial}M_{24}}{{\partial}x_{i}}}\det M-M_{24}{\frac{{\partial}\det M}{{\partial}x_{i}}}}}{\det M^{2}}}\), for \(i=1,2,\ldots,8\).
Next, one computes the partial derivatives of the sub-determinants \(M_{ij}\) and of the determinant detM:
Equivalently, one has
Moreover, it holds that
Additionally, it holds that
In a similar manner one obtains
Equivalently one has
Following this procedure one gets
Additionally, it holds that
In this context one obtains
Additionally, one has
Furthermore, one has
Continuing in this manner one gets
Besides, one has
Equivalently, one obtains
In a similar manner one gets
Finally, one has that
About the partial derivatives of the determinant detM one has for \(i=1,2,\ldots,8\)
Next, the derivatives of the elements of the inertia matrix M are computed.
It holds that \(m_{11}=m(\sin^{2}(x_{3})\cos^{2}(x_{7})+\sin^{2}(x_{7})){L^{2}}+2mL{x_{3}}\cos(x_{7})\sin(x_{3})+(m+M){x_{3}^{2}}+J\). Thus one has:
Besides, it holds that \(m_{12}=m_{21}=-mL\sin(x_{7})\), thus \({\frac{{\partial}m_{12}}{{\partial}x_{i}}}={ \frac{{\partial}m_{21}}{{\partial}x_{i}}}=0\) if \(i=1,2,\ldots,8\) and \(i{\neq}7\), \({\frac{{\partial}m_{12}}{{\partial}x_{7}}}={ \frac{{\partial}m_{21}}{{\partial}x_{7}}}=-mL\cos(x_{7})\).
Moreover, it holds that \(m_{13}=m_{31}=-mL\cos(x_{5})\times \cos(x_{7})\sin(x_{7})\), thus \({\frac{{\partial}m_{13}}{{\partial}x_{i}}}={ \frac{{\partial}m_{31}}{{\partial}x_{i}}}=0\) if \(i=1,2,\ldots,8\) and \(i{\neq}5,7\), \({\frac{{\partial}m_{13}}{{\partial}x_{5}}}={ \frac{{\partial}m_{31}}{{\partial}x_{5}}}= m{L^{2}}\sin(x_{5})\cos(x_{7})\sin(x_{7})\), \({\frac{{\partial}m_{13}}{{\partial}x_{7}}}= { \frac{{\partial}m_{31}}{{\partial}x_{7}}} =-m{L^{2}}\cos(x_{5})[-\sin^{2}(x_{7})+\cos^{2}(x_{7})]\).
Additionally, it holds that \(m_{14}=m_{41}=mL({x_{3}}\cos(x_{7})+L\sin(x_{5}))\), thus \({\frac{{\partial}m_{14}}{{\partial}x_{i}}}={ \frac{{\partial}m_{41}}{{\partial}x_{i}}}=0\) for \(i=1,2,\ldots,8\). and \(i{\neq}3,5, 7\), \({\frac{{\partial}m_{14}}{{\partial}x_{3}}}={ \frac{{\partial}m_{41}}{{\partial}x_{3}}}=mL\cos(x_{7})=mL\cos(x_{7})\), \({\frac{{\partial}m_{14}}{{\partial}x_{5}}}={ \frac{{\partial}m_{41}}{{\partial}x_{5}}}=mL\cos(x_{7})=m{L^{2}}\cos(x_{5})\), \({\frac{{\partial}m_{14}}{{\partial}x_{7}}}={ \frac{{\partial}m_{41}}{{\partial}x_{7}}}=mL\cos(x_{7})= -mL{x_{3}}\sin(x_{7})\).
Furthermore, it holds that \(m_{23}=m_{32}=mL\cos(x_{5})\times \cos(x_{7})\), thus \({\frac{{\partial}m_{23}}{{\partial}x_{i}}}={ \frac{{\partial}m_{23}}{{\partial}x_{i}}}=0\) for \(i=1,2,\ldots,8\). and \(i{\neq}5,7\), \({\frac{{\partial}m_{23}}{{\partial}x_{i}}}={ \frac{{\partial}m_{32}}{{\partial}x_{i}}}=-mL\sin(x_{5})\cos(x_{7})\), \({\frac{{\partial}m_{23}}{{\partial}x_{7}}}={ \frac{{\partial}m_{32}}{{\partial}x_{7}}}= -mL\cos(x_{5})\sin(x_{7})\).
Additionally, it holds that \(m_{34}=m_{43}=-mL\sin(x_{5})\times \cos(x_{7})\), thus \({\frac{{\partial}m_{34}}{{\partial}x_{i}}}={ \frac{{\partial}m_{43}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\). and \(i{\neq}5,7\), \({\frac{{\partial}m_{34}}{{\partial}x_{5}}}={ \frac{{\partial}m_{43}}{{\partial}x_{5}}}=-mL\cos(x_{5})\cos(x_{7})\), \({\frac{{\partial}m_{34}}{{\partial}x_{7}}}={ \frac{{\partial}m_{43}}{{\partial}x_{7}}}= mL\sin(x_{5})\sin(x_{7})\).
Finally, about the computation of the partial derivatives of the Coriolis forces vector one has
It holds that for \(i=1.3,5,7\)
and also
Equivalently it holds that for \(i=1.3,5,7\)
and also
Similarly, it holds that for \(i=1.3,5,7\)
and also
Finally, it holds that for \(i=1.3,5,7\)
and also
Next, the following partial derivatives of the elements \(c_{ij}\) \(i=1,2,3,4\) and \(j=1,2,3,4\) of the Coriolis matrix are computed. It holds
Thus, \({\frac{{\partial}c_{11}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{11}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}c_{11}}{{\partial}x_{3}}}=(m+M)x_{4}+ mL\cos(x_{5})\cos(x_{7})x_{6}-mL\sin(x_{5})\sin(x_{7})x_{8}\), \({\frac{{\partial}c_{11}}{{\partial}x_{4}}}= (m+M)x_{3}+mL\sin(x_{5})\sin(x_{7})\), \({\frac{{\partial}c_{11}}{{\partial}x_{5}}}=-mL{x_{3}}\sin(x_{5})\times \cos(x_{7})x_{6}-mL{x_{3}}\cos(x_{5})\sin(x_{7})x_{8}+ mL\cos(x_{5})\sin(x_{7})x_{4}+m{L^{2}}[\cos^{2}(x_{5})-\sin^{2}(x_{5})]\cos^{2}(x_{7})x_{6}- m{L^{2}}[-2\cos(x_{5})\times \sin(x_{5})\sin(x_{7})\cos(x_{7})]x_{8}\), \({ \frac{{\partial}c_{11}}{{\partial}x_{6}}}= mL{x_{3}}\cos(x_{5})\cos(x_{7}) + m{L^{2}}\sin(x_{5})\cos(x_{5})\cos^{2}(x_{7})\), \({ \frac{{\partial}c_{11}}{{\partial}x_{7}}}= -mL{x_{3}}\cos(x_{5})\times \sin(x_{7})x_{6}-mL{x_{3}}\sin(x_{5}) \cdot \cos(x_{7})x_{8}+ -mL\sin(x_{5})\cos(x_{7})x_{4} +m{L^{2}}\sin(x_{5})\cos(x_{5})[-2\cos(x_{7})\sin(x_{7})]x_{6} -m{L^{2}}\cos^{2}(x_{5})\times [\cos^{2}(x_{7})-\sin^{2}(x_{7})]x_{8}\), \({\frac{{\partial}c_{11}}{{\partial}x_{8}}}=-mL{x_{3}}\sin(x_{5})\sin(x_{7})+ m{L^{2}}\cos^{2}(x_{5})\sin(x_{7})\cos(x_{7})\).
Additionally, it holds that
Thus, \({\frac{{\partial}c_{12}}{{\partial}x_{7}}}=0\), \({\frac{{\partial}c_{11}}{{\partial}x_{2}}}=mL\sin(x_{5})\cos(x_{7})+(m+M)x_{3}\), \({\frac{{\partial}c_{12}}{{\partial}x_{3}}}=(m+M)x_{2}\), \({\frac{{\partial}c_{12}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{12}}{{\partial}x_{5}}}=mL\cos(x_{5})\cos(x_{7})x_{2}\), \({\frac{{\partial}c_{12}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{12}}{{\partial}x_{7}}}=-mL\sin(x_{5})\sin(x_{7})x_{2}\), \({\frac{{\partial}c_{11}}{{\partial}x_{8}}}=0\).
Moreover, it holds that
Thus, \({\frac{{\partial}c_{13}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{13}}{{\partial}x_{1}}}=mL{x_{3}}\cos(x_{5})\cos(x_{7})+ m{L^{2}}\sin(x_{5})\cos(x_{5})\cos^{2}(x_{7})\), \({\frac{{\partial}c_{13}}{{\partial}x_{3}}}=mL\cos(x_{5}) \cdot \cos(x_{7})x_{2}\), \({\frac{{\partial}c_{13}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{13}}{{\partial}x_{5}}}=-mL{x_{3}}\sin(x_{5})\cos(x_{7})x_{2}-m{L^{2}}\cos(x_{5})\times \sin(x_{7})\cos(x_{7})x_{6}+ m{L^{2}}[\cos^{2}(x_{5})-\sin^{2}(x_{5})]\cos^{2}(x_{7})x_{2}- m{L^{2}}\sin(x_{5})\sin^{2}(x_{7})x_{8}\), \({\frac{{\partial}c_{13}}{{\partial}x_{6}}}=m{L^{2}}\sin(x_{5})\sin(x_{7})\cos(x_{7})\), \({\frac{{\partial}c_{13}}{{\partial}x_{7}}}=-mL{x_{3}}\cos(x_{5}) \cdot \sin(x_{7})x_{2}+m{L^{2}}\sin(x_{5})\cos(x_{5}) \cdot [-2\cos(x_{7})\sin(x_{7})]x_{2}+m{L^{2}}\cos(x_{5})[2\sin(x_{7})\cos(x_{7})]x_{8}\), \({\frac{{\partial}c_{13}}{{\partial}x_{8}}}=m{L^{2}}\cos(x_{5}) \cdot \sin^{2}(x_{7})\).
Additionally, it holds that
Thus, one obtains \({\frac{{\partial}c_{14}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{14}}{{\partial}x_{2}}}=-mL{x_{3}}\sin(x_{5})\sin(x_{7})+m{L^{2}}\cos^{2}(x_{5})\sin(x_{7})\cos(x_{7})\), \({\frac{{\partial}c_{14}}{{\partial}x_{3}}}=-mL \cdot \sin(x_{5})\sin(x_{7})x_{2}-mL\sin(x_{7})x_{8}\), \({\frac{{\partial}c_{14}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{14}}{{\partial}x_{5}}}= -mL{x_{3}} \cdot \cos(x_{5})\sin(x_{7})x_{2}+ m{L^{2}}[-2\cos(x_{5})\sin(x_{5})] \cdot \sin(x_{7})\cos(x_{7})x_{2}-m{L^{2}}\sin(x_{5})\times \sin^{2}(x_{7})x_{6}\), \({\frac{{\partial}c_{14}}{{\partial}x_{6}}}=m{L^{2}}\cos(x_{5})\sin^{2}(x_{7})\), \({\frac{{\partial}c_{14}}{{\partial}x_{7}}}=-mL{x_{3}}\times \sin(x_{5})\cos(x_{7})x_{2}-mL{x_{3}}\cos(x_{7}){x_{8}}-m{L^{2}}\cos^{2}(x_{5}) [\cos^{2}(x_{7})-\sin^{2}(x_{7})]x_{2}+m{L^{2}}\cos(x_{5})[2\sin(x_{7})\cos(x_{7})]x_{6}\), \({\frac{{\partial}c_{14}}{{\partial}x_{8}}}= -mL{x_{3}}\sin(x_{7})\).
Additionally, it holds that
Thus, \({\frac{{\partial}c_{21}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{21}}{{\partial}x_{2}}}=-(m+M)x_{3}-mL\sin(x_{7})\cos(x_{7})\), \({\frac{{\partial}c_{21}}{{\partial}x_{3}}}=-(m+M)x_{2}\), \({\frac{{\partial}c_{21}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{21}}{{\partial}x_{5}}}=-mL\cos(x_{5})\cos(x_{7})x_{2}\), \({\frac{{\partial}c_{21}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{21}}{{\partial}x_{7}}}=mL\sin(x_{5})\sin(x_{7})x_{2}+mL\sin(x_{7}){x_{8}}\), \({\frac{{\partial}c_{21}}{{\partial}x_{8}}}=-mL\cos(x_{7})\).
Furthermore, it holds that \(c_{22}=0\). Thus, one obtains \({\frac{{\partial}c_{22}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Moreover, it holds that
Thus, \({\frac{{\partial}c_{23}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{23}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}c_{23}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{23}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{23}}{{\partial}x_{5}}}= -mL(\cos(x_{5})\cos(x_{7})x_{6}-\sin(x_{5})\sin(x_{7})x_{8})\), \({\frac{{\partial}c_{23}}{{\partial}x_{6}}}=-mL \sin(x_{5})\cos(x_{7})\), \({\frac{{\partial}c_{23}}{{\partial}x_{7}}}= -mL(-\sin(x_{5})\sin(x_{7})x_{6}+\cos(x_{5}) \cos(x_{7})x_{8})\), \({\frac{{\partial}c_{23}}{{\partial}x_{8}}}=-mL\cos(x_{5})\sin(x_{7})\).
Furthermore, it holds that
Thus, one obtains \({\frac{{\partial}c_{24}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{24}}{{\partial}x_{2}}}=-mL\cos(x_{7})\), \({\frac{{\partial}c_{24}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{24}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{24}}{{\partial}x_{5}}}=-mL(-\sin(x_{5})\sin(x_{7})x_{6}+\cos(x_{5})\cos(x_{7})x_{8})\), \({\frac{{\partial}c_{24}}{{\partial}x_{6}}}=-mL\cos(x_{5})\sin(x_{7})\), \({\frac{{\partial}c_{24}}{{\partial}x_{7}}}=-mL(\cos(x_{5})\cos(x_{7})x_{6}-\sin(x_{5})\sin(x_{7})x_{8})-\sin(x_{7})x_{2}\), \({\frac{{\partial}c_{24}}{{\partial}x_{8}}}=-mL\sin(x_{5})\cos(x_{7})\).
Additionally, one has that
Thus, \({\frac{{\partial}c_{31}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{31}}{{\partial}x_{2}}}=-mL\cos(x_{5})\cos(x_{7})(x_{3}+L\sin(x_{5}) \cos(x_{7}))\), \({\frac{{\partial}c_{31}}{{\partial}x_{3}}}=-mL\cos(x_{5})\cos(x_{7})x_{2}\), \({\frac{{\partial}c_{31}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{31}}{{\partial}x_{5}}}= -mL(-\sin(x_{5}))\cos(x_{7})(x_{3}+L\sin(x_{5})\cos(x_{7}))x_{2}+ mL\times \cos(x_{5})\cos(x_{7})(L\cos(x_{5})\cos(x_{7}))x_{2}+m{L^{2}}\sin(x_{5})\cos(x_{7})x_{8}\), \({\frac{{\partial}c_{31}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{31}}{{\partial}x_{7}}}=mL\cos(x_{5})\sin(x_{7})(x_{3}+L\sin(x_{5})\cos(x_{7}))x_{2}+mL\cos(x_{5})\cos(x_{7}) \cdot (L\sin(x_{5})\sin(x_{7}))+m{L^{2}}\cos(x_{5})\times (2\cos(x_{7})\sin(x_{7}))x_{8}\), \({\frac{{\partial}c_{31}}{{\partial}x_{8}}}=-m{L^{2}}\cos(x_{5})\cos^{2}(x_{7})\).
Furthermore, it holds that \(c_{32}=0\). Thus, one obtains \({\frac{{\partial}c_{32}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Moreover, it holds that
Thus, \({\frac{{\partial}c_{33}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{33}}{{\partial}x_{7}}}= -m{L^{2}}[\cos^{2}(x_{7})-\sin^{2}(x_{7})]x_{8}\), \({\frac{{\partial}c_{33}}{{\partial}x_{8}}}=-m{L^{2}}\sin(x_{7}) \cos(x_{7})\).
Additionally, it holds that
Thus, \({\frac{{\partial}c_{34}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{34}}{{\partial}x_{2}}}=-m{L^{2}}\cos(x_{5})\cos^{2}(x_{7})\), \({\frac{{\partial}c_{34}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{34}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{34}}{{\partial}x_{5}}}=-m{L^{2}}(-\sin(x_{5})\cos^{2}(x_{7})x_{2}-\cos(x_{5})\times \cos(x_{7})x_{6})\), \({\frac{{\partial}c_{34}}{{\partial}x_{6}}}=-m{L^{2}}(\sin(x_{5})\cos(x_{7}))\), \({\frac{{\partial}c_{37}}{{\partial}x_{7}}}= -m{L^{2}}(-2\cos(x_{5})\cos(x_{7})\sin(x_{7})x_{2}-\sin(x_{5})\sin(x_{7})x_{6})\), \({\frac{{\partial}c_{34}}{{\partial}x_{8}}}=0\).
Furthermore, one has that
Thus, \({\frac{{\partial}c_{41}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{41}}{{\partial}x_{1}}}=mL(m\sin(x_{5})\sin(x_{7})-L\cos^{2}(x_{5}) \sin(x_{7})\cos(x_{7}))+m{L^{2}} \cos(x_{5})\cos^{(}x_{7})\), \({\frac{{\partial}c_{41}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{41}}{{\partial}x_{4}}}= mL\cos(x_{7})\), \({\frac{{\partial}c_{41}}{{\partial}x_{5}}}=mL(m\cos(x_{5})\sin(x_{7})-2L\cos(x_{5})\times \sin(x_{5})\sin(x_{7})\cos(x_{7}))x_{2} -m{L^{2}} \cdot \sin(x_{5})\cos^{2}(x_{7})x_{2}\), \({\frac{{\partial}c_{41}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{41}}{{\partial}x_{7}}}=mL(m\sin(x_{5})\cos(x_{7})-L\cos^{2}(x_{5}))[\cos^{2}(x_{7})- \sin^{2}(x_{7})]x_{2} -2m{L^{2}}\cos(x_{5}) \cdot \cos(x_{7})\sin(x_{7})x_{2}-mL\sin(x_{7})x_{4}\), \({\frac{{\partial}c_{41}}{{\partial}x_{8}}}=0\).
Moreover, it holds that
Thus, \({\frac{{\partial}c_{42}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{42}}{{\partial}x_{2}}}=mL\cos(x_{7})\), \({\frac{{\partial}c_{42}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{42}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{42}}{{\partial}x_{5}}}=0\), \({\frac{{\partial}c_{42}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}c_{42}}{{\partial}x_{7}}}=-mL\sin(x_{7})x_{2}\), \({\frac{{\partial}c_{42}}{{\partial}x_{8}}}=0\).
Furthermore, it holds that
Thus, \({\frac{{\partial}c_{43}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}c_{43}}{{\partial}x_{2}}}=m{L^{2}}\cos(x_{5})\cos^{2}(x_{7})\), \({\frac{{\partial}c_{43}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}c_{43}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}c_{43}}{{\partial}x_{5}}}=m{L^{2}}(-\sin(x_{5})\cos^{2}(x_{7})x_{2}+\cos(x_{5})\cos(x_{7})x_{6})\), \({\frac{{\partial}c_{43}}{{\partial}x_{6}}}=m{L^{2}}(\sin(x_{5})\cos(x_{7}))\), \({\frac{{\partial}c_{43}}{{\partial}x_{7}}}= m{L^{2}}(-2\cos(x_{5})\cos(x_{7})\sin(x_{7})-\sin(x_{5})\sin(x_{7})x_{6})\), \({\frac{{\partial}c_{43}}{{\partial}x_{8}}}=0\).
Finally, it holds that \(c_{44}=0\). Thus, one obtains \({\frac{{\partial}c_{44}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
In a similar manner one computes the partial derivatives of the elements of the gravitational forces matrix. It holds that \(g_{11}=0\) that one obtains \({\frac{{\partial}g_{11}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Additionally, it holds that \(g_{21}=0\) that one obtains \({\frac{{\partial}g_{21}}{{\partial}x_{i}}}=0\), for \(i=1,2,\ldots,8\).
Moreover it holds that
Thus, one obtains \({\frac{{\partial}g_{31}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}g_{31}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}g_{31}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}g_{31}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}g_{31}}{{\partial}x_{5}}}=gmL\cos(x_{5})\sin(x_{7})\), \({\frac{{\partial}g_{31}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}g_{31}}{{\partial}x_{7}}}=gmL\sin(x_{5})\times \cos(x_{7})\), \({\frac{{\partial}g_{31}}{{\partial}x_{8}}}=0\).
Finally it holds that
Thus, one obtains \({\frac{{\partial}g_{41}}{{\partial}x_{1}}}=0\), \({\frac{{\partial}g_{41}}{{\partial}x_{2}}}=0\), \({\frac{{\partial}g_{41}}{{\partial}x_{3}}}=0\), \({\frac{{\partial}g_{41}}{{\partial}x_{4}}}=0\), \({\frac{{\partial}g_{41}}{{\partial}x_{5}}}=-gmL\sin(x_{5})\sin(x_{7})\), \({\frac{{\partial}g_{41}}{{\partial}x_{6}}}=0\), \({\frac{{\partial}g_{41}}{{\partial}x_{7}}}=gmL\cos(x_{5})\times \cos(x_{7})\), \({\frac{{\partial}g_{41}}{{\partial}x_{8}}}=0\).
4 Design of an H-infinity nonlinear feedback controller
4.1 Equivalent linearized dynamics of the tower crane
After linearization around its current operating point, the dynamic model for the tower crane is written as
Parameter \(d_{1}\) stands for the linearization error in the tower crane’s model that was given previously in Eq. (17). The reference setpoints for the state vector of the aforementioned dynamic model are denoted by \({\mathbf{{x_{d}}}}=[x_{1}^{d},\ldots,x_{8}^{d}]\). Tracking of this trajectory is achieved after applying the control input \(u^{*}\). At every time instant the control input \(u^{*}\) is assumed to differ from the control input u appearing in Eq. (88) by an amount equal to Δu, that is \(u^{*}=u+{\Delta}u\)
The dynamics of the controlled system described in Eq. (88) can be also written as
and by denoting \(d_{3}=-Bu^{*}+d_{1}\) as an aggregate disturbance term one obtains
By subtracting Eq. (89) from Eq. (91) one has
By denoting the tracking error as \(e=x-x_{d}\) and the aggregate disturbance term as \(\tilde{d}=d_{3}-d_{2}\), the tracking error dynamics becomes
The above linearized form of the tower crane’s model can be efficiently controlled after applying an H-infinity feedback control scheme.
4.2 The nonlinear H-infinity control
The initial nonlinear model of the tower crane is in the form
Linearization of the model of the tower crane is performed at each iteration of the control algorithm around its present operating point \({(x^{*},u^{*})}=(x(t),u(t-T_{s}))\). The linearized equivalent of the system is described by
where matrices A and B are obtained from the computation of the previously defined Jacobians and vector d̃ denotes disturbance terms due to linearization errors. The problem of disturbance rejection for the linearized model that is described by
where \(x\in R^{n}\), \(u\in R^{m}\), \(\tilde{d}\in R^{q}\) and \(y\in R^{p}\), cannot be handled efficiently if the classical LQR control scheme is applied. This is because of the existence of the perturbation term d̃. The disturbance term d̃ apart from modeling (parametric) uncertainty and external perturbation terms can also represent noise terms of any distribution.
In the \(H_{\infty}\) control approach, a feedback control scheme is designed for trajectory tracking by the system’s state vector and simultaneous disturbance rejection, considering that the disturbance affects the system in the worst possible manner. The disturbances’ effects are incorporated in the following quadratic cost function:
The significance of the negative sign in the cost function’s term that is associated with the perturbation variable \(\tilde{d}(t)\) is that the disturbance tries to maximize the cost function \(J(t)\) while the control signal \(u(t)\) tries to minimize it. The physical meaning of the relation given above is that the control signal and the disturbances compete to each other within a min-max differential game. This problem of min-max optimization can be written as \({\min_{u}}{\max_{\tilde{d}}}J(u,\tilde{d})\).
The objective of the optimization procedure is to compute a control signal \(u(t)\) which can compensate for the worst possible disturbance, that is externally imposed to the tower crane. However, the solution to the min-max optimization problem is directly related to the value of the parameter ρ. This means that there is an upper bound in the disturbances magnitude that can be annihilated by the control signal.
4.3 Computation of the feedback control gains
For the linearized system given by Eq. (96) the cost function of Eq. (97) is defined, where coefficient r determines the penalization of the control input and weight coefficient ρ determines the reward of the disturbances’ effects. It is assumed that (i) The energy that is transferred from the disturbances signal \(\tilde{d}(t)\) is bounded, that is \({\int _{0}^{\infty}}{\tilde{d}^{T}(t)}\tilde{d}(t)\,{dt}<\infty \), (ii) matrices \([A, B]\) and \([A, L]\) are stabilizable, (iii) matrix \([A, C]\) is detectable. In the case of a tracking problem the optimal feedback control law is given by
with \(e=x-x_{d}\) to be the tracking error, and \(K={\frac{1}{r}}{B^{T}}P\) where P is a positive definite symmetric matrix. As it will be proven in Sect. 5, matrix P is obtained from the solution of the Riccati equation
where Q is a positive semi-definite symmetric matrix. The worst case disturbance is given by
The solution of the H-infinity feedback control problem for the tower crane and the computation of the worst case disturbance that the related controller can sustain, comes from superposition of Bellman’s optimality principle when considering that the robotic crane is affected by two separate inputs: the control input u and the cumulative disturbance input \(\tilde{d}(t)\). Solving the optimal control problem for u, that is for the minimum variation (optimal) control input that achieves elimination of the state vector’s tracking error, gives \(u=-{\frac{1}{r}}{B^{T}}Pe\). Equivalently, solving the optimal control problem for d̃, that is for the worst case disturbance that the control loop can sustain gives \(\tilde{d}={\frac{1}{\rho ^{2}}}{L^{T}}Pe\).
The diagram of the considered control loop for the tower crane is depicted in Fig. 2.
5 Lyapunov stability analysis
5.1 Stability proof
Through Lyapunov stability analysis it will be shown that the proposed nonlinear control scheme assures \(H_{\infty}\) tracking performance for the underactuated tower crane, and that in case of bounded disturbance terms asymptotic convergence to the reference setpoints is achieved. The tracking error dynamics for the tower crane is written in the form
where in the tower crane’s case \(L=\in R^{8{\times}8}\) to be the disturbance inputs gain matrix. Variable d̃ denotes model uncertainties and external disturbances of the tower crane’s model. The following Lyapunov equation is considered
where \(e=x-x_{d}\) is the tracking error. By differentiating with respect to time one obtains
The previous equation is rewritten as
Assumption
For given positive definite matrix Q and coefficients r and ρ there exists a positive definite matrix P, which is the solution of the following matrix equation
Moreover, the following feedback control law is applied to the system
By substituting Eq. (107) and Eq. (108) one obtains
which after intermediate operations gives
or, equivalently
Lemma
The following inequality holds
Proof
The binomial \(({\rho}{\alpha}-{\frac{1}{\rho}}b)^{2}\) is considered. Expanding the left part of the above inequality one gets
The following substitutions are carried out: \(a=\tilde{d}\) and \(b={e^{T}}{P}L\) and the previous relation becomes
Equation (115) is substituted in Eq. (112) and the inequality is enforced, thus giving
Equation (116) shows that the \(H_{\infty}\) tracking performance criterion is satisfied. The integration of V̇ from 0 to T gives
Moreover, if there exists a positive constant \(M_{d}>0\) such that
then one gets
Thus, the integral \({\int _{0}^{\infty}}{\Vert e\Vert _{Q}^{2}}\,dt\) is bounded. Moreover, \(V(T)\) is bounded and from the definition of the Lyapunov function V in Eq. (102) it becomes clear that \(e(t)\) will be also bounded since \(e(t) \in \Omega _{e}=\{e|{e^{T}}Pe\leq 2V(0)+{\rho ^{2}}{M_{d}} \}\). According to the above and with the use of Barbalat’s Lemma one obtains \(\lim_{t \rightarrow \infty}{e(t)}=0\).
After following the stages of the stability proof one arrives at Eq. (116) which shows that the H-infinity tracking performance criterion holds. By selecting the attenuation coefficient ρ to be sufficiently small and in particular to satisfy \(\rho ^{2}<\Vert e\Vert ^{2}_{Q} / \Vert \tilde{d}\Vert ^{2}\) one has that the first derivative of the Lyapunov function is upper bounded by 0. This condition holds at each sampling instance and consequently global stability for the control loop can be concluded. □
5.2 Robust state estimation with the use of the \(H_{\infty}\) Kalman filter
The control loop has to be implemented with the use of information provided by a small number of sensors and by processing only a small number of state variables. To reconstruct the missing information about the state vector of the tower crane it is proposed to use a filtering scheme and based on it to apply state estimation-based control [1, 36]. By denoting as \(A(k)\), \(B(k)\) and \(C(k)\) the discrete-time equivalents of matrices A, B and C of the linearized state-space model of the system, the recursion of the \(H_{\infty}\) Kalman Filter for the model of the tower crane, can be formulated in terms of a measurement update and a time update part.
Measurement update:
Time update:
where it is assumed that parameter θ is sufficiently small to assure that the covariance matrix \({P^{-}(k)}^{-1}-{\theta}W(k)+C^{T}(k)R(k)^{-1}C(k)\) will be positive definite. When \(\theta =0\) the \(H_{\infty}\) Kalman Filter becomes equivalent to the standard Kalman Filter. One can measure only a part of the state vector of the crane, for instance state variables \(x_{1}\), \(x_{3}\), \(x_{5}\), and \(x_{7}\) and can estimate through filtering the rest of the state vector elements (rate of change of ϕ, η, \(\delta _{1}\) and \(\delta _{2}\)). Moreover, the proposed Kalman filtering method can be used for sensor fusion purposes.
6 Simulation tests
The global stability properties of the control method and the elimination of the state vector’s tracking error which were previously proven through Lyapunov analysis are further confirmed through simulation experiments. To compute the stabilizing feedback gains of the controller, the algebraic Riccati equation of Eq. (107) had to be repetitively solved at each iteration of the control algorithm. The parameters of the dynamic model of the tower crane which have been used in the simulation experiments were according to [2, 3]. All parameters and variables of the crane’s model are measured in SI units. The obtained results are depicted in Fig. 3 to Fig. 18. The real values of the state variables of the tower crane are printed in blue, their estimates which are provided by the H-infinity Kalman Filter are printed in green colour while the associated setpoints are printed in red. The performance of the nonlinear optimal control method was very satisfactory. Actually, through all test cases it has been shown that the control method can achieve fast and accurate tracking of reference trajectories (setpoints) under moderate variations of the control inputs. The simulation tests come to confirm that the control method has global (and not local) stability properties. Under the nonlinear optimal control method the state variables of the tower crane can track precisely setpoints with fast and abrupt changes. Moreover, the convergence to these setpoints is independent from initial conditions.
Regarding the selection of values for the controller gains it can be noted that parameters r, ρ and Q which appear in the method’s algebraic Riccati equations are assigned offline constant values, where the gains vector K is updated at each sampling instance, based on the positive definite and symmetric matrix P which is the solution of the method’s algebraic Riccati equation. The tracking accuracy and the transient performance of the control scheme depends on the values of coefficients r, ρ and on the values of the elements of the diagonal matrix Q. Actually, for relatively small values of r one achieves elimination of the state vector’s tracking error one. Moreover, for relatively high values of the diagonal elements of matrix Q one achieves fast convergence the state variables’ reference trajectories, Finally, the smallest value of the attenuation coefficient ρ that results into a valid solution of the method’s Riccati equation in the form of the positive definite and symmetric matrix P, it the one that provides the control loop with maximum robustness.
Comparing to past attempts for solving the H-infinity control problem for nonlinear dynamical systems, the article’s control approach is substantially different [16]. Preceding results on the use of H-infinity control to nonlinear dynamical systems were limited to the case of affine-in-the-input systems with drift-only dynamics and considered that the control inputs gain matrix is not dependent on the values of the system’s state vector. Moreover, in these approaches the linearization was performed around points of the desirable trajectory whereas in the present article’s control method the linearization points are related with the value of the state vector at each sampling instant as well as with the last sampled value of the control inputs vector. The Riccati equation which has been proposed for computing the feedback gains of the controller is novel, so is the presented global stability proof through Lyapunov analysis.
The proposed H-infinity (optimal) control method for the robotic tower crane exhibits several advantages when compared against other linear or nonlinear control schemes [16]. For instance: (i) In contrast to global linearization-based control schemes (Lie algebra-based control and differential flatness theory-based control) it does not need complicated changes of state-variables (diffeomorphisms) and does not come against singularity problems in the computation of the control inputs, (ii) In contrast to sliding-mode control or to backstepping control the proposed nonlinear optimal control scheme does not require the state-space model of the system to be in a specific form (e.g. triangular, canonical, etc.) (iii) In contrast to PID control the proposed nonlinear optimal control method is globally stable and functions well at changes of operating points, (iv) In contrast to multi-models based control and linearization around multiple operating points, the nonlinear optimal control scheme requires linearization around one single operating point and thus it avoids the computational load for solving multiple Riccati equations or LMIs.
To elaborate on the tracking performance and on the robustness of the proposed nonlinear optimal control method for the ball and plate system the following Tables are given: (i) Table 1 which provides information about the accuracy of tracking of the reference setpoints by the state variables of the tower crane’s state-space model, (ii) Table 2 which provides information about the robustness of the control method to parametric changes in the model of the tower crane’s dynamics (change \({\Delta}a\%\) in the mass M of the trolley), (iii) Table 3 which provides information about the precision in state variables’ estimation that is achieved by the H-infinity Kalman Filter, (iv) Table 4 which provides the approximate convergence times of the tower crane’s state variables to the associated setpoints.
7 Conclusions
Tower cranes are mechatronic systems with complicated nonlinear and multivariable dynamics which exhibit also underactuation. They are also exposed to undesirable swinging and swaying motions of the payload and such phenomena may prevent the precise positioning of the transferred cargos or may slow down the execution and completion of load transport tasks. To circumvent such deficiencies, full automation of tower cranes’ operation has been pursued with the development of elaborated nonlinear control algorithms. In the present article a novel nonlinear optimal control approach has been proposed for the dynamic model of the 4-DOF underactuated tower crane. At a first-stage the tower crane’s dynamic model undergoes approximate linearization with the use of the first-order Taylor series expansion and through the computation of the associated Jacobian matrices. The linearization point is updated at each sampling instance and is defined by the present value of the system’s state vector and by the last sampled value of the control inputs vector.
At a second stage a stabilizing H-infinity feedback controller is designed. To compute the stabilizing feedback gains of the H-infinity controller an algebraic Riccati equation had to be repetitively solved at each time-step of the control algorithm. The global stability properties of the control scheme have been proven through Lyapunov analysis. To implement state estimation-based control, the H-infinity Kalman Filter has been used as a robust state estimator. The nonlinear optimal control approach retains the advantages of the standard linear optimal control, that is fast and accurate tracking of reference setpoints under moderate variations of the control inputs. Finally, it is noted that the nonlinear optimal control method is of generic use and can be applied to a variety of robotic cranes, such as 4-DOF underactuated overhead (moving bridge and trolley) cranes, offshore boom cranes, double-pendulum overhead cranes, 4-DOF underactuated tower cranes, and quay-side cranes and so on.
Availability of data and materials
Data about this research work are available upon reasonable request.
Code availability
Source code is subject to confidentiality constraints but software applications can be demonstrated upon reasonable request.
References
G. Rigatos, K. Busawon, Robotic Manipulators and Vehicles: Control, Estimation and Filtering (Springer, Cham, 2018)
T. Yang, N. Sun, H. Chen, Y. Fang, Observer-based nonlinear control for tower cranes suffering from uncertain function and actuator constraints with experimental verification. IEEE Trans. Ind. Electron. 68(7), 6192–6204 (2021)
N. Sun, Y. Wu, H. Chen, Y. Fang, Antiswing cargo transportation of underactuated tower crane systems by a nonlinear controller embedded with an integral term. IEEE Trans. Autom. Sci. Eng. 16(3), 1387–1398 (2019)
M. Zhang, Y. Zhang, B.J.C. Ma, X. Cheng, Adaptive sway reduction for tower crane systems wwith variable cable lengths. Autom. Constr. 119, 10342–10351 (2020)
S.C. Duong, E. Uezato, H. Kinjo, T. Yamamoto, A hynrid evolutionary algorithm for recurrent neural network control of a three-dimensional tower crane. Autom. Constr. 49, 1318–1325 (2013)
Y. Qian, Y. Fang, Switching logic-based nonlinear feedback control of offshore ship-mounted tower cranes: a disturbance observer-based approach. IEEE Trans. Autom. Sci. Eng. 16(3), 1125–1136 (2019)
J. Kim, D. Lee, B. Kiss, D. Kim, An adaptive unscented Kalman filter with selective scaling (AUKF-SS) for overhead cranes. IEEE Trans. Ind. Electron. 68(7), 6131–6140 (2021)
M. Boek, A. Kugi, Real-time nonlinear model-predictive path-following control of a laboratory tower crane. IEEE Trans. Control Syst. Technol. 22(4), 1461–1473 (2014)
T.S. Wu, M. Karkoub, W.S. Yu, C.T. Chen, M.G. Henand, K.W. Wu, Anti-sway tracking control of tower cranes with delayed uncertainty using a robust adaptive fuzzy control, in Fuzzy Sets and Systems, vol. 290 (Elsevier, Amsterdam, 2016), pp. 118–137
T.S. Wu, M. Karhoub, H. Wang, H.S. Chen, T.H. Chen, Robust tracking control of MIMO underactuated nonlinear systems with dead-zone band and delayed uncertainty using an adaptive fuzzy control. IEEE Trans. Fuzzy Syst. 25(4), 905–918 (2017)
H. Chen, N. Sun, Nonlinear control of underactuated systems subject to both actuated and unactuated state constraints with experimental verification. IEEE Trans. Ind. Electron. 67(9), 7702–7714 (2020)
Z. Liu, T. Yang, N. Sun, Y. Fang, An antiswing trajectory planning method with state constraints for 4-DOF tower cranes: design and experiments. IEEE Access 7, 62142–62151 (2019)
A.T. Le, S.G. Lee, 3D comparative control of tower cranes using robust adaptive techniques. J. Franklin Inst. 354, 8333–8357 (2017)
N. Sun, Y. Fang, X. Zhang, Energy coupling output feedback control of 4-DOF underactuated cranes with saturated inputs. Automatica 49, 1318–1325 (2013)
Y. Wu, N. Sun, H. Chen, Y. Fang, Adaptive output feedback control for 5-DOF varying-cable-length tower cranes with cargo mass estimation. IEEE Trans. Ind. Inform. 17(4), 2453–2464 (2021)
G. Rigatos, E. Karapanou, Advances in Applied Nonlinear Optimal Control (Cambridge Scholars Publishing, Newcastle-upon-Tyne, 2020)
G. Rigatos, M. Abbaszadeh, P. Siano, Control and Estimation of Dynamical Nonlinear and Partial Differential Equation Systems: Theory and Applications (The Institution of Engineering and Technology, London, 2022)
F. Rauscher, O. Sawodny, Modeling and control of tower cranes with elastic structure. IEEE Trans. Control Syst. Technol. 25(1), 64–79 (2021)
J. Yoon, S. Nution, W. Singhose, J.E. Vaugham, Control of crane payloads that bounce during hoisting. IEEE Trans. Control Syst. Technol. 22, 1233–1238 (2014)
N. Sun, Y. Fang, H. Chen, B. Lu, Y. Fu, Slow / translational positioning and swing suppression for 4-DOF tower cranes with parametric uncertainties: design and hardware experimentation. IEEE Trans. Ind. Electron. 63(10), 6407–6418 (2016)
H. Chen, Y. Fang, N. Sun, An adaptive tracking control method with swing suppression for 4-DOF tower crane systems. Mech. Syst. Signal Process. 123, 426–442 (2019)
M. Zhang, X. Jing, Z. Zhu, Disturbance obverver-based sliding-mode control for 4-DOF tower crane systems. Mech. Syst. Signal Process. 161, 107946–107954 (2021)
M. Zhang, Y. Zhang, B.J.C. Ma, X. Cheng, Modeling and energy-based sway reduction control for tower-crane systems with double-pendulum and spherical-pendulum effects. Meas. Control 53(1–2), 141–150 (2020)
T. Yang, N. Sun, Y. Fang, Neuroadaptive control for complicated underactuated systems with simultaneous output and velocity constraints exerted on both actuated and unactuated states, in IEEE Transactions on Neural Networks and Learning Systems (2022)
T. Yang, H. Chen, N. Sun, Y. Fang, Adaptive neural network output feedback control of uncertain underactuated systems with actuated and unactuated state constraints, in IEEE Transactions on Systems, Man and Cybernetics (2022)
J. Ye, J. Huang, Control of beam-pendulum dynamics in a tower crane with a slender jib transporting a distributed mass-load, in IEEE Transactions on Industrial Electronics (2022)
M. Zhang, X. Jing, Adaptive neural network tracking control for double-pendulum tower crane systems with nonideal inputs. IEEE Trans. Syst. Man Cybern. 52(4), 254–2530 (2022)
S.M. Fasih ur Rahman, M.A. Abbasi, Input shaping with an adaptive scheme for swing control of an underactuated tower crane under paylod hoisting and mass variation. Mech. Syst. Signal Process. 175, 109106–109151 (2022)
J. Huang, W. Wang, J. Zhou, Adaptive control design for underactuated cranes with guaranteed transient performance: theoretical design and experimental verification. IEEE Trans. Ind. Electron. 69(3), 2822–2832 (2022)
G. Rigatos, P. Siano, M. Abbaszadeh, Nonlinear H-infinity control for 4-DOF underactuated overhead cranes, in Transactions of the Institute of Measurement and Control (Sage, Thousand Oaks, 2017)
G. Rigatos, P. Siano, P. Wira, F. Profumo, Nonlinear H-infinity feedback control for asynchronous motors of electric trains. Intell. Industr. Syst. 1, 85–98 (2015)
G.G. Rigatos, S.G. Tzafestas, Extended Kalman filtering for fuzzy modelling and multi-sensor fusion, in Mathematical and Computer Modelling of Dynamical Systems, vol. 13 (Taylor & Francis, London, 2007), pp. 251–266
M. Basseville, I. Nikiforov, Detection of Abrupt Changes: Theory and Applications (Prentice Hall, New York, 1993)
G. Rigatos, Q. Zhang, Fuzzy model validation using the local statistical approach, in Fuzzy Sets and Systems, vol. 60 (Elsevier, Amsterdam, 2009), pp. 882–904
G. Rigatos, Modelling and Control for Intelligent Industrial Systems: Adaptive Algorithms in Robotcs and Industrial Engineering (Springer, Berlin, 2011)
G. Rigatos, Nonlinear Control and Filtering Using Differential Flatness Approaches. Applications to Electromechanical Systems (Springer, Cham, 2015)
G. Rigatos, Intelligent Renewable Energy Systems: Modelling and Control (Springer, Cham, 2016)
G.J. Toussaint, T. Basar, F. Bullo, \(H_{\infty}\) optimal tracking control techniques for nonlinear underactuated systems, in Proc. IEEE CDC 2000, 39th IEEE Conference on Decision and Control, Sydney, Australia (2000)
Z. Shengzheng, H. Xiongxiong, Z. Haiyut, L. Xiaocong, L. Xingguo, PID-like coupling control of underactuated oberhead cranes with input constraints. Mech. Syst. Signal Process. 178, 109274–109283 (2022)
M. Zhai, T. Yang, N. Sun, Y. Fang, Observer-based adaptive fuzzy control of underactuated offshore cranes for cargo stabilization with respect to ship decks. Mech. Mach. Theory 175, 104927–104942 (2022)
Z. Liu, Y. Fu, N. Sun, T. Yang, Y. Fang, Collaborative antiswing hoisting for dual rotary cranes with motion constraints. IEEE Trans. Ind. Inform. 18(9), 6120–6130 (2022)
Y. Wu, N. Sun, H. Chen, Y. Fang, New adaptive dynamic output feedback control of double-pendulum ship-mounted cranes with accurate gravitational compensation and constrained inputs. IEEE Trans. Ind. Electron. 69(9), 9196–9205 (2022)
I. Golovin, A. Maksakov, M. Shysh, S. Palis, Discrepancy-based control for positioning of large gantry crane. Mech. Syst. Signal Process. 163, 108199 (2022)
G.O. Tysse, A. Cibicik, O. Egeland, Vision-based control of a knuckle boom crane with online cable length estimation. IEEE/ASME Trans. Mechatron. 26(1), 416–426 (2021)
S. Zhang, H. Zhou, X. He, Y. Feng, C.K. Pang, Passivity-based coupling control for underactuated three-dimensional overhead cranes. ISA Trans. 126, 352–360 (2022)
G.O. Tysse, A. Cibicik, L. Tingelstad, O. Egeland, Lyapunov-based damping controller with nonlinear MPC control of payload position for a knuckle boom crane. Automatica 140, 110219–110229 (2022)
Funding
This research work has been partially supported by Grant Ref. “CSP contract 040322”—“Nonlinear control, estimation and fault diagnosis for electric power generation and electric traction/propulsion systems” of the Unit of Industrial Automation of the Industrial Systems Institute.
Author information
Authors and Affiliations
Contributions
The contribution of the members of the research team is indicated by their order of appearance in the list of authors. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
No conflict of interest exists with third parties about the content of the present article.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rigatos, G., Abbaszadeh, M. & Pomares, J. Nonlinear optimal control for the 4-DOF underactuated robotic tower crane. Auton. Intell. Syst. 2, 21 (2022). https://doi.org/10.1007/s43684-022-00040-4
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43684-022-00040-4