1 Introduction

The new generation information technology and advanced manufacturing technology have become the core driving force of the fourth industrial revolution. At present, artificial intelligence (AI) based models, such as computing vision, deep learning, and knowledge graph, have significantly shown advances in smart product design, production optimization and maintenance management [1, 2]. With the continuous shortening of product life cycle, the manufacturing paradigm has gradually shifted from large-scale production to multi-variety and small-batch personalized production, which makes human–robot collaboration (HRC) to become an important and frequent activity. Traditionally, industrial robots are not flexible enough to quickly adapt to production changes, and workers are often lacking in efficiency and endurance. Nowadays, the collaboration between industrial robots and workers can significantly improve machining efficiency and reduce production cost. At the same time, promoting the integration of the artificial intelligence technology and industrial robots can bring new changes to the smart manufacturing [3–5]. Among them, smart industrial robot has three characteristics: single robot autonomy, multi-robots collaboration, and human–robot integration [6]. Human–robot integration service is a new type of “human–robot–environment” interaction relationship, in which workers and industrial robots can work together autonomously through multi-directional, multi-level and multi-scale operations. At present, there are bottlenecks in human–robot collaboration on CNC (Computer Number Control) machine tools: The adaptability of complex operations. Traditional CNC machine tools are committed to high precision as the goal to complete fixed and heavy operations; while the new generation CNC machine tools focus more on deep human–robot collaboration, and the operations are flexible. The friendliness of human–robot interaction. Traditional CNC machine tools have low friendliness and intelligence; while the new generation CNC machine tools can provide a variety of interaction modes such as voice and gesture to actively recognize workers’ behavior intention [7].

In the context of human–robot interaction, workers and industrial robots have their own significant advantages. The advantage of workers lies in their strong cognitive ability especially when dealing with complex operation tasks; the advantage of industrial robots lies in high strength, fast speed and high accuracy. In the industrial scenario of human–robot interaction, the primary problem to be solved is the rational operations allocation between workers and industrial robots. Therefore, this paper takes the human–robot collaboration for CNC machine tools as the research object, and investigates the allocation strategy of complex operations. By measuring the complexity of workers and industrial robots’ operations, an optimization function based on multi-attribute evaluation was proposed. The main contributions of this paper are outlined as follows:

  1. 1)

    A human–robot collaborative operations framework on CNC machine tool was proposed. According to the characteristics of the collaborative operations, it was divided into three stages: pre-machining, machining and post-machining.

  2. 2)

    A three-layer hierarchical model of “production line-operations-actions” was established. A human–robot operation allocation model was built and solved by simulated annealing algorithm.

The rest of this paper is organized as follows. Section 2 presents literature review of human–robot collaboration. A human–robot collaborative operation framework on CNC machine tool is proposed in Sect. 3. Section 4 shows the actions analysis in the context of human–robot interaction. In Sect. 5, a collaboration operations allocation model is established. Section 6 uses a simulated annealing algorithm to solve above model. Section 7 is a case study. Conclusions and future work are shown in Sect. 8.

2 Literature review

As an emerging mode, human–robot collaboration has attracted increasing attentions in recent years, both in academia and in industry [8]. At present, it has been widely studied in construction, assembly, disassembly and other scenarios [9–11]. Focusing on the allocation strategy of collaboration operations, typical study was outlined as follows: Gervasi et al. proposed a general framework to evaluate the collaboration between humans and robots considering different configuration profiles [12]. Malik and Brem explored the feasibility of using a digital twin to address the complexity of collaborative production systems through an industrial case and a demonstrator [13]. Roveda et al. proposed a Model-Based Reinforcement Learning (MBRL) variable impedance controller to assist human operators in collaborative tasks [14]. Parsa and Saadat proposed a disassembly planning method based on human–robot collaboration. Based on cleanability, reparability and economy of remanufacturing components, genetic algorithm was used to find a nearoptimal collaborative disassembly process [15]. Then Tram and Raweewan studied human–robot task allocation when designing for semi-automation considering total operating cost, cycle time, and ergonomic difficulty through building a multi-objective linear programming model [16]. Baenziger et al. established the production time and ergonomics during a production cycle as a function of the human–robot task allocation, and used genetic algorithm to optimize the task allocation in human–robot teams for a given workplace [17]. Also, Zhang et al. adopted a human–robot collaborative reinforcement learning algorithm to optimize the task sequence allocation scheme in assembly processes [18]. To sum up, most of the current literature is about the task allocation of product disassembly and assembly line. There is a lack of research on human–robot operations allocation in production line, especially CNC machine tools.

In terms of human–robot collaborative operations allocation of the production line, different workpieces processes and different types of CNC machine tools can lead to more complex collaborative schemes between workers and industrial robots. Therefore, human–robot collaborative operations allocation is a complex nonlinear combination problem. Many studies have shown that intelligent optimization algorithms have outstanding advantages in solving the above NP-hard problems [19]. For example, Ren et al. summarized the research on the smart management of intelligent optimization algorithms in manufacturing equipment from the four aspects: task analysis and management of intelligent manufacturing equipment in big data environment, task decomposition and resource allocation, task network analysis and evaluation, and task integration analysis and verification evaluation progress [20]. Qawqzeh et al. investigated the recent publications of swarm intelligence algorithms (particle swarm optimization (PSO), ant colony optimization (ACO), artificial bee colony (ABC), and the firefly algorithm (FA)) in scheduling and optimization problems [21]. It must be noted that as an intelligent algorithm for solving large-scale combinatorial optimization problems based on Monte Carlo iterative flow measurement, simulated annealing algorithm has been widely studied [22]. Compared with the traditional iterative algorithms, simulated annealing algorithm has some significant advantages: It cannot fall into a local minimum. Because it is always possible to deviate from the local minimum when the system operates at a non-zero temperature. Simulated annealing algorithm is adaptive. The general outline of the system can be seen in the high temperature process, and its specific details can be seen in the low temperature. Due to its above unique optimization mechanism and less dependence on problem information, versatility and flexibility, SA has been widely used in the field of optimization, such as production scheduling, control engineering, machine learning, neural networks, and signal processing [23–25]. Therefore, simulated annealing algorithm was adopted to solve the operations allocation model of human–robot interaction.

3 Human–robot collaborative operation framework on CNC machine tool

In production line, the related physical elements include the CNC machine tools, AGVs (Automatic Guided Vehicle), RFID (Radio Frequency Identification), industrial robots, workers, and various sensing devices, which are connected through industrial Internet. As shown in Fig. 1, the machining process of workpieces involve the pre-machining, machining, and post-machining. The corresponding human–robot collaboration services on CNC machine tool can be divided into three stages:

  1. 1)

    Pre-machining stage

Figure 1
figure 1

Human–robot collaboration operations

Full size image

When the production line receives the machining tasks, it must determine the process planning and fixture arrangement. In this pre-machining stage, the collaborative content of human–robot interaction includes the grasping, placement, positioning of workpieces, installation and setting of cutting tools.

  1. 2)

    Machining stage

In the machining stage, it is essential to realize the real-time collection of machining process information and smart decision-making. If the abnormal state of the machining process was identified, the data-driven and knowledge-guided decision-making mechanism was triggered. The collaborative content of human–robot interaction includes the real-time monitoring based on machine vision, the optimization strategy based on knowledge and machine learning, etc.

  1. 3)

    Post-machining stage

In the post-machining stage, it is essential to inspect and test the finished workpieces. After passing the inspection, the workplaces were moved to the next process through AGV, workers or forklifts. The collaborative content of human–robot interaction includes cleaning, deburring, inspection, condition test and other inspection operations, as well as the packaging, transportation.

The goal of human–robot interaction is to ensure the stability of machining accuracy and improve production efficiency. Due to the diversity and complexity of collaboration operations in workpieces machining, it needs to consider the flexibility of workers and the repeatability of industrial robots. Through normalizing the time, cost, efficiency, accuracy and complexity of human–robot interaction, collaboration effectiveness was proposed to evaluate the operations allocation strategy.

4 Action analysis in the context of human–robot interaction

When machining complex workpieces, detailed process design was needed. The process on the production line can be subdivided into several steps. For each step, there are different combinations of human–robot interaction, such as fully automated machining, independent worker machining, collaborative machining of workers and industrial robots. The reasonable arrangement of these human–robot interaction combinations can not only improve the machining efficiency and accuracy, but also reduce the working difficulty of workers. This paper mainly focuses on the operations allocation in pre-machining stage.

4.1 Description of actions

In the production line, different operations are composed of basic actions. Workers can finish complex operations by using different actions and varying their sequence. According to the characteristics of industrial robots, some actions were described as shown in Table 1 [26, 27].

Table 1 Partial actions description of industrial robots
Full size table

4.2 Hierarchical model of operations

The operation model was divided into three layers: production line layer, operation layer, and action layer. As shown in Fig. 2, in the human–robot collaboration, the action layer represents the specific actions that industrial robots or workers can perform; the operation layer represents the sum of a series of actions based on a machine tool; the production line layer represents the sum of multiple machine tools that can complete the production of different batches of workpieces.

Figure 2
figure 2

Three-layers structure of human–robot interaction operations model

Full size image

Figure 3 shows an example about “workpieces loading”. According to the hierarchical rules of operation model, its action layer included four specific actions: obtain the spatial position of the workpieces; grab the workpieces from the current position; move to the next position; place the workpieces.

Figure 3
figure 3

The hierarchy model of workpieces loading

Full size image

4.3 Complexity evaluation of operations

An operation consists of multiple actions. In the process of actions execution, the action can be completed not only by workers, but also by industrial robots. In a smart production line, industrial robots have been able to replace most workers. For example, using industrial robots instead of workers to deal with workpieces can greatly reduce the labor intensity and repeatability of workers. However, industrial robots cannot replace workers in some complex or important operations based on the operation accuracy and professional experience. Even in some operations, workers and industrial robots need to collaborate with each other. For the above reasons, we need to consider the complexity evaluation of the different operations based on human–robot interaction. Referring to the complexity model of operation proposed by Malik and Bilberg, this paper evaluates the complexity of actions from scale and difficulty [28].

  1. 1)

    Scale H

In the process of human–robot collaboration to complete the operations, the scale only considers the number of each operation’s actions, such as workpieces loading. The scale H is denoted by information entropy as follows

$$ H_{i} = \lg C_{i}, $$
(1)

where \(H_{i}\) is the scale of ith operation; \(C_{i}\) is the number of ith operation’s actions.

  1. 2)

    Difficulty K

Difficulty refers to the difficulty of finishing the operations. Here, the difficulty is evaluated by analyzing the actions. The difficulty of operation depends on the respective difficulty and the total number of all actions. Therefore, the relative operation difficulty can be denoted as:

$$ K_{i} = \frac{{B}_{i}}{{C}_{i}}, $$
(2)

where \(B_{i}\) denotes the sum of relative difficulty in ith operation’s actions.

The factors affecting the action difficulty K have coupling characteristics with each other. Neural network can be adopted to evaluate the difficulty of each action [29]. Table 2 is the description of the action difficulties related to several key steps.

Table 2 Difficulty of different actions
Full size table

Then, the complexity measurement model of operations can be denoted as:

$$ L_{i} = K_{i}H_{i}, $$
(3)

where \(L_{i}\) is the complexity of the ith operation; \(H_{i}\) is scale of the ith operation; \(K_{i}\) is difficulty of the ith operation.

5 Operations allocation model of human–robot interaction

5.1 Relevant assumptions

Considering that the complex actions in operations involve professional experience and knowledge, it is defined as that the accuracy completed by workers is greater than that completed by industrial robots. Therefore, the order of completion accuracy is as follows: human–robot collaboration > workers > industrial robots. The following conditions are assumed: Each action does not affect each other, but needs to meet the sequence requirements;  The completion of each operation needs different industrial robots and different workers; The completion of the operation can meet the requirements.

Given the above assumptions, find an optimization scheme to minimize the human–robot collaboration effectiveness under certain conditions, such as certain total machining time, total machining cost, worker labor complexity, machining accuracy, machining efficiency and so on.

5.2 Variable definition

In human–robot interaction, it is assumed that there are M operations, and each operation has N actions. Human–robot collaboration allocation is conducted on each operation. Suppose each operation has N actions, which are denoted as: \(N = \{ N_{1}, N_{2}, \ldots , N_{N}\}\); Describe the actions as follows: \(N_{i} = \{ I, PM_{I}, A_{I}, C_{I}, T_{I}, Y_{I}, E_{I}, L_{I}\}\).

The corresponding variable descriptions are shown in Table 3.

Table 3 Variable definition
Full size table

5.3 Objective function

Collaboration effectiveness refers to the evaluation of the cost, time, complexity, and other factors involved in the collaborative interaction between workers and industrial robots in completing complex actions. It is a comprehensive evaluation index of the collaborative interaction effectiveness. In this paper, the factors are normalized as the optimization goal of collaborative operations allocation [30]. Collaboration effectiveness (Q) is defined as:

$$ Q = \sum_{1}^{n} \bigl(w_{1} \vert T \vert + w_{2} \vert C \vert + w_{3} \vert A \vert + w_{4} \vert E \vert + w_{5} \vert L \vert \bigr), $$
(4)

where \(|T |\) is the normalized time; \(|C |\) is the normalized cost; \(|A |\) is the normalized accuracy; \(|E |\) is the normalized efficiency; \(|L |\) is the normalized labor complexity; \(w_{n}\) is the weight determined by linear weighting method, \(\sum_{1}^{{n}} w_{n} = 1\).

5.4 Constraints

Constraints are divided into cost constraints, time constraints, adjacency matrix constraints and equilibrium degree. The calculation method is as follows:

Cost constraint

$$ C < \mathop{C}\limits ^{ \bullet} = \mathop{w_{1}}\limits ^{ \bullet} \sum _{i = 1}^{n} \min (c_{ij}) + \mathop{w_{2}}\limits ^{ \bullet} \sum_{i = 1}^{n} \max (c_{ij}), $$
(5)

where \(c_{ij}\) denotes the cost to complete the jth action in the ith operation. \(\mathop{w_{1}} ^{ \bullet} \), \(\mathop{w_{2}} ^{ \bullet} \) is the weight, \(\mathop{w_{1}} ^{ \bullet} + \mathop{w_{2}} ^{ \bullet} = 1\), \(i = 1,2,\ldots,N\); \(j = 0,1,2\).

Time constraint

$$ T < \mathop{T}\limits ^{ \bullet} = \mathop{w_{3}}\limits ^{ \bullet} \sum _{i = 1}^{n} \min (t_{ij}) + \mathop{w_{4}}\limits ^{ \bullet} \sum_{i = 1}^{n} \max (t_{ij}), $$
(6)

where \(t_{ij}\) denotes the time to complete the jth action in the ith operation. \(\mathop{w_{3}} ^{ \bullet} \), \(\mathop{w_{4}} ^{ \bullet} \) is the weight, \(\mathop{w_{3}} ^{ \bullet} + \mathop{w_{4}} ^{ \bullet} = 1\), \(i = 1,2,\ldots,N\); \(j = 0,1,2\).

Equilibrium constraint

It is the ratio of the number of workers’ continuous actions to the sum of all actions in an operation.

$$ F_{1} = \frac{N_{A}}{N}, $$
(7)

where \(F_{1}\) denotes the degree of equilibrium; \(N_{A}\) denotes the maximum number of actions continuously completed by workers, and N denotes the sum of all actions in an operation.

Adjacency matrix constraint

Each operation is completed by multiple actions, and each action in the operation has coupling relationships. That is, different actions under the same operation can lead to mutual influence. An adjacency matrix is established to represent the relationship between their actions, which is shown as follows:

$$ \begin{aligned} &U_{MN} = \textstyle\begin{cases} 1 & \mathrm{Relevant}, \\ 0 & \mathrm{Irrelevant}, \end{cases}\displaystyle \\ &\quad M = 1,2,\ldots,M;N = 1,2,\ldots,N, \end{aligned} $$
(8)

where M is the number of operations; N is the number of actions.

6 Operations allocation optimization based on simulated annealing algorithm

6.1 Parameter setting

  1. 1)

    Initial temperature \(T_{0}\) and temperature decay function

There are many forms of attenuation function. The common attenuation function is

$$ T_{{t} + 1} = \alpha T_{{t}}, $$
(9)

where α is a constant, generally 0.95.

  1. 2)

    The selected parameters are as follows:

Initial temperature \(T_{0} = 100\).

Cooling function \(T_{{t} + 1}\ = \alpha T_{{t}}\). Then the temperature at time t:

$$ T_{{t} + 1} = \alpha T_{{t}} = 100 \times 0.95^{{t}}. $$
(10)

Time function:

$$ C_{t} = \frac{1}{T_{t}} = \frac{1}{100 \times 0.95^{t}}. $$
(11)

Probability function of accepting new solution:

$$ p_{t} = e^{ - \vert A_{1} - A_{1\_n} \vert \times C_{t}}. $$
(12)

6.2 Optimization process of simulated annealing algorithm

As shown in Fig. 4, the basic flow of the algorithm is described.

Figure 4
figure 4

Flow chart of simulated annealing algorithm

Full size image

Step 1: Input the initial data, constraint function and its weight, collaboration efficiency weight, and input the number of iterations and initial temperature;

Step 2: Initialize the temperature \(T_{0}\), cooling function \(T_{t+1}\), time function \(C_{t}\) and initialization solution, and calculate the human–robot collaboration effectiveness Q;

Step 3: Generate new solutions;

Step 4: Bring the new solution into the constraint function (C•, T•), if the conditions are not met, go to Step 3 again;

Step 5: Calculate human–robot collaboration effectiveness \(Q\_1\);

Step 6: \(Q\_1 < Q\), accept the new solution; \(Q\_1 > Q\), accept the new solution according to a certain probability \(p_{t}\);

Step 7: Judge whether the number of iterations has been reached. If not, go to Step 3;

Step 8: If the algorithm fails to meet the exit conditions, reduce \(T_{0}\), iterate again, and go to Step 3.

7 Case study

7.1 Scenario description

Taking the positioning and drilling of a workpiece as an example to verify the feasibility of the proposed simulated annealing algorithm to solve the human–robot collaboration operations allocation model. The specific scenario description was shown in Fig. 5.

Figure 5
figure 5

Process of positioning and drilling the workpieces

Full size image

During this period, works and industrial robots need to constantly interact, collaborate with each other and help complete the operation. Taking the workpieces placement as an example, it can be assumed that industrial robot grasped the workpieces, and the worker assisted in positioning and placing the workpieces. The interaction scene between worker and industrial robot was shown in Fig. 6.

Figure 6
figure 6

Human–robot interaction scene

Full size image

7.2 Actions analysis

Figure 7 shows the actions obtained after further decomposition of the above scene operations.

Figure 7
figure 7

Partial actions involved in workpieces operation

Full size image

In the machining process of workpieces, positioning plays an important role. Accurate positioning is a key prerequisite for ensuring the machining accuracy. The positioning methods mainly include double pin positioning, long side guiding positioning, surface combination positioning and so on. In the positioning of workpiece installation, it can be divided into multiple actions to complete the combination. The main actions analysis was shown in Table 4.

Table 4 Positioning of workpiece installation
Full size table

Through the actions analysis, the partial process of workpieces installation and positioning was shown in Fig. 8.

Figure 8
figure 8

Flow chart of workpiece installation and positioning

Full size image

7.3 Result analysis

Set the algorithm’s iterations number to 300, and its convergence curve was shown in Fig. 9. The calculated minimum human–robot collaboration effectiveness was 34.2163.

Figure 9
figure 9

Convergence curve

Full size image

In order to prove the effectiveness of the algorithm, we compared the solving performance of SA, (Genetic Algorithm) GA and PSO. Set the number of iterations to 300, and the results were shown in Fig. 10. SA has better optimization ability than the other two algorithms. In terms of optimal solution, SA was 34.2163, which was 7.5% less than GA (36.782); in terms of running time, SA was 6.5 s, which was 12.3% less than PSO (7.3 s).

Figure 10
figure 10

Comparison of algorithm results

Full size image

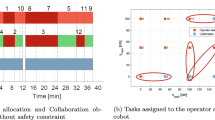
Based on the simulated annealing algorithm, the human–robot collaboration scheme for workpieces was shown in Fig. 11. The equilibrium degree \(F_{1} = \frac{5}{23} \approx 0.2174\). It meets the requirements.

Figure 11
figure 11

Human–robot collaboration scheme

Full size image

8 Conclusions

Human–robot interaction has a broad application prospect in smart manufacturing. By deploying industrial robots, we can make full use of the advantages of workers and industrial robots to improve machining efficiency and reduce production costs. This paper studies the human–computer interaction on CNC machine tools, and the conclusions are as follows:

  1. 1)

    A three-layers hierarchical model “production line-operations-actions” was used to describe the human–computer collaboration. The complexity measurement of human–computer operations was given, which provided an important foundation for the operations allocation.

  2. 2)

    A collaboration effectiveness-based operations allocation model was established through normalizing the time, cost, efficiency, accuracy and complexity of human–robot interaction.

  3. 3)

    A simulated annealing algorithm was used to solve preferable interaction scheme. Compared with GA and PSO, SA has better solving performance in optimal solution and running time. The optimal collaboration effectiveness was 34.2163 and equilibrium degree was 0.2174, which met the expected collaboration requirements.

This paper focuses on the human–robot collaborative operations allocation in pre-machining stage. The future work is to investigate the collaborative operations allocation in machining stage, as well as the operations allocation of the whole production line.