1 Introduction

Graphene is a single layer of carbon atoms arranged in a hexagonal lattice structure. It is incredibly thin, lightweight, transparent, strong, excellent conductor of heat and electricity, flexible, and stretchable [1,2,3,4,5]. Graphene-based materials have various shapes and structures, each with unique properties, such as graphene sheets [6], oxide [7], nanoribbons [8], nanotubes [9], and nanoplatelets [10]. Due to its remarkable electronic, mechanical, and thermal properties, it holds immense potential for diverse applications, such as energy storage [2] and conversion [11], electronics and photonics [4], sensors [3], water purification [12], and reinforced composite materials [10]. Numerous properties of graphene-based materials can be enhanced by changing their structural orientations. Thermal transport is one of them, which is very important for improving existing technologies and developing new ones where heat transport and heat management play a crucial role [7, 13,14,15].

Polycrystalline graphene consists of many grains with random orientation, and it can be produced through numerous methods, such as chemical vapor deposition (CVD) on metal substrate, reducing graphene oxide, and annealing process [5, 16]. Graphene nanoribbons (GNRs) have been extensively studied, such as the effects of grain boundaries on charge transport [17], the impact of graphene performance [5, 16], and bilayer graphene has tunable band gaps [18]. Polycrystalline graphene overcomes the disadvantage of single-layer graphene lacking band gaps. Especially in 2018, Cao et al. discovered that superconductivity was observed in twisted bilayer graphene when the twist angle was close to 1.1° [19, 20], which sparked interest in the study of this special structure. The bilayer GNRs are also intriguing due to their potential to blend the electronic properties of GNRs with the unique features of bilayer graphene [21]. Reducing interfacial thermal resistance (ITR) is crucial in applications like thermal interface materials, where efficient heat dissipation is necessary to prevent electronic devices from overheating. ITR is the main obstacle to heat flow from one layer to another in multi-layer materials [1]. With the penetration of semiconductor technology into other applications, the problem of ITR has been encountered in many new fields and devices, such as light-emitting diodes [22], quantum cascade lasers [23], phase change memories [24], thermoelectric devices [11], wearable devices [25], photovoltaic cells [26], and three-dimensional architecture chips [27]. Graphene is a good heat-dissipation material and has ultra-high thermal conductivity. Still, due to its two-dimensional structure limitations, its out-of-plane thermal conductivity is far inferior to in-plane thermal conductivity [28]. Therefore, how to improve its out-of-plane thermal conductivity to reduce the ITR of devices has become a hot topic of concern.

Researchers explore various techniques to minimize ITR, such as introducing intermediate layers with compatible atomic structures, optimizing chemical bonding, and controlling surface roughness [29]. These efforts aim to enhance the overall thermal performance of graphene-based materials in practical applications, making them more effective for thermal management and other heat-related technologies [30]. During the process of rotating bilayer single-crystal graphene, researchers found that the ITR increased with the rotation angle from 0° to 30° [13], and the in-plane thermal conductivity first decreased and then increased from 0° to 30° [31]. The thermal transport of polycrystalline graphene has been extensively investigated through theoretical calculations [32, 33], molecular dynamics (MD) simulations [7, 15, 30, 34,35,36], and CVD [14, 29] from different perspectives. For example, Krasavin et al. [33] predicted the effects of grain boundary structure, size, and shape on the phonon thermal conductivity of polycrystalline graphene. MD simulations were performed to compute the effects of grain size, alignment, and temperature by Wang et al. [34], grain boundary and grain-sized by Liu et al. [13], grain size, tensile strain, and temperature by Wu et al. [15], fatigue by Zhang et al. [36] and recently grain, vacancy and strain by Li et al. [30] on phonon thermal transport of polycrystalline graphene. Mu et al. calculated the thermal conductivity of oxidized polycrystalline graphene [7]. In addition, researchers have attempted to regulate the thermal transport properties of bilayer graphene by doping carbon atoms between layers [37]. Previous literature has reported on the frictional mechanics of multi-layer polycrystalline graphene [38] and on the effect of layer number on the thermal transport of polycrystalline graphene [29]. However, there are few reports on the effects of interlayer forces, grain size, and vacancy defect on the thermal transport of bilayer polycrystalline graphene, and thus the related mechanism is still unclear.

In this paper, the in-plane and out-of-plane thermal transport properties of the polycrystalline graphene nanoribbon (pGNR) bilayer and GNR bilayer are calculated by using the MD simulation method, respectively. The effects of interlayer forces, grain size, and vacancy defects on ITR and in-plane thermal conductivity are discussed for pGNR and GNR bilayers. The impact and mechanism of vacancy defects on the ITR of the pGNR bilayer are addressed from the perspective of phonon transport. This study contributes to a deeper understanding of the physical mechanism of thermal transport in the pGNR bilayer. It provides essential guidance for experimental research on regulating the phonon thermal conductivity and ITR in polycrystalline graphene layered materials.

2 Models and methods

2.1 Bilayer pGNR model and structure relaxation

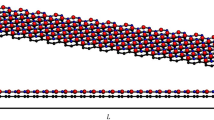
The structure model of monolayer pGNR is formed by the Thiessen polygon method [30, 39] with the open-source software Atomsk [40]. Upon acquiring a model of monolayer pGNR, adjustments were made to the interlayer spacing between the two layers, setting it precisely at d = 0.34 nm, see Fig. 1a. The MD simulations were implemented with the large-scale atomic/molecular massively parallel simulator (LAMMPS) package [41]. The AIREBO potential [42] was applied to describe the C-C interactions in the pGNR and GNR monolayers, and this potential has widely been used to calculate the thermal conductivity of graphene-based nanomaterials [43, 44]. The interlayer Van der Waals interactions are modeled by the Lennard-Jones potential [38]. The relevant parameters of the Lennard-Jones potential are taken from some commonly used in previous calculations for bilayer graphene [13]. In order to ensure stability and computational efficiency, a time step of 0.5 fs was used in the MD simulation to calculate the required properties. The periodic boundary conditions are applied on the layer plane (x and y directions). The pGNR monolayer/bilayer model underwent a comprehensive relaxation process as follows: initially heating up to 1000K over the duration of 0.5 ns in the NPT ensemble. Subsequently, a cooling phase took place for another 0.5 ns, bringing the system down to 300 K. It was followed by a 1.0-ns relaxation period in both the 300 K NPT and NVT ensembles and, ultimately, an additional 1.0-ns relaxation phase in the NVE ensemble to achieve the desired equilibrium state.

Fig. 1
figure 1

Schematics of bilayer models: a pGNR/pGNR, b pGNR/GNR, and c GNR/GNR

Full size image

2.2 Calculation method of ITR

The ITR is estimated by using the transient pump–probe method, as described in the reference [45]. This method has been widely used to investigate ITR in diverse two-dimensional heterostructures, as demonstrated in previous studies [46,47,48]. The MD simulation imitates the process of the transient pump–probe experiment, also called the heat dissipation method [45]. The simulation process is as follows: the two-layer heterostructure model undergoes complete relaxation initially at room temperature. After attaining the NVE equilibrium state, a thermal pulse of 50.0 ps is applied to one of the layers. During this process, the temperature of the heating layer (T1) rapidly increases to 400 K while the temperature of the undisturbed layer (T2) remains unchanged at 300 K within the NVT ensemble. Following the heat pulses of 50.0 ps, the thermostat is removed, and heat energy dissipates through interface thermal conduction until the system attains a new thermal equilibrium, as shown in Fig. 2a. Throughout the relaxation process, the temperature evolution of each layer and the total energy of the heat-applied layer are recorded at each time step. Due to the vacuum in the surrounding environment, the only thermal channel between monolayers is the exchange of heat energy between interfaces. The energy dissipation change of the heating layer over time is described as

$$\frac{\partial {E}_t}{\partial t}=A\times \left(\frac{T_1-{T}_2}{R}\right)$$
(1)

where Et is the total energy of the heating layer during the time t, R is the ITR, A is the effective heat transfer area between the two layers, and T1/T2 is the temperature of the heating layer/undisturbed layer, respectively. In order to reduce data fluctuations, the collected data points are averaged once every 100 steps. The energy Et after integration becomes as,

$${E}_t={E}_0+\left(\frac{A}{R}\right).{\int}_0^t\left(T{}_1-{T}_2\right) dt$$
(2)

where E0 represents the initial energy of the heating layer. As shown in Fig. 2b, the ITR is obtained from the linear fitting relationship of Et and the time integral of the temperature difference (T1-T2). The initial data for 100 ps was excluded from linear fitting due to the significant energy disturbance caused by the thermal pulse in the early stages of the thermal relaxation process.

Fig. 2
figure 2

a The evolution of heating layer temperature (T1), undisturbed layer temperature (T2), and heating layer energy (E1) versus time t during the heat dissipation process. b The relationship between the total energy of the heating layer and the time integral of (T1-T2)

Full size image

2.3 Phonon density of state analysis

In solid-state physics, phonons are the quantized form of lattice vibration, and the room-temperature thermal conduction of crystals is mainly determined by the interaction of phonons. Phonon density of state (PDOS) is an important parameter that reflects the thermal properties of crystals at the microscopic level. The degree of overlap of PDOS of layered materials determines the phonon transmission behavior of the interface. Based on MD simulations, PDOS can be obtained by Fourier transform of the velocity autocorrelation function as [49]

$$D\left(\omega \right)={\int}_0^t\Gamma (t)\exp \left(-\omega t\right) dt$$
(3)

where ω is the frequency, D(ω) is the frequency of PDOS, Г(t) is the velocity autocorrelation function, written as Γ(t) = 〈v(t) ⋅ v(0)〉. The thermal resistance of the interface between heterostructure interfaces is closely related to the overlap factor S of PDOS on both sides of the interface [50]

$$S=\frac{\int_{-\infty}^{+\infty }{D}_1\left(\omega \right){D}_2\left(\omega \right) d\omega}{\int_{-\infty}^{+\infty }{D}_1\left(\omega \right) d\omega {\int}_{-\infty}^{+\infty }{D}_2\left(\omega \right) d\omega},$$
(4)

where the D1 and D2 are the PDOS of the materials on both sides of the interface. The larger the S value of the overlap factor, the stronger the phonon coupling between the two layers, and thus the more conducive it is to phonon transport.

3 Results and discussion

3.1 Effect of interlayer interaction

In the stable state of two-dimensional layered materials, interlayer forces, commonly referred to as van der Waals forces, exist between the layers. The Lennard-Jones potential is frequently used in MD simulations to describe the van der Waals interactions between atoms. The van der Waals interaction can be characterized by a potential functionU(r) = χV(r), where V(r) is the Lennard-Jones potential in the initial state and χ is the proportional coefficient used to adjust the strength of the interaction. In order to analyze disparities between pGNR and GNR, three different bilayer structures were considered: pGNR/pGNR, pGNR/GNR, and GNR/GNR, as shown in Fig. 1. This selection allowed for observing how varying interlayer interaction strengths influence in-plane phonon thermal transport and the ITR within the bilayer system. Here the GNR and pGNR models with dimensions of 40 nm × 10 nm are specifically selected, and the average grain area size of pGNR is 50.0 nm2. A uniform χ value within the collapse limit was consistently applied to ensure the system’s stability amid fluctuating interlayer interaction strengths.

Figure 3 illustrates that the ITR of the GNR/GNR bilayer is higher than that of the pGNR/GNR heterostructure under the same χ. Moreover, the ITR of the pGNR/pGNR bilayer is the lowest. For example, at χ = 1, the ITR of pGNR/GNR reduces to 64% of the ITR of GNR/GNR. Similarly, the ITR of pGNR/pGNR reduces to 55% of the ITR of GNR/GNR. This indicates that the grain boundaries of pGNR enhanced phonon transport at the interface, leading to significantly improved out-of-plane thermal conduction in the bilayers. The decrease in ITR can be explained by the increased friction caused by the enhancement of interface roughness and defects, resulting in an enhancement of phonon coupling. When the interlayer interaction strength increases as χ = 2, 4, 6, 8, and 10, the ITR of GNR/GNR bilayer decreases to 90%, 74%, 62%, 56%, and 46%, respectively, of the original value (χ = 1). The ITR of pGNR/GNR heterostructure decreases to 92%, 72%, 67%, 54%, and 53% of the original value (χ = 1), respectively. The ITR of the pGNR/pGNR bilayer is reduced to the original 78%, 55%, 48%, 39%, and 28%, respectively. Obviously, the ITR of the pGNR/pGNR bilayer is more susceptible to interlayer forces.

Fig. 3
figure 3

The variation of ITR (R) with the intensity of interlayer interaction (χ)

Full size image

Figure 4 displays the influence of interlayer interaction strength on the in-plane phonon thermal conductivity (κ) of studied bilayer structures. At χ = 1, our presented κ value for the GNR/GNR bilayer was compatible with earlier reported work [9, 51]. With the rise in χ, the in-plane κ of the bilayer structures decreases to varying degrees. The in-plane κ of pGNR/pGNR decreased to the original 94%, 91%, 84%, 82%, and 76%, while the in-plane κ of GNR/GNR decreased to the original 95%, 91%, 88%, 84%, and 80%, respectively, for χ = 2, 4, 6, 8, and 10. Interestingly, the in-plane κ of pGNR/GNR is lower than that of GNR/GNR and higher than that of pGNR/pGNR at the same χ. This phenomenon arises due to the distinct grain orientations and defects in various grain domains within pGNR. All in all, introducing interlayer interaction is analogous to imposing strain in the out-of-plane direction, thereby influencing the overall structure of the model. The larger interlayer interaction intensity corresponds to the larger van der Waals interaction which reduces in-plane phonon thermal conductivity because of suppressing the contribution of the out-of-plane acoustic mode (ZA) [52].

Fig. 4
figure 4

The variation of in-plane thermal conductivity (κ) with the intensity of interlayer interaction (χ). Here the GNR and pGNR models with dimensions of 40 nm × 10 nm are specifically selected, and the average grain area size of pGNR is 50.0 nm2

Full size image

3.2 Effect of grain size

Figure 5 shows the pGNR grain size effect on the ITR of pGNR-based bilayers. Three randomly generated models with the same grain size were selected for simulation, and the average value was taken to reduce computational fluctuations. Upon reaching a dimension of 400 nm2, corresponding to a bilayer GNR model, the ITR measures 2.82 × 10−2 m2K/MW, aligning with findings reported in the relevant literature [13]. When the average grain size of pGNR is 25, 50, 100, and 200 nm2, the ITRs of the pGNR/pGNR bilayer (pGNR/GNR bilayer) decrease to be 55% (60%), 62% (67%), 74% (89%), 91% (96%) of ITR of GNR/GNR, respectively. The surface of GNR is smooth and complete, resulting in lower phonon coupling strength compared to pGNR in bilayer structures. As the grain size of pGNR increases, the corresponding grain boundaries and defects decrease. Thus weakening phonon coupling between two layers may be unfavorable for phonon thermal transport at the interface.

Fig. 5
figure 5

The variation of ITR (R) of bilayer structures with the average grain area size of pGNR layer. Here the GNR and pGNR models with dimensions of 40 nm × 10 nm are specifically selected

Full size image

3.3 Effect of vacancy defect

Due to the inevitable occurrence of vacancy defects in layer materials in practical applications, it is important to study the influence of vacancy defects on thermal transport at interlayer interfaces. Figure 6 shows the ITRs of the GNR/GNR bilayer and pGNR/pGNR bilayer under the influence of random vacancy defects rate (ε), respectively. Here vacancy defects rate is generally defined as the ratio between the number of vacancies and the number of atoms in a perfect crystal. From Fig. 6, it can be seen that the ITR decreases with the increase of ε both in the GNR/GNR bilayer and in the pGNR/pGNR bilayer. However, the sensitivity of the ITR to ε is inconsistent during these two bilayer models. As the ε increases by 1%, 3%, and 5%, the ITR of GNR/GNR bilayer (pGNR/pGNR bilayer) is 89% (97%), 61% (85%), and 52% (68%), of the initial state (ε = 0), respectively.

Fig. 6
figure 6

The variation of ITR (R) of GNR/GNR and pGNR/pGNR bilayer structures versus random vacancy defect rate (ε). Here the bilayer models with dimensions of 40 nm × 10 nm are specifically selected, and the average grain area size of pGNR is 50.0 nm2

Full size image

Figure 7 shows the out-of-plane PDOS (PDOSz) of the pGNR/pGNR bilayer under different vacancy defect rates ε. It is found that when the ε is 0, 1%, 3%, and 5%, the corresponding overlap factors S are 0.0036, 0.0041, 0.0051, and 0.0052, respectively. The increase in overlap factor S indicates that the increase in vacancy defect rate enhances the heat transfer at the interface, leading to a decrease in ITR. From a structural perspective, as the number of vacancy defects increases, the horizontal binding of atoms decreases while the out-of-plane vibration increases.

Fig. 7
figure 7

The out-of-plane PDOS (PDOSz) of pGNR/pGNR bilayer under different vacancy defect rates (ε)

Full size image

4 Conclusions

In this paper, MD simulations have been performed to calculate the in-plane phonon thermal conductivity and ITR of pGNR-based bilayers. The effects of interlayer forces, grain size, and vacancy defects on phonon thermal transport were studied systematically. It was found that the in-plane phonon thermal conductivity of pGNR is lower than that of GNR with the same size, regardless of whether it is a single layer or a bilayer, and weakens with the increase of interlayer forces in the bilayer structure. This is because the interface distance between bilayer membranes decreases with the increase of interlayer interaction intensity, and the contribution of phonon bending mode (ZA) is suppressed. More significant interlayer interaction intensity corresponds to a larger van der Waals interaction, which reduces the in-plane phonon thermal conductivity. The ITR of the bilayer structure will decrease with the increase of interlayer force, the decrease of crystal grain size, and the increase of vacancy defects. The ITR of the pGNR bilayer is smaller than that of the GNR bilayer, which can be explained by the increased friction caused by the enhancement of interface roughness and defects, resulting in an enhanced phonon coupling in the pGNR-based bilayers, compared to the GNR bilayer. The research results of this paper help to understand the interlayer thermal transport properties of pGNR and also provide meaningful guidance for the regulation of phonon thermal transport between layers of pGNR.