Abstract
We theoretically investigate the polaron physics of an impurity immersed in a two-dimensional Fermi sea, interacting via a p-wave interaction at finite temperature. In the unitary limit with a divergent scattering area, we find a well-defined repulsive Fermi polaron at short interaction range, which shows a remarkable thermal stability with increasing temperature. The appearance of such a stable repulsive Fermi polaron in the resonantly interacting limit can be attributed to the existence of a quasi-bound dressed molecule state hidden in the two-particle continuum, although there is no bound state in the two-particle limit. We show that the repulsive Fermi polaron disappears when the interaction range increases or when the scattering area is tuned to the weakly interacting regime. The large interaction range and small scattering area instead stabilize attractive Fermi polarons.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Fermi polaron is a well-established research area that addresses the fate of an impurity when it moves and interacts with the surrounding environment of a quantum many-fermion system [1]. The ability of a free particle-like motion of the impurity under interactions can be intuitively described by a fundamental concept of many-body physics — quasiparticle [2]. For many decades, the determination of quasiparticle properties, such as energy, residue, and lifetime, provides valuable insights on intriguing quantum many-fermion systems in the different branches of physics [3,4,5,6,7,8,9,10].
Over the past two decades, the investigation of Fermi polarons with ultracold atoms attracts particular interests [6, 7, 11,12,13,14,15,16,17]. Due to the unprecedented controllability on the interatomic interaction (i.e., through Feshbach resonance [18]), purity and dimensionality of ultracold atomic Fermi gases [19, 20], new interesting features of Fermi polarons can be revealed in a quantitative manner [21,22,23]. For example, repulsive Fermi polaron, which is an excited polaron state with well-defined residue and lifetime, has been theoretically predicted [24, 25] and experimentally observed in an interacting imbalanced spin-1/2 Fermi gas with s-wave contact interactions [12, 13, 15]. This repulsive branch appears on the tightly bound side of the Feshbach resonance, with a deep two-body bound state. Towards the strongly interacting unitary limit at resonance where the two-body bound state dissolves, the decay rate of repulsive Fermi polaron increases too rapidly to behave like a well-defined quasiparticle [15, 25].
In this work, we predict the existence of a well-defined repulsive Fermi polaron in a two-dimensional Fermi gas, under a resonant p-wave interaction between impurity and fermions, in the absence of a two-body bound state. This resonant unitary limit is described by an infinitely large scattering area \(a_{p}=\pm \infty\), together with a nonzero effective interaction range \(R_{p}\) [26, 27]. The repulsive Fermi polaron appears at small interaction range, due to a quasi-bound dressed molecule state hidden in the two-particle continuum, although no two-body bound state can exist.
To describe the repulsive polaron branch, we apply a many-body T-matrix theory [28,29,30,31] that allows us to go beyond the earlier zero-temperature study of p-wave Fermi polarons (in three dimensions) [32] and to explore their finite-temperature properties. Remarkably, the p-wave repulsive Fermi polaron appears to be robust against thermal fluctuations. This thermal stability of p-wave repulsive Fermi polaron could be crucial for its experimental observation, since a p-wave interacting Fermi gas often suffers severe atom loss at low temperature [33,34,35].
The rest of the paper is organized as follows. In the next section (Section 2), we outline the model Hamiltonian for the p-wave interacting Fermi polaron and present the many-body T-matrix approach that is capable to describe the one-particle-hole excitation at finite temperature, which is the key ingredient of polaron physics. In Section 3, we first discuss the zero-momentum spectral function of the impurity and show the appearance of the p-wave repulsive Fermi polaron in the unitary limit. We then present the spectral function of the molecule to reveal the existence of a quasi-bound dressed molecule state. Finally, we explore the parameter space for p-wave repulsive Fermi polaron, by changing either the scattering area or the effective interaction range. The conclusions follow in Section 4.
2 Model Hamiltonian and many-body T-matrix approach
We consider a highly imbalanced spin-1/2 Fermi gas of ultracold atoms near a p-wave Feshbach resonance in two dimensions. In the extreme limit of vanishing population of minority atoms, we treat minority atoms as individual impurities, interacting with a non-interacting Fermi sea of majority atoms via an interaction potential \(V_{p}\left( \textbf{k},\textbf{k}'\right)\). Our system can then be well-described by the single-channel model Hamiltonian,
where \(c_{\textbf{k}}^{\dagger }\) and \(d_{\textbf{k}}^{\dagger }\) are the creation field operators for the majority of atoms and the single impurity, respectively. The first two terms in the Hamiltonian are the single-particle terms with dispersion relations \(\xi _{\textbf{k}}=\hbar ^{2}\textbf{k}^{2}/(2m)-\mu =\epsilon _{\textbf{k}}-\mu\) and \(E_{\textbf{k}}=\hbar ^{2}\textbf{k}^{2}/(2m)\), while the last term describes the interaction term. Here, \(\mu\) is the chemical potential of the majority of atoms and at finite temperature T is given by, \(\mu =k_{B}T\ln \left[ \exp (\varepsilon _{F}/k_{B}T)-1\right]\). At low temperature, the chemical potential approaches the Fermi energy \(\varepsilon _{F}=\hbar ^{2}k_{F}^{2}/(2m)=2\pi n\hbar ^{2}/m\), where n is the density of the majority of atoms in two dimensions.
For the p-wave interaction potential \(V_{p}\left( \textbf{k},\textbf{k}'\right)\), for concreteness, we choose the chiral \(p_{x}+ip_{y}\) channel, by assuming that experimentally one can carefully tune the magnetic field very close to a p-wave Feshbach resonance with azimuthal quantum number \(m=+1\). In practice, it is convenient to take a separable interaction potential in the form [27, 36],
where \(\lambda\) is the interaction strength and
is a dimensionless \(p_{x}+ip_{y}\) form factor function with a cut-off momentum \(k_{0}\), a polar angle \(\varphi _{{\textbf {k}}}=\arctan (k_{y}/k_{x})\) and an exponent n that is introduced for the convenience of numerical calculations. The wavevector k is measured in units of the Fermi wavevector \(k_{F}=(4\pi n)^{1/2}\).
2.1 Two-body T-matrix and the renormalization of p-wave interaction
While it is convenient to use the set of the three parameters (\(\lambda ,k_{0},n\)) to describe the p-wave interaction potential, physically we would better use the scattering area \(a_{p}\) (in two dimensions) and the effective range of interaction \(R_{p}\), which are formally defined through the p-wave phase shift \(\delta _{p}\left( k\right)\) in the low-energy limit (i.e., \(k\rightarrow 0\)) [27, 33],
The p-wave phase shift \(\delta _{p}\left( k\right)\) can be easily obtained by calculating the low-energy two-body T-matrix in vacuum [27], \(T_{2}^{(\text {vac})}({\textbf {k}},{\textbf {k}};E)=\left| \Gamma ({\textbf {k}})\right| ^{2}\tilde{T}_{2}^{(\text {vac})}(E)\) with
where \(E\equiv \hbar ^{2}k^{2}/m\). Using the well-known relation \([T_{2}^{(\text {vac})}({\textbf {k}},{\textbf {k}};E)]^{-1}=-m[\cot \delta _{p}(k)-i]/(4\hbar ^{2})\), we find that in the low-energy limit \(k\rightarrow 0\),
where \(\mathscr {P}\) stands for taking the Cauchy principal value. By carrying out the summation over \(\textbf{p}\), we find that [27]
Throughout this work, we take an exponent \(n=1.0\). For the given scattering area \(a_{p}\) and effective range \(R_{p}\), we then determine the interaction strength \(\lambda\) and the cut-off momentum \(k_{0}\) by using the above two expressions. Physical results of course will not depend on the choice of the exponent n. In Appendix 1, we explicitly show the n-independence of the separable interaction potential \(V_{p}\left( \textbf{k},\textbf{k}'\right)\), by calculating the impurity self-energy.
2.2 Many-body T-matrix theory of Fermi polarons
We now turn to solve the Fermi polaron problem by applying the many-body T-matrix theory with the ladder approximation [28,29,30]. The theory has been outlined in greater detail in the previous work for Fermi polarons with an s-wave interaction potential [31], so here we only briefly sketch the key ingredients and emphasize the changes due to the p-wave interaction potential.
Following the same derivation as in the previous work [31], it is easy to show that the many-body T-matrix is given by
where
By taking \(\textbf{q}=0\), \(\mu =0\) and the Fermi-Dirac distribution function \(f(x)=0\) (i.e., by considering the two-body scattering in vacuum), \(\tilde{T}_{2}(\textbf{q};\omega )\) reduces to the two-body T-matrix Eq. (5). In other words, the many-body T-matrix can be understood as the effective interaction in the medium. According to the interaction Hamiltonian in Eq. (1), diagrammatically this effective interaction comes with two incoming legs with momenta \(\textbf{q}/2\pm \textbf{k}'\) and with two out-going legs with momenta \(\textbf{q}/2\pm \textbf{k}\). Therefore, by winding back the out-going leg of majority atoms (i.e., with the momentum \(\textbf{q}/2+\textbf{k}\)) and connecting it to the incoming leg with the momentum \(\textbf{q}/2+\textbf{k}'\) (so \(\textbf{k}=\textbf{k}'\)) [31], we obtain the approximate impurity self-energy in the many-body T-matrix theory,
where \(\mathscr {G}\) is the non-interacting Green function of the Fermi sea and we use \(\mathcal {Q}=(\textbf{q},i\nu _{n})\) and \(\mathcal {K}'=(\textbf{k}',i\omega _{m'})\) to denote the four-dimensional momenta with the bosonic Matsubara frequency \(\nu _{n}=2\pi nk_{B}T\) and the fermionic Matsubara frequency \(\omega _{m'}=\pi (2m'+1)k_{B}T\) at finite temperature T. We have also used the abbreviation \(\sum _{\mathcal {Q}}\equiv \sum _{\textbf{q}}k_{B}T\sum _{i\nu _{n}}\). For the impurity self-energy, it is convenient to change to \(\mathcal {K}=\mathcal {Q}/2-\mathcal {K}'=(\textbf{k},i\omega _{m}\)), so \(\Sigma (\mathcal {K})=\sum _{\mathcal {Q}}G(\mathcal {Q}-\mathcal {K})\tilde{T}_{2}(\mathcal {Q})\left| \Gamma (\textbf{q}/2-{\textbf {k}})\right| ^{2}\). By summing over the bosonic Matsubara frequency \(\nu _{n}\) and taking the analytic continuation \(i\omega _{m}\rightarrow \omega +i0^{+}\) [31], we find the impurity self-energy,
In comparison with the case of an s-wave interaction potential [31], the many-body T-matrix Eq. (10) and the impurity self-energy Eq. (12) take essentially the same forms, apart from the additional interaction form factors \(\Gamma ({\textbf {k}})\) and \(\Gamma ^{*}({\textbf {k'}})\) that are necessary to characterize the p-wave interaction [27, 36]. These interaction form factors do not introduce too many numerical workloads, and the numerical difficulty still lies on the handling of the pole structure that might appear in the summation over the momentum \(\textbf{p}\) in \(\tilde{T}_{2}^{-1}(\textbf{q},\omega )\). A detailed discussion of \(\tilde{T}_{2}^{-1}(\textbf{q},\omega )\) is included in Appendix 2. We note that the summation over the momentum \(\textbf{q}\) in the self-energy \(\Sigma (\textbf{k},\omega )\) may also suffer from the existence of a well-defined molecule state, which manifests itself as a pole or a delta-peak of \(\tilde{T}_{2}(\textbf{q},\omega )\).
3 Results and discussions
Once the impurity self-energy is obtained, we directly calculate the impurity Green function [14, 31],
Fermi polarons can be well-characterized by the impurity spectral function
where each quasiparticle is visualized by the appearance of a sharp spectral peak, with its width reflecting the lifetime or decay rate of quasiparticle [25, 28]. Mathematically, we may determine the quasiparticle energy \(\mathcal {E}_{P}(\textbf{k})\), either the attractive polaron energy or the repulsive polaron energy, from the pole position of the impurity Green function (\(\omega \rightarrow \mathcal {E}_{P}(\mathbf {k)}\)), i.e.,
By expanding the self-energy near the zero momentum \(\textbf{k}=0\) and the polaron energy \(\mathcal {E}_{P}\equiv \mathcal {E}_{P}\left( \textbf{0}\right)\), we directly determines various quasiparticle properties, including the polaron residue,
and the polaron decay rate,
3.1 Repulsive Fermi polaron in the unitary limit
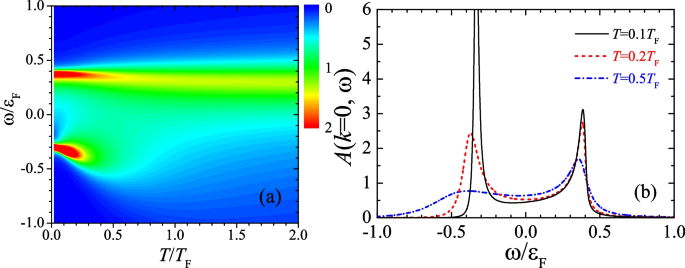
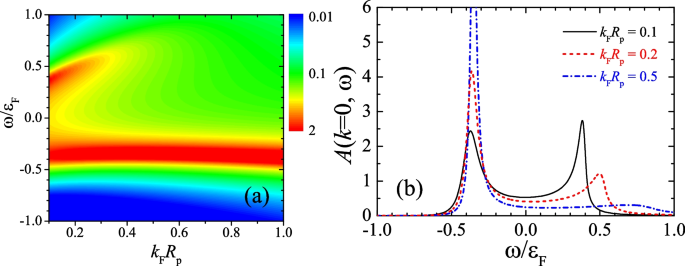
Let us first focus on the unitary limit, where the scattering area diverges, i.e., \(a_{p}=\pm \infty\). In Fig. 1a, we report the temperature evolution of the zero-momentum spectral function \(A(\textbf{k}=0,\omega\)) at a small interaction range \(k_{F}R_{p}=0.1\), in the form of a two-dimensional contour plot in the linear scale. The one-dimensional plots of the spectral functions at the three typical temperatures \(T=0.1T_{F}\), \(0.2T_{F}\) and \(0.5T_{F}\) are shown in Fig. 1b, by using black solid, red dashed, and blue dot-dashed lines, respectively.
Zero-momentum spectral function \(A(\textbf{k}=0,\omega )\) of the impurity as a function of the reduced temperature \(T/T_{F}\). The two-dimensional contour plot in (a) is shown in the linear scale. The three lines in (b) show the spectral functions at \(T=0.1T_{F}\) (black solid), \(T=0.2T_{F}\) (red dashed), and \(T=0.5T_{F}\) (blue dot-dashed). Here, we consider the unitary limit \(1/(k_{F}^{2}a_{p})=0\) and take an interaction range \(k_{F}R_{p}=0.10\). The spectral functions are measured in units of \(\varepsilon _{F}^{-1}\)
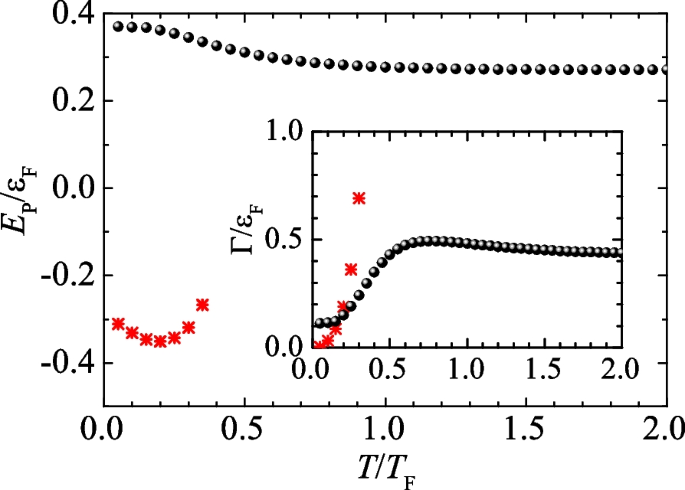
At very low temperature (i.e., \(T\sim 0\)), we find two dominant peaks in the spectral function at the positions \(\omega \simeq -0.31\varepsilon _{F}\) and \(\omega \simeq +0.37\varepsilon _{F}\), which correspond to the attractive Fermi polaron and the repulsive Fermi polaron [21,22,23, 25], respectively. By increasing temperature, both polaron states show a red shift in energy, similar to the s-wave case [31]. The initially sharp attractive polaron peak quickly dissolves into a broad distribution at \(T\sim 0.3T_{F}\) and eventually disappears at \(T\sim 0.6T_{F}\). In sharp contrast, the repulsive polaron appears to be very robust against thermal fluctuations. In particular, once the temperature is larger than \(0.6T_{F}\), the position and the width of the repulsive polaron peak essentially do not change with temperature.
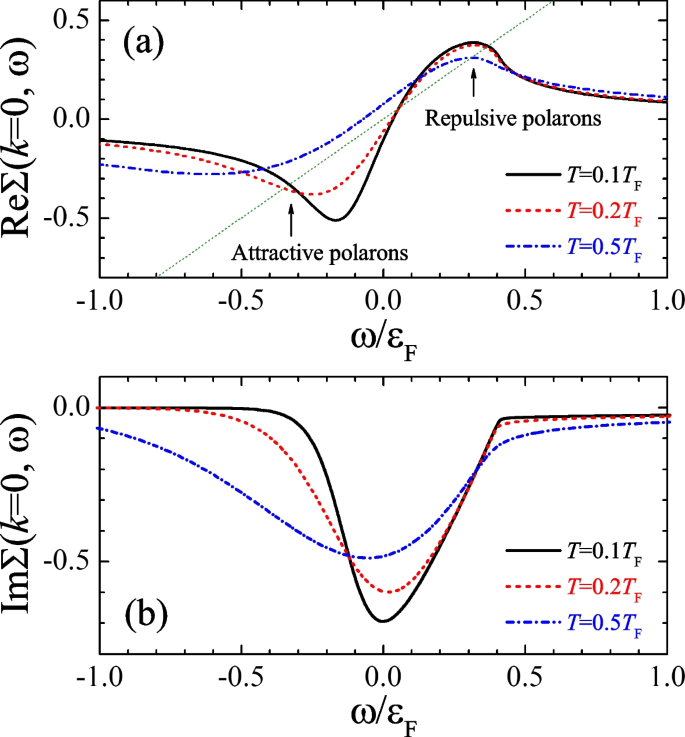
To confirm the existence of a repulsive Fermi polaron, in Fig. 2, we present the real part (a) and the imaginary part (b) of the self-energy at the same three typical temperatures as in Fig. 1b. At zero momentum (i.e., \(E_{\textbf{k}}=0\)), a pole of the impurity Green function occurs when \(\omega =\text {Re}\Sigma (k=\textbf{0},\omega )\). Therefore, in Fig. 2a, the intercept between the green dotted line (i.e., \(y=\omega\)) and the curves \(\text {Re}\Sigma (k=\textbf{0},\omega )\) determines the polaron energy. On the negative frequency side (\(\omega <0\)), we find that the green dotted line fails to intercept with the curve \(\text {Re}\Sigma (k=\textbf{0},\omega )\) at the temperate \(T=0.5_{F}\), consistent with our earlier observation that the attractive polaron develops into a broad structure once \(T>0.3T_{F}\). On the positive frequency side (\(\omega >0\)), the green dotted line always crosses with the curves \(\text {Re}\Sigma (k=\textbf{0},\omega )\) at different temperatures, indicating the persistence of the repulsive polarons with increasing temperature. The position of the crossing points or the repulsive polaron energies do not change too much as temperature increases. Remarkably, at those repulsive polaron energies, the imaginary part of the self-energy \(\text {Im}\Sigma (k=\textbf{0},\omega )\) turns out to be reasonably small, and more importantly to be temperature insensitive.
Real part (a) and imaginary part (b) of the impurity self-energy as a function of the frequency \(\omega\). Both self-energy and frequency are measured in units of the Fermi energy \(\varepsilon _{F}\). The three lines show the self-energy at \(T=0.1T_{F}\) (black solid), \(T=0.2T_{F}\) (red dashed), and \(T=0.5T_{F}\) (blue dot-dashed). In (a), we also show the curve \(y=\omega\) using a dotted line. The crossing points of this curve with the three lines for the real part of self-energy determine the polaron energies, which are indicated using arrows for both the attractive polaron branch and the repulsive polaron branch. As in Fig. 1, we consider the unitary limit \(1/(k_{F}^{2}a_{p})=0\) and take an interaction range \(k_{F}R_{p}=0.10\)
The thermally stable repulsive polaron is not expected to appear in the unitary limit, because a well-defined two-body bound state does not exist [14, 25]. This situation might be compared with an s-wave Fermi polaron in three dimensions [31]. In that case, in the same unitary limit, where the s-wave scattering length \(a_{s}\) diverges, the impurity spectral function only shows an extremely broad background at positive energy, without any signal for a repulsive polaron. The analysis of the real part of the self-energy confirms the absence of a repulsive polaron, since no solution exists for the condition \(\omega =\text {Re}\Sigma (k=\textbf{0},\omega )\) when \(\omega >0\) [31]. Under the s-wave interaction between the impurity and the Fermi sea, repulsive polaron only appears in the tightly bound limit, where a well-defined two-body bound state exists. Towards the s-wave unitary limit, the decay rate of the s-wave repulsive polaron will quickly increase with both the scattering length \(a_{s}\) and temperature. As a result, there is no meaningful s-wave repulsive polaron near the strongly interacting regime of the unitary limit.
The existence of a thermally robust repulsive polaron, without a two-body bound state, is therefore an unique feature of p-wave Fermi polarons. To understand its formation mechanics, we consider the dressed molecule state in the presence of the many-body environment of a Fermi sea, which is an analog of a Cooper pair in the limit of an extreme population imbalance. In the many-body T-matrix theory, the dressed molecule state is simply described by its effective Green function, i.e, the many-body T-matrix \(T_{2}(\textbf{q},\omega )\) [28, 29, 31]. Thus, we introduce a molecule spectral function,
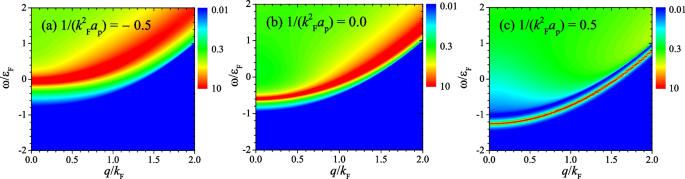
In Fig. 3, we report the two-dimensional contour plots of the molecule spectral function in the logarithmic scale across the unitary limit at the temperature \(0.2T_{F}\), with the inverse scattering areas \(1/(k_{F}^{2}a_{p})=-0.5\) (a), 0.0 (b), and \(+0.5\) (c). To be consistent with the results in Fig. 1, we have taken the same effective interaction range \(k_{F}R_{p}=0.1\).
Two-dimensional contour plots of the molecule spectral function \(A_{\text {mol}}(\textbf{q},\omega )\) at different inverse scattering areas: \(1/(k_{F}^{2}a_{p})=-0.5\) (a), \(1/(k_{F}^{2}a_{p})=0\) (b), and \(1/(k_{F}^{2}a_{p})=+0.5\) (c). The contour plots are shown in the logarithmic scale in arbitrary units, as indicated by the color bar. We take an interaction range \(k_{F}R_{p}=0.1\) at temperature \(T=0.2T_{F}\)
On the molecule side of the Feshbach resonance in Fig. 3c, it is ready to see a sharp peak starting at energy \(\omega \sim -1.2\varepsilon _{F}\), which is well-separated from the two-particle continuum. Moreover, at the momentum \(q<k_{F}\), the spectral weight at the bottom of the two-particle continuum is depleted. The separate, sharp peak arises from of the existence of an undamped dressed molecule state, which in the two-particle limit reduces to a two-body bound state that must exist with a positive scattering area.
In the unitary limit on resonance (see Fig. 3b), although a separate undamped peak does not exist, we do observe that a sharp peak emerges at energy \(\omega \sim -0.6\varepsilon _{F}\) and becomes broader when the momentum q is larger than \(0.5k_{F}\). We would like to attribute the existence of a well-defined repulsive polaron in the unitary limit to this quasi-bound dressed molecule state, which is hidden slightly above the bottom of the two-particle scattering continuum. Although it is a quasi-bound molecule state, it effectively depletes fermions surrounding the dressed molecule and eventually leads to the excited repulsive polaron [25]. This idea is also supported by the weak temperature dependence of the quasi-bound dressed molecule state (not shown in the figure), which may explain the observed thermal stability of the repulsive polaron.
We finally consider a negative scattering area, as shown in Fig. 3a. The dressed molecule state now becomes less well-defined, with a much broader peak and with its energy blue-shifted to \(\omega \sim 0\) at zero momentum. In this situation, the repulsive polaron may fail to exist, as we shall see.
To complete our analysis of the repulsive polaron in the unitary limit, we show in Fig. 4 the temperature dependence of the energy (in the main figure) and the decay rate (in the inset) of both attractive Fermi polaron and repulsive Fermi polaron. As illustrated by the red stars in the inset, the decay rate of the attractive Fermi polaron rapidly increases with increasing temperature. It becomes larger than the Fermi energy when \(T>0.3T_{F}\), in agreement with the observation in Fig. 1a that the attractive polaron ceases to exist at this temperature. On the other hand, as indicated by black dots in the inset, the decay rate of the repulsive Fermi polaron increases from \(0.1\varepsilon _{F}\) at \(T\sim 0\) to about \(0.5\varepsilon _{F}\) at \(T\sim 0.7T_{F}\). By further increasing temperature, the decay rate only slightly decreases, with a polaron energy almost fixed at \(0.27\varepsilon _{F}\) (see the main figure). This provides a quantitative measure of the thermal robustness of the repulsive Fermi polaron in the unitary limit.
3.2 Parameter space for repulsive Fermi polarons
We now turn to explore the parameter window of repulsive Fermi polarons, for a p-wave interaction strength that does not support a two-body bound state. We focus on the cases of a fixed temperature \(T=0.2T_{F}\), but with varying effective interaction range \(k_{F}R_{p}\) and with varying scattering area \(1/(k_{F}^{2}a_{p})\).
In Fig. 5, we report the evolution of the zero-momentum spectral function \(A(\textbf{k}=0,\omega )\) as the interaction range \(k_{F}R_{p}\) increases in the unitary limit. From the two-dimensional contour plot in Fig. 5a, we find that the lower attractive polaron branch becomes increasingly dominant with respect to the increase in the interaction range. However, the interesting new feature of repulsive polaron branch quickly disappears when \(k_{F}R_{p}\) becomes larger than 0.3. At the interaction range \(k_{F}R_{p}=0.5\), as shown in Fig. 5b by the blue dot-dashed line, one can observe an extremely broad bump at about \(\omega \sim 0.7\varepsilon _{F}\), as a reminiscent of the repulsive polaron. Therefore, we conclude that a large interaction range does not favor the formation of a repulsive Fermi polaron.
Zero-momentum spectral function \(A(k=0,\omega )\) of the impurity as a function of the interaction range \(k_{F}R_{p}\) in the unitary limit \(1/(k_{F}^{2}a_{p})=0\). The two-dimensional contour plot in (a) is shown in the logarithmic scale, in units of \(\varepsilon _{F}^{-1}\). The three lines in (b) show the spectral functions at \(k_{F}R_{p}=0.1\) (black solid), \(k_{F}R_{p}=0.2\) (red dashed), and \(k_{F}R_{p}=0.5\) (blue dot-dashed). Here, the temperature is set to \(T=0.2T_{F}\)
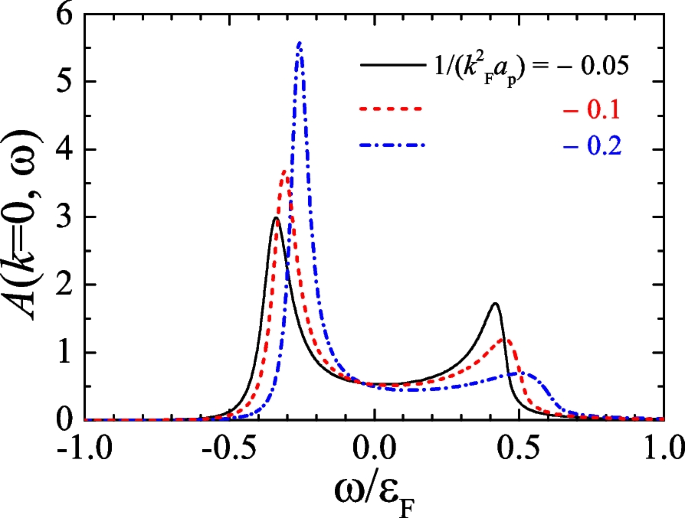
In Fig. 6, we present the zero-momentum spectral function at three inverse scattering areas \(1/(k_{F}^{2}a_{p})=-0.05\) (black solid line), \(-0.1\) (red dashed line) and \(-0.2\) (blue dot-dashed line), and at a fixed interaction range \(k_{F}R_{p}=0.1\). By decreasing the inverse scattering area, the attractive Fermi polarons show a blue shift in energy. More importantly, the attractive polaron peak becomes sharper. The repulsive Fermi polarons also show a blue shift in energy. However, their width becomes much wider with increasing inverse scattering area. At \(1/(k_{F}^{2}a_{p})=-0.2\), we may hardly identify the peak as a well-defined repulsive polaron. This finding is consistent with the earlier observation from Fig. 3a that the quasi-bound dressed molecule state becomes less well-defined as the inverse scattering area decreases and moves away from the Feshbach resonance.
Zero-momentum spectral function \(A(k=0,\omega )\) of the impurity at different inverse scattering areas: \(1/(k_{F}^{2}a_{p})=-0.05\) (black solid), \(1/(k_{F}^{2}a_{p})=-0.1\) (red dashed) and \(1/(k_{F}^{2}a_{p})=-0.2\) (blue dot-dashed). Here, we take an interaction range \(k_{F}R_{p}=0.1\) and set the temperature \(T=0.2T_{F}\)
4 Conclusions and outlooks
In conclusion, we have investigated p-wave Fermi polarons in two dimensions at finite temperature, which potentially can be experimentally realized in a population imbalanced spin-1/2 Fermi gas, where minority atoms in one hyperfine state act as impurities and interact with majority atoms in another hyperfine state near a p-wave Feshbach resonance. In contrast to the conventional s-wave case that the existence of a repulsive Fermi polaron requires a two-body bound state [15, 25, 31], a p-wave repulsive Fermi polaron can arise in the absence of two-body bound state near the Feshbach resonance, due to a quasi-bound dressed (many-body) molecule state that is hidden inside the two-particle scattering continuum. The p-wave repulsive polaron shows a remarkable stability against temperature. This extraordinary thermal robustness would be very useful for its experimental observation, since a p-wave Fermi gas is not blessed by the Pauli exclusion principle and often has severe atom loss below the Fermi temperature for degeneracy [34, 35].
Instead of using a spin-1/2 Fermi gas with two hyperfine states, one may also consider a mass-imbalanced Fermi-Fermi mixture such as \(^{6}\)Li-\(^{40}\)K atomic mixture near Feshbach resonances, with a strong atom-dimer attraction occurring between \(^{40}\)K atoms and weakly-bound \(^{6}\)Li-\(^{40}\)K molecules in odd partial-wave channels [37]. This higher partial-wave attraction is mainly p-wave and is recombination-free (and therefore stable), as experimentally observed [37]. We may tune down the number of weakly bound \(^{6}\)Li-\(^{40}\)K molecules to treat them as impurities. In this case, the mass of impurity is slightly larger than the mass of the fermions in the Fermi sea. Our results of repulsive Fermi polarons, based on equal mass, should be qualitatively applicable. Quantitative predictions however require the extension of our work to account for an arbitrary impurity mass. Another crucial issue of the atom-dimer p-wave attraction is that weakly bound dimers may spontaneously dissociate on a time scale of about tens mill-seconds [37]. We would like to leave a careful investigation of these two issues (i.e., the unequal mass effect and the short lifetime of impurity) to a future study.
Availability of data and materials
The data generated during the current study are available from the contributing author upon reasonable request.
References
A.S. Alexandrov, J.T. Devreese, Advances in Polaron Physics, vol. 159 (Springer, New York, 2010)
L.D. Landau, Electron Motion in Crystal Lattices. Phys. Z. Sowjetunion 3, 664 (1933)
P. Nozières, C.T. De Dominicis, Singularities in the X-Ray Absorption and Emission of Metals. III. One- Body Theory Exact Solution. Phys. Rev. 178, 1097 (1969)
A.G. Basile, V. Elser, Stability of the ferromagnetic state with respect to a single spin flip: Variational calculations for the \(U=\infty\) Hubbard model on the square lattice. Phys. Rev. B. 41, 4842(R) (1990)
G.-M. Zhang, H. Hu, L. Yu, Marginal Fermi Liquid Resonance Induced by a Quantum Magnetic Impurity in d-Wave Superconductors. Phys. Rev. Lett. 86, 704 (2001)
F. Chevy, Universal phase diagram of a strongly interacting Fermi gas with unbalanced spin populations. Phys. Rev. A. 74, 063628 (2006)
A. Schirotzek, C.-H. Wu, A. Sommer, M.W. Zwierlein, Observation of Fermi Polarons in a Tunable Fermi Liquid of Ultracold Atoms. Phys. Rev. Lett. 102, 230402 (2009)
M. Sidler, P. Back, O. Cotlet, A. Srivastava, T. Fink, M. Kroner, E. Demler, A. Imamoglu, Fermi polaron-polaritons in chargetunable atomically thin semiconductors. Nat. Phys. 13, 255 (2017)
Y. Cao, J. Zhou, Fermi polarons in a driven-dissipative background medium. Sci. China Phys. Mech. Astron. 65, 110312 (2022)
H. Hu, J. Wang, R. Lalor, X.-J. Liu, Two-dimensional coherent spectroscopy of trion-polaritons and exciton-polaritons in atomically thin transition metal dichalcogenides. AAPPS Bull. 33, 12 (2023)
Y. Zhang, W. Ong, I. Arakelyan, J.E. Thomas, Polaron-to-Polaron Transitions in the Radio-Frequency Spectrum of a Quasi-Two-Dimensional Fermi Gas. Phys. Rev. Lett. 108, 235302 (2012)
C. Kohstall, M. Zaccanti, M. Jag, A. Trenkwalder, P. Massignan, G.M. Bruun, F. Schreck, R. Grimm, Metastability and coherence of repulsive polarons in a strongly interacting Fermi mixture. Nature (London) 485, 615 (2012)
M. Koschorreck, D. Pertot, E. Vogt, B. Fröhlich, M. Feld, M. Köhl, Attractive and repulsive Fermi polarons in two dimensions. Nature (London) 485, 619 (2012)
P. Massignan, M. Zaccanti, G.M. Bruun, Polarons, dressed molecules and itinerant ferromagnetism in ultracold Fermi gases. Rep. Prog. Phys. 77, 034401 (2014)
F. Scazza, G. Valtolina, P. Massignan, A. Recati, A. Amico, A. Burchianti, C. Fort, M. Inguscio, M. Zaccanti, G. Roati, Repulsive Fermi Polarons in a Resonant Mixture of Ultracold \(^{6}\)Li Atoms. Phys. Rev. Lett. 118, 083602 (2017)
R. Schmidt, M. Knap, D.A. Ivanov, J.-S. You, M. Cetina, E. Demler, Universal many-body response of heavy impurities coupled to a Fermi sea: a review of recent progress. Rep. Prog. Phys. 81, 024401 (2018)
J. Wang, Functional determinant approach investigations of heavy impurity physics. AAPPS Bull. 33, 20 (2023)
C. Chin, R. Grimm, P. Julienne, E. Tiesinga, Feshbach resonances in ultracold gases. Rev. Mod. Phys. 82, 1225 (2010)
I. Bloch, J. Dalibard, W. Zwerger, Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885 (2008)
H. Hu, X.-C. Yao, X.-J. Liu, Second sound with ultracold atoms: a brief review. AAPPS Bull. 32, 26 (2022)
O. Goulko, A.S. Mishchenko, N. Prokof’ev, B. Svistunov, Dark continuum in the spectral function of the resonant Fermi polaron. Phys. Rev. A 94, 051605(R) (2016)
J. Wang, X.-J. Liu, H. Hu, Exact Quasiparticle Properties of a Heavy Polaron in BCS Fermi Superfluids. Phys. Rev. Lett. 128, 175301 (2022)
J. Wang, X.-J. Liu, H. Hu, Heavy polarons in ultracold atomic Fermi superfluids at the BEC-BCS crossover: Formalism and applications. Phys. Rev. A 105, 043320 (2022)
X. Cui, H. Zhai, Stability of a fully magnetized ferromagnetic state in repulsively interacting ultracold Fermi gases. Phys. Rev. A. 81, 041602(R) (2010)
P. Massignan, G.M. Bruun, Repulsive polarons and itinerant ferromagnetism in strongly polarized Fermi gases. Eur. Phys. J. D 65, 83 (2011)
H. Hu, B.C. Mulkerin, L. He, J. Wang, X.-J. Liu, Quantum fluctuations of a resonantly interacting p-wave Fermi superfluid in two dimensions. Phys. Rev. A 98, 063605 (2018)
H. Hu, X.-J. Liu, Resonantly interacting p-wave Fermi superfluid in two dimensions: Tan’s contact and the breathing mode. Phys. Rev. A 100, 023611 (2019)
R. Combescot, A. Recati, C. Lobo, F. Chevy, Normal State of Highly Polarized Fermi Gases: Simple Many-Body Approaches. Phys. Rev. Lett. 98, 180402 (2007)
H. Hu, B.C. Mulkerin, J. Wang, X.-J. Liu, Attractive Fermi polarons at nonzero temperatures with a finite impurity concentration. Phys. Rev. A 98, 013626 (2018)
H. Tajima, S. Uchino, Thermal crossover, transition, and coexistence in Fermi polaronic spectroscopies. Phys. Rev. A. 99, 063606 (2019)
H. Hu, X.-J. Liu, Fermi polarons at finite temperature: Spectral function and rf spectroscopy. Phys. Rev. A 105, 043303 (2022)
J. Levinsen, P. Massignan, F. Chevy, C. Lobo, p-Wave Polaron. Phys. Rev. Lett. 109, 075302 (2012)
J. Levinsen, N.R. Cooper, V. Gurarie, Stability of fermionic gases close to a p-wave Feshbach resonance. Phys. Rev. A 78, 063616 (2008)
C. Luciuk, S. Trotzky, S. Smale, Z. Yu, S. Zhang, J.H. Thywissen, Evidence for universal relations describing a gas with p-wave interactions. Nat. Phys. 12, 599 (2016)
J. Yoshida, T. Saito, M. Waseem, K. Hattori, T. Mukaiyama, Scaling Law for Three-Body Collisions of Identical Fermions with p-Wave Interactions. Phys. Rev. Lett. 120, 133401 (2018)
S.S. Botelho, C.A.R. Sa de Melo, Quantum Phase Transition in the BCS-to-BEC Evolution of p-wave Fermi Gases. J. Low Temp. Phys. 140, 409 (2005)
M. Jag, M. Zaccanti, M. Cetina, R.S. Lous, F. Schreck, R. Grimm, D.S. Petrov, J. Levinsen, Observation of a Strong Atom-Dimer Attraction in a Mass-Imbalanced Fermi-Fermi Mixture. Phys. Rev. Lett. 112, 075302 (2014)
Acknowledgements
The present work is dedicated to the memory of Professor Lee Chang, whose contributions to physical science and education were longstanding and far-reaching. He enthusiastically carried out the research on ultracold atomic physics in Tsinghua University twenty-five years ago and guided the authors (HH and XJL) into this fantastic field.
Funding
This research was supported by the Australian Research Council’s (ARC) Discovery Program, Grants No. FT230100229 (J.W.).
Author information
Authors and Affiliations
Contributions
All the authors equally contributed to all aspects of the manuscript. All the authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: the n-dependence of the separable interaction form
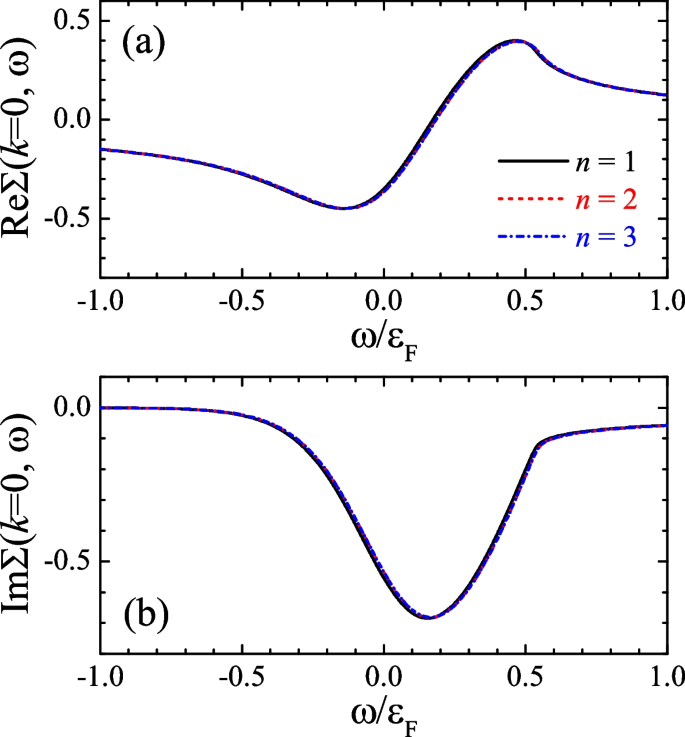
Throughout the work, we have taken \(n=1\) in our separable interaction form \(V_{kk'}=\) \(\lambda \Gamma (k)\Gamma (k')\), with a p-wave form factor \(\Gamma (k)=(k/k_{F})[1+(k/k_{0})^{2n}]^{3/2}\). After the renormalization, physical results (at low energy) should only depend on the scattering area \(1/(k_{F}^{2}a_{p})\) and interaction range \(k_{F}R_{p}\), independent on the choice of the value of n. In Fig. 7, as an example, we explicitly examine this independence for the impurity self-energy in the unitary limit \(1/(k_{F}^{2}a_{p})=0\). We find negligible differences when we change the value of n from 1 to 3, as anticipated.
Appendix 2: the numerical calculation of \(T_{2}^{-1}(\textbf{q},\omega )\)
In numerical calculations, it is convenient to take the natural units, where \(m=\hbar =k_{B}=1\). In other words, we set the units of energy and momentum as \(\varepsilon _{F}\) and \(k_{F}\), respectively. The inverse of the many-body T-matrix then takes the form,
where we have defined an angle-integrated function,
The integral Eq. (19) is well defined if \(y\equiv (\omega +\mu )/2-q^{2}/4<0.\) In this case, we find that,
Otherwise (\(y\ge 0\)), we may use the identity
to recast the real and imaginary parts of \(T_{2}^{-1}(q,\omega )\) into the forms,
Here, by taking the Cauchy principle value, we have defined two integrals,
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, H., Wang, J. & Liu, XJ. Thermally stable p-wave repulsive Fermi polaron without a two-body bound state. AAPPS Bull. 33, 27 (2023). https://doi.org/10.1007/s43673-023-00100-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43673-023-00100-8