Uniform and non-uniform sampling of bandlimited functions at minimal density with a few additional samples

Abstract

A family of sampling theorems for the reconstruction of bandlimited functions from their samples is presented. Taking one or more additional samples is shown to yield more rapidly convergent series with lower truncation errors, as well as to facilitate the reconstruction of bandlimited functions with polynomial growth on the real line. The theorems apply to both uniform sampling and a large class of non-uniform sampling sets, i.e., complete interpolating sequences for the Paley–Wiener space. A number of examples and numerical illustrations accompany the general theory. These include uniform sampling, uniform sampling with finitely many points moved, periodic non-uniform sampling, and sampling at the zeros of Bessel functions $J_\nu (\pi x)$ for non-integer $v > -1$.

1 Introduction

We consider the reconstruction of functions of at most polynomial growth on the real line whose Fourier transform has compact support, from their samples on certain discrete sets. For functions $f\in L^1({\mathbb {R}})$ the Fourier transform is given by $\hat{f}(\xi ) = \int _{-\infty }^\infty f(x) e^{-ix\xi } dx$. This definition can be extended to larger classes of functions and to distributions (generalized functions), see, e.g., [45]. A $\sigma$-bandlimited function is a function whose (distributional) Fourier transform has support in the interval $[-\sigma , \sigma ]$. A well-known and widely used space of $\sigma$-bandlimited functions is the Paley–Wiener space $\mathcal{P}\mathcal{W}_\sigma ^2$, which contains the functions $f \in L_2({\mathbb {R}})$ that can be represented as

$$\begin{aligned} f(z)=\int _{-\sigma }^{\sigma }g(t)\,e^{izt}\,dt \end{aligned}$$

(1)

for some function $g\in L^{2}[-\sigma ,\sigma ]$. $\mathcal{P}\mathcal{W}_\sigma ^2$ is a Hilbert space when equipped with the usual $L_2$ inner product. In the present work we consider the following spaces of bandlimited functions with at most polynomial growth on the real line.

Definition 1

For $N=0,1,2,\ldots$ let $B_N(\sigma )$ denote the space of $\sigma$-bandlimited functions f such that $\int _{-\infty }^\infty \frac{|f(x)|^2}{(1+|x|)^{2N}}\,dx < \infty$, that is, $f(x)\,(1+|x|)^{-N}$ is square integrable. The space of $\sigma$-bandlimited functions that are bounded on the real line is denoted by $B^\infty (\sigma )$. The spaces $B_N(\sigma )$ are nested, i.e., $\mathcal{P}\mathcal{W}_\sigma ^2= B_0(\sigma ) \subset B^\infty (\sigma ) \subset B_1(\sigma ) \subset B_2(\sigma ) \ldots$.

Without loss of generality, we will set $\sigma = \pi$ throughout most of this paper. We are interested in the reconstruction of bandlimited functions from their samples on a discrete set. A fundamental result in this area is the Whittaker-Kotelnikov-Shannon (WKS) sampling theorem [21, 49, 59], which allows for the reconstruction of a function $f \in \mathcal{P}\mathcal{W}_\pi ^2$ from its sampled values on the integers.

Theorem 1

(WKS Theorem) Let $f \in \mathcal{P}\mathcal{W}_\pi ^2$. Then f can be reconstructed from its samples f(k), $k\in \mathbb {Z}$, by means of the ‘cardinal series’

$$\begin{aligned} f(t)=\sum _{k=-\infty }^{\infty }f(k)\,\frac{\sin \pi \left( t-k\right) }{\pi \left( t-k\right) },\quad t\in \mathbb {R}. \end{aligned}$$

(2)

The series converges absolutely, in the $L^2$-sense, and uniformly on $\mathbb {R}$.

The WKS Theorem, its applications and generalizations have given rise to a rich literature; see, e.g., the introductions and surveys [6, 10, 11, 14, 18, 52], monographs [15, 32, 67], and collections [8, 33, 41].

Our approach to non-uniform sampling is based on Theorem 3 in Sect. 3, which generalizes the WKS theorem to allow for non-uniform sampling sets of minimal density that are complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2=B_0(\pi )$. Sampling bandlimited functions in $B_N(\pi )$ for $N>0$ requires some additional information, which can be obtained in different ways. In the present paper this additional information is provided by samples of f at $M\ge N$ additional points. For $M=N$ such sampling sets are minimal in the sense that upon removal of any point there exists a function in $B_N(\pi )$, not identically zero, that vanishes at all the remaining sampling points. Related results were obtained by Walter [56] and Shin et al. [50]. Our approach builds on ideas in Walter’s work, in particular Lemma 2.1 and Corollary 2.2 in [56]. Shin et al. [50] proved a very general sampling theorem using the contour integral method. The present work differs from [50] by its exploration of achieving faster convergence by choosing $M>N$; by considering a larger class of non-uniform sampling sets; and by deriving the main results with a different method.

An alternative approach obtains the needed information for $f\in B_N(\pi )$ by including N samples of derivatives of f at one or more points. As noted by Butzer, Schmeisser and Stens [6, p. 96], this approach was already present in a classical paper by Valiron [53, p. 204, formula (9)]. The case with one additional sample $f'(0)$ is also known as Valiron-Tschakaloff formula, see, e.g., [6, p. 91], [14, pp. 53–55], [15, p. 60]. A non-uniform Valiron-Tschakaloff formula was derived in [1, Theorem 8]. Furthermore, a family of formulas was obtained with this approach by Hoskins and De Sousa Pinto [16], who generalized results by Pfaffelhuber [40, Theorem 2] and Lee [24, Theorem 1]. Corollary 3.3 in Walter [57] falls in this category as well.

Other approaches involve oversampling, i.e., sampling at a higher rate than $\sigma /\pi$, where $\sigma$ denotes the bandwidth of f. The resulting sampling sets are no longer minimal in the above sense, but allow for the construction of very rapidly converging methods. Zakai [66, Theorem 3] showed that (2) remains valid with uniform convergence on compact subsets of ${\mathbb {C}}$ for functions f in $B_1(\sigma )$ with $\sigma < \pi$. The method of multipliers also restricts the bandwidth $\sigma$ of f to be less than $\pi$. One can then replace the ‘cardinal sine’ $\text{ sinc }(t-k) = \frac{\sin \pi \left( t-k\right) }{\pi \left( t-k\right) }$ in (2) by the ‘damped cardinal sine’ $\psi (t-k)\,\text{ sinc }(t-k)$, where $\psi$ is a more rapidly decaying function with bandwidth $\delta < \pi - \sigma$ that satisfies $\psi (0)=1$, e.g., $\psi (t) = \left( \text{ sinc }\left( \frac{\delta t}{\pi m}\right) \right) ^m$ [12, p. 180]. For applications to uniform sampling see, e.g., Piranashvili [42], Campbell [7, Theorem 2], Lee [24, Theorem 3], and Madych [31]. Choosing a Gaussian function for $\psi$ incurs an aliasing error but nevertheless leads to highly accurate approximate formulas with exponential rates of convergence; see, e.g., Qian [43] and Schmeisser and Stenger [46]. Voss [55] applied the multiplier method to a large class of non-uniform sampling sets. Walter [56, 57] used oversampling and $(C,\alpha )$ Cesaro summability instead of pointwise convergence, and also considered convergence in the sense of generalized functions [57].

In the following, we will first present the results together with the information necessary to apply them, and later on follow up with proofs and further theory. Accordingly, the next two sections contain the results for uniform sampling and non-uniform sampling, respectively, and provide a number of examples and numerical experiments, as well as some useful tools for constructing additional examples for non-uniform sampling. Formal definitions, proofs, and some further theoretical considerations are then given in Sect. 4, and conclusions are offered in the final section.

2 Uniform sampling

The following theorem generalizes Theorem 1 for functions $f\in B_N(\pi )$.

Theorem 2

(Uniform sampling) Let $f\in B_N(\pi )$, $M\ge N$, and $\mu _1,\ldots ,\mu _M \in {\mathbb {C}}$ be distinct non-integer points. Let $P_\mu (z) = \prod _{l=1}^M (z-\mu _l)$. Then

$$\begin{aligned} f(z)= & {} F(z) + P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{f(k)}{P_\mu (k)} \,\text{ sinc }(z-k)\nonumber \\ \text{ with }{} & {} F(z)\; =\; \sum _{m=1}^M f(\mu _m)\, \frac{\sin (\pi z)}{\sin (\pi \mu _m)} \, \prod _{j=1, \; j\ne m}^{M} \frac{z-\mu _j}{\mu _m-\mu _j}. \end{aligned}$$

(3)

The convergence is uniform on compact subsets of ${\mathbb {C}}$.

For $M=0$, i.e., when no additional samples are taken, one has $P_\mu (z) = 1$, $F(z) = 0$, and (3) reduces to the cardinal series (2). For $M = 1$ one has $P_\mu (z) = z-\mu _1$ with $\mu _1\not \in {\mathbb {Z}}$. Then the expansion (3) reads

$$\begin{aligned} f(z) = f(\mu _1) \,\frac{\sin (\pi z)}{\sin (\pi \mu _1)} \;+\; (z-\mu _1)\, \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{f(k)}{k-\mu _1} \,\text{ sinc }(z-k), \end{aligned}$$

and is valid for $f\in B_1(\pi )$. The product $\prod _{j=1, \; j\ne m}^{M} \frac{z-\mu _j}{\mu _m-\mu _j}$ occurring in (3) can alternatively be written as

$$\begin{aligned} \prod _{j=1, \; j\ne m}^{M} \frac{z-\mu _j}{\mu _m-\mu _j} \;=\; \frac{P_\mu (z)}{P_\mu '(\mu _m) \, (z-\mu _m)}. \end{aligned}$$

(4)

Theorem 2 is a special case of Theorem 4 below, which will be proved in Sect. 4. It sharpens a result obtained by Shin et al. [50]. In order to reconstruct a function in $B_N(\pi )$, Theorem 2 requires a minimum of N additional samples, compared to the $N+1$ additional samples required in [50, Example 3.7]. The sampling series (3) also refines Corollary 2.2 in Walter [56] by removing the interpolating polynomial from the sampling series; cf. Eq. (50) in Sect. 4 below. This refinement enables the improved rates of convergence for larger values of M.

We proceed with a numerical example. The general set-up for our numerical examples is as follows. In practice the infinite series in the reconstruction formula (3) has to be truncated to a finite summation. We will explore how the error incurred by this truncation is reduced by taking additional samples, i.e., by letting $M > N$. In particular, we consider the situation where, for x in an interval $[-a,a]$, f(x) is approximated by a function $f_K(x)$, $K \in {\mathbb {N}}$, which is obtained from restricting the summation in the infinite series occurring in (3) to values of k such that $|k|\le K$. That is,

$$\begin{aligned} f_K(z)= & {} F(z) \;+\; P_\mu (z)\,\sum _{k=-K}^K \,\frac{f(k)}{P_\mu (k)} \, \text{ sinc }(z-k). \end{aligned}$$

(5)

Let $E_K$ denote the maximum truncation error for the interval $[-a,a]$:

$$\begin{aligned} E_K = \max _{x\in [-a,a]} |f(x)-f_K(x)|. \end{aligned}$$

(6)

We will explore how rapidly $E_K$ decays as $K\rightarrow \infty$. The numerical computations will be carried out using MATLAB. For the experiments we will use the family of $\pi$-bandlimited functions

$$\begin{aligned} g_\nu (z)= & {} 2^\nu \varGamma (\nu +1) \,\frac{J_\nu (\pi z)}{(\pi z)^\nu }, \quad \nu > -\frac{1}{2}, \end{aligned}$$

(7)

where $J_\nu (z)$ denotes the Bessel function of the first kind with index $\nu$. One has $\max _{x\in {\mathbb {R}}} |g_\nu (x)| =g_\nu (0) = 1$, and $|g_\nu (x)| = O\left( |x|^{-\nu -\frac{1}{2}}\right) \; \text{ as } x \rightarrow \pm \infty$. For $\nu =1/2$ one has $g_{\frac{1}{2}}(x) = \text{ sinc }(x)$. The Fourier transform of $g_\nu$ is given by

$$\begin{aligned} \widehat{g_\nu }(\xi ) \;=\; \left\{ \begin{array}{ll} \frac{2 \, \varGamma (\nu +1)}{\sqrt{\pi }\, \varGamma \left( \nu +\frac{1}{2}\right) }\, \left( 1-\left( \frac{\xi }{\pi }\right) ^2\right) ^{\nu -\frac{1}{2}} &{} \text{ for } |\xi |< \pi \\ 0 &{} \text{ for } |\xi |> \pi . \end{array} \right. \end{aligned}$$

It follows that $g_\nu \in B^\infty (\pi )$ for $\nu > -1/2$; $g_\nu \in \mathcal{P}\mathcal{W}_\pi ^2=B_0(\pi )$ for $\nu > 0$; and $x^n g_\nu (x) \in B_N(\pi )$ for $N > n -\nu$.

Fig. 1

Uniform sampling according to Theorem 2 for $f(x) = g_\nu (x-c)$ with $\nu = 0.1, c = -\sqrt{63}$ and $g_\nu$ as in (7). Plots of $E_K$ given by (6) with $a = 20$ for $K = 10 \cdot 2^m, m=1,\ldots ,12$. Points labeled with ‘x’ correspond to $M=0$, i.e., the WKS Theorem without additional samples. Points labeled with ‘*’ correspond to $M=1$, with one additional sample taken at $\mu _1=10.5$. Points labeled with ‘+’ correspond to $M=2$, with two additional samples taken at $\mu _1=10.5$ and $\mu _2 = -15.3$. In each case $E_K$ decays as $O(K^{-0.6-M})$

For a numerical experiment, consider the function

$$\begin{aligned} f(x) = g_\nu (x-c), \quad \nu = 0.1,\quad c = -\sqrt{63}. \end{aligned}$$

(8)

For $x\rightarrow \pm \infty$ one has $|f(x)| = O(|x|^{-\nu -1/2}) = O(|x|^{-0.6})$. Hence $f \in \mathcal{P}\mathcal{W}_\pi ^2$, the WKS Theorem applies, and no additional sampling points would be required. However, without additional sampling points the convergence of $f_K$ to f is very slow. This is illustrated by the numerical experiment in Fig. 1. Even for $K=40960$ the maximum error $E_K$ in the interval $[-20,20]$ is still greater than $10^{-4}$. Taking just one or two additional samples leads to a dramatic improvement. If Theorem 2 with one additional sample at $\mu _1=10.5$ is used, then $E_K < 10^{-4}$ for $K > 640$. If two additional samples at $\mu _1=10.5$ and $\mu _2 = -15.3$ are used, then $E_K < 10^{-4}$ for $K \ge 64$. In general, if $|f(x)| = O(|x|^\alpha )$ as $x\rightarrow \pm \infty$, the terms in the series $\sum _{k} \frac{f(k)}{P_\mu (k)} \text{ sinc }(z-k)$ in (3) decay as $O(|k|^{\alpha -M-1})$ as $k\rightarrow \pm \infty$. Hence the errors $E_K$ may be expected to decay as $O(K^{\alpha -M})$ as $K\rightarrow \infty$. In the experiments of Fig. 1 we have $\alpha =-0.6$ and in each case the error $E_K$ does indeed decay as $O(K^{-M-0.6})$ as expected.

The experiment above demonstrates that convergence can already be considerably improved by adding just one or two additional sampling points. However, many sampling points outside the interval of interest $[-a,a]$ may still be required for a desired accuracy. For higher accuracy one could increase the number of additional sampling points. Then the question of optimal placement of the additional points arises. We will not investigate this question in detail, but wish to offer the following consideration. The truncation error of the finite sum in (5) is amplified by the factor $P_\mu (z)$. It then seems natural to place the additional points in such a way that $\max _{-a\le x\le a} |P_\mu (x)|$ is as small as possible. This is achieved by choosing the Chebychev nodes $\mu _j = a \cos (\pi (2j-1)/(2M))$, $j=1,\ldots ,M$. In the above example this choice with $M=8$ leads to an error $E_{24} = 4.3\cdot 10^{-5}$ for $a=20$, $K=24$. For the larger interval $[-a,a]=[-100, 100]$, and $M=20$ additional sampling points, one obtains an error of $E_{110}= 2.2\cdot 10^{-7}$ for $K=110$. Hence for larger values of M only a few samples outside the interval of interest may be needed. If K is increased to 140, the error decreases to $E_{140} = 2.5\cdot 10^{-11}$.

3 Non-uniform sampling

For sampling in $\mathcal{P}\mathcal{W}_\pi ^2$ we seek sampling sets $\varLambda =\{\lambda _k, \,k\in {\mathbb {Z}}\}$ that are complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2$ in the following sense (cf. [64, pp. 142-143], [15, Ch. 10]).

Definition 2

A set $\varLambda =\{\lambda _k, \, k\in {\mathbb {Z}}\}$ of real or complex numbers is called a complete interpolating sequence (CIS) for $\mathcal{P}\mathcal{W}_\pi ^2$ if the following two conditions hold.

• 1. For any sequence $\{c_k\}_{ k\in {\mathbb {Z}}}$ such that $\sum _{k\in {\mathbb {Z}}} |c_k|^2 < \infty$ the interpolation problem

  $$\begin{aligned} f(\lambda _k) = c_k, \quad k\in {\mathbb {Z}}, \end{aligned}$$

  has a unique solution $f\in \mathcal{P}\mathcal{W}_\pi ^2$.

• 2. For all $f\in \mathcal{P}\mathcal{W}_\pi ^2$ one has

  $$\begin{aligned} A \parallel f\parallel ^2_{L^2} \;\, \le \; \sum _{k\in {\mathbb {Z}}} |f(\lambda _k)|^2 \;\le \;B \parallel f\parallel ^2_{L^2} \end{aligned}$$

  with constants $0< A \le B < \infty$ that are independent of f.

Equivalently, $\varLambda$ is a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$ if and only if the set of functions $\{e^{i\lambda _k t}, \,k\in {\mathbb {Z}}\}$ is a Riesz basis for $L^2[-\pi ,\pi ]$ [64, p. 143, Theorem 9]. Unless otherwise specified the $\lambda _k$ are enumerated with non-decreasing real parts, i.e., $\text {Re } \lambda _k \le \text {Re } \lambda _{k+1}$, and such that $\text { Re }\lambda _k \le 0$ for $k\le 0$, and $\text { Re }\lambda _k \ge 0$ for $k\ge 0$. If $0 \in \varLambda$, then $\lambda _0 = 0$.

A complete interpolating sequence is both a set of interpolation and a set of stable sampling in the sense of Landau [22]. All complete interpolating sequences are uniformly discrete sets, i.e., $\inf _{n\ne m} |\lambda _m-\lambda _n| > 0$. Two basic examples for complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2$ are given by the sampling set for uniform sampling $\varLambda = {\mathbb {Z}}$, and by non-uniform but periodic sets of the form

$$\begin{aligned} \varLambda = \bigcup _{j=1}^{J} (J{\mathbb {Z}}+ x_j) \end{aligned}$$

(9)

with distinct shifts $x_j \in [0,J)$. A ‘generating function’ associated with a CIS $\varLambda = \{\lambda _k, \,k\in {\mathbb {Z}}\}$ is a function $\varphi \in B_1(\pi )$ given by the canonical product

$$\begin{aligned} \varphi \left( z\right) = c\, (z-\lambda _0) \prod _{k=1}^\infty \left( 1-\frac{z}{\lambda _{k}}\right) \, \left( 1-\frac{z}{\lambda _{-k}}\right) \end{aligned}$$

(10)

where c is a non-zero constant that can be chosen for convenience. A generating function exists for every CIS and can in many cases be explicitly evaluated [15, p. 108], [60, p. 238]. For example, if $\varLambda ={\mathbb {Z}}$, then a generating function is given by $\varphi (z) = \sin \left( \pi z\right)$. The non-uniform sampling theorem for $\mathcal{P}\mathcal{W}_\pi ^2$ now reads as follows.

Theorem 3

Let $f\in \mathcal{P}\mathcal{W}_\pi ^2$, and $\varLambda = \left\{ \lambda _{k}, \, k\in \mathbb {Z}\right\}$ be a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function $\varphi$ as in (10). For $k\in {\mathbb {Z}}$ define

$$\begin{aligned} \varphi _k(z) = \frac{\varphi (z) }{\varphi '(\lambda _k)\,(z-\lambda _k)} \end{aligned}$$

(11)

for $z\ne \lambda _k$, and $\varphi _k(\lambda _k) = 1$. Then the set $\{\varphi _k, \,k\in {\mathbb {Z}}\}$ is a Riesz basis for $\mathcal{P}\mathcal{W}_\pi ^2$, and

$$\begin{aligned} f(z) = \sum _{k\in \mathbb {Z}} f(\lambda _k)\, \varphi _k(z). \end{aligned}$$

(12)

The series converges absolutely, in $L^2({\mathbb {R}})$, and uniformly on any horizontal strip in ${\mathbb C}$ of finite width.

The expansion (12) is a Lagrange-type interpolation formula (cf. [68]) and simplifies for $\varLambda = {\mathbb {Z}}$ to give the cardinal series (2). Versions of Theorem 3 that apply to smaller classes of sampling sets are well known. Most widely known are complete interpolating sequences $\varLambda \subset {\mathbb {R}}$ that are perturbations of the integers in the sense that $\sup _k |\lambda _k-k| < 1/4$ [19]. For this case the expansion (12) follows from seminal work by Paley and Wiener [38, p. 115, Theorem XXXIX], and Levinson [27, p. 48], and is called the Paley–Wiener–Levinson Theorem by some authors; see, e.g., Zayed [67, pp. 41-43], Yao and Thomas [61], Higgins [13, 15, pp. 107–108], and Pak and Shin [37, Theorem 3.4]. García [9, 10] gives a different proof based on an infinite product expansion for bandlimited functions by Titchmarsh [51, Theorem VI]. Further classes of complete interpolating sequences for which (12) is known to hold include the zero sets of sine-type functions [6, p. 93–94], [25, p. 165], [34, 64, p. 144]; perturbations of zero sets of sine-type functions [2]; and when $\varLambda$ is both a CIS and a symmetric real sequence [64, pp. 124–126]. While the content of Theorem 3 in its full generality is also not unknown, cf. [5, Theorem 2], [29, p. 254], [30, p. 367], [35, p. 5497], we have not been able to find a reference with a complete proof. We therefore provide a proof in Sect. 4.

The next theorem is the main theoretical result of this paper. It extends Theorem 3 to functions in $B_N(\pi )$ and will be proved in Sect. 4.

Theorem 4

Let $f\in B_N(\pi )$, and $\varLambda = \left\{ \lambda _{k}, \,k\in \mathbb {Z}\right\}$ a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function $\varphi$ as in (10), and $\varphi _k(z) = \frac{\varphi (z)}{\varphi '(\lambda _k)\,(z-\lambda _k)}$, $k\in {\mathbb {Z}}$. For $M \ge N$ let $\mu _1,\ldots , \mu _M \in {\mathbb {C}}$ be distinct points not contained in $\varLambda$, and let $P_\mu$ denote the polynomial $P_\mu (z) = \prod _{l=1}^M (z-\mu _l)$. Then,

$$\begin{aligned} f(z) = \sum _{m=1}^M f(\mu _m) \frac{ \varphi (z)}{ \varphi (\mu _m)}\frac{P_\mu (z)}{ P_\mu ^{\prime }(\mu _m)(z-\mu _m)} \;+\; P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{f(\lambda _k)}{P_\mu (\lambda _k)} \varphi _k(z). \end{aligned}$$

(13)

The convergence is uniform on compact subsets of $\mathbb {C}$.

If $f \in \mathcal{P}\mathcal{W}_\pi ^2= B_0(\pi )$, then no additional samples are required, and for the choice $M=0$ one has $P_\mu (z) = 1$ and Eq. (13) reduces to (12). Shin, Chung and Kim [50, Example 3.12] give the expansion (13) for $f\in B^\infty (\pi )$, sampling sets $\varLambda \subset {\mathbb {R}}$ that satisfy Kadec’s 1/4-Theorem, and $M=3$. Since $B^\infty (\pi ) \subset B_1(\pi )$, Theorem 4 shows that $M\ge 1$ is sufficient in this case.

Application of Theorems 3 and 4 in concrete cases may require verification that a sampling set $\varLambda$ is a CIS, as well as the evaluation of the associated generating function. Necessary and sufficient conditions characterizing complete interpolating sequences are established in [17, p. 239], [30, 39], and are discussed in the next section. However, these conditions may not always be convenient to verify. Therefore, it is useful to have a sufficiently large class of established examples as well as some tools to find new complete interpolating sequences from known ones. For example, for $c\in {\mathbb {C}}$ and $\varLambda$ a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function $\varphi (z)$, the translated set $\tilde{\varLambda } = \varLambda + c$ is also a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$, and its generating function $\tilde{\varphi }(z)$ is a constant multiple of $\varphi (z-c)$. The following very useful criterion is due to Pak and Shin [37, Lemma 3.1]. It generalizes a result obtained by Yen [62, Theorem I] for the case $\varLambda = {\mathbb {Z}}$.

Lemma 1

Moving finitely many points of a CIS $\varLambda$ for $\mathcal{P}\mathcal{W}_\pi ^2$ to distinct new locations in ${\mathbb {C}}\backslash \varLambda$ will yield another CIS for $\mathcal{P}\mathcal{W}_\pi ^2$.

Young [63, p. 106], [64, p. 164] showed that the points of a real-valued CIS can be vertically displaced to obtain a complex-valued CIS:

Lemma 2

Let $\varLambda = \{\lambda _k, \,k\in {\mathbb {Z}}\} \subset {\mathbb {C}}$ satisfy $\sup _k |\text { Im }\lambda _k| < \infty$. If $\{\text { Re }\lambda _k, \, k\in {\mathbb {Z}}\}$ is a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$, then so is $\varLambda$.

A suitable class of examples is furnished by the zero sets of so-called $\pi$-sine type functions, and certain perturbations of such sets, which are known to give complete interpolating sequences [3, 20]. The fundamental example of a $\pi$-sine type function is $\varphi (z) = \sin (\pi z)$ whose zero set is the integers, i.e., the sampling set for uniform sampling. The function $\varphi (z) = \cos (\pi z)$ is a $\pi$-sine type function as well. Periodic sets of the form (9) with distinct shifts $x_j \in [0,J)$ are zero sets of the $\pi$-sine type functions $\varphi (z) = \prod _{j=1}^J \sin \left( \frac{\pi }{J} (z-x_j)\right)$ [44, p. 295]. A $\pi$-sine type function is always a generating function for the CIS given by the set $\varLambda$ of its zeros [28, Theorem 1.4]. The formal definition of a $\pi$-sine type function is given in the next section. In this section only the three examples above will be required.

We consider two kinds of perturbations of the zero set of a $\pi$-sine type function that lead to new complete interpolating sequences. The first criterion follows immediately from a theorem by Levin and Ostrovskii [26, p. 85].

Lemma 3

Let the set $\varLambda = \{\lambda _k,\, k\in {\mathbb {Z}}\} \subset {\mathbb {C}}$ be uniformly discrete and satisfy

$$\begin{aligned} \sum _{k\in {\mathbb {Z}}} |\lambda _k-\lambda ^{*}_k|^p< \infty \;\; \text{ for } \text{ some } 1<p<\infty , \end{aligned}$$

(14)

where $\{\lambda ^{*}_k, \, k\in {\mathbb {Z}}\}$ is the zero set of some $\pi$-sine type function. Then the canonical product (10) corresponding to $\varLambda$ is a $\pi$-sine type function, and consequently $\varLambda$ is a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$.

In particular, moving finitely many zeros of a $\pi$-sine type function to new locations without creating any multiple zeros yields another $\pi$-sine type function. We also wish to consider perturbations where $\lambda _k-\lambda ^{*}_k$ does not necessarily converge to zero as $k \rightarrow \pm \infty$. For example, a frequently encountered class of non-uniform sampling sets are sets $\varLambda = \{ \lambda _k, \, k\in {\mathbb {Z}}\} \subset {\mathbb {R}}$ that satisfy $\sup _k |\lambda _k - k| \le d < \infty$. We will call such a sampling set $\varLambda$ a d-perturbation of the integers ${\mathbb {Z}}$. Kadec’s $\frac{1}{4}$-Theorem [19, 64, p. 36] states that for $0\le d < 1/4$ one obtains complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2$. The next definition generalizes this notion to perturbations of zero sets of $\pi$-sine type functions.

Definition 3

Let $\varLambda ^{*}= \{\lambda ^{*}_k,\, k\in {\mathbb {Z}}\}\subset {\mathbb {C}}$ denote the zero set of a $\pi$-sine type function, ordered such that $\text {Re } \lambda ^{*}_{k+1} \ge \text {Re } \lambda ^{*}_k$ for all $k\in {\mathbb {Z}}$. A set $\varLambda = \{\lambda ^{*}_k + \delta _k,\,k\in {\mathbb {Z}}\} \subset {\mathbb {C}}$ is called a d-perturbation of $\varLambda ^{*}$ for some $d\ge 0$, if $\varLambda$ is uniformly discrete, $\sup _{k\in \mathbb {Z}}\left| \text {Im } \delta _k \right| < \infty$, and

$$\begin{aligned} \left| \text {Re } \delta _k \right|\le & {} d\, \rho _k \; \text{ for } \text{ all } k\in {\mathbb {Z}}, \end{aligned}$$

(15)

where $\rho _k = \inf _{l\ne k} |\text { Re }(\lambda ^{*}_l-\lambda ^{*}_k)| = \min \{ \text { Re }(\lambda ^{*}_{k+1}-\lambda ^{*}_{k}),\, \text { Re }(\lambda ^{*}_{k}-\lambda ^{*}_{k-1})\}$.

The family of all d-perturbations of $\varLambda ^{*}$ is denoted by $\mathcal {S}_d(\varLambda ^{*})$. Finally, let $\mathcal {S}_d$ denote the family of all sets $\varLambda$ that are d-perturbations of some zero set of a $\pi$-sine type function.

Katsnel’son [20] established the following criterion:

Lemma 4

Let $\varLambda \in S_d$ with $0\le d < \frac{1}{4}$. Then $\varLambda$ is a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$.

An even stronger result where the condition (15) can be replaced by an averaged analogue has been obtained by Avdonin; see [3, Theorem C].

In the remainder of this section we provide various examples and numerical experiments. We begin with an explicit expansion for the case of uniform sampling with one point moved, followed by a numerical example for uniform sampling with 2001 points moved. We then consider periodic sampling, and conclude with sampling at the zero crossings of Bessel functions $J_\nu (\pi z)$, for non-integer index $\nu > -1$. The general set-up for the numerical experiments is the same as described in Sect. 2 above.

3.1 Moving finitely many sampling points to distinct new locations

According to Lemma 1, one can move finitely many points of a complete interpolating sequence to new distinct locations and obtain another CIS. Therefore, if only finitely many points are sampled, this opens up the attractive possibility to choose all points where samples are taken entirely freely. However, for certain choices, such as when there are larger gaps in the sampling sets, the resulting function $\varphi (x)$ in (16) may exhibit very large oscillations that may impact numerical stability. In the following we explore the case of uniform sampling with a single point moved and conduct a numerical experiment for uniform sampling with a large number of points moved.

Our theoretical framework does accommodate the replacement of finitely many sampling points as follows. Let $\varLambda ^{*}= \{\lambda ^{*}_k, \,k\in {\mathbb {Z}}\}$ be a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$ with associated generating function $\varphi ^{*}(z)$. Assume that the points $\lambda ^{*}_{k_1} \ldots , \lambda ^{*}_{k_J}$ are replaced by distinct points $\tilde{\lambda }_{1}, \ldots , \tilde{\lambda }_{J}$ that do not lie in $\varLambda ^{*}$. The resulting sampling set $\varLambda = \{\lambda _k, \, k\in {\mathbb {Z}}\}$ is again a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$ and satisfies $\lambda _{k_j} = \tilde{\lambda }_j$, $j=1,\ldots ,J$, and $\lambda _k = \lambda ^{*}_k$ for $k\in {\mathbb {Z}}\backslash \{k_1,\ldots ,k_J\}$. A generating function $\varphi (z)$ is then given by

$$\begin{aligned} \varphi (z) = \varphi ^{*}(z) \, \prod _{j=1}^{J} \frac{z-\tilde{\lambda }_{j}}{z-\lambda ^{*}_{k_j}}. \end{aligned}$$

(16)

We first consider uniform sampling with $\varLambda ^{*}= {\mathbb {Z}}$, with a single point $\lambda ^{*}_{k_1} = l \in {\mathbb {Z}}$ changed to a new point $\tilde{\lambda }_1 = \lambda \not \in {\mathbb {Z}}$. In this case $\varphi ^{*}(z) = \sin (\pi z)$, and

$$\begin{aligned} \varphi (z)= & {} \sin (\pi z) \,\frac{z-\lambda }{z-l} \;=\; (-1)^{l}\, \pi \,(z-\lambda ) \,\text{ sinc }(z-l). \end{aligned}$$

(17)

Observing that

$$\begin{aligned} \frac{\varphi (z)}{(z-\lambda )\varphi '(\lambda )}= & {} \frac{\text{ sinc }(z-l)}{\text{ sinc }(\lambda -l)},\\ \frac{\varphi (z)}{(z-k) \varphi '(k)}= & {} \frac{k-l}{k-\lambda }\,\frac{z-\lambda }{z-l} \,\text{ sinc }(z-k), \end{aligned}$$

applying Theorem 4, and using (4) yieds

Corollary 1

(Uniform sampling with one point moved) Let $f\in B_N(\pi )$, $M\ge N$, $l\in {\mathbb {Z}}$, $\lambda \not \in {\mathbb {Z}}$, and $\varLambda = \{\lambda \}\cup ({\mathbb {Z}}\backslash \{l\})$. Let $\mu _1,\ldots ,\mu _M \in {\mathbb {C}}\backslash \varLambda$ be distinct points and $P_\mu (z) = \prod _{m=1}^M (z-\mu _m)$. Then,

$$\begin{aligned} f(z)= & {} \sum _{m=1}^M f(\mu _m) \frac{(z-\lambda )\; \text{ sinc } (z-l) }{(\mu _m-\lambda )\; \text{ sinc } (\mu _m-l)} \prod _{j=1, j\ne m}^M \frac{z-\mu _j}{\mu _m-\mu _j} \nonumber \\{} & {} +\; \;P_\mu (z) \left( \frac{f(\lambda )}{P_\mu (\lambda )}\,\frac{\text{ sinc } (z-l)}{\text{ sinc } (\lambda -l)}\;\; + \;\; \sum _{k\in {\mathbb {Z}}\backslash \{l\}} \frac{f(k)}{P_\mu (k)} \,\frac{k-l}{k-\lambda }\,\frac{z-\lambda }{z-l} \,\text{ sinc } (z-k) \right) .\nonumber \\ \end{aligned}$$

(18)

The convergence is uniform on compact subsets of ${\mathbb {C}}$.

For a numerical experiment we consider the function $f(x) = g_\nu (x-c), \quad \nu = -0.4,\quad c = -\sqrt{63}$, with $g_\nu$ given by (7). This function lies in $B^\infty (\pi )$ but is not square integrable, so $M\ge 1$ is required. The sampling point $k_1 = -8$, which is closest to the maximum of f, is replaced by the point $\lambda = -6.5$. This creates a gap of width 2 in the sampling set. The maximum of f lies within this gap. The function f decays as $O(|x|^{-0.1})$ for $x\rightarrow \pm \infty$. The results of the experiment with $M=1,2,3,4$, are displayed in Fig. 2. In each case the error $E_K$ decays at the expected asymptotic rate of $O(K^{-0.1-M})$. For $M=4$ and large K the error $E_K$ bottoms out at $5\cdot 10^{-13}$ due to round-off.

Fig. 2

Uniform sampling with one point moved for $f(x) = g_\nu (x-c), \nu = -0.4, c = -\sqrt{63}$, and $g_\nu$ as in (7). The function f decays as $O(|x|^{-0.1})$ for $|x|\rightarrow \infty$. The sampling point $l=-8$ was moved to $\lambda = -6.5$. Plots of $E_K$ given by (6) with $a = 20$ for $K = 10 \cdot 2^m, m=1,\ldots ,12$. Additional sampling points are $\mu _1 = 10.5$, $\mu _2 = -15.3$, $\mu _3 = -17.8$, and $\mu _4= 21.4.$ Points labeled with ‘$\cdot$’ correspond to $M=1$, with $\mu _1$ as the only additional sampling point. Points labeled with ‘x’ correspond to $M=2$, with $\mu _1$ and $\mu _2$ being used. Points labeled with ‘*’ correspond to $M=3$, with $\mu _1,\mu _2$, and $\mu _3$. Points labeled with ‘+’ correspond to $M=4$ with all four additional points used. In each case the maximum error $E_K$ decays asymptotically as $O(K^{1.1-M})$

As mentioned above, moving finitely sampling points to arbitrary new locations, while yielding a new CIS, may induce numerical instability if there are large gaps in the sampling set that cause the generating function to oscillate with very large amplitudes. The following experiment indicates that such drastic and undesirable effects do not appear to occur when the new sampling set is in the class $\mathcal {S}_d({\mathbb {Z}})$ for d not overly large. We generated a sampling set $\varLambda \in \mathcal {S}_d({\mathbb {Z}})$, $d=0.245$, such that $\lambda _k$ is randomly chosen from the interval $[k-0.245, k+0.245]$ for $|k|\le 1000$, and $\lambda _k = k$ for $|k|> 1000$. That is, in (16) we have $\varphi ^{*}(z) = \sin (\pi z)$, and randomly chosen new sampling points $\tilde{\lambda }_{j}$ such that $|k_j-\tilde{\lambda }_{j}|\le 0.245$, $k_j = j-1001$, $j = 1,\ldots ,J=2001$. We sample the function

$$\begin{aligned} f(x) = (x/c)^2 g_\nu (x-c), \quad \nu = +0.4, \quad c = -\sqrt{63}. \end{aligned}$$

(19)

One has $|f(x)| = O(|x|^{\alpha })$ with $\alpha = 1.1$ as $x\rightarrow \pm \infty$, so $f\in B_2(\pi )$. The results are reported in Fig. 3. The function $\varphi (x)$ does not exhibit large oscillations. The asymptotic decay of the error $E_K$ is of order $O(K^{1.1-M})$ as expected.

Fig. 3

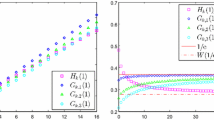
Uniform sampling with 2001 points moved. Upper left: Graph of $f(x) = (x/c)^2 g_\nu (x-c), \nu = 0.4, c = -\sqrt{63}$ for the interval $x\in [-20,20]$. The function f satisfies $|f(x)| = O(|x|^{1.1})$ for $x \rightarrow \pm \infty$. Upper right: Graph of $\varphi (x)$ for the sampling set with $\lambda _k$ randomly chosen from the interval $[k-0.245, k+0.245]$ for $|k|\le 1000$, and $\lambda _k = k$ for $|k|> 1000$. Lower left: Maximum error $E_K$ for $a=20$. The minimum number of additional sampling points is $N = 2$. The additional sampling points are $\mu _1 = 10.5$, $\mu _2 = -15.3$, $\mu _3 = -17.8$, and $\mu _4= 21.4.$. Points labeled with ‘x’ correspond to $M=2$, with $\mu _1$ and $\mu _2$ being used. Points labeled with ‘*’ correspond to $M=3$, with $\mu _1,\mu _2$, and $\mu _3$. Points labeled with ‘+’ correspond to $M=4$ with all four additional points used. In each case the maximum error $E_K$ decays asymptotically as $O(K^{1.1-M})$

3.2 Periodic non-uniform sampling

We next consider periodic sampling, where the sampling set is a union of shifted copies of $J {\mathbb {Z}}$, $J\in {\mathbb {N}}$, i.e.,

$$\begin{aligned} \varLambda= & {} \bigcup _{j=1}^{J} (J{\mathbb {Z}}+ x_j), \quad x_j \in [0,J), \; j=1,\ldots ,J, \quad x_j\ne x_l \text{ for } j\ne l. \end{aligned}$$

(20)

We denote the sampling points by

$$\begin{aligned} \lambda _{j,k} = Jk + x_j, \quad k\in {\mathbb {Z}}, \quad j=1,\ldots ,J. \end{aligned}$$

The sampling set $\varLambda$ is the zero set of the $\pi$-sine type function

$$\begin{aligned} \varphi (z) = \prod _{j=1}^{J} \sin (\pi (z-x_j)/J). \end{aligned}$$

(21)

As already mentioned, a $\pi$-sine type function is a generating function for the set of its zeros. From

$$\begin{aligned} \varphi '(z) = \frac{\pi }{J} \sum _{j=1}^J \cos (\pi (z-x_j)/J) \prod _{n=1, n\ne j}^{J} \sin (\pi (z-x_n)/J) \end{aligned}$$

we obtain

$$\begin{aligned} \varphi '(Jk + x_j) \;=\; \frac{\pi }{J} \cos (\pi k) \prod _{n=1, n\ne j}^{J} \sin (\pi k + \pi (x_j-x_n)/J) \;=\; (-1)^{Jk} C_j, \end{aligned}$$

with

$$\begin{aligned} C_j \;=\; \frac{\pi }{J} \prod _{n=1, n\ne j}^{J} \sin (\pi (x_j-x_n)/J). \end{aligned}$$

(22)

For $f\in \mathcal{P}\mathcal{W}_\pi ^2$ and no oversampling, Theorem 3 now gives the sampling series

$$\begin{aligned} f(z) = \varphi (z) \,\sum _{j=1}^{J} \frac{1}{C_j} \sum _{k\in {\mathbb {Z}}} (-1)^{Jk} \frac{f(Jk+x_j)}{(z-Jk-x_j) }, \end{aligned}$$

(23)

with $\varphi$ and $C_j$ given by (21) and (22), respectively. The expansion (23) was first obtained by Yen [62]. The above derivation based on Theorem 3 is different from, and considerably shorter than, Yen’s original proof. Theorem 4 now yields

Corollary 2

(Periodic sampling) Let $f\in B_N(\pi )$, $\varLambda$ as in (20), $M\ge N$, $\mu _1,\ldots ,\mu _M$ be distinct points in ${\mathbb {C}}\backslash \varLambda$, and $P_\mu (z) = \prod _{m=1}^M (z-\mu _m)$. Then

$$\begin{aligned} f(z)= & {} \sum _{m=1}^M f(\mu _m) \frac{\varphi (z)}{\varphi (\mu _m)} \frac{P_\mu (z)}{P_\mu ^{\prime }(\mu _m) (z-\mu _m) } \nonumber \\{} & {} +\;\; P_\mu (z) \, \sum _{j=1}^{J}\frac{1}{C_j}\, \sum _{k\in {\mathbb {Z}}} \frac{f(Jk+x_j)}{ P_\mu (Jk+x_j) }\frac{(-1)^{Jk} \varphi (z)}{(z-Jk-x_j) } \end{aligned}$$

(24)

with $\varphi (z)$ and $C_j$ as given by (21), and (22), respectively. The convergence is uniform on compact subsets of ${\mathbb {C}}$.

For the numerical implementation of (23) and (24) it may be helpful to use (4) and to note that

$$\begin{aligned} \frac{\varphi (z)}{z-Jk-x_j}= & {} (-1)^k \frac{\pi }{J}\, \text{ sinc }((z-Jk-x_j)/J)\,\prod _{n=1,n\ne j}^{J} \sin (\pi (z-x_n)/J). \end{aligned}$$

For a numerical illustration we again consider the function $f \in B_2(\pi )$ given in (19), which has a pronounced local maximum near $x = -8$. Periodic sampling sets allow for clustering sampling points with sizable gaps between clusters. We choose a periodic sampling set with $J=5$ and shifts $\{x_1,\ldots ,x_5\} = \{-0.5, -0.6, -0.7, -0.8, -0.9\}$, with additional sampling points taken from the set $\{\mu _1,\mu _2,\mu _3,\mu _4\} = \{0.6, 0.7, 0.8, 0.9\}$. The peak of f near $x=-8$ falls within the interval $[-10.5,\,-5.9]$ that contains no sampling points. Numerical results for $M=2,3,4$ are reported in Fig. 4. The asymptotic decay of $E_K$ is again $O(K^{1.1-M})$ as expected.

Fig. 4

Periodic sampling. $\varLambda = \bigcup _{j=1}^5 (5{\mathbb {Z}}+ x_j)$, $\{x_1,\ldots ,x_5\} = \{-0.5, -0.6, -0.7, -0.8, -0.9\}$. Additional sampling points taken from $\{\mu _1,\mu _2,\mu _3,\mu _4\} = \{0.6, 0.7, 0.8, 0.9\}$. Left side: Graph of $f(x) = (x/c)^2 g_\nu (x-c), \nu = 0.4, c = -\sqrt{63}$ for the interval $x\in [-20,20]$. Points of $\varLambda$ in this interval are marked with a black ‘x’. The additional sampling points are indicated by red stars. The function f satisfies $|f(x)| =O(|x|^{1.1})$ for $x\rightarrow \pm \infty$, so $f\in B_2(\pi )$. Right side: Numerical experiment for $M=2,3,4$. Points labeled with ‘x’ correspond to $M=2$, with $\mu _1$ and $\mu _2$ being used. Points labeled with ‘*’ correspond to $M=3$, with $\mu _1,\mu _2$, and $\mu _3$. Points labeled with ‘+’ correspond to $M=4$ with all four additional points used. In each case the maximum error $E_K$ decays asymptotically as $O(K^{1.1-M})$

3.3 Sampling at the zeros of Bessel functions $J_\nu (\pi z)$

The sampling sets for our final family of examples are the zero sets of the Bessel functions $J_\nu (\pi z)$ for non-integer index $\nu > -1$. We denote by $j_{\nu ,k}$ the $k-th$ positive zero of $J_\nu$ (when listed in increasing order). We begin with considering the case $0< \nu < 1$ and define the sampling set

$$\begin{aligned} \varLambda _\nu= & {} \{\lambda _{\nu ,k}, \, k\in {\mathbb {Z}}\}, \quad \text{ with } \nonumber \\{} & {} \lambda _{\nu ,0} = 0, \; \lambda _{\nu ,k}= j_{\nu ,k}/\pi , \; \lambda _{\nu ,-k} = -\lambda _{\nu ,k},\; k=1,2,\ldots \end{aligned}$$

(25)

The property $\lim _{k\rightarrow \infty } \left| j_{\nu ,k}- \left( k + \frac{1}{2}\nu -\frac{1}{4}\right) \pi \right| = 0$ implies that for $0< \nu < 1$ all but finitely many of the $\lambda _{\nu ,k}$ satisfy $|\lambda _{\nu ,k}- k | \le d_\nu$ for some $d_\nu < 1/4$. It then follows from Lemmas 1 and 4 that $\varLambda _\nu$ is a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ for $0< \nu < 1$. On the other hand, for the limiting cases $\nu =0$ and $\nu = 1$ one has $|\lambda _{\nu ,k}-k| < 1/4$ for all k, but $\lim _{k\rightarrow \infty } |\lambda _{\nu ,k}-k| = 1/4$, so that these sampling sets do not lie in $S_d({\mathbb {Z}})$ for any $d < 1/4$ and Lemma 4 no longer applies. It will be shown in the next section (following Lemma 6) that one does not obtain complete interpolating sequences for integer values of $\nu$. In practice, the $\lambda _{\nu ,k}$ can be conveniently computed to the desired accuracy by using McMahon’s approximation [36, §10.21] followed by a few iterations of Newton’s method. For given $0< \nu < 1$ let

$$\begin{aligned} \varphi (z) \;=\; (\pi z)^{1-\nu } J_\nu (\pi z) \; = \; \frac{\pi z}{2^\nu \varGamma (\nu +1)} \, \prod _{k=1}^\infty \left( 1-\frac{z^2}{\lambda _{\nu ,k}^2}\right) . \end{aligned}$$

(26)

One has $\varphi '(0) = \pi /(2^\nu \varGamma (\nu +1))$, and using the property $J_\nu '(j_{\nu ,k}) = J_{\nu -1}(j_{\nu ,k})$ one finds

$$\begin{aligned} \varphi '(\lambda _{\nu ,k})= & {} \pi \frac{J_{\nu -1}(\pi \lambda _{\nu ,k})}{\left( \pi \lambda _{\nu ,k}\right) ^{\nu -1}}. \end{aligned}$$

(27)

Now Theorem 3 yields

Corollary 3

Let $f \in \mathcal{P}\mathcal{W}_\pi ^2$, $0< \nu < 1$, and $\varLambda _\nu = \{\lambda _{\nu ,k}, \, k\in {\mathbb {Z}}\}$ as in (25), i.e., the zero set of $\varphi (z) = (\pi z)^{1-\nu } J_\nu (\pi z)$. Then

$$\begin{aligned} f(z)= & {} \frac{J_\nu (\pi z)}{(\pi z)^\nu } \left( 2^\nu \varGamma (\nu +1) f(0) \;+\; z \,\sum _{k\ne 0} \; \frac{\left( \pi \lambda _{\nu ,k}\right) ^{\nu -1}}{J_{\nu -1}\left( \pi \lambda _{\nu ,k}\right) }\;\; \frac{f(\lambda _{\nu ,k})}{z-\lambda _{\nu ,k}}\right) . \end{aligned}$$

(28)

The convergence is uniform on compact subsets of ${\mathbb {C}}$.

For $\nu = 1/2$ one has $\lambda _{\frac{1}{2},k} = k$, $J_{\frac{1}{2}}(\pi z) = \sqrt{\frac{2}{\pi }} \frac{\sin (\pi z)}{\sqrt{\pi z}}$, $J_{-\frac{1}{2}}(\pi z) = \sqrt{\frac{2}{\pi }} \frac{\cos (\pi z)}{\sqrt{\pi z}}$, and (28) simplifies to the classical cardinal series (2). Corollary 3 provides a family of examples for the Paley–Wiener–Levinson Theorem as well as Kadec’s 1/4-Theorem. To our surprise, we have not found it in the literature. Theorem 4 yields

Corollary 4

Let $f\in B_N(\pi )$, $0<\nu <1$, and $\varLambda _\nu = \{\lambda _{\nu ,k}, \, k\in {\mathbb {Z}}\}$ as in (25), i.e., the zero set of $\varphi (z) = (\pi z)^{1-\nu } J_\nu (\pi z)$. For $M \ge N$ let $\mu _1,\ldots , \mu _M \in {\mathbb {C}}$ be distinct points not contained in $\varLambda _\nu$, and let $P_\mu$ denote the polynomial $P_\mu (z) = \prod _{l=1}^M (z-\mu _l)$. Then,

$$\begin{aligned} f(z)= & {} F(z) \;+\;2^\nu \varGamma (\nu +1)\frac{f(0)}{P_\mu (0)} \, \frac{J_\nu (\pi z)}{(\pi z)^\nu }\;+\; \sum _{k\ne 0} \frac{f(\lambda _{\nu ,k})}{P_\mu (\lambda _{\nu ,k})}\, \varphi _k(z)\\{} & {} F(z) = \sum _{m=1}^M f(\mu _m) \frac{\varphi (z)}{\varphi (\mu _m)} \prod _{l=1, l\ne m}^M \frac{z-\mu _l}{\mu _m-\mu _l} \nonumber \\{} & {} \varphi _k(z) = \frac{\left( \pi \lambda _{\nu ,k}\right) ^{\nu -1}}{\pi \, J_{\nu -1}\left( \pi \lambda _{\nu ,k}\right) }\; \frac{\varphi (z)}{z-\lambda _{\nu ,k}}, \quad k\ne 0\nonumber \end{aligned}$$

(29)

The convergence is uniform on compact subsets of $\mathbb {C}$.

One has $|\varphi _k(x)| = O\left( |k|^{\nu -\frac{3}{2}}\right)$ for fixed x and $k \rightarrow \pm \infty$, which follows from the asymptotic properties of Bessel functions (31) and (40) below. Therefore, if $|f(x)| = O(|x|^\alpha )$ as $x\rightarrow \pm \infty$, the truncation error $E_K$ for (29) can be expected to decay as $O(K^{\alpha +\nu -\frac{1}{2}-M})$. Hence, for $0< \nu < \frac{1}{2}$ the non-uniform sampling sets $\varLambda _\nu$ can be expected to slightly outperform the uniform sampling set $\varLambda _{\frac{1}{2}} = {\mathbb {Z}}$ with regard to this measure. These expectations are confirmed in the numerical experiment reported in Fig. 5, where we sampled the bounded bandlimited function $f(z) = z\left( \cos (\pi z) - \cos (\pi \sqrt{z^2-1})\right) \in B^\infty (\pi )$ (cf. [15, p. 108]) on the set $\varLambda _\nu$ with $\nu = 0.01$.

Fig. 5

Sampling on the set $\varLambda _\nu$ defined in (25) for $\nu = 0.01$. The sampled function is $f(x-c)$, with $f(x) = z\left( \cos (\pi z) - \cos (\pi \sqrt{z^2-1})\right) \in B^\infty (\pi )$, and $c = -\sqrt{63}$. Shown are plots of $E_K$ given by (6) with $a = 20$ for $K = 10 \cdot 2^m, m=1,\ldots ,8$. Additional sampling points are $\mu _1 = 10.5$, $\mu _2 = -15.3$, and $\mu _3 = -17.8$. Points labeled with ‘$\cdot$’ correspond to $M=0$, i.e., no additional sampling points. Points labeled with ‘x’ correspond to $M=1$, with $\mu _1$ as the only additional sampling point. Points labeled with ‘*’ correspond to $M=2$, with $\mu _1$ and $\mu _2$ being used. Points labeled with ‘+’ correspond to $M=3$, with all three additional samplng points used. In each case the maximum error $E_K$ decays asymptotically as $O(K^{\nu -\frac{1}{2}-M})$

From the numerical experiment we note that even for $M=0$, where convergence of $f_K$ to f is not guaranteed by the theory presented here, the error appears to go to zero at the predicted rate of $O(K^{\nu -1/2}) = O(K^{-0.49})$ . For a partial explanation we consider the rate of decay of $\varphi (x)$ as $x\rightarrow \pm \infty$. For $x \rightarrow \pm \infty$ one has $|\varphi (x)| = O(|x|^{\frac{1}{2}-\nu })$. It follows that $\varphi$ is unbounded on the real line for $0< \nu < \frac{1}{2}$, and bounded on the real line for $\frac{1}{2}\le \nu < 1$. That is, $\varphi \in B_1(\pi )\backslash B^\infty (\pi )$ for $0< \nu < \frac{1}{2}$, and $\varphi \in B^\infty (\pi )$ for $\frac{1}{2}\le \nu < 1$. This leads to the following observation.

Corollary 5

Let $\varLambda$ be a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function $\varphi$. Then $\varLambda$ is a set of uniqueness for $B^\infty (\pi )$, the space of $\pi$-bandlimited functions bounded on the real line, if and only if $\varphi$ is unbounded on ${\mathbb {R}}$.

To see this, assume that $\varphi$ is unbounded on ${\mathbb {R}}$ and assume two functions $f,g\in B^\infty (\pi )$ agree on the set $\varLambda$. Then the difference function $h(z) = f(z)-g(z)$ is a function in $B^\infty (\pi )$ that vanishes on $\varLambda$. Assume there is a point $\mu _1\in {\mathbb {C}}\backslash \varLambda$ such that $h(\mu _1)\ne 0$. Applying Theorem 4 with $M=1$ gives $h(z) = h(\mu _1) \frac{\varphi (z)}{\varphi (\mu _1)}$. Hence h is a scalar multiple of $\varphi$, and since $\varphi \in B_1(\pi )\backslash B^\infty (\pi )$, it follows that $h\in B_1(\pi )\backslash B^\infty (\pi )$, contradicting that $h\in B^\infty (\pi )$. Therefore such a point $\mu _1$ can not exist and h must vanish identically, implying that $f=g$. On the other hand, if $\varphi$ is bounded on ${\mathbb {R}}$, then $\varphi \in B^\infty (\pi )$, and $\varLambda$ is not a set of uniqueness since $\varphi$ vanishes on $\varLambda$ but is not identically zero.

The following lemma generalizes the findings for $\nu \in (0,1)$ to all non-integer $\nu > -1$. It turns out that the zero sets of Bessel functions of non-integer order $\nu > -1$ can be augmented to form complete interpolating sequences, and that the choice $\nu = n + \frac{1}{2}$, $-1\le n\in {\mathbb {Z}}$, yields sine type functions. We will show in the next section following Lemma 6, that for integer $\nu$ one does not obtain a CIS by adding finitely many points to the zero set of $(\pi z)^{-\nu } J_\nu (\pi z)$.

Lemma 5

Let $\nu > -1$ and let n denote the largest integer that is no greater than $\nu$. Let $\tilde{\varLambda }_\nu$ be the set of zeros of the entire function $(\pi z)^{-\nu }J_\nu (\pi z)$. For $n=-1$ let $p(z) = 1$ and $\varLambda _\nu =\tilde{\varLambda }_\nu$. For $n\ge 0$ let $p(z) = (z- \tau _0)\cdot \ldots \cdot (z- \tau _n)$, with $\tau _0,\ldots ,\tau _n$ distinct points in ${\mathbb {C}}\backslash \tilde{\varLambda }_\nu$, and let $\varLambda _\nu = \{\tau _0,\ldots ,\tau _n\}\cup \tilde{\varLambda }_\nu$. If $\nu$ is not an integer, then $\varLambda _\nu$ is a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function

$$\begin{aligned} \varphi (z) = p(z)\, (\pi z)^{-\nu } J_\nu (\pi z). \end{aligned}$$

(30)

If $\nu = n + \frac{1}{2}$, then $\varphi$ is a $\pi$-sine type function.

Proof

Since $\nu > -1$, the zeros of $J_\nu (z)$ are real and simple [36, §10.21], and it follows from the infinite product representation for $z^{-\nu }J_\nu (z)$ [58, p. 498] that $\varphi$ is a generating function for $\varLambda _\nu$. Let $-1 < \nu \not \in {\mathbb {Z}}$ and write $\nu$ in the form $\nu = n + \frac{1}{2} + \gamma$ with $-1\le n\in {\mathbb {Z}}$ and $-\frac{1}{2}< \gamma < \frac{1}{2}$. Consider the case that n is odd, i.e., $n = 2l-1$, $l\in {\mathbb {N}}$. We will show that the zeros $\lambda _k$ of $\varphi$ can be viewed as perturbations of the zeros of the $\pi$-sine type function $\cos (\pi z)$, which vanishes at the points $\lambda ^{*}_k = k - \frac{1}{2}$, $\lambda ^{*}_{-k}=-\lambda ^{*}_k$, $k\in {\mathbb {N}}$. Let $t_k = j_{\nu ,k}/\pi$ denote the k-th positive root of $J_\nu (\pi z)$. The asymptotic approximation for the zeros of $J_\nu$ [58, p. 506] gives

$$\begin{aligned} t_k= & {} \left( k + \frac{\nu }{2}\,-\frac{1}{4}\right) \; + \; O(k^{-1}) \;=\; \left( k + l -\frac{1}{2} + \frac{\gamma }{2}\right) \;+\; O(k^{-1}). \end{aligned}$$

(31)

In order to apply Lemma 4 we now associate each element $\lambda _k$ of $\varLambda _\nu$ to a corresponding $\lambda ^{*}_k$. Let m be a fixed integer that is greater than $\max _{j=0,\ldots ,n} |\text { Re }\tau _j|$, as well as sufficiently large such that, according to [58, p. 497], the function $(\pi z)^{-\nu }\, J_\nu (\pi z)$ has exactly m zeros $t_1,\ldots ,t_m$ between 0 and $m + \frac{\nu }{2} + \frac{1}{4} = m + l + \frac{\gamma }{2}$. The set ${\mathbb {N}}- \frac{1}{2}$ has $m + l$ elements in this open interval. Taking into account the corresponding negative zeros, $2l=n+1$ additional zeros are needed, which are supplied by the polynomial p(z) in (30). Therefore we let $\lambda _k = t_{k-l}$ and $\lambda _{-k}=-\lambda _k$ for $k > m+l$, while $\{\lambda _k, k=-m-l,\ldots , -1\} \cup \{\lambda _k, k=1,\ldots , m+l\}$ is given by $\{\tau _0,\ldots , \tau _n\}\cup \{\pm t_1, \ldots , \pm t_{m}\}$, ordered by nondecreasing real parts. Then, for any d such that $\left| \frac{\gamma }{2}\right|< d< \frac{1}{4}$ one has $|\lambda _k-\lambda _k^*|\le d$ for all but finitely many k. Hence, by Lemmas 1 and 4, $\varLambda _\nu$ is a complete interpolating sequence. In case of $\nu = n + \frac{1}{2}$, i.e., $\gamma = 0$, (31) implies that $d_k = \lambda _k-\lambda ^{*}_k$, $k\in {\mathbb {Z}}\backslash \{0\}$ is square summable. Hence, by Lemma 3, $\varphi$ is a $\pi$-sine type function. The case of even n is treated in an analogous way, viewing the $\lambda _k$ as perturbations of the zeros of $\sin (\pi z)$. $\square$

4 Theory

In this section we provide the formal definition of a $\pi$-sine type function; discuss the conditions characterizing complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2$; state an infinite product representation for functions in $B_N(\pi )$; and prove Theorems 3 and 4. Theorem 2 follows from Theorem 4 by letting $\varLambda = {\mathbb {Z}}$ and thus does not require a separate proof.

In the derivations below we will also use the following characterization of $\pi$-bandlimited functions, which follows from [45, Theorem 7.23]: A function f is $\pi$-bandlimited if and only if f is an entire function and satisfies the growth condition

$$\begin{aligned} \left| f(z)\right| \,\le \,\gamma \left( 1+|z|\right) ^{n}\,e^{\pi \left| \text {Im }z\right| } \end{aligned}$$

(32)

for all $z\in {\mathbb {C}}$, and some non-negative integer n and constant $\gamma > 0$. It follows that a function f is in $B_N(\pi )$ if and only if f is entire, satisfies (32), and $\int _{-\infty }^\infty |f(x)|^2 (1+ |x|)^{-2N} \, dx < \infty$.

4.1 Definition of a sine type function

Definition 4

($\pi$-sine type function) An entire function f is said to be a $\pi$-sine type function if

• 1. f is of exponential type $\pi$, i.e., $\limsup _{r\rightarrow \infty } \frac{\log M(r)}{r} = \pi$, where $M(r) \;= \;\max \{|f(z)|, \,|z|=r\}$. Equivalently, $\pi$ is the smallest non-negative number $\sigma$ such that $|f(z)|\;\le \; e^{(\sigma + \epsilon ) r}$ for all $\epsilon > 0$ as soon as r is sufficiently large.

• 2. There exist positive constants A, B, and $\eta$ such that

  $$\begin{aligned} A e^{\pi \mid \text {Im } z \mid }\;\le \;\mid f(z)\mid \;\le \; B e^{\pi \mid \text {Im }z\mid } \end{aligned}$$

  for all $z\in {\mathbb {C}},$ such that $\mid \text{ Im } z \mid \,\ge \,\eta$.

• 3. The zeros $\lambda _k$ of f are simple and satisfy the separation condition

  $$\begin{aligned} \inf _{n\ne m} |\lambda _n-\lambda _m| > 0. \end{aligned}$$

Some authors omit the third condition from the definition of a sine type function. For more information on the properties of sine type functions see, e.g., [3, 25, 26, 28, 44, 64, 65].

4.2 Characterization of complete interpolating sequences

Next we discuss necessary and sufficient conditions for a set $\varLambda = \{\lambda _k, \, k\in {\mathbb {Z}}\}$ to be a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$. These conditions are established in [17, 30, 39]. Since the elements of any Riesz basis $\{g_k, k\in {\mathbb {Z}}\}$ must satisfy $\sup _{k\in {\mathbb {Z}}} \parallel g_k\parallel < \infty$, and $\parallel e^{i \lambda _k t}\parallel _{L^2[-\pi ,\pi ]}^2 \;=\; \int _{-\pi }^\pi e^{-2 (\text {Im }\lambda _k) t } \, dt$, it follows that

$$\begin{aligned} \sup _{k\in {\mathbb {Z}}} |\text {Im } \lambda _k| < \infty . \end{aligned}$$

(33)

That is, $\varLambda$ must be contained in a horizontal strip of finite width. We note that in [30] a broader definition of a CIS is used that allows for cases where the sequence $(\text {Im } \lambda _k)_{k\in {\mathbb {Z}}}$ is unbounded. The set $\varLambda$ must also satisfy the Carleson condition, which because of (33) simplifies to the requirement that $\varLambda$ is uniformly discrete [17, p. 225], i.e.,

$$\begin{aligned} \inf _{n\ne m} |\lambda _n - \lambda _m| > 0. \end{aligned}$$

(34)

Third, the associated generating function $\varphi$ must be an entire function of exponential type $\pi$.

Fourth, $\varLambda$ must be relatively dense [30], a condition which in the light of (33) simplifies to the requirement that there exists an $r>0$ such that

$$\begin{aligned} \{\text {Re } \lambda _k, \; k\in {\mathbb {Z}}\} \cap [x,x+r] \ne \emptyset \quad \text{ for } \text{ all } x\in {\mathbb {R}}. \end{aligned}$$

The fifth and final condition requires that there exists a relatively dense subsequence $\varGamma = \{\gamma _j, \, j\in {\mathbb {Z}}\} \subset \varLambda$ such that the sequence $w_j = |\varphi '(\gamma _j)|^2$ satisfies the discrete Muckenhoupt ($A_2$) condition [30]

$$\begin{aligned} \sup _{k\in {\mathbb {Z}}, n > 0} \left( \frac{1}{n} \sum _{j=k+1}^{k+n} w_j\right) \, \left( \frac{1}{n} \sum _{j=k+1}^{k+n} \frac{1}{w_j}\right) \;< \; \infty . \end{aligned}$$

(35)

For further details and continuous versions of the last condition we refer the reader to [17, 30, 39] as well as [3, 47, 48]. Of course, for $\varLambda \subset {\mathbb {R}}$, the five conditions above also collectively imply that $\varLambda$ satisfies Landau’s necessary density condition $\lim _{r \rightarrow \infty } \frac{n(r)}{2r} = 1$, where n(r) denotes the number of points in $\varLambda$ contained in the interval $[-r,r]$, cf. [15, Theorem 10.4], [22, 23, 47, Ch. 6]. It is also worth noting that there are zero sets of $\pi$-sine type functions, and hence complete interpolating sequences for $\mathcal{P}\mathcal{W}_\pi ^2$, for which $|\lambda _k-k|$, $k\in {\mathbb {Z}}$ is unbounded [65].

As an example we verify that the zero set $\varLambda$ of a $\pi$-sine type function is a CIS for $\mathcal{P}\mathcal{W}_\pi ^2$. The first three conditions follow directly from the definition of a $\pi$-sine type function $\varphi$ and the fact that $\varphi$ is a generating function (10) of its zero set [28]. Lemma 3 in [25, p. 164] and its proof establish that $\varLambda$ is relatively dense. Finally, Lemma 2 in [25, p. 164] shows that there are constants $N_1$, $N_2$ such that $0< N_1< |\varphi '(\lambda _k)|< N_2 < \infty$ for all $k\in {\mathbb {Z}}$. This in turn implies immediately that condition (35) is satisfied. More generally, Semmler [48, Lemma 5] showed that if there is $\alpha \in \left( -\frac{1}{2},\,\frac{1}{2}\right)$ and positive constants $c_1$, $c_2$ such that

$$\begin{aligned} c_1 (1+|j|)^{2\alpha } \; \le \; w_j \;\le \; c_2 (1+|j|)^{2\alpha } \end{aligned}$$

(36)

for all $j\in {\mathbb {Z}}$, then the sequence $(w_j)_{j\in {\mathbb {Z}}}$ satisfies the Muckenhoupt condition (35). The Muckenhoupt condition does neither rule out that $|\varphi '(\lambda _k)|\rightarrow \infty$ nor that $|\varphi '(\lambda _k)|\rightarrow 0$ for large |k|, but it does restrict both the rate of growth and of decay. The following lemma gives two necessary conditions for complete interpolating sequences that reflect similar restrictions. These conditions are easier to check in some cases and can be useful for establishing counterexamples. The first condition is used in proofs by Young [64, p. 105] and Vellucci [54, pp. 91–92]. The second condition, which we have not found in the literature, is a consequence of $\varphi$ being an element of $B_1(\pi )$.

Lemma 6

Let $\varLambda = \{\lambda _k, \, k\in {\mathbb {Z}}\}$ be a complete interpolating sequence for $\mathcal{P}\mathcal{W}_\pi ^2$ with generating function $\varphi$. Then

$$\begin{aligned} \sum _{k\ne 0} \left| \frac{1}{\varphi '(\lambda _k) \,\lambda _k}\right| ^2< & {} \infty , \text{ and } \end{aligned}$$

(37)

$$\begin{aligned} \sum _{k\ne 0} \left| \frac{\varphi '(\lambda _k)}{\lambda _k}\right| ^2< & {} \infty . \end{aligned}$$

(38)

Proof

To begin, we note that since $\varLambda$ is uniformly discrete, relatively dense, and contained in a horizontal strip, there exist positive constants $c_1$, $c_2$, $k_0$ such that

$$\begin{aligned} c_1 \,|k| \;\le \; |\text { Re }\lambda _k|\;\le \; c_2\, |k| \;\;\text{ whenever } |k|\ge k_0. \end{aligned}$$

(39)

To show the condition (37) one can either use the same argument as in [54, pp. 91–92], or slightly adapt the reasoning in [64, p. 105]. To show the second assertion we consider the function

$$\begin{aligned} g(z) = \frac{\varphi '(z)-\varphi '(0)}{z}, \quad z\ne 0, \quad g(0) = \varphi ''(0). \end{aligned}$$

To see that $g\in \mathcal{P}\mathcal{W}_\pi ^2$ we recall that $\varphi \in B_1(\pi )$. Zakai [66, pp. 149–150] showed that any $f\in B_1(\pi )$ can be written as $f(z) = f(0) + z h(z)$ with $h\in \mathcal{P}\mathcal{W}_\pi ^2$. Applying this relation to $f=\varphi$ and differentiating gives $\varphi '(z) = h(z) + zh'(z)$. Since it follows directly from (1) that $h \in \mathcal{P}\mathcal{W}_\pi ^2$ implies $h' \in \mathcal{P}\mathcal{W}_\pi ^2$, one has $\varphi '\in B_1(\pi )$. Applying Zakai’s relation to $\varphi '$ then establishes that $g \in \mathcal{P}\mathcal{W}_\pi ^2$. Expanding g in the Riesz basis $\{\varphi _k,\,k\in {\mathbb {Z}}\}$ gives $g = \sum _k g(\lambda _k) \varphi _k(z)$ with $\{g(\lambda _k)\}\in l^2$. One has

$$\begin{aligned} \frac{\varphi '(\lambda _k)}{\lambda _k} = g(\lambda _k) + \frac{\varphi '(0)}{\lambda _k}, \quad k\ne 0. \end{aligned}$$

Since (39) implies that $\{1/\lambda _k\}_{k\ne 0} \in l^2$, the condition (38) follows. $\square$

The inequalities (39) also imply that (37) and (38) can be replaced by the equivalent conditions $\sum _{k\ne 0} \left| \frac{1}{\varphi '(\lambda _k) \,k}\right| ^2 < \infty$, and $\sum _{k\ne 0} \left| \frac{\varphi '(\lambda _k)}{k}\right| ^2 < \infty$, respectively. It is then readily apparent that if the inequalities (36) hold for $w_j = |\varphi (\lambda _j)|^2$ and some $\alpha$ with $|\alpha |\ge 1/2$, then $\varLambda$ is not a CIS.

We are now ready to show that one cannot obtain a CIS by adding finitely many points to the zero set of $z^{-n} J_n(\pi z)$ for n a non-negative integer. Assume $m\ge 0$ points are added, so that a generating function would be $\varphi (z) = q(z) z^{-n} J_n(\pi z)$, with $q(z) = (z-\tau _1)\cdot \ldots \cdot (z-\tau _m)$, or $q(z) = 1$ if $m=0$. The positive zeros of $J_n(\pi z)$ are $t_k = j_{n,k}/\pi = k + \frac{n}{2} - \frac{1}{4} + O(k^{-1})$. Using $J_n'(z) = \frac{n}{z}J_n(z) - J_{n+1}(z)$, (31), and the limiting form of $J_\nu (t)$ for large |z|, i.e.,

$$\begin{aligned} J_\nu (z)= & {} \sqrt{\frac{2}{\pi z}} \left[ \cos \left( z - \frac{(2\nu +1)\pi }{4}\right) \,+\, e^{|\text { Im }z|} o(1)\right] \end{aligned}$$

(40)

one has $\lim _{k\rightarrow \infty } \frac{|\varphi '(t_k)|}{C_{m,n}(k)} = 1$, with $C_{m,n}(k) = \frac{\sqrt{2}}{\pi }\,\left| k + \frac{n}{2}-\frac{1}{4}\right| ^{m-n-\frac{1}{2}}$. It follows that (36) holds with $\alpha = m-n-\frac{1}{2}$, and for no choice of m is $|\alpha | < \frac{1}{2}$. Of course, deleting finitely many points from the zero set of $z^{-n} J_n(\pi z)$ would lead to a more rapidly decaying canonical product that would be an element of $B_0(\pi )$ and therefore could not be the generating function of a CIS.

4.3 Infinite product expansion for functions in $B_N(\sigma )$

The following theorem about the infinite product expansion and the distribution of zeros of functions in $B_N(\sigma )$ is of intrinsic interest and will be used in the proof of Theorem 3. Its content stems from [25, Lecture 17]. We state its hypothesis in terms of the Fourier transform instead of the indicator function of f.

Theorem 5

Let $f\in B_N(\sigma )$ for some $\sigma > 0$, and let [a, b] the smallest interval that contains the support of the (distributional) Fourier transform of f. If $a<b$, then f has infinitely many zeros $a_n$, $a_n\ne 0$, ordered with non-decreasing absolute values, such that

$$\begin{aligned} f(z) = A z^m\,e^{i(a+b)z/2}\, \prod _{n=1}^\infty \left( 1-\frac{z}{a_n}\right) , \end{aligned}$$

(41)

where m is a non-negative integer. The infinite product converges conditionally. The convergence is uniform on compact subsets of ${\mathbb {C}}$. Furthermore,

$$\begin{aligned} \sum _{n=1}^\infty \text { Im }\left( \frac{1}{a_n}\right)< & {} \infty , \nonumber \\ \lim _{R\rightarrow \infty } \sum _{|a_n|<R} \frac{1}{a_n}{} & {} \text{ exists },\\ \lim _{R\rightarrow \infty } \frac{n_+(R,\alpha )}{R}= & {} \lim _{R\rightarrow \infty } \frac{n_-(R,\alpha )}{R} \;=\; \frac{b-a}{2\pi },\nonumber \end{aligned}$$

(42)

where $0< \alpha < \pi$, and $n_+(R,\alpha )$, $n_-(R,\alpha )$ denote the number of zeros of f in the sectors $\{z\in {\mathbb {C}}: |z|\le R, \, |\arg (z)| \le \alpha \}$, and $\{z\in {\mathbb {C}}: |z|\le R, \, |\pi -\arg (z)| \le \alpha \}$, respectively.

Theorem 5 can be derived from results in [25, Lecture 17] along the following lines. If $f(0)=0$, then we set m equal to the multiplicity of this root. Otherwise $m=0$. Consider the function $g(z) = z^{-m} e^{-i(a+b)z/2} \, f(z)$. Clearly, $g(0)\ne 0$ and the smallest interval that contains the support of the Fourier transform of g is the interval $[-d/2,d/2]$ with $d = (b-a)$. The condition $a<b$ rules out that g is a polynomial, hence g is an entire function of exponential type. It follows that g is in the Cartwright class defined in [25, p. 115]. Next one verifies that the indicator function of g ([25, p. 53]) is given by $h_g(\theta ) = \frac{d}{2} |\sin \theta |$. One way to see this is as follows. Consider the family of functions $g_\tau (z) = e^{i\tau z} g(z)$, $\tau \in {\mathbb {R}}$. The interval $[\tau -\frac{d}{2},\,\tau + \frac{d}{2}]$ is the smallest interval containing the support of the Fourier transform of $g_\tau$. It then follows from (32) that the exponential type of $g_\tau$ equals $\frac{d}{2} + |\tau |$ and assumes its minimal value of $\frac{d}{2}$ for $\tau = 0$ and $g_0 = g$. On the other hand, according to [25, p. 126] there is $\lambda \in {\mathbb {R}}$ such that the indicator function of $g_{\lambda }$ has the form $h_{g_\lambda }(\theta ) = \sigma _0 |\sin \theta |$. Since $g_\tau (z) = e^{i(\tau -\lambda )z} g_\lambda (z)$, it follows from the definition of the indicator function that $h_{g_\tau }(\theta ) = \sigma _0 |\sin \theta | + (\tau -\lambda ) \sin \theta$. The exponential type of $g_\tau$ is given by $\max h_{g_{\tau }}(\theta ) \,=\, \max (\sigma _0 - (\tau -\lambda ),\, \sigma _0+(\tau -\lambda ))$ (cf. [4, p. 75, Theorem 5.4.1]) and assumes its minimal value of $\sigma _0$ for $\tau = \lambda$. Hence $\lambda = 0$, $g_\lambda = g_0 = g$, and $\sigma _0 = \frac{d}{2}$. The theorem now follows by applying Theorem 1 in [25, p. 127] and the infinite product expansion given in [25, p. 130] to the function g.

Theorem 5 generalizes a theorem by Titchmarsh [51, Theorem VI] that is better known in sampling theory [2, 9, 67, p. 39]. From the above derivation it also becomes apparent that the factor $e^{(a+b)z/2}$ occurring in Titchmarsh’s theorem should correctly be $e^{i (a+b)z/2}$ as in (41).

4.4 Proof of Theorems 3 and 4

Proof of Theorem 3

Since $\varLambda$ is a CIS, there is a unique function $\varphi _0\in \mathcal{P}\mathcal{W}_\pi ^2$ that solves the interpolation problem

$$\begin{aligned} f(\lambda _l)= & {} \delta _{0l} ,\quad l\in {\mathbb {Z}}, \quad f \in \mathcal{P}\mathcal{W}_\pi ^2, \end{aligned}$$

(43)

where $\delta _{kl}$ denotes the Kronecker delta. The uniqueness of $\varphi _0$ implies the following. First, $\varphi _0$ does not have any other zeros. If $\varphi _0(\mu )=0$ for $\mu \not \in \varLambda$, then the function $g(z) = \frac{\lambda _0-\mu }{z-\mu } \varphi _0(z) \in \mathcal{P}\mathcal{W}_\pi ^2$ would be another solution of (43). We use the convention that if $0\in \varLambda$, then $\lambda _0 =0$. It then follows that $\varphi _0(0) \ne 0$. Similarly, the $\lambda _k$, $k\ne 0$ must be simple zeros of $\varphi _0$, since otherwise the function $g(z) = \frac{\lambda _0-\lambda _k}{z-\lambda _k}\,\varphi _0(z)$ would be another solution. Finally, the interval $[-\pi ,\pi ]$ is the smallest interval that contains the support of the Fourier transform of $\varphi _0$. For if the support of $\widehat{\varphi _0}$ is contained in a proper subinterval of $[-\pi ,\pi ]$, then there is $0\ne \tau \in {\mathbb {R}}$ such that $e^{i\tau z} \varphi _0 \in \mathcal{P}\mathcal{W}_\pi ^2$, and $g(z) = e^{i\tau (z-\lambda _0)} \varphi _0(z)$ would be another solution of (43). Now Theorem 5 gives the representation

$$\begin{aligned} \varphi _0(z) = \varphi _0(0) \; \lim _{K\rightarrow \infty } \prod _{1\le |k| \le K} \left( 1-\frac{z}{\lambda _k}\right) , \end{aligned}$$

(44)

the convergence being conditional and uniform on compact subsets of ${\mathbb {C}}$. It follows that

$$\begin{aligned} \varphi (z)= & {} (z-\lambda _0) \varphi _0(z)/\varphi _0(0) \nonumber \\= & {} (z-\lambda _0) \; \lim _{K\rightarrow \infty } \prod _{1\le |k| \le K} \left( 1-\frac{z}{\lambda _k}\right) \end{aligned}$$

(45)

is in $B_1(\pi )$ and the functions $\varphi _k$, $k\in {\mathbb {Z}}$, are the unique solutions in $\mathcal{P}\mathcal{W}_\pi ^2$ of the interpolation problems $f(\lambda _l) = \delta _{kl}$, $l\in {\mathbb {Z}}$. Next we show that $\{\varphi _k,\, k\in {\mathbb {Z}}\}$ is a Riesz basis of $\mathcal{P}\mathcal{W}_\pi ^2$. We note that the Fourier transform $\hat{f}(\xi ) = \int _{\mathbb {R}}f(x) e^{-ix\xi }\,dx$ is an isometry between $\mathcal{P}\mathcal{W}_\pi ^2$ and the space $L_2[-\pi ,\pi ]$ equipped with the inner product $\langle f,\,g\rangle = \frac{1}{2\pi } \int _{-\pi }^\pi f(\xi )\,\overline{g}(\xi ) \,d\xi .$ Since $\varLambda$ is a CIS, the exponentials $\{e^{i\lambda _k t}, \, k\in {\mathbb {Z}}\}$ are a Riesz basis of $L_2[-\pi ,\pi ]$ [64, p. 143, Theorem 9]. Since complex conjugation does not change the Riesz basis property, the functions $\{e^{-i\,\overline{\lambda _l}\, t}, \, l\in {\mathbb {Z}}\}$ are also a Riesz basis of $L_2[-\pi ,\pi ]$. From

$$\begin{aligned} \delta _{kl} \;=\; \varphi _k(\lambda _l) \;=\; \frac{1}{2\pi } \int _{-\pi }^\pi \widehat{\varphi _k}(t) \,e^{i\lambda _l t}\,dt \;=\; \langle \widehat{\varphi _k},\, e^{-i\,\overline{\lambda _l}\, t} \rangle \end{aligned}$$

(46)

it follows that $\{\widehat{\varphi _k},\,k\in {\mathbb {Z}}\}$ is the biorthogonal Riesz basis associated with $\{e^{-i\overline{\lambda _l} t}, \, l\in {\mathbb {Z}}\}$. Since the Fourier transform is an isometry, it follows that $\{\varphi _k, \, k\in {\mathbb {Z}}\}$ is a Riesz basis of $\mathcal{P}\mathcal{W}_\pi ^2$. Hence $f\in \mathcal{P}\mathcal{W}_\pi ^2$ enjoys the expansion $f = \sum _{k\in {\mathbb {Z}}} \langle f, \,\psi _k\rangle \,\varphi _k$, where $\{\psi _l, \,l\in {\mathbb {Z}}\}$ denotes the corresponding biorthogonal sequence. From (46) and $\delta _{kl} = \langle \varphi _k, \psi _l\rangle = \langle \widehat{\varphi _k},\, \widehat{\psi _l}\rangle$ one obtains $\widehat{\psi _l}(t) = e^{-i\overline{\lambda _l} t}$. This leads to

$$\begin{aligned} \langle f, \psi _k\rangle = \langle \hat{f},\, \widehat{\psi _k}\rangle = \langle \hat{f},\, e^{-i\,\overline{\lambda _l}\, t}\rangle = \frac{1}{2\pi } \int _{-\pi }^\pi \hat{f}(t)\, e^{i\lambda _k t}\,dt = f(\lambda _k), \end{aligned}$$

which establishes (12). The Riesz basis property of $\{\varphi _k, \, k\in {\mathbb {Z}}\}$ also implies the convergence properties of the sampling expansion (12). $\square$

The following Lemma will be used in the derivation of Theorem 4.

Lemma 7

Let $h\in B_N(\pi )$, $M\ge N$, and $\mu _1,\ldots ,\mu _M\in {\mathbb {C}}$ be distinct points such that $h(\mu _m) = 0$ for $m=1,\ldots ,M$. Let $P_\mu (z) = \prod _{m=1}^M (z-\mu _m)$. Then $G(z) = h(z)/P_\mu (z) \in \mathcal{P}\mathcal{W}_\pi ^2$.

Proof

One needs to verify that G is $\pi$-bandlimited and square integrable. Since h is $\pi$-bandlimited, h is an entire function and satisfies (32) for some integer $n=n_1$ and constant $\gamma > 0$. Since the roots $\mu _m$ of $P_\mu$ are simple and $h(\mu _m) = 0$, the singularities of G at the points $\mu _m$ are removable. Defining $G(\mu _m) = \lim _{z\rightarrow \mu _m} G(z)$, $m=1,\ldots ,M$, makes G an entire function. Let $R = \max _{1\le m\le M} |\mu _m|$. Then $|P_\mu (z)| \ge C_1 (1+|z|)^M$ for $|z|> 1+R$ and some constant $C_1>0$. Since G is entire, G is bounded for $|z|\le 1+R$, and for $|z| > 1+R$ one has

$$\begin{aligned} |G(z)| \;=\; \left| \frac{h(z)}{P_\mu (z)}\right| \;\le \; \frac{|h(z)|}{C_1 (1+|z|)^M}. \end{aligned}$$

(47)

It follows that G satisfies (32) with n replaced by $\max \{0,n_1-M\}$, hence G is $\pi$-bandlimited. Since $M\ge N$ and $h(x) (1+|x|)^{-N}$ is square integrable, (47) also implies that G is square integrable on the real line. Hence $G\in \mathcal{P}\mathcal{W}_\pi ^2$. $\square$

Proof of Theorem 4

Consider the function

$$\begin{aligned} F(z) = \sum _{m=1}^M f(\mu _m) \frac{\varphi (z)}{\varphi (\mu _m)} \frac{P_\mu (z)}{P_\mu ^{\prime } (\mu _m) (z-\mu _m)} \end{aligned}$$

(48)

for $z \ne \mu _m$, and $F(\mu _m) = \lim _{z\rightarrow \mu _m} F(z) = f(\mu _m)$, $m=1,\ldots ,M$. Then F is entire. According to Theorem 3 the function $\varphi _0(z) = \frac{\varphi (z)}{\varphi '(\lambda _0)(z-\lambda _0)}$ is in $\mathcal{P}\mathcal{W}_\pi ^2= B_0(\pi )$. This implies that $P_\mu (z)\varphi (z)/(z-\mu _m) = \frac{z-\lambda _0}{z-\mu _m}P_\mu (z)\varphi '(\lambda _0) \varphi _0(z) \in B_M(\pi )$. Hence, $F\in B_M(\pi )$. Let $q_M$ denote the polynomial of degree at most $M-1$ that interpolates f (and thereby also F) at the points $\mu _1,\ldots ,\mu _M$. Any polynomial is a $\pi$-bandlimited function, and since $q_M(x)/(1+|x|)^M$ is square integrable, one has $q_M\in B_M(\pi )$. Now consider the function

$$\begin{aligned} G(z) = \frac{F(z)-q_M(z)}{P_\mu (z)} \end{aligned}$$

for $z \ne \mu _m$, and $G(\mu _m) = \lim _{z\rightarrow \mu _m} G(z)$. Applying Lemma 7 to the function $h_1(z) = F(z)-q_M(z)$ yields $G\in \mathcal{P}\mathcal{W}_\pi ^2$. Applying Theorem 3 to G together with the observation that $F(\lambda _k) = 0$, $k\in {\mathbb {Z}}$, now yields

$$\begin{aligned} G(z)= & {} \frac{F(z)-q_M(z)}{P_\mu (z) } \;=\; \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} G(\lambda _k) \varphi _k(z) \\= & {} -\lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{q_M(\lambda _k)}{ P_\mu (\lambda _k)} \varphi _k(z) \end{aligned}$$

with uniform convergence on any horizontal strip of finite width. Multiplication by $P_\mu (z)$ yields

$$\begin{aligned} F(z)= & {} \sum _{m=1}^M f(\mu _m) \frac{\varphi (z)}{\varphi (\mu _m)}\frac{P_\mu (z)}{P_\mu '(\mu _m)(z-\mu _m)} \;=\; q_M(z) + P_\mu (z) G(z) \nonumber \\= & {} q_M(z) - P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{q_M(\lambda _k)}{ P_\mu (\lambda _k)} \varphi _k(z) . \end{aligned}$$

(49)

Now consider the function $h_2(z) = f(z) - q_M(z)$. Since $f\in B_N(\pi )$ and $q_M\in B_M(\pi )$, it follows that $h_2\in B_M(\pi )$. Applying Lemma 7 to $h_2$ yields that the function $g(z) = (f(z)-q_M(z))/P_\mu (z)$ lies in $\mathcal{P}\mathcal{W}_\pi ^2$. Application of Theorem 3 to g yields

$$\begin{aligned} f(z)= & {} q_M(z) + P_\mu (z) g(z) \;=\; q_M(z) + P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} g(\lambda _k) \varphi _k(z) \nonumber \\= & {} q_M(z) + P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{f(\lambda _k)-q_M(\lambda _k)}{P_\mu (\lambda _k)} \,\varphi _k(z) \end{aligned}$$

(50)

$$\begin{aligned}= & {} q_M(z) - P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{q_M(\lambda _k)}{P_\mu (\lambda _k)} \,\varphi _k(z) \nonumber \\ {}{} & {} \;+\; P_\mu (z) \lim _{K\rightarrow \infty } \sum _{k=-K}^{K} \frac{f(\lambda _k)}{P_\mu (\lambda _k)} \,\varphi _k(z) \end{aligned}$$

(51)

Before proceeding we wish to mention that for uniform sampling Eq. (50) gives Corollary 2.2 in [56]. Now substituting (49) in (51) yields (13). Theorem 3 gives uniform convergence on horizontal strips of finite width. Since $P_\mu (z)$ is unbounded on horizontal strips but bounded on compact sets, the multiplication by $P_\mu (z)$ changes this to uniform convergence on compact subsets of ${\mathbb {C}}$. $\square$

5 Conclusions

A family of sampling theorems for the reconstruction of bandlimited functions from their uniform or non-uniform samples is presented. The bandlimited functions may be square-integrable or may have polynomial growth on the real line. It is demonstrated that taking one or more additional samples can accelerate the convergence of the partial sums of the infinite sampling series, and thus reduce truncation errors. With regard to an optimal placement of the additional samples within an interval of interest, the Chebychev nodes are recommended. The oversampling with very few additional samples that is considered in the present work does not require to increase the sampling rate, and is thus different from oversampling achieved by slightly increasing the sampling rate (or, equivalently, reducing the admissible bandwidth of the sampled function).

General sampling expansions are derived for a large class of sampling sets $\varLambda = \{\lambda _k, \,k\in {\mathbb {Z}}\}$ consisting of the complete interpolating sequences for the Paley–Wiener space $\mathcal{P}\mathcal{W}_\pi ^2$. The conditions characterizing complete interpolating sequences are discussed and practically useful tools and criteria to obtain new such sampling sets are provided. Specific expansions and numerical experiments are given for uniform and periodic non-uniform sampling sets, as well for the zero sets of the Bessel functions $J_\nu (\pi z)$, $0<\nu <1$. The latter encompasses uniform sampling when $\nu = 1/2$. Furthermore, the theory accommodates the movement of finitely many sampling points to new locations, and this is demonstrated with a numerical experiment where 2001 points were moved.

The sampling expansions are of Lagrange interpolation type and have the general form $f(z) = \lim _{K \rightarrow \infty } f_K(z)$, with

$$\begin{aligned} f_K(z) = F(z) + P_\mu (z)\sum _{k=-K}^K \frac{f(\lambda _k)}{P_\mu (\lambda _k)} \varphi _k(z), \end{aligned}$$

where F(z) interpolates f at the additional sampling points $\mu _1,\ldots ,\mu _M$, $P_\mu$ is the polynomial $P_\mu (z) = \prod _{m=1}^M (z-\mu _m)$, and $\varphi _k$ is determined by the sampling set $\varLambda = \{\lambda _k, k\in {\mathbb {Z}}\}$. For the rate of convergence of $f_K$ to f as $K\rightarrow \infty$ one has the following general guideline. If, for real x, $|f(x)| = O(|x|^\alpha )$ as $|x|\rightarrow \infty$, and, for fixed z, $|\varphi _k(z)| = O(|k|^\beta )$ as $|k|\rightarrow \infty$, then $|f(z)-f_K(z)| = O(K^{\alpha + \beta + 1 -M})$, with uniform convergence on compact sets. For sampling sets that are uniform or periodic, with possibly finitely many points moved, one has $\beta =-1$, while for the zero sets $\varLambda _\nu$ of the Bessel functions $J_\nu (\pi z)$, $0<\nu <1$, one has $\beta = \nu - \frac{3}{2}$. Hence, for $0<\nu <1/2$ the non-uniform sampling set $\varLambda _\nu$ leads to slightly faster convergence than the uniform set $\varLambda = {\mathbb {Z}}$.

The numerical experiments were provided as an illustration of the theory and were conducted with noise-free samples. A deeper investigation of numerical aspects including the case of noisy samples will be the subject of future work. The case where the additional samples may be both values of the function itself and/or its derivatives will be explored in a forthcoming paper.