Health status, life expectancy and early claiming of pension

Abstract

Prior to 2011, individual life expectancy played no role in the Norwegian old-age pension system. However, after the 2011 reform, life expectancy became a central factor for early pension take-up. Asymmetric information is crucial in most insurance markets, including the new pension system, where employees can flexible claim a public pension from the age of 62. Individuals who expect to live longer than the average for their birth cohort can maximize their pension wealth by deferring pension claiming, while those with a shorter life expectancy should draw their pension as early as possible. This raises concerns that adverse selection may pose a risk to the sustainability of the new pension system. To investigate this issue, we use chronic disease as a proxy for life expectancy and examine its relationship with employment and pension decisions. Our findings show that individuals with a chronic health condition are more likely to draw a pension and continue working when they reach 62 years of age compared to those without a chronic health condition. This suggests potential adverse selection issues in the pension system, although our results suggest small effects after adjusting for unobservables.

Introduction

Life expectancy has been steadily increasing across OECD countries, with the average life expectancy at birth being 81 years, which is more than ten years higher than in 1970 (OECD 2021). Additionally, individuals at age 65 can now expect to live an additional 19.9 years. While this trend is generally considered positive, it does pose longevity risks to pension providers. If future improvements in life expectancy are not considered, pension funds and annuity providers may face an expected shortfall in the provisions set aside to fund future obligations (OECD 2014). Therefore, it is crucial for policymakers and pension providers to address these risks to ensure the sustainability of pension schemes in the face of increasing longevity.

As individual expected longevities may deviate from the average longevity of a birth cohort, there is a potential for adverse selection in a flexible pension system. Adverse selection in our context means that individuals are capable of assessing their individual life expectancy using this information to make choices that are subject to uncertainty. Adverse selection has negative consequences for the National Insurance Scheme if longer-lived individuals postpone claiming, and shorter-lived individuals claim early, all other things being equal.¹

The main research question in this paper is whether the adverse selection hypothesis related to longevity can be substantiated by empirical evidence in the pension system. In particular, we analyse how chronic disease, of which one of the potential consequences is shorter life expectancy, affects early claiming. Empirical analyses examining the relationship between mortality and pension claiming (e.g., Hurd et al. (2004), Van Solinge and Henkens (2010), Shoven and Slavov (2014), Coile (2015)) have yielded inconclusive results regarding the actual influence of mortality risk on behavior. As discussed by Altig et al. (2022), even though maximizing lifetime benefits would typically require most American workers to delay pension collection beyond the age of 65, only a small percentage actually choose to do so. On the other hand, drawing from US data too, Goda et al. (2018) discover a robust association between claiming decisions and life expectancy. In a Dutch study conducted by Vanajan et al. (2020), it is revealed that the retirement preferences of older workers are contingent upon the specific chronic health conditions (CHCs) they experience. Interestingly, retirement preferences are influenced to varying degrees by subjective life expectancy, perceived health-related work limitations, and vitality. This study provides evidence that retirement behavior is influenced not solely by financial incentives but also affected by various other factors.

Of recent contributions studying the relationship between claiming behavior and a model for expected longevity, Brinch et al. (2018) is of particular interest in relation to our study. Firstly, they measure the overall association between claiming at age 62 and expected longevity in the Norwegian pension system. Secondly, they study the extent to which individuals claim pensions early partly because they act on information about their expected longevity. They simulate expected longevities and expected present values of pensions conditional on claiming at age 62 and at age 67. They then calculate the relative money’s worth (RMW) as the income stream from claiming at age 67 versus age 62, and find that those who benefit from claiming at age 67 rather than at age 62 due to longer life expectancy (based on estimated mortality probabilities) have lower claiming rates at age 62. This indicates that individuals act on information about their expected longevity.

In our study, we utilize a direct measure of health as a proxy for shorter life expectancy. This approach is motivated by the suggestion made by Finkelstein and Poterba (2002) that individuals may possess private information regarding their life expectancy, such as their own health or the mortality of their parents. Hence, we consider one’s own health as a direct indicator or signal of their life expectancy, which, in turn, influences individual claiming behavior. We construct our proxy/signal of life expectancy by utilizing the detailed diagnostic information available in health registers, particularly those from GP filings.² The proxy variable is a categorical variable that divides the sample into two groups: those with one or more chronic health conditions indicating reduced health and longevity, and those without such conditions. We thus rely on a treatment-control framework in our empirical set-up. Several studies, to which we return in the next section, find that specific health conditions or a combination of such significantly affect life expectancy. The presence of certain health conditions is thus an objective signal, albeit possibly an imperfect and noisy one, of a shorter expected life span compared to people without such conditions. When individuals make decisions regarding retirement, they must rely on signals of life expectancy, and health plays a crucial role within their available information set. However, since individual life expectancy is unobserved and chronic disease is a noisy signal, it is difficult to fully establish whether the measured effect is attributable to lower life expectancy or to other consequences of chronic disease that are unrelated to life expectancy.

We study early take-up and continued employment using detailed individual data from several longitudinal data registers, not least data from health registers combined with socio-economic background characteristics along with labour market outcomes. The two groups of people – those with chronic health conditions and those without – are likely to behave differently in terms of choices between work and early claiming. We match the groups so that they are equal along all the measured characteristics. In addition, we run regressions to analyse the effect of health on claiming and employment decisions using a large set of background variables for three birth cohorts (1949-1951). The key assumption for causal interpretation is that individuals with a chronic health condition would have had similar outcomes to their matched counterparts without health issues, and that a chronic health condition is a valid signal of shorter life expectancy. We also test for robustness to omitted variables following a procedure developed in Altonji et al. (2005) and Oster (2019). Below, we will be more precise about our theoretical and empirical estimand, and what we can learn from the data (Lundberg et al. 2021).

Our findings reveal a significant association between our signal or proxy indicating shorter life expectancy and the joint occurrence of early claiming and continued employment in our regression models. Individuals are influenced by health information, leading them to have a higher likelihood of opting for pension payments and continuing their employment at the age of 62, as compared to individuals without health issues. This effect remains consistent for women even after adjusting for unobservables. However, for men, the effect is close to zero following the adjustment for unobservables.

Pension take-up, health and life expectancy

The new pension system in Norway, implemented in 2011, comprises two main components relevant to our study³: a) adjustments are made for increasing life expectancy in the population,⁴ and b) the possibility of combining work and claiming pension after the age of 62 for all workers without a reduction in pension payments.

The pension system operates in a manner where the present value of pension payments is, in principle, unaffected by the withdrawal age, thereby introducing actuarial neutrality into the system, assuming that individuals have no knowledge of their own life expectancy. If pension withdrawal is deferred, the annual pension payment amount increases. The present value remains unaffected due to a reduction in the remaining average life years with pension payments. The system is intentionally designed to incentivize individuals to stay in the labor market longer. If a person postpones pension uptake and continues working for one year, the annual pension benefit increases by approximately 7.5%.

Individuals eligible for early pension uptake can claim pension benefits within the age range of 62 to 75, irrespective of whether they retire from the labor force or not. These pension benefits are granted for the entirety of their life and are not subject to an earnings test.⁵ The neutrality of the pension system is based on the calculation of average life expectancy at age 61 for each birth cohort. The actual impact of claiming age on the net present value depends on an individual’s life expectancy relative to the cohort’s average life expectancy.

The decoupling of claiming age and continued employment introduces individuals to a new set of considerations related to a monetary inter-temporal choice problem. One may ask how well-informed soon-to-be pensioners are concerning these choices about early or deferred claiming and employment. The Norwegian Labour and Welfare Administration (NAV) administers a third of the national budget through schemes such as unemployment benefit, work assessment allowance, sickness benefit, pensions, child benefit, and cash-for-care benefit. NAV informs people individually when they approach the age of 62 years about their pension entitlements, i.e. basic pension and income-related pension. An individual may keep track of their pension entitlements and accumulated pension on their individual webpage at NAV. Importantly, the webpage facilitates easy-to-perform simulations of the annual pension and pension level, depending on choices made for (i) the age at which pension payments start, (ii) the percentage of the pension to be paid (20%-100%); and (iii) the decision to work full-time or part-time (as low as 20%). It is easy to contact NAV and receive information through Internet-based chats. Furthermore, most employers inform their employees about the choices they can make and the consequences for annual pension and accumulated pension. Labour unions inform their members on pension issues, too. Private banks do the same for their customers. News media regularly cover topics related to pensions, including discussions on how individual longevity may impact the net present value of pension payments.

The value of delaying pension claims is positive for long-lived individuals and negative for short-lived individuals, all other things being equal. Despite the pension system’s neutrality regarding average longevity, asymmetric information might lead to non-neutral behavior.⁶ Individuals can incorporate private information about their health status as a signal of longevity in their decision-making process to maximize the net present value of pension payments.⁷

Several studies are of interest in relation to health outcomes and life expectancy. DuGoff et al. (2014) analyse the life expectancy of Medicare beneficiaries aged 67 years or more by numbers of chronic conditions. They conclude that life expectancy decreases with each additional chronic condition. A 67-year-old individual with no chronic conditions will on average live for 22.6 additional years. A 67 year-old individual with five chronic conditions and $\ge$10 chronic conditions will live 7.7 and 17.6 fewer years, respectively. The average marginal decline in life expectancy is 1.8 years with each additional chronic condition, ranging from 0.4 fewer years with the first condition to 2.6 fewer years with the sixth condition. Vanajan and Gherdan (2022) also conclude that having a chronic health condition is associated with a change in subjective life expectancy, in particular newly diagnosed ones, relative to having no chronic health condition.

Franco et al. (2007) calculate the association of having diabetes mellitus with life expectancy, and years lived with and without cardiovascular disease (CVD) among populations aged 50 years and older. They conclude that diabetic men and women aged 50 years and older lived on average 7.5 and 8.2 years less than their nondiabetic equivalents. The differences in life expectancy free of CVD were 7.8 and 8.4 years, respectively. Livingstone et al. (2015), a study based on Scottish data, confirm that diabetes mellitus has consequences for expected lifetime. The estimated life expectancy of patients with type 1 diabetes in Scotland based on data from 2008 to 2010 indicated an estimated loss of life expectancy at age 20 years of approximately 11 years for men and 13 years for women, compared with the general population without type 1 diabetes.

Franco et al. (2005) analyse the life course of people with high blood pressure levels at age 50 in terms of total life expectancy and life expectancy with and without cardiovascular disease compared with people with normal blood pressure (normotensives). Compared with hypertensives, the total life expectancy was 5.1 and 4.9 years longer for normotensive men and women, respectively. Increased blood pressure in adulthood is associated with a great reduction in life expectancy and more years lived with cardiovascular disease. This effect is greater than estimated previously and affects both sexes similarly.

Based on our own calculations using register data spanning a limited number of years, and with descriptive statistics and regression results available upon request, we have identified a strong association between chronic disease and objective measures of hospitalization and mortality. The risk of dying between age 62 and 64 doubles in relative terms for the chronic disease group, but the absolute numbers are small: 1.2 % in the chronic disease group dies between age 62–64, while 0.5 % dies in the group having no such diagnosis.

The number of papers on subjective measures of health and life expectancy is increasing, but they are not reviewed in this context. The utilization of register data on health outcomes, in comparison to self-reported health status, helps mitigate potential biases arising from social class or other factors that might influence the self-assessment of health (see for instance Lindeboom and Van Doorslaer (2004), Baker et al. (2004), and McFadden et al. (2009)). Henceforth, rather than subjective or self-rated health indicators, our study uses diagnostic information for each individual registered by general practitioners (GPs) after each visit.

Data sources

Our dataset is sourced from public longitudinal registers, allowing us to follow individuals over time and conduct a comprehensive analysis of work and claiming decisions alongside changes in health status. The available data spans up to and includes the year 2014. For our analysis, we focus on the initial three cohorts born in 1949, 1950, and 1951, representing the first groups to reach the age of 62 following the implementation of the new pension system in 2011.

The information on work and income is extracted from the FD-Trygd database, which integrates administrative data from the National Insurance Administration, Statistics Norway, and the Directorate of Labour. This database encompasses the entire Norwegian population and provides details on work, income, and social security aspects (such as sick leave, disability, retirement, etc.), along with background characteristics such as age, gender, education, marital status, children and grandchildren, employment status, potential pension payments, interest payments, sick leave history, and more.

Individual health information is obtained from the Norwegian Health Economics Administration (HELFO) and merged with data from FD-Trygd. HELFO is responsible for the Norwegian primary care patient list scheme. GPs are remunerated through the social security system, based on a combination of fee-for-service and capitation contributions. GPs have the role as gatekeepers, i.e. apart from emergency admission to hospital, a patient must generally be referred to specialist/hospital care by a GP before being admitted to either inpatient or outpatient treatment. There are more than 4,100 registered primary care physicians (GP), with a total listed population of approximately 5 million inhabitants (99.6% of the population). After each patient consultation, GPs submit an invoice to HELFO. The register includes information on patients’ age and gender, date and time of contact, and diagnosis according to the ICPC-2-diagnosis code and codes from a detailed tariff for types of contact. HELFO data is available from 2006 and onwards. The inclusion of data from this particular database distinguishes our study from other studies of the Norwegian pension system, for instance Brinch et al. (2015), Hernæs et al. (2016), Brinch et al. (2018) and Hernæs et al. (2019).

To identify individuals with a potential shorter life expectancy, we utilize specific diagnoses or combinations thereof, as presented in Table 1. This table serves as a reference to establish our treatment group, which comprises individuals presumed to have a shorter life expectancy. In contrast, our comparison group consists of individuals without documented health issues.

Table 1 Definition of chronic disease

ICPC-2 classifies patient data and clinical activity in the domains of GP practice and primary care based on the patient’s reason for the encounter, the problems/diagnosis managed, and interventions. Health information is based on data prior to the earliest claiming age of 62, in particular in the 57–61 age span (2006–2012).

Sample selection and descriptive statistics

The current pension system provides individuals with shorter life expectancies, relative to the average life expectancy of their respective cohorts, incentives to opt for early pension claiming instead of deferring. However, it is important to acknowledge that not all individuals from the three cohorts born in 1949, 1950, and 1951 were eligible for early pension take-up due to insufficient accumulated pension capital. Additionally, a significant portion of individuals who were not employed in the last quarter before reaching the age of 62 received disability pension, precluding them from pursuing early claiming in conjunction with employment. Accounting for these necessary considerations, our final sample encompasses 90,216 individuals, as depicted in Table 2.

Table 2 Individuals from three cohorts (1949–1951)

The main outcome or dependent variable is a binary variable for which 1 indicates early claiming ($P=1$) in combination with work ($W=1$), and 0 otherwise at the age of 62. This choice would enable us to more effectively isolate the selection issues related to individuals with shorter and longer life expectancies, without being confounded by the work decision and its correlates. Early claiming in combination with work generates the greatest increase in annual pension payments compared to all other combinations, for those with lower life expectancy. Thus, we examine the likelihood of individuals with a relatively short life expectancy choosing the joint outcome of work and early claiming, compared to those with a longer life expectancy. We also analyse all four combinations of P and W in a multinomial regression model. Based on the available data, we are unable to analyse late claiming, since we only have three years of follow-up data after 2011. Our target population is solely those who are eligible for early claiming, so that all persons in our estimation sample are employed in the month before reaching 62 and have sufficient accumulated pension capital.

The available panel data is rich in terms of variables relevant to our empirical study. Our main explanatory variable is whether a person has a chronic disease or not, distinguishing between the treatment (chronic disease) and control (no chronic disease) groups. This serves as our indicator variable, signaling shorter life expectancy, as the chronic diseases under study are associated with lower life expectancy. To address differences between the two groups, we adjust for various background variables, including gender, marital status, parenthood and grandparent status, level of education, employment sector, interest payments on debt, prior work status (full-time or part-time), and occupation type (blue-collar or white-collar). Additionally, factors such as days on sick leave and the number of GP visits in a year are included as they may indicate aspects of an individual’s health status at age 61, influencing choices regarding work and claiming. Detailed information on all explanatory variables is presented and discussed in an appendix (available upon request).

While the pension system, as mentioned earlier, does not make adjustments based on these factors when calculating pension payments - relying solely on cohort-estimated life expectancy - it is crucial to control for heterogeneity related to these variables. These factors are significant in pension decisions as they correlate with life expectancy. Separate analyses are conducted for females and males.

Table 3 presents the mean of the dependent variable for both the entire sample and various sub-groups within the data. We have only selected a few variables for this table. All background variables are measured at age 61. A table which includes all subgroup variables is available upon request. The outcome variable reported in Column (1) in Table 3 is an indicator variable for the combination of working ($W=1$) and pension take-up ($P=1$). The outcome variable is assessed during the final quarter prior to reaching the age of 63. Column (1) shows the mean of the dependent variable for different subgroups of the sample. Column (2) shows the number of observations, Column (3) shows the mean difference in the dependent variable, while Column (4) shows the difference in percent.

Table 3 The effect of having a chronic disease, which signals shorter life expectancy, on joint early claiming and employment

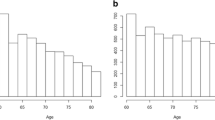
It is clear from Column (1) in Table 3 that early claiming behaviour varies considerably between subgroups of the sample. The raw/unadjusted mean is 27.6% for the full sample, meaning that 27.6% of the sample claim retirement benefits early and continue working at the age of 62. The table shows that men claim earlier than women. The difference between chronic disease and the comparison group, reported in Column (3), is also greater for men. The unadjusted effect is 3.49 percentage points for men and 0.57 percentage points for females, with an overall effect of 2.86 percentage points. In terms of the decision to claim early and continue working, women are relatively less affected by the signal indicating a shorter life expectancy compared to men. This is also illustrated in Fig. 1, which shows the difference evolving over time for men and women separately after the age of 62.

The estimated associations between the proxy/signal of shorter life expectancy and early claiming are positive for all subgroups of the data – shorter life expectancy is associated with early claiming. This is also predicted by theory. Highly educated people also act on the signal to a greater degree than those with medium or lower education. The association appears to be considerably stronger among workers in the public sector than in the private sector, and among full-time employed people compared to part-time workers at age 61. This is also the case for white-collar workers compared to blue-collar workers. The association is also strong for individuals with a relatively high level of accrued pension payments at 61. The difference between the chronic disease group and the comparison group within subgroups is as high as 5 percentage points.

Fig. 1

Difference in claiming/work by chronic disease for males and females. Note: The figure illustrates the effect of shorter life expectancy for men and women born 1949–1951. Shorter life expectancy is proxied by chronic disease. The figure shows the effect up to 9 quarters (3 years) after the age of 62. The y-axis shows the effect in percentage points, where the average outcome variable for men and women is 37.6% and 13.8%, respectively, see Table 3

Analytical strategies

The two groups of people, those with chronic conditions and those without, which serve as an indicator of shorter life expectancy, are different, and are likely to display distinct behaviors when it comes to work and early claiming decisions. We begin by matching the two groups to ensure that they are equivalent in all the measured characteristics.

Conditional on the variables used in the matching procedure, the key assumption is that individuals having a chronic condition would have had similar outcomes as their matched counterparts without health issues, i.e. in the absence of the illness, or that there are no systematic differences in the potential outcomes of treatment and control group members (Morgan and Winship 2015). This assumption is not possible to test, but it is possible to produce evidence for considering treatment status to be conditionally independent.

Formally, for individual i, $T_i$ is an indicator variable denoting whether the individual is a member of the treatment group ($T_i = 1$) or the control group ($T_i = 0$). Furthermore, $Y_i^1$ is the potential outcome for individual i in the treatment state and $Y_i^0$ is the potential outcome for individual i in the control state. The individual causal effect, which can never be directly observed in the data, is defined as the difference in the potential outcomes in the treatment and control states, ${\delta }_i = (Y_i^1 - Y_i^0)$. The average treatment effect is theoretically defined as the average over the two potential states for all individuals:

$$\begin{aligned} {\delta }_{ATE} = \frac{1}{N} \sum _{i=1}^{N} (Y_i^1 -Y_i^0). \end{aligned}$$

(1)

The average treatment effect for the treated (${\delta }_{TT}$) is defined in the same manner by summing over the number of individuals in the treatment group ($N_T$). Our target group $N_T$ thus includes individuals eligible for retirement at age 62 and defined in the group having shorter life expectancy. $Y_i$ is in our case an indicator variable for whether an individual draws a pension and continues to work after the age of 62. We also condition on specific values of background variables ($X_i$) making the theoretical estimand a conditional treatment effect parameter: ${\delta }_{ATE_x} = 1/N_x \sum _{i: X_i=x}^{N_x} (Y_i^1 - Y_i^0)$.

Matching is used to adjust for non-random assignment to treatment, which in our case is selection into health status. Matching is based on variables prior to the measurement of the outcome variable $Y_i$, i.e., when the person is 61 years old. To conduct the matching, we use coarsened exact matching (CEM), see Blackwell et al. (2009) and Iacus et al. (2012). Part of a class of methods labelled “Monotonic Imbalance Bounding,” the key feature of CEM is that it sets bounds, prior to the matching, on the maximum allowable imbalance between the matched treatment and control group on all variables used in the matching procedure. While commonly used matching procedures, such as propensity score matching, generate balance on all variables used to predict selection into treatment in expectation, CEM ensures balance on all variables used in the matching procedure within the sample.

As described in Iacus et al. (2012), CEM involves three steps. First, matching variables are “coarsened” into intervals for those variables that are not indicator variables to begin with. Second, all observations are placed within strata of the matching variables, and matches are made within strata of the coarsened variables. Third, strata that do not include members of both the treatment and the control groups are discarded. The resulting estimates produced after eliminating strata that do not include members of both groups are referred to as “local sample average treatment effects on the treated” by Iacus et al. (2012). This label is used to emphasize the fact that estimates do not generalize to a wider population, nor do they apply to the entire sample. Instead, estimates apply to the segment of the sample that is successfully matched. The coarsening of continuous variables, create some remaining imbalances in the matched data. It is reasonable to try to adjust for the remaining imbalance using a regression model, as we do in our analyses. After matching, where common support is provided, our estimation sample reduces from 90,216 to 74,157. Matching does a good job in making the two groups equal. More details about the matching process are available upon request.

Our empirical estimand is constructed by averaging over our two groups defined by health status. It is the difference in the observed outcomes for birth cohorts 1949-1951 between those in the shorter life expectancy group ($T=1$) defined by health status and those not in that group ($T=0$). This involves only observable quantities (no potential outcomes)

$$\begin{aligned} {\hat{\delta }}_{ATE} = \frac{1}{N_M^1} \sum _{i \in \mathbb {S}_1} Y_i (X_i) - \frac{1}{N_M^0} \sum _{i \in \mathbb {S}_0} Y_i (X_i) \end{aligned}$$

(2)

where $N_M^1$ is the number of observations in the treated group (shorter life expectations) for our matched sample and $N_M^0$ is the number in the untreated group. It is natural to express our empirical estimand within the framework of a regression model. i.e. conditional mean:

$$\begin{aligned} {\hat{\delta }}_{ATE} = \frac{1}{N} \sum _{i=1}^N \mathbb {\hat{E}}[Y_i | X_i, T=1] - \frac{1}{N} \sum _{i=1}^N \mathbb {\hat{E}}[Y_i | X_i, T=0] \end{aligned}$$

(3)

where $X_i$ are pre-treatment covariates. This can be implemented as a simple dummy variable regression specification:

$$\begin{aligned} Y_i = X_i \hat{\beta } + \hat{\delta } T_i + \hat{\epsilon _i} \end{aligned}$$

(4)

There is no one-to-one mapping between the theoretical estimand in equation (1) and the empirical estimand in equation (3) unless the last term in equation (3) represents the outcome individuals with shorter life expectancy would have experienced had they not had shorter life expectancy. This is the case if $X_i$ adjusts for differences between the two groups, i.e., $\mathbb {\hat{E}}[Y_i | X_i, T=0] = \mathbb {{E}}[Y_i^0|X_i,T=1]$. This is the assumption of selection on observables. To differentiate between $\hat{\delta }_{ATE}$ and ${\hat{\delta }}_{TT}$ we could split equation (4) by T to run two separate regressions: $Y_i = X_i \hat{\beta _1} + \hat{\epsilon _i}$ if $T=1$ and $Y_i = X_i \hat{\beta _0} + \hat{\epsilon _i}$ if $T=0$, and calculate $X_i(\hat{\beta _1} - \hat{\beta _0})$ by prediction for the full sample to retrieve ATE, and for the sample of treated to retrieve TT, assuming selection on observables only. The alternative to this procedure is to use the imputation method (Hahn 1998). This opens for an analysis of heterogeneous effects, which in our case involves interaction terms and subgroup/stratification analysis.

The matching and regression models employed in our analysis account for observed confounders, aiming to mitigate potential biases. To assess the robustness of our estimates in relation to omitted or unobserved variables that could lead to bias, we adopt an approach that involves examining coefficient changes upon incorporating pre-treatment predictors (Altonji et al. 2005). A procedure proposed by Oster (2019) calculates estimates of the potential endogenous variable and relative degree of selection in linear models. These estimators are consistent under the assumption that the selection on observed variables is proportionate to the selection on unobserved variables. If the regression coefficient is stable after inclusion of background variables, this could be a sign that omitted variable bias is limited, see for instance Chiappori et al. (2012), Lacetera et al. (2012). It is also possible to calculate the degree of selection on unobservables relative to observables which would be necessary to explain away the results, see Oster (2019). A related approach is given in Aakvik (2001), where estimated effects are scrutinized to see whether they are sensitive to selection bias due to correlation between unobserved factors and the potential endogenous treatment variable. This procedure, however, is not used within the framework of a regression model, but directly on a matching estimator.

Regression results

We have argued that the new pension system gives people with shorter life expectancy than the average life expectancy of their respective cohorts’ incentives to claim early rather than delaying. There is an incentive in the pension system to continue working, as this will always increase yearly pension payments. The main outcome variable is therefore a binary variable for which 1 indicates early claiming ($P=1$) in combination with work ($W=1$). We report the full regression results in, where all the background variables are included. In this table we report both the full sample results and the estimated results based on the matched sample using regression models. Table 4 in the text below presents only a selection of results for the matched sample, both overall and for males and females separately. The overall estimated effect of chronic disease indicates a strong link between (relatively) short life expectancy and early claiming in combination with work at the age of 62. The significant association holds for the matched sample regardless of gender. Individuals with an assumed relatively shorter life expectancy are approximately 1.45 percentage points more inclined to opt for early claiming in conjunction with work, compared to those with a longer life expectancy, see Column 1 in Table 4. Since the mean of the outcome variable, $\Pr (P=1 \cap W=1)$, is around 0.3, the effect translates to 5%, which is lower than the unadjusted effect of 10.4% from Table 3 in Sect. 4.

Table 4 The effect of chronic disease on joint early claiming and employment. Males and females

The results of our analysis indicate that the proxy variable of shorter life expectancy has a stronger effect on early claiming among males than females. Specifically, the estimated effect in terms of percentage points is 1.65 for males and 1.08 for females, as shown in Columns (2) and (3) of Table 4. However, in relation to the mean of the dependent variable, the effect is actually greater for women, at 8.2% (0.0108/0.132), than for men, at 4.2% (0.0165/0.394). Notably, the estimated effect for women is higher in the matched sample compared to the unadjusted coefficient effect reported in Table 3. The estimated effect for men decreases from 9.3% to 4.2% after controlling for other factors through matching and regression adjustments, compared to the unadjusted effect.

We now test for robustness to omitted variables. Our original estimate of our proxy of life expectancy on early claiming in combination with continued work is 1.45 percentage points, see Table 4, Column (1). This effect is reduced to 1.28 percentage point if we assume that bias due to selection on observed background variables equals bias due to omitted variables, i.e. using $delta=1$ and $Rmax=1$ in the procedure used in Oster (2019). If we assume that selection on unobservables is 50% of the selection on observables ($delta=0.5$), our bias-adjusted estimate changes to 1.37 percentage points. Our robustness test confirms that our estimates are not affected by omitted variable bias, using different values of delta and Rmax. We find that the unobservables would need to be almost four times as important as the observables to produce an estimated effect of zero. This is a very large number, given that we include a lot of background variables in our estimation equations.

The findings for females remain robust, with a positive effect of approximately 1 percentage point, which is around 8% in relative terms. The bias-adjusted estimate for males moves towards zero, assuming that bias due to selection on observed background variables equals bias due to omitted variables $(delta=1)$. However, this result hinges on setting $Rmax=1$, which is the maximum an R-squared value can be. Oster (2019) discusses reducing Rmax by a proportion of the actual R-squared in the regression model. If we reduce Rmax to two times the actual R-squared, together with $delta=1$, the bias-adjusted estimate is very close to its original estimate of 1.65 percentage points for men (not reported in the table). Even when using four times the estimated R-squared produces an estimate close to the original. In that case, the bias-corrected estimate for men is 1.3 percentage points.

While the stability of coefficients is a useful indicator of bias, it is important to note that it does not provide a complete assessment of potential omitted variable bias (Oster 2019). Nonetheless, the robustness checks performed in our analysis indicate that the potential bias from omitted variables is limited, strengthening the credibility of our results. Our results indicate that the effect of our life expectancy signal for early claiming is statistically significant, but relatively small in magnitude.

In order to add to the knowledge concerning claiming behaviour and how life expectancy may influence choices, it is essential to analyse those who continue to work and claim early, relative to those choosing one of the other three choices available. The choice of work/early claiming captures the essence of the new pension system, while allowing us to study the effect of life expectancy on benefit claiming. An eligible individual can make one of four mutually exclusive choices related to claiming and work.

• (i) quit working and not claim early (Group 1: $W=0$, $P=0$);

• (ii) quit working and claim early (Group 2: $W=0$, $P=1$);

• (iii) continue to work and not claim early (Group 3: $W=1$, $P=0$); and

• (iv) continue to work and claim early (Group 4: $W=1$, $P=1$).

In our data, Groups 1 and 2 are smaller in terms of numbers of individuals. Group 1 consists of 6,503 individuals, Group 2 consists of 4,978 individuals, and Group 3 consists of 41,225 individuals, while Group 4 consists of 21,451 individuals. Table 5 also shows numbers of men and women in each group.

To check the robustness of our results, we estimate the multinomial logit model with the four outcomes detailed above. The coefficients reported in Table 5 show the difference in probability of belonging to the group with relatively short life expectancy, versus those with relatively long life expectancy, i.e. $\Pr (W,P|CD=1,X) - \Pr (W,P|CD=0,X)$ for each of the four joint claiming and employment outcomes.

Table 5 Multinomial logit model, marginal effects

The results reported in Table 5 confirm the difference between the two groups: people with chronic conditions, our proxy for shorter life expectancy, make different choices regarding work and early claiming, compared to people without such conditions. People with chronic diseases/conditions have (1) a higher probability of claiming early in combination with work and (2) a lower probability of combining work with deferred claiming, as reported in the two last rows in Table 5.

Conclusion

The current pension system in Norway permits a separation between pension claiming and work, offering individuals the flexibility to simultaneously combine various degrees of take-up and work. Consequently, individuals can now balance work and leisure differently than in the old system, where this type of flexibility was not allowed due to strict earnings testing. However, the potential for early claiming raises explicit concerns regarding life expectancy and potential adverse selection.

Our main hypothesis is that individuals with a shorter life expectancy, compared to the average life expectancy of their respective cohorts, are more likely to claim their pension early and continue working than are those with an average or longer life expectancy. To test this hypothesis, we examine the effect of chronic disease on early claiming and work using empirical data. Our analysis provides some evidence to support our hypothesis. After adjusting for a large set of background variables, we find that the degree of selection is relatively low. This probably reflects the fact that any signal of shorter life expectancy could be imperfect or noisy. While asymmetric information and adverse selection play crucial roles in various markets, such as the annuity market and insurance markets in general, we did not observe strong effects of these factors in our analysis. The unadjusted/raw estimates from descriptive statistics, however, indicate a far stronger link between shorter life expectancy and early claiming compared to the matching and regression models.

Although our main results and those of Brinch et al. (2018) are in accordance with each other, it is noteworthy that the analyses are based on two different approaches in terms of how to model expected longevity. We use a predictor or signal of expected longevity constructed by exploiting detailed diagnostic health information on individuals strongly correlated with mortality, while Brinch et al. (2018) use parental longevity as an instrument for the money’s worth using a 2SLS set-up.

Our study of claiming behaviour is not without limitations. Firstly, we lack direct information on subjective life expectancy or subjective health, which is essential for a comprehensive understanding of adverse selection issues. Since we use a chronic condition as a proxy or signal of reduced life expectancy, we can expect measurement error in this variable, although we find that our proxy variable is highly correlated with mortality. Measurement errors may inflate standard errors and lead to attenuation bias, drawing our results towards zero. The fact that we still find significant coefficients indicates that attenuation bias is not detrimental to our study and the results we report. In addition, our treatment group of chronic diseases only includes the largest diagnosis groups. Our control group thus probably includes some individuals who also have health issues and shorter life expectancy. This also draws the effect towards zero. Since life expectancy is unobserved and chronic disease is a noisy signal, it is difficult to fully establish whether the measured effect is attributable to lower life expectancy or to other consequences of chronic disease unrelated to life expectancy.

Secondly, we test for robustness to omitted variables following a procedure developed in Altonji et al. (2005) and Oster (2019). Here, we find that selection due to unobserved variables would need to be almost four times as important as the observables to produce an estimated effect of zero. This is a large number, given that we include a lot of pre-treatment background variables in our estimation equations. However, this type of analysis will not provide a definitive solution to the endogeneity problem.

Thirdly, we use a selected sample of individuals born in 1949-1951 that turned 62 after 2011. These are the first cohorts affected by the pension reform characterised by flexible claiming and no earnings test. Learning might take place as the pension reform affects more and more birth cohorts. Even though the pension system adjusts for increased average remaining life expectancy after the age of 61, heterogeneity and asymmetric information regarding life expectancy also make adverse selection a potential problem going forward.

Fourthly, our variable that separates shorter-living and longer-living individuals by chronic disease might be correlated with the choice of drawing a pension for reasons other than life expectancy. For instance, a person with a chronic disease might expect higher private health expenses than a person without any such disease, which might require drawing a pension in conjunction with work. While the presence of chronic diseases might be considered a good proxy of life expectancy, one cannot claim that the only reason for the estimated effect is different life expectancy expectations. Merely having chronic disease cannot enable us to differentiate between active and passive selection for pension insurance. Moreover, the potential for part-time work and partial pension claiming might also influence how life expectancy and adverse selection impact claiming behavior.

Adding more cohorts to the study as data becomes available is a sensible direction for future research, as our study focuses on the immediate years following the implementation of the pension reform. We have solely considered one aspect of adverse selection as we look at early claiming. It would also be interesting to see whether longer life expectancy is associated with deferred claiming behaviour, for instance up to the age of 70. We should also underscore the complexity of claiming decisions, which may be influenced by various factors, such as peer effects, myopic consumption behaviour, risk aversion, spousal spillover in retirement, bequest motives, rationing, etc. Examining some of these factors is an interesting area of study.