Abstract
We define a new mathematical function that is an adaptation of a welfare function consistent with the premises of classical welfare. This function is innovative in that it enables us to specifically identify income tax functions that optimally balance the objectives of justice and efficiency in an economy. The new welfare function combines gross national product as an expression of economic performance with the Gini coefficient as a measure of its distributive justice. Afterwards we concentrate on the application of the new welfare function to the design of tax regimes and discuss the question of how to optimize income taxes. On the basis of our data, we discover interesting solutions. To find these, we compute optimal values of the welfare function under constraints of negative tax incentives; in the present case, tax avoidance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
One of the central concerns in designing an economic system lies in determining the relationship between economic freedom and economic justice, which defines its political position within the left–right spectrum. Theorists positioned on the left tend to emphasize economic justice, whereas those on the right tend to focus on economic freedom. This dispute has dominated the economic order debate since the beginning of the Industrial Revolution, or at the latest since Karl Marx with his concept of “class struggle” and the great doctrinal war between capitalism and communism.
The authors of this article share the opinion that the best economic system is the free market combined with some limitations where the free market leads to politically not desirable results. However, the relationship between freedom and justice is more a question of optimization rather than a fundamental contrast. Therefore, the purpose of this article is, firstly, to represent the relationship between freedom and justice as a condition of optimization, and to make a specific proposal as to how this optimization can be solved mathematically, and, secondly, to define income tax curves which are optimal regarding both, efficiency or freedom on the one hand, and justice on the other hand.
Research question
In the first part of the article, we investigate the question whether it is possible to define a reasonable welfare function which is not based on individual preferences. This condition is necessary, because Kenneth Arrow‘s “Impossibility Theorem” states (Arrow 1954), that it is not possible to define a welfare function based on individual preferences.
In the second part of this article, we concentrate on the question of how to define income taxes, so that they incorporate the criteria of justice and economic efficiency. To achieve this, the welfare function must be optimized under the restriction of negative tax incentives. These negative incentives emerge as soon as taxes are perceived to be excessively high.
Our article proposes a mathematically consistent way of deriving income tax curves, and we believe that this is a pioneering methodological approach. Our proposed model opens a new field of research enquiry.
Terms and necessity of conducting such research
The construction of a welfare function can provide answers regarding important economic questions such as optimal investing, optimal trade or optimal taxes. Optimal means, under the condition of that welfare function. As terms we use mathematical methods to be as objective as possible, without using ideological presumptions.
Methodology
To find a new welfare function we combine fundamental economic thinking with methods of behavioral economics. Despite the simplicity of the basic functions that we apply for our data analysis regarding welfare and tax avoidance, the derivation of our mathematical framework necessitates the use of more advanced methods (nonlinear functionals).
Main discussion
Literature review
After the second world war, it was time for economic theorists to turn their attention to economic growth in the context of welfare rather than defense. It was realized that welfare functions could play an important role as measures to be optimized, or even replace gross domestic (or national) product as being the most important economic measure. The basic idea was to define individual preferences and then aggregate these factor inputs as variables in a general welfare function.
In 1953, Kenneth J. Arrow, an American economist and subsequent Nobel Laureate (1972), proved a very astonishing fact: it is not possible, to define reasonable individual preferences and then aggregate these preferences to a general welfare function (Arrow 1954). Arrow was the first economic theorist to derive this result in a rigorous mathematical way.
This definitive conclusion almost terminated discussions about welfare functions. It was not that Arrow’s conclusion undermined the conceptual notion of a welfare function, but rather that it revealed that an aggregation of individual data under reasonable conditions is mathematically not possible.
In our proposed approach in this article, we deviate from the classic setting and define a welfare function that is not based on individual preferences. This individual aspect is replaced by the idea of distribution parameters. In order to determine the values of these parameters, we apply analytical methods from the field of behavioral economics.
A welfare function can also be seen as a consequence of the finding, that in a free market justice does not occur automatically (e.g. Söllner 2012).
Another famous result of Arrow and Debreu in the 1950s states that free market economy solves the problem of distribution in a Pareto optimal way (Arrow 1963). But Pareto optimal does not necessarily mean just, which can be seen with the example, that making rich people richer and leaving poor people where they are is Pareto optimal, but arguably not just.
To develop the new welfare function we make use of three parameters:
-
B, the gross national product (GNP),
-
h, where h is defined as 1-G and G is the well-known Gini coefficient of income inequality,
-
λ, which is a parameter defining the relative weight of B and h.
These are shortly introduced in the next sections.
Gross national product (B)
Gross national product (GNP or B) or closely related concepts such as national income are measures that are internationally used to quantify a country’s annual economic production. GNP is virtually the only measure of its kind. For this reason, it is used here as one of the three basic elements in defining the new concept of fairness.
In this article, we use GNP in its proper sense (nominal, aggregate). If we mean GNP per capita, this is mentioned explicitly.
We note that the definition of B is not undisputed (e.g. Stiglitz 2012). On one hand, different important parts of an economy are not included, e.g. unpayed homework. On the other hand, parts of the economy are included, although they do not contribute to welfare, e.g. accidents. This is an important discussion, but best left to be explored elsewhere. For our purposes, we use the generally accepted usual definition of the gross national product.
It should be mentioned that in our calculations in “Modelling tax incentives”, we approximate the GNP with the sum of all employee incomes, which represents usually around 75–80% of the classical GNP (the rest being corporate profits). This approximation proves to be very useful, leads to concrete results and keeping in mind the scalability just mentioned we do not really lose generality in forming our conclusions.
The distribution of income as the main element in the definition of economic justice
We refer to the well-known measure for inequality, the Gini coefficient G (Gini 1921). According to this definition, it holds that: \(0\le G\le 1\),
-
\(G=0\) \(\Rightarrow\) no inequality.
-
\(G=1\) \(\Rightarrow\) extreme inequality.
The Gini coefficient can also be determined for “distribution variables” other than income, e.g., wealth. In our text, G is always related to income, not to wealth.
Since G measures an uneven distribution and we seek a measure for the uniformity of a distribution, we use the complementary value \(h=1-G\).
For h, \(0\le h\le 1\), we easily see that:
-
\(h=0\) corresponds to extreme inequality.
-
\(h=1\) corresponds to no inequality.
The most important characteristic of h is that its value rises with an increasingly uniform distribution of income or wealth. See “Key aim of the new welfare formula: to link economic performance (B) and distributive justice (h)”, for a discussion about the issue of uniformity not being synonymous with justice. For a precise definition of h, the Gini coefficient will be used. This is, however, not compulsory for conceptually defining the term and other inequality measures could be theoretically used as well.
Examples of h in some countries: the highest values of h are around 0.75 (Sweden, Norway). The lowest values of h are around 0.30 to 0.35 (some African countries).
Up to a certain value of h (in practice h = 0.8) the two expressions “uniformity of distribution” and “distributive justice” are narrowly linked. If h > 0.8, GNP begins to shrink, and a higher value of uniformity is no longer linked to a higher value of “distributive justice” (see also “Key aim of the new welfare formula: to link economic performance (B) and distributive justice (h)”).
Key aim of the new welfare formula: to link economic performance (B) and distributive justice (h)
Gross national product, referred to here as B, is a key factor in economics as well as in economic policy. When referring to growth, the growth of B is implied. When referring to “depression”, a specifically defined reduction in B is implied.
The importance of B in economics is so great that it has become almost synonymous with the general prosperity of a country; therefore, the actual objective of economic policy can be perceived as the growth in B.
However, the magnitude of B is not the only factor that significantly contributes to the general well-being of mankind. Even if we only focus on economic variables, leaving aside all non-economic quantities or qualities, B is not the only factor that should be considered when investigating well-being. Most people have a basic understanding of the concept of justice or fairness. The allocation of income and assets also plays an important role in an assessment of a country’s overall economic situation. These latter factors will be used and described below to define a new mathematical measure.Footnote 1
The basic idea therefore will be to combine the measures of “economic performance” and “distributive justice” into a single mathematical measure.
If the two measures, B (gross national product) and h (distributive justice), are to be combined into a single new measure F, the following approach suggests itself:
Let g be an increasing function of h \(.\) “The power function \({\mathbf{h}}^{{\varvec{\uplambda}}}\) and the value of λ” explains why g(h) is most suitably defined as the power function:
The newly named functions and measures F, B, h and λ will be further described in more detail below.
The formula for F now reads:
As a result of this definition, the following holds true:
-
F increases with h when B remains constant. Because h is a measure of distributive justice, F increases with increasing distributive justice.
-
F increases with B when h remains constant.
Therefore, F is a measure of both economic strength and of distributive fairness in a given society. The term “fairness” (abbreviated F) was chosen to represent this concept. One could possibly use the term “welfare”, but we prefer to avoid any associations with the phrase “welfare state,” as the definition given here is not equivalent to the concept of the “welfare state”.
The measure F as a function of B and the associated h, however, is a type of welfare function. One of the greatest economists of the twentieth century, A. C. Pigou (Pigou 1920), proposed that the most important concepts when defining welfare could be gross national product as well as a measure of income or wealth distribution (Samuelson and Nordhaus 2004). To the best of our knowledge, however, this idea was not pursued any further by Pigou, or by any other social scientist.
It is now clear that optimizing F might be more useful than optimizing either B or h. Since the definition of F is based on both B and h, the optimization of F means that the combination of B and h is being optimized. This reformulation of the maximization problem provides a potential solution to the age-old, yet still relevant question of whether to focus predominantly on economic growth or alternatively on distributive fairness. In short, the use of F potentially removes the clash of interests in the classic left–right political debate. The premise of optimizing F therefore presents a methodology that would avoid this old controversy, or at least objectify it. Further aspects of this mechanism can be taken into account: if we push h too high (distributive uniformity), beyond a certain threshold, B will begin to decrease owing to a loss in incentives. This is the main argument against an excessive uniformity in income distribution. Excessive uniformity can cause F’s growth rate to slow down and ultimately decline (see end of this section).
The premise of maximizing F thus implies the rule that there is an automatic limit for values of h beyond which h starts to reduce general prosperity (F).
The use of this premise is a very specific approach that differs from John Rawls’ Difference Principle (Rawls 1971). It is much narrower in scope while being simultaneously precise and easily applicable. Therefore, a very distinct yet simple method arises that allows us to establish a methodological “third way.”
The interplay between h and B is very complex. It can certainly not be described in a simple way. There seems to be a negative dependency between h and B for very high values of h (see the end of this section), and therefore such high values of h do not exist in the real world. For lower values of h we can practically suggest independence between h and B. To show this, we add here a scatterplot for the really existing interplay between h and B (Fig. 1).
Very high values of h are extremely rare. The behavior of B for very high values of h must nevertheless be discussed, based on historical records and in the light of fundamental considerations.
One historically documented example of a country with very high levels of distributive justice is Sweden. In the 1970s, Sweden attempted to make income distribution extremely even (i.e., producing a high h value). This was enforced by implementing a steeply progressive tax rate, in addition to other measures.Footnote 2 It turned out that higher income taxpayers became less motivated to work, and it was feared that gross national product would consequently contract considerably. For this main reason, the government chose to end the program and therefore abandoned the experiment of establishing an overall high level of h.
The experience of a decreased B value when h is too high is another reason why the definition
is well founded. In other words, the premise is to optimize F and not B or h alone.
By optimizing F instead of optimizing B alone, the risk of repeating the Swedish example with a high h value does not exist. If h is too high, then B will decrease, and hence F will as well. This, however, does not apply to theoretical examples. In trial model experiments, a decrease in B when h is too high is not automatically modelled. For all theoretical examples, it is essential to model this decrease as well. In the examples in this article, the modelling of this mechanism is called the “incentive function”, as it models the fall in incentives following high values of “equality.” In many examples, it would suffice if simply an upper limit were set for h; e.g., \(h\le 0.8\).
After reviewing a vast amount of literature on theories of philosophy and economics, we found no appropriate approach, although the notion of fair income or wealth distribution (i.e., economic justice) is not an obscure philosophical concept (see, for example, the principles established by John Rawls). Aside from the aforementioned generalized hypothesis by A. C. Pigou, political economy also lacks a comparable approach.
A considerable amount of attention has been devoted recently to the work of T. Piketty (Piketty 2014). It seems that a rigorous consideration of the interplay between economic performance and inequality measures is missing in Piketty’s work, or rather, that the discussion on the topic is relatively rudimentary. The core aim of our approach here is that both measures should be addressed and analyzed simultaneously.
The power function \({\mathbf{h}}^{{\varvec{\uplambda}}}\) and the value of λ
The power function \({h}^{\lambda }\) has been chosen for the equation \(F=B{\cdot h}^{\lambda }\), because it is a fairly general functional form that allows for the representation of a large class of monotonically increasing curves. The frequent occurrence of this function in physics is no accident, illustrating its universality. Though originating in the field of physics, the approach chosen here is applied to diverse disciplines owing to its universality and simplicity.
The factor λ represents a weighting factor between B and h, that is, an adjustment ratio value to regulate the relative relationship between gross national product and the measure of distributive justice. The idea is that distributive fairness can be weighted relative to GNP as desired. If policy makers decide that distributive justice should play a more important role, then λ can be increased.
This is most clearly shown when considering corresponding differential equations. If F, B and h are assumed to be functions of the variable x (this common variable can be e.g. thought of as taxable income as is done in later sections of this work in the concrete mathematical model), then it follows thatFootnote 3:
Expressed in words, the relative change in F is composed of an addition of the relative change in B, and λ times the change in h. The relative change in B has a weight of 1, while the relative change in h has a weight of λ.
Equivalent weighting is achieved at λ = 1. For λ > 1, h is weighted more than B, for λ < 1, B is weighted more than h.
Remarks:
-
In the case of short-term constant population growth, the per capita measures f and b can be used instead of F and B, which we will do later.
-
Similar formulas apply to several variables, but partial derivatives occur. Since the meaning of λ can be seen very clearly, we will forgo the use of an explicit statement for many variables.
In the book of the first author (Lüthy 2016), there is a detailed analysis of how to find the value of λ. Basically, λ should not be thought of as a physically given endogenous constant, rather it is dependent on economical and political environment and can be determined by methods of behavioral economics (and can possibly differ for different economies or the same economy at different points in time).
We start with the fact, that λ defines the relative weight of the GNP and the parameter h as a measure of distributive justice.
The basic idea is that the value of the weighting factor λ cannot be defined by a single individual. It is possible to formulate survey questions so that the answers deliver an informative indication for the choice of λ’s value.
There are different methods to find a reasonable value of λ. Here we show an example of one method, the so-called indirect method, where we define scenarios of combinations of B and h (we do not ask directly survey participants) how they estimate the relative weight of B and h. We defined many such scenarios, and the results were always similar. As an example, we show here one pattern of B and h combinations, which we call “countries”; each “country” stands for one combination of B and h (Table 1).
The question we asked our test-persons was: in which of the five countries would you prefer to live? The answers in this specific example were: mainly countries 2 and 3.
An important condition is the veil of ignorance, first introduced by John Rawls. It means that the participants have no knowledge about their own position within the income distribution.
The next step is now to ask: for which values of λ do we get the same answer, namely the maximum of F?
This leads to the answer: 1.5 ≤ λ ≤ 2.5.
With a quite strong preference for λ = 2.
Remarks:
-
We do not look for absolute exactitude. We want to show, that it is possible, with methods of “behavioral economics” to find good estimations of λ.
-
We think, that with further developed experiments it is possible to find even more exact values of λ.
-
λ is not an exact value as in physics. It could differ between different cultures. It does not have to be an integer.
The welfare function or Fairness-Formula is therefore
or
This is the function to be optimized, which we shall call the Fairness Criterion.
Fiscal policy—an important field of application of the fairness criterion
Taxes do not serve only as a source of income for the state, although this is probably their principal purpose. Taxes normally have strong effects on the behavior of the affected people, hence they also fulfil a certain control function.
Since the state is responsible for determining tax policy and levying taxes, it is also the main addressee for achieving fairness optimization in terms of taxation. Fiscal policy is probably one of the most important fields where the fairness criterion finds application.
In “Literature review”, we note that justice does not occur in a free market automatically—it must be encouraged, fostered and legitimated politically. The most effective way to realize this postulate in practice is probably through the collection of fair taxes. But how shall we define fair taxes? Does something like objectivity exist? This is a difficult question that has been discussed very often, but without a consensual scientific solution. In politics, we arrive at roughly acceptable solutions by means of a bargaining process between different interest groups or stakeholders.
In this section, we would like to show that the premise of fairness optimization is likely, at least, to objectivize the discussion about optimal tax curves. There is no simple, unambiguous solution. Nevertheless, a model’s findings can deliver the basis for consensual solutions with respect to a fiscal policy that is fair but still does not hamper the interests of economic growth.
As the definition of F relates to income distribution, it is obvious that the premise of fairness optimization also relates to income taxes.
Without further elaboration we mention here that analogous arguments are possible for asset and inheritance taxes.
The question as to which jobs should be done privately is a political issue. Following a principle ‘In dubio pro libertate’ (in doubt, opt for freedom), the private economy should be responsible for the provision of goods and services wherever possible.
The requirement that taxes should be as low as possible has to be understood in this sense. The state has to be efficient and it has to keep taxes low. Undoubtedly, different states define the responsibilities of the state differently. Therefore, the total amount of taxes per capita differs from state to state.
This section does not discuss the question of what a certain state should be responsible for. We do not analyze or appraise different views on this question: we only discuss the distribution of the tax payments, given a certain tax substrate.
Having said that, we point out that the state can influence individuals’ incentives by increasing or decreasing the marginal rate of income tax. Individuals’ responses to the influences of these changes will in turn provide information for developing a tax incentive function, as discussed in the following sections.
In some of the examples below, we omit the assumption that taxes must be positive; i.e., earners pay tax to the state. As a consequence, the models produce tax curves that are negative for low incomes. In the following, we identify these curve segments as attributable to negative income taxes; i.e., the state pays tax to earners.
Interestingly, the resulting values of F become higher if negative income taxes are allowed. This means that the optimization of F is improved by the introduction of negative income taxes, even if not very strongly. However, taxation theorists often argue that negative income taxes can have significant disadvantages and should be replaced by forms of tax credits. This, however, does not contradict the results of the fairness optimization. Negative values on the tax curve do not necessarily imply negative income taxes; they can be interpreted in a more general way.
As mentioned in “Key aim of the new welfare formula: to link economic performance (B) and distributive justice (h)”, B and h are not independent. Especially for high values of h, B decreases as a consequence of decreasing performance incentives (see the example of Sweden in the 1970s). This association is not included automatically in theoretical models; hence, it has to be modelled explicitly. We call this mechanism “negative tax incentives” or simply “tax incentives”, i.e., the effect that taxes have on the behavior of the affected people.
The task of building a precise model of tax incentives is one of the most important challenges that our approach leaves to future researchers. No “one-size-fits-all” approach is possible owing to country-specific methods of determining the level of the tax substrate and its use. The interpretation of the model’s results when formulated into policy may have an impact on tax incentives, and therefore it is crucial that the model is conceptualized as accurately and precisely as possible. In “Modelling tax incentives”, we propose a new simple model which illustrates that a consistent mathematical modelling of tax incentives is possible and should be attempted.
The main purpose of this section is the application of the Fairness Criterion on tax policy. The tax curves will be designed in order to maximize F under certain constraints.
We derive tax curves on the basis of marginal tax rates as a function of income. The exact description of the mathematical model will follow in the next section. The necessary mathematical tools belong to the theory of nonlinear functionals (Berger 1977; Schwartz 1969), because the result we seek is a functionFootnote 4 and not a single value.
Fiscal policy: the mathematical model
We use the following assumptions:
-
We discuss mainly marginal tax rates (contrary to absolute tax rates).
-
The total of tax incomes, called the tax substrate, is given.
-
The general form of tax curves is concave.
-
In addition, we discuss curves that are first convex, then concave (logistical curves). These do not deliver good results unless we accept negative income taxes, in which case such curves are important.
-
The resulting problems are quite complex (we look for curves, not just for values). Analytical solutions are not possible in general. We therefore calculate the results numerically.
-
As mentioned above, we need the definition of “negative incentive functions” in order to model decreasing values of B for high values of h.
-
We need a definition of general parameters. This leads to a great number of variants. For simplicity, we show only a small number of examples. The examples were chosen on the basis of “intuitive realism”; further examples are, of course, possible. We show only examples with \({\varvec{\lambda}}=2\) in order to reduce complexity.
In this section, we postulate that income tax rates in a country should be set in order to maximize the measure.
subject to the condition.
Here \({TS}_{aim}\) is a constant reflecting the tax substrate that the state would like to obtain, subject to political and economic factors. We illustrate this program using Swiss data as an example. We take the empirical income distribution of Switzerland from the data provided by the Swiss Federal Statistical Office (FSO). Although it is possible to fit the income distribution using a continuous probability distribution function, resulting expressions for the Lorenz curve are cumbersome at best, and often not given in an analytically closed form (depending, of course, on the fitting distribution).
We recall that a Lorenz curve \(L(x)\) is a mapping from \([\mathrm{0,1}]\) to \([\mathrm{0,1}]\). The value \(L(x)\) represents the portion of the total income (GNP) of a country owned by the poorest \((100\cdot x)\)% of the inhabitants. Thus, if we consider the difference \(L\left(x+dx\right)-L(x)\) at the point \(x\in [\mathrm{0,1}]\), this represents the (marginal) ratio of the income that \((100\cdot dx)\)% of the citizens richer than \((100\cdot x)\)% of the population earn. Dividing \(L\left(x+dx\right)-L(x)\) by \(dx\) gives the normalizedFootnote 5 salary of an individual within this group. Letting dx \(\to\) 0, if we assume \(L\) to be (at least) once differentiable, the value of the derivative \(L^{\prime}\left( x \right)\) corresponds to the normalized salary of the individual who finds himself on the x-th rung of a hypothetical \([\mathrm{0,1}]\)-valued income ladder.
We let GNPpre denote the nominal GNP before applying taxation. We may also write
since the last integral equals 1 by the definition of the Lorenz curve (100% of the population owns 100% of the wealth). The Gini coefficient G is defined by
For the motivation and explanation of the Gini coefficient concept, see the main body of this article and the references therein. The coefficient h that forms part of the function to be optimized is given by
We let \(s(x)\) denote the effective tax rate that is applied to the salary at level x, i.e., to \(L^{\prime}\left( x \right)\). That is, s represents the effective tax rate as opposed to the marginal tax rate. Let \(f(x)\) denote the fraction of the gross salary that remains available to the employee, i.e.,
There are certain natural requirements to be imposed on the tax rates. We impose here one very natural requirement that is most conveniently defined using a condition on marginal tax rates \(m(x)\) as opposed to effective tax rates \(s\left(x\right):\) we assume that marginal tax rates are a non-decreasing function of the salary level.
We remark here that it is equivalent to speak about effective tax rates or marginal tax rates, since it is straightforward to pass from effective tax rates to marginal tax rates and vice versa. We do not elaborate on the obvious details here.
The new Lorenz curve after taxation is then given by
where the constant c is chosen so that \(\widetilde{L}\left(1\right)=1\), i.e.,
Also note that
where \(\mathop \int \nolimits_{0}^{1} s\left( w \right)L^{^{\prime}} \left( w \right)dw\) is the fraction of the original (gross) GNP retained for taxes.Footnote 6 The new Gini coefficient and the new coefficient h are then defined appropriately, i.e.,
The new net GNP is then given by
We should observe at this point that in practical and numerical considerations, one actually works with the discretely defined analogues of the quantities above, since there is a finite number of income-receiving individuals in the economy and a finite number of tax classes. Let N denote the number of tax classes. In our particular example using taxes in Switzerland, we work with 22 tax classes where the marginal tax rate changes with each CHF 1000 increase in monthly income, with the exception of the last tax class which comprises all higher incomes.
Modelling tax incentives
To take into account the empirically observed fact that high taxation leads individuals to find ways how to avoid paying taxes (negative tax incentives), we propose here a simple approach to model losses in the resulting GNP caused by this issue.
We would like to emphasize, that the notion of negative tax incentives is absolutely crucial within the contact of tax optimization. Without this empirically proven fact there would not be limits to high tax rates to maximize justice, without taking into consideration the efficiency of a certain economy.
We introduce three parameters for the tax incentives model: a multiplicative factor a, a power factor p, and a critical marginal tax rate\({m}_{crit}\). A short discussion regarding these three parameters follows at the end of this section. We model the GNP loss caused by negative incentives relating to an individual in a tax class with the marginal tax rate m(x) as:
Here \({sal}_{marginc}(x)\) is the marginal increase in salary when moving from one tax class into another (in our example, CHF 1,000), \(m\left(x\right)\) is the marginal tax rate, and \(\chi\) is the characteristic function.
The GNP loss related to all individuals in one tax class (with the marginal tax rate \(m(x)\)) is then given by
where \(g(x)\) is the ratio of the total of all individuals in the tax class being considered to the total of the whole employed population. Thus, evidently, \(\sum_{x=1}^{N}g\left(x\right)=1\), i.e., every individual is assigned to precisely one tax class.
Finally, the total loss to GNP caused by the negative tax incentives is given by
Note that the notation \({GNP}_{loss}\left(s\left(\cdot \right)\right)\) reflects the fact that the resulting loss depends on the whole tax rate curve.
The functional to be maximized is then given by:
subject to the condition
A short comment to the three parameters, mcrit, a and p:
mcrit is the critical marginal tax rate. It is not the maximal tax rate, but rather the maximal increase in the tax rate curve. In our examples, we choose mcrit = 0.3.
a is a measure for the efficiency of the tax system. That means, for a given tax substrate a is a measure for the utility which is generated through the use of the taxes.
p is a measure of the tax avoidance relative to the income. If p = 1, the tax avoidance is independent of the income. In our calculations, we set p = 1.5, mainly due to the fact that this generates reasonable results. It seems that the sensitivity of p is not very important.
It would be very helpful to define a and p based on statistical knowledge. For the time being, such statistics exist very rarely, probably due to the fact, that a and p are mainly dependent on soft factors, such as education, culture or acceptance of the government.
A wide field of analysis opens here. Such analysis would be very helpful to define optimal tax curves in an objective way.
Outcomes
Negative tax incentives, without negative income taxes
-
a)
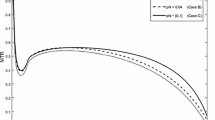
Moderate taxes (Swiss model), λ = 2 (Fig. 2)
Remark: The Tax Incentives Model used here (a = 2, p = 3/2, mcrit = 0.3) leads to the losses shown in ““Losses” corresponding to the tax curves in “Outcomes”” (as a percentage of GNP). The dampening effects are modelled in a way which should correspond to reality in countries where the welfare role of the state is somewhat limited (e.g., Switzerland, hence the name of the model).
-
b)
Higher taxes (Scandinavian Model), λ = 2 (Fig. 3)
Remark: The Tax Incentives Model used here (a = 1, p = 3/2, m_crit = 0.3) leads to the losses shown in ““Losses” corresponding to the tax curves in “Outcomes”” (as a percentage of GNP).
-
We have calibrated the parameters in the incentive function in order to obtain dampening effects which in our view come close to the current reality in some social market economies (mostly Scandinavian countries, partially Germany). We are not aware of the existence of empirical studies which attempt to quantify the dampening effects. Also, see the discussion in “Fiscal policy—An important field of application of the fairness criterion”.
-
We have calculated resulting “losses” for both diagrams. See ““Losses” corresponding to the tax curves in “Outcomes”” and the remarks there for details.
-
It is possible to define further constraints. For example, we could set the marginal tax rates so as to protect the middle class from excessive taxes.
Negative tax incentives, with negative income taxes (Swiss model only)
-
a)
Swiss model, λ = 2
-
b)
Comparison with and without negative income taxes (Swiss model only), λ = 2
Remarks: if we accept negative income taxes, we obtain the very plausible curves of Figs.4 and 5 as a result. The value of F is a little higher with the acceptance of negative income taxes. In the spirit of this article, namely maximizing F, we should therefore choose this solution. But we have to keep in mind the context, described in “Fiscal policy—An important field of application of the fairness criterion”.
Comparison with an existing marginal tax curve, an example from Zurich, Switzerland (with tax incentives, without negative income taxes)
Remarks: Figure 6 shows a comparison of the existingFootnote 7 marginal tax curve of the city of Zürich with the theoretical curve, which optimizes F, using the same tax substrate.
Comparison of the optimal income tax curve in an economy where the role of the state is moderate and no negative taxes are allowed (Fig. 2) with the existing income tax curve of the city of Zürich
Note that in our model lower taxes in lower and middle income classes are compensated by higher taxes in the highest income classes: this effect is possible due to the somewhat disproportionately high percentage of high earners in this quite wealthy city.
We would like to mention three points:
-
The theoretical curve has been calculated in order to obtain the same tax substrate, but optimizing F.
-
For very high incomes there is little effect if we limit the tax rate (e.g., at a maximal marginal rate of 0.5 or 0.6).
-
In summary: the optimal curve remains constant at the value of 0, until a yearly income of about CHF 15,000 or 20,000. Then it increases at the same rate as the existing curve until a yearly income of about CHF 150,000, when it starts approaching the existing curve: After crossing it at about CHF 230,000, it stays slightly above it.
Future outlook
In our mathematical model, we focus on the distribution of taxes in terms of aggregate income brackets and wealth categories (earnings, asset holdings and inheritance), and not in terms of absolute taxation amounts. It turns out that the criterion of fairness optimization is quite appropriate when calculating meaningful income tax curve proposals. Modelling the tax incentive function is particularly important, since there are many solutions depending on the various assumptions. It is also important to formulate appropriate framework conditions (e.g., the highest tax rate or the highest slope of the tax function). This method should prove useful when extended further to calculate optimal tax curves for asset or inheritance taxes. In order to complete this step, however, a great deal of preliminary work and data collection is still necessary.
“Losses” corresponding to the tax curves in “Outcomes”
The notion of “losses” is defined in “Modelling tax incentives”
Moderate taxes (Swiss Model), \({\varvec{\lambda}}=2\); according to Fig. 2
Salary | Marginal tax rate | Loss in % of Salary Increase (other benefits, fraud, etc.) |
|---|---|---|
12,000 | 0 | 0 |
24,000 | 0 | 0 |
36,000 | 06 | 01 |
48,000 | 11 | 03 |
60,000 | 14 | 04 |
72,000 | 17 | 06 |
84,000 | 20 | 08 |
96,000 | 22 | 09 |
108,000 | 24 | 11 |
120,000 | 26 | 13 |
132,000 | 28 | 14 |
144,000 | 30 | 16 |
156,000 | 31 | 17 |
168,000 | 33 | 19 |
180,000 | 34 | 20 |
192,000 | 36 | 22 |
204,000 | 37 | 23 |
216,000 | 38 | 24 |
228,000 | 39 | 26 |
240,000 | 41 | 27 |
252,000 | 42 | 28 |
High taxes (Scandinavian Model), \({\varvec{\lambda}}=2;\) according to Fig. 3
Salary | Marginal tax rate | Loss in % of Salary Increase (other benefits, fraud, etc.) |
|---|---|---|
12,000 | 0 | 0 |
24,000 | 0 | 0 |
36,000 | 0 | 0 |
48,000 | 0 | 0 |
60,000 | 08 | 0 |
72,000 | 17 | 02 |
84,000 | 25 | 03 |
96,000 | 33 | 05 |
108,000 | 39 | 07 |
120,000 | 46 | 10 |
132,000 | 51 | 12 |
144,000 | 57 | 15 |
156,000 | 62 | 17 |
168,000 | 67 | 20 |
180,000 | 72 | 23 |
192,000 | 77 | 26 |
204,000 | 81 | 28 |
216,000 | 86 | 31 |
228,000 | 90 | 34 |
240,000 | 90 | 37 |
252,000 | 90 | 39 |
Remarks:
The incentive functions have been defined in such a way that in a country with lower taxes such as Switzerland, the losses already occur at lower incomes. This is because a particular tax rate in Switzerland has relatively more impact than it does in a country with higher taxes. This is due to fact that in Switzerland more facilities, such as day-care nurseries, have to be financed independently than is the case in Scandinavian countries, for example.
Conclusions
Purpose of the article
The purpose of this article is to devise a solution to the controversy in the economic policy debate between “economic efficiency" and "economic justice".
It was clear from the outset that this controversy could not be solved by taking an extreme standpoint. An optimal approach for considering the relationship between these two concepts therefore had to be found, and the optimization formula, the Fairness-Formula, was proposed.
The formula is extremely simple, almost trivial, and limits itself to the sole idea of combining the measure of economic performance together with that of distribution uniformity. Additionally, we maintain that this combination must allow for a certain degree of freedom for the relative weights of the two variables.
Since one can choose different definitions of h and different values for λ, it is, strictly speaking, not a single formula, but, in fact, a family of multiple similar formulas. Their exact form can be left for further discussion.
Embedding fairness into economic science
The concept of fairness as used in this article is a generalization of the concept of GNP, and vice versa: GNP is a special case of fairness when λ is set to zero. The new definition therefore does not subvert the ideas of classical economics, but merely expands on a certain issue.
Premising fairness optimization extends the classic premise of GNP optimization to optimizing GNP and its distribution jointly and appropriately. The fairness formula can also be considered as a new form of a welfare function. According to Arrow’s impossibility theorem (Arrow 1954), it is not possible to construct a meaningful welfare function in such a way that it develops as an aggregation of individual utility functions. The fairness formula takes a different route, as it does not begin with an individual, but is established through the use of probabilities.
The inclusion of mathematics
The conceptualization of the Fairness-Formula introduces mathematics into the discussion about justice. This scientific approach to ethical controversies has an enormous advantage over traditional arguments, as it provides objective data-based evidence in support of arguments and the prospect of drawing new conclusions, thereby freeing the path for future consensus and new developments. Research shows that tremendous progress is being made in all fields of knowledge where mathematics is applied. The natural sciences are, of course, prime examples of this fact, but it has also been shown that the humanities and social sciences, particularly economics, have profited greatly from the use of mathematical methods. The section on tax policy (“Fiscal policy—An important field of application of the fairness criterion”) shows that appropriate developments are also conceivable when applied to the topic of "justice".
Mathematics also allows measurability in areas that used to be treated only qualitatively. This is not to say that “everything" must be quantifiable, but the expansion of knowledge is generally associated with measurability (where appropriate). When applied to the fairness definition, this means that fairness and its changes over time become measurable.
A new focus
Economic justice has so far not received the acknowledgement it deserves as being one of the most important issues in economics. The main focus until now has been on how to bake the cake as efficiently as possible and then divide it according to the precepts of the standard neoclassical model. Views as to whether this division was just or not were deemed to be subjective value judgements that science would have nothing to do with. It was pointed out that bigger cakes could be distributed more fairly.
The opinion of this article is that this metaphor is no longer sufficient. The issue of economic justice should be included in scientific analysis and the fairness formula is a proposal on how to do so.
Impact
One of the basic questions lies in determining to what extent GNP growth is justified if it is accompanied by growing inequality. This same question can also be applied to smaller economic units. This question has traditionally been answered in favor of GNP growth, regardless of distribution, by implementing the classical criteria for GNP growth or Pareto optimality. This answer is, however, intuitively unsatisfactory.
Our research finds that the fairness criterion always provides clear answers that accord with an intuitive sense of justice which is not measured using scientific methods.
These questions regarding the controversy between normative and positive appraisals of equitable distribution are not only of theoretical interest. They can be useful, for example, when considering the economic consequences of large investments, commercial contracts and debt, as well as the forms of income and asset distribution among different people.
Even though “Fairness Theory” is not yet fully mature and is short of comprehensive data, interesting aspects regarding its potential application can also be observed with regard to tax policy.
The overall concept discussed here, including that of the Fairness-Formula, is merely a single mosaic stone in the great colorful foundation of the future’s edifice of economic theory. “Fairness Theory” opens a rich field of research for many applications.
The relationship between freedom and justice, which impacts many other academic disciplines in the Humanities and Social Sciences, is probably one of the most important questions of mankind. World hunger, environmental destruction, even war and despotism are all connected to the fact that these basic values have not been sufficiently addressed. The creation of a global ethos that reinvents itself with successive generations, but which adheres to core values in the principles of freedom and justice, is a highly desirable vision for the future.
And a last remark: Happiness research (Frey 2017) tells us that the happiness of people, as far as the economic system is concerned, is narrowly linked to economic growth and economic fairness. Therefore, the measure F is probably close to a measure for happiness.
Data availability
Main data used in this article (income distribution of the city of Zürich) are publicly available at the webpage of the Kantonales Steueramt Zürich: https://www.zh.ch/de/steuern-finanzen/steuern/steuerstatistiken.zhweb-noredirect.zhweb-cache.html?keywords=steuerdaten&filtered=false#/. Furthermore, the values of GNP per capita and Gini coefficients for countries worldwide (used in the scatterplot in Sect. 4.4) are taken from the World Bank statistics.
Notes
The word measure is used throughout this article. It is not directly related to mathematical measure theory.
As an illustration, in 1976, the famous writer Astrid Lindgren published an article in the renowned Scandinavian newspaper “Expressen” criticizing the fact that she had to pay 102% taxes on her income.
We consider only one variable for simplicity. The meaning of \(\lambda\) can also be shown using several variables, but the expressions become more cumbersome.
i.e. a tax curve, prescribing possibly different values of the tax rate for different income classes.
Normalized using the inverse of the total amount of GNP, i.e., by GNPpre.
The tax substrate (to be used in the functional that is to be optimized) is then given by:
\(GDP_{pre} \cdot \mathop \int \nolimits_{0}^{1} L^{\prime}\left( w \right)s\left( w \right)dw\).
Data from 2016.
References
Arrow KJ (1963) Social choice and individual values, 2nd edn. Yale University Press
Arrow KJ, Debreu G (1954) Existence of an Equilibrium for a competitive economy. Econometrica 22(3):265–290
Berger MS (1977) Nonlinearity and functional analysis. Academic Press
Frey BS (2017) Wirtschaftswissenschaftliche Glücksforschung. Springer Gabler, Wiesbaden
Gini C (1921) Measurement of inequality of income. Econ J 31:124–126
Human Development Report 2016 (2016) United Nations Development Programme.
Lüthy H (2016) Die Fairness-Formel: Freiheit und Gerechtigkeit in der Wirtschaft der Zukunft. Springer Fachmedien, Wiesbaden
Pigou AC (1920) The Economics of Welfare, 1st edn. MacMillan and Co., Ltd., London
Piketty T (2014) Capital in the Twenty-First Century. Harvard University Press
Rawls J (1971) Theory of justice, Rev. Harvard University Press, Cambridge
Samuelson P, Nordhaus WD (2004) Economics, an introductory analysis. Irwin/McGraw-Hill
Schwartz JT (1969) Non-Linear Functional Analysis. Gordon & Breach Science Pub, New York
Söllner F (2012) Die Geschichte des ökonomischen Denkens. Springer Verlag
Stiglitz J (2012) The Price of Inequality. Norton, New York
Funding
The authors declare not to have received any funding for the work done on this article.
Author information
Authors and Affiliations
Contributions
The first part of the article, the definition of a concrete welfare function, was mainly developed by Herbert Lüthy. The second part, the mathematical model, was predominantly developed by Michal Chovanec.
Corresponding author
Ethics declarations
Conflict of interest
The authors confirm not having any financial or non-financial interests that are directly or indirectly related to the work submitted for publication in this article.
Ethical approval
The authors confirm that all research has been done in compliance with the Code of conduct and Regulation relating to academic integrity at the University of Basel.
Informed consent
Human participants involved in the small study (poll) described in the article have all given their informed consent. The results have been processed in an anonymous way and no disclosure of participants’ identity is possible based on the published results. There has been no risk to participants whatsoever resulting from the conducting of the poll.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lüthy, H., Chovanec, M. Optimal income taxes. SN Bus Econ 3, 36 (2023). https://doi.org/10.1007/s43546-022-00396-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43546-022-00396-y