Abstract
In this paper, steel–polyethylene hybrid fiber-reinforced strain-hardening cementitious composites (HECC) are applied in beam–column external joint core region to form a novel HECC/reinforced concrete (RC) composite beam–column joint with reduced anchorage length of beam longitudinal rebar and eliminated transverse rebar, and thus to alleviate rebar congestion and simplify the construction process efficiently especially for precast RC frame structures. Five external beam–column joint specimens are constructed and tested under cyclic loading to illustrate the influences of the anchorage length of beam longitudinal rebar and longitudinal rebar ratio on the seismic performance of beam–column joint. The effects of design parameters on seismic performance, including hysteresis behavior, degradation of strength, energy dissipation capacity, and cracking patterns are discussed in detail. Experimental results indicate that the replacement of normal concrete with HECC in beam–column joint core region could apparently reduce the amount of stirrups in the joint core area while maintaining reliable seismic behavior. Remarkably, specimen with no stirrups in the core area exhibits nearly equivalent seismic behavior to that of the control RC specimen. Furthermore, the application of HECC in joint core area allows for a substantial reduction of the required anchorage length for the beam longitudinal rebar to 9d, which further simplifies the construction process considerably.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
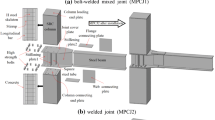
As one of the simplest, most fundamental, and most widely used structural systems, reinforced concrete (RC) frame structures often exhibit failure in the connection between the components under seismic action, leading to overall collapse of the structure [1]. Beam–column joint, serving as the transfer hinge of force resulting from beam and column, is considered as the most critical component to maintain the expected bearing capacity and ductility of the frame structure [2]. To ensure optimal seismic performance and mitigate the risk of the shear failure and local bond damage in the beam–column joint core area, standards such as ACI 318 [3] and GB 50010-2010 [4] prescribe the inclusion of sufficient transverse rebar and beam longitudinal rebar in the joint core area. In particular, for precast RC frame structures, prefabricated beams and columns are usually assembled by pouring concrete into joint area on site. In the premise of exhibiting equivalent behavior with cast-in-place ones, the design stipulations applicable for cast-in-place joint should be strictly adhered to and additional stipulation such as the longitudinal rebar of the beams should be anchored within the joint core area with 90° hooks [5] should also be complied with in precast RC frame structures. These yield intricate rebar configurations and congestion in the joint core area, augmenting the complexity and difficulty of in situ construction as depicted in Fig. 1, which not only adversely affects construction efficiency but also elevates the concealed vulnerabilities when subjected to seismic load.
Engineered cementitious composites (ECC) reinforced with randomly distributed fibers at a volume fraction of no more than 2% [6] is a novel category of fiber-reinforced concrete distinguished with outstanding characteristics [7]. It exhibits strain-hardening behavior with tensile strength and tensile strain capacity attaining 3–16 MPa and 2–10% separately [8] and saturated distributed multiple cracks with widths less than 100 μm [9]. Given the exceptional mechanical properties of ECC materials, researchers have endeavored to substitute concrete with ECC in the joint core region, aiming to enhance the seismic performance and simplify the rebar details of ECC/RC composite beam–column joints. Parra-Montesinos et al. [10] reported that beam–column joints constructed using ECC in the joint region exhibited excellent deformation capacity. Even when all the stirrups within the joint core area were omitted, and no special transverse rebar was arranged in the beam plastic hinge regions, these joints maintained satisfactorily shear-bearing capacity and energy dissipation capabilities. Previous investigations [11] have indicated that the bond behavior between rebar and ECC significantly surpasses that of conventional concrete. Deng et al. [12] studied the effect of ECC matrix strength on bond behavior, and found that the ultimate bond strength increased by 2.14 times when the compressive strength of ECC increased from 27.7 to 57.2 MPa. Chao et al. [13] indicated that the bond strength between rebar and ECC was 1.5 times of that between rebar and traditional concrete with spiral stirrups. Additionally, Cai et al. [14] found that the coordinated deformation ability between ECC and rebar was better than that of concrete due to more ECC elements could participate in the transfer of load. Therefore, several experimental studies have been conducted to reduce the anchorage length of beam longitudinal rebar in ECC joints. Zhang et al. [15] concluded that the anchorage length for the straight and headed bars could be reduced to 16d and 8.1d, respectively, in ECC joint. Additionally, Lee et al. [16] observed that ECC joints outperformed their concrete counterparts in terms of anchoring performance, resulting in mitigated pinching effect caused by beam longitudinal rebar slip.
In recent years, researchers [17] have indicated that hybrid fiber-reinforced ECC (HECC) could exhibit enhanced mechanical properties in comparison to traditional ECC because of the positive synergic effect of flexible fibers (i.e., polyethylene (PE) fiber, polyvinyl alcohol (PVA) fiber), and rigid fibers (i.e., steel (S) fiber) in various aspects [18], such as shear performance [19], elastic modulus [20], and shrinkage properties [21]. Additionally, Ding et al. [22] and Mao et al. [23] discovered that the bond strength between rebar and HECC can be further improved compared to that between ECC and rebar. However, there have been limited researches concerning the seismic performance of HECC/RC composite beam–column joints. Ghayeb et al. [24] demonstrated that joint specimen with S/PVA/PE-HECC used in core area and adjacent beam plastic hinge area possessed greater bearing capacity than PE-ECC joint and PVA-ECC joint, but lower than that of S-ECC joint. However, a noteworthy finding was that the displacement ductility coefficient of S/PVA/PE-HECC specimen increased by 21% compared to that of S-ECC. And the energy dissipation of the S/PVA/PE-HECC specimen was also higher than that of PE-ECC and PVA-ECC, suggesting that HECC joint displayed superior comprehensive seismic performance. Additionally, Chidambaram et al. [25] also pointed out that specimens using PP/S-HECC in joint core area exhibited higher ductility and energy dissipation capacity than that of PP-ECC, S-ECC, and normal RC joint specimens. Therefore, according to previous researches, it has been demonstrated that HECC/RC joint could achieve superior ductility and energy dissipation capacity than that of ECC/RC joint under seismic load. Furthermore, given that the utilization of ECC can lead to a reduction in the quantity of stirrups and the anchorage length of beam longitudinal rebar, substituting ECC with HECC could potentially preserve and even enhance these benefits. Nevertheless, it remains unclear to what extent the anchorage length of beam longitudinal rebar can be reduced and how many stirrups can be eliminated within the HECC/RC composite joint core area, which deserve further investigation.
Against this background, present research focuses on the seismic performance of HECC/RC composite beam–column external joints under cyclic loading with no stirrup rebar and shorter anchorage length of beam longitudinal rebar to simplify construction process. The considered factors include the anchorage length of beam longitudinal rebar and beam longitudinal rebar ratio. The effects of these design parameters on hysteresis behavior, degradation of strength, energy dissipation capacity, and cracking patterns are thoroughly analyzed. Furthermore, based on the analysis of slippage of beam longitudinal rebar, the anchoring performance in the HECC joint core area is discussed, and the possibility of shorter anchorage length of beam longitudinal rebar in HECC/RC composite joint is verified. The recommendations proposed in present research are vital for optimizing the rebar configurations and maintaining the seismic resistance of HECC/RC composite beam–column joints, and thus reducing the construction difficulty and enhancing the construction quality efficiently when precast beams and columns are assembled on-site.
2 Experimental program
2.1 .Specimen design
Five HECC/RC composite exterior beam–column joint specimens were designed and prepared for testing under cyclic loading. The investigated parameters include the anchorage length of beam longitudinal rebar and beam longitudinal rebar ratio. Meanwhile, a control specimen using conventional concrete was also prepared. Table 1 provides a summary of the design parameters for the tested beam–column joint specimens. Additionally, Fig. 2 depicts the geometric dimensions and rebar details for both the control specimen and the HECC/RC composite joint specimens.
Considering that the shear capacity of the joint core area is positively correlated with the size of the joint, to make the joint core area under more unfavorable stress conditions, the dimensions of the column are 360 mm × 360 mm for HECC5 specimen (Fig. 2c), while those of other specimens are 450 mm × 450 mm (Fig. 2a and b). The design of all these specimens adhered to the principle of strong column and weak beam. As depicted in Fig. 2, twelve longitudinal rebars with a diameter of 20 mm, and a number of four-leg stirrups with a diameter of 10 mm and a spacing of 100 mm are arranged in the columns for all the joints specimens. For the beams, three longitudinal rebars with diameters of 20 mm for RC and HECC1–HECC4 specimens (ρs is 1.1%) with different anchorage length in the joint core zone, while eight 20 mm longitudinal rebars for HECC5 specimen (ρs is 3.0%) to increase the shear stress of the core area are placed in the top and systematically in the bottom of the beam. Two-legged stirrups with an 8 mm diameter and spaced at 100 mm intervals are employed in the beams of all joint specimens.
According to the author’s previous research centered on the bonding behavior between rebar and HECC at the same strength designed in this study, the design anchorage length of rebar embedded in HECC could be set as 7.3d based on reliability analysis [26]. Therefore, the anchorage lengths (lab) of beam longitudinal rebars in the joint core zone are selected to vary from 6 to 18d. In contrast, the basic anchorage length of beam longitudinal reinforcement of 21d was applied to the control RC specimen, which was calculated using Eq. (1) [4]. Moreover, all the longitudinal rebars of the beam are directly anchored into the joint region.
where α is shape factor (0.14 for deformed reinforcement); fy is reinforcement yield strength; ft is tensile strength of concrete. In this study, the standard values of fy and ft were used.
Notably, to leverage the improved tensile properties and shear behavior of HECC and simplify rebar details to the maximum extent, HECC1–HECC5 specimens removes all the stirrups within the joint core zone. It is worth emphasizing that if ordinary concrete with same compressive strength is used in joint core area of HECC5 specimen, a stirrups ratio of 1.6% is required according to GB 50010–2010 [4] to avoid shear failure of the joint core area. In contrast, the control RC specimen designed according to GB 50010–2010 [4] features a four-legged stirrup with a 10 mm diameter and a 100 mm spacing in joint core area (ρsv is 0.69%) as shown in Fig. 2a.
The construction process of the joint specimens is depicted in Fig. 3. First, the reinforcements of the beam and column were assembled in the wood formwork, as shown in Fig. 3a. Then, concrete was poured into beam and column and cured until a certain strength to remove the formwork (Fig. 3b). It is worth emphasizing that some grooves were preset on the end of beams and columns to serve as shear keys to avoid interfacial shear sliding failure, as can be seen in Fig. 3b. Finally, the HECC was poured into the joint core area, as shown in Fig. 3c.
2.2 Material property
The cement-based material employed for the prefabricated columns and beams was ordinary concrete, while HECC was used exclusively within the beam–column joint core region. The prism compressive strength fc of ordinary concrete of 150 mm × 150 mm × 300 mm in size tested according to the GB/T 50081-2019 [27] was 50.5 MPa at testing day. The mix proportion of HECC could be referred to [20], and the sand-to-binder ratio was selected as 0.82. The fibers used in HECC were the PE fibers with 1% volume fraction and the steel fibers with 1% by volume, respectively. And the physical and mechanical properties of fibers are listed in Table 2.
The tensile properties of HECC were assessed through uniaxial tension tests, following the guidelines recommended by the Japan Society of Civil Engineers (JSCE) [28]. Figure 4 illustrates the tensile stress–strain curves of HECC. The results depicted in Fig. 4 reveal a distinct tensile strain-hardening behavior for HECC, with a tensile strain capacity of 4.1% and a corresponding tensile strength of 6.8 MPa. The prism compressive strength of HECC is 54.6 MPa.
The longitudinal rebars and stirrups of HRB400 with three different diameters (i.e., 6 mm, 8 mm, 20 mm) were used in this study. The mechanical properties of rebars were determined through standard tensile tests, and calculated by averaging the values of three identical samples and summarized in Table 3.
2.3 Test setup and loading procedure
The experimental setup, as dictated by the laboratory's loading equipment and support conditions, is depicted in Fig. 5. To facilitate the application of the cyclic load at the beam end, the specimens were rotated 90 degrees, and the beam was oriented vertically. Special hinge joints were used to connect the end of the columns of specimen to form a self-balancing steel frame. In this arrangement, one end of the column was supported by a roller support, while the opposite end was supported by a pin support. During the entire testing procedure, a constant axial load equivalent to 0.1fcAc (fc is the prism compressive strength of concrete, Ac is the sectional area of column), was applied to the column using a hydraulic jack with a 2000 kN capacity. It should be noted that the lower axial load ratio of 0.1 is chosen because the beam longitudinal rebar anchorage is more unfavorable at this time. Subsequently, a cyclic load was applied to the end of the beam using a hydraulic jack with a capacity of 500 kN. And the distance from the loading point to the beam–column interface was 1710 mm.
As illustrated in Fig. 5, two load cells were directly affixed to the hydraulic jack for precise measurement of the applied loading force. A linear variable displacement transducer (LVDT) was positioned at the beam-loading point to accurately measure the horizontal displacement of the beam end, which could also be employed for calculating the drift ratio. According to the purpose of this study, the slippage of longitudinal rebar in the joint core area was measured by two LVDTs, setting at the loading end (LVDT1) and the free end (LVDT2) separately, as displayed in Fig. 6.
The cyclic lateral load was applied by displacement control during the whole loading procedure as exhibited in Fig. 7. Before the yielding of specimens, a 4 mm displacement increment was applied for each controlling displacement, and then this value was increased to 8 mm. At each controlling displacement, two full loading cycles were applied. When the horizontal load at the beam end diminished to less than 85% of the peak load, the test was finished.
3 Experimental results and discussion
3.1 Failure modes
The crack distribution and failure modes of all HECC/RC composite joints and RC joint specimens under cyclic loading are shown in Fig. 8. As can be seen in Fig. 8, two failure modes, including the flexural failure of the beam end (i.e., Fig. 8a) and the anchoring failure of beam longitudinal bars (i.e., Fig. 8e) were observed in this research. Considering that specimens with the same failure mode have roughly the same crack propagation during the test, thus only the behaviors of representative specimens are described in detail as follows.
3.1.1 Beam end failure
3.1.1.1 Specimen HECC1
The HECC1 specimen, featuring an anchorage length of 18d in the joint core area, exhibited a typical flexural failure at the beam end. Figure 9 shows the crack propagation observed during the load cycles. At the displacement of 8 mm (corresponding to a drift ratio of 0.5%), flexural cracks with the width of 0.15 mm were observed in the plastic hinge zone of the beam, as shown in Fig. 9a. At this stage, the residual deformation of the beam end after unloading was only 0.26 mm, which can be ignored. With the increase of the controlling displacement, the existing cracks in the plastic hinge region of the beam continued to develop and extend, and new cracks also emerged at greater distances from the column. Despite these developed cracks, the residual deformation after unloading remained less than 1 mm until the controlling displacement reached 16 mm (corresponding to a drift ratio of 0.9%), which can be still regarded as a linear stage. As the displacement increased to 24 mm (1.4%), the specimen displayed a significant increase of residual deformation at the beam end to 6.5 mm when the load was unloaded pronouncing a nonlinear behavior, as shown in Fig. 9b. In addition, it can be found that the concrete at the beam plastic hinge area began to spall, as shown in Fig. 9c. After the peak load, large amount of concrete crushing was observed within the plastic hinge region near the beam end, as shown in Fig. 9d. It is worth mentioning that, in contrast to the RC specimen, there were no visible cracks within the joint core area of HECC1 specimen, despite the absence of transverse rebars in this region, demonstrating the fiber bridge effect of HECC restrain the development of cracks and the induced damage is limited to a small area.
3.1.1.2 Specimen HECC5
Although HECC5 specimen also experienced a flexural failure at the beam end, it synchronously developed a large number of diagonal shear cracks in the joint core area as shown in Fig. 10. At a controlling displacement of 8 mm, flexural cracks were observed in the plastic hinge zone of the beam. Different from other specimens, few fine diagonal cracks with close spacing were observed in the joint core area at a controlling displacement of 12 mm (0.7%), as shown in Fig. 10a. With the increase of the controlling displacement, tiny flexural cracks in the beam end and diagonal cracks in the core area increased and developed gradually as shown in Fig. 10b. Due to the fiber bridging effect, the crack width of diagonal cracks in the core area was within 0.2 mm. Similar to HECC1, the concrete at the beam plastic hinge area began to spall when the controlling displacement was 56 mm (3.3%) (Fig. 10c), and finally the specimen failed at a displacement of 80 mm (4.7%) (Fig. 10d) accompanied with serious crushing of the concrete and buckling of the beam longitudinal rebar.
Besides, it is worth noticing that numerous fine intersecting diagonal cracks generated in the joint core area, which differed from other specimens for more shear stress transformed into the joint core area due to larger beam longitudinal rebar ratio of 3.0%, demonstrating that the deformation of the joint core area can be well constrained by HECC although no stirrups are allocated.
3.1.2 Anchoring failure
As illustrated in Fig. 11, the HECC4 specimen, experienced an anchoring failure with a significant rebar slippage due to the inadequate anchorage length of beam longitudinal rebar in the joint core area of 6d. At a controlling displacement of 8 mm (0.5%), flexural cracks were observed in the plastic hinge zone of the beam, as shown in Fig. 11a. Notably, compared to other specimens, the HECC4 specimen exhibited larger residual deformation at the beam end after unloading, reaching approximately 1.15 mm. The distribution of cracks near the beam end is described in Fig. 11c when the controlling displacement increased to 24 mm (1.4%). It can be observed that the number of cracks near the beam end of HECC4 specimen were significantly less than those of other specimens. After the peak load, the bearing capacity of the specimen dramatically decreased, and the slip of the beam longitudinal rebar rapidly increased. As depicted in Fig. 11d, the beam plastic hinge region maintained its integrity even after the specimen failed, and no concrete spalling or crushing was observed. Furthermore, a prominent main horizontal crack at the beam end formed due to the substantial slip of the beam longitudinal rebar.
3.2 Load–displacement curves
The hysteresis load–displacement curves at the beam end of the five HECC/RC composite joint specimens as well as the RC controlling specimen are plotted in Fig. 12. As shown in Fig. 12, it can be observed that except for the HECC4 specimen, the hysteresis load–displacement curves of other specimens appear relatively plump loops with little pinching effects due to flexural failure of beam occurred. By contrast, the hysteresis curve for HECC4 (Fig. 12e) displays a significant pinching effect, which is primarily caused by the pronounced slip of the beam longitudinal rebars.
To provide a clearer and more direct understanding of the characteristics of hysteresis load–displacement curves, complete hysteresis loops at selected controlling displacements (12 mm, 40(32) mm, 56(40) mm, and 72(48) mm) of four typical specimens are presented in Fig. 13. It can be found that in the initial stage of loading (i.e., 12 mm), the unloading curve of all specimens basically coincided with the loading curve, resulting in a linear behavior. After the specimen yielded and entered the elastic–plastic deformation stage, the hysteresis curve became plumper and plumper, indicating that more energy was dissipated.
By comparing the hysteresis load–displacement loops of two cycles at a specified controlling displacement as shown in Fig. 13, a more severe pinching effect can be observed of the second cycle, resulting in a decrease in energy dissipation capacity for all specimens. This can be attributed to the cumulative effect of bonding damage between the beam longitudinal rebar and HECC in the joint core area and the increased cracks of concrete in beam end, causing more energy release. Additionally, compared to other specimens, the degradation of hysteresis responses including strength and stiffness of HECC4 specimen exacerbated obviously with the increase of cyclic numbers as shown in Fig. 13c. These observations emphasize the importance of ensuring sufficient anchorage of the beam longitudinal rebar in preserving the bearing capacity and energy dissipation capacity of a structure when subjected to seismic action.
Despite the absence of stirrups, the hysteresis curves of both HECC3 (Fig. 13b) and HECC5 (Fig. 13d) specimens closely resembled the plump shape observed in the RC specimen (Fig. 13a), with minimal pinching effects. These observations suggest that the bridging effect of hybrid fibers in HECC can provide robust and adequate confinement effect to resist shear stress and decrease shear deformation as stirrups. Thus, the use of HECC in beam–column joints can reduce or even eliminate the need for stirrups, benefitting the potential in simplifying rebar details of precast structures in seismic zone.
The load–displacement envelopes obtained by connecting the peak load of the first cycle at each controlling displacement for all the specimens are illustrated in Fig. 14. The critical experimental results, including the yielding load Py and corresponding displacement Δy, the peak load Pp and corresponding displacement Δp, the ultimate load Pu and corresponding displacement Δu, as well as the ductility factor (Δu/Δy) are summarized in Table 4. The ultimate load Pu is defined as 85% of Pp. As shown in Fig. 14, the envelope curves of HECC1, HECC2, and HECC3 specimens nearly coincide with that of RC although no stirrups were arranged. Additionally, compared to HECC3 specimen, although the bearing capacity of HECC4 specimen with anchorage length of 6d was slightly lower, the displacement ductility factor was dramatically reduced, which was only 1.84 and 1.89, decreased by 57.5% and 51.5% in the positive and negative direction, respectively. This is attributed to the insufficient bonding resistance between the beam longitudinal rebars and HECC in the joint, leading to premature specimen failure, inadequate plastic development, and poor ductility of the joint specimen.
Figure 14 also illustrates that the bearing capacity of the specimen increased with an increasing beam longitudinal rebar ratio. As observed from Table 3, the average peak load was 187.15 kN of HECC5 specimen, which was as high as 2.37 times that of HECC1 specimen for same anchorage length of beam longitudinal rebar. However, the ductility factor value of HECC5 specimen was smaller than that of HECC1 specimen, indicating that increasing the longitudinal rebar ratio had a negative influence on ductility because of the higher shear stress level in the joint core area, leading to the formation of a larger number of diagonal shear cracks.
3.3 Energy dissipation capacity
3.3.1 Energy dissipation
The energy dissipation capacity is one of the critical parameters in the research of seismic performance. During the application of cyclic loading, the dissipated energy is equal to the area enclosed by a complete hysteresis loop at a specified controlling displacement, such as the area S1 shown in Fig. 15.
Figure 16 depicts the dissipated energy of HECC3 and HECC4 of two cycles at different displacements. As can be seen from Fig. 16, the dissipated energy initially increased slowly, then entered into a rapid increase stage followed by a dramatic decrease phase with the increase of controlling displacement. During the ascending stage, a point (highlight in Fig. 16) can be observed after which the rate of energy dissipation increased rapidly, indicating that the specimens entered into nonlinear deformation stage. Irrespective of the different failure modes of HECC3 and HECC4, the energy consumption of the second loading cycle is consistently lower than that of the first cycle under the same controlling displacement. This can be attributed to the accumulation of damage under cyclic loading leads to a more severe pinching effect and a reduction in energy dissipation of the second cycle. Comparing HECC3 and HECC4 specimens, it is evident that the energy dissipated in the second cycle of HECC4 decreased more significantly. This can be attributed to the more severe strength degradation and pinching effect of HECC4 specimen in the second cycle, caused by the significant slippage of the longitudinal rebar in the joint core area.
The cumulated dissipated energy of all the specimens obtained by accumulating the energy dissipated at separate cycle during the entire cyclic loading procedure are shown in Fig. 17. It is found that the initial accumulating dissipation energy was essentially similar and small for all specimens due to the unapparent damage. With the controlling displacement increased, cracks continued to develop and extend, and the inelastic deformation of the specimens were activated and contributed more significantly to energy dissipation. Additionally, the energy dissipation capacities of specimen with larger beam longitudinal rebar ratio (i.e., HECC5) were much higher than those specimens with smaller ones. This phenomenon can be explained by that the specimen with larger beam longitudinal rebar ratio would have a relatively higher bearing capacity, which enlarged the areas of the hysteresis curves accordingly [30]. Specifically, the HECC4 specimen exhibited the lowest energy dissipation capacity due to the insufficient inelastic deformation of the beam longitudinal rebar caused by slip of beam longitudinal rebar.
3.3.2 Equivalent viscous damping coefficient
Besides the cumulated dissipated energy, the equivalent viscous damping coefficient he is also an important index to evaluate the energy dissipation capacity [29]. The equivalent viscous damping coefficient he can be calculated by Eq. (2):
where S1 and S2 denote the enclosed areas described in Fig. 15.
The relationship between the equivalent viscous damping coefficient he and the controlling displacement for different specimens are shown in Fig. 18. With the exception of HECC5 specimen, the variation trend of the equivalent viscous damping coefficient was quite similar among the other specimens. It can be observed that although the increase of longitudinal rebar ratio increased the total consumed dissipated energy of HECC5 specimen as shown in Fig. 17, the hysteresis load–displacement curve of the HECC5 was the least plump before the specimen failed (seen in Fig. 11), manifested as the smallest he values in Fig. 18. This indicates that the development of diagonal cracks in the joint core area is not conducive to the full utilization of energy dissipation capacity of the joint specimens, which needs to be avoided in practical design. Additionally, for all specimens except HECC4, the he value could continuously raise to 0.25 after peak load. It can be induced that even the load decreased obviously after peak load, the efficiency of energy dissipation capacity of specimens can still maintain at a high level. Therefore, these results indicate that the proposed HECC/RC composite beam-column joint without stirrups in the joint core area and reduced anchorage length of beam longitudinal rebar to 9d still has satisfactory energy dissipation capacity, underscoring the reliability and effectiveness of this proposed composite system in resisting seismic forces and simplifying rebar details.
3.4 Degradation of strength
The strength degradation is defined as the weakening of the bearing capacity of specimen under cyclic loading. In this study, strength degradation coefficient \(\lambda_j^2\) is used to describe the strength degradation, which can be calculated by Eq. (3) [22]:
where \(P_j^1\) and \(P_j^2\) denote the peak load of the first loading cycle and second loading cycle at a certain controlling displacement j, respectively.
Accordingly, the values of \(\lambda_j^2\) for all joint specimens at different controlling displacement are shown in Fig. 19. For specimens with flexural failure mode (RC, HECC1–HECC3, HECC5), the \(\lambda_j^2\) value ranged from 0.9 to 1.0 before reaching the peak load. It means that the peak load of the second loading cycle was nearly the same as that of the first loading cycle, indicating that the repeated loading had slight effect on the bearing capacity at this stage. As the specimens entered the failure stage, a significant decrease of strength degradation coefficient (i.e., around 0.8) was discovered. The similar trend of strength degradation coefficient curves indicates that the anchorage length and longitudinal rebar ratio have marginal influence on the degradation of strength when the joint specimens experience flexural failure at the beam end. However, for HECC4 specimen, obvious degradation of strength was found much earlier compared to other specimens due to the rapid increase in slippage of beam longitudinal rebar, and the strength of the beam longitudinal rebar cannot be fully utilized.
3.5 Analysis of anchorage performance
To ensure the desired bearing capacity, ductility, and energy dissipation capacity of the frame structure, anchorage failure of the beam longitudinal rebar should be avoided. In this study, the slip of the beam longitudinal rebar at free end (β1) and loading end (β2) were monitored as shown in Fig. 20.
The measured slippages of the beam longitudinal rebar at the free end for HECC4, HECC3, and HECC5 are shown in Figs. 21, 23, and 24, respectively. As shown in Fig. 21, the slip of the beam longitudinal rebar continuously increased with the increase of the displacement at beam end, and the maximum slippage of beam longitudinal rebar could attain to greater than 8 mm of HECC4 specimen with the anchorage length of 6d. It can be noted that as the controlling displacement increased from 24 mm (1.4%) to 32 mm (1.9%), the slip of the beam longitudinal rebar at free end increased rapidly from 0.44 mm to 1.77 mm in the first cycle, demonstrating that the bonding failure had occurred in the joint core area. Additionally, the repeated loading had an obviously negative impact on the slip of the beam longitudinal rebar. This can be attributed to that due to the inadequate anchorage length, as the relative slip increased, the interlocking resistance failed as long as the HECC keys between the rebar ribs were grounded off [31] and the accelerated damage accumulation weakened the surrounding constraints, increasing the rebar slip at the second cycle.
Comparing the beam longitudinal rebar slip of HECC4 specimen at free end and loading end in Fig. 22, it is evident that the slip at the free end consistently remained lower than that of the loading end, with a more pronounced difference in the early stages of loading when the displacement was less than 16 mm (0.9%). It can be observed that the slip at the loading end increased linearly, while the free end experienced almost no slip in the first two controlling displacements (i.e., ≤ 8 mm (0.5%)). For instance, the slip at loading end reached 0.15 mm at the displacement of 8 mm (0.5%), while the slip at free end was only 0.01 mm. It is known that the slip at loading end is composed by elastic deformation of rebar, plastic deformation of the rebar, and relative slip between rebar and HECC, while the slip at free end is only caused by relative slip. For that, the bond efficiency was fully ensured by chemical adhesion at this stage, almost no slip was occurred at free end and the slip at loading end can be attributed to the elastic deformation of rebar [32]. With the exhaust of the chemical adhesion, the free end slip began to increase with the increase of controlling displacement from 8 mm (0.5%) to 16 mm (0.9%). As the chemical adhesion invalidated, microcracks originated at the tips of the rebar ribs and steadily developed, leading to an increase in free end slip of beam longitudinal rebar. Further increasing the controlling displacement from 16 mm (0.9%) to 24 mm (1.4%), the microcracks began to coalesce into macrocracks and propagate unsteadily, a more severe HECC matrix crushing between the rebar ribs accompanied by a more severe bonding damage happened. This leads to the reduction of the difference between the slip at free end and loading end, indicating that anchorage failure occurred. After this stage, the bond efficiency is sustained by interfacial friction, and the difference between the slip at free end and loading end can be ignored.
Apparently different from the HECC4 specimen, it can be found from Fig. 23a that the difference between the slip at free end and loading end gradually increased with the increased controlling displacement of HECC3 specimen. The slip of the beam longitudinal rebar at free end remained relatively small within 0.36 mm during the entire loading process with an anchorage length of 9d. Although the slip at loading end can increase to over 4 mm, it is mainly attributed to the inelastic deformation of the beam longitudinal rebar after yielding. At peak load (corresponding to controlling displacement of 72 mm (4.2%)), the slip of the beam longitudinal rebar at free end reached a maximum value of 0.36 mm as shown in Fig. 23b, which was far less than the critical value (0.81 mm) when anchoring failure was occurred in HECC4 specimen, illustrating that the mechanical interlocking which is the major component of bond resistance is still in a good state. After the peak load, with further displacement increase, the slip value at the free end began to decrease which is different from HECC4 (Fig. 21b) indicating that there was no significant bonding damage between the longitudinal rebar and HECC in the joint core area with anchorage length of 9d. Additionally, it can be clearly seen that the slip of first cycle was generally similar with that of the second cycle, which also indicates that the longitudinal rebar had been effectively anchored.
Figure 24 shows the hysteresis slip curve of beam longitudinal rebar of HECC5 specimen with an anchorage length of 18d. Although HECC5 specimen with larger longitudinal rebar ratio experienced numerous closely spaced tiny diagonal cracks in the joint core area as shown in Fig. 8f, it is evident from Fig. 24 that the beam longitudinal rebar did not exhibit any significant slip during the whole loading process, and the maximum slip was approximately 0.07 mm. The superb bonding performance is benefitted from the fiber synergic bridging effect in HECC joint, which hindered the widening and development of microcracks effectively, and reduced and delayed the bonding damage obviously.
4 Conclusions
In this study, a novel HECC/RC composite beam–column exterior joint without stirrup rebar in the joint core region is proposed, and the influences of anchorage length of beam longitudinal rebar and longitudinal rebar ratio on its seismic performance are researched and emphasized. The following key conclusions can be summarized from the experimental findings and theoretical analysis:
-
1.
The flexural failure at beam end is observed for specimens except for HECC4 which experiences an anchoring failure mode due to insufficient anchorage length of the beam longitudinal rebar of 6d. With the increase of beam longitudinal rebar ratio, the specimen exhibits higher bearing capacity and energy dissipation capacity, but weaker ductility due to the development of more severe diagonal cracks in the joint core area.
-
2.
HECC5 specimen with higher beam longitudinal rebar ratio (3%) and no stirrups in joint core area also experienced flexural failure at beam end. However, a stirrup rebar ratio of 1.6% is required for ordinary RC joint under the same force condition, demonstrating the potential of HECC in providing confinement and preventing shear failure, and thus reducing or eliminating stirrups in the joint core zone.
-
3.
For HECC/RC composite joint core area where minimum stirrup ratio should be applied while eliminated in present research, the anchorage length of the beam longitudinal rebar can be reduced to 9d, while exhibiting effective anchoring, similar hysteresis responses, bearing capacity, energy dissipation capability, and ductility to other specimens with longer anchorage length and RC specimen with stirrup rebar.
-
4.
Replacement of ordinary concrete by HECC in the joint core area increases the confinement effect to resist shear stress and bonding behavior, which can reduce or even eliminate the need of stirrups accompanied by a reduction of the required anchorage length of beam longitudinal rebar, which can simplify the construction process of precast RC frame structure significantly. However, HECC/RC composite joint with higher level of shear stress in joint core area is recommended for further research to establish a design method for practical application.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Guo ZH, Shi XD. Principle and analysis of reinforced concrete. Tsinghua University Press; 2004.
Harajli MH. Cyclic response of concrete members with bond-damaged zones repaired using concrete confinement. Constr Build Mater. 2007;21:937–51.
ACI Committee 318. Building code requirements for structural concrete (ACI 318-14) and commentary. American Concrete Institute, Farmington Hills, Mich; 2014.
GB 50010–2010. Code for design of concrete structures. Beijing: China Building Industry Press; 2010.
JGJ1-2014. Technical specification for precast concrete structures. Beijing: China Building Industry Press; 2014.
Ding Y, Yu JT, Yu KQ, Xu SL. Basic mechanical properties of ultra-high ductility cementitious composites: from 40 MPa to 120 MPa. Compos Struct. 2018;185:634–45.
Yu KQ, Ding Y, Liu JP, Bai YL. Energy dissipation characteristics of all-grade polyethylene fiber-reinforced engineered cementitious composites (PE-ECC). Cem Concr Compos. 2020;106:103459.
Ding Y, Yu KQ, Li M. A review on high-strength engineered cementitious composites (HS-ECC): design, mechanical property and structural application. Structures. 2022;35:903–21.
Yu KQ, Yu JT, Dai JG, Lu ZD, Shah SP. Development of ultra-high performance engineered cementitious composites using polyethylene (PE) fibers. Constr Build Mater. 2018;158:217–27.
Parra-Montesinos GJ, Peterfreund SW, Chao SH. Highly damage-tolerant beam-column joints through use of high-performance fiber-reinforced cement composites. ACI Struct J. 2005;102(3):487–95.
Lee SW, Kang SB, Tan KH, Yang EH. Experimental and analytical investigation on bond-slip behaviour of deformed bars embedded in engineered cementitious composites. Constr Build Mater. 2016;127:494–503.
Deng MK, Pan JJ, Sun HZ. Bond behavior of steel bar embedded in engineered cementitious composites under pullout load. Constr Build Mater. 2018;168:705–14.
Chao SH, Naaman AE, Parra-Montesinos GJ. Bond behavior of reinforcing bars in tensile strain-hardening fiber-reinforced cement composites. ACI Struct J. 2009;106(6):897–906.
Cai JM, Pan JL, Tan JW, Li XP. Bond behaviours of deformed steel rebars in engineered cementitious composites (ECC) and concrete. Constr Build Mater. 2020;252:119082.
Zhang ZY, Ding R, Nie X, Fan JS. Seismic performance of a novel interior precast concrete beam-column joint using ultra-high performance concrete. Eng Struct. 2020;222:111145.
Lee SW, Tan KH, Yang EH. Seismic behaviour of interior reinforced-concrete beam-column sub-assemblages with engineered cementitious composites. Mag Concr Res. 2018;70(24):1280–96.
Liu JC, Tan KH. Fire resistance of strain hardening cementitious composite with hybrid PVA and steel fibers. Constr Build Mater. 2017;135:600–11.
Yu J, Chen YX, Leung CKY. Mechanical performance of strain-hardening cementitious composites (SHCC) with hybrid polyvinyl alcohol and steel fibers. Compos Struct. 2019;226:111198.
Zhou YW, Xi B, Yu KQ, Sui LL, Xing F. Mechanical properties of hybrid ultra-high performance engineered cementitious composites incorporating steel and polyethylene fibers. Materials. 2018;11(8):1448.
Mao WH, Liu JP, Ding Y. High-modulus and low-shrinkage hybrid-fiber reinforced engineered cementitious composites (ECC). Mater Struct. 2022;55(3):87.
Sun W, Chen HS, Luo X, Qian HP. The effect of hybrid fibers and expansive agent on the shrinkage and permeability of high-performance concrete. Cem Concr Res. 2001;31:595–601.
Ding Y, Liu JP, Yao G, Wei W, Mao WH. Cyclic bond behavior and bond stress-slip constitutive model of rebar embedded in hybrid fiber reinforced strain-hardening cementitious composites. Constr Build Mater. 2023;369:130582.
Mao WH, Liu JP, Ding Y, Chen YF. Bond-slip constitutive model and numerical analysis for rebar embedded in steel-polyethylene hybrid fiber-reinforced cementitious composites. Constr Build Mater. 2021;308:125092.
Ghayeb HH, Ramli Sulong NH, Razak HA, Mo KH. Enhancement of seismic behaviour of precast beam-to-column joints using engineered cementitious composite. Eng Struct. 2022;255: 113932.
Siva Chidambaram R, Agarwal P. Seismic behavior of hybrid fiber reinforced cementitious composite beam–column joints. Mater Des. 2015;86:771–81.
Ding Y, Mao WH, Wei W, Liu JP, Chen YK. Bond behavior and anchorage length of deformed bars in steel-polyethylene hybrid fiber engineered cementitious composites. Eng Struct. 2022;252:113675.
GB/T 50081–2019. Standard for test methods of concrete physical and mechanical properties. Beijing: China Building Industry Press; 2019.
JSCE. Recommendations for design and construction of high performance fiber reinforced cement composites with multiple fine cracks. Tokyo, Japan: Japan Society of Civil Engineers; 2008. p. 1–16.
Gou SK, Ding R, Fan JS, Nie X, Zhang J. Experimental study on seismic performance of precast LSECC/RC composite joints with U-shaped LSECC beam shells. Eng Struct. 2019;189:618–34.
Dong BQ, Pan JL, Cai JM, Xu L. Mechanical behavior of a new ECC-encased CFST column to RC beam connection under cyclic loading. Eng Struct. 2021;234:111915.
Huang L, Xu LH, Chi Y, Deng FQ, Zhang AL. Bond strength of deformed bar embedded in steel-polypropylene hybrid fiber reinforced concrete. Constr Build Mater. 2019;218:176–92.
Shan WC, Liu JP, Ding Y, Mao WH, Jiao YB. Assessment of bond-slip behavior of hybrid fiber reinforced engineered cementitious composites (ECC) and deformed rebar via AE monitoring. Cem Concr Compos. 2021;118:103961.
Acknowledgements
The authors are very grateful for the financial support from the National Natural Science Foundation of China (No. 52108114).
Author information
Authors and Affiliations
Contributions
Weihao Mao: Writing—original draft, Conceptualization, Methodology. Jiepeng Liu: Writing—review and editing, Investigation, Data curation. Xingjian Ou: Methodology, Investigation. Hongtuo Qi: Methodology, Validation. Tomoya Nishiwaki: Conceptualization, Supervision. Yao Ding: Methodology, Conceptualization, Supervision, Funding acquisition.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mao, WH., Liu, JP., Ou, XJ. et al. Seismic performance of HECC/RC beam–column external joint with no stirrup and reduced anchorage length in core region. Arch. Civ. Mech. Eng. 24, 158 (2024). https://doi.org/10.1007/s43452-024-00970-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43452-024-00970-1