Surface topography prediction of slider races using formed grinding wheel shape and material removal mechanism

Abstract

Compared with the roughness, the three-dimensional (3D) topography parameters, surface microstructure geometric characteristics and other information can more fully evaluate the grinding quality of the slider raceway surface. In this paper, based on the 3D topography model of the abrasive particle distribution on the surface of the formed grinding wheel, the material removal mechanism between the abrasive particle and the raceway surface is analyzed. With the undeformed chip thickness distribution model as the intermediate variable, the 3D topography model of the slider raceway surface is established, and the model verification is carried out from the roughness and the geometric characteristics of the surface microstructure, respectively. At the same time, the surface microstructure is extracted from the topography model, and the effects of different grinding process parameters on the geometric characteristics such as the height to width ratio, depth to width ratio and distribution density of groove, convex peak and peak valley structures are studied. Results are shown that A_S,T_H increase from [0.05 0.6 μm] to [0.25 0.8 μm] and FG_H grows from [0.11 1.05 μm] to [0.5 1.61 μm] when the grinding depth rises from 1 μm to 4 μm. A_S, T_H are firstly decreased from [0.17 0.61 μm] to [0.08 0.52 μm] and then increased to [0.26 0.78 μm], and the FG_H declines from [0.34 1.01 μm] to [0.16 0.86 μm] and then increases to [0.51 1.38 μm] with the feeding speed is in [25, 28 m/min]. In addition, in the range of grinding wheel linear velocity [28, 34 m/s], the A_S,T_H decreases from [0.19 0.81 μm] to [0.1 0.55 μm] and the FG_H decreases from [0.55 1.6 μm] to [0.2 1.1 μm]. This can prepare for the subsequent research on the impact of the topography characteristics on the friction coefficient and wear amount of the slider raceway surface.

1 Introduction

Roller linear guide pair is a high-precision transmission component, consists chiefly of sliding block, guide rail, roller, return device, etc. It has advantages such as high rigidity, high precision, low friction, and long service life [1, 2]. And it is mostly applied in machining centers, CNC compound machining machine tools, grinders and other heavy-duty combined machine tools [3, 4]. Mechanical actions such meshing, collision, and elastic–plastic deformation between the protrusions on the surface of the slider raceway and the roller surface can cause friction and wear during the operation of the guide rail pair [5, 6]. However, the long-term wear will bring in a deterioration on the precision and the service life of the guide rail pair determined by the raceway surface's anti-friction and wear properties. At the same time, the precision grinding surface of the slider raceway is formed by the interaction between the abrasive particles on the formed grinding wheel surface and the raceway surface to remove material [7]. Thus, the grinding surface quality of the slider raceway depends on the grinding wheel’s surface topography, the material removal mechanism between abrasive particles and the raceway surface and the grinding process [8, 9].

The grinding surfaces of the workpiece are usually the random distributed non-Gaussian surfaces [10]. And the surface micromorphology is mainly affected by the distribution of the abrasive particle protrusion height [11, 12]. Therefore, with the grinding wheel's non-Gaussian random distribution topography model, the 3D model of the workpiece surface's micro-topography can be established through the kinematics simulation method based on the interplay between the abrasives and the raceway surface [13, 14]. Whereas, during the grinding of the slider raceway surface, the shape, size, and distribution of the abrasive particles are complicated and random due to the brittleness of the single crystal corundum grinding wheel and the abrasive wear [15]. Thus, the building of the statistical model based on experimental data measured is accurate for simulating the geometric properties of abrasive particles on the surface morphology of the grinding wheel [16,17,18].

The normal distribution method is used to define the size of abrasive particles, the height of abrasive protrusions, tool friction and wear, or Rayleigh probability density function is used to describe the undeformed grinding thickness by most scholars in the actual modeling process of 3D surface morphology. For example, Liu Zhijian [19] and Ji et al. [20] respectively founded a simplified morphology model of the grinding wheel by defining the size of abrasive particles and the protrusion height of grinding wheels using the normal distribution method and assumed that the abrasive particles were not worn. Based on this, the motion trajectory equation of abrasive particles on the surface of the grinding wheel was established, and a precision grinding surface model was established in conjunction with the material removal process on the workpiece surface. And the effectiveness of the modeling method was verified through grinding experiments. Zhao Xiaotian [21] and Wang et al. [22] respectively established surface morphology models for grinding rods and grinding wheels with the assumption that the protrusion height of abrasives follows a Gaussian distribution in the ultrasonic assisted grinding process. Based on this, the grinding surface morphology models were established by combining the grinding kinematics and topological structure, and the influence of process parameters and ultrasonic vibration parameters on the surface morphology and surface roughness were analyzed. Cai et al. [23] quantified the random tool grinding error and wear through normal distribution and established the surface morphology of peripheral milling. And the effectiveness of the model prediction was verified under stable and unstable milling conditions, respectively. Chu Shuaizhen et al. [24] used the Rayleigh probability density function to describe the undeformed grinding thickness and established a GCr15 shaft sleeve inner circle grinding morphology prediction model using the surface residual material height formula. The accuracy of the surface morphology model was verified through orthogonal experiments. He et al. [25] characterized the complexity of surface morphology and the irregularity of surface protrusions based on the concept of multi frequency time interaction effects, and established an accurate 3D surface morphology model for single point diamond turning. Tao et al. [26] modeled the equivalent grinding wheel using a transient analog model by taking account the self-grinding ability, translational motion, and continuous generation of turbine wear state in grinding. Hu et al. and Mohamed et al. [27, 28] used matrix linear transformation and autocorrelation function to generate Gaussian rough surface morphology. At the same time, some scholars model the surface morphology of grinding wheels under the assumption that abrasive particles have a perfect spherical shape, uniform distribution of abrasive particles, and fixed spacing [29,30,31].

Through the micro morphology measured of abrasive particles on the wheel surface and the statistical analysis of the extracted geometric feature, it is shown that the shape, distribution, protrusion height and other characteristics of the abrasive particles have obvious randomness and cannot be fully characterized by normal distribution or Rayleigh distribution. In addition, the Monte Carlo and vibration methods include random error, uncertainty, and slow modeling speed [32,33,34]. Unlike existing research methods, the geometric distribution characteristics of the abrasive particles are extracted through the image processing technology from the wheel surface morphology measured by a 3D profilometer in order to obtain a more accurate 3D topography model of the grinding wheel surface in this paper. Statistical analysis is used to determine the quantitative relationship between the grinding wheel dressing process and the abrasive particle morphology parameters, and a 3D grinding wheel morphology model is established. On this basis, the grinding kinematic relationship between particles and the raceway surface is used as a bridge to analyze the material removal mechanism between affective abrasive particles (AAG) and raceway surfaces. At the same time, the critical protrusion height threshold value of AAGs and the variation of abrasive wear in each protrusion height interval are determined by comparing the geometric characteristics before and after grinding wheel correction during the workpiece grinding process. A 3D morphology model of the slider raceway surface is defined under the premise of considering the wear of AAGs. In addition, the influences of the grinding process parameters on the geometric characteristics of the surface microstructure are analyzed. This can provide more complete guidance for the research on the friction and wear model of the guide rail pair and the optimization of the grinding process of the raceway surface, and reduce the error between the theoretical model and practice.

2 Topography modeling of grinding wheel surface

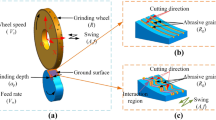
The 3D topography model of the slider raceway surface requires an accurate surface morphology model of the formed grinding wheel. As illustrated in Fig. 1, this work studies the grinding surface of the GZB45BA slider raceway. Figure 2 shows the single crystal corundum grinding wheel 1A46X25X13-SA100K-35. For slider raceway precision grinding, a diamond roller modifies the single crystal corundum grinding wheel into a wheel with the slider's cross section. The dressing procedure settings give the wheel surface a desirable morphology. After the interacting between grains and raceway surface, the material is removed and the grinding surface of the slider raceway is created.

Fig. 1

Roller type linear guide pair and slider raceway

Fig. 2

Slider grinder PLANOMATHP 408 and formed grinding wheel

Only the relevant characteristics of the AAGthat contact the raceway surface and remove material are considered in this paper. Taking the brittle material of single crystal corundum grinding wheel, abrasive wear and dressing process of the formed wheel and other conditions into account, a 3D topography model of the wheel surface is founded. To ensure the modeling accuracy of formed grinding wheel topography, its topography formation process is analyzed in this paper by extracting the shape, size, distribution and other information of grains from the measured grinding wheel topography parameters.

2.1 Shape and size of AAG

The grain size of the wheel with the type of 1A46X25X13-SA100K-35 is 100#. The particle shape is spherical crystal and the diameter R is in range of 125–160 μm before the dressing of the wheel. Based on the author's earlier research [35], the SEM topography of the grinding wheel dressed shows that abrasive grains have an irregular polyhedral shape. Considering the feasibility of modelling, the grain shape is simplified to a quadrangular pyramid, as shown in Figs. 2, 3,4, 5 [35], where V₁–V₅ are the vertices of the quadrangular pyramid and $O$ is the center point of the bottom surface of the quadrangular pyramid ${V}_{1}{V}_{2}{V}_{3}{V}_{4}$. The specific shape and size of the abrasive grain is shown in Eq. 1 [35].

$$V_{1 - 5} = \left[ \begin{gathered} V_{1} \hfill \\ V_{2} \hfill \\ V_{3} \hfill \\ V_{4} \hfill \\ V_{5} \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} x_{0} - 2Rc_{1} \sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}} \, y_{0} - 2Rc_{3} \sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}}{ 0} \hfill \\ x_{0} + 2R(1 - c_{1} )\sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}} \, y_{0} - 2R(1 - c_{4} )\sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}}{ 0} \hfill \\ x_{0} + 2Rc_{2} \sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}} \, y_{0} + 2Rc_{4} \sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}}{ 0} \hfill \\ x_{0} - 2R(1 - c_{2} )\sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}} \, y_{0} + 2R(1 - c_{3} )\sqrt[3]{{\pi t_{1} \tan \left( {{\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}} \right)}}{ 0} \hfill \\ x_{0} \, y_{0} \, R\sqrt[3]{{{{\pi t_{1} } \mathord{\left/ {\vphantom {{\pi t_{1} } {(\tan^{2} ({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}))}}} \right. \kern-0pt} {(\tan^{2} ({\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0pt} 2}))}}}} \hfill \\ \end{gathered} \right]$$

(1)

Fig. 3

Flow chart of extracting effective abrasive grain top angle

Fig. 4

a Identification and extraction of AAG; b contour extraction of AAG; c the original identification contour of contour 7; d the original identification discrete points of contour 7; e the discrete points screened by the first differential calculation of contour 7; f the discrete points screened by the second differential calculation of contour 7; g The comparison of original and fitted profiles of contour 7; h The fitted profiles of all AAGs in b

Fig. 5

a Manual extracted value of AAG’s top angle in Fig. 4a; b Comparison of manually extracted value and fitted contour extraction value

As shown in Eq. 1, the particle shape is not only related to the spatial coordinates $(x_{0} ,y_{0} ,z_{0} )$ of the point $O$, but also closely related to the volume ratio parameter $t_{1}$ and the vertex angle $\alpha$ of the abrasive particle.$t_{1}$ and $\alpha$ are mainly depend on the dressing process of the wheel, and the spatial coordinates of the point $O$ relies on the distribution of grains, which can be gained from the SEM image of the wheel surface with image processing technology. Variables $c_{1} ,c_{2} ,c_{3} ,c_{4}$ are random values which is between 0 and 1. Considering the size of abrasive particles, the random value of variables $c_{1} ,c_{2} ,c_{3} ,c_{4}$ has a negligible effect on the grain shape.

2.2 Identification and extraction of AAG

The number of AAG is affected by many elements, such as grinding depth, feed rate, grinding wheel speed, grinding wheel dressing process, grinding wheel hardness, grinding wheel particle size, etc. However, in fact, the protrusion height of the grains is the key criterion to judge whether the particles are AAG or not. Abrasive grains with alumina material of the single crystal corundum wheel has high brittleness, they are easily worn or broken during the grinding process. In order to enhance the grinding efficiency and ensure the surface grinding accuracy, it is necessary to carry out regular grinding wheel dressing to restore the grinding performance of the wheel and the sharpness of the surface particles. According to the author's previous research [35], during the grinding procedure of the GZB45BA slider raceway, the larger abrasive particles are continuously worn and the smaller grains join the grinding. In the process of the grinding amount from 0 to 100 μm, the height of the grains gradually become uniformly distributed from large differences. The wheel dressing is performed when the cumulative grinding amount approaches to 100 μm. Concurrently, the number of abrasive particles that interfere with the surface material of the raceway and participate in surface grinding is the highest. Hence, the crucial protruding height value for differentiating AAG and BAG (broken abrasive grain)is the protruding height value h0 with the highest probability of abrasive grain distribution on the wheel surface. Both the wheel dressing experiment and the slider grinding experiment yielded a result of 87 μm for h0. Particles that protrude more than two-thirds of their grain size often break or fall off during rotary cutting because of the K hardness grade of the produced wheel [35]. Consequently, the AAG’s protrusion height falls below 4R/3, and its height range is:

$$\frac{4R}{3} \ge h_{act} \ge 87$$

(2)

Equations 9–11 in [35] are substituted into Eq. 2 to get the area range S_act for extracting AAG:

$$3\pi t_{1} R^{2} \le S_{act} \le \frac{{4\pi R^{3} t_{1} }}{87}$$

(3)

After denoising, grayscale, and binarization processing of the SEM image of the grinding wheel's surface topography, the related sections are identified, marked, segmented and removed. AAG is extracted using Eq. 3’s area extraction range.

To increase the accuracy of the 3D topography model of the wheel surface, the AAG angle extraction method is improved through contour extraction and differential processing in Fig. 3 [35]. The complex contour 7 in Fig. 4b is taken as an example to carry out contour fitting and calculation of the AAG angle in this paper. The key of contour fitting is to find discrete points with large changes in contour direction. The core of the algorithm is: Firstly, the bwperim function is used to extract the AAG contour (composed of a series of discrete pixel points); Secondly, the difference operation is used to obtain the changes between adjacent discrete points and screen out the discrete points with large changes; Finally, the search and extraction of the key discrete points of the contour are carried out by cyclic calculation. The specific calculation process is as follows.

Step 1: The pixel points of the contour 7 extracted by the bwperim function are composed of a two-dimensional array 2 $\times$ 14,484, that is, each discrete point is represented by its abscissa and ordinate $\left({x}_{n},{y}_{n};n=1,...,14484\right)$. Whereas, it is necessary to increase the operation of deleting the deviation points when there will be coordinate points that deviate far from the contour range, as shown in Fig. 4d.

Step 2: Perform a differential calculation on the horizontal and vertical coordinates of adjacent discrete points respectively.

$$Xdiff = x_{n + 1} - x_{n} \left( {n = 1,...,14483} \right)$$

(4)

$$Ydiff = y_{n + 1} - y_{n} \left( {n = 1,...,14483} \right)$$

(5)

Step 3: Find the turning point of the contour trend according to the difference calculation result. That is, the abscissa and ordinate coordinates of discrete points whose difference value is less than 0 are returned by using the find function in MATLAB.

Step 4: All discrete points with difference value less than 0 are further filtered, that is, two points with adjacent distance less than 0.5 are merged into the same point, and then duplicate discrete points are deleted to obtain discrete key points of the contour.

Step 5: Store the discrete points that disappear in the range of horizontal and vertical coordinates after each difference, as shown in the discrete points in the red curve in Fig. 4e. The stored discrete points and the discrete points filtered by the last difference calculation are the key discrete points for contour fitting.

Step 6: To fit the contour more effectively, 50 is taken as the number threshold of the key dispersion points of the final fitted contour in this paper. The difference calculation is ended when the number of key discrete points is less than or equal to 50, otherwise, return to Step 2. The final number of key discrete points for fitted contour 7 is 32, and the number of difference cycles is 10.

Step 7: Calculate the tangent value of each discrete point and the center point $\left({x}_{0},{y}_{0}\right)$, complete the sequence of all discrete points according to the tangent value from small to large, and connect the discrete points in turn to obtain the final fitted contour, as shown in Fig. 4g. Finally, calculate the angles according to the sequence of discrete points, as shown in Eqs. 6–10.

$$x_{0} = \left( {x_{\max } + x_{\min } } \right)/2$$

(6)

$$y_{0} = \left( {y_{\max } + y_{\min } } \right)/2$$

(7)

$$\left\{ \begin{gathered} \alpha_{n} = arc\cos \left( {\left( {b_{n}^{2} + c_{n}^{2} - a_{n}^{2} } \right)/2b_{n} c_{n} } \right)\left( {n = 2,...,31} \right) \hfill \\ a_{n} = \sqrt {\left( {x_{n + 1} - x_{n - 1} } \right)^{2} { + }\left( {y_{n + 1} - y_{n - 1} } \right)^{2} } \, \hfill \\ b_{n} = \sqrt {\left( {x_{n + 1} - x_{n} } \right)^{2} { + }\left( {y_{n + 1} - y_{n} } \right)^{2} } \hfill \\ c_{n} = \sqrt {\left( {x_{n} - x_{n - 1} } \right)^{2} { + }\left( {y_{n} - y_{n - 1} } \right)^{2} } \hfill \\ \end{gathered} \right.$$

(8)

$$\left\{ \begin{gathered} \alpha_{1} = arc\cos \left( {\left( {b_{1}^{2} + c_{1}^{2} - a_{1}^{2} } \right)/2b_{1} c_{1} } \right) \hfill \\ a_{1} = \sqrt {\left( {x_{32} - x_{2} } \right)^{2} { + }\left( {y_{32} - y_{2} } \right)^{2} } \hfill \\ b_{1} = \sqrt {\left( {x_{2} - x_{1} } \right)^{2} { + }\left( {y_{2} - y_{1} } \right)^{2} } \hfill \\ c_{1} = \sqrt {\left( {x_{32} - x_{1} } \right)^{2} { + }\left( {y_{32} - y_{1} } \right)^{2} } \hfill \\ \end{gathered} \right.$$

(9)

$$\left\{ \begin{gathered} \alpha_{32} = arc\cos \left( {\left( {b_{32}^{2} + c_{32}^{2} - a_{32}^{2} } \right)/2b_{32} c_{32} } \right) \hfill \\ a_{32} = \sqrt {\left( {x_{31} - x_{1} } \right)^{2} { + }\left( {y_{31} - y_{1} } \right)^{2} } \hfill \\ b_{32} = \sqrt {\left( {x_{32} - x_{1} } \right)^{2} { + }\left( {y_{32} - y_{1} } \right)^{2} } \hfill \\ c_{32} = \sqrt {\left( {x_{32} - x_{31} } \right)^{2} { + }\left( {y_{32} - y_{31} } \right)^{2} } \hfill \\ \end{gathered} \right.$$

(10)

The horizontal and vertical coordinates of the key discrete points of the final fitted contour 7 and the corresponding angle extraction values are shown in Table 1. The prominent height ${h}_{act}$ of the AAG is within the range of [87, 160 μm] according to the particle size of the grinding wheel. The arithmetic square root $a$ of the AAG’s bottom surface area is within the range of [125 ${t}_{1}$,$2 \times$ 160 μm] (the value range ${t}_{1}$ can be obtained through the subsequent grinding wheel dressing experiment). Therefore, the value range of the AAG’s top angle can be obtained by Eqs. 11 and 12, it is [33.4°, 123.0°).

Table 1 Horizontal and vertical coordinates of 32 discrete points of the final fitted profile 7 μm and its corresponding angle extraction values

$$2\times 87\mathit{tan}\left(\alpha /2\right)<2\times 160$$

(11)

$$2\times 160\mathit{tan}\left(\alpha /2\right)\ge 125{t}_{1}(Max\left({t}_{1}\right)=0.77)$$

(12)

The angle of the fitted profile is screened based on the value range of AAG’s top angle and the results are 102°, 98°, and 64°, respectively, as shown in Fig. 4g. The final screening result for the angle of the fitted profile is 64°, which is very close to the manually extracted profile of 65° (Fig. 4c). AAG’s top angle interferes with the surface material and grinds the workpiece, while the grinding parts of 102° and 98° are too small to participate. All the AAG in Fig. 4b are image processed according to the above contour fitted and angle extraction process. The results are shown in Fig. 4h. The comparison between the distribution value of the AAG’s top angle and manually extracted angle value is shown in Fig. 5, which verifies the correctness and rationality of the top angle extraction results. In order to better understand the random nature of AAG’s top angle distribution, 6 SEM images of different position regions with the same size on each grinding wheel surface under different dressing process parameters are extracted, and their distribution is statistically analyzed. The top angles of the AAG are mostly between 40° and 120° and follow a normal distribution with a mean of 81.1023 and a standard deviation of 21.3197.

According to $S{T}_{act}$ and the geometric relationship with any four-edge cone shape, the size of the AAG can be obtained from Eq. 13 [35].

$$\left\{ \begin{gathered} t_{act} = ST_{act} /S_{image} \, \hfill \\ R = randi([62 \, 80],1,1) \, \hfill \\ V_{0} = 4/3\pi R^{3} \, \hfill \\ V_{act} = V_{0} t_{act} \, \hfill \\ f(\alpha_{act} ) \, = \frac{1}{{\sqrt {2\pi } \times 21.3197}}\exp \left( { - \frac{{\left( {\alpha_{act} - 81.1023} \right)^{2} }}{{2 \times 21.3197^{2} }}} \right) \, \hfill \\ h_{act} = \sqrt[3]{{{{3V_{act} } \mathord{\left/ {\vphantom {{3V_{act} } {(4\tan^{2} (\alpha_{act} /2))}}} \right. \kern-0pt} {(4\tan^{2} (\alpha_{act} /2))}}}} \, \hfill \\ a_{act} = 2h_{act} \tan (\alpha_{act} /2) \hfill \\ \end{gathered} \right.$$

(13)

where ${t}_{act}$ is the AAG volume ratio, ${ST}_{act}$ is the volume sum, ${S}_{image}$ S__image is the entire volume, V₀ is the volume before dressing, and ${V}_{act}$ is the AAG volume. ${\alpha }_{act}$ represents AAG's top angle, which follows a normal distribution. The noticeable AAG height is ${h}_{act}$ AAG's bottom surface area's arithmetic square root is ${a}_{act}$_. To conclude, parameters α__act and ${ST}_{act}$ are crucial for establishing the AAG's size model. They are primarily determined by the grinding wheel dressing process conditions and can be obtained from image processing experiments.

2.3 Distribution of AAG

The SEM image of the wheel surface morphology shows that the grains are not totally non-overlapping or filled. Grinding grains are not randomly distributed and are related to AAG area ratio and AAG number after wheel dressing. Based on AAG’s extracted features, this study calculates the area ratio, number, and size to determine its distribution. To determine AAG distribution, the distance between AAG is firstly specified. The black area of the binarized grinding wheel topography SEM image contains binders, detached grinding, and overlapping grinding grains. In this research, one-third of the black area ratio is believed to be the greatest grinding grain overlap rate since it cannot precisely calculate component areas. Secondly, the maximum AAG overlap rate determines the minimum and maximum centre-to-centre distances; Thirdly, to avoid abrasive particle overlap or separation and concentration caused by random distribution in two directions, the generatrix’s length direction is uniformly distributed and the wheel cone surface's circumference is randomly distributed to determine AAG distribution.

2.4 Experiment development and verification

The dressing experiments of the grinding wheel are conducted and the surface morphology of the grinding wheel are measured by using a morphometer after determining the quantification method for the geometric characteristics such as the shape, size, distribution, density, and quantity of abrasive particles on the surface of the grinding wheel. In addition, a mapping relationship between the grinding wheel dressing process parameters and the geometric feature parameters of the morphology is founded to establish the surface morphology model of the grinding wheel. First, the diamond roller shown in Fig. 2 is used to modify the grinding wheel into a formed grinding wheel with a slider cross-section shape; Second, the dressing experiments of the grinding wheel are conducted based on different feed rates, dressing depths, and wheel linear speeds, as shown in Table 2 [35]. To avoid experimental errors, each group of grinding wheel dressing experiments is repeated four times (three times of which are used as experimental data, and one time is used as validation experimental data); Then, a morphometer is used to measure the surface morphology of the grinding wheel obtained from each group of dressing experiments. In order to reduce the measurement error of the grinding wheel morphology, six different areas of the same size are measured on each grinding wheel surface. Image processing technology is used to extract geometric information such as the shape, size, distribution, density, quantity, etc. of the particles on the surface of the grinding wheel, and statistical analysis is performed. Simultaneously, a mapping relationship between the geometric features of the grinding wheel surface and the parameters of the dressing process is founded; Finally, a wheel surface morphology model is established based on the size, quantity, and distribution of AAGs. By comparing the quantity, density, area ratio, distribution, and size of AAG measured through simulation models and experiments [35], the effectiveness of the grinding wheel morphology modeling method is verified. On this basis, a 3D morphology model of the formed grinding wheel is further established.

Table 2 Test parameters for grinding wheel dressing experiments [35]

3 Results and discussions

3.1 3D topography modeling

According to the structure of the formed grinding wheel and the section size of GZB45BA slider in Fig. 2, the 3D model of the formed grinding wheel body is shown in Fig. 6a. It is a symmetrical structure and the two round platform sides of the upper and lower symmetry are the main contact areas during the grinding of the slider raceway. Whereas, the bus on the side of the grinding wheel platform is 7 mm, the angle between the bus and the radius of the bottom surface is 45°, the range of the lower bottom radius is [14.7, 22.6 mm]. 14.7 mm and 22.6 mm are the radius of the bottom surface of the scrapped and new dressed grinding wheel, respectively. For facilitating the calculation, the lower circle truncated cone is focused on in this paper and its 3D topography model of the surface abrasive particles is established. In Fig. 6b, the 3D coordinate system of the lower circle truncated cone is a global coordinate system and the local spatial coordinates of the five vertices that determine the shape and size of the AAG is transformed through Eq. 14 and Eq. 15.

$$\left[ \begin{gathered} BX \hfill \\ BY \hfill \\ BZ \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} \cos \left( { - 45^{ \circ } } \right) \, - \sin \left( { - 45^{ \circ } } \right){ 0} \hfill \\ \sin \left( { - 45^{ \circ } } \right){\text{ cos}}\left( { - 45^{ \circ } } \right){ 0} \hfill \\ 0 \, 0{ 1} \hfill \\ \end{gathered} \right] \times \left[ \begin{gathered} x \hfill \\ y \hfill \\ z \hfill \\ \end{gathered} \right] + \left[ \begin{gathered} \Delta x \hfill \\ \Delta y \hfill \\ \Delta z \hfill \\ \end{gathered} \right]$$

(14)

$$\left[ \begin{array}{l} {V_1}\\ {V_2}\\ {V_3}\\ {V_4}\\ {V_5} \end{array} \right] = \left[ \begin{array}{l} BX + a{c_3}\cos {45^ \circ }{\rm{ }}BY - a{c_1}\cos {45^ \circ }{\rm{ }}BZ - a{c_3}\sin {45^ \circ }\\ BX + a\left( {1 - {c_4}} \right)\cos {45^ \circ }{\rm{ }}BY + a\left( {1 - {c_1}} \right)\cos {45^ \circ }{\rm{ }}BZ - a\left( {1 - {c_4}} \right)\sin {45^ \circ }\\ BX - a{c_4}\cos {45^ \circ }{\rm{ }}BY + a{c_2}\cos {45^ \circ }{\rm{ }}BZ + a{c_4}\sin {45^ \circ }\\ BX - a\left( {1 - {c_3}} \right)\cos {45^ \circ }{\rm{ }}BY - a\left( {1 - {c_2}} \right)\cos {45^ \circ }{\rm{ }}BZ + a\left( {1 - {c_3}} \right)\sin {45^ \circ }\\ BX + h\sin {45^ \circ }{\rm{ }}BY{\rm{ }}BZ + h\sin {45^ \circ } \end{array} \right]$$

(15)

Fig. 6

3D topography model of the side surface of the lower circle truncated cone of the formed grinding wheel

The local coordinates $\left(x,y,z\right)$ of the bottom center of the single AAG are rotated -45°around the Z axis, and the coordinates translation is made. The coordinate translation amount $\left( {\Delta x,\Delta y,\Delta z} \right)$ is determined by the side position of the grinding wheel where the AAG is located, and the coordinates after translating are the global coordinates $\left(BX,BY,BZ\right)$ of the central point of AAG’s bottom center, as shown in Eq. 14. The global coordinate of each vertex is determined according to the relative position of each vertex of the AAG relative to the center point of the bottom surface in the local coordinate system (Eq. 1), as shown in Eq. 15. As demonstrated in Fig. 6b, the circular truncated cone's bus length is shorter than its circumference at different Z positions. Therefore, the AAG is evenly distributed along the bus direction and randomly distributed along the circumference of the round table according to the distribution rule of the AAG in Eq. 4. Each circumference radius and its circumference can be obtained according to the average number $n_{p}$ of AAG in the direction of the bus bar, as shown in Eqs. 16 and 17, respectively. The number of the AAG in each circular direction can be obtained according to the distribution density of the AAG and the corresponding circular length, as shown in Eqs. 2, 18. Here, the AAG density is 21/mm² which is obtained by the 3D morphometer and the SEM after the wheel dressing experiments.

$${r}_{i}=\left(20-7\times \sqrt{2}/2\right)+\left(i-0.5\right)/{n}_{p} \, \left(i=1,...,{n}_{p}\right)$$

(16)

$${C}_{i}=\pi \left({r}_{i}+{r}_{i+1}\right) \, \left(i=1,...,{n}_{p}\right)$$

(17)

$${n}_{i}=ceil\left({C}_{i}\times \sqrt{21}\right) \, \left(i=1,...,{n}_{p}\right)$$

(18)

As shown in Eq. 19, The center distance between any two adjacent AAGs is obtained through the minimum center distance $d_{\min }^{act}$, maximum center distance $d_{\max }^{act}$ and Eqs. 16–18.

$${d}_{i,j}={d}_{\mathit{min}}^{act}+\left({d}_{\mathit{max}}^{act}-{d}_{\mathit{min}}^{act}\right)r and \left[1,{n}_{i}-1\right] \, \left(i=1,...,{n}_{p} \, j={n}_{i}\right)$$

(19)

The AAGs uniformly distributed in the direction of the bus bar are the initial AAGs in each circumferential direction. Then the bottom center coordinates of each AAG distributed in the surface area of the complete round table are obtained from the clearance of any two adjacent AAGs in each circumferential directions of Eq. 19. At last, the center coordinates of each AAG distributed on the side surface of the lower circle truncated cone are transformed according to Eqs. 14 and 15. The spatial position of AAG’s each vertex in the global coordinate system is obtained, and a 3D topography model of AAGs on the side of the round table is established, as shown in Fig. 6c. From the local magnification Fig. 6d, e of Fig. 6c, the number of AAG on the wheel surface is large and its shape, size and distribution are random and the distribution density and protruding height of the AAG can be determined by the dressing process parameters. The surface topography of the slider raceway is formed by the cumulative effect of the chip removal, and the distribution of the maximum undeformed chip thickness (MUCT) distribution is identical to the distribution of the grooves and protrusions. Therefore, taking the distribution model of MUCT as the intermediate variable, the 3D surface morphology model of slider raceway under different grinding parameters can be established based on the surface topography of the formed grinding wheel and the material removal mechanism between AAGs and raceway surface.

3.2 Material removal mechanism

Based on the research [36], the MUCT distribution model may be created by analyzing the material removal process, MUCT size and distribution, and the AAG-raceway surface interference depth. Figure 7 shows the process of the material removal and surface topography formation in the slider raceway. Figure 7b shows how the AAG in Fig. 7a with varying protrusion heights and shapes interacts with the raceway surface to remove surface material. Figure 7a expresses that the number of AAGs is large and its distribution is random. The particle–workpiece interference depth is affected by the AAG shape, distribution, and protrusion height affect. Compared with the AAG labeled 1, the AAG labeled 3 has a larger protruding height and larger interference depth to the workpiece, resulting in the production of the larger chip. Figure 7c is a single feed cutting trajectory of a single AAG. During the grinding process, AAGn begins to contact the raceway surface at point N and travels along a curved path to the point $B_{n}$ where it begins to separate from the raceway surface and the chip is generated, as shown in the green area $NN{\prime} N^{^{\prime\prime}} C_{n} B_{n}$. The cutting path $NN^{^{\prime\prime}} C_{n} B_{n}$ is cycloid relative to the reciprocating linear movement of workpiece feeding, which is generated by the superposition of the circular movement with velocity $v_{s}$ and the workpiece feeding movement with velocity $v_{w}$. According to the grinding process of slider raceway surface, Fig. 7d is the cross-section simulation diagram of the material removal between the single AAG and workpiece surface in a single grinding wheel dressing cycle according to the grinding allowance of 100 μm and the grinding depth of 2 μm. The circumferential cross-sectional profile of all AAGs on the grinding wheel’s circle truncated cone surface is shown in Fig. 7e. Under the spinning grinding wheel, the AAG and workpiece interact to produce a large number of chips, which form a groove on the slider raceway in the grinding direction, as shown in Fig. 7f. Based on this, the MUCT distribution model can be established to obtain the 3D topography model of slider raceway surface. In the process of establishing MUCT model, first, image processing technology is combined with 3D topography measurement to extract the prominent height, shape, distribution and density of AAGs. Second, probability distribution function and DS (Dempster/Shafer) evidence theory quantify AAG wear, and grinding process parameters define the interference depth between the single AAG and raceway surface. The notable height, grinding depth, and AAG wear influence the AAG interference depth. Using the material removal mechanism, the chip formation process and MUCT size produced by a single AAG are calculated, as indicated in Eq. 20 [36] based on the AAG cutting track.

$$h^{\prime}_{muct} = r^{\prime} - \left( {\left( {r^{\prime}} \right)^{{^{2} }} A^{{^{2} }} \theta_{na}^{{^{2} }} + \left( {r^{\prime}} \right)^{{^{2} }} - 2\left( {r^{\prime}} \right)^{{^{2} }} A\theta_{na}^{{^{2} }} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} + h^{\prime}_{{\text{int}}}$$

(20)

Fig. 7

a The AAG’s distribution in the circumferential direction of the formed wheel and its motion with the slider raceway; b the relationship between the chip size and the protruding height of the AAG; c the chip generation process of single AAG; d grinding simulation between a single AAG and the workpiece surface during the wheel dressing cycle; e cross-sectional profile of all AAGs in a certain circular direction of the wheel; f 3D topography of the slider raceway surface

MUCT amount and distribution can be estimated after analyzing the effect of wheel–workpiece and abrasive–workpiece contact area deformation on the contact arc length and effective cutting-edge density. Due to the random pyramid shape of the AAG, only one cutting edge is produced when it contacts the slider raceway surface at any grinding depth, hence the effective cutting-edge density is 21/mm². The contact area $S_{cont}$ between the grinding wheel and the workpiece is governed by the contact arc length $l_{r}$ and workpiece width $w_{workpiece}$ and it determines the number of effective cutting edges.

The length of the contact arc is affected by the randomness of AAG's size, shape, and distribution due to complex phenomena in the grinding area, unlike the geometric and moving contact arc lengths. Hertz contact theory states that the geometric contact arc length of the nth AAG on the i th small round table of the formed grinding wheel can be calculated from the contact deformation between wheel and slider raceway, AAG and slider raceway, and AAG wear [36]:

$${l}_{ri}^{n}={\left(\frac{8}{\pi }\left({r}_{i}+{r}_{i+1}\right)W{P}_{i}+{d}_{si}{\delta }_{gi}^{n}+\frac{8}{\sqrt{\pi }}{\left(W{\delta }_{gi}^{n}{d}_{si}\frac{{r}_{i}+{r}_{i+1}}{2}{P}_{i}\right)}^\frac{1}{2}+\left({{h}{\prime}}_{\mathit{int}}^{n}+ap\right){d}_{si}\right)}^\frac{1}{2}\left(i=\mathrm{1,2},...,33\right)$$

(21)

where $W = {{\left( {1 - u_{{_{1} }}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - u_{{_{1} }}^{2} } \right)} {E_{1} }}} \right. \kern-0pt} {E_{1} }} + {{\left( {1 - u_{{_{2} }}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - u_{{_{2} }}^{2} } \right)} {E_{2} }}} \right. \kern-0pt} {E_{2} }}$.

Therefore, the size and distribution model of MUCT are created which can be confirmed by surface grinding the slider raceway.

3.3 Modeling the surface topography

According to the chip formation process and the material removal mechanism, the surface morphology is the cumulative result of the chip removal, and the distribution of the MUCT is like the replication of the surface grooves and bulges. Therefore, the 3D surface topography model of slider raceway under different grinding parameters can be established by using the intermediate variable of MUCT distribution model on the basis of the AAG model. The weight coefficient of the number of AAGs in each height distribution zone is calculated by statistical analysis of the probability density distribution of AAG protruding heights after grinding wheel treatment experiment (Eq. 22).

$${W}_{grain}^{90}=0.0438,{W}_{grain}^{100}=0.1347,{W}_{grain}^{110}=0.1246,{W}_{grain}^{120}=0.1414,{W}_{grain}^{135}=0.1178$$

(22)

According to Eq. 22, the ratio of the AAG’s number in each height distribution interval can be obtained, as shown in Eq. 23. And AAGs’ protrusion height is calculated through Eq. 24 by considering the small difference in each height interval.

$${W}_{AAG}^{90}=0.0787,{W}_{AAG}^{100}=0.2362,{W}_{AAG}^{110}=0.2205,{W}_{AAG}^{120}=0.2520,{W}_{AAG}^{135}=0.2126$$

(23)

$$\left\{ \begin{gathered} H_{AAG}^{90} { = }87{ + }3 \times rand\left( {1,1} \right) \hfill \\ H_{AAG}^{100} { = }90{ + }10 \times rand\left( {1,1} \right) \hfill \\ H_{AAG}^{110} { = }100{ + }10 \times rand\left( {1,1} \right) \hfill \\ H_{AAG}^{120} { = }110{ + }10 \times rand\left( {1,1} \right) \hfill \\ H_{AAG}^{135} { = }120{ + }15 \times rand\left( {1,1} \right) \hfill \\ \end{gathered} \right.$$

(24)

The grinding process parameters of the single factor experiment for the slider raceway are taken as the input parameters. Working table feeding speeds are 25, 26, 27, 28 m/min, grinding wheel linear speeds are 28, 30, 32, 34 m/s, and grinding depths are 1, 2, 3, 4 μm. In Eqs. 25 and 26, the AAG protrusion height, deformation of the wheel–workpiece and abrasive–workpiece contact areas, and influence factors of AAG wear are used to calculate the number of cutting edges and the actual contact arc length.

$$Nace_{i} = ceil\left( {21 \times 7 \times l_{ri} /1000} \right) \, \left( {i = 1,2,...,33} \right)$$

(25)

$${l}_{ri}={\left(\frac{8}{\pi }\left({r}_{i}+{r}_{i+1}\right)W{P}_{i}+{d}_{si}{\delta }_{gi}+\frac{8}{\sqrt{\pi }}{\left(W{\delta }_{gi}{d}_{si}\frac{{r}_{i}+{r}_{i+1}}{2}{P}_{i}\right)}^\frac{1}{2}+\left({h}_{\mathit{int}}{\prime}+5\right){d}_{si}\right)}^\frac{1}{2}\left(i=\mathrm{1,2},...,33\right)$$

(26)

From Eqs. 24 and 25, the number of the AAG and the protruding height of each AAG in the contact area of grinding wheel and slider raceway can be obtained. The protruding height of each AAG is calculated after considering the influence of AAG wear and substituted into Eq. 20 to obtain the MUCT and its distribution. On this basis, the raceway surface roughness profile with different process parameters can be determined. Then the 3D surface topography model of slider raceway is founded after the difference fitting in the vertical direction of the roughness profile. The results are shown in Fig. 8.

Fig. 8

3D topography model of the raceway surface. (X-grinding direction, Y-raceway width direction) a–d Vw = 25 m/min, Vs = 32 m/s; e–h ap = 2 μm, Vs = 32 m/s; i–l ap = 2 μm, Vw = 25 m/min

3.4 Experimental validation

To verify the effectiveness of surface morphology models for slider raceway under different grinding process parameters, firstly, grinding experiments are conducted on the raceway grinding machine PLAMATH408 shown in Fig. 9. Based on workshop experience and actual process parameters, the experimental parameters for slider raceway grinding are designed as shown in Table 3. Among them, for each group of grinding experiments, four identical sliders are ground simultaneously to reduce experimental errors; Second, the 3D surface morphology of the raceway is measured using the Rtec dual focus 3D profilometer (UP) shown in Fig. 9, and the results are shown in Fig. 10. Then, the roughness profile is extracted based on the surface morphology of the slider raceway measured by a 3D profilometer and the established 3D surface morphology model of the raceway; Finally, based on the extraction of roughness values and surface microstructures such as grooves, peaks, width, depth (height), and aspect ratio from roughness contours, statistical analysis and comparison are conducted to verify the effectiveness of the surface morphology model of the slider raceway.

Fig. 9

Slider grinder PLANMATHP408 and 3D profilometer

Table 3 Specific grinding process parameters

Fig. 10

Raceway surface 3D topography testing. a–d Vw = 25 m/min, Vs = 32 m/s; e–h Vw = 25 m/min, ap = 2 μm; i–l Vs = 32 m/s, ap = 2 μm

The roughness and feature information of the slider raceway surface microstructure are used to evaluate the 3D topography model’s accuracy.

Experiment Results: The roughness value of the surface contour is usually characterized by the parameter Ra (arithmetic mean deviation of the contour), whose calculation process is shown in Eq. 27. This shows that Ra values are only related to the size and distribution number of grooves and bulges, but not to their specific surface distribution positions. Therefore, the surface simulation rough contour can be generated using the random distribution method that does not affect the roughness value Ra of the profile after establishing the MUCT distribution model.

$$Ra_{profile} = f\left( {\left[ {\left\{ {h_{MUCT}^{1} ,w_{MUCT}^{1} } \right\},...,\left\{ {h_{MUCT}^{n} ,w_{MUCT}^{n} } \right\}} \right]} \right) = f\left( {\left[ {\left\{ {h_{MUCT}^{random1} ,w_{MUCT}^{random1} } \right\},...,\left\{ {h_{MUCT}^{randomn} ,w_{MUCT}^{randomn} } \right\}} \right]} \right)$$

(27)

According to the surface topography simulation model of slider raceway under different grinding process parameters in Fig. 8, 30 surface roughness simulation profiles are extracted and roughness simulation values are calculated according to Eq. 27. Meanwhile, for the experimental test topography corresponding to each simulation model in Fig. 10, the Gwyddion software built in the confocal 3D topography instrument is used to identify the roughness contour at 30 arbitrary positions in the topography map, and the average roughness value is counted (Fig. 11).

Fig. 11

Extraction of the roughness profile measurement

As shown in Fig. 12, the 30 simulated roughness values are compared with the average roughness values measured in 30 experiments. Ra increases with the grinding depth, decreases first and then increases with the increasing feeding speed of the working platform, while diminishes with the growing of the wheel speed. In addition, the predicted values and experimental values and their variation trends are highly consistent in the 30 simulation processes. At the same time, the relative error between the mean value of roughness simulation and the experimental mean value shown in Fig. 13 is basically controlled within 7%, which can verify the correctness and rationality of the topography modeling method. In addition, the simulation model of slider raceway surface topography can be also verified from the perspective of the geometric characteristic information of the surface microstructure. With the 3D topography model of the slider raceway surface established in Fig. 8, not only the surface roughness profile can be extracted to obtain its roughness value, but also the geometric features of the microstructure can be extracted from the roughness contour [36].

Fig. 12

Comparison of the roughness values between experimental and simulation measurements

Fig. 13

Relative errors between simulated and experimental roughness values of the surface profiles in the 3D topography model

For the roughness profiles extracted from the topography simulation model and experimental test topography under different grinding process parameters, the microstructure geometric features such as grooves and convex peaks in the surface rough contour are calculated and their average values are compared and analyzed, the results are shown in Fig. 14a and c shows that the simulation value and experiment value of A_S(groove depth), A_SW(depth to width ratio of the groove),T_H(peak height), T_HW (height to width ratio of the peak) and the average of the FG_H (peak valley height)are very close. At the same time, due to the value of A_W(groove width), T_W(peak width), FG_W (peak valley width) are determined using the random selection method in the range of [$0.6a{{h_{UCT} } \mathord{\left/ {\vphantom {{h_{UCT} } h}} \right. \kern-0pt} h},\sqrt {3.92} a{{h_{UCT} } \mathord{\left/ {\vphantom {{h_{UCT} } h}} \right. \kern-0pt} h}$], which leads to the simulation value and experimental value has a certain fluctuation (Fig. 14b). In general, the relative error of the simulation value and experiment value of the surface microstructure is basically controlled within 10%, only the relative error of a small number of geometric features is 10% to 15% (Fig. 14d). As a result, the correctness and effectiveness of the raceway surface topography model can be validated. This allows the extraction of surface microstructure feature information under varied grinding process parameters and the study of how process parameters affect groove, convex peak, and peak-valley structure size in surface topography.

Fig. 14

Comparison between simulation and experimental values of (a) AS, TH, and FGH, (b) AW, TW, and FGW, (c) ASW and THW, and (d) relative error

3.5 Impact of process parameters on microstructures

Different surface morphologies of the workpiece are processed through the different grinding process parameters. The difference in topographies is mainly reflected in the different geometric dimensions and distributions of surface microstructures such as pits, convex peaks, and peak valley structures. At the same time, the different surface morphology of the slider raceway will bring about different performance parameters of the linear guide pair during operation, such as the dynamic and static friction coefficients and wear resistance of the guide pair under different loads and operating speeds. Therefore, it is necessary to study the influence of grinding process parameters on the geometric characteristics of microstructure in surface morphology, which can lay a theoretical foundation for the study of the friction and wear resistance performance of slider raceway surfaces.

Figures 15, 16, 17 show the statistical analysis results of the geometric features of surface microstructures, respectively. The geometric feature information of surface microstructure is extracted according to the raceway surface topography simulation model under different grinding process parameters.

Fig. 15

Comparison of geometric characteristics of groove, peak and peak-valley structure in surface topography of slider raceway with different grinding depths

Fig. 16

Comparison of geometric characteristics of groove, peak and peak-valley structure in surface topography of slider raceway with different feeding speeds

Fig. 17

Comparison of geometric characteristics of groove, convex peak and peak-valley structure in surface topography of slider raceway with different grinding wheel linear velocities

3.5.1 The influence of grinding depth on the geometric characteristics of surface microstructure

Figures 15a–h show the statistical analysis results of surface microstructure geometric features extracted from the surface morphology of the raceway obtained under the grinding process parameters that the feed rate of 25 m/min, grinding wheel linear speed of 32 m/s, and grinding depth of 1 μm increase to 4 μm, respectively.

From Fig. 15a and Fig. 15d, within the scope of the grinding depth [1, 4 μm], A_S and T_H increase from [0.05 0.6 μm] to [0.25 0.8 μm] with the growing of grinding depth. Similarly, the distribution range of the FG_H increases with the grinding depth from [0.11 1.05 μm] to [0.5 1.61 μm], as shown in Fig. 15g. According to the material removal mechanism on the surface of the workpiece, it can be inferred that the thickness of undeformed chips is determined by the actual interference depth model between the AAGs and the workpiece surface (Eq. 20), which increases with the rising of the interference depth. Among them, the actual interference depth of AAGs is mainly affected by the protrusion height of the abrasive particles, the grinding depth, and the amount of abrasive wear [37]. According to the grinding trajectory of a single abrasive particle, it can be found that the interference depth of the abrasive particles grows with the increase of grinding depth. Therefore, with the growing of grinding depth, the actual interference depth between the AAG and the workpiece surface increases, resulting in the increase of chip thickness, which is reflected in the increase of A_S and T_H in the topography.

Whereas, the A_W, T_W and FG_W has changed little (Fig. 15b, e, h). The reason is that the chip width is calculated by random value within the range of [$0.6a{{h_{UCT} } \mathord{\left/ {\vphantom {{h_{UCT} } h}} \right. \kern-0pt} h},\sqrt {3.92} a{{h_{UCT} } \mathord{\left/ {\vphantom {{h_{UCT} } h}} \right. \kern-0pt} h}$] due to the difficulty in obtaining the relative position of the cutting edges when the AAG interference with the raceway surface. The surface topography is the cumulative effect of the interplay between a large number of AAGs and the slider raceway surface. The superposition of the groove width is formed based on the cumulative interaction of the randomly distributed abrasive particles in removing material. Therefore, the range of A_W is larger than that of T_W, as displayed in Fig. 15b, e. The range of A_W is [0.05 1.1 μm] and the range of T_W is [0.05 0.54 μm], respectively. By the same token, the T_HW and A_SW increase with grinding depth and the scope of T_HW is larger than that of the A_SW, as list in Fig. 15c and Fig. 15f, respectively.

3.5.2 The influence of feed rate and wheel linear speed on the geometric characteristics of surface microstructure

The statistical analysis results of the surface microstructure geometric features extracted from the surface morphology of the raceway obtained under grinding process parameters with the grinding depth of 2 μm, the grinding wheel linear speed of 32 m/s and a feed rate increasing from 25 m/min to 28 m/min are shown in Figs. 16a–h, respectively. Meanwhile, the statistical analysis results of the surface microstructure geometric features extracted from the surface morphology of the raceway obtained under grinding process parameters with the grinding depth of 2 μ m, the feed rate of 25 m/min and the grinding wheel linear speed increasing from 28 m/s to 34 m/s are shown in Figs. 17a–h), respectively.

When the feeding speed is in [25, 28 m/min], the chip thickness decreases first and then increases with the growing of the feeding speed. As a result, the A_S and T_H are firstly lowered and then growing with the increase of the feeding speed, and their distribution range decreased from [0.17 0.61 μm] to [0.08 0.52 μm] and then increased to [0.26 0.78 μm], as list in Fig. 16a, d. The FG_H declines from [0.34 1.01 μm] to [0.16 0.86 μm] and then increases to [0.51 1.38 μm], as displayed in Fig. 16g.

In the range of grinding wheel linear velocity [28, 34 m/s], chip thickness declines with the growing of wheel linear velocity. Therefore, the A_S and T_H continuously decrease with the rising in the wheel linear velocity, as noted in Fig. 17a, d, and the distribution range decreases from [0.19 0.81 μm] to [0.1 0.55 μm]. Meanwhile, the FG_H decreases from [0.55 1.6 μm] to [0.2 1.1 μm], as shown in Fig. 17h. Similarly, A_W, T_W and FG_W has little change with different feeding speeds and wheel linear velocities (Fig. 16(b, e, h) and Fig. 17b, e, h). Meanwhile, it can be inferred that the surface topography of the raceway is the cumulative effect of the interaction between a large number of AAGs and the surface according to the material removal mechanism and the groove width is formed based on the cumulative interaction of the randomly distributed abrasive particles in removing material. Therefore, the range of A_W is larger than that of T_W, as displayed in Fig. 16b, e and Fig. 17b, e. By the same token, the T_HW and A_SW increase with grinding depth and the scope of T_HW is larger than that of the A_SW, as list in Fig. 16c, f and Fig. 17c, f.

By comparing the variation trend of surface microstructure geometric characteristics that changes with the process parameters with the variation of surface roughness, it is found that the larger the surface roughness is, the larger the geometric characteristic size of the surface microstructure is.

3.5.3 The significance of studying the geometric characteristics of surface microstructures

In addition, during the running process of the guide rail pair, friction will be generated due to the adhesion between contact irregularity, the ploughing effect between roughness, and the appearance of hydrodynamic frictional stress under lubrication [37]. The tribological properties of raceway surface are highly dependent on surface topography, except for the preload of slider, loading of the guide rail pair, lubrication conditions and running speeds. On the one hand, the distribution and size of the microstructure in the topography can be used as a lubricant pocket to preserve the lubricating oil in the contact area, capture wear particles in the process of movement, and reduce wear. On the other hand, the distribution of surface microstructure will produce a rougher surface, thereby reducing the actual area of contact and reducing the friction coefficient. Thus, groove size, convex peaks, and peak-valley topologies vary with grinding process parameters and affect slider raceway friction and wear [38]. The constructed 3D surface topography model of slider raceway and the distribution and size characteristics analysis of surface microstructure in this chapter can be used to establish a friction and wear model and examine its features. At the same time, raceway surface grinding process optimization can overcome theory–practice gaps and provide more complete guidance.

4 Conclusions

Based on the 3D topography model of the wheel, the characteristics of the abrasive particle distribution on the side of the symmetrical round table of the formed grinding wheel are analyzed.

• The local spatial coordinates of AAG’s five vertices are transformed by taking the circular 3D coordinate system as the global coordinate system. At the same time, according to the principle of uniform distribution of AAGs along the bus direction and random distribution in the circumferential direction, a 3D topography model of AAGs distribution is founded.

• Secondly, the probability density distribution of AAG protrusion height determines the number of AAGs in each height distribution interval and their unique protrusion height values. The MUCT model also calculates slider raceway surface roughness profiles under varied grinding parameters. Multiple cycle calculation and profile difference fitting create the slider raceway surface's 3D topography model.

• Experiments with various grinding depths, feeding speeds, and wheel linear speeds are conducted for raceway grinding. The surface topography tested by the morphometer is compared with the topography simulation model, and the raceway topography model is verified from the perspectives of surface roughness and surface microstructure geometric characteristics. It is found that the A_S, T_H and FG_H grows with the grinding depth, and declines with the wheel linear speed and decreases first and then increases with the feeding speed in its range of [25, 28 m/min]. The change trend of the microstructures’ geometric characteristics changing with the grinding process parameters is compared with the surface roughness. And results show that the larger the roughness is, the larger the geometric feature size of the surface microstructure is.

• In future works, the influence of the topography model and the features of the surface microstructure on the slider raceway surface friction coefficient and wear amount will be studied. In addition, a more comprehensive guidance for the optimization of raceway surface grinding technology will also be provided to break through the limitations or reduce the error between theory and practice.