1 Introduction

Many types of timber structural elements (i.e., columns, trusses, and frame structures) undergo axial compression or combined axial compression and bending during their lifetime functions; the risk that they deflect laterally, under this load conditions, is called flexural buckling.

The load-bearing capacity of timber members is not easy to predict as it is influenced by several variables which can be gathered in two groups: the first one involves the geometrical features, the boundary conditions, the material and environmental properties (i.e., strength and service class) and the load duration; the second comprises the geometrical (i.e., initial curvature) and structural imperfections (i.e., knots, growth deviations, amount of moisture content). The effect of these latter variables was deeply investigated in Refs. [1,2,3,4,5] while the influence of the material properties on the load‐bearing capacity was analyzed by Blaß [6,7,8].

Furthermore, two key aspects should be considered: (i) a geometric effect called P‐delta which describes the non‐linear increasing of deformations due to the increasing eccentricity of the axial load, as well as (ii) the non-linear behavior of timber material under compression actions parallel to the grain. A large investigation on the P-delta effect on axial compressed timber elements was carried on by Tetmajer [9] and confirmed by test campaign by Larsen and Pedersen [10], the influence of non-linearity of timber on the interaction between moment and axial force was numerically defined by Buchanan [11, 12].

The current National codes and Standards (i.e., Eurocode 5 [13]) provide two methods for the calculation of the load-bearing capacity of axially compressed columns with and without eccentricity; the most simple one is based on the effective length method (ELM), while, the other accounts for a second-order analysis of the structure. This latter method, by the way, considers timber as an elastic material so it is not able to take into account its material non-linearity.

The ELM considers a simple equivalent column hinged at both ends; the P-delta effect is taken implicitly into account through a buckling factor, kc. The buckling factor is used here to reduce the compressive strength of the timber column in the direction parallel to the grain and depends on the effective length of the structural element which can be expressed by the slenderness ratio λ.

Several experimental tests have been performed to define the influence of slenderness ratios on failure modes strain and ultimate bearing capacity of glulam columns made of different timber species: bamboo [14], larch [15], European beech [16]. Moreover, the effect of imperfections such as knots [17] and cracks [18], was also investigated as experimentally as performing FEM fittings and parametric analyses.

A novel strain-based model to analyze the load-bearing capacity with and without eccentricity is proposed in Ref. [19] for solid elements; in this work, it is highlighted how the non-linear behavior of timber when subjected to compression parallel to the grain considerably influences the load-bearing capacity. Based on this latter model and accounting for the Glos’ stress–strain relation [20], in Ref. [21], Monte Carlo simulations were performed with the aim of investigating the influence of the varying material properties and slenderness.

Among the aforementioned solid and engineered wood products, an in-depth study of cross-laminated timber (CLT) column components has not yet been carried out. These latter structural elements result from the cut of prefabricated solid slabs made of adjacent planks layers glued together at a right angle.

In the last few decades, CLT has become popular in the mass timber construction field [22], especially for mid- and high-rise buildings, due to the numerous advantages [23] such as the high dimensional stability, elevated in-plane isotropic strength and stiffness with respect to sawn timber, high speed of installation [24], and the environmental benefits compared to other construction materials like steel, concrete, and masonry.

The growing interest on CLT for design purposes and its great mechanical properties has led several authors to analyze deepen its mechanical characteristics as bending, tensile, shear, and compressive strength [25,26,27,28,29,30,31]. Although, as previously highlighted, many studies have been conducted to clarify the in-plane and out-of-plane mechanical behavior of CLT panels, up to now, just limited research has been carried out to invesigate the stability bearing capacity of CLT members under axial compression loads. In Ref. [32], the different axial compression behaviors of cross-laminated timber columns (CLTCs) and control glued-laminated timber columns (GLTCs) were investigated. The GLT column specimens had a greater compressive loading capacity than CLT column specimens but the latter highlighted a better ductility and energy absorption than GLT. In Ref. [33], the main aims were to define the stability bearing capacity of the CLT members in axial compression and to propose a CLT stability coefficient calculation method by suitably modifying that implemented for GLT in the Chinese Standard. In Ref. [34], Ye et al. accounted for the CLT rolling shear sensitivity arising from the out-of-plane bending and compression load combination; an analytical model which takes rolling shear effects into account to predict the load-carry capacity of CLT compression-bending members was provided.

Stability issues have to be addressed in view of challenging aims such as those analyzed in [35,36,37,38]. In the case of timber engineering, it is to realize increasingly high-rise timber buildings. Because of the low modulus of elasticity parallel to the grain of timber in general and of the even lower shear modulus which affects the ortogonal layers [39], CLT is more prone to undergo instability phenomena. Timber exhibits about one third of the modulus of elasticity of concrete in parallel to the grain, and the radial-tangential shear stiffness is roughly two order of magnitude lower than the longitudinal one [40], and as a consequence, timber structures may suffer from buckling.

Considering the technology of cross-laminated timber, the orthogonal layers are influenced by the radial-tangential shear stiffness, usually called rolling shear stiffness [41], and, therefore, it is expected that shear effects are important in this type of wood-based composite.

Some researches pointed out how the properties of the entire CLT panel are strongly influenced by the type of wood of which its layers are made [42, 43], their thickness [44], and the type of glue adopted [45, 46]. Other studies [47,48,49,50], have investigated panels made with wood species other than fir and spruce, which are currently the most used species for CLT industrial manufacturing. In this context, panels made of some native hardwoods species such as beech, yellow-poplar, and tropical hardwood (i.e., rubberwood, batai) have shown an excellent behavior. This evidence is relevant considering the impact that the use of hardwood, especially local, would have on the production of CLT panels. The development of a short supply chain of wood is a possible mean to economically enhance the woodlands and to achieve environmental and social benefits [51]. Wood can be effectively used to manufacture products for structural purposes, but it is necessary to investigate the potential of each local species to identify the most suitable technology to employ. An interesting research case was carried out in Italy, where maritime pine from Sardinia was employed to produce cross-laminated timber panels. Preliminary tests were required to evaluate the physical and mechanical properties so as to demonstrate the suitability of this locally grown species to produce CLT panels [52]. In addition, the activation of a short supply chain of timber could lead to a sustainable forest management and to a better exploitation of the raw material [53]. Nowadays in Europe, the attention is focusing on hardwoods especially for manufacturing wood-based composite due to their great mechanical properties [54]. Despite the fact that softwood has played a central rule in the market of glue-laminated timber and cross-laminated timber, the abundance of hardwoods in European forests has determined the need to analyze their performances [55].

The current work aims to deeply analyze the buckling and post-buckling behavior of CLT panels. The specimens’added value lies in (i) the short supply chain origin of both hardwood beech an softwood Corsican pine and in (ii) the homogeneous beech and hybrid beech–Corsican pine configuration, devised for defining a possible optimization of material. To reach the purposed aim, an experimental test campaign is first carried on. As a result, the ultimate load and the failure modes are accounted for. At a second stage, analytical models are formulated and fitted with the previous evidences and then discussed.

2 Materials and methods

2.1 Specimens description

To carry on this experimental campaign, two of the most interesting Italian hardwood and softwood timber species, beech and Corsican pine, were chosen. The raw material for both species came from Calabrian forests, South Italy. All the steps that led to obtaining the final product were carried out with short supply chain procedures. An amount of 365 beech boards and 90 Corsican pine boards were specifically classified as D40 and C20 [50] and planed to a thickness of h = 18 mm to guarantee the adequate planar surface necessary for the face gluing. Two different series of three-layered cross-laminated timber (CLT) panels, made, respectively, of beech and Corsican pine and only beech, were realized to carry out an extended experimental campaign to assess their mechanical properties prior to the industrial production. The hybrid configuration is composed by two beech outer layers and one Corsican pine inner layer. The layering of the boards and the gluing process were performed by hand.

Timber boards were tiled, overlapped, and glued together by a melamine urea formaldehyde (MUF) adhesive [GripPro™ Design—AkzoNobel, that was obtained by mixing with the ratio 2–1 the two components: hardener (H002) and liquid flexible resin (A002)]. The narrow board edges were not bonded. The choice of employing the melamine adhesive was due to the usage of beech hardwood boards in both homogeneous and hybrid beam configurations with Corsican pine boards. In particular, the GripPro™ adhesive is specifically designed for softwood as well as for hardwood timber, such as beech, birch, oak, and chestnut. The average of glue grammage was 190 g/m2. The adhesive was applied in a factory condition of 17 °C, with an environmental moisture of 50%. Formed beams were then cold-pressed for 2 h, with a pressure of 1.4 N/mm2. No finger joints were forecasted in cross-laminated panels of this experimental campaign.

From this production, an amount of seven specimens for each series was accounted for these tests, their features are summarized in Table 1.

Table 1 Size (B = width; T = thickness; L = length), configuration, and test type of the examined CLT specimens
Full size table

2.2 Central axial compressive test

The experimental tests were performed at the Laboratory of Structures, Tests and Materials of the University of L’Aquila (Italy), Department of Civil, Architecture and Building and Environmental Engineering. The typical duration of buckling experiments was in the range of 30 min long and an appropriate setup was developed, to provide the desired loading and boundary conditions to the tested CLT panel. Each specimen was positioned between a couple of one-way knife hinges whose shape has been designed to ensure the right positioning in the underlying and overlying wedges (Fig. 1a, c). The distance between the axes of end hinges is \(l = 1064\;{\text{mm}}\). The wedges were connected to the machine test support devices by bolts.

Fig. 1
figure 1

Setup description: a machine test; b displacement transducers position and knifes; c setup design detail

Full size image

During the test, a total of four laser displacement transducers were used. Their position (Fig. 1b) was on both sides of the span area of the specimen; the transducers 1 and 3 were used to measure the middle deflections of the specimen, while the transducers 2 and 4 could measure some torsional effects. The in-plane compressive load F, continuously monitored by means of a load cell, was applied by means of an Instron-Schenck hydraulic servo-controlled jack along the width B.

In the process of specimen loading, a preload F0 was applied to the specimen to eliminate the gap between the ends of the specimen and the supports. In this experimental test, the preloaded load value F0 was taken as 30% of the estimated ultimate load value of the specimen.

The tests were carried out under displacement control; in particular, a limit of 15 mm was fixed for the vertical lowering of the machine crossbeam. Two different speed rates have been set: the first, until the critical load was reached, was equal to 0.44 mm/s, and once the critical load was reached, the speed rate has been reduced to 0.33 mm/s.

2.3 Experimental results

The ultimate loads Fb and the failure modes are summarized in Table 2. Some examples of failure modes are defined in Fig. 2. Regardless of configuration, panels reached similar average limit load levels equal to 200 kN for the homogeneous configuration and 192 kN for the hybrid configuration. Panels having an homogeneous configuration were characterized by a bending due to bucking (tension and compression) failure while the main failure mode of hybrid specimens was rolling shear. The standard deviation sy and the 5th percentile mk are given in Table 2.

Table 2 Axial compression test campaign evidence
Full size table
Fig. 2
figure 2

Failure modes: a–c bending–buckling; d–f rolling shear; g, h delamination

Full size image

The axial displacement versus compressive load F curves are shown in Fig. 3, both for the seven homogeneous specimens (Fig. 3a) and for the seven hybrid specimens (Fig. 3b). The curves of the homogeneous and hybrid specimens reach the final slope after an initial settlement of the specimens. It is worth observing that after such initial settlement, the slope of the linear increasing branches of the curve is almost the same both for the homogeneous and hybrid panels.

Fig. 3
figure 3

Axial displacement versus compressive load F: a homogeneous HB specimens; b hybrid HB specimens

Full size image

The recorded mid-span displacement versus compressive load F curves are shown in Fig. 4, both for the homogeneous (Fig. 4a) and hybrid (Fig. 4b) specimens. They all show the existence of some problems of the experimental apparatus. Specifically, due to the unavoidable imperfections of the experimental setup, it was necessary to re-elaborate the acquired data to extract the displacement component linked to the deformation of the specimen only. The imperfections of the setup that cannot be fully eliminated include: the misalignment of the two hinges with respect to the longitudinal axis of the specimen, the imperfect contact of the end sections of the specimen with base and top steel plates, and the presence of a gap between the lateral steel plates of the end restraints and the specimen. The accurate procedure to clean up the experimental curves from the imperfections is described in the Appendix. Finally, the re-elaborated mid-span displacement versus compressive load F curves are shown in Fig. 4c, d for the homogeneous and hybrid specimens, respectively.

Fig. 4
figure 4

Midspan displacement versus compressive load F: a and, top b recorded curves for the homogeneous and hybrid specimens, respectively; c and, bottom d re-elaborated curves for the homogeneous and hybrid specimens, respectively

Full size image

3 Analytical model

3.1 General glued multilayer beam model

To understand the results of the experimental campaign and in the attempt to extend such results for practical use, an analytical model is here developed. A general model is first introduced with the aim to approach the buckling of a glued multilayer beam subject to a concentrated compression load, after which it will be adapted to the three layers CLT panel object of the present paper. As the model is intended to interpret the experimental results described before, it will be made reference to an initial imperfection of the panels as in Fig. 5. It is worth observing that the length l is taken equal to the distance between the two end hinges of the experimental apparatus (l = 1064 mm), even though the panel length is of 800 mm (see Table 1), since it is assumed that the entire system between the hinges undergoes bending–buckling deformation.

Fig. 5
figure 5

Reference system: imperfect beam under a concentrated compression load

Full size image

The general mechanical model is made of N overlapped planar Timoshenko beams, with rectangular cross-sections of different height hi (i = 1…, N) and unique width b; the beams are connected through N − 1 glue lines, represented by a continuous distribution of linear elastic springs that work along the tangential and normal directions, as in Refs. [56, 57]. Since the model aims to analyze its buckling behavior, it is developed according to the classical linearized theory approach, which consider the hypothesis of small displacements and small strains, though imposing the equilibrium in a deformed shape adjacent to the reference equilibrium configuration (trivial solution).

The mathematical model is defined by three sets of three equations (kinematic, static, and constitutive) for each layer, which involve kinematic and static quantities related to the glue lines.

3.1.1 Kinematics

With reference to Fig. 6a, b, the kinematics on the entire system is described by a 3N displacement components vector \({\mathbf{u}}(x) = \left\{ {{\mathbf{u}}_{1} (x),..,{\mathbf{u}}_{i} (x),..,{\mathbf{u}}_{N} (x)} \right\}^{{\text{T}}}\), expressed as a function on a unique variable x, lying along the beam length, in which \({\mathbf{u}}_{i} (x) = \left\{ {u_{i} (x),v_{i} (x),\varphi_{i} (x)} \right\}^{{\text{T}}}\) encompasses the displacements of the i-th layer.

Fig. 6
figure 6

Kinematic quantities: a undeformed shape; b deformed shape

Full size image

By neglecting the dependence on the variable x for simplicity, a generalized 5N − 2 strain vector follows as \({{\varvec{\upvarepsilon}}} = \left\{ {{{\varvec{\upvarepsilon}}}_{1} ,{{\varvec{\upvarepsilon}}}_{g1,2} ..,{{\varvec{\upvarepsilon}}}_{gi - 1,i} ,{{\varvec{\upvarepsilon}}}_{i} ,{{\varvec{\upvarepsilon}}}_{gi,i + 1} ..,{{\varvec{\upvarepsilon}}}_{N} } \right\}^{{\text{T}}}\) in which the classical beam strains for the i-th layer are defined, adopting from now on the Lagrangian notation, as \({{\varvec{\upvarepsilon}}}_{i} = \left\{ {\varepsilon_{i} ,\gamma_{i} ,\kappa_{i} } \right\} = \left\{ {u^{\prime}_{i} ,v^{\prime}_{i} - \varphi_{i} ,\varphi^{\prime}} \right\}\), while for the i, i + 1-th glue line (to be intended as: between layers i and i + 1) (Fig. 7):

$$ {{\varvec{\upvarepsilon}}}_{gi,i + 1} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{ni,i + 1} } \\ {\varepsilon_{ti,i + 1} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {v_{i} - v_{i + 1} } \\ {\left( {u_{i} + \frac{{h_{i} }}{2}\varphi_{i} } \right) - \left( {u_{i + 1} - \frac{{h_{i + 1} }}{2}\varphi_{i + 1} } \right)} \\ \end{array} } \right\}. $$
(1)
Fig. 7
figure 7

Detail (in the deformed shape) of the kinematic and static quantities of the glue line between i-th and i + 1-th layers

Full size image

It should be observed that, since the thickness of a real glue line may be of difficult estimation or control, it is worthy to express the components of \({{\varvec{\upvarepsilon}}}_{gi,i + 1}\) independently from the thickness ti,i+1; therefore, such components represent displacements, and thus they are dimensionally equal to a length.

3.1.2 Statics

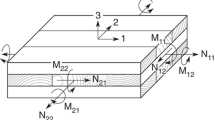
The static quantities of the general model, (represented in Figs. 7, 8 as positive), are the generalized internal forces \(N_{i} (x),\,\,T_{i} (x)\) and \(M_{i} (x)\) (i = 1,..,N), which represent the axial force, the shear force, and the bending moment, respectively, acting on the i-th layer, whereas quantities \(\overline{\sigma }_{i,i + 1} (x)\) and \(\,\overline{\tau }_{i,i + 1} (x)\) are, respectively, the normal and tangential stresses (per unit of length) acting along the contact interface between layers i and i + 1. These can be collected into a (5N − 2) × 1 force vector \({\mathbf{t}}(x) = \left\{ {{\mathbf{t}}_{1} (x),{\mathbf{t}}_{g1,2} (x)..,{\mathbf{t}}_{gi - 1,i} (x),{\mathbf{t}}_{i} (x),{\mathbf{t}}_{gi,i + 1} (x)..,{\mathbf{t}}_{N} (x)} \right\}^{{\text{T}}}\) with (neglecting again the dependence on the variable x for simplicity) \({\mathbf{t}}_{i} = \left\{ {\begin{array}{*{20}c} {N_{i} } & {T_{i} } & {M_{i} } \\ \end{array} } \right\}^{T}\) and \({\mathbf{t}}_{gi,i + 1} = \left\{ {\begin{array}{*{20}c} {\overline{\sigma }_{i,i + 1} } & {\overline{\tau }_{i,i + 1} } \\ \end{array} } \right\}^{T}\).

Fig. 8
figure 8

Static quantities in the deformed configuration and global resultants

Full size image

With reference to Fig. 8, the equilibrium equations, for each layer, should be written with respect to the adjacent deformed configuration defined by the angles \(\theta_{i} = v^{\prime}_{i}\) (i = 1,..,N), which may include some initial imperfection and, in general, should be different for each layer as the glue lines are allowed to deform out of their plane. Since the forces Ni and Ti (i = 1,..,N) are not parallel and the sections stepwise, it may be convenient to express the equilibrium condition with reference to an infinitesimal portion of the deformed beam, cut by two vertical sections, spaced dx, and projecting the forces Ni and Ti in the horizontal and vertical direction.

In Fig. 9, the forces involved in the equilibrium of the single layer are portrayed and the apex \(( \cdot )^{ + }\) indicates the small increment derived by a series expansion up to the first order, so that \(\alpha (x)^{ + } = \alpha (x) + \alpha^{\prime}(x)dx\), \(\alpha (x)\) being one of the kinematic or static entities shown in Fig. 9.

Fig. 9
figure 9

Static equilibrium for the i-th layer

Full size image

In the same figure, the rotations of the axis line are split in two parts, having distinguished the initial rotation \(\theta_{i0} = v^{\prime}_{0i}\), which may be present in the unloaded imperfect beam (Fig. 5), from the relative rotation \(\theta_{i} = v^{\prime}_{i}\), which rise from the initial imperfect shape, as an effect of the applied loads. It should be recalled that while the bending response of the layer is related to the (relative) rotation \(\theta_{i}\), the bending effect induced by the horizontal force \(H_{i}^{ + }\) depends on the (total) rotation \(\theta_{it} = \theta_{i0} + \theta_{i}\).

With reference to Fig. 9, it should be also observed that strictly the glue stress \(\overline{\sigma }\) and \(\,\overline{\tau }\) vary in an unknown way along the layer’s border; however, for simplicity, they are supposed uniform in dx and acting under the rotation \(\theta_{it}\).

For the i-th layer, it can be then demonstrated that the equilibrium equations read:

$$ \begin{gathered} N^{\prime}_{i} - (T_{i} \theta_{it} )^{\prime} - \overline{\sigma }_{i - 1,i} \theta_{it} + \overline{\sigma }_{i,i + 1} \theta_{it} + \overline{\tau }_{i - 1,i} - \overline{\tau }_{i,i + 1} = 0 \hfill \\ T^{\prime}_{i} + (N_{i} \theta_{it} )^{\prime} + \overline{\sigma }_{i - 1,i} - \overline{\sigma }_{i,i + 1} + \overline{\tau }_{i - 1,i} \theta_{it} - \overline{\tau }_{i,i + 1} \theta_{it} = 0 \hfill \\ M^{\prime}_{i} + T_{i} - ({{h_{i} } \mathord{\left/ {\vphantom {{h_{i} } 2}} \right. \kern-0pt} 2})(\overline{\tau }_{i - 1,i} + \overline{\tau }_{i,i + 1} - \overline{\sigma }_{i - 1,i} \theta_{it} - \overline{\sigma }_{i,i + 1} \theta_{it} ) = 0. \hfill \\ \end{gathered} $$
(2)

However, recalling that \(H = \sum\nolimits_{i} {H_{i} } = - F\) for the reference system (Fig. 5), the equilibrium equations can be simplified supposing that \(\theta_{it}\) is small enough for each layer, such as \(N_{i} \approx H_{i}\), and hence \(N = \sum\nolimits_{i} {N_{i} } \approx - F\), which implies that \(N^{\prime} = \sum\nolimits_{i} {N^{\prime}_{i} } \approx 0\); similarly the terms \(\overline{\sigma }\,\theta_{t}\) and \(\overline{\tau }\,\theta_{t}\) can be overlooked, thus determining the equilibrium equations in the form:

$$ \begin{gathered} N^{\prime}_{i} + \overline{\tau }_{i - 1,i} - \overline{\tau }_{i,i + 1} = 0 \hfill \\ T^{\prime}_{i} + (N_{i} \theta_{it} )^{\prime} + \overline{\sigma }_{i - 1,i} - \overline{\sigma }_{i,i + 1} = 0 \hfill \\ M^{\prime}_{i} + T_{i} - ({{h_{i} } \mathord{\left/ {\vphantom {{h_{i} } 2}} \right. \kern-0pt} 2})(\overline{\tau }_{i - 1,i} + \overline{\tau }_{i,i + 1} ) = 0. \hfill \\ \end{gathered} $$
(3)

3.1.3 Constitutive laws

Finally, the constitutive laws are introduced, based on a linear elastic uncoupled behavior for all the materials, according to the following expressions: \({\mathbf{t}}_{i} = \left[ {C_{i} } \right]{{\varvec{\upvarepsilon}}}_{i}\) with \(\left[ {C_{i} } \right] = {\text{diag}}\left\{ {E_{i} A_{i} ,G_{i} A_{ti} ,E_{i} I_{i} } \right\}\), for the i-th layer, and \({\mathbf{t}}_{gi,i + 1} = \left[ {C_{gi,i + 1} } \right]{{\varvec{\upvarepsilon}}}_{gi,i + 1}\) with \(\left[ {C_{gi,i + 1} } \right] = diag\left\{ {k_{i,i + 1} ,g_{i,i + 1} } \right\}\), for the i,i + 1-th glue line. Specifically, \(A_{i}\), \(A_{it} = 5/6\;A_{i}\) (as the layers present a rectangular section), \(I_{i}\), \(E_{i}\), and \(G_{i}\) are, respectively, the cross-section area, the shear area, the moment of inertia, the Young modulus, and the shear modulus of the i-th layer. For the glue line between layers i and i + 1, the stiffness of the two continuous bed of springs in the normal and tangential direction is defined, respectively (Fig. 7):

$$ k_{i,i + 1} = \frac{{E_{gi,i + 1} \;b}}{{t_{i,i + 1} }}\quad g_{i,i + 1} = \frac{{G_{gi,i + 1} \;b}}{{t_{i,i + 1} }} $$
(4)

having considered the glue as an elastic continuum with Young modulus \(E_{gi,i + 1} \;\) and shear modulus \(G_{gi,i + 1}\). In the next numerical calculations, it is always assumed \(t_{i,i + 1} = 0.1\) mm.

It can be noted that globally, the general mechanical model is defined by 13N − 4 kinematic and static unknowns against 13N − 4 equations; therefore, the algebraic-differential problem associated to the proposed model is balanced.

3.2 Three-layer CLT beam model

The base mechanical system described above can be adapted to fit the specific three-layer CLT panels (N = 3) used in the experimental campaign described in the previous sections, resulting in a global simplification of the mathematical formulation. Since the three layers of the specimens have the same thickness h and the same width b, a unique cross-section area \(A_{i} = A = bh\), shear (rectangular) area \(A_{it} = A_{t} = (5/6)\;bh\), and moment of inertia \(I_{i} = I = bh^{3} /12\) is considered for each layer (\(\forall i = 1,2,3\)).

Due to the mechanical symmetry of the section of the CLT panels, as the outer layers are made of the same kind of wood, a single value for the elastic modulus \(E_{1} = E_{3}\) and for the shear modulus \(G_{1} = G_{3}\) are taken into account for the external layers.

Finally, for both the two glue lines, the same thickness t, Young modulus Eg, and shear modulus Gg are supposed; therefore, a single normal stiffness \(k = k_{1,2} = k_{2,3}\) as well as a single shear stiffness \(g = g_{1,2} = g_{2,3}\) are considered.

Equilibrium Eq. (3) now became:

$$ \begin{array}{*{20}c} \begin{gathered} N^{\prime}_{1} - \overline{\tau }_{1,2} = 0 \hfill \\ N^{\prime}_{2} + \overline{\tau }_{1,2} - \overline{\tau }_{2,3} = 0 \hfill \\ N^{\prime}_{3} + \overline{\tau }_{2,3} = 0 \hfill \\ \end{gathered} &\vline & \begin{gathered} T^{\prime}_{1} + (N_{1} \theta_{1t} )^{\prime} - \overline{\sigma }_{1,2} = 0 \hfill \\ T^{\prime}_{2} + (N_{2} \theta_{2t} )^{\prime} + \overline{\sigma }_{1,2} - \overline{\sigma }_{2,3} = 0 \hfill \\ T^{\prime}_{3} + (N_{3} \theta_{3t} )^{\prime} + \overline{\sigma }_{2,3} = 0 \hfill \\ \end{gathered} &\vline & \begin{gathered} M^{\prime}_{1} + T_{1} - \frac{h}{2}\overline{\tau }_{1,2} = 0 \hfill \\ M^{\prime}_{2} + T_{2} - \frac{h}{2}\left( {\overline{\tau }_{1,2} + \overline{\tau }_{2,3} } \right) = 0 \hfill \\ M^{\prime}_{3} + T_{3} - \frac{h}{2}\overline{\tau }_{2,3} = 0 \hfill \\ \end{gathered} \\ \end{array} . $$
(5)

The CLT beam model can be further simplified by introducing some internal constraints, based on suitable assumptions on the mechanical behavior of the system. These constraints are expressed as follows:

$$ \begin{gathered} \varepsilon_{n12} = 0 \to v_{1} = v_{2} = v \hfill \\ \varepsilon_{n23} = 0 \to v_{3} = v_{2} = v \hfill \\ \gamma_{1} = 0 \to \varphi_{1} = v^{\prime} = \theta_{1} = \varphi \hfill \\ \gamma_{3} = 0 \to \varphi_{3} = v^{\prime} = \theta_{3} = \varphi \hfill \\ N_{2} = 0. \hfill \\ \end{gathered} $$
(6)

By means of Eq. (6)1,2, the impossibility of the layers to detach from each other in the normal direction is introduced, thus resulting in a single displacement component \(v_{1} = v_{2} = v_{3} = v\) orthogonal to the layers’ axes. Likewise it is supposed that the initial imperfection \(v_{i0}\) is equal for each layer, thus assuming \(v_{i0} = v_{0}\) \(\forall i = 1,2,3\) (Fig. 5). Based on the low thickness to length ratio of each layer, Eq. (6)3,4 enforces the shear non-deformability of the external timber layers (Euler–Bernoulli beam theory); such a constraint makes the rotation angles \(\varphi_{1}\) and \(\varphi_{3}\) slave quantities of the orthogonal displacement v, thus assuming the same value \(\varphi\). Finally, Eq. (6)5 is based on the fact that often in CLT panels, as in the case of the ones tested experimentally, the cross layers are made of planks whose narrow borders are not glued or not even in contact; it is then supposed that the central layer is unable to bear any axial force. Nevertheless, as the inner planks hold some cross bending stiffness, which can be involved by the deflection of the outer layers, it is supposed that the central layer is able to bear some bending moment \((M_{2} \ne 0)\).

From Eqs. (6)5 and (5)2, it can now be written \(\overline{\tau }_{1,2} = \overline{\tau }_{2,3} = \overline{\tau }\), which means that the two glue lines are subject to the same shear stress \(\overline{\tau }\) and the same shear strain \(\overline{\tau }/g = \varepsilon_{t} = \varepsilon_{t1,2} = \varepsilon_{t2,3}\) while the global compressive force acting on the panels (Fig. 5) reads: \(N = N_{1} + N_{3} = - F\) keeping itself constant along the panel.

Due to the internal constraints, some internal forces (\(T_{1}\), \(T_{3}\), \(\overline{\sigma }_{1,2}\), \(\overline{\sigma }_{2,3}\)) become reactive quantities, as they cannot be expressed by the constitutive laws. Such reactive quantities can be then obtained by solving Eq. (5)7,9 with respect to \(T_{1}\) and \(T_{3}\), and Eq. (5)4,6 with respect to \(\overline{\sigma }_{1,2}\) and \(\overline{\sigma }_{2,3}\). Together with Eq. (5)1,3, the condensed equilibrium equations are, hence, obtained by substituting the relationships that provide the reactive forces \(\overline{\sigma }_{1,2}\) and \(\overline{\sigma }_{2,3}\) into Eq. (5)5, and finally substituting, in the same equation, the derivatives of \(T_{1}\), \(T_{2}\), and \(T_{3}\) expressed from Eq. (5)4,5,6. The condensed equilibrium equations, thus, read:

$$ \begin{gathered} N^{\prime}_{1} - \overline{\tau } = 0 \hfill \\ N^{\prime}_{3} + \overline{\tau } = 0 \hfill \\ (M_{1} + M_{2} + M_{3} )^{\prime\prime} - 2N^{\prime\prime}_{1} \;h + F(v + v_{0} )^{\prime\prime} = 0 \hfill \\ M^{\prime}_{2} + T_{2} - \overline{\tau }h = 0 \hfill \\ \end{gathered} $$
(7)

in which it has been considered, from Eq. (6)3,4, that \(\sum\nolimits_{i} {(N_{i} \theta_{it} )^{\prime}} = \sum\nolimits_{i} {N_{i} \theta^{\prime}_{it} = - F(v^{\prime\prime} + v^{\prime\prime}_{0} )}\).

By substituting the constitutive laws (Sect. 3.1.3), and the kinematics equations (Sect. 3.1.1) (modified according to Eq. (6)) into Eq. (7), the field equations are obtained as:

$$ \begin{gathered} E_{1} A\;u^{\prime\prime}_{1} - g\varepsilon_{t} = 0 \hfill \\ E_{1} A\;u^{\prime\prime}_{3} + g\varepsilon_{t} = 0 \hfill \\ 2E_{1} I\;\varphi^{\prime\prime\prime} + E_{2} I\;\varphi^{\prime\prime\prime}_{2} - 2E_{1} A\;u^{\prime\prime\prime}_{1} \;\;h + F(v + v_{0} )^{\prime\prime} = 0 \hfill \\ E_{2} I\;\varphi^{\prime\prime}_{2} + G_{2} A_{t} (\varphi - \varphi_{2} ) - g\varepsilon_{t} h = 0 \hfill \\ \end{gathered} $$
(8)

which represent a system of four coupled linear differential equations facing five kinematic unknowns (\(u_{1}\), \(u_{3}\), \(\varepsilon_{t} ,\)\(v\),\(\varphi_{2}\)); therefore, since the system is indeterminate, a new constraint is needed. However, before doing this, further considerations have to be made.

It should be now taken into account the relationships that exist among the various displacement components (Fig. 10), according to Eq. (1), from which the two axial displacements for the external layers are obtained in the form:

$$ \begin{gathered} u_{1} = u_{2} - \frac{h}{2}\left( {\varphi + \varphi_{2} - \frac{2}{h}\varepsilon_{t} } \right) \hfill \\ u_{3} = u_{2} + \frac{h}{2}\left( {\varphi + \varphi_{2} - \frac{2}{h}\varepsilon_{t} } \right). \hfill \\ \end{gathered} $$
(9)
Fig. 10
figure 10

Kinematics of the generic section in the CLT panel

Full size image

Summing both sides of Eq. (9) and deriving it, it follows: \(\varepsilon_{1} + \varepsilon_{3} = 2\varepsilon_{2}\) which means that the axial displacement and strain of the central layer identify, respectively, the mean displacement and strain of the outer layers. Therefore, it can be written \(- F = E_{1} A\varepsilon_{1} + E_{1} A\varepsilon_{3} = E_{1} A(\varepsilon_{1} + \varepsilon_{3} ) = 2E_{1} A\varepsilon_{2}\) and then \(\varepsilon_{2} = - {F \mathord{\left/ {\vphantom {F {(2E_{1} A)}}} \right. \kern-0pt} {(2E_{1} A)}}\) which implies that the central layer axial strain is constant along the panel. This means that deriving twice Eq. (9) and substituting them into the field equations, Eq. (8)1,2 become equals, thus resulting in a differential system twice indeterminate (three independent equations against five unknowns). Therefore, two more constraints are needed.

3.2.1 Coupling parameters

To eliminate the indetermination of the problem, a simple but consistent attempt, from a mechanic standpoint, is to introduce the following two non-dimensional parameters:

$$ \eta = \frac{{\varphi_{2} }}{\varphi }\quad \psi = \frac{2}{h}\frac{{\varepsilon_{t} }}{\varphi }. $$
(10)

Although \(\eta\) as well as \(\psi\) should be, generally, functions of x, it is now supposed that they are both constant showing later the conditions under which such a hypothesis turns to be true. Then introducing Eq. (10) into Eq. (9), after derivation, the outer layers axial strains become:

$$ \begin{gathered} \varepsilon_{1} = u^{\prime}_{1} = - \frac{F}{{2E_{1} A}} - \frac{h}{2}\left( {1 + \eta - \psi } \right)\varphi^{\prime} \hfill \\ \varepsilon_{3} = u^{\prime}_{3} = - \frac{F}{{2E_{1} A}} + \frac{h}{2}\left( {1 + \eta - \psi } \right)\varphi^{\prime}. \hfill \\ \end{gathered} $$
(11)

From Eqs. (10) and (11)1, the field Eqs. (8), which have now become an algebraic-differential system of three equations facing three unknowns (\(v\), \(\eta\), \(\psi\)), read:

$$ \begin{gathered} E_{1} A\;(1 + \eta - \psi )\;\varphi^{\prime\prime} + g\,\psi \varphi = 0 \hfill \\ E_{1} \left[ {I\left( {2 + \rho_{E} \,\eta } \right) + Ah^{2} (1 + \eta - \psi )} \right]v^{IV} + F(v + v_{0} )^{\prime\prime} = 0 \hfill \\ 2E_{2} I\,\eta \varphi^{\prime\prime} + 2G_{2} A_{t} \varphi (1 - \eta ) - gh^{2} \psi \varphi = 0 \hfill \\ \end{gathered} $$
(12)

in which the elastic modulus ratio \(\rho_{E} = {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }}\) has been introduced. Equation (12)2 can be then written in a compact form:

$$ E_{1} I_{eq} v^{IV} + F(v + v_{0} )^{\prime\prime} = 0 $$
(13)

which, in absence of an initial imperfection (i.e..\(v_{0} = 0\)), clearly recalls the classic elastic curve equation for the buckling of a Euler–Bernoulli’s beam, having introduced the equivalent moment of inertia:

$$ I_{eq} = I\left( {2 + \rho_{E} \,\eta } \right) + Ah^{2} (1 + \eta - \psi ). $$
(14)

The two parameters \(\eta\) and \(\psi\) can now be determined from Eq. (12)1,3, thus obtaining:

$$ \begin{aligned} \psi &= \frac{{E_{1} A\,(1 + \eta )\;\varphi^{\prime\prime}}}{{E_{1} A\,\,\varphi^{\prime\prime} - g\,\varphi }} \\ \eta & = - \frac{{2G_{2} A_{t} \varphi + E_{1} Ah^{2} (1 - \psi )\varphi }}{{(2E_{2} I + E_{1} Ah^{2} )\varphi^{\prime\prime} - 2G_{2} A_{t} \varphi }}. \end{aligned} $$
(15)

These last equations effectively express two constant quantities provided that the differential Eq. (13) admits a solution \(v\) in the form \(v(x) = - \;e\;\sin \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} l}} \right. \kern-0pt} l}} \right)\). As known, such a circumstance may stem out assuming \(v_{0} (x) = - \;e_{0} {\kern 1pt} \,\sin \left( {{{\pi x} \mathord{\left/ {\vphantom {{\pi x} l}} \right. \kern-0pt} l}} \right)\) for the imperfect beam problem of Fig. 5, which, from now on, will be considered as the reference system for the analytical model, as it can be directly associated to the experimental set up.

From the abovementioned sine solution, it can be determined:

$$ \begin{aligned} \psi & = \frac{{2E_{1} A\;\pi^{2} ( {2G_{2} A_{t} \,l^{2} + E_{2} J\pi^{2} } )}}{{2G_{2} A_{t} g\;l^{4} + [ {E_{1} A ( {2G_{2} A_{t} + gh^{2} } ) + 2E_{2} I\,g} ]l^{2} \pi^{2} + 2E_{1} A\;E_{2} I\pi^{4} }} \\ \eta & = \frac{{2G_{2} A_{t} \,l^{2} - E_{1} A\;h^{2} \pi^{2} ( {1 - \psi } )}}{{2G_{2} A_{t} \,l^{2} + E_{1} A\;h^{2} \pi^{2} + 2E_{2} I\pi^{2} }} \end{aligned} $$
(16)

which, according to Eq. (14), determines the degree of coupling of the external layers. In this context, the parameter \(\psi\) represents the coupling flexibility of the glue lines whereas the parameter \(\eta\) represents the coupling efficiency of the central layer. Among all the parameters that appear in Eq. (16), those, which a specific attention is given to in this paper, are the glue line shear stiffness g and the shear modulus G2, the latter representing the rolling shear modulus of the central layer. With reference to Fig. 11, it is possible to define some limit conditions associated to the extreme values that g and G2 may achieve.

Fig. 11
figure 11

Limit configurations for the single section

Full size image

Full composite beam

$$ \left. {\begin{array}{*{20}c} {g \to \infty } \\ {G_{2} \to \infty } \\ \end{array} } \right\}\;\, \Rightarrow \;\;\psi \to 0\;\; \Rightarrow \;\eta \to 1\; \Rightarrow \;I_{eq} \to I_{FC} = I\left( {2 + \rho_{E} \,\eta } \right) + 2Ah^{2} $$
(17)

No slip in the glue lines, with the global section remaining plane while the quantity \(Ah^{2} (1 + \eta - \psi )\) (Steiner’s term) reaches its maximum value as \(1 + \eta - \psi = 2\).

Coupled beam

$$ g \to \infty \; \Rightarrow \;\psi \to 0\; \Rightarrow \;\eta \to \eta_{C} = \frac{{2G_{2} A_{t} \,l^{2} - E_{1} A\;h^{2} \pi^{2} }}{{2G_{2} A_{t} \,l^{2} + E_{1} A\;h^{2} \pi^{2} + 2E_{2} I\pi^{2} }} \Rightarrow I_{eq} \to I_{C} = I\left( {2 + \rho_{E} \,\eta_{C} } \right) + Ah^{2} (1 + \eta_{C} ) $$
(18)

No slip in the glue lines, with the global section that exhibits a broken line profile.

Uncoupled beam

$$ g \to 0\;\; \Rightarrow \;\;\psi \to \psi_{U} = 1 + \frac{1}{{1 + \frac{{E_{2} I\pi^{2} }}{{G_{2} A_{t} \,l^{2} }}}}\;\; \Rightarrow \;\;\eta \to \eta_{U} = \frac{1}{{1 + \frac{{E_{2} I\pi^{2} }}{{G_{2} A_{t} \,l^{2} }}}}\;\; \Rightarrow \;I_{eq} \to I_{U} = I\left( {2 + \rho_{E} \,\eta_{U} } \right) $$
(19)

With no tangential stress in the glue line, with a stepwise global section and with the Steiner’s term that vanishes, the uncoupled panel behaves as if it was made of three stacked independent beams.

On the basis of the geometrical dimensions exposed in Table 1 and the mechanical properties shown in Table 3 (Sect. 4) for beech wood and glue, the variation of the coupling parameters \(\eta\) and \(\psi\) with g and G2 is portrayed in Fig. 12. As can be observed especially from the right graphs of the figure, whatever value of the rolling shear stiffness G2, both the coupling parameters \(\eta\) and \(\psi\) depend very little on the stiffness of the glue g, since over a very small value of g > 10,000 N/mm2, the curve is substantially horizontal.

Table 3 Mechanical properties of the wood species used for the CLT specimens
Full size table
Fig. 12
figure 12

Diagrams of the coupling parameters \(\psi\) and \(\eta\) varying with g and G2 within their ranges of interest for CLT panels

Full size image

3.2.2 Euler’s buckling load and the elastic solution for the imperfect three-layer CLT beam

Recalling Eq. (13), the Euler’s critical load for the three-layer CLT panels follows the classical form:

$$ F_{cr} = \frac{{\pi^{2} }}{{l^{2} }}E_{1} I_{eq} $$
(20)

over which, according to Eq. (14), it is possible to evaluate the influence of g and G2. With reference to the geometrical (Table 1) and mechanical (Table 3, Sect. 4) values associated to the HO-CLT panel, in Fig. 13, the variation of Fcr with g and G2 is portrayed, by means of a buckling load efficiency \(\eta_{{F_{cr} }} = F_{cr} /F_{cr,FC}\), being \(F_{cr,FC}\) the critical load for the full composite beam.

Fig. 13
figure 13

Buckling load efficiency varying with g and G2 within their ranges of interest for CLT panels

Full size image

Clearly, the influence of glue stiffness g is negligible whereas the rolling shear modulus plays a crucial role.

From the sine initial imperfection \(v_{0} (x)\), the solution of Eq. (13), assuming the following boundary conditions \(v(0) = v(l) = v^{\prime\prime}(0) = v^{\prime\prime}(l) = 0\) (Fig. 5), reads:

$$ v(x) = - \;e\;\sin \left( {\frac{\pi }{l}x} \right) = - \frac{{e_{0} \;F}}{{F_{cr} - F}}\sin \left( {\frac{\pi }{l}x} \right) $$
(21)

in which the applied force \(F\) and the initial eccentricity \(e_{0}\) are assumed known. Specifically, the initial imperfection \(e_{0}\) can be estimated by comparing the experimental mid-span displacement–compressive load F curves of Fig. 4c, d and the correspondent analytical (\(v(l/2){\text{ versus }}F\)) curves obtained from the solution of Eq. (21). Figure 14 shows the experimental mid-span displacement–compressive load F of the homogeneous specimens HO-1, HO-4, HO-5, and HO-7, already shown in Fig. 4c (thin lines), and the analytical curves (thick lines) obtained for different initial imperfection \(e_{0}\). As can be observed, the best fitting among experimental and analytical curves occur for \(e_{0} = 0.25\) mm (≈ L/4000). As a final clarification, the curves in Fig. 14 are shown in a zoomed window with respect to those shown in Fig. 4c. Moreover, Fig. 14 shows the absolute value of the mid-span displacement. In the next section, the value of \(e_{0} = 0.25\) mm will be always used.

Fig. 14
figure 14

Experimental (thin line) and analytical (thick line) mid-span displacement versus compressive load F

Full size image

From Eq. (21), it is now possible to evaluate all the displacements, strains, and forces of the system. In particular, focusing on the static quantities, introducing the single i-th (i = 1, 2, 3) layer’s critical load as \(F_{cri} = E_{i} I\;{{\pi^{2} } \mathord{\left/ {\vphantom {{\pi^{2} } {l^{2} }}} \right. \kern-0pt} {l^{2} }}\)\((F_{cr1} = F_{cr3} )\) and recalling the kinematic and constitutive equations of Sect. 0, it can be written from Eq. (11)1:

$$ N_{1} = E_{1} A\;u^{\prime}_{1} = - \frac{F}{2} - \;\frac{{E_{1} \,A\;h\;\pi^{2} (1 + \eta - \psi )}}{{2\;l^{2} }}e\;\sin \left( {\frac{\pi }{l}x} \right) $$
(22)
$$ M_{1} = M_{3} = E_{1} I\;v^{\prime\prime} = \;F_{cr1} \;e\;\sin \left( {\frac{\pi }{l}x} \right) $$
(23)
$$ M_{2} = E_{2} I\;\eta \;v^{\prime\prime} = F_{cr2} \;\eta \;e\;\sin \left( {\frac{\pi }{l}x} \right) $$
(24)

from Eq. (10)2:

$$ \overline{\tau } = g\varepsilon_{t} = - \;g\frac{\psi \;h\;\pi }{{2\;l}}e\;\cos \left( {\frac{\pi }{l}x} \right) $$
(25)

from Eq. (5)7,9:

$$ T_{1} = T_{3} = - M^{\prime}_{1} + \frac{h}{2}\overline{\tau } = - \;\frac{\pi }{l}\left( {F_{cr1} + \frac{{g\;\psi \,h^{2} }}{4}} \right)e\;\cos \left( {\frac{\pi }{l}x} \right) $$
(26)

from Eq. (10)1:

$$ T_{2} = G_{2} A_{t} (1 - \eta )\;v^{\prime} = - \frac{{G_{2} A_{t} \pi (1 - \eta )}}{l}\;e\;\cos \left( {\frac{\pi }{l}x} \right) $$
(27)

eventually from Eq. (5)4,6:

$$ \overline{\sigma }_{1,2} = \frac{{\pi^{2} e}}{{4\;l^{4} }}\left\{ {2E_{1} A\;h\;\pi^{2} \left( {1 + \eta - \psi } \right)\;e\;\cos \left( {\frac{2\pi x}{l}} \right) \quad + \left[ {4E_{1} I\;\pi^{2} + l^{2} \left( {gh^{2} \psi - 2F} \right)} \right]\sin \left( {\frac{\pi }{l}x} \right)} \right\} $$
(28)
$$ \overline{\sigma }_{2,3} = \frac{{\pi^{2} e}}{{4\;l^{4} }}\left\{ {2E_{1} A\;h\;\pi^{2} \left( {1 + \eta - \psi } \right)\;e\;\cos \left( {\frac{2\pi x}{l}} \right) \quad - \left[ {4E_{1} I\;\pi^{2} + l^{2} \left( {gh^{2} \psi - 2F} \right)} \right]\sin \left( {\frac{\pi }{l}x} \right)} \right\} $$
(29)

On the basis of the geometrical dimensions exposed in Table 1 and the mechanical properties shown in Table 3 (Sect. 4) for beech wood and glue, the elastic response of the homogeneous three-layer CLT panel is then described by the functions portrayed in Fig. 15.

Fig. 15
figure 15

Elastic response of the imperfect HO-CLT panel under a tip load expressed by functions of the abscissa x (F = 0,5 Fcr − e0 = 0.25 mm).

Full size image

3.2.3 Stability verification

Recalling the theoretical nature of the Euler’s buckling load and the fact that, in principle, it could never be reached, at least within the boundaries of the linearized theory, to interpret the results of the experimental campaign, it is now necessary to define some specific failure criteria, as in Ref. [58].

Basically, as it was described in Sect. 2.3, three failure modes have been observed in the tests: a bending–buckling mode, occurring in the middle of the panel, a rolling shear mode, detected at the ends, and a delamination mode, involving the glue at the extremities as well. To each of these modes, it is possible to associate an ultimate compression load which account for the achievement of the relevant failure stress in a specific part of the structural element. The ultimate load of the panel will be then the lowest of the three, for which an assessment is here presented.

Bending buckling mode

The flexural failure mode stems from the minimum (absolute maximum) compression stress reached in the middle of the panel at the very external surface of layer 1. Recalling the classical Navier’s formula, such a stress can be calculated as:

$$ \sigma_{x,\min } = \frac{{N_{1} (l/2)}}{A} - \frac{{M_{1} (l/2)}}{I}\frac{h}{2} $$
(30)

and therefore, from Eqs. (22) and (23)

$$ \sigma_{x,\min } = - \frac{F}{2A} - \frac{{E_{1} \;h\;\pi^{2} \left( {2 + \eta - \psi } \right)\;}}{{2\;l^{2} }}\frac{{e_{0} \;F}}{{F_{{{\text{cr}}}} - F}}. $$
(31)

Given \(f_{{{\text{cu}}}}\) the compression failure stress of the layer’s wood, it determines a limit compression load, for the straight panel, equal to \(F_{{{\text{cu}}}} = 2\;A\;f_{{{\text{cu}}}}\). The search for the ultimate load \(F = F_{{{\text{cb}}}}\), which makes \(\sigma_{x,\min } = f_{{{\text{cu}}}}\) according to Eq. (31), follows the Ayrton–Perry criterion. After introducing the following non-dimensional parameter:

$$ \beta_{c} = \frac{{(2 + \eta - \psi )A\;h\;e_{0} }}{{I_{eq} }} $$
(32)

from Eq. (31) it can be written:

$$ \frac{{F_{{{\text{cb}}}} }}{{F_{{{\text{cu}}}} }}\left[ {1 + \beta_{c} \left( {1 - \frac{{F_{{{\text{cb}}}} }}{{F_{{{\text{cr}}}} }}} \right)^{ - 1} } \right] = 1. $$
(33)

It is now introduced the relative slenderness in the form:

$$ \overline{\lambda } = \sqrt {\frac{{2\;f_{{{\text{cu}}}} \;A}}{{F_{{{\text{cr}}}} }}} $$
(34)

from which, defining:

$$ \phi = \frac{1}{2}\left( {1 + \beta_{c} + \overline{\lambda }^{2} } \right) $$
(35)

and:

$$ \chi = \frac{1}{{\phi + \sqrt {\phi^{2} - \overline{\lambda }^{2} } }} $$
(36)

finally:

$$ F_{cb} = \chi \;F_{cu} $$
(37)

Rolling shear mode

The rolling shear failure appears once the shear stress in the inner layer has reached the rolling shear strength \(f_{{{\text{ru}}}}\). Such a circumstance may occur at the ends of the panel, where the shear force T2 achieves its maximum (minimum) value. For simplicity it is considered a uniform distribution of the shear stress across the central layer section:

$$ \tau_{r} = \tau_{xy,2} = T_{2} /A $$
(38)

from which, recalling Eq. (27):

$$ \tau_{r,\max } = \frac{{T_{2} (x = l)}}{A} = \frac{5}{6}\frac{{G_{2} \pi \;(1 - \eta )}}{l}\;\frac{{e_{0} \;F}}{{F_{{{\text{cr}}}} - F}}\widehat{ABC}. $$
(39)

This can be modified introducing:

$$ \beta_{r} = \frac{5}{6}\frac{{G_{2} \;\pi \;(1 - \eta )\;e_{0} }}{l}\; $$
(40)

and then writing:

$$ \tau_{r,\max } = f_{{{\text{ru}}}} = \;\beta_{r} \frac{{F_{{{\text{rb}}}} }}{{F_{cr} - F_{{{\text{rb}}}} }}, $$
(41)

where \(F_{{{\text{rb}}}}\) represents the limit compression load which determines the achievement of the rolling shear strength in the inner layer. This is, hence, defined as:

$$ F_{{{\text{rb}}}} = \frac{{f_{{{\text{ru}}}} \;F_{{{\text{cr}}}} }}{{\beta_{r} + f_{{{\text{ru}}}} }}. $$
(42)

Delamination mode


The delamination of the glue at the ends of the panel should likely derive from the combined action of the shear stress \(\overline{\tau }\) and the normal traction \(\overline{\sigma }\) (Fig. 15); however,in this paper, for the sake of simplicity, it will be considered solely the first one.

The maximum shear stress (per unit of length) is evaluated from Eq. (25) for \(x = l\), thus obtaining:

$$ \overline{\tau }_{\max } = \;g\frac{\psi \;h\;\pi }{{2\;l}}\frac{{e_{0} \;F}}{{F_{cr} - F}}. $$
(43)

Given the failure shear stress of the adhesive, which determines the delamination, its associated value \(\overline{\tau }_{u} = \tau_{u} b\) stems from an ultimate load \(F = F_{gb}\) which makes \(\overline{\tau }_{u} = \overline{\tau }_{\max }\) according to Eq. (43). Therefore, defining:

$$ \beta_{g} = g\frac{\psi \;h\;\pi }{{2\;l}}e_{0} $$
(44)

it can be written:

$$ \overline{\tau }_{\max } = \overline{\tau }_{u} = \;\beta_{g} \frac{{F_{gb} }}{{F_{cr} - F_{gb} }} $$
(45)

and finally:

$$ F_{gb} = \frac{{\tau_{u} \,b\;F_{cr} }}{{\beta_{g} + \tau_{u} \,b}} $$
(46)

Finally, the limit compression load for the CLT panel reads:

$$ F_{b} = {\text{Min}}\left\{ {F_{cb} ,F_{rb} ,F_{gb} } \right\} $$
(47)

4 Comparison between analytical and experimental results

The numerical value of the mechanical properties of the wood species considered in this analysis is reported in Table 3. The mean elastic moduli E1 and E2 were identified in Ref. [59], where the same CLT panels were mechanically characterized from bending tests.

For beech wood, the rolling shear modulus and strength have been taken from [60], whereas the compression strength has been approximately defined from EN338, considering the mean experimental MOR shown in Ref. [59].

For Corsican pine wood, the rolling shear modulus has been calculated from EN338, as a fraction of 10% of the shear modulus normal to grain for a C20 graded soft wood, while the rolling shear strength derives from [50].

On the basis of a shear modulus of the glue Gg = 642 N/mm2, [59] and of an alleged glue line thickness t = 0.1 mm, it can be calculated from Eq. (4), the shear stiffness of the glue: g = 924.480 N/mm2. However, regarding this last value, it should be considered the uncertainty related to the thickness of the glue line; therefore, it seems reasonable to consider g in the range 105 ÷ 106 N/mm2.

The adhesive shear strength has been taken from [61].

The limit failure loads of the CLT panel are reported in Table 4. Specifically, the theoretical critical load for both the homogeneous and hybrid specimens is shown in the first line of Table 4. Such a critical load Fcr is obtained from Eq. (20). The limit loads that refer to the three different failure modes of the CLT panel are reported in the second, third, and fourth rows of Table 4. They are obtained from Eqs. (37), (42), and (46), respectively. Finally, the limit compression load Fb for the CLT panel, identified with the minimum value of the previous three limit loads, is reported in the last row of Table 4.

Table 4 Critical and limit loads from the analytical model
Full size table

A comparison among the experimental and the analytical limit loads, here obtained, is finally performed. The analytical limit loads of the homogeneous and hybrid configuration of the CLT panels are displayed in the first row of Table 5. The mean experimental limit loads are reported in the second row of the same table. As can be observed, the percentage differences among analytical and experimental values are quite small. Specifically, the analytical model seems to evaluate better the limit failure behavior of the homogeneous CLT panels.

Table 5 Comparison between analytical and experimental results
Full size table

The minor ability of the analytical model to describe the failure limit behavior of the hybrid CLT panels seems to be related to the statistically scattered values provided by the experimental test. From a deeper observation of the numerical data in Table 2, the limit loads of the specimens HB-1 and HB-4 are higher than the highest limit load provided from the homogeneous CLT panels, which are supposed to be of higher resistance as the inner layer holds better mechanical properties. Since such a result appeared conceptually implausible, and thus to be traced back exclusively to the material uncertainty, it was deemed of interest to consider, beside the full range of test results for hybrid panels, also a reduced range in which the most unlikely results were excluded. This fact suggests to remove the results of the specimens HB-1 and HB-4 from the calculus of the experimental mean value of the limit load. The updated experimental limit load of the hybrid CLT panels, obtained from the HB-2, HB-3, HB-5, HB-6, and HB-7 specimens, is reported in the second row of Table 6. Considering this updated value, the relative difference between the analytical and experimental values decreases and becomes of the same order of magnitude of that of the homogeneous CLT panels.

Table 6 Comparison between analytical and updated experimental results
Full size table

Clearly, the comparison presented before relies on the specific value of the initial imperfection calibrated on the basis of the experimental results (Fig. 14). However, for designing purposes, the practical application of the analytical model would require the adoption of a general value of the initial imperfection \(e_{0}\), consistent with the standard production’s tolerance. Obviously higher imperfections would result in lower limit compression loads for the CLT panel. For example, applying a value \(e_{0} = 1.00\) mm (≈ L/1000) to the reference system described before, it can be calculated a limit compression load \(F_{b} = 161\) kN for HO specimens and \(F_{b} = 140\) kN for HB specimens, with a relative reduction, with respect to the use of \(e_{0} = 0.25\) mm, respectively, of almost 13% and 11%.

5 Conclusion

In this paper, the buckling behavior of three-layered CLT panels was investigated, first by means of 14 experimental tests and then by developing an analytical formulation calibrated on the specific test setup.

The experimental campaign was conducted on two different groups of seven specimens, each one related to a specific configuration characterized by the panels cross-section’s arrangement. The first configuration (homogeneous, labeled HO) presented three layers made of the same timber specie (beech), whereas, in the second one (hybrid, labeled HB), the inner layer was made of a different timber specie (Corsican pine). The experimental tests aimed to evaluate the failure limit loads of the specimens, under an increasing tip compression force. The homogeneous panels showed almost exclusively a mid-span bending failure mode while for the hybrid panels, different failure mechanisms, such as rolling shear failure, as well as delamination failure, were observed at the ends, singularly or in conjunction. Such a circumstance is likely to follow from the lower rolling shear strength of the inner layer in the hybrid panels. Nevertheless, the two groups showed quite similar average limit loads; however, the hybrid specimens presented results with a higher standard deviation with respect to those related to the homogeneous ones.

An analytical model was then developed in the attempt to describe theoretically the system object of the experimentation. The moderately high length to width ratio of the specimens, the absence of side restraints in the test setup and, above all, the intent to develop a simplified approach to the problem at hand, led straight to a beam-based theoretical formulation. This was first introduced for a panel with a generic number of layers, modeled as a stack of planar Timoshenko beams connected each other by continuous distributions of normal and tangential elastic springs representing the glue lines. The general model was then adapted to a three-layer system, similar to the panels of the experimental campaign, by means of some internal constraints, and considering a side displacement field in the form of a sine, as a result of an initial sine shape for the imperfect panel’s longitudinal axis line. From such a model, a closed-fform solution for the elastic problem, together with the related Eulerian critical load, was determined; this was performed by introducing two non-dimensional parameters, \(\psi\) and \(\eta\) which express the interaction among the wooden layers due, respectively, to the tangential stiffness of the glue and the rolling shear tangential stiffness of the inner layer. It should be noted that the abovementioned closed-form solution stems from the hypothesis on the initial imperfect axis line’s sine shape, which introduces some strict similarities with the \(\gamma\)-process [62]. Nevertheless, the proposed model includes the influence of the elastic response of the glue lines, which represents the novelty of the presented theoretical approach with respect to others [62] which generally overlook the presence of the adhesive layers. However, although it was recognized that the influence of the glue stiffness on the critical load is negligible, it should be highlighted that the modeling of the adhesive layers, beyond allowing a richer description of the response of the three-layer CLT panel, permitted the investigation of the delamination failure mode observed during the laboratory tests. Such a delamination mode enlarges the range of possible failure modes for a CLT panel, which includes the classical bending mode and the shear mode [58].

On the basis of the achieved closed-form solution and recalling the different failure mechanisms [63,64,65] detected during the experimental campaign, three different failure criteria were introduced, leading to a unique theoretic compression limit load. The first one accounts for the bending–buckling failure, the second refers to the rolling shear failure mechanism of the inner layer, and finally the last takes into account the delamination phenomena.

A comparison among the experimental and the theoretic limit loads was performed after the calibration of the analytical model on the basis of some of the experimental results as well as on some parameters derived from the literature. The comparison showed that the analytical formulation describes sufficiently well the real behavior of the CLT panels, both with a homogeneous or hybrid configuration, with relative differences on the limit loads lower than 20%.

As a beam-based formulation, the proposed model, besides being adopted for a comparison with the specific test described above, seems to configure a potential preliminary design tool for stability verification, since it considers one of the most demanding configuration for a three-layer panel wall, though substantially unusual in the construction practice, with no vertical sides’ restraints and hinges on both the horizontal ends. However, it should be recognized that the model is clearly unable to describe the two-dimensional buckling behavior of a panel wall in the presence of restraints along its vertical border and/or of a width to height ratio higher than unity.