Abstract
Operational Modal Analysis (OMA) is becoming a mature and widespread technique for Structural Health Monitoring (SHM) of engineering structures. Nonetheless, while proved effective for global damage assessment, OMA-based techniques can hardly detect local damage with little effect upon the modal signatures of the system. In this context, recent research studies advocate for the use of wave propagation methods as complementary to OMA to achieve local damage identification capabilities. Specifically, promising results have been reported when applied to building-like structures, although the application of Seismic Interferometry to other structural typologies remains unexplored. In this light, this work proposes for the first time in the literature the use of ambient noise deconvolution interferometry (ANDI) to the structural assessment of long bridge structures. The proposed approach is exemplified with an application case study of a multi-span reinforced-concrete (RC) viaduct: the Chiaravalle viaduct in Marche Region, Italy. To this aim, ambient vibration tests were performed on February 4\(^{\text {th}}\) and 7\(^{\text {th}}\) 2020 to evaluate the lateral and longitudinal dynamic behaviour of the viaduct. The recorded ambient accelerations are exploited to identify the modal features and wave propagation properties of the viaduct by OMA and ANDI, respectively. Additionally, a numerical model of the bridge is constructed to interpret the experimentally identified waveforms, and used to illustrate the potentials of ANDI for the identification of local damage in the piers of the bridge. The presented results evidence that ANDI may offer features that are quite sensitive to damage in the bridge substructure, which are often hardly identifiable by OMA.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Classical bridge maintenance policies mainly lie on visual inspections, which can hardly detect early-stage damage and the inspection outcomes are often subject to manifold conditioning factors. It is worth noting the survey report published by the US Department of Transportation in 2001 [1], which concluded that inspection reports may considerably differ depending on the lighting conditions, fear of traffic, and experience of the inspectors. Nowadays, there is a broad consensus on the importance of adopting SHM strategies for preventing catastrophic failures and excessive infrastructure downtimes. This concern has acquired a social dimension after some tragic collapses, such as the I-35 W Mississippi river [2] or the Genoa bridge [3] in August 2007 and 2018, respectively, which evidenced the large risks associated with ageing degradation and inefficient maintenance. This has promoted a vast volume of research on SHM since 1970s, as well as the publication of a multitude of technical standards of SHM worldwide [4]. These include from the first SHM guide in 2001 by the SIS Canada Research Network [5], until the last guidelines of the monitoring of viaducts published by the Italian Ministry of Infrastructure and Transport [6]. Nonetheless, despite the large research efforts made in this field, the reality is that these have yielded relatively few routine industrial applications [7]. Among the reasons explaining the slow technological transfer of SHM to industry pinpointed by Cawley in reference [8], it is worth stressing the lack of performance validation of damage identification techniques on full-scale structures under real operating conditions.
Structural Health Monitoring based on OMA has become a mature and ubiquitous technology in the realm of condition-based maintenance of structures. These techniques exploit ambient vibration records to extract the modal properties of structures as damage sensitive features. Readers may find a comprehensive review of OMA techniques in references [9, 10]. Given that these systems work under operational conditions, the degree of invasiveness on the monitored structure is minimal. Nevertheless, although these techniques have proved highly effective for detecting global damage, they may fail at detecting local pathologies with little influence upon the modal features of the system. In this light, the application of seismic interferometric techniques to civil engineering structures offers promising avenues for complementing OMA with local damage detection capabilities. Seismic interferometry (SI) is a technique originally developed in Geophysics [11] to characterize the Earth’s subsurface by cross-correlating seismic observations at different receiver locations. When applied to civil engineering structures, this technique conceives their dynamic response as a superposition of propagating waveforms [12]. Unlike non-destructive testing (NDT) of materials using ultrasonic waves, seismic interferometry exploits seismic waves with wavelengths of \(\approx\)5–500 m and experiencing little attenuation, being possible to characterize large-scale systems without any actuating device [13]. This may be accomplished by implementing a variety of data processing techniques, typically cross-correlation, cross-coherence or deconvolution [14]. In particular, deconvolution interferometry has proved well-suited for the characterization of mono-dimensional structures such as high-rise buildings or towers as evidenced by Todorovska and Trifunac [15] in the 25.48 m high Imperial County Services Building in the El Centro, California. The motivation of this approach for damage identification lies in the fact that the scattering and attenuation of travelling pulses depend upon the constitutive properties of the propagating medium. Therefore, the identification of wave velocities between pairs of sensors along the structure provides an indirect assessment of the system’s stiffness distribution [16]. On this basis, two main advantages of SI compared to OMA-based approaches are often highlighted. Firstly, since damage-induced stiffness degradation leads to localized increases in the pulse travel times across the damaged region of the structure, SI-based damage identification is local in essence [17]. Secondly, SI-based damage identification (detection, localization and, to some extent, quantification) can be performed in a fully data-driven way and no stationary assumptions over the excitation need to adopted [18].
Most research works on the application of SI to engineering structures has coped with the system identification of RC buildings under seismic actions. The theoretical fundamentals of SI to extract the response of buildings under strong base motions were laid out by Snieder and Şafak [12], who presented an application case study of the 9-storey RC Millikan Library in Pasadena (US) during the Yorba Linda earthquake in 2002. A similar approach was used by Todorovska and Trifunac [19], who investigated the wave propagation in the Van Nuys 7-story hotel under 11 seismic events over 24 years. Their results reported considerable wave delays during the 1971 San Fernando and 1994 Northridge earthquakes, which coincides with the damage observed by in-situ inspections. Rahmani and Todorovska [20] developed a shear beam model for wave propagation analysis and reported good agreements with experimentally observed waveforms. Interestingly, the presented numerical results showed that, since phase velocities are computed through motion differences between the floors of the building, the identified velocity profile is minimally affected by soil-structure interaction (SSI) effects. The shear beam model was recently adopted by Bulajić and co-authors [21] for damage detection purposes in a 12-story office building in Skopje (Macedonia) under 11 earthquakes between 1980 and 2004. While such a modelling performs well for shear-like buildings, some discrepancies with experimental evidence can be observed when bending deformation is significant. Specifically, this model cannot explain the dispersion effects observed in high-rise bending-type buildings, where the wavelength of propagating pulses changes with frequency. In order to solve this limitation and reproduce dispersion effects, Ebrahimian and Todorovska [22] developed a layered Timoshenko beam (TB) model including both shear and bending deformation. Those authors demonstrated the contribution of the latter to the dispersion of the wave velocities in high-rise buildings. Recently, the authors [23] extended the TB formulation to investigate the application of acceleration- and strain-based wave propagation analysis for damage identification of masonry towers under seismic actions.
The number of works on the use of ANDI for SHM of structures under ambient vibrations remains scarce. Amongst them, one of the first contributions was made by Prieto et al. [24] who applied ANDI for the system identification of a 17-storey steel moment-frame building in Los Angeles (US) by implementing a deconvolution approach with temporal averaging. A similar approach was also adopted by Nakata and Snieder [25], who investigated the daily fluctuations in the wave velocities identified in an 8-storey building in Japan under ambient vibrations. These studies suggest the compatibility of ANDI with OMA since both approaches exploit identical monitoring data and their sensing layouts and monitoring equipments can be easily combined. In this line, one of the first research efforts was made by Bindi et al. [26] who explored the simultaneous application of ANDI and Frequency Domain Decomposition (FDD) to an 8-storey RC hospital in Thessaloniki (Greece). Sun and co-authors [27] exploited impulse response functions (IRFs) extracted by ANDI in a 21-storey concrete building in Massachusetts (US) for the Bayesian updating of a numerical model of the structure. The synergistic application of OMA and ANDI for the full dynamic identification of architectural heritage structures was explored by the authors in reference [28] through three case studies of historic buildings in Umbria, Italy. The first approach towards the coupled application of OMA and ANDI for long-term SHM of structures was made by Lacanna et al. [29], who reported their application to 36 hours of ambient vibrations recorded in the Giotto’s bell-tower in Florence (Italy). A step beyond was recently made by the authors in reference [30], where the system identification of an historical tower in Perugia (Italy) using automated OMA and ANDI during three weeks was reported. The presented results evidenced substantial environmental effects both upon the modal and wave propagation properties of the structure, and pinpointed the need for their removal through pattern recognition to achieve early-stage damage detection. Another recent contribution was made by Todorovska et al. [31] who reported the implementation of an ANDI-based SHM system in a 48-story skyscraper located in Kunming, China.
From the previous literature review, it seems clear that the implementation of ANDI and its combination with standard OMA-based SHM systems will experience an upward trend. In particular, although considerable research efforts have been exerted to the application to building-like structures, the potentials of ANDI for the SHM of other structural typologies remain virtually unexplored. In this regard, long bridge structures may offer a fruitful application line to delve into the benefits of ANDI for the development of new vibration-based SHM systems with superior damage identification capabilities. In these structures, if is often possible to locate accelerometers with considerable separation so that wave velocities can be assessed without requiring excessively high data acquisition rates. Additionally, since the vibration behaviour of the bridge superstructure is largely conditioned by bearings and piers, it may be possible to infer the health condition of the substructure by assessing local wave delays in the bridge deck. In this light, this paper proposes for the first time in literature the application of ANDI for the full structural system identification of the lateral dynamic behaviour of long multi-span concrete viaducts. The proposed SHM system combines OMA and ANDI and it is exemplified with an application case study of a multi-span RC viaduct: the Chiaravalle viaduct in Marche (Italy). The Chiaravalle viaduct has been the subject of study of a number of research works conducted to assist the design of an important seismic upgrade realized in 2017 (for further details refer to references [32,33,34,35,36]). The dynamic response of the viaduct under normal operating conditions was recorded in an experimental campaign conducted on February 4\(^{\text {th}}\) and 7\(^{\text {th}}\) 2020. The ambient acceleration records are used to extract the modal features of the viaduct by OMA, as well as to identify the propagation of ambient noise waves through ANDI. A simplified numerical model of the bridge is constructed and used to interpret the experimental waveforms, as well as to shed light into the dispersion relation of the bridge. Finally, the numerical model is used to simulate several damage scenarios and to illustrate the potential application of ANDI for damage identification of the piers of the viaduct.
The remaining of this paper is organised as follows. Section 2 overviews the fundamentals of ANDI. Sections 3 and 4 respectively describe the Chiaravalle viaduct and the ambient vibration testing campaign. Section 5 reports the construction of a simplified numerical model of the viaduct. Section 6 presents the numerical results and discussion and, finally, Sect. 7 concludes this work.
2 Ambient noise deconvolution interferometry (ANDI): theoretical background
Seismic interferometry is based upon the assessment of the spatial distribution of the velocity of waves travelling through a structure. This is achieved by constructing the Green’s function of the system describing the propagation of elastic waves between sets of sensors deployed along the monitored structure [37]. In this work, let us consider a bridge structure instrumented with an array of accelerometers recording lateral ambient vibrations a(x, t) along its length \(0 \le x \le L\) as sketched in Fig. 1, with t being the time variable and L the total length of the bridge covered by the measuring chain. Assuming the bridge as a linear time-invariant system, the acceleration records of a reference sensor \(a(x_{ref},t)\) and an arbitrary one a(x, t) can be related in the time domain t as [14]:
or, alternatively, in the frequency domain \(\omega\) as:
where \(*\) indicates convolution, and a hat represents the Fourier transform. Functions \(\widehat{h}(x,x_{ref},\omega )\) and \(h(x,x_{ref},t)\) denote the transfer function (TF) and the IRF between the output signal a(x, t) and the input signal \(a(x_{ref},t)\), respectively. Equation (2) implies that, at the position of the reference sensor \(x=x_{ref}\), \(\widehat{h}(x_{ref},x_{ref},\omega )=1\) and, thus, \(h(x_{ref},x_{ref},t)=\delta (t)\), with \(\delta (t)\) being the Dirac Delta impulse. Hence, the IRFs physically relate the responses of the system to a virtual impulse applied at the reference station. The IRFs can be computed by taking the inverse Fourier transform of the corresponding TFs as follows:
with \(\mathscr {F}^{-1}\) denoting the inverse Fourier transform operator. Nonetheless, since ambient vibrations can only be sampled discretely in practice, the IRFs are only obtained for a finite frequency band \(\left| \omega \right| < \omega _{max}=\pi Fs\), with Fs being the acquisition sampling frequency, that is:
In addition, a regularized version of the TFs in Eq. (3) needs to be introduced as:
where the bar indicates complex conjugate, and \(\epsilon\) denotes a regularization parameter used to avoid numerical instability due to division by small numbers. In this work, we use \(\epsilon\) equal to 0.1% of the average power spectrum of the reference input signal. When used consistently, such a small value does not affect the SHM analysis, which copes with the detection of changes in the identified wave velocities.
The IRFs provide a representation of the propagating waveforms in the bridge, being possible to identify the spatial distribution of wave velocities by simple peak-picking analysis as exemplified in Fig. 1. Following the approximate Snell’s law, ray paths between the monitoring stations are traced first. Then, the i-th time-lag \(\tau _i\) between the motions recorded at stations \(x_{i+1}\) and \(x_{i}\) can be obtained by peak-picking the maxima of their corresponding IRFs \(h (x_{i+1},t)\) and \(h (x_{i},t)\) along an identified ray path [13]. The velocity of the pulses can be computed as \(v_i=l_i/\tau _i\), with \(l_i\) being the separation between the stations \(l_i=x_{i+1}-x_{i}\). The number of IRFs that can be computed in a bridge monitored at N different stations equals N and, therefore, the resolution of the identified wave velocity distribution is \(N-1\). It is worth noting that, since the velocity of the pulse \(v_i\) is directly related to the stiffness of the structure between the i-th and the \(i+1\)-th stations, local damage-induced stiffness reductions can be detected in a fully data-driven manner in the shape of increases in the wave travel time \(\tau _i\).
An important aspect to be considered in the application of deconvolution interferometry concerns the potential existence of a dispersive behaviour. When the system is dispersive, different frequency components travel at different speeds [38]. Specifically, propagating waveforms can be characterized by their phase and group velocities as \(c^p=\omega /k\) and \(c^g=\partial \omega /\partial k\), respectively, k being the wavenumber. The phase velocity determines the velocity of the individual one-frequency pulses packed in the overall waveform, while the group velocity defines the velocity of propagation of the envelope or modulation of the compound waveform. When the propagation medium is non-dispersive, its phase and group velocities coincide, i.e. \(c^p=c^g\). In order to identify the wave velocities in a dispersive system, the contribution of certain frequency bands to the resulting waveforms can be isolated by applying a band-pass filter \(\widehat{S}\) to the TFs as [28]:
with \(\omega _2>\omega _1\) denoting the cut-off frequencies. This filter can be defined as a shifted box function as follows:
In order to minimize the variance of the estimates on the wave velocities when applied to ambient vibration testing, it is convenient to implement the formulation in Eq. (6) considering time windows. Hence, the deconvolved waveforms can be stacked over Nw intervals of duration T and certain overlapping as follows [30]:
where \(\widehat{h}_n(x,x_{ref},\omega )\) stands for the TF extracted from the n-th time window.
3 The Chiaravalle viaduct
The Chiaravalle viaduct links the state road 76 (SS76) and the Marche airport (also known as the Raffaello Sanzio Airport) straddling the municipalities of Falconara Marittima and Chiaravalle in central Italy (Fig. 2). The viaduct has been studied in several research works in the literature, so interested readers can find further information on the bridge structure in references [32,33,34,35,36]. The overall length of the viaduct is 875 m and it consists of four kinematic chains (KC#), separated by structural joints (Fig. 3). The KCs, involving 13, 10, 3 and 5 spans, respectively, are constituted by simply supported girders connected by steel post-tensioned tendons at the level of the concrete slab. The span length is 27.5 m with exception of the span between piers 24 and 25, crossing the Orte-Falconara Marittima railway line, which has a total length of 51.80 m. The layout of the viaduct consists of a horizontally curved alignment between piers 17 and 29 with radius of curvature of 425 m, and joined to two tangent straight segments of 495 m and 55 m along the centre line.
The deck along the viaduct is 12.10 m wide and is constituted by three twin simply supported V-shaped prestressed concrete beams underlying a 0.25 m thick concrete slab (Fig. 4a). The span between piers 24 and 25 is an exception, because its deck consists in an adjacent box beam ending with two Gerber saddles (Fig. 4b), on which the trapezoidal beams of the adjacent spans are connected. The substructure of the viaduct was originally defined by column bent piers constituted by two circular columns with a diameter of 1.4 m (Figs. 4c,d), with the exception of pier 17, which is characterised by a single wall pier with a rounded rectangular cross section. The foundations of the piers were originally defined by 1.70\(\times\)9.00\(\times\)5.00 m plinths on two rows of three \(\varnothing\)1000 mm piles. Nonetheless, the viaduct, built in the early 1990s, was seismically upgraded in 2017 after a survey campaign evidenced the presence of advanced surface degradation of the viaduct [32]. The degradation was particularly acute in the foundation structures where coring samples revealed low values of concrete compressive strength, with reductions in the piles of up to 70% of the project design values. The seismic upgrading works considered a new foundation structure constituted by \(\varnothing\)300 mm micropiles in the perimeter of the rafts, new rafts superimposed to the original ones, and 0.3 m thick concrete jacketing of the pillars [33]. The upgrading also included the substitution of steel-teflon elastomeric bearings with double concave friction pendulum isolators, as well as auxiliary dissipative viscous dampers between the deck and the substructure on the abutments and pier 17. The final configuration of the piers has heights ranging between 6.25\(\sim\)8.72 m for KC1, 8.60\(\sim\)10.75 m for KC2, 8.95\(\sim\)11.42 m for KC3, and 4.50\(\sim\)9.01 m for KC4.
4 Ambient vibration tests and operational modal analysis
Ambient vibration tests (AVTs) were performed to evaluate the dynamic behaviour of the viaduct on February 4\(^{\text {th}}\) and 7\(^{\text {th}}\) 2020. The monitoring instrumentation consisted of high sensitivity (10 V/g) uniaxial PCB 393B12 accelerometers fastened to steel supports by threaded screws (Fig. 5a). The accelerometers were placed on the curb side of the bridge deck, and connected by coaxial cables to a data acquisition system (DAQ) model NI cDAQ-9188 with NI 9234 modules (24-bit resolution, 102 dB dynamic range and anti-aliasing filters) (Fig. 5b). Because of limited availability of sensors, three different sensor configurations were adopted to achieve a sufficient spatial coverage of the viaduct as illustrated in Fig. 6. Note that the adopted sensor layout has been designed similar to the one installed by Gara et al. [36] for subsequent comparison purposes. The first set-up was aimed at characterizing the dynamic behaviour of KC1, and included 14 accelerometers aligned in the transverse direction of the bridge’s centre line and located on the piers and the first abutment, as well as 3 accelerometers aligned in the longitudinal direction on piers 6 and 13. The second set-up focused on KC2, including 12 accelerometers aligned in the transverse direction on the piers, and 3 aligned in the longitudinal direction on piers 13, 18 and 23. Channels 1, 2 and 13, coincident with channels 13, 14, and 17 from the first set-up, are used as reference sensors to evaluate any degree of continuity of the modes between the kinematic chains. From preliminary numerical analyses and previous literature on the viaduct, one single roving sensor (Ch. 14) was assumed sufficient to characterize both the longitudinal mode shapes and wave velocities of KC2. Finally, the third set-up covered KC3 and KC4, comprising 10 accelerometers on the piers and aligned in the transverse direction, and 4 accelerometers in the longitudinal direction on piers 23, 26, 28, and the second abutment. In this set-up, channels 12, 13 and 14 are used as reference sensors coincident with channels 11, 12 and 15 from the previous one. For each set-up, 30 minutes of ambient vibrations were recorded by two asynchronous acquisitions at a sampling frequency rate of 1652.89 Hz (the largest rate allowed by the data acquisition equipment). A LabView toolkit was implemented for data acquisition and preliminary real-time processing, including amplitude and spectral plots for quality-control inspections. With regard to the environmental conditions, February 4\(^{\text {th}}\) was characterized by strong winds with speeds up to about 15 m/s in the transverse direction of the bridge, and environmental temperatures in the order of 10–15 \(^\circ\)C . Conversely, almost no wind was present on February 7\(^{\text {th}}\) and cooler temperatures ranging between 5 and 10 \(^\circ\)C were registered.
The modal identification of the viaduct was performed using MOVA, an in-house code recently developed by the authors and reported in reference [39]. This code includes specific toolboxes for signal preprocessing, automated OMA, and post-identification merging for multi-setup OMA. Firstly, the acceleration records were thoroughly inspected, and the presence of anomalous spikes and spurious trends were eliminated through Hanning window filtering and moving average baseline correction, respectively. Then, the signals were filtered with a Butterworth band-pass filter with cut-off-frequencies of 1 and 30 Hz and, finally, the resulting signals were down-sampled at 100 Hz to decrease the computational cost in the subsequent modal identification. Afterwards, the Covariance-driven Stochastic Subspace Identification (COV-SSI) method was used to identify the modal properties of the viaduct. The parameters used in the identification included maximum and minimum numbers of block rows/columns in the Toeplitz matrix of covariances j of 300 and 400, respectively, with steps of 10, and model’s orders running from 10 to 80 with steps of 2 for Set-ups 1 and 2, and from 140 to 300 with steps of 4 for Set-up 3. The modal features were extracted using the automation algorithm proposed in reference [40], which allows the elimination of spurious modes and automates the interpretation of the stabilization diagrams from the considered series of block rows in the Toeplitz matrix through hierarchical clustering. Figure 7 furnishes an example of the obtained stabilization diagrams, corresponding to the first asynchronous acquisition of Set-up 1. The mode shapes extracted from the considered set-ups were merged using the least squares approach proposed by Au [41].
Table 1 collects the resonant frequencies (\(f_i\)) and damping ratios (\(\zeta _i\)) identified in the frequency range 0–10 Hz, and Fig. 8 plots the first eight mode shapes. For comparison purposes, the identification results from previous AVTs on the viaduct and reported in references [32, 34,35,36] are also included in Table 1. The modes descriptions in Table 1 have been based on a simple inspection of the identified mode shapes. In comparison with the testing campaign carried out right after the seismic upgrading of the viaduct in 2017 by Gara et al. [32], four new modes have been observed in the present survey, including one longitudinal and three transverse modes. Regarding the modes identified in both surveys, only small deviations are found in the resonant frequencies (with maximum relative differences below 3%), which are essentially attributable to differences in the environmental conditions of the tests. Note that it is well known that the resonant frequencies of bridges are highly dependent upon the environmental and operational conditions, being common to find daily fluctuations around \(\pm 2-3\%\) of the average values (see e.g. [42]). It is interesting to note that the natural frequencies identified in both campaigns for the transverse modes are significantly larger (on average by a factor of \(\approx 2\)) than those identified in 2014 [34,35,36], that is before the seismic upgrading. These results confirm the effectiveness of the overall stiffening of the viaduct after the rehabilitation. Regarding the identified mode shapes in Fig. 8, it is noted that these do not seem to exhibit any relative rotations at the piers. This fact indicates that the pendulum isolators did not activate due to friction, which is ascribed to the low in-service loading conditions (wind and traffic) registered during the tests with ambient vibrations of the order of a few thousandths of g. Thence, the modal forms of the viaduct in the horizontal plane resembles the behaviour of a continuous beam structure with elastic supports accounting for the stiffness/mass properties of the piers.
5 Finite element modelling of the Chiaravalle viaduct
In order to interpret the propagating waveforms reported in the subsequent section, a finite element model (FEM) of the Chiaravalle viaduct has been modelled in SAP2000 as shown in Fig. 9. For the sake of clarity and ease in the interpretation of the results, a simplified 2D continuous multi-span beam model has been developed. This choice is supported by the experimental evidence, where the identified mode shapes evidence the transverse continuity of the deck, being possible to conclude that the pendulum isolators behave as rigid deck-pier constraints. The material properties of the model are retrieved from the experimental data reported in reference [36], including the elastic moduli of the columns, columns bent, and beams of 25.80 GPa, 29.68 GPa and 33.52 GPa, respectively. Equivalent 2-nodes elastic Timoshenko beam elements are used to model the deck, accounting for the inertial/mass properties of the V-shaped (Fig. 4a) and the adjacent box beam (Fig. 4b) cross-sections. In order to tune the shear area values of the equivalent Timoshenko beams, two local FEMs of the bridge’s cross-sections have been developed separately using the commercial software ANSYS as shown in the inserts of Fig. 9. For each model, a section of the bridge’s deck is simulated in parallel using 3D 8-nodes SOLID185 elements and 2-nodes BEAM188 Timoshenko beam elements. Parametric analyses were performed considering clamped boundary conditions and increasing tip transverse displacements, so that the shear areas of the Timoshenko beams were sought to minimize the mismatch between the reaction forces of both modellings.
The piers are modelled through elastic supports defined by three elastic springs with longitudinal \(k_l\), transverse \(k_t\), and rotational \(k_\phi\) stiffness constants. The elastic constants of these supports have been computed using local FEMs of the piers in ANSYS as shown in the inserts of Fig. 9. Specifically, three different model types have been developed, including the two-column bent piers, the wall pier (P17), and the single-column bent piers (P24 and P25). These local models have been defined using BEAM188 elements, including rigid links to take into account the real position of the elements’ centroids. For simplicity, and given the considerable increase in the foundation stiffness achieved by the seismic upgrading of the viaduct, the soil-foundation interaction is neglected and fixed base conditions are assumed. On this basis, the elastic constants (\(k_l\), \(k_t\), and \(k_\phi\)) have been extracted by sub-structuring analysis of the local pier models, condensing the stiffness/mass properties of the piers to a master node located at the deck’s centroid. It is important to mention that the consideration of perfect bonding between the original columns and the concrete jacketing added in the seismic retrofit resulted in a too stiff model, with numerical resonant frequencies substantially exceeding the experimental ones. This fact indicates that, instead of performing as a solid section, the jacketing-column ensemble behaves as a composite section. In order to account for this effect, the formulation prescribed in the Eurocode 4 EN 1994-1-1 [43] for the design of composite steel and concrete structures has been adopted. According to this formulation, the effective flexural stiffness \((EI)_{eff}\) of the composite section reads:
with \((EI)_{c}\) and \((EI)_{j}\) being the flexural stiffness of the original column and of the concrete jacketing, respectively, and \(k_c\) standing for an efficiency factor. Factor \(k_c\) has been adjusted by manual tuning, achieving a reasonably good agreement between the experimental and numerical modal features for a value of \(k_c=0.55\). On this basis, the resulting longitudinal and transverse stiffness of the piers of the viaduct are furnished in Fig. 10. The comparison between the first four experimental modal features and the predictions of the resulting FEM is presented in Table 2. Specifically, the comparison is appraised in terms of relative differences between experimental \(f_{exp}\) and numerical \(f_{FEM}\) resonant frequencies, as well in terms of Modal Assurance Criterion (MAC) values. In addition, the comparison of the experimental/numerical mode shapes is depicted in Fig. 11. Relatively good agreements are found in terms of natural frequencies and mode shapes, with mean relative differences in frequency and MAC values of 7.2% and 0.88, respectively. Although there is a number of uncertain model parameters that may be refined to achieve better agreements, such as the consideration of flexible connections between the kinematic chains, distinct definition of the correction factor \(k_c\) for each pier, or soil-structure interaction effects, the accuracy of the FEM reported in Table 2 is deemed to be sufficient for the purpose of the present work.
6 Ambient noise deconvolution interferometry: numerical results and discussion
This section reports the system identification results of the Chiaravalle viaduct using ANDI. The reported results assess the wave propagation properties of the viaduct, including the effects of ambient excitations, frequency bands of analysis, wave velocity distribution, and dispersion phenomena. The previously reported FEM is used to gain insight into the propagation of ambient noise waves and interpret the experimentally identified waveforms. Finally, the model is used to simulate different damage scenarios and illustrate the potential application of ANDI to identify the appearance of damage in the piers of the viaduct.
6.1 Ambient noise propagating waveforms
In order to minimize the variance of the estimates of the wave velocities, the IRFs have been computed considering 10-min-long windows with 50% overlap and stacked (averaged) over every 30-min long vibration record. In these analyses, ambient vibrations sampled at a sampling rate of \(F_s=1500\) Hz are used to accurately assess the wave propagation velocities. In addition, virtual sources (VSs) have been considered at the most distant stations. Figures 12a,c, b,d show the IRFs experimentally identified in KC1 in the transverse (Channels 1–14) and longitudinal (Channels 15–17) directions, respectively. In this first set-up, VSs have been considered at the first abutment (\(x_{ref}=0.0\) m) and at P13 (\(x_{ref}=357.5\) m). In order to cover the main resonant frequencies of the viaduct, the IRFs have been filtered in the broad-band frequency of 0.5–10 Hz according to Eq. (7). It is noted in these figures that two quasi-symmetric pulses can be clearly identified (with ray paths denoted by blue lines). This behaviour coincides with the waveforms obtained by Nakata and Snieder [25] for building structures under ambient excitations. Those authors pointed out that, unlike buildings under seismic excitations where the physical source relates to a single base motion [12], ambient vibrations are characterized by multiple load sources inside and outside the structure (e.g. micro-tremors, wind loads or traffic), giving origin to both causal and acausal pulses. In general, waves propagate in three directions throughout the structure with multiple reflections from boundaries and nonhomogeneities. Nevertheless, the relative simplicity of the waveforms in Fig. 12 suggests the wave propagation is predominantly one-dimensional in KC1, thereby the wave velocities can be readily computed by peak-picking analysis. It is also interesting to note that the wave velocity is clearly larger in the longitudinal direction, which may be expected considering that the longitudinal and shear-wave velocities in an elastic material are defined as \(c_L=\sqrt{E/\rho }\) and \(c_s=\sqrt{G/\rho }\), respectively, with E, G and \(\rho\) being the Young’s modulus, shear modulus, and mass density.
The IRFs experimentally identified in KC2 and KC3 are shown in Figs. 13a,c, b,d, respectively. As evidenced in these figures, no clear travelling pulses were identified in set-ups 2 and 3. The poor identification results in these testing set-ups is ascribed to two main causes. Firstly, the low ambient vibration levels registered on February 7\(^{\text {th}}\) 2020, when the last two set-ups were conducted, led to low signal-to-noise ratios, hampering the identification of travelling pulses. Secondly, the curved geometry of the last three kinematic chains may result in complex reflection, scattering and diffraction patterns. An in-depth analysis is required to exploit the potentials of ANDI to assess the health condition of the last three curved chains, which falls out of the scope of the present work and deserves a separate study. Thereby, only ANDI results and discussion from the first straight kinematic-chain are presented hereafter.
Stacking waveforms over 10-min long IRFs of the Chiaravalle viaduct in the first set-up conducted on February 4\(^{\text {th}}\) 2020 and filtered in the broad-band frequency of 0.5–10 Hz. Transverse (a, c) and longitudinal (b, d) directions, and VS (\(\blacktriangledown\)) at the first abutment (\(x_{ref}=0.0\) m) and P13 (\(x_{ref}=357.5\) m)
With the purpose of interpreting the waveforms previously reported in Fig. 12, numerical waves have been also extracted by time-history analysis of the FEM of the viaduct presented in Sect. 5. To do so, two different load cases are considered: one single random transverse point load applied at the first abutment (LC1) (Fig. 14), and random point loads applied at all the piers of the viaduct (LC2) (Fig. 15). The point loads are defined as Gaussian white noise processes, and the time-history analysis is conducted using the Hilbert-Hughes-Taylor linear direct integration method with a time step of 6.67E-4 s (i.e. 1500 Hz). The Rayleigh damping model is adopted considering the resonant frequencies and damping ratios of modes 2 and 11 from Table 1 to compute the mass/stiffness proportionality coefficients. Ten seconds long acceleration response time series of the first abutment and 13 piers of KC1 are extracted and processed using the ANDI approach introduced in Sect. 2. For the first load case, Figs. 14a, b report the numerical transverse and longitudinal IRFs, respectively, considering the VS at \(x_{ref}=0.0\) m (coincident with the physical source in this particular load case). It is observed in this figure that, when one single physical source is considered, only causal travelling pulses (positive time values) are found, as well as some reflections from the piers in the transverse direction in Fig. 14a. Such a behaviour resembles the waveforms in building structures under seismic excitations reported by previously published works (see e.g. [12, 20]), where only causal pulses are found alongside some reflections from the roof level when the virtual source coincides with the physical one. On the other hand, when random loads are located all throughout the viaduct, the numerical waveforms furnished in Fig. 15 approximate the experimental ones previously reported in Fig. 12. This supports the co-existence of multiple excitation sources as the driving mechanism of the experimentally observed causal and acausal travelling pulses. The numerical longitudinal waves in Figs. 14b and 15b also propagate at a considerably higher velocity likewise the experimental ones from Fig. 12b. These results thus evidence the potential of ANDI to achieve a meaningful representation of the physics underlying the dynamic response of bridge structures. Apart from epistemic uncertainty in the modelling, it is important to mention that discrepancies between the experimental and numerical waveforms may arise as a result of differences in the loading conditions (being unknown in practice), as well as distinct wave attenuation due to simplicity assumptions in the adopted damping model. Nevertheless, the wave velocities depend upon the local stiffness properties of the structure, thereby both the experimental and numerical IRFs must yield similar values irrespective of the loading and/or damping conditions.
The comparison of the experimental and numerical IRFs is further analysed in Fig. 16 in terms of wave arrival times. In this figure, the arrival times obtained from the numerical IRFs considering the two aforementioned load cases (Figs. 14 and 15) are benchmarked against the experimental counterparts from Fig. 12. The numerical results corresponding to LC1 are obtained by peak-picking analysis of the IRFs considering the VS coincident with the physical one (\(x_{ref}=0.0\) m), while the results for LC2 are estimated as the average arrival times between the causal and acausal pulses. Considerably good agreements are found between the numerical and experimental arrival times of transverse waves, while some discrepancies are observed for longitudinal waves. Specifically, the global waves velocities (traversing the whole kinematic chain) obtained from the numerical transverse waves are 661.3 m/s and 672.0 m/s for LC1 and LC2, respectively, while the experimental velocities for VSs at \(x_{ref}=0.0\) m and \(x_{ref}=357.5\) m are 606.7 m/s and 601.3 m/s, respectively. As mentioned earlier, the discrepancies are larger for longitudinal waves, with global wave velocities of 2837.6 m/s and 3025.23 m/s for LC1 and LC2, in contrast to the experimental results with 2242.8 m/s and 2381.22 m/s for VSs at \(x_{ref}=0.0\) m and \(x_{ref}=357.5\) m, respectively. These differences are ascribed to epistemic uncertainties in the modelling, as well as the effect of the dissipative devices installed during the upgrading works in the viaduct (namely concave friction pendulum isolators and viscous dampers [33]), which were disregarded in the modelling. Note that the effect of these uncertainties is magnified in the longitudinal direction, where waves travel faster and sampling errors due to a limited acquisition rate also increase. Nonetheless, since the primary goal of these analyses is to interpret the experimentally identified waveforms, the model is assumed accurate enough for the present work and more advanced modelling approaches are left for future research work.
6.2 Dispersion effects
In order to investigate the presence of dispersive effects in the ambient vibration response of the Chiaravalle viaduct, Fig. 17 depicts the experimental band-pass filtered IRFs obtained in KC1 considering increasing cut-off frequencies, namely 0.5–5 Hz, 0.5–15 Hz, and 0.5–30 Hz. In order to ease the interpretation of the results, inserts with the time distances between upward and downward pulses are included in Fig. 17. The effect of considering wider frequency bands can be readily noted in this figure in the shape of narrower propagating pulses. As discussed by the authors in a previous work [28], the pulse at the reference level is defined as a sinc function, whose width of the central lobe is inversely proportional to the width of the box filter in Eq. (7). Therefore, the use of wider frequency bands may facilitate the identification of separate travelling pulses, although high-frequency secondary propagation modes may arise hampering the identification. For instance, in the case of high-rise buildings, Ebrahimian and Todorovska [38] demonstrated the existence of a critical frequency \(f_{cr}=2 \pi c_s\sqrt{k_G}/r_g\) (with \(k_G\) and \(r_g\) being the shear correction factor and the radius of gyration of the building), above which a secondary propagation mode intervenes in the waveforms generating complex interference patterns. In this work, the use of cut-off frequencies above 40 Hz resulted in too complex waveforms, precluding the clear identification of travelling pulses. With regard to the wave velocities, it is noted in Fig. 17a that transverse waves propagate at slightly faster velocities, whilst the opposite effect is observed for longitudinal waves in Fig. 17b.
Dispersion curves in the longitudinal (a, c) and transverse (b, d) directions of KC1 of the Chiaravalle viaduct obtained by peak-picking analysis of the ambient noise band-pass filtered IRFs. The error bars in (a, b) represent the minimum/maximum values of the computed wave velocities in the experimental 10-min long stacking IRFs
In light of the previous discussion, the degree of dispersion in the dynamic response of the Chiaravalle viaduct is further investigated in Fig. 18. In this figure, the dispersion relations for longitudinal (a,c) and transverse waves (b,d) are reported in the frequency band between 5 and 40 Hz. To do so, both the experimental and numerical waveforms have been filtered to different frequency bands with increasing cut-off frequencies, namely 5 Hz, 10 Hz, 15 Hz, 20 Hz, 25 Hz, and 40 Hz, and the wave velocities have been obtained through peak-picking analysis. The experimental dispersion curves in Figs. 18a, b agree with the previous discussion regarding the results of Fig. 17. In these figures, the error bars in the graph represent the minimum/maximum values of the computed wave velocities in the 10-min long time-windowed IRFs. The velocity of the longitudinal waves experiences fast decreases in the low-frequency range until it tends to an asymptotic value for cut-off frequencies above 15 Hz. Such a behaviour agrees with the theoretical dispersion relation observed in axially loaded road-like structures [44]. On the other hand, the dispersion relation for transverse waves exhibits the opposite behaviour, with increasing phase velocities for larger frequencies. Similar dispersion relations are also observed in beam-like buildings as reported by Ebrahimian and Todorovska [38]. Those authors pinpointed the contribution of bending deformation as an essential factor in the dispersive propagation of shear waves through beam-like structures. Similar analyses have been also conducted using the numerical acceleration time-series from the FEM of the viaduct as reported in Fig. 18c, d. While noticeable discrepancies are found in terms of absolute wave velocities, it is noted that the dispersion relations exhibit a qualitatively similar behaviour to the experimental ones. The comparison is particularity accurate when a single load point is considered (LC1), while poorer identification results are obtained for LC2. The reason for the latter is ascribed to errors in the identification of travelling pulses when random loads are defined all throughout the viaduct, giving origin to complex interference patterns when simple peak-picking fails to accurately asses the wave velocity. This contrasts with the clear pulses formerly observed in Fig. 12, indicating that the real loading conditions of the viaduct (mainly wind and traffic actions) facilitate the propagation of one-dimensional waves throughout the structure.
6.3 Damage identification of piers through ANDI
This last section investigates the potential application of ANDI for damage identification of the piers of the Chiaravalle viaduct. To this aim, the FEM of the viaduct is used to simulate different damage scenarios with increasing severity through stiffness reductions of the piers. Specifically, three different damage severities are considered, with stiffness reductions of \(D=15\)%, 25% and 35%. On this basis, nine different damage scenarios are defined by applying the three considered stiffness reductions to piers P2, P6, and P11. With the aim of assessing local wave delays and so identify the damage (localization and quantification), the first kinematic chain is divided into three layers: L1 \(x \in \left[ 0.0,110.0\right]\) m (Ab1-P4); L2 \(x \in \left[ 110.0,220.0\right]\) m (P4-P8); and L3 \(x \in \left[ 220.0,357.5.0\right]\) m (P8-P13). The wave velocities of the layers are computed following the peak-picking procedure previously overviewed in Sect. 2. Specifically, wave travel times \(\tau _i\) are computed at the end stations of the layers by peak-picking the maxima of their corresponding IRFs along an identified ray path, and the local wave velocities are computed as \(v_i=l_i/\tau _i\), with \(l_i\) being the length of the layers. In light of the previous discussion, the analysis is performed in terms of transverse waves considering one single random point load at the first abutment (LC1). Likewise previous analyses, 10 s long acceleration response time-series are computed with two different sampling rates, namely 1500 Hz and 5000 Hz in Figs. 19 and 20, respectively.
Damage identification results of the Chiaravalle viaduct using numerical transverse IRFs filtered in the broad-band frequency of 0.5–10 Hz when damage is imposed in piers P2 (a, d), P6 (b, e), and P11 (c, f). The identification results are reported in terms on local wave velocities (a, b, c), and relative variations of local wave velocities \(\Delta v_i\) with respect to the undamaged condition (d, e, f) (\(F_s=1500\) Hz)
Damage identification results of the Chiaravalle viaduct using numerical transverse IRFs filtered in the broad-band frequency of 0.5–10 Hz when damage is imposed in piers P2 (a,d), P6 (b,e), and P11 (c,f). The identification results are reported in terms on local wave velocities (a,b,c), and relative variations of local wave velocities \(\Delta v_i\) with respect to the undamaged condition (d,e,f) (\(F_s=5000\) Hz)
Figure 19 furnishes the damage identification results for the nine considered damage scenarios in terms of local wave velocities \(v_i\) (a,b,c), and relative variations with respect to the undamaged condition \(\Delta v_i\) (d,e,f) considering a sampling rate of 1500 Hz. In general terms, it is clearly noted that wave delays concentrate in the layers where the damaged pier is effectively localized. This is particularly evident when damage is localized in layers L1 and L2 (d,e), with reductions between 1 and 2%. In addition, the wave delays increase with the damage severity, which demonstrates the ability of ANDI not only for damage detection and localization, but also to some extent for quantification. The identification fails to clearly identify the damage when localized in the third layer L3 (see Figure 19f), finding similar wave delays in both L2 and L3 for stiffness reductions of 15% and 25%. In this case, since L3 is longer than L1 and L2, the relative effect of the damaged pier upon the wave velocity is smaller. Thereby, errors in the peak-picking analysis of the IRFs due to the limited sampling rate gain importance, restraining the effectiveness of the damage identification. This highlights one of the key factors in the success of ANDI for damage identification: the need for high data acquisition rates. Specifically, given a wave velocity \(v_i\) and a separation \(l_i\) between sensors, i.e. a wave lag \(\tau _i=l_i/v_i\), the relationship between the minimum observable reductions in the wave velocity \(\delta v_i\) and the sampling frequency \(F_s\) reads \(\delta v_i=-\frac{l_i}{F_s \tau _i^2 +\tau _i}\). In order to verify this aspect, the same study is also conducted considering an higher sampling frequency of 5000 Hz in Fig. 20. In this figure, it is noted that the damage identification results when damage is localized in L1 and L2 (d,e) experience some improvements, with reduced wave delays in the undamaged layers due to sampling errors. More interestingly, the damage identification considerably improves when damage is localized in L3, having monotonically decreasing wave velocities as the damage severity increases. Also, although some wave delays remain in L2, these are approximately the half of the previously observed ones in Fig. 19. It is important to mention that the decays of the resonant frequencies of the FEM of the viaduct achieved maximum values of 0.6% in the fourth resonant frequency, and less than 0.4% in the fundamental frequency. Damage-induced variations in the mode shapes cannot be easily identified either, and only some differences between the fourth undamaged and damaged mode shapes are found when the damage is localized at P11, with a minimum MAC value of 0.94 for the highest damage severity.
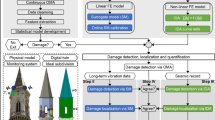
It is important to remark that the aforementioned low frequency decays and small variations in the mode shapes are at the limit of what is actually detectable with long term OMA-based detection techniques. On the other hand, ANDI exhibits a higher sensitivity to local defects since it directly exploits features that are local in-nature, i.e. local wave delays. Additionally, note that ANDI operates on the analysis of the complete IRFs, while OMA typically uses ambient vibration records to identify a dynamic model (typically a state-space system) and extracts a reduced set of modal signatures. In this regard, it is important to pinpoint that modal features (resonant frequencies, damping ratios and mode shapes) can be also extracted from the IRFs as a particular case (see e.g. [23, 27]). Therefore, in light of the presented numerical results, it is suggested that ANDI may offer a quite complementary approach to provide OMA with enhanced local damage identification capabilities. A final discussion on the advantages and disadvantages of OMA and ANDI is presented in Fig. 21. Future research efforts are still required to appraise the effects of noise upon the wave velocity assessment in ANDI, as well as to establish a fair comparison of such effects on the damage identification capabilities of OMA and ANDI.
7 Conclusions
This paper has proposed, for the first time in the literature, the implementation of ANDI for SHM of long multi-span RC viaducts, with an example application to the Chiaravalle bridge in Marche Region, Italy. Ambient vibration tests have been performed on the bridge to assess its lateral and longitudinal dynamic behaviour, using the recorded ambient vibrations to extract the modal features of the viaduct through OMA (resonant frequencies, damping ratios, and mode shapes), as well as to identify the propagation of ambient noise waves through ANDI. With the aim of interpreting the experimental waveforms, a simplified stepped non-uniform Timoshenko beam model with elastic supports has been constructed. Qualitatively similar results between the numerical results and the experimental ones have been reported, both in the time and frequency domain. Finally, several damage scenarios of increasing severity have been simulated and used to illustrate the application of ANDI for damage identification (detection, localization, and to some extent quantification) of the piers of the viaduct. The key findings of this work can be summarised as follows:
-
The experimentally identified waveforms of propagating ambient noise waves (lateral and longitudinal) in the straight section of the Chiaravalle viaduct exhibit a clear one-dimensional behaviour. This makes it possible to easily identify travelling pulses and assess local wave velocities by means of peak-picking analysis, that is, in a fully data-driven way.
-
The FEM of the viaduct has confirmed the experimental evidence, reporting qualitatively similar results to the experimental ones in terms of waveforms and dispersion relations. The identification of propagating waveforms through ANDI offers a valuable information which, along with the modal signatures extracted by OMA, may minimize ill-conditioning limitations in model updating applications.
-
ANDI has been proved to provide features that are quite sensitive to small/moderate damage in the piers of the viaduct, which can be hardly found by OMA-based techniques. The presented numerical results suggest that ANDI may perform well at detecting many other local damage mechanisms in bridge substructures such as corrosion in piers, scouring of foundations, earthquake-induced damage in substructures, etc., which are typically difficult to detect with OMA.
References
Moore M, Phares BM, Graybeal B, Rolander D, Washer G, Wiss J, Reliability of visual inspection for highway bridges, volume I, Tech. rep. (2001).
Salem HM, Helmy HM. Numerical investigation of collapse of the Minnesota I-35W bridge. Eng Struct. 2014;59:635–45.
Domaneschi M, Pellecchia C, De Iuliis E, Cimellaro GP, Morgese M, Khalil AA, Ansari F. Collapse analysis of the Polcevera viaduct by the applied element method. Eng Struct. 2020;214:110659.
Moreu F, Li X, Li S, Zhang D. Technical specifications of structural health monitoring for highway bridges: New Chinese structural health monitoring code. Front Built Environ. 2018;4:10.
ISIS Canada, Guidelines for Structural Health Monitoring, ISIS Canada, 2001, pp. 539–541.
Ministero delle Infrastrutture e dei Trasporti Consiglio Superiore dei Lavori Pubblici, Linee guida per la classificazione e gestione del rischio, la valutazione della sicurezza ed il monitoraggio dei ponti esistenti (2020).
Mitchell JS. From vibration measurements to condition-based maintenance: Seventy years of continuous progress. Sound and Vibration (magazine). 2007;41(1):62–79.
Cawley P. Structural health monitoring: Closing the gap between research and industrial deployment. Struct Health Mon. 2018;17(5):1225–44.
Fan W, Qiao P. Vibration-based damage identification methods: a review and comparative study. Struct Health Mon. 2011;10(1):83–111.
Reynders E. System identification methods for (operational) modal analysis: review and comparison. Arch Comput Methods Eng. 2012;19(1):51–124.
Claerbout JF. Synthesis of a layered medium from its acoustic transmission response. Geophysics. 1968;33(2):264–9.
Snieder R, Şafak E. Extracting the building response using seismic interferometry: theory and application to the Millikan Library in Pasadena. California Bull Seismol Soc Am. 2006;96(2):586–98.
Todorovska MI, Rahmani MT. System identification of buildings by wave travel time analysis and layered shear beam models-Spatial resolution and accuracy. Struct Control Health Mon. 2013;20(5):686–702.
Snieder R, Miyazawa M, Slob E, Vasconcelos I, Wapenaar K. A comparison of strategies for seismic interferometry. Surveys Geophys. 2009;30(4–5):503–23.
Todorovska MI, Trifunac MD. Earthquake damage detection in the Imperial County Services Building III: analysis of wave travel times via impulse response functions. Soil Dyn Earthquake Eng. 2008;28(5):387–404.
Trifunac MD, Ivanović SS, Todorovska MI. Wave propagation in a seven-story reinforced concrete building: III, Damage detection via changes in wavenumbers. Soil Dyn Earthq Eng. 2003;23(1):65–75.
Rahmani M, Ebrahimian M, Todorovska MI. Time-wave velocity analysis for early earthquake damage detection in buildings: application to a damaged full-scale RC building. Earthq Eng Struct Dyn. 2015;44(4):619–36.
Ebrahimian M, Rahmani M, Todorovska MI. Nonparametric estimation of wave dispersion in high-rise buildings by seismic interferometry. Earthq Eng Struct Dyn. 2014;43(15):2361–75.
Todorovska MI, Trifunac MD. Impulse response analysis of the Van Nuys 7-storey hotel during 11 earthquakes and earthquake damage detection. Struct Control Health Mon. 2008;15(1):90–116.
Rahmani M, Todorovska MI. 1D system identification of buildings during earthquakes by seismic interferometry with waveform inversion of impulse responses-method and application to Millikan library. Soil Dyn Earthq Eng. 2013;47:157–74.
Bulajić, B. Đ., Todorovska, M. I., Manić, M. I., Trifunac, M. D., Structural health monitoring study of the ZOIL building using earthquake records, Soil Dyn Earthquake Eng 133 (2020) 106105.
Ebrahimian M, Todorovska MI. Structural system identification of buildings by a wave method based on a nonuniform Timoshenko beam model. J Eng Mech. 2015;141(8):04015022.
García-Macías E, Ubertini F. Seismic interferometry for earthquake-induced damage identification in historic masonry towers. Mech Syst Signal Process. 2019;132:380–404.
Prieto GA, Lawrence JF, Chung AI, Kohler MD. Impulse response of civil structures from ambient noise analysis. Bull Seismol Soc Am. 2010;100(5A):2322–8.
Nakata, N., Snieder, R., Monitoring a building using deconvolution interferometry. II: ambient-vibration analysis, Bull Seismol Soc Am 104 (1) (2013) 204–213.
Bindi D, Petrovic B, Karapetrou S, Manakou M, Boxberger T, Raptakis D, Pitilakis KD, Parolai S. Seismic response of an 8-story RC-building from ambient vibration analysis. Bull Earthq Eng. 2015;13(7):2095–120.
Sun H, Mordret A, Prieto GA, Toksöz MN, Büyüköztürk O. Bayesian characterization of buildings using seismic interferometry on ambient vibrations. Mech Syst Signal Process. 2017;85:468–86.
García-Macías E, Kita A, Ubertini F. Synergistic application of operational modal analysis and ambient noise deconvolution interferometry for structural and damage identification in historic masonry structures: three case studies of Italian architectural heritage. Struct Health Mon. 2019;19(4):1250–72.
Lacanna G, Ripepe M, Coli M, Genco R, Marchetti E. Full structural dynamic response from ambient vibration of Giotto’s bell tower in Firenze (Italy), using modal analysis and seismic interferometry. NDT & E Int. 2019;102:9–15.
García-Macías E, Ubertini F. Automated operational modal analysis and ambient noise deconvolution interferometry for the full structural identification of historic towers: A case study of the Sciri Tower in Perugia. Italy Eng Struct. 2020;215:110615.
Todorovska MI, Niu B, Lin G, Cao C, Wang D, Cui J, Wang F, Trifunac MD, Liang J. A new full-scale testbed for structural health monitoring and soil-structure interaction studies: Kunming 48-story office building in Yunnan province, China. Struct Control Health Mon. 2020;27(7):e2545.
Gara, F., Regni, M., Roia, D., Caratterizzazione dinamica del Viadotto “Chiaravalle” per il controllo e monitoraggio ante operam e post operam, Tech. rep., Relazione Tecnica per ANAS S.p.A. – Compartimento per la viabilità per le Marche (2017).
Dezi, L., Merlino, M., Sturbini, C., Seismic Upgrading of Chiaravalle Viaduct along the SS 76 - Falconara Airport Link Road, in: Italian Concrete Days, (2018).
Roia, D., Regni, M., Gara, F., Carbonari, S., Dezi, F., Current state of the dynamic monitoring of the “Chiaravalle viaduct”, in: 2016 IEEE Workshop on Environmental, Energy, and Structural Monitoring Systems (EESMS), IEEE, (2016), pp. 1–6.
Regni, M., Gara, F., Dezi, F., Roia, D., Carbonari, S., Soil-Foundation Compliance Evidence of the “Chiaravalle Viaduct”, Springer, (2017), pp. 871–881.
Gara F, Regni M, Roia D, Carbonari S, Dezi F. Evidence of coupled soil-structure interaction and site response in continuous viaducts from ambient vibration tests. Soil Dyn Earthq Eng. 2019;120:408–22.
Wapenaar K, Draganov D, Snieder R, Campman X, Verdel A. Tutorial on seismic interferometry: Part 1-Basic principles and applications. Geophysics. 2010;75(5):75A195–209.
Ebrahimian M, Todorovska MI. Wave propagation in a Timoshenko beam building model. J Eng Mech. 2013;140(5):04014018.
García-Macías E, Ubertini F. MOVA/MOSS: two integrated software solutions for comprehensive structural health monitoring of structures. Mech Syst Signal Process. 2020;143:106830.
Ubertini F, Gentile C, Materazzi AL. Automated modal identification in operational conditions and its application to bridges. Eng Struct. 2013;46:264–78.
Au SK. Assembling mode shapes by least squares. Mech Syst Signal Process. 2011;25(1):163–79.
Anastasopoulos, D., De Roeck, G., Reynders, E. P. B., One-year operational modal analysis of a steel bridge from high-resolution macrostrain monitoring: influence of temperature vs. retrofitting, Mechanical Systems and Signal Processing 161 (2021) 107951.
Committee, E., Eurocode 4 EN 1994-1-1. Design of composite steel and concrete structures, European Committee: Brussels, Belgium.
Miklowitz J. The theory of elastic waves and waveguides, vol. 22. Amsterdam: Elsevier; 2015.
Acknowledgements
The authors would like to express their gratitude to ANAS S.p.A (Marche section) for providing information on the case study bridge and for supporting the ambient vibration tests by a research contract with the Laboratory of Structural Dynamics of the Department of Civil and Environmental Engineering of the University of Perugia, Italy.
Funding
Open access funding provided by Università degli Studi di Perugia within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
García-Macías, E., Ubertini, F. Structural assessment of bridges through ambient noise deconvolution interferometry: application to the lateral dynamic behaviour of a RC multi-span viaduct. Archiv.Civ.Mech.Eng 21, 123 (2021). https://doi.org/10.1007/s43452-021-00273-9
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43452-021-00273-9