Abstract
For the last 30 years, the economy has been undergoing a massive digital transformation. Intangible digital assets, like software solutions, Web services, and more recently deep learning algorithms, artificial intelligence, and digital platforms, have been increasingly adopted thanks to the diffusion and advancements of information and communication technologies. Various observers argue that we could rapidly approach a technological singularity leading to explosive economic growth. The contribution of this paper is on the empirical and the modelling sides. On the empirical side, we present a cross-country empirical analysis assessing the correlation between the growth rate of both tangible and intangible investments and different measures of productivity growth. Results show a significant correlation between intangible investments and both labor and total factor productivity in the period after the 2008 financial crisis. Similarly, both measures of productivity growth are correlated with a combination of both tangible and intangible investments which include information and communication technologies and software and database. These results are used to inform the enrichment of the agent-based macro-model Eurace that we employ to assess the long-term impact on unemployment of digital investments. Computational experiments show the emergence of technological unemployment in the long run with a high pace of intangible digital investments.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In his 1930 lecture “Economic possibilities for our grandchildren,” John Maynard Keynes predicted that in 100 years from then, i.e., around 2030, the production problem would be solved and there would be enough for everyone but machines would cause “technological unemployment.” McKinsey Global Institute in a recent reportFootnote 1 stated that the increasing adoption of automation technologies, including artificial intelligence and robotics, will generate significant benefits for the economy, raising productivity and economic growth, but with a far-reaching impact on the global workforce. In particular, according to the study, around half of current work activities are subject to be technically automatable by adapting current available technologies and, by 2030, 75 million to 375 million workers will be displaced by automation with the need to change occupation to avoid unemployment.
Brian Arthur, one of the pioneers in studying the economics of the digital age, recently statedFootnote 2 that we reached, or we are close to, the abovementioned “Keynes point,” i.e., a new economic era where we are witnessing the “third morphing” of the digital revolution. In particular, while the first morphing in the 1970s/1980s was characterized by the microchip and the availability of cheap digital calculus, and the second morphing in the 1990s/2000s by the widespread diffusion of computer networks, the third morphing is bringing intelligent machines. The combination of computers, sensors, big data, and statistical learning techniques provides machines characterized by the sort of associative intelligence typical of biological beings, then potentially able to substitute humans in a large set of activities. Indeed, the higher efficiency related to the introduction of new digital technologies generally determines a higher productivity which in turn can lead to lower employment (see Pianta (2009)). Furthermore, it is worth noting that while most of innovations introduced in the production process until the end of the twentieth century empowered workers with additional mechanical energy able to overcome the limits imposed by human physical force, “The Second Machine Age” (Brynjolfsson and McAfee 2014) characterized by robotics, automation, software, and artificial intelligence (AI) might be able to surmount also the limits imposed by the human mind. Technological unemployment is then becoming the concern not only of “blue collars” but also of “white collars” workers. However, empirical studies have shown a job polarization not completely consistent with the so-called skill-biased technical change (see Goos et al. (2007, 2014), Autor and Dorn (2013)). Indeed, the advent of new digital technologies has led to a decreasing demand of mid-range workers performing routine manual and cognitive tasks and, at the same time, to an increasing demand of high-salary non-routine cognitive jobs and low-salary non-routine manual jobs.
According to the so-called theory of compensation, the technological progress itself triggers different compensation mechanisms that countervail technological unemployment deriving from process innovation (see Petit (1993)). As highlighted by Vivarelli (2014), six different economic forces counteracting the process innovation labor-saving effect can be distinguished, namely the compensation mechanism “via additional employment in the capital goods sector,” “via decrease in prices,” “via new investments,” “via decrease in wages,” “via increase in incomes,” and “via new products.” All these six mechanisms contribute to counterbalance the negative effects on employment caused by technological progress. However, not all economists have been completely optimistic and confident about these compensation mechanisms (see Piva and Vivarelli (2017)). A considerable part of economists argues that, thanks to the compensation mechanisms, digital technologies will not have a deep impact on employment. In this respect, according to Vermeulen et al. (2018), automation is determining only a typical structural change rather than the so-called end of work. On the other hand, Acemoglu and Restrepo (2017, 2018a, b, c, d) argue that the only effective way able to counterbalance the “displacement effect” created by robotics, automation, and AI is represented by the creation of new labor-intensive tasks, as the productivity effect, the capital accumulation, and the deepening of automation are not able to absorb the disruptive impact of digital technologies.
The key element of intelligent machines is software, i.e., the collection and combination of procedures, instructions, and algorithms that set machine and computer behaviors based on environment and input. Software is an intangible good which is non-rivalrous since it is characterized by zero (or quasi-zero) marginal costs. Arthur has investigated since the 1980s the economic features of software and generally of intangible digital technologies as well as their effects for business and the economy as whole (see Arthur (1989, 1990, 1994, 1996)). In particular, he pointed out the existence of two different economic realities: the so-called diminishing and increasing returns world. The former is represented by traditional mass-production systems whose products require a huge amount of resources and a relatively lower contribution of knowledge, whereas the latter is represented by high-tech companies such as digital technology producers: their products are characterized by a high knowledge content and a scarce quantity of resources. Several economic features distinguish increasing returns business worlds from traditional bulk-production worlds. Arthur mentions network effects, positive feedback, path dependence, winner-takes-most/winner-takes-all outcomes, and then technological lock-in. In particular, positive feedbacks reinforce market position of growing companies and, at the same time, negatively affect producers with declining market share.
A considerable effort has been spent for years in order to assess the impact of intangible assets on productivity at both firm, industry, and national levels (see Marrocu et al. (2011), Corrado et al. (2016), and Hao and Van Ark (2009), respectively). In particular, a sizeable number of researches using different estimation methods underline the positive effect that intangible assets have on labor and total factor productivity growth (see Roth (2019)).
Building on the pioneering insights of Arthur and on the recent contribution by Haskel and Westlake (2017), this study enriches the previous empirical work on the relation between measures of productivity and intangible investments. In particular, we consider a high number of countries and different kinds of intangible investments, also in combination with tangible investments in information and communication technologies. Results show a significant correlation between intangible investments and both labor and total factor productivity in the period after the 2008 financial crisis. Similarly, both measures of productivity growth are correlated with a combination of both tangible and intangible investments which includes information and communication technologies and software and database. We integrate the empirical analysis by modelling the digital automation process within a well-known agent-based macroeconomic model (see recent contributions by Teglio et al. (2019), Bertani et al. (2020), and Petroviċ et al. (2020)) and by performing computational experiments to study its impact on unemployment. Computational experiments show the emergence of technological unemployment in the long run with a high pace of intangible digital investments.
It is worth noting that one of the main feature of the agent-based approach lies in considering multiple interacting agents, which give rise to macroeconomic aggregates by exchanging goods, services, or assets in the different markets. Particularly relevant for this work is the presence of multiple firms with autonomous decision making, and direct interactions with other agents (households, banks, digital assets developers). This allows for a differentiation among firms, which evolve in the system according to their previous choices, reaching different potential outcomes, including bankruptcy. In particular, the occurrence of bankruptcies is structurally omitted in representative agent models, but it can be significantly related to the dynamics of unemployment; therefore, it can play an important role in this sense. Moreover, our modelling framework is characterized by a realistic and decentralized labor market mechanism, and thus it is particularly appropriate to capture the unemployment dynamics. Monte Carlo experiments allow us to compare alternative scenarios, extracting statistically relevant economic indicators that can show the different implications of the chosen scenarios.
The paper is organized as follows. The empirical analysis concerning productivity and investments is provided in Section 2. Section 3 presents the extension of the Eurace model that includes investments in intangible digital assets, and the related results. Concluding remarks are in Section 4.
2 Productivity and digital assets: an empirical assessment
Following the previous considerations about the potential disruptive impact of the digital transformation on both the working of our economies and on the labor market, the aim of this section is to provide an empirical and quantitative evidence about the impact of intangible investments on the economy, in particular on the productivity of production factors, i.e., labor and capital, taken singularly and in combination. The investigation is based on a correlation analysis between the growth rates of different measures of investments and productivity, along the line of the analysis presented in the recent book by Haskel and Westlake (2017), which we extend in many dimensions, in particular, in the number of variables considered, in the number of countries, and in the length of the time period examined. The results will inform the development of the new modelling features introduced in the Eurace agent-based macromodel to address the impact of the digital transformation on the economy and in particular on the level of unemployment that we will present in section 3.
The role of intangible investments in our economy is becoming increasingly important over time. In fact, intangible investments have surpassed tangible ones in certain markets, as for example in the United Kingdom (UK) (see Goodridge et al. (2012)). In addition to software and databases (Soft&DB), other kinds of intangible investments are represented for example by investments in R&D, design and engineering, mineral exploration, and brands and advertising (see Thum-Thysen et al. (2017) and Corrado et al. (2005)).
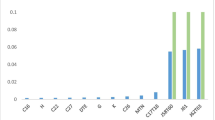
As far as digital technologies are concerned, Fig. 1 shows several time series representing the ratio between intangible investments in software and database and gross value added (GVA) for various countries. The ratio between investments in Soft&DB and GVA represents a relative measure which allows comparing the entity of these intangible investments between countries regardless of their size and GDP. In fact, although the bigger countries tend to invest more in absolute terms, their relative data can be lower than that in some smaller countries; see the case of the USA and Netherlands in Fig. 1a. Except for Italy (IT) and Luxembourg (LU) (see Fig. 1b and c respectively), these investments increased between 1995 and 2016; in particular Netherlands (NL), France (FR), and Sweden (SW) have experienced the hugest enhancement. This shows the growing importance that digital assets have in our economic system.
Various time series representing the trend between 1995 (1997 only for USA) and 2016 of ratio between software and database intangible investments and gross value added for several countries. Time series are authors’ elaboration of on EU-KLEMS data (www.euklems.net) based on a Hodrick–Prescott filter with a smoothing parameter equal to 10. HP filtering has been performed to dampen excessive fluctuations and highlight the general trend. Time series are organized in sub-figure according to their values: (a) time series with highest values are displayed and (d) time series with lowest ones; (b) and (c) time series with intermediate values are reported
Along the line of Haskel and Westlake (2017), we have carried out a correlation analysis in order to investigate the relation among different measures of productivity and types of investment. Our study takes into account a larger number of countries and it is focused on a longer time period of 22 years, from 1995 to 2016. We split this time span into pre- and post-crisis time periods, i.e., from 1995 to 2007 and from 2008 to 2016. The fifteen countries considered are as follows: Italy (IT), Germany (DE), Netherlands (NL), United Kingdom (UK), the United States (USA), France (FR), Sweden (SW), Spain (ES), Denmark (DK), Portugal (PT), Austria (AT), Finland (FI), Ireland (IE), Greece (GR), and Luxembourg (LU).
Moreover, while Haskel and Westlake (2017) productivity-investments correlation analysis focused mainly on total factor productivity (TFP), we extend the analysis to different measures of productivity, namely labor productivity (PL) and capital productivity (PK)Footnote 3. As for investments, we consider the following investment items:
-
Total intangible investments (Tot Int): they represent the sum of R&D, software, databases, mineral exploration and artistic originals investments;
-
Intangible investments in software and database (Int Soft&DB);
-
Intangible investments in R&D (Int R&D);
-
Total tangible investments (Tot Tang): they represent the sum of ICT equipment, transportation equipment, cultivated assets, non-residential structures, other machinery equipment and weapons investments. We do not consider investments in residential structures because the research focuses on those investments that generate productive assets.
-
Tangible investments in ICT equipment (Tang ICT).
-
Tangible investments in ICT equipment together with intangible investments in software and databases (ICT&Soft&DB). The combination of these investments turns out to be crucial because of the intrinsic complementarity characterizing hardware and software. Hardware is useless without software and vice versa and combining these investments we can assess the real importance that digital technologies have in our society. Indeed, besides the distinction between “tangible” and “intangible” capital, another kind of common grouping is represented by “ICT” and “Non-ICT” capital (or assets), where ICT capital includes IT, CT, and computerized information, namely Soft&DB (see Adarov and Stehrer (2019) and Basu et al. (2004)). Software and hardware are also strictly related to each other from a technological progress point of view. In fact, according to Brynjolfsson et al. (2018), AI software and machine learning improvements are related to the creation of more powerful computer hardware (and the availability of a larger database). Therefore, complementary investment in hardware turns out to be crucial in order to obtain further software developments.Footnote 4
The correlation analysis has been performed combining the EU KLEMS databaseFootnote 5 (https://euklems.eu), which provided information about investments, and the OECD database (https://stats.oecd.org) for information on productivity growth rates.
For each country, time averages of growth rates of different measures of productivity and investments have been calculated for each of the three time periods considered. Table 1 reports correlation coefficients and p values (in brackets) between this set of country average growth rates. Asterisks point out statistically significant resultsFootnote 6.
Table 2 reports main statistical moments, i.e., mean and standard deviation σ, of investments and productivity growth rates for four representative countries among those analyzed: Greece (EL), Ireland (IE), Germany (DE), and the United States (USA). These countries have been chosen according to their position in the data distribution. In particular, Greece has been chosen as the representative of the lower bound, Ireland as the representative of the upper one, and Germany as median. USA is included because of its importance in the world economy. Statistical moments refer to two different time periods, namely 1997–2007 and 2008–2016, except for IE whose data refers to time intervals 1997–2007 and 2008–2014 because of the lack of data.
Significant results underline positive correlations between variables in all the cases except for the negative correlation between capital productivity and intangible R&D investments average growth rates in the 1997–2016 time periods. In this respect, it is worth noting that capital productivity, measured as the ratio between GDP and capital services, has been decreasing in most OECD countries for the past 20 years (see OECD (2019)), and this fact may have affected the result.
In the time period 2008–2016, a considerable part of the results turns out to be highly significant, highlighting a positive correlation between productivity and investments. In this time period, TFP average growth rate is significantly and positively correlated with total intangible, R&D, total tangible, ICT equipment, and ICT&Soft&DB investments average growth rates. Also, labor productivity PL is positively correlated with total intangible, R&D, ICT equipment, and ICT&Soft&DB investments.
Even though the 1997–2007 time period is characterized mainly by positive relations among variables, we did not find significant results.
Figure 2 show the scatter plot between TFP and total intangible investments average growth rates in the 1997–2007 and 2008–2016 time periods. The comparison of these two plots highlights an increase in the correlation between variables in the 2008–2016 time period, even though the growth rates tend to be lower. The same considerations hold also for R&D and ICT&Soft&DB investments average growth rates, presented in Figs. 3 and 4. In 2008–2016 time periods, even though the positive correlation coefficient between TFP and Soft&DB intangible investments is not significant, TFP turns out to be significantly and positively correlated with the sum of Soft&DB and ICT equipment that has been called ICT&Soft&DB (the correlation coefficient is equal to 0.6519). This fact points out the complementary roles of hardware and software.
Two scatter plots between country TFP and total intangible investments average growth rates (%). Country averages are considered for two different time periods, namely 1997–2007 (a) and 2008–2016 (b), except for IE whose time average in the subplot (b) refers to a shorter interval because of the lack of data, i.e., 2008–2014. The correlation index is equal to 0.20 (a) and 0.7025 (b). Source: authors’ estimations based on EU-KLEMS (https://euklems.eu) and OECD (https://stats.oecd.org) data
Two scatter plots between country TFP and R&D investments average growth rates (%). Country averages are considered for two different time periods, namely 1997–2007 (a) and 2008–2016 (b), except for IE whose time average in the subplot (b) refers to a shorter interval because of the lack of data, i.e., 2008–2014. The correlation index is equal to 0.19 (a) and 0.465 (b) respectively. Source: authors’ estimations based on EU-KLEMS (https://euklems.eu) and OECD (https://stats.oecd.org) data
Two scatter plots between country TFP and ICT&Soft&DB investments average growth rates (%). Country averages are considered for two different time periods, namely 1997–2007 (a) and 2008–2016 (b), except for IE whose time average in the subplot (b) refers to a shorter interval because of the lack of data, i.e., 2008–2014. The correlation index is equal to 0.19 (a) and 0.6519 (b), respectively. Source: authors’ estimations based on EU-KLEMS ((https://euklems.eu)) and OECD (https://stats.oecd.org) data
The higher correlation coefficients in the post-crisis period of 2008–2016 might also be explained along the lines of the cleansing effect of recessions, introduced by Caballero and Hammour (1994). According to this idea, recessions can be seen as times of “cleansing” when outdated or relatively unprofitable techniques and products are pruned out of the productive system. Therefore, after the crisis of 2007, investments in new technology induced a higher productivity growth with respect to the previous decade. Of course, many other factors might have affected this result, in particular the political response in terms of institutional reforms or economic policies. However, it is worth noting that the cleansing effect typically occurs in all countries, irrespective of their local institutional arrangement or market structure.
3 Modelling the digital transformation
3.1 Literature overview
Modelling the digital transformation turns out to be crucial in order to assess the consequences for the economy related to the advent of digital technologies. To this purpose, the debate on how to represent the potential effects deriving from their adoption in production processes is still open.
Current literature includes different methods that have been developed in order to assess unemployment, productivity change, and wage inequality deriving from the digital transformation. One of these is represented by including AI within production functions as a new (production) factor; see Hanson (2001), Lankisch et al. (2019), and DeCanio (2016). Moreover, as pointed out by Acemoglu and Restrepo (2018d), several researchers have modelled the introduction of automation and AI in the manufacturing sector as a factor augmenting technical change and digital transformation is represented by an increase in factor productivity; see Acemoglu (2003). For instance, Nordhaus (2015), Graetz and Michaels (2018), and Sachs and Kotlikoff (2012) frame automation and AI impact as a capital-augmenting technical change, whereas Bessen (2016, 2018, 2019) represents automation as labor-augmenting.
It is worth noting however that Acemoglu and Restrepo (2017, 2018a, b, c, d) point out some weaknesses of the factor-augmenting approach in equilibrium modelsFootnote 7 and they adopt the so-called task-based approach based on the pioneering contribution by Zeira (1998): automation advent is represented as an increase in the number of tasks that can be performed by machines. Similarly, Aghion et al. (2017) developed AI through a task-based model.
It is worth noting however that the criticism by Acemoglu and Restrepo holds in equilibrium models, whereas it is not directly applicable to the disequilibrium approach which is the distinguishing feature of agent-based simulation models as the one presented in the section. In particular, differently from equilibrium models whose main purpose is to find the static vector of prices equating agents’ demand and supply schedules and making their expectations self-fulfilling, agent-based computational modelling studies how agents’ actions, strategies, or expectations endogenously change out-of-equilibrium and the aggregate economic patterns that this dynamic process creates; see Arthur (2006, 2010). An example of how micro-level behavior gives rise to a macro-level regularity, which is interesting in our context, is the network effect in the adoption of a technological standard, i.e., the empirically grounded modelling feature according to whom the likelihood of adoption depends not only on the (not perfectly known) quality of the standard but also on the number of its current users. This micro-choice behavior can give rise in the long run to a winner-takes-all standard, which is not necessarily the superior one from the technological standpoint; see Arthur (1989). Furthermore, who is the winner can not be foreseen ex-ante based on agents’ preferences, as in a standard equilibrium models, since the final outcome is path-dependent and small unpredictable exogenous stochastic disturbances during the dynamic selection process can give rise to different final outcomes. This macro-level regularity can then be compared with the empirical evidence; see, e.g., the case of software industry (Arthur 1996).
3.2 The Eurace model with intangible assets
Building on the empirical analysis presented in the previous section, which shows a clear effect of investments in ICT&Soft&DB on TFP, we have developed a new extension of the well-known large-scale macroeconomic model Eurace (see Raberto et al. (2012), Teglio et al. (2012, 2019), Petrovic et al.(2017), Mazzocchetti et al. (2018, 2020), Ponta et al. (2018), Bertani et al.(2020)).
Agent-based macroeconomic model arose as an alternative to neoclassical economic models, describing the economy as a complex evolving system in which macrodynamics (e.g., business cycle, long run growth) emerge out of the micro-interactions among bounded rational agents (see LeBaron and Tesfatsion2008). Differently from the structural macromodels of the 1970s, agent-based macroeconomics introduce explicit microfoundations based on empirically observed behaviors of individuals and organizations. Agents’ decisions and adaptation are embedded in a world characterized by true Knightian uncertainty and dispersed information.
The Eurace model is populated by several types of economic agents, characterised by limited capabilities of computation and information gathering, which interact through different markets. Each agent is represented as a dynamic balance sheet which contains the details regarding its assets and liabilities; see Godley and Lavoie (2012) and Raberto et al. (2018) for details. Most agents’ decisions occur at a weekly, monthly, quarterly, or yearly periodicity, and are asynchronous.
The household (HH) operates in the financial market, labor market, goods market, and housing market. As a trader, it allocates its financial wealth among the available assets, which are bonds issued by the government and stocks issued by firms and banks. As a worker, it receives a monthly salary, which constitutes, along with the financial returns on bonds and stocks, the total income of the household. On the basis of total income, households decide the consumption budget, according to a target wealth to income ratio, in line with the buffer-stock saving behavior theory; see Carroll (2001). Households’ decision about the product to buy is driven by purchasing probabilities based on the price.
The consumption good producer (CGP) produces and sells an homogeneous good, taking decisions about the factors of production and how to finance them. In this respect, once the CGP has estimated the expected demand based on past sales, it determines the labor demand (posting new vacancies or firingFootnote 8) and the investment demand, by comparing the net present value of future additional cash flows with the current cost of the investment. The CGP tries to finance these costs according to the pecking order theory: first retained earnings, then debt, then equity. If rationed, the CGP reduces costs in order to make the total financial needs consistent with the available resources. If insolvent, the CGP defaults and undergoes a restructuring process to increase the equity over debt ratio.
The commercial bank (B) role in the model is to provide credit to private agents. The bank evaluates loan requests by firms, and eventually offers the loan at a price that depends on the risk associated to the default probability of the firm. A similar procedure is used by the bank to assess the creditworthiness of households asking for mortgage loans (details are in Ozel et al. 2019). Bank’s lending is also limited by the obligation to respect the minimum capital requirements enforced by Basel II regulation. It is worth noting that money in the model is endogenous, as new deposits are created every time a bank issues new credit.
The other main agents in the model are the capital good producer (KGP), which produces investment goods and sells them to CGPs, and the policy maker agents, which are in charge of economic policy and regulation. In particular, the government (G) ensures a welfare system through fiscal policy. Taxes come from corporate earnings, consumption (VAT), financial income, and labor income. Government expenditures include the public sector wage bill, unemployment benefits, transfers, and interest payment on debt. On a monthly basis, if in short of liquidity, the government issues new bonds, which are perpetuities that pay a monthly fixed coupon. Teglio et al. (2019) show some of the main results related to fiscal policy in the Eurace model.
The central bank (CB) provides liquidity in infinite supply to banks, acting as lender of last resort. It also sets the policy rate according to a dual mandate rule, i.e., low unemployment and stable prices, and the capital requirement for banking regulation. Teglio et al. (2012) and Cincotti et al. (2012) show some of the main results related to monetary policy and banking regulation policy in the Eurace model.
The main novelty of the enriched version of Eurace introduced in this study is the introduction of a new type of capital asset employed in the production process, say intangible digital asset, as well as a new type agent, say digital assets developer. Intangible digital assets in the model shall be considered as software or any other digitalized knowledge-based assets, e.g., algorithms, advanced routines, and instructions, which can support the production process. Intangible digital assets are developed and supplied by a specific agent, namely the intangible digital assets developer (DAD), and are employed by CGPs with the purpose of rising total factor productivity. Intangible digital assets are heterogeneous among the different DADs, depending on their accumulated digital knowledge, which increases over time based on the R&D investments made. DADs compete among each other for providing firms with new digital technology.
Digital assets developers
(DADs) embody the essence of Schumpeterian entrepreneurship: they represent the engine of innovation and technological progress within the Eurace macroeconomic system. In fact, they invest a fixed fraction of revenues in R&D activity by hiring skilled workforce employed in developing a more productive version of their digital assetFootnote 9. As explained in detail below, more productive digital technologies attract customers (CGPs) and allow expanding market shares. In fact, DADs compete with each other on the digital technologies market innovating and varying the price of their products. Therefore, digital asset innovation assumes a fundamental importance in Eurace from both entrepreneurship and macroeconomic growth perspectives.
Intangible digital assets are assumed non-rivalrous, i.e., characterized by zero marginal production costs; see, e.g., Haskel and Westlake (2017). Production costs are given only by the R&D costs, which are determined by the cumulated labor costs of the skilled labor force employed at any DAD agent. On a monthly basis, each DAD has a chance to develop a new version of its digital asset, endowed with higher productivity when employed in the production process by CGPs. The probability probd of a successful completion of the new digital asset version depends on the cumulated person months Md employed by the DAD d since the latest version developed, as follows:
where η is a shape parameter setting the development speed, i.e., the higher is η, the higher is the probability to develop an improved version of the digital assets, for any level of cumulated person months Md employed. The rationale behind (1) is to set the probability as an increasing monotone function of the human efforts devoted to R&D, but with decreasing returns to scale. It is also worth noting that R&D is modelled here as an uncertain activity whose positive outcome is never granted in principle, since the probability is equal to 1 only asymptotically for an infinite number of person months. DADs determine the number of employees on a monthly base, according to the DAD monthly turnover. The number of employees in the DADs sector depends also by the average wage in the economy. As regards the hiring process, DADs perform the same procedures of CGPs and the KGP. However, while CGPs and the KGP hire households from the highest to the lowest education level without distinctionsFootnote 10, DADs hire only highly educated workers (from the third level upwards) in order to perform research activities and develop digital assets.
Consumption good producers
(CGPs) employ digital assets to increase their productivity. In particular, digital assets, namely software, are integrated within “hard” capital purchased by the KGP. “Hard” capital shall be considered as a generalized mean of production which represents the physical part of machine tools, computerized numerical control machines, robots, computing equipment (or computer hardware), communications equipment, etc. These means of production need software in order to work; in particular, we assume that each unit of “hard” capital needs to be associated with a digital asset license, thus each CGP selects a specific digital asset to install on its own stock of hard capital among the different digital technologies available on the market. The choice depends both on the efficiency of the production process provided by the digital asset, on the license unit price and on the training costs of the workforce (see Eq. 6). The modelling assumptions of integrating digital assets with “hard” capital in the consumption goods production process and associating them with productivity are grounded on the empirical analysis presented in the previous section, where we found a positive correlation between ICT equipment (hard capital) and Soft&DB (digital assets) investments with total factor productivity. This modeling assumption embodies the concept of complementarity between hardware and software.
The production process of the various firms (CGPs) is modelled through a Cobb-Douglass production function with constant return to scale as follows:
where Nf and Kf are the labor force employed and the capital endowment owned by a generic firm f and γf represents the total factor productivity (TFP), which is heterogeneous across firms. According to the empirical findings reported in the previous section, in particular the positive correlation between TFP and both R&D and ICT&Soft&DB investments, we model the impact of digital assets innovation on production processes as total factor augmenting, namely as increasing the value of TFP. In particular, the TFP γf of a generic firm f has been modelled as follows:
where ηγ is a scale parameter homogeneous across all CGPs while κd is an index number representing the innovation level of the digital asset adopted. The TFP growth has been formulated as exponential in order to model a strong and significant impact of digital technological progress on the economy. In particular, an exponential growth trend allows considering an increasing relevance of digital technologies on the production process and then on the labor market. Moreover, growth rates productivity data provided by OECD suggests a long-term exponential trend of TFP, albeit with a declining rate, and this further justifies our modelling assumption.
The total factor-augmenting influence of digital assets on production processes affects input factors equally and higher values of TFP, linked to more advanced technologies, determine a decrease in the amount of input factors needed, which in turn leads to a production costs reduction. Finally, the latter is reflected in a decrease in the consumption goods sales price. Therefore, process innovation allows CGPs to save money and decrease their prices in order to compete in the consumption goods market. In fact, the lower the price, the higher the probability to sell their product since the price is assumed as a discriminating factor in the consumption goods choice by households.
Each CGP can adopt only one kind of digital asset at a time and if the R&D activity of the corresponding DAD is successful, with probability set by Eq. 1, then κd will be increased by a fixed tick equal to δκ as reported in the following relation:
The number of digital assets licenses required by each CGP is equal to its stock of hard capital Kf. Therefore, each CGP pays to the DAD owner of the digital asset a money amount Mf set by:
where \(p_{D_{d}}\) is the license unit price set by the DAD.
Each month, the CGP has a given exogenous probability to take into consideration the switching to a different digital asset. The decision to switch depends on the assessment of costs and benefits of adopting any other digital asset d∗ available in the market with respect to one already adopted d. In particular, costs and benefits analysis is performed by computing the net present value (NPV ) of expected net future cash flows that the CGP would get in case of switching:
where the first term provides the present value of gain (or loss) in future revenues given, ceteris paribus, by different TFP and then output of the two digital assets, the second term refers to the license unit price difference between the present digital asset and the one under evaluation, and the third term represents the training costs that the CGP would incur for its employees in order to use the new digital assets in the production process. rD is the weighted average cost of capital proxied by the corporate loan rate. In our framework, CGPs usually face a trade-off between higher (lower) future revenues related to a more (less) productive digital asset and higher (lower) unit license price, since higher (lower) digital asset productivity is usually linked to higher (lower) unit license price, as outlined in Bertani et al. (2020).
3.3 License unit price dynamics
In order to use digital assets in their production processes, each month, CGPs pay a money amount to the reference DAD d equal to Mf (see 5). The license unit price \(p_{D_{d}}\) is given by the following relation:
where w represents the average wage in the economy and λ is the markup. The latter can increase or decrease over time according to the past sales trend. If the DAD has increased its sales, it decides to increase also the markup by a fixed tick equal to δλ, otherwise it decreases the markup by the same amount:
DADs try to manage the market uncertainty which characterizes the economic environment by means of this variable markup policy because, in case of sales contractions, lower prices could determine higher market shares at the expense of competitors. Indeed, CGPs can evaluate the possibility to switch digital supplier in order to increase their profitability and the license unit price \(p_{D_{d}}\) represents one of the costs and benefits analysis key factors (see Eq. 6). In other words, this pricing behavioral assumption allows DADs to handle the sales fluctuations through a trade-off between markup and market share. Moreover, it allows DADs to exploit expansion phases of their sales increasing profits by enhancing markup λ (see Fraser (1985), Goldstein (1986a, b)).
It is worth noting that, through this markup mechanism, DADs try to manage the competition with other software developers. Indeed, they can try to cope with shortcomings in productivity with a decrease in the license unit price. In other words, the continuous R&D activity which characterizes the digital sector could result in being outdated in terms of digital asset productivity and, in turn, this can lead to the loss of part of its customers. In this case, a price reduction could compensate productivity differences and make the product still considerable in terms of economic efficiency (see Eq. 6). However, in the competition among DADs, digital innovation, which determines an increase of the digital assets productivity, results to be a more critical element compared with the pricing strategy and leads to the emergence of a market leader in the long term, as shown in Bertani et al. (2020): price reductions are not able to compensate significant differences in terms of productivity.
Digital innovation is determined by R&D activities: the more intense the R&D activity, the higher the probability of innovating (see Eq. 1), and the R&D intensity, represented by the person months employed by the DAD, is strictly related to the markup λ. In this respect, each month, DADs use the largest part of their turnover to hire researchers to develop more productive versions of digital assets. Revenues are mainly linked to the sale of licensesFootnote 11 and their price, besides w, is influenced by λ (see Eq. 7). Therefore, for equal sales, higher turnover related to higher value of the markup λ determines more intense R&D activitiesFootnote 12.
It is worth stressing that R&D activities, which represent the higher fraction of DADs revenues, assume a crucial role in the competition among DADs. In fact, although competition is managed by both innovating and varying the license unit prices, this last dynamics is carried out with the purpose of increasing revenues in order to enhance R&D intensity. As mentioned in the previous paragraph, high R&D intensities are linked to a higher probability to update digital assets and in the long term innovation allows companies to leave competitors behind, acquiring most of the market shares. In this respect, Bertani et al. (2020) show that Eurace is able to capture the long-term emergence of a market leader whose digital assets are characterized by the highest productivity value. This happens despite the active variation in the prices of competitors aimed at curbing the spreading of the most technologically advanced digital asset.
3.4 Workers’ digital skills
Households are endued with a set of digital skills which represent the worker’s ability to manage different types of digital assets. We assume that in order to acquire these skills, workers must be trained by the DAD owner of the digital asset. CGPs then face training costs for their personnel to handle the new digital technologies in case of switching or new hiring. Total training costs are given by the the number of employees that are still not trained with the specific digital asset times the training cost per worker which is represented by the average wage characterizing the economy in that moment. These training costs are taken into account in the costs and benefits analysis performed by CGPs in order to evaluate potential digital technology changes (see Eq. 6), and through this modelling assumption we want to model an indirect network effect according to which economic benefits arise indirectly from the interaction of different groups (Farrell and Klemperer 2007; Belleflamme and Peitz 2018). Indeed, CGPs benefit from the digital skills of their workers when they assess a possible digital technology switching: the greater the number of workers with that skill, the lower the transition costs to the new digital technology under consideration. Moreover, DADs benefit from workers’ skill: the greater the number of employees able to manage their digital technologies, the higher the probability to sell their products.
These training costs represent intangible investments in human capital which are complementary to digital assets: in order to manage digital technologies, workers must acquire specific knowledge, otherwise digital assets would not be exploitable within production processes. In this respect, Brynjolfsson (2000, 2018) argues that information technology (i.e., computers and digital communication technology) and AI require other complementary intangible investments, such as training and organizational investments. In fact, a higher level of information technology within firms is associated with a higher level of skill in the workforce (see Bresnahan et al. (2002)).
3.5 Computational results
In order to evaluate the potential effects of digital technological progress on the economic system and, in particular, on the labor market, we consider six different values of η, which is the shape parameter of the innovation probability function (see Eq. 1). It is worth noting that η sets the success probability of R&D activity performed by DADs: the higher the value of η, the higher the probability to develop an improved version of the digital asset. We consider also a “no intangible investments” case, characterized by no innovation in digital technologies, which can be considered the baseline scenario. The analysis is based on Monte Carlo experiments, i.e., we run twenty different simulations (where each simulation is associated to a different seed of the pseudorandom number generator) for each of the seven scenarios under investigation, for a total of 140 simulations. We present ensemble averages over twenty seeds, along with related standard errors, of time averages over a 20-years-long period of the most relevant economic variables (see Table 3). In addition, considering a single fixed seed, we plot some time series of selected economic variables.
Table 3 shows that digital assets average productivity (γf) increases with η: the higher the value of η the higher the endogenous rate of technological progress in the model (see also Fig. 5). Furthermore, this higher digital assets productivity for high values of η leads to higher unemployment level in the economic system. In fact, Fig. 6 shows that for high η values the “displacement effect” caused by digital technologies increases dramatically: digital assets substitute workers in jobs that they previously performed in the mass production industrial sector represented in the model by consumption good producers (CGPs)Footnote 13. However, for low η values (i.e., 0.05 and 0.1), the unemployment level is not extremely high (see Table 3).
It is worth noting that, as reported in Table 3, in case of no intangible investments, the unemployment level tends to be higher compared with the case η = 0.05. This is related to the interaction of two different effects: the “displacement effect” and the compensation mechanism “via additional employment in the (digital) capital goods sector” (see Acemoglu and Restrepo (2018a) and Vivarelli (2014)). The former refers to the destruction of job places in the CGPs industrial sector, whereas the latter is related to the creation of new job opportunities in the DADs industrial sector (see Table 4). For the lowest value of η, the compensation mechanism is able to absorb effectively the unemployment generated by digital technologies in CGPs creating also additional job places, while for higher value of η, “displacement effect” takes over on it leading in certain case to mass unemployment.
Table 4 shows a decrease in the CGPs employment level with the increase of η, and this holds also for the capital good producer (KGP). In this respect, the higher digital assets productivity implies not only a lower level of employment, but also a lower level of (hard) capital in the production processes and this is why the KGP employment decreases with η, whose increase determines a higher endogenous technological progress rate. As regards the DADs employment, it increases until η = 0.2, after that it starts to decrease. This trend is related to the high average digital assets productivity which characterizes the economy for a high value of η. In fact, the number of licenses sold by DADs is strictly related to the capital level inside the CGPs: the higher the productivity, the lower the capital level inside CGPs and the lower the licenses sold because each unit of capital is associated to a license (see Table 4). Therefore, for a high value of η, the technological progress affects negatively also the DADs. In this regard, Fig. 5 shows that in the long term the average TFP γf is higher for η = 0.4 compared with η = 0.5; this fact witnesses a decrease of R&D activities related to a very high endogenous rate of technological change which determines in the long term a lower capital level and in turn lower revenues in the DAD sector for η = 0.5. Indeed, the average productivity level is higher in this case until the 19th year, then the curve flattens. This fact highlights the complexity characterizing the digital economy in which the various industrial sectors are interrelated with each other.
Table 3 shows an increase of the average real wage until η = 0.2, after that it starts to decrease slightly. This increase in the real wage is strictly related to a decrease in the consumption goods price level. In fact, firms set their prices through a markup pricing rule on unit costs, and the higher productivity related to digital technological progress allows CGPs to hire fewer workers reducing production costs. In other words, Eurace is able to capture the so-called compensation mechanism “via decrease in price”: the costs reduction leads to a prices decrease which in turn determines a higher demand of goods. However, this compensation mechanism is not able to counteract effectively the displacement effect in the CGPs industrial sector related to the higher average TFP. Therefore, the lower consumption goods price level determines a higher CGPs sold quantity (see Table 3), and comparing η scenarios, there emerges a strong relation between these two variables. Although process innovation determines a higher average real wage linked to lower consumption goods price level and the government provides an unemployment benefit, for high values of η the dramatic unemployment level leads to a contraction of real consumption if compared with lower η values, as shown in Table 3. A low real consumption level causes a decrease of CGP revenues which in turn determines a lower capital endowment: the lower the capital stock owned by CGPs, the lower the licenses sold by DADs. According to this, low levels of real consumption affect also DAD revenues and their R&D activities which determine product innovation within the economy. Therefore, not only high levels of productivity can explain low capital endowments within CGP industrial sector as explained above, this is also related to a lower level of real consumption.
For high values of η, i.e., η = 0.4; 0.5, the economic system is strongly affected by digital technological progress whose impact results to be very significant also because of the exponential TFP growth shape. In this regard, this results in a difficulty to imagine a future characterized by such high unemployment levels. However, since we do not have a perfect ability to foresee the future, considering high values of η gives us a complete overview of the long-term possible scenarios even if they seem to be unrealistic or catastrophic. Moreover, testing a large range of values gives us the possibility to verify the functioning and validity of our model.
These strong negative effects on the economy are partly related to the lack of other compensation mechanisms, as for example the introduction of new products in the market. In this respect, the compensation mechanism “via new products” represents one of the most effective counterbalancing effects to process innovation. In fact, literature highlights a positive relationship between product innovation and employment (see Pianta (2009)). However, being the consumption goods homogeneous, this type of compensation mechanism can not be modelled in Eurace at the current state.
It is worth noting that not all the compensation mechanisms can coexist together and can be captured by a model at the same time. For example, the compensation mechanism “via increase in incomes” is in clear contrast with the “via decrease in wages” one, as highlighted by Vivarelli (2014).
Obviously, all these results are strictly linked to the modelling assumption influenced by the empirical analysis: the total factor augmenting technological progress. As explained above, the positive and significant correlations between TFP–ICT&Soft&DB and TFP–R&D has led us to assume a positive effect of these investments on the TFP. Therefore, in Eurace, technological progress affects input factors, namely capital and labor, increasing their marginal productivity in the same proportion.
4 Concluding remarks
The research work has highlighted the growing importance of intangible digital investments in our economic system. First, we performed an empirical analysis taking into account various European countries and USA data in order to assess the relation between productivity and different kinds of tangible and intangible investments. This analysis shows a high positive and significant correlation between total factor productivity and two key investment kinds: ICT&Soft&DB (or ICT capital) and R&D.
According to these main empirical findings, we have presented a model extension of the Eurace agent-based model and simulator that includes new intangible digital investment assets as well as new agents in charge of their development, say digital assets developers (DADs). Consumption goods producers (CGPs) are then allowed to add to the traditional investment in (tangible) physical capital also an investment in a new type of digital productive asset which increase their total factor productivity.
Digital assets developers invest a fixed fraction of their revenues in R&D activities that have a likelihood to bring to light a smarter version of the digital asset with an increased impact on the total factor productivity of its users, i.e., the CGPs.
R&D activities performed by DADs then lead to an innovation process inside the economic system, whose speed, that we control through an exogenous parameter, turns out to be crucial in order to understand the potential implications of intangible digital technology adoption on the economy and the labor market. In this respect, we observe that for a moderate rate of innovation, compensation mechanisms (“via decrease in price” and via “additional employment in the capital goods sector”) counteract the displacement effect caused by digital technologies in the traditional mass production system represented by consumption goods producers. Conversely, for a high rate of technological progress, the unemployment increases dramatically. Furthermore, the increasing DAD employment level with higher levels of technological progress highlights a clear labor market transformation: the economic system experiences a transition from a mass production economy to a digital services one.
Finally, it is worth noting that results also depend on the exponential form of the TFP growth and the absence of other compensation mechanisms, as for example product innovation. In particular, the latter could provide a relevant contribution of new jobs related to the opening of other markets. However, the co-presence of all the mechanisms belonging to the compensation theory turns out to be impossible because, in some cases, they are not compatible. Furthermore, government interventions aimed at counteracting actively the digital technological unemployment are out of the scope of this study. In this regard, future research will investigate the feasibility of targeted policy interventions, e.g., a robot tax or a reduction of working hours aimed to counteract the digital technological unemployment.
Notes
McKinsey Global Institute, Jobs Lost, Jobs Gained: Workforce Transitions in a Time of Automation, December 2017.
Arthur (2017) Where is technology taking the economy, McKinsey Quarterly
Labor productivity PL measures how efficiently labor input is used in the production of goods and services. It can be measured as the ratio between GDP and all the persons employed in the production process or as the ratio between GDP and total hours worked. However, in the first case, the measure does not differentiate between full-time and part-time employment. Therefore, in our analysis, we consider the hours worked as labor input variable in the productivity measurement because “it bears a closer relation to the amount of productive services provided by workers than simple head counts”; see OECD (2001). So, in our case, PL represents the amount of goods and services produced in 1 h.
As regards capital productivity PK, it measures how efficiently capital input is used within production and it is given by the ratio between GDP and capital services. The latter “refer to the flow of productive services provided by an asset that is employed in production” and “are the appropriate measure of capital input in production analysis”; see OECD (2001).
Finally, total factor productivity (or multifactor productivity) reflects how efficiently labor and capital inputs are employed together in the production process. Several factors can determine TFP variations, as for example technological progress, organizational changes, network effects, and spillovers. TFP is measured as the “residual growth that cannot be explained by changes in labour and capital inputs”; see OECD (2019).
Besides tangible investments in ICT assets, Brynjolfsson et al. (2018) argue that AI software needs complementary investments in other intangible assets, namely databases, human capital, and organizational capital.
EU KLEMS database (where KLEMS stands for capital (K), labor (L), energy (E), material (M), and service (S) inputs) collects data on industry-level measures of productivity, capital formation, technological change, economic growth, and employment creation for the European union members, Japan, and the USA. These data are meant to be used as effective inputs for policy evaluation and statistical analysis. For our research, we have gathered investments data from the EU KLEMS Release 2019; see Stehrer et al. (2019) and Adarov and Stehrer (2019).
Assuming a null hypothesis of non-correlation, we consider three different levels of significance: a single asterisk is used when p values are lower than 0.1 whereas two and three asterisks are used when p values are lower than 0.05 and 0.01, respectively.
Acemoglu and Restrepo (2018d) argue that “factor-augmenting technologies have a limited scope to reduce the demand for labor.” Another criticism made by the same authors refers to the impact of technology on labor share in national income: it is strictly related to the elasticity of substitution between production factors. Conversely, they argue that task-based approach “always reduces the labor share and it reduces labor demand and the equilibrium wage unless the productivity gains from automation are sufficiently large.”
In particular, if the number of workers exceeds the amount of workforce needed to meet the production target, the CGP fires employees in excess, otherwise it enters the decentralized labor market in order to hire new households to employ in the production process. As regards the wage setting, first, the CGP sets an initial wage offer which, in case of failure in hiring the amount of workers needed, is increased by a fixed parameter in order to start a second round. If the employment target is not reached for the second time, it exits the labor market. However, it increases the wage offer again and this will represent the initial wage offer for the next labor market session. It is worth noting that, in case of low unemployment levels within the economy, firms have difficulties in hiring workers and this could involve an increase of wages according to the wage setting mechanism described above. In turn, higher wages involve an increase of prices that are determined through a markup pricing on unit costs and this fact could trigger a price inflation.The same hiring procedures are adopted also by the capital goods producer (KGP) and the digital assets developers (DADs) described in the following paragraphs.
It is worth noting that, since digital assets are non-rivalrous goods, DADs face only workers’ wages costs in order to supply their products.
Although CGPs hire households regardless of their education level, during the hiring process they prioritize highly educated workers.
DADs provide also training courses for workers to manage their digital assets.
Higher revenues do not necessarily involve more intense R&D activities because they could be related also to an increase of the average wage w characterizing the economic system. Therefore, for equal sales, higher turnover could be used in order to compensate for higher salaries.
References
Acemoglu D (2003) Labor- and capital- augmenting technical change. J Eur Econ Assoc 1:1–37
Acemoglu D, Restrepo P (2017) Robots and jobs: evidence from us labor markets. Working Paper 23285, National Bureau of Economic Research
Acemoglu D, Restrepo P (2018a) Artificial intelligence, automation and work. Working Paper 24196, National Bureau of Economic Research
Acemoglu D, Restrepo P (2018b) Automation and new tasks: the implications of the task content of production for labor demand. J Econ Perspect 33 (2):3–30
Acemoglu D, Restrepo P (2018c) Low-skill and high-skill automation. J Hum Cap 12(2):204–232
Acemoglu D, Restrepo P (2018d) Modeling automation. AEA Papers Proc 108:48–53
Adarov A, Stehrer R (2019) Tangible and intangible assets in the growth performance of the eu, japan and the us. wiiw, research report no. 442
Aghion P, Jones BF, Jones CI (2017) Artificial intelligence and economic growth. Working Paper 23928, National Bureau of Economic Research
Arthur WB (1989) Competing technologies, increasing returns, and lock-in by historical events. Econ J 99(394):116–31
Arthur WB (1990) Positive feedbacks in the economy. Sci Am 262(2):92–99
Arthur WB (1994) Increasing returns and path dependence in the economy. University of Michigan Press
Arthur WB (1996) Increasing returns and the new world of business. Harvard Bus Rev 74(4):100–109
Arthur WB (2006) Out-of-equilibrium economics and agent-based modeling, Handbook of computational economics, vol 2. Elsevier, pp 1551–1564
Arthur WB (2010) Complexity, the santa fe approach, and non-equilibrium economics. History Econ Ideas 18:149–166
Autor DH, Dorn D (2013) The growth of low-skill service jobs and the polarization of the US Labor Market. Amer Econ Rev 103:1553–1597
Basu S, Fernald JG, Oulton N, Srinivasan S (2004) The case of the missing productivity growth, or does information technology explain why productivity accelerated in the United States but not in the United Kingdom?. The MIT Press, pp 9–82
Belleflamme P, Peitz M (2018) Platforms and network effects. In: Handbook of game theory and industrial organization: applications, vol 2, pp 286–317
Bertani F, Ponta L, Raberto M, Teglio A, Cincotti S (2020) The complexity of the intangible digital economy: an agent-based model. Journal of Business Research
Bessen JE (2016) How computer automation affects occupations: technology, jobs, and skills. Law & Economics Working Paper No. 15-49, Boston University School of Law
Bessen JE (2018) AI and jobs: the role of demand. Working Paper 24235, National Bureau of Economic Research
Bessen JE (2019) Automation and jobs: when technology boosts employment. Law & Economics Working Paper No. 17-09, Boston University School of Law
Bresnahan TF, Brynjolfsson E, Hitt LM (2002) Information technology, workplace organization, and the demand for skilled labor: firm-level evidence. Quart J Econ 117(1):339–376
Brynjolfsson E, Hitt LM (2000) Beyond computation: Information technology, organizational transformation and business performance. J Econ Perspect 14(4):23–48
Brynjolfsson E, McAfee A (2014) The second machine age: work, progress, and prosperity in a time of brilliant technologies. W. W. Norton & Co Inc
Brynjolfsson E, Rock D, Syverson C (2018) Artificial intelligence and the modern productivity paradox: a clash of expectations and statistics. In: The economics of artificial intelligence: an agenda, NBER Chapters. National Bureau of Economic Research, Inc, pp 23–57
Caballero RJ, Hammour ML (1994) The cleansing effect of recessions. Amer Econ Rev 84(5):1350–1368
Carroll CD (2001) A theory of the consumption function, with and without liquidity constraints. J Econ Perspect 15(3):23–45
Cincotti S, Raberto M, Teglio A (2012) Macroprudential policies in an agent-based artificial economy. Revue de l’OFCE (5):205–234
Corrado C, Hulten CR, Sichel DE (2005) Measuring capital and technology: an expanded framework. The University of Chicago Press, Chicago, pp 11–46
Corrado C, Haskel J, Jona-Lasinio C (2016) Intangibles, ICT and industry productivity growth: evidence from the EU. Cambridge University Press, Cambridge, pp 319–346
DeCanio SJ (2016) Robots and humans - complements or substitutes?. J Macroecon 49:280–291
Farrell J, Klemperer P (2007) Chapter 31: coordination and lock-in: competition with switching costs and network effects. In: Handbook of industrial organization, vol 3, pp 1967–2072
Fraser RW (1985) Uncertainty and the theory of mark-up pricing. Bull Econ Res 37(1):55–64
Godley W, Lavoie M (2012) Monetary economics: an integrated approach to credit, money, income, production and wealth. Palgrave Macmillan, UK
Goldstein J (1986a) Markup variability and flexibility: theory and empirical evidence. J Bus 59(4):599–621
Goldstein JP (1986b) Mark-up pricing over the business cycle: the microfoundations of the variable Mark-Up. South Econ J 53(1):233
Goodridge P, Wallis G, Haskel J (2012) UK innovation index: productivity and growth in UK industries. Nesta working paper
Goos M, Manning A (2007) Lousy and lovely jobs: the rising polarization of work in Britain. Rev Econ Stat 89(1):118–133
Goos M, Manning A, Salomons A (2014) Explaining job polarization: routine-biased technological change and offshoring. Amer Econ Rev 104:2509–2526
Graetz G, Michaels G (2018) Robots at work. Rev Econ Stat 100:753–768
Hanson R (2001) Economic growth given machine intelligence. Journal of Artificial Intelligence Research - JAIR
Hao MVJX, Van Ark B (2009) Intangible capital and growth- an international comparison. Working Paper D3.6
Haskel J, Westlake S (2017) Capitalism without capital. Princeton University Press
Lankisch C, Prettner K, Prskawetz A (2019) How can robots affect wage inequality?, vol 81
LeBaron B, Tesfatsion L (2008) Modeling macroeconomies as open-ended dynamic systems of interacting agents. Amer Econ Rev 98(2):246–250
Marrocu E, Paci R, Pontis M (2011) Intangible capital and firms’ productivity. Ind Corp Chang 21(2):377–402
Mazzocchetti A, Raberto M, Teglio A, Cincotti S (2018) Securitization and business cycle: an agent-based perspective. Ind Corp Chang 27:1091–1121
Mazzocchetti A, Lauretta E, Raberto M, Teglio A, Cincotti S (2020) Systemic financial risk indicators and securitised assets: an agent-based framework. J Econ Interac Coord 15:9–47
Nordhaus WD (2015) Are we approaching an economic singularity? Information technology and the future of economic growth. Working Paper 21547, National Bureau of Economic Research
OECD (2001) Measuring productivity - OECD manual: measurement of aggregate and industry-level productivity growth. OECD Publishing, Paris
OECD (2019) OECD Compendium of productivity indicators 2019. OECD Publishing, Paris
Ozel B, Nathanael RC, Raberto M, Teglio A, Cincotti S (2019) Macroeconomic implications of mortgage loan requirements: an agent-based approach. J Econ Interac Coord 14(1):7–46
Petit P (1993) Employment and technical change. Cepremap working papers, CEPREMAP
Petrovic M, Ozel B, Teglio A, Raberto M, Cincotti S (2017) Eurace open: an agent-based multi-country model. Working Paper 2017/09 Economics Department, Universitat Jaume I, Castellón
Petroviċ M, Ozel B, Teglio A, Raberto M, Cincotti S (2020) Should i stay or should i go? An agent-based setup for a trading and monetary union. J Econ Dyn Control 113:103866
Pianta M (2009) Innovation and employment. In: The Oxford handbook of innovation
Piva M, Vivarelli M (2017) Technological change and employment: were Ricardo and Marx right? IZA Discussion Papers 10471, Institute of Labor Economics (IZA)
Ponta L, Raberto M, Teglio A, Cincotti S (2018) An agent-based stock-flow consistent model of the sustainable transition in the energy sector. Ecol Econ 145(C):274–300
Raberto M, Teglio A, Cincotti S (2012) Debt, deleveraging and business cycles: an agent-based perspective. Econ - Open-Access Open-Assess E-J 6:1–49
Raberto M, Ozel B, Ponta L, Teglio A, Cincotti S (2018) From financial instability to green finance: the role of banking and credit market regulation in the Eurace model. Journal of Evolutionary Economics, pp 1–37
Roth F (2019) Intangible capital and labour productivity growth: a review of the literature. Hamburg Discussion Papers in International Economics, pp 4
Sachs JD, Kotlikoff LJ (2012) Smart machines and long term misery. Technical Report 18629, National Bureau of Economic Research
Stehrer R, Bykova A, Jäger K, Reiter O, Schwarzhappel M (2019) Industry level growth and productivity data with special focus on intangible assets. Technical report, The Vienna Institute for International Economic Studies (wiiw
Teglio A, Raberto M, Cincotti S (2012) The impact of banks’ capital adequacy regulation on the economic system: an agent-based approach. Adv Complex Syst 15:1–27
Teglio A, Mazzocchetti A, Ponta L, Raberto M, Cincotti S (2019) Budgetary rigour with stimulus in lean times: policy advices from an agent-based model. J Econ Behav Organ 157:59–83
Thum-Thysen A, Voigt P, Bilbao-Osorio B, Maier C, Ognyanova D (2017) Unlocking investment in intangible assets. Quarterly report on the euro area (qrea)
Vermeulen B, Kesselhut J, Pyka A, Saviotti PP (2018) The impact of automation on employment: just the usual structural change? Sustainability 10:1–27
Vivarelli M (2014) Innovation, employment and skills in advanced and developing countries: a survey of economic literature. J Econ Issues 48(1):123–154
Zeira J (1998) Workers, machines, and economic growth. Q J Econ 113:1091–1117
Funding
Open access funding provided by Universitàdegli Studi di Genova within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bertani, F., Raberto, M. & Teglio, A. The productivity and unemployment effects of the digital transformation: an empirical and modelling assessment. Rev Evol Polit Econ 1, 329–355 (2020). https://doi.org/10.1007/s43253-020-00022-3
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s43253-020-00022-3
Keywords
- Intangible assets
- Digital transformation
- Total factor productivity
- Technological unemployment
- Agent-based economics