1 Introduction

In recent years, along with rising environmental pollution issues and declining fossil energy resources, the use of renewable-based distributed generation systems (such as photovoltaic, wind energy, etc.), FACTS devices (such as STATCOM, UPFC, UPQC, etc.), active power filters (APFs), and grid connected converters in a wide variety of applications such as high-voltage and low-voltage systems as well as some specific applications, has increased [1]. Among grid-connected converters, multilevel converters are one of the most widely employed in high power applications [2]. This is due to their advantages, which include the ability to operate at high-power, low-distortion output voltage waveforms, and lower voltage stress (dv/dt) when compared to conventional inverters [2].

The three most prominent types of multilevel converters are diode clamped, flying capacitors, and cascaded [3]. Compared to other multilevel converters, cascaded multilevel inverters are preferred for medium and high power applications as well as modular structures [5].

The pulse width modulation (PWM) strategy in multilevel inverters consists of two main categories that are suitable for high and low switching frequencies. In high switching frequencies, sinusoidal pulse width modulation (SPWM) and space-vector modulation are commonly used. Meanwhile, in low switching frequencies, selective harmonics elimination and selective harmonic reduction methods are usually employed [4].

There are various PWM methods to control the DC link voltage in grid-connected cascaded H-bridges (CHBs). Carrier-based modulation techniques, including phase shift PWM (PSPWM) and level shift PWM (LSPWM), are among the most widely used [6].

Generally, two types of passive coupling (L and LCL) are used to reduce switching current harmonics. The LCL filter structure is used in power conversion applications due to its advantages such as lower switching frequencies, better damping, and reduced current ripple when injecting more current into the grid [7]. Although the complexity of closed-loop stabilization is the major drawback of LCL filters when compared to L filters, the design and control structure of LCL filter-based inverters is a challenging task that requires a high-quality current, low amount of harmonic distortion (THD), fast dynamic response, and robust closed-loop stability of the system [7]. In contrast to the advantages mentioned above, LCL filters can disrupt the grid current due to the resonant frequency. Therefore, this problem should be resolved by using active or passive damping methods [8]. Various authors have proposed methods for reducing the problems caused by the resonant frequency for LCL filters. In [7], a method was proposed for a full delay compensation strategy for the unit capacitor-voltage feedforward inverters with LCL filters used in distributed generation systems. Sampath and Moin [9] proposed a design for the LCL filters of grid-connected voltage source inverters, and they fully explained how to calculate all of the filter parameters for this structure.

State-space models for multilevel converters have been presented in a number of scientific papers. In [10], a switching-cycle state-space model was proposed for a modular multilevel converter. This model differs from similar models in that it is analyzed on the basis of a switching function and has capacitance relationships for each individual cell. Moreover, voltage-based state-space modeling for modular multilevel converters was presented in [11]. In [12], a method was presented for the harmonic state-space modeling of modular multilevel inverters with zero-sequence voltage compensation. In [13], Chaves et al. proposed a method for a diode clamp multilevel converter state-space model, which is a generalized m-level model. However, the need for several linear and nonlinear controllers in different converter loops can reduce the complexity and cost of the system. Other scientific papers have also proposed state-space models for multilevel converters [14, 15]. However, LCL coupling for a GCCMI with SPWM has not been presented. Nonlinear loads, such as diode rectifiers with capacitive or inductive loads, inject reactive and harmonic current into the grid, which results in a low efficiency, low power factor, high harmonic distortion (THD), and harmful disturbances to other network equipment [16]. Numerous studies have been conducted to solve the problems caused by nonlinear loads. Recently, simple passive, parallel, and hybrid filters have been investigated to improve the power factor and to compensate for selective harmonics [17]. Another solution to these problems is to use SAPFs. Among active filters, the SAPF is one of the most practical structures used in this field [16]. Different control methods for shunt active power filters (SAPFs) have been proposed in a number of papers. In [18], artificial neural network model predictive control (ANN-MPC) was implemented on a neutral point clamped (NPC) converter using a shallow neural network. In [19], a method was presented for the sliding mode control modeling of three-phase active power filtering using the vector technique. However, that paper mainly focused on obtaining a nonlinear large-signal model of different reference frames according to the vector operation technique (VOT). In [20], an adaptive backstepping control method of a single-phase SAPF with two series control was proposed. An adaptive backstepping controller was used to control the filter current in the inner loop, and the DC input voltage of the inverter in the inner loop was adjusted by a proportional integral (PI) controller. The use of the Lyapunov function in the controller structure made it robust to dynamic changes.

This manuscript presents a general state-space model for a multilevel GCCMI with LCL coupling, which can be used for the controller design in an arbitrary number of H-bridges for the implementation of multilevel inverters. Considering that this model is used in the design of power electronic structures and controllers, its effectiveness is of great importance. In Sect. 3, the obtained model is verified, and simulation results as well as practical results in the steady and dynamic states are presented. In Sect. 4, a Lyapunov function-based nonlinear controller for grid-connected SAPF is designed by using the generalized model of a GCCMI with LCL coupling. Thus, the voltage of the DC link capacitors is stabilized by a PI controller at a desired value. The generalized design of the controller also has the advantage of having a flexible design. Therefore, the number of inverter H-bridges can be easily increased. In the manuscript, an example of this SAPF with three H-bridges is simulated using EMTC/PSCAD software. The results show that the load current THD is within the IEEE-519 standard range, and that it is stable and robust in a wide range of operation. Figure 1 presents the overall structure of the work done in this manuscript.

Fig. 1
figure 1

Overall structure of the work in this paper

Full size image

2 Mathematical modeling

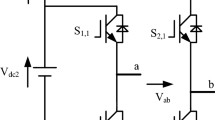
In Fig. 2, the general structure of the GCCMI, including a cascaded multilevel inverter, an LCL coupling, and a nonlinear load is shown. To model the GCCMI with an LCL coupling, considering Fig. 3 and assume that all of the inverter bridges are turned on. Kirchhoff's laws for this structure can be written as follows:

Fig. 2
figure 2

General structure of SAPF based on a cascaded multilevel inverter with LCL coupling

Full size image
Fig. 3
figure 3

General structure of the cascaded multilevel inverter with LCL coupling, assuming that all of inverter bridges are turned on

Full size image
$$\left\{\begin{array}{l}{V}_{S}={V}_{C}+{R}_{f}{i}_{f}+{L}_{f}\frac{{d}_{{i}_{f}}}{dt}\\ {i}_{dc}={i}_{f}-C\frac{{d}_{{V}_{C}}}{dt}\\ {V}_{C}=\left({V}_{DC1}+{V}_{DC2}+\dots +{V}_{DCn}\right)+\left({R}_{c}+nr\right){i}_{inv}+{L}_{c}\frac{{d}_{{i}_{dc}}}{dt}\\ {i}_{inv}={c}_{1}\frac{{d}_{{V}_{DC1}}}{dt} , {i}_{inv}={c}_{2}\frac{{d}_{{V}_{DC2}}}{dt} , \dots , {i}_{inv}={c}_{n}\frac{{d}_{n}}{dt}\end{array}\right.$$
(1)

By defining state-space variables as follows:

$${x}_{1}={i}_{f}, {x}_{2}={v}_{c}, {x}_{3}={i}_{inv}, {x}_{4}={v}_{DC1}, {x}_{5}={v}_{DC2}, \cdots , {x}_{n+3}={v}_{DCn}$$
(2)

The state-space equations are written as follows:

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ {\dot{x}_{5} } \\ \vdots \\ {\dot{x}_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 & 0 & \cdots & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 & 0 & \cdots & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + nr}}{{L_{c} }}} & { - \frac{1}{{L_{c} }}} & { - \frac{1}{{L_{c} }}} & \cdots & { - \frac{1}{{L_{c} }}} \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 & 0 & \cdots & 0 \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 & 0 & \cdots & 0 \\ \end{array} } \right] \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \\ {x_{5} } \\ \vdots \\ {x_{n} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array} } \right]$$
(3)

If the capacitance of the DC link capacitors of the inverter bridges is equal to C1, the VDC1 state variable can be considered constant for all of the H-bridges, and the values of the voltages VDC1, VDC2, … and VDCn are also equal to the average value of VDC1. It is assumed that the state-space equations for multilevel inverters with N–H-bridges are as follows:

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + nr}}{{L_{c} }}} & { - \frac{n}{{L_{c} }}} \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(4)

According to Fig. 4, inverter switching is performed using the unipolar PWM method [6], where switching signals are generated by comparing the high frequency carrier wave (Vtri) and the desired AC control wave (Vcontrol). Due to the high frequency of the switching, it can be assumed that the control signal is almost constant over a switching cycle [20]. Then by examining two cases of cascaded multilevel inverters with the N–H-bridge structure, the general state-space model of this inverter is obtained.

Fig. 4
figure 4

Unipolar PWM switching structure of the cascaded multilevel inverter

Full size image

Figure 5 shows carrier and control waves of the cascaded multilevel inverter with two H-bridges for the positive semicircle of the control signal (Vcontrol). As shown in Fig. 5a, in a switching cycle, there are eight working modes per control signal in the range of (1/2 < Vcontrol < 1) for the two H-bridges. The inverter1 switching signals are obtained by comparing Vtri1 with the Vcontrol signals. Similarly, the inverter2 switching signals are obtained by comparing Vtri2 with the Vcontrol signals. For the operating modes 1a, 3a, 5a, and 7a there is only one H-bridge in the positive position. According to Fig. 3 and Eq. (4), the state-space equation of the switching modes 1a, 3a, 5a, and 7a are written as 5 and the state-space equation of the switching modes 2a, 4a, 6a, and 8a are written as 6.

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + 4r}}{{L_{c} }}} & { - \frac{1}{{L_{c} }}} \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(5)
$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + 4r}}{{L_{c} }}} & { - \frac{2}{{L_{c} }}} \\ 0 & 0 & {\frac{1}{{c_{1} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(6)
Fig. 5
figure 5

Carrier and control signal of the cascaded multilevel inverter with a two H-bridge structure for a positive semicircle of the control signal: a control signal in the range of (1/2 < Vcontrol < 1); b control signal in the range of (0 < Vcontrol < 1/2)

Full size image

Considering the above switching modes, the average state-space equations in a switching cycle for a series multilevel inverter including two H-bridges can be obtained as follows:

$$\dot{X}={A}_{avg}X+{B}_{avg}$$
(7)
$${A}_{avg}=\left(\frac{1}{T}\right)\left({t}_{1a}{A}_{1}+{t}_{2a}{A}_{2}+\cdots +{t}_{8a}{A}_{8}\right) except {A}_{33}$$
(8)
$${A}_{avg33}=\left(1/T\right)\left({t}_{1a}{A}_{1}+{t}_{2a}{A}_{5}+{t}_{2a}{A}_{2}+{t}_{2a}{A}_{4}+{t}_{2a}{A}_{6}+{t}_{8a}{A}_{8}\right)$$
(9)
$${B}_{avg}=\left(1/T\right)\left({t}_{1a}{B}_{1}+{t}_{2a}{B}_{2}+\cdots +{t}_{8a}{B}_{8}\right)$$
(10)

Considering the times of different switching modes:

$${t}_{1a}={t}_{3a}={t}_{5a}={t}_{7a}=DT , D\in \left[0,\frac{1}{4}\right]$$
(11)
$${t}_{2aa}={t}_{4a}={t}_{6a}={t}_{8a}=\frac{1-4D}{4}T , D\in \left[0,\frac{1}{4}\right]$$
(12)

With respect to Eqs. (5, 6, 7, 8, 9, 10, 11, 12) and considering Fig. 5, the values of Aavg and Bavg are given as follows:

$${A}_{avg}=4D{A}_{1}+\left(1-4D\right){A}_{2}\mathrm{ except }{A}_{33} , {A}_{avg33}=2\mathrm{D}{A}_{1}+\left(1-4\mathrm{D}\right){A}_{2},$$
$${A}_{avg}=\left[\begin{array}{cccc}-\frac{{R}_{f}}{{L}_{f}}& -\frac{1}{{L}_{f}}& 0& 0\\ \frac{1}{C}& 0& -\frac{1}{C}& 0\\ 0& \frac{1}{{L}_{c}}& -\frac{{R}_{c}+4r}{{L}_{c}}& -\left(1-2D\right)\frac{2}{{L}_{c}}\\ 0& 0& \left(1-2D\right)\frac{1}{{c}_{1}}& 0\end{array}\right]$$
(3)
$${B}_{avg}=4D+\left(1-4D\right){B}_{=}\left[\begin{array}{c}\frac{1}{{L}_{f}}{V}_{S}\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$
(14)

In the case of Aavg, 3,3 in Eq. (15), given that only one DC link capacitor is considered and that each of the DC link capacitors is connected to the network in only two of the working modes 1a, 3a, 5a, and 7a of Eq. (6), the matrix of Eq. (9) is used to average this layer. According to the OAB triangle in Fig. 5, and based on trigonometric relations, the following equations for this structure can be written as follows:

$$MN\parallel AB \Rightarrow \frac{ON}{{OB}} = \frac{MN}{{AB}}$$
(15)
$$\frac{{t_{2} + t_{3} + t_{4} + t_{5} /2}}{T/2} = \frac{{V_{control} + \hat{V}_{tri} }}{{2\hat{V}_{tri} }} \Rightarrow \frac{{\frac{{\left( {1 - 4D} \right)T}}{4} + DT + \frac{{\left( {1 - 4D} \right)T}}{4} + \frac{DT}{2}}}{\frac{T}{2}} = \frac{1}{2}\left( {1 + \frac{{V_{control} }}{{\hat{V}_{tri} }}} \right)$$
(16)
$$\frac{{V_{control} }}{{\hat{V}_{tri} }} = 1 - 2D \Rightarrow u = \frac{{V_{control} }}{{\hat{V}_{tri} }}$$
(17)

The expression (1 − 2D) can be defined as a control variable:

$$u = \left( {1 - 2D} \right) , u \in \left[ {0,\frac{1}{2}} \right]$$
(18)
$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + 4r}}{{L_{c} }}} & { - \frac{2u}{{L_{c} }}} \\ 0 & 0 & {\frac{u}{{c_{1} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(19)

and:

$$u=1-2D, \left\{\begin{array}{c}0<D<\frac{1}{4}\\ \frac{1}{2}<u<1\end{array}\right.$$
(20)

The final form of the state-space equations of the cascaded multilevel inverter including two H-bridges in the range of 1 / 2 ≤ u ≤ 1 is obtained as follows (Eq. 19).

Given Eq. (17) and assuming \({\widehat{V}}_{tri}=1\), the parameter u as the controller output can be used as the input signal of the PWM segment.

Similarly, according to Fig. 5b, for the control signal in the range of 0 < Vcontrol < 1/2 for the two H-bridges, there are eight working modes in a switching cycle. In addition, for the 1b, 3b, 5b, and 7b working modes, the two H-bridges are always off. According to Fig. 3 and Eq. (4), the equations of these modes are written as Eq. (21). Moreover, for the switching modes 2b, 4b, 6b, and 8b there is only one H-bridge in the positive position that is on, and Eq. (7) represents its state equations.

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + 4r}}{{L_{c} }}} & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(21)

Given the above switching modes and considering the equations of states 5 and 21, similar to the previous section, the average state-space equations in a switching cycle for a cascaded multilevel inverter consisting of two H-bridges (0 < Vcontrol < 1/2) can be obtained as (19) and (22).

$$u=2D, \left\{\begin{array}{c}0<D<\frac{1}{4}\\ 0<u<1/2\end{array}\right.$$
(22)

Similarly for the negative half-cycle of the control signal, state-space equations in the ranges of -1 < Vcontrol < − 1/2 and − 1/2 < Vcontrol < 0 are obtained as Eqs. (19, 23, and 24).

$$u=1-2D, \left\{\begin{array}{c}0<D<\frac{1}{4}\\ -1<u<-\frac{1}{2}\end{array}\right.$$
(23)
$$u=-2D, \left\{\begin{array}{c}0<D<\frac{1}{4}\\ -\frac{1}{2}<u<0\end{array}\right.$$
(24)

Finally, considering the state-space Eq. (19) through (20) and (22) through (24), the general equations of the cascaded multilevel inverter connected to the grid with LCL filters including two H-bridges can be written as (19) and as follows:

$$\left\{\begin{array}{l}0\le D\le \frac{1}{4}\\ u=1-2D ,\frac{1}{2} \le u\le 1\\ u=2D , 0\le u\le \frac{1}{2}\\ u=-(1-2D) ,- 1 \le u\le -\frac{1}{2}\\ u=-2D ,-\frac{1}{2}\le u\le 0\end{array}\right.$$
(25)

Similarly, when the number of H-bridge converters increases, the general structure of the state-space equations for the GCCMI are given as (26) and (27).

$$\left[ {\begin{array}{*{20}c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \\ {\dot{x}_{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{f} }}{{L_{f} }}} & { - \frac{1}{{L_{f} }}} & 0 & 0 \\ \frac{1}{C} & 0 & { - \frac{1}{C}} & 0 \\ 0 & {\frac{1}{{L_{c} }}} & { - \frac{{R_{c} + 4r}}{{L_{c} }}} & { - \frac{2u}{{L_{c} }}} \\ 0 & 0 & {\frac{u}{{c_{1} }}} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \\ {x_{4} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{L_{f} }}V_{S} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]$$
(26)
$$\left\{\begin{array}{c}0\le D\le \frac{1}{2n}\\ ---------------------\\ u=1-2D ,\frac{n-1}{n} \le u\le 1\\ u=\frac{n-2}{n}+2D ,\frac{n-2}{n}\le u\le \frac{n-1}{n}\\ u=\frac{n-3}{n}+2D ,\frac{n-3}{n}\le u\le \frac{n-2}{n}\\ \vdots \\ u=\frac{1}{n}+2D ,\frac{1}{n}\le u\le \frac{2}{n}\\ u=2D , 0\le u\le \frac{1}{n}\\ ---------------------\\ u=-(1-2D) ,- 1 \le u\le -\frac{n-1}{n}\\ u=-\left(\frac{n-2}{n}+2D\right) ,-\frac{n-1}{n}\le u\le -\frac{n-2}{n}\\ u=-\left(\frac{n-3}{n}+2D\right) ,-\frac{n-2}{n}\le u\le -\frac{n-3}{n}\\ \vdots \\ u=-\left(\frac{1}{n}+2D\right) ,-\frac{2}{n}\le u\le -\frac{1}{n}\\ u=-2D , -\frac{1}{n}\le u\le 0\end{array}\right.$$
(27)

3 Results and verification of the designed model

Based on the averaged state-space Eqs. (19) and (25), Fig. 6 shows a box diagram of this modeling for a multilevel inverter with two H-bridges. In addition, Fig. 7 shows a block diagram of this system for the structure in Fig. 3 with two H-bridges. Considering the parameters presented in Table 1, the obtained model in Fig. 6 and the system in Fig. 7 are simulated by EMTDC/PSCAD software, and the results are compared with practical results obtained with the laboratory setup shown in Fig. 8. A single-phase rectifier with an RC load is employed as a nonlinear load. Insulated-gate bipolar transistor (IGBT) switches are used in the inverters. Measurement of the filter and load currents are performed using Hall-effect LEM sensors. It should be noted that the parameters of the practical sample are also in accordance with Table 1. The following is a review of the above results.

Fig. 6
figure 6

Model of the GCCMI for n = 2

Full size image
Fig. 7
figure 7

Block diagram of the GCCMI with LCL coupling

Full size image
Table 1 Parameters of the GCCMI with LCL coupling for n = 2
Full size table
Fig. 8
figure 8

Experimental setup of a GCCMI with LCL coupling (n = 2)

Full size image

3.1 Steady state results

To investigate the steady state performance, the system in which the control signal (u) with 0.85 amplitude carrier waves (Vtri), and a phase difference of 35 degrees on the grid voltage is investigated. According to Fig. 9, the voltage of the DC-link with a small ripple on a value of 31 V is stabilized, and if and iinv currents are alternately in fluctuation with approximate values of 9.4 A and 9.45 A. The x1 and x2 current values are 9.6 A and 9.52 A, respectively. In addition, the LCL filter capacitor voltage has a peak value of 66 V. Figure 9 indicates the cascaded multilevel converter voltage with two H-bridges, the control signal waveform (u) with 0.85 amplitude carrier waves (Vtri), and a 35-degree phase difference on the grid voltage.

Fig. 9
figure 9

Waveforms of GCCMI with LCL coupling and two H-bridges for the control signal (u) with Vtri = 0.85 < 35°: a if and x1 state variables obtained from the simulation; b if from the experimental setup; c Vc and × 2 state variables obtained from the simulation; d Vc obtained from the experimental setup; e iinv and × 3 state variables obtained from the simulation; f iinv from the experimental setup; g VDC and × 4 variables obtained from the simulation; h VDC obtained from the experimental setup; i output voltage of the converter from the simulation; j output voltage of the converter from the experimental setup

Full size image

3.2 Dynamic results

To show the system performance in the dynamic mode, Fig. 10 depicts the modeling, simulation, and practical results of the system in which the control signal (u) with a phase difference of 35 degrees on the grid voltage is reduced from a 0.8 amplititude carrier wave (Vtri) to 0 with step changes. As observed in Fig. 10, when the control signal with a 35-degree phase difference on the grid voltage is reduced from a 0.8 amplitude carrier wave to zero, the if current increases from 9.34 to 14.35 A, iinv increases from 9.31 to 14.45 A, the LCL filter capacitor voltage decreases from 66 to 24.5 V, and the DC link voltage of the converters changes to an approximate voltage of 26 V. Figure 10 shows cascaded multilevel inverter voltage waveforms, control signal waveforms, and grid voltage waveforms obtained from the simulation and practical results. The voltage level of the multilevel inverter is reduced from 56 to 26 V. According to the figures, it is clear that these changes occur in less than one period, which indicates the high operating speed of the system in the presence of dynamic changes.

Fig. 10
figure 10

Waveforms of GCCMI with LCL filter and two H-bridges for the control signal (u) with an 0.85 carrier wave (Vtri) amplitude (with a step change of 0.8, the carrier wave (Vtri) is reduced to 0): a if and x1 state variables obtained from the simulation; b if from the experimental setup; c Vc and × 2 state variables obtained from the simulation; d Vc obtained from the experimental setup; e iinv and × 3 state variables obtained from the simulation; f iinv from the experimental setup; g VDC and × 4 variables obtained from the simulation; h VDC obtained from the experimental setup; i output voltage of the converter from the simulation; j output voltage of the converter from the experimental setup; k control signal (u) and source voltage from the simulation; l control signal (u) and source voltage from the experimental setup

Full size image

4 Lyapunov based nonlinear control design

Figure 2 shows the general structure of a grid-connected SAPF with cascaded multilevel inverter and LCL coupling, and Fig. 11 depicts a block diagram of the nonlinear controller based on the Lyapunov function. In this control method, the main objective is to generate a compensating reference current. However, eliminating the load current harmonics should also be considered. A network power factor (iS) of one is obtained as follows:

$$i_{s}^{*} = I_{m} \left( t \right)\sin \left( {\omega t} \right)$$
(28)
Fig. 11
figure 11

Block diagram of a nonlinear SAPF based on the Lyapunov function

Full size image

4.1 PI controller

If the inverter switching control variable (u) is completely sinusoidal, the DC link capacitor voltage of the inverter bridges is equal to a certain value. However, due to the nature of shunt active filters, this control variable is completely nonlinear and usually has an undetermined value. Therefore, during the compensation process, the voltage of the DC link capacitors are not balanced between charge and discharge, which prevents these voltages from being fixed to a certain value (VDC-avg). This in turn, leads to inefficiency of the controller. If the instantaneous difference of the DC link voltages with the reference value (V*DC-avg) is defined as follows:

$$\left\{ {\begin{array}{*{20}c} {e_{1} = V_{DC1} - V_{DC - avg}^{*} } \\ {e_{2} = V_{DC2} - V_{DC - avg}^{*} } \\ \vdots \\ {e_{n} = V_{DCn} - V_{DC - avg}^{*} } \\ \end{array} } \right.$$
(29)

and the minimum value of these errors is given as follows:

$$e_{min} = min\left\{ {e_{1} ,e_{2} , \ldots ,e_{n} } \right\}$$
(30)

the Im value can be obtained using a PI controller as follows:

$$I_{m} \left( t \right) = K_{p} \left( {e_{min} } \right) + K_{i} \smallint \left( {e_{min} } \right)dt$$
(31)

Then the value of \(i_{s}^{*}\) is calculated using Vs. According to Fig. 11, the compensation flow can be defined as follows:

$$i_{f}^{*} = i_{s}^{*} - I_{l}$$
(32)

For the closed loop system, the compensation current if must follow its reference value (\(i_{f}^{*}\)), where \(i_{s}^{*}\) has a value that is close to a sine with a power factor of about one. According to Eqs. (19) and (27) and considering the state variables in Eq. (2), equations of the grid-connected shunt active filter with the N-level cascaded multilevel inverter and LCL filter are written as follows:

$$V_{S} = V_{C} + R_{f} i_{f} + L_{f} \dot{x}_{1}$$
(33)
$$i_{dc} = i_{f} - C\dot{x}_{2}$$
(34)
$$V_{C} = nuV_{DC1} + \left( {R_{c} + 2nr} \right)i_{dc} + L_{c} \dot{x}_{3}$$
(35)
$$ui_{dc} = c_{1} \dot{x}_{4}$$
(36)

By inserting Vc from (33) into (35) and idc from (34) into (35) and (36), the following is obtained:

$$L_{c} \dot{x}_{1} + \left( {R_{c} + 2nr} \right)x_{1} - CL_{c} \ddot{x}_{2} - C\left( {R_{c} + 2nr} \right)\dot{x}_{2} + L_{f} \dot{x}_{1} + R_{f} x_{1} = V_{s} - nux_{4}$$
(37)
$$c_{1} \dot{x}_{4} = ux_{1} - Cu\dot{x}_{2}$$
(38)

Considering the filter reference current (\({\text{i}}_{{\text{f}}}^{*}\)) and the DC inverter link voltage (\({\text{V}}_{{{\text{DC}}}}^{*}\)), the associated errors of these references are given as follows:

$$z_{1} = x_{1} - x_{1}^{*} ,\quad z_{2} = x_{4avg} - x_{4}^{*}$$
(39)

By placing (39) into Eqs. (37) and (38), the following is obtained:

$$(L_{f} + L_{c} )\dot{z}_{1} = V_{s} - (L_{f} + L_{c} )\dot{x}_{1}^{*} - \left( {R_{c} + 2nr + R_{f} } \right)z_{1} - \left( {R_{c} + 2nr + R_{f} } \right)x_{1}^{*} + CL_{c} \ddot{x}_{2} + C\left( {R_{c} + 2nr} \right)\dot{x}_{2} - nuz_{2} - nux_{4}^{*}$$
(40)
$$c_{1} \dot{z}_{2} = uz_{1} + ux_{1}^{*} - Cu\dot{x}_{2} - c_{1} \dot{x}_{4}^{*}$$
(41)

4.2 Lyapunov function relationships and control strategy

The proposed control strategy is based on Lyapunov’s direct method [20]. The main idea of this method is to verify that the total energy of the system is decreasing along the system trajectories. This, in turn, implies that the system states are confined to a bounded set of the phase plane. An energy-like function V(x), often referred to as the Lyapunov function is chosen in terms of the system states.

According to Lyapunov’s stability theorem, any linear or nonlinear system is globally asymptotically stable if V(x) meets the following criteria:

  1. 1.

    \(V\left( 0 \right)\, =\, 0;\)

  2. 2.

    \(V\left( x \right) > 0\, for\, all\, x\, \ne\, 0;\)

  3. 3.

    \(\dot{V}\left( x \right) < 0 \,for\, all\, x\, \ne\, 0;\)

  4. 4.

    \(V\left( x \right) \to \infty\, as\, x\, \to\, \infty .\)

Which is a matter of intuition, analytical skills, and trial–error.

Considering the Lyapunov function as follows:

$$V\left( x \right) = \frac{1}{2}(L_{f} + L_{c} )z_{1}^{2} + \frac{n}{2}c_{1} z_{2}^{2} , {\text{n}} = 1,2,3, \ldots$$
(42)
$$V(\dot{x}) = z_{1} (L_{f} + L_{c} )\dot{z}_{1} + nz_{2} c_{1} \dot{z}_{2}$$
(43)

By placing \((L_{f} + L_{c} )\dot{z}_{1}\) from (42) and \(c_{1} \dot{z}_{2}\) from (41) into (43) the following is obtained:

$$V(\dot{x}) = \emptyset_{1} z_{1} + \emptyset_{2} z_{2} - \left( {R_{c} + 2nr + R_{f} } \right)z_{1}^{2}$$
(44)

where:

$$\emptyset_{1} = V_{s} - (L_{f} + L_{c} )\dot{x}_{1}^{*} - \left( {R_{c} + 2nr + R_{f} } \right)x_{1}^{*} + CL_{c} \ddot{x}_{2} + C\left( {R_{c} + 2nr} \right)\dot{x}_{2} - nU_{0} x_{4}^{*}$$
(45)
$$\emptyset_{2} = nux_{1}^{*} - nCu\dot{x}_{2} - nc_{1} \dot{x}_{4}^{*}$$
(46)

Considering Eq. (44), it is clear that:

$$\emptyset_{1} = - q_{1} z_{1}$$
(47)
$$\emptyset_{2} = - q_{2} z_{2}$$
(48)

Equation (44) is negative. Using Eqs. (47) and (48) it is possible to write:

$$u\left( t \right) = \frac{1}{{nx_{4}^{*} }}\left[ {V_{s} - (L_{f} + L_{c} )\dot{x}_{1}^{*} - \left( {R_{c} + 2nr + R_{f} + q_{1} } \right)x_{1}^{*} + q_{1} x_{1} + CL_{c} \ddot{x}_{2} + C\left( {R_{c} + 2nr} \right)\dot{x}_{2} } \right]$$
(49)

Here, q1 is a real constant value. This method makes the PWM converter control very stable in the presence of significant changes.

4.3 Nonlinear controller simulation results

To simulate the system, according to Fig. 11, a structure with three H-bridges and a completely nonlinear load is investigated. The voltage of the DC link capacitors is stabilized by the PI controller at 310, and this structure is simulated considering the parameters in Table 2 using EMTDC/PSCAD software, and the obtained results are further discussed. The LCL filter parameters (μ, k, and fres) have been designed and calculated using the method in [9], and the PI controller coefficients have been obtained by trial and error.

Table 2 System parameters
Full size table

To assess the steady state and transient state, the shunt active filter is illuminated at t = 1.5 s. As shown in Fig. 12, when the SAPF is off, the grid current is nonlinear and the THD is 35% of the grid current. When the filter is turned on, the network current is completely sinusoidal with a THD reaching 1.3%, which is within the IEEE range. Moreover, the DC link voltages of the cascaded inverter are stabilized at 310 V. Figure 13 also shows load current harmonics before and after the active filter is switched on.

Fig. 12
figure 12

Grid-connected SAPF waveforms with a cascaded multilevel inverter and an LCL filter before and after switching on: a grid voltage; b grid current; c nonlinear load current; d SAPF current; e DC link capacitor voltages; f THD of network current

Full size image
Fig. 13
figure 13

Grid current harmonics: a before SAPF is switched on; b after SAPF is switched on

Full size image

Similarly, Fig. 14 shows the results of the system simulation for a state where the load current increases from 47.8 A to 69.3 A, and returns to the same value. As shown in this figure, the grid current also increases and decreases again with changes from 34 to 55 A. The DC link voltages of all three inverter bridges decrease as the load current drops slightly from 310 to 300 V, and returns to the same range. The THD of the load current remains below the 1.5% range during load flow changes.

Fig. 14
figure 14

Grid-connected SAPF waveforms with a cascaded multilevel inverter and LCL coupling that increase and decrease the load current: a grid voltage; b grid current; c nonlinear load current; d DC link capacitor voltages; e THD of the grid current

Full size image

5 Conclusion

Since all systems require a state-space model to use in different controllers, it is necessary to obtain this model. In this manuscript, a generalized state-space model of a GCCMI with LCL coupling for an N-level general structure was acquired. The results obtained from the simulation and the laboratory sample confirm the accuracy of the model in the permanent and dynamic states. This model can be employed in applications with cascaded multilevel inverters in different power system structures. The model uses multicarrier phase shifted PWM, which allows the converter to be used at high power and high switching frequencies. To confirm the performance of the obtained model, a grid-connected SAPF was studied using a cascaded multilevel inverter with LCL coupling and PSPWM modulation. In addition, a nonlinear controller was designed for it based on the Lyapunov function. Using a minimum error algorithm to stabilize the DC link voltages in the converter H-bridges is one of the advantages of this controller. The studied system is also fast and robust due to the use of Lyapunov stability in the controller design. Results from SAPF simulations show that the THD is in compliance with the IEEE-519 standard. The obtained state-space model in this manuscript can be used in other structures of grid-connected power converters and for the design of nonlinear controllers.