Hedonic real estate price estimation with the spatiotemporal geostatistical model

Abstract

This study argues that the spatiotemporal geostatistical model for real estate prices, which accounts for and incorporates spatial autocorrelation, can be estimated successfully using the Bayesian Markov Chain Monte Carlo (MCMC) estimation. While this procedure often encounters difficulty in calculating probabilistic densities in the Metropolis–Hastings (MH) algorithm, this study introduces a feasible and practical estimation method, providing useful estimated parameters for the model. Using single-family house transaction data, we show that ordinary estimations of real estate prices, with respect to certain explanatory variables, may lead to the underestimation of standard errors of coefficients for explanatory variables with spatial effects unless spatial autocorrelation is controlled for. Our model also makes it possible to obtain accurate in-sample predictions and moderately improved out-of-sample predictions for real estate prices. This study further estimates a “decay rate:” a diminishing correlation between real estate prices and increasing distance, showing that geographical proximities are likely to have an important impact on real estate prices, especially at a range under 600 m.

1 Introduction

Based on the theoretical foundation of the hedonic model formulated by Rosen (1974), Freeman (1974), and others, many works, including those of Muth (1969) and Polinsky and Ellwood (1979), have used hedonic estimation to explain real estate prices, with respect to some explanatory variables. As Kanemoto (1988) describes the nature of such a hedonic approach in that period as “particularly attractive,” this approach can be applied to nonmarket interactions such as existence of externalities and public goods, even though there are many potential theoretical and empirical biases that need to be cautioned against. Hedonic analysis and regression, ranging from ordinary linear regression to sophisticated non-linear models and other estimation techniques, have attempted to retrieve certain effects from explanatory variables, including infrastructure provision, environmental changes, and other elements that affect real estate prices. In doing so, they assume that such changes in a particular location or city will eventually be reflected in real estate prices, through revealed preferences for certain properties.

This type of analysis has been conducted in many different fields, including regional studies and transportation economics, where researchers are interested in the effect of particular environmental characteristics and the provision of infrastructure or facilities. While the present study provides valuable insights into the estimation of coefficients for explanatory variables and spatiotemporal variance–covariance matrices, one of its focuses is on the prediction performance of the dependent variable (real estate price) in the estimated hedonic model. The strategy for improving the prediction performance of the model involves incorporating “spatial effects” in the estimation model, where the unexplained effects of explanatory variables maybe correlated with spatial proximity.

Between the late 1960s and the 1970s, several researchers used statistics to explore such spatial interactions. For example, Ord (1975) uses the maximum likelihood estimator to estimate a certain output via the spatial weight matrix, assuming the existence of spatial autocorrelation. Prof. Jean Paelinck coined the term "spatial econometrics,” pointing out the principles used to specify spatial econometric models (Paelinck (1978)). In a textbook, he published a specification estimation that incorporated spatial autocorrelation and included some empirical results (Paelinck and Klaassen 1979). Given the rapid advances in the analysis of spatial autocorrelation in recent decades (see e.g., Anselin and Bera (1998), LeSage and Pace (2009), and Anselin (2010)), analytical methods that consider spatial autocorrelation have emerged and accumulated in many strands of research.

These studies take similar approaches, employing a spatial weight matrix to capture the geographical distance between datasets. Naturally, this technique has been applied to hedonic real estate price analyses, reflecting the fact that real estate prices always incur a decent level of spatial autocorrelation, while location has a significant impact on real estate prices. Such studies apply the spatial weight matrix, estimated using GLS, maximum likelihood, or other methods that should be appropriate for statistical assumptions about explanatory variables and error terms.

Since real estate prices have many implications for our daily lives and the economy, capturing the effect of the surrounding environment, infrastructure provision, and other attributes, a wide range of estimation methods account for the spatially autocorrelated nature of real estate prices. The effect of spatial autocorrelation on real estate prices has thus attracted much attention and been analyzed by various researchers and academic societies.¹

One notable example is the research carried out by Basu and Thibodeau (1998), who exhibit superior performance in predicting house prices, using an estimation model called the Kriged EGLS, which outperformed the OLS method in six out of eight submarkets. Case et al. (2004) held a competition to estimate real estate prices, using the suggested estimation models and comparing their performances. While the Case’s model has some advantages, in terms of the mean squared errors for predicted values, the performance of the other spatial econometric model (the spatial Durbin Model) does not seem to improve, in contrast to the OLS method and its variants. Thus, incorporating neighboring information does not necessarily improve prediction. It is more important to include other attributes of real estate as explanatory variables.²

The present study employs a geostatistical model, which can extract spatial effects ignored in the OLS estimation. While the process would be asymptotically the same if this study focused on estimating the coefficients, here it shows that the captured spatial effect of the geostatistical model can be used to predict prices and improve accuracy. Geostatistics, as the name suggests, were originally used in the earth sciences; they have recently been applied to other natural sciences, including ecological and health sciences. In these fields, geostatistical models that capture spatiotemporal effects have begun to emerge in the literature. For example, Conn et al. (2015) have estimated animal abundance in certain geographical areas (mesh data in the Bering Sea), whereas Paul et al. (2020) have estimated the progression of COVID-19 via county-level data in the United States, using Bayesian Markov Chain Monte Carlo (MCMC) algorithms. Alegana et al. (2016) have applied a geostatistical method to map malaria for elimination, using mesh data from Namibia via a Bayesian maximum likelihood estimation. Although several earth science studies have applied point-level data (e.g., Babcock et al. (2018), Beloconi et al. (2018), Guhaniyogi et al. (2013), and Yang and Ng (2019)), such studies do not use a spatiotemporal specification of variance–covariance matrices for their estimations. In line with previous research on the application of geostatistics to socio-economic research, Muto et al. (2021) have shown that the geostatistical model, which explicitly captures the spatial error structure in their estimation model, substantially improves in-sample prediction and can also improve out-of-sample forecast performance in the context of a panel data regression, when used with the Monte Carlo experiment and real data. This can explain the regional vacant house ratio, with respect to regional age composition.

Unlike other geostatistics research with spatiotemporal effects, the present study is distinct in that it examines real estate data, and our model captures the effect from point data in terms of spatial and temporal continuous spaces. Such research is rare, due to data availability issues and analytical complexities. One feature of real estate price data is that they cannot be captured at one time, such as governmental statistics. Instead, transactions occur at random, both spatially and temporally, within a certain geographical area and time frame, with real estate price and observed characteristics, such as the transaction price, floor area, and building age, recorded separately for each transaction. The present study extends the existing method to include a hedonic real estate price analysis, based on a spatiotemporal weight matrix. This succeeds in explicitly modeling the variance–covariance relationship in real estate transactions that occur at various locations and points of time and applying them to other locations and periods in the data. As this study shows, the chosen geostatistical model not only provides a certain level of goodness-of-fit for predicted prices, but also derives useful parameters of interest with a proper statistical foundation.

Another issue in hedonic price analyses is the probabilistic distribution of predicted values. In other words, even if real estate prices can be estimated and explained using a certain explanatory variable or spatial effect, it is impossible to obtain a deterministic prediction. In other words, there is always a certain probability distribution when predictions are made, based on the estimated model. In fact, it is analytically and practically necessary to estimate such a probabilistic distribution appropriately. This study therefore uses a Bayesian MCMC estimation to estimate the geostatistical model, making it possible to obtain the posterior probabilistic densities for the parameters of interest.³

After overcoming various issues associated with hedonic analyses in this way, the present analysis shows that a geostatistical hedonic real estate estimation model incorporates geographical and temporal information, has multiple benefits for researchers and practitioners alike. First, the geostatistical model captures spatial autocorrelation through its error structure, leading to a proper estimation of coefficients, including their estimates and standard errors. We find that an ordinary hedonic estimation of real estate prices with respect to explanatory variables affected by the surrounding environment, tends to underestimate the standard errors of such coefficients because it overlooks spatial autocorrelation. This may lead to an erroneous assertion of the statistical significance of some estimated coefficients in the OLS estimation or in any estimation model that does not control for spatial autocorrelation.

Second, a method of spatial complementation known as Bayesian kriging can predict the probability distribution of real estate prices in a certain out-of-sample location derived from the estimated model. Thus, it provides a useful perspective in terms of spatial correlation at specific points if we can assume geographical continuity among the points of interest and the points in the data. As this study shows, the model predicts the posterior density of real estate prices for a desired location both inside and outside the geographical boundaries of the estimated model. The estimated posterior densities provide point estimates, spatial effect surface plots, and out-of-sample estimations; these are used in real estate research and practical studies. Third, we have found that the geostatistical model can substantially improve in-sample prediction performance, enhancing the performance of the out-of-sample prediction method, which derives from the Bayesian Kriging technique, with moderately higher R² and smaller Mean Squared Errors (MSEs). Finally, because we have estimated the scale parameter for a spatial distance in the model, the posterior probability density for estimated scale parameters translates directly into the spatial decay rate, indicating the correlation between real estate prices and various spatial distances in the dataset.

This paper is structured as follows: Sect. 2 formulates the spatiotemporal geostatistical model employed in this study and introduces a scale parameter, which enables the estimation of a real estate price analysis. Section 3 describes the data and the regional context needed to understand the nature of the data. Section 4 estimates the results. While certain characteristics of the estimated model are introduced and analyzed in relation to a specific dataset, the model can be applied to many settings in other real estate markets. Such extensions and limitations are discussed in the later and concluding sections.

2 The geostatistical estimation model

Geology and other earth science fields deal with the estimation of unobserved variables of interest under spatial autocorrelation, incorporating geographical information into the statistical model via spatial effects to represent potential spatial heterogeneity, rather than adjusting the correlation in error terms. Following Gelfand et al. (2003) and Banerjee et al. (2014), the present study has employed the following regression model with spatial effects, referred to here as the “geostatistical model:”

$$y = X\beta + \omega + \varepsilon ,{\text{where}}\;\varepsilon \sim N\left( {0, \tau^{2} I_{n} } \right),\omega \sim N\left( {0, \sigma^{2} H\left( {\phi ,\delta } \right)} \right)$$

(1)

where $y={\left({y}_{1},\dots ,{y}_{n}\right)}^{T}$ is the n-dimensional vector of real estate price; X denotes the $n\times p$ matrix of the explanatory variables;, ${I}_{n}$ is the $n\times n$ identity matrix; $\varepsilon$ and $\omega$ are mutually independent error terms and spatiotemporal effects, respectively; and $H\left(\bullet \right)$ is the spatiotemporal correlation matrix in which the $\left(i, j\right)$-element includes a spatial correlation of ${\rho }_{S}({s}_{i}-{s}_{j};\phi )$ as well as temporal correlation${\rho }_{T}({t}_{i}-{t}_{j};\delta )$. Here, ${\rho }_{S}$ is a valid isotropic correlation function indexed by an unknown range parameter$\phi$, and ${s}_{1},\dots {s}_{n}$ are typically two-dimensional vectors of longitude and latitude. Typical correlation function options include Gaussian correlation ${\rho }_{SGij}$ and exponential correlation ${\rho }_{SEij}$ as follows:

$$\rho_{SGij} \left( {s_{i} - s_{j} ;\phi } \right) = \exp \left( { -\frac{||s_{i} - {s_{j} |\left. \right|^{2} }}{{\phi^{2} }}} \right),\rho_{SEij} \left( {s_{i} - s_{j} ;\phi } \right) = {\text{exp}}\left( { - \frac{{\left| {\left| {s_{i} - s_{j} } \right|} \right|}}{\phi }} \right)$$

(2)

To accommodate typical real estate data, which contain temporal information related to transaction registration times and spatial information on the transaction locations, we introduce an additional unknown or estimated time range parameter $\delta$, which signifies a certain transaction ${t}_{i}$ and ${t}_{j}$, which also has the Gaussian correlation ${\rho }_{TGij}$ and exponential correlation ${\rho }_{TEij}$

$${\rho }_{TGij}\left({t}_{i}-{t}_{j};\delta \right)=\mathrm{exp}\left(-\frac{{|{t}_{i}-{t}_{j}|}^{2}}{{\delta }^{2}}\right),{\rho }_{TEij}\left({t}_{i}-{t}_{j};\delta \right)=\mathrm{exp}\left(-|{t}_{i}-\frac{{t}_{j}|}{\delta }\right)$$

(3)

We assume the $\left(i, j\right)$-element of $H\left(\bullet \right)$ as the product of ${\rho }_{SGij}$ or ${\rho }_{SEij}$ and ${\rho }_{TGij}$ or ${\rho }_{TEij}$, namely, the correlation between spatial effects at $({s}_{i},{t}_{i})$ and $({s}_{j},{t}_{j})$ is described as

$$\mathrm{exp}\left(-\frac{{||{s}_{i}-s}_{j}|{\left.\right|}^{k}}{{\phi }^{k}}-\frac{{|{t}_{i}-{t}_{j}|}^{m}}{{\delta }^{m}}\right), k,m\in \left\{\mathrm{1,2}\right\}.$$

(4)

The two range parameters $\phi$ and $\delta$ can be interpreted as weights for geographical and time difference, respectively. As the above form shows, the degree of correlation decreases when the temporal distance increases, even for transactions that take place in the same space. In addition, the degree of correlation decreases if the spatial distance increases, even for transactions that take place at the same time. This correlation structure is known as a “separable” correlation; more complicated nonseparable spatiotemporal models are also available (e.g., Cressie and Huang 1999). As results based on such advanced models are not always easy to interpret, here we use the simple separable form of spatiotemporal correlation, and four versions of the combination above can be used. They are: i) exponential ${\rho }_{SEij}$ and exponential ${\rho }_{TEij}$, ii) exponential ${\rho }_{SEij}$ and Gaussian ${\rho }_{TGij}$, iii) Gaussian ${\rho }_{SGij}$ and exponential ${\rho }_{TEij}$, and iv) Gaussian ${\rho }_{SGij}$ and Gaussian ${\rho }_{TGij}$ When we execute the MCMC and use our own datasets to estimate Eq. (1), the Gaussian correlation based specification ${\rho }_{SG}$ for geographical distances (specifications iii) and iv)) exhibits unstable performance because it is difficult to estimate and invert the near singular matrix $H\left(\phi ,\delta \right)$. Among the two specifications that use the exponential correlation ${\rho }_{SE}$ for geographical distances, the one that uses the exponential time correlation ${\rho }_{TE}$ performs better than the other in terms of the MCMC chain convergence for parameter $\delta$, based on the Geweke’s Chi-square test, as specified by LeSage (1999). We therefore report the estimation results using the exponential correlation ${\rho }_{SE}$ for exponential distance and the Gaussian correlation ${\rho }_{TG}$ for time difference (specification i)) to ensure the stability of the MCMC algorithm.

In model (1), $\omega$ is a vector of spatial and time effects, and the marginal distribution of $y$ is$N(X\beta , {\tau }^{2}{I}_{n}+{\sigma }^{2}H\left(\phi ,\delta \right))$, a spatiotemporal correlation is introduced in $y.$ The distinction between the spatial econometric literature and the geostatistical literature stems from the distance matrix,$H$,$\left(\phi ,\delta \right)$, which may be a counterpart of the spatial weight matrix, often referred to as the W matrix in the spatial econometric model. To estimate model (1), Bayesian techniques via MCMC have been widely adopted (e.g., Banerjee et al. 2014). After introducing prior distributions for the unknown model parameters$(\beta ,{\sigma }^{2},{\tau }^{2},\phi , \delta )$, the posterior distribution of the unknown parameters is given as:

$$\pi \left(\beta ,{\sigma }^{2},{\tau }^{2},\phi , \delta | y\right)\propto \pi \left(\beta ,{\sigma }^{2},{\tau }^{2},\phi , \delta \right) p(y;X\beta ,\Sigma )$$

(5)

where $\pi$ $\left(\beta ,{\sigma }^{2},{\tau }^{2},\phi , \delta \right)$ are the prior distributions; $p(y;X\beta ,\Sigma )$ are the probability density functions of $N(X\beta ,\Sigma )$, and $\Sigma ={\sigma }^{2}H\left(\phi \right)+{\tau }^{2}{I}_{n}$. Throughout the MCMC estimation in this study, the prior distribution for $\beta$ is set as N (${\beta }_{0}$, ${V}_{\beta }$), where ${\beta }_{0}=0, {V}_{\beta }$= 1,000, and that for the error structures, which are $\sigma ,\tau ,\phi$ and $\delta$, employs the inverse gamma prior (IG(1,1)).⁴

The MCMC algorithm that generates posterior samples of $\left(\beta ,{\sigma }^{2},{\tau }^{2},\phi , \delta \right)$ consists of iteratively generating random samples from the complete conditional distributions of $\beta$ and (${\sigma }^{2},{\tau }^{2},\phi , \delta$). The complete conditional of $\beta$ is given by:

$$\beta | {\sigma }^{2}, {\tau }^{2}, \phi ,\delta , y\sim N \left({D}_{\beta }{d}_{\beta }, {D}_{\beta }\right)$$

(6)

where ${D}_{\beta }={(X{\Sigma }^{-1}{X}^{\prime}+{V}_{\beta }^{-1})}^{-1}$,${d}_{\beta }=X{\Sigma }^{-1}y+{V}_{\beta }^{-1}{\beta }_{0}$

However, the logarithm of the complete conditional distribution of (${\sigma }^{2},{\tau }^{2},\phi , \delta$) is:

$$\mathrm{Log}\left(\pi \left({\sigma }^{2},{\tau }^{2},\phi , \delta | \beta ,y\right)\right)\propto \mathrm{log}\pi \left({\sigma }^{2},{\tau }^{2},\phi , \delta \right)-\frac{1}{2}\mathrm{log}\left(\left|\Sigma \right|\right)-\frac{1}{2} {\left(y-X\beta \right)}^{T}{\Sigma }^{-1}(y-X\beta )$$

(7)

The log of the determinant in Eq. (7) is calculated using the Cholesky decomposition, adding the logarithm of the diagonal element of the matrix to speed up the calculation. We then execute the random walk Metropolis–Hastings (MH) algorithm to generate a random sample from the distribution above. Using posterior samples of the model parameters, we generate posterior samples of the spatial error term $\omega$ from the following conditional distribution⁵:

$$\omega | \beta , {\sigma }^{2},{\tau }^{2},\phi , \delta , y\sim N \left({D}_{\omega }{d}_{\omega }, {D}_{\omega }\right)$$

(8)

where ${D}_{\omega }=({{\sigma }^{-2}H\left(\phi ,\delta \right)}^{-1}+{\uptau }^{-2}{I}_{n}{)}^{-1}$,${d}_{\omega }={\tau }^{-2}(y-X\beta )$

In a later section, we show that spatiotemporal information from the posterior samples of $\omega$ substantially improves in-sample predictions and moderately improves out-of-sample predictions.

While this use of the geostatistical model to estimate real estate prices is relatively straightforward, researchers may encounter a situation in which the MH algorithm above does not perform well because $\left|\Sigma \right|$ in Eq. (7) takes an extremely small (close to zero) or large value when the sample size is large. When the determinant is evaluated as infinity or zero by the MH algorithm, using a computer, it is impossible to judge the acceptance or rejection of proposal densities. We have overcome this problem by including a scale tuning parameter in the MH algorithm when estimating the proposal and current density of Eq. (8), as shown in the Appendix.⁶

3 Data

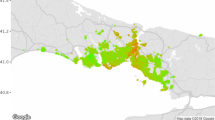
The present study uses real estate data obtained in Yokosuka City, Japan, 50 km south of central Tokyo. The city has various different housing areas within its compact boundary, which is diamond shaped and approximately 7.1 km from east to west and 6.5 km from north to south in our transaction data (Fig. 1a). In this suburban city, transaction samples are less dense than those taken in a major city center. To conduct a practical and useful analysis, we should consider a method of spatial complementation for out-of-sample predictions. As it is impossible to obtain sufficient samples that are spatially close, we must also refer to samples spanning several years from the transaction time.

Fig. 1

Location of hillside and promotion areas and their district-level information

The Tokyo metropolitan area has a monocentric city structure along commuter railways and a high homeownership rate (Kubo 2020). Many people commute to central Tokyo by train, traveling to the station on foot or taking buses that connect the station with suburban residential areas. The population of Yokosuka City is around 0.4 million; it has continued to decline from its peak in 1990, known as the “bubble period,” when real estate prices in Japan soared rapidly. At that time, this city faced acute urbanization, even on one difficult-to-access hillside, where direct car access to residential properties was limited or impossible. While the northeastern side of the city faces the coastline, Yokosuka is rather mountainous, with limited flat areas suitable for residential development. After the bubble period, the city experienced population loss and the number of vacant homes increased, particularly on the inaccessible hillside. As houses have become increasingly affordable, due to declining real estate prices, the demand for suburban housing has shifted to more convenient parts of the city. Furthermore, Yokosuka City has a military port and accumulated heavy industries. Factory closures have significantly accelerated the population decline. On the western edge of the city, there is a newly formed upscale residential complex, with some public facilities and a research institute. Some residential development has continued in neighborhoods that offer a sufficiently convenient commute to Tokyo or another larger city.

Thus, Yokosuka City has various residential areas, including distressed areas and a more upscale single-family housing complex within the geographically compact area; the city boundary and geographic characteristics are shown in Fig. 1a. In terms of the district information used in our estimation, the blue districts in Fig. 1b represent the hillside, which is surrounded by small mountains and contains significant numbers of long-term vacant houses and lots. The red districts in Fig. 1b represent the so-called “promotion area,” where the city financially supports the sale and purchase of existing houses to ensure an inflow of younger generation residents. Specifically, families with children can receive a maximum subsidy of 0.5 million JPY when they purchase an existing house, listed with the property bank. The promotion area was selected because it provides a suitable residential environment for raising a family: locations with low rise buildings, accessible by automobiles, and with easy access to train stations and/or bus stops. Compared to the hillside, a typical promotion area is composed of divided and orderly districts, with a low density of long-term vacant houses.

This study has employed property-level transaction data on detached houses, provided by the Real Estate Information Network System (REINS), a database for real estate agents, which shares property information. Registration is required by law for some forms of dedicated intermediary transactions, carried out by real estate agents. We use data registered by real estate agents or companies after the transaction through REINS is completed. While the registration of prices and other attributes is not necessarily mandated by laws after a transaction, the government and the REINS network encourage this; the data are thought to cover a sufficient proportion of transactions in this region.⁷

The present analysis uses data on newly built and existing single-family houses, purchased and sold between 2016 and 2019, for a total sample size of 1,136 observations. Table 1 shows the summary statistics for the entire sample, which include prices and property-specific characteristics, such as the age of each transacted building and its building and floor areas. The data have been classified using access to the closest station, bus usage, and daily passenger numbers at the closest stations as property-level spatial variables. To reflect development history and each property location’s susceptibility to natural disasters, we include data detailing the construction period of developments in densely inhabited districts (DID) for each decade from the 1960s through the 2010s. The public data include risk areas for sediment related disasters and 3 m deep inundations, caused by tsunamis of a certain level, as property-level spatial dummy variables. The local characteristics discussed in this section, include both hillside and promotion areas. The ratio of residents who have lived in the development for twenty years or more is included as a district-level dummy variable to characterize the age of the development. To convert the longitude and latitude data to geographical distance, this study uses distances calculated via the GRS80 ellipsoid from the website of the Geospatial Information Authority of Japan. Distance related to longitude and latitude was measured by 0.1 points at the center of the data sample. We then converted 0.1 points of longitude to 9,100.741 m and 0.1 points of latitude to 11,094.52 m.⁸

Table 1 Descriptive statistics

4 Estimation result

4.1 Estimation of coefficients for explanatory variables.

In comparing the OLS and geostatistical models, Table 2 shows the results of estimating the transaction price of single-family housing in Yokosuka City as an explanatory variable, using the data described in the previous section.

Table 2 Comparison of estimation and in-sample prediction of the OLS and the geostatistical model. (Data Year: 2016–2019)

In terms of the estimates of coefficients for the explanatory variables, the posterior standard errors of the coefficients for the geostatistical model are greater than those of the OLS estimation for the property-level spatial variable, which includes district-level variables and the time it takes to walk to the railway station. This tendency toward larger standard errors using OLS for explanatory variables with spatial effects, thought to be spatially correlated with each other, reflects the likelihood of encountering underestimated standard errors for the hedonic estimated coefficients of such variables when spatial autocorrelation is not incorporated. In regard to property-specific explanatory variables, such as building age, floor size, and land area, such underestimations have not been observed. In addition, the standard errors associated with the geostatistical model tend to be smaller than those in OLS.

At the same time, we observe the largely robust nature of estimates, which are the posterior means in the geostatistical model, depending on the estimation model and the inclusion of various explanatory variables. As shown by Lee (2002), OLS estimates can be consistent even when spatial autocorrelation exists.⁹ Thus, as standard errors for coefficients with spatial effects can be underestimated, researchers should be cautious in interpreting the statistical significance of such explanatory variables, taking steps to avoid causal judgment of the effect of explanatory variables by considering the existence of spatial autocorrelation. For example, while one might expect the presence of a tsunami hazard area to bring down house prices, this assumption contradicts the seemingly positive premium on prices in such areas, based on the OLS estimation result for specifications (2) and (4) in Table 2. These coefficients for the geostatistical model, although still positive, are less than their standard errors for the geostatistical model. We can see that these explanatory variables have a statistically insignificant effect on real estate price when estimations are made using the geostatistical model. Among various area specific explanatory variables, the presence of a sediment disaster risk has a consistently negative impact on real estate prices, even when spatial autocorrelation is controlled for using the geostatistical model. In addition, the data confirm the positive effect on real estate prices of mitigating hazards in such areas. From a regional policy perspective, there is a case for policy interventions to alleviate or mitigate landslides in this city. Such a policy could be introduced by increasing property tax revenue and regional revitalization.

We should note that we can employ spatial econometric models, such as the spatial lag of X (SLX) model and the spatial Durbin error model (SDEM), to correctly estimate the coefficients when considering spatial effects on real estate prices. In relation to our model, SLX and SDEM have been estimated, with the results compared in Table 4. They show the similarity between spatial econometric models and the geostatistical model for the coefficients of development age, disaster risk, and other district-level variables, which are captured by the specification, considering spatial effects. These variables tend to lose their explanatory power, which has a “significant” effect, according to OLS estimates. Moreover, the findings show a moderately improved fit to the observed data, in terms of the coefficient of determination (R²), when the spatial error specification in SLX and SDEM is included. The advantage of the SLX and SDEM models is evident for studies that aim to infer the direction and significance of estimated coefficients, in relation to the computational intensity of a geostatistical model. At the same time, there is a certain limitation in applying these models to our analysis, which explores the continuous spatiotemporal nature of the correlation.

4.2 Bayesian kriging and out-of-sample prediction, based on geostatistical models

The geostatistical model is effective in providing a statistically sound model by determining separately the effects of the explanatory variables and spatiotemporal effect. This model is particularly useful in situations where the predictive rationale has been questioned, including real estate appraisals. It is insufficient to simply question its price prediction performance. The geostatistical model estimated using Bayesian MCMC provides various forms of posterior densities, conditioned on the data and relatively non-informative prior distributions. One useful output of the estimation is the conditional distribution of the unobserved spatial effect (${\omega }_{{k}_{0}}$) at a certain out-of-sample point (${k}_{0})$ on $\omega$, which is defined by the following equation:

$${\omega }_{{k}_{0}} | \omega , \beta , {\sigma }^{2},{\tau }^{2},\phi , \delta , y \sim N \left({z}_{k0}{\left(\phi ,\delta \right)}^{T}{H\left(\phi ,\delta \right)}^{-1}\omega , {{\sigma }^{2}-{\sigma }^{2}{z}_{{k}_{0}}{(\phi ,\delta )}^{T}H\left(\phi ,\delta \right)}^{-1}{z}_{{k}_{0}}\left(\phi ,\delta \right)\right)$$

(9)

where Eq. (9) assumes multivariate normality between ${\omega }_{{k}_{0}}$ and ${\omega }_{{k}_{0}}$ and ${\sigma }^{2}{z}_{{k}_{0}}$ is its spatiotemporal covariance vector. Thus, the posterior mean value of ${\omega }_{{k}_{0}}$ is derived, as in Banerjee et al. (2014):

$${E[\omega }_{{k}_{0}} \left| \omega , \beta , {\sigma }^{2},{\tau }^{2},\phi , \delta , y\right]= {\sigma }^{2}{Z}_{k}\left(\phi ,\delta \right){\Sigma }^{-1}(y-X\beta )$$

(10)

While we can retrieve the Kriged value of spatial effect (${\omega }_{{k}_{0}}$) at any spatial or temporal data point, we fix the temporal data toward the period, which is the end of 2019, and build an argument using the spatial correlation among geographical spaces. Using model specification (4) in Table 2, we obtain the posterior distribution of ${\omega }_{{k}_{0}}$ for specific locations using the point’s longitude and latitude information, which marks particular locations in (a) the hillside area, (b) the intermediate residential neighborhood, and (c) the upscale neighborhood at the southwest edge of our sample, shown in Fig. 2.

Fig. 2

Posterior distribution of ${\omega }_{{k}_{0}}$ in different locations. (Specification of Table 2 (4))

This figure shows the effect of spatial information, which cannot be explained by explanatory variables. It not only shows the mean value of the predicted posterior densities in each location, but also the probabilistic distribution of posterior densities in a statistically consistent way. In other words, properties with the same characteristics (i.e., building age, building size, land area, transportation, and other attributes) are evaluated in each transaction, giving a house in the upscale residential complex a premium of around 17.8 million JPY and a house on the hillside a discount worth around 8.0 million JPY, according to the mode values of the posterior distribution shown in Fig. 2. These premiums and discounts derived from our data exhibit a fairly wide distribution. The shape of the distribution varies among data points. Seemingly, the narrower the posterior distribution of ${\omega }_{{k}_{0}}$ is, the more support is obtained from the correlation among surrounding observed data. We can derive such posterior densities in any location in or near the sample area. The distribution and its mean values can be useful for any individual or professional who wants to infer the real estate price for a particular property, using coherent information on real estate transaction data. These distributions can be easily combined with real estate prices; such combined probabilistic distributions are useful for mass evaluations, which are often conducted by financial institutions that manage multiple properties in a particular region.¹⁰

The other metric that may help to identify the spatial effect is the surface plot derived from the Kriged values for grid points, using the posterior means of the error structure defined in Eq. (10). We can derive the posterior mean surface plot, as shown in Figs. 3a and b; these surface plots show a premium or discount that cannot be explained by property- or area-specific variables. Such variables include walking routes and bus access, as well as building age and floor and land area. We can therefore derive a numerical value from the premium or discount for a property at a certain location, which indicates positive or negative neighborhood quality, a characteristic that is sometimes referred to by real estate professionals in Japan as “land class.”

Fig. 3

a Posterior mean values of ${\omega }_{{k}_{0}}$ for Geographical grid points. (Specification of Table 2 (4): data points are expressed as red circle dots) b 3D Surface plot of the posterior means values of ${\omega }_{{k}_{0}}$ for grid points (Specification of Table 2 (4))

Using the posterior mean value of ${\omega }_{{k}_{0}}$ defined in Eq. (10), we can also conduct out-of-sample predictions, using the estimated coefficients and error structure variables, when we know certain characteristics about a property. Specifically, we estimate the model without data in the most recent year. We then make a counterfactual forecast or out-of-sample prediction for the real estate price in the latest year, assuming that we have correct information on the location and attributes of the transacted house.¹¹ As Table 3 shows, the benefit of the improved in-sample predictive performance of the geostatistical model is reflected in the out-of-sample predictions or forecasts. Under specifications (1) and (2), the geostatistical model provides moderately better predictions with higher R² and smaller MSEs.

Table 3 Comparison of out-of-sample prediction of the OLS and the geostatistical model. (In-Sample Data Year: 2016–2018, Out-Of-Sample Data Year: 2019)

When OLS or another non-spatial estimation method is used, one strategy for avoiding erroneous assertions about the effect of explanatory variables on spatially correlated dependent variables is to include district-specific variables, such as specification (5) in Table 2 and specification (3) in Table 3. The present study employs district dummy variables, including one for the finest unit in the town segment, totaling 250 districts, following the spatial heterogeneity in detail. However, we would argue that this use of dummy variables should be limited to the analysis of coefficients and is not appropriate for a prediction analysis, while the prediction of the real estate price is often of interest to academic researchers or practitioners.¹²

According to the results shown in Table 3, the out-of-sample prediction for the estimation model with district dummy variables is less accurate than the predictions of models without regional dummy variables in both the OLS and geostatistical models. This may reflect the over fitting of the estimation model with the district dummy variable, since there are few samples for each district and the biases associated with each transaction may lead to erroneous estimates of the district-specific effect. As there are large standard errors for the district dummy variable in the geostatistical model, researchers should avoid making predictions based on the estimated coefficients of those dummy variables. However, geostatistical models consistently perform better in estimating out-of-sample real estate prices. In other words, the bias between the posterior mean and the actual value of a real estate price has a larger R² and smaller MSEs in the geostatistical model, even with fewer explanatory variables in the dataset. The improved MSEs in the out-of-sample prediction come to 0.049 out of the 0.375 from OLS, a smaller result than one might expect, given the drastic improvement in the in-sample prediction. This figure could be improved through the use of better property-specific data, such as the number of rooms or other specific property characteristics.

4.3 Spatial decay rate for correlation (variogram)

Having estimated the error structure variable that accounts for spatial autocorrelation, which is $\phi$ in our specification, we can derive a spatial decay rate to measure how real estate prices are spatially and temporally correlated. Specifically, the spatial decay rate (${D}_{S}$) was derived from the following equation:

$${D}_{S}=\mathrm{exp}(-d/\phi )$$

(11)

where $d$ denotes the geographical distance (km).¹³

Figure 4 shows the curve of the posterior mean values, which are shown as solid lines. The 10% and 90% tile values obtained from their posterior densities are shown as dashed lines for geographical distances and time differences. According to the results, the spatial correlation of real estate prices diminishes to 0.5 at around 200 m distant data points, according to the median value of the decay rate. When we infer the real estate price of a specific property with past surrounding data points, we need data within a radius of approximately 600 m, where the price correlation dissipates at a distance of approximately 0.1. This decay rate should be especially useful for appraisers, who regularly collect transaction data for “surrounding” areas for comparison purposes. While the results of our study have been obtained in a limited geographic space for a specific type of property—the transaction price for a single-family property in Yokosuka City, Japan between 2016 and 2019—we expect to obtain standardized figures with certain levels of variation by accumulating similar analyses with different datasets.

Fig. 4

Spatial decay rate (Specification of Table 2 (4))

4.4 Limitations and possible extensions of future analyses

This study has analyzed the applicability and usefulness of the geostatistical model for real estate price analyses. The findings show that various numerical values ​​can be obtained with statistical consistency in relation to coefficient estimation, prediction implementation, and the measurement of spatiotemporal correlations. Currently, the main limitation of this analytical method is its calculation intensity. The data used for this study include 1,136 data points, suggesting that the geographical matrix required for this analysis is 1,136 times 1,136 square matrices. As a Bayesian MCMC estimation requires a significant amount of time to implement an estimation with larger numbers, such analyses will be difficult or infeasible using an ordinary personal computer if the sample size becomes significantly larger than our datasets.

At present, the analysis described in this paper can be used to treat a relatively small amount of data, up to approximately 1,000 data points. The advantage of the present analysis lies in its ability to estimate the parameters of the error structure variable. We can estimate the necessary parameters with a certain precision, using a relatively limited amount of data. As computational capabilities progress rapidly, this issue should be overcome by technological advances in the future. In other words, researchers should implement “big data” analyses using millions of data points, and this sample size problem should be addressed as soon as possible. Although it is beyond the scope of the present study, an estimation can be carried out with relatively limited spatial correlation structures, using an approximated version of the large-scale Gaussian process, as in the predictive Gaussian process (Banerjee et al. 2008 and Latimer et al. 2009) and the nearest-neighbor Gaussian process (Datta et al. 2016). This will be possible when we can use a large dataset with spatial information to estimate real estate prices.

Although it is important to extend the analysis in this direction, it is also essential to conduct multiple analyses in different locations, using different types of properties. Since our analyses have uncovered some parameters that may have universal implications for real estate price analyses, such as the spatial decay rate, a comparison of different analyses can help researchers and practitioners ascertain the nature and formation of real estate prices, which hold a significant portion of our assets and affect individual lives, as well as the economy as a whole.

5 Conclusion

This study has developed a geostatistical model that uses explanatory variables and spatially autocorrelated error structures to explain real estate prices. The estimation has been carried out via the Bayesian MCMC method and MH within the Gibbs procedure. This type of estimation often suffers from computational difficulties, especially when calculating the determinant of the variance–covariance matrix, which often takes an extremely large or small value. We propose a scale tuning parameter to coordinate the determinant value within a computable value range and make it possible to estimate the spatiotemporal geostatistical model, using data from real estate transactions.

The results of this study demonstrate several findings of applying a model that considers a spatial autocorrelation that can be applied to real estate across a whole city, using transaction data from detached houses in Yokosuka City, Japan. First, the coefficients of explanatory variables with a spatial effect may underestimate the standard errors under OLS for some explanatory variables with spatial heterogeneities. Second, using the estimated geostatistical model, we have checked the predictive performance of the in-sample prediction and obtained a substantially improved margin of error for the predicted and actual values. The out-of-sample prediction performance has been examined and found to achieve moderately improved MSEs for the predicted values, in comparison to the actual values. Thus, the estimated model can improve the accuracy of real estate price estimates in the future and at points where there are no regional data by extracting the spatial effect on real estate prices. It can also derive statistically appropriate probability distributions. Third, from the spatial correlation perspective, our estimated model shows that the influence of real estate prices affects a relatively small range of properties, less than 600 m away. Such figures can be an important indicator for appraisers and real estate agents, who collect transaction cases in the surrounding area and judge their importance in the data. It is important in real estate analysis to generalize these boundaries through various studies based on different property types and geographical areas.

Although this analysis is limited in relation to geography and real estate types, the overall structure of the model should be universally applied to all hedonic real estate price analyses. Geographical space has a significant impact on real estate prices and this fact is unlikely to change, even with modern technology. Hedonic analyses carried out using a geostatistical model that allows for the structural analysis of autocorrelated space and time are expected to advance significantly in the near future.

Appendix. MCMC estimation and introducing a scale tuning parameter to the MH step

See Tables

Table 4 Comparison of estimation results with the SLX and the SDEM. (Specification (4) of Table 2)

4,

Table 5 Convergence check of the algorithm

5

To estimate with the MH step in the Bayesian MCMC estimation in this study, it is necessary to calculate the determinant values to obtain and compare the value of the proposal density and current density, as in Eq. (7).

Since the value of $\left|\Sigma \right|$ often takes too large or too small a value to compute, especially for a large amount of data, the calculation is scale sensitive, and we use the following “scale tuning parameter” (${s}_{tu}$), which is a scalar within some reasonable bounds in Eq. (7). More specifically, we can rewrite the Eq. (7) as follows by introducing ${s}_{tu}$:

$$\mathrm{log}(p\left(Y;\beta , \sigma ,\phi ,\tau \right))\propto \frac{1}{2}\mathrm{log}\left(|\Sigma \cdot {{s}_{tu}}^{2}|\right)-\frac{1}{2}{\left(\left(y-X\beta \right)\cdot {s}_{tu}\right)}^{T}{(\Sigma \cdot {{s}_{tu}}^{2})}^{-1}((y-X\beta )\cdot {s}_{tu})$$

(7A)

It is clear that a scaler ${s}_{tu}$ should be analytically dropped when comparing the log of the proposal and current posterior target densities if we use the same ${s}_{tu}$ for both the proposal and current densities. This analytically meaningless parameter is necessary for us to conduct the MH step by keeping the value of the determinant within the range of numerical values ​​that can be calculated by ordinary calculation software, and we update ${s}_{tu}$ in each iteration so that $|\Sigma \cdot {{s}_{tu}}^{2}|$ takes a value within a certain bound. In our analysis, we set the update procedure as follows.

• i. If $|\Sigma \cdot {{s}_{tu}}^{2}|$ is larger than 100, ${s}_{tu}$ is tuned such that $|\Sigma \cdot {{s}_{tu}}^{2}|$ equals 100.

• ii. If $|\Sigma \cdot {{s}_{tu}}^{2}|$ is smaller than 0.01, ${s}_{tu}$ is tuned so that $|\Sigma \cdot {{s}_{tu}}^{2}|$ equals to 0.01.

• iii. If (i) or (ii) are not applicable, ${s}_{tu}$ is kept at the same value as in the previous iteration.

The chain value of ${s}_{tu}$ for estimating specification (4) in Table 2 at each iteration is shown in Fig. 

Fig. 5

The chain value of ${s}_{tu}$ for the geostatistical model estimation

5 and the chain values of the coefficient and error structure parameters are shown in Fig. 

Fig. 6

The chain value for the coefficients and the error terms in estimating geostatistical model (Specification (4) of Table 2)

6.