A TMB Approach to Study Spatial Variation in Weather-Generated Claims in Insurance

Abstract

In this paper, we use TMB to study spatial variation in weather-generated claims in insurance. Our motivation is twofold. By comparing with INLA, we first find that TMB is a robust and efficient approach to deal with spatial variation of covariates and the dependent variable in a case with sparse data. Second, we demonstrate how examining the spatial pattern of random effects may offer auspicious suggestions for model extensions, represented by added covariates accounting for relevant spatial characteristics. Both the approach and the results represent useful input in reaching an efficient spatial diversification of premium rates in non-life insurance.

1 Introduction and Motivation

In this paper, we use TMB (Template Model Builder) [1] and [2] to estimate model formulations accounting for the possible presence of spatial dependence in data. Spatial dependence means that there is a systematic spatial pattern in the phenomenon being studied, see e.g. [3]. The impact of variations in specific covariates on the response variable may differ systematically across locations, and this may not be adequately captured by variation in the selected covariates. Ignoring such spatial patterns in the model formulation may lead to seriously biased estimates of how variations in covariates affect the response variable, see for instance [4].

Data are often defined for a specific subdivision of the geography into administrative units. In such cases, one option is that each unit, zone, is represented by separate fixed effects in the model formulation. This may lead to a model formulation that fits data reasonable well, but such an approach may prove to have some shortcomings for example when it comes to providing reliable out-of-sample predictions. This could for instance be to predict the response to an unfortunate incident in a zone outside the region that was used for estimation. Significant location-specific fixed effects may reflect the impact of omitted information on spatial characteristics. Hence, such effects can prove to be useful in attempts to improve the model formulation, and to uncover general spatial patterns in the response to variations in risk factors.

The Gaussian conditional autoregressive model (CAR) represents one possible approach to account for systematic spatial dependencies in data, see e.g. [5]. A concise presentation of the intrinsic CAR model can be found in [6]. This model accounts for the possibility that neighbouring zones may respond similarly to variations in risk factors. Accounting for such spatial patterns may contribute to improved explanatory power, and in particular it potentially contributes to more precise predictions concerning the local impact of specific incidences. Based on a CAR-model, [7] find that accounting for spatial dependencies results in a significantly improved explanatory power, and more reliable estimates.

Accounting for spatial dependencies in general leads to a complex likelihood function, which results in a challenging optimization problem. One approach to overcome this problem is to employ Markov-Chain Monte Carlo (MCMC) simulations in estimating the model parameters. Recently, however, a few approaches have been introduced that enable us to do the estimation by maximizing a likelihood function, see for instance [8] for a presentation of the so-called SPDE-approach. Software packages like TMB (Template Model Builder) and INLA (the integrated nested Laplace approximation) use Matérn correlation parameters to impose a spatial dependence structure in the model formulation, see for example [8]. The specification of a likelihood function in general allows for a more flexible approach, both in terms of what information that can be utilized in the data, and in terms of estimated output on the relationship between variations in the covariates and the response variable.

In this paper, TMB is used to discuss spatial variation in weather-related property claims. However, our motivation is not solely methodological. Studying property claims due to extreme weather conditions is highly relevant in times of climate change. Insurance companies are aiming for an efficient pricing regime, introducing incentives that contribute to prevent or reduce future claims. This involves geographical variations in insurance premiums, reflecting the local variations in the likelihood of claims. In the perspective of reaching reliable estimates of the likelihood of claims, it is important to account for spatial dependencies in risk factors. Such dependencies may reflect local variations in weather conditions, but also in the response to unfortunate weather, represented for instance by the soil, the topography, local building regulations and construction technologies.

As a first step, we use exploratory approaches to demonstrate and test how weather-related claims vary systematically across the geography. We focus primarily on the frequencies of claims in different geographies, but we also have some information on the size of claims (the insurance payout). One observation in the descriptive part of the paper, is a tendency of more claims per insurance policy in relatively large urban areas than in more rural areas.

The literature offers some results on the relationship between weather conditions and insurance claims. According to [9], the insurance payouts due to water claims in Norway were increased by more than six times in the period from 1993 to 2003. They further distinguish between claims from instant rain, and claims from accumulated rainfall, measured by the total precipitation over the last five days and nights. They found a tendency that counties in western and southern Norway were slightly less sensitive to instant rain than the rest of the country, and suggest that this might reflect that the construction technology in coastal areas are better prepared for heavy rain [10] find that frequency plots “indicate that densely populated areas exhibit larger vulnerability than do municipalities in rural districts”. It is our ambition to enter in more detail into this observation.

Based on a very large dataset with more than 6.7 million observations from the period 2011–2018, [6] study model for insurance premium rating taking spatial effects into account. They do not study the impact of meteorological and hydrological defined covariates, but in general find that accounting for random effects when modeling water claims yields better model fit and that this is the best way of taking the geographical location into account. [6] use the R-package mgcv to estimate the parameters in random effects. mgcv is also compared to utilizing INLA, but they have not been considering TMB. In this paper, we present results from both TMB and INLA, as a basis for evaluating the robustness and efficiency of the TMB approach.

The size of premium rates in private insurance is based on the expected value principle, with an addition for overhead costs. The expected value principle is stating that the expected value of discounted payments from policyholders equals the total expected value of payouts from the insurance companies. In a spatial context, it is important to account for the possibility that both the occurrence of risk factors and the response to variation in risk factors may vary systematically across space. This represents the justification for geopricing; correct pure premium rates call for reliable predictions of expected payouts. One important problem is whether the premium rates should be differentiated across spatial units, like municipalities or counties, or according to a more continuously defined geography, corresponding to a more spatially smoothed pattern in the likelihood of claims. Approaches based on INLA or TMB allow for a continuous, coordinates-based specification of the geography. In this paper, however, all the observations are assigned to the corresponding municipality center; information on location is restricted to the coordinates of the municipality center. Hence, we have not spatially detailed enough information to discuss the possibility that claims may vary continuously within municipalities. However, an important ambition of this paper is to demonstrate how examining the spatial pattern of random effects contributes to an improved, extended, model formulation, which is in addition suggesting additional guidelines for spatially diversification of premium rates.

The data and descriptive statistics are presented in Section 2, before Section 3 provides a presentation of the basic modelling and conceptual framework. The estimation procedures are introduced and explained in Section 4. Estimation results are presented and discussed in Section 5, while Section 6 provides concluding remarks.

2 Data Source and Data Exploration

The data used in this paper is obtained from regular water claims inflicted to properties in the portfolio of a Norwegian insurance company. The stock data and registered water claims are given for policy holders at the time in the 429 Norwegian municipalities included in our data, before a process of merging municipalities and counties in later years. The stock data includes information on the number of policies, the insurance premiums, as well as claim frequencies and claim size by data. Meteorological and hydrological information are also given by date, provided for the insurance company by the Norwegian Meteorological Institute and the Norwegian Water Resource and Energy Directorate (NVE).

Table 1 Weather-related covariates to be included in our model formulation

Table 1 offers definitions of the weather-related covariates that are included in the data, and will be used in our model formulation. Notice that the information of the variables is in general available for the period 1961–2006, but stock data are only available in the period after 1996. In this paper, we utilize information for the period from 1999–2006. Drain represents a measure of the total draining away of water from the surface of an area, which is the precipitation minus evaporation. Snow (the snow water equivalent) is the amount of precipitation represented by an amount of water.

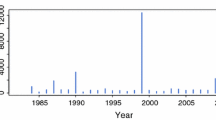
Both as a starting point for the formulation of interesting hypotheses and for the evaluation of estimation results, it may be useful to study temporal and spatial patterns in data. Figure 1 illustrates time series of some basic insurance-related measures for the period from 1999 through 2006.

Fig. 1

The development in the number of insurance policies, the sum insured and the insurance premium in the period from 1999 through 2006

It follows from Fig. 1b that the insurance sum paid to the clients increased substantially over the period under study. This does not solely reflect the increased number of insurance policies. Another reason is that Norway experienced a strong growth in housing prices in this period. The irregularities at the turn of each year in the graphs of Fig. 1, are due to a yearly indexation of construction costs.

Figure 2 provides an illustration of the development in the frequency of claims. It clearly appears from the figure that the claims do not take place in a regular pattern over time. As stated in the introduction, one ambition of this paper is to study how claim frequencies depend on meteorological and hydrological risk factors. Figure 2 reveals no specific time trend in the frequencies of claims but the number of claims was at the lowest in 2004. The figure further illustrates that trends may be more visually apparent in a figure where the chosen time scale is relatively aggregated.

Fig. 2

Number of claims in the period from 1999 through 2006 at three different aggregation levels

Both the risk factors and the number of water claims vary systematically over space. Figure 3 visualizes county-wise deviations from national averages in precipitation and snow melting. Notice that all the maps, and the corresponding text, apply to the situation prior to the process of merging counties in more recent years. The maps reveal expected patterns of heavy rain in the counties of Western Norway, while in particular Northern Norway has a lot of snow melting. The variance of these risk factors may also be relevant in explaining the frequency of water claims. County-wise estimates of this variance show a pattern very similar to the pattern of averages in Fig. 3

Fig. 3

County-wise variation in deviations from national averages in meteorological and hydrological risk factors. The average for the years 1999–2006, and the average for the different measuring points in the municipalities in each county

Figure 4 provides information on the county-wise variation in the number of water claims, and the average size of the claims. The number of claims is naturally closely related to the housing stock, which reflects the population size. It is for example reasonable that the most populous counties (Oslo, Akershus, Rogaland, and Hordaland) have the highest number of water claims. There is apparently no such relationship regarding the average size of the claims. The high value for Finnmark may reflect the dominance of a few abnormal observations.

Fig. 4

County-wise variation in the number of water claims and the average size of the water claims, over the period from 1999 through 2006

From an insurance perspective, it is more interesting to study the number of water claims per policy, since this measure does at least not to the same degree reflect the population size. Figure 5a visualizes the county-wise variation in the number of water claims per policy, measured by an average of the municipalities of the county, over the period 1999–2006. Once again, there is a pattern with high values for densely populated counties, while the sparsely populated Hedmark and Oppland stand out with a low number of water claims per policy. The number of policies per inhabitant reflects both the regional variation in the propensity to buy insurance, and regional variation in the market share of the insurance company being studied. As visualized in part b of Fig. 5, it is in particular Hedmark and Oppland that has a high number of policies per inhabitant. More densely populated areas in eastern and western Norway have a lower number of policies per inhabitant, while the two sparely populated counties furthest north have the lowest number of policies per inhabitant.

Fig. 5

County-wise variation in the number of water claims per policy, and the number of policies per inhabitant, measured over the period from 1999 through 2006

Figure 6 provides information on the spatial variation in risk factors at the municipality level. Comparing these maps to the maps in Fig. 3 serves as an example that heterogeneities potentially represent a potential source of bias in statistical analysis based on an aggregated representation of the geography into zones. In some counties, like Sogn og Fjordane in Western Norway, there are coastal municipalities with loads of rain, while some inner parts have considerably less precipitation than the national average. By using average values for counties extending over relatively large areas, we fail to account for the effect of local variations in risk factors. Hence, potentially important information are not accounted for, and the results can be expected to be sensitive to the level of spatial aggregation used in the analysis. This is called “the modifiable areal unit problem” (MAUP) in the literature. An early contribution to study such problems can be found in [11]. The chosen level of spatial aggregation for the analysis is in general a compromise between what is theoretically desirable and what data are available.

Fig. 6

Variation across municipalities in deviations from national average values of meteorological and hydrological risk factors. The average for the years 1999–2006

3 The Modelling Framework

This section provides a presentation of the modelling framework that is being used for the estimation and predictions. As mentioned in the introduction, approaches based on TMB are in general referring to a continuous, coordinate-based definition of the geography. Our data are point-based, assigned to the coordinates of the municipality centers. Ideally, TMB would come into its own with a more continuously defined, coordinate-based specification of the geography, but this paper demonstrates that such a geo-statistical approach still provides useful results and insight. The subdivision of Norway into $m=429$ municipalities allows for a reasonable estimation of spatial dependence, in terms of the Matern correlation function.

3.1 Generalized Linear Mixed Models (GLMM)

Generalized Linear Models (GLM) may be considered as a generalization of the classical linear regression [12]. The first element of a GLM is the dependent variable, which is assumed to follow a distribution from the exponential family. In non-life insurance, the Poisson distribution has typically been used to model claim frequency, while the claim size is often modelled by the gamma distribution. We focus on claim frequencies, while both [10] and [6] also discuss claim size.

The second element in the GLM specification is the linear predictor, $\eta _i$. This is a linear combination of the parameter vector, $\mathbf{\beta } = (\beta _0, \beta _1,...,\beta _p)^t$, and the vector of covariates, $x_{ij}$:

$$\begin{aligned} \eta _i=\beta _{0} + \sum _{j=1}^{p}{x_{ij} \beta _j}. \end{aligned}$$

(1)

where $i=1,...,n$ and n is the number of insurance policies.

Finally, the third element of a GLM is the link function, g, which is connecting the linear predictor to the expected value, $\mu$, of the dependent variable:

$$\begin{aligned} g(\mu _i) = \eta _i = \beta _{0} + \sum _{j=1}^{p}{x_{ij} \beta _j}. \end{aligned}$$

In this paper, the GLM-formulation is extended by adding a spatially referenced random effect, $u_{R[i]}$, to the linear predictor:

$$\begin{aligned} g(\mu _i) = \eta _i = \beta _{0} + \sum _{j=1}^{p}{x_{ij} \beta _j} + u_{R[i]}. \end{aligned}$$

$u_{R[i]}$ refers to the random effect assigned to each policy i belonging to municipality $R[i] \in {1,..., m}$. The extension of a GLM with random effects is called Generalized Linear Mixed Models (GLMM) ([13]).

3.2 Gaussian Markov Random Fields (GMRF)

As stated in [14], one of the main drawbacks working with Gaussian fields has been the so-called “big m problem” related to the computational cost of algebraic operations with dense covariance matrices. When the number of municipalities, m, increases, factorization of the dense covariance matrix of order mxm will require a general cost of $O(m^3)$ [8].

One way to overcome the “big m problem” is by formulating a Gaussian Markov Random Field (GMRF) representation of the Gaussian field. As described in [15], this is done by introducing a Markovian element, such that only neighbouring sites will have covariance values different from zero. Hence, the precision (inverse covariance) matrix becomes sparse, and the computational cost is reduced to $O(m^{3/2})$.

3.3 Matern Correlation Function

The Matern correlation function defines the statistical correlation between measurements made at two spatial points. In [15] the Matern correlation function is defined as follows:

$$\begin{aligned} \textrm{corr}_{Matern} \left( u_{R[i]}, u_{R[j]} \right) = \dfrac{2^{1-\nu }}{\Gamma (\nu )} \left( \kappa ||s_i - s_j|| \right) ^\nu K_\nu \left( \kappa ||s_i - s_j|| \right) . \end{aligned}$$

(2)

The term $||s_i - s_j||$ represents the Euclidean distance between these locations. $K_\nu$ is the Bessel function of the second kind. As described in [15], $\kappa >0$ is a scaling parameter that is linked to the range parameter r. According to Lindgren and Rue (2011), empirical evidence concludes that the relationship between r and $\kappa$ can be more precisely expressed by

$$\begin{aligned} r = \dfrac{\sqrt{8\nu }}{\kappa }, \end{aligned}$$

(3)

where r is the distance where the correlation has been reduced to 0.1.

The Matern covariance matrix of the spatial random effects, $\mathbf \Sigma$, has elements:

$$\begin{aligned} {\Sigma _{ij}} = \sigma _u^2 \cdot \textrm{corr}_{Matern} \left( u_{R[i]}, u_{R[j]} \right) \end{aligned}$$

(4)

where $\sigma _u^2$ represents the marginal variance of the random effects. Hence, the covariance of the spatial Gaussian fields can be defined by this Matern covariance function, and we are then left with estimating the two parameters $\sigma _u^2$ and $\kappa$. However, working with large sample sizes, $\mathbf{\Sigma }$ tends to be large, and this causes challenges in the estimation procedure. represented by the “big m problem” that was mentioned in Section 3.2. The SPDE approach is a method to estimate the parameters in a computationally effective way.

3.4 The Stochastic Partial Differential Equation (SPDE)

As explained in Section 3.2, the introduction of a Markovian element leads to a sparse precision matrix of the GMRF, with substantially reduced computational costs. The SPDE approach was introduced in [8], and may be used for estimation of the unknown parameters in the covariance function of a Gaussian field. A presentation of the approach is provided in Appendix A.

This approach calls for a specification of a spatial domain that is represented by irregular grids called a mesh, that is based on subdividing the geography into non-intersecting triangles. The mesh is explained in “Mesh”. The last step of solving the model, and estimating spatial dependence, is the finite element approach, see [8].

4 TMB Estimation Approach

In this paper, the estimation of the GMRF is performed using the SPDE-approach by the software package TMB. Like INLA, TMB uses the Laplace approximation Appendix B. While INLA can be considered as a Bayesian method, TMB represents a frequentist approach, using maximum likelihood estimator.

Consider, for simplicity, a model with only one hyperparameter ($\sigma$) and two regression parameters, $\beta _1$ and $\beta _2$:

$$\begin{aligned} y = \beta _1 X_1 + \beta _2 X_2, \end{aligned}$$

where y is the response variable. By using Bayes theorem and the theory of conditional probability, the following expression follows for the joint distribution:

$$\begin{aligned} f(\beta _1, \beta _2, \sigma |y) \propto f(y|\beta _1, \beta _2, \sigma )f(\beta _1, \beta _2 | \sigma )f(\sigma ), \end{aligned}$$

where $f(\beta _1, \beta _2 | \sigma )$ and $f(\sigma )$ are the priors. When working with GMRF’s, the $\beta$’s are assumed to be normally distributed and independent. The results of the Bayesian estimation approach are given by the posteriori marginal distribution, i.e. $f(\beta _1|y)$, $f(\beta _2|y)$ and $f(\sigma |y)$.

In general, the marginal distribution of a continuous random variable can be found by integrating the joint distribution over the desired variable. Hence, we need to factor out the parameters of interest. Working with complex models with latent variables (like GMRF’s) such integrals will become high-dimensional and solving them analytically might be impossible. Because of this, traditional estimation routines have involved Markov Chain Monte Carlo (MCMC) (see for example [16] and [4]). However, recent contributions involving Laplace Approximation have proven to be successful in approximating marginal distribution ([17] and [18]).

While MCMC represents a simulation based algorithm for Bayesian inference, the INLA-algorithm was introduced by [18], and represents a deterministic algorithm. INLA enables us to compute accurate approximations to the posterior marginals in shorter time than MCMC.

Skaug and Fournier [17] introduced a method of fitting hierarchical random effects models by Laplace approximation and automatic differentiation. This method is further implemented in TMB. As described in [1], TMB can be considered as an interface between R and C++. The user defines the likelihood for the data and the random effects in C++, while other operations are performed in R. Recently, a version of TMB, referred to as RTMB (https://github.com/kaskr/RTMB), allows all the code to be written in R. The fact that the user do not have to know C++ can be expected to expand the TMB user base. It is not clear to us if all TMB models can be implemented in RTMB, but the models used in the present paper can be formulated in RTMB. Although the analysis performed in this manuscript has been done using ordinary TMB we have chosen to present RTMB for the model, because the code is shorter and easier to understand. The code and a simulated dataset is described in Appendix C.

Thorson and Kristensen [19] discuss how the TMB software has been modified to reduce bias resulting from non-linear transformation of random effects, and adjust under-estimation of uncertainty. [2] provide a detailed description of the TMB technology and source code. They describe the approach as exceptionally flexible, computationally efficient, and applicable to a wide class of spatial models. [2] in addition provide an elaborate comparison between TMB and INLA, concluding that “the predictive fields from both methods are comparable in most situations even though TMB estimates for fixed and random effects may have slightly larger bias than R-INLA”. In general, however, [2] were “pleasantly surprised” to find near concurrence in spatial field estimation distributions in TMB and INLA.

5 Results

The data we use in this paper to some degree represent dated information, as they are utilizing information of claims and meteorological and hydrological observations from the period 1999–2006. One advantage of using these data is that the results can be directly compared to other studies based on alternative approaches, but the same data set, see for instance [10]. Another advantage is that old data are not to the same degree subject to strict confidentiality policies at the insurance companies, which for instance prevents [10] from showing the results in full. In addition, data are relatively sparse, involving numerous entries with ‘zero’. This is in general no advantage, and it is demanding from a methodological, calibration, point of view. However, as a basis for evaluating TMB, it is an advantage that data are challenging. If a calibration approach deals satisfactorily with this problem, there is reason to claim that it is relatively robust.

5.1 The Basic Model Formulation

Let DC denote the number of weather-related claims. In modelling DC we use a zero-inflated Poisson model (ZIP). Early contributions to ZIP models can be found in [20] and [21]. Yip and Yau [22] find that a ZIP model is a suitable approach to study the number of claims with extra dispersion in insurance. The model to be estimated can be formulated as follows:

$$\begin{aligned} DC\sim ZIP(\eta _i, p), \end{aligned}$$

(5)

$$\begin{aligned} \eta _i=\alpha +\beta _1\cdot RAIN_i + \beta _2\cdot TEMP_i + \beta _3\cdot DRAIN_i + \beta _5\cdot SNOW_i + u_{R[i]}, \end{aligned}$$

(6)

$$\begin{aligned} \left( u_1, ..., u_m \right) \sim N(\textbf{0}, \mathbf {\Sigma }). \end{aligned}$$

(7)

Here, $\mathbf {\Sigma }$ is the covariance matrix, defined by Eq. 4 in Section 3.3, and the covariates are defined in Table 1. $\left( u_1,..., u_m \right)$ is the vector of the random effects for all municipalities.

5.2 The Estimated Impact of Variations in Weather-Related Covariates

As a basis for evaluating the TMB approach, we have also estimated the model by INLA, as an alternative approach to TMB. While we have been working with this paper, new versions have been released of both approaches. From a computational perspective there was a convergence problem in using earlier versions of the INLA approach for our full dataset, while TMB had no such problems. The underlying problem was that the daily observations of the weather-related variables, as well as claims, leave us with a high number of entries with zero, that is with very sparse data. In earlier versions of INLA, we treated this by aggregating over the time dimension, that is be defining the weather-related observations for a specific number of days. The lowest number of days which resulted in a number of entries with zeros that did not cause convergence problems in the previous version of INLA was found to be 7. However, with the updated version of INLA, documented in [23], we did not enter into convergence problems, even in cases where the full dataset is used. Hence, both the results represented by INLA and TMB in Table 2 correspond to a definition of the covariates on a daily resolution. It follows from the table that INLA and TMB give more or less identical parameter estimates in this case. Without entering into more details, our experiments demonstrate that this is the case for any version of the model where the level of time aggregation is the same in the two approaches. The analysis were performed on a regular desktop computer with 16 GB of memory with an Intel(R) Core(TM) i7-11800 H@2.30GHz with 8 cores.

Likewise, we will not enter into details on the results based on the iCAR model, estimated by MCMC in the WINBUGS software. We have used the same dataset for experiments based on this specification, but they proved to be considerably more time-consuming than the INLA and TMB-estimations, and we entered into problems with convergence in cases where the full dataset was used. This also underpins our perception of TMB as a very robust and efficient procedure.

Table 2 Results based on alternative estimation and model formulations. TMBX represents the extended model, accounting for CENTRALITY, MOUNTAIN and NORTH

As mentioned above, we have run experiments where the covariates are defined for a longer period than the daily observations. This may be necessary to reach convergence in cases with a very high number of zero entries. In general, it is not desirable to use data averaged over a long time period in predicting the number of property damages following from unfortunate weather conditions. This corresponds to intuitively reasonable tendency that the estimated impact of bad weather is scaled down over a longer time perspective, and time aggregation may lead to a severely underestimation of weather-related property claims. Hence, it is fortunate that both TMB and the new version of INLA proved to be robust towards this problem for the sparse dataset that we are using.

Other studies based on the same dataset have distinguished between instant rain and accumulated rain, see for instance [9] and [24]. [24] defines accumulated rain as the total rainfall over the last 5 days. If aggregation of time has to be made in order to reach convergence, RAIN captures both the effect of accumulated and instant rain. This complicates the interpretation of the corresponding parameter estimate. Based on estimation by MCMC simulations of a conditional autoregressive model formulation (iCAR), [24] reported parameter estimates attached to rainfall that was overall higher than the estimate following from TMB (and INLA) in Table 2. At the same time, however, the parameter estimates attached to accumulated rain was substantially lower than the TMB-estimates of variations in RAIN. Hence, a reasonable hypothesis is that the estimates attached to variations in RAIN in Table 2 reflect a mixture of instant and accumulated rain.

Table 2 also provides estimated standard deviations for the parameter estimates, and it is straightforward to see for example that all the covariates are estimated to have a positive impact on the number of property claims in the approach given by TMB (and INLA).

5.3 The Matern Correlation

In a spatial dependency context, the most important of the hyperparameters in Table 2 is $\kappa$. As stated in Section 3.3, Matern correlation defines statistical correlation between measurements made at two spatial points that are at a specific distance from each other. The estimates of $\kappa$ offers information about this correlation. If $\kappa$ is estimated to be high, this means that the two points have to be close to each other to be statistically dependent. The so-called correlation range, r, that was also discussed in Section 3.3 is closely related to $\kappa$; $r=\frac{\sqrt{8}}{\kappa }$, for $\nu =1$ (Eq. 3). The range offers information of the distance where the spatial correlation more or less can be ignored. According to Table 2, the range is estimated to be around 70 km for the different estimation approaches. As illustrated in Fig. 7, the spatial dependency ceases at around 70 km, with corresponding values of the Matern correlation below 0.1. This result supports the hypothesis that there is a strong spatial dependency between the risk of property claims at sites located close to each other.

Fig. 7

Estimated spatial correlation is reduced with increasing distance between two locations

5.4 The Spatial Random Effects

As was made clear in Section 1, both INLA and TMB estimate the random effects of each municipality center, reflecting spatial variation that is not captured by the covariates or the estimated parameters of the Matern correlation function.

The literature provides some unfortunate experiences in terms of convergence and computing costs of using INLA. This is for example reported in [6], who find that by using INLA “….. not possible to fit the frequency model using the full dataset from Gjensidige in a reasonable time”. INLA was found to give a very long run time compared to the other approaches that were considered. However, according to [6] “It should be noted that INLA is in rapid development, with new features added continuously. Hence, the difference in run times may be smaller in the future than those reported here”. This is very much in line with our experience. In fact, things have improved considerably in a relatively short time, and the differences in computing time for our problems were relatively marginal between TMB and INLA. We provide another demonstration that both TMB and INLA are now extremely efficient from a computational perspective. INLA “was designed, in part, to be a computationally efficient and quick alternative to MCMC samplings” ([2]).

Fig. 8

Estimated spatial random effects (u) for Norwegian municipalities in the model presented in Section 5.1 (TMB)

In our data, the municipalities marked in blue in Fig. 8 have a higher number of weather-related claims than what should be expected from the structural part of the model that is formulated in Section 5.1. Correspondingly, the model overpredicts the number of claims in the municipalities marked in red.

Figure 8 demonstrates that the values of the random effects display a systematic spatial pattern and spatial dependencies. This is potentially helpful in suggesting model extensions accounting explicitly for spatial structure characteristics. As mentioned above, the blue marked municipalities represent areas where the model underpredicts the risk of weather-related property claims. From a basic knowledge of the Norwegian geography, the blue marked areas tend to be found in Northern Norway, and in prosperous, centrally located, coastal areas in southern Norway. This suggests a model extension where a measure of centrality is explicitly accounted for, as well as a covariate identifying Northern Norway. In addition, the municipalities marked in red, or with statistically insignificant contributions to explain the dependent variable, tend to be located in mountainous areas in Southern Norway.

5.5 A Model Accounting for Centrality and Location

Exploring the spatial pattern of random effects discloses a potential for increasing the explanatory power of the spatial distribution of claims. The systematic spatial pattern of the random effects suggests that the following covariates are added to the linear predictor of the model formulation:

• CENTRALITY = a measure of the centrality of a municipality

• MOUNTAIN = a dummy variable identifying mountainous areas

• NORTH = a dummy variable representing municipalities in Northern

The hypotheses from studying the random effects are that

• high values of CENTRALITY and a location in NORTH contribute to increase the number of claims related to unfortunate weather conditions, beyond the predictions from the basic model formulation.

• the parameter attached to MOUNTAIN in the linear predictor of the extended model should be expected to be negative.

Hence, the basic model is hypothesized to underpredict the number of claims in centrally located areas and in municipalities in Northern Norway, while it overpredicts the number of claims in mountainous areas. The operationalization of centrality for our purpose is based on an index developed by Statistics Norway ([25]). Centrality is based on the travelling time to the working places that can be reached by car within 90 min, and how many different kinds of services that can be reached within a travelling time by car of 90 min. The location of jobs and services are weighted by the distance from the residential site. All calculations are made for census tracts, and then aggregated to a value at the municipality level. Statistics Norway publishes values of the index both on a continuous scale, and for a categorization, where municipalities are classified into 6 mutually exclusive groups, according to centrality levels.

The results from using the continuous and categorized scale of the index naturally were quite similar. Only the results based on the continuous scale are reported in Table 2, since this variant of the index gave a somewhat better model performance, in terms of AIC values. This makes sense, since the continuous scale utilize more of the available information on centrality. The centrality index from Statistics Norway applies for the situation in 2017, rather than the period for which the rest of our data refers to. We have made no attempts to adjust centrality relative to the situation in 1999–2006. This is hardly a serious source of error, since adjustments in centrality values for municipalities should be expected to be very sluggish.

All the hypotheses are supported by the results. Consider the results of the extended model TMBX in Table 2. Notice first that the parameter estimates attached to the four covariates that were incorporated also in the basic model TMB do not change significantly for the extended model formulation. Second, it follows from the values of AIC that TMBX performs better than the basic model TMB. Third, the partial effects of variations in CENTRALITY, MOUNTAIN and NORTH are according to a priori expectations, reflected in the hypotheses that was stated above. All the relevant parameters are estimated to be different from zero, at any reasonable level of significance.

Fig. 9

The linear predictor ($\eta _i$) partial impact of variations in CENTRALITY, NORTH and MOUNTAIN. CENTRALITY is limited to values between 600 and 800, which covers the majority of the municipalities

The partial impact of variations in CENTRALITY is illustrated in Fig. 9. Values of the centrality index are measured on the horizontal axis, while the vertical axis measures $\eta _i$ in Eq. 1, representing the number of claims in a scenario where random effects are ignored. Centralized, national average, values are used for the covariates included in Eq. 6. The solid curve illustrates how $\eta _i$ responds to variations in CENTRALITY, for a municipality that is not located in Northern Norway, and not in a mountainous area. The curve indicates that variations in CENTRALITY have a substantial quantitative impact on the frequency of damage claims. However, this does not to the same degree apply to variations in NORTH and MOUNTAIN. The dashed curve illustrates the relationship between $\eta _i$ and CENTRALITY for a municipality in Northern Norway, while the dotted curve represents the relationship for a municipality that is located in a mountain area, but not in Northern Norway. Despite the fact that both NORTH and MOUNTAIN were found to have a clearly significant impact on the number of claims, the quantitative effect is not found to be substantial. This in particular applies for mountainous areas.

Notice also from Table 2 that incorporating relevant spatially defined covariates leads to a reduction in the estimated values of $\sigma _u^2$, which represents the variance of the spatial random effects. This is according to a priori expectations, since spatial random effects capture the effect of omitted spatial characteristics. The substantial reduction in the estimated values of $\sigma _u^2$ indicates that the covariates CENTRALITY, MOUNTAIN and NORTH in sum represent important spatial characteristics in explaining spatial variation in damage claims due to unfortunate weather conditions. In addition, introducing additional spatial characteristics results in a slightly lower estimate of the spatial dependency between observations of damage claims at two points located close to each other. With this model formulation, the spatial correlation ceases at around 68 km.

6 Concluding Remarks

In our study, TMB, like INLA, turned out to be a robust and efficient approach in calibrating a model aiming at studying spatial variation in weather-generated claims from a demanding, sparse, data set. First, we were examining the spatial pattern of random effects that was estimated by TMB from a basic model formulation. Besides introducing an assumption regarding the distribution of random effects, this basic model incorporates covariates which are defining local weather conditions in Norwegian municipalities. Examining the spatial structure of the random effects in the basic model turned out to offer useful input and justification for an extended model, defined by the introduction of a set of spatial characteristics. This extended model was accounting for the effect of the location in a rural/urban dimension, altitude information, and some matters that seem to be specific to Northern Norway. Each of these added covariates contributes significantly to explain the spatial variation in weather related claims. Taken together, this resulted in an extended model formulation representing a substantially improved explanation of the problem under study. Besides contributing with a more complete list of relevant covariates, our approach offers useful information of spatial correlation in local claims.

In general, our results give support for TMB to be a very suitable approach to estimate a model formulation with spatial dependence in data. The results further demonstrate that it is important to account for spatial dependencies in reaching reliable estimates of the likelihood of events like weather-related claims. Estimating the likelihood of such claims is potentially important for insurance companies, in establishing efficient pricing regimes. The likelihood reflects local variation in risk factors related to weather, but also local variation in the response to the weather condition, like the building regulations. As such, spatial variation in insurance premiums involves relevant incentives to prevent or reduce future claims.

Wahl et al. [6] use a similar data set to what has been used in this paper to compare different spatial models to make reliable out-of-sample predictions for claim frequencies and claim sizes resulting from water claims. They find that all spatial models outperform a baseline, non-spatial, model and that all the models taking the geography into account by using random effects, outperform models based on spatial spline. Most of the random effect models are found to have a very similar performance. However, [6] do not study the spatial pattern of random effects in terms of the potential for adding new covariates, and they do not use meteorological and hydrological information in explaining the frequencies and sizes of water claims. In addition, they do not consider how TMB performs in dealing with random effect models.

Correct premium rates call for reliable predictions of expected payouts. In many cases, there are substantial spatial variation in risk factors and substantial spatial correlation, that should be accounted for in the predictions. One potential advantage of approaches like TMB is that they allow a continuous, coordinate-based specification of the geography. Hence, it may estimate a spatially smoothed pattern in the likelihood of claims. In the results presented in this paper, data were available only for municipalities. Ideally, the estimation and predictions should be made at a more disaggregated subdivision of the geography, but this will often be restricted by data availability. If data were collected at a finer geographical scale, this would improve the potential for setting more efficient insurance premiums. Still, information on for example centrality and altitude may be constructed for instance for census areas, and contribute to a spatially more smoothed estimation of risk factors, allowing for more spatially differentiated premium rates. Our results on claim frequencies pull in the direction of recommending that insurance premiums are set relatively high in centrally located, urban, areas, low in mountainous areas, and high in Northern Norway, ceteris paribus. However, as demonstrated in [10] this recommendation may be modified by examining the spatial pattern of claim sizes.

Appendices

Appendix A: The Stochastic Partial Differential Equation (SPDE)

The stochastic partial differential equation (SPDE) for a Gaussian field, $U(\mathbf{s)}$, with location coordinates $s_1,...,s_N$ is expressed by:

$$\begin{aligned} \left( \kappa ^2 - \Delta \right) ^{\alpha / 2} \tau U(\textbf{s}) = \omega (\textbf{s}). \end{aligned}$$

(8)

Here, $\Delta$ is the Laplacian and $\omega (\textbf{s})$ is a Gaussian spatial white noise process. The parameter $\kappa$ is the spatial range parameter, $\alpha$ is a parameter controlling the smoothness of the realisations, while $\tau$ controls the variance (see [26]). The Gaussian field with the Matern covariance function defined in Eq. 4 is the exact and stationary solution to the SPDE (see for example [8] and/or [14]). Hence, the parameters in Eq. 8 are linked to the parameters in Eq. 4. More precisely, [14] show that the link between the parameters of the SPDE in Eq. 8 and the parameters of the Matern covariance function in Eq. 4 for a d-dimensional space is given by the following expressions:

$$\begin{aligned} \nu = \alpha - 1 \end{aligned}$$

and

$$\begin{aligned} \sigma _u^2 = \dfrac{\Gamma (\nu )}{\Gamma (\alpha ) (4\pi )^{d/2} \kappa ^{2\nu } \tau ^2}. \end{aligned}$$

Given a solution to Eq. 8, these expressions can be used to find all the parameters needed to specify the covariance matrix of the GMRF. The default value is $\alpha =2$ in the estimation procedures R-INLA and TMB that will be reviewed in Section 4. $\alpha =2$ corresponds to $\nu =1$, which leads to a simplified expression of the Matern correlation function, and the following simplified relationships between the basic parameters of the Matern covariance function:

$$\begin{aligned} r = \dfrac{\sqrt{8}}{\kappa } \end{aligned}$$

(9)

$$\begin{aligned} \sigma _u^2 = \dfrac{1}{4\pi \kappa ^{2} \tau ^2}. \end{aligned}$$

(10)

Lindgren and Rue [8] show that the basic parameters of the Matern covariance function follow from the solution of Eq. 8 in a case defined on a regularly spaced lattice. However, geostatistical data are in general not based on such a regular lattice. Lindgren and Rue [8] proved that the solution of the SPDE gives the relevant parameter estimates of spatial dependence also in cases where the geography is represented by an irregular grid. Hence, the specification of an irregular grid, also called a mesh, is an important step in the formulation of a modelling framework.

1.1 Mesh

A mesh can be considered as a triangulation of the spatial domain. As described in [8], the spatial domain is subdivided into a set of non-intersecting triangles. Any two triangles meet in at most a common edge or corner. The three corners of a triangle are called vertices. A high number of vertices in a mesh increases the accuracy of the GMRF representation, but also the computational cost. The mesh to be used should give a sufficient GF approximation at a reasonable computational cost.

In the mesh that we will be using, all our spatial data points (municipality centers) are on one of the vertices. To avoid boundary problems in cases where a triangle is located at the edge of the geography under study, the triangularization in addition includes an outer area to the geography under study. The number of triangles is determined by the specification of the maximum edge length. However, it is often reasonable to let this upper limit be larger for the outer area than for the inner area of the mesh, since it is in general essential to work with a more accurate, finer grid, of the inner area. Our results are based on the mesh that is presented in Fig. 10, where the circles represents the center of each municipality.

Fig. 10

The mesh; the triangulation of the spatial domain

Appendix B. Laplace Approximation

Both INLA and TMB make use of the Laplace approximation. As explained in [14], Laplace approximation is used to approximate integrals of the form

$$\begin{aligned} \int \exp ^{M \cdot g(\textbf{u})}d\textbf{u}, \end{aligned}$$

(11)

where $\textbf{u} = [u_1,..., u_n]^T$ and $g(\cdot )$ a scalar function of $\textbf{u}$ and M is a large number. To find an approximated solution to Eq. 11, a second order Taylor expansion evaluated in $\textbf{u}_0$ is performed:

$$\begin{aligned} g(\textbf{u}) \approx g(\textbf{u}_0) + \bigtriangledown g(\textbf{u}_0)(\textbf{u} - \textbf{u}_0) + \dfrac{1}{2}(\textbf{u} - \textbf{u}_0)^T + \bigtriangledown ^2 g(\textbf{u}_0)(\textbf{u} - \textbf{u}_0) \end{aligned}$$

(12)

$\bigtriangledown g(\textbf{u}_0)$ and $\bigtriangledown ^2 g(\textbf{u}_0)$ represent the gradient and the Hessian matrix for $g(\textbf{u})$. If $g(\textbf{u})$ has a unique global maximum in ${\hat{\textbf{u}}}$, $\bigtriangledown g({\hat{\textbf{u}}}) = \textbf{0}$ and $\bigtriangledown ^2 g({\hat{\textbf{u}}})$ is negative definite. Hence, the Taylor expansion of $g(\textbf{u})$ around ${\hat{\textbf{u}}}$ becomes:

$$\begin{aligned} g(\textbf{u}) \approx g({\hat{\textbf{u}}}) + \dfrac{1}{2}(\textbf{u} - {\hat{\textbf{u}}})^T + \bigtriangledown ^2 g({\hat{\textbf{u}}})(\textbf{u} - {\hat{\textbf{u}}}). \end{aligned}$$

(13)

Inserted in Eq. 11 it follows that

$$\begin{aligned} \int \exp ^{M \cdot g(\textbf{u})}d\textbf{u} \approx \exp ^{M \cdot g({\hat{\textbf{u}}})} \int \exp ^{\frac{1}{2}(\textbf{u} - {\hat{\textbf{u}}})^T + M \cdot \bigtriangledown ^2 g({\hat{\textbf{u}}})(\textbf{u} - {\hat{\textbf{u}})}} d\textbf{u} \end{aligned}$$

(14)

The integrand in Eq. 14 is the kernel density of a multivariate Normal distribution with mean ${\hat{\textbf{u}}}$ and covariance matrix $[-M \cdot \bigtriangledown ^2 g({\hat{\textbf{u}}})]^{-1}$. Hence, the approximated solution of the integral is given by:

$$\begin{aligned} \int \exp ^{M \cdot g(\textbf{u})}d\textbf{u} \approx \left( \dfrac{2 \pi }{M} \right) ^{\frac{n}{2}} | - \bigtriangledown ^2 g({\hat{\textbf{u}}}) |^{-\frac{1}{2}} \exp ^{M \cdot g({\hat{\textbf{u}}})} \end{aligned}$$

(15)

where $| - \bigtriangledown ^2 g({\hat{\textbf{u}}}) |$ represents the determinant of the matrix $- \bigtriangledown ^2 g({\hat{\textbf{u}}})$.

Appendix C: TMB Code

A TMB program consists of an R file and a C++ file. However, recently a pure R interface to TMB has become available via the R package https://github.com/kaskr/RTMB. Because we expect that most users would prefer this to the C++ interface, we present RTMB code for a simplified version of of model. We use simulated data based on parameter values from Table 2. The R code is available in the subfolder Thorsen_etal of https://github.com/skaug/Supplementary.

The R code has three sections: 1) Use INLA to set up the spatial mesh and calculate the sparse matrices needed for building the precision matrix, 2) Simulate data, and 3) Specify and fit the model in RTMB. For the benefit of the user the R code in Section 3 refers to equations in the paper.