1 Introduction

Train planning, sometimes referred to as timetabling, is the long process of producing new feasible train timetables that satisfy certain service requirements (e.g., three trains per hour from station A to station B), rolling stock constraints, planned maintenance disruptions, and robustness levels. In this work, we refer to timetabling as the train planning process carried out by the railway infrastructure managers, lasting from 1 year to 1 day, sometimes also called short-term timetabling. This should not be confused with long-term timetabling (also called strategic timetabling), which is a longer process lasting multiple years with the main purpose of investigating changes in the capacity of a railway network by proposing additional/different train services, infrastructure upgrades, or both. The two processes differ in scope but also in the input provided to them. In long-term timetabling, one must usually produce a new timetable from scratch given a desired set of train services and a possibly modified railway infrastructure. In (short-term) timetabling, one usually starts from a given (possibly infeasible) timetable and makes modification based on new preferences/constraints of the train operators, planned maintenance work, and customer satisfaction. This process typically lasts about a year, but it also continues after a timetable has been finalized and entered into operation. In fact, even from 1 day to another, a timetable might require small adjustments or planning of additional trains (usually freight or service trains). A summary of the entire process is described in Table 1.

Table 1 A summary of a typical timetabling process carried out by European railway infrastructure managers to determine the annual timetable
Full size table

Depending on the chosen planning horizon, different levels of flexibility are adopted and different requirements can apply. For example, a new timetable for the next year could require a complete overhaul of the previous year’s timetable, maybe because new infrastructure was built and additional capacity has been added to the network. On the other hand, when planning the timetable for the next day, the timetable adopted in the current year is used as a starting point, and very limited modifications are allowed. Therefore, the planning process can take from a couple of hours (for the next day) to several weeks (for the next year). In this work, we propose a MILP model and an interactive tool that can be used to support the short-term timetabling process in modern railway infrastructure management, both for the next-day timetable and the next-year timetable.

The route planners that are tasked to produce new timetables usually have many years of experience and a huge domain knowledge, which is difficult to transfer into a mathematical model that automatically builds optimal timetables. Moreover, the concept of an optimal timetable is still very vague and not well defined. And when new models are proposed to take into account typical measures of optimality (e.g., robustness, average passenger travel time), the increase in complexity usually makes them impractical for real-life instances. This is probably the reason why, to the best of our knowledge, there is currently no optimization-based decision support tool available off-the-shelf.

As described above, in a typical timetabling process, the route planners start from an existing timetable (or at least a sketch of it) and then adjust it in order to make it feasible. This adjustment is a tedious manual work that takes a large portion of their time, which could instead be spent more efficiently by letting them exploit their expertise to test, for example, different timetable scenarios or configurations.

Therefore, we consider attacking the timetabling problem from a different angle compared to the existing optimization literature (see, e.g., the survey papers and tutorials [1,2,3,4,5,6,7]). Unlike previous work that aims at producing an “optimal” timetable based on a combination of different objective functions, we mainly focus on producing a feasible timetable. In other words, we wish to aid the planning process rather than hoping to replace it. As in many previous works, we also make use of a mixed-integer linear programming approach, based on a so-called big-M formulation, as, e.g., [8,9,10,11,12]. The idea is simple. Starting from an existing (possibly infeasible) timetable T, route planners can use an interactive interface to add trains, modify them (e.g, shift/extend/shorten their schedules, change the minimum dwell times or running times in specific station and tracks), and set specific preferences (e.g., train A should have precedence over train B, train A should only run on Sundays). The resulting modified timetable \(T^{'}\) will likely be infeasible, and the objective of our model would be to find a new timetable \(T^{'^*}\) that is feasible and as close as possible to \(T^{'}\) (according to some reasonable distance measure). This way, we relieve the route planners from the tedious work of making small adjustments to a tentative timetable in order to make it feasible, giving them the possibility of trying and testing many more tentative timetables. We call this process incremental timetabling.

This approach has several advantages when it comes to the complexity of the MILP model. First of all, we do not need to deal with complex objective functions to represent, for example, the robustness of a timetable. But we also do not need to consider uncertainty in the passenger distribution or, in general, deal with stochastic constraints. Instead, we assume that route planners, through their extensive expertise, are able to guide this process towards an “optimal” timetable, incrementally improving the quality of a timetable after each modification.

In this paper, we adapt and extend the model and approach developed in [10] to cope with this specific application and with a yearly timetable. In particular, we show that by carefully taking into consideration operational periods (i.e., trains having the same timetable across several days of the week), we can project all trains running throughout a year into a single day. This makes it possible to re-plan the yearly timetable for a busy railway line in Norway in just a few minutes. As of 2023, the same process is done manually and may require several hours. The idea of projecting trains with different operational periods is not entirely new as it was already introduced in [13] for a PESP formulation of the problem of finding (what they call) a partially periodic timetable. The authors show that, under certain assumptions, the original problem and the projected (periodic) problem are equivalent, and they use the latter to compute a daily timetable where trains can have different periodicity at different hours of the day.

2 A MILP Formulation for Incremental Timetabling

Given a tentative (possibly infeasible) timetable for all trains, we aim to solve the problem of finding new feasible schedules for all trains such that the schedule of each train is as close as possible to its corresponding schedule in the given timetable. Here, we use the term “feasible” to identify a schedule that satisfies all operational rules: free-running, precedence, safety margin, and connection rules (all described below). In other words, the problem is very similar to a classical train scheduling problem, but with a somewhat uncommon objective function. Train scheduling problems have been studied for many years. Two main MILP formulations arose: time-indexed and big-M. The formulation we use in this paper is based on the big-M formulation extensively in described in [14] and later applied to many real-world applications (see, for example, [10] and [15]). In this section, we present the formulation described in [15] for train scheduling, while in the next section, we describe how to project all trains running within a year into a single day.

We consider a set of trains A and a set of resources R. Each train \(a\in A\) has an associated route, that is a sequence of resources \((r_1, \dots , r_{|R^a|})\), where \(R^a\) is the set of resources in the route of train a. We assume that the first and last resources are always stations. Tracks are simply resources with capacity 1, while stations are resources with capacity greater or equal than 1. The exact decomposition approach described in [14] considers a mesoscopic representation of the network [16], and it consists of repetitively solving a train scheduling problem that initially ignores operational rules in the stations, generating appropriate constraints on the fly only when those rules are violated by the incumbent schedule. Whenever no rules are violated, the incumbent solution is optimal. But one could also go one step further and actually initially ignore a larger set of operational rules, both in the stations and the tracks. This iterative constraint-generation algorithm has several nice properties. First, the initial problem formulation is relatively small. Secondly, determining whether a certain incumbent solution violates any rule can be done independently for each resource, effectively decomposing the problem of identifying conflicts into a set of very small problems.

Following [14], we model the train scheduling problem as an extension of the job-shop scheduling problem with blocking and no-wait constraints first described in [17]. We introduce a scheduling variable \(t_r^a \in \mathbb {R}\) to indicate the time train \(a\in A\) enters resource \(r\in R^a\). With a slight abuse of notation, we define by \(t_{r+1}^a\) the time train a enters the resource immediately after r in its route. Then, the time train \(a\in A\) leaves resource \(r\in R\) can simply be defined as \(t_{r+1}^a\). We assume R contains a fictitious resource \(r^\text {out}\) that we can append to the end of the route of each train so that we can use the scheduling variable \(t_{r^\text {out}}^a \in \mathbb {R}\) to indicate the time train a leaves the last station of its route and exits the railway network. For consistency and simplicity, we denote by \(t_{r^\text {in}}^a\) the time train a enters the first station in its route.

Free-Running Rules

We can start building our MILP model by limiting the minimum and maximum running time of each train in each resource:

$$\begin{array}{ll} t_{r+1}^a - t_r^a \ge \lambda _r^a &{} a\in A, r\in R^a,\\ t_{r+1}^a - t_r^a \le \Lambda _r^a &{} a\in A, r\in R^a, \end{array}$$
(1)

by limiting the arrival and departure time at the first and last station, respectively:

$$\begin{array}{ll} t_{r^\text {in}}^a \ge \phi ^a &{} a\in A,\\ t_{r^\text {out}}^a \le \Phi ^a &{} a\in A, \end{array}$$
(2)

and by limiting the total travel time:

$$\begin{aligned} \begin{array}{ll} t_{r^\text {out}}^a - t_{r^\text {in}}^a \le \theta ^a&a\in A. \end{array} \end{aligned}$$
(3)

When r represents a track, (1) restricts the minimum and maximum running time in the track (usually dependent on the type of train, number of wagons and locomotives, and its weight). Instead, when r represents a station, (1) restricts the minimum and maximum dwell time in the station. All constraints (1)–(3) are usually called “free-running” constraints because they model the basic behavior of a train without considering interactions with other trains.

Precedence Rules

When planning two or more trains in the same network, violations of the precedence rules may arise. In this paper, we refer to precedence rules as all those rules that make sure two or more trains will not interfere with each other within a resource, that is whether one or more trains need to give precedence to other trains in a resource. Here, we assume that given a set of trains (with their routes) and a resource, there exists an oracle able to determine whether these trains can be feasibly scheduled (and routed) within the resource whenever they happen to “meet” simultaneously in the resource. If the oracle returns a negative answer, then there must be no positive time interval in which all trains of this set can occupy the resource at the same time. For example, in a single track, a train must leave the track before another train can enter, and therefore, no set of two trains traversing the same track can ever meet in that track at the same time. Similarly, in a small station with two tracks but only a single platform track, two passenger trains can never be present at the same time (since they both need to use the platform). The oracle can take into account the characteristics of the trains (e.g., length, type), the infrastructure of the resource (e.g., length of tracks and platforms), the available feasible routes, et cetera. Like any model, this is an abstraction of reality. However, as long as the information provided to the oracle is rich enough, this abstraction is sufficient to produce schedules that would also be feasible in a very realistic environment, as proven in other recent works (see, for example, [15, 18]). The details of the oracle are not particularly relevant for this work, and some examples include both simpler implementations based on graph coloring algorithms [14] and more complex algorithms based on very precise microscopic station models [19]. Note that, in general, determining whether trains can be feasibly scheduled inside a resource is computationally hard, especially if the resource represents a large, complex piece of the railway infrastructure (e.g., a large station serving several lines). However, in our macroscopic approach, resources represent either single tracks or stations with relatively simple feasibility rules, and the computational time spent on the oracle is negligible compared to solving the MILPs.

Now that we know which trains can and cannot be in each resource at the same time, we simply need the model to be able to measure the train occupancy of each resource. To formulate this, we can start by looking at the interactions between each pair of trains within a resource. Later, we will see how to combine interactions across pairs of trains to deduce interactions among larger sets of trains and therefore measure the train occupancy. Note that only two situations can occur when there is a possibility for two trains to meet in a resource. Either they actually meet in the resource (i.e., the intervals of time spent in the resource by each train overlap at least in one point) or one train leaves the resource before the other enters. The latter gives rise to two symmetric cases, as we will see below. Note that not all trains can meet in every resource; therefore, we can limit the number of binary variables based on the potential interactions.

Define the set \(\Omega ^+ \subseteq R \times A \times A\) as the set of (resource, train, train) triplets (r, a, b) such that \(r\in R^a\cap R^b\). Note that \(\Omega ^+\) is symmetric: Whenever \((r,a,b) \in \Omega ^+\), so is (r, b, a). To avoid redundancy in the model due to this symmetry, we also define \(\Omega \subset \Omega ^+\) such that when \((r,a,b) \in \Omega ^+\), then either \((r,a,b) \in \Omega\) or \((r,b,a) \in \Omega\), but not both. The choice of which is arbitrary.

Then, the interactions between pairs of trains can be described with the following binary variables:

  • \(p_r^{ab} \in \{0,1\}\), \((r,a,b) \in \Omega ^+\): this precedence variable is equal to 1 whenever train a exits the resource r before train b enters it (i.e., a precedes b in resource r), 0 otherwise. In other words, if \(p_r^{ab} = 1\), then \(t_r^b \ge t_{r+1}^a\).

  • \(m_r^{ab} \in \{0,1\}\), \((r,a,b) \in \Omega\): this meeting variable is equal to 1 whenever train a meets train b in resource r, 0 otherwise. In other words, if \(m_r^{ab} = 1\), then \(t_r^b \le t_{r+1}^a \ \wedge \ t_r^a \le t_{r+1}^b\), that is, train b enters resource r before train a leaves and train a enters resource r before train b leaves. Note that \(m_r^{ab}\) is defined for the smaller set \(\Omega\), and its symmetric version \(m_r^{ba}\) does not exist.

Then, we can model these variables with the following constraints:

$$\begin{array}{ll} p_r^{ab} + p_r^{ba} + m_r^{ab} = 1 &{} (r,a,b) \in \Omega , \\ t_{r+1}^a - t_r^b \le M (1 - p_r^{ab}) &{} (r,a,b) \in \Omega ^+,\\ t_r^b - t_{r+1}^a \le M (1 - m_r^{ab}) &{} (r,a,b) \in \Omega ,\\ t_r^a - t_{r+1}^b \le M (1 - m_r^{ab}) &{} (r,a,b) \in \Omega , \end{array}$$
(4)

where M is a large enough constant (i.e., the infamous big-M coefficient). The first constraint makes sure that either one train precedes the other train in the resource or they actually meet in the resource. The other constraints tie these binary variables to the scheduling variables. For example, if \(p_r^{ab} = 1\), then the second constraint becomes active and \(t_r^b \ge t_{r+1}^a\), that is, train b can enter resource r only after train a has left, and all the remaining big-M constraints become inactive (i.e., always satisfied). The observant reader might notice that the set of constraints in (4) can be simplified by eliminating one of the binary variables. However, we use this slightly redundant formulation here and throughout the rest of the paper in the interest of a clearer presentation.

Now that we established a way to determine whether two trains meet in a certain resource, we can use the well-known Helly’s Theorem to extend this concept to a set of trains. In fact, it is easy to show that given a set of trains S, they will all meet simultaneously in a resource r if and only every pair meets in r, that is if and only if \(\sum _{\{a,b\}\subseteq S} m_r^{ab} = \left( {\begin{array}{c}|S|\\ 2\end{array}}\right)\). Recall our assumption on the oracle, that for every set of trains \(S\subseteq A\) and for every resource \(r\in R\), we can determine whether they can all meet simultaneously in that resource. Define by \(\mathcal {S}^r\) the set of (minimal) subsets of trains that would receive a negative answer from the oracle in resource r. Then, we can make sure that all precedence rules are satisfied simply by making sure that none of those sets of trains will ever meet simultaneously in each specific resource:

$$\begin{aligned} \begin{array}{ll} \sum _{\{a,b\}\subseteq S} m_r^{ab} \le \left( {\begin{array}{c}|S|\\ 2\end{array}}\right) - 1&r\in R, S\in \mathcal {S}^r. \end{array} \end{aligned}$$
(5)

Safety Margin Rules

After modeling the basic free-running behavior of trains and preventing them from colliding by introducing the precedence rules, we still need additional constraints to model safety margin rules. These rules come in the form of required minimum time separation between events. One typical example is when two passenger trains running in opposite direction along single-tracks are approaching at the same time a station with two platforms. Since each train will be routed to a different platform and they enter the station from different directions, they are not expected to collide or interfere with each other within the station. However, one of the trains could miss its assigned route due to a malfunction (in the infrastructure or the brakes, for example) and hit the other incoming train. In this situation, safety margin rules usually impose that the train entering the station last may do so only after a certain amount of time has passed since the first train has entered the station.

In general, there may be rules for all combinations of events on each pair of trains in each resource. The following separation times then apply when the specific event for train a happens before the specific event for train b in resource r:

  • \(\alpha _r^{ab}\): The minimum time separation in resource r between the arrival events of trains a, b;

  • \(\beta _r^{ab}\): The minimum time separation in resource r between the arrival of train a and the departure of train b;

  • \(\gamma _r^{ab}\): The minimum time separation in resource r between the departure of train a and the arrival of train b;

  • \(\delta _r^{ab}\): The minimum time separation in resource r between the departure events of train a, b.

Note that \(\alpha _r^{ab}\), for example, could be different from \(\alpha _r^{ba}\), depending on the train characteristics or the railway infrastructure. For the arrival-vs-departure restrictions, we can reuse the precedence variables introduced in (4):

$$\begin{array}{ll} t_{r+1}^b - t_r^a \ge \beta _r^{ab} - M p_r^{ba} &{} (r,a,b) \in \Omega ^+, \\ t_r^b - t_{r+1}^a \ge \gamma _r^{ab} - M (1 - p_r^{ab}) &{} (r,a,b) \in \Omega ^+, \end{array}$$
(6)

The first constraint says that if train b does not exit resource r before train a enters (i.e., \(p_r^{ba} = 0\)), then train b can leave that resource only after \(\beta _r^{ab}\) time has passed since train a has entered (i.e., \(t_{r+1}^b \ge t_r^a + \beta _r^{ab}\)). The second has a similar meaning. However, note that the second constraint in (6) is a generalization of the second constraint in (4), which could then be omitted.

Whenever we have that \(m_r^{ab}=1\) (i.e., train a meets train b in resource r), \(p_r^{ab}=p_r^{ba} = 0\), and we cannot use these variables to determine which train entered the resource first. Moreover, their arrival order might be different from their departure order, e.g., when one train overtakes another in a station. Therefore, additional binary variables are needed to enforce the remaining two time restrictions. For every \((r,a,b) \in \Omega ^+\), we introduce variable \(u_r^{ab} \in \{0,1\}\) to model the relation between train arrivals. Specifically, if \(u_r^{ab}=1\), then train a enters resource r before train b enters the same resource, i.e., \(t_r^a \le t_r^b\). Similarly, we introduce variable \(v_r^{ab} \in \{0,1\}\) to model the relation between train departures. If \(v_r^{ab}=1\), then train a exits resource r before train b exits the same resource, i.e., \(t_{r+1}^a \le t_{r+1}^b\). These variables and the corresponding remaining safety margin restrictions can then be modeled with the following constraints:

$$\begin{array}{ll} u_r^{ab}+u_r^{ba}=1 &{} (r,a,b) \in \Omega ,\\ t_r^b - t_r^a \ge \alpha _r^{ab} - M (1 - u_r^{ab}) &{} (r,a,b) \in \Omega ^+,\\ v_r^{ab}+v_r^{ba}=1 &{} (r,a,b) \in \Omega ,\\ t_{r+1}^b - t_{r+1}^a \ge \delta _r^{ab} - M (1 - v_r^{ab}) &{} (r,a,b) \in \Omega ^+,\\ \end{array}$$
(7)

Connection Rules

Some trains are intended to be serviced by the same rolling stock, usually turning around at a terminal station. When this is the case, we must impose a minimum time between the first train’s arrival and the second’s departure. There are also cases where two trains should meet in a station to exchange passengers, leading to similar constraints.

Define \(\Gamma \subseteq R \times A \times A\) as the set of (resource, train, train) triplets (r, a, b) such that a connects to b in station r. The connection time is modeled by the constraint

$$\begin{aligned} \begin{array}{ll} t_{r+1}^b - t_r^a \ge \zeta _r^{ab}&(r,a,b) \in \Gamma , \end{array} \end{aligned}$$
(8)

where \(\zeta _r^{ab}\) is the minimum time between a’s arrival and b’s departure. In the case where one physical rolling-stock is assigned to trains a, b, running in that order, we have \((r,a,b) \in \Gamma\), where station r is the last resource in a’s route and the first in b’s route. In the case where trains a, b meet in some station r to exchange passengers, we have both \((r,a,b) \in \Gamma\) and \((r,b,a) \in \Gamma\).

Objective Function

As mentioned in the introduction and at the beginning of this section, we consider an objective function that is quite uncommon in the literature of train timetabling. In fact, we disregard the more common objectives such as robustness or average passenger travel time, and we simply measure the distance of the incumbent timetable from a given timetable. The idea is that route planners would have already taken into account these considerations while making a tentative (but likely infeasible) timetable. Although they cannot optimize over robustness or average passenger travel time, they have many years of experience and a huge domain knowledge, both of which can prove to be more significant than an approximated robustness measure, for example.

The model receives as input a timetable T, that is, a target value \(\bar{t}_r^a\) for each scheduling variable \(t_r^a\), \(a\in A, r\in R^a\). The objective of the model is to find new values for the scheduling variables \(t_r^a\) such that all constraints are satisfied and the new incumbent timetable is as close as possible to the given one. To measure this distance, we start by considering the absolute difference \(d_r^a \in \mathbb {R}^+\), \(d_r^a = |t_r^a - \bar{t}_r^a|\), which can be modeled with the following linear constraints:

$$\begin{array}{ll} t_r^a - \bar{t}_r^a \le d_r^a &{} a\in A, r\in R^a,\\ \bar{t}_r^a - t_r^a \le d_r^a &{} a\in A, r\in R^a. \end{array}$$
(9)

Then, two common choices for measuring the total distance between a given timetable and the incumbent timetable consist of the following:

  • \(\sum \limits _{a\in A, r\in R^a} d_r^a\): Total sum of absolute differences;

  • \(\max \limits _{{a\in A, r\in R^a}} d_r^a\): Maximum absolute difference.

We choose the former for two reasons. First, minimizing the maximum absolute difference requires additional constrains (to linearize the maximum value) and it usually introduces symmetry, both of which could impact the computation time. Secondly, we have been asked by Norwegian route planners to have the possibility of limiting the absolute differences for some trains, which can then also be used to limit their maximum value:

$$\begin{aligned} \begin{array}{ll} d_r^a \le \psi ^a&a\in A, r\in R^a. \end{array} \end{aligned}$$
(10)

In some cases, a subset of trains is known to have already feasible schedules, and these schedules should remain fixed. In other cases, the new schedules of some trains should not deviate too much from the schedules of the given timetable. Then, route planners have the possibility of imposing these preferences through the parameter \(\psi ^a\).

In conclusion, the entire problem consists of minimizing \(\sum _{a\in A, r\in R^a} d_r^a\), subject to constraints (1)–(10).

3 Solution Algorithm

The full MILP model grows quickly in size when the number of trains in the problem increases. The number of constraints of types (4), (6), and (7) is quadratic in the number of trains (assuming that all trains run on the same line), and the number of constraints of type (5) can grow even quicker, when there are stations where many trains can meet. More significantly, the number of binary variables needed to express the constraints is also quadratic in the number of trains. This can make the full problem challenging to solve to optimality. However, only relatively few of these constraints are actually needed, because most of them forbid situations that only occur when trains deviate significantly from the given timetable. Since the objective precisely aims at producing a solution similar to the given timetable, these constraints are unlikely to be relevant for the optimal solution.

We solve the problem using an iterative algorithm that exploits this fact and add constraints in a lazy fashion, which has been shown to be very successful in reducing the computation time in the context of traffic management (see, for example, [20] and [21]). To start, we set up a MILP that excludes all constraints of types (4)–(7). Thus, each train is considered to be free running, except that train connections must be observed. Each iteration then consists of the following steps:

  1. (i)

    Solve the current MILP.

  2. (ii)

    If infeasible, the timetabling problem as a whole is infeasible. Stop.

  3. (iii)

    Check whether the solution violates any constraint of type (4)–(7).

  4. (iv)

    If not, the solution is feasible and optimal. Stop.

  5. (v)

    Otherwise, augment the MILP with the violated constraints.

  6. (vi)

    Repeat

Steps iii and v are described in more detail below for each class of constraint.

Precedence Rules

Constraints (4) serve to define the binary precedence and meeting variables in terms of the scheduling variables. The binaries \(p_r^{ab}\), \(p_r^{ba}\) and \(m_r^{ab}\) are not present in the initial MILP, nor are the constraints, but by substituting the solution’s values of \(t_r^a\) into (4), we may discover what values \(p_r^{ab}\), \(p_r^{ba}\) and \(m_r^{ab}\) must have for the solution to be feasible. The found values of \(m_r^{ab}\) can then be substituted into (5) to discover the train subsets \(S\in S^r\) for which that constraint is violated.

While the above procedure is correct, we use a more direct way to find the violated precedence rules, based on a standard algorithm to identify maximal cliques in interval graphs. For each resource r, we collect the arrival and departure times \(t_r^a\) and \(t_{r+1}^a\) for all visiting trains and sort them in ascending order. Now, we can run through the sorted sequence while maintaining a set S of present trains, which starts empty. When we encounter an arrival \(t_r^a\), we add a to S, and when we encounter a departure \(t_{r+1}^a\), we remove a from S. Every time we add a train to S, we ask the oracle to check whether the current set of trains can be meeting in that resource at the same time. Whenever we have an S for which the oracle returns a negative answer, we have found a violated instance of (5).

When (5) is found to be violated for some S, we add it to the MILP. We also add \(p_r^{ab}\), \(p_r^{ba}\), and \(m_r^{ab}\) and constraints (4) for all \(\{a,b\} \subseteq S\) where this has not yet been done.

Safety Margin Rules

The procedure for safety margin rules is similar. We order all arrivals and departures in resource r by time and run through them, checking whether any are closer than allowed. If so, the corresponding equation from (6) or (7) and associated binary are added to the MILP. When this involves \(p_r^{ab}\), \(m_r^{ab}\) or \(p_r^{ba}\), they must all be added, along with the corresponding set of constraints from (4).

4 Modeling a Yearly Timetable

So far, we have described a timetabling problem that does not take into account train periodicity, that is trains that have the same exact schedule on different days of the year. A naive application of the method described above would result in the unnecessary modeling of such trains, making the problem intractable. When looking at a busy Norwegian railway line with about 100 trains a day (see Sect. 5.2 about the real-life experiments), this would result in a problem with roughly 36,500 trains. However, it turns out that only 160 of those trains have unique schedules. This is very common. Neither do route planners have the capacity to create customized timetables for each day of the year, nor is it desirable from a traveler’s point of view to have different timetables from day to day and week to week. In this section, we describe how to model periodic trains when solving for a yearly timetable.

As before, we consider a set of trains A and a timetable T. In addition, for each train a, we are given a pattern \(D_a \subseteq D = \{1, 2,..., 365\}\). This pattern indicates on which days during the year the train runs. So instead of representing a single point in time, the scheduling variable \(t_r^a\) now represents the time at which train a enters resource r on each day present in pattern \(D_a\).

The canonical interval in which time is expressed is the interval \([0, \eta )\), where 0 represents midnight at the start of some day in D, and \(\eta\) represents midnight at the end of the same day. The timetable is expressed so that the target time at the first station in any train’s route is always within the interval \([0, \eta )\). The subsequent target times along a train’s route must be increasing, with no wraparound taking place. Thus, if a train’s timetable starts late in the day and continues into the next day, it will contain target times \(\ge \eta\). The scheduling variables \(t_r^a\) likewise normally take values in the interval \([0, \eta )\), but may exceed \(\eta\) when the train runs across midnight. Additionally, \(t_r^a\) is allowed to take negative values, which is rare, but may happen if a train that is targeted to start soon after midnight receives an earlier start time before midnight in the MILP solution.

The general structure of the MILP model and algorithm for the periodic case are the same as of the non-periodic case described above, but we must now take into account that time \(t+\eta\) on some day \(d \in D\) represents the same time as t on day \(d+1\). Thus, two trains may conflict if their times on the same resource differ by approximately \(\eta\). We must also consider the fact that not all trains run on all days, and if two trains do not both run on any common day in D, then they do not actually conflict when they have similar times on the same resource.

As a concrete example, consider the safety margin rule for time between arrivals, expressed by the two first constraints of (7). We wish to check if this rule is violated for trains a, b in resource r, and if so, add the appropriate variables and constraints. The algorithm runs as follows:

  1. 1.

    First, check whether \(D_a\) and \(D_b\) have any common element. If \(D_a \cap D_b = \emptyset\), the trains never run on the same day. Go to step 3.

  2. 2.

    Check if \(t_r^b < t_r^a + \alpha _r^{ab}\) and \(t_r^a < t_r^b + \alpha _r^{ba}\). If so, the rule is violated. Add \(u_r^{ab}\), \(u_r^{ba}\) and the associated constraints from (7) to the MILP.

  3. 3.

    Next, check if for any \(d \in D_a\), we have \(d+1 \in D_b\). If so, the trains may conflict when a runs one day and b the next day. Otherwise, go to step 5.

  4. 4.

    Check if \(t_r^b + \eta < t_r^a + \alpha _r^{ab}\) and \(t_r^a < t_r^b + \eta + \alpha _r^{ba}\). If so, the rule is violated: Train a starting on day d and train b starting on day \(d+1\) arrive too close. Add to the MILP \(u_r^{ab}\), \(u_r^{ba}\) and the associated constraints, modified with the offset \(\eta\) to take into account the 1-day difference:

    $$\begin{aligned} u_r^{ab}&+u_r^{ba}=1 \\ t_r^b - t_r^a \ge \alpha _r^{ab} &- \eta - M (1 - u_r^{ab}) \\ t_r^a - t_r^b \ge \alpha _r^{ba} &+ \eta - M (1 - u_r^{ba}) \end{aligned}$$
    (11)
  5. 5.

    To handle violations when a runs the day after b, repeat steps 3 and 4 with a and b swapped.

The modifications in handling the remaining rules are analogous: In the form given in (4)–(8), the constraints apply only when the patterns of both trains share a day. But also, a modified form, where \(t_r^b\) is offset by \(\eta\) or \(-\eta\), applies when for some \(d \in D_a\), \(d+1 \in D_b\) or \(d-1 \in D_b\), respectively. We do not describe the remaining rules in detail, but note the following points:

  • The connection rules (8) are all added to the initial LP. Only one form of each is needed, whose offset (\(-\eta\), 0 or \(\eta\)) is chosen as the one most similar to the difference between the connected target times.

  • When searching for violations of the precedence rules, we add three versions of each time to the collection of times to be sorted, i.e., \(t_r^a -\eta\), \(t_r^a\) and \(t_r^a+\eta\) for an arrival time, and record the offset that belongs to each. Each train in the set S of trains present has an associated offset, and the sets given to the oracle are those subsets of S whose patters and offsets imply that they all meet on some common day in D.

5 Real-Life Experiments

This section presents how the model described in this paper can be used in a real-life setting and evaluates its performance. Section 5.1 presents the main features of a graphical user interface that was developed in collaboration with Norwegian route planners, which they can use to interact directly with the model and the algorithm. Section 5.2 describes a set of representative test instances and the algorithm’s performance on these instances.

5.1 User Interface

For railway planning professionals to make productive use of the algorithm described above, it is helpful to have a graphical user interface where they can load and save timetables, display and manipulate timetables graphically, set various parameters, start the algorithm, and monitor its progress.

Fig. 1
figure 1

The user interface. From the top menu bar, timetables can be loaded and saved as files, and connection to the back-end computation server is initiated. On the left, algorithm parameters are set, and the solver’s log output can be monitored. On the right, the graphical timetable is displayed and can be directly manipulated by the mouse

Full size image

We have developed such a user interface in collaboration with Norwegian route planners. The software uses a server-client architecture, with a computation back-end server running the algorithm and using Gurobi v10.0 [22] for solving the MILP problems, and a graphical front-end running on Windows for manipulating the timetable graphically. An overview of the graphical user interface is shown in Fig. 1. Timetables are loaded and saved in the railML v2.2 file format.

When loading a timetable, that timetable is set as the reference timetable and drawn in black in the graphical timetable. The timetable’s time range covers midnight to midnight of a single day. Because some trains run across the date limit (i.e., midnight), an additional 6 h before and after midnight are displayed with a darker background. By default (for overview), all trains are drawn in this same 1-day timetable, even those running on different days. The operation period selection can be used to narrow down the displayed trains to days-of-week, date ranges, or individual dates.

The user can make direct modifications of the reference timetable by clicking the trains in the graphical timetable. Available operations include the following:

  • Clone train: Creates a new train that has the same timetable as an existing train. This is useful to add more trains for specific train services, and the new trains can be slotted into new times using the move train operation described below.

  • Move train: Offsets arrival and departure times of all stations by the same amount. This is useful to provide the same train service at a different time of day.

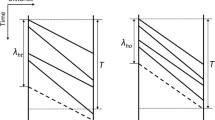
  • Stretch range: Increase or decrease the operational reserve (running times and/or dwelling times) over a selected range. This is useful to make trains arrive/depart earlier or later at specific stations while leaving other parts of its timetable unmodified (see Fig. 2).

Fig. 2
figure 2

Stretching running times can be used to make trains faster or slower by decreasing or increasing the operational reserve proportionally over the selected range

Full size image

There are also further basic operations available, such as canceling (removing) a train, changing the operational period, setting arrival/departure times, locking (“fixing") parts of the reference timetable, and moving a range (shifting operational reserve between before and after the range). All of these operations are performed by pointing and clicking with the mouse in the graphical timetable, letting the planning professionals work more graphically compared to most commercially available timetabling software. The idea is that a timetable is best manipulated and experimented with by working graphically and seeing the timetable as a whole, and then the tedious detail work required to make the timetable feasible can largely be left to the algorithm.

When the desired modifications to the reference timetable have been made, conflicts may have been introduced, and the user can start the algorithm to compute a new conflict-free timetable that is as close as possible to the reference one. The algorithm has two main modes: (1) Adjust timetable for all trains, which solves the problem described in Section 2 above, and (2) Find slot, which will modify only the timetables of currently selected trains. Both modes produce a feasible suggested timetable from the potentially infeasible reference timetable. When a suggested timetable has been found by the algorithm, it is drawn in red over the black reference timetable. The user may inspect the suggestion and continue making modifications to the reference timetable or the algorithm’s parameters. If the user is satisfied with the suggested timetable, they can accept the suggestion, setting it as the new reference timetable.

5.2 Performance Evaluation

To demonstrate that the algorithm runs fast enough for interactive use, we produced a set of 40 reference timetables that represent incremental modifications of the kind that Norwegian route planners were interested in performing. All the modifications are based on the real 2021 full-year timetable for 160 trains on the Norwegian Dovrebanen line from Eidsvoll (near Oslo) to Trondheim, a 485-km long line with 28 stations with passenger exchange. The original timetable contained detailed input data from the real 2021 production timetable, including train schedules, train types (class, length, etc.), passenger exchanges, minimum dwelling times, minimum running times, and rolling stock correspondences. The timetable (and corresponding infrastructure model) also included the line from Oslo Central Station to Eidsvoll, where Dovrebanen begins, because most trains running on Dovrebanen will arrive or depart from Oslo. However, since the timetable’s scope was limited to Dovrebanen, the parts of the trains between Oslo and Eidsvoll were considered fixed (locked) and would not be modified as part of the Dovrebanen timetabling process (i.e., setting \(\psi ^a=0\)). This allows route planners to add and modify trains on Dovrebanen and find feasible slots for them to travel also on the Oslo-Eidsvoll line, without changing the existing Oslo-Eidsvoll timetable.

We have produced modifications of four kinds, with 10 instances of each kind:

  • add-long: Cloning a long-distance train (running the whole 500 km) and offsetting its times.

  • add-short: Cloning a short-distance train (running locally near the terminal station) and offsetting its times.

  • stretch: Shortening or lengthening a section of a train timetable.

  • move: Offsetting a train timetable.

The modified timetables were produced manually using the graphical operations described in Section 5.1 above, based on the route planners’ examples of how they modify timetables in practice. This means that the modified timetables are made to be reasonable, in the sense that one does not, for example, make two trains with very overlapping timetables, or a train that blocks a single-track section for an unreasonable amount of time. But aside from more or less obviously irreparable timetables, the modifications were made without regard for detailed feasibility, such as trains meeting in the middle of a single-track section.

For each of the add-long and add-short instances, we calculated feasible timetables using each of the two algorithm modes (adjust timetable and find slot). For each of the stretch and move instances, only the adjust timetable mode was used. The algorithm was run on a server machine with an Intel Xeon Gold 6240 processor and 20 GB of memory. Running time results are shown in Table 2. All cases had the maximum time deviation from the reference timetable set to 60 min for all trains (expect for the fixed trains mentioned above). The table shows that all instances were solved in less than a minute, enabling a highly interactive workflow for timetable modifications. Across these computational experiments, 73% of the running time is spent on solving the MILP problem, while 11% is spent on the oracle finding conflicts (i.e., checking for violations of (4)–(7)). Each call to the oracle takes on average only 1.24 µs. When conflicts are found, most of the corresponding constraints involve only two trains (99.2% of conflicts) and only a very few involve larger number of trains: 3 trains (0.5% of conflicts) and 4 trains (0.2%). Only a handful of oracle calls resulted in conflicts between more than 4 trains.

Table 2 Running time results for incremental timetabling problem instances. The two leftmost columns indicate the instance category, each containing 10 problem instances. The Avg. iter. column averages the number of algorithm iterations. The Avg. confl. column averages the total number of conflict constraints that were added to the MILP model. The Min. time, Avg. time, and Max. time columns describe the minimum, average, and maximum running times, respectively, of the 10 cases in the category
Full size table

The effect of setting the maximum time deviation to other values (than our default 60 min) is shown in Fig. 3. When lowering the maximum time deviation, the problems are solved somewhat faster, but the objective value (i.e., the sum of deviations) increases. If the maximum time deviation is set too low, the problem becomes infeasible. For example, this happens in the cases presented in Fig. 3 when the maximum deviation is set to less than 8 min.

In our experience (and also in these experiments), we see that the running time of our algorithm on real-life instances is influenced by the number of conflicts and the number of iterations. The intuition is that denser timetables or busier infrastructures will lead to a higher number of conflicts and iterations, but these relationships are not easily quantifiable. For example, if a timetable is almost feasible, the algorithm is likely to terminate almost immediately regardless of the density timetable or the available capacity in the infrastructure. However, we can report that the timetable used in these experiments was chosen by Norwegian route planners as a case study due to its length, high density, and little available capacity ([23]), all of which made manual modifications very time consuming.

Fig. 3
figure 3

Objective value and running time for a single problem instance (add-long case #1) as a function of the maximum deviation constraint. Top: using the adjust timetable algorithm mode. Bottom: using the find slot algorithm mode. Crosses indicate infeasible values for the max deviation

Full size image

6 Discussion and Future Work

For several years, one important objective of the Operations Research community was to develop algorithms to produce “optimal” timetables. Unfortunately, while some of these algorithms have been validated on realistic instances, their usage in practical settings is still nonexistent, to the best of our knowledge. Two main reasons can be identified. First, the actual complexity and size of real-life instances can produce an unacceptable increase in computation time. Second, practitioners struggle with providing a precise definition of optimality, and timetables which are optimal according to an agreed objective function may eventually not satisfy the route planners.

In this work, we take a step back, and rather than trying to replace the work of a route planner, we just aid it. We consider the typical workflow of a route planner in the context of short-term timetabling, which consists of iterative adjustments of an existing timetable. Most of the time spent in this process by route planners goes into regaining feasibility after modifications to the timetable have been made. This is exactly what our model is designed to achieve. After the route planner applies changes to a timetable and this becomes infeasible, our model tries to adjust it to regain feasibility by making as little modifications as possible. This method has the advantage of dealing with both issues discussed above. First, the model remains simple enough that it can be applied to real-life instances. Second, we do not need to deal with a vague definition of optimality, leaving to the route planner the decision of how to make major changes in a timetable while only focusing on the very fine adjustments.

Another important aspect of the proposed approach has to do with the human factor. Route planners may not want a tool that tells them how an optimal timetable looks like. Rather, they may prefer a tool that helps them build one.

The decision support tool presented in this paper has been tested and validated over several weeks by the Norwegian route planners on a busy railway line in Norway, who reacted positively to the possibility of using this tool in the future. However, a few things are still missing before the tool is ready for introduction into the daily routine of a route planner. As it was presented, the algorithm does not support hourly periodicity (e.g., a train should leave a certain station at minute hh:05 of every hour), and we do not take that into account when regaining feasibility. This is important, because passengers expect most of the trains to be periodic throughout the day (i.e., they depart at regular intervals). To fix this, we plan to implement the concept of quasi-periodicity as described in [15], which would let us produce an almost perfectly periodic timetable that can be presented to the public as a perfectly periodic timetable.

A more detailed oracle function that supports a precise microscopic modeling of more complex resources is also under development. This requires abundant care as to not ruin the assumption of our approach that the time spent on the oracle should be negligible in respect to the time spent on the main problem itself. Indeed, understanding the relationship between the running time of the algorithm and the complexity/number of oracle calls is an interesting avenue for future work.

Another useful feature would be the ability to relax parts of the model. Certain rules, e.g., the connection rules, are less important than the others and could be modeled as part of the objective rather than as constraints. Other small things that are missing from the current implementation include a more detailed interface to the railML format, support for more precise routing in stations, support for pre-signals, and some more, all of which we plan to include into the software in the following years.