A Simple Characterization of Assignment Mechanisms on Set Constraints

Abstract

We consider the problem of allocating divisible/indivisible goods to agents according to agents’ ordinal preferences. Hashimoto et al. [15] provided a nonalgorithmic and axiomatic characterization of well-studied probabilistic serial (PS) mechanism. Recently, Fujishige et al. [12] generalized the PS mechanism where goods are enlarged from a fixed set to a family of sets which is a polytope defined by a system of linear inequalities associated with submodular functions. The above extended PS (EPS) greatly improved the flexibility of allocations. Based on these two results, in this paper, we investigate the nonalgorithmic and axiomatic characterization of EPS. We show that the EPS rule is the only mechanism satisfying the ordinal fairness and a newly defined non-wastefulness. The submodularity plays a crucial role in our arguments.

1 Introduction

We study the problem of allocating divisible/indivisible goods among agents. Various studies have been conducted on this subject. Over the last decade, many studies treated fair assignments over indivisible goods; see a recent survey paper [1] for more details. However, after a seminal paper by Bogomolnaia and Moulin [6] introducing the PS mechanism, various extensions and characterizations of PS have been proposed. Refer to recent papers and references therein [2, 3] for more details, and see [14] for general problems.

The following two types of research on PS are related to our work:

• 1. Recently, Fujishige et al. [12, 13, 18] proposed an extended PS (EPS) mechanism which enlarged the points (i.e., the goods with fixed quotas) to polytopes of good resources called base polyhedra defined in Sect. 2.

• 2. Approximately 10 years after Bogomolnaia and Moulin’s paper, a completely nonalgorithmic characterization of PS was presented by Hashimoto et al. [15].

In this paper, we generalize the characterization of PS by Hashimoto et al. [15] to the EPS allocation mechanism [12]. Precisely:

We used two concepts, ordinal-fairness and non-wastefulness to characterize EPS. We keep the same definition of ordinal fairness as the one given in [15], and redefined the non-wastefulness in a simple form. Therefore, the difference between PS and EPS can be viewed as the difference between the two non-wasteful concepts. Submodularity, the property of tight sets given in Proposition 1 plays a crucial role in the proofs associated with the non-wastefulness.

Although we assume a submodularity in our problem, the resource space is a polytope defined by a system of linear inequalities including many special cases. The results provide possibilities for further research, e.g., Doğan et al. [9] showed that some of their results used the ordinal-fairness. Refer to our papers [11,12,13, 18] for what the generalization means about EPS.

Here are some related works of literature.

Bogomolnaia and Moulin [6] proposed the well-studied PS mechanism. A fundamental property of the assignments obtained using the PS mechanism is the ordinal efficiency with respect to agents’ preferences, along with envy-freeness and weak strategy-proofness. Since then, PS has been extended or generalized to various settings, see, e.g., [2, 3, 14].

We enlarged the fixed quotas of goods to polytopes such that the quotas of goods vary [12, 18], and we also include the layer structure in [7], as pointed in [12, 18]. Comparing the allocation problems in [6, 15], our setting is multi-unit demands with submodular constraints on goods, which change the weak-strategyproof into a weaker concept called Nash equilibrium; see [12] for more details.

Furthermore, e.g., Chatterji and Li [8] treated the assignments of bundles. The mechanism is equivalent to PS under a restricted domain. Preferences are defined over bundles of goods with fixed quota for each good, which differs from our setting, polytopes, defined later.

After a decade of elusiveness, as indicated in [5], nonalgorithmic, axiomatic characterization was provided in [15], followed by a leximin characterization given in [4].

Our result is based on that of Hashimoto et al. [15], which is a redefinition of PS. Precisely, Hashimoto et al. provided two characterizations. Meanwhile, our work is a generalization of the first one¹ which includes a new concept ordinal fairness defined later. Besides, the axiomatic characterization proposed in [15] significantly depends on the fixed quotas of goods.

Heo and Yilmaz [17] generalized the characterization in [15] to weak preferences [17]. The mechanism with weak preferences and submodular constraints on goods has been completed by Sano and Zhan [18]. We restrict ourselves to the assignment problem with strict preferences in our characterization.

The following example shows the difference between PS and EPS, what agents can obtain when fixed quotas of goods are released, and related characterization.

Example 1

Consider three agents $\{1,2,3\}$ and three goods $\{e_1,e_2,e_3\}$, respectively, and let the quota of each good be 1. Suppose that the agents’ preferences are as follows:

$$\begin{array}{cc} 1 \qquad &{} e_1 \quad e_2 \quad e_3 \\ 2 \qquad &{} e_1 \quad e_2 \quad e_3 \\ 3 \qquad &{} e_3 \quad e_1 \quad e_2 \end{array}$$

i.e., agents 1 and 2 prefer $e_1$ to $e_2$ to $e_3$, and agent 3 prefers $e_3$ to $e_1$ to $e_2$. Here is an assignment:

(1)

where each entry P(i, j) of P means the proportion of good $e_j$ that agent i obtained.

Next, suppose that the resource of goods is formalized as²

$$\begin{aligned} &x_P(e_i)+x_P(e_j) \le 2 \qquad \mathrm{for} \; i,j \in \{1,2,3\},\\ &x_P(e_1)+ x_P(e_2)+x_P(e_3) \le 3, \end{aligned}$$

where $x_p \in \mathbb {R}^3$ is a vector, and each component of $x_P(e_i)$ $(i \in \{1,2,3\})$ is the column sum of P. We can obtain the following assignment:

(2)

Although the total resource is 3 in both cases, the resource associated with (2) is more flexible than fixed quota 1. Agents 1 and 2 obtain 1, more portion of their most preferred good $e_1$ in (2), comparing $\frac{1}{2}$ in (1). Assignments of (1) and (2) are computed from PS and EPS, respectively.

The rest of this article is organized as follows. Section 2 introduces the model, notations, and preliminary results. Section 3 describes the EPS mechanism. Section 4 gives the definitions of non-wastefulness and ordinal fairness. The main theorem is presented in Sect. 5. Section 6 gives the concluding remarks.

2 The Model

Let $N=\{1,2,\dots ,n\}$ be a set of agents and E be a set of goods. Each good $e \in E$ is considered as a type of goods and the number of available goods e can be more than one. Each agent $i\in N$ wants to obtain a certain amount of goods, denoted by $d(i) \in \mathbb {Z}_{>0}$. The vector $\mathbf{d}=(d(i) \mid i \in N) \in \mathbb {Z}_{>0}^N$ is called the demand (upper bound) vector.³

Suppose that each agent $i \in N$ has an ordinal preference

$$\begin{aligned} L^i: \ e^i_1 \succ _i \cdots \succ _i e^i_m, \end{aligned}$$

(3)

where $\{e^i_1, \dots , e^i_m \}=E$. Let ${\mathcal L}$ denote the profile of preferences $L^i \ (i\in N)$.

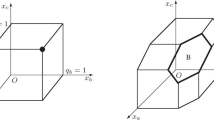
The resource space of goods is defined as a polytope $\{ x \in \mathbb {R}^m _{\ge 0} \mid A x \le \mathbf{b}\}$, where A is a nonnegative $k \times m$ matrix, and $\mathbf{b}$ is a k-dimensional vector. By a slight abuse of notation, we also use $(A,\mathbf{b})$ to denote a set of solutions induced by a system of linear inequalities.

For a given economy $(N,E,\mathcal{L}, \mathbf{d},(A,\mathbf{b}))$, denoted by RA, a random assignment, also called an expected allocation, is a nonnegative matrix $P \in \mathbb {R}_{\ge 0}^{N\times E}$ satisfying

• (i) $\sum _{e \in E} P(i,e) \le d(i) \;\; \text{for all}\ \ i \in N$  

• (ii) $\sum _{i \in N} P^i \in \{ x \in \mathbb {R}^m \mid A x \le \mathbf{b}\},$

where $P^i$ is the ith row vector of P, representing the probability of goods allocated to the agent i.

Note that $\sum _{i \in N} P^i$ is a vector $x_P \in \mathbb {R}^m$, each element of $x_P$ associated with a column sum of P, denoted as $x_P(e)$ for $e \in E$. Hence, we have $\sum _{i \in N} P^i =(x_P(e) \mid e \in E) =x_P$.

Next, we give a further definition of $(A,\mathbf{b})$.

Given a set function $\rho :2^E \rightarrow \mathbb {R}$, the family of sets of goods is a polytope $\mathbf{P}(\rho ) \subset \mathbb {R}^{E}$ satisfying

$$\begin{aligned} \mathbf{P}(\rho )=\{x\in \mathbb {R}^E \mid x(X) \le \rho (X), \; \forall X \subseteq E \}. \end{aligned}$$

(4)

where $x(X)=\sum _{e \in X} x(e)$.

To get desirable properties, we assume that $\rho$ satisfies the following submodular inequalities

$$\begin{aligned} \rho (X) + \rho (Y) \ge \rho (X \cup Y)+\rho (X \cap Y), \; \forall X,Y \in 2^E, \end{aligned}$$

(5)

and $\rho$ is non-decreasing, i.e., $\rho (X)\le \rho (Y)$ if $X \subseteq Y$ with $\rho (\emptyset )=0$. Polytope $\mathbf{P}(\rho )$ associated with a pair $(E, \rho )$ called a submodular system satisfying these conditions is a polymatroid and $\rho$ is a rank function. Note that polymatroid $\mathbf{P}(\rho ) \subset \mathbb {R}^E_{\ge \mathbf{0}}$. See [10] for more details about submodular functions.

Next, assume that goods are in high demand and the resource is completely allocated. In other words, the total goods assigned are on the maximal vectors of $\mathbf{P}(\rho )$ satisfying

$$\begin{aligned} \mathrm{B}(\rho )=\{x\in \mathbb {R}^E \mid x \in \mathbf{P}(\rho ), x(E)=\rho (E) \}. \end{aligned}$$

(6)

We call $\mathrm{B}(\rho )$ in (6) the base polyhedron of the submodular system $(E, \rho )$, and $\mathrm{B}(\rho )\ne \emptyset$.

In what follows, we treat assignment problem $\mathbf{RA}=(N,E,\mathcal{L},\mathbf{d}=(d(i) \mid i \in N), (E,\rho ))$.

Remark 1

We have the following relation between rank function $\rho$ and base polyhedron $\mathrm{B}(\rho )$ [10, 12].

$$\begin{aligned} \rho (X) =\max \{ x(X) \mid x \in \mathrm{B}(\rho ) \} \qquad (\forall X \subseteq E). \end{aligned}$$

(7)

By the assumption of demand upper bound $\mathbf{d}$ satisfying $\sum _{i \in N} d(i) \ge \rho (E)$, from (6) and (7), we obtain output $x_P \in \mathrm{B}(\rho )$ while maximizing $\mathbf{d}$ in $\mathrm{P}(\rho )$ during the execution of EPS defined in the next section.

Here are some economic properties related to submodularity. If we rewrite (5) as

$$\begin{aligned} \rho (X) -\rho (X \cap Y) \ge \rho (X \cup Y) -\rho (Y) , \; \forall X,Y \in 2^E, \end{aligned}$$

(8)

inequalities (8) is called “diminishing return” or economies of scale/scope. Property (8) allows goods with higher preferences to share more portion of total goods than those with lower preferences since more preferred goods were chosen earlier, as shown in Example 1 of the introduction, where submodularity acts on goods. When assigning lectures to professors, submodularity implies higher specialities bringing higher effects [16].

The following proposition is fundamental in the theory of submodular functions and optimizations.

Proposition 1

Given a vector $x \in \mathbf{P}(\rho )$ and $X,Y \subseteq E$, if we have $x(X)=\rho (X)$ and $x(Y)=\rho (Y)$, then $x(X\cup Y)=\rho (X\cup Y)$ and $x(X\cap Y)=\rho (X\cap Y)$. That is, the x-tight sets are closed with respect to the set union and intersection.

For any $e \in E$, define $\chi _e$ to be the unit vector in $\mathbb {R}^E$ such that $\chi _e(f)=1$ if $f=e$ and $\chi _e(f)=0$ if $f \in E \setminus \{e\}$.

For each $x \in \mathrm{P}(x)$, by Proposition 1, there exists a unique maximal x-tight set, denoted by sat(x), which is equal to the union of all tight sets for x. The function sat: $\mathrm{P}(\rho ) \rightarrow 2^E$ is called the saturation function.

Later, we use the following notation in the newly non-wastefulness. For $x \in \mathrm{B}(\rho )$ and $e \in \mathrm{sat}(x)$, define

$$\begin{aligned} \mathrm{dep}(x,e) = \{ e' \in E \mid \exists \alpha >0: x + \alpha (\chi _e - \chi _{e'}) \in \mathrm{B}(\rho ) \}, \end{aligned}$$

(9)

which is called the dependence function for $(E, \rho )$. It is known that [10, Chap. 2]

$$\begin{aligned} \mathrm{dep}(x,e) = \bigcap _{e \in\, X\, \subseteq\, E} \{ X \mid x(X) = \rho (X) \}. \end{aligned}$$

(10)

Using Proposition 1, we have $x(\mathrm{dep}(x,e))= \rho (\mathrm{dep}(x,e)).$

We will repeat chains in the sequel. It is essential to know [10, 12, Sec. 7] that for $\forall x \in \mathrm{B}(\rho )$, the family of tight sets $\{ X \subseteq E \mid x(X) = \rho (X) \}$ is completely determined by a maximal chain:

$$\begin{aligned} \hat{\mathcal {C}}: {S}_0=\emptyset \subset \hat{S}_1 \subset \dots \subset \hat{S}_p=E, \end{aligned}$$

(11)

where $x(\hat{S}_i)=\rho (\hat{S}_i)$ for $i=0,1,\dots ,p.$

Let $\hat{T}_i = \hat{S}_i \setminus \hat{S}_{i-1}$ for $i=1,\dots ,p$, then $\{\hat{T}_1, \dots , \hat{T}_p\}$ form a partition of E. By the maximal chain, we mean that for each $X\subseteq E$ with $x(X)=\rho (X)$, we have $X=\hat{T}_{\ell _1} \cup \cdots \cup \hat{T}_{\ell _k}$, $1 \le \ell _1 \le \cdots \le \ell _k \le p$.

In the following, we write one element set $\{e\}$ as e for simplicity.

3 Extended PS Mechanism

Fix a random assignment problem $\mathbf{RA}=(N,E,\mathcal{L}, \mathbf{d},(E,\rho ))$. A mechanism is a mapping from $\mathbf{RA}$ into allocation $P \in \mathbb {R}^{N \times E}_{\ge 0}$ meeting some requirements.

As mentioned earlier, EPS is an extension of the standard PS mechanism of [6], which was proposed by Fujishige et al., and for more details, the reader can refer to [12].

Recall that for each $i \in N$, agent i’s preference is given by $L^i$ in (3), and $\mathcal {L}=(L^i \mid i \in N)$. Based on the collection (a multiset) of the first (most favorite) elements $e^i_1$ for all agents $i \in N$, define a nonnegative integral vector $b(\mathcal{L})\in \mathbb {Z}_{\ge 0}^E$ by

$$\begin{aligned} b(\mathcal{L})= \sum _{i\in N} d(i)\chi _{e_1^i}, \end{aligned}$$

(12)

where we may have $e_1^i=e_1^j$ for distinct $i, j\in N$ and d(i) is the integral demand upper bound of agent $i \in N$.

During the execution of the following algorithm, the current lists $L^i$ ($i \in N$) may get shorter because of removal of exhausted goods. Also note that $S_p$ is the set of types of goods saturated at stage p.

Algorithm I

Extended Probabilistic Serial Algorithm (EPS) [3, 12]

Input::

A random assignment problem $\mathbf {RA}=(N,E,\succ ,\mathbf {d},(E, \rho ))$.

Output::

An expected allocation $P\in \mathbb {R}^{N \times E}_{\ge 0}$.

Step 0::

For each $i\in N$ put $x^i\leftarrow \mathbf {0}\in \mathbb {R}^E$ (the zero vector), and put $S_0\leftarrow \emptyset$.

Put $p\leftarrow 1$, $x^*\leftarrow \mathbf {0}$, and $\lambda _0 \leftarrow 0$.

Step 1::

For current (updated) $\mathcal{L}=(L^i\mid i\in N)$, using $b(\mathcal{L})$ in (12), compute

$$\begin{aligned} \lambda _p = \max \{t \ge \lambda _{p-1}\mid x^*+(t-\lambda _{p-1}) b(\mathcal{L})\in \mathrm{P}(\rho )\}. \end{aligned}$$

(13)

For each $i\in N$ put $x^i\leftarrow x^i+(\lambda _p-\lambda _{p-1})d(i) \chi _{e^i_1}$.

Put $x^*\leftarrow x^*+(\lambda _p-\lambda _{p-1}) b(\mathcal{L})$ and $S_p\leftarrow \mathrm{sat}(x^*)$.

Step 2::

Put $T\leftarrow S_p\setminus S_{p-1}$.

Update $L^i$ by removing all elements of T from current $L^i$ $(i\in N)$.

Step 3::

If $\rho (S_p)<\rho (E)$, then put $p\leftarrow p+1$ and go to Step 1.

Otherwise ($\rho (S_p)=\rho (E)$) put $P(i,e)\leftarrow x^i(e)$ for all $i\in N$ and $e\in E$.

Return P.

When Algorithm I terminates, we obtain a chain:

$$\begin{aligned} \mathcal {C}: \quad \emptyset =S_0 \subset S_1 \subset \cdots S_p = E \end{aligned}$$

(14)

satisfying $\rho (S_t)=x_P(S_t)$ for all $0 \le t \le p$. Chain (14) is a subchain of the maximal chain of $x_P$ defined in (11).

Remark 2

Recall that agent $i \in N$ can be viewed as d(i) subagents, and each subagent eats goods at unit speed. As in paper [6], the parameter t in (13) can be considered as time. The monotonic assumption of $\rho$ implies that the agents eat at nonnegative consecutive time intervals.

Fix a preference profile $\mathcal {L}=(L^i \mid i \in N)$. Given two assignments P and Q, recall that $P^i=(P(i,e) \mid i \in N)$ and $Q^i=(Q(i,e) \mid i \in N)$. We say that $P^i$ stochastically dominates (sd) $Q^i$, denoted by $P^i \succeq _i^\mathrm{sd} Q^i$, if $\sum _1^\ell P(i,e^i_\ell ) \ge \sum _1^\ell Q(i,e^i_\ell )$ for all $\ell =1, \dots , m$. We say that Q is stochastically dominated by P if we have $P^i \succeq _i^\mathrm{sd} Q^i$ for all $i \in N$ and $P \ne Q$. An assignment P is ordinally efficient if P is not stochastically dominated by any other allocation.

An allocation P is normalized sd-envy-free if for all $i,j \in N$, $\frac{1}{d(i)} P^i \succeq _i^{sd} \frac{1}{d(j)} P^j$.

Theorem 2

(Theorems 5.1 and 5.2 [12]) Algorithm I computes an expected allocation that is ordinally efficient and normalized envy-free.

Example 2

Suppose $N=\{1,2,3,4\}$ and $E=\{a,b,c,g\}$. The preference profile is given as follows,

$$\begin{aligned} \begin{array}{cc} 1 &{} a\succ _1 b \succ _1 c \succ _1 g \\ 2 &{} a \succ _2 c \succ _2 b \succ _2 g \\ 3 &{} a \succ _3 c \succ _3 g \succ _3 b \\ 4 &{} b \succ _4 a \succ _4 g \succ _4 c \end{array} \end{aligned}$$

(15)

The demand upper bound vector is given by $\mathbf{d}=(4,2,1,1) \in \mathbb {Z}^N_{>0}$, and the submodular function $\rho$ on E is defined by

$$\begin{aligned} \rho (X)={\left\{ \begin{array}{ll} 4 |X |&{}\mathrm{if} \; |X |\le 2 \\ \;\;\ 8 \quad &{} \mathrm{if} \; |X |> 2 \end{array}\right. } \quad (\forall X \subseteq E). \end{aligned}$$

(16)

Each good in E can be interpreted as a shop in a tenant, where the value of $\rho$ represents the area. Here, The total area is eight. To keep diversity, the area of each shop is at most four, while the popular shop can also get larger portions of the area.

The following matrix P is an assignment obtained using EPS.

(17)

After Step 1, agents 3 and 4 get ${\frac{4}{7}}$ of their best goods, agent 2 gets ${2 \times \frac{4}{7}}$, and agent 1 gets ${4 \times \frac{4}{7}}$. At Step 2, they get the remaining goods. The (maximal) set of goods exhausted at steps 1 and 2 of EPS are $\{a\}$ and $\{a,b,c,g\}$, respectively.

Using the same $\mathrm{B}(\rho )$ in (16), if we change the preference profile (15) by swapping goods a and g while keeping the others, we obtain an assignment P as follows,

(18)

Now good g, instead of a, shares a portion 4 from the total resources 8 to sufficiently satisfy agents’ preferences.

4 Non-wastefulness and Ordinal Fairness

Two concepts, namely, non-wastefulness and ordinal fairness, are essential for characterizing the EPS mechanism introduced in Sect. 3.

Let $\mathbf{RA}=(N,E,\mathcal{L}, \mathbf{d},(E,\rho ))$.

Definition 1

A random assignment P is non-wasteful at $\mathcal {L}$ if $\forall (i, e) \in N \times E$ such that $P(i,e)>0$, we have:

$$\begin{aligned} e \notin \mathrm{dep}(x_P,e') \quad \forall e' \succ _i e. \end{aligned}$$

(19)

Recall that $\mathrm{dep}(x_P,e')$ is also a well-define $x_P$-tight set, i.e., $x_P(\mathrm{dep}(x_P,e'))=\rho (\mathrm{dep}(x_P,e'))$ as indicated in (10).

Compared with the case of PS where each good $e \in E$ with a fixed quota $q_e$, the non-wastefulness at $\mathcal {L}$ is $\forall e' \succ _i e$ such that $P(i,e)>0$, we have $x_P(e')=q_{e'}$. Our definition is also simple despite the bind being a set function.

To understand definition (19) further, let us define a notation on triple $(L^i,e,P^i)$ as

$$\begin{aligned} \overline{W}(L^i,e,P^i) \equiv \bigcup _{e' \succ _i e} \mathrm{dep}(x_P,e'). \end{aligned}$$

(20)

Then, for any good $e\in E$ with $P(i,e)>0$, we can see that all $e'\in E$ satisfying $e'\succ _i e$ are in a saturated set $\overline{W}(L^i,e,P^i)$ which does not include good e from following facts.

• (i) $e \notin \overline{W}(L^i,e,P^i)$,

• (ii) $\{ e' \mid e' \succ _i e \} \subseteq \overline{W}(L^i,e,P^i))$,

• (iii) $x_P(\overline{W}(L^i,e,P^i))= \rho (\overline{W}(L^i,e,P^i))$

We have: (i) follows from the definitions of non-wasteful and $\overline{W}$. (ii) follows from $e' \in \mathrm{dep}(x_P,e')$. Since $\mathrm{dep}(x_P,e')$ is a $x_P$-tight set, we obtain (iii) by Proposition 1. All $\overline{W}(L^i,e,P^i)$ form a chain of $x_P$-tight sets with $P(i,e)>0$ because this is an inductive property on preferences for each pair $(i,e) \in N \times E$.

Proposition 3

Algorithm I computes an expected allocation $\widehat{P}$ that is non-wasteful.

Proof

Suppose that $\widehat{P}$ is not non-wasteful. Then, by the definition, there exists $i \in N$, $e \in E$, and $\widehat{P}(i,e)>0$ such that

$$\begin{aligned} e \in \mathrm{dep}(x_{\widehat{P}},e') \quad \forall e' \succ _i e. \end{aligned}$$

(21)

By the definition of dep function (9), there exists $\epsilon >0$, and the vector $x_{\widehat{P}}+\epsilon (\chi _{e'}-\chi _e) \in \mathrm{B}(\rho )$. Then, we can obtain a new assignment $\widehat{P}'$ by replacing $\widehat{P}'(i,e)=\widehat{P}(i,e) -\epsilon$, $\widehat{P}'(i,e)=\widehat{P}(i,e')+\epsilon$, and keeping other entries the same as those of $\widehat{P}$. Assignment $\widehat{P}'$ sd-dominates ${\widehat{P}}$. This contradicts the ordinal efficiency of EPS by Theorem 2.

Recall that $\mathrm{dep}(x_{\widehat{P}},e')$ is a well-defined $x_{\widehat{P}}$-tight set by Proposition 1 because of submodularity. $\square$

Let $U(L^i,e) \equiv \{e' \in E \mid e' \succeq _i e \}$ be the upper contour set of good e at $\succ _i$. For an assignment P, let $F(L^i,e,P^i)$ be the probability that agent i is allocated at least as good as e under $P^i$ which satisfies

$$\begin{aligned} F(L^i,e,P^i)=\frac{1}{d(i)} \sum _{\;e' \in U(L^i,e)} P(i,e'), \; \; \forall (i,e) \in N \times E, \end{aligned}$$

(22)

we call $F(L^i,e,P^i)$ agent i’s (normalized) surplus at e under $P^i$.

Definition 2

An assignment P is ordinally fair⁴ at $\mathcal {L}$ if $\forall i,j \in N, \; e \in E$ such that $P(i,e)>0$, we have:

$$\begin{aligned} F(L^i,e,P^i) \le F(L^j,e,P^j). \end{aligned}$$

(23)

As mentioned in the introduction, ordinal fairness in Definition 2 is the same as the one in [15], which defines a fair property. From (23), we obtain that for any ordinally fair assignment, agents must share the same surplus value if they have a positive probability on the same good.⁵

Example 2, continues

For assignment (17), we have $F(L^1,a,P^1) =F(L^2,a,P^2) = F(L^3,a,P^3) = 4/7$. All of the remaining $F(L^i,e,P^i)$ are 1.

The following Proposition 4 follows from [15]. It gives a relation with the chain (14) of EPS, and we provide its proof for completeness.

Proposition 4

Algorithm I computes an expected allocation $\widehat{P}$ that is ordinally fair.

Proof

For the chain (14) obtained after Algorithm I, denote $\Delta S_t= S_t \setminus S_{t-1}$ ($1 \le t \le p$).

Suppose $P(i,e)>0$, $e=e^i_1 \in \Delta S_t$ at Step t for agent i, then each agent j has $e^j_1 = e'\succeq _j e$ in current $L^j$. We have $e' \in \Delta S_t$ or $e' \in S_{t+\ell }$, where $\ell >1$. In the former case, we have both $e, e'\in \Delta S_t$. Hence, $F(L^i,e,\widehat{P}^i) = F(L^j,e, \widehat{P}^j)$. In the latter case, we have

$$\begin{aligned} F(L^i,e,\widehat{P}^i) < F(L^j,e', \widehat{P}^j) \le F(L^j,e, \widehat{P}^j), \end{aligned}$$

(24)

where the first inequality from $e\in \Delta S_t$ and $e' \in S_{t+\ell }$, the second one from $e' \succeq _j e$. Both cases mean

$$\begin{aligned} F(L^i,e,\widehat{P}^i) \le F(L^j,e, \widehat{P}^j), \; \forall e \in \Delta S_t \; (t \ge 1), \forall i,j \in N. \end{aligned}$$

(25)

Since t, i, and j are arbitrary, and $S_t$, $\Delta S_t$, and $S_{t+\ell }$ $(\ell >1)$ include all goods, i.e., (25) is satisfied by $\forall e\in E$ and $\forall i,j \in N$. Hence, $\widehat{P}$ is ordinally fair. $\square$

Example 2 continues

Assignment (17) can only have two values of $F(L^i,e,P^i)$. It is easy to check that Proposition 4 is satisfied since (17) is obtained using the EPS. The smaller values of $F(L^i,a,P^i)$ with $P(i,a)>0$ are equal.

5 Main Results

We now state our main characterization of the EPS mechanism. The proof follows closely to that of Theorem 1 given by [15]. However, we give the proofs related to non-wastefulness for completeness.

Theorem 5

A mechanism is ordinally fair and non-wasteful if and only if it is EPS.

The “if” part of Theorem 5 has been proved by Propositions 3 and 4. Hence, we will show the converse. The main difference from [15] is the non-wastefulness associated with submodularity.

We need some notations.

Fix an assignment P. For all $e \in E$, define

$$\begin{aligned} \pi (e)=\min _{i \in N} F(\succ _i,e,{ P}^i), \end{aligned}$$

(26)

we get different values $\pi _1< \cdots < \pi _p$ of $\pi$ with $1 \le p \le m$. Grouping goods satisfying

$$\begin{aligned} T_s(e)=\{ e \in E \mid \pi (e)= \pi _s\}, \end{aligned}$$

(27)

we obtain a partition $\{T_1, \dots , T_p\}$ of E. Moreover, let $\mathbf{S}_s=T_1 \cup \cdots \cup T_s$ with $\mathbf{S}_0=\emptyset$.

For each ${\bar{e}}_s \in E \setminus \mathbf{S}_{s-1}$, define

$$\begin{aligned} N_s({\bar{e}}_s) =\{i \in N \mid {\bar{e}}_s \succeq _i e', \forall e' \in E \setminus \mathbf{S}_{s-1} \} \end{aligned}$$

(28)

as the set of agents who prefer ${\bar{e}}_s$ most in the complement of set $\mathbf{S}_{s-1}$. Additionally, if ${\bar{e}}_s \in T_s$, we denote above ${\bar{e}}_s$ as ${\bar{e}}_{T_s}$.

Lemma 6 is about the ordinal fairness, and its proof is similar to that of Theorem 1 (Steps 1 and 2) [15].

Lemma 6

If P is an ordinally fair assignment, we have:

$$\begin{aligned} P(k,{\bar{e}}_{T_s})=0 \quad { if} \; k \notin N_s({\bar{e}}_{T_s}), \end{aligned}$$

(29)

$$F(\succ _i,{\bar{e}}_{T_s},{ P}^i) =\pi ({\bar{e}}_{T_s}), \quad \forall i \in N_s({\bar{e}}_{T_s}).$$

(30)

Note that there is no corresponding part of Lemma 7 in the paper [15] since the non-wastefulness is simple for each good with a fixed quota.

Lemma 7

If P is a non-wasteful assignment, then

$$\begin{aligned} x_P(\mathbf {S}_s) = \rho (\mathbf {S}_s) \quad \forall s=1,\dots , p. \end{aligned}$$

(31)

Proof

We prove it by induction. This is true for $\mathbf{S}_0=\emptyset$. Assuming that it is true for $\forall t < s$, we show that it is true for s.

First, we show

$$\begin{aligned} \mathrm{dep}(x_P,e_s) \subseteq \mathbf{S}_{s} \quad \forall e_s \in T_s. \end{aligned}$$

(32)

For a contradiction, suppose $\exists \hat{e} \in \mathrm{dep}(x_P,e_s)$ such that $\hat{e} \in E\setminus \mathbf{S}_{s}$. Let $\hat{e} \in T_t$ with $t>s.$

If there exists $i \in N$ such that $P(i,\hat{e})>0$ and $e_s \succ _i \hat{e}$, by the definition of non-wastefulness, we have $\hat{e} \notin \mathrm{dep}(x_P,e_s),$ which is a contradiction to the assumption. Otherwise, for all $P(i,\hat{e})>0$, we have $\hat{e} \succ _i e_s$. By the definition of (22) and (26), we obtain another contradiction of $t>s$.

Since $e_s \in \mathrm{dep}(x_P,e_s)$ and from (32), we obtain

$$\begin{aligned} T_s \subseteq \bigcup _{e_s\in T_s}\mathrm{dep}(x_P,e_s) \subseteq \mathbf{S}_{s}. \end{aligned}$$

(33)

From definition $T_s \cup \mathbf {S}_{s-1} = \mathbf {S}_{s}$ and (33), we get

$$\begin{aligned} \mathbf {S}_{s-1} \bigcup _{e_s\in T_s}\mathrm{dep}(x_P,e_s) = \mathbf{S}_{s}. \end{aligned}$$

(34)

Now, by the inductive assumption $x_P(\mathbf{S}_{s-1} )= \rho (\mathbf{S}_{s-1})$, $x_P(\mathrm{dep}(x_P,e_s)) = \rho (\mathrm{dep}(x_P,e_s))$, and Proposition 1, we have (31), this ends the proof. $\square$

From Lemmas 6 and 7, we have: If P is an ordinally fair and non-wasteful assignment, then

$$\begin{aligned} \sum _{{\bar{e}}_{T_s}\in T_s} \sum _{j\, \in\, N} P(j,{\bar{e}}_{T_s})=\sum _{{\bar{T_e}}_s\in T_s} \sum _{j\, \in\, N_s({\bar{e}}_{T_s})} P(j,{\bar{e}}_{T_s}) =\rho (\mathbf{S}_s)-\rho (\mathbf{S}_{s-1}),\;\ 1 \le s \le p. \end{aligned}$$

(35)

The rest of the proof of Theorem 5 can be shown in a very similar way as Steps 4 and 5 in [15]. (Arguments that do not use non-wastefulness can be extended, these are omitted.)

Let $\widehat{P}$ represent the random assignment obtained from EPS. We prove it by induction.

Suppose that for $\forall t < s$, (i) $\forall {\bar{e}}_{T_t} \in T_t$ and $\forall i \in N_t({\bar{e}}_{T_t})$, we have $F(L^i,{\bar{e}}_{T_t},{ P}^i) = F(L^i,{\bar{e}}_{T_t}, \widehat{P}^i)=\pi ({\bar{e}}_{T_t})$, (ii) $\forall {\bar{e}}_{T_t} \in T_t$ and $\forall k \notin N_t({\bar{e}}_{T_t})$, we have $P(k,{\bar{e}}_{T_e})=\widehat{P}(k,{\bar{e}}_{T_e})=0$. The inductive assumption holds trivially for $s=1$. We prove that they hold for Step s and thus $P=\mathrm{EPS}$.

By the same arguments as that given in [15], we can show at Step s of EPS,

$$\begin{aligned} F(L^i,{\bar{e}}_{T_s},\mathrm{\widehat{P}}^i)\ge \pi ({\bar{e}}_{T_s}) \quad \forall {\bar{e}}_{T_s} \in T_s, \; \forall i \in N_s({\bar{e}}_{T_s}). \end{aligned}$$

(36)

Now, we show that for each ${\bar{e}}_{T_s} \in T_s$ and $j \in N_s({\bar{e}}_{T_s})$, we have $\pi ({\bar{e}}_{T_s})=F(L^j, {\bar{e}}_{T_s}, \widehat{P}^j)$ and $\widehat{P}(k,{\bar{e}}_{T_s})=0$ $\forall k \notin N_s({\bar{e}}_{T_s})$. Proving the first claim is sufficient since ${\bar{e}}_{T_s}$ cannot be allocated to agent k in this case.

Suppose for a contradiction that there exists ${\bar{e}}_s \in T_s$ and $i \in N_s({\bar{e}}_{T_s})$, $F(L^i, {\bar{e}}_{T_s}, P^i)= \pi ({\bar{e}}_{T_s}) < F(L^i, {\bar{e}}_{T_s}, \widehat{P}^i)$. Then,

$$\begin{aligned} \begin{aligned} \sum _{{\bar{e}}_{T_s}\in T_s} \sum _{j\, \in\, N_s({\bar{e}}_{T_s})} P(j,{\bar{e}}_{T_s}) =&\ \sum _{{\bar{e}}_{T_s}\in T_s} \sum _{j\, \in\, N_s({\bar{e}}_{T_s})} \Bigl \{ F(L^j,{\bar{e}}_{T_s},{ P}^j)- \sum _{e'\succ _j \,{\bar{e}}_{T_s}}{P}(j,e') \Bigr \} \\ <&\sum _{{\bar{e}}_{T_s}\in T_s} \sum _{j\, \in\, N_s({\bar{e}}_{T_s})} \Bigl \{ F(L^j,{\bar{e}}_{T_s},\widehat{P}^j)- \sum _{e'\succ _j\,{\bar{e}}_{T_s}}\widehat{P}(j,e') \Bigr \} \\ =&\sum _{{\bar{e}}_{T_s}\in T_s} \sum _{j\, \in\, N_s({\bar{e}}_{T_s})} \widehat{P}(j,{\bar{e}}_{T_s})= \rho ({\mathbf{S}}_s)-\rho ({\mathbf{S}}_{s-1}), \end{aligned} \end{aligned}$$

where the strict inequality follows from (36), Lemma 6, the supposition, and $P(j,{\bar{e} }_{T_s})=\widehat{P}(j,{\bar{e}}_{T_s})$ for all ${\bar{e}}_{T_s} \in T_s, j \in N_s({\bar{e}}_{T_s}$) by the inductive assumption. Therefore,

$$\begin{aligned} \sum _{t \le s} \sum _{{\bar{e}}_{T_t} \in T_t} \sum _{j\, \in\, N_t({\bar{e}}_{T_t})} P(j,{\bar{e}}_{T_t}) < \rho (T_1 \cup \cdots \cup T_s) =\rho (\mathbf{S}_s), \nonumber \end{aligned}$$

this contradicts $\sum _{i \in N} P^i \in \mathrm{B}(\rho )$ if $s=p$, violates Lemma 7. Hence, P coincides with $\widehat{P}$. $\square$  

6 Concluding Remarks

We considered the problem of allocating a family of good sets to agents using agents’ ordinal preferences.

• We provide a new definition of non-wastefulness given in (19), despite the constraints are defined on the sets of goods. From Lemma 6, and the ordinal fairness in (23), we obtain the original form of submodular constraints on sets shown in Lemma 7. We adapted the arguments by Hashimoto et al. [15], and submodularity plays a central role in our setting.

• The main result is given in Theorem 5, a simple nonalgorithmic redefinition, or characterization of the EPS mechanism developed by Fujishige et al. [12]. The EPS mechanism greatly increases the flexibility of assignments.

The leximin maximization, a characterization given in [4], can also be extended to the EPS mechanism for a random assignment with a family of good sets, as shown in [11, 18].

Recently, the related simultaneous eating mechanism (which is a mechanism presented in Sect. 3 with different agents’ eating speed) is also generalized on polytopes [3]. The unified characterization here will provide a clue for further research in these assignment problem.