Abstract
In the Inventory Routing Problem, customer demand is satisfied from inventory which is replenished with capacitated vehicles. The objective is to minimize total routing and inventory holding cost over a time horizon. If the customers are located relatively close to each other, one has the opportunity to satisfy the demand of a customer by inventory stored at another nearby customer. In the optimization of the customer replenishments, this option can be included to lower total costs. This is for example the case for ATMs in urban areas where an ATM-user that wants to withdraw money could be redirected to another ATM. To the best of our knowledge, the possibility of redirecting end-users is new to the operations research literature and has not been implemented, but is being considered, in the industry. We formulate the Inventory Routing Problem with Demand Moves in which demand of a customer can (partially) be satisfied by the inventory of a nearby customer at a service cost depending on the quantity and the distance. We propose a branch-price-and-cut solution approach which is evaluated on problem instances from the literature. Cost improvements over the classical IRP of up to 10% are observed with average savings around 3%.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Inventory Routing Problem (IRP) combines the optimization of inventory management and routing of the replenishments for a set of customers. This problem is relevant in vendor-managed inventory settings, in which a supplier (the vendor) takes both the routing and replenishment decisions. The customers need to be served over a given time horizon and the vendor needs to decide when to replenish each customer, how much to deliver, and how to combine the visits in feasible vehicle routes while minimizing total routing and inventory holding costs. Each customer faces a certain demand per period which must be satisfied from the customer’s inventory, this demand is composed of demands of multiple end-users. If the customers are located relatively close to each other, one may have the opportunity to satisfy a part of the demand of a customer by another nearby customer by redirecting some of the end-users. This is for example the case when considering ATMs in urban areas where ATMs are often located in close proximity. This provides the opportunity to redirect ATM-users (“end-users”) who want to withdraw money from one ATM to another in case of a cash shortage, hence, to move demand between ATMs (“customers”). The same principle could also be applied to, e.g., urban bike sharing systems. Our business partner considers this a realistic option to reduce their ATM replenishment costs. Moreover, in the future, it might be possible to provide ATM-users with information upfront via a mobile application which can increase customer service by avoiding visits to out-of-service ATMs. Besides that, it is also an option to give the user a small discount if they withdraw cash from certain ATMs. Note that, for example in the Netherlands, a user can withdraw money at every ATM without transaction costs, even if an ATM is not owned by his own bank but by a competing bank. Hence, stimulating a user to withdraw at a certain ATM does not result in transaction costs for the user.
The possibility of redirecting end-users can be incorporated in the optimization of the customer replenishments to reduce total costs. We define the Inventory Routing Problem with Demand Moves (IRPDM) in which demand of a customer can (partially) be satisfied by another customer. We assume that a service cost is incurred by the vendor for each demand move. This cost can, for example, reflect a loss in service experienced by the end-user or the actual cost of the discount provided to the end-users. Hence, the IRPDM consists of deciding on the timing and quantity of deliveries to each customer, both to satisfy its own demand and potential demand moved from other customers to this customer, deciding on the vehicle routes to perform the replenishments and on demand moves between customers. The objective of the IRPDM is to minimize the total routing, inventory holding and service costs.
The contributions of this paper can be summarized as follows. We introduce the notion of demand moves and define the IRPDM. We solve the problem with a branch-price-and-cut (BPC) solution method based on the approach by Desaulniers et al. [1] for the IRP. Valid Inequalities (VIs) from the IRP literature are not directly applicable to the IRPDM. Non-trivial modifications of these inequalities are proposed to ensure that they capture the effect of the demand moves in the IRPDM. Experiments on synthetic IRP instances from the literature illustrate the performance of the proposed solution approach and offer insight in the benefits of allowing demand moves in inventory routing problems. Moreover, sensitivity analysis, for example on the service costs, is conducted to derive managerial insights.
The paper is organized as follows. Section 2 provides an overview of related literature. In Section 3, we formally describe the problem and we present a mathematical programming formulation for the IRPDM. Section 4 describes the solution method and contains an extensive description of the VIs. The results of the computational experiments are detailed in Section 5. Finally, Section 6 discusses conclusions and directions for future research.
2 Literature
Inspired by a real-life case on ATM replenishment, this paper contributes to a recent stream of papers on cash supply chains. Van Anholt et al. [2] propose a three-step heuristic to solve a combined inventory management and routing problem for so-called Recirculation ATMs (RATM). At an RATM, a user can both withdraw and deposit money; hence, the IRP solutions contain both delivery and pick-up activities. Money that is picked up at one ATM can be used for a replenishment of another ATM. Hence, transshipments performed by a vehicle are included in the model. Instances are based on real-life data with up to 200 customers and one vehicle per depot for a planning horizon of 6 days. Larrain et al. [3] consider an IRP which allows stock-outs and the replenishment policy consists of swapping new cassettes of a chosen amount for the old cassettes that can still contain bank notes. The authors propose a matheuristic to solve instances with up to 60 locations, 3 vehicles, and up to 18 periods (in at most 6 days). Geismar et al. [4] provide a literature overview on currency supply chains by reviewing studies that look into the supply chain from the supply side (national banks), the demand side (commercial banks and ATM networks), and the private sector logistics providers’ side. In their analysis of ATM replenishment-related literature, Geismar et al. [4] mention the study by Van Anholt et al. [2] on RATMs and suggest as future research to investigate possible incentives to rebalance RATM inventories by steering users to a certain RATM (either withdraw from a full RATM or deposit at an empty RATM). As incentive they suggest a premium for making a deposit at a certain RATM and these premiums can be reviewed online by the user. In this paper, we investigate the IRPDM to examine possible supply chain savings when implementing a similar system for ATMs.
The IRPDM is related to the IRP with Transshipment (IRPT) introduced by Coelho et al. [5]. In the IRPT, one can move goods from an origin customer or depot to a destination customer in order to redistribute merchandise between stores of the same chain to cover unexpected demand variations, redistribute inventory to reduce handling costs, and in case storage capacity is limited at certain locations. It is assumed that these transshipments are performed by an outsourced carrier. Coelho et al. [5] propose an ILP formulation for this problem and develop an adaptive large neighborhood search heuristic for the single vehicle case. The heuristic is tested on instances from the literature with one vehicle, with up to 30 customers and 6 periods and with up to 50 customers and 3 periods. The heuristic’s stopping criterion is 25,000 iterations or 1 h of computation time (which was reached for some of the largest instances). Coelho and Laporte [6] use a branch-and-cut (BC) algorithm without problem specific VIs for the IRPT, solving instances up to 30 customers with 6 periods and 50 customers with 3 periods with a maximum running time of 12 hours per instance. Lefever et al. [7] propose an improved formulation for the IRPT which is solved by BC and uses two problem specific VIs. Compared with [6], the computation times are lower and two more instances with 6 periods are solved.
On the one hand, for certain features, the IRPDM can be seen as a special case of the IRPT. First, in the IRPT, it is possible to transship goods and store the goods at the destination customer to be used during multiple periods. In the IRPDM, the goods are not transshipped, but the demand is moved. Therefore, a demand move in one direction, is equivalent to a transshipment of goods in the other direction if these transshipped goods are immediately consumed. Second, in the IRPDM, demand moves to the depot are not possible while in the IRPT, goods can be moved directly from the depot to a customer.
On the other hand, the IRPDM contains some features that generalize the IRPT. First, we handle the multiple vehicle case, while in [5] and [6], only the single vehicle case is considered. Second, in the IRPDM, a large distance between customers would make a demand move impractical. Therefore, we restrict demand moves for each customer to a small subset of neighboring customers in close proximity and this subset can be different for each customer. In contrast, both in [5] and [6], the set of customers from which goods can be transshipped is limited to a depot and a subset of the customers, and this set is fixed for all customers. Hence, there is a set of “source” locations from which goods can be transshipped to any other customer. This can be modeled as a special case in the framework of neighbors that we define for the IRPDM. Although the limitation to a general set of source locations is modeled in [5], this feature does not seem to be used in the computational experiments. Concluding, in the IRPDM, any customer can be a “source” location, not only a predetermined subset of the customers, and in the IRPDM, the “source” customers can be different for each customer.
For extensive surveys on variants and solution methods for the IRP, we refer to [8] and [9]. Next to solution methods mentioned in these surveys, Desaulniers et al. [1] present a new formulation for the IRP that performs better for instances with multiple vehicles. In [1], a BPC algorithm is proposed to solve the IRP. In the model, columns represent a combination of a route and a so-called route delivery pattern (RDP) specifying the quantity delivered to each customer along the route. In the master problem, the optimal combinations of routes and RDPs are selected to minimize total routing and inventory holding costs. In the pricing problem (PP), routes and associated RDPs are generated based on the dual variables retrieved from the master problem. To model demand moves in the IRP, we extend the IRP formulation as introduced by Desaulniers et al. [1]. The main differences are the handling of initial inventory at the customers at the beginning of the planning horizon, the introduction of the neighboring customers, and the non-trivial adjustments to the VIs. Section 3 provides more details on the IRP formulation by Desaulniers et al. [1] and the extension for the IRPDM.
3 Problem Description and Formulation
In the IRPDM, a supplier replenishes inventory for a set of customers over a certain planning horizon. The supplier has an initial inventory at the beginning of the planning horizon and a known quantity becomes available in each period. A given number of vehicles with a load capacity restriction is available to perform the replenishments. A customer can be serviced at most once per period, i.e., split deliveries are not allowed. Each customer has an initial inventory at the beginning of the planning horizon, faces a given demand per period, and has an inventory capacity that must be respected. Via demand moves, part of a customer’s demand can be satisfied by another nearby customer. Note that we consider moving a part of the demand of the customer (the ATM) which implies that in practice, the demand of several end-users of the customer is moved. For each demand move, a cost is incurred that depends on the quantity moved and the distance between the customers involved. The other costs consist of routing costs for the distance traveled by the vehicles and inventory holding costs at the supplier and the customers. The objective of the IRPDM is to minimize the routing, inventory holding, and demand move costs. The inventory holding costs are charged on the quantity in stock at the end of each period assuming the following order of events in a period: increase inventory at the supplier, delivery of goods to the customers, consumption, inventory calculation. This order of events coincides with most literature on the IRP [10].
More formally, a single supplier, denoted by 0, needs to serve a set of customers N over a time horizon P = {1,2,…,ρ}. A fictitious period ρ + 1 is considered to handle end inventories. At each discrete time moment p ∈ P, a quantity \({d_{0}^{p}}\) becomes available at the supplier 0 and each customer i ∈ N faces a demand \({d_{i}^{p}}\). A homogeneous fleet of K vehicles with capacity Q is available to deliver the goods to the customers. For each customer i ∈ N, a holding capacity Ci needs to be respected and backlogging is not allowed. A customer i ∈ N (the supplier 0) has an initial inventory \({I_{i}^{0}}\) (\({I_{0}^{0}}\)) and a unit holding cost hi (h0). A Maximum Level inventory policy is adopted for the customers which means the delivery quantity can be chosen freely as long as inventory capacity is respected. The distance between the depot and each customer, and between all customers is given and denoted by cij. Each customer can redirect (part of) its demand to another customer. Therefore, for each customer i ∈ N, a set of neighboring customers \(\mathcal {N}_{i}\) is established; the demand of the customers in \(\mathcal {N}_{i}\) can be satisfied by i via demand moves. So, if a demand move from i to j is possible, this means that \(i \in \mathcal {N}_{j}\), i.e., j can satisfy demand of i. If a demand move takes place, a cost mij is charged per unit moved and per unit distance between i and j. Adding these costs in the objective is similar to incorporating costs of, for example, backlogging [11] and lost sales [3] in IRP settings.
In most IRP formulations, the model involves variables indicating the quantity delivered in a period to a certain customer. Inventory balance constraints keep track of the use of the inventory to satisfy the demand in the different periods. In contrast, in the formulation for the IRP proposed by Desaulniers et al. [1], the model uses variables indicating for which periods the delivered quantities are dedicated. The authors use the fact that there always exists an optimal solution that respects the first-in, first-out (FIFO) principle. Hence, it is possible, given the period of delivery, to determine the periods to which a delivered quantity is assigned. Moreover, if there is initial inventory, FIFO implies that this inventory is used to cover the demand in the first periods of the planning horizon. Therefore, so-called residual demands \(\bar {d}_{i}^{p}\) can be calculated. In periods for which the initial inventory cannot cover the demand, customers have a positive residual demand. Constraints that make sure all demand is covered are only needed for periods with a positive residual demand. In the IRPDM, initial inventory can also be used to satisfy moved demand of another customer. Therefore, we cannot use residual demands as in [1], but we have to model the use of the initial demand explicitly. This also implies that these constraints are needed for all customers and all periods.
Given the FIFO rule, let \(I_{i}^{0,s} = {\max \limits } \{0, {I_{i}^{0}} - {\sum }_{\ell = 1}^{s} d_{i}^{\ell } \}\) be the quantity remaining from initial inventory at customer i at the end of period s if initial inventory is only used to satisfy demand of customer i itself. Let \(P_{ijp}^{+}\) denote the subset of periods associated with subdeliveries delivered in period p ∈ P to customer i ∈ N dedicated to customer \(j \in \mathcal {N}_{i} \cup \{i\}\). The deliveries for periods \(P_{ijp}^{+}\) and customers \(j \in \mathcal {N}_{i} \cup \{i\}\) are so-called subdeliveries. Note that a subdelivery can be zero, then no delivery is made for the corresponding period and customer. The set \(P_{ijp}^{+}\) can be determined as follows:
The set \(P_{ijp}^{+}\) should be large enough such that possible solutions for the IRP are not excluded, which can be derived as follows. If i = j and \(\mathcal {N}_{i} \neq \emptyset \), there are neighbors for which the initial inventory can satisfy the demand. Set \(P_{ijp}^{+}\) is then largest if all periods are included such that inventory capacity of the customer is not exceeded by the total delivery made. If i = j and \(\mathcal {N}_{i} = \emptyset \), all initial inventory is used to satisfy demand of customer i itself, and subdeliveries are only needed for periods with a positive residual demand, and such that inventory capacity is not exceeded. If i≠j, because of the FIFO principle, demand of customer i needs to be satisfied from inventory before satisfying (part of) the demand of a neighbor j. This means that a subdelivery for a customer j in a period s is possible if the total demand of customer i up to and including period s does not exceed Ci. For ease of notation, denote \(P_{ip}^{+} = P_{iip}^{+}\), and introduce \(P_{ip}^{+\ell }\) denoting the latest period in set \(P_{ip}^{+}\).
Let \(u_{ijp}^{s}\) denote the upper bound on the quantity of a subdelivery in period \(s \in P_{ijp}^{+}\). For the visited customer i \(u_{ip}^{s} := u_{iip}^{s}\) is computed as follows:
and the upper bound \(u_{ijp}^{s}\) for a neighboring customer \(j \in \mathcal {N}_{i}\) is given by:
Note that delivering goods for the fictitious ending period will be in inventory at the same customer i ∈ N, no matter whether these goods are dedicated to the customer itself or one of its neighbors. Therefore, without changing the solutions, we set the upper bound for the quantity dedicated to each neighbor to 0 for this fictitious period. Also note that it is never optimal to have an incoming demand move and outgoing demand move in the same period. Therefore, first the customer’s own demand needs to be satisfied before using goods in inventory to satisfy the demand of a neighbor. This influences the upper bound on the delivered quantity that is dedicated to a neighbor. The set of feasible routes is denoted by R. For each route, r ∈ R, Nr indicates the set of visited customers and Ar the set of arcs used in the route. Let ari be equal to 1 if customer i ∈ N is visited in route r ∈ R and 0 otherwise. An RDP w corresponding to period p details the quantities \(q_{wij}^{s} \in [0,u_{ijp}^{s}]\) delivered to customer i ∈ Nr dedicated to satisfy the demand of customer \(j \in \mathcal {N}_{i} \cup \{i\}\) in period \(s \in P_{ijp}^{+}\). As in [1], \(q_{wij}^{s} = 0\) corresponds to a zero subdelivery, \(q_{wij}^{s} = u_{ijp}^{s}\) to a full subdelivery, and a partial subdelivery if \(0 < q_{wij}^{s} < u_{ijp}^{s}\). An extreme RDP contains at most one partial subdelivery. A set of extreme RDPs \({W_{r}^{p}}\) is associated with each route r ∈ R in period p ∈ P. Note that with a convex combination of multiple extreme RDPs any combination of delivered quantities can be constructed. The total quantity delivered in RDP \(w \in {W_{r}^{p}}\) is denoted by \(q_{w} = {\sum }_{i \in N_{r}} {\sum }_{j \in \mathcal {N}_{i} \cup \{i\}} {\sum }_{s \in P_{ijp}^{+}} q_{wij}^{s}\).
Given a route r ∈ R and an extreme RDP \(w \in {W_{r}^{p}}\), we can identify the quantity \(\hat {b}_{wi}^{s}\) delivered to customer i ∈ N that will be in inventory at the end of period \(p \leq s \leq P_{ip}^{+\ell }\). Compared with [1], we use \(\hat {b}_{wi}^{s}\) instead of \(b_{wi}^{s}\) to indicate that in our case deliveries dedicated to neighboring customers are also included. Let \(c_{rw} = {\sum }_{(i,j)\in A_{r}} c_{ij} + {\sum }_{i \in N_{r}} {\sum }_{s \in P_{ip}^{+}} h_{i} \hat {b}_{wi}^{s}\) be the costs associated with route r and RDP w in which the first term is the routing costs and the second term is the inventory holding costs of all units delivered to the visited customers. Note that a unit dedicated to satisfy the demand of a neighboring customer stays in inventory at the customer until consumption. Denote by \(P_{ijs}^{-} = \{p \in P| s \in P_{ijp}^{+}\}\) the set of periods in which a subdelivery can be made to customer i ∈ N to satisfy the demand of customer \(j \in \mathcal {N}_{i} \cup \{i\}\) in period s ∈ P. Use \(P_{is}^{-}\) to represent the union of sets \(P_{ijs}^{-}\) over all \(j \in \mathcal {N}_{i} \cup \{i\}\).
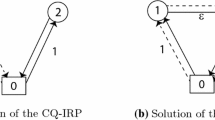
To model the IRPDM, we use the following decision variables. Continuous variables \(y_{rw}^{p} \in [0,1]\) are indicating the proportion of route r ∈ R with RDP \(w \in {W_{r}^{p}}\) in period p ∈ P. To clarify some of the notation, Figure 1 illustrates a variable \(y_{rw}^{p}\) for a route 0-1-2-0 and RDP w in a period p, corresponding delivery quantities \(q_{wij}^{p}\) for the visited customers (solid arrows) and the involved demand move (dotted arrow). Nonnegative variables \({I_{0}^{p}}\) indicate the inventory level at the supplier at the end of period p ∈ P. Nonnegative, integer variables \(z_{ij}^{p}\) indicate the quantity out of initial inventory at customer i ∈ N used to satisfy demand of customer \(j \in \mathcal {N}_{i} \cup \{i\}\) in period p ∈ P.
To comply with the FIFO principle, we prevent a demand move from i to j if customer i still has inventory left. Therefore, we introduce binary decision variables \({v_{i}^{s}}\). This variable will be equal to 1 if there is a positive inventory level at customer i ∈ N at the end of period s ∈ P and 0 otherwise. Hence, if \({v_{i}^{s}} = 0\), a demand move from customer i to j (\(i \in \mathcal {N}_{j}\)) in period s is possible. If \({v_{i}^{s}} = 1\), customer i still has inventory left that should be used first and a demand move is definitely not possible.
We can now formulate the IRPDM as follows:
The objective function (1a) minimizes the total routing, inventory holding, and demand move costs. Note that the demand move costs consist of the moves satisfied by initial inventory and by deliveries made during the planning period. Constraints (1b) balance the inventory level at the supplier between periods. Constraints (1c) make sure that, for each customer j ∈ N, all demand is satisfied by deliveries to customer j itself, to one of the customers i for which \(j \in \mathcal {N}_{i}\), or from initial inventory. Constraints (1d) are the capacity constraints at the customers. Note that the inventory level at customer i in a period is highest after the deliveries and before consumption. The highest inventory level is thus equal to the remaining initial inventory, plus past deliveries (dedicated to i or to \(j \in \mathcal {N}_{i}\)) that are not consumed yet at the end of the period, plus the demand satisfied for other customers \(j \in \mathcal {N}_{i}\) in this period and the demand at i in this period. Split deliveries are prevented by constraints (1e) and the number of used vehicles per period is limited by constraints (1f). Constraints (1g) make sure that the amount used from initial inventory does not exceed the actual initial inventory. In (1h), the left hand side is equal to the ending inventory at customer i in period s. If the ending inventory is positive, variable \({v_{i}^{s}}\) must be equal to 1. Note that in this case, constraints (1d) are more restrictive than (1h). If \({v_{i}^{s}} = 0\) then there cannot be any ending inventory. By constraints (1i), a demand move from j to i can only occur if \({v_{j}^{s}} = 0\) which implies that there cannot be any ending inventory in the same period.
Note that the maximum number of periods in which demand can be satisfied from initial inventory is limited, for example, if the demand is the same every period, the number of periods is \(\lceil {I_{i}^{0}} / d_{i} \rceil \). Hence, the variables \(z_{ij}^{p}\) only need to be introduced for those periods.
3.1 Limiting the Moved Demand
In the current formulation of the problem, it is possible that one customer is never replenished by a vehicle, but that all of its demand is satisfied from the customer’s initial inventory and via demand moves. In practice, this might not be desirable, for example for an ATM that is closest to a hospital. Therefore, as a general rule, we limit the quantity that is satisfied by another customer via demand moves to a certain percentage 𝜃 of the demand. The left hand side of the constraint should be the quantity of the demand of customer j ∈ N in period s ∈ P satisfied via demand moves, either via a delivery to another customer i such that \(j \in \mathcal {N}_{i}\) or from initial inventory. The right hand side should limit the quantity to \(\theta {d_{j}^{s}}\). The left hand side of this constraint is identical to the left hand side of constraint (1i), hence, we can merge the two types of constraints as follows:
3.2 Using Initial Inventory for Demand Moves
In Section 4, we will present a BPC algorithm to solve the IRPDM. Existing cuts for the IRP are no longer valid and need to be adjusted to handle demand moves. Because initial inventory can be used to satisfy moved demand, it is not straightforward how the cuts can be properly adjusted. Therefore, we first study a simplified variant of the problem, in which initial inventory can only be used to satisfy demand of the customer itself. In the remainder of the paper, we consider this variant of the problem, unless indicated otherwise. In formulation (1a)–(1n), this variant can be modeled by setting \(z_{ij}^{p} = 0\) for all i≠j or by considering a formulation with residual demands as in [1]. Moreover, we need to adjust the calculations of \(P_{ijp}^{+}\) and \(u_{ijp}^{s}\) since goods only need to be delivered for periods with a positive residual demand. The set of periods to which a delivery in period p to customer i can be dedicated is given by:
An upper bound \(u_{ip}^{s}\) on the quantity dedicated to each period \(s \in P_{ijp}^{+}\) is computed as follows for the visited customer:
and the upper bound \(u_{ijp}^{s}\) for a neighboring customer \(j \in \mathcal {N}_{i}\) is given by:
4 Solution Method
A BPC method is used to solve model (1a)–(1n). Column generation is applied to the master problem consisting of the linear relaxation of (1a)–(1l) and (1n) to compute lower bounds within a branch-and-bound algorithm. Columns represent a route and an extreme RDP, and these are generated by the PP. This solution method can be applied to both the case in which the initial inventory can be used to satisfy moved demand and the case in which initial inventory cannot be used for this purpose. VIs are added dynamically to the master problem to tighten the linear relaxations. The VIs are based on inequalities proposed in the literature for the IRP, we adjust these for the case in which initial inventory cannot be used to satisfy moved demand. An integer feasible solution is found by branching on the appropriate variables. Below, we describe the column generation process, the PP, the VIs, and the branching procedure.
4.1 Column Generation
Column generation is an iterative procedure that solves a linear program (LP). The procedure to solve the linear relaxation of (1a)–(1l) and (1n) starts with an LP with a limited set of variables \(y_{rw}^{p}\), which is called the restricted master problem (RMP). Then, new variables are added which are found by solving one or more PPs and with these new variables, the RMP is resolved. The PPs generate negative reduced cost variables \(y_{rw}^{p}\) (also called columns) with respect to the dual values of the current RMP. This process continues until the PPs do not generate new variables.
Initially, artificial columns with very high costs are added to guarantee a feasible solution for the RMP, such that dual values can be retrieved to be used in the PP. To obtain a better initial solution, an additional set of columns is computed in the following greedy way. Consider, for each period p, the customers \(\mathcal {S}\) that have residual demand in this period, if there are none, consider the customers with residual demand in period p + 1. For each customer, consider the RDP with a full delivery in period p (or p + 1) and zero deliveries for other periods. Create a route to visit the customers in \(\mathcal {S}\) by applying the nearest neighbor heuristic starting at the depot and adding customers as long as vehicle capacity is not violated. Each customer that is added to the route is marked as visited. If no customers in \(\mathcal {S}\) can be added anymore without violating vehicle capacity, the route is finished. If there are still unvisited customers in \(\mathcal {S}\), create another route.
4.2 Pricing Problem
For the IRPDM, there is a PP for each period p ∈ P in the planning horizon. A column generated by the PP corresponds to a delivery route r ∈ R and an extreme RDP \(w \in {W_{r}^{p}}\) that are feasible with respect to the constraints of the problem. Hence, the PP consists of a routing part and a delivery part which results in solving an Elementary Shortest Path Problem with Resource Constraints (ESPPRC) combined with the linear relaxation of a knapsack problem. After providing more explanation on the PP, the details on solving the ESPPRC will be discussed in Section 4.2.1. The PP for the IRPDM is an extension of the one for the IRP in [1].
Associate dual variables \({\pi }_{p}^{\text {1b}},~{\pi }_{is}^{\text {1c}},~{\pi }_{is}^{\text {1d}},~{\pi }_{ip}^{\text {1e}},~{\pi }_{p}^{\text {1f}},~{\pi }_{is}^{\text {1h}}\), and \({\pi }_{js}^{\text {1i}}\) with constraints (1b)–(1f) and (1h)–(1i) respectively. The reduced cost of a variable \(y_{rw}^{p}\) is given by:
in which \(c_{rw} = {\sum }_{(i,j)\in A_{r}} c_{ij} + {\sum }_{i \in N_{r}}{\sum }_{s = p}^{P_{ip}^{+\ell }} h_{i} \hat {b}_{wi}^{s}\) are the routing and inventory holding costs for a route r and RDP w.
For the routing part of the problem, define a graph Gp = (Vp,Ap) in which Vp is the set of nodes and Ap is the set of arcs with arc travel costs cij, (i,j) ∈ Ap. The set of nodes includes nodes corresponding to the customers vi, and to a depot source node vS and sink node vE. Set Ap contains all arcs between the customers (i,j) ∈ N × N, i≠j, all arcs from the source node (vS,i), i ∈ N and all arcs entering the sink node (i,vE), i ∈ N. In the ESPPRC, define the cost of an arc to be:
For the delivery part of the problem, a linear relaxation of a knapsack problem needs to be solved with the extra feature that the delivery quantity for a customer consists of goods to satisfy the demand of the customer itself and of its neighbors. Therefore, introduce two sets of variables. First, associate with each customer i ∈ N and period \(s \in P_{is}^{+}\) the variable \({\xi _{i}^{s}} \in [0, u_{ip}^{s}]\) specifying the quantity delivered to customer i that is dedicated to satisfy the demand of customer i in period s if s ∈ P or to the end inventory if s = ρ + 1. Second, associate with each customer i ∈ N, each of its neighbors \(j \in \mathcal {N}_{i}\) and each period \(s \in P_{ijp}^{+}\) variable \(\psi _{ij}^{s} \in [0, u_{ijp}^{s}]\) specifying the quantity delivered to customer i dedicated to satisfy the demand of customer j in period s. As indicated before, \(\rho + 1 \notin P_{ijp}^{+}\) for \(j \in \mathcal {N}_{i}\). Given a route r ∈ R, variables \({\xi _{i}^{s}}\), \(s \in P_{is}^{+}\), and \(\psi _{ij}^{s}\), \(s \in P_{ijp}^{+}\), must be 0 for customers i ∈ N ∖ Nr. Moreover, it must hold that \({\sum }_{i \in N_{r}} \left ({\sum }_{s \in P_{ip}^{+}} {\xi _{i}^{s}} + {\sum }_{j \in \mathcal {N}_{i}} {\sum }_{s \in P_{ijp}^{+}} \psi _{ij}^{s} \right ) \leq Q\) to respect vehicle capacity. Given the conditions above, \(({\xi _{i}^{s}})_{i \in N,s \in P_{ip}^{+}}\) and \((\psi _{ij}^{s})_{i \in N, j \in \mathcal {N}_{i}, s \in P_{ijp}^{+}}\) define an RDP w associated with route r. The reduced cost can be rewritten as follows:
An extreme RDP has at most one partial subdelivery; hence, in an extreme RDP at most one variable \({\xi _{i}^{s}}\) or \(\psi _{ij}^{s}\) can take a value in the open interval \(]{0}{u_{ip}^{s}}[\) and \(]{0}{u_{ijp}^{s}}[\), respectively.
4.2.1 Labeling Algorithm
Labeling algorithms have been proposed in the literature to solve the PPs of a wide variety of routing problems [12]. To solve the PP of the IRPDM, we propose a labeling algorithm in which a label represents both a partial route (path) and an associated extreme RDP. The labeling algorithm starts with a label at the source node vS in the graph Gp, this label is extended to subsequent nodes if such extensions are feasible. An extension to the sink node vE results in a route with corresponding extreme RDP. During the algorithm, a dominance rule can be used to discard labels that will not result in the optimal solution of the PP.
An extreme RDP consists of full subdeliveries, zero subdeliveries and at most one partial subdelivery. During the execution of the labeling algorithm, the quantity delivered in the partial subdelivery is unknown, because this quantity can depend on the other deliveries made. When a label is extended to the sink node vE, the size of the partial subdelivery is determined. Following [1], we keep track of the possible contribution of the partial subdelivery to the reduced costs.
A label Li corresponding to a partial route ending in node i with associated RDP w contains the following elements:
-
\(T_{i}^{\text {cost}}\): Reduced cost of the route/RDP (r,w), excluding the dual contribution of the partial subdelivery if i≠vE.
-
\(T_{i}^{\text {loadF}}\): Total quantity delivered along (r,w), the quantity of full subdeliveries only if i≠vE.
-
\(T_{i}^{\text {cust}_{k}}\): Binary value indicating whether or not customer k ∈ N has been visited in the route.
-
\(T_{i}^{\text {part}}\): Binary value indicating whether or not RDP w contains a partial subdelivery.
-
\(T_{i}^{\text {rateP}}\): Unit rate of contribution of the partial subdelivery to the reduced costs, if applicable.
-
\(T_{i}^{\text {maxP}}\): Maximum quantity that can be delivered in the partial subdelivery, if applicable.
Therefore, the label is denoted by \(L_{i} = \left (T_{i}^{\text {cost}}, T_{i}^{\text {loadF}}, \left (T_{i}^{\text {cust}_{k}}\right )_{k \in N}, T_{i}^{\text {part}},\right . T_{i}^{\text {rateP}},\) \(\left . T_{i}^{\text {maxP}} \right )\). There are three subdelivery types: a full (F), partial (P), and zero (Z) subdelivery. An extreme RDP consists of the subdelivery types for the visited customers and their neighbors for the periods in \(P_{ip}^{+}\) and \(P_{ijp}^{+}\), respectively, which we call a customer delivery pattern (CDP). For example, for a visit to customer i with one neighbor j, the CDP FF–P means that full subdeliveries are made for the two periods in \(P_{ip}^{+}\) for customer i and that a partial subdelivery is made to satisfy a demand move from customer j in the single period in \(P_{ijp}^{+}\). A CDP can contain at most one partial subdelivery, since an RDP can contain at most one, and the full subdeliveries cannot exceed vehicle capacity Q. For each customer i ∈ N and period p ∈ P, we determine a list of feasible CDPs Γip that we consider in the labeling algorithm at a node corresponding to customer i in period p. To make this list as short as possible, which will speed up the labeling algorithm, the list can be filtered to exclude CDPs that do not comply with the FIFO rule. For example, for customer i without neighbors, a CDP FPF cannot be optimal, and hence, this CDP is excluded from the list. Note that the FIFO rule can only be applied to the part of the CDP that indicate the subdeliveries for the visited customer itself and cannot be applied to the part of the CDP indicating the deliveries for the neighboring customers. For example, a CDP FFF-FPF is feasible with respect to the FIFO rule and can be in the optimal solution if the neighboring customer receives a delivery in the second period of \(P_{ijp}^{+}\).
To express the resource extension functions, define binary parameters \(f_{\gamma }^{s}\) (respectively, \(f_{\gamma j}^{s}\)) which is equal to 1 if CDP γ ∈Γip contains a full subdelivery for period s for the visited customer (respectively, neighbor j). Similarly, define \(g_{\gamma }^{s}\) (respectively, \(g_{\gamma j}^{s}\)) which is equal to 1 for a partial subdelivery in period s for the visited customer (respectively, neighbor j). Now, we can define for each CDP γ ∈Γip the cost \(\tau _{\gamma }^{\text {cost}}\), the load of the full deliveries \(\tau _{\gamma }^{\text {loadF}}\), an indicator whether there is a partial subdelivery in the CDP \(\tau _{\gamma }^{\text {part}}\), the rate of the partial delivery \(\tau _{\gamma }^{\text {rateP}}\), and the maximum size of the partial delivery \(\tau _{\gamma }^{\text {maxP}}\), which are defined as follows:
Any CDP with a partial subdelivery for which \(\tau _{\gamma }^{\text {rateP}} \geq 0\) can be discarded, since replacing the partial subdelivery with a zero subdelivery provides a solution with at most the same reduced cost.
The resource extension functions are defined as follows. Assume we have a label \(L_{i} = \left (T_{i}^{\text {cost}}, T_{i}^{\text {loadF}}, \left (T_{i}^{\text {cust}_{k}}\right )_{k \in N}, T_{i}^{\text {part}}, T_{i}^{\text {rateP}}, T_{i}^{\text {maxP}} \right )\) corresponding to a node i≠vE and the label is extended along an arc (i,j) ∈ Ap (j≠vE), for every CDP in Γjp. Let γ ∈Γjp be one of those CDPs. The extended label is given by \(L_{j} = \left (T_{j}^{\text {cost}}, T_{j}^{\text {loadF}}, \left (T_{j}^{\text {cust}_{k}}\right )_{k \in N}, T_{j}^{\text {part}}, T_{j}^{\text {rateP}}, T_{j}^{\text {maxP}} \right )\) with:
The resulting label is feasible if \(T_{j}^{\text {loadF}}\leq Q\), \(T_{j}^{\text {cust}_{k}} \leq 1\) for all k ∈ N, and \(T_{j}^{\text {part}} \leq 1\). When extending to the sink node j = vE, the cost computation differs to account for the partial subdelivery:
The number of labels can become very large; therefore, a dominance rule is used to reduce the number of labels. The dominance rule introduced for the IRP by Desaulniers et al. [1] still holds for the IRPDM:
Definition 1
A label \(L_{1} = \left (T_{1}^{\text {cost}}, T_{1}^{\text {loadF}}, \left (T_{1}^{\text {cust}_{k}}\right )_{k \in N}, T_{1}^{\text {part}}, T_{1}^{\text {rateP}}, T_{1}^{\text {maxP}} \right )\) is said to dominate a label \(L_{2} = \left (T_{2}^{\text {cost}}, T_{2}^{\text {loadF}}, \left (T_{2}^{\text {cust}_{k}}\right )_{k \in N}, T_{2}^{\text {part}}, T_{2}^{\text {rateP}}, T_{2}^{\text {maxP}} \right )\) if both labels L1 and L2 are associated with the same vertex and the following conditions are satisfied:
-
(a)
\(T_{1}^{\text {loadF}} \leq T_{2}^{\text {loadF}}\);
-
(b)
\(T_{1}^{\text {cust}_{k}} \leq T_{2}^{\text {cust}_{k}}\);
-
(c)
\(T_{1}^{\text {part}} \leq T_{2}^{\text {part}}\);
-
(d)
\(T_{1}^{\text {cost}} - T_{1}^{\text {maxP}}T_{1}^{\text {rateP}} \leq T_{2}^{\text {cost}} - T_{2}^{\text {maxP}}T_{2}^{\text {rateP}}\);
-
(e)
\(T_{1}^{\text {cost}} - \left (T_{2}^{\text {loadF}} - T_{1}^{\text {loadF}}\right )T_{1}^{\text {rateP}} \leq T_{2}^{\text {cost}}\);
-
(f)
\(T_{1}^{\text {cost}} - \left (T_{2}^{\text {loadF}} + T_{2}^{\text {maxP}} - T_{1}^{\text {loadF}}\right )T_{1}^{\text {rateP}} \leq T_{2}^{\text {cost}} - T_{2}^{\text {maxP}}T_{2}^{\text {rateP}}\).
4.2.2 Heuristic Labeling Algorithms
Before applying the exact labeling algorithm described above, two heuristic labeling algorithms are applied. First, for each route/RDP combination in the current RMP solution, optimize the CDPs for the given route with respect to the current dual variables. To optimize the CDPs, the labeling algorithm is solved with only the arcs in the given route. Second, the labeling algorithm is performed on a graph that contains only a subset \(\hat {A}^{p}\) of the arcs Ap for each period p ∈ P. The arcs are selected by the procedure proposed in [13]. Arcs that do not belong to the κ least reduced cost out of an origin node, or into a destination node, are removed. To compute the reduced cost of an arc A, the average cost over all possible CDPs for the destination node is computed (or similarly, the average cost over the CDPs of the origin node of an arc) and added to the reduced cost. In this calculation, we assume that no quantity is delivered in the partial deliveries. Then, for each node, the κ arcs with the lowest reduced cost, both incoming and outgoing, are kept in the graph. We set a dynamic value for κ, which starts at 1 and is incremented by 2 if no columns are generated in every subproblem for κ = 1.
4.2.3 Acceleration Techniques
Next to the heuristic labeling procedures, the following acceleration techniques are implemented to speed up the column generation procedure.
First, the list of CDPs Γip associated with a customer i ∈ N in period p ∈ P can be established once before the solution procedure starts. The costs and values associated with each CDP γ ∈Γip need to be updated at each iteration with the corresponding dual variables. Before the (heuristic) labeling algorithm solves the PP, we filter the list of CDPs by applying the dominance conditions as in Definition 1, except for condition (b), in which all T values are replaced by the current τ values of the CDPs.
Second, ng-path relaxation is applied as defined in [14]. This relaxation of the PP allows for cycles in the paths. To apply ng-paths, define for each node v ∈ Vp in network Gp = (Vp,Ap) a subset of customers NGv. Let NGv contain v itself and a subset of vertices that are closest to v such that |NGv| = b. Here, b is a predefined parameter (which is set to 7 in our experiments). An ng-path can contain a sequence of visits v − v1 − v2 −… − v only if at least one node w∉NGv is visited in between two visits of v. The labeling algorithm is adjusted to accommodate ng-paths as explained in [15].
Finally, since constraints (1e), which limit the number of visits to a customer in one period to one, are numerous and often not binding in the optimal solution, these constraints are relaxed first and added only if violated in a BC form. Moreover, Desaulniers et al. [1] showed that for the IRP some holding capacity constraints (equivalent to 1d) are redundant with the constraints equivalent to 1c and 1e. However, for the IRPDM, it is not possible to establish a comparable statement. Hence, all capacity constraints (1d) are now present in the master problem. Yet, it is likely that for each customer this constraint is only binding in one or two periods. Therefore, we add the holding capacity constraints (1d) also in a dynamic way similar to constraints 1e.
4.3 Valid Inequalities
Next to the heuristic labeling described in Section 4.2.2 and the acceleration techniques described in Section 4.2.3, VIs are implemented to strengthen linear relaxations of the problem and hence, to speed up the solution method. Only one family of VIs that was proposed for the IRP can immediately be applied to the IRPDM. For the variant of the IRPDM in which initial inventory cannot be used to satisfy moved demand, existing VIs can be adjusted, although the adjustments are not trivial. For the variant of the IRPDM in which initial inventory can be used to satisfy moved demand, it is not clear whether or how some of the existing IRP VIs can be adjusted. Therefore, we restrict ourselves to developing VIs for the variant in which initial inventory cannot be used to satisfy moved demand.
First, in Section 4.3.1, we describe a family of VIs proposed in [1] for the IRP and we argue why this family of inequalities is also valid for the IRPDM. Second, we propose a generalization of the first family of inequalities in Section 4.3.2. Third, Sections 4.3.3 to 4.3.6 propose VIs for the IRPDM that are derived from VIs for the IRP. Finally, in Section 4.3.7, we elaborate why the VIs in Sections 4.3.3 to 4.3.6 need structural changes for the variant of the IRPDM in which initial inventory can be used to satisfy moved demand.
4.3.1 Valid Inequalities on the Minimum Number of Routes per Time Interval
In the IRP, given the total quantity that must be delivered and the vehicle capacity, one can compute the minimum number of vehicle routes needed to deliver all goods. So, if one adds up the residual demand of all customers up to period ρ ∈ P, a lower bound can be established on the number of routes to fulfill the total residual demand. This also holds for the number of routes needed up to a certain period ℓ ∈ P. We denote these inequalities as Route Inequalities (RIs). In the IRPDM, both in case initial inventory can and cannot be used to satisfy moved demand, the total quantity that needs to be delivered by vehicles remains the same as in the IRP. Therefore, these inequalities can be applied to the IRP and both variants of the IRPDM without adjustments. A lower bound on the number of routes is given by \(lb_{\ell }^{R} = \left \lceil {\sum }_{i \in N}{\sum }_{s=1}^{\ell } \bar {d}_{i}^{s} / Q \right \rceil \) and the following VIs hold:
Let \({\pi }_{\ell }^{\text {13}},~\ell \in P\) be the dual variables associated with VIs (13). The reduced cost is adjusted the same way as in [1]:
4.3.2 Generalized Valid Inequalities on the Minimum Number of Routes per Time Interval
The cuts in Section 4.3.1 can be generalized to time intervals \([\ell , \ell ^{\prime }]\) where \(\ell , \ell ^{\prime } \in P\) are such that \(\ell ^{\prime } > \ell \). For example, suppose there is one customer and it has the following residual demands: 25, 40, 40, 40, 40, 40 for the six periods in the planning horizon, the vehicle capacity is Q = 100, and inventory capacity at the customer is C = 80. Then, at the end of period 4, there can be at most an inventory of 40; hence, at least one vehicle must visit this customer in the interval [5,6]. All residual demands for this customer can be covered with 3 vehicles, but if, in a fractional solution, this customer receives a visit of one vehicle in periods 1, 3, and 4, and of 0.4 vehicle in period 5, the inequality for interval [5,6] will be violated. We denote these inequalities as Generalized Route Inequalities (GRIs). If ℓ = 1, the inequalities are the same as in Section 4.3.1.
Define a new lower bound \(lb_{ll^{\prime }}^{\bar {R}} = \left \lceil \frac {{\sum }_{i \in N} \left ({\sum }_{p = \ell }^{\ell ^{\prime }} {d_{i}^{p}} - \left (C_{i} - d_{i}^{\ell -1}\right )\right )}{Q} \right \rceil \). The numerator now accounts for the maximum possible inventory level at the end of period ℓ − 1 at each customer. Note that the fraction can be rounded up because all terms are known at the beginning of the planning horizon. We propose the following generalized VIs:
Associating dual variables \({\pi }_{\ell \ell ^{\prime }}^{\text {15}},~\ell , \ell ^{\prime } \in P\) with these inequalities, then the modified arc reduced costs \(\bar {c}_{ij}\) become:
4.3.3 Valid Inequalities on the Minimum Number of Visits per Customer
For the IRP, given the residual demand at a customer over periods 1 to ℓ ∈ P, the inventory capacity at the customer and the vehicle capacity, one can compute how many visits are at least needed to satisfy a customer’s demand [16, 17]. In the IRPDM, demand at a customer i cannot only be satisfied via deliveries by a vehicle but also via other customers \(j: i \in \mathcal {N}_{j}\). Hence, a delivery to such a customer j should also be counted as a “visit” to customer i. Note that Cj can also decrease the number of visits needed for customer i, if residual demand is satisfied via a customer j. Therefore, define \(C_{i}^{\max \limits } = \max \limits _{j: i\in \mathcal {N}_{j} \cup \{i\}} \{C_{j} \}\). Then the minimum number of visits needed to a customer between periods 1 and ℓ is given by \(lb_{i\ell }^{V} = \left \lceil \frac {{\sum }_{p=1}^{\ell }\bar {d}_{i}^{p}}{\min \limits \{Q, C_{i}^{\max \limits }\}} \right \rceil \). The following VIs hold:
Associate dual variables \({\pi }_{i\ell }^{\text {17}}\), i ∈ N, ℓ ∈ P with the VIs. In the PP for period p, the arc reduced costs are adjusted as follows:
Lefever et al. [7] adjust a different version of these VIs for the IRPT in which the right-hand side contains the variable representing the inventory level. Lefever et al. [7] include transshipments by adding the fraction of transshipped demand to the left-hand side. Since variables are included in these terms, rounding is not possible.
4.3.4 Valid Inequalities on the Minimum Number of Subdeliveries per Demand
Inequalities on the minimum number of subdeliveries per demand (MNSDIs) for the IRP were proposed by Desaulniers et al. [1] based on the idea of Desaulniers [18] on similar inequalities for the Split Delivery Vehicle Routing Problem (SDVRP). The idea is that the residual demand \(\bar {d}_{i}^{s}\) of customer i ∈ N in period s ∈ P can be fulfilled via one subdelivery of size \(\bar {d}_{i}^{s}\), or via at least two smaller subdeliveries in different periods. We extend the inequalities to incorporate demand moves.
A given residual demand \(\bar {d}_{i}^{s} > 0\) can, in the IRPDM, be fulfilled in four different ways: (i) either by performing one subdelivery to customer i in a period \(p \in P_{is}^{-}\), (ii) at least two subdeliveries to customer i in different periods \(p \in P_{is}^{-}\), (iii) one subdelivery to a customer \(j : i \in \mathcal {N}_{j}\) in a period \(p \in P_{jis}^{-}\) or (iv) at least two subdeliveries to a customer j in different periods \(p \in P_{jis}^{-}\). Define \(a_{ijw}^{S}\) (respectively, \(a_{ijw}^{M}\)) as a binary parameter equal to 1 if ari = 1 and \(\bar {d}_{j}^{s}\) (respectively, less than \(\bar {d}_{j}^{s}\)) units are delivered in the subdelivery to customer i dedicated to customer \(j \in \mathcal {N}_{i} \cup \{i\}\) and period \(s \in P_{ijp}^{+}\) in RDP w, 0 otherwise. Define \(a_{wi}^{S} = a_{wij}^{S}\) if i = j, and similarly for \(a_{wi}^{M}\). The MNSDIs can be stated as follows:
Define \({\pi }_{is}^{\text {19}},~i \in N,~s \in P\) as the dual variables of VIs (19). To take the dual variables into account in the PP for period p ∈ P, modify parameters \(\tau _{\gamma }^{cost}\) as follows:
4.3.5 Multiperiod Capacitated Subtour Inequalities
Avella et al. [19] formulate Multiperiod Capacitated Subtour Inequalities (MCSIs) for the IRP. The MCSIs exploit that over a given set of subsequent periods p1 to p2, one can determine the minimum vehicle flow needed to satisfy the demand of a subset of customers \(S \subseteq N\). Before deriving the MCSIs for the IRPDM, we will rewrite the VIs of [19] for the IRP in the terminology of our paper.
Let (E : F) denote the set of arcs (i,j) ∈ A for which i ∈ E and j ∈ F with A the complete set of arcs. Suppose there is a subset of customers \(S \subseteq N\) and a time interval [p1,p2] in which p1 ≤ p2, p1,p2 ∈ P. Define arij to be a binary parameter indicating whether arc (i,j) is traversed in route r ∈ R. The following inequalities hold for the IRP:
The left hand side computes the vehicle flow into \(S \subseteq N\) during the periods p1 to p2. In the nominator of the right hand side, for each customer in S, we add up the demand over the periods in the time interval, minus the largest possible inventory at the end of period p1 − 1. The largest possible ending inventory at a customer i is equal to the holding capacity Ci minus the demand in period p1 − 1. Note that for p1 = 1, the right hand side can be improved to \(\left \lceil \frac {{\sum }_{i \in S}{\sum }_{t=1}^{p_{2}} \bar {d}_{i}^{t}}{Q} \right \rceil \) since there is no delivery possible before this time period and the remaining (residual) demand is known.
Avella et al. [19] introduce a quadratic program to solve the separation problem for this family of inequalities, which is rewritten as follows for the IRP:
in which \(\bar {y}_{rw}^{t}\) are the values of the current fractional solution, αi = 1 if i ∈ S and 0 otherwise for i ∈ N, and 𝜖 is a very small positive constant. γ represents the value of the right hand side of (21). Solutions with a negative objective correspond to violated cuts.
In the IRPDM, the demand of a customer j ∈ S cannot only be satisfied by vehicles going into the set S (first term of (26)) but also by deliveries to a customer i ∈ N ∖ S for which \(j \in \mathcal {N}_{i}\) (second term of (26)). Note that if there are customers j,k ∈ S and \(k \in \mathcal {N}_{j}\), flow into j does not have to contribute twice to the flow into S to account for a possible demand move. We therefore adjust the MCSIs as follows for the IRPDM:
The second term represents deliveries to customers i ∈ N ∖ S for which \(j \in S \cap \mathcal {N}_{i}\), but only for the periods 1 ≤ t ≤ p2 in which the subdelivery periods \(P_{ijt}^{+}\) have any overlap with the interval [p1,p2] under consideration. Again, for p1 = 1, the right hand side can be improved to \(\left \lceil \frac {{\sum }_{i \in S}{\sum }_{t=1}^{p_{2}} \bar {d}_{i}^{t}}{Q} \right \rceil \).
To separate the inequalities for the IRPDM, the programs (22)–(25) can still be used, but with the following extended objective function:
Associate dual variables \({\pi }_{S\ell \ell ^{\prime }}^{\text {26}},~S \subseteq N,~\ell ,\ell ^{\prime } \in P\) with inequalities (26). In the subproblem for period p ∈ P, the reduced costs are adjusted as follows:
with \(\bar {z}_{ij}\) a parameter equal to 1 if customer i ∈ N ∪{vS}∖ S and j ∈ S, and \(\hat {z}_{p\ell \ell ^{\prime }}\) equal to 1 if \(P_{ijp}^{+} \cap [\ell , \ell ^{\prime }] \neq \emptyset \).
4.3.6 Capacity Inequalities
The Capacity Inequalities (CIs) were introduced for the Capacitated Vehicle Routing Problem (CVRP) [20]. For the CVRP, given a subset of customers \(U \subseteq N\) and a lower bound κ(U) on the number of vehicles required to service these customers given the vehicle capacity, the total flow of vehicles incident to subset U must be at least 2κ(U). Desaulniers et al. [1] propose an adaptation of these VIs for the IRP. Instead of a subset of customers, the authors use subsets of positive residual demands to define the CIs. For the CVRP, a graph depicting the flow between customers is used for separating the VIs. For the IRP, an auxiliary graph is used which depicts the flow between consecutive residual demands assuming the FIFO principle.
For the IRPDM in which initial inventory cannot be used to satisfy moved demand, we extend the notion of the flow between residual demands. We will use a similar auxiliary graph as in [1]; however, the underlying structure of the graph per period changes. Define the set of residual demands \(RD = \{(i,s)\!\in \! N\! \times \! P~\!|~\!\bar {d}_{i}^{s}\! > \!0\}\) and the auxiliary graph \(G^{*} = \left (V^{*},E^{*}\right )\). Node set V∗ contains a depot node 0 and a node for each residual demand in RD. The edge set E∗ contains the following types of edges. First, an edge is present between the depot node and each residual demand node. Secondly, edges are present between consecutive nodes that correspond to the same customer, i.e., an edge exists between (i,s) and (i,s + 1). Third, there is an edge between nodes (i,s) and \((i^{\prime }, s^{\prime })\), \(i \neq i^{\prime }\), if there exists a period p ∈ P such that s is the latest period in \(P_{ip}^{+} \cap P\) and \(s^{\prime }\) is the earliest period in \(P_{i^{\prime }p}^{+} \cap P\). Until now, this definition is the same as in [1]. Additionally, for the IRPDM, an edge exists between (i,s) and \((i^{\prime }, s^{\prime })\), \(i \neq i^{\prime }\), if i is in \(\mathcal {N}_{k}\) for some \(k \neq i, i^{\prime }\) and there is a period p ∈ P such that s is the latest period in \(P_{kip}^{+}\) and \(s^{\prime }\) is the earliest period in \(P_{i^{\prime }p} \cap P\). Edges that do not have any weight can be discarded.
For the weights on the edges, for a given (fractional) solution, we look into a network per period Gp = (Vp,Ap). For the IRP, a node in this network for a given period p represents a customer and the periods for which a subdelivery can be made \(P_{ip}^{+}\). For the IRPDM, a node represents both a customer and its neighbors, and the periods for which a subdelivery can be made for these customers in period p, i.e., the periods in \(P_{ip}^{+}\) and \(P_{ijp}^{+}\) for all \(j \in \mathcal {N}_{i}\). To illustrate the structure of the auxiliary graph for the IRPDM, consider the example in Fig. 2.
Consider the example with N = {c1,c2} and P = {1,2,3}. Customer c1 has a positive residual demand in period 3 and customer c2 has a positive residual demand in periods 2 and 3. Moreover, customer c2 is a neighbor of customer c1, i.e., \(\mathcal {N}_{c1} = \{c2\}\). The nodes in the networks in Fig. 2a–c represent both the customer and their neighbor, if applicable. Period 4 = ρ + 1 is the fictitious period and recall that this period is never included in the delivery periods for a neighbor. Figure 2d gives the corresponding auxiliary graph G∗ in which customer i and period s are indicated by ci.s.
To illustrate the association of the arcs with the edges, consider as an example the edge between c1.3 and c2.2. This edge is present because the latest period in \(P_{c2,1}^{+}\) is 2 and the first period in \(P_{c1,1}^{+}\) is 3. The edge represents the flow between the residual demands and can be computed by summing the flow on arc (c2,c1) ∈ A1 (arc c), the incoming arcs of node c1 ∈ V1 (arcs a and c) and the incoming arcs of node c1 ∈ V2 (arcs g and i). The last two sets are added since customer c2 is a neighbor of customer c1, the last period of \(P_{c1,c1,1}^{+} \cap P\) and \(P_{c1,c1,2}^{+} \cap P\) is period 3, and the first period of \(P_{c1,c2,1}^{+}\) and \(P_{c1,c2,2}^{+}\) is period 2. Note that arc c is added twice to this edge flow; counting arcs twice for one edge was not possible in the auxiliary graph for the IRP but is now necessary to account for the demand moves.
Since we only change the underlying auxiliary graph for the IRPDM, the VIs as defined in [1] and the impact on the reduced cost remain the same and are not repeated here for conciseness. They use three separation heuristics for the CIs for the IRP. The first one is the separation routine of the CVRPSEP package [21] developed by Lysgaard et al. [22] which is followed by a filter to incorporate that, for the IRP, the flow through a node can be higher than one. Second, current routes/RDPs with exactly one partial subdelivery in a current solution are considered to construct subsets \(U \subseteq N\) on which the VI is evaluated. Finally, a route-based connected component heuristic is applied which was proposed by Archetti et al. [23] for the SDVRP with Time Windows. For details on the separation heuristics, which are also used for the IRPDM, we refer to [1].
4.3.7 IRPDM in Which Initial Inventory Can Satisfy Moved Demand
The inequalities presented in Sections 4.3.3 to 4.3.6 cannot be adjusted without changing their structure and effectiveness for the variant of the IRPDM in which initial inventory at a customer can be used to satisfy the demand of another customer via a demand move. For the inequalities in Sections 4.3.3 to 4.3.5, two main reasons preventing effective adjustments are (1) the “flow” resulting from the use of initial inventory should be accounted for in the left hand side and (2) residual demand can no longer be used in the right hand side of the inequalities. For the CIs in Section 4.3.6, similar to the other inequalities, the residual demands can no longer be used to construct the auxiliary graph. Hereafter, we discuss the two main reasons in more detail by reflecting on the VIs on the minimum number of visits per customer (Section 4.3.3).
(1) If it is possible to satisfy a demand move from initial inventory, potentially all demand at a customer j is satisfied from the initial inventory of customers j and \(i : j \in \mathcal {N}_{i}\). In that case, no visits by a vehicle (to j or i) are needed to satisfy the demand of j. The idea of considering the use of initial inventory of i to satisfy demand of j as a “visit” could be applied to adjust the VI in two ways. A first approach could be to add the initial inventory variables to the left hand side; however, it would not be counting visits, but units of goods. One could divide by the demand and round up, but this would be non-linear. A second approach could be to add supplementary binary variables, which are equal to 1 if initial inventory is used to satisfy a demand move. However, these binary variables must be added to the master problem and moreover, a set of big-M constraints is needed to make sure the binary variables have the correct value.
(2) In the right hand side of the inequality, residual demands \(\bar {d}_{j}\) can no longer be used since initial inventory of customer j can be used to satisfy demand of a customer \(k \in \mathcal {N}_{j}\). Hence, not all initial inventory is necessarily available to satisfy demand of customer j itself. In the right hand side of inequality (17), we could therefore incorporate the variables that represent the use of initial inventory to satisfy moved demand. The disadvantage of that is that decision variables are included in the fraction and rounding the fraction would make the inequality non-linear.
Concluding, both on the left and the right hand side of the VI, the structure has to be changed to handle the possibility of using initial inventory to satisfy moved demand, making the inequalities weaker. A similar reasoning can be followed for the VIs in Sections 4.3.4 and 4.3.5. Therefore, the inequalities cannot be adjusted for this variant of the IRPDM without changing their structure and effectiveness.
4.4 Branching
To find a feasible solution to the problem, seven types of branching decisions are evaluated if a fractional solution of the linear relaxation is computed. The branching decisions are defined on the following variables:
-
1.
The total number of routes over all periods \(\left ({\sum }_{p \in P}{\sum }_{r \in R}{\sum }_{w \in {W_{r}^{p}}} y_{rw}^{p}\right )\).
-
2.
The number of routes per period p ∈ P \(\left ({\sum }_{r \in R}{\sum }_{w \in {W_{r}^{p}}} y_{rw}^{p}\right )\).
-
3.
The number of visits per customer i ∈ N \(\left ({\sum }_{p \in P}{\sum }_{r \in R}{\sum }_{w \in {W_{r}^{p}}} a_{ri} y_{rw}^{p}\right )\).
-
4.
\({v_{i}^{s}}\) variables.
-
5.
\(z_{ij}^{p}\) variables.
-
6.
The flow through each customer vertex i ∈ N in each period p ∈ P \(\left ({\sum }_{r \in R}{\sum }_{w \in {W_{r}^{p}}} a_{ri} y_{rw}^{p}\right )\).
-
7.
The flow on each edge < i,j > in each period p ∈ P which is equal to the sum of the flows on the corresponding arcs (i,j) and (j,i) in Ap \(\left ({\sum }_{r \in R}{\sum }_{w \in {W_{r}^{p}}} (a_{rij} + a_{rji}) y_{rw}^{p}\right )\).
Compared with the solution method proposed by Desaulniers et al. [1] for the IRP, we added three types of variables to branch on 3, 4, and 5. Types 4, 5, and 7 are sufficient to guarantee an optimal integer solution. For a discussion on the arc and edge flows, we refer to [1]. Branching decisions are imposed in the model by adding a constraint, except for setting the flow on an edge to zero for which both corresponding arcs are removed from the arc set Ap. Adding an extra constraint to the master problem implies an adjustment in the reduced costs; specifics are omitted here for conciseness.
The next steps are followed to decide which branching decision is imposed. Compute the values of the variables for each type of decisions 1 to 7 and select for each type the candidate variable with a value closest to 0.5. If the candidates for types 6 and 7 have fractional values between 0.25 and 0.75, then branch on the variable with the value closest to 0.5 out of these two (at equality, select the type 3 decision). If there are no type 6 or 7 variables to branch on, if there is a candidate variable of type 1 or 2, select the candidate with the value closest to 0.5. If no candidate exists in the previous types, branch on the candidate variable of type 3 if one exists. Otherwise, choose the candidate variable of type 4 or 5 of which the value is closest to 0.5 to branch on.
A local-depth first search approach as described in [1] is applied to select the next node in the branch-and-bound tree to explore.
5 Computational Experiments
To assess the impact of including the demand moves in the IRP, we performed computational experiments using the described BPC algorithm that was implemented using C++ and the Gencol library. CPLEX 12.6 is used to solve all restricted master problems during the solution procedure. These experiments are run on an Intel Core i7-4770 processor at 3.40 GHz, with 8 cores and 16 GB RAM. For all tests, only a single core is used and a time limit of 2 h is imposed for each instance. To evaluate the benefits of demand moves, the IRPDM results are compared to the IRP by using the solution values obtained by Coelho and Laporte [17] and Desaulniers et al. [1] (see instances and results in [24]).
To design our test set, we use the benchmark instances proposed by Archetti et al. [16] for the IRP. The time horizon in these instances is either 3 or 6 periods, instances have a multiple of five customers, and there is one vehicle with a given capacity. Moreover, an instance contains for each customer the location, the initial inventory level, the maximum inventory capacity, the demand, and the inventory holding rate. For the depot, the quantity becoming available is given instead of the demand and there is no maximum on the inventory. There are two levels for the inventory holding rate. Based on that, there are four classes of instances denoted by their inventory holding rate level (High or Low) and planning horizon (3 or 6 periods), resulting in classes H3, H6, L3, and L6. The instances originally include a single vehicle, but the instances have been used for the multi-vehicle case by dividing the vehicle capacity by the chosen number of vehicles. Details on the instances are available in [16].
To incorporate demand moves, we determine for each customer i ∈ N the closest customer j ∈ N ∖{i} that is within 150 units of distance and set \(\mathcal {N}_{i} = \{j\}\). All VIs are added in a dynamic way in each node of the branch-and-bound tree. The CIs and MCSIs are only added in nodes that are at most at depth two in the tree. The costs for demand moves are set to mij = 0.01 per unit of goods and per unit of distance between locations i and j (following [5]) and there is no limit on the amount of demand that can be moved, unless indicated otherwise.
In Section 5.1, we present results to assess the effectiveness of the new GRIs (Section 4.3.2), the MCSIs (Section 4.3.5), and the CIs (Section 4.3.6). Thereafter, generating results for the IRPDM with the most efficient settings, Section 5.2 compares the solution values of the IRPDM with the solution values of the IRP. In Section 5.2.1, the cost of a demand move is set to mij = 0.05 and mij = 0.1 to assess the impact of changing this cost. In practice, it might not be desirable that all demand of a customer is satisfied by another customer as described in Section 3.1. Hence, Section 5.2.2 reports the effect of limiting the percentage of demand that can be moved to 25%, 50%, and 75% of the demand of one customer in each period.
5.1 Effectiveness of Valid Inequalities
We assess the effectiveness of the GRIs, MCSIs, and CIs by solving the IRPDM with different combinations of VIs. The first setting includes the CIs and the GRIs, while the second setting includes the MCSIs and the GRIs. For the third and fourth settings, both the CIs and MCSIs are included. Additionally, setting three includes the GRIs, while setting four uses the original RIs. The remaining VIs are used in all settings. For each setting, the IRPDM is solved for a subset of the instances. The algorithm is tested on the instances with 3 and 4 vehicles (“K”), with 5 and 10 customers for 3-period horizon, and with 5 customers for 6-period horizon, for both high and low inventory holding costs. Hence, for each H3/L3 class (“Class”), there are 10 instances, and for each H6/L6 class, there are 5 instances in this subset.
Table 1 reports for each class and number of vehicles the average integrality gap at the root node before adding VIs (“Gapr”), which is the same for all settings. Thereafter, the table compares for each setting the number of instances solved to optimality (“Opt”), the average running time of instances solved to optimality (“T(s)”), the average integrality gap at the root node after adding VIs (“Gap”), and the average number of CIs (“CI”) and MCSI (“MCSI”) inequalities added during the execution of the algorithm, respectively. Only the instances solved to optimality are considered when computing the averages. The integrality gap is computed as \((\overline {z} - \underline {z})/\overline {z}\) with \(\underline {z}\) the lower bound computed at the root node of the branch-and-bound tree and \(\overline {z}\) the optimal value. The row “overall” shows the overall average, overall minimum, or maximum reported in each of columns.
Table 1 shows that with all four settings, the same number of instances can be solved. Moreover, the CIs and MCSIs are effective since the integrality gap is approximately halved by adding these VIs. This can be observed from the overall integrality gaps of 2.1% and 1.9% for settings 1 and 2 respectively, compared to the gap of 4.2% in the root node before adding VIs. In tests with the RIs (without the CIs and MCSIs), still 55 instances can be solved to optimality, but the average running time is more than 2.5 times as high and the integrality gap is more than twice as high as in setting 4. Details on these tests are not reported, but are available on request.
The results indicate that the MCSIs are slightly more effective than the CIs since setting 2 gives both a lower average computation time and lower integrality gap after adding the VIs than setting 1. Combining these types of inequalities in settings 3 and 4 increases the efficiency since the running time goes down, even tough the integrality gap is the same as for settings 2 and 3. In settings 3 and 4, the average number of identified CIs is much lower than in setting 1, but since the MCSIs are slightly more effective, the average computation time is still lower in settings 3 and 4 than in setting 1. Comparing settings 3 and 4 shows that the integrality gaps are the same, which implies that using the GRIs does not seem to improve the solution method for the IRPDM. Note that the average number of CIs and MCSIs differs slightly between settings 3 and 4. Although the generalization of the route inequalities is not effective for the IRPDM, this cannot immediately be concluded for other problems. Based on these observations, setting 4 will be used for the remainder of the experiments.
5.2 Comparing IRP and IRPDM
To evaluate the benefit of exploiting demand moves in the IRP, the solutions of the IRPDM are compared to the solutions of the IRP. We look into the (percentage) cost improvement that is achieved for the test instances, and examine the number of moves and their size that actually take place in the IRPDM solutions. The solutions for the IRP are collected from [24].
Table 2 shows the obtained results. For each class of instances (“Class”), fleet size (“K”), and number of customers (“N”), Table 2 first shows the number of instances that are solved to optimality for both the IRP and IRPDM (“Opt.”). Secondly, the average computation time for the BC IRP algorithm by Coelho and Laporte [17] (“T(s)-BC”), for the BPC IRP algorithm by Desaulniers et al. [1] (“T(s)-BPC”), and for the IRPDM (“T(s)”) are reported. Thereafter, the average (“Av. Impr”), maximum (“Max. Impr”), and minimum (“Min. Impr”) percentage cost improvement of the IRPDM over the IRP are stated. Finally, the average number of demand moves (“Av. Nr. of DMs”) and the average size of a demand move are reported (“Av. Sz. of DM”).
We run the algorithm on instances with up to 25 customers for a 3-period horizon and up to 10 customers for a 6-period horizon. All detailed results are reported in Appendix 1. Two instances can be solved for the IRPDM while no feasible solution for the IRP exists. Hence, these instances are not included in the results since there are no IRP results to compare with. For instances with a 6-period horizon, we can only solve instances with five customers to optimality. This is limited, however, note that for the IRP not all instances with a 6-period horizon and ten customers have been solved to optimality with BPC in state-of-the-art literature [1] and the proposed IRPDM is a more complicated problem.
The average computation times show that the IRPDM instances require more time to be solved than the IRP with the BPC solution method. This can be expected since the BPC solution method for the IRPDM is an extension of the one for the IRP. Compared to the BC method for the IRP, solving the IRP is in general easier. The higher computation times are caused by having a more extensive master problem which includes additional binary variables and new constraints. Also, the capacity constraints are not redundant with the other constraints in the master problem which was the case for the IRP [1]. Moreover, the number of CDPs per customer increases substantially since the patterns include the deliveries dedicated to the neighboring customers. Consequently, the number of labels is greater which slows down the PP. However, for some instances, the BPC method for the IRPDM solves them more quickly, for example class H3 with 4 vehicles and 10 customers.
The average cost improvement is around 2.35% for instance classes with high holding costs and above 3.5% for instance classes with low inventory holding costs, respectively. In general, it can be observed that the average improvements are higher for low inventory holding costs while the average number and the average size of the demand moves do not differ much. This can be explained by the fact that for high holding costs, the routing costs are a smaller part of the solution value than for low holding costs. Since the demand moves decrease the routing costs and increase the holding costs, the savings yielded by including demand moves are larger when holding costs are lower.
The maximum improvements go up to 10% and for only three classes of instances, the minimum cost improvement equals zero. A zero cost improvement means that solving the IRPDM results in the same solution as the IRP, i.e., exploiting demand moves does not result in a cost saving. Looking into the detailed results in Appendix 1 shows that out of 96 instances, only three instances do not result in a cost improvement. The number of demand moves per instance is 2.6 and 2.8 for short time horizons, and 5.3 and 5.5 for long horizons, respectively. This implies that there is on average one demand move per period of the planning horizon. The higher number of moves for longer horizons can be explained by the fact that in a longer planning horizon, there are more opportunities to incorporate a demand move for multiple periods. Note that the percentage cost improvement is not higher for a longer planning horizon than for a shorter planning horizon. If a demand move takes place, the number of units moved is quite substantial with averages between 30 and 45 units, which is approximately between half and three-quarters of the average demand (the demand is between 10 and 100).
5.2.1 Impact of the Demand Move Costs
In the previous experiments, the service fee incurred for a demand move (per unit of goods and per unit of distance) is set to m = 0.01. This section examines the impact of this parameter on the IRPDM solutions by solving the IRPDM for different values of m. For a subset of instances (instance sizes 5, 10 and 15 for 3-period horizon and sizes 5 and 10 for 6-period horizon), the IRPDM is solved for m = 0.005, m = 0.05 and m = 0.1 as well. The latter two values were also tested by Coelho et al. [5] for the IRPT. Table 3 reports the average cost improvement over the IRP (“Av. (%)”), the maximum cost improvement (“Max. (%)”), the average number of demand moves (“Av. Nr.”), and the average size of the demand move (“Av. Sz.”) per instance class and fleet size. Only instances that are solved to optimality for all parameter values of m are considered (the number of instances solved is indicated in column “Opt.”); therefore, averages can differ marginally from the reported results in Table 2 for m = 0.01. Detailed results can be found in Appendix 2.
The results in Table 3 show that the improvement over the IRP by using demand moves diminishes if the cost of demand move increases, which can be expected. Increasing the value of m from m = 0.01 to m = 0.05 results in average improvements that are approximately a factor five lower, as illustrated in Fig. 3. The average number of demand moves decreases more rapidly as planning horizons become longer. Increasing the value of m to 0.1 results in very few demand moves, and hence, a very minor cost improvement of only 0.1% and 0.2% on average for high and low inventory holding costs, respectively. Moreover, if a demand move takes place, the number of units moved is very limited and approximately half of the size for m = 0.05.
Lowering m from m = 0.01 to m = 0.005 leads to higher improvements, as can be expected. Note that mainly for 6-period horizon instances, the number of demand moves increases which results in an average cost improvement twice the improvement for m = 0.01. The average size of the demand moves does not change substantially for this change in demand move cost m.
Overall, it can be observed that the value of m has a larger impact for instances with a 6-period horizon. Figure 3 shows that when m is increased, the average cost improvement decreases faster for a longer than for a shorter planning horizon. Also the number of demand moves declines faster for a longer planning horizon, starting at averages of well above one move per period for m = 0.005, but reducing to almost zero for m = 0.05 and m = 0.1.
5.2.2 Impact of Limit on Moved Demand
As discussed in Section 3.1, the IRPDM allows that all demand of one customer is moved to another customer (after using the initial inventory). This could imply that some customers are never replenished by a vehicle. From a service point of view, this might be unacceptable. In this section, we therefore analyze the impact on the solutions when the moved demand per customer per period is limited to a given percentage, as discussed in Section 3.1. We solve the IRPDM for a maximum of 25%, 50%, and 75%, additionally to the results already obtained for 100% (which allows moving all demand). The same instances are used as in Section 5.2.1 and Table 4 reports similar information as Table 3. Only instances solved to optimality for all settings are taken into account; therefore, the averages for 100% can deviate slightly from the reported results in Table 2. Appendix 2 reports the detailed results.
Table 4 shows that the average number of units moved decreases if the maximum demand moved becomes smaller. For example, for class H3, the average size is only 6 units if the limit is 25% compared to 32.3 units if there is no maximum. It is interesting to observe that the average number of units declines stronger for a shorter planning horizon than for a longer planning horizon. For instance, for class H6, the average number of units is 15.6 for a 25% limit, which is much larger than the 6 units for class H3 while the differences between the classes are small if there is no limit imposed (32.3 vs. 37.8 units). The same observation holds for classes with low holding costs.
Furthermore, the results show that the difference in cost improvement is small between a limit of 25% and 50%. Figure 4 shows that the largest difference can be observed between maxima of 75% and 100% (i.e., no limit). Restricting the demand moved to 75% of the demand per customer per period approximately halves the percentage cost improvement over the IRP. As an example, consider instance class L3 which has an average cost improvement of 4.0% if there is no limit, and only 1.5% in case of a maximum of 75%. This shows that if there is any restriction on the amount of demand that can be moved, a large share of the potential cost improvement is lost. This can be explained by the fact that in case of a limit, some customers must be served by a vehicle while their demand would have been moved and no visit would be required if there was no limitation on the moved demand. Therefore, routing costs increase and the improvement over the IRP is lower. The number of required replenishments is also enhanced by the limitation that demand can only be moved if there is no inventory left. Hence, replenishing a customer once and spreading this inventory over multiple periods combined with moving some demand every period is not possible; instead, replenishments with a vehicle are necessary.
Although limiting the demand that can be moved, to 25% for example, clearly results in lower cost improvements over the IRP than imposing no limit. From a service perspective, this can still be preferable. Even with moving a very limited amount of goods, we still find average cost improvements between 0.5 and 1.1%, and up to 4.8% maximally, which can be substantial in practice.
6 Conclusion
In this paper, we introduced the Inventory Routing Problem with Demand Moves (IRPDM). This problem is an extension of the IRP with the addition that a customer can satisfy (part of) the demand of another customer. Although originally inspired by redirecting ATM-users to nearby ATMs, the IRPDM can prove useful to a variety of settings, such as bicycle sharing systems where users can collect or return a bicycle at several stations. We formulate a mathematical model for the IRPDM as an extension of the IRP formulation of Desaulniers et al. [1] and we develop a BPC solution method including non-trivially adjusted VIs stemming from the IRP.
The IRPDM is solved on IRP benchmark instances from the literature [16] and the performance of three types of VIs is analyzed. The tests show that MCSIs (see [19] for the IRP) adjusted for the IRPDM are more effective than adjusted CIs (see [1] for the IRP), and that using both these types of inequalities results in the best performance of the algorithm. To assess the impact of allowing for demand moves in the IRP, we compare the solutions of the IRPDM to those of the IRP. Moreover, we analyze the average number and size of demand moves to develop management insights.
Cost improvements of up to 10% are achieved for a demand move cost of m = 0.01 per unit of demand and unit of distance and if there is no limit on the moved demand. Moreover, it is observed that there is on average approximately one demand move per day, which implies that these improvements are achieved without a large change in the solutions compared to the IRP. The designed algorithm can solve instances with up to twenty customers, three periods, and five vehicles to optimality, which is limited. It must be noted that the IRPDM is much more difficult than the IRP, for which instances up to fifty customers can be solved to optimality with a state-of-the-art BPC method [1]. Sensitivity analysis on both the demand move costs and the maximum on the moved demand per customer per period is performed. Varying the demand move costs shows that the impact of increasing the costs is larger for a longer planning horizon than for a shorter planning horizon on both the percentage cost improvement over the IRP and the number of demand moves performed. Limiting the demand that can be moved per period of one customer to 75% of its demand already has a considerable impact on the cost improvement over the IRP compared with the cost improvement if there is no limit. The percentage cost improvement is approximately halved in case of 75% compared to 100%. Even by allowing only 25% of the demand to be moved, we observe cost improvements up to 4.8% and around 1% on average compared to the classical IRP.
In this paper, we limit ourselves to the case in which initial inventory can only be used to satisfy demand of the customer itself for algorithmic reasons. An extension would be to develop an exact solution method that does accommodate satisfying moved demand with the initial inventory. A challenge can especially be found in the design of VIs for this problem as discussed in Section 4.3.7. Moreover, the results show that allowing for demand moves can lead to significant cost savings. Therefore, the design of a heuristic solution method for the IRPDM capable of solving larger scale IRPDM instances is an interesting future research direction. A helpful insight obtained in this paper which can be used in the development of heuristics is that the number of demand moves taking place in optimal solutions is rather limited. Finally, in our model, we only consider a load capacity constraint on the vehicles. In practice, the number of ATMs that can be served by one vehicle in one period is often limited by time, which is now not considered in the IRPDM. Hence, demand moves can also be useful if there is insufficient vehicle time capacity to replenish all ATMs in a certain area. It would be interesting to investigate the impact of allowing demand moves if the number of customers that can be replenished is further limited, for example, by limiting the number of customers served per vehicle.
References
Desaulniers. G, Rakke JG, Coelho LC (2016) A branch-price-and-cut algorithm for the inventory-routing problem. Transp. Sci. 50(3):1060–1076
Van Anholt RG, Coelho LC, Laporte G, Vis I FA (2016) An inventory-routing problem with pickups and deliveries arising in the replenishment of automated teller machines. Transp. Sci. 50(3):1077–1091
Larrain H, Coelho LC, Cataldo A (2017) A variable MIP neighborhood descent algorithm for managing inventory and distribution of cash in automated teller machines. Computers & Operations Research 85:22–31
Geismar HN, Sriskandarajah C, Zhu Y (2017) A review of operational issues in managing physical currency supply chains. Prod. Oper. Manag. 26 (6):976–996
Coelho LC, Cordeau J-F, Laporte G (2012) The inventory-routing problem with transshipment. Computers & Operations Research 39(11):2537–2548
Coelho LC, Laporte G (2013) The exact solution of several classes of inventory-routing problems. Computers & Operations Research 40 (2):558–565
Lefever W, Aghezzaf E-H, Hadj-Hamou K, Penz B (2018) Analysis of an improved branch-and-cut formulation for the inventory-routing problem with transshipment. Computers & Operations Research 98:137–148
Andersson H, Hoff A, Christiansen M, Hasle G, Løkketangen A (2010) Industrial aspects and literature survey: Combined inventory management and routing. Computers & Operations Research 37(9):1515–1536
Coelho LC, Cordeau J-F, Laporte G (2014) Thirty years of inventory routing. Transp. Sci. 48(1):1–19
Archetti C, Bianchessi N, Irnich S, Speranza MG (2014) Formulations for an inventory routing problem. Int. Trans. Oper. Res. 21(3):353–374
Abdelmaguid TF, Dessouky MM, Ordóñez F (2009) Heuristic approaches for the inventory-routing problem with backlogging. Computers & Industrial Engineering 56(4):1519–1534
Irnich S, Desaulniers G (2005) Shortest path problems with resource constraints. In: Desaulniers G, Desrosiers J, Solomon MM (eds) Column generation, pp 33–65. Springer
Desaulniers G, Lessard F, Hadjar A (2008) Tabu search, partial elementarity, and generalized k-path inequalities for the vehicle routing problem with time windows. Transp. Sci. 42(3):387–404
Baldacci R, Mingozzi A, Roberti R (2011) New route relaxation and pricing strategies for the vehicle routing problem. Oper. Res. 59(5):1269–1283
Desaulniers G, Madsen OliBG, Ropke S (2014) The vehicle routing problem with time windows. In: Toth P, Vigo D (eds) Vehicle routing: Problems, methods, and applications, 2nd edition, pp 119–159. MOS-SIAM series on optimization (SIAM, Philadelphia)
Archetti C, Bertazzi L, Laporte G, Speranza MG (2007) A Branch-and-Cut algorithm for a vendor-managed inventory-routing problem. Transp. Sci. 41(3):382–391
Coelho LC, Laporte G (2014) Improved solutions for inventory-routing problems through valid inequalities and input ordering. Int. J. Prod. Econ. 155:391–397
Desaulniers G (2010) Branch-and-price-and-cut for the split-delivery vehicle routing problem with time windows. Oper. Res. 58(1):179–192
Avella P, Boccia M, Wolsey LA (2018) Single-period cutting planes for inventory routing problems. Transp. Sci. 52(3):497–508
Laporte G, Nobert Y, Desrochers M (1985) Optimal routing under capacity and distance restrictions. Oper. Res. 33(5):1050–1073
Lysgaard J (2004) Cvrpsep. https://econ.au.dk/research/researcher-websites/jens-lysgaard/cvrpsep/, Accessed: 29 August 2020
Lysgaard J, Letchford AN, Eglese RW (2004) A new branch-and-cut algorithm for the capacitated vehicle routing problem. Math. Program. 100(2):423–445
Archetti C, Bouchard M, Desaulniers G (2011) Enhanced branch and price and cut for vehicle routing with split deliveries and time windows. Transp. Sci. 45(3):285–298
Coelho LC (2021) Problem instances inventory routing. http://www.leandro-coelho.com/instances/inventory-routing/, Accessed: 4 December 2017
Acknowledgments
We are grateful to François Lessard for the support on the implementation of the algorithm.
Funding
This work was supported by the Netherlands Organisation for Scientific Research (NWO) [project number 407-13-050].
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the Topical Collection on Decomposition at 70
Appendices
Appendix 1: Results per instance
Tables 5, 6, and 7 show detailed results on the instances used for Section 5.2 when m = 0.01 and no maximum on the moved demand. The fleet size differs per table (K= 3,4,5). The three tables report per instance the computation time for the IRPDM if the instance is solved within 2 h of running time and whether the instance was solved to optimality (y/n). Thereafter, the upper bound (“UB”), the root lower bound (“LBroot”), and the lower bound after adding valid inequalities (“LBcuts”) is given. The size of the tree (“Tree”), the number of added CIs (“CI”) and MCSIs (“MCSI”) are then given, followed by the percentage cost improvement over the IRP (“Impr.”), the number of demand moves (“Nr.DM”), and the average size of the demand moves (“Sz.DM”) of the solution. Finally, the best upper bound found for the IRP is reported (“UB”), retrieved from [24] and an indication (“Opt.”) whether the instance was solved to optimality (y/n). The instance is indicated in the following format C_Hp_Nc_Kv_i with C the level of holding costs, p the number of periods, c the number of customers, v the number of vehicles, and i the index of the instance. If no solution is available because the instance is not solved to optimality, a dash is filled out. We only include instances for which at least the root node is solved. For two IRP instances, there is no feasible solution possible, and their upper bounds are therefore unknown (Unk).
Appendix: 2: Results on impact of m and maximum on moved demand
Tables 8, 9, and 10 show detailed results on the instances used for Sections 5.2.1 and 5.2.2. The fleet size differs per table (K = 3,4,5). The three tables show for each instance details on the time (“T(s)”), the upper bound (“UB”), and the best lower bound (“LBbest”). The details are shown for different values of m (0.01, 0.005, 0.05, 0.1) and varying maxima on the moved demand (100%, 25%, 50%, 75%). Remind that instances with up to 15 customers and horizon three, and with five customers and horizon six are tested. The formatting of the instance number is the same as in Appendix 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Baller, A.C., Dabia, S., Desaulniers, G. et al. The Inventory Routing Problem with Demand Moves. SN Oper. Res. Forum 2, 6 (2021). https://doi.org/10.1007/s43069-020-00042-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43069-020-00042-z