Abstract
Let \({\mathcal {B}}\) be a class of finite-dimensional Banach spaces. A \({\mathcal {B}}\)-decomposed Banach space is a Banach space X endowed with a family \({\mathcal {B}}_X\subset {\mathcal {B}}\) of subspaces of X such that each \(x\in X\) can be uniquely written as the sum of an unconditionally convergent series \(\sum _{B\in {\mathcal {B}}_X}x_B\) for some \((x_B)_{B\in {\mathcal {B}}_X}\in \prod _{B\in {\mathcal {B}}_X}B\). For every \(B\in {\mathcal {B}}_X\) let \(\mathrm {pr}_B:X\rightarrow B\) denote the coordinate projection. Let \(C\subset [-1,1]\) be a closed convex set with \(C\cdot C\subset C\). The C-decomposition constant \(K_C\) of a \({\mathcal {B}}\)-decomposed Banach space \((X,{\mathcal {B}}_X)\) is the smallest number \(K_C\) such that for every function \(\alpha :{\mathcal {F}}\rightarrow C\) from a finite subset \({\mathcal {F}}\subset {\mathcal {B}}_X\) the operator \(T_\alpha =\sum _{B\in {\mathcal {F}}}\alpha (B)\cdot \mathrm {pr}_B\) has norm \(\Vert T_\alpha \Vert \le K_C\). By \(\varvec{{\mathcal {B}}}_C\) we denote the class of \({\mathcal {B}}\)-decomposed Banach spaces with C-decomposition constant \(K_C\le 1\). Using the technique of Fraïssé theory, we construct a rational \({\mathcal {B}}\)-decomposed Banach space \(\mathbb {U}_C\in \varvec{{\mathcal {B}}}_C\) which contains an almost isometric copy of each \({\mathcal {B}}\)-decomposed Banach space \(X\in \varvec{{\mathcal {B}}}_C\). If \({\mathcal {B}}\) is the class of all 1-dimensional (resp. finite-dimensional) Banach spaces, then \(\mathbb {U}_{C}\) is isomorphic to the complementably universal Banach space for the class of Banach spaces with an unconditional (f.d.) basis, constructed by Pełczyński (and Wojtaszczyk).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A Banach space X is (complementably) universal for a given class of Banach spaces if X belongs to this class and every space from the class is isomorphic to a (complemented) subspace of X.
In 1969 Pełczyński [15] constructed a complementably universal Banach space for the class of Banach spaces with a Schauder basis. In 1971 Kadec [10] constructed a complementably universal Banach space for the class of spaces with the bounded approximation property (BAP). In the same year Pełczyński [13] showed that every Banach space with BAP is isomorphic to a complemented subspace of a Banach space with a basis. Pełczyński and Wojtaszczyk [16] constructed in 1971 a (complementably) universal Banach space for the class of spaces with a finite-dimensional decomposition. A simple construction of the Pełczyński universal space was suggested by Schechtman [17]. Applying Pełczyński’s decomposition argument [14], one immediately concludes that all three universal spaces are isomorphic. It is worth mentioning a negative result of Johnson and Szankowski [9] saying that no separable Banach space can be complementably universal for the class of all separable Banach spaces.
Lindenstrauss and Tzafriri showed in [12, 1.g.5] that a Banach space with an unconditional finite-dimensional decomposition is isomorphic to a subspace of a space with an unconditional basis.
In [7] the second author constructed an isometric version of the Kadec-Pełczyński-Wojtaszczyk space. The universal Banach space from [7] was constructed using the general categorical technique of Fraïssé limits [11]. In [1, 2] the authors constructed some isomorphic copies of the Pełczyński universal spaces, which are isometrically universal for the class of rational based Banach with some restrictions on the suppression or unconditional basis constants. However, as was discovered in [2], the language of based Banach spaces and base preserving morphisms does not work well for based Banach spaces with unconditional constant \(>1\).
In this paper we propose an alternative language of decomposable Banach spaces which is free of this drawback and allow us to establish nice almost universality properties of rational Banach spaces constructed in [1, 2]. Our approach also allows to consider simultaneously the suppression and unconditional constants, which are just special cases of the C-decomposition constant \(K_C\), for C equal to \(\{1\}\) and \(\{-1,1\}\), respectively. Also the notion of a decomposed Banach space generalizes the notions of a Banach space with unconditional base and of a Banach space with uncounditional f.d. base, which was considered in [16].
For a set X by \([X]^{<\omega }\) we denote the family of all finite subsets of X. The sets of rational and real numbers are denoted by \(\mathbb Q\) and \(\mathbb R\), respectively. All Banach spaces considered in this paper are separable and are over the field \(\mathbb R\) of real numbers.
Let \((x_\alpha )_{\alpha \in A}\) be a sequence of points of a Banach space X, indexed by elements of a set A. We say that a series \(\sum _{\alpha \in A}x_\alpha \)converges (more precisely, unconditionally converges) to a point \(x\in X\) if for every \(\varepsilon >0\) there exists a finite subset \(F\subset A\) such that \(\Vert x-\sum _{\alpha \in B}x_\alpha \Vert <\varepsilon \) for any finite subset \(B\subset A\) that contains F.
1.1 Decomposed Banach spaces
Let \({\mathcal {B}}\) be a class of finite-dimensional Banach spaces such that for any linear bijective isometry \(f:X\rightarrow Y\) between Banach spaces the inclusion \(X\in {\mathcal {B}}\) implies \(Y\in {\mathcal {B}}\). Banach spaces from the class \({\mathcal {B}}\) will be called basic Banach spaces. For example, for \({\mathcal {B}}\) we can take the class of all 1-dimensional Banach spaces (or all finite-dimensional Banach spaces).
By a \({\mathcal {B}}\)-decomposed Banach space we understand a pair \((X,{\mathcal {B}}_X)\) consisting of a Banach space X and a family \({\mathcal {B}}_X\subset {\mathcal {B}}\) of finite-dimensional subspaces of X such that every \(x\in X\) can be uniquely written as the sum of an unconditionally convergent series \(\sum _{B\in {\mathcal {B}}_X}x_B\) consisting of points \(x_B\in B\) for \(B\in {\mathcal {B}}_X\). The convergence \(x=\sum _{B\in {\mathcal {B}}_X}x_B\) means that for every \(\varepsilon >0\) there exists a finite subfamily \({\mathcal {F}}\subset {\mathcal {B}}_X\) such that \(\Vert x-\sum _{B\in {\mathcal {E}}}x_B\Vert <\varepsilon \) for any finite subfamily \({\mathcal {E}}\subset {\mathcal {B}}_X\) that contains \({\mathcal {F}}\). In this case the family \({\mathcal {B}}_X\) is called the \({\mathcal {B}}\)-decomposition of X. If the class \({\mathcal {B}}\) is clear from the context, then we shall speak about decomposed Banach spaces instead of \({\mathcal {B}}\)-decomposed Banach spaces.
Fix a class \({\mathcal {B}}\) of finite-dimensional Banach spaces. For every \(B\in {\mathcal {B}}_X\) let \(\mathrm {pr}_B:X\rightarrow B\) denote the coordinate projector. It assigns to each point \(x\in X\) the B-th term \(x_B\) of the unique sequence \((x_{E})_{E\in {\mathcal {B}}_X}\) with \(x=\sum _{E\in {\mathcal {B}}_X}x_E\). The Open Mapping Principle implies that the coordinate projector \(\mathrm {pr}_B:X\rightarrow B\subset X\) is bounded (see [4, p. 33] for more details).
For every finite subfamily \({\mathcal {F}}\subset {\mathcal {B}}_X\), consider the projector
For every \(x\in X\) the unconditional convergence of the series \(\sum _{B\in {\mathcal {B}}_X}\mathrm {pr}_B(x)\) implies the set \(\{\Vert \mathrm {pr}_{\mathcal {F}}(x)\Vert :{\mathcal {F}}\in [{\mathcal {B}}_X]^{<\omega }\}\) is bounded and then by the Banach-Steinhaus Uniform Boundedness Principle, the real number
is well-defined. This number will be called the suppression constant of the decomposed Banach space \((X,{\mathcal {B}}_X)\).
1.2 The decomposition constants of a decomposed Banach space
Let \((X,{\mathcal {B}}_X)\) be a decomposed Banach space with the suppression constant \(K_s\).
For every function \(\alpha :{\mathcal {F}}\rightarrow \mathbb R\) defined on a finite subfamily \({\mathcal {F}}\subset {\mathcal {B}}_X\), consider the operator
For a bounded subset \(C\subset \mathbb R\) let
be the family of functions \(\alpha :{\mathcal {F}}\rightarrow C\) defined on finite subfamilies \({\mathcal {F}}\) of \({\mathcal {B}}_X\).
The number
is called the C-decomposition constant of the decomposed Banach space \((X,{\mathcal {B}}_X)\). Observe that \(K_{\{1\}}\) is equal to the suppression constant \(K_s\) of X. The \(\{-1,1\}\)-decompositional constant \(K_{\{-1,1\}}\) is called the unconditional constant and is denoted by \(K_u\) (cf. [5, §4.5], [8, 6.6]).
The decomposition constants have the following properties.
Lemma 1
Let \((X,{\mathcal {B}}_X)\) be a decomposed Banach space with suppression constant \(K_s\). For any bounded subset \(C\subset \mathbb R\) the following statements hold:
- 1.
\(K_C\ge K_s\cdot \sup _{c\in C}|c|\ge \sup _{c\in C}|c|\);
- 2.
\(K_C\le K_s\cdot \sum _{c\in C}|c|\);
- 3.
\(K_C=K_{C\cup \{0\}}\);
- 4.
\(K_C=K_{\mathrm {conv}({\bar{C}}\cup \{0\})}\);
- 5.
\(K_C\le K_s\cdot \mathrm {diam}(\mathrm {conv}(C\cup \{0\}))<\infty \);
- 6.
\(K_{tC}=|t|\cdot K_C\) for any real number t.
Proof
- 1.
To prove that \(K_C\ge K_s\cdot \sup _{c\in C}|c|\), assume that this inequality does not hold. Then there exists \(c\in C\) and a finite subfamily \({\mathcal {F}}\subset {\mathcal {B}}_X\) such that \(K_C<|c|\cdot \Vert \mathrm {pr}_{\mathcal {F}}\Vert \). Now consider the constant function \(\alpha :{\mathcal {F}}\rightarrow \{c\}\subset C\) and observe that \(T_\alpha =c\cdot \mathrm {pr}_{\mathcal {F}}\) and hence
$$\begin{aligned} K_C<|c|\cdot \Vert \mathrm {pr}_{\mathcal {F}}\Vert =\Vert T_\alpha \Vert \le K_C, \end{aligned}$$which is a desired contradiction completing the proof.
- 2.
To prove that \(K_C\le K_s\cdot \sum _{c\in C}|c|\), observe that for every function \(\alpha :{\mathcal {F}}\rightarrow C\) defined on a finite subset \({\mathcal {F}}\subset {\mathcal {B}}_X\) we have
$$\begin{aligned} \Vert T_\alpha \Vert= & {} \left\| \sum _{B\in {\mathcal {F}}}\alpha (B)\cdot \mathrm {pr}_B\right\| =\left\| \sum _{c\in C}c\cdot \mathrm {pr}_{\alpha ^{-1}(c)}\right\| \\\le & {} \sum _{c\in C}|c|\cdot \Vert \mathrm {pr}_{\alpha ^{-1}(c)}\Vert \le \sum _{c\in C}|c|\cdot K_s. \end{aligned}$$ - 3.
The inequality \(K_C\le K_{C\cup \{0\}}\) follows from the inclusion \(C\subset C\cup \{0\}\); the inequality \(K_{C\cup \{0\}}\le K_C\) follows from the observation that for every function \(\alpha \in (C\cup \{0\})^{<{\mathcal {B}}_X}\) the operator \(T_\alpha \) is equal to the operator \(T_\beta \) for the function
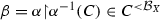 .
. - 4.
The inequality \(K_C\le K_{\mathrm {conv}({\bar{C}}\cup \{0\})}\) follows from the inclusion \(C\subset {\mathrm {conv}({\bar{C}}\cup \{0\}})\). To prove the reverse inequality, we need to prove that \(\Vert T_\alpha \Vert \le K_C\) for any function \(\alpha :{\mathcal {F}}\rightarrow {\mathrm {conv}({\bar{C}}\cup \{0\}})\) defined on a finite set \({\mathcal {F}}\subset {\mathcal {B}}_X\).
Let \(C_0=C\cup \{0\}\) and for every \(n\in \omega \) let \(C_{n+1}:=\{\frac{1}{2}x+\frac{1}{2}y:x,y\in C_n\}\). It is easy to see that the union \(C_\omega =\bigcup _{n\in \omega }C_n\) is a dense subset of \(\mathrm {conv}({\bar{C}}\cup \{0\})\). By induction we shall show that for every \(n\in \omega \) and every function \(\alpha :{\mathcal {F}}\rightarrow C_n\) the operator \(T_\alpha \) has norm \(\Vert T_\alpha \Vert \le K_C\). For \(n=0\) this follows from the equality \(K_{C_0}=K_{C\cup \{0\}}=K_C\), which was proved in the preceding statement.
Assume that for some \(n\in \omega \) we proved that for every \(\alpha :{\mathcal {F}}\rightarrow C_n\) the operator \(T_\alpha \) has norm \(\Vert T_\alpha \Vert \le K_C\). Given any function \(\alpha :{\mathcal {F}}\rightarrow C_{n+1}\), find two functions \(\beta ,\gamma :{\mathcal {F}}\rightarrow C_n\) such that \(\alpha (B)=\frac{1}{2}\beta (B)+\frac{1}{2}\gamma (B)\) for every \(B\in {\mathcal {F}}\). Then \(T_\alpha =\frac{1}{2}T_\beta +\frac{1}{2}T_\gamma \) and hence
Now we see that for any function \(\alpha :{\mathcal {F}}\rightarrow C_\omega \) the operator \(T_\alpha \) has norm \(\Vert T_\alpha \Vert \le K_C\). The density of \(C_\omega \) in \({\mathrm {conv}({\bar{C}}\cup \{0\}})\) and the continuity of the projectors \(\mathrm {pr}_B\) for \(B\in {\mathcal {F}}\) imply that for every function \(\alpha :{\mathcal {F}}\rightarrow {({\bar{C}}\cup \{0\}})\) the operator \(T_\alpha \) has norm \(\Vert T_\alpha \Vert \le \sup \{\Vert T_\beta \Vert :\beta \in C_\omega ^{\mathcal {F}}\}\le K_C\).
- 5.
By the boundedness of the set C, the convex set \({\mathrm {conv}({\bar{C}}\cup \{0\})}\) coincides with the closed interval [a, b] for the real numbers \(a=\min ({\bar{C}}\cup \{0\})\) and \(b=\max ({\bar{C}}\cup \{0\})\). By the statements (4) and (2), we obtain
$$\begin{aligned} K_C=K_{[a,b]}=K_{\{a,b\}}\le K_s\cdot (|a|+|b|)=K_s\cdot \mathrm {diam}(C\cup \{0\})<\infty . \end{aligned}$$ - 6.
For any \(t\in \mathbb R\), the definition of the constants \(K_C\) and \(K_{tC}\) ensure that
$$\begin{aligned} K_{tC}= & {} \sup \big \{\Vert T_\alpha \Vert :\alpha \in (tC)^{<{\mathcal {B}}_X}\big \}=\big \{\Vert T_{t\alpha }\Vert :\alpha \in C^{<{\mathcal {B}}_X}\big \}\\= & {} |t|\cdot \big \{\Vert T_\alpha \Vert :\alpha \in C^{<{\mathcal {B}}_X}\big \}=|t|\cdot K_C. \end{aligned}$$
\(\square \)
1.3 Rational decomposed Banach spaces
A decomposed Banach space \((X,{\mathcal {B}}_X)\) is a subspace of a decomposed Banach space \((Y,{\mathcal {B}}_Y)\) if \(X\subseteq Y\) and \({\mathcal {B}}_X\subseteq {\mathcal {B}}_Y\).
For a Banach space X by \(\Vert \cdot \Vert _X\) we denote the norm of X and by
the closed unit ball of X.
A finite-dimensional decomposed Banach space \((X,{\mathcal {B}}_X)\) is rational if its unit ball is a convex polyhedron spanned by finitely many points that have rational coordinates in some basis \(\{e_1,\dots ,e_n\}\subset \bigcup _{B\in {\mathcal {B}}_X}B\) of X. It is easy to see that any decomposed subspace of a rational finite-dimensional decomposed Banach space is rational.
A decomposed Banach space \((X,{\mathcal {B}}_X)\) is rational if each finite-dimensional decomposed subspace of \((X,{\mathcal {B}}_X)\) is rational.
1.4 Categories
Let \({\mathfrak {K}}\) be a category. For two objects A, B of the category \({\mathfrak {K}}\), by \({\mathfrak {K}}(A,B)\) we denote the set of all \({\mathfrak {K}}\)-morphisms from A to B. A subcategory of \({\mathfrak {K}}\) is a category \({\mathfrak {L}}\) such that each object of \({\mathfrak {L}}\) is an object of \({\mathfrak {K}}\) and each morphism of \({\mathfrak {L}}\) is a morphism of \({\mathfrak {K}}\). Morphisms and isomorphisms of a category \({\mathfrak {K}}\) will be called \({\mathfrak {K}}\)-morphisms and \({\mathfrak {K}}\)-isomorphisms, respectively.
A subcategory \({\mathfrak {L}}\) of a category \({\mathfrak {K}}\) is full if each \({\mathfrak {K}}\)-morphism between objects of the category \({\mathfrak {L}}\) is an \({\mathfrak {L}}\)-morphism.
A category \({\mathfrak {L}}\) is cofinal in \({\mathfrak {K}}\) if for every object A of \({\mathfrak {K}}\) there exists an object B of \({\mathfrak {L}}\) such that the set \({\mathfrak {K}}(A,B)\) is nonempty. A category \({\mathfrak {K}}\) has the amalgamation property if for every objects A, B, C of \({\mathfrak {K}}\) and for every morphisms \(f\in {\mathfrak {K}}(A,B)\), \(g\in {\mathfrak {K}}(A,C)\) there exist an object D of \({\mathfrak {K}}\) and morphisms \(f'\in {\mathfrak {K}}(B,D)\), \(g'\in {\mathfrak {K}}(C,D)\) such that \(f'\circ f=g'\circ g\).
In this paper we shall work in the category \(\varvec{{\mathcal {B}}}\), whose objects are \({\mathcal {B}}\)-decomposed Banach spaces \((X,{\mathcal {B}}_X)\). For two decomposed Banach spaces \((X,{\mathcal {B}}_X)\), \((Y,{\mathcal {B}}_Y)\), a morphism of category \(\varvec{{\mathcal {B}}}\) is a linear injective continuous operator \(T: X\rightarrow Y\) such that \(T(B)\in {\mathcal {B}}_Y\) for every \(B\in {\mathcal {B}}_X\). To shorten notation, we shall often denote decomposed Banach spaces \((X,{\mathcal {B}}_X)\) by X.
A morphism \(T:X\rightarrow Y\) of the category \(\varvec{{\mathcal {B}}}\) is called an isometry (or else an isometry morphism) if \(\Vert T(x)\Vert _Y=\Vert x\Vert _X\) for any \(x\in X\). By \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\) we denote the category whose objects are decomposed Banach spaces and morphisms are isometry morphisms of decomposed Banach spaces. The category \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\) is a subcategory of the category \(\varvec{{\mathcal {B}}}\).
By \({\mathfrak {f}}\varvec{{\mathcal {B}}}\) (resp. \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}\)) we denote the full subcategory of \(\varvec{{\mathcal {B}}}\) (resp. \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)), whose objects are finite-dimensional decomposed Banach spaces, and by \({\mathfrak {r}} \varvec{{\mathcal {B}}}\) (resp. \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}\)) the full subcategory of \(\mathfrak f\varvec{{\mathcal {B}}}\) (resp. \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}\)) whose objects are rational finite-dimensional decomposed Banach spaces.
1.5 \(\varvec{{\mathcal {B}}}\)-universal decomposed Banach spaces
Definition 1
A decomposed Banach space U is defined to be \(\varvec{{\mathcal {B}}}\)-universal if \(U\in \varvec{{\mathcal {B}}}\) and each decomposed Banach space \(X\in \varvec{{\mathcal {B}}}\) is \(\varvec{{\mathcal {B}}}\)-isomorphic to a decomposed subspace of U.
Applying the decomposition method of Pełczyński [15], we can prove the following uniqueness result.
Theorem 1
Any two \(\varvec{{\mathcal {B}}}\)-universal decomposed Banach spaces are \(\varvec{{\mathcal {B}}}\)-isomorphic.
1.6 The categories \(\varvec{{\mathcal {B}}}_C\) and \(\varvec{{\mathcal {B}}}{\mathfrak {I}}_C\)
Given a closed convex set \(C\subset [-1,1]\), let \(\varvec{{\mathcal {B}}}_{C}\) (resp. \(\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)) be the full subcategory of \(\varvec{{\mathcal {B}}}\) (resp. \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)) whose objects are decomposed Banach spaces with C-decomposition constant \(K_C\le 1\). For a decomposed Banach space X we shall write \(X\in \varvec{{\mathcal {B}}}_{C}\) if X is an object of the category \(\varvec{{\mathcal {B}}}_{C}\) (that is X has C-decomposition constant \(K_C\le 1\)).
Also consider the full subcategory \({\mathfrak {f}}\varvec{{\mathcal {B}}}_{C}=\mathfrak f\varvec{{\mathcal {B}}}\cap \varvec{{\mathcal {B}}}_{C}\) of the category \(\varvec{{\mathcal {B}}}\) and the full subcagories \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}={\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}\cap \varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) and \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}={\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}\cap \varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) of the category \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\).
From now on we assume that \(C\subset [-1,1]\) is a fixed closed convex set such that
where \(C\cdot C=\{xy:x,y\in C\}\).
2 Amalgamation
In this section we prove that the categories \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) and \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) have the amalgamation property.
Lemma 2
(Amalgamation Lemma) Let X, Y, Z be objects and \(i:Z\rightarrow ~X\), \(j:Z \rightarrow Y\) be morphisms of the category \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\). Then there exist an object W of the category \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) and \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphisms \(i':X\rightarrow W\) and \(j':Y\rightarrow W\) such that the diagram

is commutative.
Moreover, if the decomposed Banach spaces X, Y, Z are rational, then so is the decomposed Banach space W.
Proof
We shall prove this lemma in the special case when the isometries i, j are identity inclusions; the general case is analogous but has more complicated notation. Our assumptions on i, j ensure that \(Z\subset X\cap Y\) and \({\mathcal {B}}_Z\subset {\mathcal {B}}_X\cap {\mathcal {B}}_Y\), where \({\mathcal {B}}_X,{\mathcal {B}}_Y,{\mathcal {B}}_Z\subset {\mathcal {B}}\) are the decompositions of the decomposed Banach spaces X, Y, Z. It follows from \({\mathcal {B}}_Z={\mathcal {B}}_X\cap {\mathcal {B}}_Y\) that the coordinate projectors of the decompositions \({\mathcal {B}}_X\) and \({\mathcal {B}}_Y\) agree on the intersection \(Z=X\cap Y\).
Consider the direct sum \(X\oplus Y\) of the Banach spaces X, Y endowed with the norm \(\Vert (x,y)\Vert =\Vert x\Vert _X+\Vert y\Vert _Y\). Let \(W=(X\oplus Y)/\varDelta \) be the quotient by the subspace \(\varDelta =\{(z,-z):z\in Z\}\).
We define linear operators \(i':X\rightarrow W\) and \(j':Y\rightarrow W\) by \(i'(x)=(x,0)+\varDelta \) and \(j'(y)=(0,y)+\varDelta .\)
Let us show \(i'\) and \(j'\) are isometries. Indeed, for every \(x\in X\)
On the other hand, for every \(z\in Z\)
and hence \(\Vert x\Vert _X \le \inf _{z\in Z} \Vert (x,0)-(z,-z)\Vert =\Vert i'(x)\Vert _W\). Therefore \(\Vert i'(x)\Vert _W=\Vert x\Vert _X\). Similarly, we can show that \(j'\) is an isometry.
We shall identify X and Y with their images \(i'(X)\) and \(j'(Y)\) in W. In this case we can consider the union \({\mathcal {B}}_W:={\mathcal {B}}_X\cup {\mathcal {B}}_Y\) and can show that \({\mathcal {B}}_W\) is a decomposition of the (finite-dimensional) Banach space W.
Let us show that the decomposed Banach space \((W,{\mathcal {B}}_W)\) has C-decomposition constant \(K_C\le 1\). Given any function \(\alpha :{\mathcal {B}}_W\rightarrow C\), we should prove the upper bound
for every \(w\in W\). Since 0 is a non-isolated point of the convex set C, we lose no generality assuming that for every \(B\in {\mathcal {B}}_W\) the number \(\alpha _B:=\alpha (B)\) is not equal to zero.
Taking into account that the decomposed Banach spaces \((X,{\mathcal {B}}_X)\) and \((Y,{\mathcal {B}}_Y)\) have C-unconditional constant \(\le 1\), we obtain:
If the finite-dimensional based Banach spaces X and Y are rational, then so is their sum \(X\oplus Y\) and so is the quotient space W of \(X\oplus Y\). \(\square \)
3 \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach spaces
Definition 2
A decomposed Banach space X is called \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal if
each finite-dimensional decomposed subspace of X is an object of the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\), and
for any object A of the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\), any \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \(f:\varLambda \rightarrow X\) defined on a decomposed subspace \(\varLambda \) of A can be extended to an \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \({\bar{f}}:A\rightarrow X \).
We recall that \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) denotes the full subcategory of \(\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) whose objects are rational finite-dimensional decomposed Banach spaces with C-decomposition constant \(K_C\le 1\). Obviously, up to \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-isomorphisms the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) contains countably many objects. By Lemma 2, the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) has the amalgamation property. We now use the concepts from [11] for constructing a “generic” sequence in \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\). A sequence \((X_n)_{n\in \omega }\) of objects of the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) is called a chain if each decomposed Banach space \(X_n\) is a subspace of the decomposed Banach space \(X_{n+1}\).
Definition 3
A chain \((U_n)_{n\in \omega }\) of objects of the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) is Fraïssé if for any \(n\in \omega \) and \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \( f: {U_n} \rightarrow Y\in {\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_C\) there exist \(m > n\) and an \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \(g: Y\rightarrow {U_m}\) such that \(g \circ f:U_n\rightarrow U_m\) is the identity inclusion of \(U_n\) to \(U_m\).
Definition 3 implies that the Fraïssé sequence \(\{U_n\}_{n\in \omega }\) is cofinal in the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) in the sense that each object A of the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) admits a \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \(A\rightarrow U_n\) for some \(n\in \omega \). In this case the category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) is countably cofinal.
The name “Fraïssé sequence”, as in [11], is motivated by the model-theoretic theory of Fraïssé limits developed by Roland Fraïssé [6]. One of the results in [11] is that every countably cofinal category with amalgamation has a Fraïssé sequence. Applying this general result to our category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) we get:
Theorem 2
[11] The category \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) has a Fraïssé sequence.
From now on, we fix a Fraïssé sequence \((U_n)_{n\in \omega }\) in \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\). Let \(\mathbb {U}_{C}\) be the completion of the union \(\bigcup _{n\in \omega }U_n\) and \({\mathcal {B}}_{\mathbb {U}_{C}}=\bigcup _{n\in \omega }{\mathcal {B}}_{U_n}\). The proof of the following theorem literally repeats the proof of Theorem 4.4 in [1].
Theorem 3
\((\mathbb {U}_{C},{\mathcal {B}}_{\mathbb {U}_{C}})\) is an \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space.
To shorten notation, the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space \((\mathbb {U}_{C},{\mathcal {B}}_{\mathbb {U}_{C}})\) will be denoted by \(\mathbb {U}_{C}\). The following theorem shows that such space is unique up to \(\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-isomorphism. It can be proved by analogy with Theorem 4.5 in [1].
Theorem 4
Any two \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach spaces X, Y are \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-isomorphic, which means that there exists a linear bijective isometry \(X\rightarrow Y\) preserving the decompositions \({\mathcal {B}}_X\) and \({\mathcal {B}}_Y\).
Corollary 1
Any \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space X is \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-isomorphic to the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space \(\mathbb {U}_{C}\).
The following universality property of the space \(\mathbb {U}_C\) can be proved by analogy with Theorem 5.5 in [1].
Theorem 5
For any rational decomposed Banach space \(X\in \varvec{{\mathcal {B}}}_C\) there exists an isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow \mathbb {U}_C\).
4 Almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universality
By analogy with an \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space, one can try to introduce an \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space. However such notion is vacuous as each decomposed Banach space has only countably many finite-dimensional decomposed subspaces whereas in general the category \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\) contains continuum many pairwise non \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-isomorphic 2-dimensional decomposed Banach spaces. A “right” definition is that of an almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space, introduced with the help of \(\varepsilon \)-isometries.
For a positive real number \(\varepsilon \), a linear operator \(f:X\rightarrow Y\) between Banach spaces X and Y is called an \(\varepsilon \)-isometry if
for every \(x\in X\backslash \{0\}\). This definition implies that each \(\varepsilon \)-isometry is an injective linear operator.
Definition 4
A decomposed Banach space X called almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal if for any \(\varepsilon >0\) and finite-dimensional decomposed Banach space \(A\in {\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_C\), any \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:\varLambda \rightarrow X\) defined on a decomposed subspace \(\varLambda \) of A can be extended to an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \({\bar{f}}:A\rightarrow X \).
Theorem 6
Any \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space X is almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal.
Proof
We shall use the fact, that the norm of any finite-dimensional decomposed Banach space can be approximated by a rational norm.
To prove that X is almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal, take any \(\varepsilon >0\), any finite-dimensional decomposed Banach space \(A\in {\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_C\) and an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:\varLambda \rightarrow X\) defined on a decomposed subspace \(\varLambda \) of A. For every function \(\alpha :{\mathcal {B}}_A\rightarrow C\), consider the linear operator \(T_{\alpha }:A\rightarrow A\), \(T_\alpha :x\mapsto \sum _{B\in {\mathcal {B}}_A}\alpha (x)\cdot \mathrm {pr}_B(x)\). By \(\Vert \cdot \Vert _A\) and \(\Vert \cdot \Vert _\varLambda \) we denote the norms of the Banach spaces A and \(\varLambda \). The morphism f determines a new norm \(\Vert \cdot \Vert _\varLambda '\) on \(\varLambda \), defined by \(\Vert a \Vert _\varLambda '=\Vert f(a)\Vert _X\) for \(a\in \varLambda \). Taking into account that the decomposed Banach space X is rational with C-unconditional constant \(K_C\le 1\), we conclude that \(\Vert \cdot \Vert '_\varLambda \) is a rational norm on \(\varLambda \) such that \(\Vert T_{\alpha }(a)\Vert '_\varLambda \le \Vert a\Vert '_\varLambda \) for every \(a\in \varLambda \) and every function \(\alpha :{\mathcal {B}}_\varLambda \rightarrow C\).
Since f is an \(\varepsilon \)-isometry, \((1+\varepsilon )^{-1}<\Vert a\Vert _\varLambda '<(1+\varepsilon )\) for every \(a\in \varLambda \) with \(\Vert a\Vert _\varLambda =1\). By the compactness of the unit sphere in \(\varLambda \), there exists a positive \(\delta <\varepsilon \) such that \((1+\delta )^{-1}<\Vert a\Vert '_\varLambda <(1+\delta )\) for every \(a\in \varLambda \) with \(\Vert a\Vert _\varLambda =1\). This inequality implies \(\frac{1}{1+\delta }B_\varLambda \subset B_\varLambda '\subset (1+\delta )B_\varLambda \), where \(B_\varLambda =\{a\in \varLambda : \Vert a\Vert _\varLambda \le 1\}\) and \(B_\varLambda '=\{a\in \varLambda : \Vert a\Vert '_\varLambda \le 1\}\) are the closed unit balls of \(\varLambda \) in the norms \(\Vert \cdot \Vert _\varLambda \) and \(\Vert \cdot \Vert _\varLambda '\). Choose positive real numbers \(\delta ',\varepsilon '\) such that \(\delta< \delta '<\varepsilon '<\varepsilon \). Next, choose rational numbers \(-1\le c\le 0<c'\le 1\) such that \(C\subset [c,c']\subset \frac{1+\delta '}{1+\delta }C\) and \(C\cdot [c,c']\subset [c,c']\).
Since the norm \(\Vert \cdot \Vert '_\varLambda \) is rational, there exists a basis \(\{e_1,\dots ,e_n\}\subset \cup {\mathcal {B}}_A\) of the Banach space A such that the ball \(B'_\varLambda \) is a convex polyhedron whose vertices have rational coordinates in the basis \(e_1,\dots ,e_n\). Such a polyhedron in A will be called rational.
Let \(B_A=\{a\in A: \Vert x\Vert _A\le 1\}\) be the closed unit ball of the Banach space A. Choose a rational polyhedron P in A such that \(P=-P\) and
Next consider the convex hull \(B_A':=\mathrm{conv} (P')\) of the set
Repeating the proof of Lemma 1(4), one can show that \(B_A'\) coincides with the convex hull of the set
which implies that \(B_A'\) is a rational polyhedron in the decomposed Banach space A.
Taking into account that \([c,c']\subset \frac{1+\delta '}{1+\delta }C\), \(P\subset \frac{1}{1+\delta '}B_A\), and A is a decomposed Banach space with C-decomposition constant \(\le 1\), we conclude that
Then
and hence
The convex symmetric set \(B_A':=\mathrm {conv}(P')\) determines a rational norm \(\Vert \cdot \Vert _A'\) on A whose unit ball coincides with \(B_A'\). By \(A'\) we denoted the decomposed Banach space A endowed with the norm \(\Vert \cdot \Vert '_A\). We claim that the decomposition \({\mathcal {B}}_{A'}={\mathcal {B}}_A\) of the Banach space \(A'\) has C-unconditional constant \(K_C\le 1\). Indeed, for any function \(\alpha :{\mathcal {B}}_A\rightarrow C\) the inclusion \(C\cdot [c,c']\subset [c,c']\) implies
and hence
which means that the operator \(T_{\alpha }:A'\rightarrow A'\) has norm \(\Vert T_\alpha \Vert \le 1\) and hence the decomposed Banach space \(A'\) has C-unconditional constant \(K_C\le 1\).
It remains to check that \(\Vert a\Vert '_A=\Vert a\Vert '_\varLambda \) for each \(a\in \varLambda \), which is equivalent to the equality \(B_A'\cap \varLambda =B_\varLambda '\). The inclusion \(B_\varLambda '\subset B_A'\cap \varLambda \) is evident. To prove the reverse inclusion \(B_\varLambda '\supset B_A'\cap \varLambda \) observe that \(P'\subset B_\varLambda '\cup \frac{1}{1+\delta }B_A\) and hence
The inclusions \(\frac{1}{1+\varepsilon '}B_A\subset B_A'\subset (1+\delta )B_A\) imply the strict inequality
holding for all \(a\in A\backslash \{0\}\).
Let \(\varLambda '\) and \(A'\) be the decomposed Banach spaces \(\varLambda \) and A endowed with the new rational norms \(\Vert \cdot \Vert _\varLambda '\) and \(\Vert \cdot \Vert _A'\), respectively. It is clear that \(\varLambda '\subset A'\). The definition of the norm \(\Vert \cdot \Vert '_\varLambda \) ensures that \(f:\varLambda '\rightarrow X\) is a \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism. Using the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universality of X, extend the \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \(f:\varLambda '\rightarrow X\) to a \(\varvec{{\mathcal {B}}}{\mathfrak {I}}\)-morphism \({\bar{f}}:A'\rightarrow X\). The inequalities (2) ensure that \({\bar{f}}:A\rightarrow X\) is an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism from A, extending the \(\varepsilon \)-isometry f. This completes the proof of the almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universality of X. \(\square \)
Theorem 7
Let X and Y be almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach spaces and \( \varepsilon >0\). Each \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X_0\rightarrow Y\) defined on a finite-dimensional decomposed subspace \(X_0\) of the decomposed Banach space \(X\in \varvec{{\mathcal {B}}}_{C}\) can be extended to an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-isomorphism \(\bar{f}:X \rightarrow Y\).
Theorem 7 can be proved by analogy with Theorem 5.3 in [1].
Corollary 2
For any almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach spaces X and Y and any \( \varepsilon >0\) there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-isomorphism \(f:X \rightarrow Y\).
Corollary 3
Any almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space is \(\varvec{{\mathcal {B}}}\)-isomorphic to the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space \(\mathbb {U}_{C}\).
Theorem 8
Let U be an almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space. For any \(\varepsilon >0\) and any decomposed Banach space \(X\in \varvec{{\mathcal {B}}}_{C}\), there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow U\).
Theorem 8 can be proved by analogy with Theorem 5.5 in [1]. Applying Theorems 6 and 8 to the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal space \(\mathbb {U}_{C}\) we obtain its \(\varvec{{\mathcal {B}}}_{C}\)-universality.
Corollary 4
For any \(\varepsilon >0\) and any decomposed Banach space \(X\in \varvec{{\mathcal {B}}}_{C}\), there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow \mathbb {U}_{C}\).
Corollary 5
Each almost \({\mathfrak {f}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal decomposed Banach space U is \(\varvec{{\mathcal {B}}}\)-universal and hence is \(\varvec{{\mathcal {B}}}\)-isomorphic to the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{[0,1]}\)-universal space \(\mathbb {U}_{[0,1]}\).
Proof
Given a \(\varvec{{\mathcal {B}}}\)-decomposed Banach space X, we need to prove that X is \(\varvec{{\mathcal {B}}}\)-isomorphic to a subspace of the decomposed space U. Denote by \(X_1\) the decomposed Banach space X endowed with the equivalent norm
Using the inclusion \(C\cdot C\subset C\), it is easy to check that \(X_1\) has C-decompostion constant \(\le 1\) and hence \(X_1\in \varvec{{\mathcal {B}}}_C\). By Theorem 8, for \(\varepsilon =\frac{1}{2}\) there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X_1\rightarrow U\). Then f is a \(\varvec{{\mathcal {B}}}\)-isomorphism between X and the decomposed (and hence complemented) subspace \(f(X)=f(X_1)\) of the decomposed Banach space U.
Therefore, the decomposed Banach space U is \(\varvec{{\mathcal {B}}}\)-universal. By Theorem 1, U is \(\varvec{{\mathcal {B}}}\)-isomorphic to any other \(\varvec{{\mathcal {B}}}\)-universal decomposed Banach space, in particular, to \(\mathbb {U}_{[0,1]}\). \(\square \)
5 Some special cases
In this section we survey some implications of the results obtained in the preceding sections for some special choices of the class \({\mathcal {B}}\) of basic Banach spaces and the convex set \(C\subset [-1,1]\).
5.1 \(\varvec{{\mathcal {B}}}\)-Decomposed Banach spaces with bounds on suppression or unconditional constants
Let us recall that for a decomposed Banach space X its suppression constant \(K_s\) is equal to \(K_{[0,1]}\) and its unconditional constant \(K_u\) is equal to \(K_{[-1,1]}\). Then for every real number \(K\ge 1\) the category \(\varvec{{\mathcal {B}}}_{[0,\frac{1}{K}]}\) coincides with the category of decomposed Banach spaces with suppression constant \(\le K\) and the category \(\varvec{{\mathcal {B}}}_{[-\frac{1}{K},\frac{1}{K}]}\) coincides with the category of decomposed Banach spaces with uncondional constant \(\le K\).
Applying Theorems 3, 5, 6 to the convex subsets \([0,\frac{1}{K}]\) and \([-\frac{1}{K},\frac{1}{K}]\) we get the following two corollaries.
Corollary 6
For every real number \(K\ge 1\), there exists a rational \(\varvec{{\mathcal {B}}}\)-decomposed Banach space U such that
- (1)
U has suppression constant \(K_s\le K\);
- (2)
for any rational \({\mathcal {B}}\)-decomposed Banach space X with suppression constant \(\le K\) there exists an isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow U\);
- (3)
for any \({\mathcal {B}}\)-decomposed Banach space X with suppression constant \(\le K\) and any \(\varepsilon >0\) there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow U\).
Corollary 7
For every real number \(K\ge 1\), there exists a rational \(\varvec{{\mathcal {B}}}\)-decomposed Banach space U such that
- (1)
U has unconditional constant \(K_u\le K\);
- (2)
for any rational \({\mathcal {B}}\)-decomposed Banach space X with unconditional constant \(\le K\) there exists an isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow U\);
- (3)
for any \({\mathcal {B}}\)-decomposed Banach space X with unconditional constant \(\le K\) and any \(\varepsilon >0\) there exists an \(\varepsilon \)-isometry \(\varvec{{\mathcal {B}}}\)-morphism \(f:X\rightarrow U\).
5.2 Universal Banach spaces with unconditional f.d. bases
If \({\mathcal {B}}\) is the class of all finite-dimensional Banach spaces, then \(\varvec{{\mathcal {B}}}\)-decomposed Banach spaces are called Banach spaces with unconditional f.d. base. In [16] Pełczyński and Wojtaszczyk constructed a Banach space \(\mathbb {U}_{fd}\) with unconditional f.d. base such that every Banach space with unconditional f.d. base is isomorphic to a complemented subspace of \(\mathbb {U}_{fd}\).
Applying Corollaries 6, 7 and Theorem 1 to the class \({\mathcal {B}}\) of all finite-dimensional Banach spaces, we get the following universal spaces, which are isomorphic copies of the Pełczyński-Wojtaszczyk space \(\mathbb {U}_{fd}\).
Corollary 8
For every real number \(K\ge 1\), there exists a rational Banach space U with uncounditional f.d. base such that
- (1)
U has suppression constant \(K_s\le K\);
- (2)
for any rational Banach space X with unconditional f.d. base and suppression constant \(\le K\) there exists a linear isometry \(f:X\rightarrow U\) preserving the f.d. decompositions of the spaces X and U;
- (3)
for any \(\varepsilon >0\) and any Banach space X with unconditional f.d. base and suppression constant \(\le K\), there exists a linear \(\varepsilon \)-isometry \(f:X\rightarrow U\) preserving the f.d. decompostions of the spaces X and U;
- (4)
there exists an isomorphism \(U\rightarrow \mathbb {U}_{fd}\) preserving the decompositions of the spaces U and \(\mathbb {U}_{fd}\).
Corollary 9
For every real number \(K\ge 1\), there exists a rational Banach space U with uncounditional f.d. base such that
- (1)
U has unconditional constant \(K_u\le K\);
- (2)
for any rational Banach space X with unconditional f.d. base and unconditional constant \(\le K\) there exists a linear isometry \(f:X\rightarrow U\) preserving the f.d. decompositions of the spaces X and U;
- (3)
for any \(\varepsilon >0\) and any Banach space X with unconditional f.d. base and unconditional constant \(\le K\), there exists a linear \(\varepsilon \)-isometry \(f:X\rightarrow U\) preserving the f.d. decompostions of the spaces X and U;
- (4)
there exists an isomorphism \(U\rightarrow \mathbb {U}_{fd}\) preserving the decompositions of the spaces U and \(\mathbb {U}_{fd}\).
5.3 Universal Banach spaces with unconditional bases
If \({\mathcal {B}}\) is the class of all 1-dimensional Banach spaces, then \(\varvec{{\mathcal {B}}}\)-decomposed Banach spaces can be identified with based Banach spaces, considered in [1, 2]. We recall that a based Banach space is a pair \((X,\mathcal {B}_X)\) consisting of a Banach space X and a subset \(\mathcal {B}_X\subset X\) such that every \(x\in X\) can be uniquely written as the sum of an unconditionally convergent series \(\sum _{b\in \mathcal {B}_X}x_b\cdot b\) for some sequence of real numbers \((x_b)_{b\in \mathcal {B}_X}\). The set \(\mathcal {B}_X\) is called the unconditional basis of X. Each unconditional basis \(\mathcal {B}_X\) induces a 1-dimensional decomposition \({\mathcal {B}}_X:=\{\mathbb R\cdot b\}_{b\in \mathcal {B}_X}\subset {\mathcal {B}}\) of the Banach space X. Conversely, for any decomposition \({\mathcal {B}}_X\subset {\mathcal {B}}\) of a Banach space X, in each 1-dimensional subspace \(B\in {\mathcal {B}}_X\) we can choose an element \(e_B\in B\) of norm \(\Vert e_B\Vert =1\) and obtain an unconditional basis \(\mathcal {B}_X:=\{e_B\}_{B\in {\mathcal {B}}_X}\) for X. The suppression and unconditional constants of the obtained base \(\mathcal {B}_X\) coincides with the suppression and decomposition constants of the decomposition \({\mathcal {B}}_X\).
A based Banach space \((X,\mathcal {B}_X)\) is called a subspace of a based Banach space \((Y,\mathcal {B}_Y)\) if \(X\subset Y\) and \(\mathcal {B}_X=X\cap \mathcal {B}_Y\). For two based Banach spaces \((X,\mathcal {B}_X)\) and \((Y,\mathcal {B}_Y)\) a linear operator \(T:X\rightarrow Y\) is called
base-preserving if
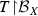 is an injective map from X to Y;
is an injective map from X to Y;decomposition-preserving if for every \(x\in \mathcal {B}_X\) there exists a unique \(y\in \mathcal {B}_Y\) with \(T(x)\in \mathbb R\cdot y\).
It is clear that each base-preserving operator is decomposition-preserving.
In [1] (resp. [2]) for every real number \(K\ge 1\) we have constructed a rational based Banach space \((\mathbb {U}_{K},\mathcal {B}_{\mathbb {U}_{K}})\) with suppression (resp. unconditional) constant \(\le K\) such that for any rational based Banach space \((A,\mathcal {B}_A)\) with suppression (resp. unconditional) constant \(\le K\), any base-preserving linear isometry \(f:\varLambda \rightarrow \mathbb {U}_{K}\) defined on a finite-dimensional based subspace \((\varLambda ,\mathcal {B}_\varLambda )\) of \((A,\mathcal {B}_A)\) can be extended to a base-preserving linear isometry \(f:A\rightarrow \mathbb {U}_{K}\). The based space \((\mathbb {U}_K,\mathcal {B}_{\mathbb {U}_K})\) will be called the universal rational based Banach space with suppression (resp. unconditional) constantK. In [1] (resp. [2]) it was shown that the universal space \(\mathbb {U}_K\) is isomorphic to the universal Banach space \(\mathbb {U}\) with unconditional basis, constructed by Pełczyński [15].
By [1, 3] (resp. [2]), for \(K=1\) and any \(\varepsilon >0\) the universal based Banach space \((\mathbb {U}_K,\mathcal {B}_{\mathbb {U}_K})\) has the following \(\varepsilon \)-universality property: for any based Banach space \((A,\mathcal {B}_A)\) with suppression (resp. unconditional) constant \(\le K\), any base-preserving linear \(\varepsilon \)-isometry \(f:\varLambda \rightarrow \mathbb {U}_{K}\) defined on a finite-dimensional based subspace \((\varLambda ,\mathcal {B}_\varLambda )\) of \((A,\mathcal {B}_A)\) can be extended to a base-preserving linear \(\varepsilon \)-isometry \(f:A\rightarrow \mathbb {U}_{K}\). By [2, 3], the latter \(\varepsilon \)-extension property of \(\mathbb {U}_{K}\) does not hold for \(K>1\). However, Theorem 6 implies the following weaker \(\varepsilon \)-universality property of \((\mathbb {U}_K,\mathcal {B}_K)\), holding for every \(K>1\).
Corollary 10
Let \(K\ge 1\) and \((\mathbb {U}_K,\mathcal {B}_{\mathbb {U}_K})\) be a rational universal based Banach space with suppression (resp. unconditional) constant K. For every \(\varepsilon >0\) and any based Banach space \((A,\mathcal {B}_A)\) with suppression (resp. unconditional) constant \(\le K\), any decomposition-preserving linear \(\varepsilon \)-isometry \(f:\varLambda \rightarrow \mathbb {U}_{K}\) defined on a finite-dimensional based subspace \((\varLambda ,\mathcal {B}_\varLambda )\) of \((A,\mathcal {B}_A)\) can be extended to a decomposition-preserving linear \(\varepsilon \)-isometry \(f:A\rightarrow \mathbb {U}_{K}\).
This corollary follows from Theorem 6 and the observation that the universal rational based Banach sppace \((\mathbb {U}_K,\mathcal {B}_{\mathbb {U}_K})\) endowed with the 1-dimensional decomposition generated by its basis \(\mathcal {B}_{\mathbb {U}_K}\) is a rational \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_C\)-universal \({\mathcal {B}}\)-decomposed Banach space for \(C=\left[ 0,\frac{1}{K}\right] \left( \mathrm{resp.} \left[ -\frac{1}{K},\frac{1}{K}\right] \right) \).
6 Conclusions
In this paper we consider the notion of a decomposed Banach space, which is more flexible comparing to a more restrictive notion of a based Banach space, exploited in [1, 2]. In particular, it allowed us to introduce a true notion of an almost universal space and establish an almost universality of the \({\mathfrak {r}}\varvec{{\mathcal {B}}}{\mathfrak {I}}_{C}\)-universal based Banach spaces, constructed in [1, 2].
Moreover, using the C-unconditional constants \(K_C\) allowed us to generalize the results of the papers [1,2,3] related to Banach spaces with some restrictions on suppression or unconditional of unconditional bases.
References
Banakh, T., Garbulińska-Wȩgrzyn, J.: The universal Banach space with a \(K\)-suppression unconditional basis. Comment. Math. Univ. Carolin. 59(2), 195–206 (2018)
Banakh, T., Garbulińska-Wȩgrzyn, J.: A universal Banach space with a \(K\)-unconditional basis. Adv. Oper. Theory 4(3), 574–586 (2019)
Banakh, T., Garbulińska–Wȩgrzyn, J.: Corrigendum to the paper “The universal Banach space with a \(K\)-suppression unconditional basis”. To appear in Comment. Math. Univ. Carolin
Diestel, J.: Sequences and Series in Banach Spaces. Springer, New York (1984)
Fabian, M., Habala, P., Hájek, P., Montesinos, V., Zizler, V.: Banach Space Theory. The Basis for Linear and Nonlinear Analysis. Springer, New York (2011)
Fraïssé, R.: Sur quelques classifications des systèmes de relations. Publ. Sci. Univ. Alger. Sér. A. 1, 35–182 (1954)
Garbulińska, J.: Isometric uniqueness of a complementably universal Banach space for Schauder decompositions. Banach J. Math. Anal. 8(1), 211–220 (2014)
Heil, C.: A Basis Theory Primer. Birkhauser/Springer, New York (2011)
Johnson, W.B., Szankowski, A.: Complementably universal Banach spaces. Stud. Math. 58, 91–97 (1976)
Kadec, M.I.: On complementably universal Banach spaces. Stud. Math. 40, 85–89 (1971)
Kubiś, W.: Fraïssé sequences: category-theoretic approch to universal homogeneous structures. Ann. Pure Appl. Logic 165, 1755–1811 (2014)
Lindenstrauss, J., Tzafriri, L.: Classical Banach Spaces I and II. Springer, New York (1996)
Pełczyński, A.: Any separable Banach space with the bounded approximation property is a complemented subspace of a Banach space with a basis. Stud. Math. 40, 239–243 (1971)
Pełczyński, A.: Projections in certain Banach spaces. Stud. Math. 19, 209–228 (1960)
Pełczyński, A.: Universal bases. Stud. Math. 32, 247–268 (1969)
Pełczyński, A., Wojtaszczyk, P.: Banach spaces with finite-dimensional expansions of identity and universal bases of finite-dimensional subspaces. Stud. Math. 40, 91–108 (1971)
Schechtman, G.: On Pełczyński paper “Universal bases”. Israel J. Math. 20, 181–184 (1975)
Acknowledgements
The authors would like to express their sincere thanks to the (anonymous) referee of their paper [2] who advised the authors to modify the definition of a morphism between based Banach spaces, which eventually lead us to introducing the notion of a decomposed Banach space, a rational morphism between such spaces, and a correct notion of almost universality. Research of the second author was partially supported by NCN Grant DEC-2013/11/N/ST1/02963.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jan Stochel.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Banakh, T., Garbulińska-Wȩgrzyn, J. Universal decomposed Banach spaces. Banach J. Math. Anal. 14, 470–486 (2020). https://doi.org/10.1007/s43037-019-00003-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s43037-019-00003-7





 .
.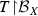 is an injective map from X to Y;
is an injective map from X to Y;