Abstract
In the setting of non-type \(\mathop {\mathrm{{II_1}}}\) representations, we propose a definition of deformed Fredholm module \(\big [D_{{\mathcal {T}}}|D_{{\mathcal {T}}}|^{-1},\,\mathbf{\cdot }\,\big ]_{{\mathcal {T}}}\) for a modular spectral triple \({{\mathcal {T}}}\), where \(D_{{\mathcal {T}}}\) is the deformed Dirac operator. \(D_{{\mathcal {T}}}\) is assumed to be invertible for the sake of simplicity, and its domain is an “essential” operator system \({{\mathcal {E}}}_{{\mathcal {T}}}\). According to such a definition, we obtain \(\big [D_{{\mathcal {T}}}|D_{{\mathcal {T}}}|^{-1},\,\mathbf{\cdot }\,\big ]_{{\mathcal {T}}}=|D_{{\mathcal {T}}}|^{-1}d_{{\mathcal {T}}}(\,\mathbf{\cdot }\,)+d_{{\mathcal {T}}}(\,\mathbf{\cdot }\,)|D_{{\mathcal {T}}}|^{-1}\), where \(d_{{\mathcal {T}}}\) is the deformed derivation associated to \(D_{{\mathcal {T}}}\). Since the “quantum differential” \(1/|D_{{\mathcal {T}}}|\) appears in a symmetric position, such a definition of Fredholm module differs from the usual one even in the undeformed case, that is in the tracial case. Therefore, it seems to be more suitable for the investigation of noncommutative manifolds in which the nontrivial modular structure might play a crucial role. We show that all models in Fidaleo and Suriano (J Funct Anal 275:1484–1531, 2018) of non-type \(\mathop {\mathrm{{II_1}}}\) representations of noncommutative 2-tori indeed provide modular spectral triples, and in addition deformed Fredholm modules according to the definition proposed in the present paper. Since the detailed knowledge of the spectrum of the Dirac operator plays a fundamental role in spectral geometry, we provide a characterisation of eigenvalues and eigenvectors of the deformed Dirac operator \(D_{{\mathcal {T}}}\) in terms of the periodic solutions of a particular class of eigenvalue Hill equations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that in noncommutative approach to mathematics, the concept of “point” is meaningless. The same happens in quantum physics in an attempt to unify electromagnetic, weak and strong interactions with the gravitation where, at Planck scale, any reasonable measurement process is lost.
Another fundamental long-standing problem in number theory, and thus in a different direction even if connected with the previous one, concerns the attempt to prove the Riemann hypothesis about the location of the zeroes of the Riemann zeta-function \(\zeta (z)\), see e.g. [11]. Therefore, motivated by the two potential applications described above, Connes’ noncommutative geometry grew impetuously in the last decades.
Regarding other relevant applications of noncommutative geometry, we mention that the quantum Hall effect can be explained by the Connes–Chern character \(\mathrm{Ch}(P_F)\) of the eigen-projection \(P_F\) of the Hamiltonian on energies smaller than or equal to the Fermi level. Therefore, for some relevant applications, the pairing between the cyclic cohomology and K-theory plays a crucial role.
We note that it would be difficult to provide an exhaustive list of the involved literature. However, for a natural starting point, we refer the reader to the seminal monographs [6, 9, 21], and the standard available references on this topic.
Taking into account the above introductory facts, a “noncommutative manifold” might describe the physics of the quantum Hall effect (see e.g. [2] and the references therein), or that arising from Connes’ standard model and the relative spectral action (cf. [7, 12]). Also, any commutative manifold can be considered as a particular case of a noncommutative one. In this last case, Connes’ reconstruction theorem (cf. [9]) allows to reconstruct all relevant properties of the manifold under consideration in terms of the natural axioms of noncommutative geometry in which the concept of spectral triple assumes a quite relevant role.
Therefore, one of the main ingredients in noncommutative geometry is then the so-called (undeformed) spectral triple and the associated Fredholm module, the last being also the candidate to encode many important properties of the manifold under consideration, and then to keep together K-theory, topology, measure theory and many others.
On the other hand, the discovery of a deep connection between the quantum statistical mechanics, in particular Kubo–Martin–Schwinger (KMS for short) condition (cf. [23, 31, 33]) and, on the mathematical side, Tomita theory (e.g. [41]) dealing with fundamental questions of operator algebras (see e.g. [8]), suggests the necessary need to take the modular data into account.
To the knowledge of the authors, the idea to take into consideration the modular data in defining the spectral triples has been started in [13] with the perspective of the application to the theory of foliations.
The project of exhibiting twisted spectral triples according to the modular data is indeed carried out in detail in [14]. There, the twisting comes from inner and bounded perturbations of the canonical trace of the noncommutative 2-torus, thus in the context of type \(\mathop {\mathrm{{II_1}}}\) representations. Such spectral triples were called modular.
Many other works have been devoted to the investigation of deformed spectral triples whose twist arises, or does not directly arise, from the modular data. We mention e.g. [5, 22, 36] and, for some potential applications to quantum field theory, [32].
The program to provide examples of twisted spectral triples arising from type \(\mathop {\mathrm{{III}}}\) representations, and thus exhibiting a highly nontrivial modular structure, is carried out in [19] for noncommutative 2-tori. In this paper, it was considered irrational rotations by the angle \(2\pi \alpha \), provided that \(\alpha \) is a Liouville number, that is an irrational number admitting a “fast” approximation by rationals.
Since the last mentioned paper, as well as the present one, can be considered as a kind of generalisation of [14], we denote the spectral triples considered here again as modular, with the aim to point out the fact that the nontrivial modular structure plays a crucial role.
Such a preliminary but essential step to construct non-type \(\mathop {\mathrm{{II_1}}}\) representations of the noncommutative torus is done by considering suitable \(C^\infty \)-diffeomorphisms  of the unit circle \({{\mathbb {T}}}\). Then the Gel’fand–Naimark–Segal (GNS for short) representations of the \(C^*\)-algebra \({{\mathbb {A}}}_{\alpha }\) of the noncommutative torus generated by states
of the unit circle \({{\mathbb {T}}}\). Then the Gel’fand–Naimark–Segal (GNS for short) representations of the \(C^*\)-algebra \({{\mathbb {A}}}_{\alpha }\) of the noncommutative torus generated by states  with central support in the bidual, and canonically associated to the diffeomorphism
with central support in the bidual, and canonically associated to the diffeomorphism  , provide the searched type \(\mathop {\mathrm{{III}}}\) representations.
, provide the searched type \(\mathop {\mathrm{{III}}}\) representations.
The modular spectral triples considered in [19], whose associated twisted commutator is automatically defined to be “real” in its own domain, satisfy the following basic requirements. The first one concerns the associated twist of the Dirac operator and the relative twisted derivation, which should come from the Tomita modular operator. We remark that, in the non-type \(\mathop {\mathrm{{II_1}}}\) cases, the modular operator is unbounded and not inner, in particular it should not come from a bounded inner perturbation.
According to the standard definition of any spectral triple, such a suitably deformed Dirac operator should have compact resolvent, and in addition the unbounded twisted derivation should include in its domain sufficiently many elements (e.g. typically a dense \(*\)-subalgebra or, as considered in the recent paper [15], merely an essential operator system). We note that the examples of modular spectral triples constructed in [14] for the noncommutative 2-torus arise from bounded (indeed “smooth”) inner perturbations of the canonical trace, and thus provide only type \(\mathop {\mathrm{{II_1}}}\) GNS representations.
The previous facts are relevant because they constitute the minimal requirements for a spectral triple to encode the main metric properties and the associated measure theoretic ones, that is the noncommutative counterpart of the volume form, i.e. a state. Moreover, the spectral triple may also furnish possible pairings involving the K-Theory and the (equivariant) KK-Theory, and thus the corresponding local index formula for which the modular data may play a crucial role.
Concerning the last aspect involving pairings with K-theory and K-homology, the concept of Fredholm module assumes a fundamental meaning, see e.g. [9, 24], and the literature cited therein. Therefore, it is natural to address the investigation about Fredholm modules arising from such new spectral triples, suitably deformed by the use of the modular data.
By the considerations set out above, it is natural to expect that such Fredholm modules should be again deformed according to the underlying modular structure. Hence, with \(D_{{\mathcal {T}}}\) and \({{\mathcal {E}}}_{{\mathcal {T}}}\) the deformed Dirac operator and the operator system in the domain of the deformed commutator associated to the modular spectral triple \({{\mathcal {T}}}\), we provide a definition of a deformed commutator \([D_{{\mathcal {T}}}|D_{{\mathcal {T}}}|^{-1}, A]_{{\mathcal {T}}}\) between the “sign” \(F_{{\mathcal {T}}}=D_{{\mathcal {T}}}|D_{{\mathcal {T}}}|^{-1}\) of the Dirac operator and the elements A of \({{\mathcal {E}}}_{{\mathcal {T}}}\). According to such a definition, this deformed commutator differs from the usual one also in the tracial case when the Tomita modular operator is trivial.
Under some technical assumptions about the domains of the involved unbounded operators, for the deformed commutator in the definition of the Fredholm module, and for \(d_{{\mathcal {T}}}\) the deformed derivation associated to \({{\mathcal {T}}}\), we show that
and thus it still produces compact operators.
We want to point out that the “quantum differential” \(1/|D_{{\mathcal {T}}}|\) appears in a symmetric manner in the above formula. In addition, in order to obtain such a symmetric displacement of the quantum differential, the Fredholm modules associated to undeformed spectral triples (i.e. arising from the tracial cases) should be also deformed in a canonical way.
It would then be expected that such a new definition of Fredholm module may be more suitable for the investigation of some relevant noncommutative manifolds exhibiting nontrivial modular structure.
Similarly, such objects arising from modular spectral triples and deformed Fredholm modules (e.g. the cohomologies), should take into account the non-cyclicity associated to the presence of the modular operator. Therefore, they might be new objects which have to be identified yet. For general details concerning previous investigations involving these aspects of cyclic cohomology, the reader is referred to the monograph [9], and the survey paper [27].
The present paper is organised as follows. Apart from the introduction and a preliminary section in which some basic notions are reported, in Section 3, we provide a slightly modified definition (w.r.t. Definition 2.4 in [19]) of modular spectral triple which, according to [15], takes also into account the possibility to deal with operator systems.
Section 4 is devoted to show that the models arising from non-type \(\mathop {\mathrm{{II_1}}}\) representations of the noncommutative 2-torus described in Sections 7 and 8 of [19], indeed provide nontrivial examples of modular spectral triples according to Definition 3.1.
Section 5 deals with the new definition of Fredholm module for which, under natural assumptions on domains of the involved unbounded operators, we prove the key formula (1.1). We also prove that all above-mentioned examples for the noncommutative torus enjoy the properties of providing deformed Fredholm modules.
Section 6 concerns with a simple but illustrative one dimensional example. Compared with the twin one in Section 3.1 of [20], such an example helps the reader to clarify the framework.
In Section 7, it is outlined that the combination of examples in Section 9 of [19] and those in Section 7 of [18], indeed provides deformed Fredholm modules. We are leaving to the reader the involved technical computations because those do not add anything else to the conceptual meaning of the topic. For some of such examples of deformed Fredholm modules, their domains contain a dense \(*\)-algebra. The price to pay is that the intrinsic undeformed Dirac operator must be suitably modified using the growth sequence of the diffeomorphism  , whose modular state
, whose modular state  enters in the definition of spectral triple. Therefore, the arising Fredholm modules are losing some degree of intrinsicity.
enters in the definition of spectral triple. Therefore, the arising Fredholm modules are losing some degree of intrinsicity.
Since the detailed knowledge of the spectrum of the Dirac operator plays a fundamental role, we added Section 8 in which the crucial problem to diagonalise such an operator is equivalent to find all periodic solutions of a class of eigenvalue equations, first introduced by Hill in [25].
We end by mentioning some further investigations (i.e. metric aspects, spectral geometry, index theory, cohomologies and many others) involving modular spectral triples and deformed Fredholm modules considered in the present paper. The reader is referred to [9], and the survey-paper [6], for the corresponding objects arising from the tracial (i.e. untwisted) standard situation. Therefore, it should be desirable to come back to these aspects somewhere else in future.
2 Preliminaries
We gather here some facts useful for the forthcoming sections.
Basic notions. We denote by \({{\mathbb {T}}}\) the unit circle
where \(z=e^{\imath \theta }\). It is a compact group whose Haar measure is the normalised Lebesgue measure

If Y is a point-set, \({{\mathcal {B}}}(Y)\) denotes the unital \(C^*\)-algebra consisting of all bounded complex-valued functions on Y.
Given an irrational number which is not diophantine, it is possible to prove that it is a Liouville number, that is it satisfies the following condition.
- (L):
-
A Liouville number \(\alpha \in (0,1)\) is a real number such that for each \(N\in {{\mathbb {N}}}\) the inequality
$$\begin{aligned} \left| \alpha - \frac{p}{q}\right| < \frac{1}{q^N} \end{aligned}$$has an infinite number of solutions for \(p,q\in {{\mathbb {N}}}\) with \((p,q)=1\).
- (UL):
-
Among Liouville numbers, we also consider those such that, for each \(\lambda >1\) and \(N\in {{\mathbb {N}}}\), the inequality
$$\begin{aligned} \left| \alpha - \frac{p}{q}\right| <\frac{1}{\lambda ^{q^N}} \end{aligned}$$again admits infinite number of solutions for p, q as above.
The numbers satisfying (UL), which have a prescribed faster approximation by rationals, are called ultra-Liouville numbers. Concerning the Liouville numbers, the reader is referred to the standard monograph [28]. Following the line in [39], in Section 3 of [19] it was exhibited a Liouville number satisfying the faster approximation (UL).
Let \(\varphi \in {{\mathcal {S}}}({{\mathfrak {A}}}):={{\mathfrak {A}}}^*_{+,1}\) be a state on the \(C^*\)-algebra \({{\mathfrak {A}}}\). We denote by \(({{\mathcal {H}}}_\varphi ,\pi _\varphi ,\xi _\varphi )\) its GNS representation, see e.g. [42]. If the cyclic vector \(\xi _\varphi \in {{\mathcal {H}}}_\varphi \) is also separating for \(\pi _\varphi ({{\mathfrak {A}}})''\), we call \(\varphi \) a modular state. We also note that \(\varphi \) being a modular state is equivalent to \(s({\varphi })\in Z({{\mathfrak {A}}}^{**})\), where \(s(\varphi )\) is the support (of the normal extension) of \(\varphi \) in the bidual \({{\mathfrak {A}}}^{**}\), see e.g. [37], pag. 15.
Concerning the Tomita modular theory, we use the notations in [40]. For example, \(S_\varphi \), \(J_\varphi \) and \(\Delta _\varphi \), with \(S_\varphi =J_\varphi \Delta _\varphi ^{1/2}\), denote the Tomita involution, Tomita conjugation and modular operator associated to the modular state \(\varphi \in {{\mathcal {S}}}({{\mathfrak {A}}})\), respectively.
Let \({1}{\mathrm{I}}_{{\mathfrak {A}}}\in {{\mathfrak {S}}}={{\mathfrak {S}}}^*\subset {{\mathfrak {A}}}\) be a, not necessarily closed, self-adjoint subspace of the unital \(C^*\)-algebra \({{\mathfrak {A}}}\) which contains the identity \({1}{\mathrm{I}}_{{\mathfrak {A}}}\). It is called a (concrete) operator system.
Noncommutative 2-torus. For a fixed \(\alpha \in {{\mathbb {R}}}\), the noncommutative torus \({{\mathbb {A}}}_{2\alpha }\) associated to the rotation by the angle \(4\pi \alpha \), is the universal \(C^*\)-algebra with identity I generated by the commutation relations involving two noncommutative unitary indeterminates U, V:
The factor 2 is considered for the sake of convenience, see below.
We express \({{\mathbb {A}}}_{2\alpha }\) in the so-called Weyl form. Indeed, let \(\mathbf{a}:=(m,n) \in {{\mathbb {Z}}}^2\) with \({\textbf {0}}=(0,0)\), and define
Obviously, \(W(\mathbf{0})=I\), and the commutation relations (2.1) become
where the symplectic form \(\sigma \) is defined by
We now fix a function \(f:{{\mathbb {Z}}}^2\longrightarrow {{\mathbb {C}}}\), which we may assume to have finite support. The element \(W(f)\in {{\mathbb {A}}}_{2\alpha }\) is then defined as
The set \(\{W(f)\in {{\mathbb {A}}}_{2\alpha }\mid f\in {{\mathcal {B}}}({{\mathbb {Z}}}^2)\,\text {with finite support}\}\) provides a dense \(*\)-algebra of \({{\mathbb {A}}}_{2\alpha }\).
For \(\alpha \) irrational, which is tacitly assumed from now on, we recall that \({{\mathbb {A}}}_{2\alpha }\) is simple and has a necessarily unique faithful trace \(\tau \) given by
Conversely, by Remark 1.7 of [3], any element \(A\in {{\mathbb {A}}}_{2\alpha }\) is uniquely determined by the corresponding Fourier coefficients
The relations (2.2) transfer to the generators W(f) as follows:
where
is a twisted convolution.
Suppose that the double sequence \(f(\mathbf{a})\equiv f(m,n)\) satisfies (2.4) for some \(A\in {{\mathbb {A}}}_{2\alpha }\). It is then easily seen that, for each fixed \(n\in {{\mathbb {Z}}}\), \(f^{(n)}(m):=f(m,n)\) defines a sequence whose Fourier anti-transform

where the convergence is meant in norm in the Cesáro sense (e.g. [17]), provides a continuous function  . Here, for “Fourier anti-transform”, we simply mean that in the series (2.5), we are using \(z^m\) instead of \(z^{-m}\) as in the usual definition of the Fourier transform:
. Here, for “Fourier anti-transform”, we simply mean that in the series (2.5), we are using \(z^m\) instead of \(z^{-m}\) as in the usual definition of the Fourier transform:  .
.
On topological dynamical systems on the unit circle. If  is an invertible map on the point-set Y:
is an invertible map on the point-set Y:
-
 , and the inverse of
, and the inverse of  is denoted by
is denoted by 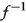 ;
; -
for the n-times composition,
 ;
; -
for the n-times composition of the inverse,
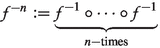 .
.
Thus,  is meaningful for any \(n\in {{\mathbb {Z}}}\) with the above convention.
is meaningful for any \(n\in {{\mathbb {Z}}}\) with the above convention.
We now specialise the matter to Y being the unit circle. Given a \(C^1\)-diffeomorphism  of the unit circle \({{\mathbb {T}}}\), its growth sequence
of the unit circle \({{\mathbb {T}}}\), its growth sequence  is defined as
is defined as

where, with a slight abuse of notation and \(z=e^{\imath \theta }\), \(\partial :=\frac{\mathrm{d}\,\,}{\mathrm{d}z}=\frac{1}{\imath e^{\imath \theta }}\frac{\mathrm{d}\,\,}{\mathrm{d}\theta }\) is the derivative w.r.t. the variable z.
To simplify, we reduce the situation to \(C^\infty \)-diffeomorphisms  , called simply “diffeomorphisms”. The diffeomorphisms considered in the present paper are topologically conjugate to the rotation \(R_\alpha \), that is
, called simply “diffeomorphisms”. The diffeomorphisms considered in the present paper are topologically conjugate to the rotation \(R_\alpha \), that is

for a unique homeomorphism  of \({{\mathbb {T}}}\) with
of \({{\mathbb {T}}}\) with  .
.
If  is \(C^1\)-conjugate to the rotation by some angle \(2\pi \alpha \), i.e.
is \(C^1\)-conjugate to the rotation by some angle \(2\pi \alpha \), i.e.  , then the sequence
, then the sequence  is bounded. As pointed out before, this happens for \(C^\infty \)-diffeomorphisms
is bounded. As pointed out before, this happens for \(C^\infty \)-diffeomorphisms  with rotation number
with rotation number  (see e.g. Section 11 of [26] for the definition of rotation number) whenever \(\alpha \) is diophantine.
(see e.g. Section 11 of [26] for the definition of rotation number) whenever \(\alpha \) is diophantine.
Conversely, suppose that \(\beta \in (0,1)\backslash {{\mathbb {Q}}}\) and  is an orientation-preserving diffeomorphism with
is an orientation-preserving diffeomorphism with  . In this case, the Denjoy Theorem (e.g. [26]) asserts that there exists a unique homeomorphism
. In this case, the Denjoy Theorem (e.g. [26]) asserts that there exists a unique homeomorphism  of the unit circle such that
of the unit circle such that  satisfying (2.6) for the rotation \(R_\beta \). Then
satisfying (2.6) for the rotation \(R_\beta \). Then

is the unique invariant measure, which is ergodic for the natural action of  on \({{\mathbb {T}}}\). For a diophantine number \(\beta \),
on \({{\mathbb {T}}}\). For a diophantine number \(\beta \),  is indeed smooth (cf. [43]) and thus
is indeed smooth (cf. [43]) and thus  . For a Liouville number \(\beta \), things are quite different. There are diffeomorphisms as above for which the unique invariant measure
. For a Liouville number \(\beta \), things are quite different. There are diffeomorphisms as above for which the unique invariant measure  is singular w.r.t. the Haar measure
is singular w.r.t. the Haar measure  :
:  . For \(\beta =2\alpha \), to exhibit non-type \(\mathop {\mathrm{{II_1}}}\), and then type \(\mathop {\mathrm{{III}}}\) representations of the noncommutative torus \({{\mathbb {A}}}_{2\alpha }\), we will actually look at such diffeomorphisms, that is those satisfying the above-mentioned singularity condition. As before, the factor 2 is pure matter of convenience, and will be clarified in the sequel.
. For \(\beta =2\alpha \), to exhibit non-type \(\mathop {\mathrm{{II_1}}}\), and then type \(\mathop {\mathrm{{III}}}\) representations of the noncommutative torus \({{\mathbb {A}}}_{2\alpha }\), we will actually look at such diffeomorphisms, that is those satisfying the above-mentioned singularity condition. As before, the factor 2 is pure matter of convenience, and will be clarified in the sequel.
Note that, for the class of diffeomorphisms  considered in the present paper, the asymptotic of
considered in the present paper, the asymptotic of  is at most \(o(n^2)\), see [44]. However, for the diffeomorphisms constructed in [34], Proposition 2.1 when \(\alpha \) is a Liouville number, or in [19], Proposition 3.1 for ultra-Liouville numbers, we have
is at most \(o(n^2)\), see [44]. However, for the diffeomorphisms constructed in [34], Proposition 2.1 when \(\alpha \) is a Liouville number, or in [19], Proposition 3.1 for ultra-Liouville numbers, we have  or
or  , respectively.
, respectively.
It is of interest to note that it would be possible to select Liouville numbers with sufficiently fast approximation by rationals, providing diffeomorphisms of the kind considered in the present paper such that its growth sequence enjoys any unbounded prescribed asymptotic slower than o(n).
Modular states and non-type \(\mathop {\mathrm{{II_1}}}\) representations. We consider an orientation-preserving diffeomorphism  on \(C^\infty ({{\mathbb {T}}})\) with rotation number
on \(C^\infty ({{\mathbb {T}}})\) with rotation number  . Then it is conjugate to the rotation \(4\pi \alpha \) through an essentially unique homeomorphism as in (2.6). For such diffeomorphism, we consider a uniquely determined measure
. Then it is conjugate to the rotation \(4\pi \alpha \) through an essentially unique homeomorphism as in (2.6). For such diffeomorphism, we consider a uniquely determined measure  , and take advantage of the construction in [19], Section 4, of a state \(\omega _\mu \) associated to any probability Radon measure \(\mu \in C({{\mathbb {T}}})^*\).
, and take advantage of the construction in [19], Section 4, of a state \(\omega _\mu \) associated to any probability Radon measure \(\mu \in C({{\mathbb {T}}})^*\).
Indeed, let \(\mu \in {{\mathcal {S}}}(C({{\mathbb {T}}}))\) be a probability measure on \({{\mathbb {T}}}\). As shown in [1], Proposition 2.1,

is well defined, positive and normalised, so it defines a state on \({{\mathbb {A}}}_{2\alpha }\).
Notice that, if \(\mu \) is the Haar–Lebesgue measure, then

and thus  , i.e. the trace, by (2.7) and (2.3).
, i.e. the trace, by (2.7) and (2.3).
Remark 2.1
For the states \(\omega _\mu \), we have
-
(i)
\(\omega _\mu \in {{\mathcal {S}}}({{\mathbb {A}}}_{2\alpha })\) is faithful if and only if \(\mathop {\mathrm{supp}}(\mu )={{\mathbb {T}}}\) (cf. [19], Proposition 4.1);
-
(ii)
if for \(n\in {{\mathbb {Z}}}\), \(\mu \circ R_{2\alpha }^{n}\preceq \mu \) (and thus \(\mu \circ R_{2\alpha }^{n}\sim \mu \)), then the support of \(\omega _\mu \) in the bidual is central: \(s(\omega _\mu )\in Z({{\mathbb {A}}}_{2\alpha }^{**})\) (cf. [19], Proposition 4.2).
Now we specialise the situation to

which is quasi-invariant and ergodic for the natural action of the rotation \(R_{2\alpha }\) by the angle \(4\pi \alpha \), and thus  acts in standard form on
acts in standard form on  .
.
Denoting by  the dual action of the rotations \(R_{2\alpha }\) on functions, and in particular on
the dual action of the rotations \(R_{2\alpha }\) on functions, and in particular on  , it is possible to see that such an action is also free (e.g. [42], pag. 363). Let now
, it is possible to see that such an action is also free (e.g. [42], pag. 363). Let now  be the dual action of
be the dual action of  on
on  , as well as on \(C({{\mathbb {T}}})\).
, as well as on \(C({{\mathbb {T}}})\).
Since the dynamical systems  and
and  are conjugate, we get (cf. [19], Proposition 6.2) that
are conjugate, we get (cf. [19], Proposition 6.2) that  is indeed a von Neumann crossed product (e.g. [4], Section 2.7):
is indeed a von Neumann crossed product (e.g. [4], Section 2.7):

where in addition  is a factor containing the image of
is a factor containing the image of  , or equivalently that of
, or equivalently that of  , as a maximal abelian subalgebra, see [42], Theorem XIII.1.5, and Corollary XIII.1.6. As \({{\mathbb {Z}}}\) is amenable,
, as a maximal abelian subalgebra, see [42], Theorem XIII.1.5, and Corollary XIII.1.6. As \({{\mathbb {Z}}}\) is amenable,  is also hyperfinite by [30], Theorem 4.4.
is also hyperfinite by [30], Theorem 4.4.
Since \({{\mathbb {A}}}_{2\alpha }\) is a simple \(C^*\)-algebra, we also have

where the involved products are \(C^*\)-crossed products, see [4], Section 2.7.
Concerning the type of the von Neumann factors, we are obtaining, trivially  cannot be of type \(\mathop {\mathrm{{I}}}\) because
cannot be of type \(\mathop {\mathrm{{I}}}\) because  is nonatomic. It is of type \(\mathop {\mathrm{{II_1}}}\) if and only if the measure class
is nonatomic. It is of type \(\mathop {\mathrm{{II_1}}}\) if and only if the measure class  contains a probability measure which is invariant under the action generated by \(R_{2\alpha }\), see Theorem XIII.1.7 in [42]. In this case,
contains a probability measure which is invariant under the action generated by \(R_{2\alpha }\), see Theorem XIII.1.7 in [42]. In this case,  and
and  by uniqueness, and this always occurs when \(\alpha \) is diophantine.
by uniqueness, and this always occurs when \(\alpha \) is diophantine.
In the remaining cases, if  is not of \(\mathop {\mathrm{{II_1}}}\), its type is determined by the Connes invariant
is not of \(\mathop {\mathrm{{II_1}}}\), its type is determined by the Connes invariant  , or equally well by the Krieger–Araki–Woods ratio-set (cf. [29])
, or equally well by the Krieger–Araki–Woods ratio-set (cf. [29])  associated to the underlying commutative dynamical systems
associated to the underlying commutative dynamical systems  , because they coincide:
, because they coincide:

We remark that diffeomorphisms of the prescribed ratio-set are constructed in [34] through limits of a suitable sequence of diffeomorphisms conjugate to rational rotations which approximate the Liouville number \(\alpha \).
We want also to note that  is of type \(\mathop {\mathrm{{II_\infty }}}\) if and only if the measure class
is of type \(\mathop {\mathrm{{II_\infty }}}\) if and only if the measure class  contains an unbounded \(\sigma \)-finite measure which is invariant under the rotation \(R_{2\alpha }\), and it is of type \(\mathop {\mathrm{{III}}}\) if and only if the measure class
contains an unbounded \(\sigma \)-finite measure which is invariant under the rotation \(R_{2\alpha }\), and it is of type \(\mathop {\mathrm{{III}}}\) if and only if the measure class  contains no \(\sigma \)-finite measure, invariant under such a rotation \(R_{2\alpha }\).
contains no \(\sigma \)-finite measure, invariant under such a rotation \(R_{2\alpha }\).
To take into account the intrinsic differential structure of \({{\mathbb {A}}}_{2\alpha }\), and therefore to define the twisted Dirac operator by deforming the untwisted one, associated to such an intrinsic differential structure, we directly work on the space  dealing with the action
dealing with the action  induced by the diffeomorphism
induced by the diffeomorphism  on measurable complex valued functions on the unit circle \({{\mathbb {T}}}\).
on measurable complex valued functions on the unit circle \({{\mathbb {T}}}\).
Also the “square-root” T of  , given by
, given by

plays a crucial role. Indeed, T is a canonical choice for the square root of  :
:  .
.
Concerning the GNS representation of  , whose support in the bidual is central by construction in the situation of the present paper, it was shown in [19] that
, whose support in the bidual is central by construction in the situation of the present paper, it was shown in [19] that

Considering  , for \(n\in {{\mathbb {Z}}}\) and \(z\in {{\mathbb {T}}}\), the related modular structure is then given by
, for \(n\in {{\mathbb {Z}}}\) and \(z\in {{\mathbb {T}}}\), the related modular structure is then given by

where, as before, \(\partial =\frac{\mathrm{d}\,\,}{\mathrm{d}z}\) stands for the derivative w.r.t. the variable \(z\in {{\mathbb {T}}}\).
For \(z\in {{\mathbb {T}}}\) and \(n\in {{\mathbb {Z}}}\), we set

so that the modular operator is given by

with \(M_g\) denoting the multiplication operator by the function g.
3 Modular spectral triples
We provide a slightly modified definition of modular spectral triple w.r.t. that appeared in Definition 2.4 of [19]. It takes into account the possibility to deal with operator systems as explained in [15]. To put in evidence only the topological and the main algebraic aspects, we limit the analysis to spectral triples of dimension 2, by noticing that it can be straightforwardly generalised to an arbitrary dimension.
Let \({{\mathfrak {A}}}\) be a unital \(C^*\)-algebra. With \({{\mathfrak {A}}}\ni a\mapsto *(a):=a^*\in {{\mathfrak {A}}}\), we denote the star operation.
Definition 3.1
A spectral triple considered in the present paper, named as modular spectral triple according to the terminology in [14], is a triplet \({{\mathcal {T}}}:=(\omega ,{{\mathcal {L}}},{{\mathcal {E}}})\) where, with a slight abuse of notation, we write \({{\mathcal {E}}}\equiv {{\mathcal {E}}}_{{\mathcal {T}}}\), made of a modular state \(\omega \in {{\mathcal {S}}}({{\mathfrak {A}}})\), an operator \({{\mathcal {L}}}:{{\mathcal {A}}}\subset {{\mathfrak {A}}}\rightarrow {{\mathfrak {A}}}\) defined on a unital dense \(*\)-algebra \({{\mathcal {A}}}\subset {{\mathfrak {A}}}\), and finally an operator system \({{\mathcal {E}}}_{{\mathcal {T}}}\) acting on \({{\mathcal {B}}}({{\mathcal {H}}}_\omega )\), satisfying the properties listed below.
First, we put \({{\mathcal {L}}}^\star :=-*{{\mathcal {L}}}\,*\) and, for \(a\in {{\mathfrak {A}}}\), we denote by \(a_\omega \in {{\mathcal {H}}}_\omega \) the natural embedding of a in \({{\mathcal {H}}}_\omega \), i.e. \(a_\omega =\pi _\omega (a)\xi _\omega \).
-
(i)
With \({{\mathcal {H}}}_\omega \supset {{\mathcal {A}}}_\omega \ni a_\omega \mapsto L_\omega ^\#a_\omega :=({{\mathcal {L}}}^\#a)_\omega \subset {{\mathcal {H}}}_\omega \), where \({{\mathcal {L}}}^\#\) and \(L_\omega ^\#\) stand for \({{\mathcal {L}}},{{\mathcal {L}}}^\star \) and \(L_\omega ,L^\star _\omega \), respectively, the deformed Dirac operator
$$\begin{aligned} D^{(o)}_{{\mathcal {T}}}:=\begin{pmatrix} 0 &{}\Delta _\omega ^{-1}L_\omega \\ L_\omega ^\star \Delta _\omega ^{-1}&{} 0\\ \end{pmatrix} \,, \end{aligned}$$(3.1)acting on its own domain \({{\mathcal {D}}}_{D^{(o)}_{{\mathcal {T}}}}\subset {{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \), uniquely defines a self-adjoint operator with compact resolvent: \(D^{(o)}_{{\mathcal {T}}}\) is densely defined essentially self-adjoint with closure \(D_{{\mathcal {T}}}\), and \(\big ((1+D_{{\mathcal {T}}})^2\big )^{-1/2}\) is compact.
-
(ii)
There exists a dense \(*\)-subalgebra \({{\mathcal {B}}}\subset {{\mathfrak {A}}}\), and a set \(\mathbf{P}=(P_\iota )_{\iota \in {{\mathcal {I}}}}\subset {{\mathcal {B}}}({{\mathcal {H}}}_\omega )\) of (increasing) self-adjoint projections with \(\sup _\iota P_\iota =:P\le I_{{{\mathcal {H}}}_\omega }\), such that
$$\begin{aligned} \mathcal {E}_\mathcal {T}:=\mathrm{span}\big \{P,P_\iota \pi _\omega (\mathcal {B})P_\iota \mid \iota \in \mathcal {I}\big \}\subset P\mathcal {B}(\mathcal {H}_\omega )P\,, \end{aligned}$$and for each \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\), the deformed commutator
$$\begin{aligned} d^{(o)}_{{\mathcal {T}}}(A):=\imath \begin{pmatrix} 0&{}\Delta _\omega ^{-1}[L_\omega ,A]\\ [L_\omega ^\star ,A]\Delta _\omega ^{-1}&{} 0\\ \end{pmatrix} \end{aligned}$$(3.2)uniquely defines a bounded operator, denoted by \(d_{{\mathcal {T}}}(A)\): \(\overline{{{\mathcal {D}}}_{d^{(o)}_{{\mathcal {T}}}(A)}}={{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \) and
$$\begin{aligned} \sup \big \{\big \Vert d^{(o)}_{{\mathcal {T}}}(A)\xi \big \Vert \mid \xi \in {{\mathcal {D}}}_{d^{(o)}_{{\mathcal {T}}}(A)},\,\,\Vert \xi \Vert \le 1\big \}<+\infty . \end{aligned}$$
Remark 3.2
-
(a)
The usual case of undeformed spectral triples associated to tracial states leads to \({{\mathcal {I}}}\) being the singleton \(\{\iota _o\}\) with \(P_{\iota _o}=I_{{{\mathcal {H}}}_\omega }\). The same situation emerges when \(\omega \) is an “inner” deformation of a trace considered in [14].
-
(b)
The main case described in [15] corresponds to \(\Delta _\omega =I_{{{\mathcal {H}}}_\omega }\) occurring when \(\omega \) is a trace, and \({{\mathcal {I}}}\) being a singleton with corresponding projection \(P< I_{{{\mathcal {H}}}_\omega }\). In order not to lose any information possibly encoded into the spectral triple, it is natural to consider a set of projections such that \(\sup _\iota P_\iota =I_{{{\mathcal {H}}}_\omega }\). In such a situation, we say that \({{\mathcal {E}}}_{{\mathcal {T}}}\) is essential.
-
(c)
We may decide not to include in \({{\mathcal {E}}}_{{\mathcal {T}}}\) the irrelevant subspace \({{\mathbb {C}}}P\), where \(P=\sup _{\iota \in {{\mathcal {I}}}} P_\iota \). In such a situation,
$$\begin{aligned} {{\mathcal {E}}}_{{\mathcal {T}}}:=\mathrm {span}\big \{P_\iota \pi _\omega ({{\mathcal {A}}})P_\iota \mid \iota \in {{\mathcal {I}}}\big \}\subset P\mathcal {B}(\mathcal {H}_\omega )P. \end{aligned}$$ -
(d)
The models in [19], Sections 8 and 9, provide modular spectral triples \({{\mathcal {T}}}=(\omega ,{{\mathcal {L}}},{{\mathcal {E}}}_{{\mathcal {T}}})\) associated to a nontrivial modular structure, see Sections 4 and 7 below. Therefore, we indeed have nontrivial examples of spectral triples satisfying all properties listed in Definition 3.1.
For a spectral triple \({{\mathcal {T}}}\) as above, we can define a norm on \({{\mathcal {E}}}_{{\mathcal {T}}}\) as follows:
Notice that this norm is nothing but an analogue of a \(C^1\)-norm on a space of \(C^1\)-functions, and can be considered as a kind of a Lipschitz norm on the involved operator systems. Moreover, since \(d_{{\mathcal {T}}}(A^*)=d_{{\mathcal {T}}}(A)^*\) for each \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\), the \(*\)-operation in \({{\mathcal {E}}}_{{\mathcal {T}}}\) is isometric also w.r.t. the above norm.
Proposition 3.3
The completion \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) w.r.t. the norm (3.3) of \({{\mathcal {E}}}_{{\mathcal {T}}}\), can be viewed as a, non-necessarily closed, operator system contained in \({{\mathcal {B}}}({{\mathcal {H}}}_\omega )\), and \(d_{{\mathcal {T}}}\) uniquely extends to the whole \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\), providing again bounded operators.
Proof
We start by noticing that, since \([]A^* []_{{\mathcal {T}}}=[]A []_{{\mathcal {T}}}\), \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) is equipped with a \(*\)-operation in a natural way, and thus \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) is an (abstract at this stage) operator system as well.
Let \({\widetilde{A}}\in \overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\), and choose a sequence \((A_n)_n\subset {{\mathcal {E}}}_{{\mathcal {T}}}\) converging to \({\widetilde{A}}\) in the topology generated by \([]\,\,\, []_{{\mathcal {T}}}\). It is a Cauchy sequence w.r.t. the norm (3.3), and thus both sequences \((A_n)_n\subset {{\mathcal {B}}}({{\mathcal {H}}}_\omega )\) and \(\big (d_{{\mathcal {T}}}(A_n)\big )_n\subset {{\mathcal {B}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\) are Cauchy sequences w.r.t. the norms of \({{\mathcal {B}}}({{\mathcal {H}}}_\omega )\) and \({{\mathcal {B}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\), respectively.
Let A and B the limits in \({{\mathcal {B}}}({{\mathcal {H}}}_\omega )\) and \({{\mathcal {B}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\) of the sequences \((A_n)_n\) and \(\big (d_{{\mathcal {T}}}(A_n)\big )_n\), respectively, and define \(j({\widetilde{A}}):=A\). It is matter of routine to verify that such a map is well defined, and realises a homeomorphism between \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) and \(j\big (\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\big )\subset {{\mathcal {B}}}({{\mathcal {H}}}_\omega )\). In addition, after putting \(d_{{\mathcal {T}}}({\widetilde{A}}):=B\), we obtain the required extension of \(d_{{\mathcal {T}}}\) to the whole \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) by bounded operators. \(\square \)
Remark 3.4
By identifying \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) with its image \(j\big (\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\big )\subset {{\mathcal {B}}}({{\mathcal {H}}}_\omega )\), we can suppose that \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\), as well as the operators \(\{d(A)\mid A\in \overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\}\), are directly acting on the Hilbert space \({{\mathcal {H}}}_\omega \) and \({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \), respectively. In particular, \(\overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\) can be considered as a concrete operator system.
To take into account the whole modular structure associated to a spectral triple \({{\mathcal {T}}}\), we define
acting on its own domain, which is a dense subspace of \({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \) and
which, with \(\gamma =\begin{pmatrix} I&{}0\\ 0&{}-I\\ \end{pmatrix}\), leads to \(J_{{\mathcal {T}}}^2=-I\) and \(J_{{\mathcal {T}}}\gamma =-\gamma J_{{\mathcal {T}}}\), the last being the prescription of a (real) spectral triple of dimension 2.
We also note that, with \({{\mathcal {A}}}_\omega =\{a_\omega \mid a\in {{\mathcal {A}}}\}\subset {{\mathcal {H}}}_\omega \), \({{\mathcal {A}}}\) as in Definition 3.1, we have \([\Lambda _{{\mathcal {T}}},S_{{\mathcal {T}}}]=0\) on the dense subspace \({{\mathcal {A}}}_\omega \bigoplus {{\mathcal {A}}}_\omega \). The above properties can be viewed as the generalisation to the modular case of the tracial one in Definition 3 of [10], or in Definition 2.1 of [35].
We point out that it is not still completely clear the role of the “charge conjugation” \(J_\omega \) and the doubled one \(J_{{\mathcal {T}}}\) in the context of modular spectral triples.
4 Modular spectral triples for the noncommutative 2-torus
The present section is devoted to check in a detailed way that the models described in Section 8 of [19] provide modular spectral triples which are mainly associated to non-type \(\mathop {\mathrm{{II_1}}}\) representations as explained above.
Indeed, we start with a \(C^\infty \)-diffeomorphism  of the unit circle which is conjugate to the rotation \(R_{2\alpha }\) of the angle \(4\pi \alpha \) as in (2.6) by the unique homeomorphism
of the unit circle which is conjugate to the rotation \(R_{2\alpha }\) of the angle \(4\pi \alpha \) as in (2.6) by the unique homeomorphism  satisfying
satisfying  . To simplify the notations, we put
. To simplify the notations, we put  and remark that, according to (2.10),
and remark that, according to (2.10),  does not depend on the normal faithful state \(\omega \), up to unitary equivalence. In particular, it always coincides with \({{\mathcal {H}}}_\tau \) associated to the canonical trace \(\tau \). We then put
does not depend on the normal faithful state \(\omega \), up to unitary equivalence. In particular, it always coincides with \({{\mathcal {H}}}_\tau \) associated to the canonical trace \(\tau \). We then put

for all states \(\omega \) considered in the present paper.
On the Hilbert space

we put
the undeformed Dirac operator, where L and \(L^\star \) are the operators acting on the \(L^2\)-spaces coming from the corresponding ones \({{\mathcal {L}}}\) and \({{\mathcal {L}}}^\star \) acting on a norm-dense \(*\)-algebra \({{\mathcal {A}}}\subset {{\mathbb {A}}}_{2\alpha }\), as explained in (i) of Definition 3.1. Indeed,
where \(\partial _i:=\frac{\partial \,}{\partial \theta _i}\), \(i=1,2\), are the partial derivatives of functions \(g\big (e^{\imath \theta _1},e^{\imath \theta _2}\big )\) on the 2-torus \({{\mathbb {T}}}^2\) w.r.t. the angles, and for \({{\mathcal {A}}}\) one can make the choice
We also recall that another reasonable choice would be the dense \(*\)-subalgebra \( \{W(f)\in {{\mathbb {A}}}_{2\alpha }\mid f\in {{\mathcal {S}}}({{\mathbb {Z}}}^2)\}, \) \({{\mathcal {S}}}\) standing for the rapidly decreasing functions.
After passing to the Fourier anti-transform (2.5) w.r.t. the m-index, (4.1) assumes the form
After some easy computations, we get
where \(D^{(\mathrm und)}_n= \begin{pmatrix} 0 &{}L_n\\ L_n^\star &{} 0\\ \end{pmatrix}\), with
both acting on their own domains which are dense subspaces of \({{\mathcal {H}}}\).
For the convenience of the reader, we report the spectral resolution of \(D:=\overline{D^{(\mathrm und)}}\), obtaining \(\sigma (D)=\left\{ \pm \sqrt{m^2+n^2}\mid m,n\in {{\mathbb {N}}}\right\} \). Concerning the eigenspaces, we put \(\varepsilon _{00}^{(\pm )} = \frac{1}{\sqrt{2}}\begin{pmatrix} 1\\ \pm 1\\ \end{pmatrix}\), and
With
we see that the orthonormal system \(\big \{e_{nm}^{(\pm )}\mid m,n\in {{\mathbb {Z}}}\big \}\) is a basis for \({{\mathcal {H}}}\bigoplus {{\mathcal {H}}}\) made of eigenvectors of the untwisted Dirac operator D corresponding to the eigenvalues \(\pm \sqrt{m^2+n^2}\). Therefore, each of such eigenspaces is generated by the single eigenvector \(e_{nm}^{(\pm )}\) whenever \((m,n)\ne (0,0)\). The eigenspace corresponding to 0 (i.e. the kernel of D) is degenerate, and is generated by the two eigenvectors \(e_{00}^{(\pm )}\).
The deformed Dirac operator with the twisting determined by the modular operator, is here defined as follows. Pointing out the state \(\omega \) fixed in the sequel, we put \(\Gamma _\omega :=\begin{pmatrix} \Delta _\omega &{}0\\ 0&{} I\\ \end{pmatrix}\), and define \(D^{(o)}_\omega :=\Gamma _\omega ^{-1}D^{(\mathrm und)}\Gamma _\omega ^{-1}\).
The operator \(D^{(o)}_\omega \) is essentially self-adjoint in its own domain, whose closure \(D_\omega \) is easily described as follows. Denote with \(AC({{\mathbb {T}}})\) the set of all absolutely continuous complex valued functions on the unit circle. The Sobolev–Hilbert space \(H^1({{\mathbb {T}}})\) is given by

For each \(n\in {{\mathbb {Z}}}\), we put

and define the (unbounded) operators
where the \(L_n\) and \(L_n^\star \) are given in (4.5).
The deformed Dirac operator \(D_\omega \) is then defined as
on the domain
Notice that \(D_{\omega ,n}\) has compact resolvent for each \(n\in {{\mathbb {Z}}}\), and in addition is invertible for each \(n\ne 0\).
For the convenience of the reader, we report the main properties of the deformed Dirac operator summarised in the following
Theorem 4.1
The operator \(D_\omega \) with domain \({{\mathcal {D}}}_{D_\omega }\) is self-adjoint. In addition, it has compact resolvent if and only if

and if

Proof
It is matter of routine to check that \(D_\omega \) is self-adjoint in \({{\mathcal {D}}}_{D_\omega }\), see [19], Proposition 7.1. Here, we report the details of the proof of Theorem 7.3 in [19] concerning compactness.
By disregarding the kernel of the Dirac operator, we can suppose that it is invertible. Therefore, \(D_\omega \) has compact resolvent if and only if \(D^{-1}_\omega \) is compact. Then it is enough to consider
which is invertible with inverse
We now note that, by the form of the operators \(D_{\omega ,n}\) given in (4.6), the \(D^{-1}_{\omega ,n}\) are compact operators.
Suppose now that (4.8) holds true, \(D^{-1}_\#\) is manifestly compact being norm limit of the sequence of compact operators \(\big (\bigoplus _{0<|n|\le N}D^{-1}_{\omega ,n}\big )_N\). Conversely, suppose (4.8) were not true. Then there would exist a sequence \((\xi _k)_{k\in {{\mathbb {N}}}}\subset {{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \) of unit vectors such that for \(k,l\in {{\mathbb {N}}}\) \(k\ne l\),
Therefore, the sequence \(\big ((D_\#)^{-1}\xi _k\big )_{k\in {{\mathbb {N}}}}\) is not relatively compact.
Finally, by [19], Lemma 7.2,  , \(n\ne 0\). Thus, if (4.9) is satisfied, then \(\big \Vert D^{-1}_{\omega ,n}\big \Vert =o(1)\) and the second half follows by the first one. \(\square \)
, \(n\ne 0\). Thus, if (4.9) is satisfied, then \(\big \Vert D^{-1}_{\omega ,n}\big \Vert =o(1)\) and the second half follows by the first one. \(\square \)
We now exhibit modular spectral triples, some of them arising from non-type \(\mathop {\mathrm{{II_1}}}\) representations of the noncommutative torus, provided \(\alpha \) is a Liouville number. For such a purpose, define

Let \(J\subset {{\mathbb {Z}}}\) be a finite subset. For \(F_k\in {{\mathcal {C}}}_0\), consider the function \(f_k(m,n):=\widehat{F_k}(m)\delta _{n,0}\), and set \(g_k(m,n):=\delta _{m,0}\delta _{n,k}\). We define \({{\mathcal {B}}}_0\subset {{\mathcal {B}}}({{\mathbb {Z}}}^2)\) as the set of all functions
and put
To obtain a modular spectral triple as in Definition 3.1, we set  . Here,
. Here,  is the Radon probability measure on \({{\mathbb {T}}}\) defined in (2.8), and \(\omega \) in (2.7) is nothing else that
is the Radon probability measure on \({{\mathbb {T}}}\) defined in (2.8), and \(\omega \) in (2.7) is nothing else that  . It is quasi-invariant w.r.t. the multiple of the rotations by the angle \(4\pi \alpha \), and thus
. It is quasi-invariant w.r.t. the multiple of the rotations by the angle \(4\pi \alpha \), and thus  has central support in the bidual.
has central support in the bidual.
The intrinsic derivatives \({{\mathcal {L}}}\) and \({{\mathcal {L}}}^\star \) given by (4.1), assuming in our picture the form (4.3), act on the dense \(*\)-algebra \({{\mathcal {A}}}\subset {{\mathbb {A}}}_{2\alpha }\) given in (4.2) providing the required property \({{\mathcal {L}}}^\star =-*{{\mathcal {L}}}*\). It is then possible to get the deformed Dirac operator  given by (4.7). It has compact resolvent if the growth sequence satisfies
given by (4.7). It has compact resolvent if the growth sequence satisfies  , see Theorem 4.1. The operator system is finally provided by the self-adjoint subspace of
, see Theorem 4.1. The operator system is finally provided by the self-adjoint subspace of  given by
given by

where \(P_N\) is the self-adjoint projection in  onto
onto  . Notice that
. Notice that  is an operator system, and \(\sup _NP_N=I\). Therefore,
is an operator system, and \(\sup _NP_N=I\). Therefore,  is essential according to Definition 3.1.
is essential according to Definition 3.1.
Remark 4.2
By (2.12), any  is an entire element w.r.t. the adjoint action
is an entire element w.r.t. the adjoint action  on
on  of the one-parameter group generated by the modular operator, see the proof of Theorem 5.4 below.
of the one-parameter group generated by the modular operator, see the proof of Theorem 5.4 below.
Theorem 4.3
The triple  is a modular spectral triple, provided (4.8) is satisfied.
is a modular spectral triple, provided (4.8) is satisfied.
Proof
With  , we start by noticing that the deformed Dirac operator \(D_\omega \) given in (4.7) has compact resolvent if and only if (4.8) is satisfied. We notice that a sufficient condition for having compact resolvent is
, we start by noticing that the deformed Dirac operator \(D_\omega \) given in (4.7) has compact resolvent if and only if (4.8) is satisfied. We notice that a sufficient condition for having compact resolvent is  . Then, we have to verify (ii) in Definition 3.1.
. Then, we have to verify (ii) in Definition 3.1.
Indeed, we have only to check that \(\Delta _\omega ^{-1}[L,P_N\pi _\omega ({{\mathbb {A}}}_{2\alpha }^{oo})P_N]\) provides bounded operators on the common dense domain \(\pi _\omega ({{\mathcal {A}}})\xi _\omega \) for \({{\mathcal {A}}}\) given in (4.2), the other part concerning the anti-diagonal term in (3.1) being similar.
Since \(P_N\pi _\omega ({{\mathcal {A}}})\xi _\omega \subset \pi _\omega ({{\mathcal {A}}})\xi _\omega \) and, on such a dense domain \(P_N\) commutes with L and \(\Delta _\omega \), we have
and thus the assertion follows by [19], Theorem 8.1. We report those computations for the convenience of the reader.
Indeed, for the linear generator \(a=x \lambda ^l\), where \(x:=W(\widehat{F}(m)\delta _{n,0})\) and \(\lambda ^l:=W(\delta _{m,0}\, \delta _{n,l})\) the l-step shift on the direct sum  , we have
, we have
We note that \(\pi _\omega (x)\) is diagonal with  . Then, setting \(A=\pi _\omega (x)\), [L, A] is diagonal as well, providing
. Then, setting \(A=\pi _\omega (x)\), [L, A] is diagonal as well, providing

Using (2.11) and (2.12), we get

and thus

On the other hand, by (8.3) in [19], we have

where  is the growth sequence of the diffeomorphism
is the growth sequence of the diffeomorphism  .
.
Collecting together, on the domain \(\pi _\omega ({{\mathcal {A}}})\xi _\omega \) we get

\(\square \)
Remark 4.4
For all models considered in the present paper, to obtain the estimate (4.10), in the Definition 3.1 of the modular spectral triple, we should use the modular operator  of the state
of the state  on the commutant
on the commutant  . The meaning of such a fact is still unclear.
. The meaning of such a fact is still unclear.
As noticed before, the type of the representation  to which the modular spectral triple is associated, is uniquely determined by the ratio-set
to which the modular spectral triple is associated, is uniquely determined by the ratio-set  . For \(\alpha \) being a Liouville number and for the diffeomorphisms
. For \(\alpha \) being a Liouville number and for the diffeomorphisms  considered in Section 2 of [34], by taking into account [19], Proposition 3.1 (vi), it is possible to exhibit modular spectral triples arising from non-type \(\mathop {\mathrm{{II_1}}}\) representations of the noncommutative torus \({{\mathbb {A}}}_{2\alpha }\). In such a situation,
considered in Section 2 of [34], by taking into account [19], Proposition 3.1 (vi), it is possible to exhibit modular spectral triples arising from non-type \(\mathop {\mathrm{{II_1}}}\) representations of the noncommutative torus \({{\mathbb {A}}}_{2\alpha }\). In such a situation,  cannot be chosen as a \(*\)-algebra, except trivial cases, i.e. when the involved states come from inner perturbations of the canonical trace.
cannot be chosen as a \(*\)-algebra, except trivial cases, i.e. when the involved states come from inner perturbations of the canonical trace.
5 Deformed Fredholm modules
Concerning the question of whether a modular spectral triple \({{\mathcal {T}}}=(\omega ,{{\mathcal {L}}},{{\mathcal {E}}}_{{\mathcal {T}}})\) determines some kind of Fredholm module, we could conjecture that such Fredholm modules themselves have to be consequently deformed. The reader is referred to [36] for similar computations relative to the usual (i.e. undeformed) Fredholm module. To provide a totally symmetric formula for the quantum differential, we find that such a formula is indeed deformed also when the Dirac operator is not deformed, i.e. in the tracial case.
For the sake of simplicity, we tacitly suppose that \(D_{{\mathcal {T}}}\) is invertible. Since \(\hbox {Ker}_{D_{{\mathcal {T}}}}\) is finite dimensional, the assumption of invertibility does not affect the substance of the analysis in the present paper, even if the kernel of the Dirac operator encodes some information which are relevant for other aspects of noncommutative geometry (e.g. [9]). Therefore, we can reduce the matter to the subspace of finite codimension \(P^\perp _{\hbox {Ker}_{D_{{\mathcal {T}}}}}{{\mathcal {H}}}_\omega \), on which \(D_{{\mathcal {T}}}P^\perp _{\hbox {Ker}_{D_{{\mathcal {T}}}}}\) is invertible.
In such a situation, the polar decomposition for \(D_{{\mathcal {T}}}\) leads to the phase (or, more precisely, the sign) \(F_{{\mathcal {T}}}\) and the modulus \(|D_{{\mathcal {T}}}|\) satisfying
Here, the inclusion \(F_{{\mathcal {T}}}\ \supset |D_{{\mathcal {T}}}|^{-1}D_{{\mathcal {T}}}\) means that \(|D_{{\mathcal {T}}}|^{-1}D_{{\mathcal {T}}}\) is closable on its natural domain \({{\mathcal {D}}}_{D_{{\mathcal {T}}}}\) and \(\overline{|D_{{\mathcal {T}}}|^{-1}D_{{\mathcal {T}}}}=F_{{\mathcal {T}}}\).
To deal with the (deformed) Fredholm module, we set
as operators acting on \({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \), see also (3.4).
To avoid technicalities, conceptually inessential at this stage, we start by supposing that, for each \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\),
Note that, if \(\Gamma _{{\mathcal {T}}}^{\pm 1} \underline{A}\Gamma _{{\mathcal {T}}}^{\mp 1}\) is closable with bounded closure \(\overline{\Gamma _{{\mathcal {T}}}^{\pm 1} \underline{A}\Gamma _{{\mathcal {T}}}^{\mp 1}}\), then \( \underline{A}\) is in the domain of the analytic continuation of the function \({{\mathbb {R}}}\ni t\mapsto \mathrm{ad}_{\Gamma _{{\mathcal {T}}}^{\imath t}}\in \mathrm{aut}\big ({{\mathcal {B}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\big )\) at \(t=\mp \imath \).
We then define in its own domain,
Definition 5.1
The modular spectral triple \({{\mathcal {T}}}\) in Definition 3.1 is called a deformed Fredholm module if in addition, for any \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\), the deformed commutator \([F_{{\mathcal {T}}},A]^{(o)}_{{\mathcal {T}}}\) in (5.3) uniquely defines a compact operator denoted by \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\): \(\overline{{{\mathcal {D}}}_{[F_{{\mathcal {T}}},A]^{(o)}_{{\mathcal {T}}}}}={{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \),
and \(\overline{[F_{{\mathcal {T}}},A]^{(o)}_{{\mathcal {T}}}}=:[F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\in {{\mathcal {K}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\).
Theorem 5.2
Suppose that the modular spectral triple \({{\mathcal {T}}}\) considered in Definition 3.1, in addition to \(\mathrm {(iii)}\) in (5.2), also satisfies the following conditions:
-
(iv)
\(\underline{A}{{\mathcal {R}}}_{\Gamma _{{\mathcal {T}}}^{-1}}\subset {{\mathcal {D}}}_{\Gamma _{{\mathcal {T}}}}\), \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\);
-
(v)
for \(\iota \in {{\mathcal {I}}}\), \(P_{\iota }\bigoplus P_{\iota }\) strongly commutes with \(\Gamma _{{\mathcal {T}}}\), i.e. \(\Gamma _{{\mathcal {T}}}\big (P_{\iota }\bigoplus P_{\iota }\big )\supset \big (P_{\iota }\bigoplus P_{\iota }\big )\Gamma _{{\mathcal {T}}}\), and \(\big (P_{\iota }\bigoplus P_{\iota }\big ){{\mathcal {R}}}_{\Lambda _{{\mathcal {T}}}\Gamma _{{\mathcal {T}}}^{-1}}\subset {{\mathcal {D}}}_{\Gamma _{{\mathcal {T}}}^{-1}}\);
-
(vi)
\(\overline{\Gamma _{{\mathcal {T}}}\underline{A}\Gamma ^{-1}_{{\mathcal {T}}}}{{\mathcal {D}}}_{D_{{\mathcal {T}}}}\subset {{\mathcal {D}}}_{D_{{\mathcal {T}}}}\), \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\).
Then, for \({{\mathcal {T}}}\),
and thus it provides a deformed Fredholm module.
Proof
Using (iii), (vi) and the polar decomposition (5.1) of \(F_{{\mathcal {T}}}\), from (5.3) we get, first that the domain of \([F_{{\mathcal {T}}},A]^{(o)}_{{\mathcal {T}}}\) is \({{\mathcal {D}}}_{D_{{\mathcal {T}}}}\), and on such a dense domain,
We now check that \(D_{{\mathcal {T}}}\,\overline{\Gamma _{{\mathcal {T}}}\underline{A} \Gamma _{{\mathcal {T}}}^{-1}}- \overline{\Gamma _{{\mathcal {T}}}^{-1} \underline{A} \Gamma _{{\mathcal {T}}}}\,D_{{\mathcal {T}}}\supset d^{(o)}_{{\mathcal {T}}}(A)\). Indeed, by recalling (3.1) and using (3.2) from Definition 3.1, by (iv) and (v) we have
Therefore, we find from (5.5),
We now suppose that \(\xi \in {{\mathcal {D}}}_{d^{(o)}_{{\mathcal {T}}}(A)}\). Firstly, \(\xi \in {{\mathcal {D}}}_{\Gamma _{{\mathcal {T}}}\underline{A} \Gamma _{{\mathcal {T}}}^{-1}}\),
and
Secondly, \(\xi \in {{\mathcal {D}}}_{D_{{\mathcal {T}}}^{(o)}}\),
and
By (ii) in Definition 3.1 and the previous computations, \( \overline{|D_{{\mathcal {T}}}|^{-1} d_{{\mathcal {T}}}^{(o)}(A)}\subset |D_{{\mathcal {T}}}|^{-1} d_{{\mathcal {T}}}(A) \) and \(|D_{{\mathcal {T}}}|^{-1}d_{{\mathcal {T}}}^{(o)}(A)\) is bounded. Therefore, \( \overline{|D_{{\mathcal {T}}}|^{-1} d_{{\mathcal {T}}}^{(o)}(A)}=|D_{{\mathcal {T}}}|^{-1} d_{{\mathcal {T}}}(A). \) At the same time, we also get \( \overline{d_{{\mathcal {T}}}^{(o)}(A)|D_{{\mathcal {T}}}|^{-1}}= d_{{\mathcal {T}}}(A)|D_{{\mathcal {T}}}|^{-1}. \)
Collecting together the last computations and (5.6),
and thus \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}=|D_{{\mathcal {T}}}|^{-1} d_{{\mathcal {T}}}(A)+d_{{\mathcal {T}}}(A)|D_{{\mathcal {T}}}|^{-1}\) since the r.h.s. is bounded.
Since the r.h.s. is also compact, \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\) provides a compact operator for each \(A\in {{\mathcal {E}}}_{{\mathcal {T}}}\). \(\square \)
We note that, when \(\omega =\tau \) is a trace and then \(\Delta _\tau =I\), (iv) and (v) in Theorem 5.2 are automatically satisfied, whereas (vi) reduces to
-
(vi’)
\(A{{\mathcal {D}}}_{D_{{\mathcal {T}}}}\subset {{\mathcal {D}}}_{D_{{\mathcal {T}}}}\),
which coincides with (1) in Definition 1.1 of [20].
Remark 5.3
The deformed commutator \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\) is also meaningful for \(A\in \overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\), providing compact operators acting on \({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega \) as well, again obtaining
Proof
With \(\Vert \,\,\,\Vert =\Vert \,\,\,\Vert _{{{\mathcal {B}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )}\), we consider \(A\in \overline{{{\mathcal {E}}}_{{\mathcal {T}}}}\), together with a sequence \((A_n)_n\subset {{\mathcal {E}}}_{{\mathcal {T}}}\) converging to A in the norm \([]\,\,\,[]_{{\mathcal {T}}}\). Since
the sequence \(\big ([F_{{\mathcal {T}}},A_n]_{{\mathcal {T}}}\big )_n\subset {{\mathcal {K}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\) is a Cauchy sequence which converges to a compact operator as \({{\mathcal {K}}}({{\mathcal {H}}}_\omega \bigoplus {{\mathcal {H}}}_\omega )\) is complete. Since such a limit does not depend on the sequence converging to A in the norm \([]\,\,\,[]_{{\mathcal {T}}}\), it uniquely defines a compact operator which we still call \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\). \(\square \)
We point out that, differently to the usual case, the “quantum differential” \(1/|D_{{\mathcal {T}}}|\) appears symmetrically in the formula defining \([F_{{\mathcal {T}}},A]_{{\mathcal {T}}}\). Also for the undeformed spectral triples, that is when \(\omega \) is a trace, this leads to the additional deformed term \(\big (F_{{\mathcal {T}}}|D_{{\mathcal {T}}}|A|D|_{{\mathcal {T}}}^{-1}-|D_{{\mathcal {T}}}|^{-1}A|D_{{\mathcal {T}}}|F_{{\mathcal {T}}}\big )\) to the usual commutator \([F_{{\mathcal {T}}},A]\).
We now provide nontrivial examples associated to the modular spectral triples considered in the present paper for the noncommutative 2-torus, which are indeed deformed Fredholm modules.
Theorem 5.4
The spectral triples  given in Theorem 4.3 are indeed deformed Fredholm modules.
given in Theorem 4.3 are indeed deformed Fredholm modules.
Proof
To simplify, we put  . We also recall the definition of
. We also recall the definition of  in (4.7), and
in (4.7), and

We start by noticing that (iv) and (v) in Definition 5.1 are easily achieved by (2.12) and (4.4).
We now argue that, by (2.12) and (4.7),
Since  , by (5.7) we have for
, by (5.7) we have for 

Therefore, \(\underline{A}\) is an entire element for the group \(\mathrm{ad}_{\Gamma _\omega ^{\imath t}}\), and thus (iii) in (5.2) is satisfied.
Concerning (vi), we reason as in the proof of Theorem 4.3. Indeed, for the linear generator \(a=x\lambda ^l\), with \(x=W(\widehat{F}(m)\delta _{n,0})\) and \(\lambda ^l=W(\delta _{m,0}\delta _{n,l})\) as above, we first note that \(P_N\) commutes with \(\pi _\omega (x)\). Therefore, we reduce the matter when A is either \(P_N\pi _\omega (x)\) or \(P_N\pi _\omega (\lambda )^lP_N\).
By (5.8), and taking into account that the \(\delta _n\) and F are \(C^1\)-function on \({{\mathbb {T}}}\), we easily get (vi) for such a situation. For the case \(A=P_N\pi _\omega (\lambda )^lP_N\), we obtain the assertion after applying again (5.8). Indeed, if \(\xi _k\in H^1({{\mathbb {T}}})\bigoplus H^1({{\mathbb {T}}})\) and

since the \(\delta _n\) are smooth, \(\pi _\omega (\lambda )^l\xi =\bigoplus _{n\in {{\mathbb {Z}}}}\delta _{n,k-l}\xi _k\) is in the domain of \(D_\omega \) as well. \(\square \)
6 A simple illustrative example
We briefly discuss a simple example of one-dimensional spectral triple concerning the unit circle \({{\mathbb {T}}}\) for which the involved \(C^*\)-algebra is \(C({{\mathbb {T}}})\). This example is borrowed from [20], Section 3.1 where, indeed, it was instead considered the algebra C([0, 1]). Clearly, the Dirac operator \(D:=z\frac{\mathrm{d}\,\,}{\mathrm{d}z}=-\imath \frac{\mathrm{d}\,\,}{\mathrm{d}\theta }\) is nothing else than the “square root” of the (opposite of) the Laplacian \(-\frac{\mathrm{d}^2\,\,}{\mathrm{d}\theta ^2}\) on the circle. In such a way, we have an essentially different example of spectral triple from that considered in the previous mentioned paper.
We start with the multiplication operator \(a:=M_f\) for the function \(f(z)=z^l\) and \(\xi (z)=\sum _k \xi _k z^k\in L^2\left( {{\mathbb {T}}},\frac{\mathrm{d}z}{2\pi \imath z}\right) \), where the sum is over a finite set. As explained above, for our purposes we can disregard the kernel of D.
Since the modular operator is trivial, we put \(D|D|^{-1}=F=F_{{\mathcal {T}}}\) and compute
We remark that we are obtaining the perfect analogous formula corresponding to Eq. (5.4), even for this simple example of dimension one.
For this simple example, the arising spectral triple \({{\mathcal {T}}}\equiv ({{\mathcal {A}}},{{\mathcal {L}}},{{\mathcal {E}}}_{{\mathcal {T}}})\) of dimension 1, which is also a Fredholm module by the just seen computation, would be chosen as follows. For the dense \(*\)-algebra \({{\mathcal {A}}}\), we can choose
where \([]\,\,[]_{{\mathcal {T}}}\) is the norm in (3.3) corresponding to that of the uniform convergence of functions together with their 1st derivative. Correspondingly, \({{\mathcal {L}}}:=D\lceil _{{\mathcal {A}}}\). Finally, the state \(\omega \) is obviously given by the Haar-Lebesgue measure \(\frac{\mathrm{d}z}{2\pi \imath z}\) on \({{\mathbb {T}}}\).
We would like to point out that, conversely to the simple model just described above, Example 3.1 in [20] might not provide a Fredholm module for both definitions, the usual undeformed one, and the deformed one in Definition 3.1 adapted to spectral triples of dimension 1.
Indeed, on \(C([0,2\pi ])\) with one of the usual self-adjoint Dirac operators \(D_\chi \), for \(|\chi |=1\), given by \(-\imath \frac{\mathrm{d}\,\,}{\mathrm{d}\theta }\) with
(e.g. Example in [38], Section VIII.2), any dense \(*\)-subalgebra of \(C([0,2\pi ])\) on which the commutator with \(D_\chi \) provides bounded operators acting on \(L^2([0,2\pi ])\) would contain a smooth function f for which \(f(0)\ne f(2\pi )\).
For such a kind of function \(a :=f(z)\), the asymptotic of the Fourier coefficients \(\{{\hat{f}}(k)\}_{k\in {{\mathbb {Z}}}}\) is at most 1/|k| or worst. Therefore, the deformed commutator \([F,a]_{{\mathcal {T}}}\) is meaningless. On the other hand, [F, a] corresponding to the usual definition of Fredholm module, and again defined on any appropriate domain, although giving rise to bounded operators, cannot always provide compact ones as shown in [20].
However, it is an interesting fact that, on \(C({{\mathbb {T}}})\) and for \(D=z\frac{\mathrm{d}\,\,}{\mathrm{d}z}\), the associated undeformed Fredholm module \([F,M_f]=[D|D|^{-1},M_f]\) for \(\{M_f \mid f(z)=\sum _{|l|\le K} f_l\, z^l,\,\,K\in {{\mathbb {N}}}\}\) produces finite rank operators, hence compact ones. Indeed, set \(a=M_f\) with \(f(z)=z^l\), and \(\xi =\sum _{|k|\le K}\xi _k z^k\) with \(K\in {{\mathbb {N}}}\).
To simplify, we first suppose \(l>1\) and compute
where \(\lambda \) is the one-step shift defined as \((\lambda \xi )(z)= \sum _k \xi _{k-1} z^k\), and \(P_L\) is the self-adjoint projection given by \((P_L \xi )(z) = \sum _{k\in L} \xi _k z^k\).
Now, to manage the general case \(l\in {{\mathbb {Z}}}\), define
and, by reasoning as in (6.1), it is straightforward to check that
We would like to point out that, for \(a=M_f\) with \(f(z)=\sum _{|l|\le K} f_l\, z^l\) as above, by (6.1) |D|[F, a] uniquely defines a bounded operator satisfying
Therefore, denoting by \(B_a\) the bounded closure of |D|[F, a], we re-obtain the well-known Connes’ formula \([F,a]= |D|^{-1}B_a\).
7 Other examples of modular spectral triples
In the present section, we briefly describe other examples of modular spectral triples and deformed Fredholm modules for the noncommutative 2-torus \({{\mathbb {A}}}_{2\alpha }\), leaving technical details to the reader.
The first case we are interested in is described in Section 9 of [19], and provides spectral triples \({{\mathcal {T}}}\) for which \({{\mathcal {E}}}_{{\mathcal {T}}}\) is a dense \(*\)-algebra. Indeed, to obtain a \(*\)-algebra, we need to fix any orientation-preserving diffeomorphism  of the circle having a rotation number
of the circle having a rotation number  , where \(\alpha \) is a ultra-Liouville number, see Section 2. As usual, we use the notation
, where \(\alpha \) is a ultra-Liouville number, see Section 2. As usual, we use the notation  for the involved \(*\)-algebra.
for the involved \(*\)-algebra.
As previously seen in [19], Section 9, \({{\mathcal {L}}}\), and consequently \({{\mathcal {L}}}^\star \), should be modified as

where  is the multiplier defined in its own domain by
is the multiplier defined in its own domain by

with

Here, the Fourier transform and anti-transform involve only the 2nd variable w, and  is the growth sequence of the diffeomorphism
is the growth sequence of the diffeomorphism  .
.
Notice that, for these cases, the choice of \({{\mathcal {L}}}\) and \({{\mathcal {L}}}^\star \) heavily depend on  , and thus on the state
, and thus on the state  entering in the Definition 3.1 of the modular spectral triple. The reader is indeed referred to [19], Proposition 3.1 and Section 9, for the proofs and further details.
entering in the Definition 3.1 of the modular spectral triple. The reader is indeed referred to [19], Proposition 3.1 and Section 9, for the proofs and further details.
A second set of examples is proposed in Section 7 of [18] for each \(\eta \in [0,1]\). With an abuse of notation, we denote by \({{\mathcal {T}}}_\eta \) the modular spectral triples under consideration. We then have a parametric family of deformed Dirac operators given by
defined in their own domains. Here, \(\mathrm {L}_\omega \) and \(\mathrm {L}^\star _\omega \) are the operators in (4.1) or in (7.1) acting on the \(L^2\)-space on their own domains, and (4.1) can be clearly viewed as a particular case of (7.1).
Correspondingly, for the deformed derivation \(d_{{{\mathcal {T}}}_\eta }\) on \({{\mathcal {E}}}_{{{\mathcal {T}}}_\eta }\),
would still provide bounded operators.
For all values of \(\eta \) and \({{\mathcal {T}}}_\eta \) the relative spectral triples, if we consider the models associated to (4.1), the construction can be carried out for all Liouville numbers, and the undeformed Dirac operator \(\begin{pmatrix} 0&{}\mathrm {L}_\omega \\ \mathrm {L}^\star _\omega &{} 0\\ \end{pmatrix}\equiv \begin{pmatrix} 0&{}L_\omega \\ L^\star _\omega &{} 0\\ \end{pmatrix}\) does not depend on the diffeomorphism  . For this situation, the price to pay is that the domain \({{\mathcal {E}}}_{{{\mathcal {T}}}_\eta }\) of the deformed commutator \(d_{{{\mathcal {T}}}_\eta }\) is merely an (essential) operator system.
. For this situation, the price to pay is that the domain \({{\mathcal {E}}}_{{{\mathcal {T}}}_\eta }\) of the deformed commutator \(d_{{{\mathcal {T}}}_\eta }\) is merely an (essential) operator system.
In the second case when we use (7.1) for the undeformed Dirac operator \(\begin{pmatrix} 0&{}\mathrm {L}_\omega \\ \mathrm {L}^\star _\omega &{} 0\\ \end{pmatrix}\), \({{\mathcal {E}}}_{{{\mathcal {T}}}_\eta }\) is a dense \(*\)-algebra, but our construction can be performed only for ultra-Liouville numbers (UL) described in Section 2. In addition, the undeformed Dirac operators do depend on  according to (7.1), that is they are not intrinsic objects associated to the noncommutative manifold under consideration.
according to (7.1), that is they are not intrinsic objects associated to the noncommutative manifold under consideration.
After setting
we find that (7.2) and (7.3) are obtained respectively as
It is expected that for all cases described in the present section, we would still get deformed Fredholm modules. Indeed, with \(F_{{{\mathcal {T}}}_\eta }\) the phase of \(D_{{{\mathcal {T}}}_\eta }\) and disregarding its kernel, similarly to (5.3) for the closure \([F_{{{\mathcal {T}}}_\eta },A]_{{{\mathcal {T}}}_\eta }\) of
we would obtain \([F_{{{\mathcal {T}}}_\eta },A]_{{{\mathcal {T}}}_\eta }=|D_{{{\mathcal {T}}}_\eta }|^{-1}d_{{{\mathcal {T}}}_\eta }(A)+d_{{{\mathcal {T}}}_\eta }(A)|D_{{{\mathcal {T}}}_\eta }|^{-1}\) as in Theorem 5.2.
8 The spectrum of the Dirac operator and the Hill equation
We now want to discuss the, in general difficult, problem to diagonalise the deformed Dirac operator \(D_\omega \) for the noncommutative 2-torus considered in the present paper and given in (4.7).
In Section 4, we have already noted that the set of eigenvectors of \(D_\omega \) generates the whole Hilbert space. This easily follows as the \(D_{\omega , n}\) have compact resolvent for any \(n\in {{\mathbb {Z}}}\), and thus \(\sigma (D_{\omega , n})\) are discrete sets. Therefore, \(\sigma (D_\omega )=\overline{\bigcup _{n\in {{\mathbb {Z}}}}\sigma (D_{\omega , n})}\). Theorem 4.1 provides conditions under which \(D_\omega \) has compact resolvent, and thus \(\sigma (D_\omega )=\bigcup _{n\in {{\mathbb {Z}}}}\sigma (D_{\omega , n})\) if this is the case. We also note that \(\sigma (D_\omega )\) might still be a discrete set even if \(D_\omega \) has not compact resolvent. This happens when some eigenvalue has infinite multiplicity.
We show that the characterisation of eigenvalues and eigenvectors of \(D_\omega \) is given in terms of a particular class of eigenvalue Hill equations.
The undeformed Dirac operator \(\overline{D^{(\mathrm und)}}=\begin{pmatrix} 0 &{}\overline{L} \\ \overline{L^\star } &{} 0\\ \end{pmatrix}\) gives rise to the eigenvalues equation \(\Big (\frac{\mathrm{d}^2\,}{\mathrm{d}\theta ^2}+(\lambda ^2-n^2)\Big )H=0\) for the periodic function H and each fixed \(n\in {{\mathbb {Z}}}\), providing eigenvalues and eigenvectors given at the beginning of Section 4.
Setting \(d_n(\theta ):=\delta _n(e^{\imath \theta })\), where the \(\delta _n\) are defined in (2.11), the result concerning the Hill equation and the diagonalization of \(D_\omega \), independently on the fact that it has compact resolvent, are summarised as follows.
Theorem 8.1
The real number \(\lambda \) is an eigenvalue of the deformed Dirac operator \(D_\omega \) in (4.7) if and only if there exists \(n\in {{\mathbb {Z}}}\) such that the homogeneous Hill equation
admits a periodic \(C^2\) (and therefore necessarily \(C^\infty \)) nontrivial solution.
Proof
The real number \(\lambda \) is an eigenvalue of \(D_\omega \) if, for some n, there exist non-vanishing periodic functions f, g on the unit circle, necessarily smooth, satisfying
By replacing g from the 2nd equation in the 1st of (8.2), and defining \(h:=\delta _n^{-1}f\), we obtain
By passing to \(H(\theta ):=h(e^{\imath \theta })\) and \(d_n(\theta )=\delta _n(e^{\imath \theta })\), it becomes
which leads to the homogeneous Hill equation (8.1).
Suppose now that (8.1) admits a non-zero smooth periodic solution for some \(\lambda \ne 0\) and \(n\in {{\mathbb {Z}}}\), the case \(\lambda =0\) being trivial.
By putting \(H(\theta )d_n(\theta )=f(z)\) with \(z=e^{\imath \theta }\), and
an easy calculation shows that the vector-valued function
provides an eigenvector corresponding to the eigenvalue \(\lambda \).
Indeed, for \(\lambda \ne 0\) and \(n\in {{\mathbb {Z}}}\), (8.2) reads \(\delta _n^{-1}L_ng=\lambda f\) and \(L_n^\star (\delta _n^{-1} f)=\lambda g\), where \(L_n\) and \(L_n^\star \) are the differential operators given in (4.5).
We first note that (8.3) is nothing else than the first condition above. Concerning the second, using the Hill equation, we get
Summarising,
and this concludes the proof. \(\square \)
The eigenvalue problem arising from the deformed Dirac operators
defined for \(\eta \in [0,1]\) in (7.2), provides a generalisation that can be achieved as follows. By (8.4), we get
By arguing as in the case corresponding to \(\eta =0\) previously described, with \(H(\theta ):=d_n(\theta )^{\eta -1}f(e^{\imath \theta })\), we obtain after some computations,
References
Acerbi, F.: Nonregular representation of CCR algebras, ISAS PhD Thesis, available online at ISAS digital Library (1993)
Bellissard, B., van Elst, A., Schulz-Baldes, H.: The noncommutative geometry of the quantum Hall effect. Topology and physics. J. Math. Phys. 35, 5373–5451 (1994)
Boca, F.-P.: Rotation C\(^{*}\)-algebras and Almost Mathieu Operators. Theta, Bucharest (2001)
Bratteli, O., Robinson, D.W.: Operator Algebras and Quantum Statistical Mechanics 1. Springer, New York (2002)
Carey, A.L., Phillips, J., Putnam, I.F., Rennie, A.: Families of type III KMS states on a class of C*-algebras containing \(O_n\) and \({\mathbb{Q}}_N\). J. Funct. Anal. 260, 1637–1681 (2011)
Carey, A. L., Phillips, J., Rennie, A.: Spectral triples: examples and index theory. In: Carey (Ed.), Noncommutative Geometry and Physics: Renormalisation, Motives, Index Theory, in: ESI Lect. Math. Phys., pp. 175–265 (2011)
Chamseddine, A.H., Connes, A.: The spectral action principle. Commun. Math. Phys. 186, 731–750 (1997)
Connes, A.: Une classification des facteurs de type III. Ann. Sci. École Norm. Sup. 6, 133–252 (1973)
Connes, A.: Noncommutative Geometry. Academic Press, San Diego (1994)
Connes, A.: Noncommutative geometry and reality. J. Math. Phys. 36, 6194–6231 (1995)
Connes, A.: Trace formula in noncommutative geometry and the zeros of the Riemann zeta function. Journées Équations aux dérivées partielles , pp 1–28 (1997)
Connes, A., Lott, J.: Particle models and noncommutative geometry. Nuclear Phys. B Proc. Suppl. 18B, 29–47 (1991)
Connes, A., Moscovici, H.: Type III and spectral triples. Aspects Math. E 38, 57–71 (2008)
Connes, A., Moscovici, H.: Modular curvature for noncommutative two-tori. J. Amer. Math. Soc. 27, 639–684 (2014)
Connes, A., van Suijlekom, W.D.: Spectral truncations in noncommutative geometry and operator systems. Commun. Math. Phys. 383, 2021–2067 (2021)
Correia Ramos, C., Martins, N., Pinto, P.R., Sousa Ramos, J.: Orbit equivalence and von Neumann algebras for expansive interval maps. Chaos Solit. Fract. 33, 109–117 (2007)
Davidson, K. R.: \(C^*\)-algebras by Example. Providence RI (1996)
Fidaleo, F.: Fourier analysis for type III representations of the noncommutative torus. J. Fourier Anal. Appl. 25, 2801–2835 (2019)
Fidaleo, F., Suriano, L.: Type III representations and modular spectral triples for the noncommutative torus. J. Funct. Anal. 275, 1484–1531 (2018)
Forsyth, I., Mesland, B., Rennie, A.: Dense domains, symmetric operators and spectral triples. New York J. Math. 20, 1001–1020 (2014)
Gracia-Bondía, J.M., Várilly, J.C., Figueroa, H.: Elements of Noncommutative Geometry. Springer, New York (2013)
Greenfield, M., Marcolli, M., Teh, K.: Twisted spectral triples and quantum statistical mechanical systems. P-Adic Numbers Ultrametric. Anal. Appl. 6, 81–104 (2014)
Haag, R., Hugenholtz, N.M., Winnink, M.: On the equilibrium states in quantum statistical mechanics. Commun. Math. Phys. 5, 215–236 (1967)
Hadfield, T.: Fredholm modules on certain group \(C^*\)-algebras. J. Oper. Theory 51, 141–160 (2004)
Hill, G.W.: On the part of the motion of lunar perigee which is a function of the mean motions of the sun and moon. Acta Math. 8, 1–36 (1886)
Katok, A., Hasselblatt, B.: Introduction to the Modern Theory of Dynamical Systems. Encyclopedia of Mathematics and Its Applications, 54. Cambridge University Press, Cambridge (1995)
Khalkhali, M.: A short survey on cyclic cohomology. Clay Math. Proc. 11, 283–311 (2010)
Ya, A.: Khinchin. Continued Fractions. The University of Chicago Press, Chicago (1964)
Krieger, W.: On the Araki-Woods asymptotic ratio set and non singular transformations of a measure space. In: Ergodic Theory and Probability (Proc. Conf., Ohio State Univ., Columbus, Ohio, 1970), Lecture Notes in Mathematics, Springer, New York, 160, pp. 158–177 (1970)
Krieger, W.: On constructing non \(*\)-isomorphic hyperfinite factors of type III. J. Funct. Anal. 6, 97–109 (1970)
Kubo, R.: Statistical-Mechanical theory of irreversible processes I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jpn. 12, 570–586 (1957)
Landi, G., Martinetti, P.: Gauge transformations for twisted spectral triples. Lett. Math. Phys. 108, 2589–2626 (2018)
Martin, P.C., Schwinger, J.: Theory of many-particle systems I. Phys. Rev. 115, 1342–1373 (1959)
Matsumoto, S.: Orbit equivalence types of circle diffeomorphisms with a Liouville rotation number. Nonlinearity 26, 1401–1414 (2013)
Mayer, R.: Real Spectral Triples and Charge Conjugation. In: Noncommutative Geometry and the Standard Model of Elementary Particle Physics. Lecture Notes in Phys. 596 (2002) Springer, New York, pp. 11–20
Moscovici, H.: Local index formula and twisted spectral triples. In: Quanta of maths, pp. 465–500, Clay Math. Proc. 11, Amer. Math. Soc., Providence, RI (2010)
Niculescu, C.P., Ströh, A., Zsidó, L.: Noncommutative extensions of classical and multiple recurrence theorems. J. Oper. Theory 50, 3–52 (2003)
Reed, M., Simon, B.: Functional Analysis. Academic Press, New York (1980)
Sondow, J.: An irrationality measure for Liouville numbers and conditional measures for Euler’s constant. arXiv:0307308
Strǎtilǎ, Ş: Modular Theory in Operator Algebras. Abacus Press, Tunbridge Wells, Kent (1981)
Takesaki, M.: Tomita’s Theory of Modular Hilbert Algebras and its Applications. LNM 128. Springer, Berlin (1970)
O Takesaki, M.: Theory of Operator Algebras I, III. Springer, Berlin (1979, 2003)
Yoccoz, J.-C.: Conjugaison différentiable des difféomorphismes du cercle dont le nombre de rotation vérifie une condition diophantienne. Ann. Sci. École Norm. Sup. 17, 333–359 (1984)
Watanabe, N.: Growth sequences for circle diffeomorphisms. Geom. Funct. Anal. 17, 320–331 (2007)
Acknowledgements
The authors acknowledge MIUR Excellence Department Project awarded to the Department of Mathematics, University of Rome “Tor Vergata”, CUP E83C18000100006, and Italian INdAM-GNAMPA. The first-named author is partially supported by MIUR-FARE R16X5RB55W QUEST-NET. The second-named author is grateful to the Faculty of Mathematics and Computer Science of University of Würzburg for the kind hospitality in occasion of the Prodi-Chair position (winter 2021–2022), where the present work was finalised.
Funding
Open access funding provided by Università degli Studi di Roma Tor Vergata within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by M. S. Moslehian.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ciolli, F., Fidaleo, F. Modular spectral triples and deformed Fredholm modules. Ann. Funct. Anal. 13, 67 (2022). https://doi.org/10.1007/s43034-022-00200-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s43034-022-00200-w
Keywords
- Noncommutative geometry
- Noncommutative torus
- Type III representations
- Spectral triples
- Fredholm modules
- One-dimensional topology
- Diffeomorphisms of the circle
- Quasi-invariant ergodic measures




 , and the inverse of
, and the inverse of  is denoted by
is denoted by 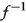 ;
; ;
;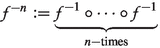 .
.