Zeros of Gaussian power series, Hardy spaces and determinantal point processes

Abstract

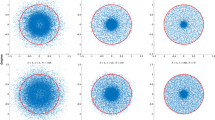
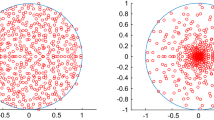
Given a sequence $(\xi _n)$ of standard i.i.d complex Gaussian random variables, Peres and Virág (in the paper “Zeros of the i.i.d. Gaussian power series: a conformally invariant determinantal process” Acta Math. (2005) 194, 1-35) discovered the striking fact that the zeros of the random power series $f(z) = \sum _{n=1}^\infty \xi _n z^{n-1}$ in the complex unit disc ${\mathbb {D}}$ constitute a determinantal point process. The study of the zeros of the general random series f(z), where the restriction of independence is relaxed upon the random variables $(\xi _n)$ is an important open problem. This paper proves that if $(\xi _n)$ is an infinite sequence of complex Gaussian random variables, such that their covariance matrix is invertible and its inverse is a Toeplitz matrix, then the zero set of f(z) constitutes a determinantal point process with the same distribution as the case of i.i.d variables studied by Peres and Virág. The arguments are based on some interplays between Hardy spaces and reproducing kernels. Illustrative examples are constructed from classical Toeplitz matrices and the classical fractional Gaussian noise.