The Limit Empirical Spectral Distribution of Gaussian Monic Complex Matrix Polynomials

Abstract

We define the empirical spectral distribution (ESD) of a random matrix polynomial with invertible leading coefficient, and we study it for complex $n \times n$ Gaussian monic matrix polynomials of degree k. We obtain exact formulae for the almost sure limit of the ESD in two distinct scenarios: (1) $n \rightarrow \infty$ with k constant and (2) $k \rightarrow \infty$ with n constant. The main tool for our approach is the replacement principle by Tao, Vu and Krishnapur. Along the way, we also develop some auxiliary results of potential independent interest: We slightly extend a result by Bürgisser and Cucker on the tail bound for the norm of the pseudoinverse of a nonzero mean matrix, and we obtain several estimates on the singular values of certain structured random matrices.

1 Introduction

Given $n \times n$ matrices $C_0, C_1, \dots , C_k \in \mathbb {C}^{n \times n}$, consider the square matrix polynomial of degree k

$$\begin{aligned} P(x) = \sum _{j=0}^k C_j x^j; \end{aligned}$$

(1)

a finite eigenvalue of P(x) is then defined [9, 12] as a number $\lambda \in \mathbb {C}$ such that

$$\begin{aligned} \mathrm {rank}_\mathbb {C}P(\lambda ) < \mathrm {rank}_{\mathbb {C}(x)} P(x). \end{aligned}$$

The polynomial eigenvalue problem (PEP) is to find all such eigenvalues [1, 8,9,10,11,12, 15, 21], possibly (and depending on the application) together with other objects—such as eigenspaces, infinite eigenvalues, minimal indices and minimal bases—whose precise definition is not relevant for this paper. Under the generic assumption that $\det P(x) \not \equiv 0$, the finite eigenvalues of P(x) are the roots of its determinant. Polynomial eigenvalue problems are common in several areas of applied and computational mathematics; their applications include acoustics, control theory, fluid mechanics and structural engineering [10, 11, 21].

Clearly, two very classical mathematical problems arise as special cases of polynomial eigenvalue problems: finding the roots of a scalar polynomial corresponds to $n=1$, while finding the eigenvalues of a matrix corresponds to $k=1$ and $C_1=I_n$. When randomness enters the game, these two extremes are well understood. It is known that when the polynomial coefficients are i.i.d. normally distributed random variables and in the limit $k \rightarrow \infty$, then the roots of scalar polynomials are uniformly distributed on the unit circle. Similarly, classical results in random matrix theory state that when the entries of an $n \times n$ matrix are i.i.d. normally distributed random variables with mean 0 and variance $n^{-1}$, and in the limit $n \rightarrow \infty$, then the eigenvalues are uniformly distributed on the unit disc. Moreover, the phenomenon of universality is well known: there exist works that, under relatively mild assumptions, extend these results to several other distributions of coefficients or entries.

To our knowledge, nothing was so far explicitly known about the eigenvalues of random matrix polynomials, except for the two extremal cases above described. In this paper, we fill this gap by computing the empirical eigenvalue distribution of monic ($C_k=I)$ square matrix polynomials of size n and degree k, with all but the leading coefficient being i.i.d. complex Gaussian random matrices, in two different limits: when $n \rightarrow \infty$ with k constant and when $k \rightarrow \infty$ with n constant. Moreover, our results can equivalently be interpreted as results on the empirical eigenvalue distribution of certain structured random matrices: indeed, given a monic matrix polynomials P(x), a linearization of P(x) is a matrix whose eigenvalues (as well as their geometric and algebraic multiplicities) coincide with those of P(x). In the numerical linear algebra literature, numerous constructions of linearizations are known, see, e.g., [8, 10, 15] and the references therein. In particular, the prototype of all linearizations is the so-called companion matrix, which plays a central role in this paper.

In previous research on matrix polynomials, probability theory was used in the context of analyzing the condition number of PEPs. Namely, in [2] Armentano and Beltrán computed the average eigenvalue condition number for Gaussian random complex matrix polynomials, and in [4], Beltrán and Kozhasov extended the analysis to the case of real Gaussian matrix polynomials. In [12], Lotz and Noferini went beyond the classical idea of condition by imposing a uniform probability distribution on the sphere for perturbations of a fixed singular matrix polynomial. However, we are not aware of any previous work where the exact distribution of the eigenvalues of a random matrix polynomial is obtained. In addition to being interesting per se, our results can potentially be valuable to numerical analysts in the context of testing numerical methods for the solution of the PEP. Indeed, although randomly generated problems are expected not to be very challenging from the numerical point of view (by the results in [2, 4]), it is common practice to use them as benchmark for minimal performance requirements; in published research papers on this subject, tests on random input are in fact often included among the numerical experiments. The analytic knowledge of the limit eigenvalue distributions that we obtain in this article can help to predict the behavior of randomly generated problems: when scrutinizing a novel algorithm, if the numerically computed eigenvalues should significantly deviate from the expectations, then this fact can raise legitimate suspicions on the accuracy of the computations.

The structure of the paper is as follows. In Sect. 2, we review some necessary background material on linear algebra, matrix polynomial theory, probability theory and random matrix theory. Moreover, we define the empirical spectral distribution of a random matrix polynomial with invertible leading coefficient. In Sect. 3, we obtain our first main result: the almost sure limit, for $n \rightarrow \infty$, of the empirical spectral distribution of a random $n \times n$ monic complex Gaussian matrix polynomial of degree k. In Sect. 4, our second main result is discussed: the almost sure limit, for $k \rightarrow \infty$, of the empirical spectral distribution of a random $n \times n$ monic complex Gaussian matrix polynomial of degree k. In Sect. 5, we draw some conclusions and propose new lines of research. To keep the main part of the paper as easily readable as possible, the proof of some technical lemmata, needed in Sects. 3 and 4, is postponed to “Appendix A”; however, we believe that some of those results could have independent interest. In particular, we slightly improve known results on the tail bounds for pseudoinverses of random matrices with nonzero mean, and we study the extremal singular values of certain structured random matrices.

2 Mathematical Background

2.1 Linear Algebra

Given an $m \times n$ complex matrix X, we denote it singular values by $\sigma _1(X) \ge \dots \ge \sigma _{\min }(X) \ge 0$, having introduced the shorthand $\sigma _{\min }(X) :=\sigma _{\min (m,n)}(X)$. The spectral norm of X is denoted by $\Vert X \Vert :=\sigma _1(X)$, while the Frobenius norm of X is

$$\begin{aligned} \Vert X \Vert _F = \left( \sum _{i=1}^m \sum _{j=1}^n |X_{ij}|^2 \right) ^{1/2} = \sqrt{\mathrm {tr}(X^* X)} = \sqrt{\sigma _1(X)^2 + \dots + \sigma _{\min }(X)^2} . \end{aligned}$$

Recall that any X admits a singular value decomposition $U\Sigma V$ with $U\in \mathbb {C}^{m\times m}$, $V\in \mathbb {C}^{n\times n}$ unitary matrices and $\Sigma \in \mathbb {R}^{m\times n}$ diagonal real matrix whose diagonal elements are the singular values $\sigma _i(X)\ge 0$. The Moore–Penrose pseudoinverse of X is the matrix $X^\dagger =V^*\Sigma ^\dagger U^*$, where $\Sigma ^\dagger \in \mathbb {R}^{n\times m}$ is a diagonal real matrix whose diagonal entries are $\Sigma _{i,i}^\dagger =\Sigma _{i,i}^{-1} = \sigma _i(X)^{-1}$ if $\sigma _i(X)>0$ and zero otherwise.Note that, if X has full rank, then $\Vert X^{\dagger }\Vert = 1/\sigma _{\min }(X)$. We also use the induced 1 and $\infty$ matrix norms, defined, respectively, as

$$\begin{aligned} \Vert X\Vert _1 = \max _{1\le j\le n} \sum _{i=1}^m |X_{ij}|, \qquad \Vert X\Vert _\infty = \max _{1\le i\le m} \sum _{j=1}^n |X_{ij}|. \end{aligned}$$

Since $\mathbb {C}^{m \times n}$ is finite-dimensional, various norms mentioned above are of course equivalent to each other, and the following relations will be useful to us:

$$\begin{aligned} \Vert X\Vert \le \Vert X\Vert _F,\qquad \Vert X\Vert \le \sqrt{ \Vert X\Vert _\infty \Vert X\Vert _1 }. \end{aligned}$$

(2)

An interlacing result for the singular values arises when we consider low rank perturbation of matrices.

Theorem 2.1

(Interlacing Singular Values for Low-Rank Perturbations [20]) Let A and E be $n\times n$ matrices, where E has rank at most k. If $B = A+E$ and the singular values of A and B are, respectively,

$$\begin{aligned} \alpha _1\ge \alpha _2 \ge \dots \ge \alpha _{n}, \qquad \beta _1\ge \beta _2 \ge \dots \ge \beta _{n}, \end{aligned}$$

then

$$\begin{aligned}&\alpha _i\ge \beta _{i+k},&i=1,2,\dots ,n-k,\\&\beta _i\ge \alpha _{i+k},&i=1,2,\dots ,n-k. \end{aligned}$$

If the norm of the perturbation, as opposed to its rank, is to be used to estimate the singular values, then we can appeal to the following result attributed to Mirsky, which is a corollary of the minimax principle for singular values.

Theorem 2.2

(Perturbation Theorem [14]) Given two ${ n\times n}$ matrices A, B, with singular values, respectively,

$$\begin{aligned} \alpha _1\ge \alpha _2 \ge \dots \ge \alpha _n, \qquad \beta _1\ge \beta _2 \ge \dots \ge \beta _n, \end{aligned}$$

then

$$\begin{aligned} |\alpha _i-\beta _i|\le \Vert A-B\Vert , \qquad i=1,2,\dots ,n. \end{aligned}$$

2.2 Matrix Polynomial Theory

Let P(x) be the matrix polynomial defined in (1). We give here a brief overview of those aspects in the spectral theory of square complex matrix polynomials that are relevant to this paper. More detailed discussions can be found, e.g., in [1, 9, 10, 12] and the references therein. As mentioned in introduction, an element $\lambda \in \mathbb {C}$ is said to be a finite eigenvalue of P(x) if

$$\begin{aligned} \mathrm {rank}_{\mathbb {C}}(P(\lambda )) < \mathrm {rank}_{\mathbb {C}(x)}(P(x)) =: r, \end{aligned}$$

where $\mathbb {C}(x)$ is the field of fractions of $\mathbb {C}[x]$, that is, the field of rational functions with coefficients in $\mathbb {C}$.

If the leading coefficient $C_k$ of the matrix polynomial P(x) in (1) is invertible, then P(x) has kn finite eigenvalues. Under this assumption, one can define the companion matrix of P(x) as (see, e.g., [1])

$$\begin{aligned} M=\begin{bmatrix} -C_k^{-1}C_{k-1} &{} -C_k^{-1}C_{k-2} &{} \dots &{} -C_k^{-1}C_{1} &{} -C_k^{-1}C_{0}\\ I_n &{} 0 &{} 0 &{} \dots &{} 0\\ 0&{} I_n &{} 0 &{} \dots &{} 0\\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \dots &{} 0 &{} I_n &{} 0 \end{bmatrix} \in \mathbb {C}^{kn \times kn}, \end{aligned}$$

(3)

where $I_n$ and 0 are, respectively, the $n\times n$ identity and zero matrices. It is well known that the eigenvalues of M, defined in the classical sense, coincide with the finite eigenvalues of P(x). As a consequence, under the assumption that $C_k$ is invertible, studying the finite eigenvalues of P(x) is equivalent to studying the eigenvalues of the structured matrix M. Observe that, if P(x) is monic, then $C_k = I$ so that the assumption is automatically satisfied.

We can identify, say via an arbitrary but fixed rearrangement of the real and imaginary parts of the entries of each coefficient, the (real) vector space of $n \times n$ complex matrix polynomials of degree up to k with $\mathbb {R}^{2(k+1)n^2}$. In this setting, let ${\mathcal {S}} \subset \mathbb {R}^{2(k+1)n^2}$ correspond to the subset of matrix polynomials that are regular and have kn distinct finite eigenvalues. We conclude this subsection by observing that ${\mathcal {S}}$ is a nonempty Zariski open set, and hence, its complement has Lebesgue measure zero: in this sense, being regular with kn distinct finite eigenvalues is a generic property of matrix polynomials.

2.3 Random Matrix Theory

Often, within our probabilistic arguments it will be crucial to consider matrices that have some deterministic entries and some other entries corresponding to (complex) random variables, which in turn can be seen as pairs of real random variables. We implicitly identify those matrices with a vector in $\mathbb {R}^N$, N being the number of real random variables involved, and equipping $\mathbb {R}^N$ with an appropriate probability measure. In this context, we will often invoke, without explicit justification, the well-known fact that events that happen in (subsets of) proper Zariski closed sets of $\mathbb {R}^N$ have probability zero: for example, we may claim that a certain square random matrix is almost surely invertible. Recalling that any proper Zariski closed set has Lebesgue measure zero, it follows immediately that the claimed property is true for any absolutely continuous probability measure (as are all the ones we discuss in this paper). The verification that, in all the instances where we make such a claim, the corresponding algebraic set is indeed contained in a proper algebraic set is a straightforward exercise in linear algebra, and we therefore omit the details.

2.3.1 Empirical Spectral Distributions

Given a deterministic matrix $A\in M_{m}(\mathbb {C})$ with eigenvalues $\lambda _1(A),\dots ,\lambda _m(A)$ we say that its empirical spectral distribution (ESD) is the atomic measure

$$\begin{aligned} \mu _A = \frac{1}{m} \sum _{i=1}^{m} \delta _{\lambda _i(A)}, \end{aligned}$$

where the eigenvalues are considered with their respective algebraic multiplicities. A random matrix $A_n$ can be seen as a random variable with values in the appropriate space of matrices that will usually be $M_{nk}(\mathbb C)$, where n and k are fixed parameters. We can extend the concept of ESDs to random matrices as follows.

Definition 2.3

Given a random matrix A, its empirical spectral distribution (ESD) is a random variable with values in the space of probabilities on $\mathbb C$, defined as

$$\begin{aligned} \mu _A(\omega ) := \mu _{A(\omega )} = \frac{1}{m} \sum _{i=1}^{m} \delta _{\lambda _i(A(\omega ))}. \end{aligned}$$

The space of probabilities on $\mathbb C$ is a measurable subset of ${\mathcal {M}}^b(\mathbb C)$, the space of signed measure of $\mathbb C$ with bounded total variation, that is a Hausdorff space when equipped with the vague (or weak $-^*$) convergence of measures.

We will study the spectral distribution for some families of random matrices $\{A_{n}\}_n$ and find that in our cases the sequence $\{\mu _{A_n}\}_n$ always converges almost surely (a.s.) to a constant random variable that can be identified with a probability measure $\mu \in \mathbb P(\mathbb C)$. In this case, we simply write

$$\begin{aligned} \mu _{A_n}\xrightarrow {a.s.} \mu . \end{aligned}$$

The measure $\mu$ will thus be our candidate for the asymptotic spectral distribution of the family $\{A_{n}\}_n$.

Finally, having let us consider a random matrix polynomial $P(x;\omega )$ of shape $n \times n$ and degree k, under the assumption that, for all $\omega \in \Omega$, $P(x;\omega )$ has invertible leading coefficient. This implies, in particular, that $P(x;\omega )$ has kn finite eigenvalues that we denote by $\lambda _1(P(x;\omega )),\dots ,\lambda _{kn}(P(x;\omega ))$.

Definition 2.4

Let $P(x;\omega )$ be a random matrix polynomial of size n and degree k, such that its leading coefficient is invertible for all $\omega \in \Omega$. Its empirical spectral distribution (ESD) is a random variable with values in the space of probabilities on $\mathbb {C}$, defined as

$$\begin{aligned} \mu _P(\omega ) := \mu _{P(x;\omega )} =\frac{1}{kn} \sum _{i=1}^{kn} \delta _{\lambda _i(P(x;\omega ))}. \end{aligned}$$

It is immediate by Definitions 2.3 and 2.4 that the ESD of a random matrix polynomial coincides with the ESD of its (random) companion matrix (3). Indeed, in this paper we will strongly rely on its equivalence.

2.3.2 The Replacement Principle and the Circle Law

Central to our arguments to derive the empirical spectral distributions is the so-called replacement principle: a tool in random matrix theory developed by Tao, Vu and Krishnapur. We recall it below.

Theorem 2.5

(Replacement Principle [18]) Let $A_m, B_m$ be two $m \times m$ random matrices. Assume that

• 1. The quantity $\frac{1}{m^2} \left( \Vert A_m \Vert _F^2 + \Vert B_m\Vert ^2_F \right)$ is bounded a.s.;

• 2. For a.e. $z \in \mathbb {C}$,

  $$\begin{aligned} \frac{1}{m} \log \left| \frac{\det ( m^{-1/2}A_m - z I ) }{\det ( m^{-1/2}B_m - z I )} \right| \xrightarrow {a.s} 0. \end{aligned}$$

  Then, $\mu _{\frac{1}{\sqrt{m}}A_m} - \mu _{\frac{1}{\sqrt{m}}B_m} \xrightarrow {a.s.} 0$.

Remark 2.6

The random variable $\mu _{\frac{1}{\sqrt{m}}A_m} - \mu _{\frac{1}{\sqrt{m}}B_m}$ takes values in the space of signed measures on $\mathbb C$ with total variation bounded by 2.

Thanks to the replacement principle, we will be able to generalize a well-known result on random Gaussian matrices to the case of monic Gaussian matrix polynomials.

Theorem 2.7

(Strong Circle Law [13]) Let $A_m$ be the ${m\times m}$ random matrix whose entries are iid Gaussian random variables with mean 0 and variance 1. Then, the ESDs of $\frac{1}{\sqrt{m}} A_m$ converge almost surely to the uniform distribution on the unit disc.

3 Empirical Spectral Distribution for $n \times n$ Monic Complex Gaussian Matrix Polynomials of Degree k, in the Limit $n \rightarrow \infty$

Let X be a complex random variable, normally distributed with mean 0 and variance 1. We consider the $n \times n$ monic matrix polynomial of degree $k \ge 2$

$$\begin{aligned} P_n(x) = I_n x^k + \sum _{j=0}^{k-1} C_j x^j, \end{aligned}$$

(4)

where, for $j=0,\dots ,k-1$ every coefficient $C_j$ is an $n \times n$ random matrix whose entries are i.i.d. copies of X. Note that each $C_j$ depends on j and on n, but we omit the dependence on n in the notation. It is intended moreover that all $C_j$ are independent of each other for varying j and n.

The finite eigenvalues of $P_n(x)$ coincide with the eigenvalues of its companion matrix: in particular, substituting $C_k=I_n$ in (3), we obtain

$$\begin{aligned} M:=\begin{bmatrix} -C_{k-1} &{} \dots &{} -C_1 &{} -C_0\\ I_n &{} &{} &{} \\ &{} \ddots &{} &{} \\ &{} &{} I_n &{} \end{bmatrix} =: Z + E_1 C^T \end{aligned}$$

(5)

where $E_1^T = \begin{bmatrix} I_n&0&\dots&0 \end{bmatrix}$ and $C^T = -\begin{bmatrix} C_{k-1}&\dots&C_1&C_0 \end{bmatrix}$. Note that the spectrum of the matrix $E_1 C^T$ consists of the eigenvalues of the random matrix $-C_{k-1}$, with the addition of the eigenvalue 0, which appears with algebraic multiplicity $n(k-1)$. As $C_{k-1}$ is a Gaussian random matrix, the almost sure limit ESD of $n^{-1/2} C_{k-1}$ follows the circular law (Theorem 2.7), i.e., is distributed with the uniform measure on the unit disc. Hence, the ESD of $n^{-1/2} E_1 C^T$ converges almost surely, in the limit $n \rightarrow \infty$, to $\frac{k-1}{k} \mathbf{1}_0 + \frac{1}{k} \mathbf{1}_D$, where $\mathbf{1}_0$, $\mathbf{1}_D$ denote the uniform probability measures on, respectively, the set $\{ 0 \}$ and the unit disc. Since $n^{-1/2}M$ is a perturbation of $n^{-1/2} E_1 C^T$, one can expect that the almost sure limit ESD of $n^{-1/2}M$ and thus the almost sure limit ESD of $P_n(n^{1/2}x)$ coincide with the limit ESD for $n^{-1/2} E_1 C^T$.

Fig. 1

Scatter plots of the eigenvalues of $P_n(x)$ for growing n, multiplied by $\frac{1}{\sqrt{n}}$

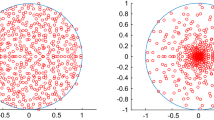
This conjecture is also empirically confirmed by the experiments. For example, in Fig. 1, we plotted the complex eigenvalues, multiplied by $n^{-1/2}$, of N realization of the polynomial $P_n(x)$ for different values of the triple (k, n, N) under the constraint $knN=c$ for some positive integer c (so that the number of the eigenvalues plotted is the same in every image). We display several subfigures organized as a matrix: the degree of the polynomial is constant on each row (namely $k=6$ for the first row and $k=4$ for the second row), while the columns are characterized by different values of n, increasing from left to right. To facilitate the visual comparison with the above claim, we also superimpose the unit circle on each image.

We prove the claim as Theorem 3.1. Its proof relies on several technical lemmata on the behavior of the singular values of certain matrices: in order to improve the readability of the paper, these are collected in “Appendixes A.2 and A.3.” Since, for $k=1$, we recover the well-known limit distribution of the eigenvalues of a Gaussian random matrix, within the proof we tacitly assume that $k \ge 2$.

Theorem 3.1

Let $P_n(x)$ be a monic $n \times n$ complex random matrix polynomial of degree k as in (4), where the entries of each coefficient $C_j$ are i.i.d. complex random variables normally distributed with mean 0 and variance 1. Then, for $n \rightarrow \infty$, the empirical spectral distribution of $P_n(n^{1/2}x)$ converges almost surely to

$$\begin{aligned} \frac{k-1}{k} \mathbf{1}_0 + \frac{1}{k} \mathbf{1}_D, \end{aligned}$$

where $\mathbf{1}_0$, $\mathbf{1}_D$ denote the uniform probability measures on, respectively, the set $\{ 0 \}$ and the unit disc.

Proof

The strategy of the proof is to apply the Replacement Principle (Theorem 2.5) in the special case where $m=kn$, $A_m = M$ and $B_m = E_1 C^T$, where $M,E_1,C$ are the matrices defined in (5) and immediately below. Indeed, by the observations above, this immediately implies the statement. Thus, we need to verify that the two assumptions of Theorem 2.5 hold.

• 1. Consider the random variable

  $$\begin{aligned}R_n = \frac{1}{k^2 n^2} \sum _{i=1}^{2kn^2} |X_i|^2, \end{aligned}$$

  where $X_i$ are i.i.d. normally distributed complex random variables with mean 0 and variance 1. The $X_i$ depend also on n, and it is intended that all $X_i$ are i.i.d. for varying i and n. Since $\frac{1}{m^2} \left( \Vert A_m \Vert _F^2 + \Vert B_m \Vert _F^2 \right)$ has the same distribution as $R_n + \frac{k-1}{k^2n}$, it suffices to prove that $R_n$ is bounded almost surely. This is tantamount to $\mathbb {P}( \limsup _n R_n < \infty ) =1$. On the other hand, by the strong law of large numbers,

  

  it follows that $\mathbb {P}\left( \limsup _n R_n < \infty \right) \ge \mathbb {P}\left( \limsup _n R_n = \frac{2}{k}\right) =1 .$

• 2. Fix a nonzero complex number $w \ne 0$. We need to verify that, for almost every w,

  $$\begin{aligned} \frac{1}{kn} \left( \log \left| \det \left( \frac{1}{\sqrt{kn}} E_1 C^T - wI \right) \right| - \log \left| \det \left( \frac{1}{\sqrt{kn}} M - wI \right) \right| \right) \xrightarrow {a.s.} 0. \end{aligned}$$

  Defining $z:=w \sqrt{k}$, we readily see that this is equivalent to showing

  $$\begin{aligned} \frac{1}{n} \sum _{i=1}^{kn} \left[ \log \sigma _i \left( \frac{1}{\sqrt{n}} E_1 C^T - z I \right) - \log \sigma _i \left( \frac{1}{\sqrt{n}} M - z I \right) \right] \xrightarrow {a.s.} 0 \end{aligned}$$

  (6)

  for every $z\ne 0$. Now let $0<\delta <1/2$ and set $f(n):=\lfloor kn-n^{1-\delta } \rfloor$. Observe that, for any n large enough, $kn> f(n) > kn-n$. Rather than verifying (6) directly, we will prove a somewhat stronger statement. Indeed, we claim that the following three facts all hold:

  $$\begin{aligned}&\frac{1}{n} \sum _{i=f(n)+1}^{kn} \log \sigma _i \left( \frac{1}{\sqrt{n}} M - z I \right) \xrightarrow {a.s.} 0. \end{aligned}$$

  (7)
  $$\begin{aligned}&\frac{1}{n} \sum _{i=f(n)+1}^{kn} \log \sigma _i \left( \frac{1}{\sqrt{n}} E_1 C^T - z I \right) \xrightarrow {a.s.} 0. \end{aligned}$$

  (8)
  $$\begin{aligned}&\frac{1}{n} \sum _{i=1}^{f(n)} \left[ \log \sigma _i \left( \frac{1}{\sqrt{n}} E_1 C^T - z I \right) - \log \sigma _i \left( \frac{1}{\sqrt{n}} M - z I \right) \right] \xrightarrow {a.s.} 0. \end{aligned}$$

  (9)

  It is clear that (7), (8) and (9), together, imply (6). It now remains to prove each statement separately.

  • Proof of (7). By Lemma A.6 and Lemma A.8, almost surely, for all n sufficiently large, the following is true:

    $$\begin{aligned} \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right)&\ge \sum _{i=f(n)+1}^{kn}\log ( n^{-a-2})\\&\ge (n^{1-\delta }+1)(-a-2) \log (n),\\ \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right)&\le \sum _{i=f(n)+1}^{kn}\log (d) \le (n^{1-\delta }+1)\log (d), \end{aligned}$$

    where a and d are the positive constants appearing in Lemma A.6 and Lemma A.8, and d can be chosen greater than 1. Hence, dividing by n,

    $$\begin{aligned} (n^{-\delta } + n^{-1}) (-a-2) \log (n)&\le \frac{1}{n} \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) \nonumber \\&\le (n^{-\delta } + n^{-1}) \log (d). \end{aligned}$$

    (10)

    Thus, (7) follows by the sandwich rule.

  • Proof of (8). By Lemma A.7 and Lemma A.8, there are positive constants $\widetilde{a}$ and $d>1$ such that almost surely, for all n sufficiently large,

    $$\begin{aligned} \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} E_1C^T -zI \right)&\ge \sum _{i=f(n)+1}^{kn}\log ( n^{-\widetilde{a}-2})\ge (n^{1-\delta }+1)\\&(-\widetilde{a}-2) \log (n),\\ \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} E_1C^T -zI \right)&\le \sum _{i=f(n)+1}^{kn}\log (d) \le (n^{1-\delta }+1)\log (d). \end{aligned}$$

    The latter inequalities imply

    $$\begin{aligned} (n^{-\delta } + n^{-1}) (-\widetilde{a}-2) \log (n)\le & {} \frac{1}{n} \sum _{i=f(n)+1}^{kn}\log \sigma _i\left( \frac{1}{\sqrt{n}} E_1C^T -zI \right) \nonumber \\\le & {} (n^{-\delta } + n^{-1}) \log (d). \end{aligned}$$

    (11)

    yielding in turn (8) via the sandwich rule.

  • Proof of (9). We start by the algebraic manipulation

    $$\begin{aligned}&\frac{1}{n} \sum _{i=1}^{f(n)} \left[ \log \sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) - \log \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) \right] \\&\quad = -\frac{1}{n} \sum _{i=1}^{f(n)} \left[ \log \frac{\sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) }{\sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right] . \end{aligned}$$

    Thanks to Mirsky’s Theorem (Theorem2.2), we know that, for every i,

    $$\begin{aligned} \left| \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) - \sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) \right| \le \frac{1}{\sqrt{n}}\Vert M - E_1 C^T\Vert = \frac{1}{\sqrt{n}} \end{aligned}$$

    so, for $i=1,\dots ,f(n)$ there exist $d_i$ satisfying $|d_i| \le \frac{1}{\sqrt{n}}$ and such that

    $$\begin{aligned} \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) = \sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) +d_i. \end{aligned}$$

    Thus,

    $$\begin{aligned}&\left| \frac{1}{n} \sum _{i=1}^{f(n)} \left[ \log \sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) - \log \sigma _i\left( \frac{1}{\sqrt{n}} M -zI \right) \right] \right| \le \frac{1}{n} \sum _{i=1}^{f(n)} \nonumber \\&\quad \left| \log \left( 1 + \frac{d_i}{\sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right) \right| \end{aligned}$$

    (12)

    Observe now that, using Lemma A.9, we have that, for some positive constants $t,\varepsilon$, almost surely, for all n sufficiently large and for every $i\le f(n)$,

    $$\begin{aligned} |x| := \left| \frac{d_i}{\sigma _i(n^{-1/2}E_1 C^T-zI)}\right| \le \left| \frac{n^{-1/2}}{\sigma _{f(n)}(n^{-1/2}E_1 C^T-zI)}\right| \le t^{-1}n^{-\varepsilon } . \end{aligned}$$

    For sufficiently large n (i.e., $n > t^{-1/\varepsilon }$), the right-hand side of the latter inequality is bounded above by 1. Noting that $|x| < 1 \Leftrightarrow |\log (1+x)| \le - \log (1-|x|)$, we obtain the following upper bound for the right-hand side of (12):

    $$\begin{aligned}&0\le - \frac{1}{n} \sum _{i=1}^{f(n)} \log \left( 1 - \frac{|d_i|}{\sigma _i\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right) \le - \frac{f(n)}{n} \\&\quad \log \left( 1 - \frac{n^{-1/2}}{\sigma _{f(n)}\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right) \end{aligned}$$

    which in turn is bounded above by

    $$\begin{aligned}- k \log \left( 1 - \frac{n^{-1/2}}{\sigma _{f(n)}\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right) . \end{aligned}$$

    Invoking again Lemma A.9, we have that almost surely

    $$\begin{aligned}&0\le \frac{n^{-1/2}}{\sigma _{f(n)}\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \le t^{-1}n^{-\varepsilon }\rightarrow 0 \\&\implies - k \log \left( 1 - \frac{n^{-1/2}}{\sigma _{f(n)}\left( \frac{1}{\sqrt{n}} E_1 C^T -zI \right) } \right) \xrightarrow {a.s.} 0, \end{aligned}$$

    and this concludes the proof.

$\square$

Remark 3.2

The relations (7) and (8) still hold if the entries of $C_i$ are i.i.d. copies of any centered random variable with unit variance, using slight variations in the reported results.

4 Empirical Spectral Distribution for $n \times n$ Monic Complex Gaussian Matrix Polynomials of Degree k in the Limit $k \rightarrow \infty$

Consider again¹ the monic matrix polynomial

$$\begin{aligned} P_k(x) = I_n x^k + \sum _{j=0}^{k-1} C_j x^j, \end{aligned}$$

(13)

so that for all $j=0,\dots ,k-1$ every coefficient $C_j$ is a $n\times n$ random matrix where all the entries are i.i.d. Gaussian complex random variables with mean zero and variance 1. Note that each $C_j$ depends on j and on k, but we omit the dependence on k in the notation. It is intended, moreover, that all $C_j$ are independent of each other for varying j and k.

The finite eigenvalues of $P_k(x)$ coincide with those of its companion matrix M as in (5). However, this time we decompose M as the sum of a deterministic circulant matrix and a random matrix with rank at most n

$$\begin{aligned}&M= B + A,\qquad B = \begin{bmatrix} &{} &{} &{} I_n\\ I_n &{} &{} &{} \\ &{} \ddots &{} &{} \\ &{} &{} I_n &{} \end{bmatrix},\qquad A = \begin{bmatrix} -C_{k-1} &{} \dots &{} -C_1 &{} -(C_0+I_n)\\ &{} &{} &{} \\ &{} &{} &{} \\ &{} &{} &{} \end{bmatrix} \nonumber \\&\quad = E_1 \widehat{C}^T, \end{aligned}$$

(14)

where $\widehat{C}^T = C^T - e_k^T\otimes I_n$, $E_1^T = \begin{bmatrix} I_n&0&\dots&0 \end{bmatrix}$ and $C^T = -\begin{bmatrix} C_{k-1}&\dots&C_1&C_0 \end{bmatrix}$. In particular, B is a circulant matrix [7], with spectrum

$$\begin{aligned} \Lambda (B) = { \exp ( 2\pi ij/k ) | j=0,1,\dots ,k-1 } \end{aligned}$$

where each eigenvalue has multiplicity n. It is thus easy to see that the almost sure limit ESD of B is the uniform (singular) probability measure on the unit circle $\mathbf{1}_U$. The problem can be seen through the lens of the theory of perturbations for Toeplitz matrices and sequences (see, for example, [3, 22]), but since the perturbation $E_1{\hat{C}}^T$ is a rank n correction to the Teoplitz matrix B, this case does not fall in the classical settings, where it is required that the random perturbation is not singular with high probability. Since the rank of the perturbation is small when compared with the growing size kn of the matrices, we may anyway expect that the ESD of M also converge almost surely to the same distribution $\mathbf{1}_U$.

This claim is also empirically supported by the experiments. For example, in Fig. 2 we plot the complex eigenvalues of N realization of the polynomial $P_k(x)$ for different values of the triple (k, n, N). The interpretation of Fig. 2 is the same as Fig. 1 after swapping the roles of the matrix sizes and the degrees: we fix n on each row (to 6 and 4, respectively) and we increase the degree of the polynomial on the columns. The unit circle is drawn on top of each scatter plot to make easier the comparison with the claim above; N is always chosen so that the number of eigenvalues plotted, equal to knN, is the same in every image.

Fig. 2

Scatter plots of the eigenvalues of $P_k(x)$ for growing k

In Theorem 3.1, we thus show that the ESD of M also converges almost surely to $\mathbf{1}_U$. Note that the statement includes, as a special case when $n=1$, the well-known limit distribution of random scalar polynomials, for which we thus provide a novel proof. For the sake of a clearer exposition, below we focus on the major lines of thought that lead to the proof, postponing to “Appendix A.4” a more detailed analysis of some technicalities that appear as intermediate steps.

Theorem 4.1

Let $P_k(x)$ be a monic $n \times n$ complex random matrix polynomial of degree k as in (4), where the entries of each coefficient $C_j$ are i.i.d. complex random variables normally distributed with mean 0 and variance 1. Then, for $k \rightarrow \infty$, the empirical spectral distribution of $P_k(x)$ converges almost surely to $\mathbf{1}_U$, the uniform probability measure on the unit circumference.

Proof

The strategy of the proof follows very closely that of Theorem 3.1: we verify that the two assumptions of Theorem 2.5 hold in the special case where $m=kn$, $A_m = \sqrt{kn} \ M$ and $B_m =\sqrt{kn} \ B$, where M, B are the matrices defined in (14) and immediately below.

• 1. The first item is treated analogously to Theorem 3.1, and we omit the details.

• 2. Fix a nonzero complex number z such that $|z|\not \in {0,1}$. We show that, for every such z,

  $$\begin{aligned} \frac{1}{kn} \left( \log \left| \det \left( M - zI \right) \right| - \log \left| \det \left( B - zI \right) \right| \right) \xrightarrow {a.s.} 0, \end{aligned}$$

  that is equivalent to

  $$\begin{aligned} \frac{1}{k} \sum _{i=1}^{kn} \log ( \sigma _i\left( M -zI \right) ) - \log (\sigma _i\left( B -zI \right) ) \xrightarrow {a.s.} 0. \end{aligned}$$

  (15)

  We claim that the following facts are true:

  $$\begin{aligned}&\frac{1}{k} \sum _{i=1}^{n}\log ( \sigma _i\left( M -zI \right) ) \xrightarrow {a.s.} 0, \qquad \frac{1}{k} \sum _{i=kn -n+1}^{kn}\log ( \sigma _i\left( M -zI \right) ) \xrightarrow {a.s.} 0. \end{aligned}$$

  (16)
  $$\begin{aligned}&\frac{1}{k} \sum _{i=1}^{n}\log ( \sigma _i\left( B -zI \right) ) \xrightarrow {a.s.} 0, \qquad \frac{1}{k} \sum _{i=kn -n+1}^{kn}\log ( \sigma _i\left( B -zI \right) ) \xrightarrow {a.s.} 0. \end{aligned}$$

  (17)
  $$\begin{aligned}&\frac{1}{k} \sum _{i=n+1}^{kn -n} \log ( \sigma _i\left( M -zI \right) ) - \log (\sigma _i\left( B -zI \right) ) \xrightarrow {a.s.} 0. \end{aligned}$$

  (18)

  It is clear that (16), (17) and (18), together, imply (15). It now remains to prove each statement separately.

  • Proof of (16). By Lemma A.10, almost surely, for all k sufficiently large, the following are true almost surely for some positive constant r:

    $$\begin{aligned} \sigma _{1}(M-zI) \le r\sqrt{k} + 1 + |z|, \qquad \sigma _n(M-zI)\ge |1-|z||. \end{aligned}$$

    These facts are enough to conclude that

    $$\begin{aligned} \frac{1}{k}\sum _{i=1}^{n}|\log ( \sigma _i\left( M -zI \right) )| \le \frac{n}{k} \max \left\{ |\log (r\sqrt{k} + 1 + |z|)|, |\log ( |1-|z|| )| \right\} \xrightarrow {a.s.} 0 \end{aligned}$$

    and thus the first a.s. limit in (16) holds. Moreover, by Lemma A.11, almost surely, for all k sufficiently large,

    $$\begin{aligned} \sigma _{kn} \left( M - z I \right) \ge tk^{-2} \end{aligned}$$

    for some positive constant t. Hence, it suffices to estimate

    $$\begin{aligned}&\frac{1}{k} \sum _{i=kn -n+1}^{kn}|\log ( \sigma _i\left( M -zI \right) ) | \le \frac{n}{k}\max \{ |\log (\sigma _1(M -zI))|,\\&|\log (\sigma _{kn}(M -zI))| \} \le \frac{n}{k}\max \{ |\log ( r\sqrt{k} + 1 + |z|)|, |\log (tk^{-2})| \}\xrightarrow {a.s.} 0. \end{aligned}$$

    Thus, the second part of (16) also holds.

  • Proof of (17). Observe that $B-zI$ is a circulant matrix, and hence, in particular it is normal. Its spectrum is

    $$\begin{aligned} \Lambda (B-zI) = { \lambda - z | \lambda \in \Lambda (B)}. \end{aligned}$$

    Since all eigenvalues of B have unitary norm, we can bound the singular values of $B-zI$ as

    $$\begin{aligned} \sigma _i(B-zI) = |\lambda _i - z|, \qquad | 1 - |z|| \le |\lambda _i - z| \le 1 + |z|. \end{aligned}$$

    (19)

    Importantly, these bounds do not depend on k. As a consequence,

    $$\begin{aligned}&\frac{n\log (| 1 - |z|| )}{k} \le \frac{1}{k} \sum _{i=kn -n+1}^{kn}\log ( \sigma _i\left( B -zI \right) ) \le \frac{n\log (1 + |z|)}{k}, \\&\frac{n\log (| 1 - |z|| )}{k} \le \frac{1}{k} \sum _{i=1}^{n}\log ( \sigma _i\left( M -zI \right) ) \le \frac{n\log (1 + |z|)}{k}, \end{aligned}$$

    and (17) follows by the sandwich rule.

  • Proof of (18). We start by noting that the statement is implied by

    $$\begin{aligned} \frac{1}{k} \sum _{i=n+1}^{kn -n} \left| \log \left( \frac{\sigma _i\left( M -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| \xrightarrow {a.s.} 0. \end{aligned}$$

    Assume now that $k>2$. Observe that $M-zI$ is a perturbation of rank at most n of $B-zI$. As a consequence, by Theorem 2.1, we find that

    $$\begin{aligned} \sigma _{i+n}(B-zI)\le \sigma _i(M-zI) \le \sigma _{i-n}(B-zI) \end{aligned}$$

    (20)

    for every $n<i\le nk-n$. Thus,

    $$\begin{aligned} \frac{1}{k} \sum _{i=n+1}^{kn -n} \left| \log \left( \frac{\sigma _i\left( M -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| \le&\frac{1}{k} \sum _{i=n+1}^{kn -n} \max \left\{ \left| \log \left( \frac{\sigma _{i-n}\left( B -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| , \right. \\&\left. \left| \log \left( \frac{\sigma _{i+n}\left( B -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| \right\} \end{aligned}$$

    The singular values of $B-zI$ are the moduli of $\lambda _i-z$ where $\lambda _i$ are the eigenvalues of B. For the rest of this argument, and for the sake of notational simplicity, let us now drop the dependence on the argument matrix and simply refer to the rth singular value of $B-zI$ as $\sigma _r$. Since all the eigenvalues of B have multiplicity n, then $\sigma _{i-n}= |\lambda _j -z|$, $\sigma _{i} = |\lambda _i -z|$ and $\sigma _{i+n} = |\lambda _s -z|$, where necessarily i, j, s are pairwise distinct; specifically, j and s are determined by z coherently with the decreasing ordering of the singular values. We conclude that $\sigma _{i} - \sigma _{i+n}$ and $\sigma _{i-n} - \sigma _{i}$ are both bounded above by

    $$\begin{aligned}&\min _{j \ne s \ne i \ne j} \max \{ ||\lambda _i -z| - |\lambda _j -z||, ||\lambda _i -z| - |\lambda _s -z|| \} \le \min _{j \ne s \ne i \ne j}\\&\quad \max \{ |\lambda _i -\lambda _j|, |\lambda _i -\lambda _s | . \} \end{aligned}$$

    In particular, as $k>2$, we can choose

    $$\begin{aligned} \lambda _j = \lambda _i \exp (2\pi \text {i}/k),\qquad \lambda _s = \lambda _i \exp (-2\pi \text {i}/k), \end{aligned}$$

    and hence,

    $$\begin{aligned} \min _{j \ne s \ne i \ne j} \max \{ |\lambda _i -\lambda _j|, |\lambda _i -\lambda _s | \} \le |1-\exp (2\pi \text {i}/k)| = 2\sin (\pi /k). \end{aligned}$$

    Therefore, for all values of k large enough so that $0<2\sin (\pi /k)<|1-|z||$, we use (19) to obtain

    $$\begin{aligned}&\left| \log \left( \frac{\sigma _{i+n}}{\sigma _i} \right) \right| = - \log \left( 1 - \frac{\sigma _i -\sigma _{i+n}}{\sigma _i}\right) \le - \log \left( 1 - 2\frac{\sin (\pi /k)}{|1-|z||}\right) , \\&\left| \log \left( \frac{\sigma _{i-n}}{\sigma _i} \right) \right| = \log \left( 1+ \frac{\sigma _{i-n} -\sigma _{i}}{\sigma _i} \right) \le \log \left( 1 + 2\frac{\sin (\pi /k)}{|1-|z||}\right) . \end{aligned}$$

    and, since $0<x<1 \implies -\log (1-x) > \log (1+x)$, we conclude that

    $$\begin{aligned}&\frac{1}{k} \sum _{i=n+1}^{kn -n} \max \left\{ \left| \log \left( \frac{\sigma _{i-n}\left( B -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| , \left| \log \left( \frac{\sigma _{i+n}\left( B -zI \right) }{\sigma _i\left( B -zI \right) } \right) \right| \right\} \\&\quad \le -\frac{kn-2n}{k} \log \left( 1 - 2\frac{\sin (\pi /k)}{|1-|z||}\right) \end{aligned}$$

    that goes to zero as $k\rightarrow \infty$, implying (18).

$\square$

5 Conclusions

We have rigorously obtained the limit of empirical spectral distribution for monic complex i.i.d. Gaussian matrix polynomials. To our knowledge, and in spite of the relatively common use of random matrix polynomials in the context of numerical experiments to test algorithms for the polynomial eigenvalue problem, the study in the present paper is the first attempt to study analytically the distribution of eigenvalues of a class of random matrix polynomials.

We hope that this work may open the path to further future research on eigenvalues of random matrix polynomials. In particular, we believe that it would be of interest to extend our results by considering, for instance, different ways to send $k,n \rightarrow \infty$, non-monic polynomials, coefficients restricted to be real (and/or otherwise structured) and more general distributions of the entries.

In a forthcoming document, the authors will show further progress about proving the convergence of non-monic non-Gaussian polynomial empirical spectral distribution in both cases $n,k\rightarrow \infty$.

Appendix: Technical Results

In this appendix, we provide the full details on some technical steps that are necessary for our analysis. For convenience, we have split the appendix into various subsections, according to the specific nature of the results contained therein.

1.1 Preliminaries and Known Results

A result we frequently use in our arguments is the following interlacing property of the singular values of submatrices.

Theorem A.1

(Interlacing Singular Values for Submatrices [19]) Given any matrix A and any $p\times q$ submatrix B,

$$\begin{aligned} \Vert A\Vert \ge \Vert B\Vert , \qquad \sigma _{\min (p,q)}(A) \ge \sigma _{\min } (B). \end{aligned}$$

Moreover, we recall the useful Woodbury identity.

Lemma A.2

(Woodbury [23]) Let A, B, U, V be complex matrices satisfying $B = A + UV$ with A, B square. If A and $I + VA^{-1}U$ are both invertible, then

$$\begin{aligned} B^{-1} = A^{-1} - A^{-1}U(I + VA^{-1}U)^{-1}VA^{-1}. \end{aligned}$$

When dealing with sequences of random matrices, one can estimate the distribution of eigenvalues, singular values, or related quantities such as, for instance, trace, determinant, norms. Here we collect some of the estimations we use further on. We do not claim that the bounds we mention below are the best possible ones; yet, they suffice for our purposes.

First, we provide a probabilistic upper bound for the norm of a Gaussian random matrix.

Theorem A.2

( [16]) Suppose that the coefficients of a random matrix N of size ${n\times n}$ are i.i.d. copies of a normal random variable. Then, there exist absolute constants $C,c>0$ such that

$$\begin{aligned} \mathbb P\left( \Vert N\Vert >A\sqrt{n}\right) \le C \exp (-cAn) \end{aligned}$$

for all $A\ge C$.

A very different kind of estimate, due to Tao and Vu, is needed for the least singular value of random matrices having nonzero mean.

Theorem A.3

( [17]) Let c, d be positive constants, and let X be a complex-valued random variable with non-zero finite variance. Then, there are positive constants a and b such that the following holds: if $N_n$ is the $n \times n$ random matrix whose entries are i.i.d. copies of X, and M is an $n \times n$ deterministic matrix with spectral norm at most $n^{c}$, then

$$\begin{aligned} \mathbb P\left( \Vert (M+N_n)^{-1}\Vert \ge n^a \right) \le bn^{-d}. \end{aligned}$$

Note that, in Theorem A.3, we can always choose $d>1$ so that the probability is summable. Thus, we can use Borel–Cantelli lemma to obtain a lower bound for the last singular value valid for all sufficiently large n.

A widely used distribution in the theory of probability for real random variables is the Beta distribution on [0, 1] that depends on two positive parameters $\alpha , \beta$ and it is described by its density function

$$\begin{aligned} Y\sim B(\alpha ,\beta ) \implies \mathbb P \left( Y\le \lambda \right) = \frac{\Gamma (\alpha + \beta )}{\Gamma (\alpha )\Gamma (\beta )} \int _0^\lambda x^{\alpha -1}(1-x)^{\beta -1}\, {\mathrm{d}}x,\quad \forall \, 0\le \lambda \le 1, \end{aligned}$$

where $\Gamma (z) = \int _0^\infty t^{z-1} e^{-t} dt$ is Euler’s gamma function. It is known that if z is a positive integer, then $\Gamma (z) = (z-1)!$.

Consider now a real random vector X with N components, uniformly distributed on the unit sphere $S^{N-1}:=\{ X \in \mathbb {R}^N : \Vert X \Vert _2 =1 \}$. It is known [12, Sec. 4.1.1] that the squared norm of the projection of X onto a k-dimensional space is Beta distributed with parameters $B(k/2,(N-k)/2)$. Note that a complex random vector with N complex components, uniformly distributed on the respective complex spherical surface, can be seen as a real vector with 2N real components and uniformly distributed on $S^{2N-1}$. As a consequence, the squared norm of the projection of such a vector onto a k-dimensional complex space is Beta distributed with parameters $B(k,N-k)$. In particular, if $k=1$, then

$$\begin{aligned} \mathbb P\left( \Vert P_1(X)\Vert ^2\le \lambda \right)= & {} \frac{\Gamma (N)}{\Gamma (1)\Gamma (N-1)} \int _0^\lambda (1-x)^{N-2}\, {\mathrm{d}}x = 1 - (1-\lambda )^{N-1} ,\nonumber \\&\forall \ \lambda \in [0,1]. \end{aligned}$$

(21)

1.2 A Variation on a Result by Bürgisser and Cucker: A Formula for the Tail Bounds of the Norm of the Pseudoinverse of a Non-zero Mean Random Matrix

Theorem A.5 yields a tail bound on the norm of the Moore-Penrose pseudoinverse of a random Gaussian complex rectangular matrix with nonzero mean. It is a modification of the results obtained by Bürgisser and Cucker in [5, Sec. 3] and [6, Ch. 4], with two differences. A minor one is that we work with complex, as opposed to real, numbers and random variables (as noted already in [6], this extension is not at all difficult). A more significant one is that we are interested in the limit case where $\lambda = \frac{n-1}{N} \rightarrow 1$, and we therefore state the result in such a way that it covers that case, unlike [5, 6] that provide formulae for the regime $\lambda <1$. For these reasons, as well as for the sake of self-containedness, we provide a full proof (which still follows very closely the lead of [5, 6]).

Theorem A.5

Let G be an $n \times N$ (with $N \ge n$) complex random matrix with i.i.d. normally distributed entries with mean 0 and variance $n^{-1}$. Suppose $R=R_D + G$ where $R_D \in \mathbb {C}^{n \times N}$ is a deterministic matrix, and let $R^\dagger$ be the Moore–Penrose pseudoinverse of R. Then, given $\tau > 0$,

$$\begin{aligned} \mathbb {P}\left( \sigma _n(R)\le \tau \right) \le \frac{ \tau ^{2(N-n+1)}}{\sqrt{2\pi } } \frac{ (nNe^2)^{N-n+1} }{(N-n+1)^{2(N-n+1) + 1/2} }. \end{aligned}$$

Proof

We know that there exists an unit vector $u \in \mathbb {C}^n$ such that

$$\begin{aligned} \Vert R^\dagger u\Vert = \Vert R^\dagger \Vert \end{aligned}$$

and that, for almost every²R, u is unique up to multiplication by a unit of $\mathbb {C}$. If $v \in \mathbb {C}^n$ is any unit vector, then for some $\beta \in \mathbb {C}$ it can be decomposed as

$$\begin{aligned} v = (u^*v)u +\beta u^\perp \end{aligned}$$

where $u^\perp \in \mathbb {C}^n$ is a unit vector orthogonal to u. On the other hand, since $R^\dagger u$ is orthogonal to $R^\dagger u^\perp$, we have

$$\begin{aligned}&\Vert R^\dagger v\Vert ^2 = | u^*v|^2\Vert R^\dagger u\Vert ^2 + \Vert \beta R^\dagger u^\perp \Vert ^2 \ge |u^*v|^2\Vert R^\dagger \Vert ^2 \\&\implies \Vert R^\dagger v\Vert \ge |u^*v| \Vert R^\dagger \Vert . \end{aligned}$$

Thus, for any $s\in (0,1)$ and $t>0$ we have

$$\begin{aligned} \mathbb {P}_{R,v} \left( \Vert R^\dagger v\Vert \ge t\sqrt{1-s^2} \right) \ge \mathbb {P}_{R,v} \left( |u^*v|\ge \sqrt{1-s^2} \text { and } \Vert R^\dagger \Vert \ge t \right) \end{aligned}$$

or equivalently

$$\begin{aligned} \mathbb {P}_{R,v} \left( \Vert R^\dagger v\Vert \ge t\sqrt{1-s^2} \right) \ge \mathbb {P}_{R} \left( \Vert R^\dagger \Vert \ge t \right) \mathbb {P}_{R,v} \left( |u^*v|\ge \sqrt{1-s^2} \Bigm \vert \Vert R^\dagger \Vert \ge t \right) , \end{aligned}$$

where we choose v uniformly over the unit vectors on $\mathbb C^n$. Observe that, by unitary invariance,

$$\begin{aligned} \mathbb {P}_{R,v} \left( |u^*v|\ge \sqrt{1-s^2} \Bigm \vert \Vert R^\dagger \Vert \ge t \right) = \mathbb {P}_{v} \left( |e_1^*v|\ge \sqrt{1-s^2} \right) = \mathbb {P}_{v} \left( |v_1|\ge \sqrt{1-s^2} \right) . \end{aligned}$$

The vector v can be then seen as a unit real random vector with 2n entries, uniformly distributed on the unit sphere $S_{2n-1}$. From (21),

$$\begin{aligned} \mathbb {P}_{v} \left( |v_1|\ge \sqrt{1-s^2} \right) = (n-1) \int _{1-s^2}^1 (1-x)^{n-2} = (s^2)^{n-1}. \end{aligned}$$

Therefore,

$$\begin{aligned} \mathbb {P}_{R,v} \left( \Vert R^\dagger v\Vert \ge t\sqrt{1-s^2} \right) \ge \mathbb {P}_{R} \left( \Vert R^\dagger \Vert \ge t \right) s^{2n-2} \end{aligned}$$

$$\begin{aligned} \implies \mathbb {P}_{R} \left( \Vert R^\dagger \Vert \ge t \right) \le \mathbb P_{R,v} \left( \Vert R^\dagger v\Vert \ge t\sqrt{1-s^2} \right) s^{2-2n}. \end{aligned}$$

(22)

Note now that

$$\begin{aligned} \mathbb P_{R} \left( \Vert R^\dagger v\Vert \ge t\sqrt{1-s^2} \right) = \mathbb P_{R} \left( \Vert R^\dagger e_1\Vert \ge t\sqrt{1-s^2} \right) \end{aligned}$$

(23)

since any unitary action on R does not change its property to be the sum of a Gaussian matrix with mean 0 and variance $n^{-1} I$, plus a deterministic matrix. Moreover, $w = R^\dagger e_1$ is the first column of $R^\dagger$, and from $RR^\dagger = I$ (which is true with probability 1 since R is almost surely full rank), we know that $w^*$ is orthogonal to all the rows of R but $r^T=e_1^T R$. Furthermore,

$$\begin{aligned} r^T w = 1. \end{aligned}$$

Let $r_\perp$ be the component of r orthogonal to the vector space ${\mathcal {V}}$ generated by the other rows of R. Since $RR^*$ is almost surely invertible, with probability 1 we have $w^* = e_1^T (RR^*)^{-1} R$, so $w^*$ belongs to the row space of R. Since it is also orthogonal to ${\mathcal {V}}$, we conclude that $w^*$ and $r_\perp ^T$ are parallel, and

$$\begin{aligned} 1 = r^Tw = r_\perp ^Tw \implies 1 = \Vert r_\perp \Vert \cdot \Vert w\Vert . \end{aligned}$$

Let $\varphi$ be the density of the random matrix R that can be split into $\varphi = \psi \rho$ where $\psi$ is the density of r and $\rho$ is the density of the rest of the rows, say, $R_1$. We have

$$\begin{aligned} \mathbb {P}_{R} \left( \Vert R^\dagger e_1\Vert \ge p^{-1} \right) = \int _{\Vert w\Vert \ge p^{-1}} \varphi (R) \, {\mathrm{d}}R = \int _{R_1} \rho \int _{\Vert r_\perp \Vert \le p} \psi \, {\mathrm{d}}r\, {\mathrm{d}}R_1 \end{aligned}$$

(24)

Let us focus on the integral over r. Fix $R_1$ as a set of $n-1$ linearly independent (almost surely) vectors, with span ${\mathcal {V}}$. On the other hand, $r_\perp$ is the projection of r over ${\mathcal {V}}^\perp$. If we split $r = r_N + r_D$ where $r_N$(the first row of G) is a random Gaussian vector $N(0,n^{-1}I)$ and $r_D$ (the first row of $R_D$) is a deterministic vector of bounded norm, then we conclude

$$\begin{aligned} UU^*r = r_\perp = UU^*r_N + UU^* r_D. \end{aligned}$$

Here, U is a $N\times N-n+1$ matrix such whose columns are an orthonormal basis of ${\mathcal {V}}^\perp$. We can rewrite $U=QE$ where Q is unitary and $E^T= [I\,\, 0]$, so that

$$\begin{aligned} UU^* = Q \begin{pmatrix} I &{} 0\\ 0 &{} 0 \end{pmatrix} Q^*. \end{aligned}$$

The vector $Q^* r_N$ is still a random Gaussian vector with mean 0 and variance $n^{-1}I$, and hence,

$$\begin{aligned} Q^*r_\perp = \begin{pmatrix} \widetilde{r}_N \\ 0 \end{pmatrix} + \begin{pmatrix} \widetilde{r}_D \\ 0 \end{pmatrix} \end{aligned}$$

where $\widetilde{r}_N$ is a random Gaussian vector, of length $N-n+1$, with mean 0 and variance $n^{-1}$, while $\Vert \widetilde{r}_D\Vert \le \Vert r_D\Vert$. Setting $\widetilde{r}_\perp =\widetilde{r}_N + \widetilde{r}_D$, then

$$\begin{aligned} Q^* r = \begin{pmatrix} \widetilde{r}_\perp \\ * \end{pmatrix} \end{aligned}$$

so

$$\begin{aligned} \int _{\Vert r_\perp \Vert \le p} \psi \, {\mathrm{d}}r = \int _{\Vert \widetilde{r}_\perp \Vert \le p} \widetilde{\psi }\, {\mathrm{d}}\widetilde{r} \end{aligned}$$

(25)

where $\widetilde{\psi }$ is the distribution of $\widetilde{r}_\perp$, and $\widetilde{r}$ is a generic vector of length $N-n+1$. In other words, we are restricting to the first $N-n+1$ coordinates of r, up to a unitary transformation. Now, observe that, from (24) and (25),

$$\begin{aligned}&\mathbb {P}_{R} \left( \Vert R^\dagger e_1\Vert \ge p^{-1} \right) = \int _{R_1} \mathbb {P}_{v\sim {\mathcal {N}}(v_\star ,n^{-1}I)}\left( \Vert v\Vert \le p \right) \, \rho \, {\mathrm{d}}R_1 \nonumber \\&\quad \le \int _{R_1} \mathbb {P}_{v\sim {\mathcal {N}}(0,2I)}\left( \Vert v\Vert ^2 \le 2 np^2 \right) \, \rho \, {\mathrm{d}}R_1 \end{aligned}$$

(26)

where $v_\star$ is a generic complex vector of dimension $N-n+1$ and v is a random complex vector of the same rank. Note further that a complex normally distributed vector v of length $N-n+1$ and variance 2 can be seen as a real normally distributed vector $v_\mathbb {R}$ of length $2(N-n+1)$ and variance 1. Taking this viewpoint, we write

$$\begin{aligned} \mathbb {P}_{v\sim {\mathcal {N}}(0,2I)}\left( \Vert v\Vert \le \sqrt{2 n}p \right)= & {} \mathbb {P}_{v_{\mathbb {R}}\sim {\mathcal {N}}(0,I)}\left( \Vert v_{\mathbb {R}}\Vert \le \sqrt{2 n}p \right) \\= & {} \frac{1}{(2\pi )^{N-n+1}} \int _{\Vert X\Vert \le \sqrt{2 n}p } e^{-\Vert X\Vert ^2/2} \, {\mathrm{d}}X \\\le & {} \frac{1}{(2\pi )^{N-n+1}} \int _{\Vert X\Vert \le \sqrt{2 n}p } 1 \, {\mathrm{d}}X = \frac{ (\sqrt{2 n}p)^{2(N-n+1)} \pi ^{N-n+1} }{(2\pi )^{N-n+1} (N-n+1)! }\\= & {} \frac{( np^2 )^{N-n+1}}{(N-n+1)!}. \end{aligned}$$

Recalling Stirling’s bound

$$\begin{aligned} (N-n+1)! \ge \sqrt{2 \pi (N-n+1)} \left( \frac{N-n+1}{e} \right) ^{N-n+1}, \end{aligned}$$

we get the estimate

$$\begin{aligned} \mathbb {P}_{v\sim N(0,2I)}\left( \Vert v\Vert \le \sqrt{2 n}p \right) \le \frac{1}{\sqrt{2\pi }} \frac{(np^2e)^{N-n+1}}{ (N-n+1)^{N-n+3/2} }. \end{aligned}$$

The latter upper bound does not depend on $R_1$, so plugging it into (26) we obtain

$$\begin{aligned} \mathbb {P}_{R} \left( \Vert R^\dagger e_1\Vert \ge p^{-1} \right)\le & {} \int _{R_1} \frac{1}{\sqrt{2\pi }} \frac{(np^2e)^{N-n+1}}{ (N-n+1)^{N-n+3/2} } \, \rho \, {\mathrm{d}}R_1 \nonumber \\= & {} \frac{1}{\sqrt{2\pi }} \frac{(np^2e)^{N-n+1}}{ (N-n+1)^{N-n+3/2} } \end{aligned}$$

(27)

and, using (22) and (23),

$$\begin{aligned} \mathbb {P}_{R} \left( \Vert R^\dagger \Vert \ge t \right) \le \frac{1}{\sqrt{2\pi }} \frac{\left( \frac{ne}{t^2} \right) ^{N-n+1}}{ (N-n+1)^{N-n+3/2} } \frac{1}{(1-s^2)^{N-n+1}(s^2)^{n-1}} \end{aligned}$$

for every $s\in (0,1)$ and $t>0$. We now sharpen the bound by optimizing in the parameter $s^2$: to this goal, we need to find a maximum over (0, 1) of

$$\begin{aligned} q(Y) = (1-Y)^{N-n+1}Y^{n-1}.\end{aligned}$$

If $n>1$, then a straightforward computation shows that the maximum is achieved at

$$\begin{aligned} Y = \frac{n-1}{N} =: \lambda \in (0,1)\end{aligned}$$

and since

$$\begin{aligned} \lambda ^{-(n-1)} = \lambda ^{-N\lambda } = (\lambda ^{-\frac{\lambda }{1-\lambda }} )^{N(1-\lambda )} \le e^{N(1-\lambda )}, \end{aligned}$$

we have that

$$\begin{aligned} \frac{1}{q(\lambda )} = \frac{1}{(1-\lambda )^{N-n+1}\lambda ^{(n-1)}} \le \frac{e^{N(1-\lambda )}}{(1-\lambda )^{N-n+1}} = \frac{(Ne)^{N-n+1}}{(N-n+1)^{N-n+1}}. \end{aligned}$$

On the other hand, if $n=1$, then $\sup _Y q(Y) = 1$ and

$$\begin{aligned} 1\le e^N = \frac{(Ne)^{N-n+1}}{(N-n+1)^{N-n+1}}. \end{aligned}$$

Thus,

$$\begin{aligned} \mathbb {P}_{R} \left( \Vert R^\dagger \Vert \ge t \right) \le \frac{1}{\sqrt{2\pi } t^{2(N-n+1)} } \frac{\left( ne \right) ^{N-n+1}}{ (N-n+1)^{N-n+3/2} } \frac{(Ne)^{N-n+1}}{(N-n+1)^{N-n+1}}, \end{aligned}$$

and hence, by taking $\tau = t^{-1}$,

$$\begin{aligned} \mathbb {P}\left( \sigma _n(R)\le \tau \right) \le \frac{ \tau ^{2(N-n+1)}}{\sqrt{2\pi } } \frac{ (nNe^2)^{N-n+1} }{ (N-n+1)^{2(N-n+1) + 1/2} }. \end{aligned}$$

This concludes the proof. $\square$

1.3 Estimates on the Singular Values of Certain Random Matrices in Sect. 3

In Lemma A.6, we obtain (in probability) a lower bound for the smallest singular value of the matrix $n^{-1/2}M - zI$, where M is defined in in (5).

Lemma A.6

Let M be the $kn \times kn$ matrix defined as in (5) and $0 \ne z \in \mathbb {C}$. There exist constants $a,b >0$ such that, for every large enough n,

$$\begin{aligned} \mathbb {P}\left( {\sigma _{kn}(n^{-1/2}M - zI)} < n^{-a-2} \right) \le 2bn^{-2} \end{aligned}$$

and in particular, with probability 1,

$$\begin{aligned} {\sigma _{kn}(n^{-1/2}M - zI)} \ge n^{-a-2} \end{aligned}$$

for all large enough n.

Proof

Using the same notation introduced in (5), let us rewrite

$$\begin{aligned} n^{-1/2}M - zI =n^{-1/2}E_1C^T + n^{-1/2}Z - zI \end{aligned}$$

and denote $N:=Z - n^{1/2} z I$. recall that the inverse of the least singular value of an invertible square matrix X is equal to the spectral norm of $X^{-1}$. By Woodbury Lemma (Lemma A.2), we see that

$$\begin{aligned}&(n^{-1/2}E_1C^T + n^{-1/2}Z - zI)^{-1} = n^{1/2} (N + E_1C^T)^{-1} = n^{1/2}\\&\quad \left[ N^{-1} - N^{-1}E_1( I + C^TN^{-1}E_1 )^{-1} C^T N^{-1} \right] \end{aligned}$$

Here we used that $(I + C^TN^{-1}E_1)$ is invertible with probability 1 and that N is invertible since $z\ne 0$. As a consequence

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}M - zI)} \le n^{1/2}\Vert N^{-1}\Vert \left( 1 + \Vert ( I + C^TN^{-1}E_1 )^{-1}\Vert \Vert C^T\Vert \Vert N^{-1}\Vert \right) . \end{aligned}$$

Observe now that $N = Z - n^{1/2}zI$ is a block Toeplitz matrix lower triangular matrix. It follows that its inverse is also a block Toeplitz lower triangular matrix, and it is easily verified that the first block column of $N^{-1}$ is

$$\begin{aligned} N^{-1} = \begin{pmatrix} (\sqrt{n} z)^{-1}I &{} \\ -(\sqrt{n} z)^{-2}I &{} \ddots \\ \vdots &{} \ddots \\ (-1)^{k-1}(\sqrt{n} z)^{-k}I &{} \ddots \end{pmatrix}. \end{aligned}$$

Using $\Vert N^{-1}\Vert \le \sqrt{\Vert N^{-1}\Vert _1\Vert N^{-1}\Vert _{\infty }} =\Vert N^{-1}\Vert _1$ we can bound the norm from above with

$$\begin{aligned} \Vert N^{-1}\Vert&\le \Vert N^{-1}\Vert _1 = \sum _{i=1}^k (\sqrt{n} |z|)^{-i} = (\sqrt{n} |z|)^{-1} \frac{ (\sqrt{n} |z|)^{-k} -1 }{(\sqrt{n} |z|)^{-1} - 1 } = \frac{ 1-(\sqrt{n} |z|)^{-k} }{\sqrt{n} |z| - 1 }\\&\le \frac{2}{\sqrt{n} |z| } \end{aligned}$$

where we are assuming $n \ge 4/|z|^2$. Hence,

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}M - zI)} \le \frac{2}{|z|} \left( 1 + \frac{2}{\sqrt{n} |z| }\Vert ( I + C^TN^{-1}E_1 )^{-1}\Vert \Vert C^T\Vert \right) . \end{aligned}$$

Note that $C^T$ is a $n\times kn$ matrix, and can be seen as a submatrix of a $kn\times kn$ random matrix $\widetilde{C}$ where every entry is an i.i.d copy of a Gaussian complex random variable X. Thanks to an interlacing theorem for singular values (Theorem A.1), we have that $\Vert C^T\Vert \le \Vert \widetilde{C}\Vert$. On the other hand, by Theorem A.2,

$$\begin{aligned} \mathbb {P}(\Vert C^T\Vert> r\sqrt{n}) \le \mathbb {P}(\Vert \widetilde{C}\Vert > r\sqrt{n}) \le s\exp (-crn) \end{aligned}$$

(28)

where $c,s,r>0$ are absolute constants. As a consequence, with high probability (at least $1 - s\exp (-crn)$),

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}M - zI)} \le \frac{2}{|z|} ( 1 + \frac{2r}{ |z| }\Vert ( I + C^TN^{-1}E_1 )^{-1}\Vert ). \end{aligned}$$

(29)

Consider now the matrix

$$\begin{aligned} C^TN^{-1}E_1 = \sum _{i=1}^{k} (-1)^{i} (\sqrt{n} z)^{-i} C_{d-i}. \end{aligned}$$

Clear, each of its entry is a linear combination of i.i.d. Gaussian variables all having mean 0, and this is still a normally distributed variable with mean 0. Moreover, the variance is

$$\begin{aligned} \sum _{i=1}^{k} (\sqrt{n} |z|)^{-2i} = (\sqrt{n} |z|)^{-2}\frac{ (\sqrt{n} |z|)^{-2k} -1 }{(\sqrt{n} |z|)^{-2} - 1 } = \frac{1- (\sqrt{n} |z|)^{-2k} }{(\sqrt{n} |z|)^{2} - 1 } =: \frac{c(n)^2}{n} = \Theta ( \frac{1}{n}). \end{aligned}$$

Hence,

$$\begin{aligned} \Vert ( I + C^TN^{-1}E_1 )^{-1}\Vert ^{-1} = \sigma _{n} (I+ C^TN^{-1}E_1) = \frac{c(n)}{\sqrt{n}} \sigma _{n} \left( I \frac{\sqrt{n}}{c(n)} + G\right) \end{aligned}$$

where now G is a matrix where all entries are i.i.d copies of a complex Gaussian random variable X having mean 0 and variance 1. Since for large values of n, $\Vert I \frac{\sqrt{n}}{c(n)}\Vert \le n$, we can apply Theorem A.3 and conclude that there exist positive constants a, b such that

$$\begin{aligned} \mathbb {P}\left( \sigma _{n}\left( I \frac{\sqrt{n}}{c(n)} + G\right) \le n^{-a} \right) \le bn^{-2} \end{aligned}$$

meaning that, with high probability (at least $1-bn^{-2}$), it holds

$$\begin{aligned} \Vert ( I + C^TN^{-1}E_1 )^{-1}\Vert ^{-1} \ge \frac{c(n)}{\sqrt{n}} n^{-a} \ge n^{-a-1} \end{aligned}$$

(30)

for sufficiently large n. As a consequence, from (29) and (30),

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}M - zI)} \le \frac{2}{|z|} ( 1 + \frac{2r}{ |z| }n^{a+1} ) \end{aligned}$$

and thus

$$\begin{aligned} {\sigma _{kn}(n^{-1/2}M - zI)} \ge \frac{1}{\frac{2}{|z|} ( 1 + \frac{2r}{ |z| }n^{a+1} )} \ge n^{-a-2} \end{aligned}$$

with probability at least

$$\begin{aligned} 1 - bn^{-2} - s\exp (-crn)\ge 1 - 2bn^{-2} \end{aligned}$$

for any large enough values of n. In particular, we can conclude the proof by invoking the Borel–Cantelli lemma. $\square$

Lemma A.7 is the analogue of A.6 when the matrix $E_1C^T$ is considered.

Lemma A.7

Let $E_1$ and $C^T$ be the matrices defined in (5) and immediately after it. There exists a constant $\widetilde{a}>0$ such that, for all large enough n,

$$\begin{aligned} \mathbb {P}\left( {\sigma _{kn}(n^{-1/2}E_1C^T - zI)} < n^{-\widetilde{a}-2} \right) \le 2n^{-2} \end{aligned}$$

and in particular, with probability 1,

$$\begin{aligned} {\sigma _{kn}(n^{-1/2}E_1C^T - zI)} \ge n^{-\widetilde{a}-2} \end{aligned}$$

for all sufficiently large n.

Proof

The proof is very similar to Lemma A.6, so we only sketch it. In this case, set $N := -n^{1/2}zI$ and

$$\begin{aligned} (n^{-1/2}E_1C^T - zI)^{-1} = n^{1/2}\left[ N^{-1} - N^{-1}E_1( I + C^TN^{-1}E_1 )^{-1} C^T N^{-1} \right] \end{aligned}$$

where N is invertible since $z\ne 0$ and $I + C^TN^{-1}E_1$ is almost surely invertible. We have $\Vert N^{-1}\Vert = n^{-1/2}/|z|$, and hence, with probability at least $1 - s\exp (-crn)$,

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}E_1C^T - zI)} \le \frac{1}{|z|} ( 1 + \frac{r}{|z| }\Vert ( I -\frac{1}{n^{1/2}z} C_{k-1} )^{-1}\Vert ). \end{aligned}$$

Again, we write

$$\begin{aligned} \Vert ( I -\frac{1}{n^{1/2}z} C_{k-1} )^{-1}\Vert ^{-1} = \sigma _n (I -\frac{1}{n^{1/2}z} C_{k-1}) = \frac{1}{n^{1/2}|z|} \sigma _n (-n^{1/2}zI + C_{k-1}) \end{aligned}$$

Note that $\Vert -I n^{1/2}z\Vert \le n$ for n big enough, so we can apply Theorem A.3 and find that with high probability (greater than $1-n^{-2}$),

$$\begin{aligned} \sigma _n (-n^{1/2}zI + C_{k-1}) \ge n^{-\widetilde{a}} \end{aligned}$$

so that

$$\begin{aligned} \frac{1}{\sigma _{kn}(n^{-1/2}E_1C^T - zI)} \le \frac{1}{|z|} ( 1 + r n^{\widetilde{a}+1} ) \end{aligned}$$

and

$$\begin{aligned} \sigma _{kn}(n^{-1/2}E_1C^T - zI) \ge \frac{|z|}{ ( 1 + r n^{\widetilde{a}+1} )} \ge n^{-\widetilde{a} - 2}. \end{aligned}$$

By the Borel–Cantelli lemma, the statement follows. $\square$

In Lemma A.8, we control the spectral norms of $M-zI$ and $E_1C^T-zI$.

Lemma A.8

Let $M,E_1,C^T$ be defined as in (5) and immediately after it. There exist constants $r,s>0$ such that for any n large enough,

$$\begin{aligned}&\mathbb {P}\left( \left\| n^{-1/2}E_1 C^T -zI\right\|> r + |z| \right) \le s\exp (-r^2n) \\&\mathbb {P}\left( \left\| n^{-1/2}M -zI\right\| > r + |z| + 1 \right) \le s\exp (-r^2n) \end{aligned}$$

and in particular, there exists $d>0$ such that, with probability 1,

$$\begin{aligned} {\sigma _{1}(n^{-1/2}E_1 C^T -zI)} \le d,\qquad {\sigma _{1}(n^{-1/2}M -zI)} \le d \end{aligned}$$

for any sufficiently large n.

Proof

Note that

$$\begin{aligned}&\left\| n^{-1/2}M -zI\right\| \le \Vert n^{-1/2}E_1 C^T\Vert + |z| + n^{-1/2}, \\&\left\| n^{-1/2}E_1 C^T -zI\right\| \le \Vert n^{-1/2}E_1 C^T\Vert + |z|, \end{aligned}$$

and $\Vert E_1 C^T \Vert = \Vert C^T\Vert$, implying (see proof of Lemma A.6)

$$\begin{aligned} \mathbb {P}(\Vert E_1 C^T\Vert > r\sqrt{n}) \le s\exp (-crn) \end{aligned}$$

where $c,s,r>0$ are absolute constants. The statement follows immediately. $\square$

Lemma A.9, whose proof relies on Theorem A.5, yields a probabilistic lower bound on the f(n)th singular value of $n^{-1/2} E_1 C^T - z I$.

Lemma A.9

Let $0< \delta < 1/2$, $E_1, C^T$ be defined as in (5) and immediately after it (so that $E_1 C^T$ is a $kn \times kn$ matrix with $k>1$), $f(n)=\lfloor kn-n^{1-\delta }\rfloor$, and $0 \ne z \in \mathbb {C}$. Then there exists a positive constant $t \le 1$ and a positive constant $\varepsilon > 0$ such that lower bound

$$\begin{aligned} \sigma _{f(n)} \left( n^{-1/2} E_1 C^T - z I \right) \ge tn^{\varepsilon -1/2} \end{aligned}$$

holds almost surely for all sufficiently large values of n.

Proof

Note first that, denoting by $\widetilde{T}$ the matrix composed by the first f(n) rows of $n^{-1/2}E_1 C^T - zI$, then by the interlacing theorem for singular values (Theorem A.1) we have

$$\begin{aligned} \sigma _{f(n)}(n^{-1/2}E_1 C^T - zI)\ge \sigma _{f(n)}(\widetilde{T}) \end{aligned}$$

so it suffices to study $\widetilde{T}$. To this goal, since $f(n)\ge n$, we partition

$$\begin{aligned} \widetilde{T} = \begin{pmatrix} H -zI &{} L &{} P\\ &{} zI &{} \end{pmatrix} \end{aligned}$$

where H is a $n\times n$ matrix, L is a $n\times ( f(n) - n )$ matrix and P is a $n\times (kn-f(n))$ matrix. Since a permutation of the columns does not change the singular values, we can equivalently study the matrix

$$\begin{aligned} T = \begin{pmatrix} L &{} H-zI &{} P\\ zI &{} &{} \end{pmatrix} = \begin{pmatrix} L &{} R\\ zI &{} \end{pmatrix} \end{aligned}$$

where $R := [H-zI\,\,\, P ]$. T is an $f(n)\times kn$ matrix, and its least singular value $\sigma _{\min }(T)$ satisfies

$$\begin{aligned} \sigma _{\min }(T)^2= & {} \inf _{\Vert v\Vert = 1} \Vert v^* T\Vert ^2 = \inf _{\Vert v\Vert = 1} \Vert v_1^* L + zv_2^*\Vert ^2 + \Vert v_1^*R\Vert ^2 \ge \inf _{\Vert v\Vert = 1} ( \Vert v_1^* L\Vert \\&- \Vert zv_2^*\Vert )^2 + \Vert v_1^*R\Vert ^2, \end{aligned}$$

where $v^* = [v_1^*\, v_2^*]$. There are three possibilities. If $v_2$ is zero, then the minimum is attained as $\sigma _{\min } ( [H-zI\,\, L\,\, P])^2$ and if $v_1$ is zero, then the minimum is simply $|z|^2$. If neither is true, we can minimize the expression over $\Vert v_1\Vert \ne 0,1$. To this goal, denote $y = \Vert v_1\Vert ^2$, so that $1-y= \Vert v_2\Vert ^2$ and define $w_1=: v_1/\sqrt{y}$, $w_2:= v_2/\sqrt{1-y}$. Then

$$\begin{aligned} ( \Vert v_1^* L\Vert - \Vert zv_2^*\Vert )^2 + \Vert v_1^*R\Vert ^2 = ( \sqrt{y}\Vert w_1^* L\Vert - \sqrt{1-y}|z| )^2 + y\Vert w_1^* R\Vert ^2. \end{aligned}$$

Define now $\alpha := \Vert w_1^* L\Vert$, $\beta := |z|$, $\gamma ^2 := \Vert w_1^*R\Vert ^2$, so that we end up with the problem of minimizing the function

$$\begin{aligned} g(y) = ( \sqrt{y}\alpha - \sqrt{1-y}\beta )^2 + y\gamma ^2 = \beta ^2 + y(\gamma ^2+\alpha ^2-\beta ^2) -2\alpha \beta \sqrt{y-y^2}. \end{aligned}$$

To further simplify the notation, it is convenient to introduce $a := \gamma ^2+\alpha ^2-\beta ^2$ and $b:=2\alpha \beta$. This trick yields

$$\begin{aligned} g(y)= & {} \beta ^2 + ya -b\sqrt{y-y^2}; \\ g'(y)= & {} a +b\frac{2y-1}{2\sqrt{y-y^2}}; \\ g''(y)= & {} \frac{b}{4} (y-y^2)^{-3/2} \ge 0. \end{aligned}$$

In particular, the computation of the second derivative shows that g(y) is a convex function, and hence, the roots of its derivative must correspond to minima. If $b>0$, then the minimum is also unique. Observe that by assumption $\beta \ne 0$, so $b=0$ implies $w_1^*L=0$ and $\sigma _{\min }(T)^2$ is surely greater than $|z|^2$ or $\min _{\Vert w_1\Vert =1} \gamma ^2$. Thus, we assume instead $b> 0$ and find a root of the derivative.

$$\begin{aligned} g'(y)= & {} 0\implies b(2y-1) = -2a\sqrt{y-y^2} \implies \mathrm {sign}(a) = \mathrm {sign}(1-2y) \\ b^2(4y^2-4y+1)= & {} 4a^2(y-y^2) \implies 4(a^2+b^2)(y^2-y+\frac{1}{4}) - a^2 = 0 \\&\implies (y-\frac{1}{2})^2 = \frac{a^2}{4(a^2+b^2)} \end{aligned}$$

so the unique root of $g'(y)$ is

$$\begin{aligned} y_\star = \frac{1}{2} -\frac{a}{2\sqrt{a^2+b^2}} \in (0,1). \end{aligned}$$

Moreover,

$$\begin{aligned} g(y_\star )= & {} \beta ^2 +\frac{a}{2} - \frac{a^2}{2\sqrt{a^2+b^2}} - \frac{b^2}{2\sqrt{a^2+b^2}} = |z|^2 +\frac{a-\sqrt{a^2+b^2}}{2} \\= & {} \frac{\gamma ^2+\alpha ^2+|z|^2-\sqrt{(\gamma ^2+\alpha ^2+|z|^2)^2 -4|z|^2\gamma ^2}}{2} \ge \frac{|z|^2}{2} \frac{\gamma ^2}{\gamma ^2+\alpha ^2+|z|^2} \end{aligned}$$

To minimize the last expression, we can maximize the denominator by

$$\begin{aligned} \gamma ^2 + \alpha ^2 = \Vert w_1^* [L\, R]\Vert ^2 \le \Vert [L\, R]\Vert ^2 \le ( \frac{1}{\sqrt{n}} \Vert C^T\Vert + |z| )^2 \end{aligned}$$

which is, with high probability (see (28)), bounded by $(r+|z|)^2$. We can thus say that there exists a constant $t>0$ such that

$$\begin{aligned} \sigma _{\min }(T)^2 \ge \min \{ \min _{\Vert w_1\Vert =1} t^2\gamma ^2, \sigma _{\min } ( [H-zI\,\, L\,\, P])^2, |z|^2 \}. \end{aligned}$$

Yet, $\min _{\Vert w_1\Vert =1} \Vert w_1^*R\Vert = \sigma _{\min }(R)$, and again by the interlacing theorem for singular values (Theorem A.1) $\sigma _{\min } ( [H-zI\,\, L\,\, P]) \ge \sigma _{\min }(R)$. We can therefore conclude that

$$\begin{aligned} \sigma _{f(n)}(n^{-1/2}E_1 C^T - zI)\ge \sigma _{\min }(T) \ge \min \{t\sigma _{\min }(R), |z|\} \end{aligned}$$

(31)

for some absolute constant $0<t\le 1$ with high probability, and almost surely for all n sufficiently large.

Almost surely, R is full rank, and thus, $\sigma _{\min }(R) = \Vert R^\dagger \Vert ^{-1}$. In particular, Theorem A.5 yields the tail bound

$$\begin{aligned} \mathbb {P}_{R} \left( \sigma _n(R)\le \tau \right) \le \left( 2\pi (n^{1-\delta }+1) \right) ^{-1/2} \left( \frac{k^2n^2 \tau ^2 e^2}{ (n^{1-\delta }+1)^2} \right) ^{\lceil n^{1-\delta }\rceil +1}, \end{aligned}$$

where we used that R is a $n\times (kn+n-f(n))$ matrix with both dimension less than kn, and

$$\begin{aligned} n^{1-\delta }+1\le \lceil n^{1-\delta }\rceil +1 = (kn+n-f(n))-n+1 . \end{aligned}$$

Now, fix any $\varepsilon$ such that $0< \varepsilon < 1/2 - \delta$ (as $0<\delta <1/2$, this is surely possible). Choosing $\tau = n^{\varepsilon - 1/2}$, this implies that for n big enough,

$$\begin{aligned} \mathbb {P}_{R} \left( \sigma _n(R)\le n^{\varepsilon - 1/2} \right) \le \frac{1}{\sqrt{ 2\pi }} n^{\delta /2-1/2} \left( \frac{(ke)^2 n^{1+2 \varepsilon }}{ n^{2-2\delta }} \right) ^{ n^{1-\delta }+1}. \end{aligned}$$

Setting $c:=1-2\delta -2\varepsilon > 0$, we conclude that

$$\begin{aligned} \mathbb {P}_{R} \left( \sigma _n(R)\le n^{\varepsilon - 1/2} \right) \le \frac{(ke)^2}{\sqrt{2 \pi }} n^{\delta /2-1/2-c} \left( (ke)^{-2/c} n \right) ^{-c n^{1-\delta }}, \end{aligned}$$

and the right-hand side goes exponentially to zero. We conclude that $\sigma _{\min }(R)$ is at least of the order $n^{\varepsilon -1/2}$ with high probability, and almost surely for sufficiently large n. From (31), we get that for some absolute constant $0<t\le 1$ and some $\varepsilon > 0$ then almost surely, for all n sufficiently large,

$$\begin{aligned} \sigma _{f(n)}(n^{-1/2}E_1 C^T - zI) \ge tn^{\varepsilon -1/2}. \end{aligned}$$

$\square$

1.4 Estimates on the Singular Values of Certain Random Matrices in Sect. 4

In Lemma A.10, we obtain probabilistic bounds for the first n singular values of the matrix $M-zI$, where M is defined in (14).

Lemma A.10

Let M be the $kn \times kn$ matrix defined as in (14) and $z \in \mathbb {C}$ with norm different from 1. There exist constants $r,s,c >0$ such that, for every $k>2$,

$$\begin{aligned} \mathbb {P}\left( \sigma _{1}(M-zI) > r\sqrt{k} + 1 +|z| \right) \le s\exp (-crk), \qquad \sigma _n(M-zI)\ge |1-|z||. \end{aligned}$$

In particular, with probability 1,

$$\begin{aligned} \sigma _{1}(M-zI) \le r\sqrt{k} + 1 + |z|, \qquad \sigma _n(M-zI)\ge |1-|z|| \end{aligned}$$

for all large enough k.

Proof

From the proof of Lemma A.6, by exchanging the roles of k and n, we know that

$$\begin{aligned} \mathbb {P}(\Vert C^T\Vert > r\sqrt{k}) \le s\exp (-crk), \end{aligned}$$

(32)

where r, s, c are absolute positive constants. As a consequence, with high probability,

$$\begin{aligned} \sigma _1(M-zI) \le \Vert C^T\Vert + 1 + |z|\le r\sqrt{k} + 1 + |z|. \end{aligned}$$

Moreover, from (19) and (20), we know that, if $k>2$,

$$\begin{aligned} \sigma _n(M-zI)\ge \sigma _{n+1}(M-zI)\ge \sigma _{2n+1}(B-zI) \ge |1-|z||>0. \end{aligned}$$

$\square$

In Lemma A.11, we obtain a lower bound (valid with probability 1) for the smallest singular value of the matrix $M-zI$, where M is defined in (14).

Lemma A.11

Let M be the $kn \times kn$ matrix defined as in (14) and $z \in \mathbb {C}$ with norm different from 1. There exist a positive constant t such that, with probability 1,

$$\begin{aligned} \sigma _{kn} \left( M - z I \right) \ge tk^{-2} \end{aligned}$$

for all sufficiently large values of k.

Proof

If we use Woodbury Lemma (Lemma A.2) on the splitting $M - zI = (B -zI) + E_1\widehat{C}^T,$ then³

$$\begin{aligned} (M-zI)^{-1} = (B -zI)^{-1} - (B -zI)^{-1}E_1(I + \widehat{C}^T(B -zI)^{-1}E_1)^{-1}\widehat{C}^T(B -zI)^{-1} \end{aligned}$$

and

$$\begin{aligned} \Vert (M-zI)^{-1}\Vert \le \Vert (B-zI)^{-1}\Vert \left[ 1 + \Vert (B-zI)^{-1}\Vert \Vert \widehat{C}^T\Vert \Vert (I + \widehat{C}^T(B -zI)^{-1}E_1)^{-1}\Vert \right] .\nonumber \\ \end{aligned}$$

(33)

$B-zI$ is a circulant matrix, so its inverse is still a circulant matrix and its norm can be estimated with (19) by

$$\begin{aligned} \Vert (B-zI)^{-1}\Vert = \sigma _{kn}(B-zI)^{-1} \le \frac{1}{|1-|z||}. \end{aligned}$$

(34)

More specifically, $(B-zI)^{-1}$ is a block circulant matrix with first block column

$$\begin{aligned} (B-zI)^{-1} = \begin{pmatrix} \frac{z^{k-1}}{1-z^k} I_n &{} \\ \frac{z^{k-2}}{1-z^k} I_n &{} \ddots \\ \vdots &{} \ddots \\ \frac{1}{1-z^k} I_n &{} \ddots \end{pmatrix}. \end{aligned}$$

Consider now the matrix

$$\begin{aligned} I + \widehat{C}^T(B -zI)^{-1}E_1 = \frac{z^k}{z^k-1}I - \sum _{i=1}^k \frac{z^{k-i}}{1-z^k} C_{k-i}. \end{aligned}$$

It consists of the sum of a constant matrix, and a linear combination of i.i.d. Gaussian variables all having mean 0. Such a linear combination is still a normally distributed variable with mean 0 and variance

$$\begin{aligned} \sum _{i=1}^k \left| \frac{z^{k-i}}{1-z^k}\right| ^2 = \frac{1}{|1-z^k|^2}\sum _{i=0}^{k-1} |z|^{2i} = \frac{1}{1-|z|^2} \frac{1-|z|^{2k}}{|1-z^k|^2}:= c(k)^2 \end{aligned}$$

where $c(k) \rightarrow |1-|z|^2|^{-1/2}$ for $k\rightarrow \infty$. We can thus write

$$\begin{aligned} I + \widehat{C}^T(B -zI)^{-1}E_1 = \frac{z^k}{z^k-1}I + c(k)G \end{aligned}$$

where G is a Gaussian random $n\times n$ matrix where each entry has mean zero and unit variance. In Theorem A.5, we proved that for any deterministic matrix S, we have

$$\begin{aligned} \mathbb P \left( \sigma _n(n^{-1/2}G +S)\le t \right) \le \frac{t^2n^2e^2}{\sqrt{2\pi } }, \end{aligned}$$

(35)

so

$$\begin{aligned}&\mathbb P \left( \Vert (I + \widehat{C}^T(B -zI)^{-1}E_1)^{-1}\Vert \ge p \right) = \mathbb P \left( \sigma _n(I + \widehat{C}^T(B -zI)^{-1}E_1 )\le \frac{1}{p} \right) \\&\quad = \mathbb P \left( \sigma _n \left( \frac{z^k}{z^k-1}I + c(k)G \right) \le \frac{1}{p} \right) \\&\quad = \mathbb P \left( \sigma _n \left( \frac{n^{-1/2}z^k}{c(k)(z^k-1)}I + n^{-1/2}G \right) \le (n^{1/2}c(k)p)^{-1} \right) \\&\quad \le \frac{ne^2}{\sqrt{2\pi } c(k)^2p^2 }. \end{aligned}$$

Since $ne^2/\sqrt{2\pi }$ does not depend on k, we can choose $p=k$ and conclude by the Borel–Cantelli lemma that with probability 1 and for any k sufficiently large,

$$\begin{aligned} \Vert (I + \widehat{C}^T(B -zI)^{-1}E_1)^{-1}\Vert < k. \end{aligned}$$

(36)

Finally, from (32), we have that almost surely, for all k sufficiently large,

$$\begin{aligned} \Vert \widehat{C}^T\Vert \le \Vert C^T\Vert + 1 \le 1 + r\sqrt{k} \end{aligned}$$

(37)

for some absolute constant $r>0$. Gathering all the bounds (34), (36), (37) and substituting into (33), we find that

$$\begin{aligned}&\Vert (M-zI)^{-1}\Vert \le \frac{1}{|1-|z||}\left[ 1 + \frac{1}{|1-|z||} (r\sqrt{k} +1)k \right] \\&\qquad \le t^{-1}k^2 \implies \sigma _{kn}(M-zI) \ge tk^{-2} \end{aligned}$$

for sufficiently large k with probability 1, where t is a positive constant depending only on n and z.

$\square$