Abstract
The Natal multimammate mouse (Mastomys natalensis) is the most widespread rodent species in sub-Saharan Africa, often studied as an agricultural pest and reservoir of viruses. Its mitochondrial (Mt) phylogeny revealed six major lineages parapatrically distributed across open habitats of sub-Saharan Africa. In this study we used 1949 sequences of the mitochondrial cytochrome b gene to elaborate on distribution and evolutionary history of three Mt lineages inhabiting the open habitats of the Zambezian region (corresponding roughly to the African savannas south of the Equator). We describe in more detail contact zones between the lineages—their location and extent of co-occurrence within localities—and infer past population trends. The estimates are interpreted in the light of climatic niche models. The lineages underwent reduction in effective population size during the last glacial, but they spread widely after that: two of them after the last glacial maximum and the last one in mid-Holocene. The centers of expansion, i.e., possible long-term savanna refugia, were estimated to lie close to the Eastern Arc Mountains and lakes of the Great African Rift, geomorphological structures likely to have had long-term influence on geographical distribution of the lineages. Environmental niche modeling shows climate could also affect the broad scale distribution of the lineages but is unlikely to explain the narrow width of the contact zones. The intraspecific Mt differentiation of M. natalensis echoes phylogeographic patterns observed in multiple co-distributed mammal species, which suggests the mammal communities in the region are shaped by the same long-term processes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
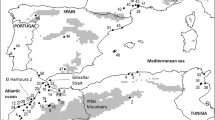
The Natal multimammate mouse (Mastomys natalensis) is the most widespread rodent species in sub-Saharan Africa, with geographical distribution spanning vast areas of Sahelo-Sudanian as well as Zambezian savannas (Fig. 1; Galster et al. 2007; Colangelo et al. 2013; Monadjem et al. 2015). Although also living in natural savanna habitats, it is particularly abundant in agricultural landscapes, where it is considered a significant rodent pest (Makundi et al. 2007; Mulungu et al. 2013). Locally, it even becomes synanthropic (Granjon and Duplantier 1993) and it has been shown to form genetically distinct urban and rural populations (Gryseels et al. 2016). The species is also known to be a reservoir of various mammarenaviruses (Olayemi et al. 2016; Goüy de Bellocq et al. 2020; Cuypers et al. 2020), including the one causing Lassa hemorrhagic fever (Monath et al. 1974). Given its impact on human society, population dynamics of the species have received a lot of attention. Like other Mastomys species, M. natalensis possesses high reproductive capacity with large litter size and short time between successive litters (Duplantier et al. 1996), it has been found promiscuous (Kennis et al. 2008) and lacking any territoriality (Borremans et al. 2014). The highest breeding rates follow one to three months after abundant rains (Leirs et al. 1994) and where the food is abundant, local population outbreaks can occur (Mwanjabe et al. 2002).
Distribution of Mt lineages of Mastomys natalensis across sub-Saharan Africa based on published CYTB sequences (listed in Supplementary material 1). Actual sampling sites were pooled to account for differential sampling effort. The black outline shows the distribution of M. natalensis specified in the IUCN Red List (IUCN 2021)
Colangelo et al. (2013) were first to study the mitochondrial phylogeography of M. natalensis across sub-Saharan Africa. They showed the species includes two major clades labeled A (distributed in the Sudanian region from West Africa to western Kenya) and B (in the Zambezian region, roughly south of the Equator) and they both split into three lineages labeled A1–3 and B4–6. (Instead of Roman numerals used by Colangelo et al. 2013 we use Arabic ones to improve readability of the labels and their automatized processing in databases.) The lineages are basically parapatric but co-occurring locally in the areas of contact (Fig. 1). More specifically, lineage A1 is present in westernmost sub-Saharan Africa from Senegal to the western part of Niger and Nigeria, where it is replaced by lineage A2, which is found from Nigeria to the Democratic Republic of Congo. Lineage A3 is known from the south-western Kenya and south-western Ethiopia. Within B clade, lineage B4 can be found from southern Kenya and Rwanda to central and eastern Tanzania, where it meets at the Eastern Arc Mountains with lineage B5, which is found in south-eastern Tanzania and northern Mozambique. The most widespread lineage, B6, inhabits a large part of Southern Africa—from south-western Tanzania to South Africa and Angola. The contact between lineage B6 and the other two clade B lineages follows the Great Rift Valley along the lakes Malawi, Rukwa and Tanganyika (Fig. 1).
While parapatric mitochondrial lineage ranges might simply be a sign of their stochastic expansion history within a single population under isolation by distance, a survey across the contact zone of Mt lineages B4 and B5 shows abrupt (20 km) changes in not only Mt lineage frequency, but also microsatellite markers on autosomes and a single nucleotide polymorphism (SNP) on the Y chromosome (Gryseels et al. 2017). The switch between these mitochondrial types is therefore marking the position of a multilocus species barrier within the M. natalensis range, a barrier that also appears to apply to rodent-borne viruses: Gairo mammarenavirus is found on the B4 lineage side of the contact zone, Morogoro mammarenavirus on the B5 lineage side, both being present at the center of contact (Gryseels et al. 2017; Cuypers et al. 2020). Given similar genetic distances between each pair of Mt lineages that we consider here (Colangelo et al. 2013; Hánová et al. 2021a) it seems likely each Mt lineage pair’s contact marks its own multilocus barrier.
The high abundance (i.e., availability of samples), wide distribution and phylogeographic structure of the Natal multimammate mouse make it an excellent model for the study of spread and contraction of savanna ecosystems in Pleistocene and adaptation of savanna species to novel conditions of cultivated landscapes and human dwellings. At the same time, it became a promising model for the study of incipient speciation and evolution of pathogen specificity. Building up on the work of Colangelo et al. (2013), the present study uses a much more extensive data set to examine what population processes and ecological factors contributed to the distribution of mitochondrial lineages in the Zambezian region. More specifically, we estimated timing and putative centers of population expansions, which brought the lineages into their current distribution ranges, and examined whether they occupy different climatic niches.
Materials and methods
Sequence data
This work is based on a total of 1949 sequences of mitochondrial cytochrome b (CYTB) gene of M. natalensis, which were taken from published studies, many of them genotyped by the authors of this study (e.g., Gryseels et al. 2016; Hánová et al. 2021a).
Out of those 1949 sequences 1784 were longer than 700 bp, which was our threshold for distinguishing “long” and “short” sequences. The long sequences comprised 659 unique haplotypes. The whole data set is documented in Supplementary material 1, which also cites sources of the published data, and the alignment of all CYTB sequences is provided in Supplementary material 2. All included sequences were georeferenced, originating from 342 distinct sampling sites. Their spatial distribution reflects differential sampling effort in various regions, however. Therefore, sites were pooled so that we worked with a spatial resolution at which their distribution is as even as possible (Fig. 1). This was achieved by successive merging of the nearest sites, each time re-estimating the nearest-neighbor distances and recording their variability as estimated by interquartile range (IQR). If there is a resolution at which the sampling sites collapse to fragments of a regular grid, its IQR is equal to zero. Accordingly, the merger with the minimum IQR was retained. This procedure resulted in 100 pooled sites.
Inference of cytochrome b tree
Delimitation of Mt lineages was based on a tree inferred in MrBayes 3.2.6 (Ronquist et al. 2012). Although 659 unique long haplotypes were present, only 100 were included in the tree to ease Markov Chain Monte Carlo (MCMC) convergence. They were chosen by randomly picking one haplotype per pooled locality. Branch lengths were estimated as unconstrained and thus we also included nine outgroup sequences for post hoc rooting of the trees. They were taken from three other species of Mastomys: M. huberti, M. erythroleucus and M. kollmanspergeri (see Supplementary material 1).
Partitioning of the whole CYTB gene (1140 bp) according to codon position was selected using Bayes factors (BF; Fan et al. 2011), estimated on the 30 most divergent haplotypes. These were selected by a procedure iteratively looking for a pair of the most similar haplotypes and discarding one of its members, until the specified number of haplotypes was left. BFs were calculated as differences of log marginal likelihoods, which were calculated by stepping-stone method (Xie et al. 2011) with 50 steps and alpha = 0.4. The three partitioning schemes considered were 1 + 2 + 3, {1, 2} + 3 and {1, 2, 3}, i.e., all three positions separated, just the third position kept apart and no partitioning, respectively. The analysis supported 1 + 2 + 3 model as the best one with BF = 13.16 and 79.86 relative to the other two in the respective order. Each of the partitions was given its own nucleotide substitution model with substitution rate matrix sampled from the whole general time reversible family of models using reversible-jump MCMC (Green 1995). The substitution rate variability within each partition was modeled by a discretized gamma distribution with four categories. Four independent MCMC runs were conducted, and their convergence checked by three statistics: average standard deviation of split frequencies for tree topologies, potential scale reduction factor and effective sample size for all parameters as well as for prior and likelihood. After discarding 10% burn-in and a convergence check, the posterior samples were pooled, the trees were rooted, and the outgroup sequences removed. The maximum clade credibility (MCC) tree with common ancestor node heights (Drummond and Bouckaert 2015, p. 94) was taken to represent the final sample of trees. The convergence check was performed in R (R Core Team 2021) using packages rwty (Warren et al. 2017) and coda (Plummer et al. 2006). The MCC tree was calculated using packages ape (Paradis and Schliep 2018) and phangorn (Schliep 2011) and R functions available at https://github.com/onmikula/mcctree_mrbayes.
Delimitation of mitochondrial lineages
The delimitation of lineages on the tree was performed by the mPTP method (Kapli et al. 2017), which looks for the maximum likelihood partitioning of a tree into components (monophyletic lineages), each characterized by its own exponential distribution of branch lengths. It assumes the presence of \(K\ge 1\) terminal components and, if \(K>1\), also the presence of one basal component connecting their ancestors. Differentiation of the lineages was quantified by average uncorrected genetic distances between their members, whereas mean genetic distances within the lineages estimate their haplotype variability and can serve as estimators of the effective population size parameter (\(\theta\)).
The sequences not included in the tree were classified into the lineages using the nearest-neighbor criterion applied to uncorrected genetic distances. First, the excluded haplotypes were classified based on their distances to included ones and then the rest of sequences were compared to this enriched reference data set. Geographical distribution of lineages was described on this classification of all available CYTB data. Lineage co-occurrence was examined by depicting proportions of their haplotypes in samples collected along six transects through the contact zones. For this purpose, we kept original sampling information (locality name and geographical coordinates) and we just omitted sites with only a single individual sequenced.
Population genetic analyses
Whereas unique haplotypes were sampled for the tree estimation, spatial gradients in genetic diversity, past population trends and neutrality indices were estimated from a spatially balanced random sample of all sequences. This was achieved by randomly picking the maximum of m = 11 sequences from each of the pooled sites. The number 11 was chosen according to our predefined histogram symmetry criterion. Let ni denote sample size at site i. For every m from 2 to max (ni), every ni > m was changed to m, the frequency distribution of the resulting sample sizes was calculated, and its symmetry quantified as the mean distance between the frequencies listed in increasing and decreasing order. The symmetry should be maximum when some typical ni exists and m is not set too close to it. Using such m then keeps per site sample sizes reasonably balanced. The subsampling was performed on the whole data set, with no reference to the classification into lineages.
The Genetic hubs algorithm attempts to estimate hotspots of genetic diversity from sparse genetic data by connecting sampling sites into a graph and looking for a graph node with the best accessibility to all observed alleles (Mikula 2018). These sites (called genetic hubs) can correspond to locations of putative long-term refugia or centers of recent expansion.
Past population trends were estimated as changes in the effective population size (\({N}_{e}\)) using Bayesian skyline plots (Drummond et al. 2005) as implemented in BEAST 2 (Bouckaert et al. 2014). In short, this method assumes \({N}_{e}\) to change in a stepwise manner between a pre-specified number of periods (four here) and co-estimates boundaries of these periods, \({N}_{e}\) specific to each period and a coalescent tree of the sequences. Bayesian skyline plots were estimated separately for each of the lineages with 100 sequences taken randomly from the spatially balanced sample. Given low genetic variability within the lineages, the simplest JC substitution model (Jukes and Cantor 1969) was used to account for multiple mutations, but the alignment was partitioned to account for different mutation rates at different codon positions. The prior on molecular clock rates was normal (\(\mu =0.08,\sigma =0.01\)) in millions of years (Ma) per bp. Its choice was motivated by a preliminary multispecies coalescent analysis performed in StarBEAST 2 (Ogilvie et al. 2017) and using the CYTB data set of all Mastomys species (for details, see Supplementary material 3). The skyline plot itself was reconstructed from the posterior sample of coalescent trees in Tracer 1.7 (Rambaut et al. 2018) and visualized in R. In addition to skyline plots, two neutrality indices were calculated for lineage-specific spatially balanced samples: Tajima’s D (Tajima 1989) and R2 (Ramos-Onsins and Rozas 2002).
Environmental niche modeling
The MaxEnt inference (Phillips et al. 2006) was applied to predict probability of occurrence of lineages across the same background encompassing the whole documented distribution of lineages B4, B5 and B6. The background was discretized into quadrate cells with size of 0.5 × 0.5 degrees. All our presence records were projected to the cell grid. Climatic predictors were represented by average monthly precipitations, minimum temperatures, and maximum temperatures, downloaded from the WorldClim database (Fick and Hijmans 2017) and subsampled to 0.5° resolution. These predictors should be treated as climatic curves (not isolated monthly values) in the analyses, and we used them as described in Mikula (2021), including their superimposition and projection to natural cubic spline basis. Complexity of the spline basis was selected in a preliminary analysis using AICc (Burnham and Anderson 2002; Warren and Seifert 2011) as a measure of model fit. The superimposition was based on precipitation curves only and the model selection suggested spline bases with 3, 3, and 11 knots for precipitation, minimum temperature, and maximum temperature curves, respectively. In addition to the present data (collected between 1970 and 2000; Fick and Hijmans 2017) we also downloaded climatic data reconstructed for the Last Glacial Maximum (LGM), presented in WorldClim v. 1.4 (Hijmans et al. 2005) as simulated for a time of 21 thousand years (ka) before present using Community Climate System Model (Gent et al. 2011). LGM precipitation curves (and by extension also both temperature curves) were superimposed onto the present precipitation curves. The projected curves were used without any further transformation and lasso regularization was performed as a part of MaxEnt fit in R package maxnet (Phillips et al. 2017). The model was fitted separately for each lineage, but with the same background, to check for climatic suitability extending beyond the current lineage distributions. MaxEnt predictions come in the form of relative occurrence rates (RORs), which can be subjected to the complementary log–log transform and then (cautiously) interpreted as probabilities of presence in the cells. This allows a better comparison between the lineages. We did the comparison by calculating for every cell an index of exclusivity as the maximum of three values, which were probabilities that a given lineage is present in the cell and the other two are not. R functions necessary for handling climatic curves are available at https://github.com/onmikula/maxent_tools.
Results
Delimitation and distribution of Mt lineages
The CYTB tree of Mt B lineages of M. natalensis is presented in Fig. 2. Its maximum likelihood partitioning is congruent with the classification of Colangelo et al. (2013): three lineages with a strong phylogeographic signal (Fig. 3) were recovered. Lineage B4 is distributed from southern Kenya and Rwanda to eastern Tanzania. Lineage B5 is found in south-eastern Tanzania and northern Mozambique near Lake Malawi. Lineage B6 is sister to lineage B5 with posterior probability (PP) = 0.91 and occupies the area from south-western Tanzania to South Africa in the south and Angola in the west. The zones of contact between these lineages are shown in detail in Fig. 4. The lineages were separated by mean uncorrected genetic distances of 3.68% (B4 × B5), 3.12% (B4 × B6) and 3.05% (B5 × B6). Mean internal genetic distances were equal to 0.64% (B4), 0.75% (B5) and 1.00% (B6).
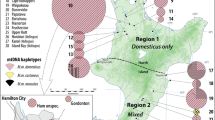
Geographical distribution of B Mt lineages of Mastomys natalensis. Colors indicate proportional representation of lineages in all sequences obtained from the site, color shades indicate site’s position on genetic diversity gradient as estimated by Genetic hubs (more intensive colors indicate higher diversity). Black dots indicate the hub sites
Area where the contact of M. natalensis B Mt lineages takes place. The names indicate the position of administrative and geographical features mentioned in the text. The numbered sub-figures at the margin show the distribution of Mt lineages in six transects through the contact zones, whose locations are indicated by gray frames in the map. In the sub-figures each pie plot corresponds to a single sampling site. For this display, we used 105 original (not pooled) sampling sites with more than one sequence, while 34 sites with a single sampled sequence were omitted
The genetic hubs analysis shows spatial gradients of genetic variation within each of the lineages, as indicated by the color tint in Fig. 3. The most pronounced is the gradient in lineage B4 whose genetic hub lies near Handeni town in Tanzania, very close to the contact with lineage B5. In contrast, the areas adjacent to Lake Tanganyika and the Albertine Rift highlands appear depleted of CYTB variation. In lineages B5 and B6 the trends are shallower, and their genetic hubs are found in Mkuranga district in the Pwani region (B5) and near the border between Malawi and Zambia close to Mchinji (B6).
History of population expansions
The Bayesian skyline plot of the B5 lineage shows a sharp recent increase in \({N}_{e}\), whereas in lineage B4 and especially lineage B6 the growth was slower and started earlier (Fig. 5). In particular, the most rapid population expansion took place 5.4 ka ago in lineage B5, whereas it is dated to 17.6 ka and 18.1 ka in lineages B6 and B4, respectively. The neutrality indices confirm this scenario. Tajima’s D was significantly negative in all three lineages: –3.02 (P = 0.0026) in lineage B4, –2.64 (P = 0.0084) in lineage B5 and –2.67 (P = 0.0075) in lineage B6, with P values based on normal approximation. The values of R2 were significantly small: 0.01 in lineage B4, 0.02 in lineage B5 and 0.01 in lineage B6 with P values always < 0.001 (according to coalescent simulations with parameters theta calculated from the observed numbers of variable sites).
Climate-based distribution models for Mt lineages
Predicted distributions (i.e., high RORs) of lineages B4 and B5 are associated mostly with their current distributions, but in the northeast of Tanzania both predicted distributions extend to the current distributions of the other lineage (Fig. 6). The predicted RORs of lineage B6 are spread over most of the considered area, although they take lower values in the current distributional range of lineage B4. Predictions for the Last Glacial Maximum show a very similar picture, but the extents of inhospitable areas are larger, and the predicted distribution of lineage B5 is smaller and largely restricted to its current distribution.
The areas where the probability of presence is high for one lineage and low for the other two are indicated in Fig. 7. The exclusive presence of lineage B4 is predicted mostly around the northern volcanoes (Kilimanjaro, Meru, Kitumbeine), the area of exclusive presence of lineage B5 is restricted to the northern part of its current distribution range, close to the Indian Ocean coast, but with lower probability it also includes the nearby contact zone with lineage B4 including its genetic hub location. Lineage B6 appears exclusive to its core distribution area in north-eastern Zambia and around Lake Malawi. Interestingly, it extends considerably into the distribution ranges of the other two lineages and in the case of lineage B5 distribution (namely the southern part of Eastern Arc Mountains, eastern side of Lake Malawi) it does so with rather high probability.
ROR-weighted climatic curves (Fig. 8) show it is lineage B6 whose preferred climate differs most from the others. It differs in the timing of precipitation peak (rainy season) and in the temperature extremes, namely, in the annual temperature minimum and in the abrupt onset of the maximum temperature peak.
Discussion
Phylogeography of M. natalensis in the Zambezian region
In this study we present the most detailed and comprehensive set of genetically confirmed presence data for the Natal multimammate mouse (M. natalensis), one of the most widespread autochthonous mammal species in sub-Saharan Africa (Hánová et al. 2021a). Compared to the previous phylogeographic study of Colangelo et al. (2013), it includes newly published sequences from the periphery of the distribution range, namely from Ethiopia (Martynov et al. 2020) and Angola (Krásová et al. 2021), as well as abundant new data from the northern Zambezian region. Phylogeographic analysis confirms the principal previous findings: in the Zambezian region M. natalensis mitochondria are structured into three haplogroups (B4-6) with limited geographical overlap. The only remaining sampling gap, which could harbor an undescribed mitochondrial lineage, now appears to be in the Horn of Africa. Here, the species occurrence is predicted by the International Union for Conservation of Nature (IUCN) Red List (IUCN 2021), but not supported by any museum record (Bryja et al. 2019, p. 164), nor by climatic niche modeling (Martynov et al. 2020). Biodiversity data from that region is very scarce, however, and new investigations are necessary to examine whether M. natalensis is present there and what type of mtDNA it harbors.
The presence of such mitochondrial differentiation is commonplace in African rodent taxa, both in forests (e.g., Bohoussou et al. 2015; Mizerovská et al. 2019; Pradhan et al. 2021) and savanna (e.g., McDonough et al. 2015; Petružela et al. 2018; Mikula et al. 2020; Zemlemerova et al. 2021) and its origin is suggested to lie in the history of climatic changes and associated habitat fragmentation (Demos et al. 2014; Huntley et al. 2019; Couvreur et al. 2021). The general idea is that under unfavorable climatic conditions, only a few small and isolated populations survive to become sources for population expansion when the conditions improve. The expansion leads to population reconnection and admixture, but in the next period of population reduction the traces of admixture may be largely erased due to local extinction. If the same happens repeatedly and in a stable coarse scale spatial setting, the species becomes internally structured and eventually can split due to reproductive incompatibilities accumulating between its phylogeographic lineages. The effects of this reduction-expansion dynamics are exaggerated by presence of migration barriers that prevent population contact, or diminish its intensity, even at the peak of expansion.
This dynamic can be reconstructed from genetic data, especially when multiple unlinked loci or the whole genome sequences are analyzed (Li et al. 2020; Coimbra et al. 2021), because overlapping effects of recombination events allow detection of events at multiple temporal scales. With contemporary sequences of a single non-recombining locus, our perspective was largely restricted to the most recent demographic events. Nevertheless, their reconstruction can still provide valuable insights into processes that have shaped current population structure. To achieve this goal, we combined inference of past population trends (Bayesian skyline plots) with estimation of the most recent centers of expansion (Genetic hubs) and climatic niche modeling (MaxEnt). In summary, our results show that all three Mt lineages underwent recent population expansion (Fig. 5) from regions that were surprisingly close to each other (Fig. 3) and that are coincident with areas estimated as the most suitable during the last glacial maximum (Fig. 6).
The effective population sizes of all three Mt lineages are similar at present, but it was not the case in the past. The most recent population expansion of lineages B4 and B6 was simultaneous, it started substantially earlier than in lineage B5, but it was not so abrupt. Overall, the effective population size of lineage B6 was higher compared to lineages B4 and B5 throughout the period covered by the analysis. Our estimates of long-term mutation rates point towards approximately mid-Holocene (5 ka) and post-LGM (18 ka) date of these expansions. During LGM (26.5–19 ka; Clark et al. 2009), lineages B4 and B6 were already expanding, while lineage B5 survived it in low numbers. The most recent expansion of lineages B4 and B6 thus took place in dry conditions of LGM and slowed down only with successive shifts towards more humid climate in the last 17 ka (Gasse 2000). The expansion of lineage B5 was more abrupt but delayed until the end of so-called African Humid Period, a period of continent-wide increase in precipitation (14.8–5.5 ka; Shanahan et al. 2015). Due to its position on the Indian Ocean coast the distribution range of lineage B5 could particularly be affected by this continent-wide increase in precipitation (cf. Tierney et al. 2011), which would prevent spread of open habitats and savanna-dwellers including M. natalensis.
The estimated demographic trends are in accord with climatic niche modeling, which predicted LGM distributions of lineages B4 and B6 to be of similar extent as the current ones, but that of lineage B5 to be smaller (Fig. 6). Even more importantly, the predicted LGM distributions are coincident with the present ones which suggests they can persist despite major changes of global climate. Consistent with this conclusion is the placement of genetic hubs, which are estimates of the centers of expansion. The Mt lineages, therefore, likely survived the last glacial in areas including our genetic hubs. It remains to be understood how restricted the areas were, but notwithstanding the details of the process, the estimates of genetic hubs and climatically suitable areas are based on entirely different data and their coincidence brings confidence into the basic scheme of this phylogeographic scenario.
Habitat suitability and contact zones
Environmental niche modeling can target either the fundamental or the realized niche of the species. The MaxEnt modeling balances the two. Its inherent tendency to the most uniform (= maximum entropy) distribution of occurrence rates targets the fundamental niche, while its reliance on constraints imposed by the presence records makes the predictions closer to the realized niche. This is necessary to consider when interpreting MaxEnt maps. The predicted distributions of three mitochondrial lineages of M. natalensis cover their observed counterparts but extend also to the observed distributions of the other lineages (Fig. 6). It means the climate differs between lineage-specific distribution ranges, cf. the ROR-weighted climatic curves (Fig. 8), but the differences are not big enough to prevent spread of the Mt lineages beyond their current distributions.
This is relevant for understanding the contact zones between the Mt lineages. They occur along the Eastern Arc Mountains as well as along the Great Rift Valley and in the lowlands of southern Tanzania and northern Mozambique. A detailed study of B4–B5 contact zone revealed limited gene flow along a transect running between two massifs of Eastern Arc Mountains. Given that frequencies of lineage-specific mitochondrial DNA, a Y-chromosome SNP, nuclear markers and even mammarenaviruses change in narrow (ca. 20 km) and coincident clines (Gryseels et al. 2017), the contact zone can be interpreted as a tension zone sustained by a balance between dispersal into the zone and selection against hybrids (Slatkin 1973; Barton and Hewitt 1985) as opposed to selection along an environmental gradient.
Our MaxEnt models show that whereas adaptation to different climates can explain broad scale distribution of the lineages, the gradient of environmental suitability is not sharp enough to explain the narrow width of the clines (Barton and Hewitt 1989). At other places, however, the mitochondrial co-occurrence seems to be more extensive (e.g., B4–B5 contact in north-eastern Tanzania, cf. Fig. 4) and its correlation with climate and other environmental parameters (primary productivity, vegetation structure etc.) is worth more detailed investigation.
As selection in a tension zone is not tied to the environment, these zones can move under differential dispersal pressures between taxa, one expanding and the other retreating until they become aligned with dispersal barriers or density troughs (Barton and Hewitt 1989). This prediction was made for short-term dynamics taking place on a fine spatial scale, but it can apply likewise to long-term dynamics on a broad spatial scale. The latter can explain the contact zones we observe here being approximately aligned with the Eastern Arc Mountains and the Great Rift Valley, where the forested hills and deep lakes can work as long-term dispersal barriers. Paleovegetation data indeed suggest the moist forest persisted during LGM on the Eastern Arc Mountains (Mumbi et al. 2008; Finch et al. 2009), although locally it could be replaced by montane grassland mosaic (Finch et al. 2014).
In any case, the current position of a contact zone may represent an equilibrium, which is most easily established where local population density is low, or a transitional state of an ongoing movement. In accord with this interpretation, the population expansion started later in lineage B5, co-occurrence of lineages B4 and B5 is limited, and it takes place where population density is presumably low. In addition, predicted RORs of lineage B5 in the current B4 range are higher under current compared to LGM conditions, while predicted RORs of lineage B4 in the current B5 range are high in both time layers. Therefore, it is possible that the contact zone has been moving in the past, more specifically that lineage B5 has expanded into the B4 range, until it was trapped at its present location. Testing this hypothesis requires, however, analysis of more and higher quality multilocus data (e.g., a genome-wide set of SNPs). The other two contact zones, B4–B6 and especially B5–B6, may have a similar history, but also in these cases more detailed geographical sampling is necessary.
Similar phylogeographic patterns are present in several small mammal taxa of the region (reviewed by Cuypers et al. 2022). In some of them, the Mt lineages were shown to match populations with separate nuclear gene pools and possibly a degree of phenotypic differentiation. Namely, this applies to Lemniscomys zebra/rosalia (Hánová et al. 2021b), Acomys muzei/ngurui (Petružela et al. 2018) and Heliophobius kapiti/argenteocinereus (Uhrová et al. 2022), whose divergences are dated to be ~ 2.5 million years (Ma) old. Other such lineages are of younger age (~ 1.0 Ma) and more detailed analyses have not been conducted yet, which is the case of Aethomys chrysophilus (Mazoch et al. 2018) or Mus minutoides (Bryja et al. 2014). According to our estimate of mutation rates, the complex of M. natalensis B lineages is even younger, just about 0.4 Ma old. The Malawi-Rukwa-Tanganyika section of the Great Rift valley was described as a phylogeographic boundary also in some large savanna mammals: roan antelope (Hippotragus equinus; Gonçalves et al. 2021), common eland (Taurotragus oryx; Lorenzen et al. 2010) or vervet monkey (Chlorocebus pygerythrus; Haus et al. 2013).
The sharing of phylogeographic patterns suggests that climatic and vegetational differentiation of the regions is stable over long periods of time, although their boundaries can change and allow colonization of the regions by immigrants from the surroundings. More detailed phylogeographic analyses of other co-distributed taxa is necessary to understand whether the regional species pools change in mutual concert. If, for instance, the demographic trends of all savanna-dwelling taxa are similar and whether their centers of expansion are coincident. Deeper understanding of biodiversity dynamics of the region will also require examining the nature of other contacts between other intraspecific lineages as the tension zone between M. natalensis B4 and B5 may not be the only one.
Data availability
All data analysed in this study are included in supplementary information files of the article.
References
Barton NH, Hewitt GM (1985) Analysis of hybrid zones. Annu Rev Ecol Evol Syst 16:113–148. https://doi.org/10.1146/annurev.es.16.110185.000553
Barton NH, Hewitt GM (1989) Adaptation, speciation and hybrid zones. Nature 341:497–503. https://doi.org/10.1038/341497a0
Bohoussou KH, Cornette R, Akpatou B, Colyn M, Kerbis PJC, Kennis J, Sumbera R, Verheyen E, N’Goran E, Katuala P, Nicolas V (2015) The phylogeography of the rodent genus Malacomys suggests multiple Afrotropical Pleistocene lowland forest refugia. J Biogeogr 42:2049–2061. https://doi.org/10.1111/jbi.12570
Borremans B, Hughes NK, Reijniers J, Sluydts V, Katakweba AAS, Mulungu LS, Sabuni CA, Makundi RH, Leirs H (2014) Happily together forever: temporal variation in spatial patterns and complete lack of territoriality in a promiscuous rodent. Popul Ecol 56:109–118. https://doi.org/10.1007/s10144-013-0393-2
Bouckaert R, Heled J, Kühnert D, Vaughan T, Wu CH, Xie D, Suchard MA, Rambaut A, Drummond AJ (2014) BEAST 2, A software platform for Bayesian evolutionary analysis. PLoS Comput Biol 10:e1003537. https://doi.org/10.1371/journal.pcbi.1003537
Bryja J, Mikula O, Šumbera R, Meheretu Y, Aghová T, Lavrenchenko LA, Mazoch V, Oguge N, Mbau JS, Welegerima K, Amundala N, Colyn M, Leirs H, Verheyen E (2014) Pan-African phylogeny of Mus (subgenus Nannomys) reveals one of the most successful mammal radiations in Africa. BMC Evol Biol 14:e256. https://doi.org/10.1186/s12862-014-0256-2
Bryja J, Meheretu Y, Šumbera R, Lavrenchenko LA (2019) Annotated checklist, taxonomy and distribution of rodents in Ethiopia. Folia Zool 68:117–213. https://doi.org/10.25225/fozo.030.2019
Burnham KP, Anderson DR (2002) A practical information theoretic approach. Model selection and multimodel inference, 2nd edn. Springer, New York, p 488
Clark PU, Dyke AS, Shakun JD, Carlson AE, Clark J, Wohlfarth B, Mitrovica JX, Hostetler SW, McCabe AM (2009) The last glacial maximum. Science 16:710–714. https://doi.org/10.1126/science.1172873
Coimbra RTF, Winter S, Kumar V, Koepfli K-P, Gooley RM, Dobrynin P, Fennessy J, Janke A (2021) Whole-genome analysis of giraffe supports four distinct species. Curr Biol 31:2929-2938.e5. https://doi.org/10.1016/j.cub.2021.04.033
Colangelo P, Verheyen E, Leirs H, Tatard C, Denys C, Dobigny G, Duplantier JM, Brouat C, Granjon L, Lecompte E (2013) A mitochondrial phylogeographic scenario for the most widespread African rodent, Mastomys natalensis. Biol J Linn Soc 108:901–916. https://doi.org/10.1111/bij.12013
Couvreur TLP, Dauby G, Blach-Overgaard A, Deblauwe V, Dessein S, Droissart V, Hardy OJ, Harris DJ, Janssens SB, Ley AC, Mackinder BA, Sonke B, Sosef MSM, Stevart T, Svenning JC, Wieringa JJ, Faye A, Missoup AD, Tolley KA, Nicolas V, Ntie S, Fluteau F, Robin C, Guillocheau F, Barboni D, Sepulchre P (2021) Tectonics, climate and the diversification of the tropical African terrestrial flora and fauna. Biol Rev 96:16–51. https://doi.org/10.1111/brv.12644
Cuypers LN, Baird SJE, Hánová A, Locus T, Katakweba AS, Gryseels S, Bryja J, Leirs H, Goüy de Bellocq J (2020) Three arenaviruses in three subspecific Natal multimammate mouse taxa in Tanzania: same host specificity, but different spatial genetic structure? Virus Evol 6:veaa039. https://doi.org/10.1093/ve/veaa039
Cuypers LN, Sabuni C, Šumbera R, Aghová T, Lišková E, Leirs H, Baird SJE, Goüy de Bellocq J, Bryja J (2022) Biogeographical importance of the Livingstone Mountains in southern Tanzania: comparative genetic structure of small non-volant mammals. Front Ecol Evol 9:742851. https://doi.org/10.3389/fevo.2021.742851
Goüy de Bellocq J, Bryjová A, Martynov AA, Lavrenchenko LA (2020) Dhati Welel virus, the missing mammarenavirus of the widespread Mastomys natalensis. J Vertebr Biol 69:20018. https://doi.org/10.25225/jvb.20018
Demos TC, Kerbis PJC, Agwanda B, Hickerson MJ (2014) Uncovering cryptic diversity and refugial persistence among small mammal lineages across the Eastern Afromontane biodiversity hotspot. Mol Phyl Evol 71:41–54. https://doi.org/10.1016/j.ympev.2013.10.014
Drummond AJ, Bouckaert RR (2015) Bayesian evolutionary analysis with BEAST. Cambridge University, Cambridge
Drummond AJ, Rambaut A, Shapiro B, Pybus OG (2005) Bayesian coalescent inference of past population dynamics from molecular sequences. Mol Biol Evol 22:1185–1192. https://doi.org/10.1093/molbev/msi103
Duplantier JM, Granjon L, Bouiganaly H (1996) Reproductive characteristics of three sympatric species of Mastomys in Senegal, as observed in the field and in captivity. Mammalia 60:629–638. https://doi.org/10.1515/mamm.1996.60.4.629
Fan Y, Wu R, Chen MH, Kuo L, Lewis PO (2011) Choosing among partition models in Bayesian phylogenetics. Mol Biol Evol 28:523–532. https://doi.org/10.1093/molbev/msq224
Fick SE, Hijmans RJ (2017) WorldClim 2, new 1-km spatial resolution climate surfaces for global land areas. Int J Climatol 37:4302–4315. https://doi.org/10.1002/joc.5086
Finch JM, Leng MJ, Marchant RA (2009) Late Quaternary vegetation dynamics in a biodiversity hotspot, the Uluguru Mountains of Tanzania. Quat Res 72:111–122. https://doi.org/10.1016/j.yqres.2009.02.005
Finch J, Wooller M, Marchant R (2014) Tracing long-term tropical montane ecosystem change in the Eastern Arc Mountains of Tanzania. J Quat Sci 29:269–278. https://doi.org/10.1002/jqs.2699
Galster S, Burgess ND, Fjeldså J, Hansen LA, Rahbek C (2007) One degree resolution databases of the distribution of 1085 species of mammals in Sub–Saharan Africa. On–line data source–Version 1.00. Zoological Museum, University of Copenhagen, Denmark
Gasse F (2000) Hydrological changes in the African tropics since the Last Glacial Maximum. Quat Sci Rev 19:189–211. https://doi.org/10.1016/S0277-3791(99)00061-X
Gent PR, Danabasoglu G, Donner LJ, Holland MM, Hunke EC, Jayne SR, Lawrence DM, Neale RB, Rasch PJ, Vertenstein M, Worley PH, Yang ZL, Zhang MH (2011) The community climate system model, version 4. J Climat 24:4973–4991. https://doi.org/10.1175/2011JCLI4083.1
Gonçalves M, Siegismund HR, Jansen van Vuuren B, Ferrand N, Godinho R (2021) Evolutionary history of the roan antelope across its African range. J Biogeogr 48:2812–2827. https://doi.org/10.1111/jbi.14241
Granjon L, Duplantier JM (1993) Social structure in synanthropic populations of a murid rodent Mastomys natalensis in Sénégal. Acta Theriol 38:39–47
Green PJ (1995) Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika 82:711–732. https://doi.org/10.1093/biomet/82.4.711
Gryseels S, Goüy de Bellocq J, Makundi R, Vanmechelen K, Broeckhove J, Mazoch V, Šumbera R, Zima J Jr, Leirs H, Baird SJE (2016) Genetic distinction between contiguous urban and rural multimammate mice in Tanzania despite gene flow. J Evol Biol 29:1952–1967. https://doi.org/10.1111/jeb.12919
Gryseels S, Baird SJE, Borremans B, Makundi R, Leirs H, Goüy de Bellocq J (2017) When viruses don’t go viral, The importance of host phylogeographic structure in the spatial spread of arenaviruses. PLoS Pathog 13:e1006073. https://doi.org/10.1371/journal.ppat.1006073
Hánová A, Konečný A, Mikula O, Bryjová A, Šumbera R, Bryja J (2021a) Diversity, distribution and evolutionary history of the most studied African rodents, multimammate mice of the genus Mastomys: an overview after a quarter of century of using DNA sequencing. J Zool Syst Evol Res 59:2500–2518. https://doi.org/10.1111/jzs.12569
Hánová A, Konečný A, Nicolas V, Denys C, Granjon L, Lavrenchenko LA, Šumbera R, Mikula O, Bryja J (2021b) Multilocus phylogeny of African striped grass mice (Lemniscomys): stripe pattern only partly reflects evolutionary relationships. Mol Phyl Evol 157:107007. https://doi.org/10.1016/j.ympev.2020.107007
Haus T, Akom E, Agwanda B, Hofreiter M, Roos C, Zinner D (2013) Mitochondrial diversity and distribution of African green monkeys (Chlorocebus Gray, 1870). Am J Primatol 75:350–360. https://doi.org/10.1002/ajp.22113
Hijmans RJ, Cameron SE, Parra JL, Jones PG, Jarvis A (2005) Very high resolution interpolated climate surfaces for global land areas. Int J of Climatol 25:1965–1978. https://doi.org/10.1002/joc.1276
Huntley JW, Keith KD, Castellanos AA, Musher LJ, Voelker G (2019) Underestimated and cryptic diversification patterns across afro-tropical lowland forests. J Biogeogr 46:381–391. https://doi.org/10.1111/jbi.13505
IUCN (2021) The IUCN red list of threatened species. Version 2021–1. https://www.iucnredlist.org
Jukes TH, Cantor CR (1969) Evolution of protein molecules. Academic Press, New York
Kapli P, Lutteropp S, Zhang J, Kobert K, Pavlidis P, Stamatakis A, Flouri T (2017) Multi–rate Poisson tree processes for single-locus species delimitation under maximum likelihood and Markov chain Monte Carlo. Bioinformatics 33:1630–1638. https://doi.org/10.1093/bioinformatics/btx025
Kennis J, Sluydts V, Leirs H, Pim van Hooft WF (2008) Polyandry and polygyny in an African rodent pest species, Mastomys natalensis. Mammalia 72:150–160. https://doi.org/10.1515/MAMM.2008.025
Krásová J, Mikula O, Bryja J, Baptista NL, António T, Aghová T, Šumbera R (2021) Biogeography of Angolan rodents: the first glimpse based on phylogenetic evidence. Divers Distrib 27:2571–2583. https://doi.org/10.1111/ddi.13435
Leirs H, Verhagen R, Verheyen W (1994) The basis of reproductive seasonally in Mastomys rats (Rodentia, Muridae) in Tanzania. J Trop Ecol 10:55–66. https://doi.org/10.1017/S0266467400007719
Li K, Zhanga S, Song X, Weyrich A, Wang Y, Liu X, Wan N, Liu J, Lövy M, Cui H, Frenkel V, Titievsky A, Panov J, Brodsky L, Nevo E (2020) Genome evolution of blind subterranean mole rats: Adaptive peripatric versus sympatric speciation. Proc Natl Acad Sci USA 117:32499–32508. https://doi.org/10.1073/pnas.2018123117
Lorenzen ED, Masembe C, Arctander P, Siegismund HR (2010) A long-standing Pleistocene refugium in southern Africa and a mosaic of refugia in East Africa: insights from mtDNA and the common eland antelope. J Biogeogr 37:571–581. https://doi.org/10.1111/j.1365-2699.2009.02207.x
Makundi RH, Massawe AW, Mulungu LS (2007) Reproduction and population dynamics of Mastomys natalensis Smith, 1834 in an agricultural landscape in the Western Usambara Mountains, Tanzania. Integr Zool 2:233–238. https://doi.org/10.1111/j.1749-4877.2007.00063.x
Martynov AA, Bryja J, Meheretu Y, Lavrenchenko LA (2020) Multimammate mice of the genus Mastomys (Rodentia, Muridae) in Ethiopia–diversity and distribution assessed by genetic approaches and environmental niche modelling. J Vertebr Biol 69:20006. https://doi.org/10.25225/jvb.20006
Mazoch V, Mikula O, Bryja J, Konvičková H, Russo IR, Verheyen E, Šumbera R (2018) Phylogeography of a widespread sub–Saharan murid rodent Aethomys chrysophilus - the role of geographic barriers and paleoclimate in the Zambezian bioregion. Mammalia 82:373–387. https://doi.org/10.1515/mammalia-2017-0001
McDonough MM, Šumbera R, Mazoch V, Ferguson AW, Phillips CD, Bryja J (2015) Multilocus phylogeography of a widespread savanna–woodland-adapted rodent reveals the influence of Pleistocene geomorphology and climate change in Africa’s Zambezi region. Mol Ecol 24:5248–5266. https://doi.org/10.1111/mec.13374
Mikula O (2018) Genetic hubs, a phylogeographer’s widget for pinpointing of ancestral populations. bioRxiv. https://doi.org/10.1101/419796
Mikula O, Nicolas V, Boratyński Z, Denys C, Dobigny G, Fichet-Calvet E, Gagaré S, Hutterer R, Nimo-Paintsil SC, Olayemi A, Bryja J (2020) Commensalism outweighs phylogeographical structure in its effect on phenotype of a Sudanian savanna rodent. Biol J Linn Soc 129:931–949. https://doi.org/10.1093/biolinnean/blz184
Mizerovská D, Nicolas V, Demos TC, Akaibe D, Colyn M, Denys C, Kaleme PK, Katuala P, Kennis J, Kerbis Peterhans JC, Laudisoit A, Missoup AD, Šumbera R, Verheyen E, Bryja J (2019) Genetic variation of the most abundant forest-dwelling rodents in Central Africa (Praomys jacksoni complex): Evidence for Pleistocene refugia in both montane and lowland forests. J Biogeogr 46:1466–1478. https://doi.org/10.1111/jbi.13604
Monadjem A, Taylor PJ, Denys C, Cotterill FPD (2015) Rodents of Sub-Saharan Africa. A biogeographic and taxonomic synthesis. Walter de Gruyter GmbH, Berlin, Munich, Boston
Monath TP, Newhouse VF, Kemp GE, Setzer HW, Cacciapuoti A (1974) Lassa virus isolation from Mastomys natalensis rodents during an epidemic in Sierra Leone. Science 185:263–265. https://doi.org/10.1126/science.185.4147.263
Mulungu LS, Ngowo V, Mdangi M, Katakweba AS, Tesha P, Mrosso FP, Mchomvu M, Sheyo PM, Kilonzo BS (2013) Population dynamics and breeding patterns of multimammate mouse, Mastomys natalensis (Smith 1834), in irrigated rice fields in eastern Tanzania. Pest Manag Sci 69:371–377. https://doi.org/10.1002/ps.3346
Mumbi CT, Marchant R, Hooghiemstra H, Wooller MJ (2008) Late quaternary vegetation reconstruction from the Eastern Arc Mountains, Tanzania. Quat Res 69:326–341. https://doi.org/10.1016/j.yqres.2007.10.012
Mwanjabe PS, Sirima FB, Lusungu J (2002) Crop losses due to outbreaks of Mastomys natalensis (Smith, 1834) Muridae, Rodentia, in the Lindi region of Tanzania. Int Biodeterior Biodegrad 49:133–137. https://doi.org/10.1016/S0964-8305(01)00113-5
Ogilvie HA, Bouckaert RR, Drummond AJ (2017) StarBEAST2 brings faster species tree inference and accurate estimates of substitution rates. Mol Biol Evol 34:2101–2114. https://doi.org/10.1093/molbev/msx126
Olayemi A, Obadare A, Oyeyiola A, Igbokwe J, Fasogbon A, Igbahenah F, Ortsega D, Asogun D, Umeh P, Vakkal I, Abejegah Ch, Pahlman M, Becker-Ziaja B, Günther S, Fichet-Calvet E (2016) Arenavirus diversity and phylogeography of Mastomys natalensis rodents, Nigeria. Emerg Infect Dis 22:694–697. https://doi.org/10.3201/eid2204.150155
Paradis E, Schliep K (2018) ape 5.0, an environment for modern phylogenetics and evolutionary analyses in R. Bioinformatics 35:526–528. https://doi.org/10.1093/bioinformatics/bty633
Petružela J, Šumbera R, Aghová T, Bryjová A, Katakweba AS, Sabuni CA, Chitaukali WN, Bryja J (2018) Spiny mice of the Zambezian bioregion-phylogeny, biogeography and ecological differentiation within the Acomys spinosissimus complex. Mamm Biol 91:79–90. https://doi.org/10.1016/j.mambio.2018.03.012
Phillips SJ, Anderson RP, Schapire RE (2006) Maximum entropy modeling of species geographic distributions. Ecol Model 190:231–259. https://doi.org/10.1016/j.ecolmodel.2005.03.026
Phillips SJ, Anderson RP, Dudík M, Schapire RE, Blair ME (2017) Opening the black box: an open-source release of Maxent. Ecography 40:887–893. https://doi.org/10.1111/ecog.03049
Plummer M, Best N, Cowles K, Vines K (2006) CODA, convergence diagnosis and output analysis for MCMC. R news 6: 7–11. URL https://cran.r-project.org/doc/Rnews/Rnews_2006-1.pdf#page=7
Pradhan N, Norris RW, Decher J, Kerbis Peterhans J, Gray CR, Bauer G, Carleton MD, Kilpatrick CW (2021) Phylogenetic relationships and biogeography of the Hybomys division (Muridae: Murinae: Arvicanthini), rodents endemic to Africa’s rainforests. J Vert Biol 70:21034. https://doi.org/10.25225/jvb.21034
R Core Team (2021) R, A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL: https://www.R-project.org
Rambaut A, Drummond AJ, Xie D, Baele G, Suchard MA (2018) Posterior summarisation in Bayesian phylogenetics using Tracer 1.7. Syst Biol 67:901–904. https://doi.org/10.1093/sysbio/syy032
Ramos-Onsins SE, Rozas J (2002) Statistical properties of new neutrality tests against population growth. Mol Biol Evol 19:2092–2100. https://doi.org/10.1093/oxfordjournals.molbev.a004034
Ronquist F, Teslenko M, Van Der Mark P, Ayres DL, Darling A, Höhna S, Larget B, Liu L, Suchard MA, Huelsenbeck JP (2012) MrBayes 3.2, efficient Bayesian phylogenetic inference and model choice across a large model space. Syst Biol 61:539–542. https://doi.org/10.1093/sysbio/sys029
Schliep KP (2011) phangorn, phylogenetic analysis in R. Bioinformatics 27:592–593. https://doi.org/10.1093/bioinformatics/btq706
Shanahan TM, McKay NP, Hughen KA, Overpeck JT, Otto-Bliesner B, Heil CW, Scholz CA, Peck J (2015) The time-transgressive termination of the African humid period. Nat Geosci 8:140–144. https://doi.org/10.1038/ngeo2329
Slatkin M (1973) Gene flow and selection in a cline. Genetics 75:733–756. https://doi.org/10.1093/genetics/75.4.733
Tajima F (1989) Statistical methods for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123:585–595. https://doi.org/10.1093/genetics/123.3.585
Tierney JE, Russell JM, Damsté JSS, Huang Y, Verschuren D (2011) Late Quaternary behavior of the East African monsoon and the importance of the Congo air boundary. Quat Sci Rev 30:798–807. https://doi.org/10.1016/j.quascirev.2011.01.017
Uhrová M, Mikula O, Bennett NC, Van Daele P, Piálek L, Bryja J, Visser JH, van Vuuren BJ, Šumbera R (2022) Species limits and phylogeographic structure in two genera of solitary African mole-rats Georychus and Heliophobius. Mol Phylogenetics Evol 167:107337. https://doi.org/10.1016/j.ympev.2021.107337
Warren DL, Seifert SN (2011) Ecological niche modeling in Maxent, the importance of model complexity and the performance of model selection criteria. Ecol Appl 21:335–342. https://doi.org/10.1890/10-1171.1
Warren DL, Geneva AJ, Lanfear R (2017) RWTY (R We There Yet), an R package for examining convergence of Bayesian phylogenetic analyses. Mol Biol Evol 34:1016–1020. https://doi.org/10.1093/molbev/msw279
Xie W, Lewis PO, Fan Y, Kuo L, Chen MH (2011) Improving marginal likelihood estimation for Bayesian phylogenetic model selection. Syst Biol 60:150–160. https://doi.org/10.1093/sysbio/syq085
Zemlemerova ED, Kostin DS, Lebedev VS, Martynov AA, Gromov AR, Alexandrov DY, Lavrenchenko LA (2021) Genetic diversity of the naked mole-rat (Heterocephalus glaber). J Zool Syst Evol Res 59:323–340. https://doi.org/10.1111/jzs.12423
Acknowledgements
This research was funded by the Czech Science Foundation (GAČR grant no. 18-19629S). This collaborative work is part of the Czech Republic—Flanders, Belgium Mobility projects 2020 (FWO number VS07521N and CAS number FWO-21-02). The study benefited from access to the National Grid Infrastructure MetaCentrum provided under the programme CESNET LM2015042.
Funding
Open access publishing supported by the National Technical Library in Prague. Grantová Agentura České Republiky, 18-19629S, Joelle Goüy de Bellocq
Author information
Authors and Affiliations
Contributions
OM, JB, JGB and SJEB developed the concept of the study, all authors collected the material in the field, AH performed laboratory analyses, OM analyzed data, JB and JGB secured funding, OM and AH wrote the first draft of the manuscript, all authors discussed the results, commented on the final version and approved the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Handling editor: J. Paul Grobler.
Supplementary Information
Below is the link to the electronic supplementary material.
42991_2023_346_MOESM1_ESM.xlsx
Supplementary material 1. Complete list of sequences included in the study, their geographical coordinates, and references to the sources of data. Supplementary file1 (XLSX 149 KB)
42991_2023_346_MOESM2_ESM.fasta
Supplementary material 2. Alignment of all CYTB sequences included in the study in fasta format. Supplementary file2 (FASTA 2455 KB)
42991_2023_346_MOESM3_ESM.pdf
Supplementary material 3. Details of the inference of time-calibrated Mastomys CYTB tree, which assisted in the choice of clock rate prior in Bayesian skyline plot analyses. Supplementary file3 (PDF 189 KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hánová, A., Bryja, J., Goüy de Bellocq, J. et al. Historical demography and climatic niches of the Natal multimammate mouse (Mastomys natalensis) in the Zambezian region. Mamm Biol 103, 239–251 (2023). https://doi.org/10.1007/s42991-023-00346-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42991-023-00346-7