Asymptotic analysis of subwavelength halide perovskite resonators

Abstract

Halide perovskites are promising materials with many significant applications in photovoltaics and optoelectronics. Their highly dispersive permittivity relation leads to a non-linear relationship between the frequency and the wavenumber. This, in turn, means the resonance of the system is described by a highly non-linear eigenvalue problem, which is mathematically challenging to understand. In this paper, we use integral methods to quantify the resonant properties of halide perovskite nano-particles. We prove that, for arbitrarily small particles, the subwavelength resonant frequencies can be expressed in terms of the eigenvalues of the Newtonian potential associated with its shape. We also characterize the hybridized subwavelength resonant frequencies of a dimer of two halide perovskite particles. Finally, we examine the specific case of spherical resonators and demonstrate that our new results are consistent with previous works.

1 Introduction

Halide perovskites are set to be at the center of the next generation of electromagnetic devices [12, 16, 17]. They are composed of crystalline lattices which have octohedral shapes and contain atoms of heavier halides, such as chlorine, bromine and iodine [1]. Their excellent optical and electronic properties, combined with being cheap and easy to manufacture, have paved the way for a perovskite revolution. A particular benefit of halide perovskites is that their high absorption coefficient enables microscopic devices (measuring only a few hundred nanometres) to absorb the complete visible spectrum. Thus, we are able to design very small devices that are lightweight and compact while also being low cost and efficient. Research is ongoing to develop perovskites capable of fulfilling their theoretical capabilities for use in applications such as optical sensors [9], solar cells [17] and light-emitting diodes [19].

The dielectric permittivity of a halide perovskite $\varepsilon$ is given, in terms of the frequency $\omega$ and wavenumber k by [16]

$$\begin{aligned} \varepsilon (\omega ,k) = \varepsilon _0 + \frac{\omega _p^2}{\omega ^2_{exc} - \omega ^2 + \hslash \omega _{exc} k^2 \mu _{exc}^{-1} - i\gamma \omega }, \end{aligned}$$

where $\omega _{exc}$ is the frequency of the excitonic transition, $\omega _p$ is the strength of the dipole oscillator, $\gamma$ is the damping factor, $\mu _{exc}$ is related to the non-local response and $\varepsilon _0$ is the background dielectric constant. This expression captures the highly non-linear dispersive characteristic of the material. We refer to [16] for the values of these constants for different halide perovskites at room temperature. Meanwhile, the dispersion relation for the halide perovskites is observed [11] to take the simplified form

$$\begin{aligned} n^2 = 1 + \frac{S_0 \lambda _0^2}{1 - \lambda _0^2 k^2}, \end{aligned}$$

where n is the refractive index, k is the wavenumber and $S_0$ and $\lambda _0$ are positive constants that describe the average oscillator strength, see [11] for the values for some different halide perovsksites. Hence, we can see how the non-linear dispersive permittivity makes our analysis non-trivial.

Dielectric nano-particles, and other electromagnetic metamaterials, have been studied using various techniques. In the case of extreme material parameters, such as small particle size or large material contrast, asymptotic methods can be used [2, 3, 6, 8]. Likewise, homogenisation has been used to characterise materials with periodic micro-structures [7, 10]. Multiple scattering formulations are popular, particularly when a convenient choice of geometry (e.g. cylindrical or spherical resonators) facilitates explicit formulas [18]. In this paper, we will use integral methods to study a general class of geometries and will extend the previous theory, e.g. [2], to the case of dispersive materials.

For simplicity, we consider the Helmholtz equation as a model of the propagation of time-harmonic waves, and for the permittivity relation, we consider the form

$$\begin{aligned} \varepsilon (\omega ,k) = \varepsilon _0 + \frac{\alpha }{\beta - \omega ^2 + \eta k^2 - i \gamma \omega }, \end{aligned}$$

(1.1)

where $\alpha ,\beta ,\gamma ,\eta$ are positive constants. We will use an approach based on representing the scattered solution using a Lippmann-Schwinger integral formulation and then using asymptotic methods to characterise the resonant frequencies in terms of the eigenvalues of the resulting integral operator (which turns out to be the Newtonian potential). This approach can handle a very general class of resonator shapes and can be adapted to study solutions to the Maxwell’s equations [5]. A similar method was used in [2] for a simpler, non-dispersive setting. This paper shows that the asymptotic theory developed in [2] and elsewhere can be developed to model real-world settings and can be used to influence high-impact design problems.

In Sect. 2 of this paper we will introduce the problem setting and retrieve its integral formulation. Then, we will study the one particle case for three and two dimensions, using integral techniques to formulate the subwavelength resonant problem and asymptotic approximations to study the resonant frequencies. In Sect. 3, we will use these methods to describe the hybridization of two halide perovskite resonators. Again, we treat the three- and two-dimensional cases separately. Passing from the integral to a matrix formulation of the problem, we obtain the hybridized subwavelength resonant frequencies. Finally, we examine the case of spherical resonators, making use of the fact that eigenvalues and eigenfunctions of the Newtonian potential can be computed explicitly in this case (see also [13]). We show that our findings are qualitatively consistent with the ones of [2]. Hence, we show that the asymptotic techniques used in [2] can be generalized to less straightforward and more impactful physical settings.

2 Single resonators

2.1 Problem setting

Consider a single resonator occupying a bounded domain $\Omega \subset {\mathbb {R}}^d$, for $d\in \{2,3\}$. We assume that the particle is non-magnetic, so that the magnetic permeability $\mu _0$ is constant on all of ${\mathbb {R}}^d$. We will consider a time-harmonic wave with frequency $\omega \in {\mathbb {C}}$ (which we assume to have positive real part). The wavenumber in the background ${\mathbb {R}}^d \setminus {\overline{\Omega }}$ is given by $k_0:=\omega \varepsilon _0\mu _0$ and we will use k to denote the wavenumber within $\Omega$. We, then, consider the following Helmholtz model for light propagation:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u + \omega ^2 \varepsilon (\omega ,k)\mu _0 u = 0 \quad &{}\text { in } \Omega , \\ \Delta u + k_0^2 u = 0 &{}\text { in } {\mathbb {R}}^d\setminus {\overline{\Omega }}, \\ u|_+ - u|_-=0 &{}\text { on } \partial \Omega , \\ \frac{\partial u}{\partial \nu }|_+ - \frac{\partial u}{\partial \nu }|_- = 0 &{}\text { on } \partial \Omega , \\ u(x) - u_{in}(x) &{}\text { satisfies the outgoing radiation condition as } |x|\rightarrow \infty ,\\ \end{array}\right. } \end{aligned}$$

(2.1)

where $u_{in}$ is the incident wave, assumed to satisfy

$$\begin{aligned} (\Delta + k_0^2)u_{in}=0 \ \ \text { in } {\mathbb {R}}^d, \end{aligned}$$

and the appropriate outgoing radiation condition is the Sommerfeld radiation condition, which requires that

$$\begin{aligned} \lim _{|x|\rightarrow \infty } |x|^{\frac{d-1}{2}} \left( \frac{\partial }{\partial |x|} - i k_0 \right) (u(x) - u_{in}(x))=0. \end{aligned}$$

(2.2)

In particular, we are interested in the case of small resonators. Thus, we will assume that there exists some fixed domain D such that $\Omega$ is given by

$$\begin{aligned} \Omega = \delta D + z, \end{aligned}$$

(2.3)

for some position $z\in {\mathbb {R}}^d$ and characteristic size $0<\delta \ll 1$. Then, making a change of variables, the Helmholtz problem (2.1) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta u + \delta ^2 \omega ^2 \varepsilon (\omega ,k)\mu _0 u = 0 \quad &{}\text { in } D, \\ \Delta u + \delta ^2 k_0^2 u = 0 &{}\text { in } {\mathbb {R}}^d\setminus {\overline{D}}, \\ \end{array}\right. } \end{aligned}$$

(2.4)

along with the same transmission conditions on $\partial D$ and far-field behaviour. The behaviour of resonators which is of interest is when $\delta \ll k_0^{-1}$, meaning the system can be described as being subwavelength. We will study this by performing asymptotics in the regime that the frequency $\omega$ is fixed while the size $\delta \rightarrow 0$.

We will characterise solutions to (2.1) in terms of the system’s resonant frequencies. For a given wavenumber k, we define $\omega =\omega (k)$ to be a resonant frequency if it is such that there exists a non-trivial solution u to (2.1) in the case that $u_{in}=0$.

2.2 Integral formulation

Let G(x, k) be the outgoing Helmholtz Green’s function in ${\mathbb {R}}^d$, defined as the unique solution to

$$\begin{aligned} (\Delta + k^2) G(x,k) = \delta _0(x) \ \ \text { in } {\mathbb {R}}^d, \end{aligned}$$

along with the outgoing radiation condition (2.2). It is well known that G is given by

$$\begin{aligned} G(x,k)= {\left\{ \begin{array}{ll} -\frac{i}{4}H^{(1)}_0(k|x|), \quad &{}d=2,\\ -\frac{e^{ik|x|}}{4\pi |x|}, &{}d=3,\\ \end{array}\right. } \end{aligned}$$

(2.5)

where $H_0^{(1)}$ is the Hankel function of first kind and order zero.

Theorem 2.1

(Lippmann-Schwinger Integral Representation Formula) The solution to the Helmholtz problem (2.1) is given by

$$\begin{aligned} u(x)-u_{in}(x) = -\delta ^2 \omega ^2 \xi (\omega ,k) \int _D G(x-y,\delta k_0) u(y) \mathrm {d}y, \ \ x\in {\mathbb {R}}^d, \end{aligned}$$

(2.6)

where the function $\xi :{\mathbb {C}}\rightarrow {\mathbb {C}}$ describes the permittivity contrast between D and the background and is given by

$$\begin{aligned} \xi (\omega ,k) = \mu _0(\varepsilon (\omega ,k) - \varepsilon _0). \end{aligned}$$

Proof

We see from (2.4) that $\Delta u + \delta ^2\omega ^2\varepsilon (\omega ,k)\mu _0u=0$ in D, so it holds that

$$\begin{aligned} \Delta u +\delta ^2 k_0^2 u = -\delta ^2 \omega ^2 \xi (\omega ,k)u, \end{aligned}$$

where $\xi (\omega ,k) = \mu _0(\varepsilon (\omega ,k) - \varepsilon _0)$. Therefore, the Helmholtz problem (2.4) becomes

$$\begin{aligned} (\Delta + \delta ^2 k_0^2)(u(y) - u_{in}(y)) = -\delta ^2 \omega ^2 \xi (\omega ,k)u(y) \chi _D(y), \ \ y\in {\mathbb {R}}^d \setminus \partial D, \end{aligned}$$

with $\chi _D$ being the indicator function of the set D. Then, we know that for $x\in {\mathbb {R}}^d$ and $y\in {\mathbb {R}}^d\setminus \partial D$, the following identity holds:

$$\begin{aligned} \nabla _y \cdot \Big [ G(x-y,\delta k_0) \nabla _y \Big ( u(y)&-u_{in}(y) \Big ) - \Big ( u(y)-u_{in}(y) \Big ) \nabla _y G(x-y,\delta k_0) \Big ] \\&= -\delta ^2 \omega ^2 \xi (\omega ,k)u(y)G(x-y,\delta k_0) \chi _D(y) - \Big ( u(y)\\&\quad -u_{in}(y) \Big )\delta _0(x-y). \end{aligned}$$

Let $S_R$ be a large sphere with radius R large enough so that $D \subset S_R$. Integrating the above identity over $y \in S_r {\setminus } \partial D$ and letting $R\rightarrow +\infty$, we can use the radiation condition (2.2) in the far field and the transmission conditions on $\partial D$ to obtain the desired integral representation formula. $\square$

We are interested in understanding how the formula from Theorem 2.1 behaves in the case that $\delta$ is small. In particular, we wish to understand the operator $K^{\delta k_0}_D: L^2(D)\rightarrow L^2(D)$ given by

$$\begin{aligned} K^{\delta k_0}_D[u](x) = - \int _{\Omega } G(x-y,\delta k_0) u(y) \mathrm {d}y, \ \ \ \ x \in D. \end{aligned}$$

(2.7)

The Helmholtz Green’s function has helpful asymptotic expansions which facilitate this. However, the behaviour is quite different in two and three dimensions, so we must now consider these two settings separately. We will first work on the three-dimensional case, and then treat the two-dimensional setting as the asymptotic expansions are more complicated.

2.3 Reformulation as a subwavelength resonance problem

In order to reveal the behaviour of the system of nano-particles, we will characterise the properties of the operator $K^{\delta k_0}_D$. We observe that the Lippmann-Schwinger formulation (2.6) of the problem is equivalent to

$$\begin{aligned} (u-u_{in})(x) = \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D[u](x). \end{aligned}$$

This is equivalent to

$$\begin{aligned} (I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)[u](x) = u_{in}(x), \end{aligned}$$

which gives

$$\begin{aligned} u(x) = (I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1}[u_{in}](x), \end{aligned}$$

for all $x\in D$, where I denotes the identity operator. Then, the subwavelength resonance problem is to find $\omega \in {\mathbb {C}}$ close to 0, such that the operator $(I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1}$ is singular, or equivalently, such that there exists $u \in L^2(D)$, $u \ne 0$ with

$$\begin{aligned} u(x) - \delta ^2 \omega ^2 \xi (\omega ,k) \int _D G(x-y,\delta k_0) u(y) \mathrm {d}y = 0, \ \ \ \text { for } x \in D. \end{aligned}$$

(2.8)

2.4 Three dimensions

We consider the three-dimensional case, $d=3$. Let us define the Newtonian potential on D to be $K^{(0)}_D: L^2(D)\rightarrow L^2(D)$ such that

$$\begin{aligned} K^{(0)}_D[u](x) := - \int _D u(y) G(x-y,0) \mathrm {d}y = - \frac{1}{4\pi } \int _D \frac{1}{|x-y|}u(y)\mathrm {d}y. \end{aligned}$$

(2.9)

Similarly, we define the operators $K^{(n)}_D: L^2(D) \rightarrow L^2(D)$, for $n=1,2,\dots ,$ as

$$\begin{aligned} K^{(n)}_D[u](x) = - \frac{i}{4\pi } \int _D \frac{(i|x-y|)^{n-1}}{n!}u(y)\mathrm {d}y. \end{aligned}$$

(2.10)

Then, in order to capture the behaviour of $K^{\delta k_0}_D$ for small $\delta$, we can use an asymptotic expansion in terms of small $\delta$.

Lemma 2.2

Suppose that $d=3$. The operator $K^{\delta k_0}_D$ can be rewritten as

$$\begin{aligned} K^{\delta k_0}_D = \sum _{n=0}^{\infty } (\delta k_0)^n K^{(n)}_D, \end{aligned}$$

where the series converges in the $L^2(D) \rightarrow L^2(D)$ operator norm if $\delta k_0$ is small enough.

Proof

This follows from an application of the Taylor expansion on the operator $K^{\delta k_0}_D$. Indeed, using Taylor expansion on the second variable of G, we can see that

$$\begin{aligned} G(x-y,\delta k_0) = \sum _{n=0}^{\infty } (\delta k_0)^n \frac{\partial ^n G}{\partial k^n}(x-y,k)\Big |_{k=0}. \end{aligned}$$

Since we are working in three dimensions,

$$\begin{aligned} G(x,k) = - \frac{e^{ik|x|}}{4\pi |x|} \end{aligned}$$

and, thus,

$$\begin{aligned} G(x-y,0) = -\frac{1}{4\pi |x-y|} \quad \text {and}\quad \frac{\partial ^n G}{\partial k^n}(x-y,k) = -\frac{i}{4\pi } \frac{(i|x-y|)^{n-1}}{n!} \quad \text {for }n>0. \end{aligned}$$

Hence,

$$\begin{aligned} G(x-y,\delta k_0)&= \sum _{n=0}^{\infty } (\delta k_0)^n \frac{\partial ^n G}{\partial k^n}(x-y,k)\Big |_{k=0} = \sum _{n=0}^{\infty } (\delta k_0)^n \left( -\frac{i}{4\pi }\right) \frac{(i|x-y|)^{n-1}}{n!}, \end{aligned}$$

and then, multiplying by u and integrating over D, gives

$$\begin{aligned} K^{\delta k_0}_D[u](y)&= \sum _{n=0}^{\infty } (\delta k_0)^n K^{(n)}_D[u](y), \end{aligned}$$

which is the desired result. $\square$

2.4.1 Eigenvalue calculation

In order to study the operator $K^{\delta k_0}_D$, we need to find its eigenvalues. From Lemma 2.2, if $k_0$ is fixed then we can write our operator as

$$\begin{aligned} K^{\delta k_0}_D = K^{(0)}_D + \delta k_0 K^{(1)}_D + O(\delta ^2) \ \ \ \text { as } \delta \rightarrow 0. \end{aligned}$$

(2.11)

Since we know that $K^{(0)}_D$ is self-adjoint, we know that it admits eigenvalues. Let us denote such an eigenvalue by $\lambda _0$, and by $u_0$ the associated eigenvector. Let us now consider the problem

$$\begin{aligned} K^{\delta k_0}_D u_{\delta } = \lambda _{\delta } u_{\delta }, \end{aligned}$$

(2.12)

where $\lambda _{\delta }$ denotes an eigenvalue of the operator $K^{\delta k_0}_D$ and $u_{\delta }$ denotes the associated eigenvector. We wish to express $\lambda _{\delta }$ as a function of $\lambda _0$, for small values of $\delta$, which is a classical idea in perturbation theory. This is possible, since $K^{(0)}_D$ is a compact operator and hence, all the eigenvalues are isolated, except from 0. Using this eigenvalue problem, we will find the resonant frequency $\omega _s$ and the associated wavenumber $k_s$ of the halide perovskite nano-particle.

Proposition 2.3

Let $\lambda _{\delta }$ denote a non-zero eigenvalue of the operator $K^{\delta k_0}_D$ in dimension three. Then, if $\delta$ is small, it is approximately given by

$$\begin{aligned} \lambda _{\delta } \approx \lambda _0 + \delta k_0 \langle K^{(1)}_D u_0, u_0 \rangle . \end{aligned}$$

(2.13)

Proof

Using Theorem 2.3 of [14], eigenvalue perturbation formulas of this kind are straightforward to obtain, provided that the unperturbed eigenvalue is semi-simple. Since $K_D^{(0)}$ is compact, all its non-zero eigenvalues are simple and isolated. Consequently, we know that there exists an expansion of the form $\lambda _{\delta }=\lambda _0+\delta A$, for some constant A which it remains to calculate. We start by truncating the $O(\delta ^2)$ term in the expansion (2.11). Then, we have that

Since $K^{(0)}_D$ is self-adjoint, we have that

$$\begin{aligned} \ \lambda _0\langle u_{\delta } , u_0 \rangle + \delta k_0 \langle K^{(1)}_D u_{\delta }, u_0 \rangle = \lambda _{\delta } \langle u_{\delta },u_0 \rangle . \end{aligned}$$

Finally, since $u_{\delta }\approx u_0$ we find that

$$\begin{aligned} \lambda _{\delta } = \lambda _0 + \delta k_0 \frac{\langle K^{(1)}_D u_{\delta }, u_0 \rangle }{\langle u_{\delta },u_0 \rangle } \approx \lambda _0 + \delta k_0 \langle K^{(1)}_D u_0, u_0 \rangle , \end{aligned}$$

which is the desired result. $\square$

The following corollary is a direct consequence of Proposition 2.13:

Corollary 2.3.1

Let $\lambda _{\delta }$ denote an eigenvalue of the operator $K^{\delta k_0}_D$ in three dimensions. Then, if $\delta$ is small, it is approximately given by

$$\begin{aligned} \lambda _{\delta } \approx \lambda _0 - \frac{i}{4\pi } \delta k_0 {\mathbb {B}}, \end{aligned}$$

(2.14)

where ${\mathbb {B}}:=(\int _D u_0(y) \mathrm {d}y)^2$ is a constant.

Proof

From (2.10), we get that

$$\begin{aligned} K^{(1)}_D[u](x) = -\frac{i}{4\pi } \int _{D} \frac{ (i|x-y|)^{1-1} }{1!}u(y)\mathrm {d}y = -\frac{i}{4\pi } \int _{D} u(y) \mathrm {d}y. \end{aligned}$$

Let us define the constant ${\mathbb {B}}:=(\int _D u_0(y) \mathrm {d}y)^2$. Then, we observe that

$$\begin{aligned} \langle K^{(1)}_D u_0, u_0 \rangle = \int _D \left( -\frac{i}{4\pi }\right) u_0(y) \int _D \overline{u_0}(x)\mathrm {d}x \mathrm {d}y = -\frac{i}{4\pi } \left( \int _D u_0(y) \mathrm {d}y \right) ^2 = -\frac{i}{4\pi }{\mathbb {B}}. \end{aligned}$$

Substituting into (2.13) gives the desired result. $\square$

2.4.2 Frequency and wavenumber

Let us now find the resonant frequency $\omega _{\delta }$ and wavenumber $k_{\delta }$ associated to this eigenvalue, which will also constitute the basis of our analysis of the operator $K^{\delta k_0}_D$. From (2.8), we see that if $u=u_\varepsilon$, then $1 = \delta ^2\omega ^2 \xi (\omega ,k) \lambda _{\delta }$ so, using Corollary 2.14 we have that

$$\begin{aligned} \varepsilon (\omega ,k) = \frac{1}{\mu _0 \delta ^2 \omega ^2 \left( \lambda _0 - \frac{i}{4\pi } \delta k_0 {\mathbb {B}} \right) } + \varepsilon _{0}. \end{aligned}$$

(2.15)

In order to study halide perovskite particles, we want the permittivity $\varepsilon (\omega ,k)$ to be given by (1.1), that is,

$$\begin{aligned} \varepsilon (\omega ,k) = \varepsilon _0+\frac{\alpha }{\beta -\omega ^2+\eta k^2 - i\gamma \omega }, \end{aligned}$$

(2.16)

where $\alpha ,\beta ,\gamma ,\eta$ are positive constants. Comparing the two expressions (2.15) and (2.16) we see that

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha \mu _0 \delta ^2 \omega ^2 \lambda _0 - \beta + \omega ^2 - \eta k^2 = 0, \\ \gamma \omega - \mu _0 \frac{1}{4\pi }\alpha \delta ^3\omega ^2k_0{\mathbb {B}}=0. \end{array}\right. } \end{aligned}$$

(2.17)

We study these two equations separately. First, we look at the second equation of (2.17). We have that

$$\begin{aligned} \omega \left( \gamma - \mu _0 \frac{1}{4\pi }\alpha \delta ^3\omega k_0{\mathbb {B}}\right) =0, \end{aligned}$$

meaning that

$$\begin{aligned} \omega = 0 \quad \text { or } \quad \omega = \frac{4\pi \gamma }{\alpha \mu _0\delta ^3 k_0 {\mathbb {B}}}. \end{aligned}$$

For $\omega = \frac{4\pi \gamma }{\alpha \mu _0\delta ^3 k_0 {\mathbb {B}}}$, we obtain that

$$\begin{aligned} \eta k^2 = (1 + \alpha \mu _0 \delta ^2 \lambda _0)\omega ^2 - \beta , \end{aligned}$$

which has solutions

$$\begin{aligned} k = \pm \sqrt{ \frac{16\pi ^2\gamma ^2(1 + \alpha \mu _0 \delta ^2 \lambda _0)}{\alpha ^2\mu _0^2\delta ^6 k_0^2 {\mathbb {B}}^2 \eta } - \frac{\beta }{\eta }}. \end{aligned}$$

(2.18)

The case of $\omega =0$ is not of physical interest here. Thus, denoting this specific frequency by $\omega _{\delta }$ and the associated wavenumber by $k_{\delta }$, we will work with

$$\begin{aligned} \omega _{\delta } = \frac{4\pi \gamma }{\alpha \mu _0\delta ^3k_0{\mathbb {B}}} \quad \text { and } \quad k_{\delta } = \sqrt{ \frac{16\pi ^2\gamma ^2(1 + \alpha \mu _0 \delta ^2 \lambda _0)}{\alpha ^2\mu _0^2\delta ^6 k_0^2 {\mathbb {B}}^2 \eta } - \frac{\beta }{\eta }}, \end{aligned}$$

(2.19)

where we have chosen the wavenumber $k_{\delta }$ to be positive.

2.4.3 Asymptotic analysis

Let us now return to the problem of studying the singularities of the operator $(I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1}$. We have the following equivalence:

$$\begin{aligned} (I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1} = 0 \ \Leftrightarrow \ \left( I - \delta ^2 \omega ^2 \xi (\omega ,k) \sum _{n=0}^{\infty }(\delta k_0)^n K^{(n)}_D \right) ^{-1}=0. \end{aligned}$$

We define

$$\begin{aligned} A_n:= \delta ^2 \omega ^2 \xi (\omega ,k) K^{(n)}_D = - \delta ^2 \omega ^2 \xi (\omega ,k) \frac{i}{4\pi } \int _D \frac{(i|x-y|)^{n-1}}{n!}u(y)\mathrm {d}y. \end{aligned}$$

Then, it holds that

$$\begin{aligned} \left( I - \delta ^2 \omega ^2 \xi (\omega ,k) \sum _{n=0}^{\infty }(\delta k_0)^n K^{(n)}_D \right) ^{-1}&= \left( I - \sum _{n=0}^{\infty }(\delta k_0)^n A_n \right) ^{-1} \\&= \sum _{i=0}^{\infty } \left( (I-A_0-\delta k_0 A_1)^{-1} \sum _{n=2}^{\infty } (\delta k_0)^n A_n \right) ^i\\&\quad (I - A_0 -\delta k_0 A_1)^{-1}\\&= (I - A_0 -\delta k_0 A_1)^{-1}\\&\ \ \ +(I - A_0 -\delta k_0 A_1)^{-1} \\&(\delta k_0)^2 A_2 (I - A_0 -\delta k_0 A_1)^{-1} + O(\delta ^4). \end{aligned}$$

Thus, the above equivalence yields

$$\begin{aligned} (I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1} = 0 \ \Leftrightarrow \ \left( I - \delta ^2 \omega ^2 \xi (\omega ,k) \sum _{n=0}^{\infty }(\delta k_0)^n K^{(n)}_D \right) ^{-1}=0 \ \Leftrightarrow \\ (I - A_0 -\delta k_0 A_1)^{-1}+(I - A_0 -\delta k_0 A_1)^{-1} (\delta k_0)^2 A_2 (I - A_0 -\delta k_0 A_1)^{-1} + O(\delta ^4)=0. \end{aligned}$$

Using this expression, we obtain the following proposition.

Proposition 2.4

Let $d=3$ and let $\omega _{\delta }$ be defined by (2.19). Then, as $\delta \rightarrow 0$, the $O(\delta ^4)$ approximation of the subwavelength resonant frequencies $\omega _s$ and the associated wavenumbers $k_s$ of the single halide perovskite resonator $\Omega = \delta D + z$ satisfy

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta } = -\delta ^4 k_0^2 \omega _s^2 \xi (\omega _s,k_s) \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle . \end{aligned}$$

(2.20)

Proof

For $\psi \in L^{2}(D)$, and dropping the $O(\delta ^4)$ term, we have

$$\begin{aligned} \Big [(I - A_0 -\delta k_0 A_1)^{-1}+(I - A_0 -\delta k_0 A_1)^{-1} (\delta k_0)^2 A_2 (I - A_0 -\delta k_0 A_1)^{-1}\Big ][\psi ]=0. \end{aligned}$$

(2.21)

We apply a pole-pencil decomposition, as it is defined in [4], to the term $(I - A_0 -\delta k_0 A_1)^{-1}[\psi ]$ and obtain

$$\begin{aligned} (I - A_0 -\delta k_0 A_1)^{-1}[\psi ] = \frac{\langle u_{\delta },\psi \rangle u_{\delta }}{1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }} + R(\delta )[\psi ], \end{aligned}$$

where the remainder term $R(\delta )[\psi ]$ can be dropped. Hence, (2.21) is, at leading order, equivalent to

$$\begin{aligned} \frac{\langle u_{\delta },\psi \rangle u_{\delta }}{1 - \delta ^2 \omega ^2 \xi (\omega _s,k_s) \lambda _{\delta }} + \frac{\langle u_{\delta },\psi \rangle u_{\delta }}{1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }} (\delta k_0)^2 A_2 \frac{\langle u_{\delta },\psi \rangle u_{\delta }}{1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }} = 0, \end{aligned}$$

which reduces to

$$\begin{aligned} \frac{u_{\delta }}{1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }} + \frac{u_{\delta }\langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle }{(1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta })^2} \delta ^4 k_0^2 \omega _s^2 \xi (\omega _s,k_s) = 0, \end{aligned}$$

which can be rearranged to give the desired result. $\square$

Remark

In the appendix, we will recover a formula for $\langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle$.

Before we move on to the consequences of this proposition, we recall that

$$\begin{aligned} K^{(2)}_D[u](x) = -\frac{i}{4\pi } \int _D \frac{i|x-y|}{2}u(y)\mathrm {d}y = \frac{1}{8\pi } \int _D |x-y|u(y)\mathrm {d}y. \end{aligned}$$

Thus, we can define the constant ${\mathbb {F}}$ to be such that

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle&= \int K^{(2)}_D[u_{\delta }](x) \overline{u_{\delta }}(x) \mathrm {d}x = \frac{1}{8\pi } \int _D \int _D |x-y| u_{\delta }(y) \overline{u_{\delta }}(x) \mathrm {d}y \mathrm {d}x =: \frac{1}{8\pi } {\mathbb {F}}. \end{aligned}$$

So, from (2.20), we see that

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta } = - \frac{\delta ^4 k_0^2 \omega _s^2 \xi (\omega _s,k_s)}{8\pi } {\mathbb {F}}. \end{aligned}$$

(2.22)

Then the following two corollaries are immediate consequences of the Proposition 2.4.

Corollary 2.4.1

Let $d=3$. Then, as $\delta \rightarrow 0$, the $O(\delta ^8)$ approximation of the subwavelength resonant frequencies of the halide perovskite resonator $\Omega = \delta D + z$ are given by

$$\begin{aligned} 1 - \frac{\omega _s^2}{\omega _{\delta }^2} \lambda _{\delta } (\varepsilon (\omega _s,k_s) - \varepsilon _0) \frac{64 \pi ^2 \gamma ^2}{\alpha ^2 \mu _0 \delta ^4 k_0^2 {\mathbb {B}}^2} = - \frac{\delta ^4 \omega _s^2 k_0^2 \xi (\omega _s,k_s)}{8\pi } {\mathbb {F}}. \end{aligned}$$

(2.23)

Proof

By a direct calculation and using (2.19), we have

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }&\ = 1 - \delta ^2 \omega _s^2 \mu _0(\varepsilon (\omega _s,k_s)-\varepsilon _0) \lambda _{\delta } \\&\overset{(2.19)}{=} 1 - \delta ^2 \frac{\omega _s^2}{\omega _{\delta }^2} \mu _0(\varepsilon (\omega _s,k_s)-\varepsilon _0) \lambda _{\delta } \frac{64 \pi ^2 \gamma ^2}{\alpha ^2 \mu _0^2 \delta ^4 k_0^2 {\mathbb {B}}^2}\\&\ = 1 - \frac{\omega _s^2}{\omega _{\delta }^2} \lambda _{\delta } (\varepsilon (\omega _s,k_s) - \varepsilon _0) \frac{64 \pi ^2 \gamma ^2}{\alpha ^2 \mu _0 \delta ^4 k_0^2 {\mathbb {B}}^2}. \end{aligned}$$

Then, using (2.22), the result follows. $\square$

Corollary 2.4.2

Let $d=3$. Then, as $\delta \rightarrow 0$, the $O(\delta ^4)$ approximation of the subwavelength resonant frequencies of the halide perovskite resonator $\Omega = \delta D + z$ can be computed as

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta } = -\frac{\omega _s^2}{\omega _{\delta }^2}(\varepsilon (\omega _s,k_s) - \varepsilon _0) \frac{8\pi \gamma ^2{\mathbb {F}}}{\alpha ^2 \mu _0 \delta ^2 {\mathbb {B}}^2}. \end{aligned}$$

(2.24)

Proof

Again, we can calculate this directly:

$$\begin{aligned} \frac{\delta ^4 k_0^2 \omega _s^2 \xi (\omega _s,k_s)}{8\pi } {\mathbb {F}}&\ = \frac{1}{8\pi } \delta ^4 \frac{\omega _s^2}{\omega _{\delta }^2} k_0^2 \mu _0 (\varepsilon (\omega _s,k_s) - \varepsilon _0) \omega _{\delta }^2 \\&\overset{(2.19)}{=} \frac{1}{8\pi } \frac{\omega _s^2}{\omega _{\delta }^2} \delta ^4 k_0^2 \mu _0 (\varepsilon (\omega _s,k_s) - \varepsilon _0) \frac{64 \pi ^2 \gamma ^2}{\alpha ^2 \mu _0^2 \delta ^4 k_0^2 {\mathbb {B}}^2}\\&= \frac{\omega _s^2}{\omega _{\delta }^2} (\varepsilon (\omega _s,k_s) - \varepsilon _0) \frac{8\pi \gamma ^2}{\alpha ^2 \mu _0 \delta ^2 {\mathbb {B}}^2}. \end{aligned}$$

Then, using (2.22), the result follows. $\square$

We finish our analysis of the three-dimensional case with the following proposition.

Proposition 2.5

Let $d=3$. For $\omega$ close to the resonant frequency $\omega _s$, the field scattered by the halide perovskite nano-particle $\Omega = \delta D + z$ can be approximated by

$$\begin{aligned} u(x)-u_{in}(x) \approx \frac{1 + \delta ^2 \omega ^2 G(x-y,\delta k_0) \xi (\omega ,k)}{\delta ^2 \omega ^2 \left( \lambda _{\delta } - \lambda _0 + \frac{i}{4\pi }\delta k_0 {\mathbb {B}} \right) \xi (\omega ,k)} \langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }. \end{aligned}$$

Proof

Our goal is to find $u\in L^{2}(D)$, $u\ne 0$ such that (2.8) is satisfied. Using the pole-pencil decomposition, we can rewrite

$$\begin{aligned} u(x)-u_{in}(x) \approx -\delta ^2 \omega ^2 \xi (\omega ,k)&G(x-y,\delta k_0) \frac{\langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{1-\delta ^2\omega ^2\xi (\omega ,k)\lambda _{\delta }} \\&+ \delta ^{4}k_0^2\omega ^2\xi (\omega ,k) \frac{\langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle \langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{(1-\delta ^2\omega ^2\xi (\omega ,k)\lambda _{\delta })^2}. \end{aligned}$$

Using (2.20) and plugging it in the above expression, we obtain

$$\begin{aligned} u(x)-u_{in}(x)&\approx \ -\delta ^2 \omega ^2 \xi (\omega ,k)G(x-y,\delta k_0) \frac{\langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{-\delta ^4 k_0^2 \omega ^2 \xi (\omega ,k) \langle K^{(2)}_D[u_{\delta }], \upsilon _{\delta } \rangle } \\&\ \ \ \ \ \ \ + \delta ^{4}k_0^2\omega ^2\xi (\omega ,k) \frac{\langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle \langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{\delta ^8 k_0^4 \omega ^4 \xi (\omega ,k)^2 \langle K^{(2)}_D[u_{\delta }], \upsilon _{\delta } \rangle ^2} \\&= \ \frac{G(x-y,\delta k_0)\langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{\delta ^2 k_0^2 \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle } + \frac{\langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }}{\delta ^4 k_0^2 \omega ^2 \xi (\omega ,k) \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle }. \end{aligned}$$

Thus, defining the constant ${\mathbb {F}}:=8\pi \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle$, we obtain

$$\begin{aligned} u(x)-u_{in}(x) \approx \ \frac{8\pi \Big (1+\delta ^2\omega ^2G(x-y,\delta k_0)\xi (\omega ,k)\Big )}{\delta ^4 k_0^2 \omega ^2 \xi (\omega ,k) {\mathbb {F}}} \langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }. \end{aligned}$$

(2.25)

From the Appendix A.1, we have that

$$\begin{aligned} {\mathbb {F}} = \frac{8\pi }{\delta ^2 k_0^2} \left( \lambda _{\delta } - \lambda _0 + \frac{i}{4\pi } \delta k_0 {\mathbb {B}} \right) . \end{aligned}$$

Plugging it into (2.25), we obtain

$$\begin{aligned} u(x)-u_{in}(x) \approx \frac{8\pi \Big (1+\delta ^2\omega ^2G(x-y,\delta k_0)\xi (\omega ,k)\Big )}{\delta ^4 k_0^2 \omega ^2 \xi (\omega ,k) {\mathbb {F}}} \frac{\delta ^2 k_0^2}{8\pi } \frac{1}{\lambda _{\delta } - \lambda _0 + \frac{i}{4\pi } \delta k_0 {\mathbb {B}}} \langle u_{in}, u_{\delta } \rangle \int _{D} u_{\delta }, \end{aligned}$$

from which the result follows. $\square$

2.5 Two dimensions

We now turn our attention to the two-dimensional setting. We define the Newtonian potential on D, $K^{(0)}_D: L^2(D)\rightarrow L^2(D)$, by

$$\begin{aligned} K^{(0)}_D[u](x) := -\int _D u(y) G(x-y,0)\mathrm {d}y = - \frac{1}{2\pi } \int _D \log |x-y| u(y) \mathrm {d}y. \end{aligned}$$

We also define the operators $K^{(-1)}_D: L^2(D)\rightarrow L^2(D)$ and $K^{(1)}_D: L^2(D)\rightarrow L^2(D)$ by

$$\begin{aligned} K^{(-1)}_D[u](x) := - \frac{1}{2\pi } \int _D u(y) \mathrm {d}y \quad \text { and } \quad K^{(n)}_D[u](x) := \int _D \frac{\partial ^n}{\partial k^n}G(x-y,k)\Big |_{k=0} u(y) \mathrm {d}y. \end{aligned}$$

Then, from the asymptotic expansion of the Hankel function, we have the following result.

Lemma 2.6

Suppose that $d=2$. Then, for fixed $k_0 \in {\mathbb {C}}$, the operator $K^{\delta k_0}_D$ satisfies

$$\begin{aligned} K^{\delta k_0}_D = \log (\delta k_0 {\hat{\gamma }}) K^{(-1)}_D + K^{(0)}_D + (\delta k_0)^2 \log ( {\hat{\gamma }} \delta k_0 ) K^{(1)}_D + O( \delta ^4 \log \delta ), \end{aligned}$$

(2.26)

as $\delta \rightarrow 0$, with convergence in the $L^2(D)\rightarrow L^2(D)$ operator norm and the constant ${\hat{\gamma }}$ being given by ${\hat{\gamma }}:=\frac{1}{2}k_0\exp (\gamma -\frac{i\pi }{2})$, where $\gamma$ is the Euler constant.

2.5.1 Eigenvalue calculation

We use the same notation for $u_{\delta }$ as in Sect 2.4.1. Let us consider the eigenvalue problem

$$\begin{aligned} K^{\delta k_0}_D u_{\delta } = \lambda _{\delta } u_{\delta }, \end{aligned}$$

(2.27)

where $\lambda _{\delta }$ denotes a non-zero eigenvalue of the operator $K^{\delta k_0}_D$, and $u_{\delta }$ denotes an associated eigenvector. As in the case of dimension $d=3$, we now wish to express $\lambda _{\delta }$ in terms of, for small values of $\delta$. This is possible since $K^{(-1)}_D$ is a compact operator.

Proposition 2.7

Let $\lambda _{\delta }$ denote a non-zero eigenvalue of the operator $K^{\delta k_0}_D$ in dimension 2. Then, for small $\delta$, it is approximately given by:

$$\begin{aligned} \lambda _{\delta } \approx \log (\delta k_0 {\hat{\gamma }})\lambda _{-1} + \langle K^{(0)}_D u_{-1}, u_{-1} \rangle + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_D u_{-1}, u_{-1} \rangle , \end{aligned}$$

(2.28)

where $\lambda _{-1}$ and $u_{-1}$ are an eigenvalue and the associated eigenvector of the potential $K^{(-1)}_D$.

Proof

Since $K^{(-1)}_D$ is a compact operator, it has simple eigenvalues so we can use Theorem 2.3 of [14]. We start by dropping the $O(\delta ^4\log (\delta ))$ term on the expansion (2.26). Then, we have that

$$\begin{aligned} K^{\delta k_0}_D u_{\delta } = \lambda _{\delta } u_{\delta }&\Leftrightarrow \ (\log (\delta k_0 {\hat{\gamma }}) K^{(-1)}_D + K^{(0)}_D + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) K^{(1)}_D)u_{\delta } = \lambda _{\delta } u_{\delta } \\&\Leftrightarrow \ \log (\delta k_0 {\hat{\gamma }}) \lambda _{-1}\langle u_{\delta } , u_0 \rangle + \langle K^{(0)}_D u_{\delta }, u_{-1} \rangle \\&\quad + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_D u_{\delta }, u_{-1} \rangle = \lambda _{\delta } \langle u_{\delta },u_{-1} \rangle . \end{aligned}$$

Therefore, assuming that $u_{\delta } \approx u_{-1}$, we can see that

which is the desired result. $\square$

The following corollary is a direct consequence of the above proposition.

Corollary 2.7.1

Let $\lambda _{\delta }$ denote an eigenvalue of the operator $K^{\delta k_0}_D$ in dimension 2. Then, for small $\delta$, it is approximately given by

$$\begin{aligned} \lambda _{\delta } \approx \log (\delta k_0 {\hat{\gamma }})\lambda _{-1} - \frac{{\mathbb {P}}}{2\pi } - \frac{i(\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}{4\pi }, \end{aligned}$$

(2.29)

where ${\mathbb {P}}$ and ${\mathbb {G}}$ are constants that depend on $u_{-1}$.

Proof

We observe that

$$\begin{aligned} \langle K^{(0)}_D u_{-1}, u_{-1} \rangle&= \int _D \left( -\frac{1}{2\pi } \int _D \log |x-y| u_{-1}(y) \mathrm {d}y \right) \overline{u_{-1}}(x) \mathrm {d}x \\&= -\frac{1}{2\pi } \int _D \int _D \log |x-y| u_{-1}(y) \overline{u_{-1}}(x) \mathrm {d}y \mathrm {d}x =: - \frac{1}{2\pi } {\mathbb {P}}. \end{aligned}$$

Then, for $u\in L^2(D)$,

$$\begin{aligned} K^{(1)}_D[u](x)&= \int _D \frac{\partial }{\partial k} G(x-y,k)\Big |_{k=0} u(y) \mathrm {d}y \\&\quad = \int _D \frac{\partial }{\partial k} \left( -\frac{i}{4} H_0^{(1)}(k|x-y|) \right) \Big |_{k=0} u(y) \mathrm {d}y= -\frac{i}{4\pi } \int _D \frac{u(y)}{|x-y|} \mathrm {d}y, \end{aligned}$$

and so, we have

$$\begin{aligned} \langle K^{(1)}_D u_{-1}, u_{-1} \rangle&= \int _D \left( -\frac{i}{4\pi } \int _D \frac{u_{-1}(y)}{|x-y|} \mathrm {d}y \right) \overline{u_{-1}}(x) \mathrm {d}x \\&\quad = -\frac{i}{4\pi } \int _D \int _D \frac{u_{-1}(y) \overline{u_{-1}}(x)}{|x-y|} \mathrm {d}y \mathrm {d}x =: -\frac{i}{4\pi } {\mathbb {G}}. \end{aligned}$$

Hence, from (2.28), we obtain the desired result. $\square$

2.5.2 Frequency and wavenumber

Let us now find the frequency $\omega _{\delta }$ and the wavenumber $k_{\delta }$ associated to this eigenvalue, which will also constitute the basis of our analysis of the operator $K^{\delta k_0}_D$. We see that (2.8) gives us that

$$\begin{aligned} 1 = \delta ^2\omega ^2 \xi (\omega ,k) \lambda _{\delta }&\Leftrightarrow \ 1 = \delta ^2\omega ^2 \mu _0 (\varepsilon (\omega ,k) - \varepsilon _0) \lambda _{\delta }. \end{aligned}$$

Using the expression (2.28) for $\lambda _{\delta }$, we see that

$$\begin{aligned} \varepsilon (\omega ,k) = \frac{1}{\mu _0 \delta ^2 \omega ^2 \left( \log (\delta k_0 {\hat{\gamma }})\lambda _{-1} - \frac{{\mathbb {P}}}{2\pi } - \frac{i(\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}{4\pi } \right) } + \varepsilon _{0}. \end{aligned}$$

Arguing in the same way as in section 2.4.4 and comparing the two permittivity expressions, we obtain the following system:

$$\begin{aligned} {\left\{ \begin{array}{ll} 4\pi \alpha \delta ^2\omega ^2\mu _0\log (\delta k_0 {\hat{\gamma }})\lambda _{-1} - 2{\mathbb {P}} \alpha \delta ^2\omega ^2\mu _0 - 4\pi \beta + 4\pi \omega ^2-4\pi \eta k^2 = 0,\\ -\alpha \delta ^4\omega ^2\mu _0 k_0^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}} + 4\pi \gamma \omega = 0. \end{array}\right. } \end{aligned}$$

(2.30)

From the second equation in (2.30), we see that

$$\begin{aligned} \omega ( -\alpha \delta ^4\omega \mu _0 k_0^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}} + 4\pi \gamma ) = 0, \end{aligned}$$

which shows us that

$$\begin{aligned} \omega =0 \ \ \ \text { or } \ \ \ \omega = \frac{4\pi \gamma }{\alpha \delta ^4\mu _0 k_0^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}. \end{aligned}$$

For $\omega = \frac{4\pi \gamma }{\alpha \delta ^4\mu _0 k_0^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}$, we obtain the equation

$$\begin{aligned}&4\pi \alpha \delta ^2\mu _0\lambda _{-1}\log (\delta k_0 {\hat{\gamma }})\frac{16\pi ^2\gamma ^2}{\alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2} - 2{\mathbb {P}} \alpha \delta ^2\mu _0 \frac{16\pi ^2\gamma ^2}{\alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}\\&\quad - 4\pi \beta + 4\pi \frac{16\pi ^2\gamma ^2}{\alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2} - 4\pi \eta k^2=0, \end{aligned}$$

which has solutions

$$\begin{aligned} k = \pm \sqrt{-\frac{\beta }{\eta } + \Big ( 2\pi \alpha \delta ^2\mu _0\lambda _{-1} \log (\delta k_0 {\hat{\gamma }}) - \alpha \delta ^2\mu _0{\mathbb {P}}+2\pi \Big )\frac{8\pi \gamma ^2}{\eta \alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}}. \end{aligned}$$

Yet again, we discard the case of $\omega =0$, as there is no physical interest. Denoting the frequency by $\omega _{\delta }$ and the wavenumber by $\lambda _{\delta }$, we will work with

$$\begin{aligned} \begin{aligned}&\omega _{\delta } = \frac{4\pi \gamma }{\alpha \delta ^4\mu _0 k_0^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}, \\&k_{\delta } = \sqrt{-\frac{\beta }{\eta } + \Big ( 2\pi \alpha \delta ^2\mu _0\lambda _{-1} \log (\delta k_0 {\hat{\gamma }}) - \alpha \delta ^2\mu _0{\mathbb {P}}+2\pi \Big )\frac{8\pi \gamma ^2}{\eta \alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}}, \end{aligned} \end{aligned}$$

(2.31)

where we have chosen the wavenumber to be positive.

2.5.3 Asymptotic analysis

Let us consider $\omega$ near $\omega _{\delta }$, and define the coefficients

$$\begin{aligned} c_n= {\left\{ \begin{array}{ll} \log (\delta k_0 {\hat{\gamma }}), \quad &{}n=-1,\\ 1, &{}n=0,\\ (\delta k_0)^{2n}\log (\delta k_0 {\hat{\gamma }}), &{}n\ge 1. \end{array}\right. } \end{aligned}$$

Then, we can write

$$\begin{aligned} K^{\delta k_0}_D = \sum _{n=-1}^{+\infty } c_n K^{(n)}_D. \end{aligned}$$

We are interested in studying the singularities of the operator $(I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1}$. Setting $B_n:= \delta ^2 \omega ^2 \xi (\omega ,k) K^{(n)}_D$, we find that $(I - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_D)^{-1} = 0$ can be written as

$$\begin{aligned} \left( I - \sum _{n=-1}^{+\infty } c_n B_n \right) ^{-1} = 0, \end{aligned}$$

which can be expanded to give

$$\begin{aligned}&\left( I - \log (\delta k_0 {\hat{\gamma }})B_{-1} - B_0 - (\delta k_0)^{2}\log (\delta k_0 {\hat{\gamma }}) B_1 - \sum _{n\ge 2}^{+\infty }c_n B_n \right) ^{-1}=0, \end{aligned}$$

which gives

$$\begin{aligned} {\mathfrak {L}} + {\mathfrak {L}} (\delta k_0)^{4}\log (\delta k_0 {\hat{\gamma }}) B_2 {\mathfrak {L}} + O(\delta ^6) =0, \end{aligned}$$

where we have defined,

$$\begin{aligned} {\mathfrak {L}} := \Big ( I - \log (\delta k_0 {\hat{\gamma }})B_{-1} - B_0 - (\delta k_0)^{2}\log (\delta k_0 {\hat{\gamma }}) B_1 \Big )^{-1} . \end{aligned}$$

(2.32)

Using this expression, we have the following proposition.

Proposition 2.8

Let $d=2$ and let $\omega _{\delta }$ be defined by (2.31). Then, as $\delta \rightarrow 0$, the $O(\delta ^4)$ approximations of the subwavelength resonant frequencies $\omega _s$ and the associated wavenumbers $k_s$ of the single halide perovskite resonator $\Omega = \delta D + z$ satisfy

$$\begin{aligned} 1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta } = - \delta ^6 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \omega _s^2 \xi (\omega _s,k_s) \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle . \end{aligned}$$

(2.33)

Proof

Applying a pole-pencil decomposition, we obtain

$$\begin{aligned} \Big ( I - \log (\delta k_0 {\hat{\gamma }})B_{-1} - B_0 - (\delta k_0)^{2}\log (\delta k_0 {\hat{\gamma }}) B_1 \Big )^{-1}[\cdot ] = \frac{\langle \cdot ,u_{\delta }\rangle u_{\delta } }{1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta }} + R(\omega _s)[\cdot ], \end{aligned}$$

where the remainder $R(\omega _s)$ is analytic in a neighborhood of $\omega _{\delta }$ and can be dropped. Thus, dropping the $O(\delta ^6)$ term, we find for $\psi \in L^2(D)$ that

$$\begin{aligned} \Big [{\mathfrak {L}} + {\mathfrak {L}} (\delta k_0)^{4}\log (\delta&k_0 {\hat{\gamma }}) B_2 {\mathfrak {L}}\Big ](\psi ) = 0. \end{aligned}$$

Applying a pole-pencil decomposition on (2.32), we get

$$\begin{aligned}&\frac{\langle \psi ,u_{\delta }\rangle u_{\delta }}{1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta }} + \frac{\langle \psi ,u_{\delta }\rangle u_{\delta } }{1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta }} \\&\quad (\delta k_0)^{4}\log (\delta k_0 {\hat{\gamma }}) B_2 \frac{\langle \psi ,u_{\delta }\rangle u_{\delta }}{1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta }} =0. \end{aligned}$$

This implies that

$$\begin{aligned} 1 - \delta ^2\omega _s^2\xi (\omega _s,k_s)\lambda _{\delta } = - \delta ^6 k_0^4&\log (\delta k_0 {\hat{\gamma }}) \omega _s^2 \xi (\omega _s,k_s) \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle , \end{aligned}$$

which is the desired result. $\square$

In order to obtain the associated consequences of this proposition, we observe that, since $d=2$, we have that

$$\begin{aligned} K^{(2)}_D[u_{\delta }](x)&= \int _D \frac{\partial ^2}{\partial k^2} G(x-y,k)\Big |_{k=0}u_{\delta }(y)\mathrm {d}y = \int _D \frac{\partial ^2}{\partial k^2} \left( -\frac{i}{4} H^{(1)}_0(k|x|) \right) \Big |_{k=0}\\&= -\frac{i}{4} \int _D - \frac{1}{\pi |x-y|^2} u_{\delta }(y) \mathrm {d}y = \frac{i}{4\pi } \int _D \frac{u_{\delta }(y)}{|x-y|^2} \mathrm {d}y. \end{aligned}$$

Hence,

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle&= \int _D \left( \frac{i}{4\pi } \int _D \frac{u_{\delta }(y)}{|x-y|^2} \mathrm {d}y \right) \overline{u_{\delta }}(x)\mathrm {d}x = \frac{i}{4\pi } \int _D \int _D \frac{u_{\delta }(y) \overline{u_{\delta }}(x)}{|x-y|^2} \mathrm {d}y \mathrm {d}x =: \frac{i}{4\pi } {\mathbb {S}}. \end{aligned}$$

(2.34)

So, we get that (2.33) is equivalent to

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta } = \frac{ - i \delta ^6 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \omega _s^2 \xi (\omega _s,k_s){\mathbb {S}}}{4\pi }. \end{aligned}$$

(2.35)

Remark

In the Appendix A.2 of this paper, we recover a formula for ${\mathbb {S}}$.

Then, the next two corollaries follow as immediate results.

Corollary 2.8.1

Let $d=2$. Then, as $\delta \rightarrow 0$, the $O(\delta ^{10}\log (\delta )^3)$ approximation of the subwavelength resonant frequencies of the halide perovskite resonator $\Omega = \delta D + z$ can be computed as

$$\begin{aligned} 1 - \frac{\omega _s^2}{\omega _{\delta }^2} \cdot \frac{16\pi ^2\gamma ^2\lambda _{\delta }\Big (\varepsilon (\omega _s,k_s)-\varepsilon _0\Big )}{\alpha ^2\delta ^6\mu _0 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2} = - \frac{ i \delta ^6 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \omega _s^2 \xi (\omega _s,k_s){\mathbb {S}}}{4\pi }. \end{aligned}$$

(2.36)

Proof

By a direct computation, we observe that

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta }&\ = \ 1 - \delta ^2 \omega _s^2 \mu _0 \Big (\varepsilon (\omega _s,k_s)-\varepsilon _0\Big ) \lambda _{\delta } \frac{\omega _{\delta }^2}{\omega _{\delta }^2}\\&\overset{(2.31)}{=} \ 1 - \delta ^2 \frac{\omega _s^2}{\omega _{\delta }^2} \mu _0 \Big (\varepsilon (\omega _s,k_s)-\varepsilon _0\Big ) \lambda _{\delta }\\&\qquad \frac{16\pi ^2\gamma ^2}{\alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}\\&\ = \ 1 - \frac{\omega _s^2}{\omega _{\delta }^2} \cdot \frac{16\pi ^2\gamma ^2\lambda _{\delta }\Big (\varepsilon (\omega _s,k_s)-\varepsilon _0\Big )}{\alpha ^2\delta ^6\mu _0 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}, \end{aligned}$$

and thus, (2.35) gives the desired result. $\square$

Corollary 2.8.2

Let $d=2$. Then, as $\delta \rightarrow 0$, the $O(\delta ^4 \log (\delta ))$ approximation of the subwavelength resonant frequencies of the halide perovskite resonator $\Omega = \delta D + z$ can be computed as

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \lambda _{\delta } = - \frac{\omega _s^2}{\omega ^2_{\varepsilon }} \cdot \frac{ 4 \pi i {\mathbb {S}} \gamma ^2 \Big ( \varepsilon (\omega _s,k_s) - \varepsilon _0 \Big ) }{ \alpha ^2 \delta ^2 \log (\delta k_0 {\hat{\gamma }}) \mu _0 {\mathbb {G}}^2 }. \end{aligned}$$

(2.37)

Proof

Again, to show this, we need to make a straightforward calculation:

$$\begin{aligned} \frac{ i \delta ^6 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \omega _s^2 \xi (\omega _s,k_s){\mathbb {S}}}{4\pi }&\ = \ \frac{i}{4\pi } \ \delta ^6 \ k_0^4 \ \log (\delta k_0 {\hat{\gamma }}) \ \frac{\omega ^2_s}{\omega _{\delta }^2} \ {\mathbb {S}} \ \mu _0 \ \Big ( \varepsilon (\omega _s,k_s) - \varepsilon _0 \Big ) \ \omega _{\delta }^2 \\&\overset{(2.31)}{=} \ \frac{i}{4\pi } \ \delta ^6 \ k_0^4 \ \log (\delta k_0 {\hat{\gamma }}) \ \frac{\omega ^2_s}{\omega _{\delta }^2} \ {\mathbb {S}} \ \mu _0 \ \Big ( \varepsilon (\omega _s,k_s) - \varepsilon _0 \Big ) \\&\qquad \frac{16\pi ^2\gamma ^2}{\alpha ^2\delta ^8\mu _0^2 k_0^4 \log (\delta k_0 {\hat{\gamma }})^2 {\mathbb {G}}^2}\\&\ = \ \frac{\omega _s^2}{\omega ^2_{\varepsilon }} \cdot \frac{ 4 \pi i {\mathbb {S}} \gamma ^2 \Big ( \varepsilon (\omega _s,k_s) - \varepsilon _0 \Big ) }{ \alpha ^2 \delta ^2 \log (\delta k_0 {\hat{\gamma }}) \mu _0 {\mathbb {G}}^2 }. \end{aligned}$$

Hence, (2.35) gives the desired result. $\square$

We continue our analysis in the same way as in the previous case.

Proposition 2.9

Let $d=2$. For $\omega$ real close to the resonant frequency $\omega _s$, the following approximation for the field scattered by the halide perovskite nano-particle $\Omega = \delta D + z$ holds:

$$\begin{aligned} u(x) - u_{in}(x) \approx \frac{ 4\pi \Big ( 1 + \delta ^2 \omega ^2 \xi (\omega ,k)G(x-y,\delta k_0) \Big ) }{i \delta ^6 k_0^4 \omega ^2 \log (\delta k_0 {\hat{\gamma }}) \omega ^2 \xi (\omega ,k) {\mathbb {S}}} \langle u_{in}, u_{\delta } \rangle \int _D u_{\delta }. \end{aligned}$$

(2.38)

Proof

As we mentioned at the beginning or our analysis, our goal is to find $u\in L^{2}(D)$, $u\ne 0$, such that (2.8) is satisfied. Using the pole-pencil decomposition on this Lippmann-Schwinger formulation of the problem, we can rewrite, as in Corollary 2.3 in [2],

$$\begin{aligned} u(x)-u_{in}(x) \ \approx -\delta ^2 \omega ^2 \xi (\omega ,k) G(x-&y,\delta k_0) \frac{\langle u_{in}, u_{\delta } \rangle \int _D u_{\delta }}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }}\\&+ \delta ^6 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \omega ^2 \xi (\omega ,k) \\&\frac{ \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle \langle u_{in}, u_{\delta } \rangle \int _D u_{\delta }}{\Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }\Big )^2}, \end{aligned}$$

which, using (2.35), becomes:

$$\begin{aligned} u(x)-u_{in}(x)&\approx \frac{G(x-y,\delta k_0)\langle u_{in}, u_{\delta } \rangle \int _D u_{\delta } }{\delta ^4 k_0^4 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle }\\&\quad + \frac{\langle u_{in}, u_{\delta } \rangle \int _D u_{\delta }}{\delta ^6 k_0^4 \omega ^2 \log (\delta k_0 {\hat{\gamma }}) \omega ^2 \xi (\omega ,k)\langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle }. \end{aligned}$$

From (2.34), this gives

$$\begin{aligned} u(x)-u_{in}(x)&\ \approx \ \frac{ 4\pi \Big ( 1 + \delta ^2 \omega ^2 \xi (\omega ,k)G(x-y,\delta k_0) \Big ) }{i \delta ^6 k_0^4 \omega ^2 \log (\delta k_0 {\hat{\gamma }}) \omega ^2 \xi (\omega ,k) {\mathbb {S}}} \langle u_{in}, u_{\delta } \rangle \int _D u_{\delta }, \end{aligned}$$

which is the desired result. $\square$

We finish our analysis with the following result.

Proposition 2.10

Let $d=2$ and $\delta$ be small enough. Then, the $o(\delta ^4)$ approximation of the subwavelength resonant frequencies $\omega _s$ of the halide perovskite nano-particle $\Omega = \delta D + z$ satisfies

$$\begin{aligned} 1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \left( -\frac{|D|}{2\pi } \log (\delta k_0 {\hat{\gamma }}) + \langle K^{(0)}_D[\hat{{\mathbb {I}}}_D], \hat{{\mathbb {I}}}_D \rangle + \delta ^2 k_0^2 \log (\delta ) \langle K^{(1)}_D[\hat{{\mathbb {I}}}_D],\hat{{\mathbb {I}}}_D \rangle \Big ) \right) = O\big ( \delta ^4 \big ), \end{aligned}$$

(2.39)

where |D| is the volume of D and $\hat{{\mathbb {I}}}_D = {\mathbb {I}}_D / \sqrt{|D|}$.

Proof

We want to find $\omega _s \in {\mathbb {C}}$ such that

$$\begin{aligned}&\Big ( I - \delta ^2 \omega _s^2\xi (\omega _s,k_s) K^{\delta k_0}_D \Big )[u](x) = 0, \end{aligned}$$

which, for small $\delta$, can be written as

$$\begin{aligned} \Big ( I - \delta ^2 \omega _s^2\xi (\omega _s,k_s) \Big (&\log (\delta k_0 {\hat{\gamma }}) K^{(-1)}_D + K^{(0)}_D + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) K^{(1)}_D\Big ) \Big )[u](x) = O\Big (\delta ^6 \log (\delta )\Big ). \end{aligned}$$

Let us denote

$$\begin{aligned} M^{\delta k_0}_D:= \log (\delta k_0 {\hat{\gamma }}) K^{(-1)}_D + K^{(0)}_D + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) K^{(1)}_D. \end{aligned}$$

We take $\nu (\delta ) \in \sigma (M^{\delta k_0}_D)$ and consider the eigenvalue problem for $M^{\delta k_0}_D$:

$$\begin{aligned} M^{\delta k_0}_D[\Psi ] = \nu (\delta ) \Psi . \end{aligned}$$

(2.40)

We employ the ansatz

$$\begin{aligned} \Psi (\delta )&= \Psi _0 + O\left( \frac{1}{\log (\delta )}\right) ,\\ \nu (\delta )&= \log (\delta ) \nu _0 + \nu _1 + \delta ^2 \log (\delta ) \nu _2 + O\Big ( \delta ^2 \Big ). \end{aligned}$$

From (2.40) and the fact that $\delta ^2\log (\delta k_0 {\hat{\gamma }})=\delta ^2\log (\delta )+O(\delta ^2)$ we have that

$$\begin{aligned}&\Big ( \log (\delta ) K^{(-1)}_D + \log (k_0{\hat{\gamma }})K^{(-1)}_D + K^{(0)}_D + (\delta k_0)^2 \log (\delta ) K^{(1)}_D \Big ) [\Psi _0] \\&\quad = \Big ( \log (\delta ) \nu _0 + \nu _1 + \delta ^2 \log (\delta ) \nu _2 \Big )[\Psi _0] + O\Big ( \delta ^2 \Big ). \end{aligned}$$

Equating the $O(\log \delta )$ terms gives

$$\begin{aligned} K^{(-1)}_D[\Psi _0] = \nu _0 \Psi _0&\Rightarrow \nu _0 \hat{{\mathbb {I}}}_D = K^{(-1)}_D [\hat{{\mathbb {I}}}_D] \Rightarrow \nu _0 \hat{{\mathbb {I}}}_D = - \frac{|D|}{2\pi } \hat{{\mathbb {I}}}_D \Rightarrow \nu _0 = - \frac{|D|}{2\pi }. \end{aligned}$$

Then, equating the O(1) terms gives

$$\begin{aligned} \log (k_0 {\hat{\gamma }}) K^{(-1)}_D[\hat{{\mathbb {I}}}_D]&+ K^{(0)}_D[\hat{{\mathbb {I}}}_D] = \nu _1 \hat{{\mathbb {I}}}_D \Rightarrow \nu _1 \hat{{\mathbb {I}}}_D = - \frac{|D|}{2\pi } \log (k_0 {\hat{\gamma }}) \hat{{\mathbb {I}}}_D + K^{(0)}_D[\hat{{\mathbb {I}}}_D] \\&\Rightarrow \nu _1 = - \frac{|D|}{2\pi } \log (k_0 {\hat{\gamma }}) + \langle K^{(0)}_D[\hat{{\mathbb {I}}}_D], \hat{{\mathbb {I}}}_D \rangle . \end{aligned}$$

Using the same reasoning for the $O\Big (\delta ^2 \log (\delta )\Big )$ terms, we get

$$\begin{aligned} \nu _2 \hat{{\mathbb {I}}}_D = k_0^2 K^{(1)}_D[\hat{{\mathbb {I}}}_D] \Rightarrow \nu _2 = k_0^2 \langle K^{(1)}_D[\hat{{\mathbb {I}}}_D],\hat{{\mathbb {I}}}_D \rangle . \end{aligned}$$

Thus,

$$\begin{aligned} \nu (\delta )&= \log (\delta ) \nu _0 + \nu _1 + \delta ^2 \log (\delta ) \nu _2 + O\Big ( \delta ^2 \Big )\\&= -\frac{|D|}{2\pi } \log (\delta ) - \frac{|D|}{2\pi } \log (k_0 {\hat{\gamma }}) + \langle K^{(0)}_D[\hat{{\mathbb {I}}}_D], \hat{{\mathbb {I}}}_D \rangle + \delta ^2 k_0^2 \log (\delta ) \langle K^{(1)}_D[\hat{{\mathbb {I}}}_D],\hat{{\mathbb {I}}}_D \rangle + O\Big ( \delta ^2 ) \Big )\\&= -\frac{|D|}{2\pi } \log (\delta k_0 {\hat{\gamma }}) + \langle K^{(0)}_D[\hat{{\mathbb {I}}}_D], \hat{{\mathbb {I}}}_D \rangle + \delta ^2 k_0^2 \log (\delta ) \langle K^{(1)}_D[\hat{{\mathbb {I}}}_D],\hat{{\mathbb {I}}}_D \rangle + O\Big ( \delta ^2 \Big ). \end{aligned}$$

Using these expressions, $1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) M^{\delta k_0}_D = O ( \delta ^6 \log (\delta ) )$ can be rewritten as

$$\begin{aligned}&1 - \delta ^2 \omega _s^2 \xi (\omega _s,k_s) \Big ( -\frac{|D|}{2\pi } \log (\delta k_0 {\hat{\gamma }}) + \langle K^{(0)}_D[\hat{{\mathbb {I}}}_D], \hat{{\mathbb {I}}}_D \rangle \\&\quad + \delta ^2 k_0^2 \log (\delta ) \langle K^{(1)}_D[\hat{{\mathbb {I}}}_D],\hat{{\mathbb {I}}}_D \rangle \\&\quad + O\Big ( \delta ^2 \Big ) \Big ) = O\Big ( \delta ^6 \log (\delta ) \Big ), \end{aligned}$$

from which the result follows. $\square$

3 Hybridization of two resonators

3.1 Three dimensions

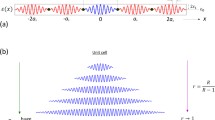
Let us consider two identical halide perovskite resontators $D_1$ and $D_2$ (e.g. the speres in Fig. 1), made from the same material. From now on, we will denote the permittivity by $\xi (\omega ,k)$, where $\omega$ is the frequency and k the associated wavenumber. In order to generalize our results, we will define it by

$$\begin{aligned} \xi (\omega ,k) := \frac{\mu _0\alpha }{\beta - \omega ^2 + \eta k^2 - i \gamma \omega }, \end{aligned}$$

(3.1)

where the positive constants $\alpha ,\beta ,\gamma$ and $\eta$ characterise the material.

Fig. 1

Two identical spherical halide perovskite resontators $D_1$ and $D_2$ of radius $\delta$, made from the same material, placed at a distance $\kappa$ from each other

Then, since there is an interaction between the two resonators, the field $u-u_{in}$ scattered by the two particles will be given by the following representation formula:

$$\begin{aligned} (u-u_{in})(x)&= - \delta ^2 \omega ^2 \xi (\omega ,k) \nonumber \\&\quad \left[ \int _{D_1} G(x-y,\delta k_0) u(y) \mathrm {d}y + \int _{D_2} G(x-y,\delta k_0) u(y) \mathrm {d}y \right] \ \ \ \text { for } x \in {\mathbb {R}}^d. \end{aligned}$$

(3.2)

Definition 3.1

We define the integral operators $K^{\delta k_0}_{D_i}$ and $R^{\delta k_0}_{D_i D_j}$, for $i,j=1,2$, by

$$\begin{aligned} K^{\delta k_0}_{D_i}: u\big |_{D_i} \in L^2(D_i) \longmapsto - \int _{D_i} G(x-y,\delta k_0) u(y) \mathrm {d}y \Big |_{D_i} \in L^2(D_i) \end{aligned}$$

and

$$\begin{aligned} R^{\delta k_0}_{D_i D_j}: u\big |_{D_i} \in L^2(D_i) \longmapsto - \int _{D_i} G(x-y,\delta k_0) u(y) \mathrm {d}y \Big |_{D_j} \in L^2(D_j). \end{aligned}$$

Then, the following lemma is a direct consequence of these definitions.

Lemma 3.2

The scattering problem (3.2) can be restated, using the Definition 3.1, as

$$\begin{aligned} \begin{pmatrix} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_1} &{} - \delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_2 D_1} \\ -\delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_1 D_2} &{} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_2} \end{pmatrix} \begin{pmatrix} u|_{D_1}\\ u|_{D_2} \end{pmatrix} = \begin{pmatrix} u_{in}|_{D_1}\\ u_{in}|_{D_2} \end{pmatrix}. \end{aligned}$$

(3.3)

Thus, the scattering resonance problem is to find $\omega$ such that the operator in (3.3) is singular, or equivalently, such that there exists $(u_1,u_2) \in L^2(D_1) \times L^2(D_2)$, $(u_1,u_2) \ne 0$, such that

$$\begin{aligned} \begin{pmatrix} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_1} &{} - \delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_2 D_1} \\ -\delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_1 D_2} &{} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_2} \end{pmatrix} \begin{pmatrix} u_{1}\\ u_{2} \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix}. \end{aligned}$$

(3.4)

Theorem 3.3

Let $d=3$. Then, the hybridized subwavelength resonant frequencies $\omega$ satisfy

$$\begin{aligned} \Big (1 - \delta ^2 \omega ^2\xi (\omega ,k)\lambda _{\delta }\Big )^2 - \delta ^4 \omega ^4 \xi (\omega ,k)^2 \langle R^{\delta k_0}_{D_1 D_2} \phi _1^{(\delta )}, \phi _2^{(\delta )} \rangle \langle R^{\delta k_0}_{D_2 D_1} \phi _2^{(\delta )}, \phi _1^{(\delta )} \rangle = 0, \end{aligned}$$

(3.5)

where $\phi _i^{(\delta )}$, for $i=1,2$, is the eigenfunction associated to the eigenvalue $\lambda _{\delta }$ of the potential $K^{\delta k_0}_{D_i}$.

Proof

We observe that (3.4) is equivalent to

$$\begin{aligned} \begin{pmatrix} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_1} &{} 0 \\ 0 &{} 1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_2} \end{pmatrix} \begin{pmatrix} u_1\\ u_2 \end{pmatrix} - \delta ^2 \omega ^2 \xi (\omega ,k) \begin{pmatrix} 0 &{} R^{\delta k_0}_{D_2 D_1} \\ R^{\delta k_0}_{D_1 D_2} &{} 0 \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = 0, \end{aligned}$$

which gives

$$\begin{aligned} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} - \delta ^2 \omega ^2 \xi (\omega ,k) \begin{pmatrix} \Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_1}\Big )^{-1} &{} 0 \\ 0 &{} \Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_2}\Big )^{-1} \end{pmatrix} \begin{pmatrix} R^{\delta k_0}_{D_2 D_1} u_2 \\ R^{\delta k_0}_{D_1 D_2} u_1 \end{pmatrix} =0. \end{aligned}$$

(3.6)

Let us now apply a pole-pencil decomposition on the operators $\Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_i}\Big )^{-1}$, for $i=1,2$. We see that

$$\begin{aligned} \Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_1}\Big )^{-1}(\cdot ) = \frac{ \langle \cdot , \phi _1^{(\delta )} \rangle \phi _1^{(\delta )} }{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} + R_1[\omega ](\cdot ) \end{aligned}$$

and

$$\begin{aligned} \Big (1 - \delta ^2 \omega ^2 \xi (\omega ,k) K^{\delta k_0}_{D_2}\Big )^{-1}(\cdot ) = \frac{ \langle \cdot , \phi _2^{(\delta )} \rangle \phi _2^{(\delta )} }{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} + R_2[\omega ](\cdot ), \end{aligned}$$

where the remainder terms $R_1[\omega ](\cdot )$ and $R_2[\omega ](\cdot )$ are holomorphic for $\omega$ in a neighborhood of $\omega _{\delta }$, so can be neglected. Then, (3.6), is equivalent to

$$\begin{aligned} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} - \delta ^2 \omega ^2 \xi (\omega ,k) \begin{pmatrix} \frac{ \langle \cdot , \phi _1^{(\delta )} \rangle \phi _1^{(\delta )} }{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} &{} 0 \\ 0 &{} \frac{ \langle \cdot , \phi _2^{(\delta )} \rangle \phi _2^{(\delta )} }{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} \end{pmatrix} \begin{pmatrix} R^{\delta k_0}_{D_2 D_1} u_2 \\ R^{\delta k_0}_{D_1 D_2} u_1 \end{pmatrix} =0. \end{aligned}$$

This gives us the system

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1 - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} \langle R^{\delta k_0}_{D_2 D_1} u_2, \phi _1^{(\delta )} \rangle \phi _1^{(\delta )}=0,\\ u_2 - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} \langle R^{\delta k_0}_{D_1 D_2} u_1, \phi _2^{(\delta )} \rangle \phi _2^{(\delta )}=0. \end{array}\right. } \end{aligned}$$

Applying the operator $R^{\delta k_0}_{D_1 D_2}$ (resp. $R^{\delta k_0}_{D_2 D_1}$) to the first (resp. second) equation, and then applying $\langle \cdot , \phi _2^{(\varepsilon )} \rangle$ (resp. $\langle \cdot , \phi _1^{(\varepsilon )} \rangle$), we find that

$$\begin{aligned} {\left\{ \begin{array}{ll} \langle R^{\delta k_0}_{D_1 D_2} u_1, \phi _2^{(\delta )} \rangle - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} \langle R^{\delta k_0}_{D_1 D_2} \phi _1^{(\delta )}, \phi _2^{(\delta )} \rangle \langle R^{\delta k_0}_{D_2 D_1} u_2, \phi _1^{(\delta )} \rangle =0,\\ \langle R^{\delta k_0}_{D_2 D_1} u_2, \phi _1^{(\delta )} \rangle - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta }} \langle R^{\delta k_0}_{D_2 D_1} \phi _2^{(\delta )}, \phi _1^{(\delta )} \rangle \langle R^{\delta k_0}_{D_1 D_2} u_1, \phi _2^{(\delta )} \rangle =0. \end{array}\right. } \end{aligned}$$

This system has a solution only if its determinant is zero. That is, if

$$\begin{aligned} 1 - \frac{ \delta ^4 \omega ^4 \xi (\omega ,k)^2 }{\Big ( 1 - \delta ^2 \omega ^2 \xi (\omega ,k) \lambda _{\delta } \Big )^2} \langle R^{\delta k_0}_{D_1 D_2} \phi _1^{(\delta )}, \phi _2^{(\delta )} \rangle \langle R^{\delta k_0}_{D_2 D_1} \phi _2^{(\delta )}, \phi _1^{(\delta )} \rangle = 0, \end{aligned}$$

which gives the desired result. $\square$

The following corollary is a direct result of Theorem 3.3.

Corollary 3.3.1

Let $d=3$. Then, the hybridized subwavelength resonant frequencies are given by

$$\begin{aligned} \omega= & {} \frac{i\gamma \pm \sqrt{-\gamma ^2 - 4 \Gamma (\beta + \eta k^2)}}{2 \Gamma }, \nonumber \\ \text {where}\qquad \Gamma= & {} -1-\delta ^2\alpha \lambda _{\delta } \pm \alpha \delta ^2 \sqrt{\langle R^{\delta k_0}_{D_1 D_2} \phi _1^{(\delta )}, \phi _2^{(\delta )} \rangle \langle R^{\delta k_0}_{D_2 D_1} \phi _2^{(\delta )}, \phi _1^{(\delta )} \rangle }. \end{aligned}$$

(3.7)

where $\phi _i^{\delta }$, for $i=1,2$, is the eigenfunction associated to the eigenvalue $\lambda _{\delta }$ of the potential $K^{\delta k_0}_{D_i}$ and the ± in the two expressions do not have to agree.

Proof

We introduce the notation ${\mathbb {K}}:= \langle R^{\delta k_0}_{D_1 D_2} \phi _1^{(\delta )}, \phi _2^{(\delta )} \rangle$ and ${\mathbb {M}}:= \langle R^{\delta k_0}_{D_2 D_1} \phi _2^{(\delta )}, \phi _1^{(\delta )} \rangle$. Then, (3.5) becomes

$$\begin{aligned}&\Big (1 - \delta ^2 \omega ^2\xi (\omega ,k)\lambda _{\delta }\Big )^2 - \delta ^4 \omega ^4 \xi (\omega ,k)^2 {\mathbb {K}} {\mathbb {M}} = 0 \\&\quad \Leftrightarrow \ 1 - \delta ^2 \omega ^2\xi (\omega ,k)\lambda _{\delta } \pm \delta ^2 \omega ^2 \xi (\omega ,k) \sqrt{{\mathbb {K}}{\mathbb {M}}} = 0 \ \Leftrightarrow \\&\quad \left( -1-\delta ^2\alpha \lambda _{\delta } \pm \alpha \delta ^2 \sqrt{{\mathbb {K}}{\mathbb {M}}} \right) \omega ^2 - i\gamma \omega + \beta + \eta k^2 = 0, \end{aligned}$$

and the roots to this second degree polynomial are given by

$$\begin{aligned} \omega = \frac{i\gamma \pm \sqrt{-\gamma ^2 - 4 \Gamma (\beta +\eta k^2)}}{2 \Gamma } \quad \text {where}\quad \Gamma =-1-\delta ^2\alpha \lambda _{\delta } \pm \alpha \delta ^2 \sqrt{{\mathbb {K}}{\mathbb {M}}}, \end{aligned}$$

with the two ± not necessarily agreeing. Finally, substituting the expressions for ${\mathbb {K}}$ and ${\mathbb {M}}$, we obtain the result. $\square$

3.2 Two dimensions

Let us move on to the case of dimension $d=2$. For simplicity, we again consider two identical halide perovskite resontators $D_1$ and $D_2$, made from the same material with permittivity given by the formula (3.1). We define the operators $K^{\delta k_0}_{D_i}$ and $R^{\delta k_0}_{D_i D_j}$, for $i,j=1,2$, as in Definition 3.1 and we continue by defining the following integral operators.

Definition 3.4

We define the integral operators $M^{\delta k_0}_{D_i}$ and $N^{\delta k_0}_{D_i D_j}$ for $i,j=1,2$ as

$$\begin{aligned} M^{\delta k_0}_{D_i} := {\hat{K}}^{\delta k_0}_{D_i} + K^{(0)}_{D_i} + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) K^{(1)}_{D_i}, \end{aligned}$$

and

$$\begin{aligned} N^{\delta k_0}_{D_i D_j} := {\hat{K}}^{\delta k_0}_{D_i D_j} + R^{(0)}_{D_i D_j} + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) R^{(1)}_{D_i D_j}, \end{aligned}$$

where

$$\begin{aligned} K^{(0)}_{D_i}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \int _{D_i} G(x-y,0)u(y)\mathrm {d}y \Big |_{D_i} \in L^{2}(D_i),\\ {\hat{K}}^{\delta k_0}_{D_i}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \log ({\hat{\gamma }} \delta k_0) {\hat{K}}_{D_i}[u]\Big |_{D_i}\in L^{2}(D_i), \\ {\hat{K}}_{D_i}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto - \frac{1}{2\pi } \int _{D_i} u(y) \mathrm {d}y \Big |_{D_i} \in L^{2}(D_i),\\ K^{(1)}_{D_i}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \int _{D_i} \frac{\partial }{\partial k} G(x-y,k)\Big |_{k=0} u(y) \mathrm {d}y \Big |_{D_i} \in L^2(D_i), \end{aligned}$$

and

$$\begin{aligned} R^{(0)}_{D_i D_j}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \int _{D_i} G(x-y,0)u(y)\mathrm {d}y \Big |_{D_j} \in L^{2}(D_j),\\ {\hat{K}}^{\delta k_0}_{D_i D_j}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \log ({\hat{\gamma }} \delta k_0) {\hat{K}}_{D_i D_j}[u]\Big |_{D_j}\in L^{2}(D_j), \\ {\hat{K}}_{D_i D_j}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto - \frac{1}{2\pi } \int _{D_i} u(y) \mathrm {d}y \Big |_{D_j} \in L^{2}(D_j),\\ R^{(1)}_{D_i D_j}: u\Big |_{D_i} \in L^2(D_i)&\longmapsto \int _{D_i} \frac{\partial }{\partial k} G(x-y,k)\Big |_{k=0} u(y) \mathrm {d}y \Big |_{D_j} \in L^2(D_j). \end{aligned}$$

We observe the following result.

Proposition 3.5

For the integral operators $K^{\delta k_0}_{D_i}$ and $R^{\delta k_0}_{D_i D_j}$, we can write

$$\begin{aligned} K^{\delta k_0}_{D_i} = M^{\delta k_0}_{D_i} + O\Big (\delta ^4 \log (\delta )\Big ), \quad \text {and} \quad R^{\delta k_0}_{D_i D_j} = N^{\delta k_0}_{D_i D_j}+ O\Big (\delta ^4 \log (\delta )\Big ), \end{aligned}$$

(3.8)

as $\delta \rightarrow 0$ and with $k_0$ fixed.

Proof

The proof is a direct result of the expansion of the Green’s function in dimension $d=2$. Indeed, for $u|_{D_i} \in L^2(D_i)$, we observe that

$$\begin{aligned} K^{\delta k_0}_{D_i}[u](x)&= - \int _{D_i} G(x-y,\delta k_0) u(y) \mathrm {d}y \Big |_{D_i}\\&= -\int _{D_i} \Big ( \log ({\hat{\gamma }} \delta k_0) \frac{1}{2\pi } + G(x-y,0) + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \frac{\partial }{\partial k} G(x-y,k)\Big |_{k=0}\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ + O\Big (\delta ^4 \log (\delta )\Big ) \Big ) u(y) \mathrm {d}y \Big |_{D_i}\\&= \Big ({\hat{K}}^{\delta k_0}_{D_i} + K^{(0)}_{D_i} + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) K^{(1)}_{D_i}\Big )[u](x) + O\Big (\delta ^4 \log (\delta )\Big )\\&= M^{\delta k_0}_{D_i}[u](x) + O\Big (\delta ^4 \log (\delta )\Big ). \end{aligned}$$

Similarly, for $u|_{D_i} \in L^2(D_i)$,

$$\begin{aligned} R^{\delta k_0}_{D_i D_j}[u](x)&= - \int _{D_i} G(x-y,\delta k_0) u(y) \mathrm {d}y \Big |_{D_j} \in L^2(D_j)\\&= -\int _{D_i} \Big ( \log ({\hat{\gamma }} \delta k_0) \frac{1}{2\pi } + G(x-y,0) + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \frac{\partial }{\partial k} G(x-y,k)\Big |_{k=0}\\&\ \ \ \ \ \ \ \ \ \ \ \ \ \ + O\Big (\delta ^4 \log (\delta )\Big ) \Big ) u(y) \mathrm {d}y \Big |_{D_j}\\&= \Big ( {\hat{K}}^{\delta k_0}_{D_i D_j} + R^{(0)}_{D_i D_j} + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) R^{(1)}_{D_i D_j} \Big )[u](x) + O\Big (\delta ^4 \log (\delta )\Big )\\&= N^{\delta k_0}_{D_i D_j}[u](x)+ O(\delta ^4 \log (\delta )). \end{aligned}$$

$\square$

Therefore, our problem is to determine the frequencies $\omega$ and the associated wavenumber k, for which the following holds:

$$\begin{aligned} \begin{pmatrix} I - \delta ^2 \omega ^2 \xi (\omega ,k)K^{\delta k_0}_{D_1} &{} - \delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_2 D_1}\\ - \delta ^2 \omega ^2 \xi (\omega ,k) R^{\delta k_0}_{D_1 D_2} &{} I - \delta ^2 \omega ^2 \xi (\omega ,k)K^{\delta k_0}_{D_2} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = \begin{pmatrix} 0\\ 0 \end{pmatrix} \end{aligned}$$

(3.9)

for nontrivial $u:=(u_1,u_2)$, such that $u|_{D_i} \in L^2(D_i)$, for $i=1,2$.

Proposition 3.6

Let $d=2$. Then, the hybridized subwavelength resonant frequencies $\omega$ satisfy

$$\begin{aligned} \begin{aligned}&1 - \delta ^2 \omega ^2 \xi (\omega ,k) \\&\quad \Big ( -\frac{|D_1|}{2\pi } \log ({\hat{\gamma }} \delta k_0) (1 \pm 1) + \langle K^{(0)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_1} \rangle + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_1} \rangle \\&\quad \pm \langle R^{(0)}_{D_2 D_1}[\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_1} \rangle \pm (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle R^{(1)}_{D_2 D_1}[\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_1} \rangle \Big ) = 0, \end{aligned} \end{aligned}$$

(3.10)

where the ± symbols coincide.

Proof

The first thing that we do is to observe that, by applying the expansion (3.8) to (3.9), we reach the problem

$$\begin{aligned} \begin{pmatrix} I - \delta ^2 \omega ^2 \xi (\omega ,k) M^{\delta k_0}_{D_1} &{} - \delta ^2 \omega ^2 \xi (\omega ,k) N^{\delta k_0}_{D_2 D_1}\\ - \delta ^2 \omega ^2 \xi (\omega ,k) N^{\delta k_0}_{D_1 D_2} &{} I - \delta ^2 \omega ^2 \xi (\omega ,k) M^{\delta k_0}_{D_2} \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \end{pmatrix} = \begin{pmatrix} O\Big (\delta ^4 \log (\delta )\Big )\\ O\Big (\delta ^4 \log (\delta )\Big ) \end{pmatrix}. \end{aligned}$$

We note that $|D_1| = |D_2|$. Then, using the symmetries of the dimer, let us denote

$$\begin{aligned} {\hat{\nu }}(\delta ) :&= - \frac{|D_1|}{2\pi } \log (\delta k_0 {\hat{\gamma }}) + \langle K^{(0)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_1} \rangle + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_1} \rangle \\&= - \frac{|D_2|}{2\pi } \log (\delta k_0 {\hat{\gamma }}) + \langle K^{(0)}_{D_2}[\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_2} \rangle + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_{D_2}[\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_2} \rangle , \end{aligned}$$

and

$$\begin{aligned} {\hat{\eta }} :&= \langle N^{\delta k_0}_{D_1 D_2} [\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_2} \rangle = \langle N^{\delta k_0}_{D_2 D_1} [\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_1} \rangle . \end{aligned}$$

In addition, we have that

$$\begin{aligned} {\hat{K}}^{\delta k_0}_{D_i D_j}[\hat{{\mathbb {I}}}_{D_i}] = {\hat{K}}^{\delta k_0}_{ D_j}[\hat{{\mathbb {I}}}_{D_j}]. \end{aligned}$$

Now, we define the quantity $\nu (\delta )$ to be the eigenvalues of the operator $M^{\delta k_0}_{D_i}$, that is,

$$\begin{aligned} \nu (\delta ) = \langle M^{\delta k_0}_{D_1}[\Psi _{D_1}], \Psi _{D_1} \rangle = \langle M^{\delta k_0}_{D_2}[\Psi _{D_2}], \Psi _{D_2} \rangle , \end{aligned}$$

for the eigenfunctions $\Psi _{D_i}(\delta ) \in L^2(D_i)$, $\Psi _{D_i}(\delta ) = \hat{{\mathbb {I}}}_{D_i} + O\left( \frac{1}{\log (d)} \right)$. Thus, we have that (3.9) is equivalent to

$$\begin{aligned}&\begin{pmatrix} u_1\\ u_2 \end{pmatrix} - \delta ^2 \omega ^2 \xi (\omega ,k) \begin{pmatrix} \Big ( I - \delta ^2 \omega ^2 \xi (\omega ,k)M^{\delta k_0}_{D_1} \Big )^{-1} &{} 0 \\ 0 &{} \Big ( I - \delta ^2 \omega ^2 \xi (\omega ,k)M^{\delta k_0}_{D_2} \Big )^{-1} \end{pmatrix}\nonumber \\&\quad \begin{pmatrix} N^{\delta k_0}_{D_2 D_1} u_2\\ N^{\delta k_0}_{D_1 D_2} u_1 \end{pmatrix} =0. \end{aligned}$$

(3.11)

Applying a pole-pencil decomposition, we observe that

$$\begin{aligned} \Big ( I - \delta ^2 \omega ^2 \xi (\omega ,k)M^{\delta k_0}_{D_i} \Big )^{-1}[\cdot ] = \frac{\langle \cdot , \hat{{\mathbb {I}}}_{D_i} \rangle \hat{{\mathbb {I}}}_{D_i}}{1 - \delta ^2 \omega ^2 \xi (\omega ,k) \nu (\delta )} + R[\omega ](\cdot ), \end{aligned}$$

where the remainder terms $R[\omega ](\cdot )$ can be neglected. Hence, (3.11) is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} u_1 - \delta ^2 \omega ^2 \xi (\omega ,k) \frac{ \langle N^{\delta k_0}_{D_2 D_1} u_2, \hat{{\mathbb {I}}}_{D_1} \rangle \hat{{\mathbb {I}}}_{D_1}}{ 1 - \delta ^2 \omega ^2 \xi (\omega ,k) \nu (\delta ) } = 0, \\ u_2 - \delta ^2 \omega ^2 \xi (\omega ,k) \frac{ \langle N^{\delta k_0}_{D_1 D_2} u_1, \hat{{\mathbb {I}}}_{D_2} \rangle \hat{{\mathbb {I}}}_{D_2}}{ 1 - \delta ^2 \omega ^2 \xi (\omega ,k) \nu (\delta ) } = 0, \end{array}\right. } \end{aligned}$$

which is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} \langle N^{\delta k_0}_{D_1 D_2} u_1, \hat{{\mathbb {I}}}_{D_2} \rangle - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k)\nu (\delta )} \langle N^{\delta k_0}_{D_1 D_2} \hat{{\mathbb {I}}}_{D_1}, \hat{{\mathbb {I}}}_{D_2} \rangle \langle N^{\delta k_0}_{D_2 D_1} u_2, \hat{{\mathbb {I}}}_{D_1} \rangle = 0,\\ \langle N^{\delta k_0}_{D_2 D_1} u_2, \hat{{\mathbb {I}}}_{D_1} \rangle - \frac{\delta ^2 \omega ^2 \xi (\omega ,k)}{1 - \delta ^2 \omega ^2 \xi (\omega ,k)\nu (\delta )} \langle N^{\delta k_0}_{D_2 D_1} \hat{{\mathbb {I}}}_{D_2}, \hat{{\mathbb {I}}}_{D_1} \rangle \langle N^{\delta k_0}_{D_1 D_2} u_1, \hat{{\mathbb {I}}}_{D_2} \rangle = 0. \end{array}\right. } \end{aligned}$$

For this to have a solution, we need the determinant of the matrix induced by this system to be zero. This gives

$$\begin{aligned}&1 - \frac{\delta ^4 \omega ^4 \xi (\omega ,k)^2}{( 1 - \delta ^2 \omega ^2 \xi (\omega ,k)\nu (\delta ) )^2} \langle N^{\delta k_0}_{D_1 D_2} \hat{{\mathbb {I}}}_{D_1}, \hat{{\mathbb {I}}}_{D_2} \rangle \langle N^{\delta k_0}_{D_2 D_1} \hat{{\mathbb {I}}}_{D_2}, \hat{{\mathbb {I}}}_{D_1} \rangle = 0. \end{aligned}$$

Given the symmetry of our setting, we have that

$$\begin{aligned} \langle N^{\delta k_0}_{D_1 D_2} \hat{{\mathbb {I}}}_{D_1}, \hat{{\mathbb {I}}}_{D_2} \rangle = \langle N^{\delta k_0}_{D_2 D_1} \hat{{\mathbb {I}}}_{D_2}, \hat{{\mathbb {I}}}_{D_1} \rangle , \end{aligned}$$

and hence, we get

$$\begin{aligned} 1 - \delta ^2 \omega ^2 \xi (\omega ,k)\nu (\delta ) \pm \delta ^2 \omega ^2 \xi (\omega ,k)\langle N^{\delta k_0}_{D_1 D_2} \hat{{\mathbb {I}}}_{D_1}, \hat{{\mathbb {I}}}_{D_2} \rangle = 0. \end{aligned}$$

This is equivalent to

$$\begin{aligned}&1 - \delta ^2 \omega ^2 \xi (\omega ,k) \Big ( - \frac{|D_1|}{2\pi } \log (\delta k_0 {\hat{\gamma }})(1\pm 1) + \langle K^{(0)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}], \hat{{\mathbb {I}}}_{D_1} \rangle + (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle K^{(1)}_{D_1}[\hat{{\mathbb {I}}}_{D_1}],\\&\quad \hat{{\mathbb {I}}}_{D_1} \rangle \pm \langle R^{(0)}_{D_2 D_1} [\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_1} \rangle \pm (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) \langle R^{(1)}_{D_2 D_1} [\hat{{\mathbb {I}}}_{D_2}], \hat{{\mathbb {I}}}_{D_1} \rangle \Big ) = 0, \end{aligned}$$

which is the desired result. $\square$

4 Example: circular resonators

Fig. 2

Behaviour of the subwavelength resonances for small circular nano-particles of radius $\delta$. The resonant frequency $\omega _s$ of a single circular methylammonium lead chloride nano-particle is shown. For two circular nano-particles, made from the same material, we see how the hybridization causes the frequencies $\omega _\mathrm {dip}$ (dipole) and $\omega _\mathrm {mon}$ (monopole) to shift either side of $\omega _s$

In this section, we illustrate our results for the case of two-dimensional circular halide perovskite resonators. We can find the resonant frequencies of a single particle $\omega _s$ by solving (2.35). Similarly, the hybridized resonant frequencies of a pair of circular resonators can be found by solving (3.10). The two solutions of (3.10) are denoted by $\omega _\mathrm {mon}$ and $\omega _\mathrm {dip}$, to describe their monopolar and dipolar characteristics. As is expected from other hybridized systems, it holds that $\omega _\mathrm {mon}<\omega _\mathrm {dip}$. We plot these three frequencies as a function of the particle size $\delta$ in Fig. 2a. Parameter values are chosen to corresponding to methylammonium lead chloride ($\text {MAPbCl}_3$), which is a popular halide perovskite [16]. We notice that the resonant frequencies for these resonators lies in the range of visible frequencies, when the particles are hundreds of nanometres in size. This puts the system in the appropriate subwavelength regime that was required for our asymptotic method.

One thing we observe from Fig. 2 is that in the $\delta \rightarrow 0$ limit, the frequencies coincide. This is because the nano-particles behave as isolated, identical resonators when $\delta$ is very small. Then, as $\delta$ increases the single-particle resonance $\omega _s$ always stays between the monopole and dipole frequencies of the hybridized case. In Fig. 2a it appears that the three resonances coincide, however in Fig. 2b, c we plot $\omega _s-\omega _\mathrm {mon}$ and $\omega _\mathrm {dip}-\omega _s$ to show that the three values differ by several hundred Hertz and satisfy $\omega _\mathrm {mon}<\omega _s<\omega _\mathrm {dip}$. The phenomenon of the dipole frequency $\omega _d$ being shifted above $\omega _s$ and the monopole frequency $\omega _m$ being shifted below $\omega _s$ is a typical behaviour of hybridized resonator systems, see e.g. [3].

5 Conclusion

We have established a new mathematical approach for modelling halide perovskite resonators. This is a significant development of the existing theory of subwavelength resonators [2, 3], as it generalizes the techniques to dispersive settings where the permittivity of the material depends non-linearly on both the frequency and the wavenumber. Given the growing use of halide perovskites in engineering applications, this theory will have a significant impact on the design of advanced devices [12, 15]. The integral methods used here are able to describe a very broad class of resonator shapes, so are an ideal approach for studying complex geometries, such as the biomimetic eye developed by [9].

A Appendix

1.1 A.1 Calculation of three-dimensional constants

We derive a formula for ${\mathbb {F}}$, which was a crucial quantity in Sect. 2.4.3, in the case of a single three-dimensional halide perovskite resonator. We have that

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle = \frac{1}{8\pi }{\mathbb {F}}. \end{aligned}$$

From (2.22), we observe that

$$\begin{aligned} \delta ^2 \omega ^2 \xi (\omega ,k)&= \frac{8\pi }{8\pi \lambda _{\delta }-\delta ^2 k_0^2 {\mathbb {F}}}. \end{aligned}$$

Also, we know that $\xi (\omega ,k)=\mu _0(\varepsilon (\omega ,k)-\varepsilon _0)$, and we have shown that

$$\begin{aligned} \varepsilon (\omega ,k) = \varepsilon _0 + \frac{1}{\mu _0\delta ^2\omega ^2\left( \lambda _0 - \frac{i}{4\pi } \delta k_0 {\mathbb {B}} \right) }. \end{aligned}$$

Substituting this into the above equation, we get

$$\begin{aligned} {\mathbb {F}} = \frac{8\pi }{\delta ^2 k_0^2} \Big (&\lambda _{\delta } - \lambda _0 + \frac{i}{4\pi } \delta k_0 {\mathbb {B}} \Big ). \end{aligned}$$

Therefore, we obtain that

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle = \frac{1}{\delta ^2 k_0^2} \Big ( \lambda _{\delta } - \lambda _0 + \frac{i}{4\pi } \delta k_0 {\mathbb {B}} \Big ). \end{aligned}$$

1.2 A.2 Calculation of two-dimensional constants

We derive a formula for ${\mathbb {S}}$, which was a crucial quantity in Sect. 2.5.3, in the case of a single two-dimensional halide perovskite resonator. We have that

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle = \frac{i}{4\pi }{\mathbb {S}}. \end{aligned}$$

From (2.35), we can obtain an expression for ${\mathbb {S}}$. Indeed, (2.35) is equivalent to

$$\begin{aligned}&4\pi = \delta ^2 \omega ^2 \xi (\omega ,k) \Big ( 4\pi \lambda _{\delta } - i \delta ^4 k_0^4 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {S}} \Big ). \end{aligned}$$

We know that $\xi (\omega ,k) = \mu _0\Big (\varepsilon (\omega ,k) - \varepsilon _0\Big )$ and we have shown that

$$\begin{aligned} \varepsilon (\omega ,k) = \frac{1}{\mu _0 \delta ^2 \omega ^2 \left( \log (\delta k_0 {\hat{\gamma }}) \lambda _{-1} - \frac{{\mathbb {P}}}{2\pi } - \frac{i(\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}) {\mathbb {G}}}{4\pi } \right) } + \varepsilon _{0}. \end{aligned}$$

Substituting this into the above equality, we get

$$\begin{aligned}&\ \ \ \ \ \ \ \ \ \ \ \ {\mathbb {S}} = \frac{-i}{\delta ^4 k_0^4 \log (\delta k_0 {\hat{\gamma }})} \Big ( 4\pi (\lambda _{\delta } - \log (\delta k_0 {\hat{\gamma }}) \lambda _{-1}) + 2 {\mathbb {P}} + i (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}){\mathbb {G}} \Big ). \end{aligned}$$

Therefore, we obtain that

$$\begin{aligned} \langle K^{(2)}_D[u_{\delta }], u_{\delta } \rangle = \frac{1}{4\pi \delta ^4 k_0^4 \log (\delta k_0 {\hat{\gamma }})} \Big ( 4\pi (\lambda _{\delta } - \log (\delta k_0 {\hat{\gamma }}) \lambda _{-1}) + 2 {\mathbb {P}} + i (\delta k_0)^2 \log (\delta k_0 {\hat{\gamma }}){\mathbb {G}} \Big ). \end{aligned}$$