Generalized Formal Model-Verifier: A Formal Approach for Verifying Static Models

Abstract

The field of software modeling has gained significant popularity in the last decades. By capturing the static aspects of the software requirements, model-driven engineering eases the development and maintenance of software. However, additional constraints, such as invariants on model elements, that the solution must conform to may be too complex to include in the structure of the model itself. External solutions are often used to describe static constraints on models, the most prevalent approach being the Object Constraint Language (OCL) and its formal variants. This paper proposes the Generalized Formal Model-Verifier (GFMV), which is a general approach for verifying static constraints on software models. GFMV employs different formal verification methods based on Kripke Structures. Kripke Structures are used to capture the static structure of the model, then the constraints are formalized using a first-order branching-time logic, the Computational Tree Logic (CTL). Finally, the NuSMV model checker is reused to verify whether the constraints formalized in CTL hold on the formal Kripke Structure. When compared to existing solutions, GFMV offers increased generality and formal proof that the constraints hold on the model. The expressive power and runtime-scalability of the approach are evaluated on a real-world example model and OCL invariants cited from literature.

Introduction

The Object Constraint Language (OCL) is a declarative, external solution for defining constraints on models. OCL is the most popular approach for this purpose, and was designed specifically with models in mind that are compatible with the Essential Meta Object Facility (EMOF) specification. The most widespread approach to modeling the static structure of a system is the UML class diagram [1] of the Object Management Group (OMG), but different approaches also exist [2,3,4,5]. Modeling approaches tend to offer high-level means to capture the most important concepts of the real-world. However, further restrictions on the model are often necessary. These restrictions cannot (or should not) be expressed in the structure of the model itself. The reason for this is that graphical modeling languages like UML are typically not expressive and precise enough to capture all the exact information of the system design. The main reason why graphical languages are preferred over textual modeling lies in their simplicity of usage. Naturally, the consequence of keeping the graphical modeling notions manageable and simple to use is the reduction of expressive power.

For instance, in the case of UML class diagrams, restrictions could be invariant rules or adding extra constraints to restrict what constitutes a valid class diagram. The latter is often referred to as checking the well-formedness of the model. For instance, consider the following constraints:

• The age of a person must be between 0 and 120.

• For every children of a person who are below 6 years old, the person is eligible for a specific sum of tax relief.

• Interfaces should not contain attributes.

• A class may implicitly inherit from any number of classes.

The first two constraints are invariants, defining more complex restrictions on the structure of the model. The second two are rules that all well-formed class diagrams must adhere to, which means that conformance to the language semantics are validated. In our work, we refer to such restrictions as static constraints in contrast to dynamic constraints, that apply restrictions on the execution of dynamic behaviour, such as methods in object-oriented models.

Over the years, formal variants of OCL had also emerged with the goal of extending OCL with formal semantics or to provide a different approach with the same purpose, but based on formal methods. The most widespread and successful of these methods is Alloy [6], which provides a simple language for modeling a system and expressing its properties. In the background, Alloy converts the model and its properties to a boolean representation and uses SAT solvers [7, 8] to check whether the defined model conforms to the defined properties.

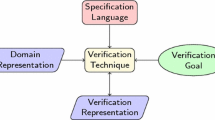
In this paper, we propose the Generalized Formal Model-Verifier (GFMV) as an alternative, general approach for defining static constraints on software models. GFMV uses different formal verification methods, specifically model checking, to verify whether the static constraints hold on the software model. In the first step, the structure of the model is transformed to a Kripke Structure. The static constraints are formalized using the Computational Tree Logic (CTL). Lastly, the CTL formulae are verified by a model checker, NuSMV [9, 10].

GFMV becomes fully automatic after defining the transformation from the original model to the Kripke Structure. By using formal methods, any and all violations are guaranteed to be found. Thus, formal, mathematically-sound proof is provided that the static constraints hold on the model, as long as the mapping between the original and the formal models had been defined as intended by the model designer.

The paper is structured as follows. In “Related Work”, we present related work and compare them with our approach. “Background”, describes the relevant theoretical background of model checking, including Kripke Structures and CTL. In “General Formal Model-Verifier”, the steps of the proposed verification process are defined. “Evaluation” evaluates GFMV by formalizing a case study and analyzing the runtime of the verification process. Finally “Conclusion” concludes the paper, highlighting the main strengths and weaknesses of the approach and discussing future work.

Related Work

One of the most widespread solutions for enforcing static constraints on models is the Object Constraint Language (OCL) [11]. OCL provides support for expressing many features, such as invariants, initialization expressions, or derived elements. It also provides its own typesystem. Nevertheless, OCL is not without weaknesses. In their work, Cabot et al. [12] performed a SWOT (Strengths-Weaknesses-Opportunities-Threats) analysis on OCL. The authors argue that the main weaknesses of OCL are the complexity of the language, and the lack of a tool ecosystem and reusable OCL libraries. As a consequence, if a custom modeling language (for which an OCL implementation does not already exist) intends to use OCL, implementing an OCL interpreter is a troublesome, relatively difficult process [13]. For this reason, one of our most important goals with GFMV is to keep it as general and simple as possible. It should be relatively easy to integrate GFMV with any custom modeling language.

Formal verification approaches offer a well-developed ecosystem of tools and methods available and have a well-defined focus for verifying constraints. They are optimized at checking constraints and provide formal, mathematically-sound proof of the correctness of the model. Thus, we believe formal verification methods to be beneficial for verifying static constraints on software models. Over the years, a number of approaches emerged that were based on formal methods. HOL-OCL [14] intends to define formal semantics for OCL by "shallow embedding of OCL into the Higher-order Logic (HOL) instance of the interactive theorem prover Isabelle." [15] presents QMaxUSE, which is a tool designed to formally verify OCL constraints on UML class diagrams with the goal of superior performance over existing solutions. [16] addresses the formalization of typically ignored UML/OCL features, such as multiple inheritance or late binding. This is achieved by transforming the UML specifications and OCL constraints to FoCaLiZe specifications. In their work, Nobakht et al. [17] extend static UML + OCL models with dynamic verification. By transforming static and dynamic aspects (class diagrams and statecharts), the entire UML specification is adapted into the UPPAAL model checker [18]. Although these approaches are formal, they are designed specifically with UML in mind, and do not (explicitly) support other types of modeling languages. In contrast, GFMV is not specific to UML models, it is usable with any modeling language.

Bill et al. [19] proposed an approach for extending OCL with the temporal operators of CTL and developed the MocOCL model checker to verify COCL (CTL OCL) properties. The purpose of their research was to express OCL properties over the full lifetime of an instance model, contrary to OCL’s capability to express invariants only in the context of a single instance model. The authors argue that a sequence of instance models capture the execution of the system, thus, defining and validating constraints on such sequences is beneficial. Consequently, in COCL, CTL is used to extend OCL constraints over sequences, whereas in GFMV, invariants can be expressed in CTL itself.

Other approaches focus on checking pre-defined properties on UML class diagrams. The goal in these cases is not to replace OCL for defining and checking constraints on instances of models, but to verify static properties on the existing UML + OCL model, including consistency, executability, reachability, liveness and satisfiability. UMLtoCSP [20] applies constraint programming to check the satisfiability of OCL constraints on a UML class diagram. Similarly, [21] focuses on improving the performance of OCL satisfiability checking. In their work, Przigoda et al. [22] propose a formal approach for verifying the structure and behavior in UML/OCL models. The possible states of the system, along with the OCL invariants are translated into a symbolic representation and SAT solvers are used to execute verification.

In OCL, the context specifies what must be verified against an invariant. In a UML class diagram, this typically, but not necessarily, means a class. However, for every invariant, only a single context can be defined. In contrast, GFMV is more flexible in this regard. It does not explicitly use contexts, the scope of a constraint can be defined by logical expressions. This offers 2 significant advantages. Firstly, any number of "contexts" can be defined for a formula. This makes it easier to reuse and manage constraints. Secondly, in GFMV, objects and classes are not explicitly separated, but are stored in the same Kripke Structure. Consequently, objects can also become contexts. This concept makes it simple to apply GFMV on multi-level modeling languages as well.

To sum up, when compared to non-formal OCL variants, GFMV has several advantages:

• GFMV uses formal verification methodologies and tools that are well developed and widespread, providing automatic, formal proof of the correctness of the model.

• GFMV is fully independent of the modeling language that is being checked, making it easier to integrate with custom modeling languages.

• GFMV focuses specifically on checking static constraints only. On one hand, it becomes easier to be used for this purpose. On the other hand, its expressive power is less than that of OCL. GFMV cannot express other features of OCL, such as querying models.

Existing formal solutions focus mainly on extending specifically UML + OCL with formal semantics or checking the satisfiability or consistency of the models. Compared to these approaches, the generality of GFMV is the main benefit.

Alloy [6] is one of the most successful of formal verification-based approaches. Alloy was inspired by the weaknesses of OCL. It provides a textual language for defining models and uses SAT solvers to formalize and check properties on the model. Similarly to OCL, it provides its own typesystem, which is more compact and easier to use. UML2Alloy [23] defines a transformation from UML class diagrams extended with OCL expressions to Alloy models. The goal of this approach is to reuse the formal aspects of Alloy to analyze UML specifications. The authors also note that defining the transformation from UML class diagrams to Alloy was “challenging”.

When compared to Alloy, GFMV works on similar grounds but with different formal methods. Additionally, it is more general, in the sense that it does not depend tightly on the NuSMV tool. This means that instead of using NuSMV and the various formal methods it employs (SAT solvers, bounded model checking etc.), it is possible to use an entirely different model checker. In this sense, our approach is easy to extend with different model checking techniques. It would also be possible to support different tools and let the model designer choose between them. This is not the case for Alloy, as it is built specifically with SAT solvers in mind. The only requirement in our case is that the Joint Relational Model (“Joint Relational Model”) should be expressed in the modeling language of the model checker and a query language similar to CTL has to be available to formulate the constraints. For example, a viable alternative to NuSMV would be Uppaal [18], with its modeling language of extended timed automata and a query language similar to CTL.

Background

Formal verification is a group of methodologies aimed at formally proving the correct behaviour of a specified system. In our work, we propose to use model checking to enforce constraints on models. One of the most typically used formal models is the Kripke Structure (KS) [24] and one of the most common and practical ways of formalizing requirements is the Computational Tree Logic (CTL) [24].

A Kripke Structure is a 4-tuple (S, I, R, L) over a set of atomic propositions AP, where:

• $AP = \{ P_1, P_2,\ldots , P_n\}$ set of atomic propositions

• $S = \{ S_1, S_2,\ldots , S_k\}$ finite set of states

• $I \subseteq S$ set of initial states

• $R \subseteq S \times S$ transition relation between states

• $L: S \mapsto 2^{AP}$ labeling of states with atomic propositions

Figure 1 illustrates a KS in a graphical representation. The model consists of 3 states: $S_1$, $S_2$ and $S_3$. The initial state is $S_1$, denoted by a double circle. $S_1$ is labeled with the atomic propositions P and Q, $S_2$ is labeled with P, and $S_3$ is labeled with Q and R. Finally, there exists a transition relation from $S_1$ to $S_2$ and $S_3$, from $S_2$ to $S_3$ and from $S_3$ to $S_1$. A path in a KS is a possible series of states along transitions. For example, in this case $S_1 \rightarrow S_2 \rightarrow S_3 \rightarrow S_1 \rightarrow S_3$ is a possible path.

Fig. 1

Graphical representation of a Kripke Structure with 3 states and 4 transitions

In CTL, requirements can be formalized using logical formulae, all of which are presented in Table 1. A CTL expression is always evaluated on a specific state, beginning with the initial state.

Table 1 CTL expressions and their semantics

Consider now the Kripke Structure depicted in Fig. 1 and the CTL formula in Eq. 1.

$$\begin{aligned} AG ( (Q \wedge P)) \implies ( (EX \lnot Q) \vee (EF (P \wedge R)) ) \end{aligned}$$

(1)

The formula prescribes that on all states of all paths in the Kripke Structure, if a state is labeled with both Q and P, then there must exist a next state that is not labeled with Q or there must exist a path on which eventually a state is labeled with both P and R. When evaluated over the example, this formula holds, because $S_1$ is the only state for which the left side of the implication holds, and the right side holds as well because $S_2$ is a potential next state and it is not labeled with Q.

General Formal Model-Verifier

Figure 2 shows the steps of the proposed approach. We propose the definition of the Joint Relational Model (JRM) as a Kripke Structure that models the structure of the original model to be checked, in the form of relations between basic model elements. In the first step of the verification approach, a JRM is created based on the software model to be verified. Secondly, the constraints that the model must conform to have to be formalized using CTL. The JRM and the CTL formulae are then forwarded as input to the NuSMV model checker tool, which verifies whether the formalized requirements hold on the JRM, and consequently, on the original model itself. For each violated CTL formula, a counter-example is generated.

Fig. 2

The steps of the proposed approach for verifying static constraints on software models

Further along this section, we present our notions of model elements and relations, Relational Models, the JRM and the formalization of constraints as CTL formulae.

Running Example—UML Class Diagram

Throughout the rest of this section, a simple example UML class diagram will be used to demonstrate the main ideas of the verification process in GFMV. The goal of this example is not to define an exhaustive formalization of UML class diagrams, but to provide a compact example to make the verification concepts easier to understand. To keep the example concise and easier to understand, the model is deliberately minimalistic and contains only a few elements.

The running example is described in Fig. 3. The diagram consists of five classes. The Factory class is abstract, with two concrete subtypes: FactoryA and FactoryB. A factory has an attribute of type string, and a method which takes a double parameter and returns an object of type Device. Factory also has an association towards Device, intended for storing the devices created in that factory. Furthermore, devices have two attributes with primitive types, as well as a method that returns a boolean value. Device has a subtype: SpecialDevice.

Fig. 3

A UML class diagram example, to be used as a running example further in this section

Relational Formal Model

When defining the formal model (in the form of a Kripke Structure), our goal is to express the structure of the original model. This means that all the elements of the original model are mapped to elements in the Kripke Structure. This way, when the various model checker algorithms employed by NuSMV traverse the state-space of the model and find violations of the constraints, the results can be mapped back to show which element of the original model violates which constraints. To achieve this, we define the notions of model element and relation.

We define a model element as the basic building block of the software model. In object-oriented models, such as a UML class diagram, model elements typically refer to classes, interfaces, attributes and methods. A relation is a structural relationship between model elements that connect them in the model. In a UML class diagram, this would include all the relationships that classes or interfaces can have with one-another, for example, association, composition, aggregation, dependency, inheritance and interface-realization, as well as holding of attributes and methods. An exhaustive mapping of UML class diagrams to formal models is given in “From UML Class Diagram To JRM”. To avoid confusion of terminologies between the Relational Models and the original model that must conform to the static constraints, we will refer to the latter as the source model.

The main idea behind Relational Models is to represent every model element of the source model as a state in the Kripke Structure. Every such state is then labeled with an identifier that corresponds to the model element that it represents. For example, if a class in the source model is called “Factory”, then in the Kripke Structure a state is created to represent this class, labeled with "Factory". At this point, we assume that every model element has a unique identifier. If this is not the case, one needs only to define an ordering on the model elements and identify them by their assigned position in the ordering.

Relations are captured in the form of transitions in the Kripke Structure. If a relation exists between model elements $m_i$ and $m_j$, then a transition is defined in the formal model between their corresponding states $S_i$ and $S_j$. Consequently, a Relational Model captures the static structure of the source model in a formal graph-like representation. Since Kripke Structures have limited ways to express information (only through labeled states and unlabeled transitions), a Relational Model is only capable of expressing a single relation. Thus, for each possible relation, a corresponding Relational Model would have to be created. At this point, let us generalize the concept of a Relational Model.

We define a Relational Model over a set of model elements $M=\{m_1, m_2,\ldots , m_k\}$ and $Relation: M^2 \mapsto \{ 0, 1 \}$ as a Kripke Structure, where:

• $AP = \{ L | \exists 1\le i \le k: m_i[ID] = L\}$

• $S = \{ IS, S_1, S_2,\ldots , S_k\}$

• $I = \{ IS \}$

• $R = \{(s,t) \in S | (s = IS \wedge \exists 1\le i \le k: \not \exists 1\le j \le k: t = S_i \wedge Relation(m_j, m_i)) \vee (\exists 1\le i, j \le k, i \ne j: S_i = s \wedge S_j = t \wedge Relation(m_i, m_j)\}$

• $L (s\in S) = \{L|\exists 1\le i \le k: S_i = s \wedge m_i[ID] = L \}$

The set of possible atomic propositions contains all the identifiers of the model elements. The set of states includes a corresponding state for each model element and an additional initial state. The transitions from the initial state point to all other states that are otherwise unreachable in the model. This way, it becomes possible to actually traverse the full model. A transition is defined between the corresponding states of two model elements $m_i$ and $m_j$ if the relation between them holds from $m_i$ to $m_j$. This is denoted by the defined Relation function, which maps two model elements to 0, if the relation does not hold from the first argument to the second, and to 1 if it holds. Finally, every state is labeled with the identifier of its corresponding model element.

Considering the example depicted in Fig. 3, for each relation defined on UML class diagrams, a Relational Model may be generated. For instance, Fig. 4 shows the inheritance model and Fig. 5 shows the attribute model of the example.

Fig. 4

The inheritance model of the UML class example. The transitions denote an inheritance relation

Fig. 5

The attribute model of the UML class example. The transitions denote an attribute relation

For every model element that is either the source or the target of the given relation in the class diagram, a state is defined labeled with the name of the model element. Henceforth, for the sake of simplicity, state names in the examples will be omitted, as they are of no semantic importance in the formal model. In these models, a transition refers to an inheritance or to the holding of an attribute between the participants, respectively. It should be emphasized that, in practice, it is sufficient to create states only for those model elements that are actually connected to any other model element through the given relation. This way, the state-space of the model can be kept much more concise.

Joint Relational Model

In practice, the previously defined Relational Models are not sufficient, as models can only capture one relation at a time. The problem is that real-world constraints typically refer to multiple relations at once, requiring more than one relation to be present in the same model in order to be evaluated successfully. Moreover, multiple relations may also be used to infer additional information based on the relations. For instance, in the examples depicted in Figs. 3 and 4, the attribute model is only capable of enumerating direct attributes. If both the inheritance and the attribute relations were present in a single formal model, derived attributes would be handled as well. Thus, a solution is needed that is capable of capturing any (finite) number of relations in a single Kripke Structure. The main reason why a Relational Model could not express more than one relation is that transitions in a Kripke Structure cannot be labeled.

Therefore, the idea is to simulate the labeling of transitions with additional states. For every relation that a model element has towards another model element, an extra relational state is defined, labeled with the name of the relation it represents. A transition is then added from the source of the relation to the relational state, and from the relational state to the target of the relation. For example, if in a UML class diagram the class “FactoryA” inherits from the class “Factory”, then: (i) A relational state is added, labeled with “Inheritance”. (ii) A transition is defined from the state labeled with “FactoryA” to the new relational state labeled with “Inheritance”. (iii) A transition is defined from the relational state of “FactoryA” labeled with “Inheritance” to the state labeled with “Factory”. This way, relational states serve as pointers to the target(s) of the relation.

The atomic propositions of a JRM consist of the union of all the propositions of the Relational Models, extended with the set of relations for labeling the relational states. Similarly, the states of the Relational Models are combined, along with adding the relational states. The initial state and its outgoing transitions remain the same, the latter denoted by $R_{IS}$. The goal here is to guarantee that the entire state-space can be traversed. Consequently, the transitions from the initial state should point to all model elements that are not accessible from any relation at all (leaves in the hierarchy). The rest of the transitions are then defined as mentioned before: from a state to its relational states, and from the relational states to the target(s) of the relation. Finally, the labeling of states remains the same as before, with the addition of labeling the relational states with the name of the relation they represent.

Let us now generalize this notion. Let Relations = {$Rel_1, Rel_2,$,...$Rel_r$} be the set of all possible relations between model elements and RelationalModels = $\{KS_1, KS_2$,..., $KS_r\}$ be the set of the corresponding Relational Models. $KS_i$[] denotes a certain part of $KS_i$ (AP—atomic propositions, S—state set, etc.), $Rel_i$ [S] denotes all of the relational states combined for the relation $Rel_i$. We define a Joint Relational Model over a set of model elements M, a set of relations Relations, and a set of Relational Models RelationalModels as a Kripke Structure, where:

• $AP = \{ KS_1 [AP] \cup \cdots \cup KS_r [AP] \cup Relations \}$

• $S = KS_1 [S] \cup \cdots \cup KS_r [S] \cup Rel_1 [S] \cup \cdots \cup Rel_r [S]$

• $I = \{ IS \}$

• $R = R_{IS} \cup \{(s,t)| \exists 1\le i \le r: \exists (sKS, tKS) \in KS_i[R], sRel \in Rel_i [S]: (s = sKS \wedge t = sRel) \vee (s = sRel \wedge t =tKS ) \}$

• $L (s \in S) = \{L | \exists 1\le i \le r: (s \in Rel_i [S] \wedge L=Rel_i) \vee (s \in KS_i[S] \wedge L = KS_i[L](s))\}$

Figure 6 demonstrates how the previously discussed Relational Models can be combined into a Joint Relational Model. Every model element is represented by a state, denoted with a circle. The attribute and inheritance relations are then modeled by states labeled with these relations. For example, the attributes of the class Device are reachable in the model by taking the transition from the state labeled with “Device” to the next state labeled with “Attributes”, from which a transition points to each and every attribute that Device holds (imei and capacity).

Fig. 6

The Joint Relational Model of the UML class example, joining the attribute and inheritance relations

Formalizing Constraints in CTL

The static constraints to be verified are formalized using CTL. However, two significant difficulties arise in a JRM, regardless of the modeling language of the source model. Firstly, most constraints should only be evaluated on states representing actual model elements, not on the relational states. Secondly, since multiple relations are now present in the formal model, navigating between them is necessary. This means that it should be possible to prescribe that when evaluating the constraint, only paths through certain relations should be considered. For example, consider a constraint on a UML class diagram that states that a certain class must be (indirectly) the base class of all classes in the model. When creating the CTL formula, it must be specified that the base class must be reachable from any non-relational state, but only through inheritance relations.

Since these problems stem from the nature of our approach, a general solution is required. With $Relations = \{Rel_1, Rel_2,\ldots , Rel_r\}$, let $R = \{Rel_i,\ldots , Rel_k\} \subseteq Relations$ be a subset of relations. To solve both problems, we define the Exclude formula in the following way:

$$\begin{aligned} Exclude(R) = \lnot Rel_i \wedge \lnot Rel_{i+1} \wedge \cdots \wedge \lnot Rel_k \end{aligned}$$

(2)

By taking the logical negation of all the given relations and joining them with logical and operators, this formula excludes all the relations in some context. For example, the problem of only evaluating constraints on states representing actual model elements, and not on relational states, can be solved in the following way:

$$\begin{aligned} AG (Exclude(R) \implies \phi ), \end{aligned}$$

(3)

where $\phi$ is the formula to be verified. By using a logical implication and the Exclude formula, the given relations can be excluded from the paths. Considering the running UML class example (Fig. 3), suppose we would like to formalize the following constraint: “An attribute (with a primitive type) cannot hold further attributes.”

Equation 4 prescribes that if a state is encountered that is labeled with “Attributes”, then there must not exist a next state, from which exists a second next state which is also labeled with “Attributes”. Since we begin from an “Attributes” state, this means that any next state will correspond to an attribute that is held by some model element. The second next state, labeled with “Attributes”, would then imply that an attribute holds another attribute, which is precisely what was prohibited in the first constraint.

$$\begin{aligned} AG ( Attributes \implies \lnot (EX EX Attributes) ) \end{aligned}$$

(4)

From UML Class Diagram To JRM

The first step of GFMV is to define the mapping from the source model to the Joint Relational Model. This means that the model elements and relations of the formal model must be defined. In terms of this transformation, GFMV works similarly to Alloy. For example, considering UML class diagrams, a mapping must be defined from UML class diagrams to the formal model. This means that the source model must be traversed, and for each element in the model, appropriate model elements and/or relations must be created in the Joint Relational Model. Currently, this procedure is manual, but will be extended to support declarative, semi-automatic transformations.

The basic model elements of a class diagram consist of the following:

• 1. Classes.

• 2. Attributes.

• 3. Methods.

• 4. Interfaces.

• 5. Enumerations.

• 6. Enumeration literals.

• 7. Associations, Compositions and Aggregations.

• 8. Typenames, such as Integer or Boolean.

• 9. Any primitive literals necessary for the constraints, including numbers, strings and booleans.

The relations of UML class diagrams are defined to be the following:

• 1. Inheritance. The source of the relation inherits from the target.

• 2. InterfaceRealization. The source of the relation realizes the target interface.

• 3. Dependency. The source of the relation depends on the target.

• 4. Attributes. The source of the relation holds the targets as its attributes.

• 5. Methods. The source of the relation holds the targets as its methods.

• 6. MethodParameters. The source of the relation holds the targets as its parameters.

• 7. ReturnType. The target of the relation is the return type of the source.

• 8. Value. The value of the source of the relation is the target.

• 9. EnumerationLiterals. The source of the relation holds the targets as its enumeration literals.

• 10. Associations, Compositions and Aggregations. The source of the relation holds the targets as its associations, compositions or aggregations, respectively. For example, suppose class A has 2 associations towards class B, with rolenames $a_1$ and $a_2$. In this case, the Associations relation of A would point to $a_1$ and $a_2$ as its targets. This is also the reason why adding associations, compositions and aggregations identified by their rolenames as model elements is necessary.

• 11. CardinalityMin. The lower bound cardinality of the source of the relation is the target. This relation is used to capture the cardinality of the previous relations.

• 12. CardinalityMax. The upper bound cardinality of the source of the relation is the target.

• 13. Type. The type of the source of the relation is the target. This relation is used to capture the type of model elements, for example in the case of attributes or method parameters.

• 14. Visibility. The visibility of the source of the relation is the target.

• 15. Modifiers. The targets of the relation are the modifiers of the source, such as abstract or static.

Let us now consider the case of objects. So far, only classes and their elements were considered. However, static constraints are defined and verified on all the objects and their corresponding elements as well. Consequently, similarly to OCL-based systems, the objects also have to be defined. The difference is that in GFMV, the objects and the classes themselves are defined in the same formal model, the JRM. To connect the objects with their respective class-elements, the Instantiation relation is defined, that points from the instance to the class-element. This applies for attributes and relations between the classes as well. For instance, if a class defines an association towards another, then all its objects will also own such an association that instantiates the association of the class.

Evaluation

In this section, we evaluate the feasibility of GFMV. We define the mapping from UML class diagrams into a JRM and present our approach on a real-world class diagram taken from existing literature depicted in Fig. 7. The model describes a simplified excerpt of Luxembourg’s personal income tax management system. The JRM is constructed as described in the previous sections. The elements of the class diagram are transformed into model elements, which are connected by relational states. The JRM of the example consists of 93 transitions, 63 states representing model elements, and 78 states representing relations. A basic proof-of-concept implementation of GFMV is publicly available on GitHub.¹ The implementation generates the NuSMV script that contains the definition of the JRM and the CTL formulae for the case study presented in this section.

Formalizing Constraints: OCL

In this section, we present the suite of constraints to be formalized. Regarding the example UML class diagram depicted in Fig. 7, Soltana et al. define the following OCL expressions. [25].

C2 prescribes that for every instance of PhysicalPerson, if the value of disabilityType is DisabilityType.None, then the value of disabilityRate must be 0. C3 states that for every instance of TaxPayer, all its addresses being registered in Luxembourg does not necessarily imply that the taxpayer is resident. C4 specifies that for every instance of TaxPayer, if there exists one of its incomes that is local and there does not exist one of its addresses that is registered in Luxembourg, then the taxpayer must not be local. C5 defines that for every instance of Income, if it is the instance of the subclass Other, then the nullable association taxcard must be undefined, otherwise it must be defined.

Formalizing Constraints: CTL

Figure 8 illustrates the objects that we defined for our experiments.

Fig. 7

The UML class diagram to be used as case study, taken from the literature [25]

Fig. 8

The objects that are validated against the invariants, represented in an object diagram

When evaluating the OCL invariants over these objects, the following results are obtained:

• C2 does not hold. The value of disabilityType is DisabilityType.None, but the disabilityRate is 1.0, which violates the requirement.

• C3 does not hold. A logical implication evaluates to false if and only if the premise holds, but the conclusion does not. In our example, this invariant does not hold if and only if all of the addresses are in Luxembourg, but the taxpayer is not resident. This is exactly the case for TaxPayer_1. Consequently, C3 does not hold.

• C4 and C5 hold.

Let us now formalize the requirements in CTL. The formulae are written using the input language of NuSMV, where & denotes logical and, ! denotes logical negation, and -> denotes logical implication. First, let us define some auxiliary subformulae, that are used often in the constraints. This way, the formulae expressing the constraints will be more concise and readable. Let T $\in AP_{JRM}$, $Relations = \{Rel_1, Rel_2,$..., $Rel_r\}$, $Exclude(Rel \subseteq Relations)$ the formula seen in Eq. 2, $R \in Relations$ any relation.

Inst(T) defines a direct instantiation relation towards the model element T.

Inherit (T) expresses that T is reachable in the model by traversing only through the Inheritance relation, all other relations are forbidden by the Exclude formula.

Conform(T) combines the previous 2 formulae: it prescribes indirect instantiation towards T. A model element M indirectly instantiates another element T, if and only if T $\ne$ M, M is a direct instance of T or M is the direct instance of an element that inherits (implicitly) from T. For example, considering the objects presented in Fig. 8, TaxPayer_1 is a direct instance of TaxPayer and an indirect instance of PhysicalPerson.

RelA(R, forbid, condition) defines that R must be an available relation in the current state and all targets of R must satisfy a given subformula, denoted by condition, if the second parameter is set to false. If it is set to true, then instead of prescribing the existence of such targets, their existence is forbidden.

RelE defines the same, but instead of all targets, at least one target is considered.

Utiziling these auxiliary formulae, the constraints C2-C5 can be formalized in CTL in the following way. Using a sub-formula at any point is denoted by a $ sign at the beginning of a formula. In OCL the invariants are defined on a single context, including, but not limited to a class in a UML class diagram. At the beginning of each formula, the context must be defined, where the rest of the formula must hold. This is equivalent to the context in an OCL expression, but is much more flexible. In our approach, any context may be defined. This can mean multiple classes, objects, or any other logical conditions. By using a logical implication with the condition as the premise and the constraint that must hold as the conclusion, the context is clearly defined. Note that by default, the InitialState is excluded from all formulae by automatically adding !InitialState to the beginning of the formula.

Formula C2 defines that for all (in)direct instances of PhysicalPerson, if there exists an attribute that instantiates PhysicalPerson.disabilityType and its value is set to Disability.None, then there must also exist the attribute PhysicalPerson.disabilityRate and its value must be set to 0. The reason why the label representing 0 is named Literal_0.0 is because the input language of NuSMV does not allow identifiers starting with a number.

C3 specifies that for all (in)direct instances of TaxPayer, considering the following conditions (1) and (2) holds, if condition (1) holds, then condition (2) must also hold. (1) For all associations, if the association instantiates PhysicalPerson.addresses then none of its association targets contain the value Country.LU. (2) There must exist an attribute that instantiates TaxPayer.isResident and its value is set to true.

C4 prescribes that for all (in)direct instances of TaxPayer, if the following conditions (1) and (2) hold, then (3) must also hold. (1) There exists an association that instantiates TaxPayer.incomes and there exists a target for this association that has an attribute that instantiates Income.isLocal, the value of which must be set to true. (2) There does not exist an association that instantiates Physicalperson.addresses and has an attribute that instantiates Address.country, the value of which is set to Country.LU. (3) There exists an attribute that instantiates TaxPayer.isResident and its value is set to false.

Considering the following conditions (1) and (2), C5 states that both condition (1) and condition (2) must hold. (1) For all (in)direct instances of Other, there must not exist an association that instantiates Income.taxCard. (2) For all in(direct) instances of Income that are not (in)direct instances of Other, there must exist an association that instantiates Income.taxCard.

The example presented in [25] also contains another invariant, C1, and some additional parts of C2, that were not covered here. These are the following.

A query is defined for the method getAge(), stating that it should return with Constants::YEAR - self.birthYear if the value of Constants::YEAR is valid, and $-1$ otherwise. C1 then defines that getAge() must return a value between 0 and 100. This is not possible to express in our approach, as it is outside of our scope of focusing on static constraints. Defining derived operations, executing them and expressing requirements on the results are not and will not be supported.

In the original solution, C2 also had another line of criteria that is not currently possible to express in our approach. Checking if a value falls in a given range ($0< disabilityRate <= 1$) is not advisable to check in the formal model. Currently, the only way it could be included in the formal model is to compute the result in an interpreter, and adding it as a relation into the model. For instance, the GreaterThan and LesserThanOrEquals relations could be defined, the results computed outside of NuSMV, generated into the model and then checked using CTL. However, this would not be a natural solution in GFMV. Instead, in the future, comparing numerical values against a given range will be done outside of NuSMV, in a high level interpreter. However, defining the operands that must be compared will still be done by navigating the JRM, only the comparison itself will be computed separately.

Performance Analysis

In this section, we evaluate the runtime of GFMV. The same model and constraints that were presented in the previous sections are used in the analysis. However, the model is not large enough to determine how the runtime scales with the size of the model. Consequently, during our analysis, we gradually increased the size by adding more instance-level elements to the model. We refer to every object and their elements (Fig. 8) as a fragment of the model. Table 2 shows the number of transitions, states representing model elements, and states representing relations. The total number of states in the model is the sum of the previous two. The number of fragments starts at 1 (the original model) and increases gradually with increments of 10 up to 100. An additional measurement was taken at 200 fragments to demonstrate that the tendency of the runtime is not linear with the size of the model. It should be noted that the number of fragments were chosen deliberately high, to simulate models that are large enough to yield representative results.

Table 2 The number of transitions, model elements and relational states for fragments ranging from 1 to 200

Fig. 9

The runtime of the verification process with regard to the number of fragments in the model

The measurements were taken using an Intel i7-7700HQ @ 2.80GHz processor. Figure 9 describes the results. At fragments 1, 10 and 20, the verification finished instantly. From 30 to 100, the runtime rises from 0.9 up to 11.3 s, in an approximately linear tendency. At 200 fragments, verification finished in 57.1 s. This is significantly more than the difference between 1 and 100 fragments. The reason for this is that the runtime of model checking CTL formulae increases exponentially with the size of the model. However, we believe 100–200 fragments already yield a large enough model that practical industrial applications would rarely surpass. Thus, for practical applications, the analysis shows that GFMV finishes verification in reasonable time to be feasible in practice.

It should be noted that creating the JRM was done fully manually. This means that the elements of the JRM were created explicitly from code, and not mapped from an actual class diagram. For this reason, the presented results do not contain the transformation time. As mentioned before, the transformation would include traversing the source model and mapping every element to model elements and relations in the JRM. Since creating the elements is negligible in terms of performance, the complexity of this process corresponds to the complexity of traversal, which is proportional to the size of the source model. Fortunately, efficient algorithms exist for traversing and processing models. Thus, we believe the complexity of the transformation will also be scalable in practice. Naturally, in the future, more experiments will be necessary to confirm this.

Conclusions

In this paper, we have presented the General Formal Model-Verifier, GFMV, that is an approach for formally verifying static constraints on models. A formal Kripke Structure is created that captures the static aspects of the original software model. The constraints to be verified are formalized using CTL and a model checker tool, NuSMV is used to verify whether the formalized CTL expressions hold on the formal model. The approach was evaluated on a real-world example UML class diagram. The model was mapped to a formal JRM, then the given OCL constraints were formalized using CTL. The runtime of the verification process was evaluated by artificially increasing the size of the example model gradually.

The main strength of GFMV lies in its formal aspect. Since a widespread model checker tool (NuSMV) is used, the verification of models is fully automatic, and formal proof is given that the model satisfies the constraints. It is guaranteed to find any violations of the formalized constraints. If no violations are found, the constraint is guaranteed to hold. The approach is general and independent of the modeling language of the source model. While this is somewhat true for OCL and its variants as well, defining a mapping between the source model and the JRM is easier and takes less effort than implementing an OCL interpreter for the given modeling language. A consequence of the generality is that the approach becomes independent of the concrete model checker behind it. It currently uses NuSMV, but could easily be extended to use a different model checker or support multiple options.

The main weakness of the approach is the expressive power of CTL. Severely complex constraints may be too difficult to express, and even if they can be expressed, it is undeniably more difficult to do so than in OCL. On the other hand, defining a context for constraints to be evaluated on is more flexible in GFMV. Multiple contexts can be defined in an arbitrary logical formula, even on objects. The second weakness is that GFMV focuses only on verifying static constraints, it does not support many other features that OCL does. Moreover, defining CTL expressions requires proficiency in formal verification methods. Naturally, this cannot be expected of the model designer. For this reason, in the future, we plan to create a Domain Specific Language (DSL) [26] to hide the complexity of writing CTL expressions from the model designer. Finally, NuSMV and other model checker tools typically detect violations of constraints in such a way that a single counter-example is generated that highlights a sequence of states on which a constraint does not hold. The reason for this is that in general, infinitely many violations may occur and exploring them all is neither possible, nor expedient. Consequently, to find all violations, running a model checker only once is not sufficient.

This weakness is vital, thus, it must be alleviated in the future. The most straight-forward solution is to modify the implementation of NuSMV in such a way that execution should not terminate with a single counter-example, but every state that violates a constraint should be collected. However, not every model checker is open-source, thus, this option is not suitable in general. The solution that could be explored is to apply counter-example guided abstraction refinement (CEGAR) [27] over the CTL constraints. By gradually filtering counter-examples that have already been found, eventually all violations can be found. Handling potential loops in the state-space is crucial, otherwise it would not be guaranteed that the abstraction refinement would ever terminate.

Developing a language over CTL is also of high priority. A syntax similar to OCL is what we strive to create, hiding the complexity of defining CTL formulae from the designer. Moreover, defining the transformations between the source models and the JRM must also be possible in a declarative, semi-automatic way.

Algorithmic performance optimizations will also be explored. Defining declarative transformations on Kripke Structures, similar to model-to-model transformations, can also help increase the expressive power of GFMV. By temporarily transforming parts of a model, constraints that are difficult to express through CTL may become easier to define.

A more thorough evaluation would also be beneficial. Although the results presented in this paper are representative and show the applicability of the approach in practice, more complex examples should also be taken into consideration. Performance evaluations should also be done iteratively, as the future work presented here may influence the algorithmic complexity of the approach.