Introduction

Knowledge graphs (KGs) have seen a surge in popularity as a flexible and intuitive way to store relational information. In order to perform complex tasks such as question answering [1] and recommendation [2] the integration of multiple KGs is crucial. Conventional data integration frameworks however struggle with the heterogeneity of KGs. Knowledge Graph Embeddings (KGE) have been found to provide a way to deal with this problem by encoding entities from different data sources into a common lower-dimensional embedding space. If done properly this technique reconstructs semantic and relational information and similar entities end up close in the embedding space [3].

While a plethora of models have been devised to obtain KGEs, their refinement in the final alignment step of the data integration pipeline has seen little attention. Sun et al. [3] have discoverd, that KGEs as many other high-dimensional data structures suffer from hubness. This phenomenon refers to the fact that some entities in the dataset become dangerously popular by dominating the nearest neighbor slots of the other entities. Hubness has been shown to plague a variety of tasks such as recommender systems [4], speech recognition [5], image classification [6] and many more. For our data integration setting hubness leads to a decrease in alignment quality.

In order to investigate the effects of hubness on entity alignment we will use 15 different Knowledge Graph Embedding approaches on 16 alignment tasks containing samples of KGs with varying properties. This provides us with 240 KGEs as input for our study.

In our evaluation we compare six different hubness reduction techniques and eight different (approximate) nearest neighbor (ANN) algorithm implementations w.r.t. their accuracy and execution time. This paper extends our previous work [7] in a variety of ways:

  • The related work section and discussion have been extended.

  • We enhanced our experiment section with another ANN library and investigate how the use of GPUs factors into our assessment.

  • While we previously used a frequentist approach [8] to check the statistical significance of our claims, we now use a more modern Bayesian testing regime [9]. This enables us to directly reevaluate our previous results and leads us to new conclusions in some cases.

Overall our work provides the following contributions:

  • We provide an extensive evaluation of hubness reduction techniques for entity alignment with Knowledge Graph Embeddings.

  • Our results suggest that using the Faiss [10] ANN library we can perform hubness reduction at practically no cost with large and small datasets, while reaping the accuracy benefits of reduced hubness.

  • Hubness-reduced nearest neighbor search for entity alignment is made practically available in our open-source library at https://github.com/dobraczka/kiez and the configurations of our experiments are available in a separate benchmark repository https://github.com/dobraczka/kiez-benchmarking.

We begin with an overview of related work, followed by an outline of hubness reduction for entity alignment in section “Hubness Reduction for Entity Alignment”. Subsequently, we present our extensive evaluation in section “Evaluation” and we close with a conclusion.

Preliminaries and Related Work

In this section we present the central concepts related to our work. We start by giving a brief outline to the notion of Knowledge Graphs, followed by an overview of Knowledge Graph Embedding approaches. Afterwards we present the hubness problem and ways to mitigate it, followed by a synopsis of entity alignment techniques for Knowledge Graph alignment.

Knowledge Graphs

Knowledge Graphs (KG) are now a widely used data structure, which is able to represent relations between entities intuitively. Especially the ability to postpone the definition a rigid schema enables a more flexible extension of data than e.g. a relational database management system. Nowadays KGs serve as backbone for a variety of tasks. For example in the use-case of semantic search, the semantically rich structure of KGs helps identify a user’s information need. Moreover, the nowadays common use of knowledge cards as search engine result, which displays the most important information about an entity (e.g. birth date, net worth, etc. of a person) relies heavily on the aggregated information contained in the KG [11].

Fig. 1
figure 1

Sample of DBpedia showing information about the movie “Parasite”

Full size image

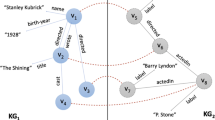
In Fig. 1 we see an example snippet of the DBpedia KG containing information about a motion picture. We see that knowledge graphs enable us to store a variety of data and relations between data points. For our purposes a KG is a tuple \(\mathcal{KG}\mathcal{}= (\mathcal {E}, \mathcal {P}, \mathcal {L}, \mathcal {T})\), where \(\mathcal {E}\) is the set of entities, \(\mathcal {P}\) the set of properties, \(\mathcal {L}\) the set of literals and \(\mathcal {T}\) the set of triples. KGs consist of triples \((h,r,t) \in \mathcal {T}\), with \(h \in \mathcal {E}\), \(r \in \mathcal {P}\) and \(t \in \{\mathcal {E},\mathcal {L}\}\).

Looking at our example graph a triple contained there is for example (dbr:Parasite_(2019_film), rdf:type, dbo:Film). For a thorough introduction into the subject of knowledge graphs we refer the reader to [12].

Knowledge Graph Embedding

Methods of machine learning belong to the standard repertoire of any data analytics endeavour nowadays. However many machine learning algorithms rely on input in the form of dense numerical vectors, which is in stark contrast to the conventional representation of knowledge graphs. To make KGs usable for machine learning tasks Knowledge Graph Embedding approaches are used to encode KG entities (and sometimes relationships) into a lower-dimensional space.

While there are different paradigms of algorithms most embedding approaches score the plausibility of a given triple (h, r, t), i.e. how likely is this statement to be true. The goal of the algorithm is then to compute the embeddings in such a way that positive examples (triples contained in the graph) are scored high, while negative examples are scored low. Negative examples are typically created by corrupting a given triple by replacing either h resp. t with \((h',r,t) \notin \mathcal {T}\) resp. \((h,r,t') \notin \mathcal {T}\). This way of self-supervised learning is highly convenient since there is no need for human labeling [12].

In the following we give a brief overview over different paradigms of embedding approaches. For a more detailed overview we direct the reader to [13, 14].

Translational

An intuitive way to make sure a model learns the plausibility of a triple is the translational approach. Algorithms that fall into this category encode relations as translations from head entity embedding to the embedding of the tail entity. This technique was popularized with TransE [15]. Suppose for a triple (h, r, t), the embedding vectors of h,r and t are \(\mathbf {h},\mathbf {r}\) and \(\mathbf {t}\) respectively, TransE utilizes the distance between \(\mathbf {h} + \mathbf {r}\) and \(\mathbf {t}\) to model the embeddings. The central idea of this approach was quickly picked up to address shortcomings of TransE, namely the problem modeling \(1-n\) or \(n-n\) relations. For example TransH [16] encodes relations in their own hyperplane, and TransR [17] even uses relation-specific spaces. While these and other generalizations of TransE enhanced the capabilities of translational models, Kazeemi and Poole [18] showed that these translational models put severe constraints on the types of relations that can be learned (at least, when these models operate solely in euclidean spaces). These fundamental limitations are adressed for example by HyperKG [19], which operates in the hyperbolic space.

Tensor-Factorization

Another paradigm of embedding approaches relies on decomposing tensors (also known as tensor-factorization). A tensor is a generalization of matrices towards arbitrary dimensions. A conventional matrix is therefore a 2-order tensor [12]. Decomposing a tensor means finding lower order tensors from which the original tensor can be (approximately) reconstructed. The lower order tensors of the decomposition capture latent factors of the original tensor. For example RESCAL [20] models KGs as a 3-order binary tensor \(\mathcal {G} \in \mathbb {R}^{n \times n \times m}\), where n and m respectively denote the number of entities and relations. Each relation is represented as a matrix \(W_r \in \mathbb {R}^{n \times n}\). The weights \(w_{i,j}\) in the matrix capture the interaction between the i-th latent factor of \(\mathbf {h}\) and j-th latent factor of \(\mathbf {t}\). We can then score the plausibility of a triple (h, r, t) by

$$\begin{aligned} f(h,r,t)=\mathbf {h}^{T} \mathbf {W}_r \mathbf {t}. \end{aligned}$$
(1)

Again the goal is to maximize the plausibility of positive examples and minimize the plausibility of negative examples. A plethora of methods belong to this paradigm. RESCAL’s representation of relations as matrices is rather costly, so for example HolE [21] models both entities and relations as vectors. Furthermore it uses a circular correlation operator, which combines the outer product of two vectors by taking the sums along their diagonals. This circular correlation compresses pairwise interactions, which makes HolE more light-weight than RESCAL [14]. Another approach called TuckER [22] utilizes Tucker Decomposition [23], which decomposes the given tensor into a sequence of three matrices \(\mathbf {A}, \mathbf {B}\) and \(\mathbf {C}\) and a smaller “core” tensor \(\mathcal {T}\). More precisely, given the knowledge graph as 3-order tensor \(\mathcal {G}\) this decomposition approximates \(\mathcal {G} \approx \mathcal {T} \otimes \mathbf {A} \otimes \mathbf {B} \otimes \mathbf {C}\), where \(\otimes \) denotes the outer product. \(\mathbf {A}\) and \(\mathbf {C}\) represent the entity embeddings and \(\mathbf {C}\) contains the relation embeddings.

Neural

The previously discussed approaches consist of either linear or bilinear (e.g., matrix multiplication) operations to compute plausibility scores. In order to incorporate non-linear scoring functions approaches rely on neural networks [12]. For example the usage of a 2-dimensional convolutional kernel has been proposed by ConvE [24]. First a matrix is generated by reshaping and concatenating \(\mathbf {h}\) and \(\mathbf {r}\). This matrix is then used as input for the convolutional layer, where different filters of the same shape return a feature map tensor. After vectorization this feature map tensor is then linearly projected into a k-dimensional space. Finally, the plausibility scores are obtained by calculating the dot product of this projected vector and \(\mathbf {t}\).

Path-Based

Oftentimes interesting information can be found in a KG, when looking not only at triples, but at longer paths. For example if a person is born in a certain city and the KG contains information about which country this city is located in we can infer the nationality of a person. PTransE [25] generalizes TransE by incorporating path-based information in the embedding process. So while TransE uses triples in the form of (h, r, t) to optimize the objective function \(\mathbf {h} + \mathbf {r} = \mathbf {t}\), PTransE uses paths like \((h,r_1,e),(e,r_2,t)\) to optimize \(\mathbf {h} + (\mathbf {r_1} \circ \mathbf {r_2}) = \mathbf {t}\), with \(\circ \) being an operator that joins the relations \(r_1\) and \(r_2\) into a unified relational path representation. Inspired by neural language models RDF2Vec [26] models paths in the knowledge graphs as sequences of entities which is akin to sentences in the language model setting. The embeddings are then trained similarly to the word2vec [27] neural language model.

Hubness

High-dimensional spaces present a variety of challenges commonly referred to under the umbrella of the curse of dimensionality. For example distances (or measures) tend to concentrate in higher dimensions. In fact, with dimensionality approaching infinity distances between pairs of objects become effectively useless by being indistinguishable [28]. This distance concentration can be explained by the fact that with increasing dimensions the volume of a unit hypercube grows faster than the volume of a unit hyperball. Consequently, numerous distance metrics (such as e.g. the euclidean distance) lose their relative contrast, i.e. given a query point the distance between the nearest and farthest neighbor decreases almost entirely [29]. This is worrisome, since neighborhood-based approaches rely fundamentally on distances.

Closely related, it has been shown that high-dimensional spaces suffer from a phenomenon known as hubness [30]. While first noticed in the field of music recommendation [31] this issue has been found harmful w.r.t result quality in a variety of tasks ranging from graph analysis [32], over clustering of single-cell transcriptomic data [33] to outlier detection [34]. In order to understand what hubness means, k-occurrence must first be introduced:

Definition 1

(k-occurrence) Given a non-empty dataset \(D \subseteq \mathbb {R}^{m}\) with n objects in an m-dimensional space. We can count how often an object \(x \in D\) occurs in the k-nearest neighbors of all other objects \(D \backslash x\). This count is referred to as k-occurrence \(O^{k}(x)\) [7].

If the distribution of the k-occurence is skewed to the right, this means there exist some hubs, that occur more frequently as nearest neighbors of other points than the rest of the dataset entries [35].

Fig. 2
figure 2

Visualization of hubness and hubness reduction on SimplE embeddings of the D-W 15K(V1) dataset. Left column shows visualization without hubness reduction, right column after NICDM hubness reduction. The value of k is 10

Full size image

Figure 2 shows how hubness means a skewed k-occurrence distribution. In the top we see that hubs (the darker, bigger points) have a much higher k-occurrence than their neighbors and how hubness reduction changes that. The bottom graphic shows the entire k-occurrence distribution. Most nodes show up rarely as nearest neighbors if at all, while a handful of nodes are nearest neighbors to more than 300 other entities. Hubness reduction techniques can mitigate this somewhat. Most notably, the 2 nodes with the highest k-occurrence (> 300) lose their prominence. More specifically, the entity that previously showed up as k-nearest neighbor (kNN) of 327 entities, now only shows up as kNN of 164 entities. Since the underlying task of this dataset is entity alignment, the practical implications of hubness reduction here are a diminished probability of wrongfully aligning entities with hub entities. We will take a closer look on hubness reduction techniques in section “Hubness Reduction”.

Initial research indicated that hubness was simply an intrinsic property of high-dimensional data [36]. However, a later study suspects that density gradients are the culprit of the hubness phenomenon [37]. In this case, density gradients refer to spatial variations in density over an empirical data distribution [38].

Hubness Reduction

Reduction of hubness has been a lively field of research since discovery of the hubness phenomenon. The objects closer to the mean of a data distribution have a higher probability to become hubs. This fact is denoted as spatial centrality of hubs [36]. One method of hubness reduction therefore aims to reduce the spatial centrality by subtracting the centroid of the data [39]. Hara et al. [40] argue that variants of these centering approaches mainly work by flattening the density gradient.

Another paradigm of hubness reduction approaches tries to repair asymmetric nearest neighbor relations. The nearest neighbor relation between two points x and y is symmetric if x is the nearest neighbor of y and vice versa. Because hubs are disproportionally more often nearest neighbors of other points than the other way round, a dataset that suffers from hubness has an asymmetry in nearest neighbor relations [38]. Some hubness reduction methods therefore transform primary distances (such as e.g. euclidean distance) to secondary distances, where these asymmetric relations are alleviated. Methods such as local scaling [41] and the (non-iterative) contextual dissimilarity measure [42] were later discoverd to actually reduce hubness. Mutual proximity [43] was specifically developed to reduce hubness. For a more comprehensive overview of hubness reduction techniques we refer to [35, 38]. In Section “Hubness Reduction” we will present a more detailed view of the mentioned approaches with regards to entity alignment.

Entity Alignment

Matching entities from different data sources has been a research effort spanning decades, ironically under a variety of terms such as record linkage, data deduplication or entity resolution [44]. While historically research in this field was centered around matching records in tables, soon enough incorporating relational information was found to be beneficial for the alignment process [45]. For example [46] use Personalized PageRank to attain a nodes importance and propagate similarities in a graph of potential matches.

The flexibility of knowledge graphs poses a challenge to the matching process, which approaches that are build for table-based matching cannot handle easily. Take a look at Figure 3, where the previously introduced snippet from DBpedia is juxtaposed with a snippet from Wikidata. We see that the heterogeneity of the data sources poses a variety of obstacles in the matching process. From different naming conventions for the same relations (e.g dbo:director and wdt:P57), to distinct representation of data (e.g. the birth dates).

Fig. 3
figure 3

Two snippets from DBpedia and Wikidata containing information about the film “Parasite”. The dark dotted lines connect entities from each source which should be matched

Full size image

A way to manage the heterogeneity of Knowledge Graphs is through the use of Knowledge Graph Embeddings. Generally entity alignment through Knowledge Graph Embeddings can be divided into two major categories: Approaches that utilize the information contained in literals (e.g. the target of the rdfs:title property) and those, that rely solely on the graph structure. While structure-only approaches initialize the entity embeddings randomly and usually have to translate the embeddings of these two different graphs into the same embedding space, approaches that utilize literal information commonly utilize pre-trained word embeddings to initialize the entity embeddings already in the same space. For the latter, the training process is then concerned with fine-tuning the initial embeddings via the structural information (and in some cases also via the attribute information). Both paradigms generally rely on seed alignment, which consists of already known matches, as training data. Finally, nearest neighbor search is used in almost all approaches to align entities from the different KGs based on how close these entities are in the embedding space.

AttrE [47] uses predicate alignment via string-similarity to create a common schema for the two given knowledge graphs. To incorporate literal information this approach uses a compositional function to aggregate the character embeddings of a given literal. Pre-trained word embeddings are not used in this approach. MultiKE [48] uses different views of the entities to capture different aspects of information, including specific “name” properties (like values of rdfs:title), attributes and relational information. The literal embeddings are initialized with pre-trained word embeddings. AttrE and MultiKE both rely on a translational approach to incorporate structural information.

An approach that does not rely on literal information is RSN4EA [49]. This algorithm relies on sampling paths via biased random walks and utilizes a so-called recurrent skipping network(RSN) [50], a refinement of recurrent neural networks (RNN) for the alignment task. Because RNNs cannot distinguish relations and entities given as a path sequence, the RSN is more fitting for entity alignment since this network is able to “skip” directly from an entity to another entity.

A more thorough overview over KGE-based entity alignment is found in [3]. This benchmarking study also first mentioned that alignment results can be improved via hubness reduction. However no systematic investigation of different hubness reduction techniques was carried out.

Hubness Reduction for Entity Alignment

In this section we formally define the task of entity alignment, present methods to measure hubness and introduce our framework for hubness reduced entity alignment. Finally we showcase the hubness reduction methods utilized for entity alignment and introduce various (approximate) nearest neighbor approaches that we employ.

Entity Alignment

As already introduced in section “Knowledge Graphs” a KG is a tuple \(\mathcal{KG}\mathcal{}= (\mathcal {E}, \mathcal {P}, \mathcal {L}, \mathcal {T})\), with the tuple elements denoting the sets of entities, properties, literals and triples respectively. Entity alignment now seeks to determine the mapping \(\mathcal {M}= \{(e_{1},e_{2}) \in \mathcal {E}_1 \times \mathcal {E}_2 \vert e_1 \equiv e_2 \}\), with \(\equiv \) denoting the equivalence relation. \(\mathcal {E}_1\) and \(\mathcal {E}_2\) are the entity sets of the respective KGs.

Hubness

Hubness can be measured in different ways. As already discussed in section “Hubness” skewness in k-occurence \(O^{k}\) can be used to determine the degree of hubness [36].

$$\begin{aligned} S^{k}=\mathbb {E}[(O^{k}-\mu _{O^{k}})^{3}]/\sigma ^{3}_{O^{k}}. \end{aligned}$$
(2)

With the commonly used notation of \(\mathbb {E}\) denoting the expected value, \(\mu \) the mean and \(\sigma \) the standard deviation. Feldbauer et al. [35] criticize k-skewness as difficult to understand and instead adapted the income inequality measure known as Robin Hood index to calculate k-occurence inequality

$$\begin{aligned} \mathcal {H}^{k}=\frac{1}{2} \frac{\sum _{x \in D} \vert O^{k}(x)-\mu _{O^{k}}\vert }{(\sum _{x \in D} O^{k}(x))-k} = \frac{\sum _{x \in D}\vert O^{k}(x) -k\vert }{2k(n-1)}, \end{aligned}$$
(3)

with D being a dataset of size n. This measure is easily interpretable, since it answers the question: “What share of ’nearest neighbor slots’ must be redistributed to achieve k-occurence equality among all objects?” [35].

Hubness Reduction

In order to align two KGs we need to find the most similar entities between the KGs.

Given the embeddings \(\mathbb {K}_s, \mathbb {K}_t\) of the two KGs we intend to align, we utilize a distance \(d_{x,y}\), with \(x \in \mathbb {K}_s\) and \(y \in \mathbb {K}_t\). The k points closest to x will be referred to as x’s k-nearest neighbors.

The implementation of our open-source framework is inspired by [51] and has been adapted to the task of hubness-reduced nearest neighbor search for entity alignment. An overview of the workflow of our framework, which we named kiez is shown in Fig. 4.

Fig. 4
figure 4

Overview of our framework. Graphic previously published in [7]

Full size image

We start by retrieving a number of kNN candidates from the two given KGEs using a primary distance (e.g. euclidean). Note that the kNN candidates for all \(x \in \mathbb {K}_s\), as well as \(y \in \mathbb {K}_t\) are retrieved. Due to asymmetric nearest neighbor relations introduced by hubness x might be a kNN candidate of y but not the other way round. However the distance between such two points x and y is the same no matter whether x is a kNN candidate of y or vice versa. These primary distances can now be utilized to perform hubness reduction and attain secondary distances. The final kNN are obtained by using these secondary distances. To offset the higher cost w.r.t speed introduced by hubness reduction we offer a variety of approximate nearest neighbor libraries. In section “Evaluation” we will see, that this gives a speed advantage on larger datasets, while still benefiting from the accuracy increase of hubness reduction. More information about the ANN approaches is given in section “(Approximate) Nearest Neighbor Search”.

We selected the best performing hubness reduction techniques reported in [38] to implement in kiez and will present them in detail now.

First introduced in [41] Local Scaling was later discovered to reduce hubness [43]. Given a distance \(d_{x,y}\) this approach calculates the pairwise secondary distance

$$\begin{aligned} LS(d_{x,y})=1 - \exp \left( -\frac{d^{2}_{x,y}}{\sigma _x \sigma _y} \right) \end{aligned}$$
(4)

with \(\sigma _x\) (or resp. \(\sigma _y\)) being the distance between x (resp. y) and their kth-nearest neighbor

A closely related technique is the non-iterative contextual dissimilarity measure (NICDM) [42] which similarly to Local Scaling was discovered by Schnitzer et. al. [43] to reduce hubness:

$$\begin{aligned} NICDM(d_{x,y})= \frac{d_{x,y}}{\sqrt{\mu _x \mu _y}}, \end{aligned}$$
(5)

where \(\mu _x\) is the mean distance to the k-nearest neighbors of x and analogously for y and \(\mu _y\)

Cross-domain similarity local scaling (CSLS) [52] was introduced to reduce hubness in word embeddings. As the previous approaches it relies on scaling locally:

$$\begin{aligned} CSLS(d_{x,y})=2 \cdot d_{x,y}-\mu _x-\mu _y \end{aligned}$$
(6)

with \(\mu _x\) being the mean distance from x to its k-nearest neighbors. Sun et al. [3] showed that this measure also successfully reduces hubness in knowledge graph embeddings.

While the previously presented approaches rely on local distances Mutual Proximity (MP) [43] counts the distances of all entities whose distances to both x and y are larger than \(d_{x,y}\):

$$\begin{aligned} MP_{emp}(d_{x,y})=\frac{\vert \{j:d_{x,j}> d_{x,y}\} \cap \{j:d_{y,j} > d_{y,x}\} \vert }{n-2} \end{aligned}$$
(7)

The presented version in Eq. 7 was adapted by [38] to normalize the range to [0, 1].

Since counting all these distances is computationally expensive, we can use an approximation:

$$\begin{aligned} MP_{Gauss}(d_{x,y})=SF(d_{x,y},\hat{\mu _x},\hat{\sigma }^{2}_{x}) \cdot SF(d_{x,y},\hat{\mu _y},\hat{\sigma }^{2}_{y}). \end{aligned}$$
(8)

where the estimated sample mean \(\hat{\mu _x}\) and variance \(\hat{\sigma _x}\) of the distances of all other objects to x is used. Furthermore, SF is the complement to the cumulative density function at \(d_{x,y}\).

Finally, we implemented DSL [40], which relies on flattening the density gradient, by estimating the local centroids \(c_k(x) = \frac{1}{k}\sum _{x' \in kNN(x)} x'\), with kNN(x) being the set of k-nearest neighbors of x. This leads to the following formula:

$$\begin{aligned} DSL(x,y)=\Vert x-y\Vert _{2}^{2} - \Vert x-c_{k}(x)\Vert _{2}^{2} - \Vert x-c_{k}(y)\Vert _{2}^{2}. \end{aligned}$$
(9)

(Approximate) Nearest Neighbor Search

Nearest neighbor (NN) search is a fundamental task in many areas of computer science. This is also true for the area of entity alignment, when utilizing knowledge graph embeddings. For higher dimensional datasets efficient exact nearest neighbor algorithms tend to suffer under the curse of dimensionality. The reason for this is again, the distance concentration mentioned in “Hubness”. Many exact NN algorithms rely on the triangle inequality to avoid making unnecessary comparisons, however with rising dimensionality distances between points become indistinguishable and all points have to be compared against all other points in the worst case [53].

Approximate nearest neighbor (ANN) algorithms have therefore been a highly active research field. While these approaches may miss some nearest neighbors they increase the speed of retrieval by creating efficient indexing structures of the search space to avoid comparing all data points with each other. These algorithms can be roughly divided into three categories: tree-based, graph-based and hashing-based.

Tree-based algorithms rely on splitting the dataset and storing these subsets in nodes of a tree. The children of a node split the dataset again and so on until the respective subset that belongs to a node is small enough to be stored there. This node becomes a leaf of the tree. When querying, the tree is traversed to find the closest points to the query.

Graph-based algorithms build a k-NN graph, where vertices are data points and edges associate true nearest neighbors. Similar to tree-based methods, given a query point this graph is traversed in greedy fashion to find the nearest neighbors.

Finally, hashing-based algorithms utilize hashing functions to encode data points as hash values. For example locality-sensitive hashing [54] creates multiple hash-codes for each entry by applying hash functions which are randomly chosen from the same function family. The NN of a query point are then determined by inspecting hash collisions. A general benchmark and overview of ANN algorithms can be found in [55].

For use in kiez, we needed libraries that provide a python implementation/wrapper. We therefore choose the following libraries similar to [35]:

  • scikit-learnFootnote 1 offers the exact methods Ball Tree [56] and KD-Tree [57] (short for k-dimensional tree). Additionally a brute-force variant simply computes pairwise distances and returns the exact nearest neighbors.

  • NMSLIBFootnote 2 implements a variety of algorithms for nearest neighbor search. In our benchmark we use their implementation of Hierarchical Navigable Small World Graphs (HNSW) [58]. This is a popular ANN algorithm that relies on hierarchical proximity graphs.

  • NGTFootnote 3 offers methods to utilize kNN graphs for approximate nearest neighbor search [59].

  • AnnoyFootnote 4 provides a tree-based approach, subsequently splitting the space with random hyperplanes until a certain depth is reached.

  • FaissFootnote 5 makes available a vast variety of algorithms of all three ANN categories. For our evaluation this library is especially interesting since it provides implementations that are capable of utilizing GPUs [10].

Evaluation

We begin the evaluation section by giving an overview of our experimental setup, presenting the used datasets and embedding approaches as well as configurations. Subsequently we will show our results in detail.

Evaluation Setup

We use 16 alignment tasks for our evaluation consisting of samples from DBpedia (D), Wikidata (W) and Yago (Y), which were introduced in [3]. These knowledge graph chunks contain a plethora of different relationships and entity types. Furthermore, they cover a cross-lingual setting in some cases (EN-DE & EN-FR). Depending on the number of entities per source there are two differently sized tasks (15 and 100 K). We show more information about the datasets in Table 1. The tasks consist of finding a 1–1 alignment between the sources, since the number of entities per KG sample is equal to the size of the gold standard mapping \(\mathcal {M}\). Differences in results between our evaluation and the outcomes of [3] are explained by the fact, that we use an updated version of the datasets.Footnote 6 We however used the same hyperparameter settings to create the KGEs as said study.

Table 1 Statistics of datasets
Full size table

The knowledge graph embeddings were created by using a wide range of approaches implemented in the framework OpenEA.Footnote 7 A summary of the 15 embedding approaches we used is shown in 2. Given these 15 embedding approaches and 16 alignment tasks we obtained 240 KGE pairs for our study.

Table 2 Embedding approaches used in the evaluation
Full size table

The exact nearest neighbor algorithms we used were on one hand scikit-learn’s implementations of BallTree and KD-Tree, as well as their brute-force variant which simply computes pairwise distances and then returns the nearest neighbors. On the other hand we used Faiss’s brute-force variant (specifically IndexFlatL2). We also used Faiss’s approximate nearest neighbor approaches. For choosing the most fitting we utilized the autofaissFootnote 8 library which automatically selects a fitting indexing approach, based on the Faiss guidelines and tunes it with the provided data. In our case this resulted in the use of HNSW as algorithm in all cases. Furthermore we used Annoy, NGT and NMSLIB’s HNSW implementation. For these algorithms we found, that their default settings gave the best results, with the exceptions of NMSLIB, where the hyperparameters M = 96 and efConstruction = 500 gave the best results. M controls the probability of adding a given point to a specific layer of the graph and efConstruction controls the recall. More details about our setup can be found in our benchmarking repository https://github.com/dobraczka/kiez-benchmarking.

The setting of our evaluation consists of doing a full alignment between the data sources, which means finding the k-NN of all source entities in the target entity embeddings. We set \(k=50\) and to obtain the primary distances we allowed 100 kNN candidates. For all algorithms the primary distance was euclidean, except for NMSLIB, where cosine was used.

We used a single machine running CentOS 7 with 4 AMD EPYC 7551P 32-Core CPUs for all experiments. For the small dataset experiments we allowed 10 GB of RAM. The experiments with the large datasets were provided 30 GB of RAM. Since Faiss is able to utilize a GPU we used a Nvidia RTX2080Ti 11 GB for the small datasets and a Nvidia Tesla V100 32 GB for the large datasets. Bear in mind, that we also included settings were Faiss didn’t use a GPU.

We use hits@k to evaluate retrieval quality:

$$\begin{aligned} hits@k(kNN)= \frac{\vert \{t: y \in kNN(x) \wedge (x, y) \in \mathcal {M}\}\vert }{\vert \mathcal {M}\vert }, \end{aligned}$$
(10)

with kNN being the calculated nearest neighbors and kNN(x) returning the k nearest neighbors of x. This metric simply counts the proportion of true matches t in the k nearest neighbors. We choose hits@k, since it is the most common metric for entity alignment tasks and is especially useful to judge the quality of neighbor-based tasks. While hits@k has it’s weaknesses, when used for evaluating the quality of the knowledge graph embeddings themselves [69], it is well-suited for our case, since any result where the correct entity is at rank \(k+1\) is in fact as bad, as a result where it is at \(k+n>> k\). Either way this correct entity would be lost in a kNN setting. In our case we present hits@50, since we wanted the 50 nearest neighbors.

For our evaluation we intend to answer four questions:

\((\mathbf {Q_{1}})\)::

Does hubness reduction improve the alignment accuracy?

\((\mathbf {Q_{2}})\)::

Does hubness reduction offset loss in retrieval quality by ANN algorithms?

\((\mathbf {Q_{3}})\)::

Can hubness reduction be used with ANN algorithms without loss of the speed advantage of ANNs?

\((\mathbf {Q_{4}})\)::

Does the answer to \((\mathbf {Q_{3}})\) change, when utilizing GPUs?

Results

Hubness Reduction with Exact Nearest Neighbors

The absolute hits@k value is to some degree determined by the quality of the given KGEs. Since our intention in \((\mathbf {Q_{1}})\) is to measure improvements through hubness reduction, we will measure the increase in hits@k compared to the baseline of using no hubness reduction. In Fig. 5 we present a boxplot representation of these improvements for exact nearest neighbor search summarized across all embedding approaches per alignment task.

Fig. 5
figure 5

Improvement in hits@50 compared to no hubness reduction. Results are aggregated over different embedding approaches. Graphic was originally published in [7]

Full size image

Any values above zero show an improvement. We can see that all hubness reduction methods have a tendency to improve the quality, albeit not to the same degree. For example both Mutual Proximity variants perform the worst.

We can see a high variance in Fig. 5 showing that the improvements vary across different embedding approaches. In Fig. 6 we therefore take a close look at some selected approaches.

Fig. 6
figure 6

Robin Hood index and hits@50 for selected embedding approaches on D-Y 100K(V2) dataset. Graphic originally published in [7]

Full size image

There is a large difference w.r.t hubness produced by the different embedding approaches. For example BootEA produces embeddings with relatively low hubness, even without hubness reduction. SimplE on the other hand has a Robin Hood index of almost 75% percent, which means almost three quarters of the nearest neighbor slots need to be redistributed in order to obtain k-occurence equality. While BootEA’s hits@50 score is already very high and leaves little room for improvement we can see that hubness reduction improves accuracy in the other approaches noticeably.

In our previous study [7] we used the frequentist analysis regime proposed in [8] to compare the performance of approaches. While this is certainly more statistically sound, than e.g. simply comparing medians of a performance metric it comes with the pitfalls of frequentist null hypothesis significance testing. This includes ignoring the magnitude of effect sizes, no real possibility to determine uncertainty and no hints about the probability of the null hypothesis. In practice this often means that given enough data minor differences can be considered significant. In this evaluation we therefore use the Bayesian testing regime proposed in [9], which comes with all benefits of Bayesian approaches. Namely, being able to not only reject, but also verify a null hypothesis, as well as being able to take actions that minimize loss. In our case this means we use a Bayesian signed rank test [70] to determine whether the difference among two classifiers is significant. Furthermore we can define a so-called region of practical equivalence (ROPE), where approaches are considered equally good. The Python package Autorank [71] makes these best practices readily available and enables us to automatically set the ROPE in relation to effect size.Footnote 9 The proposed Bayesian analysis furthermore provides us with the probability that one algorithms is better/worse than the other as well as with the probability that they are equal. We make a decision if one these probabilities is \(\ge 95\%\), else we see the analysis as inconclusive.

Fig. 7
figure 7

Decision matrix comparing hubness reduction techniques using Bayesian signed rank tests. Each cell shows the decision, when comparing the row approach to the column approach. A decision is reached if the posterior probability is \(\ge 95\%\)

Full size image

In Fig. 7 we show a decision matrix visualizing which hubness reduction methods outperform each other. We can see that NICDM, CSLS and DSL significantly outperform using no hubness reduction and the results for LS are inconclusive. Both Mutual Proximity approaches are practically equivalent to using no hubness reduction. This is in contrast to our previous study, where we determined NICDM to significantly outperform all other approaches.

In summary, we can answer our research question \((\mathbf {Q_{1}})\) positively: Yes the correct hubness reduction technique (i.e. NICDM, CSLS and DSL) improves results significantly.

Hubness Reduction with Approximate Nearest Neighbors

In order to answer \((\mathbf {Q_{2}})\) we now take a look at approximate nearest neighbor algorithms. Again we compare the improvement of hits@50 to the baseline, which is exact NN search without hubness reduction. In Fig. 8 we present a boxplot summarizing the results over all embedding approaches.

Fig. 8
figure 8

Improvement in hits@50 compared to using no hubness reduction with an exact NN algorithm. Results are aggregated over different embedding approaches

Full size image

When using ANN approaches we can see that hubness reduction cannot in all cases offset the retrieval loss of the approximation. This is especially prominent for Annoy, which not only shows the highest variance but also the worst results generally. Both HNSW implementations seem to work the best with almost all results staying in the positive range. To make sound claims about which algorithms outperform the baseline/and or other approaches we present a decision matrix containing the results of the pairwise Bayesian signed rank test in Fig. 9.

Fig. 9
figure 9

Decision matrix comparing hubness reduction techniques and ANN algorithms utilizing Bayesian signed rank tests. Each cell shows the decision, when comparing the row approach to the column approach. A decision is reached if the posterior probability is \(\ge 95\%\)

Full size image

Since we already discovered in Section Hubness Reduction with Exact Nearest Neighbors that both Mutual Proximity variants are outperformed by the other hubness reduction techniques we omit them from the decision matrix in order to keep the graphic more concise.

We can see that Annoy is generally outperformed by all other approaches and is in fact even worse than the baseline (Exact None). Faiss is the only algorithm that outperforms the baseline, but only with NICDM, CSLS or DSL as hubness reduction technique. The results for NMSLIB’s HNSW implementation is inconclusive for NICDM and DSL. Again, this is in contrast to the findings of our previous study, where we found that NMSLIB’s HNSW with NICDM/DSL was significantly better than all other approaches. We suggest the reason for this discrepancy is the fact that our new Bayesian analysis can reason about practical equivalence of two algorithms, while the previous frequentist approach could only falsify the null hypothesis, that there is no difference between the approaches. Which means minor difference can be significant given enough data.

However, the answer to \((\mathbf {Q_{2}})\) stays the same as in our previous study: “While not all ANN algorithms can achieve the same quality as the baseline, given the right algorithm and hubness reduction technique we can not only match the performance of exact NN algorithms, but we can significantly outperform them” [7]. What changes is our recommendation of ANN algorithm implementation: Faiss’s HNSW implementation in combination with either CSLS,NICDM or DSL performs significantly better than the baseline.

Execution Time

Our third question revolves around speed. Since there are large differences in execution time between the large and small datasets we show the graphs separately in Fig. 10.

Fig. 10
figure 10

Time in seconds for different (A)NN algorithms and hubness reduction methods. Results are averaged over datasets with black bar showing variance

Full size image

The slowest approaches are the exact “effective” algorithm variants (BallTree and KDTree). While they can give performance increases for low-dimensional data, they are unable to perform well for our use-case. We can also see that in most cases hubness reduction comes with some cost w.r.t speed. Especially the Mutual Proximity variants are costly. On the small datasets Faiss is the fastest approach. Faiss’s brute-force variant is in fact faster than it’s HNSW implementation. Faiss’s speed becomes especially prominent when looking at the large datasets, where it is an order of magnitude faster than Scikit-learn’s brute force variant or NMSLIB’s HNSW. While Annoy is also very fast we have already established that it is not accurate enough for our use-case. The answer to \((\mathbf {Q_{3}})\) depends on the dataset size. Using Faiss even exact hubness reduction can be used on smaller datasets with virtually no cost. For the 100K datasets Faiss’s exact and approximate approaches tend perform very similarly even when comparing fast hubness reduction methods (e.g. NICDM or CSLS) with no hubness reduction. Bear in mind, that the execution time of Faiss_HNSW depicted here includes the optimization search of autofaiss.

GPU Utilization

Finally, we investigate how the use of GPUs changes our assessments. Since the only approach capable of utilizing a GPU is Faiss we focus our comparisons on the different variants within this library. In Fig. 11 we again show the execution time in different graphs for the small and large datasets.

Fig. 11
figure 11

Time in seconds for different Faiss configurations and hubness reduction methods. Results are averaged over datasets with black bar showing variance. We differentiate indexing time by darker color and query time by lighter color

Full size image

To give a more granular view we show the time it took for each configuration to build the index and how long the query time was. Indexing time not only includes the time of Faiss to load the data or in case of HNSW build the graph, but also includes time our library needs to gather information that will be used for hubness reduction later. This is usually the primary distances from target entities to source entities, which will then be used, when we query the distances from source to target to reduce hubness. Because the hubness reduction techniques perform different calculations in this initial step the indexing times are different between them even though the same (A)NN algorithm is used. For HNSW most time is spent on building the index (except when using the expensive MP emp hubness reduction). As said before in Hubness Reduction with Approximate Nearest Neighbors this time includes the index optimization search of autofaiss. Generally we can see that the use of GPU is especially beneficial for the brute-force variant. Both NICDM and CSLS are not only the best hubness reduction techniques w.r.t to hits@50 improvement but are also the two fastest approaches (together with LS). For small datasets again the exact variant is generally faster. For the large dataset HNSW is faster, except when a GPU is available, then the exact variant is an order of magnitude faster.

More research is needed to establish a guideline w.r.t to dataset size, when HNSW on the GPU is faster than the brute variant. Our results indicate that 100.000 entities per source might very well be the point where HNSW is the more favorable choice.

Conclusion and Future Work

We investigated how hubness reduction techniques can improve entity alignment results. Our evaluation was done on a variety of real-world datasets with differing properties from knowledge graph embeddings were create with a variety of approaches. Our results suggest that mitigating hubness significantly improves alignment results, with practically no decline in retrieval speed of nearest neighbors. This is also true, when utilizing approximate nearest neighbor search for larger datasets. For example using the Faiss library with the hubness reduction technique NICDM we got a median improvement in hits@50 of 3.99% when using the exact variant and 3.88% when using their HNSW implementation. On the small datasets we saw no speed decrease for the exact algorithms, and on the large datasets we saw a negligible median decrease in speed of 1–4 s compared to using no hubness reduction. This makes hubness reduction a cheap way to get more accurate results. When a GPU is available the exact Faiss variant is noticeably the fastest even on large datasets, where we can perform hubness-reduced 50 nearest neighbor search in 8 seconds on knowledge graph embedding pairs containing 100.000 entities each.

Since we saw a negative correlationFootnote 10 between hubness and hits@50 a worthwhile investigation might be how to reduce hubness already while creating the embeddings. While nearest neighbor search is a crucial part of the alignment process it is not the final step. The hubness-reduced secondary distances can be used as input for clustering-based [74] matchers to find the definitive matching pairs. An investigation we leave for future work.