Introduction

Parkinson’s disease (PD) is a chronic, progressive neurodegenerative disorder straining health systems worldwide due to increasing prevalence rates [1]. A large global burden of disease study identified PD as one of the top five leading causes of death from neurological disorders in the US [2]. It is estimated there were approximately 6.1 million People with Parkinson’s (PwP) globally in 2016, a sharp increase compared to 2.5 million PwP in 1990 [1].

Cardinal PD symptoms include tremor, rigidity, bradykinesia, and postural instability, within the broader remit of motor, cognitive, and neuropsychiatric symptoms [3]. The breadth of motor and non-motor symptoms underscores the need for frequent, detailed, longitudinal monitoring and personalized medicine approaches [3, 4]. Comorbidities are common [5], which further complicates symptom management of symptoms [3, 4].

PD is a heterogeneous disease with considerable variation in PwP’s symptom severity trajectories, where differences in clinical phenotypes likely reflect different PD subtypes [6]. In fact, delineating subtype identification had been highlighted as one of top three PD research priorities by the National Institutes of Health [7]. Correctly determining PD subtypes is clinically important since homogeneous groups exhibit stronger clinical symptom manifestation and potentially stronger genetic coherence: this may lead to new insights towards involved biological pathways, which in turn may lead to better-informed, targeted treatment strategies [6, 8]. Ultimately, the purpose of understanding heterogeneity within disease populations in general and PD in particular, is the delivery of more personalized care tailored for individuals and the development of targeted pharmaco-therapeutic treatments. Due to the chronic, progressive, and multi-dimensional symptom constellation nature of PD, there are different approaches to define subtypes, e.g. depending on the underlying characteristics we choose to focus on (which may include motor and non-motor symptoms, cognitive ability, imaging, and symptom severity progression amongst others [9]. In practice, defining PD subtypes has been pursued using either (i) empirical clinical experience and expertise or (ii) data-driven approaches. Arguably, the former approach is subjective and as yet there is no set of empirical accepted guidelines. Different clinical experts focus on different PD symptoms during routine clinical evaluation and this choice could be the main driving force on how they would define how PwP might form groups [9]. For example, some experts might prefer to focus primarily on some of the cornerstone PD-related motor symptoms whereas others might also consider additional non-motor, cognitive, and other symptoms in their routine assessment and overall consideration of how we could define PD subtypes. There is clear potential bias inherent to this expert-based approach in defining PD subtypes [8].

For this reason, data-driven approaches to define PD subtypes have received considerable attention in the PD research community over the last few years using cluster analysis [10,11,12,13,14,15]. In the following, we aim to provide a broad overview of studies published in this area placing emphasis on recent work, however, we remark we did not attempt to pursue a systematic literature review. Indicatively, Selikhova et al. [10] used clinico-pathological characteristics; Lawton et al. [12] used standardized clinical instruments to assess motor, non-motor, and cognitive domains; Brendel et al. [14] similarly used standardized clinical instruments assessing motor, non-motor, cognitive, daily activity and sleep; and Nguyen et al. [16] used sensor-based gait pattern analysis. Extracting variables from different modalities or clinical instruments to present to clustering algorithms may potentially lead to new insights, however, it makes comparisons across studies particularly challenging and may explain discrepancies in the reported PD subtypes. For example, there is no clear consensus amongst experts on the number of subtypes or the clinical PwP characteristics within those subtypes: a recent systematic review in PD cluster analysis (summarizing the research literature published from 1999 to 2021) found that most studies report the presence of two to five clusters [13]. Almost all reviewed studies in [13] had used PD-specific clinical scales and diverse variables which were diverse across studies, e.g. some have used variables extracted from imaging techniques, additional self-reports and tests assessing cognitive status, amongst others [13]. Many of these data modalities can be expensive and/or time consuming to administer. If there was some modality that was easy to collect (ideally remotely without the need of expensive specialized equipment) and reliably inform PD clusters, that could facilitate subtype membership assignment and provide a much needed impetus to this field. The underlying motivation of this study is, therefore, the development of an approach that relies on an easy-to-collect data modality that enables meaningful PD subtype definition.

Crucially for the purposes of this study, speech as an item within comprehensive PD clinical scales has been previously shown to be very strongly associated with overall PD symptom severity as assessed using standardized clinical metrics [17, 18]. Furthermore, in the context of PD assessment we have previously used sustained vowel /a/ phonation to demonstrate: (1) differentiating a control group from PwP with almost 99% accuracy [19], (2) accurately replicating the standard clinical metric used to assess overall PD symptom severity (Unified Parkinson’s Disease Rating Scale (UPDRS)) [20,21,22], (3) automatically assessing voice rehabilitation [23]; (4) distinguishing PwP from controls and groups which are known to exhibit genetic mutations or disorders which may lead to later PD diagnosis [24, 25]; and (5) speech articulation kinematic models to characterize PD dysarthria and provide insights into the underlying vocal production mechanism [26]. Collectively, these studies and many others in the research literature convincingly demonstrate the enormous potential of using speech signals in the context of diverse PD applications.

Therefore, the use of speech towards defining PD subtypes suggests itself as a potentially useful approach. Surprisingly, this area is little explored, despite the immense interest of the research community into investigating speech-PD applications. Rueda and Krishnan [27] used sustained vowel /a/ phonations from 57 PwP and 57 matched controls aiming to cluster participants. Unfortunately, the very small sample size of that study limits the application of appropriate cluster analysis methods. Moreover, although we appreciate this was driven by the limited sample size, mixing PwP and controls is not leading to the definition of PD subtypes. Thus, to the best of our knowledge, we were the first to propose defining PD groups using clustering methods with variables extracted from sustained vowels in our two BIOSTEC-BioSignals papers [28, 29]. Both studies reported findings using data from the Parkinson’s Voice Initiative (PVI) study, the world’s largest known speech-PD dataset [30]. In brief, more than 19,000 phonations were collected across seven major geographical locations (Argentina, Brazil, Canada, Mexico, Spain, USA, and the UK) from about 10,000 participants, where approximately 18% were PwP [30, 31]. In the first study [28], we used data from the largest PVI cohort (Boston), acoustically analyzed the phonations, and used hierarchical clustering to explore PD groups. The second study [29] followed exactly the same methodology to explore how well findings generalized in two additional cohorts (Oxford and Toronto).

In this study, we aimed to extend our previous results [28, 29] by: (1) more rigorously exploring the methodology of using acoustic analysis to mine sustained vowels to extract features and select a robust feature subset that was presented into cluster analysis algorithms and (2) more formally assessing the validity of the resulting clusters to draw meaningful insights into PD subtypes. The practical significance of this study is offering a novel data-driven approach to define PD subtypes building on the sophisticated methodology we have previously developed to successfully process sustained vowels across related PD applications: given sustained vowels are easy to self-collect remotely, regularly, and inexpensively, the proposed approach may facilitate large-scale investigations in exploring PwP groupings objectively.

Data

The study draws on data from the PVI study [30, 31] for secondary analysis. The PVI invited people to contribute their voices to facilitate PD research. Self-enrolled participants called a dedicated phone number that was closest to their geographical location and were requested to provide some basic demographic information (age, gender), self-report whether they had received a clinical PD diagnosis, and record two sustained vowel /a/ phonations. The instruction for the phonations was to sustain vowel /a/ (say ‘ahh…’) for as long and as steadily as possible, following the standard speech protocol in this field [32] which we had used in similar PD studies [19, 20, 23, 25, 33]. The speech recordings were sampled at 8 kHz with 16 bits resolution, collected over standard telephone lines and stored in Aculab servers. Participants provided oral informed consent by self-enrolling and completing the requested steps during a short phone call, participating in this research project without additional incentives other than altruistically contributing to research.

In this study, we processed data from the three English-speaking sites of PVI (Boston, Oxford, Toronto), to explore how well findings compare and generalize in PwP coming from an English linguistic background. The basic demographic information for the PwP study participants is summarized in Table 1. Additional detailed information of PD-symptom specific aspects, including whether participants were “on” or “off” medication when they provided the speech recordings, or additional PD scales were not recorded in PVI. For further details on PVI please see [30, 31].

Table 1 Summary of basic demographics for the three Parkinson’s Voice Initiative (PVI) cohorts
Full size table

Methods

Data Pre-processing

We developed a speech recognition software tool which automatically transcribed the participants’ responses over the phone regarding age, gender, and whether they had received a clinical PD diagnosis (which was self-reported by answering a probe). We aurally inspected recordings where the automated speech recognition algorithm had less than 90% confidence. Furthermore, we developed an automated signap processing tool to identify and screen out unusable recordings, for example in the presence of excessive background noise. For further details please see (Arora, Baghai-Ravary, Tsanas, 2019).

Acoustic Characterization of Sustained Vowel /a/ Phonations

We used the Voice Analysis Toolbox which has been developed by the first author (freely available MATLAB source code, https://www.darth-group.com/software, last accessed 16 October 2021) to acoustically characterize each sustained vowel /a/ phonation. The toolbox computes 307 dysphonia measures, which we have developed, validated and refined over the years specifically tailored to characterize sustained vowel /a/ phonations across diverse PD datasets [19,20,21,22,23, 30, 31, 33,34,35,36], and some external non-PD applications, e.g. assessing general voice disorders [37] and processing voice fillers [38]. For the background, rationale, and detailed algorithmic expressions for the computation of the dysphonia measures and the Voice Analysis Toolbox we refer readers to our previous studies [18, 20, 22, 36]. We succinctly summarize the dysphonia algorithms in Table 2 for completeness, categorized in broad algorithmic families along with a brief description of each family.

Table 2 Broad categorization of the dysphonia measures used in the study
Full size table

The fundamental frequency (F0) estimation is one of the key characteristics of speech in general [32]. It is also intrinsically required for many of the dysphonia measures as an intermediate step, for example jitter is defined as F0 variation (there are different flavours of expressing that algorithmically, and hence we refer to these as jitter variants). The computation of F0 is particularly challenging for characterizing speech signals, and there are many F0 estimation algorithms in the research literature which have been proposed for different applications [39,40,41]. In this study, we used the Sawtooth Waveform Inspired Pitch Estimator (SWIPE) algorithm [42], building on our previous findings from a thorough empirical investigation using two databases with sustained vowel /a/ phonations and comparing 10 state-of-art F0 estimation algorithms [40].

Applying the 307 dysphonia measures to each of the sustained vowel /a/ phonations in the three dataset used in the study resulted in three design matrices with dimensions (Boston: 2097 × 307; Oxford: 536 × 307; Toronto: 198 × 307). In all cases the resulting features were continuous random variables. We linearly scaled each feature to be in the range [0, 1] following standard practice for distance-based machine learning algorithms so that no feature dominates others [43] in the subsequent clustering step.

Unsupervised Feature Selection

In datasets with high dimensionality (i.e. the presence of a large number of features in the design matrix) the available samples do not adequately populate the feature space, which is thus sparse. This well-known problem is often referred to as the curse of dimensionality, and often leads to detrimental performance of statistical learning algorithms [44, 45]. Thus, we typically employ dimensionality reduction methods, which take the form of feature transformation (transforming the original features in the design matrix to derive new features and thus operate in the new lower-dimensional space), or by feature selection (choosing a subset of the original features in the design matrix). In practical healthcare applications feature selection is typically preferred to retain the interpretability of the original features [46,47,48]. Feature selection can be further split on supervised feature selection when the response is available, and unsupervised feature selection when the aim is to select a feature subset where the response is not available. The former is much more frequently met in practice and for a recent rigorous empirical comparison into multiple diverse supervised feature selection algorithms we refer to [49].

Unsupervised feature selection is considerably less explored and more challenging than supervised feature selection [50]. Here, we used the i-Detect algorithm to select informative features where the identified feature subspace has the following property: the difference between the total volume of the space spanned by the selected feature subset and the sum of the volumes of clusters in the embedded manifolds is maximized [51]. The i-Detect algorithm has three free hyper-parameters which need to be explored and optimized: the distance metric, the kernel width and the regularization parameter. The algorithm is not very sensitive to the choice of the kernel width [51], although we still explored different values (we tried the values [0.5 1 2], 1 is the default value provided by the authors). We experimented with the Euclidean distance and the Manhattan distance, and following the authors’ suggestion we explored different values of the regularization parameter (we used the values: [0.1, 0.5, 1, 2, 3, 5, 7, 10]). Applying the i-Detect unsupervised feature selection algorithm results in a sparse feature weight vector, where the feature ranking is determined by the descending order of the weights. Thus, when exploring the application of i-Detect we operate with the selected feature subset in the lower-dimensional space (whilst retaining the original number of samples).

Cluster Analysis

Cluster analysis (or clustering) is an unsupervised learning method which aims to group a collection of samples (in the clustering literature the term ‘objects’ is more widely used, here we retain the equivalent term ‘sample’ for convenience) into clusters so that the samples within each cluster are closer to each other compared to the other clusters [44]. The output of a clustering algorithm indicates the (probabilistic) cluster membership of each sample into the possible clusters. There are many clustering algorithms in the research literature, which to large extent depend on the distances or strategy used to explore the feature space and identify the degree of similarity between samples. In this study, we used hierarchical clustering which is a popular cluster analysis method that has often been successfully used in diverse applications [44]. Hierarchical clustering constructs a dendrogram to represent the data in a tree-based form, which intuitively depicts how samples are grouped together at different levels. A major advantage that hierarchical clustering has over the commonly used k-means is that we do not need to pre-specify the number of clusters (which is not known a priori) and also enables the visualization of the data structure. We used hierarchical clustering with Ward’s linkage to cluster both the original high-dimensional data and the lower-dimensional representations obtained as we explored different feature subsets following the application of i-Detect. The number of clusters was determined following visual inspection of the dendrogram in accordance with the methodology previously described [52].

Data Visualization

In practical data analytics, it is often desirable to visualize the data in two or three dimensions for visual exploration. Here, we applied the popular t-distributed Stochastic Neighbor Embedding (t-SNE) algorithm [53] to visualize the data structure embedded in the high-dimensional space (using the original data in the 307-dimensional space and also exploring data in the lower-dimensional space with a reduced number of features following the application of i-Detect). There are a number of hyper-parameters that can be fine-tuned in t-SNE to explore different visualizations. The main ones are (i) whether to use a prior transformation of the feature space using standard Principal Component Analysis (PCA); (ii) the distance to compute pairwise sample dissimilarity; (iii) the ‘perplexity’, which can be thought of as the effective number of nearest neighbors for each sample; and (iv) the ‘exaggeration’ which is a positive scalar (1 and above) which indicates the tightness of the clusters. For further details on the hyper-parameters and how t-SNE can be used for clustering and visualization we refer to [54]. Here, we worked using different combinations of applying or not applying prior PCA before the 2D t-SNE projection, different distances (Euclidean, Manhattan, Mahalanobis), the perplexity score was sweeped through the values 5…100 (30 is the default), and the exaggeration was set sweeped through the values 2…100 (4 is the default). It is important to mention that t-SNE is a stochastic algorithm (as the name suggests) which means that setting the same hyper-parameter values and repeating the computation may lead to different visualization plots.

The resulting two-dimensional data representation may potentially lead to new insights following visual inspection, particularly since we used the two-dimensional representation to color map the samples with the cluster labels computed from the hierarchical clustering algorithm and thus visually assess the cluster analysis results. We have found this two-dimensional data projection of the feature space (or following feature selection a subset of the feature space) and color-mapping samples with labels (either from cluster algorithms or expert-provided) to be very revealing of interesting patterns across different applications [28, 29, 52, 55].

Evaluation of Cluster Findings

Given there is no underlying ground truth to compare findings against (as in supervised learning setups), the outputs of cluster algorithms can be evaluated in many different ways. One intuitive approach is to find some way to visualize the results (for example through projecting in a two-dimensional or three-dimensional space). This is one approach we have tried, as described in the preceding section. There are additional formal methods which are specific to cluster analysis and in some cases specific to the algorithms used to achieve clustering.

Here, we used the cophenetic correlation coefficient which expresses the extent to which the hierarchical structure in the dendrogram represents the underlying dissimilarities in the samples. Cophenetic correlation coefficients can be used to compare hierarchical cluster solutions, where a value close to 1 indicates a high quality clustering. We remark that it is not dependent on the threshold chosen in the dendrogram to decide on the number of clusters, it is rather a generic approach for hierarchical clustering data structure representation. For the algorithmic definition and further background details for the cophenetic correlation coefficient we refer to [44].

An additional commonly used approach to assess cluster analysis results is with silhouette plots. Silhouette plots can be used to visualize and validate the consistency of clusters both graphically and directly via the silhouette values. The silhouette value is computed for each sample and is a measure of similarity of the sample with the assigned cluster compared to the other clusters. Thus, each sample takes a silhouette value between −1 to + 1, where a value close to + 1 indicates that the sample closely matches the assigned cluster (and vice versa, a value close to − 1 indicates that the assigned cluster for the particular sample is not a good match). The average of the silhouette values provides an overall estimate of the silhouette score, which can be used to compare cluster solutions. For further background on silhouette plots and their interpretation we refer to Rousseeuw [56].

The presented methodology and all explorations and hyper-parameter optimization were done only by accessing the Boston dataset. We emphasize that we retained the other two datasets (Oxford and Toronto) separately, for external validation of assessing whether we could replicate findings by applying the same methodology to assess the cluster findings. This is an additional final step to assess how well the clustering findings are generalizable across the three datasets.

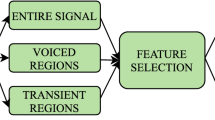
The full methodology of the study is concisely summarized in Fig. 1.

Fig. 1
figure 1

Schematic diagram with the methodology followed in the study

Full size image

Results

We started the exploration of cluster analysis by applying hierarchical clustering to the Boston dataset (retaining all features, i.e. the 307-dimensional dataset was presented into the hierarchical clustering algorithm). Figure 2a illustrates the dendrogram when using all features: following visual inspection, we placed the cut-off at 35 (highlighted with a dotted red line), which resulted in three clusters. Following the computation of the dendrogram and the decision for the cut-off, each of the samples was assigned a cluster label. Figure 2b presents the silhouette plot to visualize the validity of cluster assignment. The silhouette score was 0.32 and the cophenetic correlation coefficient 0.48. Thus, neither the silhouette score nor the cophenetic correlation inspire great confidence in the cluster membership assignment, which is also verified following visual inspection of the silhouette plot where a large number of samples appear to incorrectly match to the assigned clusters. Next, we applied t-SNE to project the original (307-dimensional) data onto a two-dimensional plot (see Fig. 3) to get an overall visual impression of how the cluster labels appear in the projected two-dimensional feature space.

Fig. 2
figure 2

a Dendrogram for the hierarchical clustering with Ward’s linkage to determine the number of clusters in the analysis using all features for the Boston dataset. Following visual inspection of the dendrogram we decided to place the cut-off at 35 (highlighted with the dotted red line), which resulted in three clusters. b Silhouette plot to depict cluster assignment validity

Full size image
Fig. 3
figure 3

Two-dimensional representation of the original high-dimensional dataset using t-SNE and marking the three clusters (denoted C1…C3) computed using hierarchical clustering with the original feature set (see dendrogram in Fig. 2a)

Full size image

Guided by the principle of parsimony, we next applied i-Detect to explore reducing the number of features that are presented into the clustering algorithm. The regularization parameter can be used to control the sparsity of the resulting weight vector, which in turn can be used to lead to the exploration of different feature subsets. Figure 4 graphically illustrates the i-Detect feature weights when we set the regularization parameter to 5, following which we can set an internal threshold to decide how many features we want to be using. In this particular case, many of the features were assigned a practically zero weight and to ensure we have a model with relatively few features we set the threshold to select only those with weight > 0.1. The further analysis with the selected feature subset refers to the 21 features where their corresponding weight was above 0.1 (see feature index in Fig. 4). Interestingly, the selected features all belong to the wavelet family (see also Table 2), we defer further elaboration for the Discussion. Using the selected feature subset, we repeated the methodology to compute the dendrogram, the cluster analysis metrics (cophenetic correlation coefficient and silhouette score) and projected the data using t-SNE.

Fig. 4
figure 4

Feature weights computed using the i-Detect algorithm, resulting in unsupervised feature selection (we set the threshold for selecting all features with weight above 0.1). The hyper-parameters chosen in i-Detect are presented in the figure as annotation for convenient referencing

Full size image

Figure 5 presents the dendrogram and the silhouette plot for the feature subset determined previously using i-Detect. The cophenetic correlation coefficient was 0.72 and the silhouette score 0.67. We remark that both these scores are considerably higher than what was computed when using the entire feature set. This is also visually illustrated intuitively by comparing the silhouette plots in Figs. 2b and 5b, where it can be clearly observed that overall there is a good matching of the cluster labels to the samples. Visual inspection of the dendrogram suggests that a threshold of 10 appears reasonable which gives four clusters. This choice was further validated when investigating the silhouette score for 2…10 clusters, and four clusters was leading to the highest overall silhouette score.

Fig. 5
figure 5

a Dendrogram for the hierarchical clustering with Ward’s linkage to determine the number of clusters in the analysis using the selected feature subset (see Fig. 4 for the i-Detect output) for the Boston dataset. Following visual inspection of the dendrogram we decided to place the cut-off at 10 (highlighted with the dotted red line), which resulted in four clusters. b Silhouette plot to depict cluster assignment validity

Full size image

Figure 6 then projected the selected features onto the two-dimensional space using t-SNE and similarly to Fig. 3 we have color-mapped the sample with the cluster labels. Following visual inspection of the projections we set perplexity to be 75 and exaggeration to be 8. Visually, it can be verified that the four clusters determined using t-SNE can be clearly visualized in the two-dimensional projection. This, along with the results above in Fig. 5b inspires confidence that the four clusters chosen are indeed separable and may be revealing certain properties of the data.

Fig. 6
figure 6

Two-dimensional representation of the Boston dataset with the selected features using t-SNE and marking the four clusters (denoted C1…C4) computed using hierarchical clustering (see dendrogram in Fig. 5a)

Full size image

The final test is to see how the presented methodology so far, using the same selected feature subset and hyper-parameter values chosen for the Boston dataset, generalize when presented with different datasets. For this last step we will use the remaining two PVI datasets from Oxford and Toronto to illustrate how the cluster solutions generalize. First we present the silhouette plots (Fig. 7) and subsequently the t-SNE derived two-dimensional plots (see Fig. 8). The silhouette score for Oxford was 0.66 and for Toronto 0.63, which are very close to the silhouette score we computed for Boston. Moreover, visually the illustrations in Figure 8 indicate that the four clusters detected using the cluster analysis methodology described above appear to be intuitively well separated in the two-dimensional space.

Fig. 7
figure 7

Silhouette plots to depict cluster assignment validity. Visually it is obvious the cluster assignment to each label match well when generalizing the methodology from the Boston cohort to these two new cohorts

Full size image
Fig. 8
figure 8

Two-dimensional representation of the Oxford and Toronto datasets with the selected features identified previously (from the Boston dataset) using t-SNE and marking the four clusters. We have retained all the hyper-parameters and choices from the Boston dataset

Full size image

Discussion

We investigated the potential of mining sustained vowel /a/ phonations collected over the standard telephone network and applying a robust cluster analysis methodology to develop a data-driven approach to define PD subtypes. We selected a robust feature subset using unsupervised feature selection with i-Detect to select 21 features to facilitate the exploration of patterns to discern meaningful lower-dimensional representation when presented into a hierarchical cluster algorithm. We found four PD subtypes in the main dataset (Boston) and externally verified findings in two additional datasets from Oxford and Toronto, all collected as part of the PVI study. We remark the computed clusters were clearly separable in the two-dimensional t-SNE projections of the selected feature space across both the Boston dataset and the two validation datasets, which inspires great confidence on the generalizability and potential clinical utility of the findings. The current study’s findings have important implications towards facilitating more personalized healthcare in PD through determining different subtypes, which may reflect different pathophysiologies and/or PD symptom severity progression trajectories. The study is part of our wider goal with the PVI study to provide new insights into PD capitalizing on a data modality (speech, and in particular sustained vowels) that is simple to collect without the need of specialized equipment, is easily administered and managed, and can be delivered remotely.

There are already a number of studies aiming to define PD subtypes using either expert-driven or data-driven approaches which have been summarized previously [9, 13, 57]. Hendricks and Khasawneh [13] authored a large systematic review in this area published in 2021, and similarly Lee et al. [57] summarized many studies which used different modalities to define PD subtypes in an extensive recent literature review. In the vast majority of data-driven approaches towards PD subtyping researches made use of clinical measures of PD symptom severity [13]. To the best of our knowledge, our work (along the lines of the two previous conference papers [28, 29]) is the first study that has approached the application of defining PD subtypes from the angle of using speech signals only from PwP in a principled matter and robustly verifying findings using different approaches.

Although there is still no clear consensus in the PD research literature regarding the number of clusters [13], interestingly a number of previous PD studies had similarly reported four PD subtypes even though using very different data modalities. For example, Lewis et al. [58] collected demographic, motor, mood, and cognitive measures from 120 early-stage PD participants and applied k-means to define four PD subtypes: (1) younger PD onset; (2) tremor-dominant; (3) non-tremor dominant with considerable cognitive impairment and mild depression; and (4) rapid disease progression but no cognitive impairment. Lawton et al. [12] used standardized questionnaires to assess motor, non-motor, and cognitive domains on two PD cohorts (comprising 1601 and 944 participants, respectively). They defined four PD subtypes: (1) fast motor progression with symmetrical motor disease, poor olfaction, cognition and postural hypotension; (2) mild motor and non-motor disease with intermediate motor progression; (3) severe motor disease, poor psychological well-being and poor sleep with an intermediate motor progression; (4) slow motor progression with tremor-dominant, unilateral disease. van Rooden et al. [59] also reported four PD subtypes: (1) mildly affected in all domains, (2) predominantly severe motor complications, (3) affected mainly on nondopaminergic domains with no major motor complications, (4) severely affected across all domains. Finally, Mu et al. [60] assessed motor and non-motor symptoms in two PD cohorts (comprising 411 and 540 participants, respectively), and also reported four clusters: (1) mild, (2) non-motor dominant, (3) motor-dominant, and (4) severe. We stress that these indicative studies had used quite different data modalities and arrived at broadly similar conclusions regarding how PwP subtypes could be defined. Given the proven validity of speech (and sustained vowels in particular) towards providing holistic information about motor and non-motor PD symptoms [18] we conjecture the findings presented in this study may be hinting that the underlying PD subtypes could be pointing to similar underlying symptoms. Other studies have reported different numbers of clusters, including, e.g. recent work by Lee et al. [57] and Brendel et al. [14] who have reported the presence of three PD clusters. Rodriguez-Sanchez et al. [15] approached the PD subtyping problem from a different perspective: instead of attempting to define PD subtypes directly using the variables available, they explored model-based multi-partition clustering to explore different approaches to define PD subtypes via the use of latent variables. Unsurprisingly, they found there are different ways to cluster PwP typically finding two or three clusters to group participants depending on the latent variables used. Collectively, it may not be straightforward to claim overall validity on the basis of the number of defined PD subtypes and agreement with the research literature, also in view of the findings in [15]. Nevertheless, we need to stress that our study has considerably more PwP than almost all existing studies in the PD subtype literature and hence as a result of greater statistical power this enables easier identification of emerging patterns and potentially exploring different ways to partition the data and explore larger numbers of resulting PwP groups.

The original high-dimensional space following the acoustic characterization of the sustained vowels (307 dysphonia measures, see Table 2) will likely obscure the identification of underlying patterns because of the inherent practical complexity with computing high-dimensional distances [53]. Indeed, we had previously reported that using the entire feature set in this application presents problems in generalizing cluster findings [28]. This motivated the use of unsupervised feature selection towards determining a robust feature subset, where patterns may emerge more clearly in a lower-dimensional space. Experimenting with i-Detect we found a feature subset comprising 21 features, all from the wavelet algorithmic family. The key insight from this finding is that wavelet-based dysphonia measures which capture detail and approximation of signal characteristics form a robust approach to characterize sustained vowels towards clustering PwP. The success of the wavelet-based dysphonia measures in previous PD-related applications [18, 20, 22] which was also verified in this study is particularly noteworthy over other dysphonia measures which have often dominated the speech signal processing field such as jitter and shimmer [32]. In accordance with results we had reported in related PVI studies in discriminating PwP from controls [30, 34], it appears that the nonlinear dysphonia measures (which were very successful in applications when sustained vowels were collected under carefully controlled acoustic conditions, e.g. to replicate UPDRS [18,19,20]), are not particularly useful towards PD subtyping. This should be interpreted very cautiously and may be because of the inherent limitation in PVI where the sample rate of the sustained vowels is 8 kHz; it would need to be further investigated in a future cluster analysis study where sustained vowels are recorded using higher sampling frequencies.

The validity and robustness of the resulting clusters in this study was evaluated using different cluster analysis approaches (the cophenetic correlation coefficient, silhouette plots, and visual inspection of two-dimensional projection of the data using t-SNE and color-mapping the resulting clusters). The cophenetic correlation coefficient is particularly useful to understand how the dendrogram summarizes the information on dissimilarities in the samples. We have found that using the feature subset selected using unsupervised feature selection the cophenetic correlation coefficient on the Boston dataset was 0.72 which indicates that the dendrogram has summarized well the intrinsic sample dissimilarities. In addition, the silhouette plots across all these datasets were visually promising, indicating that the vast majority of samples were matching well the properties within the assigned cluster as opposed to the other clusters: in the Boston dataset the silhouette score was 0.67 and only slightly lower for the other two datasets that were used to validate findings (0.66 for Oxford and 0.63 for Toronto). The silhouette plots (see Figs. 5b and 7) along with the two-dimensional t-SNE projections to visualize the clusters (see Figs. 6 and 8) make a very compelling case regarding cluster validation: using independently the two methods (cluster analysis and t-SNE) we find that the computed clusters can be visually verified.

We stress that we have not attempted any further optimization of any of the hyper-parameters in the entire methodology chain when using the two additional datasets (Oxford and Toronto) so as to have a true external validation of the presented methodology in terms of cluster assignment using a fully automated data-driven methodology relying on speech signals. Strictly speaking, we could have explored adjusting the hyper-parameters of t-SNE (particularly given that the Oxford and Toronto datasets have a considerably smaller number of samples than the Boston dataset and hence the perplexity value chosen for Boston might be too high). Nevertheless, we preferred to retain the original hyper-parameter values for consistency.

Many studies in the PD clustering literature have key methodological limitations or rely on rigid assumptions, nicely summarized in a large recent systematic review [13]. For example, k-means appears to be the most popular clustering algorithm that has been used in most PD clustering studies, often without appropriately explaining how mixed-type variables were handled or omitting crucial pre-processing details [13]. Also, most clustering PD studies do not include principled tools to assess cluster validity, e.g. silhouette plots, or approaches to visualize the resulting clusters to intuitively appreciate how samples group. To their credit, some recent studies have validated their cluster analysis methodology across two datasets (e.g. [12, 60]) which provides confidence in their findings, however, that is still not the norm for most. Further challenges in cluster analysis include selecting a robust feature subset which could improve revealing the underlying structure and groups [50] (also see the comparative results in Figs. 2 and 3 with all features versus the results in Figs. 5 and 6 with the selected feature subset). This aspect has not been explored in most studies in a principled approach, or some studies employed feature transformation (e.g. [12]) which has the practical downside of losing interpretability of the key contributing variables for the clustering. Similar constraints and methodological limitations in cluster analysis studies for other healthcare applications have been reported [61].

Our study has a number of limitations which we acknowledge. The first key limitation is the quality of the speech data: (i) the widely accepted recommendation is that for robust biomedical speech signal analysis a sample rate of at least 20 kHz should be used [32] because there is clinically useful information in the higher frequencies of the spectrum (in PVI we have 8 kHz); (ii) the PVI data have been collected under acoustically non-controlled conditions and hence contain more noise compared to lab-based data. Nonetheless, recent exploratory work on the simulated standard telephone network (thus including down-sampling data to 8 kHz and including a challenging digital communications channel introducing severe degradation) demonstrated that the loss in speech signal quality was not prohibitive for accurately replicating the standard PD clinical scale UPDRS [21]. Therefore, there is evidence to support pursuing biomedical speech signal processing applications even at the reduced sample rate. We maintain that if we want to develop innovative and disruptive practical healthcare tools accessible without undue financial and other restrictions to encourage wide adoption, we likely need to make some compromises. Moreover, we remark that all analysis in this study towards determining PD subtypes relied solely on sustained vowel /a/ phonations (the only speech modality available in PVI). Although there is a considerable body of research work to support the use of sustained vowels in different PD applications [19, 21, 25, 33, 34, 62], it is conceivable that the use of additional speech modalities (e.g. running speech) might provide additional complementary information towards informing PD subtypes. Perhaps the most important limitation of the study is that it is not obvious how well the four PD subtypes reported herein computed by processing sustained vowels match with the underlying PD subtypes (or symptom constellation) reported in other studies highlighted previously. Unfortunately, the PVI study had not collected additional PD symptoms (e.g. patient reported outcome measures or clinical assessments) to minimize participant burden and encourage participation. On the other hand, studies which have clinical evaluations and patient reported outcome measures do not have speech signal recordings which would enable to explore bridging this gap, with the ultimate aim of providing a translational path for clinical research [63,64,65]. Finally, the lack of repeated speech data collection may be a limiting factor in understanding how cluster membership might change longitudinally. For example, if repeated speech measurements at follow-up times were available, this might lead to further insights regarding the progression of specific PD subtypes reflecting PD symptom changes as expressed using speech signals [18].

We envisage this study’s findings which appear to generalize very well across the three PVI cohorts may contribute towards improving understanding of the nature of PD subtypes. We are further exploring the PVI data to investigate differences across the English-speaking and other cohorts, both towards understanding differences versus controls and also internal variability which may inform future clinical trials.

Conclusion

Sustained vowels may provide an objective, robust and streamlined approach towards informing PwP subtype assignment. The current study’s findings corroborate part of the PD research literature indicating the presence of four PD subtypes having been thoroughly validated on a large PwP cohort and externally validated on two additional PwP cohorts. There are important practical implications of defining PD subtypes using data that is easy to self-collect remotely such as speech signals and in particular sustained vowel /a/ phonations: they enable large-scale investigations and may bring us a step closer towards more personalized medicine approaches and targeted clinical management. The key limitation of the study is that we do not have additional clinical labels (e.g. UPDRS) or other self-reported outcome measures to map the resulting PD subtypes onto something that would be more tangible and comparable to related PD subtype studies. Future work could explore the extent subtypes form useful markers of symptom severity progression and conversely how PD progression might affect subtype membership for individual PwP. Similarly, further work could integrate additional modalities to speech to incorporate longitudinal passively collected modalities and self-reports which could be capturing PD-related symptoms, e.g. via using smartphones and wearables along the lines we have explored for mental disorders [63, 66,67,68,69]. Collecting additional modalities at scale using increasingly affordable technologies may provide new insights into understanding PD subtypes which may translate into understanding individual PwP similarities, related PwP symptom trajectories, and ultimately lead to better symptom management strategies.