Efficient Encoding of the Weighted MAX $k$-CUT on a Quantum Computer Using QAOA

Abstract

The weighted MAX $k$-CUT problem consists of finding a k-partition of a given weighted undirected graph G(V, E), such that the sum of the weights of the crossing edges is maximized. The problem is of particular interest as it has a multitude of practical applications. We present a formulation of the weighted MAX $k$-CUT suitable for running the quantum approximate optimization algorithm (QAOA) on noisy intermediate scale quantum (NISQ) devices to get approximate solutions. The new formulation uses a binary encoding that requires only $|V|\log _2k$ qubits. The contributions of this paper are as follows: (i) a novel decomposition of the phase-separation operator based on the binary encoding into basis gates is provided for the MAX $k$-CUT problem for $k>2$. (ii) Numerical simulations on a suite of test cases comparing different encodings are performed. (iii) An analysis of the resources (number of qubits, CX gates) of the different encodings is presented. (iv) Formulations and simulations are extended to the case of weighted graphs. For small k and with further improvements when k is not a power of two, our algorithm is a possible candidate to show quantum advantage on NISQ devices.

Introduction and Related Work

The search for quantum algorithms of practical interest has intensified since the announcement of quantum supremacy in [2]. For the foreseeable future, quantum hardware will limit the depth (length of the computation) and width (number of qubits) of the algorithms that can be run. Hybrid quantum-classical algorithms based on the variational principle are a promising approach to achieve an advantage over purely classical algorithms. The variational quantum eigensolver (VQE) [22]/quantum approximate optimization algorithm (QAOA) [8] is such a hybrid algorithm for approximately finding the solution of a problem encoded as the ground state of a Hamiltonian. In this early stage, even small reductions of the depth and/or width of an algorithm can make the difference between success and failure. In light of this, we investigate in this article how QAOA can be used to approximately solve the MAX $k$-CUT problem. The problem has interesting applications that make it practically relevant. These range from placement of television commercials in program breaks, placement of containers on a ship with k bays, partition a set of items (e.g., books sold by an online shop) into k subsets, design of product modules, frequency assignment problems, scheduling problems, and pattern matching [1, 10].

The problem discussed in this paper falls within the class of Ising models. An Ising model is a mathematical model of ferromagnetism in statistical mechanics, consisting of discrete variables $s_i$ that represent atomic “spins” that can be in one of the two states $\pm 1$. The objective function of an Ising model is given by:

$$\begin{aligned} E(\mathbf {s}) = \sum _{i=1}^N \sum _{j=i+1}^N J_{i,j} s_i s_j + \sum _{i=1}^N h_i s_i, \end{aligned}$$

(1)

where $h_i$ are the biases and $J_{i,j}$ the coupling strengths. Using the transformation $s_i = 2 x_i -1$, this can be transformed into a quadratic unconstrained binary optimization problem (QUBO) which is given by:

$$\begin{aligned} \underset{\mathbf {x}\in \{0,1\}^N}{\min } \mathbf {x}^T Q \mathbf {x} = \sum _{i\le j}^N x_i Q_{i,j} x_j, \quad x_i \in \{0, 1\}, \end{aligned}$$

(2)

where the matrix Q is an upper diagonal $N\times N$ real matrix. In this way, the Ising model without an external field is equivalently formulated as a MAX (2-)CUT problem. For an overview of other Ising-type formulations of NP problems, we refer to [20], which includes a discussion of graph coloring, but not of MAX $k$-CUT. A generalization of the Ising model is given by the Potts model, where the spin takes one of k possible values, see [25]. The MAX $k$-CUT problem is connected to the search for a ground state in the anti-ferromagnetic k-state Potts model [24]. Using Eq. (1) and replacing the terms $s_i$ with Pauli-Z operators, one arrives at an Ising Hamiltonian, which ground states, i.e., solutions of the original problem, can be found (approximatively) by the QAOA. The QAOA consists of the following main steps:

• (S1) The solution of a problem is formulated as the ground state of a Hamiltonian $H_P$ that encodes a cost function f to be optimized. It acts diagonally on the computational states, i.e., $H_P |z\rangle = f(z)|z\rangle$.

• (S2) A quantum processor prepares a parameterized quantum state $|\Psi (\theta )\rangle =U_M(\theta _{2p})U_P(\theta _{2p-1}) \cdots U_M(\theta _{2})U_P(\theta _1) |\Phi _0\rangle$, by alternatingly applying phase separation ($U_P$) and mixing ($U_M$) operators on an easy to prepare initial state $|\Phi _0\rangle$.

• (S3) Through repeated measurement, one obtains an estimate of $E(\theta )=\langle H_P \rangle _{|\Psi (\theta )\rangle }\in \mathbb {R}$ as well as a candidate solution y with probability $|\langle y||\Psi (\theta )\rangle |^2$.

• (S4) The cost function $E(\theta ) \ge E_\text {min}$ serves a classical computer that finds the ground state energy of the cost function, i.e., finds the optimal parameter $\theta$, such that $E(\theta )$ becomes minimal. This iterative process provides candidate solutions, which are typically approximate.

A general overview of hybrid quantum-classical algorithms (VQE/QAOA) is provided in, e.g., [21]. The article discusses obstacles and how to overcome them to achieve quantum advantage on noisy intermediate scale quantum devices. The QAOA was introduced by [8] where it was applied to MAX (2-)CUT. Solving small problem instances of MAX (2-)CUT with when QAOA and classical AKMAXSAT solver, the authors in [12] extrapolate to large instances and estimate that a quantum speed-up can be obtained with (several) hundreds of qubits. It has also been shown numerically that the QAOA can achieve solutions of better quality [4] then the best-known classical approximation algorithm. The authors in [26] introduce heuristic strategies inspired by quantum annealing to generate good initial points for the outer optimization loop for the MAX (2-)CUT problem. They show that this leads to large improvements in the approximation ratio achieved.

Since its inception, there have been several extensions/variants of the QAOA proposed. A recent approach, dubbed ADAPT-QAOA, presented in [27] is to create an iterative version that is problem-tailored and can adapt to specific hardware constraints. The method is exemplified on a class of MAX (2-)CUT problems, requiring fewer CNOT gates as the original method. A non-local version of QAOA is proposed in [3]. Dubbed R-QAOA, the algorithm recursively removes variables from the Hamiltonian until the remaining instance is small enough to be solved classically. Numerical evidence is provided that shows this procedure significantly outperforms standard QAOA for frustrated Ising models on random three-regular graphs for the MAX (2-)CUT problem. Another recent approach, dubbed WS-QAOA, is using the solutions of classical algorithms to improve QAOA, see [7]. An example is provided with MAX (2-)CUT, which shows numerically that warm-starting QAOA and R-QAOA provide an advantage at low depth, in the form of a systematic increase in the size of the obtained cut for fully connected graphs with random weights. Warm-starting results in a change of the mixer operator only.

To the best of our knowledge, there are only two papers discussing MAX $k$-CUT for $k>2$. The quantum alternating operator ansatz (also abbreviated as QAOA) presented in [13] considers general parameterized families of unitaries. The paper presents a suite of constrained optimization problems, such as maximum independent set, traveling sales person, and the unweighted MAX $k$-CUT. Mixing operators are adapted such that the probability of transitioning from a feasible candidate to another is non-zero and circuit compilations are described. The paper does not provide numerical simulations and the main focus is on the design of mixing operators. The one-hot encoding of the MAX $k$-CUT is further studied numerically in [23] Two approaches are presented that tackle the enforcement of the hard constraints arising from the encoding scheme. The first is to keep the X mixer, but introduce a penalty term in the phase-separating Hamiltonian and the second is to instead design an XY mixer together with consistent $W_k$-initial states to stay within the feasible set of solutions. Both articles [13, 23] present the unweighted MAX $k$-CUT, although it is not hard to generalize.

The main contributions of this article are:

• A novel decomposition of the unitary phase-separation operator $U_P$ based on the binary encoding into basis gates is provided for the MAX $k$-CUT problem for the general case $k>2$.

• Numerical simulations on a suite of test cases comparing different encodings are performed.

• We present an analysis of the resources (number of qubits, CX gates) of the different encodings.

• The formulations and simulations are extended to the case of weighted graphs.

The main advantages as compared to [13, 23] are that our approach is efficient in the number of qubits and does not require feasibility constraints to be incorporated into the circuit construction of the mixer operator. Similar to [23], we observe that the resulting energy landscape of the binary encoding might be easier to handle for the outer classical optimization loop due to fewer local minima see Table 2. As pointed out in [23], the ratio of the size of the feasible subspace, which is spanned by states corresponding to n Hamming-weight one bit strings, to the size of the full Hilbert space is:

$$\begin{aligned} \frac{\dim (\mathcal {H}_\text {feas})}{\dim (\mathcal {H})} = \left( \frac{k}{2^k}\right) ^n, \end{aligned}$$

(3)

which becomes exponentially small (for $k\ge 1$) as the graph size n grows. In contrast, the binary encoding uses the full Hilbert space as feasible space.

The rest of the article is organized as follows. We describe the classical problem and classical algorithms in “The MAX k-CUT Problem and Classical Algorithms”. After describing and comparing one-hot encoding and the proposed binary encoding scheme in “Quantum Algorithms”, we discuss implementation and results are presented in “Implementation and Results”, followed by a conclusion in “Conclusion”.

The MAX $k$-CUT Problem and Classical Algorithms

The MAX $k$-CUT problem is an extension of the well-known MAX (2-)CUT problem (or simply MAX CUT). Given a weighted undirected graph $G=(V,E)$, MAX $k$-CUT consists of finding a maximum-weight k-cut, that is a partition of the vertices into k subsets, such that the sum of the weights of the edges that have end points on different subsets is maximized. Let $w_{ij}$ be the weight assigned to each edge $(i,j)\in E$, and let $\mathcal {P}=P_1,\ldots ,P_k$ be a partition of the vertices in V. Then, the cost function for MAX $k$-CUT can be defined as:

$$\begin{aligned} \underset{|\mathcal {P}|=k}{\max } \ \sum _{1\le r<s\le k} \sum _{i\in P_r, j\in P_s, (i,j)\in E} w_{ij}. \end{aligned}$$

(4)

Alternatively, one could assign a label $x_i\in \{1, \ldots , k\}$ to each vertex $i\in V$, indicating which partition the vertex belongs to. Defining $\mathbf {x} = (x_1,\ldots ,x_{|V|})$ the optimization problem for MAX $k$-CUT can be written as:

$$\begin{aligned} \underset{\mathbf {x}\in \{1,\ldots ,k\}^n}{\max } C(\mathbf {x}), \qquad C(\mathbf {x}) = \sum _{(i,j)\in E} w_{ij} [x_i \ne x_j], \end{aligned}$$

(5)

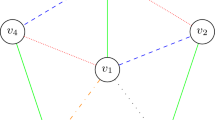
where $C(\mathbf {x})$ is the cost function and $[\cdot ]$ is the Iverson bracket, which is 1 if $x_i \ne x_j$, and 0 otherwise. An example of an optimal solution for MAX $3$-CUT is given in Fig. 1a.

The MAX $k$-CUT problem is NP-complete and it has been shown that it does not admit any polynomial-time approximation scheme, for any $k\ge 2$, unless P=NP [9]. By definition, a randomized approximation algorithm for (5) has approximation ratio $\alpha$ if:

$$\begin{aligned} \mathbb {E}[C(\mathbf {x})] \ge \alpha C(\mathbf {x}^*), \end{aligned}$$

(6)

where $\mathbf {x}^*$ is the optimal solution of (5).

Fig. 1

The MAX $k$-CUT problem and approximation guarantees for classical algorithms with polynomial runtime

A trivial algorithm that (uniformly) randomly assigns vertices to partitions has an approximation ratio of $(1-1/k)$, because each edge has a probability of $(1-1/k)$ of having endpoints in different partitions [9]. It has also been shown that there can be no polynomial-time approximation scheme (PTAS) with approximation ratio $\left( 1 - \frac{1}{34k} \right)$, unless P=NP [15]. For MAX $2$-CUT, the Goemans–Williamson algorithm [11] exploits the semidefinite programming (SDP) relaxation of the integer programming formulation of MAX $2$-CUT to achieve an approximation ratio of 0.878567. The Jerrum–Frieze algorithm [9] extended this result to MAX $k$-CUT, obtaining an approximation ratio of $\left( 1-\frac{1}{k} + \left( 1+\varepsilon (k)\right) \frac{2 \ln (k)}{k^2}\right)$, where $\varepsilon (k)$ is a function that approaches 0 as $k\rightarrow \infty$. For small k, this approximation ratio was ever so slightly improved in [6]. Figure 1b provides an overview of selected approximation ratios achieved in [6, 11].

It is interesting to note that under the unique games conjecture, both the 0.878567 approximation ratio of [11] (for $k=2$) and the $\left( 1-\frac{1}{k} + \frac{2 \ln (k)}{k^2}\right)$ approximation ratio of [9] (for large k) are optimal [18]. Given that the unique games conjecture is not valid when there are entangled provers [16, 17], it is possible that quantum algorithms may allow for an improvement over classical algorithms.

Quantum Algorithms

As a first step, we need to encode the problem described in “The MAX k-CUT Problem and Classical Algorithms” in a way that is suitable for the QAOA. There are three different possibilities (of which the first two are presented in [13], and the last is proposed in this article):

• Qudit encoding: Expressing the solutions as strings of k-dits [as in Eq. (5)] is a natural extension of the MAX (2-)CUT problem to $k>2$. The problem can be formulated using |V| qudits. To be practically relevant, it requires, however, the realization of a k-level quantum system.

• One-hot encoding: A second method is to use k bits for each vertex, where the single bit that is 1 encodes which set/color the vertex belongs to. Using this encoding requires k|V| qubits. However, the formulation requires the introduction of constraints to prevent solutions where a vertex belongs to several sets of a partition or none.

• Binary encoding: For a given k, we encode the information of a vertex belonging to one of the sets by $|i\rangle _L$, which requires $L=\lceil log_2(k)\rceil$ qubits. Here, $\lceil \cdot \rceil$ means rounding up to the nearest integer. This formulation can be executed on systems using qubits and requires L|V| qubits.

Binary encoding uses exponentially fewer qubits as compared to one-hot encoding. As an example, for $k=4$, encoding the information of a vertex belonging to one of the four sets using one-hot encoding is done through identifying color 1, 2, 3, 4 with the bit strings 0001, 0010, 0100, 1000, respectively. The binary encoding identifies colors 1, 2, 3, 4 with the bit strings 00, 01, 10, 11, respectively. Observe that, for one-hot encoding, there are $2^4-4=12$ possible bit strings in the space that encode infeasible solutions consisting of multiple colors or no color at all, whereas all possible bit strings in the binary encoding are valid encodings, see also Eq. (3).

In the following, we describe the problem Hamiltonian and unitary evolution for the one-hot encoding as well as the proposed binary encoding.

One-Hot Encoding

Here, we provide a brief description of the one-hot encoding. For details and further discussion, we refer to [13, 23]. The one-hot encoding uses k qubits per vertex, which are indexed, such that, e.g., $\sigma ^{x,y,z}_{i,a}$ applies a Pauli-X,-Y, or -Z gate to qubit number $ik+a$, for $a\in \{1,k\}$. The definition of the approximation ratio (Eq. (6) needs to be adapted to:

$$\begin{aligned} \alpha = \frac{\langle P_\text {feas} H_P P_\text {feas} \rangle }{C(\mathbf {x}^*)}, \end{aligned}$$

(7)

where $P_\text {feas}$ is the projection operator onto the feasible subspace. In practice, this means that infeasible solutions are assigned zero cost.

Problem Hamiltonian

Up to a global phase, the problem Hamiltonian is given by:

$$\begin{aligned} H_P = \sum _{(i,j)\in E} w_{i,j}\sum _{a=1}^k \sigma ^z_{i,a} \otimes \sigma ^z_{j,a}. \end{aligned}$$

(8)

One way to incorporate the constraint that the feasible subspace consists of only Hamming-weight 1-bit strings is to introduce a quadratic penalty term that results (up to global phase) in the Hamiltonian:

$$\begin{aligned} H_\text {pen} = \frac{1}{2}\sum _{v=1}^{|V|} \sum _{a=1}^{k}\sum _{b=a+1}^{k} \sigma ^z_{v,a} \otimes \sigma ^z_{v,b}. \end{aligned}$$

(9)

Overall, the phase-separating Hamiltonian becomes a weighted sum $H_P'=H_P + \beta H_\text {pen}$, where $\beta$ should satisfy $\beta \ge \frac{|V|}{k}$ and $\beta > k|E|$, see [23].

Unitary Evolution

The unitary evolution consists of creating an initial state, followed by phase-separating and mixing operators. The unitary evolution of the phase-separating operator given by the exponentiation of $H_P'$ [see Eqs. (8) and (9)] consists of terms that can be realized through the following circuit:

(10)

where $R_z(\theta ) = e^{-i\frac{\theta }{2}\sigma ^z}$. The standard X-mixing operator is given by:

$$\begin{aligned} e^{-i H_M}, \text { where } H_M = \sum _{v=1}^{|V|} \sum _{a=1}^k \sigma ^x_{v,a}, \end{aligned}$$

(11)

with each individual term realized through $R_x(\theta )=e^{-i\frac{\theta }{2}\sigma ^x}$ gates. The initial state when using the standard mixing operator is given by $|\Phi _0\rangle = H^{\otimes k|V|}|0\rangle$, where H is the Hadamard gate. However, this approach does not incorporate the feasibility constraint.

Incorporating the feasibility constraint into the mixer results in the XY mixer for each vertex $v\in V$ based on the Hamiltonian:

$$\begin{aligned} H_{XY,v} = \frac{1}{2} \sum _{a,b\in K} \sigma ^x_{v,a} \sigma ^x_{v,b} + \sigma ^y_{v,a} \sigma ^y_{v,b}, \end{aligned}$$

(12)

where K is a set consisting of certain pairs of colors (a, b). In this article, we use the parity-partitioned mixer, which can be represented as two separate Hamiltonians:

$$\begin{aligned} \begin{aligned} H_\text {odd}&= H^{XY}_{(1,2)} + H^{XY}_{(3,4)} + \ldots + H^{XY}_{(k-1,k)}\\ H_\text {even}&= H^{XY}_{(2,3)} + H^{XY}_{(4,5)} + \ldots + H^{XY}_{(k,1)},\\ \end{aligned} \end{aligned}$$

(13)

where $H^{XY}_{(j,k)} = \sigma ^x_j \sigma ^x_{j+1} + \sigma ^y_j \sigma ^y_{j+1}$. The resulting unitary operator is easily implemented in terms of two CX and one $R_X$ or $R_Y$ operation. A feasible initial state for the one-hot encoding consistent with the XY mixer is $|\Phi _0\rangle = |W_k\rangle ^{\otimes |V|}$, where the $W_k$ state is given by:

$$\begin{aligned} |W_k\rangle = \frac{1}{\sqrt{k}}\left( |100\ldots 000\rangle + |010\ldots 000\rangle + \ldots |000\ldots 001\rangle \right) . \end{aligned}$$

(14)

An efficient algorithm for this with logarithmic (in k) time complexity is presented in [5].

Binary Encoding

In the following, we describe the problem Hamiltonian for the proposed binary encoding, which is given as the sum of local terms, that is:

$$\begin{aligned} H_P = \sum _{(i,j)\in E} w_{i,j} H_{i,j}, \end{aligned}$$

(15)

where $w_{i,j}$ is the weight of the edge between vertices i and j as well as the resulting unitary evolution.

Problem Hamiltonian

The matrix $H_{i,j}$ is a diagonal matrix modeling the interaction between vertices i and j:

$$\begin{aligned} H_{i,j}= \begin{pmatrix} d_{0} &{} &{} \\ &{} \ddots &{} \\ &{} &{} d_{2^{2L}-1} \end{pmatrix}. \end{aligned}$$

(16)

From this point on, we consider the two diagonal matrices $H_P$ and $A=aI+bH_P$ to be equivalent for all $a,b\in \mathbb {R}, b\ne 0$. The reason for this is that when we compare the unitary operators $e^{-i \theta A}$ and $e^{-i \theta B}$, a parameter $a\ne 0$ results in applying a “global phase” which is irrelevant, and $b\ne 0$ can be combined with the parameter $\theta$. As mentioned in [13], “an affine transformation of the objective function [...] corresponds simply to a physically irrelevant global phase and a rescaling of the parameter”. The cost function can be easily evaluated classically, independent of the specific form of $H_P$.

From now on, we will adapt the notation that $|m\rangle _{2^n}$ is the mth basis vector of an n-qubit system. Note that for a basis vector, the decomposition $|m\rangle _{2^n}=|l_0\rangle _{2^{n-1}}\otimes |l_1\rangle _{2^{n-1}}$ both exists and is unique. The mth entry of the local Hamiltonian $H_{i,j}$ is given by:

$$\begin{aligned} d_m = {\left\{ \begin{array}{ll} -1, &{} \text { if } l_0\ne l_1 \wedge \lnot (l_0\ge k-1 \wedge l_1\ge k-1), \text { where } l_0, l_1 \text { are given by } |m\rangle _{2^n}=|l_0\rangle _{2^{n-1}}\otimes |l_1\rangle _{2^{n-1}},\\ +1, &{} \text { otherwise. } \end{array}\right. } \end{aligned}$$

(17)

This means that eigenvectors of the local Hamiltonian $H_{i,j}$ corresponding to eigenvalues $d_m=-1$ indicate a cut. When k is not a power of two the condition $\lnot (l_0\ge k-1 \wedge l_1\ge k-1)$ is introduced, such that the sets with number $k-1,\ldots , 2^L-1$ are not distinguished and become the same set. Organizing the diagonal entries $d_m$ in a matrix of size $2^L \times 2^L$, we get a particularly simple structure:

(18)

where $l = 2^L-(k-1)$, I is the identity matrix, J is a matrix of ones, and $\Gamma ^{c,d}$ is a matrix that has a one at entry c, d and is zero otherwise. Sub-indices indicate the size of the matrix. Observe that $D=D^T$ and that the sum involving terms $\Gamma$ is zero if k is a power of two. We can construct the matrix $H_{i,j}$ from D through:

$$\begin{aligned} H_{i,j} = \text {diag}\left( \text {vec}(D^T)\right) , \end{aligned}$$

(19)

where $\text {vec}(\dot{)}$ is a linear transformation which converts a matrix into a column vector by stacking the columns on top of each other, and $\text {diag}(v)$ is a matrix with the entries of the vector v along its diagonal.

Next, we will provide a few examples.

MAX (2-)CUT. For $k=2$, we can use $L=\lceil \log _2(2)\rceil =1$ qubit per vertex, where $\lceil \cdot \rceil$ means rounding up to the nearest integer. The matrix D and the local Hamiltonian are given by:

(20)

MAX 3-CUT. For the case $k=3$, we need $L=\lceil \log _2(3)\rceil =2$ qubits per vertex. Since two qubits can encode four different sets, we need to make two sets indistinguishable. Choosing sets 2 and 3 to represent one set, the entries of the matrix D and the local Hamiltonian are given by:

(21)

MAX 4-CUT. For the case when $k=4$, we need $L=\lceil \log _2(4)\rceil =2$ qubits per vertex. The entries of the matrix D and the local Hamiltonian are given by:

(22)

Unitary Evolution

For the binary encoding, there are no constraints on the binary strings to be a valid solution. Therefore, there is no need to design special mixers, and the mixing Hamiltonian is given by:

$$\begin{aligned} H_M = \sum _{j=1}^{|V|L} \beta \sigma ^x_{j}, \quad L=\lceil \log _2(k)\rceil . \end{aligned}$$

(23)

This leads to the unitary operator:

$$\begin{aligned} U_{M} = e^{-i\beta H_M} = \prod _{j=1}^{|V|L} e^{-i\beta \sigma ^x_j}. \end{aligned}$$

(24)

Each term in the above product can be implemented with an $R_x$-gate.

The unitary operator for phase separation is defined by:

$$\begin{aligned} U_{P} = e^{-i\gamma H_P} = e^{-i\gamma \sum _{(i,j)\in E} w_{i,j} H_{i,j}} = \prod _{(i,j)\in E} e^{-i\gamma w_{i,j} H_{i,j}}, \end{aligned}$$

(25)

where the last equality holds, because the terms $H_{i,j}$ trivially commute, as they are diagonal matrices. Furthermore, we can use Eq. (18) to further decompose the terms of the product:

$$\begin{aligned} e^{-i\theta H_{i,j}} = e^{-i\theta \text {diag}\left( \text {vec}(2I - J)\right) } \prod _{c,d=k+1, m\ne n}^{2^L} e^{-i 2\theta \text {diag}\left( \text {vec}(\Gamma _{c,d})\right) }. \end{aligned}$$

(26)

Again, equality holds, since only diagonal matrices are involved. The first term in Eq. (26) can be realized through the following circuit:

(27)

The qubits are enumerated, such that qubits $q_i^0, \cdots , q_i^{L-1}$ correspond to the label that is assigned to vertex enumerated i. The logic behind the circuit shown can be understood from a classical point of view. Applying CX-gates on pairs of qubits acting on basis states between vertex i and j results in the state $|q_i^0\rangle \cdots |q_i^{L-1}\rangle |q_j^0\oplus q_i^0\rangle \cdots |q_j^L\oplus q_i^L\rangle$, where the $\oplus$ operation is modulo 2. This means that the state of the qubits belonging to j has zero entries if and only if all qubits have the same basis state. Negating the state and applying a multi-controlled $'U_3(0,\phi ,0)$ gate therefore apply a phase if the original (basis) states $|q_i^0\rangle \cdots |q_i^{L-1}\rangle$ and $|q_j^0\rangle \cdots |q_j^L\rangle$ differ. After this, one can uncompute by applying X and CX-gates in reversed order, such that the overall change is that of applying a phase.

The remaining terms in Eq. (26) (which vanish if k is a power of 2) can be implemented, e.g., with the help of two ancillary qubits, $a_0, a_1$, in the following way:

(28)

The gates $N_1, N_2$ in Eq. (28) are of the form $U_0\otimes \cdots \otimes U_{L-1}$, where $U_i\in \{I,X\}$ are chosen, such that $N_1 |0\rangle _L = |c\rangle _L$, and $N_2 |0\rangle _L = |d\rangle _L$. The logic behind this circuit is that multi-controlled NOT gates are used to set two ancillary qubits to the state one if $q_i = |c\rangle _L$, and $q_j = |d\rangle _L$. Of both ancillary qubits are one, a multi-controlled $U_3(0,\phi ,0)$-gate is applied to change the phase, followed by a uncomputation steps. The ancillary qubits can be reused for all other pairs $(i,j)\in E$. An example for MAX $3$-CUT is shown in Fig. 2.

Fig. 2

Implementation of the phase operator for the edge (i, j) for MAX $3$-CUT, which consists of the circuit for MAX $4$-CUT plus two extra circuits

Table 1 Number of CX operations per layer and number of qubits of the QAOA circuit for a graph $G=(V,E)$ depending on k

Resource Analysis of One-Hot and Binary Encoding

We will give a short analysis of the number of gates required to decompose the basic building blocks of the phase operator $U_P$, the mixing operator $U_M$, and the preparation of the initial state for the two different encoding schemes. To be executable on, e.g., one of IBM’s quantum devices, all terms need to be decomposed using gates from the set of basis gates $\{U_3,CX\}$, where:

$$\begin{aligned} U_3(\theta ,\phi ,\lambda ) = \begin{pmatrix} \cos (\theta /2) &{} -e^{i\lambda } \sin (\theta /2) \\ e^{i\phi } \sin (\theta /2) &{} e^{i(\phi +\lambda )}\cos (\theta /2) \\ \end{pmatrix}, \quad CX = \begin{pmatrix} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 \\ 0 &{} 0 &{} 1 &{} 0 \\ \end{pmatrix}. \end{aligned}$$

(29)

Note that $U_3(0,\phi ,0) = \text {diag}(1, e^{i\phi })$. Throughout, we assume full connectivity of the qubits, i.e., a CX gate can be executed directly on any pair of qubits, without the need for applying SWAP or Bridge-gates [14]. Furthermore, (multi-)controlled $U_3(0,\phi ,0)$ operations can be implemented in terms of its square root $V = U_3(0,\phi /2,0)$, and $V^\dagger$, using polynomially many CX-gates, see, e.g., [19]. To implement the circuit shown in Eq. (27), one needs 2L CX-gates, 2L X-gates, and 1 (multi-)controlled $U_3$-gate. When k is not a power of two, we need to additionally execute the circuits of the form, as shown in Eq. (28). This requires 2L $C^{L}X$-gates, 2 $C^{L}U_3$-gates, and L X-gates. In general, these need to be applied $2(2^L-k)$ times. In the worst case, when $k = 2^n+1$, we need to apply these gates $2(2^n-1)$ times. Overall, Table 1 shows the width (number of qubits) and depth requirements of the complete circuit for MAX $k$-CUT. We can see that low depth and width are achieved when k is a power of two.

The analysis shows that one-hot encoding has a strong limitation when it comes to the requirement of number of qubits. In addition, preparation of $W_k$ and XY mixers is more costly than the standard X mixer sufficient for binary encoding. Furthermore, when the number of qubits is limited to a few hundred or thousand, only one-hot encoding for the cases $k=2,4$ and possibly $k=3$ will be of practical interest when quantum advantage is to be achieved.

Implementation and Results

Fig. 3

Initial guess (dotted lines with x marker) and locally optimal (solid lines with round marker) parameters $\gamma ,\beta$ for the graph shown in Fig. 5 using the interpolation-based heuristic described in the text. The results indicate a correlation of the parameters between different depths p making this a useful heuristic to avoid global optimization

In this section, we showcase numerical simulations on different types of graphs. We start by briefly describing the heuristic we employ for the classical outer optimization loop. Sampling high-dimensional target functions uniformly quickly becomes intractable for depth $p>1$. To get a good initial guess of the parameters $(\mathbf {\gamma }_p, \mathbf {\beta }_p)$ at level p for the local optimization procedure, we employ the interpolation-based heuristic described in [26], which is given by the following recursion:

$$\begin{aligned} \big [\mathbf {\gamma }_{(p+1)}^0\big ]_i = \frac{i-1}{p}\big [\mathbf {\gamma }_{(p)}^L\big ]_{i-1} + \frac{p -i+1}{p} \big [\mathbf {\gamma }_{(p)}^L\big ]_i, \quad i = 1, 2,\ldots , p + 1. \end{aligned}$$

(30)

In above formula, the superscript refers to either the initial parameter (superscript 0), or the local optimum (superscript L). The same formula holds for $\mathbf {\beta }$. For depth $p=1$, the expectation value is sampled on an $n\times m$ Cartesian grid over the domain $[0,\gamma _\text {max}]\times [0,\beta _\text {max}]$. The initial parameters $\left( \gamma _1^0, \beta _1^0 \right)$ are then given by identifying a pair of parameters which achieves the lowest expectation value on the grid. Using the starting point $\left( \mathbf {\gamma }_p^0, \mathbf {\beta }_p^0 \right)$, a local optimization algorithm, e.g., Nelder-Mead or COBYLA, is used to find the local minimum with $\left( \mathbf {\gamma }_p^L, \mathbf {\beta }_p^L \right)$. Figure 3 shows that optimal parameters are strongly correlated between different depths p, also for non-regular graphs.

The first example is a graph with two vertices connected by an edge. Using an ideal simulator, we compare the results for the binary encoding with standard X mixer, the binary encoding with the penalty term and the standard X mixer, as well as the XY mixer without penalty term and the $W_k$ initial state. The results, shown in Fig. 4, show that the binary encoding as well as the one-hot encoding with the XY mixer have approximation ratios close to one for all cases. The pure one-hot encoding becomes increasingly worse for increasing k, which is related to the exponentially small feasible subspace, see Eq. (3). Even adding a penalty term does not improve the situation noteworthy. The expectation value $E(\theta )=\langle H_P \rangle _{|\Psi (\gamma ,\beta )\rangle }$ for different parameters, often referred to as the energy landscape for all cases $k\in {2,\ldots ,8}$, is given in Table 2, which seems to indicate that the binary encoding generates optimization problems with fewer (local) minima.

The final two examples show numerical examples of larger instances of graphs: an unweighted Erdös–Rényi graph and a weighted Barabási–Albert graph with ten vertices, as presented in Fig. 5. For higher depth, we employ the interpolation-based heuristic. In all cases, the average approximation ratio achieved is considerably higher than the approximation ratio of randomly drawn a solution or the guarantees of the Goemans–Williamson, which is given as a reference. Furthermore, the average approximation ratio increases with increasing depth. One-hot encoding in the case of MAX $4$-CUT would already require 40 qubits, which quickly becomes prohibitive for a simulator.

Availability of Data and Code

All data, e.g., graphs, and the python/jupyter notebook source code of the MAX $k$-CUT implementation using QAOA for reproducing the results obtained in this article are available at https://github.com/OpenQuantumComputing.

Fig. 4

Results for a graph with two vertices connected by an edge. Using one-hot encoding, the XY mixer together with $W_k$ initial states achieves equally good results as the binary encoding. The one-hot encoding with the standard X mixer gets slightly improved by the penalty term. The low values are due to an exponentially small space of feasible solutions. The energy landscapes are shown in Table 2

Fig. 5

The results for an unweighted Erdös–Rényi with $|V|=10$ vertices and $|E|=16$ edges and a weighted Barabási–Albert with $|V|=10$ vertices and $|E|=24$ edges. $\alpha _{p}$ is the approximation ratio for depth p. #q is the number of qubits required. The number of CX-gates is per layer p. Here, − indicates that it is in principle possible to simulate classically (but we only have access to simulator with up to 32 qubits), whereas x indicates that it is infeasible to simulate even on a supercomputer (as 50 qubits are considered the threshold for that). Approximation ratios for random and Goemans–Williamson algorithm are shown as reference. The energy landscapes are shown in Table 3

Conclusion

In this article, we provide numerical evidence that NISQ device can be used to (approximately) solve the weighted MAX $k$-CUT. The analysis of the proposed binary encoding shows an exponential improvement of the number of qubits with respect to previously known results. In addition, our results indicate that the optimization problem for the one-hot encoding seems to contain many local optima, making it a more demanding problem to solve, see also the discussion in [23]. The circuit depth required is very low when k is a power of two. When this is not the case, we provide a proof of principle implementation, which requires an exponential number of CX gates with respect to k. Future research directions are, therefore, to investigate more efficient ways of decomposing the phase-separation operators. Another possibility might be to introduce penalty terms in the mixing operator, similar to the case of one-hot encoding, such that the number of possible sets is limited to k, instead of implementing the circuits, as shown in Eq. (28). Applying and testing R-QAOA and WS-QAOA to our formulation provide another future path for investigation. Finally, the performance of the proposed algorithms could be tested on simulated noise models and real machines. Another factor is to analyze the balance between number of qubits and circuit depth with respect to extra auxiliary qubits that can be introduced to minimize the number of SWAP/Bridge-gates on hardware without full qubit connectivity.

Table 2 Energy landscapes for the “Barbel” graph shown in Fig. 4

Table 3 Energy landscapes for the Erdös–Rányi and Barabási–Albert graphs shown in Fig. 5