Introduction

A Physical Unclonable Function (PUF) [1] derives the hardware signature that generates from the LSI chip based on the uncontrollable process variations. These errors make the PUF response to be unique and unclonable. In the years following this introduction, an increasing number of new types of PUFs have been proposed, with a tendency towards more LSI constructions. The practical relevance of PUFs for security applications was recognized from the start, with a special focus on the promising properties of physical unclonability and tamper evidence. Silicon based PUFs have been a promising and innovative security technology; therefore various types of PUFs such as ring-oscillator based [2, 3], SRAM based [4], bistable ring [5], etc. have been developed. In recent years, adiabatic based SRAM PUF has been first presented in [6]. This adiabatic PUF, namely, Quasi-adiabatic logic based physical unclonable function (QUALPUF) has some ultra low-power characteristics; hence it is suitable to implement in low-power portable electronic devices such RFIDs, wireless sensor nodes, etc. However, in [6], the QUALPUF was only evaluated in security metrics including reliability, uniqueness, uniformity and bit-aliasing through SPICE simulation results.

In this paper, we present the performance of QUALPUF which is implemented in 0.18 \(\upmu\)m standard CMOS process. From the post-layout simulation results with RC-extraction, we will show that the 4-bit QUALPUF has good uniqueness, and reliability. Then the measurement results of the fabricated LSI chip will be shown. The fabricated adiabatic PUF will be presented for the first time in the world. Through the fabricated adiabatic PUF, we will show that energy dissipation of the adiabatic PUF can be improved. The rest of the paper is organized as follows. In Section “Related Work of PUF”, we will introduce related works on PUFs. Section “Adiabatic Switching” describes the fundamentals of the adiabatic switching theory and the fundamental logic function of QUALPUF. Section “Design of the Quasi-Adiabatic Logic Based PUF” presents the design methodology the proposed adiabatic PUF using SRAM. The simulation results and the measurement results of PUF chip are shown in Section “Simulation and Measurement Results to Experimental Results”. Then, the adiabatic PUFs are evaluated using Figure of Merit (FoM). The conclusions are summarized in Section “Conclusion”.

Related Work of PUF

The first implementation of PUF was constructed by Pappu et al. in [1]. This PUF is classified as an optical PUF based on a transparent medium, and relies on the interaction of visible light with a randomized micro-structure. These refractive particles are in random positions, sizes, and orientations due to variations in the manufacture process. However, non-electronic PUF, like a optical PUF is hard to use in the field. Because, there are the difficulty to have a tamper-resistant measuring device and the susceptibility of the responses to the alignment of the optical equipment.

The currently prevalent PUF design is the electronic PUF, such as ring-oscillator based [2, 3], SRAM based [4], bistable ring [5]. The ring-oscillator PUF is based on a delay loop (i.e., ring oscillator) to generate random bit strings. The frequency of ring-oscillator is determined by a process variation, which cannot be predicted due to manufacturing process and other uncertain factors. This kind of PUF generates the output logic-0 or logic-1 by comparing the frequencies of two circuits selected. The SRAM PUF is formed of two cross-coupled converters switch two stable states that are normally represented by 0 and 1. The behavior of an SRAM cell depends on the difference of the threshold voltages of its transistors. Even the smallest differences will be amplified and push the SRAM cell into one of two stable states. Therefore its PUF behavior is the most straightforward and most stable way to use the threshold voltages to build an identifier. The bistable PUF is the same principle of SRAM PUF, where for certain input voltage two potential arrangements of currents and voltages across the circuit are stable.

In this paper, we will design an SRAM PUF using adiabatic logic principle. Because, when the SRAM is not powered there is no key present on the chip making the solution very secure.

Adiabatic Switching

Electronic circuit-level of adiabatic switching technology was firstly presented by Younis et al.  [7]. Several adiabatic logics have been proposed in the literature, e.g., [8, 9]. This section will review adiabatic switching which is a circuit-level approach and describe adiabatic based PUF circuit, namely QUALPUF.

Theory

Energy dissipation in conventional CMOS mainly occurs during device switching. Figure 1 shows the CMOS and adiabatic switching and their working operations. When the input signal becomes high voltage, the nMOS (or pMOS) transistor goes ON state and then the load capacitance is charged by the power supply. The nMOS (or pMOS) transistor can be modeled by the effective channel resistance of the switch and the interconnect resistance. With different power supply, the CMOS and adiabatic have different current response thereby causing different energy dissipation.

In the charging operation, the supplied energy is \(C_\mathrm{L}V_\mathrm{dd}^2\) while \(C_\mathrm{L}V_\mathrm{dd}^2/2\) is stored energy in the load capacitance and the other \(CV_\mathrm{dd}^2/2\) is dissipated energy in the resistive path. During the discharging operation, the \(C_\mathrm{L}V_\mathrm{dd}^2/2\) energy stored in the load capacitance is released to the ground terminal.

Fig. 1
figure 1

RC tree model, a CMOS charging, b adiabatic charging

Full size image

Adiabatic logic circuit employs AC power supply rather than the DC supply. It recovers the energy stored in the load capacitance back to the power source. In adiabatic power analysis, we will obtain the dissipated energy equation from the following equations:

$$\begin{aligned} Ri(t) + \frac{1}{C_\mathrm{L}}\int i(t)\mathrm{d}t = \frac{V_\mathrm{dd}}{\tau }t, \end{aligned}$$
(1)

where the \(\tau\) is rising time of ramp voltage \(V_\mathrm{dd}\). Applying the Laplace transform and inverse Laplace transform, we have

$$\begin{aligned} i(t) = \frac{V_\mathrm{dd}C_\mathrm{L}}{\tau }\left( 1 - e^{-\frac{1}{RC_\mathrm{L}}t} \right) . \end{aligned}$$
(2)

Energy dissipated over the period \(t=0\) to \(t=\tau\) is presented as:

$$\begin{aligned} E_\mathrm{charge}= & {} \int ^\tau _0 p(t)\mathrm{d}t + E(0)\nonumber \\= & {} R\frac{V_\mathrm{dd}^2C_\mathrm{L}^2}{\tau ^2}\left( 2RC_\mathrm{L}e^{\frac{-1}{RC_\mathrm{L}}t}- \frac{RC_{L}}{2}e^{\frac{-2}{RC_\mathrm{L}}t}\right. \nonumber \\&\left. - \frac{3RC_\mathrm{L}}{2} + \tau \right) . \end{aligned}$$
(3)

Using the approximation of \(\tau\)\(\gg\)RC, the dissipated energy is equal to:

$$\begin{aligned} E_{diss} = \frac{RC_\mathrm{L}}{\tau }C_\mathrm{L}V_\mathrm{dd}^2. \end{aligned}$$
(4)

From the aforementioned equations, we can observe that the dissipated energy of the conventional CMOS depends on the value of load \(C_\mathrm{L}\) and \(V_\mathrm{dd}\), while that of the adiabatic logic depends on switching time of \(\tau\); hence, by increasing the time of \(\tau\), the energy dissipation of adiabatic logic is significantly lower compared to the that of CMOS logic.

QUasi-Adiabatic Logic Based PUF (QUALPUF)

This subsection reviews the quasi-adiabatic logic based PUF (QUALPUF) which was presented in [6]. Figure 2a, b show the circuit diagram of QUALPUF, and its timing chart, respectively. In the QUALPUF, the supply clock \(V_{\mathrm{pc}}\) operates in four phases: Wait, Evaluate, Hold, and Recover as shown in Fig. 2b. When the challenge bit (\(C_{\mathrm{b}}\)) goes high state, the QUALPUF cell is operating in the Wait phase.

Fig. 2
figure 2

QUALPUF circuit and its timing chart

Full size image

Wait

In this phase, as \(V_{\mathrm{pc}}\) becomes 0V and \(C_{\mathrm{b}}\) goes high state, the QUALPUF cell keeps a preceding state. For the pMOS (P1) to be turned ON, voltage \(|V_{\mathrm{pc}}-V_{C_{\mathrm{b}}}|\) needs to be above or equal to the threshold voltage of pMOS.

Evaluate

During this phase, \(V_{\mathrm{pc}}\) goes from 0 to \(V_{\mathrm{dd}}\). Drain node of P1 starts ramping from 0 to \(V_{\mathrm{dd}}\) as transistor P1 is turned ON. When drain node of P1 reaches threshold voltage of pMOS, both P2 and P3 transistors will be conducting. The P2 and P3 will have different threshold voltage caused by the imperfections in the manufacturing CMOS process. Therefore, this leads to the flip in the outputs where one of the output leads to logic 1 and other to logic 0.

Hold

In this phase, output voltage will be hold until the recovery phase.

Recovery

In the recovery phase of the clock, the charge stored in the load capacitor is recovered back to the \(V_{\mathrm{pc}}\) through P2 or P3 and P1 transistors.

Design of the Quasi-Adiabatic Logic Based PUF

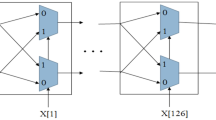
Figure 3 illustrates a simulated 4-bit adiabatic PUF, that is a 4-bit cascaded QUALPUF. Each local PUF is queried with a single challenge bit (Cb). Each local PUF is controlled by 4 clocks where each adjacent clocks differ by a phase difference of 90\(^\circ\). In this adiabatic PUF, a single cell is provided four repetitive random bits. This feature of the PUF results in making it difficult for the attackers to model the PUF. For each instance of time in the local PUF, each cell is operated with a phase difference of 90\(^\circ\) with respect to the adjacent cell. For example, if the first cell as shown in Fig. 3 is operating in the hold phase, the next cell in the same local PUF is operating in the recovery phase. Similarly, the other two PUFs are operating in the wait phase and the evaluate phase, respectively. When all the 4 outputs are sampled at a time leads to 4 bits. When these outputs are sampled at different phases of the clock, it leads to different pairs of bits. As a result of this technique, 4 PUF cell can produce 16 bits. Figure 4 draws a layout of the 4-bit cascaded QUALPUF. The area of 4-bit QUALPUF is 58.7\(\times\)15.7 \(\upmu {\mathrm{m}}^{2}\).

Simulation and Measurement Results to Experimental Results

To analysis the performance of QUALPUF, a SPICE simulation was performed using a 0.18 \(\upmu\)m standard CMOS process provided by ROHM corporation. Table 1 summarizes the MOS device parameters and the simulation conditions.

Table 1 Simulation conditions
Full size table
Fig. 3
figure 3

Cascaded structure of 4-bit QUALPUF

Full size image
Fig. 4
figure 4

Layout of 4-bit QUALPUF

Full size image

Figure 5 depicts a post-layout simulated output waveform of the 4-bit QUALPUF with parasitic and RC extraction. Figure 6 shows the Monte Carlo simulated output waveform of the 4-bit QUALPUF yielding a random bit with an even distribution of logic “1”s and “0”s. As the Reset signal (i.e., challenge bit Cb) is lowered, pMOS device M2 (or M3) is turned on and immediately begins to amplify the input to the comparator, which consists of an offset voltage and device noise. Discrete sampling of the mismatch and thermal noise thus occurs at low voltages. The cells that have larger mismatch evaluate faster and are less susceptible to thermal noise than those with a smaller mismatch.

From the Monte Carlo simulation results, we evaluate the uniqueness and reliability of the 4-bit adiabatic QUALPUF.

Fig. 5
figure 5

Post-layout simulated output waveform of 4-bit QUALPUF

Full size image
Fig. 6
figure 6

Monte-Carlo simulation of 4-bit QUALPUF

Full size image
Fig. 7
figure 7

Reliability of 4-bit QUALPUF against temperature variations

Full size image

Uniqueness

The PUF uniqueness can be evaluated by the average inter-die hamming distance (HD) of the responses produced by different PUF LSI chips. The uniqueness U for m LSI chips is expressed as

$$\begin{aligned} U = \frac{1}{m\left( m-1\right) }\sum ^{k-1}_{i=1}\sum ^{k}_{j=i+1}\frac{\mathrm{HD}(P_{i}, P_{j})}{n}, \end{aligned}$$
(5)

where i and j are two different PUF instances, \(P_{i}\) and \(P_{j}\) are the bit numbers of the n-bit length. The ideal value of the uniqueness metric is 50%. Table 2 summarizes the uniqueness of the conventional and proposed PUFs. In this work, the uniqueness calculated from the inter-die HDs of the QUALPUF is 47.58%.

Reliability

The PUF reliability is used to evaluate the stability of PUF signatures generated by the same challenge in repeated experiments. The reliability can be measured by its bit error rate (BER) by comparing the responses taken at different time with a reference response to the same challenge. The evaluation formula of reliability is

$$\begin{aligned} 100 -\frac{1}{m}\sum _{j=1}^{m} \frac{HD(R_{i}, R_{i, j})}{n}, \end{aligned}$$
(6)

where, m stands for the times of sampling, n is the number of bits of a signature generated by the PUF, and \(R_{i, j}\) is the j-th sampling of \(R_i\). The ideal value of the reliability is 100%. In our simulation, the working temperature is varied from – 40 to \(100^\circ\)C, with \(27^\circ\)C as the reference temperature. Figure 7 shows the proposed PUF reliability with temperature variations. The proposed QUALPUF has the average reliability of 95.10% as summarized in Table 2. The post-layout simulation results show that the 4-bit QUALPUF has 29.73 fJ/cycle/bit energy consumption.

Table 2 Comparison of conventional and proposed PUFs
Full size table

Figure of Merit (FoM)

Compared with the conventional and proposed PUFs, the Figure of Merits (FoMs) are defined as:

$$\begin{aligned} \mathrm{FoM}_{1}= & {} \frac{\dfrac{\min (\mathrm{Uniqueness}, 100-\mathrm{Uniqueness})}{50}}{\mathrm{Energy}\times \left( \mathrm{Area}\times \mathrm{Process\ scaling}\right) }, \end{aligned}$$
(7)
$$\begin{aligned} \mathrm{FoM}_{2}= & {} \frac{\dfrac{\mathrm{Reliability}}{100}}{\mathrm{Energy}\times \left( \mathrm{Area}\times \mathrm{Process\ scaling}\right) }. \end{aligned}$$
(8)

The first FoM represents the ratio between the Uniqueness and relative area-energy product. The second FoM shows the ration between the Reliability and relative area-energy product. The both FoM are lager, the performance of PUF is better. Compared with the existing fabricated PUF chip [4], our fabricated adiabatic PUF chip greatly can be improved. On the other hand, compared with Ring type PUF [3], and simulation level adiabatic PUF [6], our adiabatic PUF has the worst FoM; however, as well known in general, the energy dissipation of actual LSI chip increase than that of forward/back annotated simulation; the FoM of our fabricated PUF is a reasonable result considering that the LSI stands on the process rule.

Measurement Results

The 4-bit QUALPUF chip, as shown in Fig. 8 has been implemented and was evaluated as of this chip operating. Figure 9 shows the measurement results in the graph view using a digital storage oscilloscope (Rohde & Schwarz RTM3000). From this figure, we found that the correct 4-bit QUALPUF results have been outputted. After that, the outputs of 10 different IC chips were measured and then the PUF uniqueness and reliability were calculated. In the measurement results, the number of output key was set as 128-bit. The uniqueness and reliability of real QUALPUF chip are same as those of the post-layout simulation; the uniqueness is 47.58%, and the reliability is 95.10%.

Fig. 8
figure 8

Chip micro-photograph of 4-bit QUALPUF

Full size image
Fig. 9
figure 9

Transient waveform of 4-bit QUALPUF at 10 kHz

Full size image

Conclusion

In this paper, we reported the uniqueness and reliability of the 4-bit QUALPUF with post-layout RC extraction. From the simulation results, we found that the output of the QUALPUF is unique and unclonable. The uniqueness and reliability of QUALPUF are comparable with the existing PUFs. The functional measurement results of the fabricated chip are the same as the post-layout simulation results. The uniqueness and reliability characteristics along with low-energy consumption makes QUALPUF a promising candidate to provide hardware security in IoT devices.

The implemented adiabatic PUF has 16-bit internal state due to short length of identify key, this PUF seems to be vulnerable to attack, like a brute force attack. As to provide a more robust PUF scheme for security applications, we usually have set the 128-bit challenge sequence length or long. In near future, we will implement the 128-bit or 256-bit QUALPUF.