Abstract
Purpose
To biomechanically profile force generation connected to the complex role of the trunk in double poling in a representative sample of Para-Nordic sit-skiers.
Methods
Twelve male World Cup Para-Nordic sit-skiers (sport classes: LW10–12) were skiing on flat snow terrain at submaximal speed of 4.5 m/s (~ 73% maximum speed). 2D video (50 Hz) and pole force analyses (1000 Hz) were performed synchronously, examining angle, force and cycle characteristics to analyse the role of the trunk in generating propulsion.
Results
LW10–11.5 skiers lost between 21% and 4% propulsive force versus LW12 athletes only due to different geometrics of the trunk and pole angle at an equal axial pole force. While LW10–11 skiers indicated trunk extension or position maintenance during pole thrust, LW11.5–12 skiers showed strong trunk flexion combined with smaller pole angles to the ground. Hence, LW11.5–12 skiers could create larger propulsive forces and therefore greater cycle lengths at lower cycle rates at the same speed. Maximum speed increased from LW10 to LW12 and was significantly correlated to trunk flexion range of motion (r = 0.63) and cycle length (r = 0.59). Trunk flexion ROM showed a significant relationship to the impulse of propulsive force (r = 0.63) and pole angle to the ground (r = − 0.76) (all P < 0.05).
Conclusion
The impact of impairment on the force production profiles and its physiological-biomechanical consequences need further investigation also in other terrains and at wider spectrums of skiing speeds. The evident problem of low numbers of LW10–11 skiers in World Cup needs creative future solutions for research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
In Paralympic Winter sport, the International Paralympic Committee (IPC) provides a classification system to deliver fair competitions among all athletes with physical impairment [8]. The current classification process in Nordic sit-skiing assigns athletes into groups of five LW (Locomotor Winter) classes (LW10; LW10.5; LW11; LW11.5; LW12). The lower the number, the more impact the impairment has on skiing performance. Detailed class profiles are provided in the World Para Nordic Skiing classification regulations [8].
According to the IPC Position Stand, explaining the scientific principles of evidence-based classification [23], the following steps are essential in the development of any sport-specific classification system: (1) outlining a theoretical model of determinants of sports performance, (2) establishing valid measures of impairments and (3) developing standardized, sport-specific measures of performance determinants [24].
As regards Nordic sit-skiing, none of those points have been extensively developed. Only the number of studies on laboratory sit-skier impairment tests has currently increased and new methods of evaluating e.g. core function with so-called perturbation tests for Nordic sit-skiers have been introduced [18, 19], but have not yet been implemented to the IPC classification system. Another recent study examined the effect of sitting positions in different sit-ski classes and discussed that only the sitting position itself limited the trunk movement [9, 13, 17] and therefore caused distinct physiological disadvantages in classes LW10 and LW10.5 versus other classes.
For now, the sport-specific functional differences during sit-ski double poling on snow in athletes with different impairments is not understood and yet and there is a lack of studies on standardized, sport-specific measures of determinants of sit-ski performance during negotiating different slopes, mastering curves, and aerodynamic positioning during downhills. A symmetrical double poling movement and the maintenance of balance on the sit-ski during pushing on various terrains is a requirement for successful propulsive force generation, highly influenced by the skier`s ability to control the trunk. Similar to wheelchair sports [26], a suitable trunk flexion and extension is needed for a proper trunk momentum transmitted to the ski poles causing large propulsive force components during poling. This is a mechanism, which may be inefficient in skiers with severe impairments of the lower trunk (e.g. LW10). Previous biomechanical Para-Nordic sit-skiing studies described profiles of different classes by investigating more general sit-ski patterns [1, 4, 5] with only kinematic analysis in non-standardized outdoor conditions. In particular, the complex threefold role of the trunk in generating double poling propulsion with trunk momentum, trunk position, and trunk stability [18] has not been examined yet in different LW classes under standardized natural snow conditions and requires an approach measuring propulsive force and upper body kinematics synchronously.
Therefore, the general purpose of the study was to conduct a biomechanical analysis on the different force generation profiles of Para-Nordic sit-skiers representing different physical impairments on flat snow terrain at a constant submaximal speed. First time, a combined pole force and upper body kinematics analysis is applied to provide numerical description of the above mentioned threefold role of the trunk for propulsive force generation in different IPC classes. Secondary aims were to describe the maximum speed performance in sit-skiers with different impairment levels and generally relate biomechanical sit-ski double poling profiles at submaximal speed to maximum sprint performance.
Methods
Participants
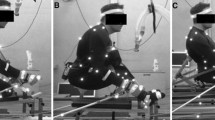
Twelve international male Para-Nordic sit-skiers representing seven nations (31 ± 6 years; 176 ± 9 cm; 61.9 ± 7 kg) with neuromusculoskeletal impairment (impairment in muscle strength due to spinal cord injury; limb deficiency), representing most LW sit-ski classes (LW10 [n = 2]; LW11 [n = 1]; LW11.5 [n = 4]; LW12 [n = 5]) volunteered in the study. The skiers participated using their proper competitive outfit and tight race suits. Consequently, significant ergonomic differences in athlete-equipment interface were notable. Athletes have chosen to use different sitting positions and sit sledges described earlier [9, 13, 16]. In Fig. 1a–g characteristic athlete-equipment setups are portrayed. The LW12 and LW11.5 skiers used the so-called “kneeling” position allowing a greater trunk range of movement (Fig. 1g). In contrast, the LW10 and LW11 skiers were sitting with the knees close to the upper body in a “high knee” position initiating trunk stability with a strong back support mounted on the sledge (Fig. 1b–d). All athletes were recruited during IPC World Cup events in Finland, regularly competed on international IPC World Cup level and had confirmed IPC classification status and certified international classifiers conducted the classification. All athletes got pre-informed about procedures and signed the informed consent with possibility to withdraw from the measurements at any point in time. The study was approved by the Ethics Committee of the University of Jyväskylä and was conducted according to the declaration of Helsinki.
a–g Calibration frame (a), definition of the kinematic variables of elbow (b), trunk (c) and pole angles (d), pole force system mounted to the pole grip (e), vector schema of the propulsive force (Fhor [prop]) calculation from the resultant (Fres [axial]) and vertical (Fvert) force vector and the pole angle α to the ground (f) and the representative sitting positions for LW10–11 sit-skiers (“high knee” position; b–d) as well as LW11.5–12 sit-skiers (“kneeling” position; g); b Elbow angle displacement (elbow angle = angle between segments Shoulder–Elbow and Elbow–Wrist) with elbow angle range of motions during flexion and extension movements during pole ground contact and the elbow angles at the events pole_in, pole_out and the minimal elbow angle during ground contact and propulsion phase, respectively. c Trunk angle displacement (trunk angle = angle of the segments Shoulder–Hip and Ski Tip–Ski Tale to each other) with trunk angle range of motions during flexion and extension movements during pole ground contact and the trunk angles at the events pole_in, pole_out and the minimal trunk angle during ground contact and propulsion phase, respectively. d Pole angle to the ground displacement (pole angle = angle between the segments Hand–Pole Tip and Ski Tip–Ski Tale (representing snow surface) with pole angle range of motions during the phases of decreasing as well as increasing pole angles during ground contact and the pole angles at the events pole_in, at minimal elbow angle during ground contact (around peak Fprop) within the stretch–shortening cycle, pole_out and the minimal pole angle during ground contact and propulsion phase, respectively
Experimental Design and Protocol
All tests took place in the Vuokatti Ski Tunnel (FIN; 1.25 km long) during the winter season under real powder snow conditions at 75%–85% air humidity and −7 °C air temperature. Maximum speed trials were performed on flat terrain (80 m) using a Radar system (Jenoptik, Germany) in order to quantify maximum sprint performance. After, athletes performed three biomechanical trials on flat terrain and an absolute constant speed of 4.5 m/s, corresponding to 73% ± 6% of maximum speed (v_max) to analyse their double poling patterns under same submaximal conditions. The speed was controlled by a visual pacing system (Protom, Finland).
Video Analyses, Radar System and Light Pacer Device
A 2D video analysis took place to analyse upper body kinematics with trunk, elbow and pole angles using 3 gen-locked video cameras (Sony HXR-NX5E, Japan; 50 Hz) to record skiing in the sagittal plane (15 m). A calibration frame was used to define the object room for each camera, creating a scale for the 2D calculations (Fig. 1a). The body model of Dempster [3] was used for the 2D coordinate determination of all digitized model points (13 point model including skiing equipment) and to calculate segment angles (Ariel Dynamics Inc., USA). For each trial of each athlete, the first three full consecutive double poling cycles were averaged.
Cycle Characteristics and Kinematic Variables
A double poling cycle during submaximal testing at 4.5 m/s speed was determined from the pole force data, dividing each cycle into a poling phase (ground contact) and a recovery phase (flight phase). The cycle time (CT), absolute (s) and relative (%CT) poling and recovery times, poling frequency (Pf = 1/CT) and cycle length (CL = CT ∙ velocity) and their ratio (Pf/CL) were determined. Figure 1b–d shows in detail the analysed and calculated kinematic angle variables with the corresponding angle definitions as angles between the shown body segments.
Pole Force Measurements
Ground reaction forces at the poles were measured (1000 Hz sample rate) with a custom made, light weight (70 g each) pole force sensor system (University of Salzburg, Austria) using uniaxial strain gauge load cells (Velomat, Germany) installed in a specifically constructed light aluminium body in the pole grips (Fig. 1e). The pole sensors were calibrated by standard procedures in accordance with previous studies [7, 10] and validity measurements against a 20 m long force platform system described in detail by Vähäsöyrinki et al. [25] proved high accuracy with a mean absolute error of 8.6 ± 5.4 N. Pole force signals were transferred via cables to an 8-channel force amplifier (Neuromuscular Research Centre, University of Jyväskylä, Finland) linked to a National Instruments A/D converter card (sampling rate 1 kHz, NI 9205). A wireless transmitter system (WLS-9163, National Instruments, Austin, USA) sent data to a portable computer with a receiver card and custom made data collection software (Labview 8.5; National Instruments, Austin, USA). The pole force system was synchronised with the video cameras by a visual event synchronization performed by hitting the pole with a wooden block while all gen-locked cameras were filming this event for each athlete.
The propulsive force was calculated from axial force (Faxial) and the pole angle to the ground (PA) (Fig. 1f):
In terms of pole forces, peak propulsive forces, average propulsive forces, impulses of Fprop as well as propulsive power were calculated and presented in relative values expressed as percentages of body weight (%BW).
Data Processing and Statistical Analyses
Data processing was conducted using IKE-master 1.38 (IKE Software Solutions, Austria). All data are presented as mean ± standard deviation or single person data (low number in different classes) for the description of the force generation profiles of Para-Nordic sit-skiers. Pearson’s product–moment correlation coefficient tests were performed to examine the interrelation of different biomechanical variables. Statistical significance was set at P < 0.05. All statistical analyses were processed using IBM SPSS Statistics 20 (IBM Corporation, USA) and Microsoft Office Excel 2010 (Microsoft Corporation, USA).
Results
Maximal Speed Performance
The maximum speed (v_max) (Fig. 2a), representing maximum speed performance in sit-skiing, in all male participants of all classes measured in the current study was of 6.2 ± 0.4 m/s, with sub-values of 5.66 ± 0.06 m/s for LW10 up to 6.42 ± 0.33 m/s for LW12. This showed a tendency of increase of maximum performance on short distance from classes with more severe impairments (e.g. reduced trunk strength due to high level thoracic spinal cord injury) to the classes with minimal impairment in sit-skiing (e.g. incomplete lumbar spinal cord injury or lower limb deficiency).
Sit-Ski Double Poling Cycle Characteristics
All variables on cycle characteristics (constant submaximal speed) are presented descriptively (mean ± standard deviation or single person data) in Fig. 2b–f. With increasing LW class, the cycle rate (poling frequency) shows tendency to drop from 76 ± 19 pushes/min down to 52 ± 8 (LW11.5) and 50 ± 7 (LW12) pushes/min while cycle length increased proportionally to the cycle rate drop (Fig. 2b, c). This pattern was also reflected by a clearly dropping cycle rate/cycle length ratio (0.4 vs. 0.15) from LW10 towards LW12 group of sit-skiers (Fig. 2d). Relative recovery and poling time increased and decreased, respectively about 10% CT from LW10 to LW12 but with no consistent linear change from class to class (Fig. 2e, f).
Upper Body Angle and Pole Force Production Profiles During Sit-Ski Double Poling
All upper body angle and force variables (constant submaximal speed) are presented descriptively (mean ± standard deviation or single person data) in Figs. 3a–d and 4a–d. The trunk range of motion (ROM) during the pushing phase in sit-ski double poling showed distinct differences between the sit-ski classes with (a) a clear trunk extension (backwards movements) during force application to the ground or trunk position maintenance (little pronounced flexion–extension pattern) in the LW10 skiers, (b) a slight, almost unrecognizable trunk flexion–extension pattern in the LW11 skier, and (c) a pronounced trunk flexion during the first two thirds of the poling phase with slightly less flexion towards the end of the double poling thrust in LW11.5 and LW12 sit-skiers (Fig. 3a). This is also reflected by the trunk angle ROMs during poling phase along with the trunk angle values at the event pole_out. In LW10 skiers trunk angle ROMs of – 20° (extension) and 2° (flexion) were observed (− 15° ± 14°) while LW11.5 and LW12 skiers showed distinct trunk flexion patterns during ground contact with trunk flexion ROMs of 16° ± 6° and 17° ± 3°, respectively (Fig. 4a). Consequently, trunk angles at the end of the pole thrust range from 94° ± 5° in LW10 skiers down to 46° ± 6° in LW12 skiers (Fig. 4b). The pole angle to the ground during poling phase and force transmission, in particular at the end of poling phase at pole release, playing a main role in the production of propulsive force, showed characteristic patterns for all classes (Figs. 3b, 4c) with values from 18° ± 1° in LW10 skiers to 14° ± 2° and 12° ± 3° in LW11.5 and LW12 athletes, respectively. Additionally, LW11.5 and LW12 showed slightly faster pole to ground angle decreases during double poling thrusts, demonstrating moreover an angle plateau towards the end of poling, which could not be found in the LW11 and LW10 (Fig. 3b). Elbow angle characteristics show basically a typical stretch–shortening cycle (SSC) pattern with a distinct elbow flexion in the first part of poling and a subsequent elbow extension phase in the second part, a pattern which is less pronounced in the single LW11 skier in the study (Fig. 3c). Elbow angle minima during the SSC occur around the peak propulsive force in classes LW11.5 and LW12, while the timing of elbow angle minimum and peak propulsive force seems to be delayed in the lower classes (Fig. 3c, d).
a–d Trunk (a), pole (b) and elbow (c) angle-time curves and propulsive force–time curves (d) in the IPC classes LW10, LW11, LW11.5 and LW12. The four vertical dotted lines indicate the elbow angle minimum or the start of elbow extension phases in each analyzed IPC sit-ski class. Only LW11.5 and LW12 sit-skiers showed a powerful trunk flexion (a) plus elbow extension phase (c) during an extended period of small pole angles to the ground (see pole angle plateau; b) with higher propulsive forces (d)
Peak propulsive pole forces (Fprop_max) were 14.5% ± 0.6%BW, 15.0%BW, 18.3% ± 3.9%BW, and 18.1% ± 2.3%BW for LW10, LW11, LW11.5 and LW12, respectively, while average Fprop was found to be 7.9% ± 2.1%BW, 8.8%BW, 10.7% ± 1.6%BW, and 11.1% ± 1.9%BW. Impulses of Fprop were 3.1% ± 0.1%BW, 1.6%BW, 5.1% ± 1.6%BW, and 5.4% ± 0.6%BW for LW10, LW11, LW11.5 and LW12, respectively. In other words, Fprop_max created at the same speed (4.5 m/s) increased 1.25-fold from class LW10 to LW11.5 and LW12, while average Fprop on top of the impulse of Fprop both increased 1.41-fold and 1.74-fold from class LW10–12, respectively (Fig. 3d).
Calculation of Propulsion Loss Due to Different Trunk and Pole Angles and Correlation Analysis
A calculation for the general relationship of pole angle at the moment of elbow angle minimum (highest forces within the cycle) to the relative and absolute loss of propulsion at a given equal axial force, is shown in Fig. 5a–d. Data of the current study were applied to this calculation, with the smallest pole angles found for the LW12 skiers with 24° vs. 44° at LW10 skiers. A LW10 skier with measured 44° degrees pole angle at the peak pole force production loses 21.3% propulsion versus the LW12 skier, a LW10.5 skier 13.7%, a LW11 skier 9.2% and a LW11.5 skier 4%, corresponding to − 29.1 N, − 18.9 N, − 12.7 N and − 5.8 N at a theoretically given assumed equal axial force of e.g. 150 N.
a–d Pole angle to the ground at the event of minimum elbow angles/peak forces versus the relative (%) (a) and the absolute (N; axial force of 150 N) (b) loss in propulsion and representative propulsive force (Fpropulsive) vector schema at 43° (LW10) (c) and 28° (LW12) (d) pole angle to the ground at the moment of axial peak pole force with a given value of 350 N
Correlations between variables at submaximal speed: the amount of trunk flexion ROM during sit-skiing double poling thrusts showed the highest correlations to the impulse of Fprop (r = 0.63; P < 0.05) and additionally correlated to the pole angle to the ground at the end of the double poling thrust (r = − 0.76; P < 0.05) (Fig. 6a, b). Both mentioned trunk angle variable correlations demonstrated variance explanations of 39% and 57%, respectively (Fig. 6a, b).
a–d Pearson’s product-moment correlations of trunk flexion range of motion (ROM) to impulse of propulsive force (Fpropolsive) (a) and to the pole angle at pole release from the snow (Pole angle_out) (b) at submaximal speed; Pearson’s product-moment correlations of maximum speed (v_max sit ski) to trunk flexion ROM (Trunk ROM) (c) and cycle length (d) realized at submaximal speed; n = 12; all P < 0.05
Maximum speed performance (v_max) was positively correlated (r = 0.63; P < 0.05) to trunk flexion ROM during pole thrust as well as cycle length (r = 0.59; P < 0.05) during sit-ski double poling at constant submaximal speed, explaining 40% and 34% of variance within the group, respectively (Fig. 6c, d).
Discussion
The main findings of the study were: (1) Classes LW10-11 showed trunk extension and/or almost no trunk movement during double poling combined with higher poling frequencies and smaller force production per cycle. In contrast, LW11.5–12 classes showed force production profiles characterized by greater trunk flexion ranges of motion and, connected to smaller pole angles to the ground and hereby better force production per pole thrust at the same submaximal speed. (2) LW10–11.5 sit-skiers lose between 21% and 4% of propulsion versus LW12 sit-skiers only due to less effective kinematics with smaller trunk ranges of motion and larger pole angles at a given equal axial force.
Numerical Description and Calculation of Force Generation Profiles Among IPC sit-ski Classes
One of the most distinct differences between LW10-11 (lower classes) and LW11.5–12 (higher classes) skiers was that lower classes were unable to resist and counteract the gravity forces acting along the poles and their upper body was forced to move backwards or maximally could be stabilized in position. In contrast, higher classes continuously flexed their trunk and pushed the poles strongly to the snow. They used stretch–shortening (flexion–extension) cycle patterns in the elbow joints and gained more propulsive power and cycle lengths, and at the same time sparing cycle rate (Fig. 2b, c). In addition, the inter-correlations of variables at submaximal speed showed that the amount of trunk flexion range of motion was strongly connected to lower pole angles and larger impulses of propulsive force, standing for an efficient force generation profiles in IPC classes LW11.5 and LW12 (Fig. 6a, b). This pattern, also found in similar sports like wheelchair racing [26], reflects the necessity of suitable trunk flexion and extension needed for a proper trunk momentum transmitted to ski poles. This part of the poling cycle is ineffective in sit-skiers with severe impairments of the lower trunk (LW10). The complex threefold role of the trunk in generating double poling propulsion with trunk momentum, trunk position, and trunk stability.
The threefold role of the trunk in generating double poling propulsion with trunk momentum, trunk position, and trunk stability could also be seen in the performed calculation model used in the current study (Fig. 5a–d). Based on exemplary data the calculation could relate (1) the pole angle to the ground at highest pole forces to (2) the sit-ski double poling forward propulsion produced at a given, theoretically equal axial pole force between sit-ski athletes, by which the effect of higher or lower strength levels or training status could be excluded. LW12 skiers gain 21.3% (LW10) to 4% (LW11.5) (Fig. 5a) more propulsion during one double poling thrust compared to the lower classes at a theoretically equal axial pole force only due to better trunk function and smaller pole angles to the ground (Fig. 4a–d). Consequently, only the geometry, without taking force production, strength capacity or training status itself into account, affects to an enormous extent the relative and absolute amount and way of force production (Fig. 5a, b) in flat terrain at a given submaximal speed. A loss of 21.3% or ~ 29 N of Fprop in e.g. LW10 was considered as meaningful (Fig. 5 a, b). The effect of training status and the hereby-caused bias in scientific classification data is a general problem, which is highly discussed among coaches, classifiers and technical delegates. The presented model takes out the factor of more or less trained force production and looks only on the geometrical, kinematic aspect of this disadvantage in low (LW10–11) sit-ski classes. Our current data about this aspect of trunk and pole kinematics and its effect on propulsion find support in earlier studies and race analyses of the research group [13, 20], which considered low pole angles to determine force transfer markedly. If one theoretically assumes an equal axial peak force of 350 N (both skiers) at the moment of the peak force and minimum elbow angle, the LW12 skier gained a propulsion benefit of 20% (50 N more propulsion) versus the LW10 skier [20]. The phenomenon of more pronounced, efficient large range of motion upper (and lower) body actions during double poling is also described in able-bodied skiers with correlations to higher pole force production or greater cycle length [6, 7, 11, 12, 21, 22].
Of note is, that the ratio of relative poling time to recovery time shows a tendency of decrease (43%–33%CT) and increase (56%–66%CT) from LW10 to LW12 classes, an aspect which is again discussed in able-bodied skiers as regards correlations to performance [7, 12]. Successful able-bodied skiers indicated a similar pattern like LW12 skiers with values of 27%CT for poling as well as 73%CT for recovery time. Longer recovery times were considered beneficial in terms of better blood flow, muscle relaxation and more time to reposition the trunk for next pole thrusts [7, 10] resulting in lower lactate and heart rate values. Solely these differences in temporal cycle patterns may be responsible for some physiological disadvantages of lower vs. higher sit-ski classes, which needs further detailed examination in future studies.
Despite the fact that it could not be directly analysed in the current study, the effects of compromised biomechanical patterns on the sit-skiing physiology must be raised at this stage, as it is a factor, which has not been analysed nor mentioned in sit-skiing until now. Similar to the three facts like (1) the impairment affected trunk and pole angle kinematics, independent from training status, (2) the forced pure sitting position [9, 13] and (3) the temporal cycle duration pattern differences, also the compensatory, higher skiing frequency (cycle rate) found in lower sit-ski classes (Fig. 2b), may have indirect impact on the sit-skiing physiology. To gain the same submaximal speed, the LW10–11 skier had to increase double poling frequencies up to almost 80 thrusts/min as such a skier cannot increase cycle length due to proven limited trunk function (Fig. 4a, b). In able-bodied skiers, double poling frequencies of 80 thrusts/min proved to create ~ 13% higher oxygen consumption, ~ 28% higher lactate values and 12% lower gross-efficiency compared to lower common frequencies in top elite skiers [10]. Additionally, the aspect of the locomotor-respiratory coupling in sport in general [14] and in physically impaired athletes, like in e.g., wheelchair racing [2, 15], highlights the direct negative impacts of this on the athlete’s breathing capacity (e.g. limited breathing muscle function in high thoracic lesions). All these physiological aspects need further and deeper analyses, but should be considered during classification conceptions besides aspects specified in the IPC Position Stand [23].
Maximum Sit-Ski Double Poling Performance and Correlations
Despite a low number of available skiers in Para-Nordic skiing worldwide in some of the IPC sit-ski classes, it can be stated that most LW11.5–12 skiers showed higher maximum speed performances on flat terrain compared to LW10–11 classes with a somewhat linear increase from LW10 to LW12 athletes. Although maximum speed has not been biomechanically analysed, it may be speculated that the typical force production and kinematic profiles of LW12 skiers at submaximal constant speeds stay valid also at maximum speed. The positive correlations of trunk flexion range of motion and cycle length at submaximal speeds to the maximum speed were standing for 40% and 35% of variance within the analysed group (Fig. 6c, d).
Shortcomings of the study are the low number of participants in the different LW classes as regards Para Nordic sit-skiers. The total number of male Paralympic athletes in all cross-country sit-skiing events e.g. in Pyeongchang 2018 Winter Paralympics is as low as 41 athletes (LW10 [n = 3]; LW10.5 [n = 4]; LW11 [n = 3]; LW11.5 [n = 7]; LW12 [n = 24]). Participation in the Winter Paralympic Games demonstrates the disproportionality between classes, with a major underrepresentation of athletes with more severe impairments. A suggestion to increase the sample size, future research could include the elite female sit-skiers in cross-country skiing and biathlon.
Future research needs to provide more knowledge about performance related issues and biomechanical-physiological movement differences in also other terrains like uphill, curve and downhill sections, a possibly slightly greater number of skiers and a wider spectrum of skiing speeds. Proper race analyses tools with split time and terrain specific performance analyses in different race distances and in combination with valid impairment measurements have to be established.
References
Bernardi M, Janssen T, Bortolan L, Pellegrini B, Fischer G, Schena F. Kinematics of cross-country sit skiing during a Paralympic race. J Electromyogr Kinesiol. 2013;23(1):94–101.
Celli B, Criner G, Rassulo J. Ventilatory muscle recruitment during unsupported arm exercise in normal subjects. J Appl Physiol. 1988;64(5):1936–41.
Dempster WT. Space requirements of the seated operator, geometrical, kinematic, and mechanical aspects of the body with special reference to the limbs. East Lansing: Michigan State University; 1955.
Gastaldi L, Mauro S, Pastorelli S. Analysis of the pushing phase in Paralympic cross-country sit-skiers–Class LW10. J Adv Res. 2016;7(6):971–8.
Gastaldi L, Pastorelli S, Frassinelli S. A biomechanical approach to paralympic cross-country Sit-Ski racing. Clin J Sport Med. 2012;22(1):58–64.
Holmberg H-C, Lindinger S, Stoggl T, Bjorklund G, Muller E. Contribution of the legs to double-poling performance in elite cross-country skiers. Med Sci Sports Exerc. 2006;38(10):1853–60.
Holmberg HC, Lindinger S, Stoggl T, Eitzlmair E, Muller E. Biomechanical analysis of double poling in elite cross-country skiers. Med Sci Sports Exerc. 2005;37(5):807–18.
IPC. World para nordic skiing classification—Rules and Regulations. Bonn: International Paralympic Committee (IPC) and World Para Nordic Skiing; 2017.
Lajunen K, Rapp W, Ahtiainen J, Lindinger S, Linnamo V. Effect of sitting posture on sit-skiing economy in non-disabled athletes. J Front Sports Active Living. 2020;2:44.
Lindinger SJ, Holmberg H-C. How do elite cross-country skiers adapt to different double poling frequencies at low to high speeds? Eur J Appl Physiol. 2011;111(6):1103–19.
Lindinger SJ, Holmberg H-C, Mueller E, Rapp W. Changes in upper body muscle activity with increasing double poling velocities in elite cross-country skiing. Eur J Appl Physiol. 2009a;106(3):353–63.
Lindinger SJ, Stoeggl T, Mueller E, Holmberg H-C. Control of speed during the double poling technique performed by Elite Cross-Country skiers. Med Sci Sports Exerc. 2009b;41(1):210–20.
Linnamo V, Rapp W, Lindinger S. Contribution of sport science to performance: Nordic skiing. In: Vanlandewijck Y, Thompson WR, editors. Training and coaching the paralympic athlete. Chichester: Wiley; 2016. pp. 216–35.
O’Halloran J, Hamill J, McDermott WJ, Remelius JG, Van Emmerik REJE. Locomotor-respiratory coupling patterns and oxygen consumption during walking above and below preferred stride frequency. Eur J Appl Physiol. 2012;112(3):929–40.
Perret C, Wenger M, Leicht CA, Goosey-Tolfrey VL. Locomotor-respiratory coupling in wheelchair racing athletes: a pilot study. J Front Physiol. 2016;7:11.
Rapp W, Lappi T, Lindinger S, Ohtonen O, Linnamo V. Force production, balance control and muscle activation in different sitting position—pilot study for disabled sit sledge cross-country skiers. In: Müller E, Kröll J, Lindinger S, Pfusterschmied J, Stöggl T, editors. Science and Skiing VI. Vallejo: Meyer & Meyer; 2014. pp. 453–64.
Rapp W, Rosso V, Ohtonen O, Gastaldi L, Vanlandewijck Y, Lindinger SJ, Vesa L. Role of muscle activation in the sit-skiing performance and classification process. In: Hakkarainen A, Linnamo V, Lindinger S, editors. Science and Nordic Skiing III. Jyväskylä: Jyväskylä University Printing House; 2016. pp. 165–72.
Rosso V, Gastaldi L, Rapp W, Lindinger S, Vanlandewijck Y, Äyrämö S, Linnamo V. Balance perturbations as a measurement tool for trunk impairment in Cross-Country Sit Skiing. Adapt Phys Activ Q. 2019;36:61–76.
Rosso V, Gastaldi L, Rapp W, Lindinger S, Vanlandewijck Y, Linnamo V. Biomechanics of simulated versus natural cross-country sit skiing. J Electromyogr Kinesiol. 2017;32:15–21.
Schillinger F, Rapp W, Hakkarainen A, Linnamo V, Lindinger SJ. A descriptive video analysis of classified Nordic disabled sit-skiers during the Nordic World Championships 2013. In: Hakkarainen A, Linnamo V, Lindinger S, editors. Science and Nordic Skiing III. Jyväskylä: Jyväskylä University Printing House; 2016. pp. 173–80.
Stöggl R, Müller E, Stöggl T. Do maximal roller skiing speed and double poling performance predict youth cross-country skiing performance? J Sports Sci Med. 2017;16(3):383.
Stöggl T, Lindinger S, Mueller E. Analysis of a simulated sprint competition in classical cross country skiing. Scand J Med Sci Sports. 2007;17(4):362–72.
Tweedy SM, Vanlandewijck Y. International Paralympic Committee position stand—background and scientific principles of classification in Paralympic sport. J Br J Sports Med. 2011;45(4):259–69.
Tweedy SM, Mann D, Vanlandewijck Y. Research needs for the development of evidence-based systems of classification for physical, vision and intellectual impairments. In: Vanlandewijck Y, Thompson WR, editors. Training and coaching the paralympic athlete. Chichester: Wiley; 2016. pp. 122–49.
Vahasoyrinki P, Komi PV, Seppala S, Ishikawa M, Kolehmainen V, Salmi JA, Linnamo V. Effect of skiing speed on ski and pole forces in cross-country skiing. Med Sci Sports Exerc. 2008;40(6):1111–6.
Vanlandewijck Y, Theisen D, Daly D. Wheelchair propulsion biomechanics: implications for Wheelchair Sports. J Sports Med. 2001;31(5):339–67.
Acknowledgements
The authors would like to express appreciation for the athletes and coaches from several Nations for their participation, enthusiasm and cooperation in this study.
Funding
Open access funding provided by University of Gothenburg.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Karczewska-Lindinger, M., Linnamo, V., Rosso, V. et al. Force Generation Profiles of Para-Nordic Sit-Skiers Representing Different Physical Impairments. J. of SCI. IN SPORT AND EXERCISE 3, 281–291 (2021). https://doi.org/10.1007/s42978-021-00117-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42978-021-00117-1