Abstract
Purpose
To challenge current conventions in paediatric sport science and use data from recent longitudinal studies to elucidate the development of aerobic and anaerobic fitness, with reference to youth athletes.
Methods
(1) To critically review the traditional practice of ratio scaling physiological variables with body mass and, (2) to use multiplicative allometric models of longitudinal data, founded on 1053 (550 from boys) determinations of 10–17-year-olds’ peak oxygen uptake (\( {{\text{V}}\text{O}}_{2} \)) and 763 (405 from boys) determinations of 11–17-year-olds’ peak power output (PP) and mean power output (MP), to investigate the development of aerobic and anaerobic fitness in youth.
Results
The statistical assumptions underpinning ratio scaling of physiological variables in youth are seldom met. Multiplicative allometric modelling of longitudinal data has demonstrated that fat free mass (FFM) acting as a surrogate for active muscle mass, is the most powerful morphological influence on PP, MP, and peak \( {{\text{V}}\text{O}}_{2} \). With FFM appropriately controlled for, age effects remain significant but additional, independent effects of maturity status on anaerobic and aerobic fitness are negated.
Conclusions
Ratio scaling of physiological variables with body mass is fallacious, confounds interpretation of the development of anaerobic and aerobic fitness, and misleads fitness comparisons within and across youth sports. Rigorous evaluation of the development of anaerobic and aerobic fitness in youth requires longitudinal analyses of sex-specific, concurrent changes in age- and maturation-driven morphological covariates. Age and maturation-driven changes in FFM are essential considerations when evaluating the physiological development of youth athletes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
High levels of aerobic and/or anaerobic fitness are essential components of performance in many youth sports. Evaluation of the interplay between aerobic and anaerobic fitness in youth sport is, however, dependent not only on the intensity, frequency, and duration of exercise but also on developmental exercise physiology. Successful talent identification, long-term athlete development, physiological monitoring, and design of training programmes are founded on knowledge of the development of aerobic and anaerobic fitness. Yet, there are remarkably few rigorous studies which have analyzed the effects of concurrent changes in age-, growth-, and maturation-driven morphological covariates on physiological variables during youth. This paper will challenge current conventions in paediatric sport science and use data from recently published longitudinal studies to elucidate the development of aerobic and anaerobic fitness, with reference to youth athletes. The potential scope of the topic is huge and with journal limits on words and number of references, complementary reviews and tutorial papers are used to support the text where appropriate.
Aerobic Fitness
Aerobic fitness defines the ability to deliver oxygen from the atmosphere to the muscles and to use it to generate energy to support metabolic demands during exercise. Peak oxygen uptake (\( {{\text{V}}\text{O}}_{2} \)), the highest rate of oxygen consumed during a progressive exercise test to exhaustion limits the capacity to perform aerobic exercise and is internationally recognized as the “gold standard” criterion measure of youth aerobic fitness [10, 49]. Although it is recognized that other variables contribute to aerobic fitness [2, 9] herein we will focus on peak \( {{\text{V}}\text{O}}_{2} \) and use the terms peak \( {{\text{V}}\text{O}}_{2} \) and aerobic fitness synonymously. Peak \( {{\text{V}}\text{O}}_{2} \) is the most researched physiological variable in paediatric exercise physiology [36], but traditional data analyses have clouded understanding of its development in relation to growth and maturation and misled comparisons of aerobic fitness both within and between youth sports [3].
The rigorous assessment of youth peak \( {{\text{V}}\text{O}}_{2} \) [25, 35] and the challenges associated with the physiological monitoring of youth athletes are well-documented [5, 24]. The importance of sport-specific ergometry is apparent in the physiological monitoring of youth swimmers where the requirement is for the determination of peak \( {{\text{V}}\text{O}}_{2} \) to reflect the major muscle groups involved in propulsion [3, 47]. However, the developmental physiology issues addressed herein are common to both healthy youth and youth athletes across all sports, so for clarity and consistency we will focus on peak \( {{\text{V}}\text{O}}_{2} \) using large muscle groups.
In paediatric sport science laboratories, peak \( {{\text{V}}\text{O}}_{2} \) is routinely determined either running on a treadmill or pedalling on a cycle ergometer, but data from different ergometers should not be combined for analyses. Longitudinal analyses of 11–16-year-olds have reported age-related, mean treadmill values of peak \( {{\text{V}}\text{O}}_{2} \) to be ~ 11%–14% higher than those determined on a cycle ergometer. However, as the total muscle mass activated during running or cycling is driven by sex-specific changes in growth and maturation, ergometer-driven differences in youth peak \( {{\text{V}}\text{O}}_{2} \) within individuals vary in accord with their biological clocks [13]. It is therefore untenable to increase sample sizes by “correcting” for ergometer-driven differences in youth peak \( {{\text{V}}\text{O}}_{2} \) through adding fixed percentages to cycle ergometer values, as has been common practice for decades (e.g. [43, 63]). Herein we will focus on the development of aerobic fitness rigorously determined on a treadmill.
Aerobic fitness and age
Peak \( {{\text{V}}\text{O}}_{2} \) (in L/min) has been consistently reported to increase with age in both boys and girls. The mean peak \( {{\text{V}}\text{O}}_{2} \) of boys is generally higher than that of similarly aged girls with the sex difference increasing with age [12]. Age-related paediatric “norms” are widely available and in common use to compare active and inactive, sporting and non-sporting, and healthy and unhealthy youth (e.g. [27]). Paediatric norms, however, only present average values of peak \( {{\text{V}}\text{O}}_{2} \) from single moments in time (“snapshots”) and provide few insights into the development of individuals’ aerobic fitness.
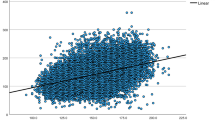
Figure 1 illustrates 1053 (550 from boys) longitudinal measures of 10–17-year-olds’ peak \( {{\text{V}}\text{O}}_{2} \) [14]. In accord with the extant literature; the data indicate that boys’ mean peak \( {{\text{V}}\text{O}}_{2} \) increases from 10 to 17 years with girls’ values increasing from 10 to 13 years of age before tapering off. Boys’ mean peak \( {{\text{V}}\text{O}}_{2} \) almost doubles from 10 to 17 years with girls’ mean peak \( {{\text{V}}\text{O}}_{2} \) increasing by ~ 50% over the same time period. Boys’ mean peak \( {{\text{V}}\text{O}}_{2} \) is ~ 11% higher than that of girls at age 10 years and the difference increases to ~ 50% by age 17 years. However, the wide individual variations in age-related peak \( {{\text{V}}\text{O}}_{2} \) and the overlap of 10–13-year-old boys’ and girls’ data, clearly expose the limitations of mean age-related “snapshot” comparisons within and between sexes and within and across sports.

Figure drawn from data reported in Armstrong and Welsman [14] and founded on 1053 determinations of peak oxygen uptake (550 from boys and 503 from girls)
Aerobic fitness in relation to age in 10–17-year-old boys and girls.
Cross-sectional analyses have consistently reported that youth athletes of both sexes, particularly those participating in endurance sports, typically present higher peak \( {{\text{V}}\text{O}}_{2} \) values than their non-athlete peers [3, 8]. This may be partially due to appropriate training [4, 47] or genetics [60] but there is a marked variation among individual youth in the timing and tempo of biological maturation which confounds age-related comparisons [45]. Some longitudinal data suggest a spurt in aerobic fitness aligned with the time of peak height velocity (PHV) [38]. But age at PHV ranges from 9.0 to 15.0 years in girls and 11.1–17.3 years in boys and it has been reported, for example, that 12–13-year-old male football players span the spectrum from prepuberty to biological maturity [45]. The aerobic fitness of a prepubertal 12–13-year-old footballer cannot be meaningfully compared with that of a biologically mature footballer of similar chronological age. These issues are a major problem in establishing a level playing field in age-group sport [3, 45].
Development of Aerobic Fitness with Growth and Maturation
Cross-Sectional Studies and the Fallacy of Ratio Scaling
In the first laboratory study of boys’ “physical fitness”, Robinson [56] recognised that his \( {{\text{V}}\text{O}}_{2} \) data were related to body size as well as age. Without providing a rationale he divided \( {{\text{V}}\text{O}}_{2} \) (in mL/min) by body mass (in kg) and presented his data in ratio with body mass as mL/kg/min. In the second laboratory study of boys’ aerobic fitness, Morse et al. [50] only reported \( {{\text{V}}\text{O}}_{2} \) data in ratio with body mass. In the first study to include girls, Åstrand [21] commented that \( {{\text{V}}\text{O}}_{2} \) should be scaled to active muscle mass rather than body mass. But as he was unable to measure active muscle mass, he suggested that \( {{\text{V}}\text{O}}_{2} \) should be interpreted in relation to fat free mass (FFM) which can be determined indirectly. He did not, however, pursue this empirically and discussed his data in ratio with body mass. Collectively, these pioneers initiated the scientific study of the exercising child but also introduced a means of “controlling” physiological variables for growth and maturation which has confused understanding of paediatric sport science ever since.
Tanner [65] unequivocally demonstrated that ratio scaling of physiological variables was fallacious but the vast majority of published paediatric sport science papers persist in reporting peak \( {{\text{V}}\text{O}}_{2} \) and other physiological variables (e.g. muscle strength, pulmonary ventilation, cardiac output) in ratio with body mass. This is probably because it is recognised as “the most convenient and traditionally accepted way” [23] and journal editors and reviewers seldom (if ever) require authors to provide a scientific rationale or statistical justification for its use.
Welsman and Armstrong [74] explained from first principles the statistical assumptions underpinning ratio scaling and empirically verified that they were not met in 20 years of cross-sectional studies from their laboratory, involving ~ 1000 determinations of the peak \( {{\text{V}}\text{O}}_{2} \) of children and adolescents. In brief, if ratio scaling effectively controls for body mass then the product-moment correlation coefficient between peak \( {{\text{V}}\text{O}}_{2} \) (in mL/kg/min) and body mass (in kg) will be not significantly different from zero. This statistical assumption was tested using data at the onset of the study illustrated in Fig. 1. Significant (P < 0.001) negative correlations of r = − 0.52 and r = − 0.54, for girls and boys, respectively, between peak \( {{\text{V}}\text{O}}_{2} \) (in mL/kg/min) and body mass (in kg) were calculated, demonstrating unequivocally the failure of ratio scaling to create a size-fee variable. Numerous reviews and tutorial papers have confirmed both theoretically and empirically the fallacy of ratio scaling of peak \( {{\text{V}}\text{O}}_{2} \) and compellingly argued that with cross-sectional data, allometric scaling with multiple covariates based in log-linear regression is the method of choice when exploring the development of youth fitness (see [71,72,73,74] for discussion of scaling paediatric data from first principles). Analyzing the data at the onset of the study illustrated in Fig. 1 with an allometric (log-linear) scaling model, revealed a mass exponent of 0.68 and correlations between allometrically scaled peak \( {{\text{V}}\text{O}}_{2} \) (i.e. mL/kg0.68/min) and body mass (kg) of r = 0.07 and r = − 0.13, for girls and boys, respectively, which were not significantly different from zero. Peak \( {{\text{V}}\text{O}}_{2} \) was therefore effectively controlled for body mass, with allometric scaling creating a size-free variable (see [3] pp 167–170 for analytical detail).
Ratio scaled data offer a different picture of youth aerobic fitness from that when absolute values (in L/min) are presented. Ratio scaling “over-scales”, disadvantages heavier youth (e.g. early maturers) and advantages lighter youth (e.g. later maturers). In several sports, body mass plays an important role in the selection of youth athletes and their retention in elite training programmes but youth athletes may be either penalised (e.g. rugby forwards) or favoured (e.g. artistic gymnasts) in ratio-scaled comparisons of fitness across sports. Moreover, the size of the real difference in aerobic (or anaerobic) fitness between youth athletes in different sports and their non-active peers is obscured in comparative studies of ratio-scaled data.
On average, instead of increasing with age, boys’ ratio-scaled peak \( {{\text{V}}\text{O}}_{2} \) remains unchanged from 10 to 17 years whereas girls’ values decline, particularly in adolescence as they accumulate more body fat. Ratio-scaled data also suggest that when body mass is controlled for, changes in maturity status have no additional or independent effect on aerobic fitness [11]. In contrast, with body mass appropriately controlled for using allometry boys’ peak \( {{\text{V}}\text{O}}_{2} \) has been demonstrated to increase from 10 to 17 years with girls’ peak \( {{\text{V}}\text{O}}_{2} \) increasing at least from 10 to 13 years before levelling-off rather than declining [75]. Moreover, allometrically scaled data have showed that maturity status exerts significant and positive effects on peak \( {{\text{V}}\text{O}}_{2} \) in both sexes, in addition to and independent of body mass and age [19].
Longitudinal Studies and Multiplicative Allometric Modelling
Some longitudinal studies have made seminal contributions to aspects of paediatric health and exercise science (e.g. [42, 48]) but to elucidate the development of physiological variables rigorous analyses of the effects of concurrent changes in age-, growth-, and maturation-driven morphological covariates are required. Longitudinal studies of aerobic fitness generally consist of a series of reports of annual analyses of absolute peak \( {{\text{V}}\text{O}}_{2} \) and peak \( {{\text{V}}\text{O}}_{2} \) in ratio with body mass. Data are consistent and reflect those from cross-sectional studies but provide few additional insights into the development of aerobic fitness.
Janz et al. [41] determined allometric scaling factors for a cohort of children and concluded that FFM was more appropriate than body mass to “normalise” peak \( {{\text{V}}\text{O}}_{2} \) when investigating physiologic changes during growth and maturation. It is, however, the emergence [1] and on-going refinement [54] of multilevel allometric modelling which has provided an elegant approach to the study of developmental exercise physiology. Nevill et al. [51] introduced multiplicative allometric modelling to paediatric sport science and with the present authors [20] demonstrated that it enabled the effects of age, maturity status, body mass, and FFM on the development of aerobic fitness to be partitioned concurrently within an allometric framework.
Using multiplicative allometric modelling, Armstrong and Welsman [13,14,15, 17] investigated the longitudinal development of the peak \( {{\text{V}}\text{O}}_{2} \) of the 10–17-year-olds described in Fig. 1, with the following baseline model where y is the physiological variable, in this case peak \( {{\text{V}}\text{O}}_{2} \),
log transformation linearized the model to form the starting point for analysis,
All parameters were fixed with the exception of the constant (a) which was allowed to vary randomly at level 2 (between individuals) and the multiplicative error ratio (ε) which also varied randomly at level 1 (within individuals) as denoted by the subscripts i (level 1 variation) and j (level 2 variation). Age was centred on the group mean. From the baseline model of age, age2, and body mass, additional explanatory variables such as sum of skinfolds were explored (see original papers for details of the analyses).
In addition to sex-specific models, the original papers explored the magnitude of sex differences in the development of aerobic fitness using the indicator variable boys = 0 and girls = 1 which sets the boys’ constant as the baseline from which the girls’ parameter is allowed to deviate. It was demonstrated that with age and body mass controlled for there was a sex difference of ~ 15% which decreased to ~ 9% when FFM replaced body mass in the models. In the 11–13-year-olds, the introduction of maximal cardiovascular covariates into models reduced the sex difference further but an unexplained ~ 4% sex difference remained [17].
As competition in youth sport is sex-specific, the primary focus herein is on single sex multiplicative allometric models to clarify the role of concurrent changes in age- and maturation-driven morphological covariates in the development of aerobic fitness. Analytical details and experimental procedures are comprehensively described in the original papers and all statistical significances were set at P < 0.05 [13,14,15, 17].
Tables 1 and 2 illustrate the multiplicative allometric models for boys and girls, respectively. The positive age terms in Model 1.1 (boys) and Model 2.1 (girls) show that (in conflict with ratio-scaled data), with body mass appropriately controlled for, aerobic fitness increases with age. The negative age2 term in each model indicates that the size of the age effect decreases in both sexes as the rate of change in growth slows. The introduction of maturity status as the stages of pubic hair described by Tanner [66] into Models 1.2 (boys) and 2.2 (girls), showed maturity status in both sexes to have an incremental, additional effect on aerobic fitness, independent of age and body mass. Again, this is in direct conflict with the ratio-scaled interpretation of peak \( {{\text{V}}\text{O}}_{2} \) and shows clearly the limitations of age-related comparisons of data ratio-scaled with body mass [14].
Body mass includes both fat mass and FFM where fat mass is largely metabolically inert [39]. In sports which involve transporting body mass fat acts as “deadweight” to be carried with a negative effect on performance, but it does not influence aerobic fitness. In this context, early maturing girls are disadvantaged as, on average, fat mass increases by ~ 50% in the 3 years post-PHV compared with ~ 12% in boys [26]. Girls’ muscle mass as a percentage of total body mass remains stable at ~ 43%–44%, from 10 to 17 years whereas boys’ muscle mass increases from ~ 46% to 54% of body mass over the same time period [46]. FFM includes tissues not involved in exercise, but in paediatric sport science FFM is well-established as a non-invasive surrogate for active muscle mass (e.g. [30, 41]).
Ideally FFM would be directly determined on each test occasion but this is not currently feasible in large studies involving several hundred assessments, moreover, “direct” measures of body fat on the same young people have been shown to vary widely across established laboratory techniques [37]. In paediatric exercise studies, FFM is commonly estimated from the youth-specific equations of Slaughter et al. [62]. It has, however, been compellingly argued that researchers should use the sum of triceps and subscapular skinfolds in conjunction with body mass as a surrogate of FFM, rather than rely on predictions from equations likely to be population-specific [57].
The introduction in Models 1.3 (boys) and 2.3 (girls) of the sum of triceps and subscapular skinfolds resulted in negative exponents with large increases in the body mass exponents and maturity status becoming non-significant. The positive age terms remained significant with negative age2 terms indicating that the size of the age effect decreases as growth slows. Collectively, skinfolds and body mass act as a surrogate for FFM and increases in the body mass exponents can be attributed to the effect that fat mass has on increasing body mass without an increase in peak \( {{\text{V}}\text{O}}_{2} \) [70]. The replacement in Models 1.4 (boys) and 2.4 (girls) of body mass and skinfold thicknesses with FFM estimated from the equations of Slaughter et al. [62] resulted in very similar models to 1.3 and 2.3. As determined by the models’ significantly smaller − 2*loglikelihoods the models with the best statistical fit were those where body mass and sum of skinfolds acted as a surrogate for FFM (i.e. Models 1.3 and 2.3) [14].
Models 1.3 and 2.3 reveal the powerful influence of FFM on the development of aerobic fitness. FFM doubles in boys from age 10–17 years and increases by ~ 60% in girls over the same time period. Sex-specific increases in FFM mask independent effects of maturation in the models as changes in FFM are strongly related to the timing and tempo of maturation. Percentage changes in FFM are at their peak around the time of PHV with boys’ values increasing by ~ 80% over a 4-year period centred on PHV and girls’ FFM increasing by ~ 30% from 1 year pre-PHV to 1 year post- PHV before tapering-off in accord with the development of peak \( {{\text{V}}\text{O}}_{2} \) [3].
Peak \( {{\text{V}}\text{O}}_{2} \) is a function of oxygen delivery to the muscles and oxygen utilisation by the muscles. As a surrogate of active muscle mass, increases in FFM augment oxygen delivery through the peripheral muscle pump which enhances venous return and increases maximal stroke volume (SV) and therefore maximal cardiac output (\( {\dot{\text{Q}}} \)) [58]. Armstrong and Welsman [15, 17] demonstrated through multiplicative allometric modelling of the data from the 11–13-year-olds described in Fig. 1, the powerful influence of increases in FFM on the development of maximal SV and maximal \( {\dot{\text{Q}}} \), in both sexes. Moreover, with FFM controlled for, there were no sex differences in maximal cardiovascular variables. Intra-muscular oxygen utilisation during exercise is enhanced by increases in active muscle mass through factors such as age and maturation- driven changes in muscle structure [46], muscle fibre activation [32], and muscle metabolism [7]. However, detailed exploration of the integrated development of intra-muscular activity during aerobic exercise awaits the ethical application of appropriate non-invasive technology.
Anaerobic Fitness
Anaerobic fitness describes the ability to generate and sustain energy through non-oxidative pathways to support metabolic demands during maximal intensity exercise. Ethical and technological constraints prevent direct measurement of intramuscular energy flux during maximal intensity exercise and current knowledge of the development of anaerobic fitness is largely founded on analyses of external power output. Unlike aerobic exercise there is no “gold standard” criterion measure of anaerobic fitness. There is a plethora of both field- and laboratory-based performance tests but paediatric research has primarily focused on external power output during the Wingate anaerobic test (WAnT) [76]. The WAnT is an “all-out” cycling test in which the determination of maximal pedalling cadence against a fixed braking force allows the assessment of external peak power output (PP) and mean power output (MP). Power output is recorded each second and PP is reached within a few seconds of the onset of the test. MP is recorded as the total power output averaged over the 30 s test.
Within studies, the WAnT is a reliable test of external power output [40] but comparisons of paediatric data across studies are problematic as several laboratories have introduced modifications to the WAnT, including a rolling start, the use of toeclips, variations in the time over which PP is determined (1 s, 3 s, or 5 s), and adaptations of cycle crank length in relation to leg length [76]. Some laboratories have factored into their calculations the internal resistance of the ergometer and the inertia of the flywheel [28]. Others have focused on the Force–Velocity test (F–VT), a variant of the WAnT which optimises the braking force to determine optimised PP (e.g. [59]). However, if the braking force is increased to optimise PP it is likely to be too high to optimise MP. Increasing fatigue reduces the pedal cadence, affects the power-to-velocity ratio, and results in a lower MP. The ability to sustain power output as estimated by MP is an important component of success in many youth sports. Although the primary energy source of MP is anaerobic, its development in youth is a function of interplay between aerobic and anaerobic metabolism which is discussed later in this paper. Despite a range of methods precluding confident comparisons of the magnitude of individual WAnT data across studies, trends within studies are consistent and much of our understanding of the development of anaerobic fitness in youth is founded on data from the WAnT.
The optimum braking force for PP varies significantly with age [29] and physiologists using variants of the WAnT in long-term development programmes of youth athletes are advised to monitor anaerobic fitness through F–VTs (for PP) with separate customised 30 s tests for MP [3]. Data from unmodified WAnTs are, however, currently in regular use to monitor the development of anaerobic fitness in youth athletes whose sport requires very different muscle recruitment and motor patterns to those in cycling [3]. Correlations of WAnT data with high-intensity sport-related activities are low to moderate (r = 0.2–0.7) with trained youth athletes and not high enough to predict sport performance with confidence [3]. Youth sports involving running-related activities are more common than cycling and well-controlled maximal sprint running tests are more appropriate than cycling tests to estimate sports-related anaerobic fitness where body mass is transported rather than supported.
Lakomy [44] was the first to estimate the anaerobic fitness of adult athletes through maximal sprint running on a non-motorised treadmill (NMT) but it was van Praagh et al. [69] who introduced the technique to youth athletes. van Praagh et al. [69] restricted performance to 10 s sprints, only published their research in abstract form, and stopped further development due to safety concerns. It was Sutton et al. [64] who developed a laboratory-based, paediatric NMT test station incorporating a safety harness, which enabled 8-year-old children to safely produce maximal sprint performances over a 30s period. The typical error of NMT test data 1 week apart was reported as 5% for MP and 6% for PP, which compares very favourably with data from WanTs [76]. The paediatric NMT test station has been used successfully with 8–16-year-olds not only in tests of PP and MP [18] but also in studies of repeated sprint ability [53], recovery profiles from maximal intensity work [55], and simulated sport-related performance [52], but more research is required to explore its full potential in the physiological assessment and monitoring of youth athletes’ performance.
Anaerobic Fitness and Age
Cross-sectional studies of WAnT-determined anaerobic fitness are plentiful, at least over the age range 11–13-years, but the wide range of methodologies outlined earlier precludes confident comparisons of data across studies Age-related paediatric norms are available (e.g. [23]) but with the same flaws as those described for aerobic fitness. Youth athletes have been persistently reported to have higher anaerobic fitness than similarly aged non-athletes but as with aerobic fitness, this is likely to be through an amalgam of training [3, 8], genetics [61], and variation in the timing and tempo of biological maturation [45].
Collectively, cross-sectional studies are consistent in reporting age-related increases in PP in both sexes with little or no significant sex difference until ~ 13 years of age. Data on MP are less readily available but generally reflect the age- and sex-related trajectories of those for PP [23, 67]. To our knowledge there is only one published longitudinal study which reports the age-related PP and MP of both boys and girls, with at least three measures separated by time [16].
Duché et al. [33] published the first longitudinal study of PP and MP, but only reported data in ratio with body mass (i.e. in W/kg). In a mixed cross-sectional-longitudinal study, Falk and Bar-Or [34], reported the PP and MP of three groups of boys to increase with age over an 18 months period of study. Santos et al. [59] reported the optimised PP of 12-year-old boys and girls to increase with age over 18 months, with no significant sex difference. MP was not determined.
Figures 2 and 3 describe 763 (405 from boys) longitudinal measures of 11–17-year-olds’ PP and MP, respectively [16]. Longitudinal data provide a more informative analysis of anaerobic fitness than cross-sectional studies and show that PP and MP increase with age in both sexes. Boys’ mean PP and MP increase by ~ 120% and ~ 115%, respectively, from 11 to 17 years. Girls’ mean PP and MP increase by ~ 66% and ~ 60%, respectively, over the same age range. There is no significant sex difference at age 11 years in either PP or MP but girls’ mean PP and MP data begin to level-off from ~ 14 years and by age 17 years the sex difference is ~ 30% in both PP and MP. However as noted with aerobic data from the same participants (Fig. 1), the wide individual differences in age-related PP and MP and the overlap of boys’ and girls’ data particularly from ~ 11 to 14 years, clearly show the marked limitations of making age-related comparisons within and between sexes and within and across sports.

Figure drawn from data reported in Armstrong and Welsman [16] and founded on 763 Wingate anaerobic tests (405 from boys and 358 from girls)
Peak power in relation to age in 11–17-year-old boys and girls.

Figure drawn from data reported in Armstrong and Welsman [16] and founded on 763 Wingate anaerobic tests (405 from boys and 358 from girls)
Mean power in relation to age in 11–17-year-old boys and girls.
Development of Anaerobic Fitness with Growth and Maturation
Cross-Sectional Studies
Cross-sectional studies of PP and MP in ratio with body mass, report age-related increases in both sexes with the sex difference increasing with age [67, 76]. As explained in the complementary section on aerobic fitness, ratio-scaled data are fallacious and mislead understanding of developmental exercise physiology.
In two rigorously analysed cross-sectional studies. Doré et al. [30, 31] adopted an allometric model to investigate the contribution of morphological variables to the optimised PP of 605 (189 girls) 7–18-year-olds. They demonstrated that both estimated FFM and estimated lean leg volume (LLV) were more strongly related to PP than body mass in both sexes. They commented that FFM reflects the total active muscle mass including muscles (e.g. trunk muscles, arm muscles, gluteus maximus) which contribute to exercise performance in addition to muscles included in LLV, and recommended FFM as the preferred scaling factor in large investigations of anaerobic fitness.
Longitudinal Studies
As indicated earlier longitudinal studies of anaerobic fitness are sparse, two studies controlled for body mass using ratio scaling and, in accord with cross-sectional data reported boys’ PP and MP to increase with age [33, 34]. Santos et al. [59] determined on four occasions 6 months apart, the optimised PP of 17 boys and 15 girls aged 12.3 years at study onset. They analysed their data using multiplicative allometric modelling and reported no significant sex differences with a model controlling for body mass and sum of triceps and subscapular skinfolds as the best statistical fit for the data.
Armstrong and Welsman [16] used multiplicative allometric modelling to analyse the data illustrated in Figs. 2 and 3. They demonstrated that with age and body mass controlled for, there was a sex difference of ~ 10% in PP and ~ 11% in MP which reduced to ~ 5% and ~ 7%, respectively, when the sum of triceps and subscapular skinfolds was introduced to the models as a surrogate for FFM. For our current purpose the sex-specific models are presented in Tables 3 and 4, for boys and girls, respectively.
In direct contrast with the development of aerobic fitness and in both sexes, once body mass and age had been controlled for [Models 3.1 and 3.3 (boys) and 4.1 and 4.3 (girls)] the introduction of maturity status had no significant effect on either PP or MP. In both sexes, models founded on FFM were superior to those with body mass as the sole morphological variable, with age exerting a significant, additional effect in all models. In all cases the introduction of body mass and sum of skinfolds as a surrogate for FFM produced a better statistical fit for the data than FFM estimated from youth-specific equations and for brevity only these models are presented herein [i.e. Models 3.2 and 3.4 (boys) and 4.2 and 4.4 (girls)]. As described earlier in the complementary section on aerobic fitness, the powerful influence of maturation-driven FFM masks any independent effects of maturity status.
135 (72 boys) of the participants described in Figs. 2 and 3 also had their PP and MP determined annually through maximal sprint running on an NMT. The study confirmed the NMT test as an appropriate method to investigate the development of both PP and MP with a methodology which is more ecologically valid for many youth sports than cycling. Absolute values of PP and MP (in W) were not comparable across ergometers but the multiplicative allometric models were remarkably similar with FFM being the most powerful morphological influence on both MP and PP in both sexes and on both ergometers, with age exerting a significant additional effect in all models [18].
The multiplicative allometric models consistently emphasise the importance of increases in FFM (representing increases in active muscle mass) in the development of both PP and MP. Active muscle mass varies with running and cycling and relative changes in magnitude have not been rigorously monitored and quantified through adolescence, although total muscle mass has been estimated to increase from 11 to 17 years by ~ 110% in boys and ~ 60% in girls [46]. Technological and ethical limitations have restricted intra-muscular investigations during maximal intensity exercise but the influence of age and maturation-driven increases in FFM on PP and MP encompass changes not only in active muscle mass but also in muscle structure, muscle metabolism, muscle fibre size, type, and activation, and neuromuscular coordination. These factors and their effects on the development of anaerobic fitness have been comprehensively reviewed elsewhere [7, 68, 76], as has their trainability in youth [3].
Anaerobic and Aerobic Fitness
Relationship Between the Development of Anaerobic and Aerobic Fitness
Coaches have noted for many years that during childhood and early adolescence, those who excel in predominantly “anaerobic” activities also excel in “aerobic” activities and Bar-Or [22] introduced the term “non-metabolic specialists” to describe the phenomenon. The present data suggest that this relationship is not one of non-metabolic specialism but can be explained by the strong, common influence of age and FFM on both aerobic and anaerobic fitness.
Peak \( {{\text{V}}\text{O}}_{2} \), PP, and MP all increase during youth but despite their common relationship with FFM, their rate of development appears asynchronous. The data illustrated in Figs. 1, 2 and 3 are from the same young people and show that there is a greater percentage increase in anaerobic fitness than in aerobic fitness from 11 to 17 years, in both sexes. Appropriate intra-muscular data are sparse and often collected at rest rather than during high intensity exercise, but the balance of evidence indicates that several changes advantageous to anaerobic fitness occur later during growth and maturation than those promoting aerobic fitness. Changes include increases in muscle pennation angle, type 2 muscle fibre activation, muscle phosphocreatine stores, muscle glycogen stores, and intra-muscular anaerobic enzyme activity [3, 6, 7].
Interplay of Anaerobic and Aerobic Metabolism in Youth Sport
Performance in youth sport almost always involves an interplay between anaerobic and aerobic metabolism which depends upon the intensity and duration of the activity and the individual’s developmental physiology, modulated by training status. The ability to quickly attain high power output and retain much of it for a sustained period is an important component of many youth sport-related activities. In many sports the contribution of different energy pathways to performance is complex and difficult to evaluate. However, MP determined over 30 s and conventionally classified as a measure of anaerobic fitness, provides a clear example of the interaction between anaerobic–aerobic energy interplay and developmental physiology.
To examine the anaerobic–aerobic interplay during high intensity exercise in youth, the peak \( {{\text{V}}\text{O}}_{2} \) and MP of 135 (63 girls) of the 11–16-year-olds described in Figs. 1, 2 and 3 were determined annually on a cycle ergometer and a treadmill. Multiplicative allometric models confirmed FFM as the most powerful morphological influence on MP, regardless of whether MP was determined on a cycle ergometer or a treadmill. However, when ergometer-specific peak \( {{\text{V}}\text{O}}_{2} \) was entered into the appropriate models it made a significant, additional contribution to FFM in explaining the development of MP, in both sexes, on both ergometers. The models including peak \( {{\text{V}}\text{O}}_{2} \) presented a significantly better statistical fit to the data than FFM alone and clearly illustrated how developmental changes in peak \( {{\text{V}}\text{O}}_{2} \) contribute to explaining developmental changes in MP [13, 18].
Conclusions
Understanding of the development of anaerobic and aerobic fitness in youth has been clouded by fallacious ratio scaling of physiological variables with body mass. A multiplicative allometric approach applied to longitudinal data has demonstrated that in both sexes peak \( {{\text{V}}\text{O}}_{2} \), PP, and MP increase with age but the most powerful influence on the development of both anaerobic and aerobic fitness is FFM. Increases in FFM encompass the effects of maturation on anaerobic and aerobic fitness as changes in FFM are strongly related to the timing and tempo of maturation. The rate of development of anaerobic and aerobic fitness is asynchronous, probably due to intra-muscular changes which promote anaerobic fitness occurring later in development than those promoting aerobic fitness. Most sport-related activities are supported by an anaerobic–aerobic energy interplay which depends not only on the intensity and duration of the activity but also on the relative development of aerobic and anaerobic fitness.
Those involved with the identification, long-term development, performance, and physiological testing of youth athletes are strongly advised to reject ratio scaling of physiological variables with body mass and focus on appropriate analyses of the concurrent effects of age and maturation-related changes in FFM. FFM can be monitored through a combination of body mass and sum of triceps and subscapular skinfold thicknesses. The multiplicative allometric equations presented herein can be used to estimate the peak \( {{\text{V}}\text{O}}_{2} \), PP, and MP of healthy youth for comparative purposes but similar longitudinal studies of sex-specific groups of elite youth athletes are required to better inform long-term athlete development programmes.
Availability of Data and Material
No unpublished data in review. All original sources cited.
References
Aitkin M, Anderson D, Hinde J. Statistical modelling of data on teaching styles. J R Stat Soc A. 1981;144(4):148–61.
Armstrong N. Top 10 research questions related to youth aerobic fitness. Res Q Exerc Sport. 2017;88(2):130–48.
Armstrong N. Development of the youth athlete. Oxford: Routledge; 2019. p. 1–250.
Armstrong N, Barker AR. Endurance training and elite young athletes. Med Sport Sci. 2011;56:59–83.
Armstrong N, Barker AR. Physiological monitoring of elite young athletes. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 527–37.
Armstrong N, Barker AR, McManus AM. Muscle metabolism changes with age and maturation. How do they relate to youth sport performance? Br J Sports Med. 2015;49(13):860–4.
Armstrong N, Barker AR, McManus AM. Muscle metabolism during exercise. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 69–87.
Armstrong N, McManus AM, editors. The elite young athlete. Basel: Karger; 2011. p. 1–205.
Armstrong N, McManus AM. Aerobic fitness. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 161–80.
Armstrong N, Tomkinson GR, Ekelund U. Aerobic fitness and its relationship to sport, exercise training and habitual physical activity during youth. Br J Sports Med. 2011;45(11):859–65.
Armstrong N, Welsman J. Assessment and interpretation of aerobic fitness in children and adolescents. Exerc Sport Sci Rev. 1994;22(1):435–76.
Armstrong N, Welsman J. Aerobic fitness: what are we measuring? Med Sport Sci. 2007;50:5–25.
Armstrong N, Welsman J. Development of peak oxygen uptake from 11–16 years determined using both treadmill and cycle ergometry. Eur J Appl Physiol. 2019;119(3):801–12.
Armstrong N, Welsman J. Sex-specific longitudinal modeling of youth peak oxygen uptake. Pediatr Exerc Sci. 2019;31(2):204–12.
Armstrong N, Welsman J. Multilevel allometric modelling of maximal stroke volume and peak oxygen uptake in 11–13-year-olds. Eur J Appl Physiol. 2019;119(11–12):2629–39.
Armstrong N, Welsman J. Sex-specific longitudinal modelling of short-term power in 11–18-year-olds. Med Sci Sport Exerc. 2019;51(5):1055–63.
Armstrong N, Welsman J. Multilevel allometric modelling of maximum cardiac output, maximum arteriovenous oxygen difference, and peak oxygen uptake in 11-13-year olds. Eur J Appl Physiol. 2020;120(2):527–37.
Armstrong N, Welsman J, Bloxham SR. Development of 11-to 16-year-olds’ short-term power output determined using both treadmill running and cycle ergometry. Eur J Appl Physiol. 2019;119(7):1565–80.
Armstrong N, Welsman JR, Kirby BJ. Peak oxygen uptake and maturation in 12-year-olds. Med Sci Sports Exerc. 1998;30(1):165–9.
Armstrong N, Welsman JR, Nevill AM, Kirby BJ. Modeling growth and maturation changes in peak oxygen uptake in 11–13 yr olds. J Appl Physiol. 1999;87(6):2230–6.
Åstrand PO. Experimental studies of physical working capacity in relation to sex and age. Copenhagen: Munksgaard; 1952. p. 103–23.
Bar-Or O. Pediatric sports medicine for the practitioner. New York: Springer; 1983. p. 1–65.
Bar-Or O, Rowland TW. Pediatric exercise medicine. 2nd ed. Champaign: Human Kinetics; 2004. p. 3–59.
Barker AR, Armstrong N. Exercise testing elite young athletes. Med Sport Sci. 2011;56:106–25.
Barker AR, Williams CA, Jones AM, Armstrong N. Establishing maximal oxygen uptake in young people during a ramp test to exhaustion. Br J Sports Med. 2011;45(6):498–503.
Baxter-Jones ADG, Mirwald RL, McKay HA, Bailey DA. A longitudinal analysis of sex differences in bone mineral accrual in healthy 8-19-year-old boys and girls. Ann Hum Biol. 2003;30(2):160–75.
Bongers BC, van Brussel BC, Hulzebos EHJ, Takken T. Pediatric norms for cardiopulmonary exercise testing in relation to sex and age. 2nd ed. Uitgeverij: Box Press; 2014. p. 1–200.
Chia M, Armstrong N, Childs D. The assessment of children’s anaerobic performance using modifications of the Wingate anaerobic test. Pediatr Exerc Sci. 1997;9(1):80–9.
Doré E, Bedu M, Franca NM, Diallo O, Duché P, van Praagh E. Testing peak cycle performance: effects of braking force during growth. Med Sci Sports Exerc. 2000;32(2):493–8.
Doré E, Bedu M, Franca NM, van Praagh E. Anaerobic cycling performance characteristics in prepubescent, adolescent and young adult females. Eur J Appl Physiol. 2001;84(5):476–81.
Doré E, Diallo O, Franca NM, Bedu M, van Praagh E. Dimensional changes cannot account for all differences in short-term cycling power during growth. Int J Sports Med. 2000;21(5):360–5.
Dotan R, Mitchell C, Cohen R, Klentrou P, Gabriel D, Falk B. Child-adult differences in muscle activation—a review. Pediatr Exerc Sci. 2012;24(1):2–21.
Duché P, Falgairette G, Bedu M, Fellmann N, Lac R, Coudert J. Longitudinal approach of bio-energetic profile in boys before and during puberty. In: Coudert J, Van Praagh E, editors. Pediatric work physiology. Paris: Masson; 1992. p. 43–55.
Falk B, Bar-Or O. Longitudinal changes in peak aerobic and anaerobic mechanical power of curcumpubertal boys. Pediatr Exerc Sci. 1993;5(4):318–23.
Falk B, Dotan R. Measurement and interpretation of maximal aerobic power in children. Pediatr Exerc Sci. 2019;31(2):144–51.
Falk B, Klentrou P, Armstrong N, Rowland T, Kemper HCG. A brief history of pediatric exercise physiology. Pediatr Exerc Sci. 2018;30(1):1–10.
Ferri-Morales A, Nascimento-Ferreira MV, Vlachopoulos D, Ubago-Guisado E, Torres-Costoso A, De Moraes ACF, Barker AR, Moreno LA, Martínez-Vizcaino V, Gracia-Marco L. Agreement between standard body composition methods to estimate percentage of body fat in young male athletes. Pediatr Exerc Sci. 2018;30(3):402–10.
Geithner CA, Thomis MA, Vanden Eynde B, Maes HH, Loos RJ, Peeters M, Claessens AL, Vlietinck R, Malina RM, Beunen GP. Growth in peak aerobic power during adolescence. Med Sci Sports Exerc. 2004;36(9):1616–24.
Goran M, Fields DA, Hunter GR, Herd SL, Weinster RL. Total body fat does not influence maximal aerobic capacity. Int J Obes. 2000;24(7):841–8.
Inbar O, Bar-Or O, Skinner JS. The Wingate anaerobic test. Champaign: Human Kinetics; 1996. p. 1–108.
Janz KF, Burns TL, Witt JD, Mahoney LT. Longitudinal analysis of scaling \( {\dot{\text{V}}\text{O}}_{2} \) for differences in body size during puberty: the Muscatine study. Med Sci Sports Exerc. 1998;30(9):1436–44.
Kemper HCG, editor. Growth, health and fitness of teenagers. Basel: Karger; 1985. p. 1–202.
Krahenbuhl S, Skinner JS, Kohrt WM. Developmental aspects of maximal aerobic power in children. Exerc Sports Sci Rev. 1985;13(1):503–38.
Lakomy HKA. The use of a non-motorized treadmill for analysing sprint performance. Ergonomics. 1987;30(4):627–37.
Malina RM. The influence of physical activity and training on growth and maturation. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 441–54.
Malina RM, Bouchard C, Bar-Or O. Growth, maturation, and physical activity. 2nd ed. Champaign: Human Kinetics; 2004. p. 1–710.
McNarry MA, Armstrong N. Aerobic trainability. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 465–75.
Mirwald RL, Bailey DA. Maximal aerobic power. London: Sports Dynamics; 1996. p. 1–80.
Mountjoy M, Andersen LB, Armstrong N, Biddle S, Boreham C, Bedenbeck HP, Ekelund U, Engebretsen L, Hardman K, Hills A, Kahlmeier S. International Olympic Committee Consensus Statement on the Health and Fitness of Young People Through Physical Activity and Sport. Br J Sport Med. 2011;45(11):839–48.
Morse M, Schlutz FW, Cassels DE. Relation of age to physiological responses of the older boy to exercise. J Appl Physiol. 1949;1(10):683–709.
Nevill AM, Holder RL, Baxter-Jones A, Round JM, Jones DA. Modelling developmental changes in strength and aerobic power in children. J Appl Physiol. 1998;84(3):963–70.
Oliver JL, Armstrong N, Williams CA. Reliability and validity of a soccer-specific test of prolonged repeated sprint ability. Int J Sports Physiol Perform. 2007;2(2):137–49.
Oliver JL, Williams CA, Armstrong N. Reliability of a field and laboratory test of repeated sprint ability. Pediatr Exerc Sci. 2006;18(3):339–50.
Rasbash J, Steel F, Browne WJ, Goldstein H. A user’s guide to MLwiN version 3.02. Bristol: University of Bristol Centre for Multilevel Modelling; 2018.
Ratel S, Williams CA, Oliver J, Armstrong N. Effects of age and mode of exercise on power output profiles during repeated sprints. Eur J Appl Physiol. 2004;92(–2):204–10.
Robinson S. Experimental studies of physical fitness in relation to age. Arbeitsphysiologie. 1938;10:251–323.
Roemmich JN, Clark PA, Weltman A, Rogol AD. Alterations in growth and body composition during puberty. I. Comparing multicompartment body composition models. J Appl Physiol. 1997;83(3):927–35.
Rowland TW. Cardiovascular function. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 147–59.
Santos AMC, Welsman JR, De Ste Croix MBA, Sharp P, Armstrong N. Optimal peak power in relation to age, sex and thigh muscle volume. Pediatr Exerc Sci. 2003;15(4):405–17.
Schutte N, Bartels M, de Gues EJC. Genetics of physical activity and physical fitness. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 293–302.
Simoneau J-M, Bouchard C. The effects of genetic variation on anaerobic performance. In: van Praagh E, editor. Pediatric anaerobic performance. Champaign: Human Kinetics; 1998. p. 5–21.
Slaughter MH, Lohman TG, Boileau R, Horswill CA, Stillman RJ, VanLoan MD, Bemben DA. Skinfold equations for estimation of body fatness in children and youth. Hum Biol. 1988;60:709–23.
Stavnsbo M, Resaland GK, Anderssen SA, Steene-Johannessen J, Domazet SL, Skrede T, Sardinha LB, Kriemler S, Ekelund U, Andersen LB, Aadland E. Reference values for cardiometabolic risk scores in children and adolescents: suggesting a common standard. Atherosclerosis. 2018;278:299–306.
Sutton NC, Childs DJ, Bar-Or O, Armstrong N. A non-motorized treadmill test to assess children’s short-term power output. Pediatr Exerc Sci. 2000;12(1):91–100.
Tanner JM. Fallacy of per-weight and per-surface area standards and their relation to spurious correlation. J Appl Physiol. 1949;2(1):1–15.
Tanner JM. Growth at adolescence. 2nd ed. Oxford: Blackwell; 1962. p. 28–39.
van Praagh E. Development of anaerobic function during childhood and adolescence. Pediatr Exerc Sci. 2000;12(2):150–73.
van Praagh E, Doré E. Short-term muscle power during growth and maturation. Sports Med. 2002;32(11):701–28.
van Praagh E, Fargeas MA, Leger L, Fellmann N, Coudert J. Short-term power output in children measured on a computerized treadmill ergometer (Abstract). Pediatr Exerc Sci. 1993;5:482.
Vanderburgh PM, Mahar MT, Chou CH. Allometric scaling of grip strength by body mass in college-age men and women. Res Q Exerc Sport. 1995;66(1):80–4.
Welsman J, Armstrong N. Statistical techniques for interpreting body size-related exercise performance during growth. Pediatr Exerc Sci. 2000;12(2):112–27.
Welsman J, Armstrong N. Interpreting performance in relation to body size. In: Armstrong N, editor. Paediatric exercise physiology. Edinburgh: Churchill Livingstone; 2007. p. 27–46.
Welsman J, Armstrong N. Scaling for size: relevance to understanding the effects of growth on performance. In: Hebestreit H, Bar-Or O, editors. The young athlete. Oxford: Blackwell Scientific; 2008. p. 50–62.
Welsman J, Armstrong N. Interpreting aerobic fitness in youth: the fallacy of ratio scaling. Pediatr Exerc Sci. 2019;32(2):184–90.
Welsman J, Armstrong N, Kirby BJ, Nevill AM, Winter EM. Scaling peak \( {\dot{\text{V}}\text{O}}_{2} \) for differences in body size. Med Sci Sports Exerc. 1996;28(2):259–65.
Williams CA, Ratel S. Maximal intensity exercise. In: Armstrong N, van Mechelen W, editors. Oxford textbook of children’s sport and exercise medicine. 3rd ed. Oxford: Oxford University Press; 2017. p. 105–20.
Funding
None.
Author information
Authors and Affiliations
Contributions
Both authors contributed to the drafting of the manuscript. Both authors reviewed and approved the final version.
Corresponding authors
Ethics declarations
Conflict of interest
The author(s) declare that they have no competing interests.
Code availability
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Armstrong, N., Welsman, J. The Development of Aerobic and Anaerobic Fitness with Reference to Youth Athletes. J. of SCI. IN SPORT AND EXERCISE 2, 275–286 (2020). https://doi.org/10.1007/s42978-020-00070-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42978-020-00070-5