Introduction

One of the most easily comprehensible of measurable variables in any defined area is the area’s species density (i.e. the total number of species in that area, often referred to loosely as “species richness”). This measure is understood by a range of stakeholders, and particularly among the conservation community. It is the common currency of debate in this area and often used by policymakers (Thompson & Starzomski, 2007). There is therefore a strong and completely understandable desire to estimate the total number of species in local species pools even when there is neither enough time nor resources to produce complete species inventories (Colwell et al., 2004).

A well-established and popular way of estimating total species pools from subsamples is using nonparametric estimators (Colwell & Elsensohn, 2014). These statistical methods rely on expected properties (and proposed underlying distributions) of the relative abundances of biological assemblages (Colwell et al., 2012). In particular, many of the methods attempt to estimate totals from the numbers of “incidence-of-one” species (occurring in only one sample/site) and “incidence-of-two” species (species that occur only in two samples/sites). (Melo, 2004).

These are standard methods and have been used extensively in terrestrial invertebrate studies, both when the assemblage is poorly studied, from tropical regions (e.g. Anderson & Ashe, 2000; Stork & Grimbacher, 2006), and also where the natural history of the species concerned is moderately well known, whether taken from the taxonomic literature (e.g. Jones et al., 2009) or from field samples (Anderson & Ashe, 2000; Jones et al., 2009; Odegaard, 2004; Southwood et al., 2004; Stork & Grimbacher, 2006; Summerville & Crist, 2004; Toti et al., 2000). Generally, however, no specific information is provided on the biology of individual species.

One of the largest hurdles to these estimates is the difficulty of measuring the number of truly rare species in a set of samples taken from the field. This problem is compounded in some taxa by ‘tourists’: species that have no intimate association with the area studied and are just passing through or resting temporarily (Odegaard, 2004). In most cases, these species will be rarely encountered and so without detailed knowledge of the environmental tolerances and habitat preferences of individual species, they will be mistakenly counted as rare ‘residents. Rare tourists are therefore potentially a source of bias in estimates of the size of species pools.

Here, we examine this problem using a case study from a ten-year longitudinal study of adult beetles from a southern English woodland. We reviewed beetles in a single self-contained stratum—the leaf litter. We show that extrapolated species density estimates that include species that are known not to be habitual occupants of the litter stratum are strongly biased and that paradoxically the bias increases with increased sampling. This re-emphasises the importance of understanding the autecology of species in community studies.

Methods

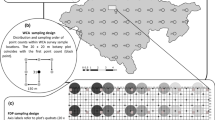
Whitley Wood is an old-growth semi-natural woodland situated in the New Forest, Hampshire, UK (OS grid ref. SU 299 056, [50_510 300 N, 1_ 340 4100 W].). It is classified as a W10 Quercus robur—Pteridium aquilinum—Rubus fruticosus woodland under the National Vegetation Classification (NVC) (Rodwell, 1991) and has two codominant tree species, oak (Quercus robur) and beech (Fagus sylvatica), and a varied understorey of hawthorn (Crataegus monogyna) and field maple (Acer campestre). The ground flora is patchy but includes bracken (Pteridium aquilinum), bramble (Rubus fruticosus agg), common dog violet (Viola riviniana) and wood spurge (Euphorbia amygaloides). The wood, like many of those in the New Forest, is browsed by ponies (Tubbs, 2001).

We sampled every month for ten years, from March 2002 to February 2012 in a ~ 2 ha area of Whitley Wood. Each month we placed a 100 m transect line at random within the area (in a different position within the 2 ha each month) and sampled at fifteen points at 7 m intervals along each monthly transect. Although this was a relatively small area, we believe it to be representative of the wood as a whole. At each sampling point, we extracted invertebrates from leaf litter. We placed sieved leaf litter from a 1 m2 quadrat into Winkler bags for three days (Krell et al., 2005). From these samples, adult beetles were identified as species (by JS [year 1–6], and SH [year 7–10]. Data from each transect were pooled and each transect was treated as a single temporal replicate, as in earlier studies (Eggleton et al., 2009).

Tourists were defined as species that, from their known autecology, are not habitual occupants of the litter stratum. We further split the tourists into (1) ‘stratum tourists’ that are found inside the woodland habitat but are not habitual residents within the litter, and (2) ‘habitat tourists’ that are not found in the same habitat (i.e. woodland) in any stratum. These definitions are not easy to apply to all species in our samples and we made the following distinctions: (1) we did not include any species that over-wintered within the woodland (e.g. a few Coccinellidae, such as Adalia decapunctatum) as residents as we could not be certain that they might not overwinter in a number of other strata or habitats, (2) we excluded aquatic beetles that are not known to inhabit leaf litter even though it is possible that some of them might have been associated with waterlogged leaf litter in the woodland. We did not exclude known wet litter specialists, such as Cyphon padi (Scirtidae), or Cercyon pygmaeus (Hydrophilidae). A list of the classifications of the species is given in the supporting information, along with general natural history information (see S1).We were conservative in our classification, treating rare species as residents unless we have strong evidence to the contrary, as it would have been circular to base status on rarity. Many of the species are just defined in the literature as “predators of mesofauna” or having a “range of terrestrial habitats including litter”. We classified all of these as residents (see S1, which also has total incidence counts for the ten-year period for each species).

The equations

The following (incidence-based) formulas are used in this paper:

Chao:

$${S}_{p}={S}_{o}+\frac{{f}_{1}^{2}}{{2f}_{2}}$$

First-order jackknife:

$${S}_{p}={S}_{o}+{f}_{1 }\frac{N-1}{N}$$

Second-order jackknife:

$${S}_{p}={S}_{o}+{f}_{1 }\frac{2N-3}{N}+{f}_{2 }\frac{{(N-2)}^{2}}{N(N-1)}$$

Bootstrap:

$${S}_{p}= {S}_{o }+ \sum_{i=1}^{{S}_{o}}{(1-{p}_{i})}^{N}$$

where Sp is the extrapolated richness in a pool, \({S}_{o}\) is the observed number of species in the collection, \({f}_{1}\) and \({f}_{2}\) are the number of species occurring only in one or only in two samples in the collection (referred to here as “incidence-of-one” and “incidence-of-two” species, respectively), \({p}_{i}\) is the frequency of species i, and N is the number of samples in the collection.

The first-order jackknife estimator therefore relies on the number of species found in one sample only (f(1), above). The Chao and second-order jackknife estimator rely on the number of species found in one (f(1)) and two (f(2)) samples only. In contrast, the bootstrap relies on the relative frequency distribution of the species in all samples. We used these estimators as they are commonly used and rely on the availability of presence-absence data, rather than count data, and are therefore more likely to be of general interest. Count data can be used to calculate some estimators (e.g. the Chao estimator for counts), but not the jackknife or bootstrap used here. Initial analyses with the count data gave essentially the same results for the Chao estimator with the incidence data (417 for the total species list for the count data, as against the 433 ± 33 estimated for the incidence data, well within the confidence limit range (Table 1).

Table 1 Results of extrapolations at three different levels. All = all species sampled in leaf litter; Habitat = all species with habitat tourists removed (i.e. stratum tourists + residents); Residents = strict leaf litter residents with habitat and stratum tourists removed
Full size table

The extrapolated estimates were all calculated using the specpool command in the vegan package (Oksanen, Blanchet et al. 2018) in R (R Core Team 2017). Each of the four estimator methods was used for the whole dataset, with stratum tourists removed, and with compartment and habitat tourists removed (thus we obtained 12 estimates).

Note that these are by no means the only extrapolation methods used in ecological research. Melo et al (2004) discuss several methods, generally using different models to fit curves on to count data. We did not use these here as they will all be equally biased by treating tourists as residents as the nonparametric estimators. We chose the nonparametric estimators as they are widely used and straightforward to calculate and they explicitly use incidence data. Incidence data are generally more common and easier to obtain than count data.

We constructed species accumulation curves, obtained using specaccum in the R package vegan, method = “random”—the sites are added in a random order (with 10,000 permutations to produce standard errors). We produced curves for all three of the residency classes (residents, residents + stratum tourists, residents + stratum tourists + habitat tourists).

Results

There were 36,687 individuals sampled during the 10-year study period from 1800 m2 samples. The total numbers of sampled species per residence category were: all species, 295; litter residents, 193; stratum tourists, 75; and habitat tourists, 35. The species accumulation curves show the effects of excluding or including the different sorts of tourists (Fig. 1). The incidences ranged from 120 (Acrotrichis intermedia agg [Ptiliidae], sampled in every month, for a total of 23,821 individuals) to one (112 species had an incidence of one). The relative abundance distribution was far more even for the resident species than for the tourist species (data in S2), with species generally far less abundant: the most abundant species for the habitat tourists was Aphthona atrocaerulea (Chrysomelidae), usually found as a herbivore on garden spurges, and for the stratum tourists was Orchestes fagi, (Curculionidae), a common herbivore of beech leaves.

Fig. 1
figure 1

Sample-based species accumulation curves, showing the difference in trajectory across the ten years of sampling between the total dataset (black lines), the woodland-specific dataset (red line), and the leaf litter-specific dataset (blue line). The vertical bars indicate standard errors from 10,000 permutations

Full size image

The species accumulation plots from the resident list give a total figure of ~ 200 resident, litter-inhabiting, species sampled in the Whitley Wood plot during the ten years (120 months) of sampling. This is a conservative estimate as we only sampled for ten years, so extremely occasional residents are potentially not included, although we have included incidence-of-one species as residents if they are not definitely non-litter inhabitants.

All extrapolations of total size of leaf litter beetle assemblage in Whitley Wood showed large overestimates if both sorts of tourists were included, or if only stratum tourists were included with litter residents (Table 1).

One-hundred-and-twelve species were found only in one sample (“incidence-of-one” species), 92% of those were singletons (i.e. there was only a single specimen). Forty-four species were found only in two samples and 86% were represented by a single specimen in each of the two samples (i.e. two individuals in total). Of the incidence of one species, 41% were tourists, while of the incidence of two species 32% were tourists.

Discussion

All four of the estimators gave much large estimates when tourists were not excluded from the dataset, compared with when they were. The calculations for the Chao estimators show clearly why this occurs. The f(1) component is overestimated by about two-thirds and the f(2) component is overestimated by about a half. These errors make an accurate estimate extremely problematic.

The mistaken assignment of tourists as residents is clearly a serious problem (e.g. (Odegaard, 2004)) when estimating missing species numbers in biodiversity samples containing highly vagile insects. Just thinking in terms of the litter stratum alone, after ten years of sampling, the tourist species (both stratum and habitat tourists) double the estimate of the total litter species pool.

A fundamental problem is that while both the total number of potential residents and tourists have a finite limit, the residents may be some 200 + species, while the total potential tourist pool is the UK beetle pool, ca. 4,000 species (Duff et al., 2012). This implies that the more sampling one does without filtering out tourists then the disproportionally higher the rates of overestimation of the total litter pool.

There is a possibility, even in such a large dataset, that we could have missed new colonisers of the woodland (i.e. new residents, due to species range shifts caused by, for example, climate change). We examined the species that occurred only in the later months of the series (Only from 2010 onwards). Of the 26 species in this category, 19 (73%) were classified as residents, four as stratum tourists (15%) and three as habitat tourists (12%). In this case, the tourists of both types were known to not be found in the leaf litter. As for the residents, there were several species that were relatively abundant and therefore appear to have colonised the wood (Mocyta negiligens (Staphylinidae) and Leiodes litura (Leiodidae), being the clearest examples). Using our conservative criteria, we recognised all these as residents and so there is no evidence of unidentified colonising rare residents causing errors in our analysis.

The overall conclusion of this analysis is that the estimation of total species pools for Coleoptera in the litter stratum is strongly constrained by our biological knowledge of the species found in that stratum. In most other regions, particularly in the tropics, where the biology of individual species is much less well known, the ability to separate, even approximately, the tourists from the residents will be far more limited, especially when the data is taken from only a few strata. This may well lead to serious overestimations of the total species pool in strata from both the original counts of numbers of species and, even more so, from extrapolations. We suggest that when such natural history data are sparse that nonparametric estimations of beetles (and by extension other freely flying insects) within well-defined strata should be approached with caution, as such estimates will, at best, be extremely inaccurate estimates of whole insect taxa or faunas.

The percentage number of singletons decline faster in the resident only dataset but stabilise at about 17%, suggesting the existence of some genuinely rare residents but at about half of the number found in the complete dataset after ten years.

The Chao (and other) estimators are undoubtedly useful in providing comparable ecological data when sampling effort differs. There is good evidence that the Chao estimator can also be successful at extrapolating species pools on a global or a regional scale (e.g. for marine biodiversity, (Tittensor et al., 2010). Ugland & Gray (2004) used simulations of marine organisms to argue that the Chao estimator will only be accurate at large sample sizes and that at low sample sizes it will seriously underestimate total species pools. (Coddington et al., 2009) used spiders in a tropical rain forest to reach similar conclusions, as does (Melo et al., 2004) using a range of real datasets. Our results suggest almost the opposite—that the Chao estimator will only yield accurate estimates when samples sizes are moderately low, and then perhaps only by chance. However, the other authors were envisaging estimating the species richness of a large species pool, with no tourists, where the number of observed rare species (i.e. of incidence one or two) declines with sample size. This is the equivalent of, say, predicting the species richness of the whole of the New Forest from Whitley Wood leaf litter data, which would, as it only deals with one stratum, of course, lead to a large underestimate. A similar problem with beetle in pitfall traps was noted by Southwood (1996).

This effect might be mitigated to some degree in multi-stratum estimates of habitat species pools where ‘stratum tourists’ would still contribute to the required habitat-level species pools. A properly designed multi-stratum sampling programme within a habitat will not remove the problem of the “true tourists”, but will improve the species density estimate for the habitat as a whole (so, for example, the inventory work undertaken in Panama Basset et al., 2012). However, sampling the litter stratum alone would clearly be an unreliable way to estimate the size of the total species pool within an entire habitat. We can only conclude that in these circumstances the estimates of leaf litter species richness must be treated either as (a) gross overestimates of numbers of beetles in the leaf litter stratum, or (b) large underestimates of number of species in larger pools (in this case within habitat or between-habitats). The best way to estimate regional species pools is by counting them directly. But this means knowing a lot more about the natural history of the species than we usually have. In the absence of species-level knowledge, we cannot know about any individual species found in a particular stratum. This argues for comprehensive sampling across multiple strata where natural history information is limited. When knowledge is limited there is always a limit to what we can find out by increasing sampling.

In addition, excluding singletons, which is sometimes resorted to ‘tidy up the data’ (particularly when considering compositional data, e.g. (Chen et al., 2011)) will clearly not work here, because (1) it would render nonparametric estimates meaningless as they all rely on estimates of single incidence species; and (2) there are singleton species that are clearly residents. There is no obvious way out of this double bind, except by separating the residents explicitly from the tourists.

As this study is intensive, but only for a single site, this does not give a definitive result. However, it is a case study that indicates some pitfalls of the nonparametric extrapolation approach. We believe that it is applicable to any site or sites where the natural history of the studied species is well known and where highly dispersive species lead to the problem of tourists. However, here may be relatively few areas, even in Western Europe, that have such comprehensive longitudinal data (10 years, sampled at consecutive monthly intervals) and so it is not possible to produce directly comparable data for context. However, we feel that this problem will apply anywhere where dispersive insects are found commonly in samples. This may not apply to wingless relatively sessile groups, such as earthworms and myriapods.

Nonparametric estimators of species richness are mathematically sound and potentially biologically revealing but may often be problematic in practice. Given that we have established that applying such estimators will compound any errors in the existing samples and that such errors are common there seems to be no compelling reason to quote anything except the observed species numbers when dealing with dispersive organisms that move long distances from patch to patch. This is because these will, in many cases, be a better estimate of total species density than any nonparametric estimator. Even more profitable would be more intensive research on the natural history and (micro-)habitat preferences of individual species within any given community, which has been undervalued as an endeavour (Able, 2016). In cases where this is not immediately possible, the estimators will be useful comparatively, but it is important to realise that they are not necessarily accurate.