Applications of Choquet expected utility to hypothesis testing with incompleteness

Abstract

The Maximin and Choquet expected utility theories guide decision-making under ambiguity. We apply them to hypothesis testing in incomplete models. We consider a statistical risk function that uses a prior probability to incorporate parameter uncertainty and a belief function to reflect the decision-maker’s willingness to be robust against the model’s incompleteness. We develop a numerical method to implement a test that minimizes the risk function. We also use a sequence of such tests to approximate a minimax optimal test when a nuisance parameter is present under the null hypothesis.

1 Introduction

Economic models may make incomplete predictions when the researcher works with weak assumptions. For example, in a discrete game, the researcher may not know the precise form of the information the players have access to, even if the researcher’s theory may fully describe the primitives of the game. Or the theory may be silent about how an equilibrium gets selected when multiple equilibria exist. In such settings, the model’s prediction is essentially the set of outcome values the incomplete theory allows. This paper considers models with set-valued predictions of the following form:

$$\begin{aligned} Y\in G(U|X;\theta ), \end{aligned}$$

(1)

where Y is an outcome variable, G is a weakly measurable correspondence that maps the observable and unobservable characteristics (X, U) and a parameter $\theta$ to a set of permissible outcome values. This structure is commonly seen across different areas of applications. Examples include discrete choices with an unknown choice set, dynamic discrete choice models, matching, network formation, and voting models (see Molinari, 2020, and references therein). This paper considers a statistical decision problem in such an environment.

The researcher is willing to choose an optimal action based on data and their incomplete theory. A noteworthy feature is that the researcher faces three types of uncertainty: sampling, parameter, and “selection”. The first two are standard in the statistical decision theory (Wald, 1939, 1945). As such, we treat them using Wald’s framework. The selection uncertainty is specific to incomplete models. The theory does not provide further information on how Y is selected from G. A possible approach is to parameterize the selection and treat it as a subcomponent of the parameter vector. Existing papers adopt parametric and nonparametric versions of this “completion” approach.¹ While the approach makes the problem tractable, it is not always straightforward to parameterize the selection because it often represents complex objects such as information structure in games (Magnolfi & Roncoroni, 2022), an initial condition in dynamic choices (Honoré & Tamer, 2006), unobserved choice set formation processes (Barseghyan et al., 2021), and so on. This paper considers a complementary robust approach. We construct robust statistical decision rules by borrowing insights from the Maximin and Choquet expected utility theories and their applications to incomplete models. In particular, the belief function expected utility allows us to encode the researcher’s lack of understanding of the selection. This approach is in line with the econometrics literature (Manski, 2003; Tamer, 2010; Molinari, 2020) that seeks partial identification and inference methods that do not require further assumptions on the incomplete parts of the model.

We define a statistical risk that incorporates the three types of uncertainty. We further demonstrate the key components of the statistical risk can be represented by the Choquet integrals of tests with respect to a belief function and its conjugate. Belief functions are Choquet capacities (or non-additive measures) that can capture a decision-maker’s perception of uncertainty when she cannot assign a unique probability but can assign an interval-valued assessment. They were introduced to the statistics literature by Dempster (1967) and Shafer (1982) as functions that summarize the “weight of evidence” for events. The belief function is also called a containment functional in the econometrics literature as it represents the law of the random set $G(U|X;\theta )$ by the probability of G being contained in events of interest. It is a crucial tool for encoding the empirical contents of the model into sharp identifying restrictions on the underlying parameter (Galichon & Henry, 2006, 2011; Beresteanu et al., 2011; Chesher & Rosen, 2017).

This paper builds on Kaido and Zhang (2019), who develop a hypothesis-testing framework for incomplete models. Using their framework, we define a statistical risk function that evaluates the performance of a test through the Choquet integral of a loss function. The criterion evaluates a test’s performance based on size and power guarantee. The latter is the value of power that is certain to realize regardless of an unknown selection mechanism. We then define an analog of the Bayes risk and call it a Bayes–Dempster–Shafer (BDS) risk because it averages a loss function over unknown parameters using a single prior distribution and integrates over unknown selection mechanisms using a belief function.

Building on Huber and Strassen (1973), Kaido and Zhang (2019) showed an optimal statistical decision rule, BDS test, was a likelihood-ratio test based on the least-favorable pair of distributions. This paper develops a numerical method to implement the BDS test. The proposed algorithm is also useful for constructing a sequence of tests that can approximate a global minimax test. In an important earlier work, Chamberlain (2000) studied applications of the maximin utility to econometric problems and developed numerical methods. Following his work, we develop an algorithm to construct a sequence of BDS tests that approximate the minimax test. Our formulation combines well-defined computational problems: convex (or concave) programming and a one-dimensional root-finding. Efficient solvers are available for these problems.

As argued earlier, the empirical contents of an incomplete model can be summarized by the sharp identifying restrictions characterizing the core of a belief function. A well-developed literature on inference based on such restrictions exists. Asymptotically valid tests and confidence regions are extensively studied (see Canay & Shaikh, 2017, and references therein). Specifically, this paper’s test and recent developments on sub-vector inference tackle testing restrictions on subcomponents of the parameter vector (Bugni et al., 2017; Kaido et al., 2019). The existing inference methods construct test statistics based on sample moment inequalities. They compute asymptotically valid critical values by bootstrapping the test statistics combined with regularization methods to ensure their asymptotic validity (see e.g., Andrews & Soares, 2010; Andrews & Barwick, 2012). This approach can be computationally costly as it typically involves solving optimization problems over bootstrapped samples. In contrast, our procedure’s critical value has a closed form. However, it requires us to solve optimization problems to construct a test statistic. We combine well-defined computational problems to mitigate its cost. Bayesian and quasi-Bayesian approaches are also considered in the recent work of Chen et al. (2018); Giacomini and Kitagawa (2021). Belief functions are also used extensively in decision theory (see Mukerji, 1997, Ghirardato, 2001, Epstein et al., 2007, Gul & Pesendorfer, 2014). In a general setting where the sample space describing repeated experiments defines payoff-relevant states, Epstein and Seo (2015) gave behavioral foundations for the type of preference (or risk) considered in this paper. Finally, we note that one may use this paper’s framework regardless of the underlying parameter being point identified or not, i.e., partially identified. An essential requirement is that the model has the structure in (1). Other statistical decision frameworks in the presence of partial identification are studied in Hirano and Porter (2012), Song (2014), and Christensen et al. (2022).

The rest of the paper is organized as follows. Section 2 sets up an incomplete model and discusses a motivating example. Section 3 provides a theoretical background behind hypothesis testing and reviews results in Kaido and Zhang (2019). Section 4 presents numerical algorithms to implement the BDS test and to approximate a minimax test.

2 Set-up

Let $Y\in \mathcal {Y}\subseteq {\mathbb {R}}^{d_Y}$ and $X\in \mathcal {X}\subseteq \mathbb R^{d_X}$ denote, respectively, observable outcome and covariates, and let $U\in \mathcal {U}\subseteq {\mathbb {R}}^{d_U}$ represent latent variables. We let $\mathcal {S}\equiv \mathcal {Y}\times \mathcal {X}$ and assume $\mathcal {S}$ is a finite set. This assumption still accommodates a wide range of discrete choice models. Relaxing $\mathcal {X}$’s finiteness is possible, but we work in a simple setting to highlight key conceptual issues.² For any metric space $\mathcal {A}$, we let $\Delta (\mathcal {A})$ denote the set of all Borel probability measures on $(\mathcal {A},\Sigma _\mathcal {A})$, and $\Sigma _\mathcal {A}$ is the Borel $\sigma$-algebra on $\mathcal {A}$. Let $\Theta \subseteq {\mathbb {R}}^d$ be a finite-dimensional parameter space. We first illustrate an incomplete structure with an example.

Example 1

(Discrete games of strategic substitution) Consider a two-player game. Each player may either choose $y^{(k)}=0$ or $y^{(k)}=1$. The payoff of player j is

$$\begin{aligned} \pi ^{(k)}=y^{(k)}\big (x^{(k)}{}{'}\delta ^{(k)}+\beta ^{(k)} y^{(-k)}+u^{(k)}\big ),~k=1,2, \end{aligned}$$

(2)

where $y^{(-k)}\in \{0,1\}$ denotes the other player’s action, $x^{(k)}$ is player k’s observable characteristics, and $u^{(k)}$ is an unobservable payoff shifter. The payoff is summarized in the table below and is assumed to belong to the players’ common knowledge.

		Player 2
		$y^{(2)}=0$	$y^{(2)}=1$
Player 1	$y^{(1)}=0$	0, 0	$0, x^{(2)}{}{'}\delta ^{(2)}+u^{(2)}$
	$y^{(1)}=1$	$x^{(1)}{}{'}\delta ^{(1)}+u^{(1)}, 0$	$x^{(1)}{}{'}\delta ^{(1)} +\beta ^{(1)}+u^{(1)}$, $x^{(2)}{}{'}\delta ^{(2)}+\beta ^{(2)}+u^{(2)}$

The strategic interaction effect $\beta ^{(k)}$ captures the impact of the opponent’s taking $y^{(-k)}=1$ on player k’s payoff. Suppose that $\beta ^{(k)}\le 0$ for both players and the players play a pure strategy Nash equilibrium (PSNE). Then, one can summarize the set of PSNEs by the following correspondence (Tamer, 2003):

$$\begin{aligned} G(u|x;\theta )= {\left\{ \begin{array}{ll} \{(0, 0)\} &{} u^{(1)}<-x^{(1)}{}'\delta ^{(1)}, u^{(2)}<-x^{(2)}{}'\delta ^{(2)},\\ \{(0, 1)\} &{} u\in S_{\theta ,(0,1)},\\ \{(1, 0)\} &{} u\in S_{\theta ,(1,0)},\\ \{(1, 1)\} &{} u^{(1)}>-x^{(1)}{}'\delta ^{(1)}-\beta ^{(1)}, u^{(2)}>-x^{(2)}{}'\delta ^{(2)}-\beta ^{(2)},\\ \{(1, 0), (0, 1)\} &{} -x^{(k)}{}'\delta ^{(k)}<u^{(k)}<-x^{(k)}{}'\delta ^{(k)}-\beta ^{(k)}, \quad j=1, 2, \end{array}\right. } \end{aligned}$$

(3)

where $\theta = (\beta ', \delta ')'$,

$$S_{\theta ,(1,0)}=\{u^{(1)}>-x^{(1)}{}'\delta ^{(1)}-\beta ^{(1)}, u^{(2)}<-x^{(2)}{}'\delta ^{(2)}-\beta ^{(2)}\}\cup \{-x^{(1)}{}' \delta ^{(1)}<u^{(1)}<-x^{(1)}{}'\delta ^{(1)}-\beta ^{(1)}, u^{(2)}<-x^{(2)}{}'\delta ^{(2)}\}$$

and

$$S_{\theta ,(0,1)}=\{u^{(1)}<-x^{(1)}{}'\delta ^{(1)}, u^{(2)}>-x^{(2)}{}'\delta ^{(2)}\}\cup \{-x^{(1)}{}' \delta ^{(1)}<u^{(1)}<-x^{(1)}{}'\delta ^{(1)}-\beta ^{(1)}, u^{(2)}>x^{(2)}{}'\delta ^{(2)}-\beta ^{(2)}\}$$

.

Recall that, conditional on $X=x$, the outcome takes values in $G(U|x;\theta )$. We summarize the model’s prediction by the following correspondence from $\mathcal {X}\times \mathcal {U}\times \Theta$ to $\mathcal {S}$:

$$\begin{aligned} \Gamma (x,u;\theta )=\{(y,x)\in \mathcal {S}: y\in G(u|x;\theta )\}. \end{aligned}$$

(4)

The map $\Gamma$ collects the values of the observable variables compatible with $(x,u,\theta )$. Let P be the joint distribution of (Y, X), $P_{Y|X}$ be the conditional distribution of Y|X, and $P_X$ be the marginal distribution of X. Suppose X’s marginal distribution is known to be $F_X$, and we assume $U|X \sim F(\cdot |\cdot ;\theta )$ for a distribution belonging to a parametric family.

Let $S=(Y,X)$ be a vector of observable variables, which takes values in $\mathcal {S}$. For each $\theta \in \Theta$, the following set describes the set of distributions of S that are compatible with the model assumption:

$$\begin{aligned} \mathcal {P}_{\theta }\equiv \Big \{P\in \Delta (\mathcal {S}): P_{Y|X}=\int _{\mathcal {U}} \eta _{Y|X,u} dF_{\theta }(u|x), \text { for some }\eta _{Y|X,u} \in \Delta (G(u|x;\theta )), P_X=F_X \Big \}, \end{aligned}$$

(5)

where $\eta _{Y|X,u}$ is a conditional law of Y supported on $G(u|x;\theta )$, which represents the unknown selection mechanism. The set $\mathcal {P}_{\theta }$ collects the probability distributions P of (Y, X) that are compatible with $\theta$ for some selection mechanism.

A statistical experiment can be summarized as follows. The nature draws $\theta$ according to a prior distribution $\mu \in \Delta (\Theta )$. Given $\theta$, (U, X) are generated according to $F(\cdot |x;\theta )$ and $F_X$. An outcome Y is selected from $G(U|X;\theta )$, but the decision-maker (DM) does not understand how the outcome was selected. Equivalently, the distribution $P\in {\mathcal {P}}_\theta$ of the realized outcome Y gets selected, but the DM does not understand how it is done. Nonetheless, the DM must make a decision based on the sample. Hence, the DM faces three types of uncertainty. Two of them, sampling and parameter uncertainty, are standard in Wald’s statistical decision theory. However, there is an added layer to the decision problem. The DM’s theory is incomplete and does not give any guidance on the selection mechanism. Hence, we assume the DM seeks a robust statistical decision rule that attains a risk guarantee regardless of the selection mechanism. As in other decision problems, robust decision rules are appealing when the DM wants to avoid further assumptions on fine details of the environment (Gilboa & Schmeidler, 1989; Bergemann & Morris, 2005; Carroll, 2019).

2.1 Belief function

We briefly review Choquet capacities and introduce belief functions. We refer to Gilboa (2009) for a review of their use in decision theory and Denneberg (1994) for technical treatments. Our treatment here is based on Gilboa and Schmeidler (1994).

Let $\Sigma _\mathcal {S}=2^\mathcal {S}$ be a finite algebra. A function $\nu :\Sigma _\mathcal {S}\rightarrow {\mathbb {R}}$ with $v(\emptyset )=0$ is a capacity. Throughout, we assume $\nu (A)\ge 0,~\forall A\in \Sigma _\mathcal {S}$, $\nu (\mathcal {S})=1$ (i.e., normalized). We also assume $\nu$ is monotone. That is, for any $A,B\in \Sigma _{\mathcal {S}}$, $A\subseteq B\Rightarrow \nu (A)\le \nu (B)$. We will use the following properties.

• 1. $\nu$ is additive if $\nu (A\cap B)=\nu (A)+\nu (B)$ for all $A,B\in \Sigma _\mathcal {S}$ with $A\cap B=\emptyset$. An additive nonnegative capacity is a measure.

• 2. $\nu$ is convex (or 2-monotone) if for any $A,B\in \Sigma _{\mathcal {S}}$, $\nu (A\cup B)+\nu (A\cap B)\ge \nu (A)+\nu (B)$.

  $\nu$ is 2-alternating if for any $A,B\in \Sigma _{\mathcal {S}}$, $\nu (A\cup B)+\nu (A\cap B)\le \nu (A)+\nu (B)$.

• 3. $\nu$ is totally monotone if it is nonnegative and, for any $A_1,\dots ,A_n\in \Sigma _\mathcal {S},$

  $$\begin{aligned} \nu \big (\cup _{i=1}^nA_i\big ) \ge \sum _{I:\phi \ne I\subseteq \{1,\dots ,n\} }(-1)^{|I|+1}\nu \big (\cap _{i\in I}A_i\big ). \end{aligned}$$

  (6)

A normalized totally monotone capacity is called a belief function.

Remark 1

The definitions above are for settings with finite ${\mathcal {S}}$. One can define capacities on a more general space that can accommodate continuous covariates by adding regularity conditions. We refer to Huber and Strassen (1973) (Section 2) who define capacities on complete separable metrizable spaces. One can use the general version to incorporate continuous covariates. The convex capacities on ${\mathcal {S}}$ still retain the key properties (in particular, Eqs. (11, 12)) introduced below.

Define the law of ${G}(U|x;\theta )$ by

$$\begin{aligned} \nu _\theta (A|x)&\equiv \int _\mathcal {U}1\{{G}(u|x;\theta )\subseteq A\}dF_\theta (u|x),~~~\forall A\in \mathcal {C}, \end{aligned}$$

(7)

where $\mathcal {C}$ is the collection of closed subsets of $\mathcal {Y}$. The map $\nu _\theta (\cdot |x)$ is non-additive in general and hence is not a measure. One can show it is a normalized totally monotone capacity and hence a belief function (Philippe et al., 1999). Also, define

$$\begin{aligned} \nu ^*_\theta (A|x)=\int _\mathcal {U}1\{{G}(u|x;\theta )\cap A\ne \emptyset \}dF_\theta (u|x),~~~\forall A\in \mathcal {C}. \end{aligned}$$

(8)

The two functions satisfy the conjugate relationship $\nu ^*_\theta (A|x)=1-\nu _\theta (A|x)$. In what follows, for any capacity $\nu$, we let $\nu ^*$ denote its conjugate. We define the unconditional version of $\nu _\theta$ and $\nu ^*_\theta$. For each, $A\subseteq \mathcal {Y}\times \mathcal {X}$, let

$$\begin{aligned} \nu _\theta (A)&=\int _\mathcal {X}\int _\mathcal {U}1\{\Gamma (x,u;\theta )\subset A\}dF_\theta (u|x)dF_X(x),\nonumber \\ \nu ^*_\theta (A)&=\int _\mathcal {X}\int _\mathcal {U}1\{\Gamma (x,u;\theta )\cap A\ne \emptyset \}dF_\theta (u|x)dF_X(x). \end{aligned}$$

Note that, for any product set $A=A_\mathcal {Y}\times A_\mathcal {X}\subseteq \mathcal {Y}\times \mathcal {X}$, one may write $\nu _\theta (A)=\int _{A_\mathcal {X}}\nu _\theta (A_\mathcal {Y}|x)dF_X(x)$ and $\nu ^*_\theta (A)=\int _{A_\mathcal {X}}\nu _\theta ^*(A_\mathcal {Y}|x)dF_X(x)$.

The core of a capacity $\nu$ is the set of distributions that are weakly bounded from below by $\nu$:

$$\begin{aligned} \mathop {\textrm{core}}{(\nu )}\equiv \left\{ Q\in \Delta (\mathcal {S}):Q(A)\ge \nu (A),A\subseteq \mathcal {S}\right\} . \end{aligned}$$

As shown in the context of cooperative games, every convex capacity has a non-empty core (Shapley, 1965). Artstein’s theorem (Artstein, 1983, Theorem 2.1) allows us to characterize all distributions of measurable selections $S=(Y,X) \in \Gamma (X,U;\theta )$ by the core of the belief function:

$$\begin{aligned} \mathcal P_\theta =\mathop {\textrm{core}}(\nu _\theta )=\left\{ Q\in \Delta (\mathcal {S}):Q(A)\ge \nu _\theta (A),A\subseteq \mathcal {S}\right\} . \end{aligned}$$

(9)

This property is crucial for econometric applications because it allows us to characterize identifying restrictions by inequalities that do not involve selection mechanisms. We also exploit this property in our numerical algorithm.

For any capacity $\nu$ and a real-valued function f on $\mathcal {S}$, the Choquet integral of f with respect to $\nu$ is defined by

$$\begin{aligned} \int fd\nu \equiv \int _{-\infty }^0(\nu (\{s:f(s)\ge t\})-\nu (\mathcal {S}))dt+\int _0^\infty \nu (\{s:f(s)\ge t\})dt, \end{aligned}$$

(10)

where the integrals on the right-hand side of (10) are Riemann integrals. In decision theory, Choquet integrals are used to represent preferences that exhibit ambiguity aversion (Schmeidler, 1989). An important property of the belief function is that, for any real-valued function³

$$\begin{aligned} \int fd\nu _\theta&=\inf _{P\in \mathop {\textrm{core}}(\nu _\theta )}\int fdP=\inf _{P\in {\mathcal {P}}_\theta }\int fdP, \end{aligned}$$

(11)

$$\begin{aligned} \int fd\nu ^*_\theta&=\sup _{P\in \mathop {\textrm{core}}(\nu _\theta )}\int fdP=\sup _{P\in {\mathcal {P}}_\theta }\int fdP. \end{aligned}$$

(12)

Hence, the infimum and supremum of the expected values of f over ${\mathcal {P}}_\theta$ coincide with the Choquet integrals with respect to $\nu _\theta$ and its conjugate. These properties play an important role in defining the statistical risk function in the next section.

3 Testing composite hypotheses

3.1 Theoretical background

This section reviews Kaido and Zhang’s (2019) hypothesis-testing framework. Many hypotheses of practical interest are composite ones:

$$\begin{aligned} H_0:\theta \in \Theta _0, ~~\text {v.s.}~~H_1:\theta \in \Theta _1. \end{aligned}$$

(13)

For example, consider testing the hypotheses on subcomponents of $\theta$. Let $\theta =(\beta ',\delta ')'\in \Theta _\beta \times \Theta _\delta$, where $\beta$ is a $k\times 1$-sub-vector of interest and $\delta$ is a $(d-k)\times 1$ vector of nuisance parameters

$$\begin{aligned} H_0:\beta =\beta _0,~\delta \in \Theta _\delta , ~~\text {v.s.}~~H_1:\beta \ne \beta _0,~\delta \in \Theta _\delta . \end{aligned}$$

(14)

Then, the two parameter sets are $\Theta _0=\{\beta _0\}\times \Theta _\delta$ and $\Theta _1=\{\beta :\beta \ne \beta _0\}\times \Theta _\delta$. In the discrete game example, the researcher may want to test whether the players interact strategically or not, which can be formulated as a problem of testing $H_0:\beta =0$. Similar problems arise in other incomplete models.⁴

The researcher’s action is binary, $a=1$ (reject) or $a=0$ (accept). Define a loss function ${\textsf{L}}:\Theta \times \{0,1\}\rightarrow \mathbb R_+$ by

$$\begin{aligned} {\textsf{L}}(\theta ,a)\equiv aI_{\Theta _0}(\theta )+\zeta (1-a) I_{\Theta _1}(\theta ), \end{aligned}$$

where $\zeta >0$. The loss from a Type-I error is normalized to 1. The parameter $\zeta$ determines the trade-off between the Type-I and Type-II errors.

A statistical decision rule (or a test) $\phi$ is a function from $\mathcal {S}$ to a probability distribution over $\{0,1\}$. We let $\Phi =\Delta (\{0,1\})$ collect all (randomized) tests. For each test $\phi \in \Phi$ and $\theta \in \Theta$, define an upper risk by

$$\begin{aligned} R(\theta ,\phi )&=\sup _{P\in {\mathcal {P}}_\theta }\int {\textsf{L}}(\theta ,\phi )dP(s) \nonumber \\&=\sup _{P\in {\mathcal {P}}_\theta }\int [\phi (s)I_{\Theta _0}(\theta )+\zeta (1-\phi (s)) I_{\Theta _1}(\theta )]dP(s). \end{aligned}$$

(15)

Recall that ${\mathcal {P}}_\theta$ collects all data-generating processes that are compatible with $\theta$ for some selection mechanism. The upper risk evaluates the risk under the scenario that nature generates data using a selection mechanism that is least favorable to the DM. We use the structure of the incomplete model to reformulate the upper risk. First, for any $\theta \in \Theta _0$, let the size of $\phi$ be

$$\begin{aligned} R_0(\theta ,\phi )\equiv \sup _{P\in {\mathcal {P}}_\theta }\int \phi dP. \end{aligned}$$

(16)

Next, for any $\theta \in \Theta _1$, let

$$\begin{aligned} \pi _\theta (\phi )=\inf _{P\in {\mathcal {P}}_\theta }\int \phi dP \end{aligned}$$

(17)

be the power guarantee of $\phi$. This is a robust measure of power at $\theta$. The value of $\pi _\theta (\phi )$ is guaranteed to realize regardless of selection mechanisms. The following proposition shows the upper risk can be expressed using Choquet integrals of $\phi$.

Proposition 1

The size and power guarantee are

$$\begin{aligned} R_0(\theta ,\phi )&=\int \phi (s)d\nu ^*_\theta (s),~\theta \in \Theta _0, \end{aligned}$$

(18)

$$\begin{aligned} \pi _\theta (\phi )&=\int \phi (s)d\nu _\theta (s),~\theta \in \Theta _1. \end{aligned}$$

(19)

The upper risk can be expressed as

$$\begin{aligned} R(\theta ,\phi )&=R_0(\theta ,\phi ) I_{\Theta _0}(\theta )+\zeta (1-\pi _\theta (\phi ))I_{\Theta _1}(\theta ). \end{aligned}$$

(20)

Equation (20) shows the upper risk trades off the size $R_0(\theta ,\phi )$ and power guarantee $\pi _\theta (\phi )$. We represent each object by a Choquet integral of $\phi$. This formulation leads us to the Bayes–Dempster–Shafer risk below.

It remains to incorporate parameter uncertainty. For this, let $\mu$ be a prior distribution over $\Theta$. We write $\mu$ as $\mu =\tau \mu _0+(1-\tau )\mu _1,$ where $\tau \in (0,1)$ and $\mu _0,\mu _1$ are probability measures supported on $\Theta _0$ and $\Theta _1$, respectively. One can interpret $\mu$ as nature’s drawing a parameter value from $\Theta _0$ according to $\mu _0$ with probability $\tau$ and from $\Theta _1$ according to $\mu _1$ with probability $1-\tau$. We now define our main performance criterion to evaluate tests.

Definition 1

(Bayes–Dempster–Shafer (BDS) risk) For each prior $\mu \in \Delta (\Theta )$ and $\phi :\mathcal {S}\rightarrow \Delta (\{0,1\})$, let

$$\begin{aligned} r(\mu ,\phi )&\equiv \int _\Theta R(\theta ,\phi )d\mu (\theta ). \end{aligned}$$

(21)

The BDS risk uses the prior probability to reflect parameter uncertainty, while it uses the belief function (and its conjugate) to incorporate the decision-maker’s willingness to be robust against incompleteness. It can also be written as follows⁵:

$$\begin{aligned} r(\mu ,\phi )= \tau \int \phi (s)d\kappa _0^*(s)+(1-\tau )\zeta (1-\int \phi (s)d\kappa _1(s)), \end{aligned}$$

(22)

where the integrals in (22) are Choquet integrals with respect to

$$\begin{aligned} \kappa _0^*=\int _{\Theta _0}\nu _\theta ^*d\mu _0,~\text { and } \kappa _1=\int _{\Theta _1}\nu _\theta d\mu _1. \end{aligned}$$

We use capacity $\kappa _0^*$ to evaluate the average size of $\phi$ across $\Theta _0$. Similarly, we use $\kappa _1$, an average belief function over $\Theta _1$, to evaluate the power of $\phi$. We call $\phi$ a BDS test if it minimizes the BDS risk.

A key component of the BDS risk in (22) is

$$\begin{aligned} \pi _{\kappa _1}(\phi )\equiv \int \phi d\kappa _1=\int _{\Theta _1}\int \phi d\nu _{\theta }d\mu _1=\int _{\Theta _1}\pi _\theta d\mu _1. \end{aligned}$$

We call this term the weighted average power guarantee. Its interpretation is similar to that of the weighted average power (Andrews & Ploberger, 1994, 1995). One may direct a test’s power guarantee toward certain alternatives by choosing a suitable $\mu _1$.

Similar to Bayesian hypothesis-testing problems, the BDS-risk contrasts the risks from the Type-I and Type-II errors. A difference is that they are the worst-case (in terms of selection) size and power guarantee averaged over the parameter space. The following lemma characterizes the BDS test. It uses the fact that the risk is written as in (22) and a result from Huber and Strassen (1973).

Lemma 1

(Lemma 5.1 in Kaido and Zhang (2019)) Let the BDS risk be defined as in (21). Suppose $core(\kappa _0)\cap core(\kappa _1)=\emptyset$. Then, there exists a BDS test such that, for any $\zeta >0$,

$$\begin{aligned} \phi (s) = \left\{ \begin{array}{ll} 1 &{} \text {if} \quad \Lambda (s)>C\\ \gamma &{} \text {if} \quad \Lambda (s)=C\\ 0 &{} \text {if} \quad \Lambda (s)<C,\\ \end{array} \right. \end{aligned}$$

(23)

where $C=\tau /\zeta (1-\tau )$, and $\Lambda$ is a version of the Radon-Nikodym derivative $dQ_1/dQ_0$ of the least-favorable pair such that $(Q_0,Q_1)\in core(\kappa _0)\times core(\kappa _1)$, and

$$\begin{aligned} Q_0(\Lambda>t)=\kappa _0^{*}(\Lambda>t),~~~\text { and }~~~ Q_1(\Lambda>t)=\kappa _1(\Lambda >t), \end{aligned}$$

(24)

for all $t\in {\mathbb {R}}_+$,

The lemma states that a BDS test takes the form of a Neyman–Pearson test, where the likelihood-ratio $\Lambda$ is formed by a representative pair $(Q_0, Q_1)$ taken from the two sets of distributions. The distribution $Q_0$ is compatible with the null hypothesis and maximizes the rejection probability of the test, whereas $Q_1$ is compatible with the alternative hypothesis and minimizes the rejection probability of the test. The theorem requires the cores of $\kappa _0$ and $\kappa _1$ not to overlap. To ensure this condition, it is sufficient to have at least one $\bar{A}\subset \mathcal {S}$ such that $P_0({\bar{A}})<P_1({\bar{A}})$ (or $P_0(\bar{A})>P_1({\bar{A}})$) for all $(P_0, P_1)\in \mathcal P_{\theta _0}\times {\mathcal {P}}_{\theta _1}$ and $(\theta _0,\theta _1)\in \Theta _0\times \Theta _1$. In the entry game example, one may take ${\bar{A}}=\{(1,1)\}\times \{x\}$ for any $x\in \mathcal {X}$.⁶

An important computational implication of Lemma 1 is that we may focus on the LFP to implement the BDS test. Furthermore, one can find the LFP by solving the following convex program (Kaido & Zhang, 2019):

$$\begin{aligned} (q_0,q_1)=\mathop {\mathrm{arg\,min}}_{(p_0,p_1)\in \Delta (\mathcal {S})^2}&~\sum _{s\in S}\ln \Big (\frac{p_0(s)+p_1(s)}{p_0(s)}\Big )(p_0(s)+p_1(s)) \nonumber \\ s.t.&~~~\kappa _{0}(A)\le \sum _{s\in A}p_0(s),~A\subset \mathcal {S}\nonumber \\&~~~\kappa _{1}(A)\le \sum _{s\in A}p_1(s),~A\subset \mathcal {S}. \end{aligned}$$

(25)

We use this result to develop numerical algorithms in Sect. 4.

3.2 Minimax test

Suppose the DM wants to maximize the weighted average power guarantee only among tests that keep their size below a prespecified level. The BDS tests are not designed to achieve uniform size control over $\Theta _0$. Hence, we need a more general treatment.

Toward this end, the following minimax theorem is useful. It characterizes the minimax test as a BDS test for the least-favorable prior (if it exists). For this, let $\mathcal M(\mu _1)\equiv \{\mu :\mu =\tau \mu _0+(1-\tau )\mu _1,\mu _0\in \Delta (\Theta _0),\tau \in (0,1)\}$, where $\mu _1$ is fixed. In what follows, we drop $\mu _1$ from the argument of ${\mathcal {M}}$, but its dependence should be understood. Also, we let $g\vee h$ be the maximum of g and h.

Theorem 1

(Theorem 5.1 in Kaido and Zhang (2019)) Let the upper risk R be defined as in (20). Suppose that $\Theta$ is compact. Then,

$$\begin{aligned} \sup _{\mu \in \mathcal {M}}\inf _{\phi \in \mathbf \Phi }\int _\Theta R(\theta ,\phi )d\mu (\theta )=\inf _{\phi \in \mathbf \Phi }(\sup _{\theta \in \Theta _0}R_{0}(\theta ,\phi )\vee R_1(\phi )), \end{aligned}$$

(26)

where $R_1(\phi )=\zeta (1-\pi _{\kappa _1}(\phi ))$. Furthermore, there exists $\phi ^\dagger$ that achieves equality in (26).

The objective function on the right-hand side of (26) is the maximum risk, $\sup _{\theta }R(\theta ,\phi )$. Hence, $\phi ^\dagger$ is a minimax test. Suppose $\zeta$ is chosen so that the minimax value is less than or equal to a prespecified level $\alpha \in (0,1)$. Then, $\phi ^\dagger$ is a level-$\alpha$ test.

The theorem suggests the minimax test can be approximated (in terms of risk) by a sequence of BDS tests $\{\phi _\ell ,\ell =1,2,\dots \}$. Each BDS test minimizes the average of $R(\theta ,\phi )$ with respect to a prior $\mu _\ell$. For complete models with nuisance parameters, numerical methods for approximating minimax tests have been developed (Chamberlain, 2000; Moreira & Moreira, 2013; Elliott et al., 2015). We aim to achieve this goal in incomplete models.

4 Numerical implementation

We develop a numerical algorithm to construct an approximating sequence to the minimax test. Our strategy is as follows. First, we approximate prior distributions over $\Theta _0$ by finite mixtures. Second, we develop a concave program for a given $\zeta$ that achieves the maximin risk over the mixture space. Third, we carry out a one-dimensional root-finding to find a value of $\zeta$ that ensures uniform size control.

Building on Chamberlain (2000), we consider a finite mixture for $\mu _0$. Let $\ell \in {\mathbb {N}}$ and $\Delta ^\ell$ be the unit simplex in ${\mathbb {R}}^\ell$. Define

$$\begin{aligned} {\mathcal {M}}_{0,\ell }\equiv \Big \{\mu _{0,\ell }\in \Delta (\Theta _0): \frac{d\mu _{0,\ell }}{d\theta }=\sum _{j=1}^\ell \eta _j\varphi _j(\theta ),\eta \in \Delta ^\ell \Big \}, \end{aligned}$$

(27)

where $\eta =(\eta _1,\cdots ,\eta _\ell )'$ is a weight vector, and $\{\varphi _j(\cdot )\}$ is a set of (basis) densities over $\Theta _0$. Let $\mu _{0,\ell }\in {\mathcal {M}}_{0,\ell }$ be a distribution over $\Theta _0$. Define $\mathcal M_\ell \equiv \{\mu _\ell \in \Delta (\Theta ):\mu _\ell =\tau \mu _{0,\ell } +(1-\tau )\mu _1,~\tau \in (0,1),\mu _{0,\ell }\in \mathcal M_{0,\ell }\}.$ Our algorithm seeks $\mu _\ell \in {\mathcal {M}}_\ell$ that solves

$$\begin{aligned} \sup _{\mu _{\ell }\in \mathcal {M}_{\ell }}\inf _{\phi \in \mathbf \Phi }\int _\Theta R(\theta ,\phi )d\mu (\theta )&=\sup _{\tau \in (0,1),\mu _{0,\ell }\in \mathcal {M}_{0,\ell }} \Big (\inf _{\phi \in \mathbf \Phi }\tau \int _{\Theta _0}R_0(\theta ,\phi )d\mu _{0,\ell }+(1-\tau )R_1(\phi )\Big )\nonumber \\&=\sup _{\tau \in (0,1),\mu _{0,\ell }\in \mathcal {M}_{0,\ell }}F_\ell (\mu _{0,\ell },\tau ). \end{aligned}$$

(28)

Let $\kappa ^*_{0,\ell }=\int \nu ^*_\theta d\mu _{0,\ell }$. Lemma 1 ensures the existence of a likelihood-ratio test $\phi ^*_\ell$ that minimizes the BDS risk. Therefore, the value of the inner optimization problem on the right-hand side of (28) is

$$\begin{aligned} F_\ell (\mu _{0,\ell },\tau )&\equiv \inf _{\phi \in \mathbf \Phi } \tau \sum _{j=1}^\ell \eta _j\int _{\Theta _0} R_0(\theta ,\phi )\varphi _j(\theta )d\theta +(1-\tau )R_1(\phi )\nonumber \\&=\tau \sum _{j=1}^\ell \eta _j\int _{\Theta _0} R_0(\theta ,\phi ^*_{\ell })\varphi _j(\theta )d\theta +(1-\tau )R_1(\phi ^*_{\ell })\nonumber \\&=\sum _{j=1}^{\ell -1}v_j\int _{\Theta _0} R_0(\theta ,\phi ^*_{\ell })\varphi _j(\theta ) d\theta +(\tau -\sum _{j=1}^{\ell -1}v_j)\int _{\Theta _0} R_0(\theta ,\phi ^*_{\ell }) \varphi _\ell (\theta )d\theta +(1-\tau )R_1(\phi ^*_{\ell })\nonumber \\&=:{\textsf{Q}}(\tau ,v_1,\dots ,v_{\ell -1}), \end{aligned}$$

(29)

where we let $v_j=\tau \eta _j$. The map $\mathsf Q(\tau ,v_1,\dots ,v_{\ell -1})$ is concave as shown below. Hence, one can find a solution to (28) by maximizing ${\textsf{Q}}$ subject to the constraint $(\tau ,v_1,\dots ,v_{\ell -1})\in (0,1)\times [0,1]^{\ell -1}$ and $\tau \ge \sum _{j=1}^{\ell -1}v_j$. One may obtain finer approximations to the left-hand side of (26) as $\ell$ increases.

Proposition 2

Let $(Q_0,Q_1)\in core(\kappa _{0,\ell })\times core(\kappa _1)$ be the LFP and $\phi ^*_\ell$ be the associated BDS test. Then,

$$\begin{aligned} {\textsf{Q}}(\tau ,v_1,\dots ,v_{\ell -1})=\tau E_{q_0}[\phi ^*_\ell ]+(1-\tau )\zeta (1-E_{q_1}[\phi ^*_\ell ]), \end{aligned}$$

(30)

and ${\textsf{Q}}$ is a concave function.

The algorithm can be summarized as follows.

Algorithm 1 (Outer optimization, Inputs: $\zeta$)

Step 1::

Choose $\ell$. For each $(\tau ,v_1,\dots ,v_{\ell -1})$, run Algorithm 2 below to obtain the LFP densities $(q_0,q_1)$ and BDS test $\phi ^*_\ell$.

Step 2::

Compute $\textsf{Q}(\tau ,v_1,\dots ,v_{\ell -1})$ using (30).

Step 3::

Maximize $\textsf{Q}$ subject to the constraints $(\tau ,v_1,\dots ,v_{\ell -1})\in (0,1)\times [0,1]^{\ell -1}$ and $\tau \ge \sum _{j=1}^{\ell -1}v_j$, which is a concave program by Proposition 2. One can use the sequential quadratic programming algorithm available in common program languages.

Remark 2

Algorithm 1 computes the objective function $\textsf{Q}$ using the size and power of the BDS test under the LFP $Q_0$ and $Q_1$, respectively. This algorithm, therefore, bypasses explicit evaluations of the Choquet integrals.

Algorithm 2 (Inner optimization, Inputs: $\tau ,v_1,\dots ,v_{\ell -1}$)

Step 1::

For each $\ell$ and $A\subseteq S$, compute

$$\begin{aligned} \kappa _{0,\ell }(A)=\sum _{j=1}^\ell \eta _j\int _{\Theta _0}\nu _\theta (A)\varphi _j(\theta )d\theta , \end{aligned}$$

(31)

where $\eta _j=v_j/\tau$ for $j=1,\dots ,\ell -1$, and $\eta _\ell =1-\sum _{j=1}^{\ell -1}\eta _j.$

Step 2::

Solve the following convex optimization problem to obtain the LFP densities $(q_0,q_1)$:

$$\begin{aligned} (q_0,q_1)=\mathop {\mathrm{arg\,min}}_{(p_0,p_1)\in \Delta (\mathcal {S})^2}&~\sum _{s\in S}\ln \Big (\frac{p_0(s)+p_1(s)}{p_0(s)}\Big )(p_0(s)+p_1(s)) \\ s.t.&~~~\kappa _{0,\ell }(A)\le \sum _{s\in A}p_0(s),~A\subset \mathcal {S}\nonumber \\&~~~\kappa _{1}(A)\le \sum _{s\in A}p_1(s),~A\subset \mathcal {S}\nonumber . \end{aligned}$$

(32)

Compute the BDS test $\phi ^*_\ell$ as in (23) with $\Lambda =q_1/q_0$.

After running Algorithm 1, one obtains $\mathsf Q(\tau ^*,v^*_1,\dots ,v^*_{\ell -1})$, which is the maximum risk in (28). We write this value as a function $\textsf{Q}^*(\zeta )$ of the input $\zeta$. If one wants the test $\phi ^*_\ell$ to achieve an approximate size control, one can run a one-dimensional root-finding with respect to $\zeta$ to solve $\textsf{Q}^*(\zeta )-\alpha =0$. A numerical experiment suggests $\textsf{Q}^*(\zeta )-\alpha$ may have multiple roots depending on the numerical tolerances used in the optimization problems in Algorithms 1–2. In such cases, we recommend plotting $\textsf{Q}^*(\zeta )$ and checking if the solution found by the root-finding algorithm is a reasonable solution.

Remark 3

When $F_X$ does not depend on $\theta$, the likelihood-ratio statistic is of the form $\Lambda (y,x)=q_0(y|x)/q_1(y|x)$ (see Section 5 in Kaido and Zhang (2019)), where $q_0(y|x)$ and $q_1(y|x)$ can be computed by solving, for each x,

$$\begin{aligned} (q_0(\cdot |x),q_1(\cdot |x))=\mathop {\mathrm{arg\,min}}_{(p_0(\cdot |x),p_1(\cdot |x))\in \Delta (\mathcal {Y})^2}&~\sum _{y\in \mathcal {Y}}\ln \Big (\frac{p_0(y|x)+p_1(y|x)}{p_0 (y|x)}\Big )(p_0(y|x)+p_1(y|x)) \\ s.t.&~~~\kappa _{0,\ell }(A|x)\le \sum _{y\in A}p_0(y|x),~A\subset \mathcal {Y}\nonumber \\&~~~\kappa _1(A|x)\le \sum _{y\in A}p_1(y|x),~A\subset \mathcal {Y}\nonumber , \end{aligned}$$

(33)

where $\kappa _{0,\ell }(A|x)=\sum _{j=1}^\ell \eta _j\int _{\Theta _0}\nu _\theta (A|x)\varphi _j(\theta )d\theta$ and $\kappa _1(A|x)=\int _{\Theta _1}\nu _{\theta }(A|x)d\mu _1$. When ${\mathcal {X}}$ is finite, one can either solve (32) once or solve (33) for each x in the support, and they yield the same BDS test. When x is continuous, one can solve (33) for each observed value of X to calculate the likelihood-ratio statistic. Hence, although finding the LFP for each x is cheap, the total computational cost can be high when the sample size is large and X is continuous.

4.1 Illustration

To illustrate, consider a simplified version of the two-player entry game. Suppose player k’s payoff is

$$\begin{aligned} \pi ^{(k)}=y^{(k)}\big (\theta ^{(k)}y^{(-k)}+u^{(k)}\big ),~ k=1,2, \end{aligned}$$

(34)

where the structural parameter is $\theta =(\theta ^{(1)},\theta ^{(2)})'$. This is a special case of Example 1 with strategic interaction parameters only, i.e., $\theta =\beta$. Consider testing the strategic interaction parameter equals 0 for one of the players. That is,

$$\begin{aligned} H_0:\theta ^{(1)}=0~~~v.s.~~~H_1:\theta ^{(1)}<0. \end{aligned}$$

The nuisance parameter $\theta ^{(2)}$ is unrestricted, while we maintain the assumption $\theta ^{(2)}\le 0$. Let $\Theta _0=\{0\}\times (-\infty ,0]$, $\Theta _1=(-\infty ,0)\times (-\infty ,0]$, and $\mu _1$ be a discrete uniform distribution over equally spaced points in $\Theta _1$.⁷ For the mixture space, we use a family of gamma distributions as basis functions $\varphi (\theta )$ in equation (31). For each $\theta \in \Theta _0$, let

$$\begin{aligned} \varphi _j(\theta )=\frac{1}{\Gamma (a_j)b_j^{a_j}}(-\theta ^{(2)})^{a_j-1}e^{\frac{x}{b_j}} \quad j=1,\ldots ,\ell , \end{aligned}$$

(35)

where the shape and scale parameters $a_j>0,b_j>0$ are chosen according to the rule described below. We restrict the shape parameter space to [1, 25] and grid it with $J_1$ equally spaced points. Similarly, the scale parameter space is [0.1, 1.5], and we grid it with $J_2$ equally spaced points. We let $\ell =J_1\times J_2$ be the number of shape and scale parameter combinations. For example, if $J_1=J_2=3$, then we set up a grid with three values for a : 1, 13, 25, and three values for b : 0.1, 0.8, 1.5, giving $\ell =9$ with $(a_j,b_j)\in \{(1,0.1), (1,0.8),\ldots , (25,0.8), (25, 1.5)\}$. We consider three cases: $\ell =9, (J_1=J_2=3)$, $\ell =16, (J_1=J_2=4)$, and $\ell =25, (J_1=J_2=5)$. We examine the approximating BDS test and its corresponding least-favorable prior for each case.

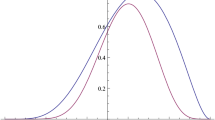
The results are as follows. Figure 1 shows the approximated least-favorable prior densities for different values of $\ell$. The densities tend to place relatively high mass near 0 but also allocate positive masses across strictly negative values of $\theta ^{(2)}$. Note that the algorithm aims at approximating the optimal value rather than the optimal solution. Hence, the approximated least-favorable prior density may change depending on $\ell$ as shown below.

Fig. 1

Least-favorable prior densities for different values of $\ell$

Table 1 Summary of the numerical illustration

The average computation time for each case is shown in Panel A of Table 1. The computer processors we employed in all of our numerical experiments were Intel(R) Core(TM) i9-9980HK CPUs 2.40 GHz. We repeat the same computation 100 times and computed the average time to complete Algorithm 1. Panel B in Table 1 reports the LFP densities $q_0, q_1$ and likelihood ratios $\Lambda$ across $\ell$. They are calculated by Step 2 in Algorithm 2.⁸ Although the convex optimization requires the belief functions as lower bound restrictions for all possible events $A\subset \mathcal {S}$, a computational trick is to use a subset of constraints that still characterize the sharp identifying restrictions. In the two-player entry game, there are $2^4=16$ possible events. However, we only need to compute the belief functions and their conjugate of the following events $\{(0,0),(1,1),(1,0)\}$. These restrictions are core determining in the sense of Galichon and Henry (2011).⁹ We set $\zeta =0.065$, under which the size of the BDS tests is below 5% across $\ell$.

Table 1 shows the LFP-based likelihood-ratio $\Lambda (y)=q_1(y)/q_0(y)$ is high for $y=(0,1),(1,0)$ and exceeds the critical value. In contrast, $\Lambda (y)$ is much lower than the critical value when $y=(1,1)$, and $\Lambda (y)$ equals 1 when $y=(0,0)$. This result can be explained as follows. First, for a given $\theta ^{(2)}$, moving the value of $\theta ^{(1)}$ from its null value (i.e., 0) to a strictly negative value raises the probability assigned to $y=(0,1)$ and decreases the probability assigned to $y=(1,1)$. Figure 2 shows the level sets of $u\mapsto G(u|\theta )$. The red region shows $\{u:G(u|\theta )=\{(0,1)\}\}$. The probability assigned to $y=(1,0)$ may stay the same or could get reduced depending on the equilibrium selection. The probability of $y=(0,0)$ remains constant regardless. The precise LFP depends on how $\mu _\ell$ assigns weights across parameter values in $\Theta _0$ and $\Theta _1$. The LFP-based likelihood ratio suggests, under $\mu _\ell$, one should expect (on average) an increase to the probabilities of $y=(0,1),(1,0)$ and a decrease to the probability of $y=(1,1)$. The BDS test uses this information to make a rejection decision.

Fig. 2

Level sets of $u \to G(u\left| {x,\theta )} \right.$. Note: $A=(0,0)$; $B=(-\theta ^{(1)},-\theta ^{(2})$. Left Panel: $\theta ^{(1)}=0$ and the model is complete. Right panel: $\theta ^{(1)}<0$. Multiple equilibria $\{(1,0),(0,1)\}$ are predicted in the blue region

5 Concluding remarks

The paper applies the belief function expected utility to a hypothesis-testing problem with incompleteness. We propose a numerical method to approximate a minimax test for incomplete models. The procedure does not require any estimator of the nuisance parameter but requires optimization of prior distributions over the null parameter space. As such, it extends the type of algorithm considered by Chamberlain (2000) to incomplete models. The proposed method is designed for finite sample problems. A direction for further research is to study ways to deal with large samples. One possibility is to incorporate large-sample approximations of experiments in the sense of Le Cam (1972) into the current framework. Such approximations often allow us to approximate the original experiments with simpler ones (Hirano & Porter, 2020).

A Proofs

Proof of Proposition 1

For the Choquet integral representation of the power guarantee, the result follows immediately from Theorem 3.2 in Gilboa and Schmeidler (1994) (see also the references there), $\mathcal P_\theta =core(\nu _\theta )$ because $\nu _\theta$ is a belief function and is a special case of a 2-monotone (or convex) capacity, and the core is non-empty.

For the size, the result follows similarly. For illustration purposes, we also give a more primitive proof to show how the definition of the Choquet integral is used. Consider $\int \phi \nu _\theta ^*$. Note that $\phi \ge 0$. Hence, only the second term in the definition of the Choquet integral in Eq. (10) is relevant. Using the definition,

$$\begin{aligned} \int \phi \nu _\theta ^*&=\int _0^\infty \nu ^*_\theta (\{s:\phi (s)\ge t\})dt\\&=\int _0^\infty Q^*_\theta (\{s:\phi (s)\ge t\})dt\\&=\int \phi (s)dQ^*_\theta (s)\\&\le \sup _{P\in {\mathcal {P}}_\theta }\int \phi (s)dP(s), \end{aligned}$$

where the second equality is due to Lemma 2.4 in Huber and Strassen (1973), which ensures the existence of a measure $Q^*_\theta$ that maximizes the probability of the event $\{s:\phi (s)\ge t\}$ for any t. The third equality uses the fact that $Q^*_\theta$ is a measure (and, hence, additive).

Similarly, noting that $\nu ^*_\theta (A)\ge P(A),\forall P\in {\mathcal {P}}_\theta$,

$$\begin{aligned} \int \phi d\nu _\theta ^*&=\int _0^\infty \nu ^*_\theta (\{s:\phi (s)\ge t\})dt\\&\ge \int _0^\infty P(\{s:\phi (s)\ge t\})dt\\&=\int \phi (s) dP(s), \end{aligned}$$

implying $\int \phi d\nu _\theta ^*\ge \int _{P\in \mathcal P_\theta }\int \phi dP.$ Combining these, conclude

$$\begin{aligned} R_0(\theta ,\phi )=\int \phi d\nu ^*_\theta . \end{aligned}$$

(36)

Eq. (20) follows because

$$\begin{aligned} R(\theta ,\phi )=R_0(\theta ,\phi )I_{\Theta _0}(\theta )+\zeta (1-\pi _\theta (\phi ))I_{\Theta _1}(\theta ). \end{aligned}$$

(37)

This completes the proof of the proposition.$\square$

Proof of Proposition 2

For (30), recall that

$$\begin{aligned} \textsf{Q}(\tau ,v_2,\dots ,v_{\ell -1})=\tau \int _{\Theta _0}R_0(\theta ,\phi ^*_\ell )d\mu _{0,\ell }+(1-\tau ) R_1(\phi ^*_{\ell }). \end{aligned}$$

(38)

Furthermore,

$$\begin{aligned} \int _{\Theta _0}R_0(\theta ,\phi ^*_\ell )d\mu _{0,\ell }=\int _{\Theta _0}\int \phi ^*_\ell d\nu ^*_\theta d\mu _{0,\ell }=\int \phi ^*_\ell d\kappa ^*_{0,\ell }=\int \phi ^*_\ell dQ_0=E_{q_0}[\phi ^*_\ell ], \end{aligned}$$

(39)

where the penultimate equality follows from $(Q_0,Q_1)$ being the LFP, which is ensured by Lemma 1. Similarly,

$$\begin{aligned} R_1(\phi ^*_\ell )=\zeta (1-\pi _{\kappa _1}(\phi ^*_\ell ))=\zeta (1-\int \phi ^*_\ell d\kappa _1)=\zeta (1-\int \phi ^*_\ell dQ_1)=\zeta (1-E_{q_1}[\phi ^*_\ell ]). \end{aligned}$$

(40)

The first claim of the proposition follows from (38)–(40).

For second claim, observe that, for any $\phi$, the following function is affine in $(\tau ,v_1,\dots ,v_{\ell -1})$

$$\begin{aligned} \sum _{j=1}^{\ell -1}v_j\int _{\Theta _0} R_0(\theta ,\phi )\varphi _j(\theta )d\theta +(\tau -\sum _{j=1}^{\ell -1}v_j)\int _{\Theta _0} R_0(\theta ,\phi )\varphi _\ell (\theta )d\theta +(1-\tau )R_1(\phi ). \end{aligned}$$

${\textsf{Q}}$ is the pointwise minimum (with respect to $\phi$) of the function above. Hence, it is concave.$\square$