Groups versus individuals, partial lying, and social image concern in a dice-rolling experiment

Abstract

This study compares the lying behavior of groups that consist of paired friends to that of individuals in a dice-rolling experiment. Both groups and individuals exhibit strong evidence of lying, but partial lying (not lying to the maximum extent possible) is more pronounced under group decisions. Furthermore, we estimate the preference parameter(s) of existing models for lying aversion. Groups are more sensitive than individuals to social image concerns of not being perceived as liars, and have a lower cost of lying than do individuals.

1 Introduction

Deception is widely observed in many social and economic contexts. Examples include accounting fraud, manipulating quality-checking data by a for-profit firm, welfare fraud by an individual or a small group of people, medical malpractice by a hospital or a doctor, and promises made by a politician in a campaign. Against the background of its bad influence on society, economists have recently begun experimentally investigating the characteristics of lying behavior (Gneezy, 2005; Mazar et al., 2008; Fischbacher & Föllmi-Heusi, 2013) (henceforth, F &FH).

Experimental evidence suggests that people often lie, but not to the maximum extent possible. F &FH developed an ingenious design to study lying behavior, in which subjects privately roll a dice, and then report the number to the experimenter. Because the payments are based on the reported number, subjects have an incentive to lie by reporting the number that would yield the highest earnings. Although we are unable to observe lying at an individual level, patterns of lying behavior can be inferred from the distribution of the reported numbers by comparing them to the uniform distribution expected under full honesty. F &FH found that as the payment that the number yields increases, the fraction of people reporting that number increases. Furthermore, the fraction of people reporting the number that yields the second highest payment (number four) was substantially higher than 1/6. This indicates that subjects disguise their lying, which F &FH refer to as partial lying. Others have reported similar findings (Abeler et al., 2019).

Using the dice-rolling experiment, this study compares the lying behavior of individuals and two-person groups. In real-life situations, decisions are often made by a group. Political, monetary policy, and some business decisions are all made by small groups in which two or more individuals interact freely. Economists and social psychologists have accumulated experimental evidence on how and why group behavior differs from individual behavior in various strategic contexts (Bornstein, 2008; Charness & Sutter, 2012; Kugler et al., 2012).

Prior studies on group versus individual lying behavior in the dice-rolling experiment examined various types of group decisions.¹ Kocher et al. (2018) examined the behavior of three-person groups in which subjects could communicate with group members via an anonymous real-time chat. Conrads et al. (2013) investigated a team incentive scheme in which a two-person group is formed randomly and anonymously, members are not allowed to communicate, and a group member’s payoff is one-half of the total earnings of the group. Muehlheusser et al. (2015) and Chytilová and Korbel (2014) examined randomly formed groups in which group members communicate face-to-face.

The important difference that distinguishes our experimental design from previous studies is that each group consists of two friends who know each other well.² During the experiment, subjects were primed to think about their friend with whom they attended the session in several ways: (1) In the recruiting process, they were requested to sign up with their friend, (2) each experimental session included only one pair of friends, and (3) they answered the questionnaire about relationship between the subjects and their friend before making a decision on the dice-rolling experiment. Examining group and individual behavior under these settings uncovers the difference between the behaviors with and without communication with a friend.

There are several reasons why we focus on groups of friends rather than randomly formed groups. First, this is intended to facilitate a discussion within a group. To reach a decision, subjects need to discuss matters which include delicate or unethical contents. Subjects might hesitate to do so if their group member is someone who they have just met for the first time. Furthermore, a lack of communication or social skills may affect the decision of randomly formed groups. Second, cheating behavior observed in many real-life situations is by a small group of acquaintances, not strangers. This design allows us to study the decisions by groups which are closer to reality. Third, a large body of literature reveal that social identity affects human behaviors in various situations (see, for example, Charness and Chen (2020) for review), including lying behaviors (Cohn et al., 2014, 2015; Ojima et al., 2021). Therefore, friends, who are one of the most familiar social groups in real life, are expected to behave differently from randomly formed groups.

The experimental results show that the distribution of the reported numbers is significantly different from the uniform distribution for both groups and individuals. Furthermore, the distribution of groups is significantly different from that of individuals. While the lying pattern of individuals is in line with previous studies, groups exhibit partial lying more saliently: the numbers with the third highest monetary payoff (number three) is reported most frequently, and four dice numbers yielding higher monetary payoffs (numbers two, three, four, and five) are reported with the fraction more than 1/6.

One possible explanation for our experimental results is that groups are more sensitive to social image concern than are individuals. Some theoretical and experimental studies reveal that the preference for appearing honest makes people averse to lying to the number that yields the maximum payment, which leads to partial lying (Abeler et al., 2019; Gneezy et al., 2018; Dufwenberg & Dufwenberg, 2018; Khalmetski & Sliwka, 2019).³ To address how well the existing models with social image concern capture the features of our experimental results, we estimate the preference parameter(s) of those models. We examine two models: Dufwenberg and Dufwenberg’s (2018; henceforth, D &D) model which incorporates the perceived size of the lie, and Khalmetski and Sliwka’s (2019; henceforth, K &S) model which includes the cost of lying and the likelihood of being perceived as a liar.

The estimation results reveal that under the D &D model, the sensitivity to the size of the lie they are perceived to have told is similar between individuals and groups. Whereas the equilibrium distribution of reported numbers under the model fits well with the individuals’ data, it does not with the groups’ data. This indicates that the D &D model fails to rationalize the hypothesis that higher sensitivity of groups to the social image concern leads stronger partial lying. Under the K &S model, on the other hand, groups are significantly more sensitive to the likelihood of being perceived as liars, and have, on average, a lower cost of lying than individuals. Furthermore, the equilibrium distribution of reported numbers under the model fits well with both groups’ and individuals’ data. Thus, the above hypothesis is supported by the logic of the K &S model.

The rest of this paper proceeds as follows: Sect. 2 presents the experimental design that allows us to analyze the lying behavior of individuals and groups. Section 3 develops our working hypotheses on how the lying pattern of groups is different from that of individuals. Section 4 reports the results of the experiment and the statistical tests. Section 5 discusses whether theoretical models support our findings that groups are more sensitive to social image concern, by estimating the preference parameters of the D &D and the K &S models. Section 6 concludes this paper.

2 Experimental design

Our experiment uses a variant of a well-known paradigm for studying lying behavior, developed by F &FH, in which subjects privately roll a six-sided dice, and report the number they observe to the experimenter. The payments were made based on the reported numbers, as follows: JPY 600 for one, JPY 700 for two, JPY 800 for three, JPY 900 for four, JPY 1000 for five, and JPY 500 for six.⁴ The payments were made in recompense for completing a questionnaire. Under the self-interested preference, a player will choose to report five, and gain the maximum payment, regardless of the actual number on the dice.

The subjects were recruited through a crowd-based subject pool software, Sona Systems.⁵ Only two persons could sign up for each time slot (experimental session). The registration page explains that participants must sign up with a friend. Furthermore, the experimenter confirmed that they were actually friends when the subjects arrived at the venue. If they were not friends (this happened because they had not carefully read the description of the experiment on the registration page), their experimental session was canceled.

At the beginning of the experimental session, subjects received and read the consent form approved by the Institutional Review Board at the Kochi University of Technology. Then, the subjects each received an envelope containing the questionnaire, and were directed to move to two separate rooms to complete the form in private. The questionnaire asked about the relationship between the subjects and their friend with whom they attended the session.⁶ After completing the questionnaire, the subjects returned to the first room. The procedures that follow distinguish between the individual and group treatments.

In the individual treatment, each subject received another envelope, which contained a six-sided dice and a copy of the instructions used to determine the payment.⁷ Subjects were again directed to move to two separate rooms, and asked to follow the instructions provided and return to the first room. Because the subjects were asked to open the envelope after entering the room, they could not communicate with their friend about the decision of a report.

In the group treatment, the two subjects received one envelope, and were directed to move to a room together and follow the instructions. The instructions informed them that they had to jointly report the number that came up on the dice, and each would be paid according to the reported number.

In both treatments, subjects were allowed to roll the dice more than once to check if it balanced. However, they were strictly instructed to fill out the number from the first throw. After filling out the number on the sheet, they returned it to the envelope and handed it to the experimenter, after which they were paid. The rooms used for the experiments were located far from the room where the experimenter waited. Thus, the subjects knew that their conversation could not be overheard, and that they were not being directly monitored by the experimenter.

Experimental sessions were conducted in October and November 2018 and December 2019 at the Kochi University of Technology. The subjects were recruited from the Kochi University of Technology and the University of Kochi. In total, 196 subjects participated in this experiment, of which 66 and 130 participated in the individual and group treatments, respectively (and hence, 66 and 65 rolls of the dice, respectively). Each experimental session lasted about 10 min. None of the subjects participated in more than one session.

3 Hypothesis

Existing studies are unable to clarify whether groups lie more or less than individuals. We can develop at least three competing hypotheses on group versus individual lying behavior. The first hypothesis is that groups are more prone to exhibit income-maximizing behavior than individuals. This hypothesis holds for several reasons. First, the majority of studies on group decision-making reveal that groups are more self-interested than individuals in various economic environments (for surveys, see (Bornstein, 2008; Charness & Sutter, 2012; Kugler et al., 2012)), even when group members are not allowed to communicate with each other (Kamijo and Tamura, 2019). Second, people tend to justify lying easily when others benefit from dishonest behavior (Schweitzer & Hsee, 2002). In our experiment, lying to the number with the maximum payment could benefit the group members. Third, members can diffuse their responsibility in a group setting (Conrads et al., 2013). Thus, the group setting mitigates the psychological burden of lying.

Hypothesis 1

(Income Maximization Hypothesis) Groups report the number with maximum payment (number five) more frequently than individuals.

The second hypothesis is that groups tend to disguise lying more saliently than individuals. People care about social image, and sacrifice monetary payoff to appear honest (Gneezy et al., 2018; Abeler et al., 2019). Furthermore, the mere presence of familiar peers strengthens social image concerns, leading people to cheat less (Pascual-Ezama et al., 2015). Thus, group setting makes people reluctant to tell a lie to preserve their reputation among their peers.

Hypothesis 2

(Partial Lying Hypothesis) Partial lying is more pronounced under group decision.

The third hypothesis is that groups are more honest than are individuals. People in a group are motivated to both perceive and present themselves in a socially desirable way (Brown, 1986; Cason & Mui, 1997). Furthermore, laboratory and field studies reveal that the existence of a moral reminder increases the level of honesty (Mazar et al., 2008; Pruckner & Sausgruber, 2013). Thus, if one of the group members behaves moralistically, the group will reach a honest decision.

Hypothesis 3

(Honesty Hypothesis) Groups are more inclined to report each number equally.

Ultimately, the question of whether groups are more or less dishonest than individuals can be answered only through the observation of actual behavior.

4 Results

Fig. 1

Distribution of reported dice numbers

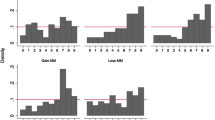
Figure 1 shows the distribution of the reported numbers, which are shown in increasing order of payoff.

Table 1 Average payoff and distribution of reports

Table 1 reports the average payoff and the share of subjects who reported the corresponding number as a percentage.

The average payoffs are 3.53 and 3.29 for the individual and group treatments, respectively, after rescaling the payoff, so that $\pi = 0$ when six is reported, and $\pi = x$, for $x\in \{1, \ldots , 5\}$, otherwise. The difference is not statistically significant ($p=0.154$, two-tailed Wilcoxon rank-sum test).

The distribution of the individual treatment exhibits a similar behavioral pattern to that of previous studies (Abeler et al., 2019).⁸ It differs significantly from the uniform distribution that would result when all subjects report honestly ($p=0.000$, chi-square goodness-of-fit test). The distribution has a significant increasing trend in payoff ($p=0.006$, $\rho = 0.986$, Spearman’s rank correlation). Numbers six, one, two, and three are reported less frequently than the expected true value of 1/6 (16.7%), with the fractions for six, one, and two being significantly less than 1/6 ($p = 0.035$ for six and one, $p=0.069$ for two, and $p = 0.310$ for three, one-sided binomial test). The fractions for four and five are significantly above 1/6 ($p=0.069$ for four and $p=0.000$ for five).

The distribution of the group treatment is also significantly different from the uniform distribution ($p=0.000$, chi-square goodness-of-fit test), but it has different characteristics from that of the individual treatment. The increasing trend in payoff is not statistically significant ($p=0.175$, $\rho = 0.657$, Spearman’s rank correlation). Only six and one are reported less frequently than 1/6 ($p=0.007$ for six, and $p=0.001$ for one). Three is reported most frequently, and is significantly above 1/6 ($p=0.030$). Five is also reported significantly above 1/6 ($p=0.060$). Two and four are above, but not significantly different from 1/6 at the 10% level ($p = 0.111$ for two and $p=290$ for four).

Consequently, we observed several differences in behavior between individuals and groups. The hypothesis that the two distributions come from the same population is rejected ($p=0.038$, chi-square test). The fractions for two and three are significantly higher in the group treatment than in the individual treatment ($p=0.029$ for two and $p=0.073$ for three, chi-square test). Conversely, one is reported significantly less frequently in the group treatment than in the individual treatment ($p=0.098$). So is number five, but not statistically significant ($p=0.102$).

From these observations, we conclude that only the partial lying hypothesis (hypothesis 2) is supported. As the fraction of five is lower in the group treatment than in the individual treatment, groups do not intend to lie to five more frequently, indicating that the income-maximization hypothesis (hypothesis 1) is rejected. As the fractions of six and one are lower in the group treatment than in the individual treatment, groups do not intend to report more truthfully, which rejects the honesty hypothesis (hypothesis 3). The fractions of two and three are above 1/6 in the group treatment, while below 1/6 in the individual treatment. This indicates that two and three are the numbers to which groups lie, but from which individuals lie to the other numbers. This suggests that groups tend to disguise their lies by misreporting to the wider range of numbers than individuals.⁹

5 Social image concern and lying behavior

This section addresses the question of how well the existing models with social image concern fit with our experimental data. As discussed in Sect. 3, we conjecture that group setting may make people more sensitive to social image concerns, which results in more salient partial lying of groups. To verify that this conjecture is correct under theoretical models that incorporate social image concerns, we estimate the preference parameters for social image concern in the D &D and K &S models, and compare the estimated values between individuals and groups. Furthermore, we examine if the equilibrium distribution of reported numbers under the estimated parameters fits well with the observed distributions.

In this section, we rename the dice number six as zero, such that an agent privately observes a state (an integer number) $\omega \in \{0,1,\dots ,5\}$. The agent then reports an integer number $x\in \{0,1,\dots ,5\}$ to the audience (e.g., experimenter). Let $p[\omega |x]$ be the probability that the audience thinks the true state is $\omega$ when x is reported, with $p[\omega |x] \in [0,1]$ for all $\omega$, and $\sum _{\omega '}p[\omega '|x]=1$. Next, we discuss the two models and their equilibrium predictions in further detail.

5.1 Perceived size of the lie

D &D incorporate disutility from the size of the lie perceived by the audience. They analyze an agent that has the following utility function:

$$\begin{aligned} u(x) = ax - \theta \sum _{\omega '}p[\omega '|x]a(x-\omega ')^+, \end{aligned}$$

where $a>0$ and $(x-\omega ')^+=\max \{x-\omega ',0\}$. The first term ax is the monetary payoff from reporting x, and $\sum _{\omega '}p[\omega '|x]a(x-\omega ')^+$ is the audience’s expectation about the amount of money earned from lying. The parameter $\theta \ge 0$ measures the agent’s sensitivity to this social image, and we will focus on its estimated value.

Let $s:\{0,\dots ,5\}\rightarrow \Delta \{0,\dots ,5\}$ be a behavioral strategy, and $s(x|\omega )$ denote the probability that s assigns to x after the agent observes $\omega$. S denotes the agent’s set of strategies. Then, $s\in S$ is a sequential equilibrium (Battigalli & Dufwenberg, 2009) if, for $\omega , \omega ', x \in \{0,\dots 5\}$, we have $p[\omega |x]\in [0,1]$, $\sum _{\omega }p[\omega |x]=1$, and the following two conditions: (a) $s(x|\omega )>0\Rightarrow x\in \text {argmax}_{x'} \,\, u(x')$, and (b) $\sum _\omega s(x|\omega )>0\Rightarrow p[\omega '|x]=\frac{\frac{1}{6}s(x|\omega ')}{\sum _\omega \frac{1}{6}s(x|\omega )}=\frac{s(x|\omega ')}{\sum _\omega s(x|\omega )}$.¹⁰

D &D show that the sequential equilibrium $s\in S$, with the properties that

• 1. if $x<\omega$, then $s(x|\omega ) = 0$,

• 2. if $\omega <5$, then $s(5|\omega ) = 1-\varepsilon _5$, where $\varepsilon _5\in (0,1)$, and

• 3. if $\omega<x<5$, then $s(x|\omega ) = (1-\varepsilon _x)\prod _{x+1\le k \le 5}\varepsilon _k$, where $\varepsilon _k\in (0,1)$,

is uniquely determined for all $\theta > 2$.¹¹ Condition (1) means that the agent never lies downward. Conditions (2) and (3) indicate that the probability that the agent lies to x is the same for all $\omega <x$. Because $s(\omega |\omega )=\prod _{\omega +1\le k\le 5}\varepsilon _k$ for $\omega < 5$ and $\varepsilon _k\in (0,1)$, all numbers are reported with positive probability.

In any sequential equilibrium with the above properties, we have

$$\begin{aligned} 1-\varepsilon _x=\frac{2}{x(\theta -2)+\theta }, \end{aligned}$$

(1)

for $x\in \{1,\cdots ,5\}$. This condition stems from the insight that the utility following any choice must be the same in equilibrium, because all numbers are reported with positive probability, and that $u(0)=0$ (see Sect. 3.4 and the proof of the proposition in Sect. 3.3 of D &D). Let $q_x(\theta )$ be the probability that the agent reports $x\in \{0,\dots ,5\}$ in equilibrium. Then, we have

$$\begin{aligned} q_x(\theta ) = \sum _{\omega \le x}\frac{1}{6}s(x|\omega ) = \left\{ \begin{array}{ll} \frac{1}{6}\prod _{1\le k \le 5}\varepsilon _k &{} \text {if }x=0 \\ \frac{1}{6}[x(1-\varepsilon _x)+1]\prod _{x+1\le k \le 5}\varepsilon _k &{} \text {if }x\in \{1,\dots ,4\} \\ \frac{1}{6}[5(1-\varepsilon _5)+1] &{} \text {if }x=5. \end{array} \right. \end{aligned}$$

Using (1), we can obtain the equilibrium distribution of the reported numbers. Figure 2 shows the equilibrium distribution of the reported numbers as a function of $\theta$. The vertical lines ($\theta = 3.629$ and $\theta = 3.946$) in the figure indicate the estimated parameters for individuals and groups, respectively, as discussed in Sect. 5.4.

Fig. 2

Equilibrium Distribution of Reported Numbers in the D &D Model. The vertical lines ($\theta = 3.629$ and $\theta = 3.946$) in the figure indicate the estimated parameters for individuals and groups, respectively, as discussed in Sect. 5.4

We present the comparative statistics results for the equilibrium lying behavior.

Claim 1

The equilibrium distribution of reported numbers in the D &D model, $q_x(\theta )$, has the following properties:

• (i) (a) When $\theta \rightarrow 2$ (from above), $q_5(\theta )\rightarrow 1$ and $q_x(\theta )\rightarrow 0$, for $x\in \{0,\dots ,4\}$. (b) When $\theta \rightarrow \infty$, $q_x(\theta )\rightarrow 1/6$, for all x.

• (ii) (a) $q_5(\theta )$ is strictly decreasing in $\theta > 2$. (b) $q_0(\theta )$ and $q_1(\theta )$ are strictly increasing in $\theta > 2$. (c) For $x\in \{2,3,4\}$, there exists $\theta > 2$, such that $q_x(\theta )>1/6$.

• (iii) $q_x(\theta )$ is strictly increasing in x, for all $\theta > 2$.

Proof

See Appendix C.

Claim 1(i) describes the results at the lower and upper limits of $\theta$; (a) states that when $\theta$ is sufficiently close to two (from above), the behavior is equivalent to the income-maximizing behavior, and (b) indicates that the agent always tells the truth, as $\theta$ becomes sufficiently large.¹² (ii) describes how the probability of reporting each number varies with $\theta$; (a) indicates that when $\theta$ increases, partial lying and/or truth-telling are revealed more often, (b) states that the two lowest numbers (zero and one) are reported more frequently as $\theta$ increases, and (c) (combined with (i)) states that the fractions of reporting two, three, and four increase in some range of $\theta$, and decrease in the other range. Finally, (iii) means that higher numbers are reported more frequently for all $\theta >2$ $\square$.

5.2 Cost of lying and likelihood of being perceived as a liar

K &S consider the cost of lying and the disutility from the probability of the agent being perceived as a liar by the audience. They analyze an agent with the following utility function:

$$\begin{aligned} u(x) = x -c\cdot I(x,\omega )-\eta \sum _{\omega '\not = x}p[\omega '|x], \end{aligned}$$

where $x\in \{0,\dots ,5\}$ is the monetary payoff by reporting x, $c>0$ is the fixed cost of lying, $I(x,\omega )$ is an indicator function, taking one if $x\not =\omega$, and zero otherwise. $\sum _{\omega '\not = x}p[\omega '|x]$ is the likelihood that the audience thinks the agent has told a lie when x is reported and $\eta >0$ captures the sensitivity to this social image, which we will focus on its estimated value.¹³ The cost of lying c is assumed to be distributed according to a strictly increasing continuous cdf F(c), with $F(0)=0$. In order to capture the characteristic of experimental data that all numbers are reported with positive probability, we assume that $F(5+\eta )<1$. This assumption means that there are some agents with a sufficiently high cost of lying, so that they never misreport.

First, we repeat the definition of a sequential equilibrium under this setting. Let $s:\{0,\dots ,5\}\times \mathbb {R}_+ \rightarrow \Delta \{0,\dots ,5\}$ be a behavioral strategy, and $s(x|\omega ,c)$ denote the probability that s assigns to x after the agent observes $\omega$ and c. Then, $s\in S$ is a sequential equilibrium if for $\omega , \omega ', x\in \{0,\dots ,5\}$, we have $p[\omega |x]\in [0,1]$, $\sum _\omega p[\omega |x]=1$, and the following two conditions: (a) $s(x|\omega ,c)>0\Rightarrow x\in \text {argmax}_{x'}\,\,u(x')$; and (b) $\sum _\omega \int _0^\infty s(x|\omega ,c)dF(c)>0\Rightarrow p[\omega '|x]=\frac{\int _0^\infty s(x|\omega ',c)dF(c)}{\sum _\omega \int _0^\infty s(x|\omega ,c)dF(c)}$.¹⁴

K &S show that there are multiple equilibria under which the distribution of the reported numbers is the same. More precisely, they show that, given $\eta >0$ and $F(\cdot )$, there exists a constant $\rho \in (\max \{0,5-\eta \},5)$ such that, in any equilibrium, for all $x\ge m(\rho )$, where $m(\rho )=\min \{x\in \{1,\dots ,5\}|x>\rho \}$,

$$\begin{aligned} x-\eta \sum _{\omega '\not =x}p[\omega '|x] = \rho , \end{aligned}$$

and $\rho$ is uniquely determined by the equation,

$$\begin{aligned} \sum _{\omega =0}^{m(\rho )-1}F(\rho -\omega )=\sum _{x=m(\rho )}^5\Bigg (\frac{x-\rho }{\eta -x+\rho }\Bigg ) \end{aligned}$$

(2)

(see Proposition 1 and Theorem 1 in K &S).¹⁵ Let $q_x(\rho )$ be the probability that the agent reports $x\in \{0,\dots ,5\}$ in equilibrium. K &S show that

$$\begin{aligned} q_x(\rho )=\left\{ \begin{array}{ll} \displaystyle \frac{\eta }{6(\eta -x+\rho )} &{} \text {if }x\ge m(\rho ) \\ \frac{1}{6}(1-F(\rho -x)) &{} \text {if }x< m(\rho ) \end{array} \right. \end{aligned}$$

(see Proposition 2).¹⁶, ¹⁷

K &S show that agents who observe $\omega <m(\rho )$ either report the true state or lie to a number $x\ge m(\rho )$, and that agents who observe $\omega \ge m(\rho )$ always report honestly (see Proposition 1 in K &S). When $\eta$ increases, $m(\rho )$ weakly decreases, and the probability that an agent lies strictly decreases (see Proposition 5 in K &S). In other words, being more concerned about social image increases the set of numbers that agents misreport, but reduces the proportion of liars. Furthermore, when $\eta$ becomes sufficiently large, all numbers other than zero are reported by liars (see Proposition 6 in K &S). When the distribution of the cost of lying F increases in the sense of first-order stochastic dominance, $m(\rho )$ weakly increases, and the probability that an agent lies strictly decreases (see Proposition 7 in K &S). In other words, a higher cost of lying decreases the range of numbers reported by liars, and decreases the proportion of liars. Finally, as under the D &D model, the probability of reporting x is strictly increasing in x for any $\eta$ and $F(\cdot )$ (see Proposition 2 in K &S). These propositions suggest that partial lying emerges with a combination of a decrease in the cost of lying and an increase in the importance of social image, which could explain the difference between experimental results for individuals and groups.

5.3 Estimation strategy

Here, we discuss our maximum likelihood estimation. Let $n_x$ be the frequency of report $x\in \{0\dots ,5\}$ observed in the experiment, and $q_x$ be the equilibrium probability of reporting x in the model. Then, the log-likelihood function is given by

$$\begin{aligned} LL = \sum _x n_x\log q_x. \end{aligned}$$

We will find $\theta > 2$ that maximizes LL in the estimation of the D &D model.

In the estimation of the K &S model, we assume that the cost of lying is distributed as a gamma distribution, with shape parameter $\alpha >0$ and scale parameter $\beta >0$. When people lie, it is likely that some non-negligible proportion of people experience a small cost of lying, the majority of people feel some cost, and a small fraction of people feel an extremely high cost. These characteristics are captured well by the gamma distribution with a broad range of parameters. Because a gamma distribution with $\alpha$ and $\beta$ as free parameters becomes quite flexible, we fix $\beta$ to two in the estimation process. The resulting distribution is equivalent to the chi-square distribution with $2\alpha$ degrees of freedom. Therefore, we will find $\eta >0$ and $\alpha >0$ that maximize LL in the K &S model.

5.4 Results

We examine the following two questions: (1) Are estimated parameters for social image concern larger in the group treatment than in the individual treatment? (2) Does the equilibrium distribution of the reported numbers with the estimated parameters fit well with the experimental data (especially, groups’ data)? (1) is the main question. A larger $\theta$ in the D &D model and a larger $\eta$ in the K &S model indicate higher sensitivity to the social image concern.¹⁸ (2) is also important because the lack of fit implies that the model cannot rationalize the observed lying behavior of individuals and groups. As both the D &D and K &S models are known as good predictors of individual lying behavior (and our data in the individual treatment is similar to that of previous studies), we expect the models to fit well with the individuals’ data. By contrast, the groups’ data is unusual relative to prior studies; therefore, it is not obvious if the models fit well with the groups’ data.

Table 2 Estimated parameter and equilibrium distribution of reported numbers under the D &D model

We first examine the results for the D &D model. Table 2 reports the estimated parameter and equilibrium distribution of reported numbers with that parameter. The estimated $\theta$ is 3.629 for individuals and 3.946 for groups. Recall that when $\theta$ is sufficiently close to two, the behavior is equivalent to the income-maximizing behavior (see (i) of claim 1). Therefore, both individuals and groups are, to some extent, sensitive to the amount of money over which they are perceived to cheat. The $\theta$ for groups is not statistically significantly different from that for individuals ($p=0.609$, t-test, and $p=0.557$, likelihood ratio test), indicating that the sensitivity to the perceived size of the lie is similar between individuals and groups under the D &D model. Because a higher $\theta$ results in a higher incidence of partial lying, we might expect that the estimated $\theta$ for groups becomes significantly higher than that for individuals; however, this is not the case. One explanation for this is that a higher $\theta$ also results in higher fractions of zero and one, which is a worse fit for the data of groups (see (ii) of claim 1).

Next, we assess how well the D &D model captures the behavioral characteristics of our experimental data. Figures 3 and 4 display the distribution of reported numbers from our experiment (black) and the percentages predicted under the models using the estimated parameter(s), respectively (gray for the D &D model and white for the K &S model).

Fig. 3

Comparison between theory and data (individual treatment)

Fig. 4

Comparison between theory and data (group treatment)

As expected, the D &D model fits well with the individuals’ data. The chi-square goodness-of-fit test reveals that the observed frequencies of all numbers are not significantly different from the equilibrium distribution under the model ($p=0.321$).¹⁹ The model significantly underpredicts the frequency of zero ($p=0.093$, one-sided binomial test). For the other numbers, the differences between the respective predicted and observed percentages are not significant ($p=0.501$ for one, $p = 0.196$ for two, $p=0.173$ for three, $p=0.519$ for four, and $p=0.134$ for five). By contrast, the model does not fit well with the groups’ data. The frequencies of all numbers are significantly different from the equilibrium distribution ($p=0.029$, chi-square test). The model significantly overpredicts the frequency of one, and underpredicts that of two and three ($p=0.025$ for one, $p=0.030$ for two, and $p=0.096$ for three).²⁰

Summarizing, our hypothesis that higher sensitivity to the social image concern results in the partial lying of groups to be more salient is not supported by the D &D model.

Table 3 Estimated parameters and equilibrium distribution of reported numbers under the K &S model

Next, we examine the performance of the K &S model. Table 3 reports the estimated parameters and its equilibrium distribution. Although $\rho$ is not a parameter to be estimated in the K &S model, we report its values because it characterizes the equilibrium lying behavior. In the K &S model, the parameter values are different between individuals and groups. The value of $\eta$ for groups (7.876) is significantly higher than that for individuals (2.892) ($p=0.011$, t-test, and $p=0.001$, likelihood ratio test). This indicates that under the K &S model, groups are more sensitive to the social image of not being viewed as liars. Recall that, under the model, being more concerned about social image (higher $\eta$) leads agents to deviate to lower numbers, which is what we observed in the group treatment relative to in the individual treatment.

The values of $\alpha$ are 1.455 and 0.328 for the individual and group treatments, respectively. The $\alpha$ for groups is significantly lower than that for individuals ($p=0.000$, t-test, and $p=0.008$, likelihood ratio test). The average values for the cost of lying are calculated as 2.910 and 0.656 in the individual and group treatments, respectively.²¹ Hence, the cost of lying is, on average, lower in the group treatment. Theoretically, a lower cost of lying results in liars reporting lower numbers. Thus, the fractions for lower numbers are more likely to be greater than 1/6, which is consistent with our findings.

As noted in Sect. 5.2, agents who observe $\omega <m(\rho )$ either report the true state or lie to a number $x\ge m(\rho )$, and agents who observe $\omega \ge m(\rho )$ always report honestly. Because $m(\rho )=\min \{x\in \{1,\dots ,5\}|x>\rho \}$, the estimated value of $m(\rho )$ is four in the individual treatment, and two in the group treatment. This is again consistent with our finding that the lowest number with a fraction above 1/6 is four in the individual treatment, and two in the group treatment.

The K &S model attains a good fit with both individuals’ and groups’ data. The chi-square goodness-of-fit test reveals that neither the observed frequencies of individuals, nor those of groups are statistically significantly different from the equilibrium distribution of reported numbers with the estimated parameters ($p=0.621$ for individuals, and $p=0.190$ for groups).²² Furthermore, the K &S model statistically neither underpredicts nor overpredicts the frequency for any given number. For the individual treatment, the p-values of the binomial test are $p=0.303$ for zero, $p=0.536$ for one, $p=0.329$ for two, $p=0.389$ for three, $p=0.330$ for four, and $p=0.538$ for five. For the group treatment, they are $p=0.188$ for zero, $p=0.137$ for one, $p=0.168$ for two, $p=0.165$ for three, $p=0.253$ for four, and $p=0.216$ for five.

In summary, under the K &S model, groups are more sensitive to the social image concern (larger $\eta$) than individuals, and the model attains a good fit with both individuals’ and groups’ data. This indicates that our hypothesis that higher sensitivity of groups to the social image concern results in the stronger partial lying observed in the experiment, is supported by the logic of the K &S model.

Finally, we turn to the question of which model better fits the experimental data. Comparing Tables 2 and 3, the K &S model outperforms the D &D model because the equilibrium distribution under the D &D model is far from the groups’ data, whereas the K &S model fits well with both individuals’ and groups’ data. However, a model with many parameters is generally more flexible, and therefore may fit observed data better than models with fewer parameters. Penalized-likelihood information criteria are widely used to compare the performance of models with different numbers of parameters. We use the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). The AIC is given by $-2{\text {LL}}^*+2m$, and the BIC is given by $-2{\text {LL}}^*+m\log (N)$, where ${\text {LL}}^*$ is the maximized log-likelihood, m is the number of parameters in the model, and N is the number of observations. The preferred model is the one with the smaller information criterion. Since both AIC and BIC is increasing in m, they penalize models that have more parameters.

Table 4 Information criteria

Table 4 reports the AIC and the BIC. For the individual data, we are unable to draw conclusions on which model is better. The AIC of the K &S model is smaller than that of the D &D model, whereas the reverse is true based on the BIC. For the group data, in contrast, both AIC and BIC of the K &S model are smaller, which means that, when taking the number of model parameters into account, the K &S model better fits the group data than the D &D model. These results suggest that the K &S model is better suited to capture the characteristics of cheating behavior across a wide range of decision makers (groups and individuals) compared to the D &D model.

6 Discussion and conclusion

We compared the lying behavior of groups of paired friends and individuals in the dice-rolling experiment developed by F &FH. The experimental data suggest that groups are more likely to disguise a lie: the fraction of reporting five, which results in the maximum monetary payoff, is lower, and the range of numbers with fractions above 1/6 is broader in the group treatment than in the individual treatment. These findings have important welfare implications. On the one hand, the average size of ill-gotten profit becomes lower for groups, but on the other hand, it becomes more difficult to infer whether a group is lying after observing a lower report, which suggests that detecting an act of dishonesty by a group is costly. In this sense, the behavior of groups is more strategic.

Group lying behavior observed in our experiment is different from those in prior studies. Groups with real-time chat (Kocher et al., 2018) and groups with team incentives (Conrads et al., 2013) lie to five more frequently than individuals. Since these experiments maintained anonymity among group members, lying did not harm their social image. Groups in Muehlheusser et al. (2015) and Chytilová and Korbel (2014) are randomly formed, and communication is face-to-face. Muehlheusser et al. (2015) found no difference in behavior between groups and individuals. Chytilová and Korbel (2014), using students at a secondary school, found that there was no significant difference between groups and individuals for older students (from 14 to 16 years old), whereas groups lied more than individuals for younger students (from 11 to 13 years old). These no or weak difference results are interpreted as follows: under randomly formed group setting, group members are typically not familiar with each other. Face-to-face communication may result in some group members hesitating to participate in a discussion within the group, because subjects need to discuss about unethical content. Thus, the group decision will be made by one or a very few people in the group, resulting in the decision being more like an individual decision. More lying by younger students in Chytilová and Korbel (2014) indicates that they have not sufficiently developed social image concerns yet.

Research on group versus individual behavior typically studies the behavior of randomly formed groups (see Bornstein 2008; Charness and Sutter 2012; Kugler et al. 2012). Our experiment suggests that the type of group (strangers, friends, family members, colleagues, etc.) matters in their decision.

In terms of external validity, since our experiment used student subjects, the results are particularly relevant to understanding cheating behavior among college students in academic contexts, such as exam cheating. However, caution should be exercised in generalizing our findings to other populations or situations. In business situations, for example, being perceived as a liar can often be a significant obstacle to building long-term relationships with business partners. In these situations, the degree of social image concern may be stronger than what we observed in the experiment.

We give one rational explanation why partial lying is more pronounced under group decision by estimating the preference parameter(s) of the models by D &D and K &S. Under the D &D model, the sensitivity to the perceived size of the lie is statistically similar between groups and individuals. Under the K &S model, groups are statistically more sensitive to the likelihood of being perceived as liars, and have a lower psychological cost of lying than do individuals. The resulting equilibrium distribution of numbers under the D &D model fail to capture some behavioral characteristics of groups, whereas that of the K &S model fits well with both individuals’ and groups’ data. The K &S model supports the hypothesis that stronger social image concern leads to stronger partial lying, as observed in the group treatment.

In our experimental setting, groups receive a prize for two people, which suggests that the benefit from misreporting is larger for groups than for individuals. Additionally, subjects in a group can benefit the other person (their friend) by misreporting and can also diffuse their responsibility for their decision, which may lead to lower costs of lying in the group treatment. At the same time, the lying behavior of subjects in a group is definitely identified by their friend in our experiment, which would hurt their social image. Consequently, subjects in a group may be hesitant to suggest and approve more greedy lying (such as misreporting for larger payments) to maintain their reputation among peers, leading to more partial lying.

Another possible method for investigating how groups and individuals are sensitive to social image concern is to develop a new experimental design to address this issue. However, it presents some difficulties, because the lying behavior is acutely affected by a small change in the environment. For example, in the experimental design of Kocher et al. (2018), the outcome of the dice roll was shown on subjects’ PC screen. As the outcome of the dice was known to the experimenter, the subjects could not disguise their lie. Possibly, subjects might get a feel of that. Consequently, they found that partial lying was rare for both groups and individuals. Thus, only a small change in experimental design might prevent us from observing what we want to observe (change in partial lying). In the light of this possibility, the estimation of parameter values in the model, adopted in this study, have some superiority, because our method does not change the experimental design at all.

This study focuses on the models that include the preference for social image concern. Of course, it is possible that other theories, not examined in this study, can explain our experimental data. It is important to evaluate the performance of these competing theories, to enhance our understanding of the human preferences behind lying behavior. We leave this for future studies.

Appendices

Appendix A: Questionnaire

Table 5 Results of questionnaire and statistical tests

Table 5 reports the results of the questionnaire administered in the experiment and the statistical tests that examine the differences between treatments. Part (1) asks about gender and affiliation. We report the number and share (in parentheses) of groups of two females, one female and one male, and two males in the gender entry. We also show the number and share (in parentheses) of groups comprising two, one, and no economics/management student(s) in the affiliation entry. Part (2) asks about the relationship between the subjects and their friend with whom they attended the experiment. We report the average and the standard deviation (in parentheses) of the answers. All answers in part (2) may be correlated within a group. To perform the statistical tests, we processed the data as follows: In Q1 and Q4, we perform the Wilcoxon rank-sum test (WRS test), with the average answer within a group as the unit of observation. In Q2, Q3, Q7, Q8, Q9, and Q10, using a seven-point Likert scale, we report two results for the Wilcoxon rank-sum test. In one test, the unit of observation is the minimum of the answers within a group; in the other, it is the maximum. In the chi-square test for Q5 and Q6, we count one if both subjects in a group answered yes, and zero otherwise.

Appendix B: Characteristics of groups and cheating behavior

In this section, we investigate how the cheating behavior of groups is influenced by the characteristics of the subjects, using the results of the questionnaire presented in Table 5. Friend is considered to be affected by the depth of their relationship and level of trust.

Table 6 Regression analysis

Table 6 reports the results of ordinary least square regression. The dependent variable is the reported number. The independent variable “Year” is the number of years (averaged within a group) that group members have known each other (Q1).²³ The variable “Influence” is the absolute difference between the answers of a seven-point scale regarding whether subjects have ever made any decision in accordance with their friend’s decision, or changed their choice as a result of their friend’s influence (Q2). This variable represents the extent to which the group members establish an equal relationship. The larger the value, the more one member depends on the other member. The variable “Help” is the average score of a seven-point scale within a group indicating how much subjects have been helped or supported by their friend (Q3). The variable “Frequency” is the number of days (averaged within a group) which subjects meet their friend in a week (Q4). The variable “Trust” is the average score of a seven-point scale within a group indicating how much subjects trust their friend (Q9).²⁴

Model (1) uses only the group data and finds that only Frequency is statistically significant at the 10 percent significance level. The coefficient is positive, indicating that the more frequently the friends meet in daily life, the larger the numbers they report in the experiment. Model (2) uses both the group and individual data, and include the interaction terms of group dummy and variables described above. However, no significant difference between groups and individuals was found.

Next, we will examine gender difference in cheating behavior. Table 7 reports the average payoffs by gender and treatment.

Table 7 Average payoff and distribution of reports by gender

In the individual treatment, the average payoff is higher for male subjects (3.72) than for female subjects (3.00) and both payoff distributions differ significantly from the uniform distribution that would lead to an average payoff of 2.50 ($p=0.000$ for males and $p=0.015$ for females, two-tailed one-sample Kolmogorov–Smirnov tests). Hence, male subjects are somewhat more prone to lying than female subjects, but the difference is not statistically significant ($p=0.108$, two-tailed Wilcoxon rank-sum test). These findings are consistent with those of Dreber and Johannesson (2008) and Muehlheusser et al. (2015). Male subjects most frequently report five to obtain the maximum possible payoff, whereas female subjects most frequently report four, which yields the second highest payoff. These results suggest that there may be gender differences in the attitudes toward feeling guilty and/or maintaining a favorable self-image.

In the group treatment, the average payoffs (3.47 for two males, 2.95 for two females, and 3.45 for mixed groups) are significantly different from 2.50 ($p=0.000$ for two males, $p=0.061$ for two females, and $p=0.030$ for mixed groups, two-tailed one-sample KS tests). The average payoff is somewhat lower for two females than for the other groups, but these differences are not statistically significant ($p = 0.307$ for two females versus two males and $p=0.444$ for two females versus mixed groups, two-tailed Wilcoxon rank-sum tests). These results are similar to the findings in Muehlheusser et al. (2015). Concerning the distributions of reported numbers, groups tend to report medium numbers (two or three), regardless of gender composition. Two male groups report five less frequently than male individuals, and two female groups report four less frequently than female individuals. These observations suggest that groups are more sensitive to the social image concern, regardless of gender.

Appendix C: Equilibrium lying behavior of the D &D model

This section provides the proof of the claim describing the characteristics of the equilibrium lying behavior of the model with the perceived size of the lie, given in Dufwenberg and Dufwenberg (2018).

Claim 2

The equilibrium distribution of reported numbers in the D &D model, $q_x(\theta )$, has the following properties:

• (i) (a) When $\theta \rightarrow 2$ (from above), $q_5(\theta )\rightarrow 1$ and $q_x(\theta )\rightarrow 0$, for $x\in \{0,\dots ,4\}$. (b) When $\theta \rightarrow \infty$, $q_x(\theta )\rightarrow 1/6$, for all x.

• (ii) (a) $q_5(\theta )$ is strictly decreasing in $\theta > 2$. (b) $q_0(\theta )$ and $q_1(\theta )$ are strictly increasing in $\theta > 2$. (c) For $x\in \{2,3,4\}$, there exists $\theta > 2$, such that $q_x(\theta )>1/6$.

• (iii) $q_x(\theta )$ is strictly increasing in x, for all $\theta > 2$.

Proof

(i)(a) It suffices to show that when $\theta \rightarrow 2$ (from above), $s(5|\omega )\rightarrow 1$, for all $\omega < 5$. Under the equilibrium,

$$\begin{aligned} 1-\varepsilon _x = \frac{2}{x(\theta -2)+\theta } \end{aligned}$$

(3)

is satisfied, for all $\theta >2$ and $x\in \{1,\dots ,5\}$ (see Sect. 3.4 and the proof of the proposition in Sect. 3.3 in D &D). Because $s(5|\omega ) = 1-\varepsilon _5$, for $\omega <5$, from the construction of the strategy, we have $s(5|\omega )\rightarrow 1$, as $\theta \rightarrow 2$, for all $\omega <5$.

(b) It suffices to show that when $\theta \rightarrow \infty$, $s(\omega |\omega )\rightarrow 1$ for all $\omega$. First, note that because there is no downward lying, from the construction of the strategy, we have $s(5|5)=1$. Because $s(\omega |\omega )=\prod _{\omega +1\le k \le 5}\varepsilon _k$, for $\omega <5$, we have $s(\omega |\omega )\rightarrow 1$ as $\theta \rightarrow \infty$.

(ii)(a) It follows immediately from the observation that $q_5(\theta )= \frac{1}{6}[5(1-\varepsilon _5)+1]$, and that $1-\varepsilon _5 = \frac{2}{5(\theta -2)+\theta }$ is strictly decreasing in $\theta >2$.

(b) For $q_0(\theta )$, it follows immediately from the observation that $q_0(\theta ) = \prod _{1\le k\le 5}\varepsilon _k$, and that $\varepsilon _k = 1 - \frac{2}{k(\theta -2)+\theta }$ is strictly increasing in $\theta >2$, for all $k\in \{1,\dots ,5\}$.

Differentiating $q_1(\theta )=\frac{1}{6}(2-\varepsilon _1)\prod _{2\le k\le 5}\varepsilon _k$, we have

$$\begin{aligned} q_1'(\theta )= & {} \frac{1}{6}[-\varepsilon _1'\varepsilon _2\varepsilon _3\varepsilon _4\varepsilon _5 + (2-\varepsilon _1)\varepsilon _2'\varepsilon _3\varepsilon _4\varepsilon _5 \\{} & {} + (2-\varepsilon _1)\varepsilon _2\varepsilon _3'\varepsilon _4\varepsilon _5 + (2-\varepsilon _1)\varepsilon _2\varepsilon _3\varepsilon _4'\varepsilon _5 + (2-\varepsilon _1)\varepsilon _2\varepsilon _3\varepsilon _4\varepsilon _5'] \\> & {} \frac{1}{6}\bigg (-\varepsilon _1' + \sum _{2\le k \le 5}\varepsilon _k'\bigg )\prod _{2\le l \le 5}\varepsilon _l. \end{aligned}$$

Here, the inequality stems from the fact that $2-\varepsilon _1>\varepsilon _x$, for all x. Because $\varepsilon _x>0$, it suffices to show that $-\varepsilon _1' + \sum _{2\le k \le 5}\varepsilon _k'>0$. Because $\varepsilon _x'=\frac{2(x+1)}{[x(\theta -2)+\theta ]^2}$, we have

$$\begin{aligned} -\varepsilon _1' + \sum _{2\le k \le 5}\varepsilon _k'= & {} -\frac{1}{(\theta -1)^2}+\sum _{2\le k\le 5}\frac{2(k+1)}{[k(\theta -2)+\theta ]^2} \\> & {} -\frac{1}{(\theta -1)^2}+\sum _{2\le k\le 5}\frac{2(k+1)}{[5(\theta -2)+\theta ]^2} \\= & {} \frac{12\theta -16}{(\theta -1)^2(3\theta -5)^2} > 0, \end{aligned}$$

for $\theta >2$.

(c) It is easy to see that

$$\begin{aligned} q_2(20)= & {} \frac{1}{6}\bigg (3-2\cdot \frac{27}{28}\bigg )\cdot \frac{36}{37}\cdot \frac{45}{46}\cdot \frac{54}{55}=\frac{1}{6}\cdot \frac{1312200}{1310540}>\frac{1}{6},\\ q_3(5)= & {} \frac{1}{6}\bigg (4-3\cdot \frac{6}{7}\bigg )\cdot \frac{15}{17}\cdot \frac{9}{10}=\frac{1}{6}\cdot \frac{1350}{1190}>\frac{1}{6}, \text { and} \\ q_4(3)= & {} \frac{1}{6}\bigg (5-4\cdot \frac{5}{7}\bigg )\cdot \frac{3}{4}=\frac{1}{6}\cdot \frac{45}{28}>\frac{1}{6}. \end{aligned}$$

(iii) Because $\varepsilon _k\in (0,1)$, for all $k\in \{1,\dots ,5\}$, we have

$$\begin{aligned} q_0(\theta )=\frac{1}{6}\prod _{1\le k\le 5}\varepsilon _k<\frac{1}{6}\prod _{2\le k\le 5}\varepsilon _k<\frac{1}{6}[(1-\varepsilon _1) + 1]\prod _{2\le k\le 5}\varepsilon _k = q_1(\theta ). \end{aligned}$$

From (1), we have

$$\begin{aligned} x(1-\varepsilon _x)+1 = \frac{1}{1-\frac{2}{\theta }\frac{x}{x+1}} < \frac{1}{1-\frac{2}{\theta }\frac{x+1}{x+2}} = (x+1)(1-\varepsilon _{x+1})+1, \end{aligned}$$

for $x\in \{1,\dots ,4\}$. It follows that, for $x\in \{1,2,3\}$,

$$\begin{aligned} q_x(\theta ) = \frac{1}{6}[x(1-\varepsilon _x)+1]\prod _{x+1\le k \le 5}\varepsilon _k< & {} \frac{1}{6}[x(1-\varepsilon _x)+1]\prod _{x+2\le k \le 5}\varepsilon _k \\< & {} \frac{1}{6}[(x+1)(1-\varepsilon _{x+1})+1]\prod _{x+2\le k \le 5}\varepsilon _k = q_{x+1}(\theta ). \end{aligned}$$

Finally,

$$\begin{aligned} q_4(\theta )=\frac{1}{6}[4(1-\varepsilon _4)+1]\varepsilon _5< \frac{1}{6}[4(1-\varepsilon _4)+1] < \frac{1}{6}[5(1-\varepsilon _5)+1] = q_5(\theta ). \end{aligned}$$

$\square$

Appendix D: Translated instructions

Thank you for responding to the survey. The amount of reward that the two of you receive (individual treatment: the amount that you receive) for today’s questionnaire survey will be determined by the number that comes up on a dice.

Please choose a representative (either you or your friend) and roll the dice in the envelope once only. The reward for each person will be determined by the number that comes up. It does not matter which of you rolls the dice (the two of you will receive the same amount). (Individual treatment: Please roll the dice in the envelope once only. Your reward will be determined by the number that comes up.) Please check the amount in the table below.

Number	Reward per person
1	600 yen
2	700 yen
3	800 yen
4	900 yen
5	1000 yen
6	500 yen

Roll the dice and write down the number that comes up.

Answer:

After the initial roll of the dice, you may roll it several times to make sure that it is not loaded. However, in the above box, write only the number that comes up first.

After writing down the number, please put this sheet in the envelope and give it to the person in charge. Thank you for your cooperation in today’s survey.