Abstract
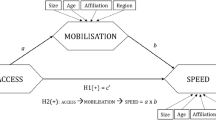
This study investigates how the structure of a domestic firm-to-firm transaction network influences the foreign direct investment (FDI) decisions of embedded firms in the network. We theoretically describe firms’ FDI decisions using an incomplete information game that considers the firm-to-firm transactions of intermediate inputs and in which firms have an incentive to collocate with their trading partners in foreign markets. We show that the probability of a firm engaging in FDI increases with its Katz–Bonacich centrality, which is defined as aggregated accessibility to all other firms and represents expected profit gained from colocation with its partners. We empirically show that this prediction is supported using disaggregated inter-firm transaction network data on Japanese firms. We also extended both theoretical and empirical frameworks to consider the dynamic aspect of FDI. When we consider existing foreign affiliates, accessibility to prior investors in the transaction network, named Katz–Bonacich accessibility, positively influences FDI as well as Katz–Bonacich centrality.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Increasingly many firms enjoy the benefits of extending their market or accessing cheap production resources from foreign direct investment (FDI). However, they also face difficulties in procuring from local firms in the host country due to a mismatch in the design and quality of the products and their delivery systems.Footnote 1 Therefore, there is an incentive to replicate transaction partnerships in the domestic market, form supply links with home-country suppliers, and maintain sales in foreign countries (e.g., Martin et al. 1995; Hackett and Srinivasan 1998). This type of FDI, which is called “follow-sourcing” (Humphrey 2003), is observed in various industries, such as the automotive industries in India and Brazil (Humphrey 2003), supermarkets (Reardon et al. 2007), and machinery sectors, which require numerous components that are supplied by subcontractors (Urata 1994).
The discussion regarding the follow-sourcing incentive implies the importance of focusing on the network of domestic firm-to-firm transactions when we consider outward FDI from a home country. Although each follow-sourcing incentive is originally generated in firm-to-firm transactions, a firm’s FDI decision influences its direct partners’ FDI decisions and, thus, is indirectly linked to partners, partners’ partners, and so on. Therefore, the outward FDI of a firm is driven by its entire domestic transaction network, and the feedback from the network differs according to the positions of firms within it.
This study investigates how domestic transaction networks yield forces that drive outward FDI by focusing on the detailed structure of the network, namely, on who transacts with whom, and on firm-level FDI decisions. According to several related empirical papers, the follow-sourcing incentive leads to the agglomeration of multinational enterprises that belong to the same industry, to vertically related industries, or to the same firm group (keiretsu; e.g., Smith and Florida 1994; Head et al. 1995, 1999; Head and Ries 1996; Belderbos and Carree 2002). However, since transaction networks are large and complex in practice (e.g., Saito et al. 2008; Atalay et al. 2011), disaggregated information on entire supply chain networks is necessary for precisely capturing the follow-sourcing incentive. Indeed, although several studies such as Yamashita et al. (2014) have analyzed detailed information on networks by considering agglomeration activities, to the best of the authors’ knowledge, no study has shown either empirical evidence on or a theoretical framework for how the network structure affects the location selection.Footnote 2
This study, which consists of both theoretical and empirical parts, expands the body of knowledge on this topic in this direction. In the theory section, we describe how firms that are embedded in a supply chain network decide whether to undertake FDI in a foreign market. We consider firm-to-firm transactions of intermediate inputs or outsourcing of various production tasks, and the basic setup of our production process is similar to those of recent studies such as Antràs and Helpman (2004), Eaton et al. (2016), and Bernard et al. (2019).
However, whereas related papers focus on how each transaction is formed, we regard the transaction network as exogenously given and we focus on the extent to which established networks affect FDI. Our model consists of two parts: the first represents the mechanism how firms yields profit and share it through transaction, and the second represents their FDI decisions. Each part is summarized as follows. First, we assume that a long-run relationship between a pair of firms yields a profit through the trading of intermediate inputs or services that have been specially customized according to a buyer’s needs, which are termed “adaptive inputs.” The profit is lost if they do not trade and the buyer procures from new transaction partner, and it is assumed that both the buyer and seller have equal bargaining power and, hence, that the profit is equally shared between them. We describe such a long-run transaction by a link of the network. Firms want to collocate with their linked partners. Despite concerns regarding the endogeneity and simultaneity of FDI and network formation, several studies have found a limited effect of FDI on domestic transactions, which suggests that transaction networks are stable in the long run (e.g., Asanuma and Kikutani 1992). Furthermore, when highlighting such relation-specific value of each product, the price should also be determined in each one-to-one relationship between firms rather than in a market that consists of many firms as in previous studies considering monopolistic competition of each differentiated products.
Second, we consider the probabilistic location choices of firms by assuming an incomplete information game.Footnote 3 When a firm decides on its FDI, it considers information on the market conditions of the destination country such as the labor costs, natural resources, product demand, and political situation. Since such conditions differ among firms, and some are the private information of each firm, the expectation (probability) of FDI by others is taken into account in addition to the observed investment when each firm decides on its FDI. Due to the probabilistic setting, the strategy of each firm is described by continuous values. Then, the diffusion of the strategy via the entire network can be described.
Our theoretical analysis shows that the probability of each firm undertaking FDI converges to a unique Bayesian Nash equilibrium in which the FDI probability is explicitly described using a network measure that is referred to as the Katz–Bonacich centrality.Footnote 4 The Katz–Bonacich centrality represents the degree of accessibility of a node, namely, a firm in this study, to all other nodes through the network. This network measure evaluates the centrality of a node within the network not only by the number of directly linked nodes to the node but also by all the indirect connections; hence, this measure describes the extent to which a node receives the influence of externalities from the entire network. The centrality index of a node increases when those of directly linked nodes increase. From the equilibrium characteristics, we deduce the empirically testable theoretical implication that the FDI incentive of a firm increases with its Katz–Bonacich centrality. Although such a “discrete choice under incomplete information” setting has been examined by Bloch and Quérou (2013) and Itoh (2014), our more generalized model can replicate the cases that are considered in these two related papers as special cases.Footnote 5Footnote 6
The novel contribution of our theoretical part to the literature of fixed network games is the introduction of firm-to-firm transactions. Our paper explicitly adopts the mechanism via which a transaction yields an additive profit compared to a new transaction and the mechanism via which each product price is endogenously determined to share the profit between the seller and the buyer, whereas previous network games simply begin with an ad-hoc payoff function. The provision of such a microfoundation in the presented network game enables us to explain why the colocation of trading firms is beneficial, how the FDI incentive spreads across networks, and, more importantly, how FDI is affected by several structural parameters such as local procurement costs in domestic and foreign markets.
In the empirical part, we test this theoretical implication using actual firm-to-firm transaction relationship data. We use disaggregated inter-firm transaction data on 115,111 Japanese firms in the manufacturing sector. This network information enables us to calculate the Katz–Bonacich centrality to represent the detailed network structure of the Japanese manufacturing sector by capturing the inter-sectoral effects among subsectors. By merging this firm-level dataset with a database of Japanese foreign affiliates, we estimate the extent to which the supply chain network affects the FDI decisions of firms by regressing firms’ FDI behavior on the Katz–Bonacich centrality.
Our empirical results demonstrate the significantly positive effects of the Katz–Bonacich centrality on firms’ FDI decisions, which imply high friction and strong colocation incentives in foreign markets according to our theoretical analysis. Even though we control for the various individual attributes of firms and characteristics of hosting countries, the Katz–Bonacich centrality maintains robust positive effects on FDI decisions. Quantitatively, the positive effects of the Katz–Bonacich centrality are large, as are the effects of productivity, which has been shown to be the main engine of FDI (Helpman et al. 2004). This finding suggests the importance of considering the supply chain network in the FDI decisions of firms.
This paper also presents an extended analysis that considers the dynamic aspect of FDI, even though our baseline model is based on a static simultaneous move game in which we focus only on the follow-sourcing incentive via expectations. The expectations of the trends of other firms are important, because as the FDI of Japanese firms has rapidly increased over the past 2 decades due to rising globalization, some firms have been forced to make snap decisions regarding FDI. Nevertheless, such FDI decisions are still made sequentially; hence, in addition to expectations, observations of others’ FDI might also play an important role. Therefore, we conduct an extended theoretical analysis in which we consider this dynamic feature of FDI and show that the FDI of firms is influenced by the Katz–Bonacich accessibility to prior investors, along with their Katz–Bonacich centrality in the network. We evaluate this prediction based on data. Hence, the Katz–Bonacich centrality, which is interpreted as the influence of expectations, still significantly affects FDI, even under such an extended setting.
Empirical studies of network effects, especially in application to social interactions, have been increasing conducted since the seminal paper of Manski (1993) (e.g., De Giorgi et al. 2010; De Giorgi and Pellizzari 2013; Blume et al. 2014). In the literature on social interactions, for example, Calvó-Armengol et al. (2009) use the model that was proposed by Ballester and Calvó-Armengol (2010) and examine the network effects under the equilibrium of the Katz–Bonacich centrality. Then, these authors structurally estimate the payoff functions of each individual and estimate the network effects using data on the educational effort of households and their networks. In contrast to that of Calvó-Armengol et al. (2009), and as discussed earlier, our model is based on a discrete choice, incomplete information setting. First, as Bernard and Jensen (1999) show only a few firms conduct FDI, while the investment of many others is zero. This is because firm must bear an initial fixed cost for FDI and initially face a discrete choice regarding whether to invest or not; hence, a continuous outcome model such as Calvó-Armengol et al. (2009) does not fit the present scenario. Second, since firms’ private information cannot be obtained exactly by competitors, an incomplete information setup is more suitable for our topic.
The remainder of this paper is organized as follows. Section 2 presents a static coordination game with a network and theoretically examines the results. Section 3 presents the data and framework that were used for our empirical analysis. Section 4 discusses our baseline empirical results, and Sect. 5 discusses the robustness of the baseline analysis by extending the model and empirical methods. Finally, Sect. 6 presents the conclusion of the paper.
2 Theoretical prediction
Consider a domestic market D, a foreign market F, and n firms for which the home country is D. In period \(t=0\), each of these firms operates its production facilities in market D, which produces a differentiated product by inputting intermediate goods that are produced by other firms. Suppose \(g_{ij}\) denotes the product quantity that firm i provides to firm j in period \(t=0\). Then, matrix \({\varvec{G}}=\{g_{ij}\}\) describes the directed transaction network. Now, given \({\varvec{G}}\), we consider a location choice in period \(t=1\) regarding whether domestic firms relocate a specified number of their facilities to the foreign market or stay in the domestic market in this period.Footnote 7 Firms that choose relocation must implement a foreign direct investment to establish a foreign affiliate. After the relocation is complete, all the relocated facilities may conduct new transactions and production to maximize their profit.
2.1 Transaction and profit sharing
Suppose the location of establishment i in period 1 is \(r=\{D,F\}\). Its production process is as follows: each establishment requires the completion of various differentiated tasks for production, each of which is conducted either via inter-firm transaction or self-production. Via the first approach, the firm inputs an adaptive intermediate product that has been specially customized by its supplier according to the task; this is equivalent to outsourcing the task. As adaptive goods are developed through long-term communication, we assume that only the trading partner in period 0 can provide the adaptive good in period 1. The second approach is a self-production. Firms can complete the task by customizing commodity goods that have been procured from the competitive market, thereby incurring self-customization cost \(c_{r}\ge 0\). It also includes outsourcing to a new firm, and it has a cost \(c_{r}\), which is interpreted as the search cost or start-up cost in the local market.Footnote 8
Also, a transportation cost \(\tau\) is incurred in the trading of an adaptive good if firms i and j are located in different countries. Although we assume that the supplier bears the transport cost, this assumption is not crucial for our analysis. Given the firms’ locations \(r_{i}\) and \(r_{j}\), the transportation cost is \(\tau (r_{i},r_{j})\), where \(\tau (r_{i},r_{j})\) equals \(\tau\) if \(r_{i}\ne r_{j}\) and zero otherwise.
Now, we consider transactions between two firms, namely, i and j, under the assumption that firm i can provide an adaptive good to firm j. The price of adaptive good \(s_{ij}\) is determined by a bargaining process between the two firms. We assume that the buyer and seller have equal bargaining power and that the profit from trading one unit of the commodity good is the respective payoff for both players. The seller’s relative profit from trading an adaptive good, compared to the profit without trading, is \(s_{ij}-\tau (r_{i},r_{j})\). In contrast, the buyer’s relative transaction profit compared to the self-production is \(-s_{ij}+c_{r_{j}}\). Since both the seller and the buyer have equal bargaining power, the price of an adaptive input is determined as \(s_{ij}=[c_{r_{j}}+\tau (r_{i},r_{j})]/2\); hence, both firms gain the same relative profit \(\tilde{\nu }_{r_{i}r_{j}}=[c_{r_{j}}-\tau (r_{i},r_{j})]/2\). The firms agree to trade if and only if the relative profit is positive. Since we assume that \(c_r\ge 0\) holds in both markets, the adaptive good is necessarily traded if the two firms are located in the same region.
Furthermore, \(\nu _{{r_{i}r_{j}}}=\max \{\tilde{\nu }_{r_{i}r_{j}},0\}\) denotes the transaction profit that firms i and j both gain if they can trade the adaptive good. Therefore, the following holds:
As \(\nu _{r_{i} r_{j}}=\nu _{r_{j} r_{i}}\) does not generally hold for \(r_{i}\ne r_{j}\), the additive profit may be asymmetric in terms of the locations of the buyer and the seller, since their location choices have different effects on the joint profit. Therefore, they may have different incentives for colocation if \(\nu _{r_{i} r_{j}}\ne \nu _{r_{j} r_{i}}\) holds.
2.2 Choice of FDI
Next, we describe the location choices of domestic firms in period 1. The ex-post profit, or the profit under all firms’ locations \((r_{1},\ldots ,r_{n})\), that is obtained by firm i while operating in country r, is as follows:
where \(z_{ir}\) is the stand-alone profit, which is gained without adaptive goods being traded through the network. This study assumes that \(q_{ir}\) is a stochastic value that differs by firm and location, which is the private information of firm i; then, firm i knows the deterministic values of \(q_{iD}\) and \(q_{iF}\) when choosing its location, while only the distribution is provided for others’ \(q_{jr}\). This is because firms differ in terms of their levels of technology, which require different skills and capital; furthermore, head-hunting for engineers and research on industrial parks are conducted confidentially. At this time, \(z_{ir}\) is also private information. In contrast, we assume that each firm has complete information on network \({\varvec{G}}\), because the current inter-firm transaction network is accessible information, which becomes available for a fee.
This study assumes that \(q_{i}\equiv q_{iF}-q_{iD}\) follows a uniform distribution with support \([-\sigma ,\sigma ]\). Therefore, \(z_{i}\equiv z_{iF}-z_{iD}\) also follows a uniform distribution as follows:
where \(\bar{z}\) is the mean value of \(z_{i}\), which denotes the average relative stand-alone profit of the foreign country. Each firm is assumed to be risk–neutral and able to form the correct expectation of all others’ probabilities of being located in each country. Hence, it chooses its location to maximize its expected profit given all the information above.
2.3 Bayesian Nash equilibrium and Katz–Bonacich centrality
In this incomplete information game, the strategy of each firm is described by its strategic threshold \(\theta _{i}\), with which firm i chooses location F if the stand-alone profit is such that \(z_{i}\ge \theta _{i}\) holds. Given threshold \(\theta _{j}\), the objective probability of firm j being located in country F is expressed as \({\rm Prob}\left[ z_{j}\ge \theta _{j}\right] =1-F \left( \theta _{j} \right)\); a lower threshold corresponds to a higher probability of engaging in FDI. Denote the vector of thresholds by \({\varvec{\theta }}=\left( \theta _{1},\ldots ,\theta _{n}\right)\). The expected profits of firm i from choosing locations F and D are expressed as follows:
Now, we define the relative profit as follows:
The location externality on the relative profit is symmetric for both sides of the transaction; namely, for both the buyer and the seller, the marginal profit from the partner’s probability is the same. However, this property depends on the assumption of equal bargaining power.
Based on the relative profit, we derive the best-response threshold from the expected profit. Since the best-response threshold \(\theta _{i}({\varvec{\theta ;G}})\) satisfies \(E\left( \pi _{iD}|{\varvec{\theta ,G}},z_{iD}\right) =E \left( \pi _{iF}|{\varvec{\theta ,G}},z_{iF}\right)\) given \(z_{i}=\theta _{i}({\varvec{\theta ;G}})\) and all others’ thresholds, \(\theta _{i}({\varvec{\theta ;G}})\) is expressed as follows:
Therefore, \(\beta =\beta '\) holds if \(\tau >{\rm max}\{c_\mathrm{F},c_\mathrm{D}\}\) is satisfied and, consequently, \(\nu _\mathrm{\mathrm DF}=\nu _\mathrm{FD}=0\) holds; otherwise, \(\beta \ne \beta '\). This is due to the asymmetric location incentive between the seller and buyer when an international transaction is possible. Equation 6 holds only if \(\theta _i\), \(\theta _j\), and \(\theta _k\) are in \(\left[ -\sigma +\bar{z}, -\sigma +\bar{z}\right]\), in which \(z_i\) is assigned; then, we can consider an interior solution.Footnote 9
Next, using a vector of the best-response thresholds, which is expressed as \({\varvec{\theta }}({\varvec{\theta ,G}})=(\theta _{1}({\varvec{\theta ,G}}),\ldots ,\theta _{n}({\varvec{\theta ,G}}))^{T}\), the system of Eq. (6) is expressed in the following matrix form:
where \(\tilde{{\varvec{G}}}\equiv {\varvec{G}}+{\varvec{G}}^{T}\) is a reciprocal transaction network in which the buyer and supplier are distinguished. When we derive the Bayesian Nash equilibrium from equation (7), we focus only on the unique interior equilibrium in which \(F(\theta _{i})\in (0,1)\) holds for all i. Since each firm chooses both markets in a strictly positive probability, our model can demonstrate the location patterns that are observed in the data. We now assume \(\sigma >|\bar{z}|+2(n-1){\rm max}\{\nu _\mathrm{FF}-\nu _\mathrm{FD},\nu _\mathrm{FF}-\nu _\mathrm{DF},\nu _\mathrm{DD}-\nu _\mathrm{FD},\nu _\mathrm{DD}-\nu _\mathrm{DF}\} \equiv \bar{\sigma }\), by which the convergence of the inverse matrix \(({\varvec{I}}-\rho \tilde{{\varvec{G}}})^{-1}\) and the interiority of equilibrium probability, namely, \(F(\theta _{j})\in [0,1]\), are sufficiently guaranteed for all the players regardless of network structure.Footnote 10 This condition is satisfied for large \(\sigma\) or small \(\nu _{rr}\); namely, the assumption of a large uncertainty or an insignificant colocation incentive renders the model tractable by excluding the corner solutions.
By solving \({\varvec{\theta }}={\varvec{\hat{\theta }}}({\varvec{\theta }})\) for \({\varvec{\theta }}\), we obtain interior equilibrium \({\varvec{\theta }}^{*}\) as follows:
\(({\varvec{I}}-\rho \tilde{{\varvec{G}}})^{-1}{\varvec{\widetilde{G}1}}\) is equivalent to the Katz–Bonacich centrality or alpha-centrality (Bonacich 1987; Ballester and Calvó-Armengol 2010), which is denoted by \(B({\varvec{\widetilde{G}}})=(b_{1}({\varvec{\widetilde{G}}}),\ldots ,b_{n}({\varvec{\widetilde{G}}}))^T\). Furthermore, the second term takes a similar form, but the asymmetry between the seller and the buyer must be considered. However, the second term disappears if \(\tau >{\rm max}\{c_\mathrm{F},c_\mathrm{D}\}\); then, \(\beta =\beta '\) holds.Footnote 11
Therefore, the equilibrium behavior of our model is characterized by the Katz–Bonacich centrality in the transaction network. Although the effect of the centrality on FDI can be positive or negative depending on the sign of \(\beta\), more central firms have larger absolute threshold values. Since a zero threshold value corresponds to the firm considering only its stand-alone profit and not the network profit when selecting its location, the Katz–Bonacich centrality in our model reflects the aggregated externalities that each firm receives from the entire network. As discussed above, \(\rho\) describes the marginal network externality from the strategy of a direct transaction partner. However, from each direct relationship in the network, one’s strategy spills over to all indirectly linked firms on all paths, with the influence diminishing as the length of each path increases; hence, the influence converges to the Katz–Bonacich centrality measure.
Therefore, we obtain the following proposition from Eq. (8).
Proposition 1
Assuming \(\tau >{\rm max}\{c_\mathrm{F},c_\mathrm{D}\}\), firms with a higher Katz–Bonacich centrality choose a foreign country with a higher (lower) probability if \(\beta\) is positive (negative).
The sign of \(\beta\) crucially influences our hypothesis. Since \(\beta =\left[ \sigma \left( c_\mathrm{F}-c_\mathrm{D}\right) +\bar{z}\left( c_\mathrm{F}+c_\mathrm{D}\right) \right] /4\sigma\) holds if \(\tau\) is sufficiently large according to Eqs. (1) and (6), it particularly depends on \(c_\mathrm{F}\), \(c_\mathrm{D}\), and \(\bar{z}\). Given a relatively weak initial advantage of the foreign market or \(\bar{z} \le 0\), \(\beta\) can be positive only if \(c_\mathrm{F}\) significantly exceeds \(c_\mathrm{D}\), which corresponds to large friction in finding a new transaction partner in the foreign country. This also corresponds to a large additional benefit from colocation with the domestic partner to cause strong network externalities, and more central firms have a higher incentive to pursue FDI, because they gain more from the network effects. Furthermore, an increase in \(\bar{z}\) increases the number of other investors in the foreign market; then, the network effect in the foreign market increases.
Now, we consider two special cases of the model, which correspond to the models of Bloch and Quérou (2013) and Itoh (2014). First, under the assumption that \(c_\mathrm{D}=0\), which means that there is no network effect in the domestic market, our best-response function (6) coincides with that of Bloch and Quérou (2013); hence, the two models are equivalent. Thus, in this scenario, more central firms have a larger incentive to enter the foreign market when the network yields a large relative profit. In this case, \(\beta\) is always positive. This is because the network is beneficial only if a firm goes to a foreign market in which searching for a new partner is difficult, then higher Katz-Bonacich centrality promotes FDI.
Second, Itoh’s (2014) model is equivalent to the case in which \(c_\mathrm{D}=c_\mathrm{F}\), which is interpreted as the two countries have equal network effects. In this case, the sign of \(\beta\) depends only on the sign of \(\bar{z}\), or on which country has an advantage in terms of stand-alone profit. If \(\bar{z}>0\), more than half of the firms are concentrated in the foreign market, and Katz-Bonacich centrality promotes FDI. However, according to our data in the preceding empirical sections, only a small proportion of Japanese firms (around 3\(\%\)) decide to pursue FDI; hence, \(\beta\) should be negative in Itoh’s (2014) case in practice.
Finally, although we almost ignored \(\tau\) in the above statement, let us discuss the role of \(\tau\) in the equilibrium behavior when it is sufficiently small. First, \(\rho\) decreases as \(\tau\) decreases; hence, the location externality decreases as the international transaction barrier diminishes. This is also the case for \(\beta\) for the same reason; hence, the role of the network diminishes as the two countries become integrated.
3 Data and empirical strategy
3.1 Data
We use a dataset that was compiled by a major credit research firm, namely, Tokyo Shoko Research Incorporated (TSR), for 2006. The dataset includes information on 826,169 large and small corporations in Japan, which represent approximately half of all incorporated firms in the country. The focus of this study is on manufacturing firms, which reduces our sample size to 142,282 firms. The dataset includes information on each firm’s name, address, industry classification code, establishment year, number of employees, sales, and credit score. Furthermore, this database includes information on each firm’s suppliers and customers. The maximum number of customers or suppliers each firm can report is 24, which may underrepresent the actual number of transaction partners. To mitigate this issue, we combine self-reported and other reported transaction information.Footnote 12
We also use a dataset of Japanese manufacturing firms that undertake foreign investment that was compiled by another major research firm, namely, Toyo Keizai Shimpo Sha (TKZ). This dataset contains information on the location (country and address), year invested, employment, names of the owners, and ownership ratio of all foreign affiliations of Japanese firms. We use the database of all foreign subsidiaries with Japanese ownership of 10% or higher that were operating in 2010. By combining the TSR dataset (according to the names of the firms) with the TKZ dataset (according to the ownership of the firms), we build a database of Japanese firms’ FDI activities and their transaction relationships in Japan. Table 1 presents the summary statistics of the dataset.
Our dataset contains 115,111 observations after merging the reduced samples of the TSR and TKZ databases. Regarding FDI behavior, 2278 manufacturing firms have at least one foreign affiliate, with 2070 of these firms having affiliates in Southeast Asia. This suggests that most FDI firms have affiliates in this region.
3.2 Empirical strategy
To evaluate our theoretical prediction, we estimate the following equation:
where \({\rm FDI}_{ir}\) is the FDI dummy, which takes the value of one if firm i conducts FDI in region r and zero otherwise; \(ln({\rm centrality}_i)\) is the natural logarithm of the Katz–Bonacich centrality; \({\varvec{X_{ir}^{\prime }}}\) represents the covariates; and \(\epsilon _{ir}\) is the error term. We estimate Eq. (9) using a linear probability model.
In the estimation, we consider the overall supply chain network in the manufacturing industry to capture the inter-sectoral effects. Since the supply chain network extends beyond the industry, the FDI decision of a firm depends on the whole manufacturing transaction network rather than on the industry network to which the firm belongs. For example, the FDI decision of a tire-producing firm that is classified as belonging to the rubber industry depends on the behavior of not only other firms that belong to the rubber industry but also firms that belong to additional industries such as the motor vehicle industry.
However, the consideration of the supply chain network of all manufacturing firms leads to computational difficulty in estimating the equation. Although this Eq. (9) appears to be linear, the centrality measure \({\rm centrality}_i\) is \(({\varvec{I}}-\rho \tilde{{\varvec{G}}})^{-1}{\varvec{\widetilde{G}1}}\). The equation is nonlinear in the parameter \(\rho\), which must be estimated. To conduct nonlinear estimation with consideration of transaction network of all manufacturing firms, we must invert the adjacency matrix \(\tilde{{\varvec{G}}}\), which is of size 115,111\(\times\)115,111; this is infeasible. To estimate the equation, it is necessary to avoid the inversion of the adjacency matrix with the full-sized sample. One approach to avoid the calculation of the inverse matrix is the use of the eigenvector centrality, which is a special case of the Katz–Bonacich centrality. Under the assumption that the value of the parameter \(\rho\) is the inverse of the largest eigenvalue of adjacency matrix \({\varvec{\tilde{G}}}\), the Katz–Bonacich centrality can be calculated without the inversion of the adjacency matrix (see Bonacich 1987). The special case of the Katz–Bonacich centrality in which the inverse of the largest eigenvalue of \({\varvec{\tilde{G}}}\) is applied as the decay parameter \(\rho\) is called the eigenvector centrality. By substituting the largest eigenvalue of adjacency matrix \({\varvec{\tilde{G}}}\) for the parameter \(\rho\), we calculate the eigenvector centrality, and we use this in the baseline analysis as a proxy for the Katz–Bonacich centrality.
However, there is no rationale from economic theory that supports the use of the eigenvector centrality instead of the Katz–Bonacich centrality; namely, economic theory does not support the correspondence of the inverse of the largest eigenvalue of \({\varvec{\tilde{G}}}\) to the parameter \(\rho\), which is determined by the trading surpluses \(\nu _{rr'}\) and the size of the support \(\sigma\) of profit shocks \(q_i\) in the model. We implement an extended estimation to support the use of the eigenvector centrality empirically. Using a subset of the supply chain network data, we regress the Eq. (9) using the Katz–Bonacich centrality in a nonlinear form, which can estimate the parameter \(\rho\). By demonstrating that the estimated value of \(\rho\) is statistically equivalent to the largest eigenvalue of \({\varvec{\tilde{G}}}\), we support the use of the eigenvector centrality in the whole sample analysis. This is conducted in Sect. 4.4.
For the other covariates \({\varvec{X_{ir}^{\prime }}}\), we first include the firm productivity. According to Helpman et al. (2004), the firm productivity is an important determinant of firms’ FDI decisions. A firm’s productivity may correlate with its location in the supply chain network. A highly productive firm may attract many customers, thereby increasing its Katz–Bonacich centrality. To respond to this endogeneity concern, we introduce the firm productivity. Unfortunately, our database does not include capital information; therefore, we cannot estimate the total factor productivity. Hence, we introduce the labor productivity, which is calculated as the sales divided by the number of workers, for the measurement of the firm productivity.
In addition to the firm productivity, the firm performance and credibility might also affect firms’ FDI decisions and, thus, their Katz–Bonacich centrality values. We include the firm age and the listed firm dummy, which takes the value of one if the firm is listed and zero otherwise. Furthermore, we include the firm credibility as a measure of comprehensive firm performance. The firm credibility is a measure of the total evaluation of a firm that was originally created by TSR using public sources of information and face-to-face interviews. This represents the total performance of a firm and is used by companies in selecting transaction partners in practice. The credibility value ranges from 0 to 100.
The endogeneity problem, namely, that an FDI decision of a firm may affect the structure of the transaction network, must also be addressed. For example, two firms in a home country that share no transaction relationship may establish foreign affiliates in close geographical proximity, which, in turn, may facilitate transactions between them. However, these new transaction relationships between foreign affiliates are extremely rare. For example, according to Asanuma and Kikutani (1992), long-term supply relationships are crucial for firm performance in the Japanese automobile industry. Indeed, firms commonly replicate their supply links with home-country suppliers and maintain their sales in foreign countries (e.g., Urata 1994; Martin et al. 1995; Hackett and Srinivasan 1998). Therefore, for the FDI of firms, only the supply chain network in the domestic market is relevant. These trunk relationships would be negligibly influenced by the decision of FDI and would be stable at least in the short run.
4 Empirical results
4.1 Baseline results
Table 1 presents the summary statistics, which highlight that firms that conduct FDI have high Katz–Bonacich centrality values compared with non-FDI firms.
Table 2 presents the results of the baseline estimation that was conducted using pooled FDI data regardless of the destination; namely, \(\text {FDI}_{ir}\) is equal to one if firm i has foreign affiliates, regardless of their locations. Column (1) in Table 2 presents the benchmark results, which include all manufacturing firms in Japan and were estimated using a linear probability model. The coefficient for the Katz–Bonacich centrality is positively significant, which implies positive \(\beta\) according to our theoretical prediction in Eq. (8). Since only a small fraction of FDI firms support negative \(\bar{z}\), this empirical result implies \(c_\mathrm{F}>c_\mathrm{D}\); there is higher network externality in the foreign market due to the substantial difficulty in finding new transactions in the foreign market. Furthermore, we obtain reasonable coefficient signs for the remaining covariates; the coefficients for worker productivity, credit score, listed firm dummy, and firm age are positively significant, thereby suggesting the validity of the model specification.
The magnitude of the supply chain network effect may differ according to firm size. To evaluate this, we separately estimate Eq. (9) based on firm size. Columns (2) and (3) present the results for the samples of small and large firms, namely, fewer than 100 and more than 100 workers, respectively. In both columns, the coefficients for the Katz–Bonacich centrality are positively significant. However, the coefficients for the Katz–Bonacich centrality are larger in large firms than in small firms. Larger firms tend to be assemblers and must procure many parts and ingredients. Thus, local procurement is more crucial for their operation compared with the operation of small firms.
The FDI decision of a firm also depends on its products. To control for such industry heterogeneity, we include industry fixed effects in the estimation equation, the results of which are presented in Columns (4)–(6) of Table 2. We use the four-digit industrial classification in the Japan Standard Industrial Classification (JSIC). Column (4) presents the results. Even after controlling for industry fixed effects, the coefficient for the Katz–Bonacich centrality is positively significant, as are the coefficients for all the other covariates. Columns (5) and (6) present the results for small and large firms, respectively. The differences in the coefficients for the Katz–Bonacich centrality between these firms become much larger. Thus, by controlling for industry fixed effects, the difference between the transaction networks’ roles in the FDI decisions of large and small firms is much sharper.
Both the FDI decisions and the centrality of the firms in the supply chain network depend on their domestic headquarter locations. Firms that are located in large metropolitan areas can find numerous transaction partners due to their locational proximity with other firms, which can reduce transaction costs; furthermore, the knowhow that is necessary for conducting FDI may spill over from the concentration of firms, thereby promoting the entrance of mediating firms that support other firms’ FDI and facilitating the FDI decisions of firms. To address to this concern, we include the prefectural-level location fixed effects of firms’ domestic headquarters. The results in Columns (7)–(9) of Table 2 suggest that even if we control for headquarter location, the Katz–Bonacich centrality still positively affects the FDI decisions of firms.
Finally, we compare the magnitudes of the Katz–Bonacich centrality and worker productivity based on their standardized coefficients, which represent the number of standard deviations that the predicted FDI probability will increase per standard deviation increase in a variable. For example, according to the results that are presented in Column (7), the standardized coefficient of the worker productivity is 0.410, whereas that of the Katz–Bonacich centrality is 0.318. This result demonstrates that the role of the supply chain network in FDI is significant and has a magnitude that is similar to that of the worker productivity, as emphasized previously (e.g., Helpman et al. (2004)). Hence, consideration of the supply chain network is necessary for understanding firms’ FDI decisions.
4.2 Heterogeneity in destination countries
In the above analysis, we included all FDI regardless of destination. However, as Baldwin and Okubo (2014) suggest, the objective and structure of the FDI by Japanese firms differ according to the destination. Thus, the role of the supply chain network in FDI decisions may also differ across host countries. To capture the differences in the roles of supply chain networks in FDI decisions across host countries, we conduct a separate analysis that focuses on Japanese FDI behavior by region. Table 3 presents the results.
Column (1) in Table 3 presents the results for FDI in Southeast Asia. In the estimation, the dependent variable is a dummy that takes the value of one if the firm conducts FDI in Southeast Asia and zero otherwise. We estimate this dummy using a linear probability model that includes industry and prefectural fixed effects. The coefficient for the Katz–Bonacich centrality is significantly positive, as are the coefficients for all the other covariates. Moreover, in the estimations for small and large firms [see Columns (2) and (3)], the coefficients for the Katz–Bonacich centrality and for the other variables are still positively significant. Furthermore, the magnitude of the Katz–Bonacich centrality is again larger for large firms than for small firms.
Columns (4)–(6) present the same estimation results for FDI in North America. Similar to the results for Southeast Asia, the coefficients for the Katz–Bonacich centrality are significantly positive. However, they are much smaller than those for FDI in Southeast Asia in every estimation (baseline, small firms, and large firms), thereby suggesting that the effects of transaction networks on FDI decisions are much larger in Asian countries than in North America. According to the theoretical result, \(\beta\) is small in North America, which is due to the small \(c_{\rm F}\) there. This is because there is relatively long history since 1970s of FDI by Japanese firms in the North American market. Therefore, a stable and certain procurement is possible in this matured market; hence, the network effect in that market is relatively small. In addition, according to Baldwin and Okubo (2014), Japanese firms form a regional value chain across Asia, thereby rendering the role of local sourcing and selling in Asian countries crucial for their profits.
Columns (7)–(9) in Table 2 present the results on Japanese FDI in China, which has recently benefited from vast FDI by Japanese firms. We find that the coefficients for the Katz–Bonacich centrality are always positively significant and that the magnitude remains larger for large firms than for small firms. Furthermore, the magnitude of the Katz–Bonacich centrality is between those in Southeast Asia and North America. This implies that the recent development of the Chinese economy may increase the quality of the local procurement.
4.3 Industry heterogeneity
To examine industry heterogeneity in FDI decisions, we re-estimate the equation for each two-digit JSIC. Since separating the samples by industry would reduce the sample size, we exclude prefectural fixed effects from this analysis. The results are presented in Table 4.
The coefficient for the Katz–Bonacich centrality is significantly positive in all industries except the lumber and wood industry, which may not require an intense production network. Although much of the related literature has focused on follow-sourcing FDI in assembly industries, as discussed by Urata (1994) and Humphry (2003), the coefficient for the Katz–Bonacich centrality is positive in most industries. This finding suggests that firms in most industries require intense production networks; hence, the location of a firm in the inter-firm network significantly affects its FDI behavior.
4.4 Validity of using eigenvector centrality
We conducted an analysis using the eigenvector centrality, which is a special case of the Katz–Bonacich centrality, by specifying the decay parameter \(\rho\) as the inverse of the largest eigenvalue of the adjacency matrix of the whole supply chain network \({\varvec{\tilde{G}}}\). However, there is no economic rationale for this correspondence between the inverse of the largest eigenvalue of \({\varvec{\tilde{G}}}\) and the decay parameter \(\rho\). To empirically support the use of the eigenvector centrality, we conduct an analysis using the Katz–Bonacich centrality and estimate the decay parameter \(\rho\).
To implement our estimation, we must reduce the size of the adjacency matrix of the whole supply chain network. For that purpose, we extract from the sample the largest 10,000 firms based on the number of employees,Footnote 13 and conduct our estimation using the nonlinear least-squares method.Footnote 14
The results are presented in Table 5. First, the coefficient for the log of the Katz–Bonacich centrality is positively significant at the 1% level. Therefore, the Katz–Bonacich centrality has a positive effect on FDI even without exogenously specifying the decay parameter. Furthermore, the point estimate of \(\gamma\) is 0.020, and this is positively significant. This finding implies that the network length has a statistically significant decay effect on FDI decisions. We cannot reject the null hypothesis that our point estimate of \(\rho\) is equal to the inverse of the largest eigenvalue of the adjacency matrix (0.023) that was used to calculate eigenvector centrality at the 10% level. Furthermore, the correlation coefficient between the estimated Katz–Bonacich centrality and the eigenvector centrality is 0.965. These results suggest the validity of using a decay parameter that is based on the inverse of the adjacency matrix eigenvalue and the validity of the results of the previous section that were obtained using this eigenvector centrality.
5 Influence of prior investors
We have demonstrated the importance of expectations on other firms’ FDI decisions under the static incomplete information game framework. However, FDI decisions are made sequentially; hence, the observation of others’ investment might also be important. To capture the dynamic features of FDI, this section extends our theory and empirical analysis.
5.1 Extension of the theoretical prediction
Here, we introduce the sequential features of FDI. In period 1, we consider two types of firms: prior investors and others. Prior investors already have an affiliate in the previous period (period 0); thus, the location choices of prior investors are provided exogenously when considering period 1. Given prior investors’ investing information, firms decide on their FDI activities to maximize their static profit.Footnote 15 Hence, prior investors decide whether to maintain established affiliations, while other firms that have no foreign affiliates decide whether to establish affiliates in the country. Therefore, all firms, including prior investors, play a simultaneous move game with incomplete information on \(z_{i}\), as represented in the baseline model that is presented in Sect. 2. However, the critical difference is the existence of prior investors, which are known by each firm.
Assume that new entrants into the foreign market must pay an investment cost \(W>0\) to establish a new affiliate, whereas prior investors can maintain their affiliates without incurring a cost. Therefore, new entrants invest if and only if their expected static profit exceeds W, whereas prior investors remain in the market only if their expected profit is nonnegative. However, even prior investors exit the market if their profit is negative.
Now, \(\eta _{i}\) describes the profile of the prior investment, which equals one if firm i has an affiliate in the previous period and zero otherwise. Therefore, firm i establishes (or maintains if it is a prior investor) an affiliate only if \(E(\pi _{iD}|{\varvec{\theta , G}}, z_{iF})- E(\pi _{iF}|{\varvec{\theta , G}}, z_{iD})> (1-\eta _{i}) W\) holds, or the additional profit of FDI exceeds the initial investment cost.
As in the previous section, we focus only on the symmetric network externalities by assuming \(\tau >{\rm max}\{c_\mathrm{F},c_\mathrm{D}\}\) and then \(\nu _\mathrm{FD}=\nu _\mathrm{DF}=0\). Under this assumption, Eq.(5) becomes as follows:
where \(\widetilde{g}_{ij}\) is a component of \(\widetilde{G}\). Therefore, given that the vector of the investment in the last period is \({\varvec{\eta }}=(\eta _1,\ldots ,\eta _n)^T\), the best-response threshold of firm in Eq. (6) is re-expressed as follows:
Representing the equations in matrix form yields \({\varvec{\theta }}({\varvec{\theta , G}})=-\beta {\varvec{\tilde{G}1}}+\rho {\varvec{\tilde{G} \theta }} +W{\varvec{(1-\eta )}}\).
Therefore, solving the model as in Sect. 2 and using \(({\varvec{I}}-\rho {\varvec{\tilde{G}}})^{-1}=({\varvec{I}}-\rho {\varvec{\tilde{G}}})^{-1}\rho {\varvec{\tilde{G}}}+{\varvec{I}}\) yield the following equilibrium:
where the first term is the Katz–Bonacich centrality which describes the accessibility all the firms, while the second term describes the accessibility only to the prior investors. In this equilibrium, firm i’s threshold is:
where \(\tilde{g}_{ij}^{\{t\}}\) denotes the ij component of \({\varvec{\tilde{G}}}^t\). We refer to \(AC_i({\varvec{\tilde{G}}}, {\varvec{\eta }})\) as the “Katz–Bonacich accessibility to prior investors.” The Katz–Bonacich accessibility between nodes i and j is calculated by summing the network paths from i to j after decaying them according to their lengths using decay parameter \(\rho\). We define the Katz–Bonacich accessibility to prior investors as the total accessibility to all prior investors, while the Katz–Bonacich accessibility is defined as the sum of the accessibilities to all firms.
According to Eq. (13), the effect of the accessibility on the probability (threshold) is positive (negative), because a prior investor is expected to remain in the market with a high probability due to the sunk cost W, as expressed in the third term of Eq. (12). This expectation diffuses from player to player through the network. For example, suppose that a direct transaction partner (j) of firm i is trading with a prior investor in a foreign market (and that firms i and j have no affiliates). The prior investor maintains its affiliate with a higher probability than starting a new investment with a positive initial cost. At this time, firm i expects firm j to invest with a high probability; thus, i also considers investing if it has an opportunity (relatively low \(z_i\)). Furthermore, although the marginal influence of the Katz–Bonacich centrality is ambiguous as in the original static model [see Eq. (8)], the effect on the investing probability is positive if \(\beta -\rho W\) is positive. This implication is almost identical to our baseline static model.
Therefore, the extended testable prediction is presented as follows:
Proposition 2
The probability of firm i deciding to conduct FDI increases (decreases) with the Katz–Bonacich centrality \(B_i({\varvec{\tilde{G}}})\) if \(\beta -\rho W\) is positive(negative), while the probability of FDI always increases with the Katz–Bonacich accessibility to prior investors, \(AC_i({\varvec{\tilde{G}}}\)).
5.2 Empirical investigation
Next, we investigate the theoretical implication of this extended model. Similar to the analysis that is presented in Sect. 4.4, to reduce the computational burden when calculating the inverse of the adjacency matrix, we restrict the samples to the largest 10,000 firms based on the number of employees. Then, we divide the sample into three groups: prior investors, post investors, and others. Prior investors are firms that already have foreign affiliates in the threshold year. Post-investors are firms that do not have any foreign affiliates in the threshold year but that conduct investments after the threshold year. The others are firms that have any foreign affiliates throughout the period.
We focus on Japanese FDI in China and Southeast Asia and set the threshold year as 2000. Japanese FDI in China and Southeast Asia increased from 2000 to 2010, especially in China. Thus, prior investors are represented here as firms that undertook FDI in 2000, and we investigate the FDI decisions of firms that did not undertake FDI in 2000. Under this definition, 470 (576) firms are defined as prior (post) investors in China compared with 1056 (307) in Southeast Asia. In both markets, there are sufficiently many post-investors.
From the theoretical prediction, we estimate the following equation:
where \(\ln ({\rm accessibility}_i)\) is the Katz–Bonacich accessibility, which is the distance to prior investors and is defined by Eq. (14). The dependent variable \({{\rm FDI}_{ir}}\) takes the value of one if firm i is a post-investor in the threshold year and zero if the firm has no foreign affiliates throughout the period.Footnote 16
Column (1) in Table 6 presents the results for China. The coefficient for the log of accessibility is positively significant, which suggests that network proximity to prior investors affects firms’ FDI decisions. Furthermore, the coefficient for the Katz–Bonacich centrality remains positively significant. Column (2) in Table 6 presents the results for Southeast Asia, which are similar to those for China. Again, the coefficients of accessibility and the Katz–Bonacich centrality are positively significant.
These results support our extended theoretical implication. The FDI of firms is stimulated by observing others’ FDI. However, even if we consider such sequential dynamic features in our estimation, the Katz–Bonacich centrality still positively affects firms’ FDI decisions significantly; namely, although firms observe prior investors’ investment information, the relationships between domestic transaction partners that do not undertake FDI are nonetheless important for FDI decisions.
6 Concluding remarks
This study investigated how the structure of a domestic market’s firm-to-firm transaction network influences the FDI of embedded firms. First, we described firms’ FDI choices using a coordination game with incomplete information on others’ location incentives. Our model begins by assuming that each firm trades intermediate inputs with its domestic transaction partners for describing colocation incentives of firms when they choose to conduct FDI. We show that the model has a unique equilibrium that is represented by the Katz–Bonacich centrality measure, which captures the diffusion of FDI expectations based on the direct and indirect network relationships.
Then, we empirically evaluated the theoretical implication using a large disaggregated dataset on Japanese firms and their supply chain networks. We demonstrated that the Katz–Bonacich centrality of each firm has a significantly positive effect on FDI, which is especially large in Asia, and is interpreted as a large network externality in the foreign market that is caused by the substantial difficulty of initiating new transactions with local firms. Furthermore, the magnitude of the Katz–Bonacich centrality is similar to that of worker productivity, which has long been emphasized in the FDI literature. This result implies that the transaction of intermediate inputs is difficult in foreign markets and that firms have an incentive to invest together with their domestic partners; namely, the location externality through the transaction network drives FDI.
The baseline result is robust even when we consider FDI by destination, industry-specific effects, and headquarter location. Although our estimations employ the eigenvector centrality, which is a special case of the Katz–Bonacich centrality in which the decay parameter is specified and is adopted to mitigate the huge computational burden, the result is the same when we use the Katz–Bonacich centrality in the small firm sample. This finding suggests that it is feasible to use the eigenvector centrality as a proxy for the Katz–Bonacich centrality. In addition, we extend the model to a sequential game to control for the effects of the observations of other firms’ investment decisions. As the result, we show an index, namely, the Katz-Bonacich accessibility, which can capture the observation effect. Then, we empirically show that even if we introduce this Katz–Bonacich accessibility to control for the observation effect, the Katz–Bonacich centrality that captures the expectation effect still affects the result positively.
Our empirical results also provide an implication for the policy of host countries in terms of attracting FDI to increase tax revenue. Since we consider mutual interactions among firms, the Katz–Bonacich centrality also suggests that all firms influence one another. Therefore, attracting investment by several leading firms, namely those with a high Katz–Bonacich centrality, should strongly stimulate investment by others. In the same vein, Itoh (2014) focuses on the strong influence of leading firms and theoretically shows that the host country can increase its total revenue by offering corporate tax incentives to these firms. By providing basic empirical support for the influence of the network on firms’ decisions, we also demonstrate the availability of such a policy in the host country.
Finally, as the most important and feasible issue for future study, researchers should aim at extending the analysis to directed transaction networks. In the present model, we considered only undirected networks in which the roles (externality) of the buyer and seller in each transaction are symmetric. Since this setting requires special assumptions such as equal bargaining power among firms and equal commodity prices between countries, future studies could distinguish buyers and sellers in the network under more general assumptions. Moreover, a simple network measure with a single discount parameter such as the eigenvector centrality is no more feasible for evaluating such an asymmetric network; hence, the discount parameter, or the degree of externality, for the buyer and seller should be estimated separately. Although this estimation is difficult to implement, as we discussed in Sect. 4.4, such an investigation would shed light on whether FDI is driven by suppliers or buyers. Differences in the location externality that are due to firm size and industry are another important issue that remains to be addressed.
Notes
A substantial body of literature discusses barriers to procurement from local firms in the host country (e.g. Lim and Fong 1982; Capannelli 1997). According to Reid (1995), the mismatch in the design and quality of the products and their delivery systems is a crucial impediment to local procurement. Kelegama and Foley (1999) discuss the importance of the production quality of local firms, and Asanuma and Kikutani (1992) identify the importance of long-term supply relationships for product quality.
Yamashita et al. (2014) use actual transaction relationship data instead of keiretsu data to empirically show that both direct and indirect transaction partners influence the FDI location decisions of firms. However, they study only a pair of firms whose distance is at most two links rather than the whole network effect.
Studies have applied the Katz–Bonacich centrality to describe the Nash equilibrium of network games (e.g., Ballester et al. 2006). Although these authors consider the choice of the continuous quantity of effort in contrast to our discrete choice model, these models share similar mathematical forms, namely a quadratic (expected) payoff function and, hence, a linear best-response function. However, the issues that are investigated in the two studies differ fundamentally. Ballester et al. (2006) consider a continuous choice model (e.g., the quantity of effort or money spent on education), whereas we consider a discrete choice model (i.e., whether to invest).
Several studies show that firms tend to close domestic establishments when they conduct foreign investments. Simpson (2012) shows this using UK data. For Japan, Matsuura (2004) shows that outward FDI to Asian countries significantly increases the probability of closure of domestic establishments for Japanese-listed electronics manufacturers. Kneller et al. (2012) show that multinational enterprises have a higher probability of closing their domestic establishments. However, some foreign direct investments may establish completely new production lines without closing domestic establishments. In the previous version of the paper, we adopted such a setting in the model. The adoption of such a setup would not change our main theoretical implication (see Itoh and Nakajima 2014).
Firms may start to trade adaptive goods via the new transactions and they may become persistent transactions, which will affect the network structure in the next period. However, this possibility is irrelevant, because our static analysis considers only the current network and profit.
However, the thresholds outside the range can be excluded, because they are not strong profit maximizers. If the right-hand side of Eq. (6) is outside the range of the interior solution, it is equivalent for firm i to select a corner value of the range. Also, if \(\theta _j\) or \(\theta _k\) assumes an outside value, its probability satisfies \(F(\theta _j)= \{0,1\}\) or it assumes a corner value. Then, the outside thresholds of other players are indifferent from some corner values.
See “Appendix” for the proof.
Equation (8) is also expressed as \({\varvec{\theta }}^{*}=-\beta ({\varvec{I}}-\rho \tilde{{\varvec{G}}})^{-1}{{\varvec{G 1}}}-\beta '({\varvec{I}}-\rho \tilde{{\varvec{G}}})^{-1}{\varvec{G^{T}1}}\), where the first and second terms are similar to the Katz–Bonacich centrality while related to supply-side and demand-side relationships, respectively.
Consider a large manufacturer such as Toyota. The firm has many suppliers and cannot report all of them. However, each supplier is relatively small and may report Toyota as a buyer. Using such other reported information, we can mitigate the upper bound problem.
The reason for sampling large firms instead of random sampling is to preserve the original network forms. Since large firms tend to be hubs in the network, omitting large firms renders the sampled network structure totally disconnected and significantly changes the relationships across the sampled firms.
We first fix \(\rho\) and calculate the Katz–Bonacich centrality with the specified \(\rho\). Next, we estimate Eq. (9) using OLS and the calculated Katz–Bonacich centrality to obtain point estimates of \(b^{\rm cent}\) and \({\varvec{b}}\) and the sum of the squared residuals (SSR). We find the value of \(\rho\) that minimizes the SSR and the other minimizers of the SSR to be the point estimates of \(\rho\), \(b^{\rm cent}\), and \({\varvec{b}}\). The standard errors for the estimated parameters are obtained through 100 bootstrap iterations.
As we consider the length of each period to be sufficiently long (at least 5 years), the proportion of the future profit is negligible compared to the present value.
We omit prior investors from the estimation and only use them to calculate the network measures.
References
Antràs, P., & Helpman, E. (2004). Global sourcing. Journal of Political Economy, 112, 552–580.
Asanuma, B., & Kikutani, T. (1992). Risk absorption in Japanese subcontracting: A microeconometric study of the automobile industry. Journal of the Japanese and International Economies, 6, 1–29.
Atalay, E., Hortaçsu, A., Roberts, J., & Syverson, C. (2011). Network structure of production. Proceedings of the National Academy of Sciences, 108(13), 5199–5202.
Bajari, P., Hong, H., Krainer, J., & Nekipolov, D. (2010). Estimating static models of strategic interactions. Journal of Business and Economic Statistics, 28, 469–482.
Baldwin, R., & Okubo, T. (2014). Networked FDI: Sales and sourcing patterns of Japanese foreign affiliates. The World Economy, 37, 1051–1080.
Ballester, C., Calvó-Armengol, A., & Zenou, Y. (2006). Who’s who in networks: Wanted the key player. Econometrica, 74(5), 1403–1417.
Ballester, C., & Calvó-Armengol, A. (2010). Interactions with hidden complementarities. Regional Science and Urban Economics, 40(6), 397–407.
Belderbos, B., & Carree, M. (2002). The location of Japanese investments in China: Agglomeration effects, Keiretsu, and firm heterogeneity. Journal of the Japanese and International Economies, 16, 194–211.
Bernard, A., & Jensen, B. (1999). Exceptional exporter performance: Cause, effect, or both? Journal of International Economics, 47(1), 1–25.
Bernard, A. B., Moxnes, A., & Saito, U. Y. (2019). Production networks, geography and firm performance. Journal of Political Economy, 127(2), 639–688.
Bloch, F., & Quérou, N. (2013). Pricing in social networks. Games and Economic Behavior, 80, 443–461.
Blume, L., Brock, W., Durlauf, S., & Jayaraman, R. (2014). Linear social interactions models. Journal of Political Economy, 123, 444–496.
Bonacich, P. (1987). Power and centrality: A family of measures. American Journal of Sociology, 92(5), 1170–1182.
Calvó-Armengol, A., Patacchini, E., & Zenou, Y. (2009). Peer effects and social networks in education. Review of Economic Studies, 76, 1239–1267.
Chang, S.-J., & Park, S. (2005). Types of firms generating network externalities and MNCs’ co-location decisions. Strategic Management Journal, 26, 595–615.
Chung, W., & Song, J. (2004). Sequential investment, firm motives, and agglomeration of Japanese electronics firms in the United States. Journal of Economics & Management Strategy, 13(3), 539–560.
De Giorgi, G., & Pellizzari, M. (2013). Understanding social interactions: Evidence from the classroom. Economic Journal, 124, 917–953.
De Giorgi, G., Pellizzari, M., & Redaelli, S. (2010). Identification of social interactions through partially overlapping peer groups. American Economic Journal: Applied Economics, 2, 241–275.
De Paula, A., & Tang, X. (2012). Inference of Signs of Interaction Effects in Simultaneous Games With Incomplete Information. Econometrica, 80, 143–172.
Eaton, J., Kortum, S., & Kramarz, F. (2016). Firm-to-firm trade: Imports, exports and the labor market. In RIETI Discussion Paper Series 16-E-048.
Farrell, J., & Saloner, G. (1985). Standardization, compatibility, and innovation. Rand Journal of Economics, 16(1), 70–83.
Hackett, S. C., & Srinivasan, K. (1998). Do supplier switching costs differ across Japanese and U.S. multinational firms? Japan World Economy, 10, 13–32.
Head, K., Ries, J., & Swenson, D. (1995). Agglomeration benefits and location choice: Evidence from Japanese manufacturing investments in the United States. Journal of International Economics, 38(3–4), 223–247.
Head, C. K., Ries, J. C., & Swenson, D. L. (1999). Attracting foreign manufacturing: Investment promotion and agglomeration. Regional Science and Urban Economics, 29, 197–218.
Head, K., & Ries, J. (1996). Inter-city competition for foreign investment: Static and dynamic effects of China’s incentive areas. Journal of Urban Economics, 40, 38–60.
Helpman, E., Melitz, M. J., & Yeaple, S. R. (2004). Export versus FDI with heterogeneous firms. American Economic Review, 94(1), 300–316.
Humphrey, J. (2003). Globalization and supply chain networks: The auto industry in Brazil and India. Global Networks, 3(2), 121–141.
Itoh, R. (2014). Tax discrimination against inter-firm networks. Regional Science and Urban Economics, 49, 25–35.
Itoh, R., & Nakajima, K. (2014). Impact of supply-chain network structure on FDI: Theory and evidence. In RIETI Discussion Paper Series, 14-E-27.
Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18, 39–43.
Kneller, R., McGowan, D., Inui, T., & Matsuura, T. (2012). Closure within multi-plant firms: Evidence from Japan. Review of World Economics, 148, 647–668.
Manski, C. F. (1993). Identification of endogenous social effects: The reflection problem. Review of Economic Studies, 60(3), 531–542.
Martin, X., Mitchell, W., & Swaminathan, A. (1995). Recreating and extending Japanese automobile buyer-supplier links in North America. Strategic Management Journal, 16, 589–619.
Matsuura, T. (2004). Outward FDI and Closure of Establishment (Kaidai chokusetsu toushi to jig yosho heisa-no jissyoubunseki). Nihon Keizai Kenkyu, 50, 124–142. (in Japanese).
Reardon, T., Henson, S., & Berdegue, J. (2007). Proactive fast-tracking diffusion of supermarkets in developing countries: Implications for market institutions and trade. Journal of Economic Geography, 7, 399–431.
Reid, N. (1995). Just-in-time inventory control and the economic integration of Japanese-owned manufacturing plants. Regional Studies, 29, 345–355.
Saito, U. Y., Watanabe, T., & Iwamura, M. (2008). Do larger firms have more interfirm relationships? Physica A, 383(1), 158–163.
Simpson, H. (2012). How do firms’ outward FDI strategies relate to their activity at home? Empirical evidence for the UK. World Economy, 35(3), 243–272.
Smith, D., & Florida, R. (1994). Agglomeration and industry location: An econometric analysis of Japanese-affliated manufacturing establishments in automotive-related industries. Journal of Urban Economics, 36, 23–41.
Urata, S. (1994). Japanese foreign direct investment and its Effect on foreign trade in Asia. In Trade and Protectionism, NBER-EASE, Vol. 2.
Yamashita, N., Matsuura, T., & Nakajima, K. (2014). Agglomeration effects of inter-firm backward and forward linkages: Evidence from Japanese manufacturing investment in China. Journal of the Japanese and International Economies, 34, 24–41.
Acknowledgements
The authors would like to thank RIETI for providing the TSR data that were used in the analysis. The authors gratefully acknowledge financial support from the JSPS (nos. 22330073, 24730216, 25380275, and 19H00598). We are also grateful to Kozo Kiyota, Daisuke Miyakawa, Yasusada Murata, Ryo Nakajima, Toshihiro Okubo, Toshimori Otazawa, and Kensuke Teshima, along with the participants of the JEA in Toyama, ARSC in Kyoto, NARSC in Atlanta, and seminars at Keio University, Kyoto University, Nihon University, Tohoku University, RIETI, and the Japan Productivity Center. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
An earlier version of this paper was circulated under the title “Impact of Supply Chain Network Structure on FDI: Theory and Evidence.”
Appendix
Appendix
To show convergence and interiority of the equilibrium, we show the following statement.
Lemma A1
Given any network structure, \(\sigma >2(n-1){\rm max}\{\nu _\mathrm{FF}-\nu _\mathrm{FD},\nu _\mathrm{FF}-\nu _\mathrm{DF},\nu _\mathrm{DD}-\nu _\mathrm{DF},\nu _\mathrm{DD}-\nu _\mathrm{FD}\}+|\bar{z}|\equiv \bar{\sigma }\) is a sufficient condition for that i) \(\mathbf {(I-\rho \tilde{G})^{-1}}=\sum _{t=0}^{\infty }(\rho \mathbf {\tilde{G}})^{t}\) holds and its every component converges to a finite value; (ii) \(F(\theta _{i}(\mathbf {G,\varvec{\theta }}))\in (0,1)\) holds for all i given any \(\varvec{\theta }\in [-\sigma +\bar{z},\sigma +\bar{z}]^n\), or the best-response threshold always takes strictly interior probability.
Proof
(i) Every component of \(\mathbf {\tilde{G}}^{t}\) is at most \(2^{t}(n-1)^{t-1}\) given any network. Therefore, when \(\rho <\frac{1}{2(n-1)}\) is given, \(\lim _{t\rightarrow \infty }(\rho \mathbf {\tilde{G}})^{t}=\mathbf {0}\) holds, and then, every component of \(\sum _{t=0}^{\infty }(\rho \mathbf {\tilde{G}})^{t}\) is finite and \(\mathbf {(I-\rho \tilde{G})^{-1}}=\sum _{t=0}^{\infty }(\rho \mathbf {\tilde{G}})^{t}\) sufficiently holds. Also, \(\rho <\frac{1}{2(n-1)}\) is equivalent to \(\sigma >(n-1)(\nu _\mathrm{FF}-\nu _\mathrm{FD}+\nu _\mathrm{FF}-\nu _\mathrm{DF})\) from Eq. (6), and the right-hand side is not larger than \(\bar{\sigma }\). Therefore, \(\sigma >\bar{\sigma }\) \(\Rightarrow \rho <\frac{1}{2(n-1)}\Rightarrow\) \(\mathbf {(I-\rho \tilde{G})^{-1}}=\sum _{t=0}^{\infty }(\rho \mathbf {\tilde{G}})^{t}\) holds.
(ii) \(F(\theta _{i}(\mathbf {G,\varvec{\theta }}))\in (0,1)\) holds for any \(\varvec{\theta }\in [-\sigma +\bar{z},\sigma +\bar{z}]^n\) if and only if \(\min _{\varvec{\theta }}\theta _{i}(\mathbf {G,\varvec{\theta }}))>-\sigma +\bar{z}\) and \(\max _{\varvec{\theta }}\theta _{i}(\mathbf {G,\varvec{\theta }}))<\sigma +\bar{z}\) holds. First, consider the first condition. From Eq. (6), the first condition becomes the following:
where \(\alpha _{1}=\frac{\nu _\mathrm{FF}-\nu _\mathrm{DD}+\nu _\mathrm{FD}-\nu _\mathrm{DF}}{2}\), \(\alpha _{2}=\frac{\nu _\mathrm{FF}-\nu _\mathrm{DD}-\nu _\mathrm{FD}+\nu _\mathrm{DF}}{2}\), \(d_{i}=\sum _{k}g_{ik}\le n-1\), and \(d_{i}'=\sum _{k}g_{ki}\le n-1\). Therefore, this condition becomes \(\sigma >(\nu _{\rm FF}-\nu _{\rm DF})d_{i}+(\nu _{\rm FF}-\nu _{\rm FD}){d_{i}^{\prime }} +\bar{z}\) whose right-hand side is at most \(\bar{\sigma }\). Therefore, \(\sigma >\bar{\sigma }\) is sufficient for \(\min _{\varvec{\theta }}\theta _{i}(\mathbf {G},\varvec{\theta }))>-\sigma +\bar{z}\).
Second, the second condition becomes the following:
Therefore, the second condition becomes \(\sigma >(\nu _\mathrm{DD}-\nu _\mathrm{FD})d_{i}+(\nu _\mathrm{DD}-\nu _\mathrm{DF}){d_{i}^{\prime }} -\bar{z}\) whose right-hand side is at most \(\bar{\sigma }\). Therefore, \(\sigma >\bar{\sigma }\) is sufficient for \(\max _{\varvec{\theta }}\theta _{i}(\mathbf {G,\varvec{\theta }}))<\sigma +\bar{z}\). \(\square\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Itoh, R., Nakajima, K. Do sourcing networks make firms global? Microlevel evidence from firm-to-firm transaction networks. JER 72, 65–96 (2021). https://doi.org/10.1007/s42973-020-00061-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42973-020-00061-9