Formation of Chinese venture capital syndication network

Abstract

Using a dataset that recorded a large number of investment transactions in China from 1991 to 2018, we examine the statistical properties of the Chinese venture capital (VC) syndication network. Our main findings are as follows. First, the number of investment transactions sharply increased after 2014. Second, more than half of the VC firms are located in Beijing, Shanghai, and Shenzhen. Third, the degree distribution becomes roughly straight on a log–log plot. Fourth, the hypothesis that the degree distribution follows a power-law distribution is not rejected for 2015 and 2016. Fifth, better connected VC firms increase their connectivity faster, which suggests the existence of preferential attachment.

1 Introduction

Venture capital (VC) firms are a class of financial intermediaries that invest their managing funds in start-up companies and thus play an important role in fostering emerging industries in both developed and developing countries. In China, which is considered a developing country, the VC market started around 1991 with the establishment of the Shanghai Stock Exchange and the Shenzhen Stock Exchange. Raising capital in these financial markets was not easy for small and medium enterprises due to the strict listing requirements; however, VC firms provided a way for these enterprises to raise capital. The number of investment transactions made by VC firms was less than 100 per year until 1998, while it rapidly increased after 1999 and reached a peak of 20,000 in 2015.

A striking feature of VC firms engaged in investment transactions is that they form syndication, that is, multiple VC firms invest in a particular start-up company at the same time. The main reason behind this behavior is to share risks associated with investing in a relatively small company and to mitigate information asymmetry between investors and investees. This suggests a fundamental question that should be addressed in corporate finance literature: how do these VC firms find their partners and what kind of statistical properties does the resulting syndication network have?

To answer this question, we use a dataset covering a large number of investment transactions in China and present basic facts regarding the development of the Chinese VC market. Specifically, we show that the number of investment transactions sharply increased after 2014, and that more than half of the VC firms are located in the three largest cities in China (Beijing, Shanghai, and Shenzhen). These time-series and geographical facts suggest that it is easier for spatially agglomerated VC firms to form the syndication network, so that they can decide and implement their investment plans more rapidly, resulting in a sharp increase in the number of investment transactions.

Next, we examine the statistical properties of the Chinese VC syndication network in three respects. First, we regard each VC firm as a node and show that the degree distribution becomes roughly straight on a log–log plot. This finding suggests that there are several giant firms that are connected with a large number of firms and many small firms that have only a few connections in the VC market. Second, following the statistical method proposed by Clauset et al. (2009), we show that the null hypothesis that the degree distribution follows a power-law distribution is not rejected for 2015 and 2016. Third, by conducting a simple regression analysis, we show that the number of connections newly established from a node is positively correlated with the number of previously established connections, which is consistent with the preferential attachment model proposed by Barabási and Albert (1999).

These findings are consistent with the hypothesis that the degree distribution of VC firms follows a power-law distribution. To support this hypothesis from a different viewpoint, we conduct two additional analyses. First, we incorporate preferential attachment into a network model and simulate it to show that the degree distribution follows a power-law distribution and its slope is similar to the observed values. Second, we examine the weighted graph of the syndication and show that the role of repeated ties among limited VC firms is small.

This study is closely related to the literature focusing on developments of the VC market, especially the aspect of network formation. Kogut et al. (2007), for example, focus on the VC syndication network in the United States to show that the degree distribution deviates from the power law and the preferential attachment hypothesis is rejected. Hochberg et al. (2007) show that American VC firms that are better connected to other firms experience higher fund performance.¹ Unlike these studies, we use a dataset covering the Chinese VC market, for which little empirical evidence has been provided.

The remainder of this paper is organized as follows. In Sect. 2, we provide an overview of the institutional background of the Chinese VC market and describe the dataset used for the analysis. We present the basic facts of the Chinese VC market in Sect. 3 and conduct statistical analyses of the syndication network in Sect.  4. In Sect. 5, we conduct simulation analyses and examine the relevance of repeated ties. Finally, we provide concluding remarks in Sect. 6.

2 Institutional background and data

2.1 Brief overview of the Chinese VC market

The concept of venture capital was first officially introduced by the Chinese central government in 1985, and the establishment of China’s capital market in 1990 offered exit channels for VC firms, facilitating the first stage of the development of the Chinese VC market. However, as Lin (2017) discussed, few VC-backed companies were able to list on the domestic secondary board due to very stringent profit requirements, which hindered the development of VC firms.

In 2009, the launch of ChiNext (China’s equivalent of NASDAQ stock exchange for start-ups) accelerated the growth of the VC market, as it erased profit restrictions for companies to go public. In addition, continuous positive changes made to the capital market during 2012–2013 have contributed significantly to the growth of the VC market. Specifically, deregulations including the split share structure reform, the launch of the National Equities Exchange and Quotations System (New Third Board), as well as the reopening of the IPO market at the end of 2013, provided important exit channels for VC firms.² In 2014, concepts such as “innovation by all” and “grassroots entrepreneurship” were raised in the Government Work Report to strongly propel mass entrepreneurship and innovation in China (Lu et al. 2018). In the same year, both the number of newly established VC firms and investment transactions doubled, and the trend further extended to 2015 on the back of significantly increasing new IPOs and the unprecedented bull market in China’s A-share market. However, this market experienced a dramatic sell-off, causing a share price reduction of more than 30% in one month; the China Securities Regulatory Commission suspended IPOs to stabilize the market.³ These IPO closures have led to freeze-ups in VC markets amid cautious market sentiment as IPOs have been the most popular exit method for VC firms in China. After 2016, VC firms experienced a “capital winter”, which means a slowdown in investment and fundraising activities. That is, in addition to the new rules for asset management released in 2018, investors grappled with a slowing economy and the end of a VC boom, although there is still a significant amount of capital flowing into VC investments in China.⁴

With soaring economic growth and the rapid advancement of Internet technology, China is now the second largest country in terms of VC deal value. According to the Zero2IPO Research Centre (2020), top-tier institutions have more resources, such that 1 percent of the VC firms in China acquired 25% of the total funds raised in the whole market in 2019. Meanwhile, opportunities in China’s growing technology sector have prompted many domestic and foreign VC firms to enter the market. Albers-Schoenberg (2018) shows that Tencent tops the ranking with the most unicorn holdings (27) and Internet giants known as BAT (Baidu, Alibaba, and Tencent) are all in the top five. American VC firms, Sequoia Capital and IDG Capital, have invested in 25 and 14 unicorns, respectively.

2.2 Data

The data used for the analysis are collected and processed by Zero2IPO. This dataset consists of investment transactions made by VC firms from August 1991 to April 2018. For each transaction, the names of the investor (VC firm) and investee (start-up company) as well as the date of execution are specified. Based on the detailed information, we can recover the group of VC firms investing in the same start-up company, or the syndication network. In addition, the amount of investments and the sector and location of start-up companies are recorded for some of these transactions.

Table 1 Summary statistics

Table 1 shows the summary statistics for the syndication network for the entire sample period. The mean of the number of links each VC firm has (degree) is approximately 10, and the standard deviation is approximately 28. (We report the 10 largest VC firms in terms of their degree in “Appendix”.) The mean distance of a given pair of VC firms is approximately 3.5.

A notable feature of the dataset is that it describes the Chinese VC market in a comprehensive way. Specifically, the number of investment transactions recorded during the entire period is 78,761, while the number of VC firms and start-up companies observable is 10,909 and 27,782, respectively. These numbers are comparable to those for the American market reported by Kogut et al. (2007), who show that the number of investment transactions from 1960 to 2005 is approximately 160,000, while the number of VC firms and start-up companies is about 5000 and 26,000, respectively. Thus, the number of investment transactions per year is almost the same across China and the United States. Moreover, our dataset covers the latest investment transactions in China, enabling us to examine recent developments in the Chinese VC market.

Fig. 1

Illustration of the syndication network

Figure 1 presents an example of the syndication network in which four venture capital (VC) firms invest in three start-ups, or venture business (VB) companies. For VB1, two VC firms (VC1 and VC2) form the syndication, so that they are connected. For VB2, three VC firms (VC2, VC3, and VC4) make investments. These firms thus constitute a circular network. Finally, VC3 is the unique investor of VB3, meaning that this investment does not generate any connections among VC firms.

3 Basic facts of the Chinese VC market

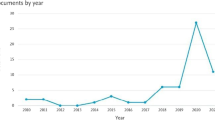
In this section, we present two basic facts of the Chinese VC market. First, Fig. 2 shows time-series developments in the number of investment transactions. The figure indicates that the number of investment transactions was quite limited in the 1990s and the early 2000s. In the late 2000s, the number of investment transactions increased gradually, while it was below 5000 per year. The figure also indicates that the number of investment transactions sharply increased after 2014 and reached a peak of 20,000 in 2015. The results are similar for the number of VC firms and connections.

Fig. 2

The number of investment transactions, VC firms, and connections from 1991 to 2017. The figure shows developments in the number of investment transactions, VC firms, and connections in the Chinese market in each year

These observations regarding the Chinese VC market are very similar to those for the American VC market. Kogut et al. (2007) for example, document that the number of investment transactions made by American VC firms was moderate from 1960 to the early 1990s, while it suddenly increased after 1999 due to the Internet bubble and reached a peak of 25,000. Put differently, the American and Chinese VC markets are similar in that the growth of these markets was moderate for many years, while they experienced a sudden increase in the number of investment transactions at some point in time.

Fig. 3

Location of VC firms in China. The figure plots the location of VC firms on a map of China. The size of each circle is proportional to the number of VC firms located in each city

Second, we plot the location of VC firms on a map of China in Fig. 3, where the size of circles denotes the number of VC firms.⁵ As can be seen, the majority of VC firms are located in the largest cities in China (such as Beijing, Shanghai, and Shenzhen), while the remaining VC firms are located in suburban cities. This figure suggests that choosing the locations close to other firms is crucial for managing VC firms.

Figure 3 highlights a new aspect regarding the formation of the syndication network. Specifically, it shows that many young VC firms became geographically agglomerated when the number of investment transactions sharply increased. While we do not rigorously test the causal relationship between these observations, geographical distance is likely one important factor for participating in syndication.

4 Statistical analyses of the syndication network

In this section, we regard each VC firm as a node and examine the syndication network in three respects. First, we graphically examine the degree distribution, which should be straight on a log–log plot if the power law applies. Second, following the method proposed by Clauset et al. (2009), we statistically test whether the degree distribution follows a power-law distribution. Third, we quantify the impact of existing connections with other VC firms on the emergence of new connections.

4.1 Graphical examination of the degree distribution

Fig. 4

Cumulative node degree distribution for the syndication network. The figure shows the counter-cumulative frequency of the node degree for 1991–2018 as well as each year from 2014 to 2017

First, we examine the degree distribution of the syndication network in China. Specifically, a VC firm’s degree is defined as the number of other VC firms that participate in the syndication of which the concerned VC firm is a member. Put differently, the degree measures the number of links each node has in the syndication network. In Fig. 4, we show the degree distribution as the counter-cumulative frequency for the entire sample period as well as each year from 2014 to 2017. The figure indicates that the degree distribution becomes roughly straight on a log–log plot.

The shape of the degree distribution provides an important implication regarding the formation of the syndication network. Specifically, the process of VC market development likely differs across China and the United States. For the U.S. market, Kogut et al. (2007) argue that the degree distribution deviates from a straight line, so that formation of the syndication network cannot be explained by the power law. In contrast, the degree distribution for the Chinese VC market has a heavier tail, suggesting that giant VC firms play a larger role, which may be explained by the power law.

However, it should be noted that graphical examination of the degree distribution cannot provide a direct test for the power law. Specifically, as demonstrated by Clauset et al. (2009), other fat-tail distributions (such as log-normal) can generate an almost straight line on a log–log plot. Thus, we conduct a more formal test of the power law in the next part.

4.2 Statistical test of the syndication network

Here we examine the hypothesis that the node degree distribution for the Chinese VC market follows a power-law distribution. Specifically, a quantity x follows the power law if it is drawn from a probability distribution such that:

$$\begin{aligned} p(x) \propto x^{-\alpha }, \end{aligned}$$

where $\alpha$ is a parameter of the distribution called the scaling parameter. Typically, the power law applies values of x greater than a certain threshold, denoted as $x_\text {min}$. The purpose of this part is to estimate the values of $\alpha$ and $x_\text {min}$, and examine whether the power-law distribution obtained under these parameters is consistent with the degree distribution observed in reality.

The estimation proceeds as follows. First, we estimate $x_{\text {min}}$ based on the Kolmogorov–Smirnov statistic, which calculates the distance between values obtained from the data and the fitted power-law model. Second, using the maximum likelihood estimation, we estimate the value of $\alpha$. Finally, we employ a goodness-of-fit test that compares a hypothetical distribution under these estimates with the distribution observed in the data, and determine whether the power law is plausible. See Clauset et al. (2009) for more detailed explanations.

Table 2 Estimation results of statistical analyses

The estimation results are shown in Table 2. First, the table shows that the scaling parameter, $\alpha$, is estimated to be between 2 and 3 for all periods. These estimated values are consistent with values obtained by existing studies such as Barabási and Albert (1999) and Newman (2005), who focus on networks including web page links on the Internet and citations of scientific papers, respectively. Second, the table also shows that the null hypothesis that the degree distribution follows a power-law distribution is not rejected at the 5% level for 2015 and 2016, while it is rejected for other periods. Investment transactions made by VC firms dramatically increased in these two years, suggesting that the syndication network developed well during this period.

The finding that the degree distribution of the VC syndication network in China follows a power-law distribution is surprising. Existing studies focusing on the VC syndication network in the United States, such as Kogut et al. (2007), argue that the degree distribution deviates from the power law. Therefore, this finding indicates that the process of VC market development differs across China and the United States.

4.3 Analysis of preferential attachment

To explore why the degree distribution for China follows a power-law distribution, we examine the preferential attachment hypothesis, which means that better connected nodes increase their connectivity faster than less connected nodes (see Jeong et al. 2003). Specifically, we estimate the following regression equation:

$$\begin{aligned} y_{i,t} = \beta _{0} + \beta _{1}x_{i,t} + \beta _{2}(x_{i,t})^{2} + D_{t} + u_{i,t}, \end{aligned}$$

(1)

where $y_{i,t}$ denotes the number of links of node i that are newly added in year t, while $x_{i,t}$ denotes the number of links of node i that exist up to the end of year $t-1$. $D_{t}$ is a dummy variable for each year. We estimate Equation (1) based on VC firms observable from 2013 to 2017.

This regression equation provides a simple test for the existence of preferential attachment. For example, Barabási and Albert (1999) assume that an entrant node obtains a certain number of connections with incumbent nodes, where the probability of these nodes being chosen is proportional to their degree. On the other hand, Jeong et al. (2003) examine the relationship between the number of new and existing connections. Considering both of these approaches, in our analysis, the dependent variable $y_{i,t}$ is set as the number of added connections from a given node to new nodes only as well as all nodes. In our regression equation, the presence of preferential attachment implies that $\beta _{1}$ is positive. Moreover, if the attachment rate linearly depends on the node degree, $\beta _{2}$ is not statistically different from zero.

Fig. 5

Scatter plots of the number of existing and new links. The figure plots the number of existing links (x) and new links (y). Panel (a) uses the number of new links from a given node to all nodes, while panel (b) uses the number of new links from a given node to new nodes only. Blue dots are raw data, while orange squares are averages for grouped observations. Observations are divided into 11 groups based on the value of x. Group 1: $0\le x < 30$, group 2: $30\le x < 60$, and so on

Before proceeding to the estimation results, we plot the number of existing links and new links in Fig. 5. Panel (a) indicates that after dividing the observations into several groups, the nodes with more existing connections acquire a larger number of new connections. This result does not change if we focus on links from a given node to entrant nodes only, as shown in panel (b).

Table 3 Estimation results for preferential attachment

The estimation results are shown in Table 3. First, columns (1)–(3) indicate that the coefficient on the number of existing connections is approximately 0.2 and is statistically positive for all three cases. This finding is consistent with the preferential attachment hypothesis, i.e., that better connected nodes increase their connectivity faster. Second, column (3) indicates that the coefficient on the square of the number of existing connections is quite small. While this coefficient is positive and statistically significant, it has quantitatively little impact. The finding that the attachment rate is almost linear in the node degree is consistent with the finding of Jeong et al. (2003). Finally, columns (4)–(6) indicate that these observations are almost unchanged if we focus on the added connections to new nodes only.

5 Numerical experiments

In this section, we employ simulation analysis to verify that the degree distribution follows a power-law distribution when better connected nodes increase their connectivity faster. We then examine the role of repeated ties among limited VC firms in the formation of the syndication network.

5.1 Simulation analysis

Simulating a network model is a popular approach in existing studies. For example, Barabási and Albert (1999) conduct a simulation incorporating both the growth of a network and preferential attachment to show that these elements are essential for generating a power-law distribution.

We conduct a simulation analysis simpler than that by prior studies. The settings are as follows. First, we prepare 10,000 nodes that potentially participate in the network. Initially, 100 nodes have one connection each, while the remaining nodes are disconnected. (There are no entrant nodes.) Second, we set the growth rate of the connections to 0.2. Thus, 20 new links are generated in the first period. Third, for each of these links, we choose two nodes that are newly connected. Specifically, we choose a node with the probability linearly depending on its degree, while picking up another node randomly. We repeat this procedure for 40 periods and examine the evolution of the degree distribution. For comparison, we also conduct simulations without preferential attachment, namely, that all nodes increase their connectivity with an equal probability.

The results are shown in Fig. 6. Panel (a) indicates that in the presence of preferential attachment, the scaling parameter of the degree distribution is stable (around 3) after the 20th period, although it is initially more volatile. This result is consistent with the estimates of the parameter obtained in Table 2. In contrast, panel (b) shows that under the setting without preferential attachment, the scaling parameter becomes much larger and the distribution likely deviates from the power law.

To obtain more precise estimates of the parameter, we apply Clauset et al.’s (2009) method to the simulated network (with preferential attachment) and report the results in Table 4. The table indicates that for the 10th and 20th periods, the scaling parameter, $\alpha$, is approximately 3, which is close to the estimated values for 2015 and 2016 in Table 2. In addition, Table 4 indicates that the null hypothesis that the degree distribution follows a power-law distribution is not rejected at the 5% level for the 20th and 30th periods.

Fig. 6

Simulation of network formation. The figure shows the counter-cumulative frequency of the node degree obtained from the simulation analysis. In panel (a), each node increases the connectivity with the probability linearly depending on its degree, while in panel (b), each node increases the connectivity with an equal probability

Table 4 Estimation results of the simulated network

This result is driven by a mechanism similar to that in Barabási and Albert (1999), namely, the combination of network growth and preferential attachment. Although there are no entrant nodes in our simulation, initially disconnected nodes gradually participate in the network, which proxies for the growth. Moreover, we incorporate preferential attachment by assuming that better connected nodes increase their connectivity with a higher probability.

5.2 Repeated ties

In this part, we examine the role of repeated ties in the formation of the syndication network. If VC firms always choose certain partners to form syndication, their degree will not increase over time. This means that the degree distribution tends to have a thin tail and is likely to deviate from the power law. To quantify the impact of such behavior, we focus on the weighted graph as in Kogut et al. (2007). Specifically, we define $w_{i,j}$ as the number of investment transactions made by VC firms i and j.

Kogut et al. (2007) argue that the degree distribution deviates from the power law in the American VC market, which can be explained by repeated ties. In particular, they show that the distribution of repeated ties (measured as $w_{i,j}$) follows a power-law distribution with a slope of − 2.26, so that it is highly fat-tailed. Is this true for the Chinese VC market?

Fig. 7

Distributions of the number of repeated ties (link weights). The figure shows the counter-cumulative frequency of link weights, which are defined as the number of investment transactions made by a given pair of VC firms

Figure 7 shows the distribution of repeated ties. The figure indicates that all distributions are roughly straight on a log–log plot, while we cannot conclude that they follow a power-law distribution due to the small variation in the sample. The figure also indicates that the slope of the distributions for 1991–2018 and each year from 2014 to 2017 is approximately − 3 and −4, respectively, which is smaller than those observed in the US data. Therefore, Chinese VC firms are less likely to choose certain partners to form syndication than American VC firms, meaning that the role of repeated ties in the formation of the syndication network is limited.

Fig. 8

Scatter plot of degree and strength. In the figure, we plot the values of degree and strength for the syndication network 1991–2018. Blue dots are raw data, while orange squares are the average strength for each degree value

Another measure of repeated ties is called the strength of node i (denoted as $s_{i}$), which is defined as $s_{i}=\sum _{\forall j}w_{i,j}$. Figure 8 plots the degree and strength of each node. The figure indicates that the strength is positively correlated with the degree, suggesting that large VC firms have more connections and more investment transactions. This observation is similar to those obtained by Gautreau et al. (2009), who focus on the US airport network.

6 Concluding remarks

In this study, we used a unique dataset covering investment transactions in China and examined the statistical properties of the venture capital syndication network. We first showed that the number of investment transactions sharply increased after 2014, and that relatively young VC firms geographically agglomerated in this period. Second, we showed that the degree distribution of the syndication network is roughly straight on a log–log plot, and that the distributions for 2015 and 2016 are consistent with the power law. Finally, we showed that better connected VC firms increase their connectivity faster than less connected VC firms, which suggests the existence of preferential attachment, one of the key ingredients for producing a power-law distribution. Thus, large VC firms tend to form syndication with new partners rather than repeatedly choose certain partners.

The findings of this study have two policy implications. The first is that policymakers need to monitor idiosyncratic shocks incurred by each VC firm. As shown by Acemoglu et al. (2012), when the degree distribution of a network follows a power-law distribution, a shock incurred by the giant node can be propagated to have a non-negligible impact on the entire network. The second implication is that the process of VC market development in China is informative for other developing countries. In particular, the fact that the statistical properties of the syndication network differ across China and the United States reflects the differences in some basic conditions of VC markets such as institutions and regulations.

Finally, we present two promising directions for future research. First, analyzing the role of each VC firm in syndication (e.g., being the lead investor or not) would be important, while we focused almost exclusively on whether VC firms are connected. Second, the primary purpose of VC firms is to pursue high fund performance, which is closely related to the degree of connectivity, although we cannot examine this point due to data limitations.

Appendix

Table 5 lists top 10 VC firms in terms of their degree, where the degree is calculated for the entire sample period. Shenzhen Capital is the top firm, with 670 connections with other VC firms. Foreign capital firms such as IDG Capital and Sequoia Capital are also ranked high.

Table 5 Top 10 VC firms in terms of their degree