How does the global network of research collaboration affect the quality of innovation?

Abstract

This study examines how research collaboration of firms affects the quality of their innovation outcomes using comprehensive patent data for firms in the world from 1991 to 2010. Identifying research collaboration by co-patenting relationships, we find that research collaboration with other firms, particularly with foreign firms, leads to substantial improvement in innovation quality. We also observe a positive effect of the brokerage in the global network, especially for firms with international collaboration links. These results are applicable to the effect on the quality of innovation achieved individually without any collaboration. Therefore, our findings emphasize the importance of links with a variety of partners, particularly with foreign partners to improve innovation performance. Finally, we find that the collaboration effect is larger in the 2000s than in the 1990s and varies depending on firm size and across countries.

Introduction

Because innovation is the ultimate source of economic growth (Romer 1990), how innovation can be promoted is one of the central issues among academic researchers, business persons, and policymakers. As innovation is mostly generated from a combination of different types of knowledge (Schumpeter 1934), knowledge diffusion through networks of individuals and organizations is an important driver of innovation (Jackson 2010; Romer 1990). Accordingly, the effect of networks on innovation performance has recently been examined extensively in the literature as surveyed in Phelps et al. (2012). In the literature, a major type of network that conduits knowledge diffusion is a research collaboration among researchers and organizations (Ahuja 2000; Belderbos et al. 2014; Fleming et al. 2007a, b; Forti et al. 2013; Gonzalez-Brambila et al. 2013; Haus-Reve et al. 2019), while some other types, such as supply chains (Fitjar and Rodríguez-Pose 2013; Todo et al. 2016) and interpersonal interactions (Brennecke and Rank 2017; Perry-Smith 2006; Sosa 2011), can also facilitate knowledge diffusion.

This paper particularly focuses on the effect of research collaboration among firms in the world economy, because inter-firm knowledge linkages across countries have been strengthened recently due to the expansion of global value chains (Baldwin 2016) and the recognition of the importance of open innovation (Chesbrough 2003). Many existing studies have already examined the effect of inter-firm research collaboration, although the mainstream of the literature has focused on collaboration between scientific researchers and between firms and universities (Chen et al. 2019; Phelps et al. 2012). However, the literature has not reached a consensus or conclusion in the following five aspects, as we will explain in more detail in the next section on the literature review.

An important aspect of research collaboration is internationality (Chen et al. 2019). On the one hand, collaboration partners in the same country are geographically and technologically similar to each other. This proximity may facilitate more diffusion of knowledge due to smaller transport and transaction costs and thus more innovation. On the other hand, proximate linkages may also lead to less innovation due to overlapped and redundant knowledge shared among neighbors (Berliant and Fujita 2008; Boschma 2005; Boschma and Frenken 2010).

The number of each firm’s collaboration partners can also affect the innovation. The number of partners, or the degree centrality, may be related to the amount of accessible knowledge and thus be positively associated with innovation. However, creating and maintaining many collaboration ties may be too costly in terms of physical transportation, social communication, and administration (Phelps et al. 2012).

How densely a firm's collaborators are connected with each other also matters to innovation. On one hand, when the firm's partners also collaborate with each other, the firm and its partners are more likely to trust each other and thus be willing to share knowledge (Coleman 1988), resulting in more innovation. On the other hand, because knowledge of a firm's partners already connected may be overlapped with each other and redundant (Burt 1992), the firm's dense ego-networks may not be able to facilitate innovation.

Further, Burt (1992) conceptualizes “structural holes” through which agents are connected directly and indirectly to diverse partners in a network. Although Burt (1992, 2004) argues that brokers that fill structural holes and connect different groups can obtain more knowledge and thus perform better, firms liked with diverse partners may not be able to exchange much knowledge due to lack of strength of ties.

Another factor that has mostly been neglected in the literature is whether or not a research collaboration improves the ability of the participant firms and thus the quality of their subsequent innovation without any collaboration. Most of the existing studies examined how research collaboration affects innovation without distinguishing between outcomes achieved by collaborative and individual research activities. Therefore, although some research collaboration is found to improve the quality of innovation achieved by the collaboration, it is still unclear whether or not the collaboration raises the ability of collaboration partners.

The present study re-examines these issues, using a comprehensive firm-level panel dataset of 534,569 patent-holding firms in the world for the period 1991–2010.¹ We identify the global research collaboration network among firms by patent co-ownership or co-patenting. We realize that co-patenting relationships capture only a subset of successful research collaboration (Briggs 2015) due to, for example, firms’ reluctance to disclose the new knowledge to the public through patenting and legal and institutional complication of value appropriation from co-patenting (Belderbos et al. 2014; Hagedoorn 2003; Hagedoorn et al. 2003). However, we use this identification so that we can cover a substantially large number of firms in the world including small- and medium-sized enterprises (SMEs) in developed, emerging, and even some developing countries, thanks to the richness of patent data.

Using the dataset, we find that co-patenting with other firms, particularly with foreign firms, leads to substantial improvement in the quality of firms’ innovation. In addition, the structure of the firm’s co-patenting network is found to influence its innovation performance. Most notably, when a firm bridges a larger variety of firms in the global co-patenting network, its performance is higher, suggesting the important role of diverse linkages in innovation. These results are applicable to the effect on the quality of innovation achieved individually without any co-patenting, although the size of the effect on innovation without co-patenting is smaller than that with co-patenting. Hence, there is a possibility that research collaboration raises the collaborating firms' innovative ability. Finally, we find that the co-patenting effect is larger in the 2000s than in the 1990s and varies across countries.

We contribute to the empirical literature on the effect of inter-firm research collaboration on innovation performance in the following five aspects. First, we use a large-scale dataset for more than a half-million firms in the world to evaluate how the global research collaboration network of firms affects the quality of their innovation. Existing studies often use smaller samples, typically of several hundred R&D-intensive firms. Although these data may capture research collaboration among firms more accurately than ours, the larger coverage of our data enables us to apply the results to more general settings. Second, we distinguish between the effect of intra- and international research collaboration, finding a substantially larger effect of the latter. This adds to the evidence in the literature supporting a larger effect of distant ties than of proximate ties. Third, we also highlight differences between intra- and international collaboration in the effect of network characteristics, showing that brokerage in the international network can promote more innovation than brokerage in an intra-national network. Fourth, we estimate the effect of collaboration on the quality of innovation achieved individually without collaboration to confirm that innovation capacity is expanded by research collaboration. This examination has not been conducted, to the best of the authors' knowledge. Finally, we carefully investigate cross-country variations in the characteristics of firms' research collaboration and the resulting effect on performance. Based on the examination, we provide practical policy implications in general as well as specific to some countries. The closest works to ours are Belderbos et al. (2014) and Briggs (2015) who also use large-scale patent data to examine the effect of international co-patenting on citations. However, these two works do not incorporate any measure of network structure.

The structure of the paper is as follows. The next section provides testable hypotheses based on theoretical considerations in the literature, whereas Sect. 3 describes the data and variables used in the estimation, including cross-country comparison and network structure. Section 4 explains the estimation equation and methodology, and Sect. 5 presents the results. Section 6 summarizes and discusses the results and provides policy implications.

Literature review, conceptual framework, and hypotheses

This section summarizes the literature on the effect of inter-firm research collaboration and alliances on innovation² to generate our conceptual framework and empirical hypotheses.

Effect of research collaboration

Inter-firm research collaboration generates knowledge networks among firms that can be a major channel of knowledge diffusion (Owen-Smith and Powell 2004). Research collaboration enables firms to exchange new knowledge and information about scientific and engineering technologies from each other and hence improves the quantity and quality of innovation outcomes. Positive effects of research collaboration on innovation are widely found in the literature using various specifications and data. For example, Ahuja (2000) and Gilsing et al. (2008) find that inter-firm alliances increase the number of patents granted to firms, a measure of the quantity of innovation widely used in the literature, whereas Phelps (2010) shows a positive effect on the number of citations received by patents of each firm, a measure of the quality of innovation. These studies use databases in which inter-firm collaborations and alliances are identified by surveys and texts, such as the MERIT-CATI database, the Dow Jones News Retrieval Text Index, Lexis-Nexis, and the SDC Alliance Database. By contrast, Belderbos et al. (2014) examine the effect of co-patenting, considering that research collaboration can result in co-patenting, and find its positive effect on the number of patents granted. Provided the literature, we re-visit the following hypothesis on the effect of research collaboration in general, focusing more on the quality of innovation, rather than its quantity.

Hypothesis 1

The firm's innovation quality with research collaboration is higher than the firms without it.

Effect of international research collaboration

In addition to the presence of research collaboration, characteristics of collaboration partners should also affect innovation. A particular characteristic examined in the literature is geographic and technological distance to collaboration partners. On the one hand, geographically and technologically proximate linkages often observed in practice (D'Este et al. 2012; Hoekman et al. 2009; Hong and Su 2013) may facilitate more diffusion of knowledge due to smaller transport and transaction costs and thus more innovation. On the other hand, proximate linkages may not be effective to innovation due to overlapped and redundant knowledge (Berliant and Fujita 2008; Boschma 2005; Boschma and Frenken 2010) as a result of knowledge sharing within regions and industries (Audretsch and Feldman 1996; Jaffe et al. 1993; Murata et al. 2014). In other words, firms can learn more from international collaboration than from intranational collaboration, because knowledge of foreign collaborators may not be available domestically.

In the inter-firm network literature, a larger positive effect of geographically distant linkages on innovation than of proximate linkages is found in some studies (Fitjar and Rodríguez-Pose 2013; Todo et al. 2016), while others find that the effect of research collaboration deteriorates with the distance between collaborators (Whittington et al. 2009). Belderbos et al. (2014) find a positive effect of inter-industry research and development (R&D) collaboration on innovation quality measured by the number of patent citations and the firm value measured by Tobin’s q, while the effect of intra-industry collaboration is mixed. According to Gilsing et al. (2008), technological distance between firms in technological alliances has an inverted U-shaped effect on the number of patents. These results suggest that the mechanism behind knowledge diffusion across geographical and technological spaces is quite complex.

A growing number of studies examine international research collaboration, a particular type of collaboration with geographically and technologically distant partners (Chen et al. 2019). The results are also mixed. For example, Briggs (2015) regards that co-patenting can capture part of research collaboration and shows a positive effect of multi-country co-patenting on the number of citations at the patent level. Gertler and Levitte (2005) find that the participation of foreign researchers improves firms’ patenting activities. However, Ebersberger and Herstad (2013) show that international collaboration does not significantly affect innovation performance of relatively backward SMEs, whereas Phelps (2010) indicates a negative effect of international alliance on the number of citations to firms’ patents. These results suggest that the benefits of international collaboration are not always realized possibly because linguistic, cultural, and institutional barriers hinder knowledge diffusion among collaborators (Chen et al. 2019). Accordingly, we propose contrasting hypotheses as follows:

Hypothesis 2a

The effect of international research collaboration on a firm's innovation quality is higher than the effect of domestic collaboration.

Hypothesis 2b

The effect of international research collaboration on a firm's innovation quality is lower than the effect of domestic collaboration.

Effect of characteristics of firms' collaboration network

Moreover, the structure of each firm's egocentric (ego) network should affect the quality of innovation. We particularly focus on the following three characteristics of the ego network often examined in the literature.

First, when firms are engaged in research collaboration with more firms, they can obtain more knowledge from their partners and hence better improve the quality of their innovation outcomes. This prediction is empirically supported by Ahuja (2000), Baum et al. (2000), Owen-Smith and Powell (2004), Shan et al. (1994) and Stuart (2000). However, creating and maintaining many collaboration ties may be costly in terms of physical transportation, social communication, and administration (Phelps et al. 2012). Accordingly, other studies, such as Guan and Liu (2016), find an inverted U-shaped relationship between the number of collaboration partners and innovation performance. Therefore, our hypotheses consider two possibilities regarding the effect of the number of collaboration links.

Hypothesis 3a

A firm's innovation quality is higher when it collaborates with more firms.

Hypothesis 3b

A firm's innovation quality is lower when it collaborates with more firms.

Second, knowledge diffusion to the focal firm is affected by not only how the focal agent is connected with its partners, but also how its partners are connected with each other (Barabási 2016; Jackson 2010). For example, in a network in which firms are densely connected with each other, agents are more likely to trust each other and thus are more willing to share information (Coleman 1988), leading to more innovation. However, because the knowledge of agents in a dense network tends to be overlapped and redundant, as in the case of geographically or technologically proximate linkages, dense networks can be less effective in the diffusion of new knowledge than networks in which agents are connected to those in different groups more (Burt 1992, 2004). The two opposing theoretical predictions are consistent with mixed empirical results. Some studies find a positive correlation between the density of a firm's ego-network, i.e., how much its partners are connected with each other, and innovation performance (Ahuja 2000; Phelps 2010). However, others show an inverted U-shaped effect of the density on innovation (Gilsing et al. 2008; Rost 2011). That is, the effect of the density is positive when the level of the density is low but negative when it is sufficiently high, and thus, the medium level of the density is optimal in promoting innovation. Accordingly, we presume the two possibilities in the following two contrasting hypotheses.

Hypothesis 4a

A firm's innovation quality is higher when its research collaboration partners are densely connected.

Hypothesis 4b

A firm's innovation quality is higher when its research collaboration partners are not densely connected.

Third, Burt (1992, 2004) argues and empirically finds that nodes that are connected with a variety of nodes and thus that bridge different groups of nodes can receive a variety of knowledge and perform better. This argument is closely related to that of Granovetter (1973), that an individual obtains more valuable information from weak ties, ties with partners the individual does not frequently meet or does not closely interact with than from strong ties, ties with close friends and relatives. Burt (1992) develops a measure to represent the level of brokerage for each node in a network. The measure, Burt's constraint measure, which is defined in detail in the next section, is negatively related to the level of brokerage and thus is small when the focal agent is bridging various types of groups in the network. Burt's constraint measure is positively correlated with innovation performance in Ahuja (2000), implying that more clustered networks lead to more innovation. However, Rost (2011) and Guan et al. (2017) find the relationship between the constraint measure and measures of innovation statistically insignificant. These findings imply that network brokerage may positively or negatively affect innovation performance, depending on the situation, as suggested by Fleming et al. (2007b). Accordingly, our hypotheses related to network brokerage are as follows:

Hypothesis 5a

A firm's innovation quality is higher when Burt’s constraint measure is higher.

Hypothesis 5b

A firm's innovation quality is higher when Burt’s constraint measure is lower.

Effect on non-collaborative innovation

When firms collaborate for a particular innovation, they can combine different types of knowledge specific to each firm, and thus are more likely to achieve innovation of higher quality than when they conduct research activities individually. However, this quality improvement from research collaboration does not necessarily mean that the knowledge base of each firm in the collaboration network expands because the knowledge exchanged in the collaboration may be specific to the innovation and may not be applied to other innovations. Alternatively, although various knowledge is utilized for the collaboration, it is not fully disclosed to collaboration partners and thus cannot be utilized afterwards. In either case, a firm's research collaboration with others may not improve the knowledge capital of the firm or the quality of innovation outcomes achieved by the firm's subsequent individual research activities without collaboration. If this is the case, the benefits of research collaboration do not persist in the long term and are quite limited.

Although this issue is important, existing studies in the literature typically examine the effect of collaboration on innovation performance at the firm level (Ahuja 2000; Belderbos et al. 2014; Gilsing et al. 2008; Owen-Smith and Powell 2004; Phelps 2010; Whittington et al. 2009), researcher level (Fleming et al. 2007a, b; Forti et al. 2013; Gonzalez-Brambila et al. 2013; Rost 2011), or patent level (Briggs 2015) and do not distinguish between innovation performance from research activities conducted individually and jointly. Therefore, this study tests the following contrasting hypotheses.

Hypothesis 6a

The quality of innovation achieved only by a firm without research collaboration improves when the firm is engaged in research collaboration.

Hypothesis 6b

The quality of innovation achieved only by a firm without research collaboration does not improve when the firm is engaged in research collaboration.

Data

Construction of data

To test the hypotheses in the previous section, our empirical analysis utilizes data for patent-holding firms in the world, taken from the Orbis dataset compiled by Bureau van Dijk (BvD). It includes various firm attributes, in addition to information on patents granted to each firm that is originally provided by PATSTAT. PATSTAT contains detailed information of patents, such as the patent identification number, date of filing, name and address of applicants and owners, country code, international patent classification, abstract, and identification numbers of patents cited by the focal patent.

In this study, we utilize data for patents that were applied for from 1991 to 2010 and granted by 2014, the final year in our dataset. We exclude patents applied for in the most recent four years because it takes several years for an applied patent to be actually granted. Harhoff and Wagner (2009) report that the average duration from the application of a patent to EPO to its grant was 4.36 and 5.10 years in 1991 and 1998, respectively. Therefore, many patents applied for in recent years have not been granted and thus are not included in our data.

BvD aggregates the patent data at the firm level. This is possible because BvD assigns an identification number to each firm in the Orbis data and identifies the identification number of each patent owner firm in PATSTAT, by matching firm names reported in PATSTAT and the Orbis. Therefore, the Orbis data can identify co-patenting networks among firms quite accurately. However, it should be noted that because BvD focuses on companies as their business target, non-firm patent owners, such as universities, public research institutions, and individuals, are excluded from our sample.

In this study, we focus on firms that were granted any patent during the period 1991–2010. The total number of patents owned by any firm with an identification number assigned by BvD in this period is 26,181,824, and the number of firms that have been granted any patent is 534,569.

To locate each firm, we use its addresses recorded in the Orbis data. Thus, a patent can be assigned to multiple countries because of possible multiple owners. The number of patents for firms located in each of the top six countries is 8,506,558 for Japan, 6,528,207 for the United States (US), 2,833,394 for Germany, 1,547,916 for South Korea, 1,043,371 for France, and 972,034 for China. These six countries account for approximately 80% of all patents.

Although patent-holding firms are generally larger than non-patent holders, we should note that our sample includes many SMEs, as the number of workers of the bottom 10% firm in our sample is just five whereas its median is 128. Accordingly, most firms in our sample do not apply for patents frequently but rather once every few years. Therefore, rather than using annual panel data, we divide the whole 20-year period into four five-year periods, 1991–1995, 1996–2000, 2001–2005, and 2006–2010.

Our rich dataset allows us to construct a measure of the citations the patents of each firm receive. Because a patent cites another patent when the former is influenced by the latter, the number of forward citations and the number of forward citations per patent are often regarded as an indicator of the quality of innovation (Griliches 1998; Nagaoka et al. 2010; Trajtenberg 1990) and are used in the literature on the effect of the firm network on innovation (Belderbos et al. 2014; Briggs 2015; Rost 2011). We first count the number of forward citations that the focal patent received from subsequent patents, excluding self-citations. A citation of patent A by patent B is defined as a self-citation if patents A and B share any firm as their owners.

Our key measure of innovation quality is the number of citations at the firm level. We count the number of citations each patent receives during the whole period in our entire data, i.e., from 1991 to 2014. Some studies fix the period (window) in which patents receive citations, e.g., for four or seven years after the application (Belderbos et al. 2014; Phelps 2010). However, we find that some patents are cited for a long period after their applications. For example, 49% of citations to patents applied for in 1991 were cited 10 years after the application or later. To incorporate the long duration of patent citations, we count all citations that each patent receives during the whole period in our data when we measure the quality of each patent. However, the number of citations tends to be smaller for more recent patents than for earlier ones. For example, a patent applied for in 1991 receives more citations than that with the same quality applied for in 2010, simply because of the longer time period after the application for the former. To account for the differences in the number of citations stemming from differences in application years, we standardize the number of citations by dividing it by the average number of citations in each year and summing it up over the 5-year period. Specifically, the standardized measure of the number of citations for firm i in 5-year period t, CITATION_it, is given by

$$\begin{array}{c}{\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it}=\sum\limits_{y\in t}\frac{{\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{iy}}{{\mathrm{a}\mathrm{v}\mathrm{g}\_\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{y}}, \end{array}$$

(1)

where citation_iy is the number of citations that patents applied for in year y and owned by firm i receive from year y to 2014 and avg_citation_y is the average number of citations to patents applied for in year y from y to 2014. Therefore, ${\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{iy}/{\mathrm{a}\mathrm{v}\mathrm{g}\_\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{y}$ represents the number of citations to patents applied for in a particular year standardized by its average.

Using the data, we also create measures of the co-patenting network of firms, i.e., the network in which firms are connected through the co-ownership of patents. Identifying the co-patenting network is possible because each owner firm of a patent is provided with an identification number in the Orbis dataset. The number of patents with more than one owner is 959,363, or 3.7% of the total number of patents, whereas the number of firms that co-own any patent with other firm or institution is 89,175, or 17% of those that own any patent. The total number of links in the co-patenting network is 166,183. The number of patents whose owners are located in more than one country, or internationally co-owned patents, is 248,909, or 0.95% of all patents, whereas the number of firms that co-own any patent with a foreign firm or institution is 20,445, or 3.8% of patent-holding firms.

We regard a co-patenting relationship between two firms as an indication of their research collaboration, because research collaboration can result in co-ownership of its outcomes, i.e., patents (Belderbos et al. 2014; Briggs 2015; Hagedoorn et al. 2003). In practice, however, firms may not co-own patents generated from their research collaboration because of their strategic decision to avoid possible legal and institutional complications in co-patenting (Hagedoorn 2003). Empirically, Hagedoorn et al. (2003) fail to show a significant correlation between research collaboration and co-patenting. Belderbos et al. (2014) find that co-patenting does not necessarily improve Tobin’s q of firms, suggesting that this may be because values from co-patenting are difficult to appropriate to patent co-owners. Therefore, some existing studies utilize firm-level data in which research collaboration and alliances are identified from surveys, news media, and business reports (Ahuja 2000; Owen-Smith and Powell 2004; Phelps 2010; Rost 2011; Whittington et al. 2009), such as the community innovation surveys (CIS) (Belderbos et al. 2006; Ebersberger and Herstad 2013; Haus-Reve et al. 2019) and the CATI database of MERIT (Gilsing et al. 2008; Hagedoorn et al. 2003). However, the present study relies on co-patenting links to identify research collaboration to cover a large number of firms around the world, following Belderbos et al. (2014) and Briggs (2015).

Firm attributes, such as sales and the number of employees, are included in the Orbis dataset. However, these attributes for most firms are available only from 2007 to 2014, while for a small sub-sample of firms they are also available from 1991 to 2010, our sample period. Therefore, our benchmark estimation does not use any firm attribute information from Orbis but only use the location and industry classification of each firm. To overcome possible shortcomings from not using standard firm attributes, we will use fixed effects at the firm level and at the country-industry-year level, as we will explain later in detail. To check the robustness of the benchmark estimations, we will also experiment with the sub-sample of firms with firm attributes.

Changes in the global co-patenting network over time by country

In this subsection, we highlight changes in the global co-patenting network over time and differences across countries so that we can later obtain more adequate interpretation and implication from our estimation results on the relationship between the network structure and innovation. In particular, we focus on the top six countries in terms of the number of patent grants, which represent approximately 80% of all patent grants.

Figure 1 shows changes in the number of patents granted by application year from 1991 to 2010. Japanese firms are granted the largest number of patents throughout the period, whereas the US is granted the second-largest number. However, in the last few years of the period examined, the number of patents in both Japan and the US declined, while China emerged as the third-largest country. These dynamics in the number of patents for each country presented here are mostly consistent with what is reported by the five largest intellectual property offices, EPO, JPO, USPTO, the Korean Intellectual Property Office, and the State Intellectual Property Office of the People's Republic of China (IP5 Offices 2012, Fig. 3.2). There are slight differences because we focus on patents granted to firms and institutions included in the firm-level Orbis dataset. Notably, the number of patents granted to China reported in IP5 Offices (2012), 312,507, is larger than that in Fig. 1.

Fig. 1

Changes in the number of patents granted

Figure 2 indicates the changes in the ratio of the average number of citations per patent for a country to the overall average number of citations per patent. Note that the ratio is standardized so that the average of this ratio in each year is one. Thus, Fig. 2 illustrates the average quality of innovation in each country relative to other countries. Then, we can see that the US has created innovations of the highest quality, while its relative quality declined from 1991 to 2003. This decline is partly because the relative quality of patents granted to Japan increased during the same period. However, the relative quality for Japan decreased after 2003, associated with an increase in the US. Thus, we conclude that both the quantity and quality of innovation generated by Japanese firms have recently deteriorated. By contrast, Chinese firms have recently increased both the quantity and quality of innovation, although the quality measure is the lowest among the six countries at the time of the year 2010.

Fig. 2

Changes in the standardized number of citations per patent

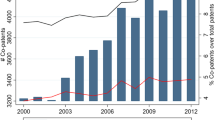
Looking at the dynamics in the extent of co-patenting for each country, we illustrate changes in the share of co-owned patents in all patents in Fig. 3. The overall co-patenting share at the patent level has been increasing from 3% in 1990 to 4.3% in 2010, indicating that research collaboration has been increasingly performed over time, possibly because of the spreading recognition of the effectiveness of open innovation (Chesbrough 2003). The share has been the highest for France in most years during the period examined, increasing substantially. The recent increase in the share of China is also prominent.

Fig. 3

Changes in the share of co-owned patents among all patents

Furthermore, we focus on the dynamics of international co-patenting in Fig. 4. We find that the share of patents internationally co-owned in all patents has also been increasing over time. However, there is a substantial gap in the share between Japan and South Korea, the lowest two countries, and the others. Because the other four countries, France and China in particular, considerably increased the share of international co-patenting in the 2000s, while Japan and South Korea were stagnant, the gap has been widened over time. This feature of Japan and South Korea will be confirmed in the visualization of the global network in the next subsection.

Fig. 4

Changes in the share of internationally co-owned patents among all patents

Structure of the global co-patenting network

To provide an overview of the structure of the global co-patenting network of firms, we visualize the network using an algorithm, ForceAtlas2 (Jacomy et al. 2014), in Gephi, open-source software for network visualization. ForceAtlas2 assumes gravity between linked nodes and repulsion between unlinked nodes. Accordingly, a set of nodes linked with each other are located closely together and form a group. Consequently, nodes linked with many others, or hubs, tend to be located in the center of the network.

Figure 5 shows the visualization in the period 1991–1995 (panel [A]) and 2006–2010 (panel [B]) for comparison across periods. The figure uses different colors for firms located in each of the top six countries in terms of the number of patents granted, Japan (red), the US (blue), Germany (green), South Korea (light blue), France (yellow), and China (black), while other firms are colored in gray. In the visualization, we pick up the largest connected component, i.e., the largest sub-network in which firms are directly or indirectly linked with each other. This is because there are many fragmented sub-networks separated from the largest connected component and located far away from the center of the visualized space, and they are less important in the big picture of the network. However, we use all firms in the estimations conducted in later sections. The share of firms in the largest connected component is 48% and 63% in the periods 1991–1995 and 2006–2010, respectively. This share varies across countries. In the period 2006–2010, 91% of Japanese firms are in the largest connected component, while the shares are substantially smaller for other countries: 69% for South Korea and China, 64% for France, 60% for Germany, and 59% for the US.

Fig. 5

Global co-patenting network

Figure 5 also illustrates that firms are likely to be linked within each country. In particular, firms in Japan and South Korea form two groups that are remarkably separated from firms in other countries. While firms in the US, Germany, and France are also located closely together, these clusters are located closely with each other. This finding implies that firms in the US, Germany, and France collaborate more across national borders with each other, while firms in Japan and South Korea mostly collaborate with other firms in the same country.

The comparison between panels (A) and (B) further indicates the following. First, the isolation of Japanese and South Korean firms has remained over time. Second, US, German, and French clusters are more closely linked with each other in the period 2006–2010 than in the period 1991–1995, implying that firms in these countries have become more active in international collaboration. Finally, Chinese firms, the black dots, are not clearly visible in the period 1991–1995 but form a cluster located closer to the combination of the US, German, and French clusters than to the Japanese and South Korean clusters in the period 2006–2010.

We further show the distribution of the number of firms linked with the focal firm, or the degree centrality (Newman 2010), in Fig. 6. The degree distribution is of great interest because if it follows the power law, i.e., there are a few nodes with an extremely large number of links or hubs, the network is classified as a scale-free network. It is well known that because in a scale-free network, most nodes are indirectly connected with each other with a small number of steps through hub nodes, diffusion of information can be quick (Barabási 2016). Many types of networks have been found to be scale free, including firms' transaction networks (Fujiwara and Aoyama 2010; Saito 2015).

Fig. 6

Degree distribution

Panels (A) and (B) of Fig. 6 show the cumulative density function (CDF) of the degree centrality by period and by country, respectively. Panel (A) illustrates the linear relationship between the log of the cumulative density and the log of degree, indicating that the global research collaboration network in any period is scale free. The gradient of the linear relationship is similar, while the size of the network (the total number of firms) increases over time. Because a larger gradient (or a smaller gradient in absolute values) of the log–log relationship indicates larger heterogeneity in the degree centrality among nodes, and a similar gradient over time implies that such heterogeneity is unchanged for the 20 years examined.

In panel (B) of Fig. 6, we observe that the gradient is different across countries. The gradient calculated by a linear regression is the largest (or the smallest in absolute values) for Japan, − 0.91, and the smallest for the US, − 1.42. This implies that there are more hubs with many links in Japan than in the US and that the median firm in Japan has more links than that in the US. These results suggest that the structure of the research collaboration network differs substantially across countries. In addition, we examine the variation across the country in assortativity of nodes, i.e. whether nodes are likely to be connected with others with a similar value of degree centrality, finding a large variation across countries. Appendix shows the details of the analysis.

Variables for co-patenting networks

This study considers three measures that represent the characteristics of the ego network of each firm in each period: the degree centrality, the local clustering coefficient, and Burt's constraint measure. When we construct the network measures, we exclude isolates, i.e., firms that do not co-own any patent with others, because the measures cannot be defined for isolates. The co-patenting network is regarded as an undirected graph, i.e., a network in which links have no direction.

The degree centrality in a network is the number of nodes directly linked to the focal node. In the co-patenting network examined in this study, degree centrality represents the number of firms that co-own any patent with the focal firm. The degree centrality is a widely used index that measures the centrality of the focal firm in the network (Ahuja 2000; Whittington et al. 2009). When we use the degree centrality in the estimations, we take its log because its distribution has a fat tail, as shown in Fig. 6.

The local clustering coefficient is an index to measure how densely each firm's partners are also connected. It is defined as the ratio of the number of pairs of firms that are connected with the focal firm and are also connected with each other to the number of all possible pairs of firms that are connected with the focal firm. When a firm is linked with only one firm, we define that its clustering coefficient is zero, following the standard literature (Barabási 2016). Because this definition is rather arbitrary, we will include a dummy variable for firms with only one link in the estimations. The clustering coefficient ranges from zero to one, and its higher value indicates that a firm's research collaboration partners are also collaborating with each other. This measure has been used in the literature on the effect of network characteristics on innovation (Fleming et al. 2007b; Gonzalez-Brambila et al. 2013; Phelps 2010; Rost 2011).

The constraint measure of Burt (1992) for node i is defined as follows:

$$\begin{array}{c}C\left(i\right)=\sum\limits_{j\in {V}_{i}, j\ne i}{\left({p}_{ij}+\sum\limits_{q\in {V}_{i}, q\ne i,j}{p}_{iq}{p}_{qj}\right)}^{2},\end{array}$$

(2)

where V_i represents the set of nodes in i's ego network, p_ij is the relative link strength between nodes i and j and is assumed to be 1/N_i for any j V_i. N_i represents the degree centrality of i, assuming the same weight across links. Everett and Borgatti (2018) show that Eq. (2) can be rewritten as

$$\begin{array}{c}C\left(i\right)=\frac{1}{{N}_{i}}+\frac{2}{{N}_{i}^{2}}\sum\limits_{j\in {V}_{i}, j\ne i}\sum\limits_{q\in {V}_{i}, q\ne i,j}{p}_{qj}+\frac{1}{{N}_{i}^{2}}\sum\limits_{j\in {V}_{i}, j\ne i}{\left(\sum\limits_{q\in {V}_{i}, q\ne i,j}{p}_{qj}\right)}^{2}.\end{array}$$

(3)

Thus, the constraint measure for node i is smaller when (a) node i is connected with more nodes (N_i is larger), (b) i's direct neighbors are not connected with each other (p_qj is zero), or (c) i's direct neighbors are connected with many more others beyond i's ego network (p_qj is smaller). In other words, this measure is small when the focal node is connected with a variety of nodes directly and indirectly, bridging between different clusters of nodes. When a firm is linked with only one firm, we assume that p_qj is zero although there is, in fact, no firm j and thus that this measure is one. Because this definition is arbitrary, similar to the case of the clustering coefficient when the degree is one, we will include a dummy for firms with one link in the estimations. This measure ranges from zero when a node is connected with an infinite number of nodes to 1.125 when a node is connected with two nodes that are also connected (Everett and Borgatti 2018). Burt's constraint measure is also used in the literature on the effect of networks on innovation (Ahuja 2000; Gonzalez-Brambila et al. 2013; Guan et al. 2017; Rost 2011). Figure 7 illustrates examples of the three cases (a), (b) and (c) as described above. The arrows (a), (b) and (c) in Fig. 7 correspond to the above three cases that affect the constraint measure for node i. The upper center example (C(i) = 1.125) in Fig. 7 is the case of the largest value of Burt’s constraint measure, and the value decreases as it follows each arrow.

Fig. 7

A Schematic figure of the concept of the Burt’s constraint measure

Descriptive statistics

In our estimation, we drop firm-period observations in singleton groups, i.e., groups with only one observation, to fully exploit the benefits of using fixed effects at the firm level and at the country-industry-period level (Correia 2015). Note that the results are essentially the same if we do not drop singletons. In addition, when we estimate the effect of the three network measures on innovation performance, we restrict the observations to firms with any co-patenting relationship because these measures can be defined only for these firms. Then, our sample contains 356,397 and 48,910 firm-period observations for the estimation of the effect of research collaboration and the three network measures, respectively.

Table 1 shows the descriptive statistics of the variable used in the estimations for the sample for estimations. Among all firms, the average number of patents granted is 63.8, although its distribution is quite skewed, as its median is only 5 and its maximum is 139,275. The number of citations is also skewed: its mean is 63.9, whereas its median is 2.41. The number of citations per patent, which can be considered as an indicator of innovation quality at the firm level, is 1.32, on average. The dummy for firms with any co-patenting relationship with other firms or institutions is 0.20, on average. The dummy for firms with any co-patenting relationship with foreign firms or institutions is 0.05, on average, indicating that international research collaboration is quite rare. It should be noted that the dummy for co-patenting and the dummy for international co-patenting are not exclusively defined. In other words, when a firm engages in international co-patenting, both dummies are one. When a firm engages in domestic co-patenting, the dummy for co-patenting is one while the dummy for international co-patenting is zero. The correlation coefficient between the dummy for co-patenting and its first lag is 0.52, whereas the corresponding figure for international co-patenting is 0.46. These figures suggest that while co-patenting behaviors are persistent, we still have sufficient variations in these key variables over time for the estimations of their effects. The dummy for firms in the largest connected component of the co-patent network, i.e., the largest sub-network of firms linked directly and indirectly with each other, is 0.13, on average. Therefore, the share of firms in the largest connected component among firms in the sample firms in the co-patenting network is approximately 65% (= 0.13/0.20). The lower rows of Table 1 show that firms with a co-patenting relationship are more likely to be granted more patents and receive more citations in total and citations per patent. Thus, it is inferred that firms that engage in research collaboration with other firms innovate more in terms of both quantity and quality. We will test this inference by econometric analysis later.

Table 1 Descriptive statistics at the firm-period level

In addition to the summary statistics of the three network measures in Table 1, we present histograms of the distributions for firms in the sample for the estimations in Fig. 8. The distribution of the degree is shown by a logarithmic scale in panel (A) of Fig. 8. We confirm a power-law distribution, as found for all firms in our data before singletons are dropped in Fig. 6. The median and mean of the number of partners are 2 and 5.36, respectively, indicating that most firms have only a few co-patenting partners. Panels (B) and (C) of Fig. 8 illustrate the distribution of the clustering coefficient and Burt's constraint measure, respectively. In these figures, we exclude firms with only one partner, which represent 43% of all firms in the estimation sample, because the clustering coefficient and Burt's constraint measure of those firms are arbitrarily defined as zero and one, respectively. Neither distribution is standard bell-shaped. The clustering coefficient is zero for 32% of firms, whereas it is one for 17%, of which 78% have two partners. Firms with a clustering coefficient between 0.5 and one are scarce. Burt's constraint is 0.5 for 20% of firms, among which all have two partners. Firms with Burt's constraint measure between 0.6 and one are scarce.

Fig. 8

Distribution of network measures

Table 2 indicates the correlation coefficients between the three network measures. Here, as mentioned before, we exclude firms with only one link in common with panels (B) and (C) of Fig. 8. As implied by Eq. (3), Burt's constraint measure includes the inverse of the degree centrality by definition. Accordingly, the correlation coefficient between the two measures is − 0.758 and quite high. We also find a negative correlation between the degree and the clustering coefficient, as often found in the literature (Barabási 2016). In addition, the correlation coefficient between Burt's constraint measure and the clustering coefficient is 0.588, a reasonably high value, because the former is related to the latter, as shown by the second term of Eq. (3).

Table 2 Correlation coefficients between network measures (firms with two or more links [N = 27,700])

Table 3 shows the international comparison in the number of firm-period observations, the number of patents per firm, and the three measures of the global co-patenting network at the firm-period level. This table conspicuously shows that Japanese firms are different from firms in other countries. The number of firm-period observations for Japan is small, compared with its large number of patents granted. Accordingly, the number of patents per firm is substantially larger for Japan than for other countries. The average of the logarithm of the degree centrality and the clustering coefficient is the largest for Japan. By contrast, Burt's constraint measure, which is smaller when the focal firm bridges different groups of firms, is the smallest for Japan. The evidence reveals that in Japan, a limited number of large firms are densely connected with many other domestic firms.

Table 3 International comparison of descriptive statistics at the firm-period level

Estimation method

Estimation equation

To test the hypotheses provided in Sect. 2, we estimate the following equation that determines the quality of innovation:

$$\begin{array}{c}ln{\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it}={\beta }_{0}+{\beta }_{1}{\text{l}}{\text{n}}{\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{N}\mathrm{T}}_{it}+{\beta }_{2}{\mathrm{N}\mathrm{E}\mathrm{T}\mathrm{W}\mathrm{O}\mathrm{R}\mathrm{K}}_{it}+{\lambda }_{i}+{\mu }_{c(i)k(i)t}+{\varepsilon }_{it}.\end{array}$$

(4)

The dependent variable, lnCITATION_it, is the log of the standardized number of citations that patents owned by firm i receive during time period t.³ Alternatively, when we test hypothesis 6 in Sect. 2, i.e., whether knowledge obtained through research collaboration is effectively utilized in the focal firm's individual research activities without any collaboration, the dependent variable is the standardized number of citations that patents owned only by the firm receive, excluding citations that co-owned patents receive. lnPATENT_it is the log of the number of patents applied for and owned by the firm during the time period t. We include lnPATENT_it as an independent variable to control for the quantity of innovation and firm size. Because Eq. (4) can be rewritten as

$$\begin{array}{c}ln\left({\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it}/{\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{N}\mathrm{T}}_{it}\right)={\beta }_{0}+\left({\beta }_{1}-1\right){\text{l}}{\text{n}}{\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{N}\mathrm{T}}_{it}+{\beta }_{2}{\mathrm{N}\mathrm{E}\mathrm{T}\mathrm{W}\mathrm{O}\mathrm{R}\mathrm{K}}_{it}+{\lambda }_{i}+{\mu }_{c(i)k(i)t}+{\varepsilon }_{it},\end{array}$$

(5)

our specification essentially estimates how the number of citations per patent, a measure of innovation quality at the firm level, is determined, controlling for the size effect. We take a natural logarithm of CITATION and PATENT because these values are quite skewed and fat-tailed (Sect. 3.5). Because CITATION is zero when no patent of a firm is cited, we add one before taking its log, following the convention.

NETWORK_it represents two sets of variables for characteristics of research collaboration at the firm level. First, using the sample of firms including those with no collaborator, we utilize three dummy variables for overall co-patenting, international co-patenting and the largest connected component of the co-patenting network. In this case, we test hypotheses 1 and 2 in Sect. 2, examining the effect of research collaboration and international research collaboration in particular on the quality of innovation. Second, using the sample of firms with at least one collaborator, we utilize the three measures of the firm's characteristics in the global co-patenting network, i.e., the logarithm of degree centrality, clustering coefficient, and constraint. Here, we test hypotheses 3–5 and examine the effect of more detailed characteristics of firms in the global co-patenting network on the quality of innovation. Because the three measures are correlated with each other, we will incorporate each of them in separate estimations. In addition, to examine possible non-linearity of the effect of the network measures found in the literature (Guan and Liu 2016; Guan et al. 2017; McFadyen and Cannella 2004; Rost 2011; Sosa 2011), we incorporate the squared term of each measure in alternative specifications and compare the results with those from linear specifications. We further check the validity of the quadratic form by experimenting with first-, third-, and fourth-order equations. As explained in Sect. 3.4, the definition of the clustering coefficient and Burt's constraint measure is arbitrary for firms with only one link. Therefore, we include the dummy variable for firms with only one link whenever either of the two measures is used.

As we mentioned earlier, our benchmark estimations do not control for firm attributes, such as sales, number of employees, and research expenditures, due to lack of data for a large number of firms. Hence, we incorporate fixed effects at the firm level, λ_i, to control for time-invariant firm attributes. In addition, we include fixed effects at the country-industry-period level, μ_c(i)k(i)t, where c(i) and k(i) represent the country and industry of firm i, respectively, to control for any unobservable factor of innovation in an industry in a country during a time period. The numbers of firms and country-industry-period groups are 139,997 and 2,137, respectively, when the co-patenting dummies are used as the key independent variable, whereas it is 19,225 and 986, respectively, when the three network measures are used.

Estimation method

We estimate Eq. (4) by fixed-effects (FE) estimations. Standard errors are clustered at the firm level, at the country-period level, and at the industry-period level to account for possible correlation between the error terms. The number of country-period and industry-period groups is 261 and 82, respectively.

There are two concerns about this estimation methodology. First, the dependent variable is zero when the firm's patents do not receive any citation. In our benchmark estimations where the key independent variables are the two dummies for research collaboration, the log of the standardized number of citations plus one is zero for 114,229 among 356,397 observations. When we focus on the sub-sample of co-patenting firms, it is zero for 5,112 among 48,910 observations. Under these circumstances where the dependent variable is above a threshold, we usually use Tobit estimations (Tobin 1958) or the extended Tobit estimations that incorporate fixed effects (Honore 1992). However, because we utilize fixed effects at two levels, one with 139,997 groups and the other with 2137, it is infeasible to achieve convergence using Tobit estimations with this large number of fixed effects. When we drop these fixed effects at two levels, we find that the results from Tobit are mostly consistent with the FE results but not robust across specifications. Therefore, we will rely on FE estimations. It should be noted that when the dependent variable is truncated at zero, FE estimations assuming linearity tend to be smaller than the true non-linear effect of the independent variables. Therefore, the FE estimates can be viewed as a lower bound of the true effect.

Second, an obvious econometric issue is biased due to endogeneity of independent variables. For example, the dependent variable, CITATION, and an independent variable, PATENT, are simultaneously determined. Our key independent variables, i.e., measures of characteristics of research collaboration networks, may be affected by firms’ innovation activities, leading to reverse causality. Although these biases may be minimized because we control for fixed effects at two levels so that the remaining disturbance is less likely to correlate with PATENT, one may still be concerned about endogeneity bias. Therefore, we will experiment with alternative specifications to address this issue in Sect. 5.8.

Results

Effect of research collaboration

Table 4 shows the benchmark results from the estimation of Eq. (4) using various independent variables. Column (1) shows the effect of the dummies for co-patenting in general and international co-patenting in particular. Because the two dummies are not exclusively defined as explained in Sect. 3.5, the coefficient of the co-patenting dummy indicates the effect of co-patenting with firms in the same country, whereas the sum of the coefficients of the two dummies represents the effect of co-patenting with foreign firms. The results show that the effect of the two dummies is positive and highly significant. The size of the coefficient of the dummy for co-patenting indicates that co-patenting with a domestic firm improves the quality of innovation by 13% because in this case, the dummy for co-patenting is one while the dummy for international co-patenting is zero. Moreover, co-patenting with a foreign firm improves the innovation quality by 36% (= 0.133 + 0.226), because in this case, the dummies for co-patenting and international co-patenting are both one.⁴ Because these independent variables are dummies whereas the dependent variable is in logs, the coefficient indicates semi-elasticity, i.e., the percentage change associated with the change of the dummy from zero to one. Therefore, our findings imply that research collaboration can lead to substantial improvement in innovation quality most likely because a variety of knowledge is combined in collaboration. Therefore, hypothesis 1 in Sect. 2 is confirmed. Moreover, the effect of international collaboration is considerably larger than the effect of domestic collaboration, confirming hypothesis 2a in Sect. 2, most likely because foreign collaborators are equipped with knowledge that is not available domestically. In addition, we incorporate a dummy variable that is one for firms in the largest connected component and zero otherwise and find a positive and significant effect of the dummy, as shown in column (2) of Table 4. This is because firms in the largest connected component are indirectly linked with more firms and thus can access more knowledge than firms in separate smaller components.

Table 4 Effect of co-patenting network on innovation (dependent variable: log of the standardized number of citations)

Effect of network structure

We further estimate the effect of each of the three measures of network characteristics, provided that the firm is engaged in any collaboration, i.e., using the sub-sample of co-patenting firms. The results in columns (3), (4), and (6) of Table 4 show that the effect of the log of the degree centrality (the number of collaboration partners) on innovation quality is positive and highly significant, and the effect of the clustering coefficient (a measure of how densely a firm's partners are connected with each other) and Burt's constraint measure (an inverse measure of brokerage) is negative and highly significant, supporting hypotheses 3a, 4b, and 5b. The size of the effect of the degree centrality and Burt's constraint measure is large. When a firm with only one collaboration partner adds one more collaborator or increases the degree by 69%, it can improve innovation quality by 10% (= 0.140 × 0.69) and a one-standard-deviation increase leads to an increase in innovation quality by 14% (= 0.140 × 1.01). A decrease in Burt's constraint measure of one standard deviation (0.36) leads to an increase in innovation quality by 18% (= -0.504 × 0.36). By contrast, the clustering coefficient has a smaller effect because a one-standard-deviation decrease improves innovation quality by only 3%.

We further check possible non-linearity of the relationship between the three measures and innovation quality using second-, third-, and fourth-order equations. Almost all the coefficients in the higher-order specifications are highly significant.⁵ Figure 9 illustrates the non-linear relationship between each of the three and innovation quality estimated by the linear and higher-order equations. Panel (A) of Fig. 9 indicates that the effect of the degree centrality is always positive, regardless of the specifications. The U-shaped relationship for the degree between one and two in the cases of the third- and fourth-order equations can be ignored because the degree must be an integer. However, the results from the higher-order specifications are slightly different from the result from the linear specification in that the marginal effect is smaller for smaller degrees, suggesting that the marginal effect is increasing with the degree centrality. Panel (C) also shows that the effect of Burt's constraint is negative, regardless of specifications employed, although the negative effect is likely to be smaller in absolute values when the measure is close to one. Because the results for the degree centrality and Burt's constraint measure from the linear specification are not substantially different from those from higher-order specifications, we will stick with the linear specification for simple presentation.

Fig. 9

Predicted relation between network measures and innovation quality $(\mathrm{ln}\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}=\widehat{{\beta }_{1}}x+\widehat{{\beta }_{2}}{x}^{2}+\widehat{{\beta }_{3}}{x}^{3}+\widehat{{\beta }_{4}}{x}^{4} )$

However, panel (B) of Fig. 9 indicates that the effect of the clustering coefficient is most likely to be inverted U-shaped when it is between zero and 0.5. Because the clustering coefficient rarely takes a value between 0.5 and one (panel [B] of Fig. 8), we can ignore substantial differences across specifications in that range. Although the coefficient of the first-order term in the quadratic specification is only weakly statistically significant (column [5] of Table 4), all other coefficients in all specifications are highly significant. These results suggest that the relation between the clustering coefficient and innovation quality is inverted U-shaped, rather than simply negative, supporting both hypotheses 4a and 4b conditional on the current value. Accordingly, we will show results from linear and quadratic specifications for the clustering coefficient in later estimations.

The benchmark results suggest that when firms collaborate with more firms, they can utilize more knowledge and thus improve innovation quality. Moreover, when firms are connected directly and indirectly with more firms, i.e., firms are bridging different groups of firms, they can exploit a variety of knowledge and thus achieve innovation of higher quality. When a firm's partners are not densely connected, increasing the density has a positive effect on innovation quality possibly because a dense network can nurture trust and thus promote knowledge sharing within the network. However, when the density is already sufficiently high, increasing it more deteriorates innovation because the knowledge of collaboration partners tends to be overlapped and redundant.

Effect on innovation without collaboration

Next, we examine whether a firm's research collaboration with others can improve not only the quality of innovation resulting from the collaboration but also the quality of innovation resulting from the firm's research activities individually conducted without any collaboration. For this purpose, we employ as the dependent variable the standardized number of citations received by patents that the firm owns without any co-owner. Columns (1) and (2) of Table 5 indicate that the dummies for co-patenting in general, international co-patenting, and co-patenting in the largest connected component significantly and positively affect the innovation quality of individual research. These effects are slightly smaller in size than the effects on the total number of citations (columns [1] and [2] of Table 4). For example, the effect of domestic and international research collaboration on the performance of individual research is 0.118 and 0.336, respectively, while their effect on the performance of overall research is 0.133 and 0.359, respectively. Thus, the results support hypothesis 6a.

Table 5 Effect of Co-patenting network on innovation without collaboration (dependent variable: log of the standardized number of citations received by patents that the firm owns without any co-owner)

Columns (3)–(6) of Table 5 show the coefficients of the three network measures. The effect of the log of the degree on the quality of innovation without collaboration is positive and highly significant (column [3] of Table 5), although it is smaller than the effect on overall innovation quality (column [3] of Table 4). Similarly, the effect of Burt's constraint measure is significant (column [6] of Table 5) but smaller in absolute values than the measure in Table 4, although the coefficient of the clustering coefficient in the linear specification is similar in column (4) of Tables 4 and 5. These findings confirm our previous conclusion that research collaboration improves the quality of innovation conducted by the same firm without any collaboration.

Comparison between firms with only domestic collaborators and those with foreign collaborators

In column (1) of Table 4, we find that international research collaboration is more effective than domestic collaboration. To examine differences between the two modes of collaboration further, we incorporate interaction terms between the three measures of network characteristics and the dummy variable for any international patent co-ownership link. The coefficient of each network measure alone can be interpreted as the effect of characteristics of firms with only domestic collaborators, whereas the sum of the coefficients of each network measure and the dummy signifies the effect of firms with foreign collaborators.

The results estimated from this specification are shown in Table 6. In column (1) of Table 6, we find that the interaction term between the degree centrality and the dummy for any international link is positive and significant. This finding suggests a larger effect of the number of collaborators on innovation quality for firms with foreign collaborators than for firms with only domestic collaborators, consistent with the previous finding. When we examine the effect of the clustering coefficient, we rely more on results from a quadratic equation shown in column (3) than results from a linear equation shown in column (2). Then, we find that the effects of the interaction term with the clustering coefficient or with its square are not statistically significant at the 5% level. This result indicates that the inverted U-shaped relationship between the clustering coefficient and innovation performance can be applied to both firms with only domestic links and those with international links. In other words, trust among firms is nurtured in a dense domestic network, as it is nurtured in a dense international network. The effect of Burt's constraint measure is larger in absolute values when firms collaborate with foreign firms than when they collaborate with only domestic firms (column [4] of Table 6). This finding indicates that bridging firms in the global research network can facilitate innovation more than bridging only domestic firms, suggesting the importance of combining a variety of knowledge across countries for high-quality innovation.

Table 6 Comparison between firms with only domestic collaboration and those with foreign collaboration (dependent variable: log of the standardized number of citations)

Heterogeneity by firm size

The effect of research collaboration and network characteristics on innovation may be heterogeneous. To check this heterogeneity, we first run the same regressions using subsamples of firms divided by measures of firm size, specifically the number of patents and the number of workers.

In Table 7, the first column shows results from regressions using the subsample of firms with the number of patents equal to or larger than its median, while the second using the subsample of firms with the number of patents smaller than its median. Similarly, the third and fourth columns respectively indicate results for the subsample of firms with a larger and smaller number of workers than its median. Note that results from five types of regressions shown in Table 4 (except for that in column [2]) are combined in each column for each subsample for the brevity of presentation.

Table 7 Heterogeneity by firm size (dependent variable: log of the standardized number of citations)

Overall, the results using the subsamples are similar to those using the full sample shown in Table 4. One difference is that although the effect of international collaboration is positive and significant in Table 4, it is positive and significant for larger firms in terms of the number of patents and the number of workers (columns [1] and [3]) but insignificant for smaller firms (columns [2] and [4]). This finding suggests that international collaboration can promote the quality of innovation only when firms are sufficiently large in terms of the size of innovation or production. In other words, firms that are not innovation-oriented cannot benefit from international collaboration possibly because of their small absorptive capacity. By contrast, in other regressions shown lower rows of Table 7, the effect of network characteristics in the larger- and smaller-firm subsamples are quite similar.

Heterogeneity across time

In addition, we examine how the effect of research collaboration and network characteristics changes over time. Because our data contain four five-year periods, we divide them into two, one in the 1990s and the other in the 2000s, and incorporate the interaction term between each network measure and the dummy variable for the 2000s. Thus, the effect in the 1990s is represented by the coefficient of a variable, whereas the effect in the 2000s is the sum of the coefficients of the variable and the interaction term with the 2000s dummy.

The results presented in Table 8 show that the effect of most network variables is larger in absolute values in the 2000s than in the 1990s. For example, column (1) indicates that domestic and international co-patenting improves the innovation quality by only 5% and 13%, respectively, in the 1990s but by 19% and 26%, respectively, in the 2000s. The coefficient of the log of the degree centrality is 0.09 in the 1990s and increases to 0.16 in the 2000s. Using the quadratic specification, the effect of the clustering coefficient is mostly negative in the 1990s but becomes inverted U-shaped in the 2000s. The effect of Burt's constraint is insignificant in the 1990s, while it is negative and highly significant in the 2000s. All of these findings suggest that the effect of research collaboration and network characteristics has increased over time.

Table 8 Heterogeneity across time (dependent variable: log of the standardized number of citations)

Heterogeneity across countries

Section 3.2 shows heterogeneity in the characteristics of research collaboration across countries. We further examine heterogeneity in the effect of network characteristics across countries by applying the same estimation method to the subset of firms in each of the top six countries. In these estimations, we keep singleton firms, although they have been dropped so far to maximize benefits of using fixed effects. This is because, if we drop singletons in country-level specifications, the number of observations for France and China amounts to only several hundred and is too small.

The first two rows of Table 9 show the effect of the two dummies for overall and international co-patenting, corresponding to column (1) of Table 4. For all countries, the effect of domestic and international collaboration is positive and highly significant. The effect is particularly large for China possibly because China is still a latecomer in the global research field in the 1900s and 2000s considered in this study and thus can benefit substantially from learning from other countries. The effect of international collaboration is also large for South Korea, France, and Germany. For South Korea, this is because of the benefit of backwardness as in the case of China. For France and Germany, the two most innovative countries in Europe, this is possible because of benefits from collaboration within the European Union, where international collaboration is officially subsidized.

The lower rows of Table 9 indicate the coefficients of the degree centrality in logs, clustering coefficient, and constraint measure from regressions using each of the three separately, corresponding to columns (3)–(6) of Table 4. For the clustering coefficient, we show the results from the quadratic specification as well. The results show that the effect of the degree is the largest for China, followed by Germany, South Korea, France, and Japan, and the smallest for the US. The effect of the clustering coefficient and Burt's constraint measure is larger for Germany, France, and South Korea than for other countries. The results indicate an important role of both clustering coefficient and Burt’s constraint in innovation in the three countries, suggesting that they benefit substantially from the global research collaboration network. By contrast, all the results shown in Table 9 imply a smaller effect of the global research network on innovation in Japan and the US.

Robustness checks

To check the robustness of the results above, we experiment with a number of alternative specifications and estimation methods.

First, we incorporate firm attributes into the set of independent variables to minimize biases due to missing variables. For example, although our measure of firm size so far, the number of patents, may not properly capture the actual firm size (Cohen 2010). For this purpose, we use balance-sheet information in the Orbis data to extract the amount of capital stocks and the number of workers. However, because these data are not available for many firms for earlier years (see Sect. 3.1), our sample size declines from 356,397 in the benchmark estimation of the effect of research collaboration to 36,633 and from 48,910 in the benchmark estimation of the effect of the network structure to 8509. The results from the alternative specification shown in column (1) of Table 10⁶ are quite similar to qualitatively and quantitatively. Only one difference is that while we found an inverted U-shaped relationship between the clustering coefficient and the measure of innovation quality in the benchmark, their relationship is insignificant in the alternative estimation (row 4 in column [1] of Table 10).

Table 9 Heterogeneity across countries (dependent variable: log of the standardized number of citations)

Table 10 Robustness checks (dependent variable: log of the standardized number of citations)

Second, an important issue of international patent data is that some patents are applied for to and granted by more than one patent office. In our data, 78.8% of all patents can be classified as patent families, i.e., patents granted by more than one patent office. Our estimations use firm-level data in which we aggregate the number of patents and citations at the firm level, rather than patent-level data. Accordingly, the number of citations each firm receives in each period and co-patenting networks among firms in each period are correctly identified. For example, suppose a particular invention of a firm is granted patent A by a patent office and patent B by another office. Then, some patents cite patent A while some others cite patent B, but no patent should cite both. Therefore, the number of citations the firm’s invention receives is the sum of the number of citations to patents A and B. However, the number of patents of each firm, which is used as an independent variable to control for the size of innovative activities, can be overvalued as we count the same patent granted by multiple patent offices multiple times. To control for this possible measurement issue, we utilize information in the Orbis data about how each patent granted by a patent office is granted by other offices and construct an alternative measure of the number of patents that account for possible double-counting and use it as an independent variable. The results in column (2) of Table 10 indicate that the results are essentially the same as the benchmark results. A difference is that the clustering coefficient has a monotonically negative and significant effect in this robustness check, while its effect is inverted U-shaped in the benchmark.

Third, another issue of international patent data is that different patent offices have different criteria for citing existing patents. For example, the patent office of a country may be stricter about citing patents than others, and thus the number of citations to patents granted by the patent office tends to be smaller. Then, the quality of patents granted by the patent office is more likely to be low in our dataset. To account for the possible variation in the number of citations, our measure of innovation quality, across patent offices, we define the following alternative index of the number of citations by standardizing the number of citations for each patent office and year:

$$\begin{array}{c}{\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it}^{\mathrm{*}}=\sum\limits_{y\in t}\sum\limits_{o}\frac{{\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{ioy}^{\mathrm{*}}}{{\mathrm{a}\mathrm{v}\mathrm{g}\_\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{oy}^{\mathrm{*}}}, \end{array}$$

(6)

where ${\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{ioy}^{*}$ is the number of citations that patents applied for to patent office o in year y and owned by firm i receive during the period from year y to 2014 and $\mathrm{a}\mathrm{v}\mathrm{g}\_{\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}_{oy}^{*}$ is the average number of citations to patents applied for to patent office o in year y from y to 2014. Column (3) of Table 10 demonstrates that the results using this alternative measure for the quality of innovation are essentially the same as the benchmark results.

Finally, a major source of estimation biases is the endogeneity of the key independent variables related to research collaboration networks. There may be missing variables in the estimations that affect both innovation quality and innovation networks. In addition, while the network variables may affect innovation quality, innovation quality may also change collaboration networks. For example, firms that achieve higher innovation quality are more likely to attract others’ request for collaboration. Although we incorporate firm and country-industry-period fixed effects and thus control for biases due to missing variables to a large extent, biases due to reverse causality may still remain.

To alleviate possible biases due to the endogeneity, we employ two approaches. We first follow the dynamic generalized method of moments (GMM) estimation developed by Blundell and Bond (1998), or the system GMM estimation. Specifically, we consider a dynamic equation in which the lagged dependent variable is added as an independent variable, first-difference it to eliminate firm fixed effects, and apply GMM estimations using lagged endogenous variables as instruments. However, Hansen J tests for over-identification always reject the null hypothesis that the instruments used are orthogonal to the error term, even though we experimented with many possible sets of instruments. Therefore, the results from the system GMM estimations, although they are quite similar to the benchmark results, may be biased and thus are not shown here.⁷

Alternatively, we take a simpler approach in which all the independent variables are lagged for one period (i.e., 5 years) to avoid endogeneity, especially because of reverse causality. It should be noted that because each period in our analysis is a 5-year period, we can most likely avoid reverse causality using the one-period lagged independent variables. Further, to account for endogeneity due to unobserved factors that affect both the innovation quality and collaboration links simultaneously, we include the lagged innovation quality as an independent variable and thus modify the regression equation as:

$$\begin{array}{c}ln{\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it}={\beta }_{0}+{\alpha \mathrm{l}\mathrm{n}\mathrm{C}\mathrm{I}\mathrm{T}\mathrm{A}\mathrm{T}\mathrm{I}\mathrm{O}\mathrm{N}}_{it-1}+{\beta }_{1}{\text{l}}{\text{n}}{\mathrm{P}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{N}\mathrm{T}}_{it-1}+{\beta }_{2}{\mathrm{N}\mathrm{E}\mathrm{T}\mathrm{W}\mathrm{O}\mathrm{R}\mathrm{K}}_{it-1}+{\lambda }_{i}+{\mu }_{c(i)k(i)t}+{\varepsilon }_{it}.\end{array}$$

(7)

Because the unobserved factors causing endogeneity are now included in lnCITATION_it−1, the error term in the equation above is less correlated with lnNETWORK_it−1, or the network variables.

The results from the use of the lagged dependent variables and additionally the lagged dependent variables shown in columns (4) and (5) of Table 10 are similar to the benchmark results, although the coefficients are smaller slightly, possibly reflecting weaker effects in a long run than immediate effects. Besides the size of the coefficients, the effect of the clustering coefficient is also different, as it is U-shaped, rather than inverted U-shaped as in the benchmark results.

Overall, these alternative specifications yield results that are quite similar to the benchmark results. One notable difference is that the effect of the clustering coefficient is not consistent across specifications. In the benchmark regression, it is inverted U-shaped, while it is U-shaped, negative, or insignificant in others.

Discussion and conclusion

This study examines how research collaboration of firms affects the quality of their innovation outcomes using comprehensive patent data for firms in the world from 1991 to 2010. We identify research collaboration by co-patenting relationships. The results above can be summarized as follows.

Most importantly, research collaboration substantially improves the quality of innovation of firms by combining a variety of knowledge in the collaboration. Further, research collaboration improves the quality of innovation conducted by the same firm without any collaboration. These results show that the effect of research collaboration can expand beyond innovation generating from the collaboration and generally improve the ability in the innovation of firms participating in the collaboration.

Moreover, we find that two of the three measures of firms' research network greatly affect the outcome of research collaboration. First, when firms collaborate with more firms, i.e., when their degree centrality is larger, they are exposed to a larger amount of knowledge and thus achieve higher innovation quality. According to our higher-order specifications, the positive effect is particularly large when firms are already collaborating with two or more firms. This finding is consistent with the findings of Ahuja (2000) and Owen-Smith and Powell (2004), although some studies, such as Guan and Liu (2016), find an inverted U-shaped relationship because of the costs of creating and maintaining many linkages. We find an increasingly positive relationship possibly because the benefits of collaboration increase as firms experience more research collaboration and thus absorb others' knowledge more easily. In other words, the marginal cost of creating and maintaining collaboration ties is likely to be diminishing, rather than increasing, as found in Guan and Liu (2016) and others.

Second, by expanding the role of brokerage, i.e., connecting with more firms indirectly and bridging a variety of firms, firms can achieve a higher quality of innovation, as suggested by Burt (1992). This finding of a positive effect of the brokerage on innovation performance is consistent with that of Ahuja (2000), while many other studies find either negative, U-shaped, or insignificant effects.

By contrast, the effect of the clustering coefficient that measures how densely a firm's collaborators are collaborating with each other is not robust to alternative samples or specifications (Sect. 5.8). Moreover, its effect is statistically significant but quantitatively small in the benchmark estimations (Sect. 5.2). Therefore, we conclude that the effect of the clustering coefficient is at most limited. This unclear and limited effect found in this study may be due to the skewed distribution of the clustering coefficient. As Fig. 8 (B) illustrates, the clustering coefficient is zero for more than one-third of firms and one for one fifth, whereas few firms have a cluster coefficient between 0.4 and 0.9. The skewness of the distribution is quite large, compared with that of the degree (Fig. 8 [A]) and Burt’s constraint (Fig. 8 [C]). This skewness is not much discussed in the literature on the effect of the clustering coefficient on performance, but our detailed analysis reveals that we need to closely look at its distribution when we examine the effect of the clustering coefficient on innovation.

In addition, we find that international research collaboration is 2.7 times more effective than domestic research collaboration. The effect of international research collaboration is more prominent for larger firms in terms of the number of patents and the number of workers. We further distinguish between firms with only domestic collaborators and those with foreign collaborators and examine the effect of the network measures for each type of firms. Then, we find that the positive effect of the number of collaborators and brokerage of firms is larger for firms with foreign collaborators than for those with only domestic collaborators. These findings suggest that because the knowledge of firms around the world varies more than the knowledge of firms in the same country, linking with a variety of foreign firms directly and indirectly is a more effective means to high-quality innovation than linking with domestic firms.

From all of these results, we can clearly conclude that links with a variety of firms in the global research collaboration network, particularly links with foreign partners, improve the quality of innovation than densely connected links with a limited number of domestic firms.

Finally, we investigate changes in the effect of research collaboration over time and find that the effect has intensified in more recent years. This is consistent with Chesbrough (2003), the seminal work in the open-innovation literature, who argues that open innovation is more important after the late 1990s than before due to the growing mobility of knowledge workers and the availability of venture capital. Rising technological complications in the high-technology sectors may also have increased the need to combine a variety of knowledge, including foreign knowledge, in innovation.

The results suggest a number of policy implications. Generally, our findings emphasize the importance of international research collaboration for better innovation performance. However, firms are often connected within each country, as shown in Fig. 5. Particularly, Japanese and South Korean firms are considerably less connected to foreign firms (Figs. 4, 5) than are firms in other countries. As the effect of international collaboration is substantially large in South Korea (Table 9), an obvious policy prescription to South Korea is to promote international collaboration. In the case of Japan, the effect of international collaboration is the lowest among the top six countries (Table 9); therefore, policies in Japan should also alleviate barriers to knowledge diffusion through international collaboration, e.g., linguistic, cultural, and institutional barriers, when promoting international collaboration. Because the innovation quantity and quality have recently deteriorated in Japan (Figs. 1, 2), increasing international collaboration and its effectiveness is an urgent policy agenda. By contrast, Chinese firms have actively collaborated with foreign firms (Fig. 4), improving the quantity and quality of innovation (Figs. 1, 2), because the effect of international collaboration on Chinese firms is extremely large (Table 9). European firms are also actively collaborating with foreign firms (Fig. 4) and generate a large effect of international collaboration on innovation (Table 9). Japan and South Korea should follow the trajectories of China and Europe.

Another important issue is that although a smaller value of Burt's constraint measure is better for higher innovation quality, its average is 0.64 and relatively high (Table 1). Therefore, policies should facilitate the creation of a network for research collaboration with a variety of partners. In addition, our analysis is shown in Sect. 5.4 (column [4] of Table 6) suggests that links with a variety of foreign partners are more important than those with a variety of domestic partners.

This conclusion is particularly important to Japanese firms because their brokerage feature is peculiar. The average constraint measure of Japanese firms is substantially lower throughout the period 1991–2010 (0.60 as shown in Table 3) than that of other countries (0.79–0.84), but they are less likely to collaborate with foreign partners (Fig. 4). These observations indicate that Japanese firms are linked with a variety of domestic firms, but not with a variety of foreign firms. Combined with another observation that performance of Japanese firms had been rising until 2003 but deteriorated since then (Fig. 2), we conclude as follows. Japanese firms performed well in the earlier period thanks to their diverse research collaboration networks but worse in the later period due to lack of collaboration with diverse foreign partners as the importance of international research collaboration has become larger (Sect. 5.5). Therefore, our analysis suggests that Japanese firms should be linked with more diverse foreign firms to improve their innovation performance.

Several caveats of this study should be noted. First, as we noted earlier, we identify inter-firm research collaboration by co-ownership of patents. Therefore, it is most likely that research collaboration identified in this study is a subset of actual research collaboration (Briggs 2015) because of legal and institutional complication associated with value appropriation from co-patenting (Belderbos et al. 2014; Hagedoorn 2003). Second, we define a firm as a legal entity and ignore parent-subsidiary relationships among firms. Although Belderbos et al. (2014) incorporate these relationships to define co-patenting between a parent firm and its subsidiary as intra-firm R&D activities, not inter-firm research collaboration, we did not distinguish parent-subsidiary relationships from other inter-firm relationships. Because subsidiaries may be equipped with knowledge different from that of their parent firms, our distinction from the previous study may be justified but should be noted. Third, our results are based on the sample of firms that are granted at least one patent in the period examined. Because firms with any patent are likely to be more innovative than those without, our results can be applied to relatively innovative firms, not to the population of firms, although we should emphasize that our sample includes SMEs. Finally, although we show the large effect of international collaboration, our analysis does not explicitly consider the costs of creating and maintaining linkages. Therefore, it is still unclear how we can reduce the costs and thus promote international linkages and whether collaborating with foreign firms results in a net positive benefit. We leave this important research agenda for future research.

Appendix

Details of data construction

Orbis dataset records patent-holding firms in the world, compiled by Bureau van Dijk (BvD). The Orbis dataset is commercially available. It includes various firm attributes, in addition to information on patents granted to each firm that is originally provided by PATSTAT. PATSTAT is the worldwide patent data created by the Organization for Economic Cooperation and Development (OECD) in corporation with the Patent Statistics Task Force consisting of patent offices in the world, such as the World Intellectual Property Organization (WIPO), the United States Patent and Trademark Office (USPTO), the European Patent Office (EPO), and the Japan Patent Office (JPO), and distributed by the EPO.⁸

When BvD aggregates the patent data at the firm level and merges them with the Orbis data, one problem in this matching process is that firm names in PATSTAT are often abbreviated or misspelled so that they are different from their formal names recorded in the Orbis. Thus, BvD employs detailed matching algorithm and, in some cases, human eyes using firms’ address, contact information, and other attributes to successfully identify the identification numbers of most patent owner firms, including SMEs. BvD also closely follows M&A deals and changes the patent owner’s identification number when an owner firm is acquired by another firm.

Assortativity

We examine the assortativity of nodes, i.e., whether nodes are likely to be connected with others with a similar value of degree centrality. Assortativity for a network can be measured by the correlation coefficient of the degrees of all pairs of connected nodes (Newman 2010) and can be positive or negative, depending on the network structure. For example, Fujiwara and Aoyama (2010) and Bernard et al. (2018) find negative assortativity in firms' transaction networks in Japan, indicating that hub firms are more likely to transact with firms with a small degree. In our research collaboration network, the correlation coefficient is 0.45, indicating positive assortativity. In other words, firms collaborating with many others are more likely to collaborate with each other, while firms collaborating with only a few others are likely to collaborate with each other. Figure 

Fig. 10

Changes in Spearman’s rank correlation coefficients between firms' own degree and the mean of their neighbors' degree

10 demonstrates the changes in assortativity over time for each country. Here, we use the average of Spearman's rank correlation between a firm's own degree and the mean of the degree of firms directly connected with the firm to define country-level assortativity. Assortativity is larger for France, the US, and Germany than for Japan and South Korea, whereas it is the smallest for China. The variation in assortativity across countries also suggest that we conduct analysis for each country.