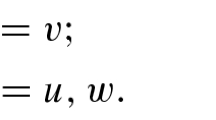Abstract
This paper concerns the superconvergence property of the ultraweak-local discontinuous Galerkin (UWLDG) method for one-dimensional linear sixth-order equations. The crucial technique is the construction of a special projection. We will discuss in three different situations according to the remainder of k, the highest degree of polynomials in the function space, divided by 3. We can prove the \((2k-1)\) th-order superconvergence for the cell averages when \(k\equiv 0\) or 2 (mod 3). But if \(k\equiv \)1 (mod 3), we can only prove a \((2k-2)\) th-order superconvergence. The same superconvergence orders can also be gained for the errors of numerical fluxes. We will also prove the superconvergence of order \(k+2\) at some special quadrature points. Some numerical examples are given at the end of this paper.
Similar content being viewed by others
References
Adjerid, S., Devine, K.D., Flaherty, J.E., Krivodonova, L.: A posteriori error estimation for discontinuous Galerkin solutions of hyperbolic problems. Comput. Methods Appl. Mech. Eng. 191(11), 1097–1112 (2002)
Adjerid, S, Issaev, D.: Superconvergence of the local discontinuous Galerkin method applied to diffusion problems. In: Proceedings of the Third MIT Conference on Computational Fluid and Solid Mechanics, vol. 3, pp. 1040–1042. Elsevier, Boston, MA (2005)
Adjerid, S., Massey, T.C.: Superconvergence of discontinuous Galerkin solutions for a nonlinear scalar hyperbolic problem. Comput. Methods Appl. Mech. Eng. 195(25), 3331–3346 (2006)
Brenner, S.C.: Poincaré-Friedrichs inequalities for piecewise \(H^1\) functions. SIAM J. Numer. Anal. 41(1), 306–324 (2003)
Cao, W., Li, D., Yang, Y., Zhang, Z.: Superconvergence of discontinuous Galerkin methods based on upwind-biased fluxes for 1D linear hyperbolic equations. ESAIM Math. Model. Numer. Anal. 51(2), 467–486 (2017)
Cao, W., Shu, C.-W., Yang, Y., Zhang, Z.: Superconvergence of discontinuous Galerkin methods for two-dimensional hyperbolic equations. SIAM J. Numer. Anal. 53(4), 1651–1671 (2015)
Cao, W., Shu, C.-W., Yang, Y., Zhang, Z.: Superconvergence of discontinuous Galerkin method for scalar nonlinear hyperbolic equations. SIAM J. Numer. Anal. 56(2), 732–765 (2018)
Cao, W., Shu, C.-W., Zhang, Z.M.: Superconvergence of discontinuous Galerkin methods for 1-D linear hyperbolic equations with degenerate variable coefficients. ESAIM: Math. Model. Numer. Anal. 51(6), 2213–2235 (2017)
Cao, W., Zhang, Z., Zou, Q.: Superconvergence of discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 52(5), 2555–2573 (2014)
Chen, A., Cheng, Y., Liu, Y., Zhang, M.: Superconvergence of ultra-weak discontinuous Galerkin methods for the linear Schrödinger equation in one dimension. J. Sci. Comput. 82(1), 22 (2020)
Cheng, Y., Shu, C.-W.: A discontinuous Galerkin finite element method for time dependent partial differential equations with higher order derivatives. Math. Comput. 77(262), 699–730 (2008)
Cheng, Y., Shu, C.-W.: Superconvergence and time evolution of discontinuous Galerkin finite element solutions. J. Comput. Phys. 227(22), 9612–9627 (2008)
Cheng, Y., Shu, C.-W.: Superconvergence of local discontinuous Galerkin methods for one-dimensional convection-diffusion equations. Comput. Struct. 87(11/12), 630–641 (2009)
Cheng, Y., Shu, C.-W.: Superconvergence of discontinuous Galerkin and local discontinuous Galerkin schemes for linear hyperbolic and convection-diffusion equations in one space dimension. SIAM J. Numer. Anal. 47(6), 4044–4072 (2010)
Cockburn, B., Shu, C.-W.: The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35(6), 2440–2463 (1998)
Dong, B., Shu, C.-W.: Analysis of a local discontinuous Galerkin method for linear time-dependent fourth-order problems. SIAM J. Numer. Anal. 47(5), 3240–3268 (2009)
Ji, L., Xu, Y.: Optimal error estimates of the local discontinuous Galerkin method for Willmore flow of graphs on Cartesian meshes. Int. J. Numer. Anal. Model. 8(2), 252–283 (2011)
Liu, H., Yan, J.: A local discontinuous Galerkin method for the Korteweg-de Vries equation with boundary effect. J. Comput. Phys. 215(1), 197–218 (2006)
Liu, Y., Shu, C.-W., Zhang, M.: Superconvergence of energy-conserving discontinuous Galerkin methods for linear hyperbolic equations. Commun. Appl. Math. Comput. 1(1), 101–116 (2019)
Liu, Y., Tao, Q., Shu, C.-W.: Analysis of optimal superconvergence of an ultraweak-local discontinuous Galerkin method for a time dependent fourth-order equation. ESAIM: Math. Model. Numer. Anal. 54(6),1797–1820 (2020)
Tao, Q., Cao, W., Zhang, Z.: Superconvergence analysis of the ultra-weak local discontinuous Galerkin method for one dimensional linear fifth order equations. J. Sci. Comput. 88(3), 63 (2021)
Tao, Q., Xu, Y.: Superconvergence of arbitrary Lagrangian-Eulerian discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 57(5), 2142–2165 (2019)
Tao, Q., Xu, Y., Shu, C.-W.: An ultraweak-local discontinuous Galerkin method for PDEs with high order spatial derivatives. Math. Comput. 89(326), 2753–2783 (2020)
Xu, Y., Shu, C.-W.: Local discontinuous Galerkin methods for high-order time-dependent partial differential equations. Commun. Comput. Phys. 7(1), 1 (2010)
Yan, J., Shu, C.-W.: A local discontinuous Galerkin method for KdV type equations. SIAM J. Numer. Anal. 40(2), 769–791 (2002)
Yan, J., Shu, C.-W.: Local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 17, 27–47 (2002)
Zhong, W.X.: On precise integration method. J. Comput. Appl. Math. 163(1), 59–78 (2004)
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
The research of Yan Xu was partially supported by the NSFC Grant No. 12071455.
Appendices
Proof of Lemma 1
We will prove this lemma by induction. Since \(\omega _u^{(0)},\,\omega _v^{(0)}\perp \mathcal {P}^{k-3}(I_j)\), we can easily deduce from the definitions of \(\omega _u^{(i)}\) and \(\omega _v^{(i)}\) that
Thus, we can write
Then, we are going to estimate \(c^1_{j,m}\) and \(d^1_{j,m}\). If \(f\perp \mathcal {P}^0(I_j)\), we can define \(D^{-1}f(x)=\overline{h_j}\int _{x_{j-\frac{1}{2}}}^x f(t)\ \textrm{d}t,\,x\in I_j\), where \(\overline{h_j}=\frac{h_j}{2}\). And \(D^{-n}=(D^{-1})^n\) for any \(n\in \mathbb {N}\). Taking \(\varphi ={D^{-3}L_{j,m}},\ m=k-5,\,k-4,\,k-3\), respectively, in (11), we have
Thus,
Similarly, we have
From (11), we can also obtain
Thus,
Thus,
Similarly, we have the estimate for \(\omega _v^{(1)}\). And we take the time derivate on both sides of (11) and (12), we can obtain the estimates for \(\partial _t^n\omega _u^{(1)}\) and \(\partial _t^n\omega _v^{(1)}\). We can prove (14) for all \(1\leqslant i\leqslant l\) by the recursion formula.
Proof of Lemma 3
Integrating (20) by part, we have
First, we take
where \(L_k\) is the standard Legendre polynomial with degree k, \(\theta =\frac{2}{h_j}\left( x-x_{j}\right) \) with \(x_j=\frac{x_{j-\frac{1}{2}}+x_{j+\frac{1}{2}}}{2}\), and \(a,\,b,\) and c are the solutions of the equations:
That is,
By the inverse inequality, we have
Clearly, there holds \(\varphi \left( x_{j-\frac{1}{2}}^+\right) =0\), \(\varphi _x\left( x_{j-\frac{1}{2}}^+\right) =0\), and \(\varphi _{xx}\left( x_{j-\frac{1}{2}}^+\right) =0\). So, by (B1) we have
thus
Next, we take \(\varphi =1\) in (B1) to obtain
thus
Next, we take \(\varphi =\frac{2(x-x_j)}{h_j}\) in (B1) to obtain
thus
Finally, we take \(\varphi =\left( \frac{2(x-x_j)}{h_j}\right) ^2\) in (B1) to obtain
thus
This finishes our proof.
Proof of Lemma 4
Since \(f_1\perp \mathcal {P}^0\), so we can define \(D^{-1}f_1(x)=\overline{h_j}\int _{x_{j-\frac{1}{2}}}^x f_1(t)\ \textrm{d}t,\,x\in I_j\), where \(\overline{h_j}=\frac{h_j}{2}\). It’s easy to check that \(D^{-1}f_1\left( x_{j\pm \frac{1}{2}}^{\mp }\right) =0\) and \(\Vert D^{-1} f_1\Vert _{I_j}\lesssim \Vert f_1\Vert _{I_j}\). Thus, we have \((f_1,\varphi )_j=-(\overline{h_j}D^{-1}f_1,\varphi _x)_j\).
Integrating the left-hand side of (22) by parts twice, we have
Taking \(\varphi =\xi _x\) and summing over j, we have
thus
By Lemma 3, we have \(\Vert \xi _{xxx}\Vert \lesssim \Vert f_1\Vert +\Vert f_2\Vert \), \(h^{-\frac{1}{2}}\left( \sum _{j=1}^N\llbracket \xi \rrbracket _{j+\frac{1}{2}}^2\right) ^{\frac{1}{2}}\lesssim h^2(\Vert f_1\Vert +\Vert f_2\Vert )\), \(h^{-\frac{1}{2}}\left( \sum _{j=1}^N\llbracket \xi _x\rrbracket _{j+\frac{1}{2}}^2\right) ^{\frac{1}{2}}\lesssim h(\Vert f_1\Vert +\Vert f_2\Vert )\), and by the discrete Poincaré inequalities, we also have
Thus,
thus
And, by (C1), we have
Proof of Lemma 5
For \(u\in L^2(I_j)\), we can have the Legendre expansion
In [10], the following expression of \(u_{j,m}\) was given:
where \(\theta =\frac{2}{h_j}(x-x_j)\) as in the proof of Lemma 3, and \(\hat{u}(\theta )=u(x(\theta ))\). If \(u\in W^{l,\infty }(I_j)\), we have
As to \(P_h^+ u\), we can also express it in the Legendre basis:
we can easily deduce from the definition of \(P_h^+\) (9) that
Substituting (D1) and (D3) into (10), we have
where
With further calculations, we know that \(\mathcal {M}_j\) is independent of h and is identical for all j, so we drop the subscript j and denote it by \(\mathcal {M}\). The reversibility of \(\mathcal {M}\) enables us to rewrite (D4) into
Then on \(I_j\), we have
where
Taking \(u=L_{j,k+1}\) in (D5), we can see that \(R_{j,k+1}\) we define here is identical with the one in (31). Therefore, from (D2), we have for \(x\in D^s_j\),
Discrete Poincaré Inequality
Let
be the piecewise \(H^1\) functions on \(\mathcal {T}\). We have the following discrete Poincaré inequality.
Lemma E1
Suppose \(u\in H^1(\Omega ,\mathcal {T})\), and u is a periodic function with a period of \(2\uppi \). Then, we have
Proof
Let \(V=\{ u\in L^2(\Omega )\!:\ u\vert _{I_j} \in \mathcal {P}^1(I_j)\ \textrm{and} \ u \ \mathrm {is \ continue}\} \), we introduce an interpolation operator \(\mathcal {I}\): \(H^1(\Omega ,\mathcal {T}) \rightarrow V\)
Let \(\uppi _{I_j}\!:\!H^1(I_j)\rightarrow \mathcal {P}^1(I_j)\) be the local interpolation operator defined by
We have the following well-known estimates:
From (E1) and (E2), we have on \(I_j\)
It is easy to check that
Along with (E3), we have
Since \(\mathcal {I}u\in H^1(\Omega )\), we can use the usual Poincaré inequality. Thus,
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, M., Xu, Y. Superconvergence of UWLDG Method for One-Dimensional Linear Sixth-Order Equations. Commun. Appl. Math. Comput. (2024). https://doi.org/10.1007/s42967-024-00390-1
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42967-024-00390-1