1 Introduction

The qualitative and quantitative analysis of the shock structure is important for many applications and a challenging subject for physics to develop a valid theory to explain the rapid and steep change of the physical quantities near the shock front [49, 52]. In order to understand the structure of strong shock waves involving a highly-nonequilibrium state beyond the validity range of the local equilibrium assumption, we need to establish an appropriate theory. Non-equilibrium thermodynamics based on the local equilibrium assumption, including the Navier-Stokes-Fourier (NSF) theory, is not able to explain the shock structure with large Mach numbers.

The kinetic approaches based on the Boltzmann equation, such as direct simulation Monte Carlo (DSMC), provide successful results on the shock structure in a rarefied monatomic gas [7].

However, due to internal modes, modeling the collision terms becomes difficult for polyatomic gases, in particular for a mixture of rarefied polyatomic gases, which is the object of the present study. For information on these subjects, please refer to the recent preliminary studies [17, 18] and the review paper [32].

Rational extended thermodynamics (RET) [30, 38, 39] is a phenomenological theory that is valid beyond the validity range of the local equilibrium assumption. In addition to the usual equilibrium quantities, the RET theory adopts dissipative fluxes, such as the viscous stress and the heat flux, as independent variables. The closure of the system is achieved by using universal principles: objectivity, entropy principle, and thermodynamic stability.

In the case of a single rarefied polyatomic gas with large bulk viscosity, as the Mach number increases, the shock structure changes from the nearly symmetric profile (Type A) to an asymmetric profile (Type B) and further to the profile with thick and thin layers (Type C) [49]. RET can explain these changes of the shock wave structure in a unified way [45, 46] in contrast to previous approaches such as the Bethe-Teller theory [5] and the prediction by NSF theory [19].

In particular, the shock structure in a rarefied polyatomic gas with large bulk viscosity (large relaxation time for the dynamic pressure) can be predicted by RET with only six independent fields (RET\(_6\)) [1, 3]: the mass density \(\rho\), the velocity \(\textbf{v}\), the temperature T, and the dynamic pressure \(\Pi\). Within the limited resolution of RET\(_6\), the thin layer is described as a sub-shock [46, 47], while it can be explained as a fine structure with very steep, but continuous change by RET\(_{14}\) with 14 independent variables, in which other than the previous 6 fields, we take into account also the 5 components of the deviatoric shear stress, and the 3 components of the heat flux.

After the successful explanation of the shock structure by RET, the numerical analysis based on the kinetic theory was done. The agreement between the theoretical predictions by RET and kinetic theory strongly supports the usefulness of the analysis based on RET [22, 23].

The next step is to analyze the shock structure in a mixture of polyatomic gases. In a recent paper [2], by using the framework of RET, the field equations of a mixture of polyatomic gases are derived in the context of the multi-temperature model where each constituent has 6 fields.

For a generic quasi-linear hyperbolic system of partial differential equations, it has been shown that the profile of the shock structure may not be continuous only when the shock velocity meets a characteristic velocity [33]. However, this necessary condition becomes also sufficient when the shock speed is greater than the maximum characteristic velocity evaluated in the unperturbed field, as was proved in a theorem by Boillat and Ruggeri [10]. The present status of the sub-shock formation is summarized in a recent survey [40] and in the book [39].

Numerical calculations of the shock structure show that a sub-shock emerges only after the maximum characteristic velocity in the context of RET theory for a single rarefied gas [44, 50]. On the other hand, sub-shock may appear before the maximum characteristic velocity, and multiple sub-shocks may also arise in the context of mixture theories [4, 8, 15] and toy models [44, 48].

In the case of the binary Eulerian mixture of rarefied polyatomic gases, the authors have given a complete classification of the regions in the plane of concentration and Mach number where both scenarios of sub-shocks before and after the maximum characteristic velocity arise [41, 42]. For a dissipative mixture of gases, we started the equivalent analysis of Eulerian mixtures in a recent paper [43], but examined only some particular values of the structural parameters and have not given a complete classification of the possible regions, that is, the aim of the present paper.

The present paper is organized as follows. In Sect. 2, we summarize the basic equations for the present analysis. In Sect. 3, the shock structure problem is presented, and in Sect. 4 the possible regions are classified depending on the concentration and Mach number in which there is the possibility of sub-shock formation. In Sect. 5, the numerical calculations of the shock structure are given and it is confirmed whether the sub-shocks arise or not. Section 6 gives the conclusions.

2 Basic Equations for a Binary Mixture of RET\(_6\) Gases

We consider a binary mixture of rarefied polytropic gases described by the following thermal and caloric equations of state:

$$\begin{aligned} p_{\alpha } = \frac{k_B}{m_{\alpha }} \rho _{\alpha } T_{\alpha }, \qquad \varepsilon _{\alpha } = \frac{k_B}{m_{\alpha }(\gamma _{\alpha } - 1)}T_{\alpha }, \end{aligned}$$

where the quantities with suffix \(\alpha\) \((= 1, 2)\) represent the corresponding quantities for the constituent \(\alpha ,\) and \(p_{\alpha }\), \(k_B\), \(m_\alpha\), \(T_{\alpha }\), \(\varepsilon _{\alpha }\), and \(\gamma _{\alpha }\) are, respectively, the pressure, the Boltzmann constant, the mass of a molecule, the temperature, the specific internal energy, and the ratio of the specific heats. In the present analysis, we consider polytropic gases in which the specific heat is independent of the temperature, and therefore also \(\gamma _\alpha\) is constant.

In the present study, we analyze plane shock waves propagating along with x-direction and hereafter, we focus on the one-dimensional problem. Furthermore, it is assumed that the mixture is inert and no chemical reactions occur.

The system of a binary mixture of RET\(_6\) gases without shear viscosity and heat conductivity has been presented in the paper [2]Footnote 1:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}}&\dfrac{\partial \rho _1 }{\partial t} + \dfrac{\partial \rho _1 v_1 }{\partial x} = 0, \nonumber \\&\dfrac{\partial \rho _1 v_1 }{\partial t}+ \dfrac{\partial }{\partial x} (\rho _1 v^2_1 + p_1 + \Pi _1 ) = {\hat{m}}_1, \nonumber \\&\dfrac{\partial }{\partial t} ( \rho _1 v^2_1 + 2 \rho _1 \varepsilon _1 ) + \dfrac{\partial }{\partial x}(( \rho _1 v^2_1 + 2\rho _1 \varepsilon _1 + 2 p_1 + 2\Pi _1 ) v_1 ) = 2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\dfrac{\partial }{\partial t}( \rho _1 v_1^2 + 3(p_1 +\Pi _1 )) + \dfrac{\partial }{\partial x}( ( \rho _1 v_1^2 + 5 (p_1 +\Pi _1 )) v_1 ) = - \dfrac{3 \Pi _1}{\tau _1} + 2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \nonumber \\&\dfrac{\partial \rho _2 }{\partial t} + \dfrac{\partial \rho _2 v_2 }{\partial x} = 0, \\&\dfrac{\partial \rho _2 v_2 }{\partial t}+ \dfrac{\partial }{\partial x} ( \rho _2 v^2_2 + p_2 + \Pi _2 ) = -{\hat{m}}_1, \nonumber \\&\dfrac{\partial }{\partial t} ( \rho _2 v^2_2 + 2 \rho _2 \varepsilon _2) + \dfrac{\partial }{\partial x}(( \rho _2 v^2_2 + 2\rho _2 \varepsilon _2 + 2 p_2 + 2\Pi _2 ) v_2 ) = -2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\dfrac{\partial }{\partial t}( \rho _2 v_2^2 + 3(p_2 +\Pi _2 )) + \dfrac{\partial }{\partial x}(( \rho _2 v_2^2 + 5 (p_2 +\Pi _2 )) v_2) = - \dfrac{3 \Pi _2}{\tau _2} -2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \nonumber \end{array}} \right. \end{aligned}$$
(1)

where v is the velocity of the center of mass and \(\tau _{\alpha } > 0\) is the relaxation time for the dynamic pressure \(\Pi _\alpha\) of the constituent \(\alpha\). The production terms, \({\hat{m}}_{\alpha }\), \({\hat{e}}_{\alpha }\), and \({\hat{\omega }}_{\alpha },\) represent the interchange of the momentum, the energy, and the momentum flux, respectively, evaluated for \(v=0\).

The expressions of \({\hat{m}}_1\), \({\hat{e}}_1\), and \({\hat{\omega }}_1\) are chosen such that the entropy production is a quadratic positive form as usual in non-equilibrium thermodynamics included in the classical approach of the thermodynamics of irreversible processes (TIP) [16]. In the present case, we have [2]

$$\begin{aligned} \begin{aligned} {\hat{m}}_1 = \psi _{11} {\hat{\Lambda }}_1, \quad {\hat{e}}_1 = 2(\theta _{11} {\hat{\eta }}_1 + \kappa _{11} {\hat{\zeta }}_1), \quad {\hat{\omega }}_1 = 2(\kappa _{11} {\hat{\eta }}_1 + \phi _{11} {\hat{\zeta }}_1 ) \end{aligned} \end{aligned}$$
(2)

with

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}}\begin{aligned} \begin{aligned}&{\hat{\Lambda }}_1 = - \frac{u_1}{T_1}\left( 1- \frac{\Pi _1}{p_1}\right) + \frac{u_2}{T_2}\left( 1- \frac{\Pi _2}{p_2}\right) , \\&{\hat{\eta }}_1 = \frac{1}{2 T_1} \left( 1- \frac{\Pi _1}{p_1}\right) - \frac{1}{2 T_2} \left( 1- \frac{\Pi _2}{p_2}\right) , \\&{\hat{\zeta }}_1 = - \frac{1}{(5-3\gamma _1)T_1}\frac{\Pi _1}{p_1} + \frac{1}{(5-3\gamma _2)T_2}\frac{\Pi _2}{p_2} \end{aligned} \end{aligned} \end{array}} \right. \end{aligned}$$
(3)

that are the components of the main field for which the system becomes symmetric hyperbolic, while \(u_\alpha = v_\alpha - v\) is the diffusion velocity.

$$\begin{aligned} \text {The coefficient } \, \psi _{11} >0 \, \text {and the matrix} \, \begin{pmatrix} \theta _{11} &{} \kappa _{11}\\ \kappa _{11} &{} \phi _{11} \end{pmatrix} \, \text {is positive definite}. \end{aligned}$$
(4)

The phenomenological coefficients \(\psi _{11}\), \(\theta _{11}\), \(\kappa _{11}\), and \(\phi _{11}\) may depend on the mass densities and temperatures and, as usual, the phenomenological theory is not able to deduce the explicit expression except for the inequalities (4). The functional forms of the coefficients may be determined for rarefied gases by kinetic theoretical consideration or, in general, by experimental data.

In the case of a mixture of rarefied Eulerian gases, some studies utilizing kinetic theory were made in [11, 28, 31].

2.1 Field Equations for Global Quantities

By taking the sum of (1), we have the following equivalent system:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}}\begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial \rho v}{\partial x} = 0, \nonumber \\&\frac{\partial \rho v}{\partial t}+ \frac{\partial }{\partial x} ( \rho v^2 + p + \Pi - \sigma ) = 0, \nonumber \\&\frac{\partial }{\partial t} \left( \frac{1}{2}\rho v^2 + \rho \varepsilon \right) +\frac{\partial }{\partial x}\left(\left( \frac{1}{2}\rho v^2 + \rho \varepsilon + p + \Pi -\sigma \right) v + q \right) = 0, \nonumber \\&\frac{\partial }{\partial t}( \rho v^2 + 3(p+\Pi )) + \frac{\partial }{\partial x}(( \rho v^2 + 5 (p+\Pi ) - 2 \sigma ) v + 2 Q ) = - 3\left( \frac{\Pi _{1}}{\tau _1}+\frac{\Pi _{2}}{\tau _2}\right) ,\nonumber \\&\frac{\partial \rho _1 }{\partial t} + \frac{\partial \rho _1 v_1 }{\partial x} = 0, \nonumber \\&\frac{\partial \rho _1 v_1 }{\partial t}+ \frac{\partial }{\partial x} (\rho _1 v^2_1 + p_1 + \Pi _1 ) = {\hat{m}}_1, \nonumber \\&\frac{\partial }{\partial t} ( \rho _1 v^2_1 + 2 \rho _1 \varepsilon _1 ) + \frac{\partial }{\partial x}(( \rho v^2_1 + 2\rho _1 \varepsilon _1 + 2 p_1 + 2\Pi _1) v_1 ) = 2({\hat{e}}_1 + {\hat{m}}_1 v), \nonumber \\&\frac{\partial }{\partial t}( \rho _1 (v_1 )^2 + 3(p_1 +\Pi _1 )) + \frac{\partial }{\partial x}(( \rho _1 v_1^2 + 5 (p_1 +\Pi _1 )) v_1 ) = - \frac{3 \Pi _1}{\tau _1} +2 ({\hat{\omega }}_1 + {\hat{m}}_1 v), \end{aligned} \end{array}} \right. \end{aligned}$$
(5)

where the global quantities mass density \(\rho\), pressure p, specific internal energy \(\varepsilon\), shear stress \(\sigma\), dynamic pressure \(\Pi\), heat flux q, and a new extra variable Q are given by

$$\begin{aligned}&\rho = \sum _{\alpha =1}^{2}\rho _\alpha , \qquad p = \sum _{\alpha =1}^{2}p_\alpha ,\\&\rho \varepsilon = \rho \varepsilon _{\textrm{int}} +\frac{1}{2} \sum _{\alpha =1}^{2}\rho _\alpha u_\alpha ^2, \quad \left( \varepsilon _{\textrm{int}} = \frac{1}{\rho } \sum _{\alpha =1}^{2}\rho _\alpha \varepsilon _\alpha \right) , \\&\sigma = { - \frac{2}{3} \sum _{\alpha =1}^{2}\rho _\alpha u_\alpha ^2} = - \frac{2}{3} \frac{\rho _{1} \rho }{\rho _{2}} u_1^2, \\&\Pi =\sum _{\alpha =1}^{2}\left( \Pi _\alpha + \frac{1}{3}\rho _\alpha u_\alpha ^2\right) = \Pi _1+\Pi _2 -\frac{\sigma }{2}, \\&q = \sum _{\alpha =1}^{2}\left( \frac{1}{2}\rho _\alpha u_\alpha ^2 + \rho _\alpha \varepsilon _\alpha + p_\alpha + \Pi _\alpha \right) u_\alpha , \\&Q = \sum _{\alpha =1}^{2}\left( \frac{1}{2}\rho _\alpha u_\alpha ^2 + \frac{5}{2}\left( p_\alpha + \Pi _\alpha \right) \right) u_\alpha . \end{aligned}$$

Here, \(\varepsilon _{\textrm{int}}\) represents the intrinsic part of the global-specific internal energy. We note that the global shear stress and global heat flux appear in the system (5) due to the diffusion velocity, even if we neglect these dissipative quantities in the field equations for each constituent.

In order to discuss the behavior of non-equilibrium average temperature \(\mathcal {T}\), we use the definition proposed in [20, 36, 37]. This average temperature is introduced such that the intrinsic internal energy \(\varepsilon _\textrm{int}\) of the multi-temperature mixture has the same expression as a single-temperature mixture:

$$\begin{aligned} \rho \varepsilon _{\textrm{int}} = \rho _1 \varepsilon _1 (\rho _1, \mathcal {T}) + \rho _2 \varepsilon _2 (\rho _2, \mathcal {T}) = \rho _1 \varepsilon _1 (\rho _1 , T_1) + \rho _2 \varepsilon _2 (\rho _2, T_2) . \end{aligned}$$

2.2 Equilibrium Subsytem

The production terms \({\hat{m}}_{\alpha }\), \({\hat{e}}_{\alpha }\), and \({\hat{\omega }}_{\alpha }\) vanish in equilibrium and from (2) and (3), we obtain \(v_1 = v_2 = v\), \(T_1 = T_2 = T\), and \(\Pi _1 = \Pi _2 = 0\), where T is the average temperature in equilibrium. In a generic equilibrium state, the total (equilibrium) pressure and the total internal intrinsic energy are the same forms as in the case of a single-component gas

$$\begin{aligned} p^{(\text{eq})} = \frac{k_{B}}{m} \rho T, \qquad \varepsilon ^{(\text{eq})}_{\textrm{int}} = \frac{k_{B}}{m(\gamma -1)} T, \end{aligned}$$

provided that we introduce following [35] average mass \(m \equiv m(c)\) and average ratio of the specific heats \(\gamma \equiv \gamma (c)\)

$$\begin{aligned} \begin{aligned} \frac{1}{m} = \frac{c}{ m_{1}} + \frac{1-c}{ m_{2}},\quad \frac{1}{\gamma -1} = \frac{m }{m_{1}} \frac{c}{\gamma _1 - 1} + \frac{m }{m_{2}} \frac{1 - c}{\gamma _2 - 1}, \end{aligned} \end{aligned}$$
(6)

where \(c=\rho _1/\rho \in ]0,1[\) denoting the concentration.

The associate equilibrium subsystem of (5) according to the definition given in [9] is given by

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{aligned} \begin{aligned}&\frac{\partial \rho }{\partial t} + \frac{\partial \rho v}{\partial x} = 0, \\&\frac{\partial \rho v}{\partial t}+ \frac{\partial }{\partial x} \left( \rho v^2 + p^{(\text{eq})} \right) = 0,\\&\frac{\partial }{\partial t} \left( \frac{1}{2}\rho v^2 + \rho \varepsilon ^{(\text{eq})}_{\textrm{int}} \right) +\frac{\partial }{\partial x}\left( \left( \frac{1}{2}\rho v^2 + \rho \varepsilon ^{(\text{eq})}_{\textrm{int}} + p^{(\text{eq})} \right) v \right) = 0, \\&\frac{\partial \rho _1 }{\partial t} + \frac{\partial \rho _1 v }{\partial x} = 0. \end{aligned} \end{aligned} \end{array}} \right. \end{aligned}$$
(7)

3 Shock Structure

The shock structure is a traveling wave solution with the constant velocity s in which all components of the field depend on a single variable \(\varphi = x - s t\) connecting two constant equilibrium states \(\textbf{u}_{0}\) and \(\textbf{u}_\textrm{I}\) at \(\varphi = \pm \infty ,\) respectively.

We can choose without loss of generality the unperturbed velocity \(v_0=0\). Taking into account the conservation laws, we have the following boundary conditions:

$$\begin{aligned} \textbf{u}_{0} = \left[ \begin{array}{c} \rho _{0} \\ v_{0} \\ T_{0} \\ \Pi _{0}\\ \left( \rho _1\right) _{0} \\ \left( v_1\right) _{0} \\ \left( T_1\right) _{0} \\ \left( \Pi _1\right) _{0}\\ \end{array} \right] , \quad \textbf{u}_\textrm{I} = \left[ \begin{array}{c} \rho _\textrm{I} \\ v_\textrm{I} \\ T_\textrm{I} \\ \Pi _\textrm{I}\\ \left( \rho _1\right) _\textrm{I} \\ \left( v_1\right) _\textrm{I} \\ \left( T_1\right) _\textrm{I} \\ \left( \Pi _1\right) _\textrm{I}\\ \end{array} \right] . \end{aligned}$$

In the unperturbed equilibrium state \(\textbf{u}_{0}\), we have

$$\begin{aligned} \left( \rho _1\right) _0 = c_{0} \rho _0, \quad \left( T_1\right) _0 = T_0, \quad v_0 = \left( v_1\right) _0 = 0, \quad \Pi _0 = \left( \Pi _1\right) _0 = 0, \end{aligned}$$
(8)

and the perturbed equilibrium state \(\textbf{u}_\textrm{I}\) is the solution of the Rankine-Hugoniot equations of the equilibrium sub-system (7):

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \begin{aligned}&\rho _\textrm{I} = \frac{(\gamma _0 + 1) M_{0}^{2}}{2 + (\gamma _0 - 1) M_{0}^{2}}\rho _0, \quad c_\textrm{I}=c_0, \quad \left( \rho _1\right) _\textrm{I} = c_{0} \rho _\textrm{I}, \nonumber \\&T_\textrm{I} ={T_1}_\textrm{I} = \frac{(2 + (\gamma _0 - 1) M_0^2)(1 + \gamma _0(2 M_0^2 - 1))}{(\gamma _0 + 1)^2 M_0^2} T_0, \\&v_\textrm{I} = {(v_1)}_\textrm{I} =\frac{2 (M_{0}^{2} - 1)}{(\gamma _0 + 1) M_{0}} a_0, \quad \Pi _\textrm{I} = \left( \Pi _1\right) _\textrm{I} = 0, \nonumber \end{aligned} \end{array}} \right. \end{aligned}$$
(9)

where \(\gamma _0\) is the function \(\gamma\) given in (6) evaluated in \(c_0\): \(\gamma _0 = \gamma (c_0)\). The unperturbed Mach number \(M_0\) is defined by

$$\begin{aligned} M_{0} =\frac{s-v_0}{a_{0}} \end{aligned}$$

with \(a_0\) being the sound velocity in the unperturbed state

$$\begin{aligned} a_{0} = \sqrt{ \gamma _0 \frac{k_{B}}{m_{0}} T_{0} }, \end{aligned}$$

and \(m_{0} = m(c_{0})\) being the equilibrium average mass of the mixture.

4 Regions Classified by the Possibility of Sub-shock Formation

Let us analyze whether the continuous shock-structure solution exists or not. Without any loss of generality, hereafter, we assume \(\begin{aligned} m_{1} \leqslant m_{2} \end{aligned}\). Following the paper [43], we will analyze the shock wave propagating in the positive direction with respect to the fluid flow introducing the characteristic velocities in an equilibrium state for constituents 1 and 2 : 

$$\begin{aligned} \lambda _1 = v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{1}} T}, \quad \lambda _2 = v + \sqrt{\frac{5}{3} \frac{k_{\textrm{B}}}{m_{2}} T}, \end{aligned}$$
(10)

and the characteristic velocities of the equilibrium subsystem

$$\begin{aligned} {\bar{\lambda }} = v + \sqrt{\gamma \frac{k_{\textrm{B}}}{m} T}\end{aligned}$$
(11)

with m and \(\gamma\) given in (6).

Let us introduce the dimensionless characteristic velocities at the unperturbed and perturbed states:

$$\begin{aligned} M_{10} \equiv \frac{\lambda _{10}}{a_0}, \quad M_{20} \equiv \frac{\lambda _{20}}{a_0}, \quad M_\textrm{1I} \equiv \frac{\lambda _\textrm{1I}}{a_0}, \quad M_\textrm{2I} \equiv \frac{\lambda _\textrm{2I}}{a_0}, \quad \end{aligned}$$

where, taking into account (10), (11) and (8), (9) the explicit expressions of these quantities are given by

$$\begin{aligned} \begin{aligned}&M_{10} = \sqrt{\frac{5 }{3 \gamma _0 ( c_{0} + (1 - c_{0}) \mu ) }}, \quad M_{20} =\sqrt{\frac{5 \mu }{3 \gamma _0 ( c_{0} + (1 - c_{0}) \mu ) }}, \\&M_\textrm{1I} = \frac{2 (M_{0}^{2} - 1)}{(\gamma _0 + 1) M_{0}} + \sqrt{ \frac{5 (2 + (\gamma _0-1) M_0^2 )( 1 + \gamma _0 (2 M_0^2 - 1) )}{3 \gamma _0 (\gamma _0+1)^2 M_0^2}\frac{m_0}{m_{1}}}, \\&M_\textrm{2I} = \frac{2 (M_{0}^{2} - 1)}{(\gamma _0 + 1) M_{0}} + \sqrt{ \frac{5 ( 2 + (\gamma _0-1) M_0^2 )( 1 + \gamma _0 (2 M_0^2 - 1) )}{3 \gamma _0 (\gamma _0+1)^2 M_0^2}\frac{m_0}{m_{2}}} \end{aligned} \end{aligned}$$
(12)

with \(\mu\) being the ratio of the masses of the constituents defined by

$$\begin{aligned} \mu = \frac{m_{1}}{m_{2}}, \quad 0< \mu \leqslant 1. \end{aligned}$$

The analogous expressions for a mixture of Eulerian gases are given in [43] and indicated with an apex (E) in Figs. 1, 2, 3, 4, 5, 6, 7.

In the previous paper [43], we have identified sufficient and necessary conditions for the sub-shock formation.

According to the theorem for the sub-shock formation given in [10],

Necessary and sufficient condition for the sub-shock formation for the shock structure of the constituent 1 (light species) is given by [43]

$$\begin{aligned} s> \lambda _{10} \quad ( \Leftrightarrow M_{0} > M_{10} ). \end{aligned}$$

While for possible sub-shocks for the shock structure of the constituent 2 (heavy species), we need to distinguish two cases: A) if \(\begin{aligned} \mu \leqslant {3 \gamma _1}/{5} \end{aligned}\) or B) if \(\mu > {3 \gamma _1}/{5}\). In fact as proven in [43], we have

Necessary condition, but in general not sufficient for the sub-shock formation for the shock structure of constituent 2 is given:

$$\begin{aligned} {\textbf {Case A) }} \nonumber \\&\text {if}\,\,\, 0 < c_0 \leqslant c_0^*, \, \, \text {when} \,\,\ \, s> \lambda _{20} \,\, (\Leftrightarrow M_{0} > M_{20}), \end{aligned}$$
(13)
$$\begin{aligned}&\text {if}\,\, c_0^*< c_0 < 1, \, \, \text {when} \,\,\ \, s> s^* \,\, (\Leftrightarrow M_{0} > M^*_{20}), \end{aligned}$$
(14)
$$\begin{aligned} {\textbf {Case B)}} \nonumber \\&\, \, \text {when} \quad s> \lambda _{20} \, (\Leftrightarrow M_{0} > M_{20}), \, \text {for any} \,\, c_0 \in \, ]0,1[ \, , \end{aligned}$$
(15)

where \({c}_0^*(\mu )\) is the solution of \(\lambda _{20} = {\bar{\lambda }}_{0}\) (\(\Leftrightarrow M_{20}(c_0^*,\mu ) = 1\)) and \(s^*\) is the solutions of \(\lambda _{\textrm{2I}}(s^*)=s^*\) (\(\Leftrightarrow M_{\textrm{2I}}(M^*_{20}) = M^*_{20}\)).

4.1 Regions in Case A)

Case A) has four possible types of regions depending on \(\mu\).

  • A\(_1\)) in which \(M^*_{20}\) intersects \(M_{10}\) and has an asymptote like in the example reported in Fig. 1. Taking into account (12), this situation is possible if

    $$\begin{aligned} 0 < \mu \leqslant \frac{3}{10}(\gamma _1 - 1). \end{aligned}$$

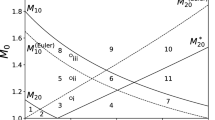
  • A\(_2\)) in which \(M^*_{20}\) intersects \(M_{10}\) and does not have an asymptote like in the example reported in Fig. 2. Taking into account (12), this situation is possible if

    $$\begin{aligned} \frac{3}{10}(\gamma _1 - 1)< \mu < \frac{15-33\gamma _1}{15\gamma _1-65}. \end{aligned}$$

  • A\(_3\)) in which \(M^*_{20}\) does not intersect \(M_{10}\) like in the example reported in Fig. 3. Taking into account (12), this situation is possible if

    $$\begin{aligned} \frac{15-33\gamma _1}{15\gamma _1-65} \leqslant \mu < \frac{3}{5}\gamma _1. \end{aligned}$$

  • A\(_4\)) in which \(M^*_{20}\) does not intersect \(M_{10}\) and the curves of \(M_{20}\) and \(M_{10}^{(E)}\) coincide with each other and \(c_0^* = 1\) like in the example reported in Fig. 4. Taking into account (12) this situation is possible if

    $$\begin{aligned} \mu = \frac{3}{5}\gamma _1. \end{aligned}$$
Fig. 1
figure 1

Regions in the plane \((c_0,M_0)\) of possible sub-shocks in Case A\(_1\) (right); \(\gamma _1=7/5\), \(\gamma _2=9/7\), and \(\mu = 0.1\). The vertical dotted line represents the asymptote of \(M^*_{20}\). The magnification of the regions around \((c_0, M_0) = (0, 1)\) is also shown (left)

Full size image
Fig. 2
figure 2

Regions in the plane \((c_0,M_0\)) of possible sub-shocks in Case A\(_2\); \(\gamma _1=7/5\), \(\gamma _2=9/7\), and \(\mu = 0.4\). The circles represent the parameters adopted for numerical calculations shown in Sect. 5

Full size image
Fig. 3
figure 3

Regions classified by the possibility of the sub-shock formation in the \(M_0\) - \(c_0\) plane in Case A\(_3\); \(\gamma _1 = 7/6\), \(\gamma _2 = 7/5\), and \(\mu = 0.65\)

Full size image
Fig. 4
figure 4

The regions classified by the possibility of the sub-shock formation in the \(M_0\) - \(c_0\) plane in Case A\(_4\); \(\gamma _1 = 7/6\), \(\gamma _2 = 7/5\), and \(\mu = 0.7\). In this case, \(c_0^* = 1\)

Full size image

4.2 Regions in Case B)

Case B) has three possible topologies of regions depending on \(\mu\).

  • B\(_1\)) in which \(M_{20}\) is always greater than one in the whole range of \(0< c_0 < 1\), and therefore \(M_{20}^*\) does not appear like in the example reported in Fig. 5. Taking into account (12), this situation is possible if

    $$\begin{aligned} \frac{3}{5}\gamma _1< \mu < \frac{\gamma _1 }{\gamma _2}. \end{aligned}$$

  • B\(_2\)) as in Case B\(_1\)) with \(M^{(E)}_{10}=M^{(E)}_{20}\) like in the exapmle reported in Fig. 6. Taking into account (12) and the results in [42], this situation is possible if

    $$\begin{aligned} \mu = \frac{\gamma _1 }{\gamma _2}. \end{aligned}$$

  • B\(_3\)) as in Case B\(_1\)), but \(M^{(E)}_{10}<M^{(E)}_{20}\) like in the exapmle reported in Fig. 7. Taking into account (12) and the results in [42], this situation is possible if

    $$\begin{aligned} \mu > \frac{\gamma _1 }{\gamma _2}. \end{aligned}$$
Fig. 5
figure 5

The regions classified by the possibility of the sub-shock formation in the \(M_0\) - \(c_0\) plane in Case B\(_1\); \(\gamma _1 = 7/6\), \(\gamma _2 = 7/5\), and \(\mu = 0.75\)

Full size image
Fig. 6
figure 6

Regions classified by the possibility of the sub-shock formation in the \(M_0\) - \(c_0\) plane in Case B\(_2\); \(\gamma _1 = 7/6\), \(\gamma _2 = 7/5\), and \(\mu = 5/6\)

Full size image
Fig. 7
figure 7

The regions classified by the possibility of the sub-shock formation in the \(M_0\) - \(c_0\) plane in Case B\(_3\); \(\gamma _1 = 7/6\), \(\gamma _2 = 7/5\), and \(\mu = 0.9\)

Full size image
Table 1 Summary of the possibility of the sub-shock formation for the classified regions in the plane \((c_0, M_0\))
Full size table

In Figs. 1, 2, 3, 4, 5, 6, 7, we enumerate the different regions, and the conclusions whether we can have or not sub-shock according to (13) are summarized in Table 1.

The word “Maybe” indicates that the condition is necessary, but not sufficient for the existence of a sub-shock. The singularity can be apparent due to an indeterminate form 0/0. For more details, see [42, 43].

At present, there is no rigorous mathematical proof to determine if the singular is apparent or not, and therefore to conclude whether the sub-shock appears in the “Maybe” case, we need to perform numerical calculations solving the field equations directly.

5 Numerical Simulation of the Shock Structure

In the present section, we solve the system of field equations numerically and clarify the possibility of the sub-shock formation.

For convenience, we introduce the following dimensionless variables to scale the state variables and the independent variable \(\varphi\) with the values evaluated in the unperturbed state:

$$\begin{aligned}&{\hat{\rho }} = \frac{\rho }{\rho _{0}}, \quad {\hat{v}} = \frac{v}{a_{0}}, \quad \hat{\mathcal {T}} = \frac{\mathcal {T}}{T_{0}}, \quad {\hat{\Pi }} = \frac{\Pi }{\rho _0\frac{k_B}{m_0}T_{0}}, \\&{\hat{\varphi }} = \frac{\varphi }{t_c \, a_0}, \quad {\hat{x}} = \frac{x}{t_c \, a_0}, \quad {\hat{t}} = \frac{t}{t_c}, \quad {\hat{\tau }} = \frac{\tau }{t_c}, \\&{\hat{\psi }} = \frac{t_c}{\rho _0 T_0}\psi _{11}, \quad {\hat{\theta }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\theta _{11}, \quad {\hat{\kappa }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\kappa _{11}, \quad {\hat{\phi }} = \frac{t_c}{\rho _0 \frac{k_B}{m_0} T_0^2}\phi _{11}, \quad \end{aligned}$$

where \(t_c\) is an arbitrary characteristic time for numerical computations.

The stability conditions, namely, \(\psi _{11} >0\) and that the matrix of (4) is positive definite, can be written in terms of the dimensionless phenomenological coefficients as follows: \({\hat{\psi }}> 0, \, {\hat{\theta }}> 0,\, {\hat{\theta }} \, {\hat{\phi }} - {\hat{\kappa }}^2 > 0\).

As done previously in the literature [13, 14, 29, 42, 44, 48], we perform numerical calculations on the Riemann problem consisting of two equilibrium states, \(\textbf{u}_0\) and \(\textbf{u}_{\textrm{I}}\) satisfying (8) and (9), and obtain the profiles of the physical quantities after a long time. Following an idea of Liu [27], a conjecture about the large-time behavior of the Riemann problem and the Riemann problem with structure [25, 26] for a system of balance laws was proposed by Ruggeri and Coworkers [12, 14, 29]. According to this conjecture, if the Riemann initial data correspond to a shock family \(\mathcal {S}\) of the equilibrium sub-system, for a large time, the solution of the Riemann problem of the full system converges to the corresponding shock structure.

We have developed numerical code adopting the uniformly accurate Central Scheme of order 2 (UCS2) [24] to solve the Riemann problem numerically.

We do not know the precise values of the phenomenological coefficients of a particular real mixture of gases, and it seems complicated to find experimental data for shock profiles in a mixture of polyatomic gases with large bulk viscosity. Nevertheless, the main goal of this paper is to analyze the qualitative behavior of shock and sub-shocks and compare the effect of dissipation with respect to the Eulerian mixture. Therefore, at the moment, we choose arbitrary values for our numerical experiments with the following parameters: \({\hat{\psi }} = {\hat{\theta }} = {\hat{\kappa }} = 0.2\), \({\hat{\phi }} = 0.3\), \({\hat{\tau }}_1 = 1\), and \({\hat{\tau }}_2 = 2\).

We show the shock structure for several Mach numbers in the case of \(\gamma _1 = 7/5\), \(\gamma _2 = 9/7\), \(\mu = 0.4\), and \(c_0 = 0.1\) in Fig. 8. These parameters correspond to circles Nos. I – III in Fig. 2. It is confirmed that the shock-structure solution predicted by the RET\(_6\) theory is continuous for \(M_0=1.2,\) while a sub-shock for the shock structure of the constituent 2 emerges for \(M_0=1.3\). If we further increase the Mach number, we observe another sub-shock for the shock structure of the constituent 1 as shown in Fig. 8 for \(M_0=1.9\).

For comparison, we also depicted the theoretical predictions by the Eulerian theory with the same parameters. As expected, the shock structure predicted by the RET\(_6\) theory is broader than the ones predicted by the Eulerian theory. Moreover, although the necessary condition for the sub-shock formation for constituent 2 is satisfied in both theories for \(M_0=1.2\), the sub-shock is observed only in the Eulerian theory. These results indicate the dissipative effect of the dynamic pressure on the shock structure and the sub-shock formation.

Fig. 8
figure 8

Shock structure of the dimensionless global mass density, mixture velocity, and average temperature (solid curves) with \(\gamma _1=7/5\), \(\gamma _2=9/7\), \(\mu = 0.4\), \(c_0 = 0.1\) for several Mach numbers; \(M_0 = 1.2\) indicated by circle No. I in Region 10 in Fig. 2 (top row), \(M_0 = 1.3\) indicated by circle No. II in Region 10 (middle row), and \(M_0 = 1.9\) indicated by circle No. III in Region 18 (bottom row). The corresponding predictions by the theory of a mixture of Eulerian gases are also shown (dashed curves)

Full size image
Fig. 9
figure 9

Shock structure predicted by the RET\(_6\) theory (solid curves) and the Eulerian theory (dashed curves) with \(\gamma _1=7/5\), \(\gamma _2=9/7\), \(\mu = 0.4\), \(c_0 = 0.15\) for \(M_0 = 1.06\) indicated by circle No. IV in Region 9 (top row) and for \(M_0=1.2\) indicated by circle No. V in Region 10 (bottom row)

Full size image

Next, let us analyze the shock structure with \(\gamma _1 = 7/5\), \(\gamma _2 = 9/7\), \(\mu = 0.4\), and \(c_0 = 0.15\) for \(M_0 = 1.06\) and for \(M_0 = 1.2\) shown in Fig. 9. The parameters correspond to circles Nos. IV and V in Fig. 2. The result for \(M_0 = 1.06\) is interesting because the necessary condition \(M_0>M_{20}\) is satisfied only in the RET\(_6\) theory, in spite of the fact that the RET\(_6\) theory incorporates the dissipative effect. Figure 9 shows that both theories predict continuous solutions without sub-shock formation for \(M_0=1.06\). If we increase the Mach number, the sub-shock formation is observed in a mixture of the Eulerian gases immediately after \(M_{20}^{*(E)},\) while the RET\(_6\) theory predicts a continuous shock-structure solution for \(M_0 = 1.2\).

Fig. 10
figure 10

Shock structure predicted by the RET\(_6\) theory (solid curves) and the Eulerian theory (dashed curves) with \(\gamma _1=7/5\), \(\gamma _2=9/7\), \(\mu = 0.4\), \(c_0 = 0.3\) for \(M_0 = 1.2\) indicated by circle No. VI in Region 9 in Fig. 2 (top row), and for \(M_0=1.3\) indicated by circle No. VII in Region 10 (bottom row)

Full size image

A similar situation is observed in the shock structure with \(\gamma _1 = 7/5\), \(\gamma _2 = 9/7\), \(\mu = 0.4\), and \(c_0 = 0.3\) for \(M_0 = 1.2\) and for \(M_0 = 1.3\) shown in Fig. 10. In these cases, parameters are indicated by circles No. VI and VII in Fig. 2. Although the necessary condition \(M_0>M_{20}^*\) is satisfied in the RET\(_6\) theory, the theoretical predictions by the RET\(_6\) theory are continuous for both \(M_0=1.2\) and \(M_0=1.3\). The sub-shock is observed only in the Eulerian theory for \(M_0=1.3\).

Fig. 11
figure 11

Shock structure predicted by the RET\(_6\) theory (solid curves) and the Eulerian theory (dashed curves) with \(\gamma _1=7/5\), \(\gamma _2=9/7\), \(\mu = 0.4\), \(c_0 = 0.45\) for \(M_0 = 1.21\) indicated by circle No. VIII in Region 9 in Fig. 2 (top row), and for \(M_0 = 1.3\) indicated by circle No. IX in Region 12 (bottom row)

Full size image

Another example is the shock structure with \(\gamma _1 = 7/5\), \(\gamma _2 = 9/7\), \(\mu = 0.4\), and \(c_0 = 0.45\) for \(M_0 = 1.21\) and for \(M_0 = 1.3\) shown in Fig. 11. These parameters correspond to circles No. VIII and IX in Fig. 2. Again, the RET\(_6\) theory predicts continuous solutions for both \(M_0=1.2\) and \(M_0=1.3,\) while the Eulerian theory predicts a sub-shock \(M_0=1.3\) in agreement with the theorem.

Fig. 12
figure 12

Shock structure predicted by the RET\(_6\) theory (solid curves) and the Eulerian theory (dashed curves) with \(\gamma _1=7/5\), \(\gamma _2=9/7\), \(\mu = 0.4\), \(c_0 = 0.75\), and \(M_0 = 1.5\) indicated by circle No. X in Region 17 in Fig. 2 (top row), and for \(M_0 = 1.7\) indicated by circle No. XI in Region 18 (bottom row)

Full size image

The last example is the shock structure with \(\gamma _1 = 7/5\), \(\gamma _2 = 9/7\), \(\mu = 0.4\), and \(c_0 = 0.7\) for \(M_0 = 1.5\) and for \(M_0 = 1.7\) shown in Fig. 12. These parameters are indicated by circles No. X and XI in Fig. 2. According to the theorem, a sub-shock for the shock structure of the constituent 1 arises in both theories. No sub-shock for the shock structure of the constituent 2 is observed in the prediction by both theories for \(M_0=1.5\), and multiple sub-shocks are predicted only in the Eulerian theory for \(M_0=1.7\).

6 Conclusions

This paper analyzes the shock structure in a binary mixture of rarefied polyatomic gases based on RET. We have used the system of the field equations derived in the context of the multi-temperature model in which the dynamic pressure’s contribution is relevant. We have classified the possible parameters by considering the necessary conditions to observe the sub-shock formation and have tested the sub-shock formation numerically. As we expect, the shock profile is more regularized with respect to the mixture of Eulerian gas, and in the case that exists sub-shocks, the amplitude of the sub-shock is reduced compared to those of non-dissipative gases. We have also observed from the numerical simulation that for very small Mach numbers in regions where existence is only necessary, the singularity is only apparent, while increasing the Mach number always has sub-shocks in this kind of region.

The present results are in agreement with the fact that the present theory satisfies the so-called K-condition [41] that, together with the convexity of entropy, take the system in the assumptions of general theorems for which if the initial data are sufficiently small, there exist smooth global solutions [6, 34, 39, 43, 51].

In the present study, we aim to analyze the qualitative behavior of the shock structure and classify all possible cases of the ratio of masses and the ratio of specific heat that have physical meaning. We adopted the parameter values from the viewpoint of including all cases rather than specific mixtures. There are several binary mixtures that belong to Case A) or Case B) with large bulk viscosity that we want to study in more detail in an upcoming paper. For example belong to Case A): H\(_2\) / CO\(_2\) (\(\gamma _1= 1.41, \gamma _2= 1.29, \mu = 0.046\)), CH\(_4\) / CO\(_2\) (\(\gamma _1= 1.31, \gamma _2= 1.29, \mu = 0.365\) ), C\(_2\)H\(_4\) / CO\(_2\) (\(\gamma _1= 1.24, \gamma _2= 1.29, \mu = 0.365\)). An example of Case B) is F\(_2\) / CO\(_2\) (\(\gamma _1= 1.36, \gamma _2= 1.29, \mu = 0.863\)) (see [21]), but it remains open to compare with experimental data because, at the moment, the authors were not able to find experimental data on the shock-wave profiles for this kind of mixture in the literature.

Instead, there are several single gases with this characteristic in which, as we say in precedence, the RET\(_6\) theory is very successful.