An Effective Model for the Simulation of Transpiration Cooling

Abstract

Transpiration cooling is numerically investigated, where a cooling gas is injected through a carbon composite material into a hot gas channel. To account for microscale effects at the injection interface, an effective problem is derived. Here, effects induced by microscale structures on macroscale variables, e.g., cooling efficiency, are taken into account without resolving the microscale structures. For this purpose, effective boundary conditions at the interface between hot gas and porous medium flow are derived using an upscaling strategy. Numerical simulations in 2D with effective boundary conditions are compared to uniform and non-uniform injection. The computations confirm that the effective model provides a more efficient and accurate approximation of the cooling efficiency than the uniform injection.

1 Introduction

To simulate transpiration cooling, the process of a cooling gas entering a hot gas flow through a porous material needs to be modeled. The problem at hand is a channel with a hot gas flow. Mounted into the wall of the channel is a porous material. A reservoir containing the cooling gas is attached to the porous material.

Compared with other active cooling techniques such as film or effusion cooling, transpiration cooling might offer advantages regarding the formation of stable films and the cooling efficiency [20,21,22]. With the availability of permeable ceramics, in particular composite carbon/carbon materials, investigated for instance in [28], the development of transpiration-cooled combustion chambers is a recent research topic, see for instance [12, 25]. Numerical simulations of hot gas flows exposed to transpiration cooling were conducted in [14] and more recently in [23]. The objective of these simulations was the investigation of the effect of the cooling gas injection on the hot gas flow, especially on the boundary layer.

The injection of cooling gas through a porous medium into a hot gas channel flow was numerically investigated in [6, 7] using a two-domain approach. Here, the injection was modeled uniformly, i.e., neglecting all roughness scales. In [17], to simulate non-uniform injection, the two-domain approach was extended by accounting for measured interface outflow distributions. The results, validated by experiments performed in a wind tunnel at ITLR Stuttgart, confirmed the assumption that microscale effects, e.g., local mass fluxes, have a significant influence on the macroscale behavior of the cooling effect such as the cooling film shape or cooling efficiency. Computations at the interface on the pore scale using reconstruction methods were presented in [31].

The channel flow and the flow within the pore-scale tubes in the porous material can be described by the Navier-Stokes equations. The resolution of all scales of the hot gas flow in the channel and the porous medium flow is not feasible due to the tremendous computational effort. In [30], the pore scale for a uniform (coarse) pore distribution was discretized to analyze the effect on the velocity. Applying well-established averaging models like Darcy-based models for the porous medium flow helps understand general effects of transpiration cooling on the macroscale at an affordable cost.

Our goal is the development of a new method that combines the advantages of an affordable averaged macroscale computation with information from the microscale at the injection interface. Here, the microscale effects that have an impact on macroscale values are of special interest. In terms of transpiration cooling, we would like to analyze how the rough porous injection interface affects the cooling film or the cooling efficiency in the channel flow. While passing through the porous material, the cooling gas is transported through microscopic channels that form the void space in the porous structure. At the interface, the cooling gas is therefore entering the channel flow through microscopic pores. The distribution of the pores is assumed to have an influence on the development of a cooling film.

Typically, the effects of the pore-scale (microscale) injection at the interface on the hot gas flow are neglected in averaged models. For a better understanding of the microscale influence at the coupling interface on macroscale quantities, we develop a macroscale model that takes into account microscale effects at the interface without resolving the entire microscale. This is done by deriving effective boundary conditions using an upscaling strategy motivated by the strategy presented in [9].

Derivations of effective boundary conditions for parallel porous medium flow can be found in [1]. A rigorous analytical derivation is presented in [13], again for parallel porous flow. In [4], this approach was used to determine boundary conditions for flows that enter the porous material at the interface. In our case, the cooling gas is injected into the hot gas flow and therefore exits the porous material at the interface. In [18], effective interfacial velocity boundary conditions based on the Stokes equations were derived. Since in our setting the hot gas flow is no creeping flow, our derivation is based on the Navier-Stokes equations.

For the derivation of an effective model for transpiration cooling, we apply an upscaling strategy proceeding in three steps. First, we solve a coupled macroscale problem by means of a two-domain approach using uniform injection. From this solution, we then extract data near the injection interface that enter local cell problems to be derived from a two-scale expansion of a multiscale problem. Finally, we solve an effective problem for the hot gas domain, where at the injection interface we impose effective boundary conditions incorporating effective coefficients determined by averages of the local cell problems.

For this purpose, we first introduce in Sect. 2 a multiscale model. By means of an upscaling strategy, we develop in Sect. 3 an effective model. The numerical setup as well as the numerical results of all components leading to an effective computation is presented in Sect. 4 and compared to solutions of a multiscale problem. A summary of the main results in Sect. 5 concludes the paper.

2 Multiscale Model

A typical transpiration cooling configuration consists of a combustion chamber and a porous medium mounted into the wall of the channel. By means of a pressure gradient between a reservoir providing the coolant at the backside of the porous media and the flow in the hot gas channel, the coolant flows through the porous structure and is injected into the hot gas. There it forms a thin cooling film reducing the wall heat flux and, consequently, the thermal load of the structure.

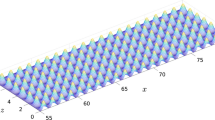
Since the microscale structure of the porous material is not known and too complex to be resolved, we consider an idealized multiscale problem, where the domain $\varOmega ^\varepsilon = \varOmega _\text{HG} \cup \varOmega ^\varepsilon _\text{PM}$ consists of the hot gas domain $\varOmega _\text{HG}$ and the union of all injection channels $\varOmega ^\varepsilon _\text{PM}$, see Fig. 1a. The hot gas enters $\varOmega _\text{HG}$ at the inflow boundary $\varGamma _\text{I}$. The coolant is injected into the domain $\varOmega ^\varepsilon _\text{PM}$ through inlets of the channels $\varGamma _{\text{I},\varepsilon }$. It is assumed to enter the hot gas flow through the outlets $\partial \varOmega _\text{HG} \cap \partial \varOmega ^\varepsilon _\text{PM}$ of the isolated channels, where it interacts with the hot gas flow. The outflow boundary of the domain $\varOmega ^\varepsilon$ is denoted by $\varGamma _\text{O}$. All other boundaries are considered to be solid walls. Here, we distinguish between the solid wall of the hot gas channel $\varGamma _{\text{W},\text{HG}} = \varGamma _{\text{W},\text{HG},\text{iso}} \cup \varGamma _{\text{W},\text{HG},\text{ad}}$ and the solid walls surrounding the idealized injection channels $\varGamma _{\text{W},\varepsilon }$. Due to the formation of a cooling film, the hot gas channel walls in between the injection channels and downstream of the injection are modeled as adiabatic walls, whereas the other hot gas channel walls are assumed to be isothermal.

Fig. 1

Multiscale problem (a) with zoom into microscale interface (b) and single pore channel (c)

The domain $\varOmega ^\varepsilon _\text{PM}$ is composed of periodic pore channel elements. Each element consists of an injection channel of height L and the surrounding solid structure, see Fig. 1c. It can be considered an idealized material crack. Here, $d_\text{S}$ is the diameter of the solid wall separating two channels, see Fig. 1b. Thus, one element of size $\varepsilon$ consists of solid structure and void space representing the injection channel. To ensure that the porosity, i.e., the ratio of the injection channel volume related to the whole volume of the element, corresponds to a given porosity $\varphi \in (0, 1)$ of some real porous media, we choose

$$\begin{aligned} \varepsilon = \frac{d_\text{S}}{1-\varphi }. \end{aligned}$$

(1)

This parameter may be very small corresponding to a large number of channels. Note that the porosity $\varphi$ and the diameter $d_\text{s}$ depend on the application at hand. The porosity is a macroscale parameter. The height L of one injection channel is the height of the entire idealized porous medium and is therefore also a macroscale parameter independent of $\varepsilon$. From a given surface area A of the porous media and a given sufficiently large number $N_{\text{pc}}$ of pore channels, we can determine $\varepsilon$ by $\varepsilon =A/N_{\text{pc}}$ and the parameter $d_\text{s}$ using (1) by

$$\begin{aligned} d_\text{s} =(1-\varphi ) \frac{A}{N_{\text{pc}}} \overset{!}{<}\varepsilon . \end{aligned}$$

(2)

The flow in $\varOmega ^\varepsilon$ is governed by the stationary compressible Navier-Stokes equations

with the density $\rho ^{\varepsilon }$, the velocity vector ${\varvec{v}}^\varepsilon$, the total energy $E^{\varepsilon }$, and the static pressure $p^{\varepsilon }$. The stress tensor ${\varvec{\tau }}^\varepsilon$ for an isotropic Newtonian fluid and the heat flux ${\varvec{q}}^\varepsilon$ modeled by the Fourier’s law are defined by

$$\begin{aligned} {\varvec{\tau }}^{\varepsilon }= -\frac{2}{3} \mu \left( \nabla \cdot {\varvec{v}}^{\varepsilon }\right) I +\mu \left( \nabla {\varvec{v}}^{\varepsilon }+\left( \nabla {\varvec{v}}^{\varepsilon }\right) ^\text{T}\right) , \qquad {\varvec{q}}^{\varepsilon }= -\kappa \nabla T^{\varepsilon } \end{aligned}$$

(4)

with the dynamic viscosity $\mu$ determined by the Sutherland’s law, the thermal conductivity $\kappa$, and the temperature $T^\varepsilon$. In particular, we assume a thermally and calorically perfect gas, i.e., the pressure $p^{\varepsilon }$ and the internal energy $e^{\varepsilon }= E^{\varepsilon }- ({\varvec{v}}^{\varepsilon })^2/2$ are closed by

$$\begin{aligned} p^{\varepsilon } = \rho ^{\varepsilon } R T^{\varepsilon }, \qquad e^{\varepsilon }= c_\text{v} T^{\varepsilon } \end{aligned}$$

(5)

with the specific gas constant R and the heat capacity at constant volume $c_\text{v}$.

The boundary conditions that are not affected by a microscale parameter are represented by

with the farfield conditions $\rho _\infty$, $p_\infty$, and $v_\infty$ for the density, the pressure, and the velocity, respectively. Here, ${\varvec{e}}_1$ is the unit vector in the streamwise direction of the hot gas. For boundaries that depend on the microscale parameter $\varepsilon$, we assume the solid walls of the porous material to be adiabatic and the no-slip conditions to hold, i.e.,

$$\begin{aligned} {\varvec{v}}^\varepsilon = {\varvec{0}}, \quad \nabla T^\varepsilon \cdot {\varvec{n}}= \frac{1}{R} \nabla \left( \frac{p^\varepsilon }{\rho ^\varepsilon }\right) \cdot {\varvec{n}}= 0 \quad \text {on } \varGamma _{\text{W},\varepsilon } \end{aligned}$$

(7)

assuming a perfect gas. At the coolant inlet boundary $\varGamma _{\text{I},\varepsilon }$ for a given temperature $T_\text{b}$, a coolant mass flow rate ${\dot{m}}_\text{c}$, and a surface area of injection $A_\text{c}$, the conservative variables are determined by

$$\begin{aligned} \rho ^\varepsilon = \frac{p^\varepsilon }{R T_\text{b}}, \quad {\varvec{v}}^\varepsilon = \frac{{\dot{m}}_\text{c}}{\varphi A_\text{c} \rho ^\varepsilon } {\varvec{e}}_2, \quad \nabla p^\varepsilon \cdot {\varvec{n}}= 0 \quad \text {on } \varGamma _{\text{I},\varepsilon }, \end{aligned}$$

(8)

where ${\varvec{e}}_2$ denotes the unit vector in direction of the cooling gas injection. For simplicity, we assume here that the coolant and the hot gas are chosen as identical fluids modeled as a perfect gas. Otherwise, we have to use a mixture of gases.

Finally, the flow equations (3) and the boundary conditions (6) as well as (7) and (8) are condensed as

for the conservative quantities ${\varvec{u}}^\varepsilon = (\rho ^\varepsilon , \rho ^\varepsilon {\varvec{v}}^\varepsilon , \rho ^\varepsilon E^\varepsilon )^\text{T}$.

We emphasize that typically the hot gas flow in the combustion chamber is turbulent due to a high Reynolds number, whereas the flow in the channels will be laminar due to a small pore Reynolds number. Thus, a direct numerical simulation (DNS) needs to resolve two microscale effects, namely, the turbulent fluctuations in the hot gas and the thin geometry of a large number of channels. This renders a DNS practically infeasible. For the sake of simplicity, we assume the hot gas flow to be laminar in the following although turbulent flows are quite different from laminar flows regarding heat transfer and mixing rates. Furthermore, in real configurations the coolant and the hot gas fluid will be different species. In particular, at higher temperatures a multispecies fluid requires a more realistic equation of state than the one for a perfect gas, cf. [5, 16]. We emphasize that the focus of this work is on the general concept rather than on a detailed physical modeling. Therefore, we deliberately confine ourselves to the above simplified model.

3 Effective Model

Since a simulation of the multiscale problem in Sect. 2 is in general not feasible, we now develop an effective strategy. This allows to investigate the influence of the injection through the small-scale pores representing the channel outlets on the efficiency of transpiration cooling without the need of resolving these structures locally.

Our envisaged strategy is based on an upscaling technique. Starting point for the derivation is the multiscale model, see Sect. 2, where coolant is injected through a large number of isolated injection channels. This multiscale model is set up such that for an increasing number of pores it is expected to coincide in the limit with a model where the coolant is injected uniformly along a smooth surface. Thus, this model in the limit can be considered a macroscale model because no small-scale features need to be resolved. Having established a multiscale and a macroscale model, we derive an effective model that can be viewed as an upgraded version of the macroscale model because it incorporates information from the microscale. The key ingredients of this effective model are effective boundary conditions that replace the uniform injection conditions of the macroscale model. Thus, the effective model is solved only in the hot gas channel. In this sense, the effective model can be considered an upscaling of the macroscale model. In the following sections, we present the macroscale model, see Sect. 3.1, and derive effective boundary conditions, see Sect. 3.2, for the effective model, see Sect. 3.3.

3.1 Macroscale Model

The idealized multiscale model presented in Sect. 2 requires a high resolution to resolve all microscale effects. For instance, for the three dimensional (3D) computations performed in [17] the grid would need to resolve over 40 000 microscopic injection channels for a porous sample of only $48$ mm $\times\,48$ mm. To reduce the computational load, we now suggest a simplified model that does not resolve the microscale structures but approximates the averaged behavior of the flow. For the derivation of the macroscale model, we make the following three heuristic hypotheses.

First, the local injection through tiny pore channels is assumed to have only little effect on the flow in the hot gas domain $\varOmega _\text{HG}$.

Second, for $\varOmega ^\varepsilon _\text{PM}$ with $\varepsilon \rightarrow 0$ the pore channel elements in the multiscale model become smaller and smaller. In turn, their number increases to infinity. Thus, the flow in such a medium is assumed to be well-approximated by an averaged model of Darcy type. This averaged model is to be solved in the porous medium domain $\varOmega _\text{PM}$. Note that $\varOmega _\text{PM}$ is not the limit of $\varOmega ^\varepsilon _\text{PM}$ for $\varepsilon \rightarrow 0$ but the union of the injection channels and the surrounding solid.

Third, through the channel outlets located at $\partial \varOmega _\text{HG}\cap \partial \varOmega ^\varepsilon _\text{PM}$ the coolant enters the hot gas flow. In the limit $\varepsilon \rightarrow 0$, the number of channel outlets tends to infinity and, thus, the union of all channel outlets tends to a smooth injection interface $\varGamma _\text{Int}$ neglecting the microscale structures.

Summarizing, the aforementioned heuristic considerations motivate to approximate the multiscale model by a two-domain model. Since this does not depend on a microscale parameter, it can be considered a zeroth-order approximation capturing all macroscale effects but failing to model the microscale effects, e.g., cracks in the porous material or pores at the interface. Thus, the macroscale problem is given by the problems in the hot gas domain $\varOmega _\text{HG}$ by

and the porous medium $\varOmega _\text{PM}$ by

coupled at the interface $\varGamma _\text{Int}$ as visualized in Fig. 2. Note that the coolant reservoir is not simulated. The reservoir conditions are set as boundary conditions of the porous medium on $\varGamma _\text{R}$.

Fig. 2

General setup of two-domain approach for macroscale model

In the following, we summarize the governing equations and boundary conditions for the two domains as well as coupling conditions following previous work in [6, 7, 11, 15,16,17, 26].

3.1.1 Hot Gas Domain $\varOmega _\text{HG}$

Since the hot gas flow is assumed to be laminar, it also can be modeled by the compressible Navier-Stokes equations (3) for the conservative flow quantities

$$\begin{aligned} {\varvec{u}}_\text{HG}=\left( \rho , \rho {\varvec{v}}, \rho E \right) ^{\text{T}}. \end{aligned}$$

(12)

In contrast to the multiscale problem in Sect. 2 we discard the superindex $\varepsilon$. The Navier-Stokes equations are complemented by suitable boundary conditions for the configuration in Fig. 2. Here, we discuss the conditions for a subsonic laminar hot gas flow. At the inflow boundary $\varGamma _{\text{I}}$, we prescribe inflow data

$$\begin{aligned} \rho =\rho _\infty ,\ {\varvec{v}}= v_\infty {\varvec{e}}_1,\ p = p_\infty \qquad \text{ on } \varGamma _{\text{I}}. \end{aligned}$$

The freestream quantities are determined from a freestream Mach number $Ma_\infty$ and a freestream temperature $T_\infty$. At the outflow boundary $\varGamma _{\text{O}}$, only the pressure is prescribed. All other variables are extrapolated from the interior, i.e., Neumann boundary conditions are used. Thus, we obtain

$$\begin{aligned} \nabla \rho \cdot {\varvec{n}}= 0,\quad \nabla v_i\cdot {\varvec{n}}= 0,\ i=1,\cdots ,d,\quad p = p_\infty \qquad \text{ on } \varGamma _{\text{O}}. \end{aligned}$$

At the solid walls, we apply no-slip conditions. The temperature of the wall is set to be isothermal ($\varGamma _{\text{W,HG,iso}}$), i.e., a constant wall temperature is given, or adiabatic ($\varGamma _{\text{W,HG,ad}}$), i.e., the wall-normal gradient of the temperature vanishes. Thus, we obtain the following boundary conditions at the solid wall:

$$\begin{aligned} {\varvec{v}}= {\varvec{0}},\quad \nabla p \cdot {\varvec{n}}= 0,\quad {\left\{ \begin{array}{ll} T = T_\text{wall} ,&{} \text{ on } \varGamma _\text{W,HG,iso} \\ \nabla T \cdot {\varvec{n}}= 0 ,&{} \text{ on } \varGamma _\text{W,HG,ad} \end{array}\right. } \qquad \text{ on } \varGamma _\text{W,HG}, \end{aligned}$$

(13)

where $T_\text{wall}$ is given data.

3.1.2 Porous Medium Domain $\varOmega _\text{PM}$

The flow through the porous material in $\varOmega _\text{PM}$ is described by

This system is solved for the variables

$$\begin{aligned} {\varvec{u}}_\text{PM} = \left( \rho _\text{f}, {\varvec{v}}, T_\text{s}, T_\text{f} \right) ^\text{T} \end{aligned}$$

(15)

which denote the fluid density, the Darcy velocity, the solid temperature, and the fluid temperature, respectively. The Darcy velocity ${\varvec{v}}$, also known as the seepage or the filtration velocity, is the average velocity over a volume that incorporates both solid and fluid material.

The continuity equation (14a) implies mass conservation and describes the behavior of the fluid density in the porous media. We consider the Darcy-Forchheimer equation (14b) to incorporate the conservation of momentum and to model the pressure-gradient-driven flow through the porous material. The temperatures of the solid and the fluid are assumed to be in non-equilibrium. Therefore, we need two heat equations (14c) and (14d). Here, $\mu$ denotes the dynamic viscosity of the fluid, ${\varvec{K}}_\text{D}$ the permeability tensor of the medium, ${\varvec{K}}_\text{F}$ the Forchheimer tensor, ${\varvec{\kappa }}_\text{s}$ the thermal conductivity tensor of the solid, $\kappa _\text{f}$ the thermal conductivity of the fluid, $c_{p,\text{f}}$ the heat capacity of the fluid, and $h_\text{v}$ the volumetric heat transfer coefficient. For our computations, ${\varvec{K}}_\text{D}$, ${\varvec{K}}_\text{F}$, and ${\varvec{\kappa }}_\text{s}$ will be diagonal matrices. The dynamic viscosity $\mu$ is computed using the Sutherland’s law. Again, to close the system we use $p= \rho _\text{f} R T_\text{f}$ with R being the specific gas constant.

Assuming that the conditions in the reservoir are constant and homogeneous, we can derive the pressure and the temperatures on the reservoir boundary by measuring the temperature $T_\text{b}$ on the backside of the porous material and the reservoir pressure $p_\text{R}$. Then, the boundary conditions on the reservoir boundary read

$$\begin{aligned} \rho _\text{f} = \frac{p_\text{R}}{R T_\text{b}} ,\quad T_\text{s}=T_\text{b}, \quad T_\text{f}=T_\text{b}, \qquad \text {on } \varGamma _\text{R} . \end{aligned}$$

We assume the solid side walls at $\varGamma _\text{W,PM}$ to be adiabatic and the slip conditions to hold, i.e.,

$$\begin{aligned} {\varvec{v}}\cdot {\varvec{n}}=0,\quad \nabla T_\text{s} \cdot {\varvec{n}}=0, \quad \nabla T_\text{f} \cdot {\varvec{n}}=0 \qquad \text {on } \varGamma _\text{W,PM}. \end{aligned}$$

(16)

Note that viscous effects are neglected in (14a) and (14b). Thus, the attached flow is parallel to $\varGamma _\text{W,PM}$, i.e., the normal velocity component must vanish, whereas non-trivial tangential velocity components have to be permitted. Therefore, (14a) and (14b) require characteristic boundary conditions on $\varGamma _\text{W,PM}$. The nonlinear term in (14b) allows the velocity ${\varvec{v}}$ to match to a physically correct tangential field at $\varGamma _\text{W,PM}$. This also implies a characteristic boundary $\varGamma _\text{W,PM}$ for (14a), i.e., in our case no boundary conditions for the density $\rho _\text{f}$ have to be imposed on $\varGamma _\text{W,PM}$.

3.1.3 Coupling Conditions on $\varGamma _\text{Int}$

So far, we have not yet addressed the boundary conditions (10c) and (11c) on the coupling interface $\varGamma _\text{Int}$ for the hot gas flow and the porous medium flow, respectively. These require data from the respective adjacent system:

PM $\leftarrow$ HG In the present work we only consider injection normal to the porous wall. Thus, for $\varOmega _\text{PM}$ the coupling conditions for ${\varvec{u}}_\text{PM} = (\rho _\text{f}, {\varvec{v}}, T_\text{s}, T_\text{f} )^{\text{T}}$ at the interface $\varGamma _\text{Int}$ consist of (i)

$$\begin{aligned} v_n = \frac{{\dot{m}}_\text{c}}{\rho _\text{mix} A_\text{c}} \text{ with } \rho _\text{mix}:= \frac{p_\text{HG}}{R T_\text{f}}, \quad v_{t_i} = 0,\ i=1,\cdots , d-1, \end{aligned}$$

(17)

where $v_n = {\varvec{v}}\cdot {\varvec{n}}_\text{Int} \geqslant 0$ and $v_{t_i} = {\varvec{v}}\cdot {\varvec{t}}_i$ denote the absolute values of the injection velocity vector ${\varvec{v}}$ normal and tangential to the porous wall, respectively, with outer unit normal vector ${\varvec{n}}_\text{Int}$ w.r.t. $\varOmega _\text{PM}$ and tangential vectors ${\varvec{t}}_i$ satisfying ${\varvec{t}}_i \cdot {\varvec{n}}_\text{Int} = 0$ for $i = 1, \cdots , d - 1$, ${\dot{m}}_\text{c}$ the prescribed coolant mass flow rate and $A_\text{c} = |\varGamma _\text{Int} |$ the surface area of the porous medium, and (ii)

$$\begin{aligned} \left( 1-\varphi \right) \left( {{\varvec{\kappa }}_\text{s}} \nabla T_\text{s} \right) \cdot {\varvec{n}}_\text{Int} = c_{p,\text{f}} \, \rho _\text{f} \, v_n \, (T_\text{f} - T_\text{s}) + \kappa _\text{HG} \nabla T_\text{HG} \cdot {\varvec{n}}_\text{Int}. \end{aligned}$$

(18)

Note that the pressure $p_\text{HG}$ and the heat flux $\kappa _\text{HG} \nabla T_\text{HG}$ of the hot gas enter as data.

HG $\leftarrow$ PM At the interface $\varGamma _\text{Int}$, coupling conditions for ${\varvec{u}}_\text{HG} = (\rho , \rho {\varvec{v}}, \rho E)^{\text{T}}$ for the hot gas domain $\varOmega _\text{HG}$ consist of

Again, we emphasize that the temperature $T_\text{s,PM}$ and the velocity ${\varvec{v}}_\text{PM}$ of the fluid are provided by the porous medium flow. All other quantities are determined by the hot gas flow.

A detailed discussion of the coupling conditions can be found in [26].

3.2 Derivation of Effective Boundary Conditions

Fig. 3

Cell problem on both scales

In the macroscale model, see Sect. 3.1, the cooling gas is uniformly injected into the hot gas channel flow. Here, in particular, the roughness of the porous material and the geometry of the channel distribution do not enter. To derive boundary conditions that capture the effects of the roughness on the hot gas channel flow as modeled in the multiscale problem in Sect. 2, we apply an upscaling approach. To do so, we need to establish a relation between the macroscale and the microscale.

Let ${\bar{{\varvec{x}}}}_\text{C} \in \partial \varOmega _\text{HG}\cap \partial \varOmega ^\varepsilon _\text{PM}$ characterize the center of the inlet of one pore channel in $\varOmega ^{\varepsilon }$ as introduced in the multiscale problem, see Fig. 3a. Then, the injection element domain $R({{\bar{{\varvec{x}}}}}_\text{C})$ consists of the free flow on top of this channel and is of height $\varepsilon$, see Fig. 3a. Note that it will not be convenient to take into account also a small portion of the injection channel itself because the solution ${\varvec{u}}^0$ of the macroscale problem may exhibit jumps at the interface $\varGamma _\text{Int}$ coupling hot gas and porous medium flow. Pressure continuity across the interface is not guaranteed in case of thermal non-equilibrium, where the interface is an idealization of a thin layer with significant pressure changes [16, 24]. Next, we introduce the transformation $\mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}{:}\;R({{\bar{{\varvec{x}}}}}_\text{C}) \rightarrow Y$ that relates each injection element $R({{\bar{{\varvec{x}}}}}_\text{C})$ on the macroscale

$$\begin{aligned} \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}}):=\frac{{\varvec{x}}-{\bar{{\varvec{x}}}}_\text{C}}{\varepsilon },\quad \forall \,{\varvec{x}}\in R({\bar{{\varvec{x}}}}_\text{C}) \end{aligned}$$

(20)

to the cell domain $Y:= \{ {\varvec{y}}= \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}}), {\varvec{x}}\in R({{\bar{{\varvec{x}}}}}_\text{C}) \}$ on the microscale as shown in Fig. 3b.

3.2.1 Upscaling

To account for microscale effects at the interface $\varGamma _\text{Int}$, we use an upscaling strategy. For this purpose, we approximate the multiscale solution ${\varvec{u}}^{\varepsilon }$ with an asymptotic expansion in terms of powers of $\varepsilon$:

$$\begin{aligned} {\varvec{u}}^{\varepsilon }({\varvec{x}}) = {\varvec{u}}^0({\varvec{x}}) + \varepsilon {\varvec{u}}^1({\varvec{x}}, \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}})) + {\mathcal {O}}(\varepsilon ^2),\hspace{20pt} \forall {\varvec{x}}\in R({\bar{{\varvec{x}}}}_\text{C}). \end{aligned}$$

(21)

Since the solution ${\varvec{u}}^0$ of the macroscale problem does not contain effects corresponding to the pore channels, these effects have to be accounted for by the term $\varepsilon {\varvec{u}}^1$. Note that the solution ${\varvec{u}}^0$ is determined only from $\varOmega _\text{HG}$ with $y_2\geqslant 0$, see Fig. 2. Following [9], we assume that the upscaling function ${\varvec{u}}^1$ depends on the macroscale variable ${\textbf{x}}$ and the microscale variable ${\varvec{y}}=\mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}})$ by

$$\begin{aligned} {\varvec{u}}^1({\varvec{x}}, \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}})):= {\varvec{\zeta }}_{{{\bar{{\varvec{x}}}}}_\text{C}} \left( \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}({\varvec{x}})\right) , \hspace{10pt} \forall {\varvec{x}}\in R({\bar{{\varvec{x}}}}_\text{C}). \end{aligned}$$

(22)

Here, the so-called cell functions ${\varvec{\zeta }}_{{{\bar{{\varvec{x}}}}}_\text{C}}$ are assumed to be sufficiently smooth functions in the cell domain Y. Note that the dependence of ${\varvec{u}}^1$ on ${\varvec{x}}$ is assumed to be only through the mapping $\mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}{:} \;{\varvec{x}}\in R({{\bar{{\varvec{x}}}}}_\text{C})\rightarrow Y$ according to (20).

3.2.2 Cell Problem

To determine the upscaling function ${\varvec{u}}^{1}$, we derive a problem on the cell domain Y. For this purpose, we consider an arbitrary but fixed injection element $R({\bar{{\varvec{x}}}}_\text{C})$. Thus, on $R({{\bar{{\varvec{x}}}}}_\text{C})$ the fluid flow can be described using the compressible Navier-Stokes equations

where $\gamma$ is the isentropic exponent and the stress tensor ${\varvec{\tau }}$ and the heat flux ${\varvec{q}}$ are determined by (4). These equations can be derived from (3) employing the perfect gas law (5). Moreover, since the flow at hand is assumed to be subsonic, we may switch to primitive variables, i.e., ${\varvec{u}}= \left( \rho , {\varvec{v}}, p\right) ^\text{T}$, which is more convenient for analytical purposes.

Plugging the asymptotic expansion (21) and the upscaling function (22) into (23) and neglecting higher order terms, for details see [9], we obtain the following nonlinear system of equations

on Y, where $\nabla _y = \varepsilon \nabla$ and $\phi$, ${\varvec{\chi }}$, $\pi$ are the upscaling functions corresponding to the density $\rho$, the velocity ${\varvec{v}}$, and the pressure p, respectively, i.e.,

$$\begin{aligned} {\varvec{u}}^1=(\phi ,{\varvec{\chi }},\pi )^\text{T}. \end{aligned}$$

(25)

For abbreviation, we introduce the stress tensor on Y relative to some vector ${\varvec{w}}$

$$\begin{aligned} {\varvec{\tau }}_y ({\varvec{w}}) = -\frac{2}{3} \mu \left( \nabla _y \cdot {\varvec{w}}\right) I +\mu \left( \nabla _y{\varvec{w}}+\left( \nabla _y {\varvec{w}}\right) ^{\text{T}}\right) . \end{aligned}$$

The cell problem is nonlinear because of the term $({\varvec{\tau }}_y({\varvec{\chi }}) \nabla _y ) \cdot {\varvec{\chi }}$ in (24c). In our computations in Sect. 4, this term has turned out to be negligible such that the system (24) becomes linear. A more detailed discussion of the nonlinear term can be found in [9].

We emphasize that the macroscale solution ${\varvec{u}}^0$ enters the system (24). Its evaluation depends on the macroscale, i.e., ${\varvec{u}}^0({\varvec{x}}({\varvec{y}})) = {\varvec{u}}^0 ( \mathcal {Y}_{{{\bar{{\varvec{x}}}}}_\text{C}}^{-1}({\varvec{y}}) ) ={\varvec{u}}^0({\bar{{\varvec{x}}}}_\text{C} + \varepsilon {\varvec{y}})$, by means of the parameter ${{\bar{{\varvec{x}}}}}_\text{C}$. For each fixed ${\bar{{\varvec{x}}}}_\text{C}$, the macroscale solution is assumed to be constant in $y_1$-direction, but it varies in $y_2$. Note that in [9] ${\varvec{u}}^0$ is assumed to be constant on Y and, thus, the gradients of ${\varvec{u}}^0$ vanish in (24).

The system has to be closed by appropriate boundary conditions for the upscaling functions at the injection boundary $\varGamma _\text{Inj}$, the walls $\varGamma _\text{W,1}$ and $\varGamma _\text{W,2}$, the inflow boundary $\varGamma _\text{in}$, the outflow boundary $\varGamma _\text{out}$ and the farfield boundary $\varGamma _\text{up}$, see Fig. 3b.

Injection boundary. Assuming that the coolant is injected in normal direction only, there is no flow in tangential direction, i.e., $v_1^\varepsilon = v_1^0 + \varepsilon \chi _1 = \varepsilon \chi _1 = 0$, resulting in $\chi _1=0$. Since the flow in the pore channel is idealized as a pipe flow, the upscaled velocity in normal direction is determined by a velocity profile of a laminar incompressible flow in a pipe, i.e.,

$$\begin{aligned} v_2^\varepsilon = v_2^0 + \varepsilon \chi _2 = v_{2,\text{max}} \left( 1 - \left( \frac{y_1}{{\bar{R}}}\right) ^2 \right) ,\quad (y_1,0) \in \varGamma _\text{Inj} \end{aligned}$$

with ${\bar{R}} = 0.5\,\varphi$, $v_{2,\text{max}}=1.5\, v_2^0/\varphi$ and $\varphi$ the given porosity. This provides $\chi _2$. Here, $v_{2,\text{max}}$ is chosen such that $1/|\varGamma _\text{Inj}|\int _{\varGamma _\text{Inj}} v_2^\varepsilon \, \text{d}\gamma = v_2^0/\varphi$. The upscaled density is assumed to be constant, i.e., $\rho ^\varepsilon = \rho ^0 + \varepsilon \phi = \rho ^0$, resulting in $\phi =0$. For the upscaling of the pressure, no boundary condition is given.

Inflow boundary. In contrast to classical homogenization techniques and also previous work on upscaling techniques [9], we cannot assume that the solutions at the boundaries $\varGamma _\text{in}$ and $\varGamma _\text{out}$ are periodic due to the flow in the hot gas domain that is significantly perturbed by the coolant injection. Instead, on $\varGamma _\text{in}$ we prescribe upscaled values for the velocity ${\varvec{v}}^\varepsilon = {\varvec{v}}^0 + \varepsilon {\varvec{\chi }}= {\varvec{v}}^\varepsilon _\text{in}$ and the temperature $T^\varepsilon = T^\varepsilon _\text{in}$ taken from an upscaled solution in the cell domain upstream to the current domain. For the upscaling of the velocity, this yields ${\varvec{\chi }}=({\varvec{v}}^\varepsilon _\text{in}-{\varvec{v}}^0)/ \varepsilon$. Assuming $\varepsilon \pi$ being negligibly small, we conclude by the perfect gas law (5) for the upscaled temperature

$$\begin{aligned} T^\varepsilon = \frac{p^0}{R (\rho ^0+\varepsilon \phi )} = \frac{p^\varepsilon _\text{in}}{R \rho ^\varepsilon _\text{in}} = T^\varepsilon _\text{in}, \quad \text {or, equivalently,}\quad \phi = \frac{1}{\varepsilon } \left( \frac{p^0 \rho ^\varepsilon _\text{in}}{p^\varepsilon _\text{in}} - \rho ^0\right) . \end{aligned}$$

Outflow boundary. We do not impose Dirichlet constraints on the upscaling functions at this boundary. The solutions are used to upscale the density, velocity and pressure there and are applied in the cell problem downstream of the current domain as explained above.

Wall boundary. At the wall, we want to ensure no-slip conditions for the upscaled velocity, i.e.,

$$\begin{aligned} {\varvec{v}}^{\varepsilon } = {\varvec{v}}^0 + \varepsilon {\varvec{\chi }}= {\varvec{0}}\quad \text {or, equivalently,} \quad {\varvec{\chi }}= -\frac{1}{\varepsilon } {\varvec{v}}^0. \end{aligned}$$

(26)

For the temperature, we consider both an adiabatic and an isothermal wall. To ensure that the wall is adiabatic w.r.t. the upscaled temperature, we need

$$\begin{aligned} \nabla T^\varepsilon \cdot {\varvec{n}}\equiv \nabla \left( \frac{p^\varepsilon }{R \rho ^\varepsilon }\right) \cdot {\varvec{n}}\approx \nabla T^0 \cdot {\varvec{n}}+ \varepsilon \, \nabla \left( \frac{\pi }{\rho ^0} - \frac{\phi \,p^0}{(\rho ^0)^2} \right) \cdot {\varvec{n}}= 0 \end{aligned}$$

(27)

providing us with a Robin type condition for the normal derivatives of $\phi$ and $\pi$. Note that here the temperature is written in terms of pressure and density using the perfect gas law (5). Higher-order powers of $\varepsilon$ are neglected in (27). Moreover, the macroscale solution is assumed to be adiabatic, i.e., $\nabla T^0 \cdot {\varvec{n}}= 0$. To impose an isothermal wall, we need

$$\begin{aligned} T^\varepsilon = \frac{p^\varepsilon }{R \rho ^\varepsilon } = \frac{p^0}{R (\rho ^0+\varepsilon \phi )} = T_\text{wall} \text {\quad or, equivalently\quad } \phi = \frac{1}{\varepsilon } \left( \frac{p^0 }{R T_\text{wall} } - \rho ^0\right) . \end{aligned}$$

(28)

Farfield boundary. Finally, with regard to a weak formulation of the cell problem, see Appendix A, that allows for a finite element method we additionally impose the boundary conditions on $\varGamma _\text{up}$ and $\varGamma _\text{out}$ as listed below.

In summary, the system (24) is closed by the following boundary conditions:

$$\begin{aligned}&\phi =\frac{1}{\varepsilon } \left( \frac{p^0 \rho ^\varepsilon _\text{in}}{p^\varepsilon _\text{in}} - \rho ^0\right) ,\quad {\varvec{\chi }}= \frac{1}{\varepsilon }\left( {\varvec{v}}^\varepsilon _\text{in}-{\varvec{v}}^0\right) \qquad \text {on } \varGamma _\text{in}, \end{aligned}$$

(29a)

$$\begin{aligned}&\left( \nabla \left( \frac{\pi }{\rho ^0} \right) - \nabla \left( \frac{\phi \,p^0}{(\rho ^0)^2} \right) \right) \cdot {\varvec{n}}_y= {\varvec{0}}\qquad \text {on } \varGamma _\text{W,ad}, \end{aligned}$$

(29b)

$$\begin{aligned}&\phi = \frac{1}{\varepsilon } \left( \frac{p^0 }{R T_\text{wall} } - \rho ^0\right) \qquad \text {on } \varGamma _\text{W,iso}, \end{aligned}$$

(29c)

$$\begin{aligned}&{\varvec{\chi }}= - \frac{{\varvec{v}}^{0}}{\varepsilon } \qquad \text {on } \varGamma _\text{W,1}\cup \varGamma _\text{W,2}, \end{aligned}$$

(29d)

$$\begin{aligned}&\phi = 0 , \quad \chi _1 = 0,\quad \chi _2 = \frac{1}{\varepsilon }\left( v_{2,\text{max}} \left( 1 - \left( \frac{y_1}{{\bar{R}}}\right) ^2 \right) - v_2^0 \right) \qquad \text {on } \varGamma _\text{Inj}, \end{aligned}$$

(29e)

$$\begin{aligned}&\nabla _y \phi \cdot {\varvec{n}}_y = 0 , \quad \left( \frac{\mu }{\varepsilon } \nabla _y {\varvec{\chi }}- \pi {\varvec{I}}\right) \, {\varvec{n}}_y = {\varvec{0}}\qquad \text {on } \varGamma _\text{up}, \end{aligned}$$

(29f)

$$\begin{aligned}&\left( \frac{\mu }{\varepsilon } \nabla _y {\varvec{\chi }}- \pi {\varvec{I}}\right) \, {\varvec{n}}_y = {\varvec{0}}\qquad \text {on } \varGamma _\text{out}. \end{aligned}$$

(29g)

For $\varGamma _\text{W,2}$, we always use adiabatic wall conditions, whereas for $\varGamma _\text{W,1}$ we use either adiabatic or isothermal wall conditions depending on the position ${\bar{{\varvec{x}}}}_\text{C}$ of the pore cell as specified in Sect. 4.1.

The solution of the system (24) with the boundary conditions (29) is used to determine effective constants by

$$\begin{aligned}&\langle \phi \rangle := \frac{1}{|\varGamma _0|} \int _{\varGamma _0} \phi \, \text{d}y_1, \end{aligned}$$

(30a)

$$\begin{aligned}&\langle \chi _i \rangle := \frac{1}{|\varGamma _0|} \int _{\varGamma _0} \chi _i\, \text{d}y_1,\ i=1,\cdots ,d, \quad \langle \pi \rangle := \frac{1}{|\varGamma _0|} \int _{\varGamma _0} \pi \, \text{d}y_1, \end{aligned}$$

(30b)

where $\varGamma _0:= \varGamma _\text{W,1} \cup \varGamma _\text{Inj} \cup \varGamma _\text{W,2}$ and $\langle \chi _2 \rangle =0$ due to the boundary conditions (29d) and (29e).

3.2.3 Effective Boundary Conditions

In Sect. 3.3, effective boundary conditions are prescribed at the interface $\varGamma _\text{Int}$. These boundary conditions are determined using the effective constant (30a) derived in Sect. 3.2.2 solving the cell problem. Applying the upscaling strategy presented in Sect. 3.2.1, the effective density is computed by

$$\begin{aligned} \rho ^\text{eff} = \rho ^0 + \varepsilon \langle \phi \rangle . \end{aligned}$$

(31)

To ensure the correct cooling gas mass flow rate, we only consider the injection velocity $v_2$ such that

$$\begin{aligned} v_i^\text{eff} = 0,\quad i\ne 2 . \end{aligned}$$

(32)

Since on top of the interface, i.e., $x_2>0$, the flow is dominated by the inflow of the cooling gas in wall-normal direction, we neglect the influence of the streamwise velocity on the hot gas flow to determine the cooling gas inflow rate. For the cooling gas mass flow rate in the effective problem to be consistent with the one in the macroscale problem, we need

$$\begin{aligned} \rho ^\text{eff} v_2^\text{eff} = \frac{{\dot{m}}_\text{c}}{A_\text{c}} \quad \text { or, equivalently, }\quad v_2^\text{eff} = \frac{{\dot{m}}_\text{c}}{A_\text{c} \rho ^\text{eff}} . \end{aligned}$$

(33)

The effective temperature is determined according to the perfect gas law (5) by

$$\begin{aligned} T^\text{eff} = \frac{p_\text{HG}}{R \rho ^\text{eff}}, \end{aligned}$$

(34)

where the pressure $p_\text{HG}$ corresponds to the pressure of the attached hot gas flow field at the interface. Note that $T^\text{eff}$ tends to $T^0$ for $\varepsilon \rightarrow 0$, i.e., the effective boundary condition is consistent with the boundary conditions of the macroscale problem.

3.3 Effective Problem

To upgrade the solution of the macroscale problem, we solve an effective problem in the hot gas domain only, where at the injection boundary we impose the effective boundary conditions (31)–(34), see Fig. 4. Note that from a geometrical point of view, $\varOmega ^\text{eff}$ coincides with $\varOmega _\text{HG}$ and $\varGamma _\text{eff}$ coincides with $\varGamma _\text{Int}$.

Fig. 4

Domain for the effective problem

Analogously to the macroscale model in Sect. 3.1.1, the flow is modeled using the laminar Navier-Stokes equations in the hot gas domain $\varOmega ^\text{eff}$ and the boundary conditions at $\varGamma _\text{I}$, $\varGamma _\text{O}$ and $\varGamma _\text{W,HG}$ are chosen correspondingly:

At the boundary $\varGamma _\text{eff}$, we use effective injection boundary conditions

$$\begin{aligned} {\mathcal {B}}^\text{eff}_{2}({\varvec{u}}^\text{eff}) = {\varvec{0}}\qquad \text {on } \varGamma _\text{eff} \end{aligned}$$

(36)

given by

$$\begin{aligned} \rho =\rho ^\text{eff}, \quad {\varvec{v}}= {{\varvec{v}}^\text{eff}}, \quad T = T^\text{eff} \end{aligned}$$

(37)

according to (31)–(34). This system is solved for the conservative flow quantities

$$\begin{aligned} {\varvec{u}}^\text{eff}= \left( \rho ^\text{eff}, \rho ^\text{eff}{\varvec{v}}^\text{eff}, \rho ^\text{eff}E^\text{eff}\right) ^\text{T}. \end{aligned}$$

(38)

4 Numerical Investigations

The effective model is investigated by means of a two-dimensional (2D) configuration using real data from an experiment [19, 27]. In the experiment, a porous carbon composite sample is mounted into the sidewall of a subsonic wind tunnel. On the backside of the porous material, a coolant reservoir is attached. The test section is $1.12 \,\text{m}$ long with the porous material beginning $0.58 \,\text{m}$ downstream of the entrance, the height is $90 \,\text{mm}$ and the width $60 \,\text{mm}$. The porous wall sample measures $61 \,\text{mm}$ $\times \, 61 \,\text{mm}$ and is $L=15 \,\text{mm}$ high. The flow conditions in the hot gas channel (air) and for the cooling gas (air) for this configuration are listed in Table 1. Parameters of the porous material are recorded in Table 2. Note that the volumetric heat transfer coefficient $h_\text{v}$ can only be estimated and not measured. More details on the experiments can be found in [19, 27]. In contrast to the experiment, we replace the porous medium in our multiscale problem by a solid with $N_{\text{pc}}$ equally distributed channels, see Fig. 1a.

Table 1 Flow parameters

Table 2 Porous material parameters

In the following, we analyze numerical results performing simulations for the multiscale model, the macroscale model and the effective model. The numerical methods and discretizations are briefly summarized in Sect. 4.1. Then, we first discuss the numerical results for the macroscale problem, see Sect. 4.2. From these simulations, we extract data that enter the cell problem. The results of the latter are discussed in Sect. 4.3. In Sect. 4.4, we perform a computation with effective boundary conditions and compare the results with simulations of the macroscale problem (uniform injection) and the multiscale problem (non-uniform injection).

4.1 Numerical Methods and Discretizations

For the numerical investigations, we perform 2D computations in the cross-section of the 3D experimental configuration along the centerline in streamwise direction of the hot gas flow. In the following, we briefly summarize the numerical discretizations of the multiscale model and of the effective model including the macroscale problem and the cell problems.

Multiscale problem. To verify the benefits of the effective model in comparison to the macroscale model, we compare its solution with the solution of the multiscale problem. The latter is determined by (3) with boundary conditions (6), (7), and (8). The multiscale domain $\varOmega ^\varepsilon$, see Fig. 1a, is composed of the hot gas channel and $N_{\text{pc}}=20$ pore channels. These are equally distributed over the porous material of width $\ell =61\,\text{mm}$ resulting in $\varepsilon =\ell /N_{\text{pc}}=3.05\,\text{mm}$.

For simulations of the multiscale model, we use the flow solver Quadflow [3], which solves the Navier-Stokes equations (3) iteratively using a fully adaptive cell-centered finite volume method on locally refined grids. The solver is initialized on a coarse grid that already comprises about 2.5 million cells. In particular in the areas of injection, a high resolution is required for stable numerical computations. The grid lines are concentrated towards all walls and in the 20 channels towards the injection using stretching functions. The final adaptive grid after four adaptations consists of approximately 2.9 million grid cells.

Macroscale problem. Following [6], we run a coupled simulation of the macroscale problem determined by (10) and (11) with uniform injection, where we perform alternately computations with Quadflow in the hot gas domain $\varOmega _\text{HG}=[0;\,1.12]\,\text{m}$ $\times \,[0;\,0.06]\,\text{m}$ and a porous medium solver in the porous medium domain $\varOmega _\text{PM}=[0.58;\,0.641]\,\text{m}$$\times\,[-0.015;\,0]\,\text{m}$, see Fig. 2. At the interface, data are exchanged between the solvers according to the coupling conditions (17), (18), and (19). For the porous medium flow, a finite element solver has been implemented using the deal.II library [2] to solve the weak formulation of the porous medium model (14).

The hot gas flow solver for $\varOmega _\text{HG}$ is initialized on a coarse grid that comprises 9 000 grid cells. The grid lines are concentrated towards the walls and the injection interface using a stretching function. The final adaptive grid after seven coupling iterations and, hence, adaptations consists of about 123 000 grid cells. The porous material $\varOmega _\text{PM}$ is discretized with about 5 000 grid cells. No adaptation is used in the porous medium domain. The grid lines are concentrated towards the injection interface.

Cell problems. For each of the 20 pore channels of the multiscale configuration, we solve a cell problem corresponding to the respective reference location ${{\bar{{\varvec{x}}}}}_\text{C}$, see Fig. 3a. For the cell problem (24), we extract solution data ${\varvec{u}}^0$ of the macroscale problem along the line $x_1 = {\bar{x}}_{\text{C},1}, x_2 \in [0; \,\varepsilon ]$ that are constantly extended in $x_1$-direction, which corresponds to $y_1=x_1/\varepsilon$ in the cell problem. For the inflow conditions at $\varGamma _\text{in}$, we also extract the upscaling data ${\varvec{u}}^1_\text{in}=(\phi _\text{in}, {\varvec{\chi }}_\text{in}, \pi _\text{in})^\text{T}$ according to (25) at $\varGamma _\text{out}$ of the cell problem solution upstream of the current cell domain. Together with the extracted macroscale data for the cell problem upstream, called ${\varvec{u}}^0_\text{in}$, we determine the upscaled input data ${\varvec{u}}^\varepsilon _\text{in}= {\varvec{u}}^0_\text{in} + \varepsilon {\varvec{u}}^1_\text{in}$ needed in (29a). Note that this requires solving the cell problems successively. For the first injection element in streamwise direction of the hot gas flow, there are no upscaling data available. Thus, we extract macroscale hot gas data at the leading edge of the porous material (here $x_1=0.58\,\text{m}$) to set up ${\varvec{u}}^0_\text{in}$ and set ${\varvec{u}}^1_\text{in}={\varvec{0}}$. Furthermore, the wall $\varGamma _\text{W,1}$ of the first cell problem is upstream of any injection of cooling gas. Hence, for the first cell problem we apply the isothermal boundary (29c) at $\varGamma _\text{W,1}$ with isothermal wall temperature $T_\text{wall}$ as given in Table 1. Otherwise, we use adiabatic wall boundary conditions (29b) at $\varGamma _\text{W,1}$ and $\varGamma _\text{W,2}$.

The cell problems are solved by a finite element method again using the deal.II library [2]. The grid for the cell domain $Y=[-0.5;\,0.5]\times [0;\,1]$, see Fig. 3b, consists of 7 680 grid cells. A stretching function leads to the concentration of the cells towards $y_2=0$ and towards $y_1=-0.5 \varphi$ and $y_1=0.5 \varphi$ such that the injection area is particularly well resolved.

Effective problem. To determine the effective coefficient (30a) on the entire interface, we solve cell problems at the $N_{\text{pc}}=20$ positions along the coupling interface and linearly interpolate the resulting effective coefficients. By means of (31)–(34), these enter the effective boundary conditions (37) of the effective problem (35a) determined by the Navier-Stokes equations (3) together with the boundary conditions (35b). Again, the flow solver Quadflow [3] is used to solve the effective problem on $\varOmega ^\text{eff}=\varOmega _\text{HG}$. Here, the grid for the flow solver has about 118 000 grid cells and a similar resolution as the final adapted grid of the macroscale problem with 123 000 cells, see above. Since the effective boundary condition (31) and, hence, also (33) and (34) depend on the macroscale solution along the interface, we extract the macroscale data from $\varOmega _\text{HG}$ at $\varGamma _\text{Int}$, see Fig. 2, according to the resolution of the grid for the effective problem such that there is one macroscale data point per grid cell at $\varGamma _\text{eff}$.

In the following, we discuss the results of our numerical simulations. Here, we will not discuss grid convergence but emphasize that the results of all problems (multiscale, macroscale, cell, effective) are grid-converged.

4.2 Macroscale Problem

To provide data needed for the cell problems and the effective problem and also for comparison with the multiscale solution, we first run a coupled simulation with uniform injection to solve the macroscale problem.

Fig. 5

Macroscale problem: distribution of temperature in the hot gas (a) and solid temperature in the porous medium (b)

In Fig. 5a, the temperature distribution in the region of the second half of the porous medium injection is shown. A cooling film forms due to the injection through the porous medium, with increasing thickness over the length of the material. In Fig. 5b, the temperature of the solid in the porous medium is presented. The temperature increases from the backside temperature $T_\text{b}=321.9\,\text{K}$ at $x_2 = -0.015\,\text{m}$ to the hot gas side at $x_2 = 0$. At the hot gas side, the solid is hotter at the leading edge of the porous material and cooler further downstream since downstream the cooling film is thicker and thus the wall heat flux is smaller.

Further results of the macroscale model are discussed in Sect. 4.4 by comparing them with the results of the multiscale and the effective model.

4.3 Cell Problem

Information from the solution of the macroscale problem enters the cell problems. Therefore, we extract data perpendicular to the interface in the range of $x_2\in [0;\,\varepsilon ]$ on and above the coupling interface $\varGamma _\text{Int}$. Thus, only data from the hot gas domain are used. Since the data strongly depend on the position ${\bar{x}}_{\text{C},1}$ on $\varGamma _\text{Int}$, we exemplarily present in Fig. 6 the extracted data for two positions ${\bar{x}}_{\text{C},1}=0.581\,525\,\text{m}$ (first cell problem) and ${\bar{x}}_{\text{C},1}=0.639\,475\,\text{m}$ (last cell problem) close to the leading edge and the trailing edge of the porous medium, respectively. We note a significant influence of the position ${\bar{x}}_{\text{C},1}$ on the density and the velocity components, while the pressure is nearly constant.

Fig. 6

Macroscale problem: hot gas information near the interface in wall-normal direction

In Fig. 7b, the solution of the cell problem is exemplarily presented for $\varepsilon \phi$ at ${\bar{x}}_{\text{C},1}=0.608\,975\,\text{m}$ (10th cell problem). Here, we scale the solution $\phi$ by $\varepsilon$ to make it physically interpretable as a density update. To visualize the effect of the update in Fig. 7, we compare the extracted macroscale solution ${\varvec{u}}^0$ and the updated version ${\varvec{u}}^0+\varepsilon {\varvec{u}}^1$. In Fig. 7a, the extracted data ${\varvec{u}}^{0}$ are extended in $y_1$-direction to cover the entire cell domain. Comparing the density distribution of the macroscale problem in Fig. 7a with its updated version in Fig. 7c, one can observe a significant difference especially close to the injection and the walls. Furthermore, the microscale effect of a local injection through one single channel, here for $y_1 \in [-0.05;\,0.05]$, becomes visible in Figs. 7b and c.

Fig. 7

Cell problem: comparison of the macroscale solution ${\varvec{u}}^0$ (a), the scaled cell solution $\varepsilon {\varvec{u}}^1$ (b) and the upscaling ${\varvec{u}}^0+\varepsilon {\varvec{u}}^1$ (c) for the density

Figure 8 depicts the density distribution resulting from the multiscale simulation around the 9th to 11th pore channels. The comparison with the upscaled density solution $\rho ^0 + \varepsilon \phi$ presented in Fig. 7c shows that the latter and, hence, the scaled update $\varepsilon \phi$, are physically meaningful.

Fig. 8

Multiscale problem: density in the area of the 9th to 11th pore channel

From each cell problem solution, the particular effective constant $\langle \phi \rangle$ is determined according to (30a) by averaging the solution along $\varGamma _0:= \varGamma _\text{W,1} \cup \varGamma _\text{Inj} \cup \varGamma _\text{W,2}$, see Fig. 3b. To cover the entire injection interface with the length of $0.061\,\text{m}$, we use linear interpolation in between the $N_{\text{pc}}$ values of $\langle \phi \rangle$. With $N_{\text{pc}}=20$, $x_1 \in [0.581\,525;\,0.639\,475]\,\text{m}$ is covered. At the leading edge of the injection, i.e., $x_1=0.58\,\text{m}$, we make use of the isothermal wall temperature and compute $\langle \phi \rangle$ according to the boundary condition (29c). Hence, we can also determine values for $x_1 \in [0.58;\,0.581\,525]\,\text{m}$ by interpolation. For the sake of simplicity, the last value at $x_1=0.639\,475\,\text{m}$ is constantly extended up to the trailing edge at $x_1=0.641\,$ m. Exemplarily, the interpolation of $\langle \phi \rangle$ is presented in Fig. 9. The plot shows that the macroscale density needs to be corrected less and less towards the trailing edge of the injection.

Fig. 9

Cell problem: $\langle \phi \rangle$ interpolated to cover the entire interface $\varGamma _\text{Int}$

Fig. 10

Macroscale problem: density at the interface $\varGamma _\text{Int}$

4.4 Effective Problem

Performing a simulation of the effective problem requires the evaluation of the effective boundary conditions (31)–(34). For this purpose, we need the effective coefficient of Fig. 9. In addition, density data from the macroscale computation enter directly. These are extracted from the hot gas flow at the interface $\varGamma _\text{Int}$, see Fig. 10. In the following, we compare the solution of the effective problem with the solutions of the macroscale problem and the multiscale problem.

In Fig. 11, the temperature distribution is compared for all three models for $x_1 \in [0.56;\; 0.81]\,\text{m}$ at $x_2=0$, which includes the cooling gas injection between $x_1=0.58\,\text{m}$ and $x_1=0.641\,\text{m}$. We observe that the cooling effect at the interface predicted with the macroscale model is significantly stronger than the cooling effect predicted with the multiscale or effective model. The effective injection clearly shows a better agreement with the results of the multiscale computation in comparison with the macroscale computation. This is also reflected in the averaged temperatures at the interfaces: $\bar{T}^{\varepsilon }=352\,\text{K}$ for the multiscale case, $\bar{T}^{0}=324\,\text{K}$ for the macroscale case, and $\bar{T}^\text{eff}=348$ K for the effective case.

Fig. 11

Comparison: temperature at $x_2=0$ in the injection area and in the wake of the injection for the multiscale, the macroscale, and the effective computation

The prediction of the effective model for the wall temperature in the wake of the cooling gas injection ($x_1 > 0.641\,\text{m}$) is nearly identical with the prediction of the multiscale model. This is crucial for establishing a reliable cooling of wall structures such as in rocket combustion chambers. In contrast to the effective model, the macroscale model fails to accurately predict the wall temperature, which is up to 12 K too low.

This trend can also be seen in the cooling efficiency $\eta$ that can be determined by relating the respective averaged temperature $\bar{T}_\text{Int}$ along the injection interface to the inflow hot gas temperature $T_{\infty }$ and the reservoir cooling gas temperature $T_\text{b}$ by

$$\begin{aligned} \eta = \frac{\bar{T}_\text{Int}- T_{\infty }}{T_\text{b}- T_{\infty }}. \end{aligned}$$

The cooling efficiencies along the porous material interface are $\eta =0.708$, $\eta =0.980$, and $\eta =0.747$ for the multiscale, macroscale, and effective simulation, respectively. Obviously, the macroscale model predicts a significantly higher cooling efficiency, whereas the effective model provides a much better approximation of the multiscale model. The relative errors are $38\,\%$ and $6\,\%$ for the macroscale model and the effective model, respectively.

Furthermore, in Fig. 12 we present the dimensionless temperature $T^{+}= T / T_{\infty }$ in the hot gas boundary layer for the positions $x_1=0.608\,975\,\text{m}$ (10th pore channel) and $x_1=0.7\,\text{m}$ (wake of the cooling gas injection) for the multiscale, the macroscale, and the effective computation. Again, the effective result better follows the trend of the multiscale result than the macroscale one, in particular in the wake of the injection.

Fig. 12

Comparison: hot gas boundary layer temperature for the multiscale, the macroscale, and the effective computation

Fig. 13

Comparison: wall shear stress for the multiscale, the macroscale, and the effective computation

From a physical point of view, we expect higher temperatures at the injection area of the multiscale problem since the wall shear stress is much higher when simulating non-uniform injection, see Fig. 13. The wall shear stress

$$\begin{aligned} \tau _\text{wall}= \mu {\left( \frac{\partial v_1}{\partial x_2}\right) }_{x_2=0} \end{aligned}$$

depends on the wall-normal gradient of the hot gas velocity in streamwise direction. Since in the multiscale simulation we have areas with injection that are separated by areas with no injection at all, see Fig. 8, the velocity gradient is locally very steep. Moreover, the non-uniform local injection interacts with the boundary layer resulting in a higher wall shear stress. This is not accurately captured by the macroscale computation that predicts a smaller wall shear stress due to a uniform injection. Since the effective coupling conditions (31)–(34) applied in the effective computation also lead to a uniform injection, the corresponding wall shear stress is close to the one of the macroscale computation. Thus, the effective model does not provide an improved approximation of the wall shear stress.

Finally, we discuss the computational efficiency of the effective model. For this purpose, we compare the numbers of cells of the final grid of the multiscale, the macroscale and the effective computation, see Table 3. We note that the number of cells of the final grid of the multiscale model is larger by factors of about 23.4 and 24.3, respectively, than the numbers of the macroscale and the effective computation. Since the effective computation is not possible without performing the macroscale computation first, their combined number of cells needs to be compared with the multiscale computation. Here, the combination is still smaller by a factor of 11.9.

Table 3 Comparison: numbers of cells on the final grid and computation times

The improved efficiency is also reflected when comparing the computation times in Table 3. All three computations were performed using 64 kernels on a cluster (one node: 2 $\times$ INTEL Xeon E5-2660 (2.6 GHz) CPU (2 $\times$ 10 kernels), 256 GB RAM). The combined computation (macroscale and effective) takes 202 min resulting in a speed-up of 6.7. Note that the total computation time of the 20 cell problems with 7 680 grid cells each is less than two minutes and neglected here.

To summarize our findings, we conclude that the effective model provides a significantly more accurate prediction of the cooling efficiency and the temperature at the injection interface than the macroscale model, the latter wrongly predicting a more efficient cooling.

Moreover, the effective computation also taking into account the computational effort of the macroscale computation is significantly more efficient by a factor of about seven in comparison to the multiscale computation. This is reflected in both the number of cells and the computation times.

We would like to emphasize that the number of pore channels $N_{\text{pc}}$ and therefore the microscale parameter $\varepsilon$ were chosen such that the simulation of the multiscale problem was feasible on the available hardware. For realistic transpiration cooling configurations, $N_{\text{pc}}$ will be much larger than 20 and $\varepsilon$ will be much smaller. This will significantly increase the computational load of the multiscale problem and result in a much higher speed-up of the effective simulations. For 3D configurations, the effective model will most likely lead to a further increase of the speed-up.

5 Conclusions

We have presented an effective model for simulating transpiration cooling taking into account microscale effects without resolving microscale pores. For this purpose, we use an upscaling strategy consisting of three steps:

• (i) with a two-domain approach, we solve a coupled macroscale problem of the hot gas flow and the porous medium flow with uniform mass injection at the interface;

• (ii) motivated by an asymptotic expansion, cell problems are solved on the microscale that depend on the data of the coupled computation;

• (iii) an effective problem is solved in the hot gas channel with effective boundary conditions at the interface using averaged data from the cell problems and data extracted from the coupled problem (uniform injection).

Experiments and numerical computations show that the cooling efficiency is reduced when using a non-uniform injection in comparison to a uniform injection. This effect is reflected in the effective computation. Thus, the effective model provides a better approximation than the coupled problem with uniform injection at reduced computational cost in comparison with a multiscale computation.

The objective of the present work has been to provide a proof of concept for the effective model applied to transpiration cooling applications. To make this a helpful tool in the engineering design, the concept has to be extended to turbulent hot gas flow and to 3D configurations and validated by experimental results. Then, the geometry of the pores and channels becomes a further parameter in the cell problem in addition to the position. Here, model order reduction strategies, e.g., [10], have to be used to reduce the computational load since a large number of cell problems has to be solved.

Furthermore, uncertainties in both the distribution of the pores at the surface and the model parameters, e.g. porosity, due to randomness in the manufacturing process of the porous material have to be taken into account. From an engineering point of view, it will be of interest to determine how much coolant is needed to ensure a safe operation of the combustion chamber, i.e., a high probability that a critical wall temperature is not exceeded. In [29], this question is investigated using probabilistic constrained Bayesian inversion. Applying the latter to the effective model might improve the efficiency of the Bayesian inversion.

Appendix A A Weak Formulation of Cell Problem

To solve the cell problem (24) with boundary conditions (29), we apply a finite element discretization. For this purpose, we need to derive the weak formulation. For trial spaces, we choose

$$\begin{aligned} U_{\phi }:= H^1_{0, \varGamma _\text{Inj} \cup \varGamma _\text{W,iso}\cup \varGamma _\text{in}}(Y), \; U_{{\varvec{\chi }}}:= \left( H^1_{0,\varGamma _\text{Inj} \cup \varGamma _\text{W} \cup \varGamma _\text{in}}(Y)\right) ^d, \; U_{\pi }:= H^1(Y), \end{aligned}$$

where $\varGamma _\text{W} = \varGamma _\text{W,1}\cup \varGamma _\text{W,2}$ and $\varGamma _\text{W,iso}=\varGamma _\text{W,1}$ for the first cell problem, otherwise $\varGamma _\text{W,iso}=\varnothing$. Here, $H^1_{0,D}(Y)$ denotes the space of functions in $H^1(Y)$ with vanishing trace on $D \subset \partial Y$. The test spaces coincide with the trial spaces, i.e., ${\varvec{U}}\times {\varvec{V}}$ with ${\varvec{V}}= {\varvec{U}}=U_{\phi } \times U_{{\varvec{\chi }}} \times U_{\pi }$. In the following, we derive the bilinear forms corresponding to (24).

Since (24a) for the upscaling function $\phi$ is only of first order, we only multiply it with a test function $t_{\phi }\in U_{\phi }$ to obtain its weak formulation

$$\begin{aligned}&b_{\phi }([\phi , {\varvec{\chi }}], t_{\phi }):= \int _{Y} \left( ({\varvec{v}}^{0}\cdot \nabla _y) \phi + \rho ^{0}\nabla _y\cdot {\varvec{\chi }}+ {\varvec{\chi }}\cdot \nabla _y \rho ^0 + \phi \nabla _y \cdot {\varvec{v}}^0\right) \, t_{\phi } \text{d}{\varvec{y}}= 0. \end{aligned}$$

(A1)

Equation (24b) for the upscaling functions ${\varvec{\chi }}$ is multiplied with the test functions ${\varvec{t}}_\chi \in U_{{\varvec{\chi }}}$. Using integration by parts for the second order terms and $\nabla _y\pi$, it holds

$$\begin{aligned}&b_{{\varvec{\chi }}}\left([\phi , {\varvec{\chi }}, \pi ], {\varvec{t}}_\chi \right) \\&:=\nonumber \int _Y {\varvec{t}}_\chi \cdot {\left( \rho ^{0} \left({\varvec{v}}^0\cdot \nabla _y \right){\varvec{\chi }}+ \nabla _y \pi +\left( \left( \rho ^0 {\varvec{\chi }}+ \phi {\varvec{v}}^0 \right) \cdot \nabla _y \right) {\varvec{v}}^0 \nonumber . - \frac{\mu }{\varepsilon } \left( \Delta _y {\varvec{\chi }}+ \frac{1}{3} \nabla _y \left(\nabla _y\cdot {\varvec{\chi }}\right) \right) \right)} \text{d}{\varvec{y}} \end{aligned}$$

(A2)

$$\begin{aligned}\\& \nonumber \\& =\int _Y {\varvec{t}}_\chi \cdot \left( \rho ^{0} ({\varvec{v}}^0\cdot \nabla _y ){\varvec{\chi }}+\left( \left( \rho ^0 {\varvec{\chi }}+ \phi {\varvec{v}}^0 \right) \cdot \nabla _y \right) {\varvec{v}}^0 \right) \end{aligned}$$

(A3)

$$\begin{aligned}&- (\nabla _y \cdot {\varvec{t}}_\chi ) \pi + \frac{\mu }{\varepsilon } \nabla _y{\varvec{t}}_\chi : \nabla _y {\varvec{\chi }}+ \frac{\mu }{3\varepsilon } (\nabla _y \cdot {\varvec{t}}_\chi ) (\nabla _y\cdot {\varvec{\chi }}) \text{d}{\varvec{y}}\nonumber \\&+ \int _{\partial Y} \left(\pi {\varvec{t}}_\chi \cdot {\varvec{n}}- \frac{\mu }{\varepsilon } {\varvec{t}}_\chi \cdot \left( (\nabla _y {\varvec{\chi }})\, {\varvec{n}}\right) - {\varvec{t}}_\chi \cdot {\varvec{n}}\frac{\mu }{3\varepsilon } (\nabla _y \cdot {\varvec{\chi }})\right)\text{d}\gamma \end{aligned}$$

with

$$\begin{aligned} \nabla _y {\varvec{\chi }}= \left( \frac{\partial \,\chi _{j}}{\partial \,y_{i}} \right) _{i,j=1,\cdots ,d},\quad \nabla _y{\varvec{\chi }}: \nabla _y {\varvec{t}}_\chi = \sum _{i,j=1,\cdots ,d} \frac{\partial \,\chi _{j}}{\partial \,y_{i}} \frac{\partial \,(t_\chi )_{j}}{\partial \,y_{i}} . \end{aligned}$$

Note that for all ${\varvec{t}}_\chi \in U_{{\varvec{\chi }}}$ it holds

$$\begin{aligned} \int _{\partial Y}\left(\pi {\varvec{t}}_\chi \cdot {\varvec{n}}- \frac{\mu }{\varepsilon } {\varvec{t}}_\chi \cdot (\nabla _y {\varvec{\chi }}{\varvec{n}})\right) \text{d}\gamma =0 \end{aligned}$$

(A4)

due to the boundary conditions (29f) and (29g) and

$$\begin{aligned} \int _{\partial Y} \frac{\mu }{3\varepsilon }{\varvec{t}}_\chi \cdot {\varvec{n}}(\nabla _y \cdot {\varvec{\chi }}) \text{d}\gamma = \int _{\varGamma _\text{up} \cup \varGamma _\text{out}} {\varvec{t}}_\chi \cdot {\varvec{n}}\frac{\mu }{3\varepsilon } (\nabla _y \cdot {\varvec{\chi }}) \text{d}\gamma . \end{aligned}$$

(A5)

Finally, we multiply (24c) for the upscaling function $\pi$ with the test function $t_\pi \in U_{\pi }$. Applying integration by parts to the Laplace operator $\Delta _y$ and introducing

$$\begin{aligned} c_0:=\frac{(\gamma -1) \kappa }{\varepsilon \, R} \end{aligned}$$

yields

$$\begin{aligned}&\quad {b}_{\pi }([\phi , {\varvec{\chi }}, \pi ], t_{\pi }) \\:= \nonumber &\int _{Y} t_{\pi } \left( ({\varvec{v}}^0\cdot \nabla _y )\pi + \gamma p^0 \nabla _y \cdot {\varvec{\chi }}+ {\varvec{\chi }}\cdot \nabla _y p^0 + \gamma \pi \nabla _y\cdot {\varvec{v}}^0 - c_0 \Delta _y \left( \frac{\pi }{\rho ^0} - \frac{\phi p^0}{(\rho ^0)^2} \right) \right. \nonumber \\&- \left. \frac{\gamma -1}{\varepsilon }\left( \left( {\varvec{\tau }}_y({\varvec{\chi }}) \nabla _y \right) \cdot {\varvec{v}}^0 + \left( {\varvec{\tau }}_y({\varvec{v}}^0)\nabla _y \right) \cdot {\varvec{\chi }}\right) -\left( \gamma -1\right) \left( {\varvec{\tau }}_y({{\bar{{\varvec{\chi }}}}}) \nabla _y \right) \cdot {\varvec{\chi }}\right) \text{d}{\varvec{y}}\\=\nonumber &\int _{Y} t_{\pi } \left( ({\varvec{v}}^0\cdot \nabla _y )\pi + \gamma p^0 \nabla _y \cdot {\varvec{\chi }}+ {\varvec{\chi }}\cdot \nabla _y p^0 + \gamma \pi \nabla _y\cdot {\varvec{v}}^0 \right. \nonumber \\& - \left. \frac{\gamma -1}{\varepsilon }\left( \left( {\varvec{\tau }}_y({\varvec{\chi }}) \nabla _y \right) \cdot {\varvec{v}}^0 + \left( {\varvec{\tau }}_y({\varvec{v}}^0)\nabla _y \right) \cdot {\varvec{\chi }}\right) -\left( \gamma -1\right) \left( {\varvec{\tau }}_y({{\bar{{\varvec{\chi }}}}}) \nabla _y \right) \cdot {\varvec{\chi }}\right) \text{d}{\varvec{y}}\nonumber \\&+ \int _{Y} c_0 \nabla _y t_{\pi } \cdot \nabla _y \left( \frac{\pi }{\rho ^0} - \frac{\phi p^0}{(\rho ^0)^2} \right) \, \text{d}{\varvec{y}}- \int _{\partial Y} c_0 t_{\pi }\nabla _y\left( \frac{\pi }{\rho ^0} - \frac{\phi p^0}{(\rho ^0)^2} \right) \cdot {\varvec{n}}\, \text{d}\gamma . \end{aligned}$$

(A6)

Here, we have linearized the term $\left( {\varvec{\tau }}_y({\varvec{\chi }}) \nabla _y \right) \cdot {\varvec{\chi }}$ by $\left( {\varvec{\tau }}_y({{\bar{{\varvec{\chi }}}}}) \nabla _y \right) \cdot {\varvec{\chi }}$. In our computations, we neglect this term. Otherwise, the weak problem has to be solved iteratively, e.g., using a Picard iteration. According to (29b), the boundary term vanishes on $\varGamma _\text{W,ad}$. To incorporate the boundary conditions (29) in the remaining parts of the boundary, we note that

$$\begin{aligned} \nabla _y\left( \frac{\pi }{\rho ^0} - \frac{\phi p^0}{(\rho ^0)^2} \right) = \frac{1}{\rho ^0} \left( \nabla _y \pi - \frac{p^0}{\rho ^0} \nabla _y\phi \right) + \pi \nabla _y \frac{1}{\rho ^0} - \phi \nabla _y \frac{p^0}{(\rho ^0)^2}. \end{aligned}$$

For $t_\pi \in U_\pi$, we deduce for the three terms

Combining (A1)–(A7), we finally conclude with the bilinear form for ${\varvec{u}}=(\phi , {\varvec{\chi }}, \pi )^\text{T}$ and ${\varvec{w}}=(t_{\phi }, {\varvec{t}}_\chi , t_{\pi })^\text{T}$ defined by

$$\begin{aligned} b_\text{cell}({\varvec{u}},{\varvec{w}}):=\;&b_{\phi }([\phi , {\varvec{\chi }}], t_{\phi }) + b_{{\varvec{\chi }}}([\phi , {\varvec{\chi }}, \pi ], {\varvec{t}}_\chi ) + b_{\pi }([\phi , {\varvec{\chi }}, \pi ], t_{\pi }) . \end{aligned}$$

To account for inhomogeneous Dirichlet boundary conditions in (29a), (29c), (29d), and (29e), we need to perform a lifting by functions $g_{\phi } \in H^1_{0, \varGamma _\text{Inj} \cup \varGamma _\text{W,iso}\cup \varGamma _\text{in}}(Y)$ and ${\varvec{g}}_{{\varvec{\chi }}} \in \left( H^1_{0,\varGamma _\text{Inj} \cup \varGamma _\text{W} \cup \varGamma _\text{in}}(Y)\right) ^d$ with traces satisfying

$$\begin{aligned}&g_{\phi } = \frac{1}{\varepsilon } \left( \frac{p^0 \rho ^\varepsilon _\text{in}}{p^\varepsilon _\text{in}} - \rho ^0\right) \text { on } \varGamma _\text{in}, \quad g_{\phi } = \frac{1}{\varepsilon } \left( \frac{p^0 }{R T_\text{wall} } - \rho ^0\right) \text { on } \varGamma _\text{W,iso},\\&{\varvec{g}}_{{\varvec{\chi }}}=\frac{1}{\varepsilon }\left( {\varvec{v}}^\varepsilon _\text{in}-{\varvec{v}}^0\right) \text { on } \varGamma _\text{in}, \quad {\varvec{g}}_{{\varvec{\chi }}} = - \frac{{\varvec{v}}^{0}}{\varepsilon } \,\, \text { on } \varGamma _{\text{W}},\\&g_{\chi _2}=\frac{1}{\varepsilon }\left( v_\text{2,max} \left( 1 - \left( \frac{y_1}{{\bar{R}}}\right) ^2 \right) - v_2^0 \right) \text { on } \varGamma _\text{Inj}. \end{aligned}$$

For $\pi$, we do not need a lifting, but for convenience of notation we set $g_{\pi }\equiv 0$.

Then, the weak formulation of the cell problem reads:

find ${\varvec{u}}=(\phi , {\varvec{\chi }}, \pi )^\text{T} \in U_{\phi } \times U_{{\varvec{\chi }}} \times U_{\pi }$ such that for each ${\varvec{w}}=(t_{\phi }, {\varvec{t}}_\chi , t_{\pi })^\text{T} \in U_{\phi } \times U_{{\varvec{\chi }}} \times U_{\pi }$ one has

$$\begin{aligned} b_\text{cell}({\varvec{u}},{\varvec{w}}) = f({\varvec{w}}) \end{aligned}$$

(A8)

with $f({\varvec{w}}):= -b_\text{cell}({\varvec{u}}^\text{L},{\varvec{w}})$ and the lifting function ${\varvec{u}}^\text{L}=(g_{\phi },{\varvec{g}}_{{\varvec{\chi }}}, g_{\pi })^\text{T}$.

Then, the weak solution of the cell problem is given by

$$\begin{aligned} {\varvec{u}}^1= {\varvec{u}}+ {\varvec{u}}^\text{L}. \end{aligned}$$

We emphasize that in the original work [8] no lifting was needed because there are no inhomogeneous Dirichlet boundary conditions. Furthermore, since the spaces $U_{\phi }$ and $U_{\pi }$ do not coincide, the existence proof for the weak formulation of the cell problem from [8] does not work for our problem.