A Space-Time Interior Penalty Discontinuous Galerkin Method for the Wave Equation

Abstract

A new higher-order accurate space-time discontinuous Galerkin (DG) method using the interior penalty flux and discontinuous basis functions, both in space and in time, is presented and fully analyzed for the second-order scalar wave equation. Special attention is given to the definition of the numerical fluxes since they are crucial for the stability and accuracy of the space-time DG method. The theoretical analysis shows that the DG discretization is stable and converges in a DG-norm on general unstructured and locally refined meshes, including local refinement in time. The space-time interior penalty DG discretization does not have a CFL-type restriction for stability. Optimal order of accuracy is obtained in the DG-norm if the mesh size h and the time step $\Delta t$ satisfy $h\cong C\Delta t$, with C a positive constant. The optimal order of accuracy of the space-time DG discretization in the DG-norm is confirmed by calculations on several model problems. These calculations also show that for pth-order tensor product basis functions the convergence rate in the $L^\infty$ and $L^2$-norms is order $p+1$ for polynomial orders $p=1$ and $p=3$ and order p for polynomial order $p=2$.

1 Introduction

The second-order scalar wave equation provides an important model for many hyperbolic wave problems in physics, engineering and life sciences. Direct applications are in acoustics and in the modeling of elastic wave propagation in mechanics and geophysics, but the scalar wave equation also serves as a model for more complicated wave phenomena in electrodynamics, fluid mechanics and quantum mechanics. This has resulted in a huge body of literature describing finite difference, finite volume and finite element discretizations of the second-order scalar wave equation. Many of these numerical discretizations follow the method of lines approach, where the wave equation is first discretized in space, after which the resulting system of ordinary differential equations is discretized with a suitable, often explicit, time integration method. This has resulted in many accurate and efficient numerical discretizations of the wave equation that can be found in nearly any text book on the numerical analysis of partial differential equations.

The need to be able to efficiently solve increasingly more complicated wave problems, however, still presents important challenges to the numerical solution of the second-order wave equation. Examples are highly heterogeneous materials and rapidly moving fronts, which require locally strongly refined unstructured meshes and local time stepping. Also, obtaining stable higher-order accurate conservative discretizations on general meshes that allow local mesh refinement, both in space and in time, without strong time step limitations is challenging. An interesting approach to deal with this type of problems is presented by space-time methods, which currently receive significant attention. In space-time methods time is treated as an extra dimension, for instance, a three-dimensional time-dependent problem is a four-dimensional problem in space-time, and the problem is then directly discretized in space-time. The space-time approach is particularly useful for problems on time-dependent domains, but is also very suitable for hp-adaptation, both in space and in time, and provides a conservative alternative to local time-stepping methods.

Several discretization approaches are possible in space-time. If one considers a fully unstructured mesh in space-time, then a “tent pitching algorithm” can be used [10, 30], and if the mesh is constructed properly, this can result in an explicit space-time discretization. Examples of the tent pitching approach and explicit in time space-time discretizations can be found in, e.g., [11, 13, 22, 23, 26]. For three-dimensional time-dependent spatial problems, the resulting four-dimensional unstructured polytopic mesh generation problem presents, however, significant challenges and still is an active area of research [10]. Also, the mesh “tent pitching algorithm” can result in locally very small time steps and/or poor mesh quality that are non-trivial to deal with in 4D space-time. The alternative is to subdivide the space-time domain into space-time slabs, that are possibly locally refined in space and/or in time, and use a tensor product structure in time for the basis functions. This alleviates the meshing problem and allows for unstructured meshes in space, but the numerical discretization will then in general be implicit in time. If the basis functions are discontinuous in time at the connection of two space-time slabs, then a time marching algorithm, where the solution is computed one space-time slab at a time, is possible, which greatly facilitates computational efficiency.

For the second-order wave equation and related wave equations space-time discretizations that are discontinuous in time, but continuous in space, were presented and analyzed in, e.g., [1, 3, 12, 14,15,16,17, 29]. Both formulations that first rewrite the second-order equations as a first-order system and formulations that directly discretize the second-order formulation have been considered. Space-time discontinuous Galerkin discretizations of the wave equation, which use basis functions that are discontinuous both in space and in time, and therefore allow optimal flexibility for hp-adaptation in space and in time, were introduced in [4, 11, 22, 26]. Recently, also Trefftz space-time discontinuous Galerkin discretizations of the second-order wave equation using non-polynomial basis functions were presented [6, 9, 19, 23, 24]. Trefftz methods incorporate local solutions of the partial differential equation into the test and trial spaces. The main benefit of this approach is that a discretization with less degrees of freedom can be obtained, which might result in improved computational efficiency.

In this article, we will present a new space-time interior penalty discontinuous Galerkin (IP-DG) discretization. The space-time IP-DG discretization uses tensor product basis functions that are discontinuous in space and in time. This provides a very natural way to construct an arbitrary higher-order accurate conservative discretization of the wave equation that allows for local mesh refinement and local time stepping. Following Johnson [17], we first rewrite the second time derivative as a first-order system and impose a special compatibility condition between the primary variable and its time derivative. This condition is useful to provide the necessary coupling in the DG discretization between the equations for the primary variable and its time derivative and is also beneficial in the stability analysis. For the spatial discretization, we use a similar approach to derive a space-time DG discretization as we presented in [27] for the parabolic advection diffusion equation, but instead of using local and global lifting operators as in [27] we now use an internal penalty method. In addition, we need to provide stable discretizations for mixed spatial-temporal derivatives. Special attention is, therefore, given to obtain a stable formulation of the time derivatives using the compatibility condition proposed in [17] and properly defined numerical fluxes. Since elements in the space-time DG discretization are only coupled through fluxes at the element faces local refinement in space and in time does not affect the discretization in neighboring elements and we will automatically obtain a conservative discretization of the second-order wave equation that is completely flexible in the choice of meshes and the polynomial order in each element [31].

After the derivation of the space-time IP-DG discretization, the main part of this article is devoted to a detailed error and stability analysis. The key components in the error analysis are several stability bounds given by Theorems 1 and 2 and Corollary 1, which are used then in a backward in time error-analysis as outlined in [28, Chapter 12]. This allows us to prove in Theorem 3 stability, convergence and optimal order accuracy of the space-time IP-DG discretization in a DG-norm for general locally refined space-time meshes and arbitrary order tensor product basis functions in space and in time and without a CFL constraint for stability.

The remainder of this work is as follows. In Sect. 2, we present the model problem and define several function spaces, followed by the definition of the space-time mesh, elements and faces and some standard DG notation in Sect. 3. In Sect. 4, the space-time IP-DG discretization is derived, including the definition of the numerical fluxes. Section 5 first proves the consistency of the space-time IP-DG discretization, followed by several stability bounds that are crucial for the a priori error analysis, which is discussed in Sect. 6. Numerical experiments to verify the theoretical analysis are presented in Sect. 7.

2 Model Problem

Given the open domain $\varOmega \subset {\mathbb {R}}^d, \,d=1,2,3,$ with Lipschitz continuous boundary $\Gamma _D{:}{=}\partial \varOmega$. We consider the wave equation for u,

$$\begin{aligned}\frac{\partial ^2 u }{\partial t^2} - {\overline{\nabla }}\cdot (A {\overline{\nabla }}u) =f \quad \text{in } \varOmega \times (0,T), \end{aligned}$$

(1a)

$$\begin{aligned}u=g_D \quad \text{at}\ \Gamma _D \times (0,T), \end{aligned}$$

(1b)

$$\begin{aligned}u=h_0,\quad \frac{\partial u}{\partial t} = h_1\qquad \text{at } \varOmega \times \{0\}, \end{aligned}$$

(1c)

where ${\overline{\nabla }}$ is the nabla operator on ${\mathbb {R}}^d$, t represents time and T the final time. The source term f, Dirichlet boundary data $g_D$, and initial conditions $h_0, h_1$ are given functions. The matrix $A \in {\mathbb {R}}^{d\times d}$ is a symmetric positive definite matrix satisfying

$$\begin{aligned} c_0x^{\mathrm{T}}x \leqslant x^{\mathrm{T}}Ax \leqslant c_1x^{\mathrm{T}}x,\quad \forall x \in {\mathbb {R}}^d \quad \text{with } c_1 \geqslant c_0 \geqslant c >0, \end{aligned}$$

where the superscript T denotes the transpose and $c_0, c_1$, and c are positive constants. We assume that the domain $\varOmega$ can be subdivided into subdomains $\varOmega _j$ in which A(x) is continuous. If we denote $u_j{:}{=}u\vert _{\varOmega _j}$ and $u_k{:}{=}u\vert _{\varOmega _k}$, and similarly for A, we have the following transmission conditions at $\Gamma _{jk}=\partial \varOmega _j\cap \partial \varOmega _k$:

$$\begin{aligned} u_j=u_k,\quad {\bar{n}}\cdot A_j{\overline{\nabla }}u_j={\bar{n}}\cdot A_k{\overline{\nabla }}u_k \end{aligned}$$

(2)

with ${\bar{n}}$ the external normal vector at $\varOmega _j$ or $\varOmega _k$.

We denote by $L^p(\varOmega )$, with $1\leqslant p \leqslant \infty ,$ the standard Lebesgue spaces on the domain $\varOmega$ with norm $\left\| {\nu }\right\| _{p,\varOmega } < \infty$ for any Lebesgue measurable function $\nu$. We denote by $W^{m,p}(\varOmega )$ the Sobolev spaces of index $m \geqslant 0$ with norm

$$\left\{ \begin{aligned}&\left\| {v}\right\| _{m,p,\varOmega } \,{:}{=}\Bigg ( \int _{\varOmega } \sum _{\vert \alpha \vert \leqslant m} \mid D^{\alpha }v \mid ^p \, {\mathrm{d}}x \Bigg )^{\frac{1}{p}}\quad \text{for } 1 \leqslant p < \infty , \\ &\left\| {v}\right\| _{m, \infty ,\varOmega } {:}{=}\underset{x \in \varOmega , \vert \alpha \vert \leqslant m}{\mathrm{sup}} \left| {D^{\alpha } \nu (x)}\right| \quad \qquad \,\, \text{for }p=\infty \end{aligned}\right.$$

(3)

with $D^\alpha$ the weak derivative with multi-index symbol $\alpha = (\alpha _1, \cdots , \alpha _d)\in {\mathbb {R}}^d$. The $W^{m,p}(\varOmega )$ seminorm is denoted as $\left| {\nu }\right| _{m,p,\varOmega }$. For $p=2$ we denote $H^m(\varOmega ) {:}{=}W^{m,2}(\varOmega )$, with $H_0^m(\varOmega )$ the space $H^m(\varOmega )$ with zero trace at $\partial \varOmega$. For $p=2$, $m=0$, we have $L^2(\varOmega ) = H^0(\varOmega )$ with $\left\| {v}\right\| _{\varOmega } {:}{=}\left\| {v}\right\| _{0,2,\varOmega }$ and similarly $\left\| {v}\right\| _{m,\varOmega } {:}{=}\left\| {v}\right\| _{m,2,\varOmega }$. We define the $L^2(\varOmega )$ inner product as $(u,v)_{\varOmega } {:}{=}\int _{\varOmega } u \, v \,{\rm{d}}x$. The negative order Sobolev norm is defined as

$$\begin{aligned} \left\| {\,w}\right\| _{-m,p,\varOmega } {:}{=}\sup _{\scriptsize{\begin{array}{c} \phi \ne 0,\forall \phi \in C_0^{\infty }(\varOmega ),\\ \left\| {\,\phi }\right\| _{m,p,\varOmega }\leqslant 1 \end{array} }} (w,\phi )_{\varOmega }, \quad \forall w \in W_0^{m,p}(\varOmega ), m\geqslant 0. \end{aligned}$$

(4)

Here, $W_0^{m,p}(\varOmega )$ denotes the space $W^{m,p}(\varOmega )$ with zero trace at $\partial \varOmega$ and $C_0^{\infty }(\varOmega )$ is the space of infinitely many times differentiable functions with compact support on $\varOmega$. For time-dependent problems, we use the Bochner spaces $L^r((0,T),W^{m,p}(\varOmega ))$, $1\leqslant r\leqslant \infty$ with norms defined on the space-time domain ${\mathscr {E}} = \varOmega \times (0,T)$ as

$$\begin{aligned}&\left\| {v}\right\| _{r,m,p,{\mathscr {E}}} \,\,{:}{=}\Bigg (\int _0^{\mathrm{T}} \left\| {v(\cdot ,t)}\right\| ^r_{m,p,\varOmega } \, {\mathrm{d}}t\Bigg )^\frac{1}{r}\quad \, \text{with} \ 1 \leqslant r < \infty , \;1\leqslant p \leqslant \infty , \\ &\left\| {v}\right\| _{\infty ,m,p,{\mathscr {E}}} {:}{=}\underset{t \in (0,T)}{\mathrm{sup}} \left\| {v(\cdot ,t)}\right\| _{m,p,\varOmega } \quad \qquad \text{with} \ 1 \leqslant p \leqslant \infty , \end{aligned}$$

where for $r=p=2$, $m=0$, we use the simplified notation $\left\| {v}\right\| _{{\mathscr {E}}}=\left\| {v}\right\| _{2,0,2,{\mathscr {E}}}$.

Given $f\in L^2((0,T);L^2(\varOmega ))$, $h_0\in H_0^1(\varOmega )$, $h_1\in L^2(\varOmega )$ and $g_D=0$, then (1) has a unique solution u on a bounded domain $\varOmega$ with

$$\begin{aligned} u\in L^2((0,T);H_0^1(\varOmega )),\quad \frac{\partial u}{\partial t}\in L^2((0,T);L^2(\varOmega )),\quad \frac{\partial ^2 u}{\partial t^2}\in L^2((0,T);H^{-1}(\varOmega )), \end{aligned}$$

see [20, Chapter 3, Theorem 8.1]. Furthermore, see [20, Chapter 3, Theorem 8.2], the solution is continuous in time with

$$\begin{aligned} u\in C^0((0,T);H_0^1(\varOmega )),\quad \frac{\partial u}{\partial t}\in C^0((0,T);L^2(\varOmega )), \end{aligned}$$

(5)

where $C^0$ denotes the space of continuous functions. If in addition $\frac{\partial f}{\partial t}\in L^2((0,T);L^2(\varOmega ))$, u satisfies the Dirichlet boundary condition (1b), and the initial conditions (1c) satisfy $h_0\in H^2(\varOmega )$ and $h_1\in H^1(\varOmega )$, and $h_0$ is compatible with the Dirichlet boundary condition (1b) and the interface condition (2), then

$$\begin{aligned} u\in L^2((0,T);H^2(\varOmega )),\quad \frac{\partial ^2 u}{\partial t^2}\in L^2((0,T);L^2(\varOmega )), \end{aligned}$$

(6)

see [21, Chapter 5, Theorem 2.1].

3 Mesh and DG Notation

3.1 Space-Time Mesh

Fig. 1

Space time slab ${\mathscr {E}}^{\;n}$ and the definition of space-time faces of a space-time element ${\mathscr {K}}^{\;n}$ in the space-time mesh ${\mathscr {T}}_h^{\;n}$

We aim to discretize the second-order wave equation by a new space-time interior penalty DG method (Fig. 1). For this purpose, the space-time formulation requires the introduction of a space-time slab, space-time elements and faces. We define the space-time domain as ${\mathscr {E}} {:}{=}\varOmega \times (0,T)$ with $\varOmega \subset {\mathbb {R}}^d$, $d=1,2,3$, and (0, T) a time interval with $T>0$ the final time. The space-time domain ${\mathscr {E}}$ has boundaries $\varOmega (0) {:}{=}\varOmega \times \{0\}, \varOmega (T) {:}{=}\varOmega \times \{T\}$ and $Q {:}{=}\partial {\mathscr {E}} \setminus (\varOmega (0) \cup \varOmega (T))$. For the space-time discretization we introduce space-time slabs. First, we partition the time interval [0, T] by an ordered series of $N+1$ time levels $0=t_0<t_1<\cdots <t_{N} = T$. Then a space-time slab is defined as ${\mathscr {E}}^{\;n} {:}{=}{\mathscr {E}} \cap ({\mathbb {R}}^d \times I_n)$, with $I_n=(t_n,t_{n+1})$. The length of $I_n$ is $\Delta t_n=t_{n+1}-t_n$. The space-time slab ${\mathscr {E}}^{\;n}$ is approximated with a non-overlapping tessellation ${\mathscr {T}}_h^{\;n}$ of $(d+1)$-dimensional open hypercube space-time elements ${\mathscr {K}} \subset {\mathbb {R}}^{d+1}$, and is denoted as ${\mathscr {E}}_h^{\;n}$. The meshes in each space-time slab can be generated independently from one another, which allows local mesh refinement and coarsening in each space-time slab. Combining the space-time slabs ${\mathscr {E}}_h^{\;n}$ for $n=0,1,\cdots ,N-1$ gives an approximation ${\mathscr {E}}_h$ to the space-time domain ${\mathscr {E}}$ with tessellation ${\mathscr {T}}_h {:}{=} \underset{n}{\bigcup } {\mathscr {T}}_h^{\;n}$. Each space-time element ${\mathscr {K}}$ is connected to the reference element $\widehat{{\mathscr {K}}} {:}{=}(-1,1)^{d+1}$ using the isoparametric mapping ${\mathscr {G}}_{{\mathscr {K}}}^{\;n} : \widehat{{\mathscr {K}}} \rightarrow {\mathscr {K}} \in {\mathscr {T}}_h^{\;n}$. A space-time element ${\mathscr {K}} \in {\mathscr {T}}_h^{\;n}$ has boundaries $K^n \subset \varOmega (t_n){{:}{=}\varOmega \times \{t_n\}}, K^{n+1} \subset \varOmega (t_{n+1}){:}{=}{\varOmega \times \{t_{n+1}\}}$ and $Q^n_{{\mathscr {K}}} {:}{=} \partial {\mathscr {K}} \setminus (K^n \cup K^{n+1})$, with exterior unit normal vector $n_{{\mathscr {K}}}$. The spatial component of $n_{{\mathscr {K}}}$ is denoted as ${\bar{n}}_{{\mathscr {K}}}$. The space-time element faces $K^n$ are collected into the set ${\mathscr {F}}_h^{n,T}$, representing the time faces at time $t=t_n$ of the space-time elements ${\mathscr {K}} \in {\mathscr {T}}_h^{\;n}$. These faces are also indicated with $\bar{{\mathscr {F}}}_h^n$ if we want to emphasize that they constitute the spatial mesh at time $t_n$. The domain $\varOmega$ is independent of time, but in case of time-dependent spatial-temporal meshes, the interface of two connecting space-time slabs must be subdivided into subfaces such that each face connects to only one space-time element on each side of the interface. For notational simplicity, we also denote this set as ${\mathscr {F}}_h^{n,T}$. The spatial domain $\varOmega$ is approximated as $\varOmega _h{:}{=}\{\cup K{:}\; \forall K\in {\mathscr {F}}_h^{n,T}\}$, which is the union of the spatial elements and does not depend on time. We assume that $\varOmega _h\rightarrow \varOmega$ as the mesh size h goes to zero.

For the space-time element faces $Q^n_{{\mathscr {K}}},\, {\mathscr {K}} \in {\mathscr {T}}_h^{\;n}$ we define the following sets: ${\mathscr {F}}_h^{n,I}$ the set of all internal faces, ${\mathscr {F}}_h^{n,D}$ the set of faces with a Dirichlet boundary condition and ${\mathscr {F}}_h^{n,I,D} = {\mathscr {F}}_h^{n,I} \cup {\mathscr {F}}_h^{n,D}$. We will also use the trace of faces in ${\mathscr {F}}_h^{n,I,D}$ at times $t_n^+{:}{=}\lim _{\epsilon \downarrow 0 } t_n + \epsilon , n=0,1,\cdots , N$. These traces will be denoted by $\bar{{\mathscr {F}}}_h^{n,I}$ for internal faces, $\bar{{\mathscr {F}}}_h^{n,D}$ for Dirichlet faces and $\bar{{\mathscr {F}}}_h^{n,I,D} {:}{=} \bar{{\mathscr {F}}}_h^{n,I} \cup \bar{{\mathscr {F}}}_h^{n,D}$.

In case of local time stepping, a space-time element ${\mathscr {K}}\in {\mathscr {T}}_h^{\;n}$, $n=0,1, \cdots ,N-1$ in the space-time slab ${\mathscr {E}}_h^{\;n}$ is split in the temporal direction into multiple space-time sub-elements ${\mathscr {K}}_i$, $i=1,\cdots ,n_t$. Similarly, faces $S\in {\mathscr {F}}_h^{n,I,D}$ connected to the space-time element ${\mathscr {K}}$ must be subdivided into sub-faces $S_i$, $i=1,\cdots ,n_t$ such that each sub-face $S_i$ connects on at least one side to only one space-time element in the space-time slab. The same applies for faces in $\bar{{\mathscr {F}}}_h^{n,I,D}$. At the intersection of two space-time sub-elements, the faces $S=\overline{{\mathscr {K}}}_i\cap \overline{{\mathscr {K}}}_j$, $i\ne j$ are treated in the same way as faces in ${\mathscr {F}}_h^{n,T}$. For details on the use of local refinement in a space-time DG discretization, where there is no fundamental difference between refinement in space or in time, see [31]. Finally, we merge the contributions of all subdivisions in time due to local time stepping into the sets ${\mathscr {T}}_h^{\;n}, {\mathscr {F}}_h^{n,T}, {\mathscr {F}}_h^{n,I,D}$, and $\bar{{\mathscr {F}}}_h^{n,I,D}$, which provides the most straightforward way to deal with the local mesh refinement and local time stepping in a space-time DG discretization.

3.2 Finite Element Spaces

Given the space-time tessellation ${\mathscr {T}}_h$, we define for $1 \leqslant p \leqslant \infty$ the following broken Sobolev spaces and norms:

$$\begin{aligned} W^{m,p}({\mathscr {T}}_h)&{:}{=}\{ v \in L^p({\mathscr {E}}){:} \, \, v|_{{\mathscr {K}}} \in W^{m,p}({\mathscr {K}}\;\,),\, \forall {\mathscr {K}} \in {\mathscr {T}}_h \}, \\ \left\| {v}\right\| _{\,m,p,{\mathscr {T}}_h}&{:}{=}\sum _{{\mathscr {K}}\in {\mathscr {T}}_h}\left\| {v}\right\| _{\,m,p,{\mathscr {K}}} \end{aligned}$$

with an equivalent formulation for the spatial tessellations $\;\bar{\!\! {\mathscr {T}}}_h^{\,n}$, $n=0,1,\cdots ,N-1$. For $p=2$, $m=0$, we use the notation $\left\| {v}\right\| _{{\mathscr {T}}_h}=\left\| {v}\right\| _{\,0,2,{\mathscr {T}}_h}$. We denote $H^m({\mathscr {T}}_h) {:}{=}W^{m,2}({\mathscr {T}}_h)$. The broken spatial gradient will be denoted by ${\overline{\nabla }}_h$, and is defined as ${\overline{\nabla }}_hv\mid _{{\mathscr {K}}} {:}{=}{\overline{\nabla }}v\mid _{{\mathscr {K}}}$ for all ${\mathscr {K}} \in {\mathscr {T}}_h$. For the space-time discontinuous Galerkin discretization we define the polynomial spaces $Q_{d+1}^{{k}}(\widehat{{\mathscr {K}}})$ as the $d+1$ tensor product of the one-dimensional Legendre polynomials $P^k(-1,1)$, with $d = \mathrm {dim}(\varOmega ) \geqslant 1$ and k the order of the polynomial basis functions. The dimension of $Q^k_{d+1}(\widehat{{\mathscr {K}}})$ is $(k+1)^{d+1}$. The space-time finite element spaces in each space-time slab ${\mathscr {E}}_h^{\;n}, \, n=0,1,\cdots ,N-1$, are defined as

$$\begin{aligned} V_h^{k,n}&{:}{=}\{ v \in L^2({\mathscr {E}}^{\;n}){:} \,v \circ G^n_{{\mathscr {K}}} \in {Q}_{d+1}^k (\widehat{{\mathscr {K}}\,}), \, \forall {\mathscr {K}} \in {{\mathscr {T}}_h^{\;n}} \}, \\ W_h^{k,n}&{:}{=}\{ w \in (L^2({\mathscr {E}}^{\;n}))^d{:} \,w \circ G^n_{{\mathscr {K}}} \in ({Q}_{d+1}^k (\widehat{{\mathscr {K}}\,}))^d, \, \forall {\mathscr {K}} \in {{\mathscr {T}}_h^{\;n}} \}, \\ U_h^{k,n}&{:}{=}V_h^{k,n} \times V_h^{k,n}. \end{aligned}$$

The space-time finite element spaces on the space-time domain ${\mathscr {E}}_h$ are then defined as

$$\begin{aligned} V_h^k&{:}{=}\{ v \in L^2({\mathscr {E}}){:} \,v \in V_h^{k,n}, n=0,\cdots ,N-1 \}, \\ W_h^k&{:}{=}\{ w \in L^2({\mathscr {E}}){:} \,w \in W_h^{k,n}, n=0,\cdots ,N-1 \}, \\ U_h^k&{:}{=}V_h^k \times V_h^k. \end{aligned}$$

3.3 Definition of Jump and Average Operators

Since the space-time discretization uses basis functions that are discontinuous both in space and in time at element faces we need to define jump and average operators to deal with the multi-valued traces at the space-time element faces. For scalar quantities $v \in {\mathbb {R}}$ we define at interior and boundary faces jump and average operators that are, respectively, denoted as

$$\begin{aligned} \begin{array}{llllllll} \{\!\{v\}\!\} {}{:}{=}\frac{1}{2} (v^L + v^R)\,\, &{} \,\,\,\,\text{at}\,\, {}{\mathscr {F}}_h^{n,I}; &{} \quad \{\!\{v\}\!\} {}{:}{=}v^L&{} \,\,\text{at}\,\, {} {\mathscr {F}}_h^{n,D},\\ \ll v\gg {}{:}{=}\,v^L \bar{{n}}^L + v^R \bar{{n}}^R &{} \,\,\,\, \text{at}\,\, {} {\mathscr {F}}_h^{n,I}; &{} \quad \ll v\gg {}{:}{=}\,\,v^L \bar{{n}}^L&{}\,\,\text{at}\,\, {}{\mathscr {F}}_h^{n,D}, \end{array} \end{aligned}$$

and for vector quantities $q \in {\mathbb {R}}^l$ as

$$\begin{aligned} \begin{array}{llllllll} \{\!\{q\}\!\} {}{:}{=}\frac{1}{2} (q^L + q^R)\,\, &{} \,\,\,\,\text{at}\,\, {}{\mathscr {F}}_h^{n,I}; &{} \quad \{\!\{q\}\!\} {}{:}{=}q^L&{} \,\,\text{at}\,\, {} {\mathscr {F}}_h^{n,D},\\ \ll q\gg {}{:}{=}\,q^L \cdot \bar{{n}}^L + q^R \cdot \bar{{n}}^R &{} \,\,\,\, \text{at}\,\, {} {\mathscr {F}}_h^{n,I}; &{} \quad \ll q\gg {}{:}{=}\,\,q^L \cdot \bar{{n}}^L&{}\,\,\text{at}\,\, {}{\mathscr {F}}_h^{n,D}. \end{array} \end{aligned}$$

Here, the L and R superscripts refer to the left and right traces at a face $S \in {\mathscr {F}}_h^{n,I}$. When considering a space-time element ${\mathscr {K}} \in {\mathscr {T}}_h$, the L-trace is always the trace taken from inside the element and the R-trace is the outside trace. At the space-time domain boundary L refers to the internal trace. The jumps in time for faces $S \in {\mathscr {F}}_h^{n,T}$ are defined as

$$\begin{aligned} \left[ v^n \right] {:}{=}v^{n,+} - v^{n,-} , \qquad \left[ q^n \right] {:}{=}q^{n,+} - q^{n,-} \end{aligned}$$

with

$$\begin{aligned} \nu ^{n,\pm } {:}{=} \lim _{\epsilon \downarrow 0 } \nu (\cdot , t_n \pm \epsilon ), \quad q^{n,\pm } {:}{=} \lim _{\epsilon \downarrow 0 } q(\cdot , t_n \pm \epsilon ). \end{aligned}$$

We will denote the spatial mesh size by h, defined by $h {:}{=} {\text{max}}_{{\bar{S}} \in \cup _n\bar{{\mathscr {F}}}_h^{n,T}} \text{diam}({\bar{S}})$.

4 Space-Time Discontinuous Galerkin Formulation

In this section, we will derive a space-time DG interior penalty discretization for the wave equation. First, we need to rewrite the scalar wave equation (1) as a first-order system. Introduce the primary variables

$$\begin{aligned} u_0(x,t) {:}{=}u(x,t), \quad u_1(x,t) {:}{=}{\dot{u}}(x,t), \end{aligned}$$

(7)

and the auxiliary variables

$$\begin{aligned} \sigma _{0}&{:}{=}A{\overline{\nabla }}u_0 , \end{aligned}$$

(8a)

$$\begin{aligned} \sigma _{1}&{:}{=}A{\overline{\nabla }}u_1, \end{aligned}$$

(8b)

where an overdot represents differentiation with respect to time. The scalar wave equation (1) can then be written as in [17]

$$\begin{aligned}&{\dot{u}}_1 - {\overline{\nabla }}\cdot \sigma _0=f\quad \text{in } \varOmega \times (0,T), \end{aligned}$$

(9)

$$\begin{aligned}&{\overline{\nabla }}\cdot {\dot{\sigma }}_0={\overline{\nabla }}\cdot \sigma _1 \quad \text{in }\varOmega \times (0,T), \end{aligned}$$

(10)

where we used the compatibility condition ${\dot{u}}_0=u_1$, which follows from (7), and the auxiliary variables (8) to obtain (10). The use of the compatibility condition (10), instead of using ${\dot{u}}_0=u_1$, which was proposed by Johnson [17], is important in the proofs of the stability results presented in Sect. 5.2 and also provides, after integration by parts of the weak formulation of the space-time IP-DG discretization, a coupling between ${\dot{u}}_0$ and $u_1$ at element faces. The Dirichlet boundary condition and initial conditions for (9)–(10) are

$$\begin{aligned} \begin{array}{llllll} &{}u_0=g_D &{} &{}&{} &{}\text{at } \Gamma _D \times (0,T),\\ &{}u_0=h_0&{} \quad \text{and }\quad &{}u_1=h_1 &{}\qquad &{}\text{at } \varOmega \times \{0\}. \end{array} \end{aligned}$$

4.1 Space-Time DG Formulation for Primary Variables

We approximate now $u_i, \sigma _i, i=0,1$, respectively, as $u_{i,h} \in V_h^k, \sigma _{i,h} \in W_h^k$, multiply (9) and (10) with test functions $v_i \in V_h^k, i=0,1$, and integrate over the space-time domain ${\mathscr {E}}_h$. This results, after subtracting the weak formulation for (10) from (9), into the space-time formulation for the scalar wave equation. Find $u_{0,h},u_{1,h} \in V_h^k$, with $\sigma _{0,h}, \sigma _{1,h} \in W_h^k$, such that ${\text {for all}}\, v_0, v_1 \in V_h^k$, we have

$$\begin{aligned} \int _{{\mathscr {E}}_h} \big ( ({\dot{u}}_{1,h} - {\overline{\nabla }}_h\cdot \sigma _{0,h}) v_1 - v_0 ({\overline{\nabla }}_h\cdot {\dot{\sigma }}_{0,h} - {\overline{\nabla }}_h\cdot \sigma _{1,h}) \big ) {\mathrm{d}}{\mathscr {E}} =\int _{{\mathscr {E}}_h} f v_1 {\mathrm{d}}{\mathscr {E}}. \end{aligned}$$

(11)

Next, we rewrite (11) into a more suitable format to obtain the space-time DG discretization. As a first step, we will use the following relation for the time derivative of $u_{1,h}\in V_h^k$:

$$\begin{aligned} \int _{{\mathscr {E}}_h} {\dot{u}}_{1,h} v_1 {\mathrm{d}}{\mathscr {E}} =\sum _{n=0}^{N-1} \int _{{\mathscr {E}}_h^{\;n}}{\dot{u}}_{1,h} v_1 {\mathrm{d}} {\mathscr {E}} +\sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \int _S \left[ u_{1,h}^n \right] v^{n,+}_{1} {\mathrm{d}}S ,\quad \forall v_1\in V_h^k, \end{aligned}$$

(12)

which is obtained by twice integrating by parts in time and using at the time levels $t_n, n=0,\cdots ,N-1$, the causality conditions ${\hat{u}}_{1}^n = u_{1,h}^{n,-}$, ${\hat{u}}_{1}^{n+1} = u_{1,h}^{n+1,-}$ for the numerical fluxes of $u_{1,h}$, which were introduced to account for the multivalued traces at time $t_n$, and $u_{i,h}^{n,\pm }{:}{=}u_{i,h}(\cdot ,t_n^\pm )$, $i=0,1$, with $t^{\pm }_{n}{:}{=} \lim _{\epsilon \downarrow 0 } t_n \pm \epsilon$. We also need the following well-known relation between sums of integrals over element boundaries and faces [5], but now used in the space-time context [27]. For $v \in V_h^k$, $w\in {W_h^k}$,

$$\begin{aligned} \sum _{ {\mathscr {K}} \in {\mathscr {T}}_h^{\;n}} \int _{Q^n_{{\mathscr {K}}}} (w \cdot {\bar{n}}) v {\mathrm{d}} S= & {} \sum _{S \in {\mathscr {F}}_h^{n,I,D}}\int _S \{\!\{w\}\!\} \cdot \ll v\gg {\mathrm{d}}S \\ &+ \sum _{S \in {\mathscr {F}}_h^{n,I}}\int _S \ll w\gg \{\!\{v\}\!\} {\mathrm{d}}S. \end{aligned}$$

(13)

This relation can be directly verified by introducing the jump and average relations defined in Sect. 3.3.

After integration by parts in space and using (12)–(13) the space-time DG formulation (11) can be expressed as: find $u_{0,h},u_{1,h} \in V_h^k$, with $\sigma _{0,h}, \sigma _{1,h} \in W_h^k$, such that ${\text {for all}}\, v_0,v_1 \in V_h^k$ we have

$$\begin{aligned}&\sum _{n=0}^{N-1}\int _{{\mathscr {E}}^{\;n}_h} \big ({\dot{u}}_{1,h}v_1 + \sigma _{0,h}\cdot {\overline{\nabla }}_hv_1 + {\dot{\sigma }}_{0,h} \cdot {\overline{\nabla }}_hv_0 - \sigma _{1,h} \cdot {\overline{\nabla }}_hv_0 \big ) {\mathrm{d}} {\mathscr {E}} \\ & -\sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}}\int _S \big ( \{\!\{{\widehat{\sigma }}_{0}\}\!\} \cdot \ll v_1\gg + \{\!\{\widehat{{\dot{\sigma }}}_{0}\}\!\} \cdot \ll v_0\gg - \{\!\{{\widehat{\sigma }}_{1}\}\!\} \cdot \ll v_0\gg \big ){\mathrm{d}}S \\ & - \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I}}\int _S \big ( \ll {\widehat{\sigma }}_{0}\gg \{\!\{v_1\}\!\} + \ll \widehat{{\dot{\sigma }}}_{0}\gg \{\!\{v_0\}\!\} - \ll {\widehat{\sigma }}_{1}\gg \{\!\{v_0\}\!\} \big ){\mathrm{d}}S \\ & +\sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \int _S \left[ u_{1,h}^n \right] v_{1}^{n,+}{\mathrm{d}}S = \int _{{\mathscr {E}}_h} f v_1 {\mathrm{d}} {\mathscr {E}}, \end{aligned}$$

(14)

where the numerical fluxes ${\widehat{\sigma }}_i, i =0,1,$ and the numerical flux for the time derivative $\widehat{{\dot{\sigma }}}_0$ account for the multivalued traces of $\sigma _{i,h}, i=0,1,$ at the faces ${\mathscr {F}}_h^{n,I,D}$of each space-time slab. For a stable and accurate space-time DG discretization, these numerical fluxes need to be carefully considered, which will be discussed in the next sections.

4.2 Space-Time DG Formulation for Auxiliary Variables

The space-time DG formulation (14) contains the auxiliary variables $\sigma _{i,h} \in W_h^k, i=0,1,$ which approximate $\sigma _i, i=0,1$, defined in (8), and the time derivative ${\dot{\sigma }}_{0,h}$. In this section, we will derive DG formulations for these auxiliary variables and define their numerical fluxes.

After multiplying, respectively, (8a) and (8b) with arbitrary test functions $\tau ={\overline{\nabla }}_hv_j \in W_h^k, v_j \in V_h^k$, $j=0,1$, integrating by parts over each space-time element ${\mathscr {K}} \in {\mathscr {T}}_h$, using $A=A^{\mathrm{T}}$, and for $n=0,1,\cdots ,N-1$ the numerical fluxes

$$\begin{aligned} {\hat{u}}_{i} = \left\{ \begin{array}{llllll} &{}\{\!\{u_{i,h}\}\!\}&{} \quad &{}\text{at}\;\; S \in {\mathscr {F}}_h^{n,I}&{}\;\;\;&{}\text{for }i=0,1,\\ &{}g_D&{} &{}\text{at}\;\; S \in {\mathscr {F}}_h^{n,D}&{}&{}\text{for }i=0, \\ &{}{\dot{u}}^L_{0,h}&{}&{}\text{at}\;\; S \in {\mathscr {F}}_h^{n,D}&{}&{}\text{for }i=1, \end{array}\right. \end{aligned}$$

(15)

and finally summing over all space-time elements ${\mathscr {K}} \in {\mathscr {T}}_h$ we obtain analogously to [27] the DG formulation for the auxiliary variables $\sigma _{i,h}$: find $\sigma _{i,h}\in W_h^k$, such that ${\text {for all}}\, v_j \in V_h^k$, for $i,j=0,1,$

$$\begin{aligned} \sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} \sigma _{i,h} \cdot {\overline{\nabla }}_hv_j {\mathrm{d}} {\mathscr {E}}&=\sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} A {\overline{\nabla }}_hu_{i,h} \cdot {\overline{\nabla }}_hv_j {\mathrm{d}} {\mathscr {E}} \\ &\quad - \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \int _S \{\!\{A {\overline{\nabla }}_hv_j\}\!\} \cdot \ll u_{i,h}\gg {\mathrm{d}}S \\ &\quad + \left\{ \begin{array}{llll} &{}{\mathop {\sum }\limits _{n=0}^{N-1}} \sum _{S \in {\mathscr {F}}_h^{n,D}}\int _S A^L {\overline{\nabla }}_hv_j^L \cdot {\bar{n}}^L g_D {\mathrm{d}}S,&{}\qquad &{}\text{if }i=0,\\ &{}{\mathop {\sum }\limits _{n=0}^{N-1}} \sum _{S \in {\mathscr {F}}_h^{n,D}}\int _S A^L {\overline{\nabla }}_hv_j^L \cdot {\bar{n}}^L {\dot{u}}_{0,h}^L {\mathrm{d}}S,&{}&{}\text{if }i=1. \end{array}\right. \end{aligned}$$

(16)

The DG formulation for ${\dot{\sigma }}_{0,h}$ can be obtained analogously to the DG formulation for $\sigma _{0,h}$ given by (16), but great care needs to be taken to account for the discontinuities in time at $t_n=0,1,\cdots , N-1$. Following the same steps as for (16), we obtain

$$\begin{aligned} \sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} {\dot{\sigma }}_{0,h} \cdot {\overline{\nabla }}_hv_0 {\mathrm{d}} {\mathscr {E}}&=\sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} A {\overline{\nabla }}_h{\dot{u}}_{0,h} \cdot {\overline{\nabla }}_hv_0 {\mathrm{d}} {\mathscr {E}} \\ &\quad - \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \int _S \{\!\{A {\overline{\nabla }}_hv_0\}\!\} \cdot \ll {\dot{u}}_{0,h}\gg {\mathrm{d}}S \\ &\quad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,D}}\int _S A^L {\overline{\nabla }}_hv_0^L \cdot {\bar{n}}^L {{\dot{u}}_{0,h}^L} {\mathrm{d}}S. \end{aligned}$$

(17)

Next, we twice integrate by parts in time the first two terms on the right-hand side of (17). To ensure causality, we use for the multivalued time traces at the faces $S \in {\mathscr {F}}_h^{n,T}$ the numerical fluxes ${\hat{u}}_0^n = u_{0,h}^{n,-}$ for $n=0,1,\cdots ,N$.

The DG formulation for ${\dot{\sigma }}_{0,h}$ then becomes: find ${\dot{\sigma }}_{0,h} \in W_h^k$, such that ${\text {for all}}\, v_0 \in V_h^k$,

$$\begin{aligned} \sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} {\dot{\sigma }}_{0,h} \cdot {\overline{\nabla }}_hv_0 {\mathrm{d}} {\mathscr {E}}&= \sum _{n=0}^{N-1} \int _{{\mathscr {E}}^{\;n}_h} A {\overline{\nabla }}_h{\dot{u}}_{0,h} \cdot {\overline{\nabla }}_hv_0 {\mathrm{d}}{\mathscr {E}} \\ &\quad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \int _S A {\overline{\nabla }}_h\left[ u_{0,h}^n \right] \cdot {\overline{\nabla }}_hv_0^{n,+}{\mathrm{d}}S \\ &\quad - \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \int _S \{\!\{A {\overline{\nabla }}_hv_0\}\!\} \cdot \ll {\dot{u}}_{0,h}\gg {\mathrm{d}}S \\ &\quad - \sum _{n=0}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \int _{{\bar{S}}} \{\!\{A {\overline{\nabla }}_hv_0^{n,+}\}\!\} \cdot \ll \left[ u_{0,h}^n \right] \gg {\mathrm{d}}{\bar{S}} \\ &\quad +\sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,D}}\int _S A^L {\overline{\nabla }}_hv_0^L \cdot {\bar{n}}^L {{\dot{u}}_{0,h}^L}{\mathrm{d}}S. \end{aligned}$$

(18)

The numerical fluxes for the auxiliary variables ${\hat{\sigma }}_i, i=0,1,$ and $\hat{{\dot{\sigma }}}_0$ in (14) are defined for $n=0,1,\cdots , N-1$, as

$$\begin{aligned} {\bar{n}} \cdot {\hat{\sigma }}_{i}= & {} \left\{ \begin{array}{ll} {\bar{n}}\cdot \{\!\{A {\overline{\nabla }}_h u_{i,h}\}\!\} &{}\quad \text{at}\ S \in {\mathscr {F}}_h^{n,I},\\ {\bar{n}}\cdot A^L{\overline{\nabla }}_h u_{i,h}^L&{}\quad \text{at}\ S \in {\mathscr {F}}_h^{n,D}, \end{array}\right. \end{aligned}$$

(19)

$$\begin{aligned} {\bar{n}} \cdot \hat{{\dot{\sigma }}}_{0}= & {} \left\{ \begin{array}{llll} {\bar{n}} \cdot \{\!\{A {\overline{\nabla }}_h {\dot{u}}_{0,h}\}\!\} &{}\quad \text{at}\ S \in {\mathscr {F}}_h^{n,I},\\ {\bar{n}} \cdot A^L {\overline{\nabla }}_h{\dot{u}}^L_{0,h} &{} \quad \text{at}\ S \in {\mathscr {F}}_h^{n,D},\\ {\bar{n}} \cdot \{\!\{[ A{\overline{\nabla }}_hu_{0,h}]\}\!\}&{}\quad \text{at} \ {\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D} . \end{array}\right. \end{aligned}$$

(20)

Note that in (20), the numerical flux at faces ${\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}$ contains a time jump, which is important to link the stabilization in between space-time slabs. In addition to (19)–(20), we also need to add to (14) the following stabilization terms:

$$\begin{aligned}&\sum _{n=1}^N \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{\mu _0}{h} \int _{{\bar{S}}} \{\!\{A\}\!\} \ll u_{0,h}^{n,-}\gg \cdot \ll v_0^{n,-}\gg {\mathrm{d}}{\bar{S}} \\ & - \sum _{n=1}^{N} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,D}} \frac{\mu _0}{h} \int _{{\bar{S}}} A^L{\bar{n}}^L {g_D^{n,-}} \cdot {\bar{n}}^L v_0^{n,-,L} {\mathrm{d}}{\bar{S}} \\ & + \sum _{n=0}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{\mu _0}{h} \int _{{\bar{S}}} \{\!\{A\}\!\} \ll \left[ u_{0,h}^n \right] \gg \cdot \ll v_0^{n,+}\gg {\mathrm{d}}{\bar{S}} \\ & +\sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \frac{\mu _1}{h} \int _S \Big ( \{\!\{A\}\!\} \ll u_{0,h}\gg \cdot \ll v_0\gg \\& + \{\!\{A\}\!\} \ll u_{1,h} -{\dot{u}}_{0,h}\gg \cdot \ll v_1-{\dot{v}}_0\gg \Big ){\mathrm{d}}S \\ & - \sum _{n=0}^{N} \sum _{S \in {\mathscr {F}}_h^{n,D}}\frac{\mu _1}{h} \int _{S} A^L{\bar{n}}^L {g_D} \cdot {\bar{n}}^L v_0^{L} {\mathrm{d}}S \end{aligned}$$

(21)

with positive stabilization coefficients $\mu _0$ and $\mu _1$. In Sect. 5, we will prove that the choices of the numerical fluxes (19)–(20) and stabilization terms (21) result in a stable and consistent space-time DG discretization.

4.3 Interior Penalty Space-Time DG Formulation for the Wave Equation

In this section, we will first introduce some definitions that allow a more compact definition of the space-time DG formulation and will also be beneficial for the error analysis. For all $v,w \in V_h^{k,n}$ we define the following bilinear forms on the space-time slabs ${\mathscr {E}}^{\;n}_h$, $n=0,1,\cdots ,N-1$,

$$\begin{aligned} (v,w)^n&{:}{=} \sum _{S \in {\mathscr {F}}_h^{n,T}} \int _S vw \,{\mathrm{d}}S, \end{aligned}$$

(22a)

$$\begin{aligned} {\bar{a}}^n(v,w)&{:}{=} \sum _{S \in {\mathscr {F}}_h^{n,T}} \int _S A {\overline{\nabla }}_hv \cdot {\overline{\nabla }}_hw \, {\mathrm{d}}S, \end{aligned}$$

(22b)

$$\begin{aligned} {\bar{b}}^n(v,w)&{:}{=} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,I,D}} \int _{{\bar{S}}} \{\!\{A {\overline{\nabla }}_hv\}\!\} \cdot \ll w\gg \, {\mathrm{d}}{\bar{S}}, \end{aligned}$$

(22c)

$$\begin{aligned} {\bar{b}}^n_S(v,w)&{:}{=} {\bar{b}}^n(v,w) + {\bar{b}}^n(w,v), \end{aligned}$$

(22d)

$$\begin{aligned} {\bar{c}}^n_{\mu }(v,w)&{:}{=} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,I,D}} \frac{\mu }{h} \int _{{\bar{S}}} \{\!\{A\}\!\} \ll v\gg \cdot \ll w\gg \, {\mathrm{d}}{\bar{S}}. \end{aligned}$$

(22e)

The restriction of ${\bar{c}}^n_{\mu }(v,w)$ to the set ${\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,D}$ with Dirichlet boundary faces is denoted as ${\bar{c}}_{D,\mu }^{n}$. Next, we introduce for all $v,w \in V_h^k$ the following bilinear forms over the space-time domain ${\mathscr {E}}_h$:

$$\begin{aligned} \left( \!\left( v,w \right) \!\right)&{:}{=} \sum _{n=0}^{N-1} \sum _{{\mathscr {K}} \in {\mathscr {T}}_h^{\;n}} \int _{{\mathscr {K}}} vw {\mathrm{d}}{\mathscr {K}}, \end{aligned}$$

(23a)

$$\begin{aligned} a\left( \!\left( v,w \right) \!\right)&{:}{=} \sum _{n=0}^{N-1} \sum _{{\mathscr {K}} \in {\mathscr {T}}_h^{\;n}} \int _{{\mathscr {K}}} A {\overline{\nabla }}_hv\cdot {\overline{\nabla }}_hw {\mathrm{d}}{\mathscr {K}},\end{aligned}$$

(23b)

$$\begin{aligned} b\left( \!\left( v,w \right) \!\right)&{:}{=} \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \int _S \{\!\{A {\overline{\nabla }}_hv\}\!\} \cdot \ll w\gg {\mathrm{d}}S, \end{aligned}$$

(23c)

$$\begin{aligned} b_S\left( \!\left( v,w \right) \!\right)&{:}{=}b\left( \!\left( v,w \right) \!\right) + b\left( \!\left( w,v \right) \!\right) , \end{aligned}$$

(23d)

$$\begin{aligned} c_{\mu }\left( \!\left( v,w \right) \!\right)&{:}{=} \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \frac{\mu }{h} \int _S \{\!\{A\}\!\} \ll v\gg \cdot \ll w\gg {\mathrm{d}}S. \end{aligned}$$

(23e)

The restriction of $b\left( \!\left( v,w \right) \!\right)$  to the set $S \in {\mathscr {F}}_h^{n,D}$ is denoted as $b_D\left( \!\left( v,w \right) \!\right)$  and the restriction of $c_{\mu }\left( \!\left( v,w \right) \!\right)$ to the set $S \in {\mathscr {F}}_h^{n,D}$ is denoted as $c_{D,\mu }\left( \!\left( v,w \right) \!\right)$ . After introducing (16) and (18)–(21) into (14), and using the notation introduced in (22)–(23), the space-time interior penalty method for the wave equation on the space-time domain ${\mathscr {E}}_h$ can be formulated as: find $u_h \in U_h^k$ such that ${\text {for all}}\, v \in U_h^k$,

$$\begin{aligned} B_h(u_h,v) =F_h(v), \end{aligned}$$

(24)

where $u_h {:}{=}(u_{0,h},u_{1,h})$ and $v {:}{=}(v_0,v_1)$. The bilinear form $B_h: U_h^k \times U_h^k \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} B_h(u_h,v)&{:}{=} \left( \!\left( {\dot{u}}_{1,h},v_1 \right) \!\right) + \sum _{n=1}^{N-1} \left( \left[ u_{1,h}^n \right] ,v_1^{n,+}\right) ^n + (u_{1,h}^{0,+},v_1^{0,+})^0 \\ &\quad + a\left( \!\left( u_{0,h},v_1 \right) \!\right) + a\left( \!\left( {\dot{u}}_{0,h}-u_{1,h},v_0 \right) \!\right) \\ &\quad + \sum _{n=1}^{N-1} {\bar{a}}^n \left( \left[ u_{0,h}^n \right] ,v_0^{n,+}\right) + {\bar{a}}^0(u_{0,h}^{0,+},v_0^{0,+}) \\ &\quad -b_S\left( \!\left( u_{0,h},v_1 \right) \!\right) -b_S\left( \!\left( {\dot{u}}_{0,h}-u_{1,h},v_0 \right) \!\right) \\ &\quad -\sum _{n=1}^{N-1} {\bar{b}}^n_S \left( \left[ u_{0,h}^n \right] ,v_0^{n,+}\right) - {\bar{b}}^0_S(u_{0,h}^{0,+},v_0^{0,+}) + \sum _{n=1}^N {\bar{c}}^n_{\mu _0} (u_{0,h}^{n,-},v_0^{n,-}) \\ &\quad + \sum _{n=1}^{N-1}{\bar{c}}^n_{\mu _0} \left( \left[ u_{0,h}^n \right] ,v_0^{n,+}\right) +{\bar{c}}^0_{\mu _0}(u_{0,h}^{0,+},v_0^{0,+}) \\ &\quad+ c_{\mu _1} \left( \!\left( u_{0,h},v_0 \right) \!\right) +c_{\mu _1} \left( \!\left( u_{1,h} -{\dot{u}}_{0,h},v_1-{\dot{v}}_0 \right) \!\right) . \end{aligned}$$

(25)

The linear form $F_h(v){:}\,U_h^k \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} F_h(v)&{:}{=} \left( \!\left( f,v_1 \right) \!\right) + (h_1,v_1^{0,+})^0 + {\bar{a}}^0(h_0,v_0^{0,+}) -{\bar{b}}^0_S(h_0,v_0^{0,+}) -b_D\left( \!\left( v_1,{g_D} \right) \!\right) \\ &\quad + {\bar{c}}^0_{\mu _0}(h_0,v_0^{0,+}) +\sum _{n=1}^N {\bar{c}}^n_{D,\mu _0} ({g_D^{n}},v_0^{n,-}) +c_{D,\mu _1} \left( \!\left( {g_D},v_0 \right) \!\right) . \end{aligned}$$

(26)

The space-time DG formulation over the complete space-time domain ${\mathscr {E}}_h$ is important for the stability and a priori error analysis, which will be discussed, respectively, in Sects. 5 and 6, but actual computations are conducted by subsequently solving for $n=0,1,\cdots ,N-1$ the space-time DG discretization for each space-time slab ${\mathscr {E}}_h^{\;n}$. Using the causality in time resulting from the choice of the numerical fluxes at the time faces $S \in {\mathscr {F}}_h^{n,T}$ in Sect. 4.1, the space-time DG discretization in the space-time slabs ${\mathscr {E}}_h^{\;n}$ can be expressed as: for $n=0,1, \cdots , N-1$, find $u_h \in U_h^{k,n}$ such that ${\text {for all}}\, v \in U_h^{k,n}$,

$$\begin{aligned} B_h^n(u_h,v) = F_h^n(v). \end{aligned}$$

The bilinear form $B_h^n: U_h^{k,n} \times U_h^{k,n} \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} B^n_h(u_h,v)&{:}{=} \int _{I_n} \big ( ({\dot{u}}_{1,h},v_1)^n + {\bar{a}}^n(u_{0,h},v_1)+{\bar{a}}^n({\dot{u}}_{0,h}-u_{1,h},v_0) \\ &\quad - {\bar{b}}^n_S (u_{0,h},v_1) - {\bar{b}}^n_S({\dot{u}}_{0,h}-u_{1,h},v_0)\big ) {\mathrm{d}}t \\ &\quad + (u_{1,h}^{n,+},v_1^{n,+})^n + {\bar{a}}^n(u_{0,h}^{n,+},v_0^{n,+}) - {\bar{b}}^n_S(u_{0,h}^{n,+},v_0^{n,+}) \\ &\quad + {\bar{c}}^{n+1}_{\mu _0} (u_{0,h}^{n+1,-},v_0^{n+1,-}) + {\bar{c}}^n_{\mu _0}(u_{0,h}^{n,+},v_0^{n,+}) \\ &\quad + \int _{I_n} \big ({\bar{c}}^n_{\mu _1}(u_{0,h},v_0) + {\bar{c}}^n_{\mu _1}(u_{1,h}-{\dot{u}}_{0,h},v_1-{\dot{v}}_0)\big ) {\mathrm{d}}t. \end{aligned}$$

(27)

The linear form $F_h^n(v){:}\,U_h^{k,n} \rightarrow {\mathbb {R}}$ is defined as

$$\begin{aligned} F_h^n(v)&{:}{=} \int _{I_n} (f,v_1)^n {\mathrm{d}}t + (u_{1,h}^{n,-},v_1^{n,+})^n + {\bar{a}}^n(u_{0,h}^{n,-},v_0^{n,+}) \\ &\quad -\int _{I_n} {\bar{b}}^n_D(v_1,{g_D}) {\mathrm{d}}t-{\bar{b}}^n_S(u_{0,h}^{n,-},v_0^{n,+}) \\ &\quad + {\bar{c}}^{n+1}_{D,\mu _0} ({g_D^{n+1}},v_0^{n+1,-}) +{\bar{c}}^n_{\mu _0} (u_{0,h}^{n,-},v_0^{n,+})+ \int _{I_n} {\bar{c}}_{D,\mu _1}({g_D},v_0){\mathrm{d}}t . \end{aligned}$$

(28)

Note that after summation of (27)–(28) over all space-time slabs, we immediately obtain the relation

$$\begin{aligned} \sum _{n=0}^{N-1}\big (B_h^n(u_h,v)-F_h^n(v)\big )=B_h(u_h,v)-F_h(v). \end{aligned}$$

(29)

For the backward in time error analysis with t replaced by $t_N-t$, which is discussed in Sect. 6, we also need the discrete dual problem: find $z_h \in U_h^k$ such that ${\text {for all}}\, v \in U_h^k$,

$$\begin{aligned} B_h(v,z_h)=F(v), \end{aligned}$$

(30)

using the following integrated by parts expression for the bilinear form (25):

$$\begin{aligned} B_h(w_h,v)&= -\left( \!\left( w_{1,h},{\dot{v}}_1 \right) \!\right) - \sum _{n=1}^{N-1} \left( w_{1,h}^{n,-},\left[ v_1^n \right] \right) ^n \\ &\quad + (w_{1,h}^{N,-},v_1^{N,-})^{N} + a\left( \!\left( w_{0,h},v_1-{\dot{v}}_0 \right) \!\right) - a\left( \!\left( w_{1,h},v_0 \right) \!\right) \\ &\quad - \sum _{n=1}^{N-1} {\bar{a}}^n \left( w_{0,h}^{n,-},\left[ v_0^n \right] \right) + {\bar{a}}^{N}(w_{0,h}^{N,-},v_0^{N,-}) -b_S\left( \!\left( w_{0,h},v_1-{\dot{v}}_0 \right) \!\right) \\ &\quad +b_S\left( \!\left( w_{1,h},v_0 \right) \!\right) + \sum _{n=1}^{N-1} {\bar{b}}_S^n\left( w_{0,h}^{n,-},\left[ v^n_0 \right] \right) - {\bar{b}}_S^{N}(w_{0,h}^{N,-},v_0^{N,-}) \\ &\quad + \sum _{n=0}^{N-1} {\bar{c}}_{\mu _0}^n(w_{0,h}^{n,+},v_0^{n,+}) + {\bar{c}}^N_{\mu _0}(w_{0,h}^{N,-},v_0^{N,-}) - \sum _{n=1}^{N-1} {\bar{c}}^n_{\mu _0} \left( \left[ w_{0,h}^n \right] ,v_0^{n,-}\right) \\ &\quad +c_{\mu _1} \left( \!\left( w_{0,h},v_0 \right) \!\right) + c_{\mu _1}\left( \!\left( w_{1,h}+{\dot{w}}_{0,h},v_1+{\dot{v}}_0 \right) \!\right) , \end{aligned}$$

(31)

and the linear form (26)

$$\begin{aligned} F_h(v)&= \left( \!\left( f,v_1 \right) \!\right) + (w_{1,h}^{N,+},v_1^{N,-})^N + {\bar{a}}^N(w_{0,h}^{N,+},v_0^{N,-}) -{\bar{b}}^N_S(w_{0,h}^{N,+},v_0^{N,-}) -b_D\left( \!\left( v_1,{g_D} \right) \!\right) \\ &\quad + {\bar{c}}^N_{\mu _0}(w_{0,h}^{N,+},v_0^{N,-}) +\sum _{n=0}^{N-1} {\bar{c}}^n_{D,\mu _0} ({g_D^{n}},v_0^{n,+}) +c_{D,\mu _1} \left( \!\left( {g_D},v_0 \right) \!\right) . \end{aligned}$$

(32)

5 Stability and Consistency of Interior Penalty Space-Time DG Discretization

5.1 Consistency

The first step in the analysis of the space-time DG discretization for the wave equation is to verify its consistency. Based on the properties of the exact solution, as stated in (5), we assume that

$$\begin{aligned} u_0&\in V_0{:}{=}C^0((0,T);{H^1}(\varOmega ))\cap H^2({{\mathscr {T}}}_h)+V_h^k,\\ u_1&\in V_1{:}{=}C^0((0,T);L^2(\varOmega ))\cap H^2({{\mathscr {T}}}_h)+V_h^k \end{aligned}$$

with $u_1={\dot{u}}_0$. The initial solutions satisfy $h_0\in H^1(\varOmega )$, $h_1\in L^2(\varOmega )$. This implies, together with the interface condition (2), that the exact solutions $u_i$ for $i=0,1$ and $n=0,\cdots , N-1$ satisfy the following jump and average relations:

$$\begin{aligned} \ll u_i^n\gg =0, \quad \{\!\{u_i^n\}\!\}=u_i^n&\quad&\text{at} \,\, S \in {\mathscr {F}}_h^{n,I} , \end{aligned}$$

(33)

$$\begin{aligned} \left[ u_i^n \right] =0&\qquad&\text{at} \,\, S \in {\mathscr {F}}_h^{n,T}, \end{aligned}$$

(34)

$$\begin{aligned} \ll h_0\gg =0&\qquad&\text{at} \,\, S \in {\mathscr {F}}_h^{0,T}, \end{aligned}$$

(35)

$$\begin{aligned} \ll A{\overline{\nabla }}u_0^n\gg =0&\quad&\text{at} \,\, S \in {\mathscr {F}}_h^{n,I}. \end{aligned}$$

(36)

Introducing the relations $u_1={\dot{u}}_0$, $u_0\vert _{\partial \varOmega }={g_D}$, $u_0(\cdot ,t_0)=h_0$ and $h_0\vert _{\partial \varOmega }={g_D^0}$ for the exact solution into (25), together with the jump and average relations (33)–(35), we obtain for $(u_0,u_1)\in V_0\times V_1$,

$$\begin{aligned} B_h((u_0,u_1),v)&= \left( \left( \frac{\partial ^2 u_0}{\partial t^2},v_1 \right) \right) + a\left( \!\left( u_0,v_1 \right) \!\right) - b\left( \!\left( u_0,v_1 \right) \!\right) \\ &\quad +(h_1,v_1^{0,+})^0 + {\bar{a}}^0(h_0,v_0^{0,+}) - {\bar{b}}^0_S(h_0,v_0^{0,+}) - b_{D}\left( \!\left( v_1,{g_D} \right) \!\right) \\ &\quad + {\bar{c}}^0_{\mu _0}(h_0,v_0^{0,+}) +\sum _{n=1}^N{\bar{c}}^{n}_{D,\mu _0}({g_D^{n,-}},v^{n,-}_0) +c_{D,\mu _1} \left( \!\left( {g_D},v_0 \right) \!\right), \quad \forall v \in U_h^k. \end{aligned}$$

(37)

Next, we use the following integration by parts formula:

$$\begin{aligned} a\left( \!\left( u_0,v_1 \right) \!\right)&= - \sum _{n=0}^{N-1} \sum _{{\mathscr {K}} \in {\mathscr {T}}_h^{\;n}} \int _{{\mathscr {K}}} v_1 {\overline{\nabla }}_h\cdot (A {\overline{\nabla }}_hu_0) {\mathrm{d}} {\mathscr {K}} + b\left( \!\left( u_0,v_1 \right) \!\right) , \quad \forall v_1 \in V_h^k, \end{aligned}$$

where we used (36). Combined with (1a), namely $\frac{\partial ^2 u_0}{\partial t^2} - {\overline{\nabla }}\cdot (A {\overline{\nabla }}u_0)=f$ on each space-time element ${\mathscr {K}}\in {\mathscr {T}}_h$, we immediately obtain for $(u_0,u_1)\in V_0\times V_1$ the relation

$$\begin{aligned} B_h((u_0,u_1),v) = F_h(v), \quad \forall v \in U_h^k. \end{aligned}$$

(38)

Hence, the space-time DG discretization is consistent, which implies the following Galerkin orthogonality: for $(u_0,u_1)\in V_0\times V_1$, $u_h\in U_h^k$,

$$\begin{aligned} B_h((u_0,u_1)-u_h,v)=0,\;\;\forall v\in U_h^k. \end{aligned}$$

(39)

5.2 Stability of Interior Penalty Space-Time DG Discretization

In this section we will prove the main result, Theorem 1, which states that the bilinear form $B_h(u_h,u_h)$ is bounded from below and above. This result is crucial for the a priori error analysis discussed in Sect. 6. We start with the following lemma.

Lemma 1

For all $u^n_{0,h} \in V_h^{k,n},$ $n = 1,2,\cdots ,N-1,$ and any $\epsilon >0$ the following inequality holds:

$$\begin{aligned}&\frac{1}{2} {\bar{a}}^n\left( \left[ u^n_{0,h} \right] ,\left[ u^n_{0,h} \right] \right) -{\bar{b}}^n\left( \left[ u^n_{0,h} \right] ,\left[ u^n_{0,h} \right] \right) +{\bar{c}}_{\mu _0}^n \left(\left[ u^n_{0,h} \right] ,{u^{n,+}_{0,h}}\right)+ {\bar{c}}_{\mu _0}^n\left( {u^{n,-}_{0,h}},{u^{n,-}_{0,h}}\right) \\ & \geqslant \sum _{S \in {\mathscr {F}}_h^{n,T}} \bigg ( \frac{1}{2} - \epsilon ^2C^2_{\text{tr},S} \bigg ) \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{\,S} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \bigg ( \mu _0 - \frac{1}{\epsilon ^2}\bigg ) \frac{1}{2h}\Big ( \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,+}}\gg }\right\| ^2_{\,{\bar{S}}} \\ & + \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,-}}\gg }\right\| ^2_{\,{\bar{S}}} \Big ) \end{aligned}$$

(40)

with $C_{\text{tr},S}$ the trace constant for faces $S \in {\mathscr {F}}_h^{n,T}$ and $\{\!\{A\}\!\}^{\frac{1}{2}}$ the matrix square root of the average of matrix A.

Proof

Using the definition of the bilinear forms (22b), (22c), (22e) and the average of A, the Schwarz inequality and the arithmetic-geometric mean inequality, we obtain for $n=1, \cdots , N-1$,

$$\begin{aligned}&\frac{1}{2} {\bar{a}}^n\left( \left[ u^n_{0,h} \right] ,\left[ u^n_{0,h} \right] \right) -{\bar{b}}^n\left( \left[ u^n_{0,h} \right] ,\left[ u^n_{0,h} \right] \right) +{\bar{c}}_{\mu _0}^n \left( \left[ u^n_{0,h} \right] ,{u^{n,+}_{0,h}}\right)+ {\bar{c}}_{\mu _0}^n({u^{n,-}_{0,h}},{u^{n,-}_{0,h}}) \\ & \geqslant \sum _{S \in {\mathscr {F}}_h^{n,T}} \frac{1}{2} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^{n} \right] }\right\| ^2_{\,S} - \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{2}h \epsilon ^2 \Big ( \left\| {\,A^{\,\frac{1}{2},L} {\overline{\nabla }}_h\left[ u_{0,h}^{n,L} \right] }\right\| ^2_{\,{\bar{S}}} + \left\| {\,A^{\frac{1}{2},R} {\overline{\nabla }}_h\left[ u_{0,h}^{n,R} \right] }\right\| ^2_{\,{\bar{S}}}\Big ) \\ & - \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{4 h \epsilon ^2} \Big ( \left\| {\,A^{\frac{1}{2},L} \ll { u_{0,h}^{n,+} }\gg }\right\| ^2_{\,{\bar{S}}} + \left\| {\,A^{\frac{1}{2},R} \ll { u_{0,h}^{n,+}}\gg }\right\| ^2_{\,{\bar{S}}} \\ & + \left\| {\,A^{\frac{1}{2},L} \ll { u_{0,h}^{n,-} }\gg }\right\| ^2_{\,{\bar{S}}} + \left\| {\,A^{\frac{1}{2},R} \ll { u_{0,h}^{n,-}}\gg }\right\| ^2_{\,{\bar{S}}}\Big ) \\ & + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{\mu _0}{2h} \Big ( \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll { u_{0,h}^{n,+}} \gg }\right\| ^2_{\,{\bar{S}}} + \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll { u_{0,h}^{n,-}} \gg }\right\| ^2_{\,{\bar{S}}} \Big ) \end{aligned}$$

(41)

with $\epsilon > 0$, arbitrary. The superscripts L and R denote, respectively, the left and right traces at faces ${\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,I,D}$. Using the definition of the average we obtain the following relation for ${\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,I,D}$ and $n=1,2,\cdots , N-1$,

$$\begin{aligned} \left\| {\,A^{\frac{1}{2},L} \ll {u_{0,h}^{n,\pm }}\gg }\right\| ^2_{{\bar{S}}} + \left\| {\,A^{\frac{1}{2},R} \ll {u_{0,h}^{n,\pm }}\gg }\right\| ^2_{{\bar{S}}} = c_S\left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,\pm }}\gg }\right\| ^2_{{\bar{S}}} \end{aligned}$$

(42)

with $c_S=2$ for faces ${\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,I}$ and $c_S=1$ for faces ${\bar{S}} \in \bar{{\mathscr {F}}_h}^{n,D}$. Since the $(d-1)$-dimensional faces ${\bar{S}}\in \bar{{\mathscr {F}}}_h^{n,I,D}$ are boundary faces of the d-dimensional faces $S\in {\mathscr {F}}_h^{n,T}$ we can use the discrete trace theorem, as stated, e.g., in [8] (Lemma 1.46), to bound the norms at ${\bar{S}}\in \bar{{\mathscr {F}}}_h^{n,I,D}$ with norms at $S\in {\mathscr {F}}_h^{n,T}$. Combined with (42) estimate (41) then gives (40) for $n=1,2,\cdots ,N-1$.

Lemma 2

For all $u^{N,-}_{0,h} \in V_h^{k,N}$ and any $\epsilon >0$ the following inequality holds:

$$\begin{aligned}&\frac{1}{2} {\bar{a}}^N(u^{N,-}_{0,h},u^{N,-}_{0,h}) -{\bar{b}}^N(u^{N,-}_{0,h},u^{N,-}_{0,h}) + {\bar{c}}_{\mu _0}^N({u^{N,-}_{0,h}},{u^{N,-}_{0,h}})\\ &\quad \geqslant \sum _{S \in {\mathscr {F}}_h^{N,T}} \frac{1}{2}( 1 - \epsilon ^2C^2_{\text{tr},S} ) \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{\,S} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \bigg ( \mu _0 - \frac{1}{2\epsilon ^2}\bigg ) \frac{1}{h}\left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{N,-}}\gg }\right\| ^2_{\,{\bar{S}}} \end{aligned}$$

(43)

with $C_{\text{tr},S}$ the trace constant for faces $S \in {\mathscr {F}}_h^{n,T}$. An identical relation holds with N replaced by 0 and the superscript $N,-$ replaced by $0,+$.

The proof of Lemma 2 is completely analogous to the proof of Lemma 1.

For the analysis, we also need the following discrete Sobolev inequality, which is a slight modification of [7] (Theorem 2.1).

Lemma 3

There exists a constant $c_I,$ depending on k,  $\vert {\varOmega _h}\vert$ and the tessellation ${\mathscr {T}}_h$ such that for all $v_h\in V_h^k$

$$\begin{aligned} \sum _{{S} \in {{\mathscr {F}}}_h^{n,T}}\left\| {\,v_h}\right\| ^2_S\leqslant c_I\left( \sum _{S \in {\mathscr {F}}_h^{n,T}}\left\| {\,A^{\frac{1}{2}}{\overline{\nabla }}_hv_h}\right\| ^2_S+ \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\frac{1}{h}\left\| {\{\!\{A\}\!\}^{\frac{1}{2}}\ll v_h\gg }\right\| ^2_S\right) . \end{aligned}$$

(44)

The discrete Sobolev inequality, stated in Lemma 3, immediately gives the following estimate.

Lemma 4

For all $u^n_{0,h}\in V_h^{k,n}, n=0,1,\cdots ,N,$ the following bound holds:

$$\begin{aligned}&\quad\frac{1}{c_I} \left( \sum _{S \in {\mathscr {F}}_h^{N,T}}\left\| {\,u_{0,h}^{N,-}}\right\| ^2_{\,{S}} + \sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \left\| {\left[ u_{0,h}^n \right] }\right\| ^2_{\,{S}} + \sum _{S \in {\mathscr {F}}_h^{0,T}} \left\| {\,u_{0,h}^{0,+}}\right\| ^2_{\,{S}} \right) \leqslant \sum _{S \in {\mathscr {F}}_h^{N,T}} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{\,{S}} \\ &\quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| {\,\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{N,-}\gg }\right\| ^2_{\,{\bar{S}}} +\sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{\,{S}} \\ &\quad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{h} \left\| {\,\{\!\{A\}\!\}^{\frac{1}{2}} \ll \left[ u_{0,h}^n \right] \gg }\right\| ^2_{\,{\bar{S}}} \\ &\quad +\sum _{S \in {\mathscr {F}}_h^{0,T}} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{\,{S}} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{\,{\bar{S}}}. \end{aligned}$$

(45)

Next, we provide lower and upper bounds for the bilinear form $B_h(u_h,u_h)$, with $B_h$ defined in (25).

Theorem 1

Given a zero Dirichlet boundary condition $g_D=0$ and a zero source term $f=0$. For $u_h\in U_h^k,$ there exists a constant ${\overline{\alpha }}> 0,$ with ${\overline{\alpha }}{:}{=}\frac{1}{2}\min (1,\frac{1}{2c_I})\min (\frac{1}{4},\frac{1}{2}\mu _0-C_{\text{tr}}^2,\mu _1),$ $\mu _0, \mu _1$ sufficiently large and trace constant $C_{\text{tr}}{:}{=}\max _{n\in \{0,1,\cdots ,N-1\}}\max _{S\in {\mathscr {F}}^{n,T}} C_{\text{tr},S},$ such that the bilinear form $B_h(u_h,u_h)$ satisfies the bounds

$$\begin{aligned}& \qquad \frac{1}{2}{\overline{\alpha }} \left( \sum _{S \in {\mathscr {F}}_h^{N,T}} \Big ( \left\| {\,u_{0,h}^{N,-}}\right\| ^2_{S} + \left\| {\,u_{1,h}^{N,-}}\right\| ^2_{S} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{S}\Big ) + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{N,-}\gg }\right\| ^2_{{\bar{S}}} \right. \\ &\qquad + \sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \bigg ( \left\| {\left[ u_{0,h}^n \right] }\right\| ^2_{S} + \left\| {\left[ u_{1,h}^n \right] }\right\| ^2_{S} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{S}\bigg ) \\ &\qquad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{h} \Big ( \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,+}}\gg }\right\| ^2_{{\bar{S}}} + \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,-}}\gg }\right\| ^2_{{\bar{S}}} \Big ) \\ &\qquad + \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big ( \left\| {\,u_{0,h}^{0,+}}\right\| ^2_{S} + \left\| {\,u_{1,h}^{0,+}}\right\| ^2_{S} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{S}\Big ) + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{{\bar{S}}} \\ &\left. \qquad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \left( \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}\gg }\right\| ^2_{S} + \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{1,h}-{\dot{u}}_{0,h}\gg }\right\| ^2_{S} \right) \right) \\ &\qquad \leqslant B_h(u_h,u_h) \\ &\qquad \leqslant \frac{1}{2{\overline{\alpha }}}(1+\mu _0)(1+C^2_{\text {tr}})^2 \left( \sum _{S \in {\mathscr {F}}_h^{0,T}}\bigg (\, \left\| {\,h_1}\right\| ^2_{S} + \left\| { \,A^{\frac{1}{2}} {\overline{\nabla }}_hh_0}\right\| ^2_{S}\bigg ) + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll h_0\gg }\right\| ^2_{{\bar{S}}}\right) . \end{aligned}$$

(46)

Proof

A. Lower bound for $B_h(u_h,u_h)$. Choose $v=u_h$ in (25), after integrating in time the contributions containing a time derivative and rearranging terms, we obtain

$$\begin{aligned} B_h(u_h,u_h)&= \sum _{S \in {\mathscr {F}}_h^{N,T}} \Big ( \frac{1}{2} \left\| {\,u_{1,h}^{N,-}}\right\| ^2_{S} + \frac{1}{2} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{S} \Big ) + \sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \Big ( \frac{1}{2} \left\| { \left[ u_{1,h}^n \right] }\right\| ^2_{S}\\ &\quad + \frac{1}{2} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{S} \Big ) \\ &\quad + \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big (\frac{1}{2} \left\| {\,u_{1,h}^{0,+}}\right\| ^2_{S} + \frac{1}{2} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{S} \Big )\\ &\quad -\sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}}\int _{{\bar{S}}} \{\!\{A {\overline{\nabla }}_hu_{0,h}^{N,-}\}\!\} \cdot \ll u_{0,h}^{N,-}\gg {\mathrm{d}}{\bar{S}} \\ &\quad -\sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \int _{{\bar{S}}} \{\!\{A {\overline{\nabla }}_h\left[ u_{0,h}^n \right] \}\!\} \cdot \ll \left[ u_{0,h}^n \right] \gg {\mathrm{d}}{\bar{S}}\\ &\quad - \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \int _{{\bar{S}}} \{\!\{A {\overline{\nabla }}_hu_{0,h}^{0,+}\}\!\} \cdot \ll u_{0,h}^{0,+}\gg {\mathrm{d}}{\bar{S}}\\ &\quad + \sum _{n=1}^N \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{\mu _0}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{n,-}\gg }\right\| ^2_{\,{\bar{S}}}\\ &\quad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{\mu _0}{h} \int _{{\bar{S}}} \{\!\{A\}\!\} \ll \left[ u_{0,h}^n \right] \gg \cdot \ll u_0^{n,+}\gg {\mathrm{d}}{\bar{S}} \\ &\quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{\mu _0}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{\,{\bar{S}}}\\ &\quad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \frac{\mu _1}{h}\Big ( \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}\gg }\right\| ^2_{\,{S}} + \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{1,h}-{\dot{u}}_{0,h}\gg }\right\| ^2_{\,{S}} \Big ). \end{aligned}$$

Using Lemmas 1 and 2, we obtain then the estimate

$$\begin{aligned} B_h(u_h,u_h)&\geqslant \sum _{S \in {\mathscr {F}}_h^{N,T}} \Big ( \frac{1}{2} \left\| {\,u_{1,h}^{N,-}}\right\| ^2_{\,{S}} + \frac{1}{2}(1-\epsilon _1^2 C_{\text {tr},S}^2) \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{\,{S}} \Big ) \\ &\quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{N,I,D}} \bigg (\mu _0 - \frac{1}{2\epsilon _1^2}\bigg ) \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{N,-}\gg }\right\| ^2_{\,{{\bar{S}}}} \\ &\quad +\sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \Big (\frac{1}{2} \left\| {\left[ u_{1,h}^n \right] }\right\| ^2_{\,{S}} + \frac{1}{2} (1-\epsilon _1^2 C_{\text {tr},S}^2) \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{\,{S}}\Big ) \\ &\quad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \bigg (\mu _0 - \frac{1}{\epsilon _1^2}\bigg ) \frac{1}{2h} \bigg ( \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,+}}\gg }\right\| ^2_{\,{\bar{S}}} + \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,-}}\gg }\right\| ^2_{\,{\bar{S}}} \bigg ) \\ &\quad + \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big (\frac{1}{2} \left\| {\,u_{1,h}^{0,+}}\right\| ^2_{\,{S}} + \frac{1}{2}(1-\epsilon _1^2 C_{\text{tr},S}^2) \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{\,{S}} \Big ) \\ &\quad +\sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \bigg (\mu _0-\frac{1}{2\epsilon _1^2}\bigg ) \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{\,{\bar{S}}} \\ &\quad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \frac{\mu _1}{h} \Big ( \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}\gg }\right\| ^2_{\,{S}} + \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{1,h}-{\dot{u}}_{0,h}\gg }\right\| ^2_{\,{S}}\Big ). \end{aligned}$$

(47)

Choose $\epsilon _1=\frac{1}{2C_{\text{tr}}^2}$ in (47). Define ${\overline{\alpha }}{:}{=}\frac{1}{2}\min (1,\frac{1}{2c_I})\min (\frac{1}{4},\frac{1}{2}\mu _0-C_{\text{tr}}^2,\mu _1)$, with trace constant $C_{\text{tr}}$ given by $C_{\text {tr}}{:}{=}\max _{n\in \{0,1,\cdots ,N-1\}}\max _{S\in {\mathscr {F}}^{n,T}} C_{\text{tr},S}$. We obtain then after using Lemma 4, and choosing the constants $\mu _0$ and $\mu _1$ large enough, the lower bound

$$\begin{aligned} B_h(u_h,u_h)&\geqslant {\overline{\alpha }} \bigg ( \sum _{S \in {\mathscr {F}}_h^{N,T}} \Big ( \left\| {\,u_{0,h}^{N,-}}\right\| ^2_{\,{S}} +\left\| {\,u_{1,h}^{N,-}}\right\| ^2_{\,{S}} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{\,{S}} \Big ) \\ &\quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{N,-}\gg }\right\| ^2_{\,{{\bar{S}}}} \\ &\quad +\sum _{n=1}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,T}} \big ( \left\| {\left[ \,u_{0,h}^n \right] }\right\| ^2_{\,{S}} + \left\| {\left[ u_{1,h}^n \right] }\right\| ^2_{\,{S}} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ u_{0,h}^n \right] }\right\| ^2_{\,{S}}\big ) \\ &\quad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{h} \bigg ( \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,+}}\gg }\right\| ^2_{\,{\bar{S}}} + \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll {u_{0,h}^{n,-}}\gg }\right\| ^2_{\,{\bar{S}}} \bigg ) \\ &\quad + \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big ( \left\| {\,u_{0,h}^{0,+}}\right\| ^2_{\,{S}} +\left\| {\,u_{1,h}^{0,+}}\right\| ^2_{\,{S}} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{\,{S}} \Big ) \\ &\quad +\sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{\,{\bar{S}}} \\ &\quad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \frac{1}{h} \Big ( \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}\gg }\right\| ^2_{\,{S}} + \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{1,h}-{\dot{u}}_{0,h}\gg }\right\| ^2_{\,{S}} \Big )\bigg ). \end{aligned}$$

(48)

B. Upper bound for $F_h(u_h)$. Choose $v_h=u_h$ in (26). Using the Schwarz, Hölder and arithmetic geometric mean inequalities and the trace inequality, we obtain

$$\begin{aligned} \left| {\,F_h(u_h)}\right|&\leqslant \sum _{S \in {\mathscr {F}}_h^{0,T}} \Bigg ( \frac{1}{2\epsilon _2^2} \left\| {\,h_1}\right\| ^2_{{S}} + \frac{1}{2} \epsilon _2^2 \left\| {\,u_{1,h}^{0,+}}\right\| ^2_{{S}} + \frac{1}{2\epsilon _2^2} \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hh_0}\right\| ^2_{{S}} + \frac{1}{2} \epsilon _2^2 \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+} }\right\| ^2_{{S}} \Bigg ) \\ &\quad +\sum _{S \in {\mathscr {F}}_h^{0,T}} \frac{1}{2} \epsilon _2^2 C_{\text{tr},S}^2 \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{{S}} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{2 \epsilon _2^2} \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll h_0\gg }\right\| ^2_{{\bar{S}}} \\ &\quad + \sum _{S \in {\mathscr {F}}_h^{0,T}} \frac{1}{2\epsilon _2^2} C_{\text{tr},S}^2 \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hh_0}\right\| ^2_{{S}} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \epsilon _2^2 \frac{1}{2h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{{\bar{S}}} \\ &\quad +\sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{\mu _0}{2h} \Big (\epsilon _2^2 \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{{\bar{S}}} + \frac{1}{\epsilon _2^2}\left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll h_0\gg }\right\| ^2_{{\bar{S}}} \Big ). \end{aligned}$$

Choose $\epsilon _2^2 = \frac{{\overline{\alpha }}}{(1+C_{\text {tr}}^2)(1+\mu _0)}$, then we obtain the bound

$$\begin{aligned} \left| {\,F_h(u_h)}\right|&\leqslant \frac{1}{2}{\overline{\alpha }} \left( \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big (\left\| {\,u_{1,h}^{0,+}}\right\| ^2_{S}+\left\| {\,A^{\frac{1}{2}}{\overline{\nabla }}_hu_{0,h}^{0,+}}\right\| ^2_{{S}}\Big ) + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll u_{0,h}^{0,+}\gg }\right\| ^2_{{\bar{S}}} \right) \\ &\quad + \frac{1}{2{\overline{\alpha }}}(1+\mu _0)(1+C^2_{\text{tr}})^2 \left( \sum _{S \in {\mathscr {F}}_h^{0,T}} \Big (\left\| {\,h_1}\right\| ^2_{S}+ \left\| {\,A^{\frac{1}{2}}{\overline{\nabla }}_hh_0}\right\| ^2_{S}\Big ) \right. \\ &\left. \quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{0,I,D}} \frac{1}{h}\left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll h_0\gg }\right\| ^2_{S} \right) . \end{aligned}$$

(49)

Using (24), we can connect the lower bound (48) and the upper bound (49). The terms with norms containing $u_{0,h}$ and $u_{1,h}$ in (49) can be directly balanced with the corresponding terms in (48).

For the a priori error analysis in Sect. 6, we also need bounds on the time derivative of $u_{0,h}$ and $u_{1,h}$, which are given by Theorem 2. Before we state these results we first give some definitions that we need in the subsequent analysis.

Definition 1

The conforming finite element space $V_h^{k,c}$ on ${\mathscr {E}}_h$ is defined as

$$\begin{aligned} V_{h}^{k,c}{:}{=}\{v\in C^0({\mathscr {E}}_h^{\;n}),n=0,1,\cdots ,N-1\;\vert \; v\in P^k({\mathscr {K}}), \forall {\mathscr {K}}\in {\mathscr {T}}_h\}\subset V_h^{k}. \end{aligned}$$

For $n=0,1,\cdots ,N$, the conforming finite element space ${\bar{V}}_{h}^{k,n,c}$ is the restriction of $V_h^{k,c}$ to $\varOmega _h$ at time $t=t_n$, and is defined as

$$\begin{aligned} {\bar{V}}_{h}^{k,n,c}{:}{=}\{v\in C^0({\varOmega _h})\;\vert \; v\in P^k(K), \forall K\in \;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h\}\subset V_h^{k,n}\vert _{\;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h}. \end{aligned}$$

We denote with ${\bar{V}}_{0,h}^{k,n,c}$ the space ${\bar{V}}_{h}^{k,n,c}$ with zero trace at $\partial \varOmega _h$.

We assume that ${\bar{V}}_{h}^{k,n,c}$ satisfies on shape and contact regular meshes for all $s\in \{0,\cdots ,k+1\}$ and for all $v\in H^{s}(\varOmega _h)$ the optimal polynomial approximation

$$\begin{aligned} \inf _{v_h\in {\bar{V}}_{h}^{n,k,c}}\left| {v-v_h}\right| _{m,\varOmega _h}\leqslant Ch^{s-m}\left| {v}\right| _{s,\varOmega }\quad \forall m\in \{0,\cdots ,s\}. \end{aligned}$$

Definition 2

The spatial $L^2$-interpolation operator ${\hat{\pi }}^n_h: L^2({\varOmega _h}) \rightarrow {\bar{V}}_{h}^{k,n,c}$ is defined as

$$\begin{aligned} ({\hat{\pi }}_h^nw(\cdot ,t),v)_{\varOmega _h} = (w(\cdot ,t),v)_{\varOmega _h},\quad \forall v \in {\bar{V}}_{h}^{k,n,c}. \end{aligned}$$

(50)

Correspondingly, we have

$$\begin{aligned} {\hat{\pi }}_h w = {\hat{\pi }}_h^n w(t),\qquad \qquad t\in I_n,\, n=0,1,\cdots ,N-1. \end{aligned}$$

(51)

Lemma 5

(Karakashian and Pascal [18], Thms. 2.2 and 2.3) Let $\;\bar{\!\! {\mathscr {T}}}_h$ be a conforming quasi-uniform polyhedral mesh satisfying the angle condition, namely, there exists a constant $\theta _0>0$ s.t. $h_K/\rho _K\geqslant \theta _0,\; \forall K\in \;\bar{\!\! {\mathscr {T}}}_h,$ where $h_K$ and $\rho _K$ denote, respectively, the diameters of the circumscribed and inscribed balls to K. Then for any $v_h\in {\bar{V}}_h^{k,n}$ there exists a ${\hat{\pi }}^n_h v_h\in {\bar{V}}_h^{k,n,c}$ satisfying

$$\begin{aligned} \sum _{K\in \;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h}\left\| {\,A^\frac{1}{2}{\overline{\nabla }}(v_h-{\hat{\pi }}^n_h v_h)}\right\| _K^2\leqslant C \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll v_h\gg }\right\| ^2_{{\bar{S}}}, \end{aligned}$$

(52)

where C is independent of h and $v_h,$ but may depend on the minimum angle $\theta _0$ in the mesh.

Remark 1

Since the interpolant ${\hat{\pi }}^n_h v_h$ constructs a conforming Lagrangian interpolant using at each mesh point the average value of the DG solution of all elements connected to that mesh point this procedure can also be used for hexahedral elements. For instance by subdividing each hexahedral element into polyhedra, or by directly generating a polyhedral mesh based on the vertices in the mesh. If necessary extra mesh points can be added in this procedure.

Theorem 2

If $u_{0,h},u_{1,h} \in V_h^{k}$ satisfy (24) with a homogeneous Dirichlet boundary condition, namely $g_D=0,$ and zero source term $f=0,$ then the time derivatives of $u_{0,h},$ $u_{1,h}$ satisfy the inequalities

$$\begin{aligned} \left\| {u_{1,h}-{\dot{u}}_{0,h}}\right\| _{{\mathscr {E}}_h}&\leqslant C\left( \sum _{n=0}^{N-1}\sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll u_{1,h}-{\dot{u}}_{0,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2}, \end{aligned}$$

(53)

$$\begin{aligned} \left\| {{\dot{u}}_{1,h}}\right\| _{1,-1,2,{\mathscr {E}}_h}&\leqslant C(1+h) \left( \left\| {\,A^\frac{1}{2}{\overline{\nabla }}_hu_{0,h}}\right\| _{{\mathscr {E}}_h}+ \left( \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll u_{0,h}\gg }\right\| ^2_S\right) ^\frac{1}{2}\right) \end{aligned}$$

(54)

with C a constant independent of $u_{0,h},$ $u_{1,h}$ and h.

Proof

A. Define the bilinear form ${\overline{a}}^n_h(v,w): {\bar{V}}_{0,h}^{k,n,c}\times {\bar{V}}_{0,h}^{k,n,c}\rightarrow {\mathbb {R}}$ with ${\overline{a}}^n_h(v,w){:}{=}(A{\overline{\nabla }}v,{\overline{\nabla }}w)_{\varOmega _h}$ for $n=0,1,\cdots ,N-1$. Consider the auxiliary problem: given $u_{0,h}, u_{1,h}\in V_{0,h}^{k,n}$, find $v_{0,h}(\cdot ,t)\in {\bar{V}}_{0,h}^{k,n,c}$ such that

$$\begin{aligned} {\overline{a}}^n_h(v_{0,h}(\cdot ,t),w)=\big ((t-t_n)(t_{n+1}-t)({\dot{u}}_{0,h}-u_{1,h}),w\big )_{\varOmega _h},\quad \forall w\in {\bar{V}}_{0,h}^{k,n,c},\,t\in I_n. \end{aligned}$$

(55)

Define

$$\begin{aligned} v_0=v_{0,h}(\cdot ,t),\quad t\in I_n, v_{0,h}(\cdot , t)\in {\bar{V}}_{0,h}^{k,n,c}, \end{aligned}$$

and set $v_1=0$. The space-time DG discretization (24) then reduces to: find $u_h\in U_h^k$ such that

$$\begin{aligned} B_h(u_h,v)=a\left( \!\left( {\dot{u}}_{0,h}-u_{1,h},v_0 \right) \!\right) -b\left( \!\left( v_0,{\dot{u}}_{0,h}-u_{1,h} \right) \!\right) =0,\quad \forall v_0\in V_h^{k,c}. \end{aligned}$$

(56)

Next, we use the spatial $L^2$-interpolator ${\hat{\pi }}_h$, given by (51), to write (56) as

$$\begin{aligned}&a\left( \!\left( {\hat{\pi }}_h({\dot{u}}_{0,h}-u_{1,h}),v_0 \right) \!\right) +a\left( \!\left( {\dot{u}}_{0,h}-u_{1,h}-{\hat{\pi }}_h({\dot{u}}_{0,h}-u_{1,h}),v_0 \right) \!\right) \\ & -b\left( \!\left( v_0,{\dot{u}}_{0,h}-u_{1,h} \right) \!\right) =0,\quad \forall v_0\in V_h^{k,c}. \end{aligned}$$

(57)

Using (55) with $w={\hat{\pi }}^n_h({\dot{u}}_{0,h}-u_{1,h})$ and (50)–(51) we can express the first term on the left-hand side of (57) as

$$\begin{aligned} a\left( \!\left( {\hat{\pi }}_h({\dot{u}}_{0,h}-u_{1,h}),v_0 \right) \!\right)&=\sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}(t-t_n)(t_{n+1}-t)\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| ^2_{\varOmega _h}{\mathrm{d}}t. \end{aligned}$$

(58)

Next, using the Schwarz inequality, Lemma 5 we can estimate the second term on the left-hand side of (57) as

$$\begin{aligned}& \quad a\left( \!\left( {\dot{u}}_{0,h}-u_{1,h}-{\hat{\pi }}_h({\dot{u}}_{0,h}-u_{1,h}),v_0 \right) \!\right) \\ &\quad \leqslant C\sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}\left( \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll {\dot{u}}_{0,h}-u_{1,h}\gg }\right\| ^2_{{\bar{S}}}\right) ^\frac{1}{2}\left\| {A^\frac{1}{2}{\overline{\nabla }}v_0}\right\| _{\varOmega _h}{\mathrm{d}}t \\ &\quad \leqslant C\left( \sum _{n=0}^{N-1}\sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll {\dot{u}}_{0,h}-u_{1,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2}\left( \sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| ^2_{\varOmega _h}{\mathrm{d}}t\right) ^\frac{1}{2}, \end{aligned}$$

(59)

where in the last step we used (55) with $w=v_{0,h}(\cdot ,t)$ and Poincare’s theorem, resulting in

$$\begin{aligned} \left\| {A^\frac{1}{2}{\overline{\nabla }}v_0}\right\| _{\varOmega _h}=(t-t_n)(t-t_{n+1})\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| _{\varOmega _h}. \end{aligned}$$

(60)

Using the discrete trace theorem, as stated, e.g., in [8] (Lemma 1.46), and (60), we have for $v_0\in {\bar{V}}_{0,h}^{k,n,c}$ the bound

$$\begin{aligned} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} h^\frac{1}{2}\left\| {\{\!\{A {\overline{\nabla }}_hv_0\}\!\}}\right\| _{{\bar{S}}} \leqslant C\left\| {\,A^\frac{1}{2}{\overline{\nabla }}v_0}\right\| _{\varOmega _h} \leqslant C(t-t_n)(t_{n+1}-t)\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| _{\varOmega _h}. \end{aligned}$$

The third term on the left-hand side of (57) then can be estimated as

$$\begin{aligned}&b\left( \!\left( v_0,{\dot{u}}_{0,h}-u_{1,h} \right) \!\right) \\ & \leqslant C\left( \sum _{n=0}^{N-1}\sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll {\dot{u}}_{0,h}-u_{1,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2}\left( \sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| ^2_{\varOmega _h}{\mathrm{d}}t\right) ^\frac{1}{2}. \end{aligned}$$

(61)

Introducing now (58), (59) and (61) into (57), using the standard inverse estimate

$$\begin{aligned} \frac{1}{C_0}\int _{t_n}^{t_{n+1}}\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| ^2_{\varOmega _h}{\mathrm{d}}t \leqslant \int _{t_n}^{t_{n+1}}(t-t_n)(t_{n+1}-t)\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| ^2_{\varOmega _h}{\mathrm{d}}t \end{aligned}$$

since ${\dot{u}}_{0,h}-u_{1,h}\in V_h^k$ (see, e.g., Thm. 2.2 in [2]), and division of all terms by $\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| _{{\mathscr {E}}_h}=\left\| {{\dot{u}}_{0,h}-u_{1,h}}\right\| _{2,0,2,{\mathscr {E}}_h}$ then gives (53).

B. Choose for each space-time slab ${\mathscr {E}}_h^{\;n}$, $n=0,1, \cdots , N-1$, the test functions as $v_0=0$, $v_1=(t-t_n)(t_{n+1}-t){\tilde{v}}_1$, with ${\tilde{v}}_1(x,t) \in C_0^{\infty }(\varOmega _h)\times P^k(I_n)$ and $g_D=0$, $f=0$. Note, this implies $\ll v_1\gg = 0, \;{\text {for all}}\, S \in {\mathscr {F}}_h^{n,I}, n=0,1, \cdots , N-1$. The function space $C_0^\infty (\varOmega _h)$ is dense in $W_0^{m,p}(\varOmega _h)$, and also in the broken Sobolev space $W_0^{m,p}(\;\bar{\!\! {\mathscr {T}}}_h)$ with zero trace at $\partial \varOmega _h$, hence we can define the negative order Sobolev norm $\left\| {\,v}\right\| _{-m,p,\;\bar{\!\! {\mathscr {T}}}_h}$ for $W_0^{s,p}(\;\bar{\!\! {\mathscr {T}}}_h)$ analogously to (4).

For this choice of test functions, we obtain from (24)

$$\begin{aligned} \left( \!\left( {\dot{u}}_{1,h},v_1 \right) \!\right) + a\left( \!\left( u_{0,h},v_1 \right) \!\right) -b\left( \!\left( v_1,u_{0,h} \right) \!\right) =0. \end{aligned}$$

Applying the Schwarz inequality and using ${\tilde{v}}_1(x,\cdot )\in C_0^\infty (\varOmega _h)$, we obtain then the estimate

$$\begin{aligned}&\sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}(t-t_n)(t_{n+1}-1)({\dot{u}}_{1,h},{\tilde{v}}_1)_{\varOmega _h}{\mathrm{d}}t \\ & \leqslant C_0\left( \sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}}\left\| {A^\frac{1}{2}{\overline{\nabla }}_hu_{0,h}}\right\| _{\bar{{\mathscr {T}}}_h^n} \left\| {\,{\overline{\nabla }}{\tilde{v}}_1}\right\| _{\varOmega _h}{\mathrm{d}}t \right. \\ &\left. \quad +\sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}h^\frac{1}{2}\left\| {{\overline{\nabla }}{\tilde{v}}_1}\right\| _{{\bar{S}}}\;\; \frac{1}{h^\frac{1}{2}} \left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll u_{0,h}\gg }\right\| _{{\bar{S}}}{\mathrm{d}}t\right) . \end{aligned}$$

(62)

Next, we use the continuous trace inequality, e.g., [8, Lemma 1.49], to estimate the ${\tilde{v}}_1(x,\cdot )$ contribution in the second term on the right-hand side as

$$\begin{aligned} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}h^\frac{1}{2} \left\| {{\overline{\nabla }}{\tilde{v}}_1}\right\| _{{\bar{S}}} \leqslant C_1\Big (h\left| {{\tilde{v}}_1}\right| _{2,\varOmega _h}+\left\| {{\overline{\nabla }}{\tilde{v}}_1}\right\| _{\varOmega _h}\Big ). \end{aligned}$$

Since ${\tilde{v}}_1(x,\cdot )\in C_0^\infty (\varOmega _h)$ and $\vert \varOmega _h\vert \leqslant C$ we have $\left| {{\tilde{v}}_1}\right| _{\,2,\varOmega _h} \leqslant C_2$. Taking the supremum of (62) for all ${\tilde{v}}_1(x,\cdot )\in C_0^{\infty }(\varOmega _h)$, with $\left\| {\,{\tilde{v}}_1}\right\| _{1,\varOmega _h} \leqslant 1$ and using a standard inverse estimate in time then gives

$$\begin{aligned}&\quad\frac{1}{C_2}\sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}} \left\| {{\dot{u}}_{1,h}}\right\| _{-1,2,\varOmega _h}{\mathrm{d}}t \\ &\quad \leqslant \sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}}(t-t_n)(t_{n+1}-t) \sup _{\begin{array}{c} {\tilde{v}}_1\ne 0,\forall {\tilde{v}}_1(x,\cdot ) \in C_0^{\infty }(\varOmega _h),\\ \left\| {\,{\tilde{v}}_1}\right\| _{\,1,\varOmega _h} \leqslant 1 \end{array} } ({\dot{u}}_{1,h},{\tilde{v}}_1)_{\varOmega _h}{\mathrm{d}}t \\ &\quad \leqslant C_0C_1(1+h) \left( \left( \sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}} \left\| {\,A^\frac{1}{2}{\overline{\nabla }}_hu_{0,h}}\right\| ^2_{\bar{{\mathscr {T}}}_h^n} {\mathrm{d}}t\right) ^\frac{1}{2}\right. \\ &\left. \quad + \left( \sum _{n=0}^{N-1}\sum _{S\in {\mathscr {F}}^{n,I,D}_h} \frac{1}{h}\left\| {\{\!\{A\}\!\}^\frac{1}{2}\ll u_{0,h}\gg }\right\| ^2_S\right) ^\frac{1}{2}\right) . \end{aligned}$$

Finally, multiplying both sides with $C_2$ gives (54).

Corollary 1

If $u_{0,h},u_{1,h} \in V_h^{k}$ satisfy (24) with a homogeneous Dirichlet boundary condition, namely $g_D=0$, and zero source term $f=0$, then the time derivatives of $u_{0,h}$, $u_{1,h}$ satisfy the inequalities

$$\begin{aligned} \left\| {u_{1,h}-{\dot{u}}_{0,h}}\right\| _{{\mathscr {E}}_h}&\leqslant C, \end{aligned}$$

(63)

$$\begin{aligned} \left\| {{\dot{u}}_{1,h}}\right\| _{1,-1,2,{\mathscr {E}}_h}&\leqslant C(1+h) \end{aligned}$$

(64)

with C a constant independent of $u_{0,h}$, $u_{1,h}$ and h.

Proof

Using the upper bound for the right-hand side in (53), provided by Theorem 1, immediately gives (63). The same applies for the second term on the right-hand side of (54). For the first term on the right-hand side define

$$\begin{aligned} q_h^2(t)=\sum _{K\in \bar{{\mathscr {T}}}_h^n}\left\| {A^\frac{1}{2}{\overline{\nabla }}u_{0,h}(\cdot ,t)}\right\| _K^2\quad \text{with }t\in I_n. \end{aligned}$$

Theorem  1 then gives the following upper bounds:

$$\begin{aligned} q_h^2(t_n^+) \leqslant C_1\quad \text{and }\quad q_h^2(t_{n+1}^-) \leqslant C_2 \quad \text{for }n=0,1,\cdots ,N-1 \end{aligned}$$

with constants $C_1, C_2$. Here, we used that ${\mathscr {T}}_h^{n,T}\subseteq \bar{{\mathscr {T}}}_h^n$ and the fact that Theorem  1 is valid for any time level $t=t_n$, $n=0,1,\cdots ,N$. Since $u_{0,h}\in V_h^k$ is a polynomial in space and in time in each space-time element ${\mathscr {K}}\in {\mathscr {T}}^{\,\;n}_h$ this implies that $q_h^2(t)\in P^{2k}(I_n)$. This, together with the bounds on $q_h^2(t)$ at times $t=t_n^+$ and $t=t_{n+1}^-$, implies that $q_h^2(t)$ is continuous and bounded on ${\bar{I}}_n$. Hence,

$$\begin{aligned} \left\| {\,A^\frac{1}{2}{\overline{\nabla }}_hu_{0,h}}\right\| ^2_{{\mathscr {E}}_h}=\sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}\sum _{K\in \bar{{\mathscr {T}}}_h^n}\left\| {A^\frac{1}{2}{\overline{\nabla }}u_{0,h}(\cdot ,t)}\right\| _K^2{\mathrm{d}}t=\sum _{n=0}^{N-1}\int _{t_n}^{t_{n+1}}q_h^2(t){\mathrm{d}}t \leqslant C, \end{aligned}$$

which completes the proof of the bound (64).

6 A Priori Error Analysis

In this section, we will provide an a priori error analysis of the space-time IP-DG discretization of the second-order wave equation (24). The main tool we use is the backward in time error analysis and the bounds stated in Theorems 1, 2 and Corollary 1. Before we state our main result, we first give some definitions.

Definition 3

(Riesz projection) For $n=0,1, \cdots , N$, the spatial $H^1$-interpolation operator ${\bar{\pi }}^n_h: H^1_0({\varOmega _h}) \rightarrow {\bar{V}}_{0,h}^{k,n,c}$ is defined as

$$\begin{aligned} ({\overline{\nabla }}{\bar{\pi }}_h^nw(\cdot ,t),{\overline{\nabla }}v)_{\varOmega _h} = ({\overline{\nabla }}w(\cdot ,t),{\overline{\nabla }}v)_{\varOmega _h},\quad \forall v \in {\bar{V}}_{0,h}^{k,n,c}. \end{aligned}$$

(65)

Correspondingly, we have

$$\begin{aligned} \pi _h w = {\bar{\pi }}_h^n w(t)\quad \text{for}\ t\in I_n,\, n=0,1,\cdots ,N-1. \end{aligned}$$

(66)

In the a priori error analysis, we will use the following bounds on the error in the Riesz projection.

Lemma 6

Let $\;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h$, $n=0,1,\cdots ,N$, be shape and contact regular meshes. Then for $w\in H^{k+1}(\varOmega _h)\cap H^1_0(\varOmega _h)$ with $k \geqslant 1$, the Riesz projection ${\bar{\pi }}^n_hw$, given by (65), satisfies

$$\begin{aligned} \left\| {w-{\bar{\pi }}^n_hw}\right\| _{\varOmega _h}+h\left\| {{\overline{\nabla }}(w-{\bar{\pi }}^n_hw)}\right\| _{\varOmega _h}&\leqslant Ch^{k+1}\left\| {w}\right\| _{k+1,\varOmega _h}, \end{aligned}$$

(67)

$$\begin{aligned} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\left\| {w-{\bar{\pi }}^n_hw}\right\| _{{\bar{S}}}&\leqslant Ch^{k+\frac{1}{2}}\left\| {w}\right\| _{k+1,\varOmega _h}, \end{aligned}$$

(68)

$$\begin{aligned} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\left\| {\{\!\{{\overline{\nabla }}w-{\bar{\pi }}^n_hw\}\!\}}\right\| _{{\bar{S}}}&\leqslant Ch^{k-\frac{1}{2}}\left\| {w}\right\| _{k+1,\varOmega _h}. \end{aligned}$$

(69)

A proof for error estimate (67) can be found in, e.g., [28, Lemma 1.1]. Error estimates (68)–(69) are a direct consequence of (67) using the continuous trace inequality, see, e.g., [8, Lemma 1.49 and also Lemma 1.59].

Definition 4

For $n=0,1, \cdots , N-1$, the temporal interpolation operator $J_h: C^0({\bar{I}}_n) \rightarrow P^k({\bar{I}}_n)$ is defined as

$$\begin{aligned} \int _{I_n}(J_h w)\, v {\mathrm{d}}t&= \int _{I_n} wv \,{\mathrm{d}}t, \quad \forall v \in P^{k-1}(I_n), \end{aligned}$$

(70a)

$$\begin{aligned} (J_h w)^{n+1,-}&= w^{n+1,-}. \end{aligned}$$

(70b)

Lemma 7

For $w\in H^{k+1}(I_n)$ with $k\geqslant 1$ the temporal projection $J_hw$ satisfies

$$\begin{aligned} \left\| {\,w-J_hw}\right\| _{\,I_n}\leqslant C(\Delta t)^{k+1}\left| {w}\right| _{\,k+1,\infty ,I_n}. \end{aligned}$$

(71)

A proof for error estimate (71) can be found in [28] in the proof of Theorem 12.1.

Definition 5

For $u_h\in U_h^{k,N-1}$, with $u_h^{N,-}=u_h\vert _{t^{N,-}}$, the DG norm at time $t=t_N$ is defined as

$$\begin{aligned} {\left| \left| \left| \,u_h^{N,-} \right| \right| \right| }^2&= \sum _{S \in {\mathscr {F}}_h^{N,T}}\Big ( \left\| {\,u_{0,h}^{N,-}}\right\| ^2_{S} + \left\| {\,u_{1,h}^{N,-}}\right\| ^2_{S} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_hu_{0,h}^{N,-}}\right\| ^2_{S}\Big ) \\ &\quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}}\ll u_{0,h}^{N,-}\gg }\right\| ^2_{{\bar{S}}}. \end{aligned}$$

(72)

Next, we state our main result, which provides an error estimate for the space-time IP-DG discretization (24).

Theorem 3

Let $u\in C^0((0,T);H_0^1(\varOmega ))\cap H^{k+1}({\mathscr {T}}_h)$, with time derivative ${\dot{u}}\in C^0((0,T);H_0^1(\varOmega ))\cap H^{k+1}({\mathscr {T}}_h)$, solve the second-order wave equation (1) with a homogeneous Dirichlet boundary condition. The error at time $t=t_N$ in the solution of the space-time IP-DG discretization of the second-order wave equation (24), given by $u_h\in U_h^k$ with $k \geqslant 1$, can be bounded as

$$\begin{aligned} {\left| \left| \left| \,(u,{\dot{u}})^{N,-}-u_h^{N,-} \right| \right| \right| } < C \big (h^k+ \varDelta t^{k}\big ) \left\| {u}\right\| _{\infty ,k+1,2,{\mathscr {E}}_h} \end{aligned}$$

with mesh size $h=\max _{K \in \;\bar{\!\! {\mathscr {T}}}_h} h_K$ and time step $\Delta t=\max _{n\in \{0,\cdots ,N-1\}}\Delta t_n$.

Proof

A. Split the error into two parts $\rho _h = J_h\pi _h u - u$ and $\theta _h = u_h - J_h\pi _h u$. Next, using (30), we define the discrete dual problem

$$\begin{aligned} B_h(v,z_h)&= (v_1^{N,-}, \theta _{1,h}^{N,-})^N + {\bar{a}}^N(v_0^{N,-},\theta _{0,h}^{N,-}) - {\bar{b}}^N_S(v_0^{N,-},\theta _{0,h}^{N,-}) +{\bar{c}}^N_{\mu _0}(v_0^{N,-},\theta _{0,h}^{N,-}). \end{aligned}$$

(73)

Choose $v=\theta _h$ in (73) then, analogously to Lemma 2 and using Lemma 3, we obtain for $(\theta _h,z_h) \in U_h^k \times U_h^k$ the estimate

$$\begin{aligned} B_h(\theta _h,z_h)& \geqslant \beta \left( \sum _{S \in {\mathscr {F}}_h^{N,T}} \Big ( \left\| {\,\theta _{0,h}^{N,-}}\right\| ^2_{S}+ \left\| {\,\theta _{1,h}^{N,-}}\right\| ^2_{S} + \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h\theta _{0,h}^{N,-}}\right\| ^2_{{S}}\Big ) \right. \\ &\left. \quad + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll \theta _{0,h}^{N,-}\gg }\right\| ^2_{{\bar{S}}} \right) \\ &=\beta {\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2 \end{aligned}$$

(74)

with $\beta = \frac{1}{2}\min (\frac{1}{2},\mu _0-2C_{\text {tr}}^N)\min (1,\frac{1}{C_p}) \geqslant \beta _0 > 0$, with $C_{\text {tr}}^N{:}{=}\max _{S\in {\mathscr {F}}^{N-1,T}} C_{\text {tr},S}$ the maximum trace coefficient for the faces $S \in {\mathscr {F}}_h^{N-1,T}$. Next, we use the orthogonality relation for $B_h$ (39)

$$\begin{aligned} B_h(\theta _h,z_h) = B_h(u_h-J_h \pi _h u,z_h) = B_h(u-J_h \pi _h u,z_h), \quad \forall z_h \in U_h^k \times U_h^k, \end{aligned}$$

and also the relation $u-J_h \pi _h u = u - \pi _h u + \pi _h u - J_h \pi _h u$ to obtain the estimate

$$\begin{aligned}&\beta {\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2 \leqslant B_h(u-\pi _h u , z_h) + B_h(\pi _h u - J_h \pi _h u, z_h), \quad \forall z_h \in U_h^k \times U_h^k. \end{aligned}$$

(75)

B. Using the time integrated by parts form of $B_h$ (31) the upper bound in (75) can be written in terms of the interpolation errors and the discrete dual solution $z_h$ as

$$\begin{aligned} \beta {\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2& \leqslant - \left( \!\left( u_1 - \pi _h u_1,{\dot{z}}_{1,h} \right) \!\right) - \sum _{n=1}^{N-1} \left( (u_1-\pi _h u_1)^{n,-},\left[ z_{1,h}^n \right] \right) ^n \\ &\quad + \left( (u_1-\pi _h u_1)^{N,-},z_{1,h}^{N,-}\right) ^{N} \\ &\quad + a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) -a\left( \!\left( u_1-\pi _h u_1,z_{0,h} \right) \!\right) \\ &\quad -\sum _{n=1}^{N-1} {\bar{a}}^n\left( (u_0-\pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) \\ &\quad + {\bar{a}}^{N}((u_0-\pi _h u_0)^{N,-},z_{0,h}^{N,-}) - b_S\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) \\ &\quad + b_S\left( \!\left( u_1-\pi _h u_1,z_{0,h} \right) \!\right) +\sum _{n=1}^{N-1} {\bar{b}}_S^n \left( (u_0 - \pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) \\ &\quad - {\bar{b}}_S^{N}((u_0-\pi _h u_0)^{N,-},z_{0,h}^{N,-}) +\sum _{n=0}^{N-1}{\bar{c}}_{\mu _0}^n ((u_0-\pi _hu_0)^{n,+},z_{0,h}^{n,+}) \\ &\quad + {\bar{c}}_{\mu _0}^N ((u_0-\pi _hu_0)^{N,-},z_{0,h}^{N,-}) - \sum _{n=1}^{N-1} {\bar{c}}_{\mu _0}^n \left( \left[ (u_0-\pi _hu_0)^n \right] ,z_{0,h}^{n,-}\right) \\ &\quad +c_{\mu _1} \left( \!\left( u_0-\pi _h u_0,z_{0,h} \right) \!\right) + c_{\mu _1} \left( \!\left( u_1{+}{\dot{u}}_0-\pi _h(u_1{+}{\dot{u}}_0),z_{1,h}{+}{\dot{z}}_{0,h} \right) \!\right) \\ &\quad - \left( \!\left( \pi _h u_1 - J_h \pi _h u_1, {\dot{z}}_{1,h} \right) \!\right) \\ &\quad - \sum _{n=1}^{N-1} \left( (\pi _h u_1 -J_h \pi _h u_1)^{n,-}, \left[ z_{1,h}^n \right] \right) ^n + ((\pi _h u_1 - J_h \pi _h u_1)^{N,-}, z_{1,h}^{N,-})^{N} \\ &\quad + a\left( \!\left( \pi _h u_0 - J_h \pi _h u_0, z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) - a\left( \!\left( \pi _h u_1-J_h \pi _h u_1, z_{0,h} \right) \!\right) \\ &\quad -\sum _{n=1}^{N-1} {\bar{a}}^n \left( ( \pi _h u_0 - J_h \pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) + {\bar{a}}^{N}((\pi _h u_0 - J_h \pi _h u_0)^{N,-},z_{0,h}^{N,-}) \\ &\quad - b_S\left( \!\left( \pi _h u_0 - J_h \pi _h u_0,z_{1,h} -{\dot{z}}_{0,h} \right) \!\right) + b_S\left( \!\left( \pi _h u_1 - J_h \pi _h u_1, z_{0,h} \right) \!\right) \\ &\quad + \sum _{n=1}^{N-1} {\bar{b}}_S^n \left( (\pi _h u_0 - J_h \pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) - {\bar{b}}_S^{N} ((\pi _h u_0 - J_h \pi _h u_0)^{N,-},z_{0,h}^{N,-}) \\ &\quad +\sum _{n=0}^{N-1}{\bar{c}}_{\mu _0}^n \left( (\pi _h u_0-J_h\pi _hu_0)^{n,+},z_{0,h}^{n,+}\right) + {\bar{c}}_{\mu _0}^N ((\pi _hu_0-J_h\pi _hu_0)^{N,-},z_{0,h}^{N,-}) \\ &\quad - \sum _{n=1}^{N-1} {\bar{c}}_{\mu _0}^n \left( \left[ (\pi _hu_0-J_h\pi _hu_0)^n \right] ,z_{0,h}^{n,-}\right) + c_{\mu _1} \left( \!\left( \pi _hu_0-J_h\pi _h u_0,z_{0,h} \right) \!\right) \\ &\quad + c_{\mu _1} \left( \!\left( \pi _h(u_1{+}{\dot{u}}_0)-J_h \pi _h(u_1{+}{\dot{u}}_0),z_{1,h}{+}{\dot{z}}_{0,h} \right) \!\right) =:\sum _{i=1}^{32} E_i. \end{aligned}$$

(76)

Many terms in (76) are zero due to the interpolants (66) and (70b).

• (i) Since $\int _{I_n}(J_hw-w)v\,{\mathrm{d}}t = 0, \, {\text {for all}}\, v \in P^{k-1}(I_n)$ we have $E_{17}=0$.

• (ii) From condition (70b), $(J_hw)^{n,-} = w^{n,-}$ for $n=1,\cdots , N$ we obtain $E_{18}=E_{19}=E_{22}=E_{23}=E_{26}=E_{27}=E_{29}=0$.

• (iii) Since $u_0(\cdot ,t),u_1(\cdot ,t) \in H^1_0({\varOmega _h})$ and $\pi _h u_0(\cdot ,t), \pi _h u_1(\cdot ,t) \in {\bar{V}}_h^{k,n,c}$ we have $\ll u_0-\pi _h u_0\gg =0$ and $\ll u_1-\pi _h u_1\gg =0$ at faces $S\in \sum _{S \in {\mathscr {F}}_h^{n,I,D}}$, $n=0,1,\cdots ,N-1$ and at faces ${\bar{S}}\in \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}$, $n=0,1,\cdots ,N$. This implies that in $E_8$, $E_9$ and $E_{24}$, $E_{25}$ we can replace $b_S\left( \!\left( u,v \right) \!\right)$ with $b\left( \!\left( u,v \right) \!\right) \,$. Similarly, in $E_{10}$, $E_{11}$ we have ${\bar{b}}^n_S(u,v)={\bar{b}}^n(u,v)$ for $n=1,\cdots ,N$. Also, we have $E_{12}=E_{13}=E_{14}=E_{15}=E_{16}=E_{28}=E_{29}=E_{30}=E_{31}=E_{32}=0$.

Collecting the non-zero terms in (76) gives

$$\begin{aligned} \beta {\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2&\leqslant -\left( \!\left( u_1-\pi _h u_1, {\dot{z}}_{1,h} \right) \!\right) - \sum _{n=1}^{N-1} \left( (u_1-\pi _h u_1)^{n,-},\left[ z_{1,h}^n \right] \right) ^n \\ &\quad + ((u_1-\pi _h u_1)^{N,-},z_{1,h}^{N,-})^{N} \\ &\quad + a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) -a\left( \!\left( u_1-\pi _h u_1,z_{0,h} \right) \!\right) \\ &\quad -\sum _{n=1}^{N-1} {\bar{a}}^n\left( (u_0-\pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) \\ &\quad + {\bar{a}}^{N}((u_0-\pi _h u_0)^{N,-},z_{0,h}^{N,-}) - b\left( \!\left( u_0-\pi _h u_0,z_{1,h}- {\dot{z}}_{0,h} \right) \!\right) \\ &\quad + b\left( \!\left( u_1-\pi _h u_1,z_{0,h} \right) \!\right) \\ &\quad + \sum _{n=1}^{N-1} {\bar{b}}^n \left( (u_0-\pi _h u_0)^{n,-},\left[ z_{0,h}^n \right] \right) - {\bar{b}}^{N}((u_0-\pi _h u_0)^{N,-},z_{0,h}^{N,-}) \\ &\quad + a\left( \!\left( \pi _h u_0 - J_h \pi _h u_0, z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) \\ &\quad - a\left( \!\left( \pi _h u_1-J_h \pi _h u_1,z_{0,h} \right) \!\right) - b\left( \!\left( \pi _h u_0 - J_h \pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) \\ &\quad + b\left( \!\left( \pi _h u_1-J_h \pi _h u_1,z_{0,h} \right) \!\right) . \end{aligned}$$

(77)

C. Next, we provide estimates for some of the terms in (77). The remaining terms are simple applications of the Schwarz and Hölder inequalities.

• i) Assume that $\left\| {u_1-\pi _h u_1}\right\| _{1,{\varOmega _h}} > 0$, then using the fact that $\phi \in C_0^{\infty }({\varOmega _h})$ is dense in $H_0^1({\varOmega _h})$ we obtain

  $$\begin{aligned} \left( \!\left( u_1-\pi _h u_1, {\dot{z}}_{1,h} \right) \!\right)&= \sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}} \frac{(u_1-\pi _h u_1, {\dot{z}}_{1,h})_{{\varOmega _h}}}{\left\| {\,u_1-\pi _h u_1}\right\| _{1,{\varOmega _h}}} \left\| {\,u_1-\pi _h u_1}\right\| _{1,{\varOmega _h}} \, {\mathrm{d}}t \\ &\leqslant \sum _{n=0}^{N-1} \int _{t_n}^{t_{n+1}} \sup _{\scriptsize{\begin{array}{c} \phi \ne 0,\forall \phi \in C_0^{\infty }(\varOmega _h),\\ \left\| {\,\phi }\right\| _{\,1,\varOmega _h}\leqslant 1 \end{array}} }(\phi ,{\dot{z}}_{1,h})_{{\varOmega _h}} \left\| {\,u_1-\pi _h u_1}\right\| _{1,{\varOmega _h}} \, {\mathrm{d}}t \\ &\leqslant \left\| {\,{\dot{z}}_{1,h}}\right\| _{1,-1,2,{\mathscr {E}}_h} \left\| {\,u_1-\pi _h u_1}\right\| _{\infty ,1,2,{\mathscr {E}}_h}. \end{aligned}$$

• ii) Using the $L^2$ interpolation (66), the term $a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right)$ can be split into

  $$\begin{aligned} a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right)&=a\left( \!\left( u_0-\pi _h u_0,{\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h}) \right) \!\right) \\ &\quad +a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h}-{\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h}) \right) \!\right) . \end{aligned}$$

  (78)

  Since ${\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h})\in V_h^{k,c}$ the Riesz projection (66) implies that the first term on the right-hand side of (78) is zero. For the second term on the right-hand side we use Lemma 5, resulting in the estimate

  $$\begin{aligned}&\Big \vert a\left( \!\left( u_0-\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) \Big \vert \\ & \leqslant C\left\| {\,A^\frac{1}{2}{\overline{\nabla }}_h(u_0-\pi _h u_0)}\right\| _{{\mathscr {E}}_h}\left( \sum _{n=0}^{N-1}\sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\,\{\!\{A\}\!\}^\frac{1}{2}\ll z_{1,h}-{\dot{z}}_{0,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2}. \end{aligned}$$

  Analogously, we obtain

  $$\begin{aligned}&\Big \vert a\left( \!\left( u_1-\pi _h u_1,z_{0,h} \right) \!\right) \Big \vert \\ & \leqslant C\left\| {\,A^\frac{1}{2}{\overline{\nabla }}_h(u_1-\pi _h u_1)}\right\| _{{\mathscr {E}}_h}\left( \sum _{n=0}^{N-1}\sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\,\{\!\{A\}\!\}^\frac{1}{2}\ll z_{0,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2},\\ &\Big \vert {\bar{a}}^N((u_0-\pi _h u_0)^{N-1},z_{0,h}^{N,-})\Big \vert \\ & \leqslant C\left\| {\,A^\frac{1}{2}{\overline{\nabla }}_h(u_0-\pi _h u_0)^{N,-}}\right\| _{\;\bar{\!\! {\mathscr {T}}}^{\;N}_h}\left( \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}}\frac{1}{h} \left\| {\,\{\!\{A\}\!\}^\frac{1}{2}\ll z_{0,h}^{N,-}\gg }\right\| ^2_{{\bar{S}}}\right) ^\frac{1}{2},\\ &\Big \vert \sum _{n=1}^{N-1}{\bar{a}}^n\left( (u_0-\pi _h u_0)^{n,-},\left[ z_{0,h}^{n} \right] \right) \Big \vert \\ & \leqslant C\left( \sum _{n=1}^{N-1}\left\| {\,A^\frac{1}{2}{\overline{\nabla }}_h(u_0-\pi _h u_0)^{n,-}}\right\| ^2_{\;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h}\right) ^\frac{1}{2}\left( \sum _{n=0}^{N-1}\sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}\frac{1}{h} \left\| {\,\{\!\{A\}\!\}^\frac{1}{2}\ll \left[ z_{0,h}^{n} \right] \gg }\right\| ^2_{{\bar{S}}}\right) ^\frac{1}{2}. \end{aligned}$$

• iii) The term $a\left( \!\left( \pi _h u_0-J_h\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right)$ is estimated as

  $$\begin{aligned}&\Big \vert a\left( \!\left( \pi _h u_0-J_h\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h} \right) \!\right) \Big \vert \\ & \leqslant \Big \vert a\left( \!\left( \pi _h u_0-J_h\pi _h u_0,{\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h}) \right) \!\right) \Big \vert \\ & +\Big \vert a\left( \!\left( \pi _h u_0-J_h\pi _h u_0,z_{1,h}-{\dot{z}}_{0,h}-{\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h}) \right) \!\right) \Big \vert \\ & \leqslant \left\| {{\overline{\nabla }}_h\cdot (A {\overline{\nabla }}_h(\pi _h u_0-J_h\pi _hu_0))}\right\| _{{\mathscr {E}}_h} \left\| {z_{1,h}-{\dot{z}}_{0,h}}\right\| _{{\mathscr {E}}_h} \\ & +C\sum _{n=0}^{N-1}\left\| {{\overline{\nabla }}_h(\pi _h u_0-J_h\pi _h u_0)}\right\| _{{\mathscr {E}}_h^{\;n}}\left( \sum _{S \in {\mathscr {F}}_h^{n,I,D}}\frac{1}{h} \left\| {\,\{\!\{A\}\!\}^\frac{1}{2}\ll z_{1,h}-{\dot{z}}_{0,h}\gg }\right\| ^2_{S}\right) ^\frac{1}{2}. \end{aligned}$$

  Here, the first term on the right-hand side is integrated by parts in space and we used $\pi _hu_0(x,\cdot ),{\hat{\pi }}_h(z_{1,h}-{\dot{z}}_{0,h})\in {\bar{V}}^{k,n,c}_{0,h}$ and the Schwarz inequality. For the second term, we used Lemma 5.

D. Combining all terms we obtain the following estimate for ${\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2$:

$$\begin{aligned}& \quad \beta {\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }^2 \\ &\quad \leqslant C \bigg ( \left\| {u_1-\pi _h u_1}\right\| ^2_{\infty ,1,2,{\mathscr {E}}_h} + \sum _{n=1}^N \left\| {(u_1-\pi _h u_1)^{n,-}}\right\| ^2_{\varOmega _h} \\ &\qquad +\left\| {A^\frac{1}{2}{\overline{\nabla }}_h(u_0-\pi _hu_0)}\right\| ^2_{{\mathscr {E}}_h}+\left\| {A^\frac{1}{2}{\overline{\nabla }}_h(u_1-\pi _hu_1)}\right\| ^2_{{\mathscr {E}}_h} \\ &\qquad + \sum _{n=1}^{N} \left\| {A^\frac{1}{2}{\overline{\nabla }}_h(u_0-\pi _h u_0)^{n,-}}\right\| ^2_{\;\bar{\!\! {\mathscr {T}}}^{\;\,n}_h} + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}}h\Big (\left\| {\{\!\{{\overline{\nabla }}_h(u_0-\pi _h u_0)\}\!\}}\right\| ^2_S \\ &\qquad + \left\| {\{\!\{{\overline{\nabla }}_h(u_1-\pi _h u_1)\}\!\}}\right\| ^2_S\Big ) \\ &\qquad + \sum _{n=1}^{N} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}}h \left\| {\{\!\{{\overline{\nabla }}_h(u_0-\pi _h u_0)^{n,-}\}\!\}}\right\| ^2_{{\bar{S}}} + \left\| {{\overline{\nabla }}_h\cdot (A^\frac{1}{2}{\overline{\nabla }}_h(\pi _h u_0-J_h\pi _h u_0))}\right\| ^2_{{\mathscr {E}}_h} \\ &\qquad +\left\| {A^\frac{1}{2}{\overline{\nabla }}_h(\pi _h u_0 - J_h \pi _h u_0)}\right\| ^2_{{\mathscr {E}}_h} +\left\| {A^\frac{1}{2}{\overline{\nabla }}_h(\pi _h u_1 - J_h \pi _h u_1)}\right\| ^2_{{\mathscr {E}}_h} \\ &\qquad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}}h\Big (\left\| {\{\!\{{\overline{\nabla }}_h(\pi _h u_0-J_h\pi _h u_0)\}\!\}}\right\| ^2_S + \left\| {\{\!\{{\overline{\nabla }}_h(\pi _hu_1-J_h\pi _h u_1)\}\!\}}\right\| ^2_S\Big ) \bigg )^{\frac{1}{2}} \\ &\qquad \times \bigg ( \left\| {{\dot{z}}_{1,h}}\right\| ^2_{1,-1,2,{\mathscr {E}}} + \left\| {z_{1,h}-{\dot{z}}_{0,h}}\right\| ^2_{{\mathscr {E}}_h}+ \sum _{n=1}^{N-1} \left\| {\left[ z_{1,h}^n \right] }\right\| ^2_{\varOmega _h}+\left\| {z_{1,h}^{N,-}}\right\| _{\varOmega _h}^2 + \sum _{n=1}^{N-1} \left\| {A^{\frac{1}{2}} {\overline{\nabla }}_h\left[ z_{0,h}^n \right] }\right\| ^2_{{\varOmega _h}} \\ &\qquad + \sum _{n=0}^{N-1} \sum _{S \in {\mathscr {F}}_h^{n,I,D}} \Big ( \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll z_{1,h}-{\dot{z}}_{0,h}\gg }\right\| ^2_{S} + \frac{1}{h} \left\| { \{\!\{A\}\!\}^{\frac{1}{2}} \ll z_{0,h}\gg }\right\| ^2_{S}\Big ) \\ &\qquad + \sum _{n=1}^{N-1} \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{n,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll \left[ z_{0,h}^n \right] \gg }\right\| ^2_{{\bar{S}}} + \sum _{{\bar{S}} \in \bar{{\mathscr {F}}}_h^{\;N,I,D}} \frac{1}{h} \left\| {\{\!\{A\}\!\}^{\frac{1}{2}} \ll z_{0,h}^{N,-}\gg }\right\| ^2_{{\bar{S}}} \bigg ) ^{\frac{1}{2}}. \end{aligned}$$

(79)

All terms in (79) containing norms of $z_h$ can be bounded using Theorem 1 and Corollary 1, applied to the backward problem (30). Using the interpolation error estimates given by Lemmas 6 and 7, it is straightforward to bound the different interpolation error terms in (79), which then gives a bound for ${\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }$. For the bound on ${\left| \left| \left| \rho _h^{N,-} \right| \right| \right| }$, we use that $(\pi _hu-J_h\pi _hu)(x,t^{N,-})=0$, which follows directly from the definition of $J_h$ in (70b), and also the continuity of $\pi _hu(x,t^{N,-})$, resulting in

$$\begin{aligned} {\left| \left| \left| \rho _h^{N,-} \right| \right| \right| }^2= & {} \sum _{K\in \;\bar{\!\! {\mathscr {T}}}_h^N}\Big ( \left\| {\,(u_0-\pi _hu_0)^{N,-}}\right\| ^2_{K} + \left\| {\,(u_1-\pi _h u_1)^{N,-}}\right\| ^2_{K}\\ &+ \left\| {\,A^{\frac{1}{2}} {\overline{\nabla }}_h(u_0-\pi _hu_0)^{N,-}}\right\| ^2_{K}\Big ), \end{aligned}$$

which can be estimated using Lemma 6. Combining the bounds for ${\left| \left| \left| \theta _h^{N,-} \right| \right| \right| }$ and ${\left| \left| \left| \rho _n^{N,-} \right| \right| \right| }$ gives the error estimate in Theorem 3.

Remark 2

The space-time DG discretization for the scalar wave equation (24) has no CFL-type restriction for stability or convergence. As long as $h=Ct$, with a constant C, the discretization has optimal convergence in the DG-norm (72).

7 Numerical Experiments

In this section, we will provide results of numerical experiments aimed to verify the order of accuracy obtained from the a priori error analysis discussed in Sect. 6. This analysis provides bounds for the error at time $t=T$ and the order of accuracy of the space-time DG discretization in the DG-norm ${\left| \left| \left| \,\cdot \right| \right| \right| }\,$. In addition, we will also compute the error at time $t=T$ and the order of accuracy in the $L^\infty (\varOmega )$ and $L^2(\varOmega )$-norms. We will consider solutions of the wave equation (1) on a domain with a constant material coefficient matrix A, with a smoothly varying material coefficient matrix A(x), and on a domain with a discontinuous material coefficient matrix A(x).

7.1 Constant Material Coefficients

In the first set of computations, we use the square domain $\varOmega =[0,2\pi ]^2$. The second-order wave equation (1) on the domain $\varOmega$ with homogeneous Dirichlet boundary conditions at $\partial \varOmega$ and zero source term f is solved with the space-time IP-DG discretization presented in Sect. 4. The matrix A in (1) is the $2\times 2$ identity matrix. The exact solution of this test problem is given by

$$\begin{aligned} u_0(x,y,t)&=\cos (\sqrt{2}t)\sin x\sin y , \end{aligned}$$

(80)

$$\begin{aligned} u_1(x,y,t)&=-\sqrt{2}\sin (\sqrt{2}t)\sin x \sin y. \end{aligned}$$

(81)

Apart from the scaling to the domain $\varOmega =[0,1]^2$, this test case is the same as in [6, Section 7.2].

Table 1 Error in $u=(u_0,u_1)$ at time $T=3$ and order of accuracy in the DG-norm of the space-time DG discretization of the second-order wave equation on the domain $\varOmega {=[0,2\pi ]^2}$ with material coefficient matrix A equal to the identity matrix and exact solution (80)–(81)

Table 2 Error in $u_0$ at time $T=3$ and order of accuracy in the $L^{\infty }$- and $L^2$-norms of the space-time IP-DG discretization of the second-order wave equation on the domain $\varOmega {=[0,2\pi ]^2}$ with material coefficient matrix A equal to the identity matrix and exact solution (80)

Table 3 Error in $u_1$ at time $T=3$ and order of accuracy in the $L^{\infty }$- and $L^2$-norms of the space-time IP-DG discretization of the second-order wave equation on the domain $\varOmega {=[0,2\pi ]^2}$ with material coefficient matrix A equal to the identity matrix and exact solution (81)

The space-time slab ${\mathscr {E}}^{\;n}$ is tessellated with a uniform $N\times N$ hexahedral mesh, with N the number of elements in each spatial direction. Each space-time element has length $h=2\pi /N$ in the spatial directions and length $\Delta t$ in the temporal direction. In the computations of the order of accuracy the CFL number is close to one. For the details, see Tables 1, 2 and 3. In the space-time DG discretization tensor product polynomial basis functions, both in space and in time, are used with polynomial order p in each direction. The polynomial orders are, respectively, $p=1,2$ and 3. Hence, the tensor product basis functions have the same polynomial order in space and in time. The stabilization coefficients $\mu _0$ and $\mu _1$ in the space-time IP-DG discretization are chosen as $\mu _0=\mu _1=Cp^2$, with the constant $C=10$ in all computations. The element and face quadrature is done using a tensor-product of 1D Gauss-Legendre quadrature rules. The order of the product Gauss quadrature rules is sufficient such that all integrals with polynomial integrants are computed exactly.

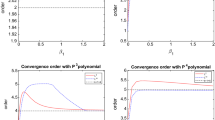
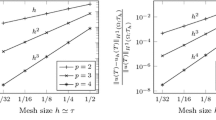
The results are shown in Tables 1, 2 and 3 for, respectively, $u=(u_0,u_1)$ in the DG-norm, and $u_0$ and $u_1$ in the $L^\infty$ and $L^2$-norms. The results in Table 1 show that the order of accuracy of $u_h=(u_{0,h},u_{1,h})$ in the DG-norm is order p, which confirms the theoretical analysis given in Sect. 6 (Theorem 3). Tables 2 and 3 show that the order of accuracy of $u_{0,h}$ and $u_{1,h}$ in both the $L^\infty$ and $L^2$-norms is $p+1$ for $p=1$ and $p=3$, which gives an optimal order of accuracy, but for $p=2$ the computed order of accuracy is p. A further theoretical analysis would be necessary to explain this result. A comparison of the results in Table 1 with the results for the Trefftz space-time DG method presented in [6, Table 7.3], whose error norm is contained in the DG-norm used in Table 1, shows that the space-time DG discretization (24) converges for the polynomial orders $p=1, 2$ and 3 at an optimal rate, whereas the Trefftz space-time DG discretization in [6] does not converge at an optimal rate for $p=1$.

7.2 Smooth Material Coefficients

In the second test case, we solve the second-order wave equation (1) with periodic boundary conditions and zero source term f on the domain $\varOmega =(0,1)$. The matrix A(x) in (1) has smoothly varying coefficients, $A(x)=\mathrm{diag}(a^2(x),\; a^2(x))$ with $a^2(x)=1+\frac{1}{2}\sin ^2(\pi x)$. The initial conditions are

$$\begin{aligned} h_0(x)=\sin (2\pi x)\quad \text{and}\quad h_1(x)=0. \end{aligned}$$

Except for the computational mesh, which now contains N-elements in the spatial direction, all numerical parameters are the same as in Sect. 7.1. Since we do not have an analytical solution that is suitable for error computations we use Richardson extrapolation [25] to compute the order of accuracy of the space-time DG discretization at time $t=T$, both in the DG-norm and in the $L^\infty (\varOmega )$ and $L^2(\varOmega )$-norms. In this procedure, we assume

$$\begin{aligned} u(x,T)-u_h(x,T)=h^sE(x,u)+O(h^{s+1}) \end{aligned}$$

with s the order of accuracy, h the mesh size and E(x, u) the error term, which is independent of h for a sufficiently fine mesh and sufficiently regular solutions. Using three uniform meshes with sizes h, h/2 and h/4 we can eliminate the exact solution u, and after neglecting the residual term $O(h^{s+1})$ and taking the norm, we obtain the following estimate for the order of accuracy:

$$\begin{aligned} s\cong \log \left( \frac{\Vert u_{h/2}-u_h\Vert }{\Vert u_{h/4}-u_{h/2}\Vert }\right) \bigg /\log 2. \end{aligned}$$

Note $\Vert \cdot \Vert$ can be any norm here, not just the $L^2$ norm. This procedure will provide accurate estimates of the order of accuracy provided that the mesh is sufficiently fine and the solution is regular. The orders of accuracy of the space-time DG discretization for the test case with smoothly varying material coefficients are shown in Tables 4, 5 and 6 for, respectively, $u_h=(u_{0,h},u_{1,h})$ in the DG-norm, and $u_{0,h}$ and $u_{1,h}$ in the $L^\infty$ and $L^2$-norms. For polynomial orders $p=1,2,3$ optimal order of accuracy for, respectively, $u_h$ in the DG-norm, and for $u_{0,h}$ and $u_{1,h}$ in the $L^\infty$ and $L^2$-norm are obtained, except for $u_{1,h}$ for $p=2$. The results in these tables confirm the theoretical results stated in Theorem 3 and verify that a smoothly varying material coefficient A(x) has no effect on the numerical accuracy of the space-time DG discretization.

Table 4 Order of accuracy of $u_h=(u_{0,h},u_{1,h})$ in the DG-norm of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(0,1)$ with smoothly varying material coefficients A(x), with $A(x)=\mathrm{diag}(a^2(x),\; a^2(x))$ and $a^2(x)=1+\frac{1}{2}\sin ^2(\pi x)$

Table 5 Order of accuracy of $u_{0,h}$ in the $L^{\infty }$- and $L^2$-norms of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(0,1)$ with smoothly varying material coefficients A(x), with $A(x)=\mathrm{diag}(a^2(x),\; a^2(x))$ and $a^2(x)=1+\frac{1}{2}\sin ^2(\pi x)$

Table 6 Order of accuracy of $u_{1,h}$ in the $L^{\infty }$- and $L^2$-norms of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(0,1)$ with smoothly varying material coefficients A(x), with $A(x)=\mathrm{diag}(a^2(x),\; a^2(x))$ and $a^2(x)=1+\frac{1}{2}\sin ^2(\pi x)$

7.3 Discontinuous Material Coefficients

In the third test case, we solve the second-order wave equation (1) with homogeneous Dirichlet boundary conditions and zero source term f on the domain $\varOmega =(-1,1)$. The matrix with material coefficients A(x) is chosen such that $A=\mathrm{diag}(1,\; 1)$ if $x< 0$ and $A=\mathrm{diag}(\frac{1}{4},\; \frac{1}{4})$ if $x> 0$. The initial conditions are

$$\begin{aligned} {h_0(x)= \left\{ \begin{array}{ll} \sin (\pi (x+1)),&{}\quad \text{if }x<0,\\ 4\sin (\pi (x+1)),&{}\quad \text{if }x>0, \end{array}\right. \quad \text{and}\quad h_1(x)=0.} \end{aligned}$$

The initial condition $h_0$ satisfies the interface condition (2). Satisfying this compatibility condition is important since otherwise at $t=0^+$ immediately a jump in the velocity at $x=0$ will occur. It will then not be possible to compute the order of accuracy of the space-time discretization for this problem due to lack of regularity. Except for the computational mesh, all numerical parameters are the same as in Sect. 7.1. The solution u of the wave equation (1) and its time derivative both have a discontinuity in the spatial derivative at $x=0$. The regularity of the exact solution is given by (5)–(6). Note for higher-order discretizations, this limited regularity will affect the order of accuracy of the numerical discretization.

The orders of accuracy of the space-time DG discretization for the test case with a discontinuous material coefficient are shown in Tables 7, 8 and 9 for, respectively, $u_h=(u_{0,h},u_{1,h})$ in the DG-norm, and $u_{0,h}$ and $u_{1,h}$ in the $L^\infty$ and $L^2$-norms. The results in Table 7 show that the order of accuracy in the DG-norm ${\left| \left| \left| \,\cdot \right| \right| \right| }$ for $p=1$ and $p=2$ is order p, which confirms the theoretical analysis given in Sect. 6 (Theorem 3). For $p=3$, the order of accuracy in the DG-norm is 2, which is not optimal and caused by the lack in regularity, see Sect. 2, and is also visible in the order of accuracy for the velocity $u_1$. For $p=1$ the order of accuracy in the $L^\infty$ and $L^2$-norms is approximately 2, which is the optimal order. Just as for the constant coefficient case considered in Sect. 7.1, for $p=2$ the order of accuracy in the $L^\infty$ and $L^2$-norms is approximately 2. For $p=3$, the order of accuracy in the $L^\infty$ and $L^2$-norms is affected by the limited regularity of the exact solution.

Table 7 Order of accuracy of $u_h=(u_{0,h},u_{1,h})$ in the DG-norm of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(-1,1)$ with discontinuous material coefficient A(x), with $A=\mathrm{diag}(1,\; 1)$ if $x< 0$ and $A=\mathrm{diag}(\frac{1}{4},\; \frac{1}{4})$ if $x> 0$

Table 8 Order of accuracy of $u_{0,h}$ in the DG-norm of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(-1,1)$ with discontinuous material coefficient A(x), with $A=\mathrm{diag}(1,\; 1)$ if $x< 0$ and $A=\mathrm{diag}(\frac{1}{4},\; \frac{1}{4})$ if $x> 0$

Table 9 Order of accuracy of $u_{1,h}$ in the DG-norm of the space-time DG discretization of the second-order wave equation on the domain $\varOmega =(-1,1)$ with discontinuous material coefficient A(x), with $A=\mathrm{diag}(1,\; 1)$ if $x< 0$ and $A=\mathrm{diag}(\frac{1}{4},\; \frac{1}{4})$ if $x> 0$