AENO: a Novel Reconstruction Method in Conjunction with ADER Schemes for Hyperbolic Equations

Abstract

In this paper, we present a novel spatial reconstruction scheme, called AENO, that results from a special averaging of the ENO polynomial and its closest neighbour, while retaining the stencil direction decided by the ENO choice. A variant of the scheme, called m-AENO, results from averaging the modified ENO (m-ENO) polynomial and its closest neighbour. The concept is thoroughly assessed for the one-dimensional linear advection equation and for a one-dimensional non-linear hyperbolic system, in conjunction with the fully discrete, high-order ADER approach implemented up to fifth order of accuracy in both space and time. The results, as compared to the conventional ENO, m-ENO and WENO schemes, are very encouraging. Surprisingly, our results show that the $L_{1}$-errors of the novel AENO approach are the smallest for most cases considered. Crucially, for a chosen error size, AENO turns out to be the most efficient method of all five methods tested.

1 Introduction

Circumventing Godunov’s theorem [8] is a 60-year old challenge to numerical mathematicians concerned with the development of high-order methods for solving hyperbolic equations. The invention of total variation diminishing (TVD) methods in the 1970s and 1980s [11, 16, 23, 29, 43] represented an important step forward in facing the challenge. However such methods, even if very effective in practice, are limited to, at most, second-order accuracy for smooth solutions. Currently, the alternative approaches relying on non-linear spatial reconstruction pioneered by Harten and others [12, 13], such as ENO, m-ENO and WENO [14, 15, 26,27,28] have become the dominant approach. Unlike TVD methods, however, ENO, m-ENO and WENO based methods cannot guarantee the absence of spurious oscillations for scalar problems. However, these methods guarantee that such oscillations vanish in the limit of mesh refinement. This is not the case for linear methods, for which, no matter how fine the mesh is, the amplitude of the oscillations will remain unchanged. The initially popular ENO method has, in recent years, been largerly discarded by most researchers and practitioners. The reconstruction scenery is currently dominated by the WENO approach, in a variety of forms. See for example [5, 31] and [6].

In this paper, we propose a novel spatial reconstruction method that is akin to both ENO and WENO. The method, called AENO, results from averaging two polynomials, the classical ENO polynomial and its closest neighbour, while the search for the stencil remains commanded by ENO. A variant of the scheme, called m-AENO, results from averaging the modified ENO (m-ENO) polynomial of Shu [26] and its closest neighbour; m-AENO is equivalent to AENO for 2nd and 3rd order of accuracy. Here, the reconstruction schemes are applied in conjunction with the fully discrete high-order ADER approach [4, 7, 30, 34, 40]. See [36] for an up-to-date review of ADER and references to the many contributions to its development. Schemes of up to 5th order of accuracy in space and time are implemented and tested, first for the linear advection equation and then for a non-linear hyperbolic system, namely the blood flow equations. For both problems, we first carry out experiments to compare numerical solutions with exact solutions for short and long evolution times. Results for three reconstruction methods are compared, namely ENO, m-ENO, WENO and the novel AENO and m-AENO schemes. Then we carry out a convergence rate study for both types of problems, the linear advection equation and the blood flow equations. Overall, the results are encouraging. For most problems, all five reconstruction methods give comparable results. Surprisingly, our results show that the $L_{1}$-errors of the novel AENO/m-AENO schemes are the smallest, for most cases considered.

The rest of this paper is structured as follows. In Sect. 2 we review the fully discrete ADER methodology to solve hyperbolic equations, first for the linear scalar case and then for non-linear systems. In Sect. 3 we briefly introduce necessary background on the ENO reconstruction method. In Sect. 4 we describe the new spatial reconstruction technique AENO and its variant m-AENO; in Sect. 5 we show results for the linear advection equation. In Sect. 6 we apply the methods to the blood flow equations and in Sect. 7 we draw conclusions.

2 Review of the ADER Methodology for Hyperbolic Equations

Here, we briefly review the ADER approach to construct one-step, fully discrete high-order Godunov methods for solving hyperbolic balance laws, whose building block is the generalized Riemann problem, a piece-wise smooth data Cauchy problem including stiff or non-stiff source terms, rather than the conventional piece-wise constant data homogeneous Riemann problem. In this section we review the ADER methodology as applied to one-dimensional systems of hyperbolic balance laws. We first deal with the scalar linear case.

2.1 ADER for the Scalar Linear Case

Before proceeding, we recall the finite volume framework for a general scalar balance law.

2.1.1 The Finite Volume Framework

Consider the one-dimensional balance law

$$\begin{aligned} \partial _{t} q + \partial _{x} f(q) = s(q), \end{aligned}$$

(1)

solved by a finite volume method, with space-time volumes

$$\begin{aligned} V=[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] \times [t_{n},t_{n+1}]. \end{aligned}$$

(2)

Exact integration of (1) on V in (2) gives

$$\begin{aligned} q^{n+1}_{i} = q^{n}_{i}-\frac{\Delta t}{\Delta x}[f_{i+\frac{1}{2}}-f_{i-\frac{1}{2}}] + \Delta t s_{i}, \end{aligned}$$

(3)

with definitions

$$\begin{aligned} \left. \begin{array}{l} q^{n}_{i} = \displaystyle \frac{1}{\Delta x} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} q(x,t_{n}) {\mathrm{d}} x, \\ f_{i+\frac{1}{2}} = \displaystyle \frac{1}{\Delta t} \int _{t_{n}}^{t_{n+1}} f( q(x_{i+\frac{1}{2}},t) ) {\mathrm{d}} t, \\ s_ {i} = \displaystyle \frac{1}{\Delta t} \frac{1}{\Delta x} \int _{t_{n}}^{t_{n+1}} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} s(q(x,t)) {\mathrm{d}} x {\mathrm{d}} t \; \end{array}\right\} \end{aligned}$$

(4)

and

$$\begin{aligned} \Delta x = x_{i+\frac{1}{2}} - x_{i-\frac{1}{2}}, \quad \Delta t = t_{n+1} - t_{n}, \quad x_{i} = \frac{1}{2}({x_{i-\frac{1}{2}}}+{x_{i+\frac{1}{2}}}). \end{aligned}$$

(5)

2.1.2 ADER for Linear Advection-Reaction

The ADER method [38] departs from the finite volume formula (3), understood as resulting from approximations to the integrals in (4). The one-step updating formula (3) updates the cell average $q_{i}^{n}$ to $q_{i}^{n+1}$, for which definitions for the numerical flux $f_{i+\frac{1}{2}}$ and the numerical source $s_{i}$ are required. The rest of the presentation of the ADER approach will be carried out with (1) as the linear advection-reaction equation, in which $f(q)= \lambda q$ and $s(q)= \beta q$, with $\lambda$ a constant wave propagation speed and $\beta$ constant reaction rate satisfying $\beta \leqslant 0$.

2.1.3 The ADER Flux and the Generalized Riemann Problem

To determine the numerical flux $f_{i+\frac{1}{2}}$ in (3) we compute a high-order accurate approximation to the flux integral in (4), which in turn requires a high-order approximation to the integrand $q(x_{i+\frac{1}{2}},t)$. This is achieved by solving, approximately, the following generalized Riemann problem

$$\begin{aligned} \left. \begin{array}{l} \hbox {PDE: } \partial _t q + \lambda \partial _x q = \beta q, \\ \\ \hbox {IC: } q(x,0) = \left\{ \begin{array}{lll} p_{i}(x) &{}\quad {\text{ if }} &{} x < 0, \\ \\ p_{i+1}(x) &{}\quad {\text{ if }} &{} x > 0, \end{array}\right. \end{array}\right\} \end{aligned}$$

(6)

in which the polynomials $p_{i}(x)$ and $p_{i+1}(x)$ are reconstruction polynomials of arbitrary degree K. To solve (6) we adopt here the Toro-Titarev [41] method, which starts from the LeFloch-Raviart expansion [18] for the approximate solution

$$\begin{aligned} q_{i+\frac{1}{2}}(\tau ) = q(0,0_{+}) + \sum _{k = 1}^{K} \left[ \partial _{t}^{(k)}q(0,0_{+}) \right] \frac{\tau ^{k}}{k!}. \end{aligned}$$

(7)

The leading term of the expansion. The leading term $q(0,0_{+})$ in (7) results from solving the conventional piece-wise-constant data Riemann problem

$$\begin{aligned} \left. \begin{array}{l} \hbox {PDE:} \quad \partial _{t} q + \lambda \partial _{x} q = 0, \\ \\ \hbox {IC:} \quad q(x,0) = \left\{ \begin{array}{lcl} p_{i}(0) &{} \quad {\text{ if }} &{} x < 0, \\ p_{i+1}(0) &{} \quad {\text{ if }} &{} x > 0, \end{array}\right. \end{array}\right\} \end{aligned}$$

(8)

in which the initial condition consists of the boundary extrapolated values $p_{i}(0)$ from the left and $p_{i+1}(0)$ from the right. The position of the interface $x_{i+\frac{1}{2}}$ corresponds to 0, in local coordinates.

The higher-order terms of the expansion. To compute the higher-order terms in (7) one requires the determination of the time derivatives $\partial _{t}^{(k)}q(0,0_{+})$. In the first version of ADER [38] it was proposed to apply the Cauchy-Kovalevskaya procedure to the governing equation in (6). Just for a moment let us assume the linear homogenous case in (6) ($\beta =0$). Then, the Cauchy-Kovalevskaya procedure gives

$$\begin{aligned} \partial _{t}q +\lambda \partial _{x} q =0, \,\, \partial _{t}q = - \lambda \partial _{x} q, \,\, \partial _{t}^{(2)}q = \lambda ^{2} \partial _{x}^{(2)} q. \end{aligned}$$

(9)

In fact, it is easily shown that for an arbitrary positive integer k,

$$\begin{aligned} \partial _{t}^{(k)} q = (-1)^{k} \lambda ^{k} \partial _{x}^{(k)} q. \end{aligned}$$

(10)

Similarly, for the inhomogeneous case with non-zero source term in (6), it can also be shown that the time derivatives can still be expressed as functions of spacial derivatives, as follows:

$$\begin{aligned} \partial _{t}^{(k)} q(x,t) = \sum _{n = 0}^{k} \left[ \frac{k!}{(k-n)! n!} \beta ^{n}(-\lambda )^{k-n}\right] \partial _{x}^{(k-n)} q(x,t). \end{aligned}$$

(11)

Now the pending problem is that of determining $\partial _{x}^{(l)}q(0,0_{+})$ in (7), for which a useful step is the construction of evolution equations for the spatial derivatives. For the homogenous case, it can be easily shown that $\partial _{x}^{(l)}q(x,t)$ obeys the same evolution equation as q(x, t), that is

$$\begin{aligned} \partial _{t} (\partial _{x}^{(l)}q(x,t)) + \lambda \partial _{x} (\partial _{x}^{(l)}q(x,t)) = 0. \end{aligned}$$

(12)

The next problem is to explore the possibility of formulating initial value problems for (12). In fact this is possible if we find suitable initial conditions. If for each computational cell we have a spatial polynomial representation $p_{i}(x)$ for $q(x,t_{n})$, via a spatial reconstruction technique for example, then it is possible to pose classical Riemann problems for spatial derivatives as follows:

$$\begin{aligned} \left. \begin{array}{l} \hbox {PDE:} \quad \partial _{t} (\partial _{x}^{(l)}q(x,t)) + \lambda \partial _{x} (\partial _{x}^{(l)}q(x,t)) = 0, \\ \\ \hbox {IC:} \quad \partial _{x}^{(l)}q(x,0) = \left\{ \begin{array}{lcl} \partial _{x}^{(l)}p_{i}(0) &{}\quad {\text{ if }} &{} x < 0, \\ \\ \partial _{x}^{(l)}p_{i+1}(0) &{}\quad {\text{ if }} &{} x > 0. \end{array}\right. \end{array}\right\} \end{aligned}$$

(13)

The initial condition for these classical Riemann problems (piece-wise constant data) consists of intercell-boundary extrapolated spatial derivatives of the reconstruction polynomials, $p_{i}(x)$ from the left and $p_{i+1}(x)$ from the right. Solutions of classical Riemann problems for the spatial derivatives, as in (13), will give the spatial derivatives $\partial _{x}^{(l)}q(0,0_{+})$ in (7), of any order l. This in turn determines the time partial derivatives in (11) and hence in (7). We have therefore found the complete solution of the homogeneous version of the generalized Riemann problem (6), which is given as

$$\begin{aligned} \displaystyle q_{i+\frac{1}{2}}(\tau )=\left\{ \begin{array}{lll} p_{i}(0) + \displaystyle {\sum _{k = 1}^{K}} \left( (-1)^{k} \lambda ^{k} \partial _{x}^{(k)} p_{i}(0)\right) \frac{(\tau )^{k} }{(k+1)!} &{}\quad {\text{ if }} &{} \lambda >0, \\ \\ p_{i+1}(0) + \displaystyle {\sum _{k = 1}^{K}} \left( (-1)^{k} \lambda ^{k} \partial _{x}^{(k)} p_{i+1}(0)\right) \frac{(\tau )^{k} }{(k+1)!} &{} \quad {\text{ if }} &{} \lambda <0. \end{array} \right. \end{aligned}$$

(14)

The solution for the inhomogeneous case is similar. The numerical flux results from an approximation to the flux integral in (4), which is now obtained as

$$\begin{aligned} f_ {i+\frac{1}{2}}= \frac{1}{\Delta t} \int _{0}^{\Delta t} f(q_{i+\frac{1}{2}}(\tau )) {\text{d}}\tau. \end{aligned}$$

(15)

Exact integration gives

$$\begin{aligned} \displaystyle f_{i+\frac{1}{2}} =\left\{ \begin{array}{lll} \lambda \left[ p_{i}(0) + \displaystyle {\sum _{k = 1}^{K}} \left( (-1)^{k} \lambda ^{k} \partial _{x}^{(k)} p_{i}(0)\right) \frac{(\Delta t)^{k} }{(k+1)!} \right] &{} {\text{ if }} &{} \lambda >0, \\ \\ \lambda \left[ p_{i+1}(0) + \displaystyle {\sum _{k = 1}^{K}} \left( (-1)^{k} \lambda ^{k} \partial _{x}^{(k)} p_{i+1}(0)\right) \frac{(\Delta t)^{k} }{(k+1)!} \right] &{} {\text{ if }} &{} \lambda <0. \end{array} \right. \end{aligned}$$

(16)

Generally, the numerical flux in (15) will require numerical integration of the appropriate order. Inserting the numerical flux (16) into the conservative finite volume formula (3) will give a numerical approximation of order $K+1$ in both space and time. In the presence of source terms in the governing equations, one must include the source terms when performing the Cauchy-Kovalevskaya procedure, as these enter in the calculation of the numerical flux. In addition, one must compute the numerical source to the appropriate order of accuracy. This requires an approximation of the source integral in (4) in the entire control volume V in (2), for which a high-order approximation to q(x, t) within V is needed. Such approximation is found in a manner similar to that of the generalized Riemann problem.

2.2 ADER for Non-linear Systems

Consider a general one-dimensional system of hyperbolic balance laws

$$\begin{aligned} \partial _{t}{} {\mathbf{Q}}(x,t) + \partial _{x} {\mathbf{F}}({\mathbf{Q}}(x,t)) = {\mathbf{S}}({\mathbf{Q}}(x,t)). \end{aligned}$$

(17)

The vectors ${\mathbf{Q}}$, ${\mathbf{F}}({\mathbf{Q}})$ and ${\mathbf{S}}({\mathbf{Q}})$ define conserved variables, fluxes and sources, respectively. Assuming the space/time domain to be discretised by finite volumes V in (2), exact integration of (17) in V gives

$$\begin{aligned} {\mathbf{Q}}_{i}^{n+1}={\mathbf{Q}}_{i}^{n} - \frac{\Delta t}{\Delta x}({\mathbf{F}}_{i+\frac{1}{2}}-{\mathbf{F}}_{i-\frac{1}{2}} ) + \Delta t {\mathbf{S}}_{i}, \end{aligned}$$

(18)

with

$$\begin{aligned} \left. \begin{array}{l} \displaystyle {{\mathbf{Q}}_{i}^{n}=\frac{1}{\Delta x} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} {\mathbf{Q}}(x,t^{n}) {\mathrm{d}}x}, \quad \displaystyle {{\mathbf{F}}_{i+\frac{1}{2}} = \frac{1}{\Delta t} \int _{t^{n}}^{t^{n+1}} {\mathbf{F}}( {\mathbf{Q}}(x_{i+\frac{1}{2}}, t) ) {\mathrm{d}} t}, \\ \displaystyle {{\mathbf{S}}_{i} = \frac{1}{\Delta t \Delta x} \int _{t^{n}}^{t^{n+1}} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} {\mathbf{S}}( {\mathbf{Q}}(x,t) ) {\mathrm{d}} x {\mathrm{d}} t}. \end{array} \right\} \end{aligned}$$

(19)

Numerically, (18)–(19) motivate the construction of finite volume methods to solve (17), in which suitable approximations to the integrals (19) determine the numerical flux ${\mathbf{F}}_{i+\frac{1}{2}}$ and the numerical source ${\mathbf{S}}_{i}$ in the approximating formula (18). See Sect. 2.1.2.

2.2.1 ADER and the Godunov Method

The classical Godunov method [8] results from (18)–(19) by assuming ${\mathbf{S}}({\mathbf{Q}})={\mathbf{0}}$ and ${\mathbf{Q}}(x_{i+\frac{1}{2}}, t)={\tilde{{\mathbf{Q}}}}_{i+\frac{1}{2}}(x/t)$ to be the similarity solution of the piece-wise constant data, homogeneous, Riemann problem

$$\begin{aligned} \left. \begin{array}{ll} \hbox {PDEs:} &{}\quad \partial _t {\mathbf{Q}} + \partial _x {\mathbf{F}}({\mathbf{Q}}) = {\mathbf{0}}, \,\, x \in (-\infty, \infty ),\,\, t>0, \\ \hbox {ICs:} &{}\quad {\mathbf{Q}}(x,0) = \left\{ \begin{array}{lll} {\mathbf{Q}}_{L}={\mathbf{Q}}_{i}^{n} &{}\quad {\text{ if }} &{} x < 0,\\ {\mathbf{Q}}_{R}={\mathbf{Q}}_{i+1}^{n} &{}\quad {\text{ if }} &{} x > 0. \end{array}\right. \end{array}\right\} \end{aligned}$$

(20)

Figure 1, top frame, depicts the initial condition (left) and the structure of the solution (right) of (20). In this simplified case the numerical flux ${\mathbf{F}}_{i+\frac{1}{2}}$ in (18) results from the exact integration in (19), namely

$$\begin{aligned} \displaystyle {{\mathbf{F}}_{i+\frac{1}{2}}^{\text{God}} = \frac{1}{\Delta t} \int _{t^{n}}^{t^{n+1}} {\mathbf{F}}({\tilde{{\mathbf{Q}}}}_{i+\frac{1}{2}}(0)) {\mathrm{d}} t ={\mathbf{F}}({\tilde{{\mathbf{Q}}}}_{i+\frac{1}{2}}(0))}. \end{aligned}$$

(21)

For exact and approximate Riemann solvers for the first-order Godunov method see [35].

Fig. 1

Riemann problems. Top: classical Riemann problem for the first-order Godunov method. Bottom: generalised Riemann problem for the ADER method. Left-hand side pictures depict initial conditions for the classical (top) and generalized (bottom) Riemann problems, while right-hand side pictures depict the respective, emerging wave structures in the x-t plane

The ADER extension of Godunov’s method [38] includes three steps.

• i) Replacing piece-wise constant data by piece-wise smooth data, as resulting from reconstruction procedures, for example; see Fig. 1, bottom frame. This leads naturally to the generalized Riemann problem

  $$\begin{aligned} \left. \begin{array}{ll} \hbox {PDEs:} &{}\quad \partial _t {\mathbf{Q}} + \partial _x {\mathbf{F}}({\mathbf{Q}}) = {\mathbf{S}}({\mathbf{Q}}), \,\, x \in (-\infty, \infty ),\,\, t>0, \\ \hbox {ICs:} &{}\quad {\mathbf{Q}}(x,0) = \left\{ \begin{array}{lll} {\mathbf{Q}}_{L}(x) &{}\quad {\text{ if }} &{} x < 0, \\ {\mathbf{Q}}_{R}(x) &{}\quad {\text{ if }} &{} x > 0. \end{array}\right. \end{array}\right\} \end{aligned}$$

  (22)

• ii) Computing ${\mathbf{Q}}_{LR}(\tau )$, the time-dependent solution of (22) at the interface, followed by evaluation of the numerical flux

  $$\begin{aligned} \displaystyle {{\mathbf{F}}_{i+\frac{1}{2}} = \frac{1}{\Delta t} \int _{t^{n}}^{t^{n+1}} {\mathbf{F}}( {\mathbf{Q}}_{LR}(\tau )) {\mathrm{d}} t}. \end{aligned}$$

  (23)

• iii) Defining a function ${\mathbf{Q}}_{i}(x,t)$ within each volume V, followed by evaluation of the numerical source

  $$\begin{aligned} \displaystyle {{\mathbf{S}}_{i} = \frac{1}{\Delta t \Delta x} \int _{t^{n}}^{t^{n+1}} \int _{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}} {\mathbf{S}}( {\mathbf{Q}}_{i}(x,t )) {\mathrm{d}} x {\mathrm{d}} t}. \end{aligned}$$

  (24)

Early communications on the ADER methodology include [38] and [25]. For an introduction to ADER methods see Chaps. 19 and 20 of [35]. The next section deals with solvers for the generalised Riemann problem (22).

2.2.2 Solvers for the Generalized Riemann Problem

Several methods for solving the generalised Riemann problem are currently available. Here we limit ourselves to brief descriptions for two of them and give appropriate references for other solvers.

The Toro-Titarev solver for the generalized Riemann problem

This solver [41] seeks an approximate solution ${\mathbf{Q}}_{LR}(\tau )$ of (22) expressed as a truncated series expansion

$$\begin{aligned} {\mathbf{Q}}_{LR}(\tau ) = {\mathbf{Q}}(0,0_{+}) + \sum _{k = 1}^{K} \left[ \partial _{t}^{(k)} {\mathbf{Q}}(0,0_{+}) \right] \frac{\tau ^{k}}{k!}, \end{aligned}$$

(25)

following [19]. The leading term is defined as

$$\begin{aligned} {\mathbf{Q}}(0,0_{+})=\lim \limits _{t \rightarrow 0_{+}} {\mathbf{Q}}(0,t) \end{aligned}$$

(26)

and is computed by solving a conventional Riemann problem, see (8). The challenge is to determine the coefficients $\partial _{t}^{(k)} {\mathbf{Q}}(0,0_{+})$ in (25) for the higher-order terms.

A precursor to the Toro-Titarev solver [41] results from a modification of the Ben-Artzi/Falcovitz second-order GRP solver [1] that departs from ${\mathbf{Q}}_{LR}(\tau ) = {\mathbf{Q}}(0,0_{+}) + \tau \partial _{t} {\mathbf{Q}}(0,0_{+})$, with ${\mathbf{Q}}(0,0_{+})$ defined as in (26). See Chap. 14 of the 1997 edition of [35]. The Cauchy-Kovalevskaya procedure is then used to determine $\partial _{t} {\mathbf{Q}}(0,0_{+})$, that is

$$\begin{aligned} \partial _{t}{} {\mathbf{Q}} + \partial _{x} {\mathbf{F}}({\mathbf{Q}}) = {\mathbf{S}}({\mathbf{Q}}) \rightarrow \partial _{t}{} {\mathbf{Q}} = - {\mathbf{A}}({\mathbf{Q}})\partial _{x}{} {\mathbf{Q}} + {\mathbf{S}}({\mathbf{Q}})\; \end{aligned}$$

(27)

and the solution then reads

$$\begin{aligned} {\mathbf{Q}}_{LR}(\tau ) = {\mathbf{Q}}(0,0_{+}) + \tau [- {\mathbf{A}}({\mathbf{Q}}(0,0_{+}))\partial _{x}{} {\mathbf{Q}}(0,0_{+}) + {\mathbf{S}}({\mathbf{Q}}(0,0_{+}))]. \end{aligned}$$

(28)

The pending problem in (28) is to compute the spatial derivative $\partial _{x}{} {\mathbf{Q}}(0,0_{+})$. First it is noted that for the linear homogeneous case

$$\begin{aligned} \partial _{t}{} {\mathbf{Q}} +{\mathbf{A}} \partial _{x}{} {\mathbf{Q}}={\mathbf{0}} \end{aligned}$$

(29)

the following evolution equations for all spatial derivatives are valid:

$$\begin{aligned} \partial _{t}(\partial _{x}^{(k)}{} {\mathbf{Q}})+ {\mathbf{A}} \partial _{x}(\partial _{x}^{(k)}{} {\mathbf{Q}})={\mathbf{0}}. \end{aligned}$$

(30)

One can then define the classical Riemann problem for (30), with $k=1$, to find $\partial _{x}{} {\mathbf{Q}}(0,0_{+})$ in (28). The numerical flux (23) then follows.

The Toro-Titarev solver for the ${\text{GRP}}_{k}$ [35] departs from the LeFloch-Raviart expansion (25) and the Cauchy-Kovalevskaya procedure, leading to

$$\begin{aligned} \partial _{t}^{(k)} {\mathbf{Q}}(x,t) = {\mathbf{P}}^{(k)} ( \partial _{x}^{(0)} {\mathbf{Q}}, \partial _{x}^{(1)} {\mathbf{Q}}, \cdots,\partial _{x}^{(k)} {\mathbf{Q}} ). \end{aligned}$$

(31)

The functionals ${\mathbf{P}}^{(k)}$ are specific to the particular system (17); their arguments are spatial derivatives, yet to be found. To determine these, evolution equations are invoked

$$\begin{aligned} \partial _t (\partial _{x}^{(k)} {\mathbf{Q}}(x,t)) + {\mathbf{A}}({\mathbf{Q}}) \partial _x (\partial _{x}^{(k)} {\mathbf{Q}}(x,t)) = {\mathbf{H}}^{(k)}. \end{aligned}$$

(32)

Then, simplified classical Riemann problems for spatial derivatives are posed

$$\begin{aligned} \left. \begin{array}{ll} \hbox {PDEs:} &{} \partial _{t}(\partial _{x}^{(k)} {\mathbf{Q}}(x,t))+{\mathbf{A}}^{(0)}_{LR} \partial _{x}(\partial _{x}^{(k)} {\mathbf{Q}}(x,t)) = {\mathbf{0}}, \\ \\ \hbox {ICs:} &{} \partial _{x}^{(k)} {\mathbf{Q}}(x,0) = \left\{ \begin{array}{lll} {\mathbf{Q}}^{(k)}_{L}(0) &{} \quad {\text{ if }} &{} x < 0,\\ {\mathbf{Q}}^{(k)}_{R}(0) &{} \quad {\text{ if }} &{} x > 0. \end{array} \right. \end{array}\right\} \end{aligned}$$

(33)

Strong simplifications have been made to the evolution equations in order to arrive at (33); the source terms ${\mathbf{H}}^{(k)}$ have been neglected and the advection term has been linearised around the leading term of the expansion (25). The coefficient matrix ${\mathbf{A}}^{(0)}_{LR}$ results from evaluating the Jacobian at the leading term of the expansion. The complete solution (25) has then been determined and the numerical flux follows from (23). A similar but simpler procedure is used to determine the source term in (24), see [41].

The Montecinos-Toro implicit GRP solver

This solver [21, 40] is implicit and can deal with stiff source terms. The key step is the following lemma.

Lemma 1 Let ${\mathbf {Q}}(x,\tau )$ be an analytical function of $\tau$. Then

$$\begin{aligned} {\mathbf {Q}}(x,\tau )= {\mathbf {Q}}(x,0_+) -\sum _{k=1}^{\infty }\frac{(-\tau )^k}{k!} \partial _t^{(k)} {\mathbf {Q}}(x,\tau ). \end{aligned}$$

(34)

This expression is the implicit counterpart of the explicit Raviart-LeFloch expansion (25). Now the implicit Cauchy-Kovalevskaya procedure leads to

$$\begin{aligned} \begin{array}{c} \partial _t^{(k)} {\mathbf {Q}}(0,\tau ) = {\mathbf {P}}^{(k)}({\mathbf {Q}}(0,\tau ),\cdots,\partial _x^{(k)}{\mathbf {Q}}(0,\tau )). \end{array} \end{aligned}$$

(35)

As for the Toro-Titarev solver, a key step is to determine the arguments of functionals ${\mathbf {P}}^{(k)}$ in (35). For details see [40] for the general case.

Example 1 Second-order scheme. In this special case, see [21] for details, we have

$$\begin{aligned} \begin{array}{c} \partial _{t}{{\mathbf {Q}}}+\partial _{x}{{\mathbf {F}}}({{\mathbf {Q}}})={{\mathbf {S}}}({{\mathbf {Q}}}), \quad {\mathbf {Q}}(0,\tau ) = {\mathbf {Q}}(0,0_+) +\tau \partial _t {\mathbf {Q}}(0,\tau ). \end{array} \end{aligned}$$

(36)

The implicit Cauchy-Kovalevskaya procedure gives

$$\begin{aligned} \begin{array}{c} {\mathbf {Q}}(0,\tau ) = {\mathbf {Q}}(0,0_+) +\tau \left[ -{\mathbf {A}}({\mathbf {Q}}(0,\tau ))\partial _x{\mathbf {Q}}(0,\tau )+ {\mathbf {S}}({\mathbf {Q}}(0,\tau )) \right]. \end{array} \end{aligned}$$

(37)

Then, applying the implicit expansion (34) we have

$$\begin{aligned} \begin{array}{c} \partial _x {\mathbf {Q}}(0,\tau ) = \partial _x {\mathbf {Q}}(0,0_+) +\tau \partial _t (\partial _x {\mathbf {Q}}(0,\tau )) \; \end{array} \end{aligned}$$

(38)

and

$$\begin{aligned} \begin{array}{c} \partial _x {\mathbf {Q}}(0,\tau ) = \partial _x {\mathbf {Q}}(0,0_+) +\tau \partial _x \left[ -{\mathbf {A}}({\mathbf {Q}}(0,\tau ))\partial _x{\mathbf {Q}}(0,\tau )+ {\mathbf {S}}({\mathbf {Q}}(0,\tau )) \right]. \end{array} \end{aligned}$$

(39)

Therefore

$$\begin{aligned} \begin{array}{c} \partial _x {\mathbf {Q}}(0,\tau ) = \left[ {\mathbf {I}}-\tau {\mathbf {B}}({\mathbf {Q}}(0,\tau )) \right] ^{-1}\partial _x {\mathbf {Q}}(0,0_+). \end{array} \end{aligned}$$

(40)

Finally, the solution ${\mathbf {Q}}(0,\tau )={\mathbf {Q}}^{*}(\tau )$ satisfies the non-linear algebraic system

$$\begin{aligned} \begin{array}{c} {\mathbf {Q}}^{*} = {\mathbf {Q}}(0,0_+) +\tau \left[ -{\mathbf {A}}({\mathbf {Q}}^{*})\left[ {\mathbf {I}}-\tau {\mathbf {B}}({\mathbf {Q}}^{*}) \right] ^{-1}\partial _x {\mathbf {Q}}(0,0_+)+ {\mathbf {S}}({\mathbf {Q}}^{*}) \right] \; \end{array} \end{aligned}$$

(41)

and the numerical flux follows. This gives a second-order, locally implicit method suitable for balance laws with stiff source terms.

Other $\mathbf{GRP}_{k}$ solvers

We have described two schemes to solve the generalized Riemann problem. The first solver is explicit, while the second one is implicit, leading to a locally implicit ADER method. The implicit method can deal with stiff source terms and the corresponding ADER methods are then able to reconcile stiffness and high accuracy, for smooth solutions. These two methods seek the solution right at the interface and extend the (explicit) Ben-Artzi/Falcovitz second-order method. Another class of solvers emerges from a re-interpretation of the high-order method of Harten et al. [13] that extends the MUSCL-Hancock second-order method. In this approach, the initial data is evolved in time and interactions at the interface are sought at selected time-integration points via classical Riemann problems [2]. The already well-established method of Dumbser et al. [4] is a numerical version of the Harten method, see also [2], whereby the data is evolved numerically via an implicit space-time discontinuous Galerkin approach. The resulting ADER scheme is suitable for stiff source terms, with the additional benefit of avoiding the Cauchy-Kovalevskaya procedure. Other recent solvers for the generalized Riemann problem are due to Götz and Iske [10], Götz and Dumbser [9], and Dematté et al. [3].

We have reviewed the ADER approach to extend Godunov’s method to high order of accuracy. Very high-order methods are essential for the following reasons: (i) there is a growing trend to use PDEs to understand the physics they embody; (ii) only very accurate solutions of PDEs will achieve this and also reveal limitations of mathematical models (PDEs themselves) and uncertainty on parameters of the problem; (iii) efficiency: given an error deemed acceptable, then high-order methods attain that error, if small, much more efficiently than low-order methods on fine meshes, by orders of magnitude. For very long time evolution simulations high-order methods are essential.

In the presentation of ADER we assumed that the solution at a time $t_{n}$ in any computing cell was represented by a polynomial resulting from some spatial reconstruction procedure. In principle, it can be any kind of reconstruction procedure, centred, biased, linear, non-linear. In what follows we review a non-linear reconstruction procedure.

3 Review of ENO Polynomial Reconstruction Methodology

To circumvent Godunov’s theorem when constructing high-order methods, it is necessary to resort non-linear schemes and hence avoid or reduce spurious oscillations in the vicinity of large gradients of the solution. A popular method to do so is the essentially non-oscillatory (ENO) reconstruction method of Harten and collaborators [12], which we briefly review here. The presentation is succinct and we follow [17] to construct the polynomial with the required properties. More popular than ENO is the WENO method, which we also use in this paper for comparison, but a review of WENO is omitted as the reader can consult the classical references [15, 27, 28]; see also [31]. There is a variant of ENO due to Shu [26], called here m-ENO. We omit all details of m-ENO here but encourage the reader to consult the original reference.

3.1 ENO Polynomial of Arbitrary Degree

We assume a set of cell integral averages of the unknown q(x, t) denoted as $\{q_{j} \}_{j=0}^{i}$ and adopt the primitive-function approach [17, 45] to construct an ENO polynomial with samples $q(x_{i+1/2})$ at the intercell boundaries $x_{i+1/2}$. Recall that a function q(x) is the primitive function of f(x), or antiderivative, if

$$\begin{aligned} f(x)=\frac{{\mathrm{d}}}{{\mathrm{d}}x}q(x), \quad {\text{ or }} \quad q(x)= \int _{x_{-1/2}}^{x}f(y){\mathrm{d}}y, \end{aligned}$$

(42)

where $x_{-1/2}$ is the left most interface.Then, the samples are defined as

$$\begin{aligned} q(x_{i+1/2}) = \sum _{j=0}^{i} \int _{x_{j-1/2}}^{x_{j+1/2}}f(y){\mathrm{d}}y = \sum _{j=0}^{i} \Delta x_{j} q_{j}. \end{aligned}$$

(43)

That is, the partial sums of cell averages are the samples of the primitive function q(x).

Now the task is to construct the interpolating polynomial P(x) of degree $N+1$ passing through $(x_{i+1/2}, q(x_{i+1/2}))$, of one degree higher than the sought reconstruction polynomial p(x), with

$$\begin{aligned} p(x)=\frac{{\mathrm{d}}}{{\mathrm{d}}x}P(x). \end{aligned}$$

(44)

For convenience, the final sought polynomial p(x) of degree N is written in Taylor form as follows:

$$\begin{aligned} p(x)= a_0 + 2a_1(x-x_i) + \cdots + (N+1)a_{N}(x-x_i)^N. \end{aligned}$$

(45)

The coefficients $a_0, a_1, \cdots, a_N$ depend on the stencil of the polynomial. Next, we find the Newton divided differences. Recalling from (43)

$$\begin{aligned} q(x_{i+\frac{1}{2}}) = \sum _{j=0}^i \Delta x_{j} {q}_j \; \end{aligned}$$

(46)

we have, for example,

$$\begin{aligned} \left. \begin{array}{l} q[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}] = \displaystyle \frac{q(x_{i+\frac{1}{2}})-q(x_{i-\frac{1}{2}})}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}} = {q}_i, \\ \\ \displaystyle q[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}, x_{i+\frac{3}{2}}] = \frac{q[x_{i+\frac{1}{2}},x_{i+\frac{3}{2}}]-q[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]}{x_{i+\frac{3}{2}}-x_{i-\frac{1}{2}}} = \frac{{q}_{i+1}-{q}_i}{2\Delta x},\\ \\ q[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}, x_{i+\frac{3}{2}}, x_{i+\frac{5}{2}} ] = \displaystyle \frac{{q}_{i+2}-2{q}_{i+1} +{q}_{i}}{6\Delta x^2}. \end{array} \right\} \end{aligned}$$

(47)

Consider the generic cell $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ with intercell boundaries $x_{i-\frac{1}{2}}$ (left) and $x_{i+\frac{1}{2}}$ (right). The polynomial is built by adding one point at the time, either left or right, to the current stencil; each time one adds one degree to the sought polynomial of degree $N+1$. The new point added, to left or to the right, depending on the relative size of divided differences in absolute value.

The general algorithm is as follows. Start with the two points $l_0(i) = i+1/2$ at the cell interface $x_{i+\frac{1}{2}}$ and $l_1(i) = i-\frac{1}{2}$ at the cell interface $x_{i-\frac{1}{2}}$. The most left point is $l_1(i) = i-\frac{1}{2}$. Then the next point in the sequence is $l_{2}(i)$. In general the new point to be added is chosen recursively as follows.

For $m=1, \cdots, N,$

$$\begin{aligned} l_{m+1}(i) = \left\{ \begin{array}{lcl} l_m(i) &{}\quad {\text{ if }} &{} |q[x_{{l_m}(i)},\cdots,x_{{l_m}(i)+m+1}]|\leqslant |q[x_{{l_m}(i)-1},\cdots,x_{{l_m}(i)+m}]|,\\ \\ l_{m}(i)-1 &{}\quad {\text{ if }} &{} |q[x_{{l_m}(i)-1},\cdots,x_{{l_m}(i)+m}]| > |q[x_{{l_m}(i)},\cdots,x_{{l_m}(i)+m+1}]|. \end{array}\right. \end{aligned}$$

(48)

The reconstruction polynomial P(x) of degree $N+1$ is

$$\begin{aligned} P(x) = \sum _{j=0}^{N+1}a_{k}(x-x_{i})^{j}. \end{aligned}$$

(49)

The coefficients $a_j$ of the polynomial (45) are as follows:

$$\begin{aligned} a_{j} = \sum _{k=0}^{N-j+1}d_{kj}q[x_{{l_{N+1}}(i)},\cdots,x_{{l_{N+1}}(i)+j+k}], \quad j=1, \cdots, N+1, \end{aligned}$$

(50)

with

$$\begin{aligned} \left. \begin{array}{lcl} d_{0j} = 1, \\ \\ d_{k0} = (x_i - x_{{l_{N+1}(i)}+k-1})d_{k-1,0}, \\ \\ d_{kj} = d_{k,j-1} + (x_i - x_{{l_{N+1}(i)}+k+j-1})d_{k-1,j}. \end{array}\right\} \end{aligned}$$

(51)

Therefore the sought polynomial (45) has been determined. For details see for example [17].

In what follows we give details for ENO polynomials of second to fourth degree.

3.2 Piecewise-Linear ENO Reconstruction

The reconstruction polynomial of degree 1 on the cell $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ is

$$\begin{aligned} p_{1}(x) = a_0 + 2a_1(x-x_i) \; \end{aligned}$$

(52)

or

$$\begin{aligned} p_{1}(x) = q_i + \frac{q_{j+1}-q_j}{\Delta x}(x-x_i) \; \end{aligned}$$

(53)

on the stencils

$$\begin{aligned} S_0 = (i-1, i), \quad S_1 = (i,i+1). \end{aligned}$$

(54)

Here

$$\begin{aligned} j = \left\{ \begin{array}{lll} i &{} \quad {\text{ if }} &{} |q_{i+1}-q_i|\leqslant |q_{i}-q_{i-1}|,\\ \\ i-1 &{} \quad {\text{ otherwise }} &{} \end{array} \right. \end{aligned}$$

(55)

and the coefficients are

$$\begin{aligned} a_1 = \frac{q_{j+1}-q_j}{2\Delta x}, \quad a_0 = q_j + 2(x_i-x_j)a_1 = {q_i}. \end{aligned}$$

(56)

As stated in Sect. 2, the ADER method requires the value of the polynomial, as well as its spatial derivatives, at the cell interfaces. The sought values of the polynomial at interface $x_{i+1/2}$ are

$$\begin{aligned} p_{1}(x_{i+1/2}) = a_0 + a_1\Delta x, \quad \frac{{\mathrm{d}}}{{\mathrm{d}}x} p_{1}(x_{i+1/2}) = 2a_1. \end{aligned}$$

(57)

3.3 Piecewise-Quadratic ENO Reconstruction

The reconstruction on the cell $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ reads

$$\begin{aligned} p_{2}(x) = a_0 + 2a_1(x-x_i) +3a_2(x-x_i)^2 \end{aligned}$$

(58)

and the relevant stencils are

$$\begin{aligned} S_0 = (i-2,i-1, i), \quad S_1 = (i-1,i,i+1), \quad S_2 = (i,i+1,i+2). \end{aligned}$$

(59)

The choice of the indexes is as follows:

$$\begin{aligned} \left. \begin{array}{l} j = \left\{ \begin{array}{lll} i &{}{\text{ if }} \; |q_{i+1}-q_i |\leqslant |q_{i}-q_{i-1}|,&{}\\ \\ i-1 &{} {\text{ otherwise}}. &{} \end{array}\right. \\ \\ k = \left\{ \begin{array}{lll} j &{}{\text{ if }} \; |q_{j+2}-2q_{j+1} +q_{j}|\leqslant |q_{j+1}-2q_{j} +q_{j-1}|, &{} \\ \\ j-1 &{} {\text{ otherwise}}.&{} \end{array}\right. \end{array}\right\} \end{aligned}$$

(60)

Then

$$\begin{aligned} \left. \begin{array}{l} a_2 = \displaystyle \frac{q_{k+2}-2q_{k+1} +q_{k}}{6\Delta x^2}, \\ \\ a_1 = \displaystyle \frac{q_{k+1}-q_k}{2\Delta x} + \frac{q_{k+2}-2q_{k+1} +q_{k}}{2\Delta x}{\left(i-k-\frac{1}{2}\right)}, \\ \\ a_0 = \displaystyle q_i -\frac{1}{24}(q_{k+2}-2q_{k+1} +q_{k}). \end{array}\right\} \end{aligned}$$

(61)

Depending on the chosen indexes we can get three different polynomials. The values at the interface are

$$\begin{aligned} \left. \begin{array}{l} \displaystyle p_{2}(x_{i+1/2})= a_0 + a_1\Delta x + \frac{3}{4}a_2 \Delta x^2,\\ \\ \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}x}p_{2}(x_{i+1/2}) = 2a_1 +3a_2\Delta x, \\ \\ \displaystyle \frac{{\mathrm{d}}^2}{{\mathrm{d}}x^2}p_{2}(x_{i+1/2}) = 6a_2. \end{array}\right\} \end{aligned}$$

(62)

3.4 Piecewise-Cubic ENO Reconstruction

The reconstruction on the cell $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ is

$$\begin{aligned} p_{3}(x) = a_0 + 2a_1(x-x_i) +3a_2(x-x_i)^2 +4a_3(x-x_i)^3. \end{aligned}$$

(63)

The stencils are

$$\begin{aligned} \left. \begin{array}{l} S_0 = (i-3,i-2,i-1,i), \quad S_1 = (i-2,i-1,i,i+1), \\ \\ S_2 = (i-1,i,i+1,i+2), \quad S_3 = (i,i+1,i+2,i+3).\\ \end{array}\right\} \end{aligned}$$

(64)

The ENO choice of indexes is as follows:

$$\begin{aligned} \left. \begin{array}{l} j = \left\{ \begin{array}{lll} i &{}\quad {\text{ if }} \quad |q_{i+1}-q_i|\leqslant |q_{i}-q_{i-1}|,&{} \\ i-1 &{} \quad {\text{ otherwise}},&{} \end{array}\right. \\ \\ k = \left\{ \begin{array}{lll} j &{}\quad {\text{ if }} \quad |q_{j+2}-2q_{j+1} +q_{j}|\leqslant |q_{j+1}-2q_{j} +q_{j-1}|, &{} \\ j-1 &{} \quad {\text{ otherwise}},&{} \end{array}\right. \\ \\ h = \left\{ \begin{array}{lll} j &{}\quad {\text{ if }} \quad |q_{k+3}-3q_{k+2}+3q_{k+1} -q_{k}|&{} \\ &{}{\qquad} \leqslant |q_{k+2}-3q_{k+1}+3q_{k} -q_{k-1}|, &{} \\ j-1 &{} \quad {\text{ otherwise}}.&{} \end{array}\right. \\ \end{array}\right\} \end{aligned}$$

(65)

The coefficients read

$$\begin{aligned} \left. \begin{array}{l} a_3 = \displaystyle \frac{q_{h+3}-3q_{h+2}+3q_{h+1} -q_{h}}{24\Delta x^3}, \\ \\ a_2 = \displaystyle \frac{q_{h+2}-2q_{h+1} +q_{h}}{6\Delta x^2} + \frac{q_{h+3}-3q_{h+2}+3q_{h+1} -q_{h}}{6\Delta x^2}(i-h-1), \\ \\ \begin{array}{ll} {a_1} = &\displaystyle{\frac{q_{h+1}-q_h}{2\Delta x} + \frac{q_{h+2}-2q_{h+1} +q_{h}}{2\Delta x}{\left(i-h-\frac{1}{2}\right)}} \\ {} & \displaystyle{+ d_{22}\frac{q_{h+3}-3q_{h+2}+3q_{h+1} -q_{h}}{24\Delta x^3},}\\ \end{array} \\ \\ a_0 =\displaystyle q_i - \frac{a_2}{4}\Delta x^2. \end{array}\right\} \end{aligned}$$

(66)

The polynomial values at the interface $x_{i+\frac{1}{2}}$ are

$$\begin{aligned} \left. \begin{array}{l} \displaystyle p_{3}(x_{i+1/2}) = a_0+a_1\Delta x +\frac{3}{4}a_2\Delta x^2 + \frac{1}{2}a_3 \Delta x^3, \\ \\ \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}x}p_{3}(x_{i+1/2}) = 2a_1 +3a_2\Delta x + 3a_3 \Delta x^2, \\ \\ \displaystyle \frac{{\mathrm{d}}^2}{{\mathrm{d}}x^2}p_{3}(x_{i+1/2}) = 6a_2 + 12a_3 \Delta x, \\ \\ \displaystyle \frac{{\mathrm{d}}^3}{{\mathrm{d}}x^3}p_{3}(x_{i+1/2}) = 24a_3. \end{array}\right\} \end{aligned}$$

(67)

3.5 Piecewise-Quartic ENO Reconstruction

The reconstruction on the cell $[x_{i-\frac{1}{2}},x_{i+\frac{1}{2}}]$ is

$$\begin{aligned} p_{4}(x) = a_0 + 2a_1(x-x_i) +3a_2(x-x_i)^2 +4a_3(x-x_i)^3 + 5a_4(x-x_i)^4. \end{aligned}$$

(68)

The stencils are

$$\begin{aligned} \left. \begin{array}{l} S_0 = (i-4,i-3,i-2,i-1,i), \quad S_1 = (i-3,i-2,i-1,i,i+1), \\ \\ S_2 = (i-2,i-1,i,i+1,i+2), \quad S_3 = (i-1,i,i+1,i+2,i+3), \\ \\ S_4 = (i,i+1,i+2,i+3,i+4). \end{array}\right\} \end{aligned}$$

(69)

The ENO choice of indexes is

$$\begin{aligned} \left. \begin{array}{l} j = \left\{ \begin{array}{lcc} i &{} {\text{ if }} &{} \quad |q_{i+1}-q_i|\leqslant |q_{i}-q_{i-1}|,\\ i-1 &{} &{} {\text{ otherwise}}, \end{array}\right. \\ \\ k = \left\{ \begin{array}{lcc} j &{} {\text{ if }} &{} |q_{j+2}-2q_{j+1} +q_{j}|\leqslant |q_{j+1}-2q_{j} +q_{j-1}|, \\ j-1 &{} &{} {\text{ otherwise}}, \end{array}\right. \\ \\ h = \left\{ \begin{array}{lcc} j &{} {\text{ if } }&{} |q_{k+3}-3q_{k+2}+3q_{k+1} -q_{k}| \\ &{} &{} \leqslant |q_{k+2}-3q_{k+1}+3q_{k} -q_{k-1}|, \\ j-1 &{} &{} {\text{ otherwise}}, \end{array}\right. \\ \\ s = \left\{ \begin{array}{lcc} h &{} {\text{ if }} &{} |q_{h+4}-4q_{h+3}+6q_{h+2} -4q_{h+1} +q_{h}|\ \\ &{} &{} \leqslant |q_{h+3}-4q_{h+2}+6q_{h+1} -4q_{h} +q_{h-1}|, \\ h-1 &{} &{} {\text{ otherwise}}. \end{array}\right. \end{array}\right\} \end{aligned}$$

(70)

To determine the coefficients we first set

$$\begin{aligned} \left. \begin{array}{l} \begin{aligned} \displaystyle d_{23} =&{}\displaystyle \Delta x^2\left[ \left( i-s-\frac{1}{2}\right) \left( i-s+\frac{1}{2}\right) +2\left( i-s-\frac{3}{2}\right) (i-s)\right. \\ &{} \left. +3\left( i-s-\frac{5}{2}\right) \left( i-s-\frac{1}{2}\right) +4\left( i-s-\frac{7}{2}\right) (i-s-1)\right], \end{aligned}\\ \\ \begin{aligned} \displaystyle d_{22} =&{} \displaystyle \Delta x^2\left[ \left( i-s-\frac{1}{2}\right) \left( i-s+\frac{1}{2}\right) +2\left( i-s-\frac{3}{2}\right) (i-s)\right. \\ &{}\left. +3\left( i-s-\frac{5}{2}\right) \left( i-s-\frac{1}{2}\right) \right], \\ \end{aligned}\\ \\ \begin{aligned} d_{31} =&{} \displaystyle \Delta x^3 \left[ \left( i-s-\frac{3}{2}\right) \left( i-s-\frac{1}{2}\right) \left( i-s+\frac{1}{2}\right) \right. \\ &{} \displaystyle + \left( i-s-\frac{5}{2}\right) \left( i-s-\frac{1}{2}\right) \left( i-s+\frac{1}{2}\right) \\ &{} \left. \displaystyle +2\left( i-s-\frac{5}{2}\right) \left( i-s-\frac{3}{2}\right) (i-s)\right], \end{aligned}\\ \\ d_{32} = \displaystyle d_{31} + \Delta x\left( i-s-\frac{7}{2}\right) d_{22}. \end{array}\right\} \end{aligned}$$

(71)

Then the coefficients are

$$\begin{aligned} \left. \begin{array}{l} a_4 = \displaystyle \frac{q_{s+4}-4q_{s+3}+6q_{s+2} -4q_{s+1} +q_{s}}{120\Delta x^4}, \\ \\ \begin{aligned} a_3 =&{} \displaystyle \frac{q_{s+3}-3q_{s+2}+3q_{s+1} -q_{s}}{24\Delta x^3} \\ &{} \displaystyle +5\varDelta x\left( i-s-\frac{3}{2}\right) \frac{q_{s+4}-4q_{s+3}+6q_{s+2} -4q_{s+1} +q_{s}}{120\Delta x^4}, \end{aligned} \\ \\ \begin{aligned} a_2 =&{} \displaystyle \frac{q_{s+2}-2q_{s+1}+q_{s}}{6\Delta x^2}+ \frac{q_{s+3}-3q_{s+2}+3q_{s+1}-q_{s}}{6\Delta x^2}(i-s-1) \\ &{} \displaystyle + d_{23}\frac{q_{s+4}-4q_{s+3}+6q_{s+2} -4q_{s+1} +q_{s}}{120\Delta x^4}, \end{aligned} \\ \\ \begin{aligned} a_1 =&{} \displaystyle \frac{q_{s+1}-q_{s}}{2 \Delta x} + \frac{q_{s+2}-2q_{s+1}+q_{s}}{2\Delta x}\left( i-s-\frac{1}{2}\right) \\ \\ &{}+ \displaystyle d_{22}\frac{q_{s+3}-3q_{s+2}+3q_{s+1}-q_{s}}{24\Delta ^3} \\ &{}+ \displaystyle d_{32}\frac{q_{s+4}-4q_{s+3}+6q_{s+2} -4q_{s+1} +q_{s}}{120\Delta x^4}, \end{aligned} \\ \\ a_0 = \displaystyle q_i -\frac{a_2}{4}\Delta x^2 -\frac{a_4}{16}\Delta x^4. \end{array}\right\} \end{aligned}$$

(72)

The polynomial values at interface $x_{i+ \frac{1}{2}}$ are

$$\begin{aligned} \left. \begin{array}{l} \displaystyle p_{4}(x_{i+\frac{1}{2}}) = a_0 + a_1\Delta x + \frac{3}{4}a_2\Delta x^2 +\frac{1}{2}a_3\Delta x^3 + \frac{5}{16}a_4 \Delta x^4, \\ \\ \displaystyle \frac{{\mathrm{d}}}{{\mathrm{d}}x} p_{4}(x_{i+\frac{1}{2}}) = 2a_1 + 3a_2\Delta x +3a_3\Delta x^2 + \frac{5}{2}a_4 \Delta x^3, \\ \\ \displaystyle \frac{{\mathrm{d}}^2}{{\mathrm{d}}x^2} p_{4}(x_{i+\frac{1}{2}}) = 6a_2 +12a_3\Delta x + 15a_4 \Delta x^2,\\ \\ \displaystyle \frac{{\mathrm{d}}^3}{{\mathrm{d}}x^3} p_{4}(x_{i+\frac{1}{2}}) = 24a_3 + 60a_4 \Delta x, \\ \\ \displaystyle \frac{{\mathrm{d}}^3}{{\mathrm{d}}x^3} p_{4}(x_{i+\frac{1}{2}}) = 120a_4. \end{array}\right\} \end{aligned}$$

(73)

As already pointed out, the evaluation of the polynomial and its derivatives at the cell interface $x_{i+\frac{1}{2}}$, from the left and the right, is needed for solving the generalized Riemann problem to determine the numerical flux. To determine the numerical source we must evaluate the volume integral (24), for which one makes use of the polynomial p(x) and its derivatives in cell i, at nodes $x_l$ of the integration formula used, e.g., a Gauss-Legendre quadrature.

We have reviewed the ENO method as implemented in the fully discrete high-order ADER methodology. The ENO reconstruction method has been criticised for a number of reasons. One of them is the abrupt change of stencil simply due to small changes in the divided differences that determine the coefficients of the ENO polynomial. In fact, even round-off errors may decide the choice of stencil. Shu [26] addressed this issue by proposing a modified ENO method, called m-ENO here. In the next section, we propose a simple averaged ENO-type method, in which the classical ENO polynomial is averaged with its closest neighbour. A variant m-AENO results from substituting ENO by m-ENO, for schemes of 4th and greater order of accuracy. The results are encouraging.

4 Novel Polynomial Reconstruction: AENO

In this section, we present a non-linear polynomial reconstruction procedure that is akin to both the existing ENO and WENO procedures [12,13,14,15, 27, 28]. We first present an example that motivates this section.

4.1 A Motivating Example: Second-Order ADER Method

We begin by considering the simplest, first-degree, polynomial reconstruction

$$\begin{aligned} p_{i}(x) = q^{n}_{i} +(x-x_{i}) \varDelta _{i} \; \end{aligned}$$

(74)

within the cell $[x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}]$, at time $t=t_{n}$. Here $x_{i}= \frac{1}{2}(x_{i-\frac{1}{2}}+x_{i+\frac{1}{2}})$ is the cell centre and $\varDelta _{i}$ is the slope of $p_{i}(x)$, still to be determined. Figure 2 depicts two polynomials of the form (74) and the results are respectively determined by choosing the slope thus

$$\begin{aligned} \varDelta _{i} \equiv \varDelta _{i-\frac{1}{2}}= \frac{q_{i}^{n}- q_{i-1}^{n}}{\Delta x} \;; \quad \varDelta _{i} \equiv \varDelta _{i+\frac{1}{2}}= \frac{q_{i+1}^{n}- q_{i}^{n}}{\Delta x}. \end{aligned}$$

(75)

Assume that the slope $\varDelta _{i}$ is chosen as the weighted average

$$\begin{aligned} \varDelta _{i} = \frac{1}{2}(1+\omega )\varDelta _{i-\frac{1}{2}}+\frac{1}{2}(1-\omega )\varDelta _{i+\frac{1}{2}}, \quad \omega \in [-1,1]. \end{aligned}$$

(76)

It is easy to show that the second-order ADER method with the linear reconstruction (74) reproduces the classical second-order schemes of Lax-Wendroff, Warming-Beam and Fromm if $\omega$ in (76) is chosen as follows:

$$\begin{aligned} \omega = \left\{ \begin{array}{cl} {-1:} &{} {\text{ Lax-Wendroff }} {\text{ method}}, \\ \;\;{0:}&{} {\text{ Fromm }} {\text{ method}}, \\ \;\;{1:}&{} {\text{ Warming-Beam }} {\text{ method}}. \\ \end{array} \right. \end{aligned}$$

(77)

Fig. 2

Two possible first-degree reconstruction polynomials $p_{L}(x)$ (left) and $p_{R}(x)$ (right) for cell $[x_{i-\frac{1}{2}}, x_{i+\frac{1}{2}}]$. These result from choosing the slope as in (75)

The classical ENO [12] second-order method chooses

$$\begin{aligned} \varDelta _{i} = \left\{ \begin{array}{lll} \varDelta _{i-\frac{1}{2}} &{}\quad {\text{ if }} &{} |\varDelta _{i-\frac{1}{2}}| \leqslant |\varDelta _{i+\frac{1}{2}}|, \\ \varDelta _{i+\frac{1}{2}} &{}\quad {\text{ if }} &{} |\varDelta _{i-\frac{1}{2}}| > |\varDelta _{i+\frac{1}{2}}|. \end{array} \right. \end{aligned}$$

(78)

In other words, the classical ENO second-order method switches non-linearly between the Lax-Wendroff and the Warming-Beam methods, depending on the relative sizes in the absolute value of the slopes $\varDelta _{i-\frac{1}{2}}$ and $\varDelta _{i+\frac{1}{2}}$.

A simple third-order method. It is interesting to note that, still in the frame of the second-order ADER method, if the weight parameter $\omega$ is chosen as

$$\begin{aligned} \omega = \frac{1}{3} (2c-{\text{sign}}(c)), \end{aligned}$$

(79)

then, a third-order accurate method results, in both space and time. Here c is the Courant number. This scheme was first presented in [33], see Eq. (13.39), and also in [37], in the setting of the MUSCL-Hancock method [44]. However, it has been shown that for the homogeneous case, the MUSCL-Hancock method is entirely equivalent to the ADER method in second-order mode (ADER2), see [20]. We have again verified this in the setting of ADER methods. The details of the analysis are omitted.

Figure 3 displays computed results for the linear advection equation, for which a Gaussian profile is used as initial condition, where comparison is made with ADER2 in conjunction with ENO reconstruction (74), (75) and (78). Table 1 shows empirical convergence rates for the linear advection equation in which it is verified that the ADER2 (formally second-order) scheme with reconstruction (74) with (76) and $\omega$ given by (79) is third-order accurate in both space and time.

Fig. 3

Numerical results for the linear advection equation for a Gaussian profile test, comparing ADER2 with ENO (circles) and ADER2 with AENO slope (76) (squares), with $\omega =\frac{1}{3}(2c-{\text{sign}}(c))$. $T_{\mathrm{out}}=100$ units, mesh $M=100$ cells and $C_{\mathrm{cfl}}=0.9$

The AENO reconstruction method presented in this paper, in fact emerges from averaging of two polynomials in the frame of the ENO scheme to choose the reconstruction stencil. The construction of ADER schemes of up to fifth order in space and time, based on averages of the type (76) were constructed by MSc student Andrea Santacá in his Master thesis [24]. Additionally, in the present paper we include a variant of AENO, called m-AENO, to be explained later.

Table 1 Empirical convergence rates for ADER2 with the particular choice of slope averaging $\omega=\frac{1}{3}(2c-{\text{sign}}(c))$ in (79)

4.2 A Joining Function for Averaging Two Polynomials

Motivated by the example of the previous Sect. 4.1 we seek an averaging procedure that can be applied to two polynomials of arbitrary degree. First we define the function

$$\begin{aligned} \omega (x) = \frac{-x}{ \sqrt{\epsilon ^{2}+x^{2}} }, \quad x \in {\mathcal {R}}, \end{aligned}$$

(80)

and $\epsilon \in {\mathcal {R}}$, a constant, with $|\epsilon | < 1$. Consider now the averaging function $J(\omega (x))$ joining smoothly two constant, real states $q_{L}$ and $q_{R}$, as follows:

$$\begin{aligned} J(w(x)) = \frac{1}{2}[1+w(x)]q_{L}+\frac{1}{2}[1-w(x)]q_{R}. \end{aligned}$$

(81)

Note the analogy between the weighted average (76) and (81). While in (76) the weight $\omega$ is constant, in (81) $\omega (x)$ is obviously variable.

Figure 4 shows the weight function $\omega (x)$ for $\epsilon ^{2}=0.2$. For $x<0$ the function $\omega (x)$ approaches 1 rapidly, while for $x>0$, $\omega (x)$ approaches $-1$. Note the following properties of $\omega (x)$:

$$\begin{aligned} \left\{ \begin{array}{l} \omega (0) = 0, \\ \\ \omega (-\epsilon ) = \frac{1}{2}\sqrt{2} \approx 0.72, \\ \\ \omega (+\epsilon ) = -\frac{1}{2}\sqrt{2} \approx -0.72. \end{array} \right. \end{aligned}$$

(82)

Note also the associated properties of $J(\omega (x))$:

$$\begin{aligned} \left\{ \begin{array}{l} J(\omega (0)) = \frac{1}{2}(q_{L} + q_{R}), \\ \\ J(\omega (-\epsilon )) = \frac{1}{2}\left( 1+\frac{1}{2}\sqrt{2}\right) q_{L}+\frac{1}{2}\left( 1-\frac{1}{2}\sqrt{2}\right) q_{R},\\ \\ J(\omega (+\epsilon )) = \frac{1}{2}\left( 1-\frac{1}{2}\sqrt{2}\right) q_{L}+\frac{1}{2}\left( 1+\frac{1}{2}\sqrt{2}\right) q_{R}. \end{array} \right. \end{aligned}$$

(83)

Fig. 4

Weight function $\omega (x)$ defined by (80) for $\epsilon ^{2}=0.2$

Figure 5 shows the distribution of $J(\omega (x))$ for $q_{L} = 3$, $q_{R} = -2$ and $\epsilon ^{2}=0.2$. It is seen that $J(\omega (x))$ approaches $q_{L} = 3$ for $x<0$, while $J(\omega (x))$ tends to $q_{R} = -2$ for $x>0$. Note that $J(\omega (x))$ is monotone, as

$$\begin{aligned} J'(\omega (x)) = \frac{1}{2}(q_{L}-q_{R})\omega '(x) \left\{ \begin{array}{ccc}< 0 &{}\quad {\text{ if }} &{} q_{L}>q_{R}, \\ \\ > 0 &{}\quad {\text{ if }} &{} q_{L}<q_{R} \; \end{array}\right. \end{aligned}$$

(84)

and

$$\begin{aligned} \omega '(x) = \frac{-\epsilon ^{2}}{(\epsilon ^{2}+x^{2})^{\frac{3}{2}}} < 0, \forall x. \end{aligned}$$

(85)

Note also that $J'(x) \rightarrow 0$ as $|\omega (x)| \rightarrow \infty$. That is the constant states $q_{L}$ and $q_{R}$ are approached asymptotically by J(x). However we note that these states are approached very rapidly. Consider a positive integer N, then

$$\begin{aligned} \omega (N\epsilon ) = \frac{-N\epsilon }{\sqrt{\epsilon ^{2}+N^{2}\epsilon ^{2}}} = -\frac{N}{\sqrt{1+N^{2}}}{\text{sign}}(\epsilon ). \end{aligned}$$

(86)

For large N,

$$\begin{aligned} \omega (N\epsilon ) \approx - {\text{sign}}(\epsilon ) =-1. \end{aligned}$$

(87)

For example, for $N=10$, $\frac{N}{\sqrt{1+N^{2}}} \approx 0.995$. That is, at a distance of $10\epsilon$ from the origin, J(x) attains the constant states with an error of less than $1 \%$. Finally, we note that the use of $\epsilon ^{2}$ in the definition of $\omega (x)$ is convenient, as it permits a precise evaluation of J(x) at a distance $\epsilon$ from the origin. In particular applications, a translation might be necessary. In this paper we use J(x) for averaging two polynomials, through the averaging of their coefficients.

Fig. 5

AENO coefficient function $C(\omega )$ derived from the joining function J, for coefficients $C_{L} = 3$ (left) and $C_{R} = -2$ (right) and $\epsilon ^{2}=0.5$. The resulting AENO coefficient $C_{\text{AENO}}$ is closer to the min

When applying the above averaging function (81) to two states $q_{L}$ and $q_{R}$ we proceed as follows. First we define

$$\begin{aligned} s=\frac{|q_{L}|}{|q_{R}|+{\mathrm{TOL}}}, \end{aligned}$$

(88)

where TOL is a small positive quantity chosen to avoid division by zero, e.g., ${\text {TOL}}=10^{-6}$. Then we redefine

$$\begin{aligned} \omega (s) = \frac{-(s-1)}{ \sqrt{\epsilon ^{2}+(s-1)^{2}} }. \end{aligned}$$

(89)

It is easy to see that for the joining function (81) we have

$$\begin{aligned} \left. \begin{array}{l} |q_{L}| \leqslant |q_{R}| \Longleftrightarrow 0 \leqslant s \leqslant 1 \Longrightarrow \frac{1}{2}[1+ \omega (s)]q_{L} {\text{ is }} {\text{ given }} {\text{ greater }}{ \text{ weight}}, \\ \\ |q_{L}| \geqslant |q_{R}| \Longleftrightarrow s \geqslant 1 \Longrightarrow \frac{1}{2}[1- \omega (s)]q_{R} {\text{ is }}{ \text{ given }}{ \text{ greater }} {\text{ weight}}. \end{array}\right\} \end{aligned}$$

(90)

In other words, in the joining function (81) acting on two states $q_{L}$ and $q_{R}$, the smaller argument in absolute value receives the larger weight and the larger argument in absolute value receives the smaller weight. This averaging procedure will be applied to two polynomials, the ENO polynomial and that closest to it, by applying it to each pair of respective coefficients. The coefficients of the ENO polynomial will receive the larger weight, as we shall see in the next section.

4.3 AENO: a Two-Polynomial Average Method

In Sect. 3 we reviewed the ENO spatial reconstruction method. In Sect. 4.1 we showed that averaging of the ENO polynomial with its closest neighbour is capable of producing encouraging results. In particular in Sect. 4.1, we showed that for the formally second-order ADER method there is an averaging for which such formally second-order ADER method is actually third-order accurate in both space and time.

In this section, we propose a reconstruction method based on a two-polynomial averaging procedure. Two schemes are proposed. Scheme 1, called AENO, results from a weighted average of the classical ENO polynomial and its closest neighbour. Scheme 2, called m-AENO, follows a similar approach and results from a weighted average of the classical m-ENO polynomial of Shu [26] and its closest neighbour. We first describe AENO.

Here we introduce a general averaging procedure as applied to two neighbouring polynomials of arbitrary degree. Assume an Nth degree polynomial p(x) on cell $[x_{i-1/2},x_{i+1/2}]$ of the form

$$\begin{aligned} p(x) = a_0 + 2a_1(x-x_i) + \cdots + (N+1)a_N(x-x_i)^N \; \end{aligned}$$

(91)

that has been obtained by differentiating a polynomial P(x) of degree $N+1$. By redefining the coefficients as

$$\begin{aligned} {\hat{a}}_1 = 2a_1, \cdots, {\hat{a}}_N = (N+1)a_N \end{aligned}$$

(92)

we write

$$\begin{aligned} p(x) = a_0 + {\hat{a}}_1(x-x_i) + \cdots + {\hat{a}}_N(x-x_i)^N. \end{aligned}$$

(93)

For the sake of simplicity, in what follows the hat is omitted.

Recall that with a reconstruction polynomial of degree N it is possible to construct an ADER numerical method of order $(N+1)$ in both space and time. Then in the context of the ENO method, we need $N+1$ stencils and following the ENO approach we find a single, best polynomial, the ENO polynomial. In the AENO approach, instead of choosing just the single ENO polynomial we consider another polynomial, the closest to the ENO polynomial and take an average of these two. Moreover, the search of the stencils for the two polynomials is commanded by the conventional ENO approach and the coefficients of the ENO polynomial take the largest weight.

Example 2 In the case of a third-order method we just need second-degree polynomials, for which we have three possible candidates, namely

$$\begin{aligned} \left. \begin{array}{l} p_{L}(x) = a_{0L} + a_{1L}(x-x_i) +a_{2L}(x-x_i)^2, \\ p_{M}(x) = a_{0M} + a_{1M}(x-x_i) +a_{2M}(x-x_i)^2, \\ p_{R}(x) = a_{0R} + a_{1R}(x-x_i) +a_{2R}(x-x_i)^2. \end{array}\right\} \end{aligned}$$

(94)

In the ENO context we choose one of these polynomials according to the ENO algorithm presented earlier. In this example, we need two stages. In the AENO case we perform just one step of the algorithm; basically, we choose the direction based on the first-order slope, which is either left or right. If the direction is left then we take an average of the coefficients of $p_L(x)$ and $p_M(x)$; otherwise we take an average of the coefficients of $p_M(x)$ and $p_R(x)$. Suppose the direction is the left one, then the sought polynomial is

$$\begin{aligned} {\tilde{p}}(x) = {\tilde{a}}_{0} + {\tilde{a}}_{1}(x-x_i) + {\tilde{a}}_{2}(x-x_i)^2, \end{aligned}$$

(95)

with

$$\begin{aligned} \left. \begin{array}{l} {\tilde{a}}_{2} = \displaystyle \frac{1}{2}(1+\omega )a_{2L} + \frac{1}{2}(1-\omega )a_{2M},\\ \\ \omega = \omega (s) = \displaystyle \frac{1-s}{\root \of {\epsilon ^{2} + (1-s)^2}}, \quad s= \frac{|a_{2L}|}{|a_{2M}|+{\text {TOL}}} \; \end{array}\right\} \end{aligned}$$

(96)

and

$$\begin{aligned} \left. \begin{array}{l} {\tilde{a}}_{1} = \displaystyle \frac{1}{2}(1+\omega )a_{1L} + \frac{1}{2}(1-\omega )a_{1M},\\ \\ \omega = \displaystyle \frac{1-s}{\root \of {\epsilon ^{2} + (1-s)^2}}, \quad s= \frac{|a_{1L}|}{|a_{1M}|+{\text {TOL}}}. \end{array}\right\} \end{aligned}$$

(97)

The coefficient ${\tilde{a}}_0$ is chosen so as to comply with the conservation property, that is

$$\begin{aligned} {\tilde{a}}_0 = q_i^n -\frac{1}{\Delta x}\int _{x_{i-1/2}}^{x_{i+1/2}}[{\tilde{a}}_1(x-x_i)+ {\tilde{a}}_2(x-x_i)^2] {\mathrm{d}}x. \end{aligned}$$

(98)

The parameter $\epsilon ^{2}$ is a positive constant, while TOL is a small positive tolerance to avoid division by zero. In practice we take ${\text {TOL}}=10^{-6}$.

Generalization: The AENO procedure is then generalized as follows.

• Step 1 ENO-determined stencil. Perform $N-1$ steps of the algorithm to choose the stencils: for $m=1,\cdots,N-1$,

  $$\begin{aligned} l_{m+1}(i) = \left\{ \begin{array}{lcl} l_m(i) &{}\quad {\text {if }}&{\quad} |q[x_{{l_m}(i)},\cdots,x_{{l_m}(i)+m+1}]|\\ &{} &{} \leqslant |q[x_{{l_m}(i)-1},\cdots,x_{{l_m}(i)+m}]|, \\ \\ l_{m}(i)-1 &{} &{} {\text {otherwise}}. \end{array} \right. \end{aligned}$$

  (99)

  This step results in two polynomials $p_{L}(x)$ and $p_{R}(x)$, with coefficients $a_{kL}$ and $a_{kR}$, respectively.

• Step 2 averaging. Take the average of the coefficients of the polynomials $p_{L}(x)$ and $p_{R}(x)$ to obtain the coefficients of the AENO polynomial, namely

  $$\begin{aligned} {\tilde{a}}_{k} = \frac{1}{2}(1+\omega )a_{kL} + \frac{1}{2}(1-\omega )a_{kR}, \end{aligned}$$

  (100)

  with

  $$\begin{aligned} \omega = \frac{1-s}{\root \of {\epsilon ^2 + (1-s)^2}}, \quad s= \frac{|a_{kL}|}{|a_{kR}|+{\text {TOL}}} \end{aligned}$$

  (101)

  and

  $$\begin{aligned} {\tilde{a}}_0 = q_i^n -\frac{1}{\Delta x}\int _{x_{i-1/2}}^{x_{i+1/2}}({\tilde{a}}_1(x-x_i)+ \cdots + {\tilde{a}}_N(x-x_i)^N){\mathrm{d}}x. \end{aligned}$$

  (102)

• Step 3 the AENO polynomial. The resulting polynomial is

  $$\begin{aligned} {\tilde{p}}(x) = {\tilde{a}}_0 + {\tilde{a}}_1(x-x_i) + \cdots + {\tilde{a}}_N(x-x_i)^N. \end{aligned}$$

  (103)

The m-AENO scheme follows a similar approach to the AENO scheme presented above. The difference is that, instead of relying on the classical ENO polynomial we rely on the classical m-ENO polynomial of Shu [26]. Then the m-AENO scheme results from a weighted averaged of m-ENO polynomial and its closest neighbour. We omit the details. For background of the m-ENO polynomial the reader is referred to the original paper of Shu [26].

In the next section, we carry out a thorough assessment of the newly proposed spatial reconstruction procedure, as applied to the linear advection equation.

5 Results for the Linear Advection Equation

Here we assess the performance of ADER with the newly proposed AENO reconstruction procedure. For the assessment we compare numerical solutions against the exact solutions and against numerical solutions with ENO, m-ENO and WENO, also in conjunction with ADER. To this end we consider four test problems, namely IVP1, IVP2, IVP3 and IVP4 given below

$$\begin{aligned}&\left. \begin{array}{ll} \hbox {PDE:} &{} \partial _{t} q + \lambda \partial _{x} q = 0, x \in [0,30], \\ \hbox {IC:} &{} q(x,0) = h(x)= \sin {\left(\frac{2}{5} \uppi x\right)}. \end{array}\right\} \quad {\text{ IVP1 }} \; \end{aligned}$$

(104)

$$\begin{aligned}&\left. \begin{array}{ll} \hbox {PDE:} &{} \partial _{t} q + \lambda \partial _{x} q = 0, x \in [0,1], \\ \hbox {IC:} &{} q(x,0) = h(x)= \sin (2 \uppi x). \end{array}\right\} \quad {\text{ IVP2 }} \; \end{aligned}$$

(105)

$$\begin{aligned}&\left. \begin{array}{ll} \hbox {PDE:} &{} \partial _{t} q + \lambda \partial _{x} q = 0, x \in [0,2], \\ \hbox {IC:} &{} q(x,0) = h(x)= \sin ^4(\uppi x). \end{array}\right\} \quad {\text{ IVP3 }} \; \end{aligned}$$

(106)

$$\begin{aligned}&\left. \begin{array}{ll} \hbox {PDE:} &{} \partial _{t} q + \lambda \partial _{x} q = 0, x \in [-1,1], \\ \hbox {IC:} &{} q(x,0) = h(x)= \left\{ \begin{array}{ll} \exp \left(\frac{\ln 2 (x+0.7)^2}{0.000\,9}\right), &{} -0.8 \leqslant x \leqslant -0.6, \\ 1, \, &{} -0.4 \leqslant x \leqslant -0.2, \\ 1-\vert 10x-1 \vert, \, &{} 0.0 \leqslant x \leqslant 0.2, \\ (1-100(x-0.5)^2)^{1/2}, \, &{} 0.4 \leqslant x \leqslant 0.6, \\ 0, \, &{} {\text {otherwise}}. \\ \end{array} \right. \end{array}\right\} {\text{ IVP4 }} \end{aligned}$$

(107)

The exact solution in each IVP is given as

$$\begin{aligned} q(x,t) = h(x-\lambda t). \end{aligned}$$

(108)

5.1 Solution Profiles for Long-Time Evolution

The purpose of this section is to illustrate the performance of the new schemes for linear IVPs for long-time evolution, which is known to be particularly challenging for low accuracy schemes. We compare results to exact solutions and to numerical solutions obtained with established reconstruction methods, namely ENO, m-ENO and WENO. To this end, we use IVP1 with smooth initial conditions and IVP4 with a combination of smooth and discontinuous parts. The second problem IVP4 is a more realistic representation of practical problems for hyperbolic equations that involve both smooth parts as well as discontinuities.

Figures 6, 7, 8, 9 and 10 show computed results (symbols) for IVP1 (104) compared to the exact solution (line) for the ADER high-order scheme with various reconstruction methods, from 2nd to 5th orders of accuracy in both space and time. For the new methods AENO and m-AENO we used $\epsilon ^{2}=\frac{1}{2}$. Obviously, for all methods, increasing the order of accuracy progressively improves the agreement between the numerical solution and the exact solution. The reconstruction method used has a visible effect on the computed solution; this is patently obvious for 2nd and 3rd orders of accuracy but it is still visible for higher orders of accuracy. Long-time evolution also contributes to differentiate between methods in terms of accuracy. Judging from the figures, AENO is clearly more accurate than both ENO and m-ENO; this is especially clear for 2nd, 3rd and 4th orders of accuracy. In fact, the new AENO schemes of this paper compare well with the sophisticated WENO; it is even reasonable to state that the new AENO schemes have a small advantage over WENO; compare carefully the profiles for 3rd and 4th orders of accuracy. For second order, WENO is superior to all other schemes.

Fig. 6

IVP1: long-time evolution test for IVP1 (104). ADER scheme with ENO reconstruction for the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}} = 500$ and $C_{\mathrm{cfl}}=0.9$

Fig. 7

IVP1: long-time evolution test for IVP1 (104). ADER scheme with m-ENO reconstruction for the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}} = 500$ and $C_{\mathrm{cfl}}=0.9$

Fig. 8

IVP1: long-time evolution test for IVP1 (104). ADER scheme with AENO reconstruction for the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}} = 500$ and $C_{\mathrm{cfl}}=0.9$

Fig. 9

IVP1: long-time evolution test for IVP1 (104). ADER scheme with m-AENO reconstruction for the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}} = 500$ and $C_{\mathrm{cfl}}=0.9$

Fig. 10

IVP1: long-time evolution test for IVP1 (104). ADER scheme with WENO reconstruction for the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}} = 500$ and $C_{\mathrm{cfl}}=0.9$

Figures 11, 12, 13, 14 and 15 show computed results for the multiple wave test IVP4 for a long evolution time $T_{\mathrm{out}} = 2\,000$ units and a coarse mesh of just $M=100$ cells. This is an exceedingly demanding test problem, as it contains the conflicting requirements of high accuracy for smooth parts and high resolution without spurious oscillations in the vicinity of discontinuities. Figure 11 shows results for ENO in conjunction with ADER for schemes of 2nd to 5th order in space and time. Clearly, for the long chosen output time and the coarse mesh used, even the 5th order scheme gives large errors; even higher order of accuracy would be required to obtain acceptable results. The challenges of this test are representative of practical computational problems involving long time evolution, such as in acoustics, seimic waves and tsunamic waves. Figure 12 shows results for m-ENO in conjunction with ADER for schemes of 2nd to 5th order in space and time. Results are comparable to those of ENO in Fig. 11.

Fig. 11

ENO results for IVP4 (107): ADER scheme with the ENO reconstruction for the linear advection with $\lambda = 1$, ${M}=100$, $T_{\mathrm{out}} = 2\,000$ and $C_{\mathrm{cfl}} = 0.9$

Fig. 12

m-ENO results for IVP4 (107): ADER scheme with the m-ENO reconstruction for the linear advection with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

Fig. 13

AENO results for IVP4 (107): ADER scheme with the AENO reconstruction for the linear advection with $\lambda = 1$, ${M}=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

Fig. 14

m-AENO results for IVP4 (107): ADER scheme with the m-AENO reconstruction for the linear advection with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

Fig. 15

WENO results for IVP4 (107): ADER scheme with the WENO reconstruction for the linear advection with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

Figure 13 shows results for the new AENO scheme. Compared to the classical ENO and m-ENO shown in Figs.  11 and  12, the new AENO scheme is clearly superior; this is more evident for 3rd and 4th orders of accuracy. Surprisingly, this observation is also true for WENO, comparing Figs. 13 and 15. Only for the 5th order case, AENO and WENO are, roughly, comparable; WENO displays some more visible undershoots and a spurious oscillation on the right-hand side. Results for the second version of our averaged ENO, m-AENO, are shown in Fig. 14. For 2nd and 3rd order accuracy, these results are identical to those of AENO. In fact, the schemes ENO and m-AENO are identical in these two cases. For 4th and 5th order cases the performance of m-AENO is visibly inferior to that of AENO. In fact, m-AENO is also inferior to the classical ENO, m-ENO and WENO schemes for this test problem and for the 4th and 5th order cases. Table 2 shows the errors in the computed solutions for the multi-wave test problem.

Table 2 $L_1$-errors for multi-wave test IVP4 (107) from the ADER scheme from 2nd to 5th order, in conjunction with ENO, m-ENO, WENO, AENO and m-AENO reconstructions, as applied the linear advection equation with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

For the multi-wave test IVP4, it is the discontinuous components of the profile that pose the most severe challenge to the numerical methods. This is a recurrent feature of high-order methods for hyperbolic equations. To highlight this feature, we carried out computations by keeping the square wave only, in the initial condition of IVP4. Results are shown in Figs. 16 and 17. Figure 16 shows four frames corresponding to ADER schemes of orders 2, 3, 4 and 5. For each order we plot results for all reconstruction schemes, noting that for orders 4 and 5 we have five distinct reconstruction schemes. For second-order ADER (ADER-2), WENO gives the best results, whereas for all higher-order ADER schemes, AENO gives the best results, by an appreciable margin, most evident for 3rd and 4th orders of accuracy. Note the undershoots in the WENO results for the 5th order scheme. Figure 17 shows four frames corresponding to four reconstruction schemes, including the two new ones of this paper, namely AENO and m-AENO. For each reconstruction schemes we see the effect of increasing the order of accuracy, from 2 to 5. Note the peculiar behaviour of m-AENO for the 4th order scheme. At this stage we note, however, that when it comes to smooth solutions, even with large derivatives, the modified AENO scheme, namely m-AENO based on m-ENO, performs very well indeed, as we shall see in the convergence rates results in Sect. 5.2.

Fig. 16

Square wave results: ADER schemes from 2nd to 5th order with ENO, m-ENO, WENO, AENO and m-AENO reconstructions for the linear advection with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

Fig. 17

Square wave results: ADER scheme with ENO, WENO, AENO and m-AENO reconstructions for the linear advection with $\lambda = 1$, $M=100$, $T_{\mathrm{out}}= 2\,000$ and $C_{\mathrm{cfl}}= 0.9$

5.2 Convergence Rate Study for the Linear Advection Equation

In this section, we carry out a convergence rate study for the linear advection equation through IVP2 (105) and IVP3 (106), for the schemes of 2nd to 5th order of accuracy in space and time. We compare the newly presented schemes AENO and m-AENO, with the established ENO, m-ENO and WENO reconstruction methods, all of them used with the fully discrete ADER approach. IVP2 (105) could be described as a smooth test of the kind commonly used in the literature to assess convergence rates. IVP3 (106) also serves the same purpose but it is recognised as an exceedingly severe test problem, for which many commonly used high-order schemes fail to give the expected rates.

Results for IVP2. Results are shown in Tables 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12, where errors and corresponding orders of accuracy are shown for the three norms $L_{1}$, $L_{2}$ and $L_{\infty }$. Results for IVP2 (105) are shown in Tables 3, 4, 5, 6 and 7. All schemes attain the theoretically expected convergence rates, for all orders, in the $L_{1}$ norm. WENO, with the exception of the second-order scheme, attains the theoretically expected convergence rates also in the $L_{2}$ and $L_{\infty }$ norms. The remaining schemes show poor performance in these norms, especially in the $L_{\infty }$ norm. Generally, ENO and m-ENO show comparable performance, perhaps with small advantage to ENO. The new AENO scheme does not perform satisfactory in the $L_{2}$ and $L_{\infty }$ norms; as a matter of fact in these norms AENO is inferior to ENO and m-ENO. The new m-AENO scheme improves with respect to AENO for the 5th order scheme.

Table 3 ENO results for IVP2 (105): convergence-rate study for the ADER scheme with the ENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 0.5$ and $C_{\mathrm{cfl}} =0.9$

Table 4 m-ENO results for IVP2 (105): convergence-rate study for the ADER scheme with the m-ENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 0.5$ and $C_{\mathrm{cfl}} =0.9$

Table 5 AENO results for IVP2 (105): convergence-rate study for the ADER schemes with the AENO reconstruction with $\epsilon ^2 = 0.5$ for the linear advection for $\lambda = 1$, $T_{\mathrm{out}} = 0.5$, $C_{\mathrm{cfl}} =0.9$

Table 6 m-AENO results for IVP2 (105): convergence-rate study for the ADER schemes with the m-AENO reconstruction with $\epsilon ^2 = 0.5$ for the linear advection for $\lambda = 1$, $T_{\mathrm{out}} = 0.5$, $C_{\mathrm{cfl}} =0.9$

Table 7 WENO results for IVP2 (105): convergence-rate study for ADER schemes with the WENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 0.5$ and $C_{\mathrm{cfl}} =0.9$

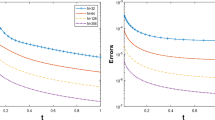
Figure 18 shows computed $L_1$-errors for IVP2 (105), as the mesh is refined, for the ADER scheme with all reconstruction schemes of this paper: ENO, m-ENO, WENO, AENO and m-AENO. With the exception of the second-order case, for which WENO is the most accurate reconstruction method, the AENO schemes of this paper outperform all the other reconstruction methods.

Fig. 18

Computed $L_1$-errors for IVP2 (105), as the mesh is refined, for the ADER scheme with reconstructions: ENO, m-ENO, WENO, AENO and m-AENO, as applied to the linear advection with $\lambda = 1$, $T_{\mathrm{out}}= 0.5$ and $C_{\mathrm{cfl}}= 0.9$

Results for IVP3. As stated previously IVP3 is an exceedingly severe test problem, for which many of the commonly used high-order schemes fail to give the expected convergence rates. Results for the schemes of this paper are shown in Tables 8, 9, 10, 11 and 12, where errors and corresponding orders of accuracy are shown for the three norms $L_{1}$, $L_{2}$ and $L_{\infty }$.

Table 8 ENO results for IVP3 (106): convergence-rate study for the ADER scheme with the ENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 4$ and $C_{\mathrm{cfl}} =0.9$

Table 9 m-ENO results for IVP3 (106): convergence-rate study for the ADER scheme with the m-ENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 4$ and $C_{\mathrm{cfl}} =0.9$

Table 10 AENO results for IVP3 (106): convergence-rate study for the ADER schemes with the AENO reconstruction with $\epsilon ^2 = 0.5$ for the linear advection for $\lambda = 1$, $T_{\mathrm{out}} = 4$, $C_{\mathrm{cfl}} =0.9$

Table 11 m-AENO results for IVP3 (106): convergence-rate study for the ADER schemes with the m-AENO reconstruction with $\epsilon ^2 = 0.5$ for the linear advection for $\lambda = 1$, $T_{\mathrm{out}} = 4$, $C_{\mathrm{cfl}} =0.9$

Table 12 WENO results for IVP3 (106): convergence-rate study for ADER schemes with the WENO reconstruction for the linear advection with $\lambda = 1$, $T_{\mathrm{out}} = 4$ and $C_{\mathrm{cfl}} =0.9$

For the ENO scheme, results are shown in Table 8. The scheme attains the expected convergence rates sub-optimally for the second and third order cases in the $L_{1}$ norm, while failing in the $L_{2}$ and $L_{\infty }$ norms. The 4th order ENO scheme fails to attain the expected rates in all three norms, while for the 5th order case computed rates are close to the expected ones, but are sub-optimal. In summary, ENO fails the convergence rate test for IVP3. For the modified ENO (m-ENO) scheme of Shu [26] we show the computed results in Table 9, where significant improvements with respect to ENO are seen; however, computed rates are sub-optimal and failure is seen in some cases for the $L_{2}$ and $L_{\infty }$ norms.

For the new AENO scheme of this paper, results are shown in Table 10. For the lower-order cases, 2nd and 3rd order, results are satisfactory, but the scheme fails to attain the expected convergence rates for the higher-order schemes, 4th and 5th order. For the new variant of AENO, called m-AENO, results are shown in Table 11. Note that m-AENO is identical to AENO for the second- and third-order schemes, see Table 10 and corresponding comments. The performance of m-AENO for the 4th and 5th order schemes is very satisfactory, attaining the expected rates in the $L_{1}$ and $L_{2}$ norms, even if sub-optimally for the $L_{2}$ norm. In the 4th order case the scheme does not attain the expected rate in the $L_{\infty }$ norm. In summary, m-AENO constitutes a significant improvement over AENO, for the higher-order range.

Results for the classical WENO scheme in conjunction with the fully discrete ADER approach are shown in Table 10. Generally, the WENO results are satisfactory for this severe test problem. For the second-order case convergence in the $L_{1}$ norm is attained, being sub-optimal for the $L_{2}$ norm and failing for the $L_{\infty }$ norm. For the higher-order schemes, convergence is attained in all norms, except for the 4th order scheme, where convergence is sub-optimal in the $L_{1}$ norm and fails in the $L_{2}$ and $L_{\infty }$ norms. In summary, out of the five reconstruction schemes, WENO gives the best convergence rate performance for this demanding IVP3 test problem.

Figure 19 shows computed $L_1$-errors for IVP3 (106), as the mesh is refined, for the ADER scheme with all five reconstructions methods: ENO, m-ENO, WENO, AENO and m-AENO. For the second-order scheme, WENO has the smallest errors, followed by AENO and then by ENO. For the third-order schemes, AENO has the smallest error, followed by WENO, m-ENO and ENO. For the 4th and 5th order schemes, m-AENO has the smallest error, while AENO’s performance deteriorates visibly as the order of accuracy increases. This observation is consistent with the convergence rate study for IVP3 discussed above.

Fig. 19

Computed $L_1$-errors for IVP3 (106), as the mesh is refined, for the ADER scheme with reconstructions: ENO, m-ENO, WENO, AENO and m-AENO, as applied to the linear advection with $\lambda = 1$, $T_{\mathrm{out}}= 4$ and $C_{\mathrm{cfl}}= 0.9$

In the next section, we assess the new AENO reconstruction method as applied to a non-linear hyperbolic system.

6 Results for the Blood Flow Equations for Arteries

In this section, we assess the methods as applied to a non-linear hyperbolic system. The ADER method is implemented with the Toro-Titarev solver [41] for the generalized Riemann problem, as described in Sect. 2.2.2. All three reconstruction methods are implemented in terms of characteristic variables, for all orders of accuracy.

6.1 The Governing Equations

Now we extend and test the new spatial reconstruction AENO method to a non-linear system of hyperbolic equations, namely the blood flow equations for arteries. The system, in general conservation-law form reads

$$\begin{aligned} \partial _{t}{} {\mathbf{Q}} +\partial _{x}{} {\mathbf{F}}({\mathbf{Q}})={\mathbf{S}}({\mathbf{Q}}), \end{aligned}$$

(109)

with

$$\begin{aligned} {\mathbf{Q}}=\left[ \begin{array}{l} A \\ Au\\ A\psi \end{array} \right], \quad {\mathbf{F}}({\mathbf{Q}})= \left[ \begin{array}{l} Au \\ Au^{2}+\gamma A^{3/2}\\ A u \psi \end{array} \right], \quad {\mathbf{S}}({\mathbf{Q}})=\left[ \begin{array}{l} 0 \\ -Ru\\ 0 \end{array} \right]. \end{aligned}$$

(110)

The first two equations are statements of conservation of mass and momentum, while the third equation represents the advection of a tracer $\psi (x,t)$ transported with the blood velocity u(x, t). Here A(x, t) is the blood vessel cross-sectional area. In the source term R is resistance, which is neglected here. The system is closed with a tube law for arteries, given as

$$\begin{aligned} p= p_{\text{ext}}+K(x) \left[ \frac{\sqrt{A}}{\sqrt{A_{0}}} -1 \right], \quad K= \frac{\sqrt{\uppi }}{1-\nu ^{2}} \frac{E(x)h_{0}(x)}{\sqrt{A_{0}}}. \end{aligned}$$

(111)

Here $A_{0}$ is the equilibrium cross-sectional area, E is the Young modulus of the vessel wall and $h_{0}$ is the vessel-wall thickness. These three quantities are parameters of the problem and in general they vary along the length of the vessel. In (110) we have assumed that all parameters of the problem are constant and

$$\begin{aligned} \gamma = \frac{K}{3 \rho \sqrt{A_{0}}}, \end{aligned}$$

(112)

where $\rho$ is the constant density of the blood. We remark that for blood flow in veins, a different tube law applies [39].

We assess the method in terms of two problems. First, we consider a Riemann problem with exact solution containing discontinuities. The purpose is to assess the performance of the non-linear reconstruction method at discontinuities, expecting absent or much reduced spurious oscillations. The second problem has a smooth exact solution and is used to evaluate the accuracy, expecting to attain the desired convergence rates.

6.2 Riemann Problem Solution Profiles

Here we assess the methods as applied to a Riemann problem test with the exact solution. For this purpose, we solve the homogeneous equations (109)–(110) with initial conditions as given in Table 13. The solution of this problem is discontinuous and therefore the objective of the exercise is to test the expected ENO character of the non-linear reconstruction methods. More particularly, to test the newly presented AENO method. We expect good resolution of smooth parts of the flow, sharp discontinuities and absence, or much reduced, spurious oscillations behind the shock.

Table 13 Riemann problem test. Initial condition for the classical Riemann problem for the blood flow equations for arteries. The left column defines the quantities on the left and right of the initial discontinuity. Here $A_{0}=3.135\,3\times 10^{-4}~{\mathrm{m}}^{2}$

Results are shown in Fig. 20 for ENO, Fig. 21 for m-ENO, Fig. 22 for AENO, Fig. 23 for m-AENO and Fig. 24 for WENO. The results show that the numerical solution approximates well the exact one for every order of accuracy and the discontinuity is handled well. For all orders, no visible spurious oscillations are present, except for WENO, and the approximation of the waves improves as the order of accuracy increases. To plotting accuracy, all methods give virtually identical results. The new method performs as well as the well-established ENO and WENO methods. As already noted, WENO differs slightly from ENO, mENO, AENO and m-AENO, in that small spurious oscillations are seen behind the shock for the 4th and 5th order methods.

Fig. 20

ENO results for a Riemann problem for blood flow. Numerical solutions from 2nd to 5th order ADER with ENO reconstruction are compared with the exact solution. Computational parameters are: $M=100$, $T_{\mathrm{out}} = 0.012$ and $C_{\mathrm{cfl}} = 0.9$

Fig. 21

m-ENO results for a Riemann problem for blood flow. Numerical solutions from 2nd to 5th order ADER with m-ENO reconstruction are compared with the exact solution. Computational parameters are: $M=100$, $T_{\mathrm{out}} = 0.012$ and $C_{\mathrm{cfl}} = 0.9$

Fig. 22

AENO results for a Riemann problem for blood flow. Numerical solutions from 2nd to 5th order ADER with AENO reconstruction are compared with the exact solution. Computational parameters are: $M=100$, $T_{\mathrm{out}} = 0.012$, $C_{\mathrm{cfl}} = 0.9$ and $\epsilon = 0.5$

Fig. 23

m-AENO results for a Riemann problem for blood flow. Numerical solutions from 2nd to 5th order ADER with m-AENO reconstruction are compared with the exact solution. Computational parameters are: $M=100$, $T_{\mathrm{out}} = 0.012$, $C_{\mathrm{cfl}} = 0.9$ and $\epsilon = 0.5$

Fig. 24

WENO results for a Riemann problem for blood flow. Numerical solutions from 2nd to 5th order ADER with WENO reconstruction are compared with the exact solution. Computational parameters are: $M=100$, $T_{\mathrm{out}} = 0.012$ and $C_{\mathrm{cfl}} = 0.9$

6.3 Efficiency Assessment on a Riemann Problem Test

A criterion of fundamental importance in assessing the performance of numerical methods is the cost/benefit relation. In other words, accuracy against cost, or equivalently error against cost. This is conventionally achieved by computing the solution to a test problem with the exact solution on a sequence of successively refined meshes $M_{k}$, and computing the corresponding errors $E_{k}$ on a given norm. Associated to each pair $(M_{k}, E_{k})$ there is a computing cost ${\text{CPU}}_{k}$. Then, one usually fits a least-square line to the set of points $({\text{CPU}}_{k}, E_{k})$ on log-log axes. The procedure is performed for each method to be assessed, which produces a graph of several straight lines, one for each method, as shown in Fig.  25.

Fig. 25

Efficiency plot for a Riemann problem for blood flow. Numerical solutions for 3rd order ADER with ENO, m-ENO, WENO and AENO reconstructions for meshes $M=25,50,100, 200, 400, 800, 1\,600$; see symbols. For the finest mesh used ($M=1\,600$), AENO is seen to be 4.3 times more efficient than WENO, for area A. For extrapolated lines to the small error $E=10^{-8}$ for area, AENO is seen to be one order of magnitude more efficient than WENO

For the efficiency exercise here, we choose the Riemann problem, with the exact solution, given in Table 14.

Table 14 Riemann problem for efficiency test. Initial condition for the classical Riemann problem for the blood flow equations for arteries. Here $A_{0}=3.14 \times 10^{-4}~{\mathrm{m}}^{2}$; length of domain = 0.5 m; position of initial discontinuity = 0.25 m

Results are shown in Fig. 25 for third-order schemes for all reconstruction methods. The top frame shows results for the error in cross-sectional area A, while the bottom frame shows results for the error in velocity u. We have used the sequence of meshes $M=25,50,100, 200, 400, 800, 1\,600$; see symbols. Then, as is customary in the literature, we have fitted least square straight lines for each scheme. From the results, it is clearly seen that as the mesh is refined, the CPU cost increases and the error decreases. The straight lines corresponding to the schemes diverge as the error decreases. It is seen that for a given cost, the smallest error is obtained from the newly proposed AENO scheme, while the largest error is given by the WENO scheme. The error lines from the remaining schemes lie in between AENO and WENO.

To assess the error/cost relation we fix an error and draw the corresponding horizontal line. For example, in Fig. 25 we first choose a constant error denoted by $E_{1\,600}^{\text{AENO}}$, this is the error of the AENO scheme for the finest mesh used with $M=1\,600$ cells. Then the intercept of this horizontal line with the least square line corresponding to AENO gives the CPU cost. For the cross-sectional area we obtain 12 827 s for AENO and 54 648 s for WENO. This means that AENO is 4.3 times more efficient than WENO.

Obviously, for even smaller errors, this difference in efficiency will increase. By extrapolating to smaller errors, assuming straight lines, we gain a clearer idea of the difference in efficiency of all methods assessed. Extrapolating the straight lines to the chosen small errors of $E=10^{-8}$ for area A and of $E=10^{-4}$ for velocity u we obtain estimates for the cost of the schemes; see corresponding arrows in Fig. 25. From the given numbers in Fig.  25 it is seen that the efficiency gain of AENO over WENO is 9.7 for area, while for velocity, bottom plot, this gain is 9.13. In other words, for small errors, the AENO reconstruction method is estimated to be one order of magnitude more efficient than WENO.

6.4 Convergence-Rate Study

To carry out an empirical convergence rate study we consider the method of manufactured solutions. First we prescribe a smooth vector-value function ${\tilde{{\mathbf{Q}}}}(x,t)$ [22] given as follows:

$$\begin{aligned} {\tilde{{\mathbf{Q}}}}(x,t) = \left[ \begin{array}{l} {\tilde{A}} + {\tilde{a}}{\text{sin}}(2\uppi x){\text{cos}}(2\uppi t)\\ -{\tilde{a}}{\text{cos}}(2\uppi x){\text{sin}}(2\uppi t) \end{array} \right], \end{aligned}$$

(113)

with

$$\begin{aligned} A_0=3.135\,3\times 10^{-4}~{\mathrm{m}}^{2}, \quad {\tilde{A}} = A_0, \quad {\tilde{a}}=A_0 \times 10^{-1}. \end{aligned}$$

(114)

After inserting (113) into (109) we obtain a new system of balance laws, namely

$$\begin{aligned} \partial _{t} {\tilde{{\mathbf{Q}}}} +\partial _{x}{} {\mathbf{F}}({\tilde{{\mathbf{Q}}}})={\mathbf{S}} ({\tilde{{\mathbf{Q}}}}) + {\mathbf{S}}_{{\rm new}}(x,t). \end{aligned}$$

(115)

The function ${\tilde{{\mathbf{Q}}}} (x,t)$ in (113) is the exact solution of the new balance law (115). We remark that for this test we considered the equations without the passive scalar.

Convergence rates are calculated with respect to the cross-sectional area A(x, t) and flow $q(x,t)=A(x,t)\,u(x,t)$. Results are shown in Tables 15, 16, 17, 18, 19, 20, 21, 22, 23 and 24. The overall results differ somehow from those for the linear advection equation. Now, essentially, the expected convergence rates are reached for all orders in all three norms, by all three reconstruction methods. In the linear advection case, the AENO method reached the expected rate only in the $L_{1}$ norm, being sub-optimal in the $L_{2}$ norm; the expected rate in the $L_{\infty }$ norm was not reached.

Regarding errors, Figs. 26 and 27 show a comparison of $L_{1}$ errors for all three methods for all orders and all meshes. Figure 26 shows results for the second (top) and third (bottom) order methods. For the second-order case all three reconstruction schemes give essentially equivalent results. For the third-order schemes, surprisingly, ENO exhibits smaller errors than AENO. Figure 27 shows results for the fourth (top) and fifth (bottom) order methods. For the fourth-order schemes, all results are virtually coincident. For the fifth-order case, the AENO schemes give the smaller errors.

Fig. 26

$L_{1}$-errors for the blood flow equations. Computed errors for cross-sectional area A for the 2nd and 3rd order ADER schemes with ENO, m-ENO, AENO and WENO

Fig. 27

$L_{1}$-errors for the blood flow equations. Computed errors for cross-sectional area A for the 4th and 5th order ADER schemes with ENO, m-ENO, AENO, m-AENO and WENO

Table 15 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the ENO reconstruction. Rates are calculated for the cross-sectional area A. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 16 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the ENO reconstruction. Rates are calculated for the flow Au. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 17 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the m-ENO reconstruction. Rates are calculated for the cross-sectional area A. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 18 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the m-ENO reconstruction. Rates are calculated for the flow Au. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 19 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the AENO reconstruction with $\epsilon ^2 = 0.5$. Rates are calculated for the cross-sectional area A. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 20 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the AENO reconstruction with $\epsilon ^2 = 0.5$. Rates are calculated for the flow Au. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 21 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the m-AENO reconstruction with $\epsilon ^2 = 0.5$. Rates are calculated for the cross-sectional area A. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 22 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the m-AENO reconstruction with $\epsilon ^2 = 0.5$. Rates are calculated for the flow Au. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 23 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the WENO reconstruction. Rates are calculated for the cross-sectional area A. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

Table 24 Convergence-rate study for the blood flow equations. ADER schemes from 2nd to 5th order of accuracy with the WENO reconstruction. Rates are calculated for the flow Au. Computational parameters are: $T_{\mathrm{out}} = 0.1$ and $C_{\mathrm{cfl}} =0.9$

6.5 Shock/Turbulence Interaction Problem

Here we assess the performance of the methods for a blood-flow analogue of the so-called shock/turbulence interaction problem for gas dynamics proposed in [14]. A variation of this test that is more suitable to assess methods for long evolution times was proposed in [42] and [32]. Our test problem here is inspired on the modified version of the problem. We solve the blood flow equations with the initial condition (Figs. 28 and 29)

Fig. 28

$L_{1}$-errors for the blood flow equations. Computed errors for flow Au for the 2nd and 3rd order ADER schemes with ENO, m-ENO, AENO and WENO

Fig. 29

$L_{1}$-errors for the blood flow equations. Computed errors for flow Au for the 4th and 5th order ADER schemes with ENO, m-ENO, AENO, m-AENO and WENO

$$\begin{aligned} \left[ A,u, \psi \right] = \left\{ \begin{array}{ll} \left[ 15 A_0, 919.7, 1 \right] &{}\quad {\text {if}} \ x \leqslant 10 \,, \\ \left[ A_0(1+0.2 \sin {\left(\frac{80}{50} \uppi x\right)}, 0, 1 \right] &{}\quad {\text {if}} \ x > 10 \,\end{array}\right. \end{aligned}$$

(116)

on a domain of length 50 cm, with the reference cross-sectional area chosen as $A_0=3.14~{\mathrm{cm}}^2$. The solution of the problem consists of a right facing shock wave running into a smooth, high-frequency fluctuation in cross-sectional area A. As time evolves, the shock runs into the fluctuation, which spreads upstream. The numerical solution is evaluated at output time $T_{\mathrm{out}} = 0.03$ s. Figures 30,  31,  32,  33 and  34 show the results obtained with ADER schemes of orders 2nd to 5th, with different reconstruction methods. This problem does not have an exact solution. We therefore compute a reference solution using the fifth order ADER scheme with WENO reconstruction on a mesh of 5 000 computational cells. In all cases the reference solution is shown in black and the numerical solution on a mesh of 1 000 cells is shown with blue dots. For orders of accuracy 2nd to 5th, Figs. 30,  31,  32,  33 and  34 compare the numerical solution with the reference solution in the portion of domain [25, 50], showing on top the shock wave and below the domain portion [28, 40] displaying the physical oscillations upstream of the shock.

Fig. 30

Shock/turbulence interaction test problem: ADER schemes from 2nd to 5th order with ENO reconstruction

Fig. 31

Shock/turbulence interaction test problem: ADER schemes from 2nd to 5th order with m-ENO reconstruction

Fig. 32

Shock/turbulence interaction test problem: ADER schemes from 2nd to 5th order with WENO reconstruction

As the order of the numerical method increases, the resolution of the physical oscillations of the solution is improved. For second order methods and all the reconstructions techniques, only two oscillations just behind the shock are captured. The WENO reconstruction method shows a small advantage over the other reconstruction schemes, for the second-order case. However, for the fourth and fifth order cases, the WENO numerical solution presents spurious oscillations and over/under shoots. For the third-order case, AENO shows a small advantage over the other methods. For the fourth-order case, AENO is comparable to ENO and m-ENO; both AENO and m-AENO show a small advantage over the remaining methods. For the fifth-order case, all methods are comparable, with the exception of WENO, which shows the worse performance, due to the spurious oscillations and over/under shoots.

Fig. 33

Shock/turbulence interaction test problem: ADER schemes from 2nd to 5th order with AENO reconstruction

Fig. 34

Shock interaction test problem: ADER schemes from 2nd to 5th order with m-AENO reconstruction

7 Conclusions

In this paper, we have presented a novel, non-linear spatial reconstruction scheme called AENO, with two variants. The method is akin to the established methods ENO, m-ENO and WENO. All reconstruction schemes have been implemented in conjunction with the fully discrete ADER scheme, from second to fifth order of accuracy, in both space and time, along with the Toro-Titarev solver for the generalized Riemann problem. The methods have been tested thoroughly for the linear advection equation and for a non-linear hyperbolic system, namely the blood flow equations. The assessment of the methods has been through comparison of profiles with exact solutions, convergence rate studies and efficiency studies. Overall, the results of the new AENO reconstruction methods are comparable to the ENO, m-ENO and WENO. However, AENO shows a distinctive advantage over ENO for long-time evolution problems; this is more obvious for second- and third-order methods, but will also be apparent for high-order methods on coarse meshes. Crucially, AENO turns out to be the most efficient of all schemes tested. Estimates reveal AENO to be up to one order of magnitude more efficient than WENO, for sought small errors. Desirable future developments are implementation and assessment of the AENO schemes in conjunction with semi-discrete methods in one and multiple space dimensions.