Abstract
In recent years the concept of multiresolution-based adaptive discontinuous Galerkin (DG) schemes for hyperbolic conservation laws has been developed. The key idea is to perform a multiresolution analysis of the DG solution using multiwavelets defined on a hierarchy of nested grids. Typically this concept is applied to dyadic grid hierarchies where the explicit construction of the multiwavelets has to be performed only for one reference element. For non-uniform grid hierarchies multiwavelets have to be constructed for each element and, thus, becomes extremely expensive. To overcome this problem a multiresolution analysis is developed that avoids the explicit construction of multiwavelets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Solutions of hyperbolic conservation laws and convection-dominated problems often reveal a heterogeneous structure: in some regions solutions are smooth whereas in other regions strong gradients or even discontinuities occur. In smooth regions a coarse resolution is sufficient to realize a certain target accuracy whereas in non-smooth regions a fine resolution is required. Thus, considering uniform grids for non-smooth solutions results in unnecessary high computational cost. To reduce the computational cost, dynamical local grid adaptation can be performed. The majority of the available adaptive strategies can be categorized into the following three different paradigms:
-
(i)
Adaptive methods based on local error estimators. A posteriori error estimates have been developed in [1, 14, 30, 38, 45,46,47, 71]. Since the estimators are in general only bounded up to some constant by the error from below but not from above, these are not reliable and efficient. The existence of an upper bound requires a stable variational formulation of the underlying partial differential equation that is still lacking for the weak formulations of nonlinear systems of conservation laws.
-
(ii)
Sensor-based adaptive methods. A sensor is used to trigger local grid adaptation. Examples for “sensors” are gradients, jumps or curvature of the solution, cf. [7, 49, 60,61,62]. These methods do usually not provide any control of the error but are used frequently in practice due to their simplicity.
-
(iii)
Perturbation methods. The key idea here is to improve the efficiency of a given reference scheme on a uniformly refined reference grid by computing only on a locally refined adapted subgrid, while preserving the accuracy of the discretization on the full uniform grid, cf. [16, 17, 40, 43, 48]. This paradigm allows at least some control of the perturbation error between reference and adaptive scheme. In this context, the terms efficiency and reliability are used, however, with different meaning from in the context of a posteriori estimator based grid adaptation, see class (i). The term efficiency is interpreted here as the reduction of the computational cost in comparison to the cost of the reference scheme. The term reliability is used here in the sense of the capability of the adaptation process to maintain the accuracy of the reference scheme.
In this work, we focus on multiresolution-based grid adaptation. This concept belongs to the class of perturbation methods and does not rely on error estimates. To decide where to coarsen the reference grid, a reliable indicator to control local grid refinement is required. To this end, a multiresolution analysis (MRA) is performed, where the data corresponding to the current solution are represented as data on a coarse level and difference information called details corresponding to data on successive refinement levels. This new representation of the data reveals insight into the local behavior of the solution. It can be shown that the details become locally small with increasing refinement level when the underlying function is locally smooth. As suggested by this so-called cancellation property, we may determine a locally refined grid performing data compression on local details using hard thresholding. This significantly reduces the amount of the data. Based on this thresholding, local grid adaptation is performed, where we refine an element whenever there exist significant details. The core issue of this strategy is to avoid using the fully refined grid at any point of the computation. Moreover, a repetition of time steps as frequently considered in estimator based adaptive schemes is not necessary.
The concept of multiresolution-based grid adaptation has originally been developed for finite volume schemes, cf. [25, 26, 33, 40, 52, 53, 56, 57, 63, 64]. It is motivated by the pioneering work of Harten [41,42,43,44] on the construction of cost-effective hybrid finite volume schemes for conservation laws using an MRA. The underlying idea of this adaptation strategy is to perform an MRA of the reference scheme and evolve only significant local contributions in time. Later on, the concept has been extended to discontinuous Galerkin (DG) schemes in [17, 48, 65]. In [48, 65] an adaptive DG scheme for one-dimensional scalar conservation laws has been derived and analyzed. In [35,36,37] it has been generalized to nonlinear systems of conservation laws in multiple space dimensions.
In contrast to this approach, adaptive multiresolution DG methods in the spirit of the work of Alpert et al. [3, 15] have been reported in [5, 66]. The basic idea in these works is to design an adaptive DG method by representing the numerical solution as well as the operators from the partial differential equation in a multiresolution representation. Thus, the evolution is carried out on the multiresolution coefficients. For that reason, their approaches strongly differ from the work of [17, 48, 65]. For the multiresolution representation multiwavelets are considered in both schemes. Both works can be considered as preliminary, since the presented adaptive strategy is not analyzed and only applied to very few numerical configurations.
A crucial part in the realization of the adaptive scheme is the construction of generators for the contributions of the orthogonal complements containing the difference information, i.e., the details between two successive refinement levels. Previous works, cf. [48, 65], are based on the explicit construction of multiwavelets, i.e., orthogonal basis functions for these complement spaces. When considering an MRA on a hierarchy consisting of rectangular elements or triangles this construction can be performed on a single reference element and then the multiwavelets are transferred to the local element by an affine transformation. However, when considering the setting of more general non-uniform hierarchies, e.g., curvilinear grids or stretched grids, the local bases functions for the orthogonal complements have to be constructed independently on each cell in the hierarchy. In principle, this is possible, but computationally expensive.
To overcome this issue we propose an alternative approach to realize the grid adaptation which does not rely on the construction of basis functions for the complements. The key idea thereby is to represent the local contributions from the orthogonal complements in terms of the basis functions for the piecewise polynomial DG space on the next finer level. To this end, we formulate the MRA in terms of projectors to enable a realization independent of the local generators. In previous work the significance of local contributions was characterized by coefficients in the basis expansion of the detail information from orthogonal complements using multiwavelets. Here, we consider a local function norm for the characterization of significance. Thereby the construction of wavelets has become superfluous. This approach enables a very efficient realization of the adaptive concept to arbitrarily shaped elements since the explicit construction of generators for the complement spaces is avoided.
The outline of the paper is thus as follows. In Sect. 2 we briefly summarize our reference DG scheme for the discretization of hyperbolic conservation laws. This scheme is going to be accelerated by incorporating local grid adaptation. The indicator for local grid refinement is based on an MRA applied to the solution of the DG scheme. The underlying concept of the MRA is presented in Sect. 3. The novelty of this work is addressed in Sect. 4 where we discuss several options how to realize the MRA. In particular, we present a wavelet-free strategy that avoids the explicit construction of multiwavelets. The MRA is then applied to the reference DG scheme, see Sect. 5, resulting in the adaptive MR-DG scheme. To compare the influence of the MRA using either the classical approach or the wavelet-free approach we perform computations for well-known benchmark problems in one and two space dimensions. We conclude in Sect. 7 with a summary of our findings.
2 DG Discretization of Hyperbolic Conservation Laws
For convenience of the reader and to fix some notation we introduce the underlying problem of interest and briefly summarize its discretization by a DG scheme.
Conservation laws. We are interested in the numerical solution of the initial-boundary value problem for hyperbolic systems of conservation laws
with the conserved quantities \(\mathbf {u}:\mathbf{R}_+ \times \Omega \rightarrow \mathcal{D}\) defined on the domain \(\Omega \subset \mathbf{R}^d\), the vector of fluxes \(\mathbf {F}(\mathbf {u}) = (\mathbf {f}_1(\mathbf {u}),\cdots ,\mathbf {f}_d(\mathbf {u}))^{\text{T}}\), \(\mathbf {f}_i\in C^1(\mathcal{D},\mathbf{R}^m)\), \(i=1,\cdots ,d\), the initial data \(\mathbf {u}_0:\Omega \rightarrow \mathbf{R}^m\) and the boundary data \(\mathbf {u}_{\text{bc}}: [0,T] \times \partial \Omega _{\text {bc}} \times \mathcal {D}\rightarrow \mathcal {D}\). Here \(\mathcal{D}\subset \mathbf{R}^m\) denotes the set of admissible states and \(\partial \Omega _{\text {bc}}\subset \partial \Omega\) is the inflow boundary.
DG discretization. To discretize the problem (1) we apply a Runge-Kutta discontinuous Galerkin (RKDG) scheme following the ideas of Cockburn et al. [20,21,22,23]. The key ingredients are the discretization of the domain \(\Omega\), the introduction of a finite-dimensional DG space and the derivation of a weak formulation,
Spatial discretization. We partition the domain \(\Omega\) by \(\mathcal {G}_h:=\{V_{\lambda }\}_{\lambda \in \mathcal {I}_h}\) with a finite number of cells \(V_\lambda\) all of them having a Lipschitz boundary. The corresponding grid is characterized by the index set \(\mathcal {I}_h\): \(\overline{\Omega } = \overline{\bigcup\limits_{\lambda \in \mathcal {I}_h} V_\lambda }\) with \(h := \inf\limits_{\lambda \in \mathcal {I}_h} \text {diam}({V_\lambda })\) the smallest diameter of the cells in the grid. The partition determines the skeleton resulting from the union of all faces by \(\Gamma _h := \bigcup\limits_{\lambda \in \mathcal {I}_h} \partial V_\lambda\) and \(\Gamma _{I} := \Gamma _h \setminus \partial \Omega _{\text {bc}}\).
Following [32], we define a unit normal vector \(\mathbf{n}_{\Gamma }\) for each face in \(\Gamma _h\) such that it coincides with the outward pointing normal vector on \(\partial \Omega _{\text {bc}}\). In particular, we fix the orientation of the normal vector on the inner faces.
DG Space. On the partition \(\mathcal {G}_h\) of \(\Omega\) we define a finite-dimensional DG space consisting of piecewise polynomials
where \(\Pi _{p-1}({V_\lambda })\) is the space of all polynomials up to total degree \(p-1\) on the cell \(V_\lambda\). Thus, functions in \(S_h\) may contain discontinuities and are not uniquely defined on the boundaries of the cells \(V_\lambda\), \(\lambda \in \mathcal {I}_h\). For reasons of stability and efficiency, the DG space is assumed to be spanned by an orthogonal basis of locally supported functions \(S_h= \mathop{\text {span}}\limits_{\lambda \in \mathcal {I}_h, i \in \mathcal {P}} \ \phi _{\lambda ,i}\), where the local degrees of freedom of \(\Pi _{p-1}\) are enumerated with the index set \(\mathcal {P}\).
Weak formulation. To determine an approximate solution in the finite-dimensional space \(S_h\) instead of solving the infinite dimensional problem (1), we derive a weak formulation following [6, 32]. This approach leads to a variational problem defining the semi-discrete DG solution of (1): find \(\mathbf {u}_{h}(\cdot ,t) \in S_h^m, t\in [0,T]\) such that for all \(v \in S_h\), there holds
with the right-hand side \(\hat{\mathcal {L}}: S_h^m\times S_h\rightarrow \mathbf{R}\) given by
Here, the \(L^2\)-inner products \(\langle \cdot , \cdot \rangle _*\) are applied component-wise for vectors and row-wise for the matrix \(\mathbf {F}(\mathbf {u}_{h})\), respectively. The jump operator \([[\cdot]]\) is defined on the skeleton as the difference of two adjacent values, cf. [6, 32]. Note that the weak formulation (3) is stabilized by replacing the normal fluxes at the cell edges as well as the boundary integrals with numerical fluxes \(\mathfrak {\hat{F}}\). For our computations we use the classical local Lax-Friedrichs flux.
Fully discrete DG scheme. The DG solutions of (3) are expanded in the basis
where the coefficients are defined by \({u}_{\lambda ,i}(t) := \langle \mathbf {u}_{h}(\cdot , t), \phi _{\lambda ,i}\rangle _{V_\lambda }\). Since the basis is not time-dependent, the temporal evolution of the DG solution is described by the evolution of the coefficients. Choosing a single basis function \({\phi }_{\lambda ,i}\) for v in (3) and using the orthogonality of the basis, we obtain a system of ordinary differential equations for the coefficients in the basis expansion of the solution (5)
where all coefficient vectors \(\mathbf {u}_{\lambda ,i}\) and right-hand sides \(\hat{\mathcal {L}}\) are comprised in the vectors \({\underline{\underline{U}}} := ( \mathbf {u}_{\lambda ,i} )_{\lambda \in \mathcal {I}_h, i \in \mathcal {P}}\) and \(\mathcal {L}({\underline{\underline{U}}}) := ( \hat{\mathcal {L}}(\mathbf {u}_{h}, \phi _{\lambda ,i}) )_{\lambda \in \mathcal {I}_h, i \in \mathcal {P}}\). Then we derive the fully-discrete DG scheme by discretizing and stabilizing the evolution equation for the coefficients (6). For that purpose, we discretize [0, T] by discrete time levels \(\{ t_n \}_{n=0}^N\). At each time level the semi-discrete DG solution \(\mathbf {u}_{h}(t_n,\cdot )\) is approximated by \({\mathbf {u}_{h}^{n}}\in S_h^m\) applying a strong-stability-preserving Runge-Kutta (SSP-RK) scheme to (6), cf. [39]. Using an explicit time discretization requires a restriction of the time step size \(\Delta t\). In case of a purely hyperbolic problem the largest possible time step size is limited by the well-known Courant-Friedrichs-Levy (CFL) condition [20, 22]: \(\Delta t \, \leqslant h\, C_{\text {CFL}}/ C_{\text {hyp}}\), where the CFL number \(C_{\text {CFL}}\) depends on the polynomial degree and \(C_{\text {hyp}}\) is a bound for the spectral radius of the Jacobian of \(\mathbf {F}\). In the nonlinear case this depends on the current solution and is recomputed in each time step.
To control oscillations near discontinuities, which typically arise in high-order schemes for hyperbolic conservation laws, we have to stabilize the fully discrete DG scheme locally by modifying high-order coefficients where we apply a projection limiter after each stage of the Runge-Kutta scheme. For our computations we choose the limiter by Cockburn et al. [21, 23], because it is comparably simple, computationally efficient and effectively suppresses oscillations. It can be applied to quadrilateral grids as well as triangular grids, cf. [23]. Instead of using a limiter for stabilization, artificial viscosity might be used, cf. [8, 9, 59, 76]. However, in numerical tests it turned out that typically this causes spurious oscillations that spoil the efficiency of our multiresolution-based grid adaptation.
3 Multiresolution Analysis
To accelerate the DG scheme presented in Sect. 2, we want to sparsify the grid \(\mathcal {G}\). To trigger grid refinement and grid coarsening we employ the MRA and perform data compression. In contrast to previous works, cf. [35,36,37, 48], we outline the concept without specifying a wavelet basis.
Hierarchy of nested grids. The concept of the MRA introduced in [55] is based on a sequence \(\mathcal{S} = \lbrace S_l\rbrace _{l\in \mathbf{N}_0}\) of nested spaces
that are closed linear subspaces of \(L^2(\Omega )\) and the union of these spaces is dense in \(L^2(\Omega )\). In the context of RKDG schemes, an appropriate multiresolution sequence can be set up by introducing a hierarchy of nested grids \(\mathcal {G}_{\ell }:=\{V_{\lambda }\}_{\lambda \in \mathcal {I}_l}\) characterized by the index sets \(\mathcal {I}_l\). These are all partitions of the domain \(\Omega\), i.e., \(\overline{\Omega }= \overline{\bigcup\limits_{\lambda \in \mathcal {G}_l }V_{\lambda }}\). The cells of two successive levels are assumed to be nested, i.e., each cell \(V_\lambda\), \(\lambda \in \mathcal {I}_l,\) is composed of cells \(V_\mu\), \(\mu \in \mathcal {M}_\lambda\), where the refinement set \(\mathcal {M}_\lambda \subset \mathcal {I}_{l+1}\) is characterized by \(\overline{V_{\lambda }} = \overline{\bigcup\limits_{\mu \in \mathcal {M}_{\lambda }} V_{\mu }}\). Obviously, the resolution becomes finer with the increasing refinement level l. For each of these grids we introduce a DG space
By definition these spaces are closed subsets of \(L^2(\Omega )\) and due to the nestedness of the grids \(\mathcal {G}_l\) they are nested. The union of these spaces is dense in \(L^2(\Omega )\) whenever it holds \(\lim\limits_{l\rightarrow \infty } \max\limits_{\lambda \in \mathcal {I}_l} {{\,\mathrm{diam}\,}}(V_\lambda ) = 0\).
We emphasize that the concept is not confined to uniform dyadic hierarchies but non-uniform hierarchies via grid mappings, cf. [34], such as triangulations are possible as well. Note that for a uniform dyadic hierarchy it holds \(|\mathcal {M}_\lambda | =2^{-d}\) and \(|V_\mu | = 2^{-d} |V_\lambda |\), \(\mu \in \mathcal {M}_\lambda\), \(\lambda \in \mathcal {I}_l\).
Multi-scale decomposition. To investigate the difference between two successive refinement levels, we consider the orthogonal complement space \(W_\ell\) of \(S_\ell\) with respect to \(S_{\ell +1}\) defined by
Since \(S_{\ell +1}\) is finite dimensional, we decompose \(S_{\ell +1}\) into the direct sum of \(S_{\ell }\) and its orthogonal complement \(W_{\ell }\), i.e., \(S_{\ell +1} = S_\ell \oplus W_\ell\), \(\ell \in \mathbf{N}_0\).
Recursively applying this two-scale decomposition yields the multi-scale decomposition of the space \(S_L\), \(L \in \mathbf{N}\), into the coarse discretization space \(S_0\) and complement spaces \(W_\ell\), \(0 \leqslant \ell \leqslant L-1\): \(S_L = S_{0} \oplus W_0 \oplus \cdots \oplus W_{L-1}.\) Thus, each function \(u \in L^2(\Omega )\) can be represented by an (infinite) multi-scale decomposition \(u = u^0 + \sum\limits_{l\in \mathbf{N}_0} d^l\) with its contributions given by the orthogonal projections
where \(P_V: L^2(\Omega ) \rightarrow V\) denotes the \(L^2\)-projection to some closed linear subspace \(V \subset L^2(\Omega )\). In particular, it holds \(u^{l+1} = u^l + d^l\), \(l\in \mathbf{N}_0\).
Applying this relation recursively we can express \(u^L \equiv P_{S_L}(u)\) for \(L \in \mathbf{N}_0\) in terms of the contributions of the orthogonal complement spaces and the coarsest discretization space \(S_0\), i.e.,
Separation of local contributions. Since the spaces \(S_l\) as well as \(W_l\) are piecewise polynomials, i.e., discontinuities are present at element interfaces, the orthogonal projections (9) can be computed locally on each element. This allows to spatially separate the local contributions in the multiscale decomposition. For \(l\in \mathbf{N}_0\) the compactly supported local contributions of the projections (9) are defined by
where \(\chi {V_\lambda }\) denotes the characteristic function on cell \(V_\lambda\). Consequently, we may decompose \(u^\ell\) and \(d^\ell\) into the sum of their local contributions, i.e.,
Based on the infinite multi-scale decomposition (9) we formulate a localized multi-scale decomposition
We emphasize that the local contributions \(d_\lambda ^l\) may become small when the underlying function is locally smooth. To see this, we note that as a consequence of Whitney’s theorem, cf. [31], we can estimate the local approximation error by
for any \(u|_{V_\lambda }\in H^p(V_\lambda )\) on a convex cell \(V_\lambda\), \(\lambda \in \mathcal {I}_l\), \(l\in \mathbf{N}_0\). From this result we infer by the Cauchy-Schwartz inequality the cancellation property
Thus, the local smoothness implies that the norm of the local contributions \(d^\ell\) decrease with order p for increasing \(\ell\). This fact allows for data compression and is the key of the multiresolution based grid adaptation.
Significance, thresholding and grid adaptation. By neglecting small contributions from the orthogonal complement spaces, we may locally sparsify the multiscale decomposition of \(u^L\) corresponding to an arbitrary but fixed refinement level \(L\in \mathbf{N}_0\) and define an approximation \(u^{L,\varepsilon }\). For this purpose, we have to find a suitable norm to measure the local significance of \(d_\lambda ^\ell\) to decide if the contribution can be neglected. First of all, we define for \(\lambda \in \mathcal {I}_{\ell }\), \(\ell \in \mathbf{N}_0\), a local complement space
equipped with a local norm \(\Vert \cdot \Vert _\lambda : W_{l,\lambda } \rightarrow \mathbf{R}\) defined by
In principle, any equivalent norm can be used giving us some flexibility and also covering the results from previous works [37, 48].
By introducing local threshold values \(\varepsilon _{\lambda ,L} \geqslant 0\) we distinguish between significant and non-significant contributions. To retain flexibility, we require only a weak constraint on the choice of the local thresholds assuming that there exists an \(\varepsilon _{\max } > 0\) such that for all \(L \in \mathbf{N}\) there holds
Then a local contribution \(d_\lambda ^l\in W^l\) is called \(\Vert \cdot \Vert _\lambda\)-significant if
For a uniform dyadic hierarchy a straightforward choice of the local thresholds is given by \(\varepsilon _{\lambda ,L} = 2^{\ell -L}\varepsilon _{L}\) with \(\varepsilon _{L} \geqslant 0\) as considered in previous works, cf. [35,36,37, 48].
If a local contribution \(d^\ell _\lambda\) is not \(\Vert \cdot \Vert _\lambda\)-significant, we discard it and, thus, sparsify the multi-scale decomposition. For this purpose, we define the sparse approximation \(u^{L,\varepsilon } \in S_L\) of \(u^L\) by
where the index set \(\mathcal {D}_\varepsilon \subset \bigcup\limits_{\ell =0}^{L-1}\mathcal {I}_\ell\) is defined as the smallest set containing the indices of \(\Vert \cdot \Vert _\lambda\)-significant contributions, i.e.,
and being a tree, i.e.,
The set \(\mathcal {D}_\varepsilon\) can be determined by adding additional indices of non-significant contributions to \(\left\{ \lambda \in \bigcup\limits_{\ell =0}^{L-1}\mathcal {I}_\ell : \Vert d_\lambda ^\ell \Vert _\lambda > \varepsilon _{\lambda ,L} \right\}\) such that the tree condition (22) is fulfilled. Then, in analogy to classical wavelet analysis, cf. [24], the error introduced by the thresholding procedure can be estimated by
for \(q \in \{1,2\}\) using (18). Moreover, by definition of the \(L^2\)-norm the thresholding procedure is \(L^2\)-stable, i.e., \(\Vert u^{L, \varepsilon } \Vert _{L^2(\Omega )} \leqslant \Vert u^{L} \Vert _{L^2(\Omega )}\).
Since \(\mathcal {D}_\varepsilon\) has a tree structure, we can identify \(u^{L, \varepsilon }\) with the orthogonal projection to a piecewise polynomial space corresponding to an adaptive grid. Hence, \(u^{L, \varepsilon }\) can be written as
where the adaptive grid \(\mathcal {G}_\varepsilon = \bigcup\limits_{\lambda \in \mathcal {I}_\varepsilon } V_\lambda\) is characterized by the index set
satisfying \(\overline{\Omega } = \bigcup\limits_{\lambda \in \mathcal {I}_\varepsilon } \overline{{V_\lambda }}\) with \({V_\lambda }\cap V_{\lambda '} = \emptyset\) for \(\lambda \ne \lambda ' \in \mathcal {I}_\varepsilon\). Then, the sparsified representation \(u^{L,\varepsilon }\) can be characterized equivalently by either the index set \(\mathcal {I}_\varepsilon\) or the index set \(\mathcal {D}_\varepsilon\) corresponding to the cells of the adaptive grid (25) and the significant local contributions of the orthogonal complements, respectively. The adaptive grid is illustrated in Fig. 1.
Relation between the adaptive grid \(\mathcal {I}_\varepsilon\) and the index set of significant contributions \(\mathcal {D}_\varepsilon\). Cells corresponding to indices in \(\mathcal {I}_\varepsilon\) and \(\mathcal {D}_\varepsilon\) are highlighted in orange (on the left) and in blue (on the right), respectively
4 Realization of the Multiresolution Analysis
To implement the MRA basis functions or rather generators for the spaces \(S_\ell\) and \(W_\ell\), \(\ell \in \mathbf{N}_0\) are required. For that purpose, we consider the general framework of stable bi-orthogonal bases for multiresolution representations that has been established in [18, 27]. The choice of the basis determines how to compute the projections (9). Thus, it strongly influences the efficiency of the implementation.
Orthogonal bases. In the following, we refer to the basis functions \(\phi _{\mathbf {i}}\) for \(S_\ell\) as scaling functions and to the basis functions \(\psi _{\mathbf {i}}\) for \(W_\ell\) as multiwavelets, i.e.,
with index sets \(\mathcal {I}^S_{\ell }\) and \(\mathcal {I}^W_{\ell }\) corresponding to the global degrees of freedom of \(S_\ell\) and \(W_{\ell }\), respectively. The local degrees of freedom of \(S_\ell\) and \(W_\ell\) on a cell \({V_\lambda }\) are enumerated with index sets \(\mathcal {P}\) and \(\mathcal {P}^{*}_\lambda\), respectively. In particular, the local degrees of freedom of the orthogonal complement spaces can be enumerated by
Due to the definition of the spaces there holds
Then we encode the spatial and polynomial degrees of freedom, i.e., \(\mathcal {I}^S_{\ell } := \mathcal {I}_\ell \times \mathcal {P}\) and \(\mathcal {I}^W_{\ell } := \mathcal {I}_\ell \times \mathcal {P}^{*}_\lambda\). For reasons of stability it is convenient to consider orthonormal bases, i.e.,
This setting is a special case of [18, 27]. Moreover, for efficiency reasons we require that the basis functions are compactly supported, i.e.,
For technical reasons, we additionally require that the zeroth scaling function is constant, i.e.,
Since the multiwavelets form a basis of \(W_\ell\), they are orthogonal to the scaling functions
We expand the global functions \(u^\ell\) and \(d^\ell\), \(\ell \in \mathbf{N}_0\) in the bases (26), i.e.,
Since \(u^\ell \equiv P_{S_\ell }(u)\) and \(d^\ell \equiv P_{W_\ell }(u)\) are defined by orthogonal projections of \(u \in L^2(\Omega )\), the coefficients are given by
Next, we make use of the locality of the bases (28) and expand the local contributions \(u_\lambda ^\ell\), \(u_\lambda ^{\ell +1}\) and \(d^\ell _\lambda\) as
For ease of notation, we comprise all local scaling functions and multiwavelets corresponding to a cell \(V_\lambda\) in vectors, i.e.,
Additionally, we merge the vectors of scaling functions \(\mathbf {\Phi }_\mu\) of all subcells in the refinement set \(\mathcal {M}_\lambda = \{\mu _{1}, \cdots , \mu _{\vert \mathcal {M}_\lambda \vert }\}\) in
Thus, we may rewrite (33) in a more compact way as
where the coefficients are comprised in vectors \({\underline{u}}_\lambda \in \mathbf{R}^{\vert P \vert }\), \({\underline{d}}_\lambda \in \mathbf{R}^{\vert P^*_\lambda \vert }\) and \({\underline{u}}_{\mathcal {M}_\lambda } \in \mathbf{R}^{\vert P \vert \, \vert \mathcal {M}_\lambda \vert }\), respectively. Due to (32) and (34), these vectors are given by
where the inner products are applied component-wise.
Based on the nestedness of the spaces, we derive two-scale relations between the scaling functions and multiwavelets of successive refinement levels. To this end, we rewrite \(\phi _\mathbf {i}\), \(\mathbf {i}\in \mathcal {I}_\ell ^S\), and \(\psi _\mathbf {j}\), \(\mathbf {j}\in \mathcal {I}^W_\ell\), in terms of scaling functions on level \(\ell +1\) by
Due to the locality of the bases (28), this reduces to
where \(\mathbf {i}= (\lambda ,i)\) and \(\mathbf {j}= (\lambda ,j)\). Then, we comprise the inner products in (38) in matrices \(\mathbf {M}_{\lambda ,0} \in \mathbf{R}^{\vert \mathcal {P}\vert \times \vert \mathcal {P}\vert \, \vert \mathcal {M}_\lambda \vert }\) and \(\mathbf {M}_{\lambda ,1} \in \mathbf{R}^{\vert \mathcal {P}^* \vert \times \vert \mathcal {P}\vert \, \vert \mathcal {M}_\lambda \vert }\), respectively. Thereby, we can write (38) equivalently in matrix-vector notation as
Since the bases are assumed to be orthonormal, the matrix
is an orthogonal matrix. Thus, \(\mathbf {M}_\lambda\) is invertible and, consequently, scaling functions on a finer level can be represented by the sum of scaling functions and multiwavelets on the next coarser level, i.e.,
Furthermore, we deduce from the orthogonality of \(\mathbf {M}_\lambda\) that
where by \(\mathbf {I}_{\vert \mathcal {M}_\lambda \vert \times \vert \mathcal {P}\vert } \in \mathbf{R}^{{\vert \mathcal {M}_\lambda \vert \, \vert \mathcal {P}\vert } \times {\vert \mathcal {M}_\lambda \vert \, \vert \mathcal {P}\vert }}\) we denote the identity matrix.
Based on (39) and (41) we derive the following relations linking the coefficient vectors (37) of successive refinement levels corresponding to the multi-scale decomposition (36):
for \(\lambda \in \mathcal {I}_\ell\), \(\ell \in \mathbf{N}_0\) with local transformation matrices \(\mathbf {M}_{\lambda ,0}\) and \(\mathbf {M}_{\lambda ,1}\) defined by (38) and (39). This provides an explicit representation of the local projections (11), i.e.,
Thus, in the discrete setting of coefficient vectors and basis expansions, cf. (36), these projections can be realized with matrix-vector multiplications. Due to the orthogonality of \(\mathbf {M}_\lambda\) there holds \(\Vert \mathbf {M}_\lambda \Vert _2 = \Vert \mathbf {M}_\lambda ^{\text{T}} \Vert _2 =1\). Hence, the two-scale transformation and its inverse, i.e.,
are well-conditioned.
Construction of multiwavelets. To determine appropriate bases with the desired properties, i.e., orthonormal and compactly supported, where in particular the construction can be performed efficiently and stable, we first need to construct the scaling functions. These can be easily computed by orthogonalization and a following normalization of a local monomial basis. A well-known example in one spatial dimension is the shifted and normalized Legendre polynomials. Since the multiwavelets are not uniquely defined by the required conditions, cf. [29], several approaches for the construction of multiwavelets, i.e., the bases for the orthogonal complement spaces, are possible.
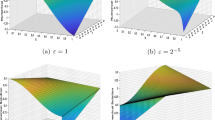
Algebraic approach. Following the ideas of [2, 3, 75] leads to an algebraic algorithm for an explicit construction of multiwavelets: in [2] Alpert proposed an algorithm for multiwavelets on uniform dyadic hierarchies in one spatial dimension. Yu et al. applied this idea in [75] for the construction of multiwavelets on a triangle with a uniform subdivision. The idea can easily be extended to the general multi-dimensional case, cf. [37]. The basic steps in this approach are: (i) construction of a local basis \(\psi _{\lambda ,i}\), \(\lambda \in \mathcal {I}_\ell\) and \(i \in \mathcal {P}\), for \(S_{\ell +1} \setminus S_{\ell }\) ensuring that \(W_{\ell ,\lambda } \subset \displaystyle\mathop{\text {span}}\limits_{i \in \mathcal {P}^*_\lambda } \psi _{\lambda , i}\), \(\lambda \in \mathcal {I}_\ell\), (ii) contribution of \(S_\ell\) in the basis functions are filtered by an orthogonalization with respect to the coarser scaling functions, (iii) orthogonalization of the basis functions among each other using a QR-decomposition, e.g., via Householder transformations, and (iv) normalization of the multiwavelets. Examples of multiwavelets are shown in Fig. 2.
Stable completion. Another possibility for the construction of multiwavelets comes from a discrete point of view. The basic idea is to find a completion of \(\mathbf {M}_\lambda\), i.e., for a given \(\mathbf {M}_{\lambda ,0}\) find \(\mathbf {M}_{\lambda ,1} \in \mathbf{R}^{\vert \mathcal {P}^* \vert \times \vert \mathcal {P}\vert \, \vert \mathcal {M}_\lambda \vert }\) such that
is an orthogonal matrix. Then, due to (39) the multiwavelets can be determined by
This idea originates from [18], where a very general setting is considered. It has been carried out in the particular setting of DG spaces for the one-dimensional uniform dyadic hierarchy in [13] and for the one-dimensional non-uniform dyadic case in [4]. In both works an explicit formula for \(\mathbf {M}_{\lambda ,1}\) is derived. The drawback of this idea is that it cannot be easily realized in the multi-dimensional case. To find a completion for the general non-uniform multi-dimensional case is not trivial and it is open whether an explicit formula similar to the one-dimensional case can be derived. Furthermore, the computation of the completions from [4, 13] for the one-dimensional case is still costly since it requires the inversion of a matrix.
Wavelet-free approach. With increasing polynomial order p and spatial dimension d the local degrees of \(W_\ell\) are increasing dramatically, e.g., in case of the dyadic hierarchy we have \(\vert \mathcal {P}^* \vert = (2^d-1)\, \vert P \vert\). Hence, the algebraic construction or the completion of the matrix separately for all cells in the hierarchy is computationally expensive. Therefore, we are interested in reducing the computational cost for the construction of multiwavelets. Whenever \(V_\lambda\) and its subcells \(V_\mu\), \(\mu \in \mathcal {M}_\lambda\), can be mapped by the same affine linear transformation \(\gamma _\lambda\) to a reference cell \(V_\lambda ^\text {ref}\) and its subcells \(V_\mu ^\text {ref}\), respectively, the construction can be performed on the reference element \(V_\lambda ^\text {ref}\). Then the multiwavelets on \(V_\lambda\) can be obtained by shifts and rescaling of the multiwavelets constructed on the reference element. Typical examples are dyadic grid hierarchies or regular triangulations, cf. [37, 75].
For reasons of efficiency it is thus of major interest to avoid the explicit construction of a basis for the complement spaces. To this end, we propose an alternative approach avoiding the explicit use of multiwavelets: since \(W_\ell \subset S_{\ell +1}\), we may express \(d_\lambda ^\ell\) in terms of scaling functions on level \(\ell +1\) using (39) by
where due to (36) and (39) the coefficients are given by
Applying (44) and (42) leads to
Notice that the rows of \(M_{\lambda ,0}\) and \(M_{\lambda ,1}\) in (40) are orthonormal with one another, hence matrices \(M_{\lambda ,0}^{\text{T}} M_{\lambda ,0}\) and \(M_{\lambda ,1}^{\text{T}} M_{\lambda ,1} = I - M_{\lambda ,0}^{\text{T}} M_{\lambda ,0}\) are orthogonal projectors. Then, (50) becomes very natural. Since \((\mathbf {I} - (\mathbf {M}_{\lambda ,0})^{\text{T}}\, \mathbf {M}_{\lambda ,0}) \in \mathbf{R}^{\vert {\mathcal {M}}_{\lambda }\vert \, \vert {\mathcal {P}}\vert \times \vert {\mathcal {M}}_{\lambda }\vert \, \vert {\mathcal {P}}\vert }\), the computation of (50) is more costly than the classical approach using (44) with multiwavelets. Since \({\underline{u}}_\lambda\) has to be computed from \({\underline{u}}_{\mathcal {M}_\lambda }\) by (43) in the two-scale decomposition, we may compute \({\underline{d}}_{\mathcal {M}_\lambda }\) in a more efficient way by
Note that the MRA is based merely on the local contributions \(d_\lambda ^\ell\) and is not influenced by the choice of the local basis functions. Due to (48) and (51), we can represent \(d_\lambda ^\ell\) without an explicit use of multiwavelets \(\mathbf {\Psi }_{\mathcal {M}_\lambda }\) or the matrix \(\mathbf {M}_{\lambda ,1}\). Thus, the construction of the multiwavelets can be avoided using (48) with (51). From the orthogonality of \(\mathbf {M}_\lambda\), in particular (40), (49) and (47), we conclude that this alternative representation of \(d_\lambda ^\ell\) is well-conditioned, i.e., \(\Vert {\underline{d}}_{\mathcal {M}_\lambda } \Vert _2 \leqslant \Vert {\underline{u}}_{\mathcal {M}_\lambda }\Vert _2\).
Implementation aspects. The computational cost for the realization of the MRA essentially relies on the approach chosen for the representation of the local wavelet spaces. In the following we discuss the classical approach based on an explicit construction of the multiwavelets, cf. (36) and (44), and the alternative wavelet-free approach by (48) and (51) avoiding the costly construction of multiwavelets or rather the completion of the matrix \(\mathbf {M}_\lambda\).
The starting point for an MRA is some given function \(u^L \in S_L \subset L^2(\Omega )\) on a fixed refinement level \(L \in \mathbf{N}_0\). This might come from a numerical scheme or from a projection of an \(L^2\)-function. The task is to compute the multi-scale decomposition (10), i.e., \(u^0\), \(d^0, \cdots ,\) \(d^{L-1}\). Due to (9), the projections in the multiscale decomposition can be computed recursively from fine to coarse, cf. Fig. 3.
Consequently, the computation of the multi-scale decomposition consists of repeated two-scale transformations. The two-scale transformation, i.e., the projections to the next coarser spaces, can be performed cell-wise.
The implementation of the multi-scale transformation depends on the basis expansions for the different spaces. The difference between the classical and the wavelet-free approach is the choice of the generating set for the orthogonal complement spaces \(W_\ell\). In the classical approach the multiwavelets are used, whereas in the wavelet-free approach the scaling functions of \(S^{\ell +1}\) are used.


Thus, the implementation of the local two-scale transformation in Algorithms 1 and 2 and its inverse in Algorithms 3 and 4, respectively, is different for the two approaches.


To compare the computational cost and memory requirements of the two approaches we focus on a local two-scale transformation on a single element described by Algorithms 1–4 neglecting the expensive multiwavelet construction in the classical approach. By this comparison the computational cost and memory requirements of the full transformations can be estimated.
In Table 1 the memory requirement, i.e., the number of coefficients for the storage of \(d_\lambda ^\ell\), \(u_\lambda ^\ell\) and \(u_\lambda ^{\ell +1}\) for \(\lambda \in \mathcal {I}_\ell\) and the number of matrix entries needed for the transformations, are compared.
To quantify the overhead in storing more coefficients in the wavelet-free approach, we consider the ratio of the number of coefficients,
The reduction of memory requirement resulting from storing less matrix entries in the wavelet-free approach can be quantified by analyzing the ratio of matrix entries,
For dyadic hierarchies the ratios (52) and (53) are listed in Table 2 for \(d=1,2,3\).
On the one hand, avoiding the explicit construction of multiwavelets has the advantage that \(\mathcal {M}_{\lambda ,1}\) is not needed anymore, cf. (51), and therefore \(\vert {\mathcal {M}}_{\lambda }\vert\)-times less matrix entries have to be stored. On the other hand, there is more memory needed for the storage of the coefficients, since \(d_\lambda ^\ell\) is expanded in the basis of the larger spaces \(S_{\ell +1}\).
Next, we compare the computational cost for the two-scale transformation and its inverse in Table 3. For that purpose, we compare the number of multiplications and additions for the computation of \(d_\lambda ^\ell\), \(u_\lambda ^\ell\) from \(u_\lambda ^{\ell +1}\) in Algorithms 1 and 2 and of its inverse in Algorithms 3 and 4.
To quantify the difference of the number of operations needed, we consider the ratio of number of total operations
In Fig. 4 the ratio of the total number of the operations \(\text {ratio}_{\text {op}}\) is plotted for different spatial dimensions d and polynomial degrees p.
Ratio of number of operations according to (54) for dyadic sub-division, i.e., \(\vert {\mathcal {M}}_{\lambda }\vert = 2^d\)
The realization of the multi-scale decomposition using the wavelet-free approach avoids the multiplication with \(\mathbf {M}_{\lambda ,1}\) and \(\mathbf {M}_{\lambda ,1}^{\text{T}}\), respectively. With increasing polynomial degree p and space dimension d the number of operations needed for the transformation is reduced significantly compared to the classical approach using multiwavelets.
In summary, we conclude that the wavelet-free approach not only avoids the costly construction of multiwavelets, but also is less expensive in terms of the computational cost in comparison with the classical approach based on multiwavelets. The only advantage of the classical approach over the wavelet-free approach is that less coefficients in the basis expansions have to be stored. However, in the classical approach more matrix entries, i.e., storage of submatrix \(\mathbf {M}_{\lambda ,1}\), have to be stored. Consequently, one may benefit from this advantage whenever it is not necessary to store \(\mathbf {M}_\lambda\) on each cell separately, e.g., in the case of a uniform dyadic hierarchy. Apart from that, the reduction of memory requirements for storing less matrix entries compensates for the overhead of storing more coefficients in the wavelet-free approach. Thus, even in terms of memory requirement, the wavelet-free approach is more efficient than the classical approach. Hence, it seems to be preferable to use the wavelet-free approach for the realization of the MRA.
5 Adaptive Multiresolution DG Scheme
We now intertwine the DG scheme and the MRA introduced in Sects. 2 and 3, respectively. The key idea is to apply the MRA to the evolution equations of the DG scheme. Then a multiscale decomposition is performed for the resulting evolution equations. We omit all equations for detail coefficients in a cell that is considered to be non-significant. The remaining evolution equations are projected back to an adaptive grid corresponding to the significant cells.
Reference scheme. The starting point for the grid adaptation is a hierarchy of nested grids. Corresponding to the grid on a fixed maximum refinement level L, we consider an MRA of the semi-discrete DG solution \(\mathbf {u}_L\) defined by (3). The weak formulations defining the evolution of this solution can be written in a compact form as
where the inner product is applied component-wise and \(\hat{\mathcal {L}}: (S_L)^m \times S_L \rightarrow \mathbf{R}^m\) is defined in (4). Note that \(\hat{\mathcal {L}}(\cdot , \cdot )\) is linear in the second argument. Due to (10) and (11) we can rewrite the semi-discrete DG solutions in terms of the single-scale coefficients of the coarsest mesh and detail coefficients as
In the following we refer to this scheme as well as to its fully-discrete counterpart as the reference scheme.
Significant local contributions. Next, we derive weak formulations for the local contributions. By choosing test functions \(v \in S_0\) and \(w \in W_\ell\), \(1 \leqslant \ell \leqslant L-1\), with compact support and using orthogonality, we conclude that the evolution of \(\mathbf {u}^0_\lambda\), \(\lambda \in \mathcal {I}_0\), and the evolution of the local contribution \(\mathbf {d}^\ell _\lambda\), \(\lambda \in \mathcal {I}_\ell\), \(1 \leqslant \ell \leqslant L-1\), are specified by
Here, the local contributions of the test functions are defined similarly to (11) by \(w_\lambda := w\, \mathbf {1}_{{{V_\lambda }}}\) and \(v_\lambda := v\, \mathbf {1}_{{{V_\lambda }}}\).
To reduce the computational cost of the reference scheme (55), we only consider significant contributions \(\mathbf {d}^\ell _\lambda\) in (58). While dealing with systems of equations, we have to account for the fact, that individual quantities might have different orders of magnitude. Thus, we augment the definition of significance (19) with a rescaling factor for vector-valued \(\mathbf {u}\in \left( S_L\right) ^m\): we call a local contribution \(\mathbf {d}_\lambda ^\ell\) \(\Vert \cdot \Vert _\lambda\)-significant iff
For this purpose, we proceed analogously to (20) and define a sparsified representation of \(\mathbf {u_{h}}(t,\mathbf {x})\) by
where evolution equations for the local contributions of the complements are partially neglected. Note that the significance of local contributions \(\mathbf {d}_\lambda ^\ell\) may change in time.
Fully discrete scheme. Note that the above ideas can be directly migrated to the fully discrete scheme where at each time step \(t_n\) we consider only significant contributions in the local multi-scale decomposition (13) of the solution of the fully-discrete scheme \(\mathbf {u}_L^n\), i.e.,
where the associated index set corresponding to significant local contributions \(\mathcal {D}^n_\varepsilon \approx \mathcal {D}_\varepsilon (t_n)\) approximates the index set of local contributions in the semi-discrete DG formulation. According to (24) and (25) this sparsified representation corresponds to a projection of \(\mathbf {u}_{L}^n\) to an adaptive grid. Here we omit the details and refer to [34] instead.
Prediction of significant contributions. To determine which local contributions become significant in the next time step, in principle the solution of the reference scheme \({\mathbf {u_{h}}^{n+1}}\) is required. However, the computation of the reference scheme has to be avoided. Thus, we have to predict the index set \(\mathcal {D}^{n+1}_\varepsilon\) of significant contributions for the next time step \(t_{n+1}\) by an index set \({\mathcal {D}}^{n+1}\). The prediction of significant contributions at the new time step \(t_{n+1}\) can only be based on available information corresponding to the old time step \(t_n\), i.e., the set \(\mathcal {D}^{n}_\varepsilon\). To ensure the reliability of the prediction, we have to avoid that future significant contributions are lost. For that purpose we want to ensure
where \(\mathcal {D}^{n+1}\) is as small as possible. Otherwise the prediction results in excessive grid refinement causing unnecessary computational overhead. Thus, the “over-prediction” has significant influence on the efficiency of the adaptive scheme. For scalar hyperbolic conservation laws in one spatial dimension a prediction strategy has been proposed in [48, 65]. This strategy is intertwined with the limiting process to ensure the reliability condition (62). For the proof of reliability of this strategy properties of the reference scheme that are only available for the scalar case in one spatial dimension are essential and therefore the extension to the multidimensional case is not trivial. Thus, we modify the idea of Harten’s heuristic strategy [43] and define \(\mathcal {D}^{n+1}\) as the smallest superset of \(\mathcal {D}^n_{\varepsilon }\) fulfilling the following constraints:
-
1)
significant contributions remain significant, i.e., \(\mathcal {D}^n_\varepsilon \subset \mathcal {D}^{n+1}\);
-
2)
contributions in a local neighborhood of a significant contribution become significant, i.e., if \(\lambda \in \mathcal {D}^n_\varepsilon\), then \(\{ \tilde{\lambda }: V_{\tilde{\lambda }} \text { neighbor of } {V_\lambda }\} \subset {\mathcal {D}}^{n+1}\);
-
3)
new discontinuities may develop causing significant contributions on higher refinement levels, i.e., if \(\max\limits_{1 \leqslant i \leqslant m}\Vert \left( \mathbf {d}_\lambda ^\ell \right) _i \Vert _\lambda > 2^{p+1} \varepsilon _{\lambda ,L}\), then \(\mathcal {M}_\lambda \subset {\mathcal {D}}^{n+1}\);
-
4)
\(\mathcal {D}^{n+1}\) is a tree, i.e., if \(\mu \in {\mathcal {D}}^{n+1}\), then \(\{\lambda : {V_\mu }\subsetneq {V_\lambda }\} \subset \mathcal {D}^{n+1}\).
This type of strategy has been originally developed for finite volume schemes. Although the reliability of this heuristic strategy has never been proven to hold, it turned out that it gives satisfactory results in the context of finite volume schemes [16, 56, 57] as well as for DG schemes [19, 35,36,37].
Adaptive MR-DG scheme. By the prediction set \(\mathcal {D}^{n}\) an adaptive grid characterized by the index set \(\mathcal {I}^n\) is defined at each time step \(t_n\) according to (25). Associated to this locally refined grid there exists a discretization space \(S^n \subset S_L\). Analogously, we denote by \(\mathcal {I}_\varepsilon ^n\) the index set characterizing the adaptive grid defined by \(\mathcal {D}^{n}_\varepsilon\) at time step \(t_n\). Furthermore, we denote by \(S^n_\varepsilon \subset S^n \subset S_L\) the associated discretization space. Thus, the adaptive DG solution \(\mathbf {u}_{L,\varepsilon }^n \in (S^n_\varepsilon )^m\) can be written equivalently in two different ways, i.e.,
A time step of the adaptive scheme consists of three steps.
-
1)
Refinement. The grid is refined via prediction of significant contributions using the multi-scale representation. Consequently, \(\mathbf {u}_{L,\varepsilon }^n\) is represented in the basis of the richer space \(S^{n+1} \supset S^{n}_\varepsilon\) corresponding to the refined grid \(\mathcal {I}^{n+1}\) of the next time step \(t_{n+1}\), i.e.,
$$\begin{aligned} \mathbf {u}_{L,\varepsilon }^n = \sum _{\ell =0}^L \sum _{\lambda \in \mathcal {I}^{n+1} \cap \mathcal {I}_\ell } \mathbf {u}_\lambda ^{\ell ,n}. \end{aligned}$$(64) -
2)
Evolution. The evolution of the DG scheme with an RK scheme including local projection limiting at each Runge-Kutta stage is computed using the single-scale representation (64). The outcome of the evolution is denoted by \(\tilde{\mathbf {u}}_{L,\varepsilon }^{n+1}\).
-
3)
Coarsening. Significant contributions might turn out to be non-significant, i.e., \(\tilde{\mathbf {u}}_{L,\varepsilon }^{n+1}\) might contain non-significant contributions. Thus, we apply the thresholding procedure (20) using the rescaled definition of significance in (59) to compute
$$\begin{aligned} \mathbf {u}_{L,\varepsilon }^{n+1} = \sum _{\ell =0}^L \sum _{\lambda \in \mathcal {I}^{n+1}_\varepsilon \cap \mathcal {I}_\ell } \mathbf {u}_\lambda ^{\ell ,n} \end{aligned}$$(65)corresponding to a coarser grid.
For a detailed representation of the adaptive MR-DG scheme we refer to previous works [34, 65], where it is discussed how to efficiently compute the integrals and how to initialize the adaptive grid avoiding the complexity of the fully refined grid. We emphasize that the MRA and the adaptive DG scheme are very much intertwined. In particular, performing the time evolution on the adaptive grid cannot be considered a DG scheme on an unstructured grid because the local numerical flux computation is connected to the numerical fluxes on the finest level by the multi-scale transformation. In the following we highlight two important conceptual issues.
Remark 1
(Choice of threshold value) Most crucial for the performance of the adaptive scheme is the choice of the local threshold values \(\varepsilon _{\lambda ,\ell }\). For reasons of efficiency and accuracy, it should be chosen neither too small nor too large to avoid over-refinement and under-refinement, respectively. Following previous works for uniform dyadic grid hierarchies, cf. [35,36,37, 48], we choose
where \(h_\ell\) and \(h_L\) denote the (uniform) diameters of the cells on level \(\ell\) and L, respectively. To determine the threshold value \(\varepsilon _L>0\) we follow Harten’s idea [42] of preserving the order of accuracy \(\beta\) of the reference solution on the uniformly refined grid at the final time step \({t=t_N}\) for \(L\rightarrow \infty\), i.e.,
For this purpose a heuristic strategy was developed in [50]: \(\varepsilon _L = C_\text {thr} h_L^\gamma\) with a constant \(C_\text {thr}\) and an exponent \(\gamma\). For a non-smooth solution we choose \(\gamma = 1\) and \(\gamma =p\) otherwise. Note that a rigorous a-priori strategy was developed in [48] for scalar conservation laws that turns out to be too pessimistic in general. Furthermore, numerous computations verified that in most cases \(C_\text {thr}=1\) is a suitable choice. However, if the solution exhibits weak discontinuities, then it is recommended to choose \(C_\text {thr}\) in the order of the strength of this discontinuity. For a more detailed discussion on the choice of the threshold and the extension to non-uniform grid hierarchies we refer to [34].
Remark 2
(Adaptation and limiting) It is well-known that the MRA provides a reliable shock detector, cf. [41, 42]. This motivates to combine adaptation and limiting: we add the MRA as an additional indicator for the detection of troubled cells, i.e., the minmod indicator and the limiter are only applied to cells on the finest refinement level, i.e., \(\mathcal {I}^n \cap \mathcal {I}_L\). In the one-dimensional adaptive scheme proposed in [48] limiting and prediction were intertwined: whenever a cell is indicated for limiting, the prediction enforces a refinement of this cell up to the finest level. Thereby, the stability of the scheme considering the additional troubled cell indicator can be ensured. Since our prediction strategy is not intertwined with the limiting process, we cannot prove the reliability of the additional troubled cell indicator. However, it turned out that if the threshold value is chosen carefully this strategy gives satisfactory results in practice, cf. [19, 35, 37].
6 Numerical Results
In [19, 35,36,37] numerical results are presented for numerous test cases using the adaptive MR-DG scheme. There, the classical approach (36) has been applied with the local norms
based on the explicit use of multiwavelets. Here we focus on the validation of the newly developed wavelet-free approach (48) with the alternative choice for the local norms (17) and compare it to the classical approach using (67). For validation purposes we first compare the classical approach and the wavelet-free approach for classical one-dimensional problems, see Sect. 6.1. Then, for real applications we consider the well-known benchmark problems of a double Mach reflection and a shock-vortex interaction with a boundary layer in Sects. 6.2 and 6.3, respectively.
6.1 One-Dimensional Test Cases
To compare the classical approach and the wavelet-free approach we first consider classical one-dimensional test cases: the Sod Riemann problem [69], the Woodward interaction problem of two blast waves [73, 74] and the Shu-Osher problem of the interaction between a moving shock and a density sine wave [67]. For each test case we determine the empirical order of accuracy to validate our reference scheme. For the “exact” solution we perform uniform computations on a very fine mesh corresponding to 12 refinement levels, i.e., 40 960 cells, instead of the analytical solution.
Problem. The system of nonlinear conservation laws (1a) is determined by the one-dimensional compressible Euler equations with the vector of conserved quantities \(\mathbf {u}= (\rho , \rho v, \rho E)^{\text{T}}\) and the flux \(\mathbf {F}(\mathbf {u}) = (\rho v, \rho v^2 + p, \rho v(E+p/\rho ))^{\text{T}}\). These equations express conservation of mass, momentum and total energy density. Here \(\rho\), v, \(E= e + \frac{1}{2}v^2\) and e denote the density, velocity, specific total energy and specific internal energy, respectively. The system is closed by the equation of state for the pressure \(p=\rho e(\gamma -1)\) for a thermally and calorically perfect gas with the ratio of specific heats \(\gamma =1.4\) for air at standard conditions.
Configuration. The three test cases differ in the initial data, the boundary conditions and the computational domain.
-
1)
Sod problem:
$$\begin{aligned} \mathbf {u}_0(x)=\left\{ \begin{array}{ll} \mathbf {u}_{0,{\text{L}}},&\text { if }x\leqslant {0},\\ \mathbf {u}_{0,{\text{R}}},&\text { if }x > {0} \end{array} \right. \end{aligned}$$with \(\mathbf {u}_{0,{\text{L}}} = (1,0,2.5)^{\text{T}}\) and \(\mathbf {u}_{0,{\text{R}}} = (0.125,0,0.25)^{\text{T}}\). Constant boundary conditions are imposed at the boundaries of the domain \(\Omega =[-0.5,0.5]\).
-
2)
Woodward problem:
$$\begin{aligned} \mathbf{u} _0(x)=\left\{ \begin{array}{ll} \mathbf{u} _{0,{\text{L}}},&\text { if }x\leqslant 0.1,\\ \mathbf{u} _{0,{\text{C}}},&\text { if }0.1< x\leqslant 0.9,\\ \mathbf{u} _{0,{\text{R}}},&\text { if }x > 0.9 \end{array} \right. \end{aligned}$$with \(\mathbf {u}_{0,{\text{L}}}=(1,0,2\,500)^{\text{T}}\), \(\mathbf {u}_{0,{\text{C}}}= (1,0,0.025)^{\text{T}}\) and \(\mathbf {u}_{0,{\text{R}}}=(1,0,250)^{\text{T}}\) corresponding to pressure values \(p_{\text{L}}=1\,000\), \(p_{\text{C}}=0.01\) and \(p_{\text{R}}=100\). Reflecting boundary conditions are imposed at the boundaries of the domain \(\Omega = [0,1]\).
-
3)
Shu-Osher problem:
$$\begin{aligned} \mathbf{u} _0(x)=\left\{ \begin{array}{ll} \mathbf {u}_{0,{\text{L}}},&\text { if }x\leqslant -4,\\ \mathbf {u}_{0,{\text{R}}}(x),&\text { if }x > -4, \end{array} \right. \end{aligned}$$with \(\mathbf {u}_{0,{\text{L}}}=(3.857\,143,10.141\,852,39.166\,66)^{\text{T}}\) and \(\mathbf {u}_{0,{\text{R}}}(x)=(1+0.2\,\sin (5x),0,2.5)^{\text{T}}\) corresponding to the pressures \(p_{0,{\text{L}}}=10.333\,33\) and \(p_{0,{\text{R}}}=1\). Constant boundary conditions are imposed at the boundaries of the domain \(\Omega =[-5,5]\).
Discretization. Simulation parameters are the following. We consider a dyadic one-dimensional grid hierarchy with uniform cells on each level, i.e., \(\vert \mathcal {M}_\lambda \vert = 2\). The computations have been performed using a third-order scheme, i.e., \(p=3\). For the time discretization an explicit third-order SSP-RK method with three stages and \(C_{\text {CFL}} =0.1\) is used. For limiting we apply the Cockburn-Shu limiter [21, 23] with an Shu constant of \(M=50\) for the Shu-Osher problem and \(M=0\) otherwise. The computations have been performed on an Intel(R) Xeon(R) Platinum 8160 CPU with 2.10 GHz CPU frequency.
Computations. We perform adaptive computations starting with a grid on level 0 containing \(N_0=10\) cells. We perform computations up to \(t=0.25\), \(t=0.038\) and \(t=0.8\) for the Sod problem, the Woodward problem and the Shu-Osher problem, respectively, with varying maximum refinement levels \(5\leqslant L \leqslant 9\). Since this test case contains discontinuities, we consider the heuristic strategy with \(\beta =1\) and \(C_\text {thr}=1\) for the choice of the threshold value, i.e., \(\varepsilon _L = h_L\). In Figs. 5, 6 and 7 the solutions (density \(\rho\)) and the adaptive grid after thresholding corresponding to the index set \(\mathcal {D}_\varepsilon ^n\) are exemplarily shown for \(L=9\) for both the classical and the wavelet-free approach. For all test cases we observe that the grids are locally refined up to the finest level only near discontinuities. For both approaches the adaptive grids are almost the same, although the thresholding is performed using different local norms.
To confirm that the adaptive computations maintain the asymptotic behavior of the reference scheme we compare in Figs. 8a, 9a and 10a the \(L^1\)-error in the density of the adaptive solution with the error of the reference solution. We observe that for Sod’s Riemann problem and Woodward’s interaction problem the errors of the adaptive solutions are very close to the discretization error of the reference scheme. For the Shu-Osher problem the error of the adaptive solutions is larger as the error of the reference scheme but the asymptotic behavior is the same. This confirms that by the choice of the threshold value the asymptotic convergence behavior of the reference scheme is maintained. This holds for both the classical and the wavelet-free approach.
To examine the efficiency of the classical approach and the wavelet-free approach, we compare the error in the density with the number of cells in the adaptive grids. Since the adaptive grids change dynamically, we consider in Figs. 8b, 9b and 10b the maximum number of cells over all time steps performing computations with different numbers of refinement levels L. We note that to realize a given error tolerance both the adaptive schemes using the classical and the wavelet-free approach require about the same number of grid cells whereas the reference scheme needs significantly more cells.
This is also reflected in the CPU times recorded in Tables 4, 5 and 6. We note that for all test cases the adaptive computations outperform the non-adaptive computation. The computations using the wavelet-free approach are only slightly faster than those using the classic approach. Here the potential of the wavelet-free approach does not become evident because for the one-dimensional-dyadic grid hierarchy the multiwavelets can be computed on a reference element once and for all.
6.2 Double Mach Reflection
Problem. Again, we consider the compressible Euler equations. In the two-dimensional case they are determined by the vector of conserved quantities \(\mathbf {u}= (\rho , \rho \mathbf{v} ^{\text{T}}, \rho E)^{\text{T}}\) and the vector of fluxes \(\mathbf {F}(\mathbf {u}) = (\rho \mathbf{v} , \rho \mathbf{v} \otimes \mathbf{v} + p \mathbf{I} , \rho \mathbf{v} (E+p/\rho ))^{\text{T}}\) with velocity vector \(\mathbf{v} =(v_x,v_y)^{\text{T}}\) and total energy \(E= e + \frac{1}{2} \mathbf{v} ^2\). The system is closed by the equation of state for the pressure \(p=\rho e(\gamma -1)\) with \(\gamma =1.4\).
Configuration. We consider the reflection of a shock making a \(60^\circ\) angle with a reflecting wall. This test case has been introduced by Woodward and Colella in [74]. Although the exact solution is not known, it is a well-known benchmark test case for numerical schemes for compressible Euler equations. Induced by the reflection of the shock wave complex wave structures develop. The computational domain is \(\Omega = [0,4] \times [0,1]\). The initial data consists of two constant states separated by a shock at \(x_1 = 1/6 + \tan (30^\circ )\, x_2\), i.e., \(\mathbf {u}(0,\mathbf {x})=\mathbf {u}_{\text{l}}\) if \(x_1 < 1/6 + \tan (30^\circ )\, x_2\) and \(\mathbf {u}(0,\mathbf {x})=\mathbf {u}_{\text{r}}\) otherwise. The values for \(\mathbf {u}_{\text{l}}\) and \(\mathbf {u}_{\text{r}}\) are depicted in Fig. 11. This flow is challenging because the flow on the left-hand side of the separating shock is supersonic, whereas the flow on the right-hand side is subsonic. This change of the flow regime is known to cause problems in the numerical simulation, cf. [23, 58].
At the lower boundary, i.e., \(x_2=0\) we impose a reflecting wall between \(x_1=1/6\) and \(x_1=4\). Since the shock position in the free flow away from the wall is explicitly known, it is used to specify suitable boundary conditions for the flow field at all other boundaries, i.e.,
where \(\mathbf {u}_{\text {ext}}\) depends on the solution \(\mathbf {u}^- = (\rho ^-, (\rho v_1)^- , (\rho v_2)^-, (\rho E)^-)^{\text{T}}\) itself. From \(\mathbf {u}_{\text {ext}}\) we compute a suitable boundary condition \(\mathbf {u}_{\text{bc}}\). The overall configuration is shown in Fig. 11.
Discretization. Simulation parameters are the following. We consider quadrilateral Cartesian grids with uniform cells on each level. The subdivision is dyadic, i.e., \(\vert \mathcal {M}_\lambda \vert = 2^d\). The computations have been performed using a third-order scheme, i.e., \(p=3\). For the time discretization an explicit third-order SSP-RK method with three stages and \(C_{\text {CFL}} =0.1\) is used. To exactly compute the integrals in the scheme we use a tensor product based Gaussian quadrature formula with \((p+1)^d\) points. To avoid limiting in regions, where the solution is smooth, we consider a Shu constant of \(M=50\), see [21, 23]. To reduce the computational cost, the computations have been performed in parallel applying the parallelization strategy described in [34] on a 16 \(\times\) Intel Xeon Gold 5118 cluster with 2.3 GHz CPU frequency using 280 nodes.
Computations. We perform adaptive computations starting with a grid on level 0 containing \(20 \times 5\) cells. We perform computations up to \({t=0.2}\) with different maximum refinement levels \(5\leqslant L \leqslant 7\). Since this test case contains discontinuities, we consider the heuristic strategy with \(\beta =1\) and \(C_\text {thr}=1\) for the choice of the threshold value, i.e., \(\varepsilon _L = h_L\). In Fig. 12 the adaptive solution (density \(\rho\)) and the corresponding adaptive grid are exemplarily shown for \(L=6\).
First, we find that all relevant structures of the solution are present in our results by comparing our adaptive results using \(L=6\) with the (uniform) results from other works, for instance [23, 51]. Furthermore, we note that the grid is only refined near to discontinuities or in areas where the solution consists of small structures needing a high resolution. In regions with less fluctuations the adaptive grid is relatively coarse.
In Fig. 13 we compare the adaptive solutions and the corresponding grids for different maximum refinement levels L in the blow-up region on the right-hand side of the domain. Thereby we note that the structures are more sharply resolved with increasing resolution. Moreover, instabilities occur at the bottom of the “red triangle” with increasing resolution. It is well-known and observed by many others that these instabilities occur, cf. [23, 58]. In fact, the absence of these instabilities is usually related to a too coarse resolution or too diffusive stabilization in the scheme, cf. [51, 70]. Thus, it seems to be reasonable that we observe the instabilities only if the maximum refinement level is sufficiently large. Moreover, this shows that the adaptive scheme is capable of resolving these features even if they develop during the computation and are not present from the very beginning.
To assess the efficiency of the adaptive scheme and to bring out the difference between the classical and the wavelet-free approach we list the maximum number of cells in the grid \(N_{\text {max}} := \max \{ \vert \mathcal {I}^{n}\vert : n=0,\cdots ,N \}\) for the different computations in Table 7. For instance, the adaptive grid for \(L=6\) consists of at most 40 768 and 33 469 cells using the wavelet-free approach and the classical approach, respectively. Again, we observe that the grids using the wavelet-free approach are slightly more refined than the grids using the classical approach. However, the uniform grid of the reference scheme on level \(L=6\) consists of 409 600 cells. Thus, the adaptive grids contain only approx 9.95% and 8.17% of the cells of the uniform grid of the reference scheme. For all considered maximum refinement levels the difference between both approaches is around 2%~3% points. Compared with the computational complexity of the reference scheme, i.e., \(N_{\text {max}}=\vert \mathcal {I}_L \vert\), this difference is of minor relevance, since the computational costs are reduced significantly with both approaches. The difference can be explained by the different local norms (17) and (67) that are equivalent but not identical. Note that due to Parseval’s identity, (17) can be computed equivalently by either \(\Vert {\underline{d}}_\lambda \Vert _2/\sqrt{\vert {V_\lambda }\vert }\) or \(\Vert {\underline{d}}_{\mathcal {M}_\lambda } \Vert _2/\sqrt{\vert {V_\lambda }\vert }\) avoiding the costly computation of \(\mathbf {M}_{\lambda ,1}\).
Finally, we summarize in Table 8 the CPU times for the adaptive computations. We note that wavelet-free computations are faster than the classic approach on lower refinement levels but become more expensive with increasing number of refinement levels. This is caused by the fact that the adaptive grids for the wavelet-free computations become denser with increasing refinement levels in comparison to the classic computations. As can be concluded from Table 7 the ratio of the maximum number of cells \(N_{\text{max}}\) for the wavelet-free approach and the classic approach increases from 1.13% (\(L=4\)) to 1.35% (\(L=7\)). We emphasize that the difference is not significant as was already observed for the 1D test cases. As it was to be expected, on Cartesian grid hierarchies the classic approach is slightly preferable. To demonstrate the benefit of the wavelet-free approach we consider the following test case.
6.3 Shock-Vortex Interaction with a Boundary Layer
So far, all computations were performed on dyadic grid hierarchies. We emphasize that for a dyadic grid hierarchy the cost for the explicit construction of multiwavelets can be significantly reduced because it needs to be done only once for a reference cell. Then the multiwavelets are mapped to the local elements by an affine mapping. Thus, the benefit of the wavelet-free approach is limited. However, in case of grid hierarchies with a non-uniform subdivision, e.g., using stretched grids, there does not exist an affine mapping to a reference element and the multiwavelets have to be constructed element wise. Then it is mandatory to apply the wavelet-free approach because for this configuration the computational costs for the classical approach are prohibitively high. For an example we consider the test case of a shock-vortex interaction with a boundary layer using stretched Cartesian grids. For this configuration we do not perform the computation for the classical approach because the construction of the multiwavelets and the evaluation is too costly as can be concluded from Tables 2 and 3 and Fig. 4.
Problem. Here we consider the two-dimensional compressible Navier-Stokes equations in dimensionless form with the vector of dimensionless conserved quantities \(\mathbf {u}= (\rho , \rho \mathbf{v} ^{\text{T}}, \rho E)^{\text{T}}\) and the vector of fluxes \(\mathbf {F}(\mathbf {u}) = \mathbf {F}^{\text{inv}}(\mathbf {u})- \mathbf {F}^{\text{vis}}(\mathbf {u},\nabla \cdot \mathbf {u})\) composed of an inviscid and viscous part. The inviscid flux vector is given by \(\mathbf {F}^{\text{inv}}(\mathbf {u}) = (\rho \mathbf{v} , \rho \mathbf{v} \otimes \mathbf{v} + p \mathbf{I} , \rho \mathbf{v} (E+p/\rho ))^{\text{T}}\). The viscous flux vector is determined by \(\mathbf {F}^{\text{vis}}(\mathbf {u},\nabla \cdot \mathbf {u}) = Re^{-1} \left( 0,{\varvec{\sigma }},{\varvec{\sigma }}\mathbf {v}- \mathbf {q}\right)\) with the shear stress tensor \({\varvec{\sigma }}= \mu (T) \left( \nabla \mathbf {v}+ (\nabla \mathbf {v})^{\text{T}} - \frac{2}{3} \nabla \cdot \mathbf {v}I\right)\) and the dimensionless heat flux \(\mathbf {q} = - \frac{\lambda (T) \gamma }{Pr} \nabla T\nonumber\) with a constant Prandtl number Pr, heat capacity ratio \(\gamma\) and dynamic viscosity \(\mu\) and thermal conductivity \(\lambda\) depending on the dimensionless temperature \(T := E - \frac{1}{2}\mathbf {v}^2\). The non-dimensionalization is performed such that there holds \(\lambda (T) = \mu (T)\). The viscosity coefficient is specified by the power law \(\mu _{\text {vis}}(T) = (T/T_{\text{ref}})^{0.7}\) where the reference temperature \(T_{\text{ref}} = 1/({Ma}^2\gamma (\gamma -1))\) is based on the reference Mach number \({Ma}\) and the heat capacity ratio \(\gamma\). Due to the viscous terms we need to modify the reference DG scheme, see Sect. 5, where we stabilize the viscous fluxes applying the BR-2 scheme by Bassi et al. [10,11,12]. Again, the system is closed by the equation of state for the pressure for a thermally and calorically perfect gas with \(\gamma = 1.4\).
Configuration. We investigate the interaction of a shock wave with the boundary layer of an adiabatic wall in two dimensions (\(d=2)\) which is a well-known test case for compressible Navier-Stokes equations, cf. [28, 54, 68, 72]. For this purpose, we consider a quadratic shock tube \([0,1]^2\) bounded by insulated adiabatic walls. The tube is filled with ideal gas at rest. Initially, a membrane is located at \(x_1 = 0.5\) separating two reservoirs containing gas with different densities and pressures. After removing the membrane at \(t=0\), a shock wave followed by a weak contact discontinuity and a weak right-moving rarefaction wave is moving to the right. Due to the presence of viscosity, boundary layers develop at the solid walls at \(x_2=0\) and \(x_2=1\). When the shock reaches the wall at \(x_1=1\) it is reflected. Then, the reflected wave interacts with the boundary layer resulting in complex wave structures.
Due to the symmetry of the problem, we compute the numerical solution only on the lower half of the tube, i.e., \(\Omega = [0,1] \times [0,0.5]\) and consider symmetry boundary conditions at \(x_2 = 0.5\). The initial configuration is shown in Fig. 14. The symmetry boundary conditions are realized by imposing \(\mathbf {u}_{\text {bc}} = (\rho ^-, (\rho v_1)^- , -(\rho v_2)^-, (\rho E)^-)^{\text{T}}\) as boundary state for the evaluation of the fluxes in the boundary integrals. The adiabatic wall boundary condition is prescribed by using the boundary state \(\mathbf {u}_{\text {bc}} = (\rho ^-, 0, 0, (\rho E)^- - \rho ^{-}\, (\mathbf {v}^-)^2 )^{\text{T}}.\) The Reynolds number is \(Re={1\,000}\).
Discretization. To adequately resolve the thin boundary layer developing at the wall \(y=0\) the grid hierarchy consists of stretched Cartesian meshes determined by applying a dyadic subdivision on the parameter domain \(\Omega\) of the grid mapping \({\varvec{\theta }}(\mathbf {x}) = (x_1, 0.5 + \tanh (\zeta (2\,x_2-1)) / (2\,\tanh (\zeta )))^{\text{T}}\), \(\mathbf {x}\in \Omega\) where the strength of the stretching is specified by \(\zeta\). For \(\zeta\) tending to zero the stretching coincides with the identity resulting in a uniform dyadic hierarchy, whereas for increasing \(\zeta\), the cells are more and more condensed toward \(x_2=0\). Here, we use \(\zeta =1.8\). The time step is calculated by \(\Delta t = \min ( C_{\text{visc}} h^2, C_{\text{CFL}}/C_{\text{hyp}} h)\) with \(C_{\text{visc}} = 0.01/ \mu\) and \(C_{\text{CFL}}=0.01\). The computations have been performed on a 16 \(\times\) Intel Xeon Gold 5118 cluster with 2.3 GHz CPU frequency using 280 nodes.
Computations. We perform adaptive computations up to \(t=1\) with different maximum refinement levels \(3 \leqslant L \leqslant 5\) based on a grid consisting of \(30 \times 15\) cells on level 0. Due to the stretching we apply a localized strategy for the threshold value choosing \(\varepsilon _{\lambda ,L}= C_{\text{thr}}\,h_{L,\lambda }^{1+\beta }/h_\lambda\) with \(h_{L,\lambda }:= \min\limits_{\mu \in \mathcal{I}_L: V_\mu \subset V_\lambda } |V_\mu |^{1/d}\) and \(h_\lambda := |V_\lambda |^{1/d}\). For details we refer to [34], Sect. 4.5.2. For the choice of the threshold value we again apply the heuristic strategy using \(C_\text {thr}=1\) and \(\beta =1\). To realize the MRA and grid adaptation, we only consider the wavelet-free approach to avoid the costly cell-wise construction of multiwavelets on the non-uniform hierarchy.
The adaptive solutions and the corresponding grids at \(t=1\) are shown in Fig. 15. First of all, we note that with sufficient resolution, i.e., sufficiently large L, our solutions reveal the same structures as computed by other groups using solvers with uniform grids, cf. [28, 68, 72]. Hence, we observe that the grid adaptation is capable of refining the relevant structures in the solution. The solution using \(L=5\) reveals some indications that this flow might be unstable. This is backed up by observations in [28, 68].
To access the efficiency of the grid adaptation, we again focus on the maximum number of cells during the computation in the adaptive grid \(N_{\text {max}}\) provided in Table 9. Here, we note that the adaptation is capable of reducing the computational cost significantly. For sake of completeness, we record in Table 10 the CPU times for the adaptive computations. Since the full grids are at least three times the size of the adaptive grids, we refrain from performing the computations on the fully refined grids.
7 Conclusion
The wavelet-free approach enables a straight forward application of the adaptation concept to general hierarchies of nested grids. This approach requires only the construction of the single-scale basis functions which have to be constructed for the (adaptive) DG scheme anyhow.
The numerical results presented here lead to the conclusion that the wavelet-free approach is a suitable alternative to the classical wavelet-based approach to overcome the issues related to the construction of wavelets. However, the grids resulting from the use of the classical approach are slightly coarser than the ones using the more general wavelet-free approach. Thereby, both approaches maintain the accuracy of the reference scheme. For that reason, the classical approach might be a good choice whenever the construction of the multiwavelets can be realized efficiently, e.g., when it is sufficient to construct them only on a single reference element. However, the additional refinement of the wavelet-free approach is comparably small in comparison to the overall gain from the grid adaptation. Thus, in most situations, especially when employing non-dyadic grids, this overhead is negligible. Moreover, the realization of the MRA and the adaptive scheme using the wavelet-free approach is computationally less costly than using the classical approach. Therefore, the wavelet-free approach is the preferable approach in the general case.
References
Adjerid, S., Devine, K., Flaherty, J., Krivodonova, L.: A posteriori error estimation for discontinuous Galerkin solutions of hyperbolic problems. Comput. Methods Appl. Mech. Eng. 191, 1097–1112 (2002)
Alpert, B.: A class of bases in \({L}^2\) for the sparse representation of integral operators. SIAM J. Math. Anal. 24, 246–262 (1993)
Alpert, B., Beylkin, G., Gines, D., Vozovoi, L.: Adaptive solution of partial differential equation in multiwavelet bases. J. Comput. Phys. 182, 149–190 (2002)
Amat, S., Moncayo, M.: Non-uniform multiresolution analysis with supercompact multiwavelets. J. Comput. Appl. Math. 235, 334–340 (2010)
Archibald, R., Fann, G., Shelton, W.: Adaptive discontinuous Galerkin methods in multiwavelets bases. Appl. Numer. Math. 61, 879–890 (2011)
Arnold, D., Brezzi, F., Cockburn, B., Marini, L.: Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39(5), 1749–1779 (2002)
Arvanitis, C., Makridakis, C., Sfakianakis, N.: Entropy conservative schemes and adaptive mesh selection for hyperbolic conservation laws. J. Hyperbol. Differ. Eq. 7(3), 383–404 (2010)
Atkins, H., Pampell, A.: Robust and accurate shock capturing method for high-order discontinuous Galerkin methods. In: 20th AIAA Computational Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences. Am. Inst. Aeronaut. Astron. (2011). https://doi.org/10.2514/6.2011-3058
Barter, G., Darmofal, D.: Shock capturing with higher-order, PDE-based artificial viscosity. In: 18th AIAA Computational Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences. Am. Inst. Aeronaut. Astron. (2007). https://doi.org/10.2514/6.2007-3823
Bassi, F., Crivellini, A., Rebay, S., Savini, M.: Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and \(k-\omega\) turbulence model equations. Comput. Fluids 34, 507–540 (2005)
Bassi, F., Rebay, S.: A high order discontinuous Galerkin method for compressible turbulent flows. In: Cockburn, B., Karniadakis, G., Shu, C.-W. (eds.) Discontinuous Galerkin Methods, Volume 11 of Lecture Notes in Comput. Science and Engineering, Springer, pp. 77–88 (2000)
Bassi, F., Rebay, S., Mariotti, G., Pedinotti, S., Savini, M.: A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows. In: Proceedings of 2nd European Conference on Turbomachinery, Fluid Dynamics and Thermodynamics, Antwerpen, Belgium, pp. 99–108 (1997)
Beam, R.M., Warming, R.: Multiresolution analysis and supercompact multiwavelets. SIAM J. Sci. Comput. 22(4), 1238–1268 (2000)
Bey, K., Oden, J.: \(hp\)-version discontinuous Galerkin methods for hyperbolic conservation laws. Comput. Methods Appl. Mech. Eng. 133(3/4), 259–286 (1996)
Beylkin, G., Keiser, J.: On the adaptive numerical solution of nonlinear partial differential equations in wavelet bases. J. Comput. Phys. 132(2), 233–259 (1997). http://www.sciencedirect.com/science/article/pii/S002199919695562X
Bramkamp, F., Lamby, P., Müller, S.: An adaptive multiscale finite volume solver for unsteady and steady state flow computations. J. Comput. Phys. 197(2), 460–490 (2004)
Calle, J., Devloo, P., Gomes, S.: Wavelets and adaptive grids for the discontinuous Galerkin method. Numer. Algorithms 39(1/2/3), 143–154 (2005)
Carnicer, J., Dahmen, W., Peña, J.M.: Local decomposition of refinable spaces and wavelets. Appl. Comp. Harm. Anal. 3, 127–153 (1996)
Caviedes-Voullième, D., Kesserwani, G.: Benchmarking a multiresolution discontinuous Galerkin shallow water model: implications for computational hydraulics. Adv. Water Resour. 86, Part A, 14–31 (2015). http://www.sciencedirect.com/science/article/pii/S0309170815002237
Cockburn, B., Hou, S., Shu, C.-W.: The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV: the multidimensional case. Math. Comp. 54(190), 545–581 (1990)
Cockburn, B., Lin, S.Y., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: one-dimensional systems. J. Comput. Phys. 84, 90–113 (1989)
Cockburn, B., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws II: general framework. Math. Comp. 52(186), 411–435 (1989)
Cockburn, B., Shu, C.-W.: The Runge-Kutta discontinuous Galerkin method for conservation laws V: multidimensional systems. J. Comput. Phys. 141, 199–244 (1998)
Cohen, A., Dahmen, W., DeVore, R.: Sparse evaluation of compositions of functions using multiscale expansions. SIAM J. Math. Anal. 35(2), 279–303 (2003). https://doi.org/10.1137/S0036141002412070
Cohen, A., Kaber, S., Müller, S., Postel, M.: Fully adaptive multiresolution finite volume schemes for conservation laws. Math. Comput. 72(241), 183–225 (2003)
Coquel, F., Maday, Y., Müller, S., Postel, M., Tran, Q.: New trends in multiresolution and adaptive methods for convection-dominated problems. ESAIM Proc. 29, 1–7 (2009)
Dahmen, W.: Wavelet and multiscale methods for operator equations. Acta Numer. 6, 55–228 (1997)
Daru, V., Tenaud, C.: Evaluation of TVD high resolution schemes for unsteady viscous shocked flows. Comput. Fluids 30(1), 89–113 (2000). http://www.sciencedirect.com/science/article/pii/S0045793000000062
Daubechies, I.: Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Philadelphia (1992)
Dedner, A., Makridakis, C., Ohlberger, M.: Error control for a class of Runge-Kutta discontinuous Galerkin methods for nonlinear conservation laws. SIAM J. Numer. Anal. 45, 514–538 (2007)
DeVore, R., Lorentz, C.: Constructive Approximation. Springer, New York (1993)
Di Pietro, D., Ern, A.: Mathematical Aspects of Discontinuous Galerkin Schemes. Mathèmatiques et Applications. Springer, New York (2012)
Domingues, M., Gomes, S., Roussel, O., Schneider, K.: Space-time adaptive multiresolution methods for hyperbolic conservation laws: applications to compressible Euler equations. Appl. Numer. Math. 59(9), 2303–2321 (2009). http://www.sciencedirect.com/science/article/pii/S0168927408002195
Gerhard, N.: An adaptive multiresolution discontinuous Galerkin scheme for conservation laws. PhD dissertation, RWTH Aachen (2017). https://doi.org/10.18154/RWTH-2017-06869
Gerhard, N., Caviedes-Voullième, D., Müller, S., Kesserwani, G.: Multiwavelet-based grid adaptation with discontinuous Galerkin schemes for shallow water equations. J. Comput. Phys. 301, 265–288 (2015)
Gerhard, N., Iacono, F., May, G., Müller, S., Schäfer, R.: A high-order discontinuous Galerkin discretization with multiwavelet-based grid adaptation for compressible flows. J. Sci. Comput. 62(1), 25–52 (2015)
Gerhard, N., Müller, S.: Adaptive multiresolution discontinuous Galerkin schemes for conservation laws: multi-dimensional case. Computat. Appl. Math. 35(2), 312–349 (2016)
Giesselmann, J., Makridakis, C., Pryer, T.: A posteriori analysis of discontinuous Galerkin schemes for systems of hyperbolic conservation laws. SIAM J. Numer. Anal. 53(3), 1280–1303 (2015)
Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability preserving high-order time discretization methods. SIAM Rev. 43(1), 89–112 (2001)
Gottschlich-Müller, B., Müller, S.: Adaptive finite volume schemes for conservation laws based on local multiresolution techniques. In: Fey, M., Jeltsch, R. (eds.) Hyperbolic Problems: Theory, Numerics, Applications. Zürich, Switzerland, February 1998. Vol. I, pp. 385–394. Birkhäuser, Basel (1999)
Harten, A.: Discrete multi-resolution analysis and generalized wavelets. Appl. Numer. Math. 12, 153–192 (1993)
Harten, A.: Adaptive multiresolution schemes for shock computations. J. Comput. Phys. 115, 319–338 (1994)
Harten, A.: Multiresolution algorithms for the numerical solution of hyperbolic conservation laws. Commun. Pure Appl. Math. 48, 1305–1342 (1995)
Harten, A.: Multiresolution representation of data: a general framework. SIAM J. Numer. Anal. 33(3), 1205–1256 (1996)
Hartmann, R., Houston, P.: Adaptive discontinuous Galerkin finite element methods for nonlinear hyperbolic conservation laws. SIAM J. Sci. Comput. 24, 979–1004 (2002)
Hartmann, R., Houston, P.: Adaptive discontinuous Galerkin finite element methods for the compressible Euler equations. J. Comput. Phys. 183, 508–532 (2002)
Houston, P., Senior, B., Süli, E.: \(hp\)-discontinuous Galerkin finite element methods for hyperbolic problems: error analysis and adaptivity. Int. J. Numer. Methods Fluids 40(1/2), 153–169 (2002)
Hovhannisyan, N., Müller, S., Schäfer, R.: Adaptive multiresolution discontinuous Galerkin schemes for conservation laws. Math. Comput. 83, 113–151 (2014). https://doi.org/10.1090/S0025-5718-2013-02732-9
Hu, G.: An adaptive finite volume method for 2d steady Euler equations with WENO reconstruction. J. Comput. Phys. 252, 591–605 (2013). http://www.sciencedirect.com/science/article/pii/S0021999113004786
Iacono, F., May, G., Müller, S., Schäfer, R.: A high-order discontinuous Galerkin discretization with multiwavelet-based grid adaptation for compressible flows. J. Sci. Comput. 62, 25–52 (2014). https://doi.org/10.1007/s10915-014-9846-9
Jaust, A., Schütz, J., Woopen, M.: An HDG Method for Unsteady Compressible Flows, Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2014, pp. 267–274. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-19800-2_23
Kaber, S., Postel, M.: Finite volume schemes on triangles coupled with multiresolution analysis. Comptes Rendus de l’Académie des Sciences - Series I - Mathematics 328(9), 817–822 (1999). http://www.sciencedirect.com/science/article/pii/S076444429980278X
Kaibara, M., Gomes, S.: A fully adaptive multiresolution scheme for shock computations. In: Godunov Methods. Theory and Applications. International conference, Oxford, GB, October 1999, pp. 497–503. New York, NY: Kluwer Academic/Plenum Publishers (2001)
Lagha, M., Zhong, X., Eldredge, J., Kim, J.: A hybrid WENO scheme for simulation of shock wave-boundary layer interaction. In: 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Aerospace Sciences Meetings. American Institute of Aeronautics and Astronautics (2009). https://doi.org/10.2514/6.2009-1136
Mallat, S.: Multiresolution approximations and wavelet orthonormal bases for \(L^2({\mathbb{R}})\). Trans. Am. Math. Soc. 315(1), 69–87 (1989)
Müller, S.: Adaptive multiscale schemes for conservation laws. Lecture Notes in Computational Science and Engineering, vol. 27. Springer, Berlin (2003)
Müller, S.: Multiresolution schemes for conservation laws. In: DeVore, R., Kunoth, A. (eds.) Multiscale, Nonlinear and Adaptive Approximation, pp. 379–408, Springer, Berlin (2009)
Pan, L., Xu, K., Li, Q., Li, J.: An efficient and accurate two-stage fourth-order gas-kinetic scheme for the Euler and Navier-Stokes equations. J. Comput. Phys. 326, 197–221 (2016). http://www.sciencedirect.com/science/article/pii/S0021999116304119
Persson, P.O., Peraire, J.: Sub-cell shock capturing for discontinuous Galerkin methods. In: 44th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings. American Institute of Aeronautics and Astronautics (2006). http://dx.doi.org/10.2514/6.2006-112
Pongsanguansin, T., Mekchay, K., Maleewong, M.: Adaptive TVD-RK discontinuous Galerkin algorithms for shallow water equations. Int. J. Math. Comput. Simul. 6(2), 257–273 (2012)
Remacle, J.F., Flaherty, J., Shephard, M.: An adaptive discontinuous Galerkin technique with an orthogonal basis applied to compressible flow problems. SIAM Rev. 45(1), 53–72 (2003)
Remacle, J.F., Frazão, S., Li, X., Shephard, M.: An adaptive discretization of shallow-water equations based on discontinuous Galerkin methods. Int. J. Numer. Meth. Fl. 52(8), 903–923 (2006). https://doi.org/10.1002/fld.1204
Roussel, O., Schneider, K.: A fully adaptive multiresolution scheme for 3D reaction-diffusion equations. In: Finite Volumes for Complex Applications III. Problems and Perspectives. Papers from the 3rd Symposium of Finite Volumes for Complex Applications, Porquerolles, France, June 24–28, 2002, pp. 833–840. Hermes Penton Science, London (2002)
Roussel, O., Schneider, K., Tsigulin, A., Bockhorn, H.: A conservative fully adaptive multiresolution algorithm for parabolic PDEs. J. Comput. Phys. 188(2), 493–523 (2003). http://www.sciencedirect.com/science/article/pii/S002199910300189X
Schäfer, R.: Adaptive multiresolution discontinuous Galerkin schemes for conservation laws. Ph.D. thesis, RWTH Aachen University (2011)
Shelton, A.: A multi-resolution discontinuous Galerkin method for unsteady compressible flows. Ph.D. thesis, Georgia Institute of Technology (2008)
Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes II. J. Comput. Phys. 83, 32–78 (1989)
Sjögreen, B., Yee, H.C.: Grid convergence of high order methods for multiscale complex unsteady viscous compressible flows. J. Comput. Phys. 185(1), 1–26 (2003). http://www.sciencedirect.com/science/article/pii/S002199910200044X
Sod, G.A.: A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 27, 1–31 (1978)
Vuik, M., Ryan, J.: Multiwavelet troubled-cell indicator for discontinuity detection of discontinuous Galerkin schemes. J. Comput. Phys. 270, 138–160 (2014)
Wang, L., Mavriplis, D.: Adjoint-based \(hp\) adaptive discontinuous Galerkin methods for the 2D compressible Euler equations. J. Comput. Phys. 228(20), 7643–7661 (2009)
Weber, Y., Oran, E., Boris, J., Anderson, J.: The numerical simulation of shock bifurcation near the end wall of a shock tube. Phys. Fluids 7(10), 2475–2488 (1995). http://scitation.aip.org/content/aip/journal/pof2/7/10/10.1063/1.868691
Woodward, P.: Trade-offs in designing explicit hydrodynamical schemes for vector computers. In: Rodrigue G. (ed.) Parallel Computations, pp. 153–172, Academic Press (1982)
Woodward, P., Colella, P.: The numerical simulation of two-dimensional fluid flow with strong shocks. J. Comput. Phys. 54(1), 115–173 (1984). http://www.sciencedirect.com/science/article/pii/0021999184901426
Yu, T., Kolarov, K., Lynch, W.: Barysymmetric multiwavelets on triangles. IRC Report 1997-006, Standford University (1997)
Zingan, V., Guermond, J.L., Popov, B.: Implementation of the entropy viscosity method with the discontinuous Galerkin method. Comput. Methods Appl. Mech. Eng. 253, 479–490 (2013)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gerhard, N., Müller, S. & Sikstel, A. A Wavelet-Free Approach for Multiresolution-Based Grid Adaptation for Conservation Laws. Commun. Appl. Math. Comput. 4, 108–142 (2022). https://doi.org/10.1007/s42967-020-00101-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42967-020-00101-6