Introduction

The discrete element method (DEM) is often applied in various particle technology fields, and studies have recently been conducted through numerical analyses or simulations. Discrete element analysis was first introduced by Cundall and Strack (1979) for analyzing the behavior of soil grains. A DEM analysis program was recently developed and is now being widely used. “PFC3D,” a program based on discrete element analysis, can be used to determine the traction and vertical forces according to soil conditions by simulating the behaviors of the soil and performing cultivation with plow blades (Chen et al., 2013). In another study using “EDEM,” agricultural products such as pepper seeds were represented as spherical shapes, and the behaviors in a grinder were analyzed and compared with their actual behaviors (Ghodki and Goswami, 2017). Using discrete element analysis, the flows and impacts of particles that cannot be analyzed through a continuum analysis method can be understood. The DEM can be applied in various situations, as an entire system can be analyzed based on a calculation of the repulsive force generated by the contact between particles, which itself can be analyzed using a linear or nonlinear equation. It is necessary to input the appropriate parameters for each analysis model (Ng, 2006). The necessary parameters include the density, modulus of elasticity, shear modulus, and Poisson’s ratio. As the analysis interval is dependent on the parameters and particle size, the required overall analysis time may also vary (Ng 2006; Lommen et al., 2014). The contact parameters for calculating the contact force include the damping coefficient, restitution coefficient, and coefficient of friction, and it is important to obtain suitable contact parameters to obtain valid results (Mishra and Murty, 2001; Malone and Xu, 2008). Studies have been conducted to measure the various parameters of actual minerals and agricultural products for application in DEM simulations (Chandramohan and Powell, 2005; Horabik and Molenda, 2016; Nam et al., 2018).

A method of deriving inter-particle properties by determining bulk properties can be used as a method for identifying the interactions between particles. The angle of repose (AOR) is a representative bulk property of particles. It is the angle between the horizontal plane and surface of particles in a heap of particulate matter; it indicates the characteristics of the friction between the particles, as well as the flow of the particles (Ileleji and Zhou, 2008). In a DEM analysis program, the influences on the AOR and flow rate of the particles can be determined according to the contact parameters between the particles, along with the flow of particles in the hopper (Yan et al., 2015). As the hopper must be able to discharge as many particles as desired, the particle flows and discharges in a hopper according to the structures of the hopper or particles have been analyzed (Sheldon & Durian, 2010). As various agricultural products, including grains, are stored in hoppers, bins, and silos after harvesting and before storage, distribution, or sowing, studies on grain flows have also been conducted (Markauskas et al., 2015). Garlic, for example, should be planted one-by-one at appropriate distances to obtain the maximum yield. To this end, a garlic planter applies a mechanism in which the seeds supplied from the hopper in the device are constantly sown one-by-one in the ground (Bakhtiari & Loghavi, 2009). Under the structure of such a garlic planter, if the garlic cannot be discharged from the hopper, the function of the planter is completely stopped. Therefore, it is necessary to determine whether garlic can be supplied smoothly. Hacıseferoğulları et al. (2005) analyzed in detail the nutritional and technological properties of garlic as a food. However, research on the inter-particle contact parameters of agricultural products required for DEM is insufficient. A DEM simulation can provide an appropriate analysis of the behavior of the garlic in a hopper and can confirm the discharge. For this reason, an analysis is required of the parameters of the garlic cloves to be applied in the simulation.

Studies on heap formation are constantly being conducted with DEM simulations, as practical results, such as the AOR, can be obtained, and various conditions can be analyzed. Nakashima et al. (2011) studied the flows of sand particles in a hopper under low-gravity conditions, which are difficult to understand in practice. Although it was found that gravity did not significantly affect the AOR, an analysis of the interactions with the ground under lunar surface conditions was possible. Alizadeh et al. (2018) employed cohesive particles treated with polyethylene glycol 400 in a DEM simulation applying a cohesive force between the particles and analyzed the AOR and shape of the particle heap. Through a correction process for the AOR, a valid analysis result was obtained, and the tendency of the experiment could be closely predicted. Measurements of the AOR for sand, soil, grain, etc. have been steadily tested in the past, and various analyses have been conducted. Geldart et al. (2006) suggested a static/dynamic AOR measurement method and found that consistent results could be easily obtained using an improved AOR measuring device. Wang et al. (2010) compared the measurement results of a discharge dynamic AOR, deposit dynamic AOR, and static AOR of pulverized coal and determined the differences in the AORs according to the particle size and moisture content. In a numerical analysis using a discrete element analysis, the AOR is affected by the particle size and thickness of the container, and the equation for the AOR is obtained according to the coefficients of the static and rolling friction between the particles and wall (2002). When considering the friction between the particles and wall when analyzing the AOR, there are many factors to consider in the simulation analysis. In one study, a swing-arm slump method was proposed for measuring the AOR, to exclude the influence of the wall (Grima & Wypych, 2011a). Moreover, through a DEM simulation in which the AOR was verified via a swing-arm slump experiment, the behavior of the particles in a high-speed conveyor could be practically analyzed (Grima & Wypych, 2011b).

In a discrete element analysis, the particles are analyzed based on a sphere with a constant curvature. However, as actual materials are not spherical in many cases, studying on the shape of the particles is required for the analysis. In recent studies, the 3D shapes of coke, rock, and iron ore were identified for a discrete element analysis; several spherical bodies were superimposed to suit the shapes, and the results were analyzed (Majidi et al., 2014; Coetzee, 2016; Li et al., 2017). Coetzee, (2016) identified 10 shapes of complex rock particles in detail using a 3D laser scanner and implemented them using two, four, and eight spherical particles. The results from measuring the AORs were compared and showed that a single spherical particle was limited in regard to showing a result similar to the actual result; an AOR comprising several particles was more similar to the actual result. In addition, the number of clumps was suggested during the calibration process. In the study of Grima and Wypych (2011b), it was found that there is a difference in the apparent density when a single particle and two spherical particles are stacked together. Regarding agricultural products, Zhang and Vu-Quoc (2000) superimposed four spheres to represent beans, and Scheffler et al. (2018) analyzed the impact forces in detail by representing apples with large number of spherical particles. Li et al. (2021) represented rice as particles and evaluated the performance of a precision seeder by DEM simulation. Markauskas et al. (2015) found that the rate of discharge from a hopper is similar to the actual rate by implementing corn as several spherical particles, and differences in behavior according to the number of spheres were identified in the discharge process. Thus, as it is necessary to organize particles to resemble the actual shape of objects for proper analysis, it is necessary to implement the non-spherical garlic cloves by clustering particles.

In this study, an analysis of the contact parameters of garlic cloves was performed using a heap formation, with the goal of performing a DEM simulation of the garlic cloves. The garlic cloves with complex shape, which could not be used for the simulation, was precisely represented as non-spherical particles. In addition, the simulation was verified more accurately with non-spherical particles. The AOR was measured for the heap, and the residual particles were counted. The sizes and shapes of the garlic cloves were identified for use in DEM simulations. The garlic particles were determined by appropriately configuring spherical particles to represent the shape of the garlic. The particle density was compared with the weight obtained from measuring the garlic. The swing-arm slump method was applied to the heap formation of the garlic cloves. As the residual number of particles was more suitable for fitting with the coefficients of friction, a prediction equation was derived for the residual number of particles. Using the coefficients of friction predicted by this equation, the heap formation of the actual garlic was appropriately simulated, and the numerical values of the contact parameters representing the practical particle flow were proposed.

Materials and Methods

Garlic Properties

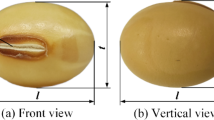
Garlic has a bulb shape made up of cloves; a clove is planted in the ground as a seed when sowing. In a garlic planter, a large number of cloves are stored in the hopper and are distributed and sown individually. To analyze the garlic cloves used for sowing, we organized particles into garlic cloves. To determine the shape of the garlic cloves, the length, width, and thickness of 150 “Daeseo” garlic cloves stored at a low temperature (2 °C) and 65% RH were measured to determine the characteristics of their sizes, as shown in Fig. 1. According to the shape of the garlic clove, the longest dimension up and down was measured as the length. The longest dimension perpendicular to the length was the width. With the garlic cloves on the floor, the thickness was measured from the bottom to the top. Each mass of the 150 cloves was recorded, and the moisture content was calculated by drying other samples stored at 105 °C for 24 h.

Fig. 1
figure 1

Appearance of a garlic clove and size definitions: a whole view, b top view, and c side view

Full size image

Heap Formation

In general, to measure the AOR, a funnel is used to accumulate particles, or grains are discharged from a rectangular hopper to measure the discharge AOR in the hopper and the deposit AOR at the bottom. However, this measurement method is not effective, as it also includes the effects of friction between the particles and wall surface and the effect of the restitution coefficient; thus, there are too many parameters to be considered for a simulation analysis. In this study, to analyze the contact parameters between pure garlic cloves, an experimental apparatus based on the swing-arm method was constructed. The swing-arm method, proposed by Grima and Wypych (2011a), quickly removes the cylinder containing the particles and allows the particles to flow freely. To measure and compare the actual AOR of the garlic, a swing-arm device was constructed, as shown in Fig. 2a. The bottom surface was made of circular acrylic with a diameter of 200 mm, and a railing was attached to the circumference at a height of 5 mm. The cylinder at the top for containing the material was 100 mm in diameter and 300 mm in height and was separated in half so that it could be removed from both sides. In the simulation, the structure was constructed with the same size as that of the actual experimental device, as shown in Fig. 2b. In the experiment, the separated cylinder was removed at a high speed (v) to avoid friction between the wall surface and material. In the simulation, after filling the particles, the upper cylinder was changed to a virtual structure that did not contact the particles, to ensure that they could flow naturally.

Fig. 2
figure 2

Experiment apparatus of swing-arm method: a actual experimental system and b simulation geometries

Full size image

The garlic cloves previously measured for their size were also used for heap formation. The garlic heap was formed by separating the cylinder after filling the cylinder with 150 garlic cloves. One hundred fifty garlic cloves are enough to fill about 200 mm in height. If the number of cloves is small, a clear heap cannot be formed. On the contrary, an excessive amount of garlic cloves will cause some cloves to flow down and not affect the heap formation. The AOR was measured from the left and right sides, as shown in Fig. 3. When the swing-arm method was applied to the garlic heap formation, a heap of garlic was created, as shown in Fig. 4. In addition, the number of garlic cloves remaining as a heap on the bottom plate was counted and recorded as the residual number of particles for further analysis. The heap formation was repeated five times to obtain the actual bulk properties of the garlic.

Fig. 3
figure 3

Manual measurement of AOR for the garlic particle heap

Full size image
Fig. 4
figure 4

Experimental heap formation of garlic

Full size image

Simulation Configuration

The DEM, developed to effectively analyze a system composed of particles, analyzes the behavior of particles based on the contact force obtained by the Hertz contact theory for spherical particles. In this study, “EDEM” software (EDEM 2019, DEM Solutions Ltd., Edinburgh, UK) applying the DEM was used to analyze the garlic cloves with particles. The irregular shapes of non-spherical particles were expressed in the form of a cluster of particles generated by superimposing multiple particles. In this case, the mass and moment of inertia of the cluster of particles could be expressed as the sum of the individual spherical particle components. In addition, by inputting the 3D shape information of a target particle for a more precise analysis, the mass and moment of inertia could be derived from the volume of the 3D shape and applied to the analysis. The motions and rotations of the particles were determined based on the relationships between the mass, moment of inertia, and contact force. The behavior of the entire particle system was analyzed using displacement values obtained by Newton’s equation of motion and was expressed by the accumulation of displacement at each analysis time step. The translational and rotational motions of the particles, according to the equation of motion, caused by the contact between particles were calculated using Eq. 1 and Eq. 2, as shown in Fig. 5 (Chen et al., 2015).

$$ {m}_i\frac{d{v}_i}{dt}={m}_ig+\sum \limits_k\left({F}_n+{F}_t\right) $$
(1)
$$ {I}_i\frac{d{\omega}_i}{dt}=-{\mu}_r{F}_n{R}_i\frac{\omega_i}{\left|{\omega}_i\right|}+\sum \limits_k{R}_i\times {F}_t $$
(2)
Fig. 5
figure 5

Particle cluster in the shape of garlic clove with a 3D template

Full size image

Here, mi, vi, g, Ii, ωi, μr, and Ri are the mass (kg), velocity (m/s), acceleration of gravity(m/s2), moment of inertia(kg·m2), angular velocity (rad/s), coefficient of rolling friction (−), and radius of the i-th particle (m), respectively. The EDEM employs the Hertz–Mindlin contact model as a basic model for analyzing the contact force. The contact force obtained using the contact model includes the vertical contact force (Fn) (N) and tangential contact force (Ft) (N), which can be expressed as shown in Eq. 3 and Eq. 4, respectively (Tsuji et al., 1992).

$$ {F}_n=-\frac{4}{3}{E}^{\ast}\sqrt{R^{\ast }}{\delta_n}^{\frac{3}{2}}+\sqrt{\frac{20}{3}}\beta {\left({m}^{\ast }{E}^{\ast}\sqrt{R^{\ast }{\delta}_n}\right)}^{\frac{1}{2}}{v}_n $$
(3)
$$ {F}_t=\min \left[{\mu}_s{F}_n,8{G}^{\ast }{\delta}_t\sqrt{R^{\ast }{\delta}_n}+\sqrt{\frac{80}{3}}\beta {\left({m}^{\ast }{G}^{\ast}\sqrt{R^{\ast }{\delta}_n}\right)}^{\frac{1}{2}}{v}_t\right] $$
(4)

In the above equations, E*, G*, R*, m*, and β are the equivalent elastic modulus (Pa), equivalent shear modulus (Pa), equivalent radius (m), equivalent mass (kg), and tangential damping coefficients (−), respectively; they are the same as 1/E* = (1 - ui2)/Ei + (1 - uj2)/Ej, 1/G* = (2 - ui)/Gi + (2 - uj)/Gj, 1/R* = 1/Ri + 1/Rj, 1/m* = 1/mi + 1/mj, and β=-lne/(ln2(e+π2))1/2, where Ei, Ej, ui, uj, Gi, Gj, Ri, Rj, mi, and mj are the elastic moduli (Pa), Poisson’s ratios (−), shear moduli (Pa), radii (m), and masses of particles i and j (kg), respectively. δn, δt, vn, vt, μs, and e are the overlap distances in the vertical and tangential directions (m), relative velocity in the vertical and tangential directions (m/s), coefficient of static friction (−), and the coefficient of restitution (−), respectively. The smaller the analysis time step in the DEM, the more accurate the analysis; however, as the total analysis time is considerably larger, an appropriate time step must be set. Malone and Xu (2008) suggested that to obtain an analysis error of less than 5%, the analysis time step should be less than 20% of the critical Rayleigh time, as shown in Eq. 5. The analysis time step in this study was set to 4 × 10−6 s, thereby satisfying the above condition.

$$ \Delta {T}_{step}<0.2\Delta {T}_R=\frac{0.2\pi {R}_i}{\left(0.163{u}_i+0.8766\right)}\sqrt{\frac{\rho_i}{G_i}} $$
(5)

Here, ΔTstep, ΔTR, and ρi are the analysis time steps (s), critical Rayleigh time (s), and particle density (kg/m3), respectively.

The parameters to be determined for the particles in the EDEM software are the Poisson’s ratio, modulus of elasticity, restitution coefficient, and coefficients of static and rolling friction. Among them, Poisson’s ratio, modulus of elasticity, and restitution coefficient are known to affect the angle of repose relatively insignificantly (Li et al., 2017). Each parameter was set as shown in Table 1, based on the values measured via compression and collision tests for garlic cloves (González-Montellano et al., 2012; Park et al., 2019). The coefficients of static and rolling friction were divided into six levels within the suggested range to perform the heap formation simulation and analyze the results.

Table 1 Input particle parameters for EDEM simulation
Full size table

Particle Size and Distribution

In the simulation, the particles were designed using a cluster method for superimposing spherical particles, as the particles needed to replace the actual garlic. Based on the measured size of the garlic, a 3D shape of garlic cloves was designed to serve as a template for composing the garlic particles and to obtain information regarding their volume. A 3D computer-aided design shape was applied as a template, and the spherical particles were superimposed to model the garlic particles as shown in Fig. 6. For the particle model, spherical particles with a radius of 2 mm and those with a radius of 1 mm at the corners were placed in close contact with the template surface. Although not all of the different shapes of actual garlic could be represented, the average value of the measured size was used as the basic size for the model, and particle cases with deviations were applied. As deviations of the length in the three-axis direction could not be applied differently in the simulation, three models with different thicknesses were developed to adapt the deviation in the thickness direction, so as to be close to the actual garlic size information. The standard deviation was the average of the standard deviations measured for the length and width of 150 garlic cloves. The standard deviation of the 150 particles generated by dividing into three cases was calculated using Eq. 6. The numbers of particles in the three cases were determined by matching the integrated standard deviation (σint) (mm) with the deviation of the actual garlic thickness.

$$ {\sigma_{int}}^2=\left(\sum \limits_{i=1}^m\left({n}_i\cdotp \left({\sigma_i}^2+{\left({\mu}_i-{\mu}_{int}\right)}^2\right)\right)\right)/\left(\sum \limits_{I=1}^m{n}_i\right) $$
(6)
Fig. 6
figure 6

Particle cluster in the shape of garlic clove with a 3D template

Full size image

In the above equations, n is the number of particles (−), μ is the mean size (mm), and σ is the standard deviation of the size (mm).

Predictive Equation Analysis

In the DEM, the AOR varies according to the coefficients of static and rolling friction in the analysis of inter-particle contact, as the force in the tangential direction generated when particles contact each other is determined by the friction coefficient. As it is difficult to directly measure the inter-particle friction and derive the friction coefficient, we attempted to determine the friction coefficient required for the simulation through an AOR that could be measured through a simple experiment. For spherical particles, an equation for predicting the AOR according to the coefficient of friction was presented and verified by comparison with actual data in previous study (Zhou et al., 2002). According to the equation, the AOR varies depending on the size of the particle and may also vary depending on the shape of the particle. As garlic cloves are not spherical, a new equation for predicting the AOR is needed. To derive the prediction equation, the heap formation simulation was repeatedly performed. The results were expressed using Eq. 7, which is a form suggested by Zhou et al. (2002). Curve fitting was performed using the least squares method to determine suitable parameters for the garlic particles for the prediction equation.

$$ X=\mathrm{A}\times {\mu}_s^{\alpha}\times {\mu}_r^{\beta } $$
(7)

In the above equations, X is the result for a bulk property (−), μs, and μr are the coefficients of static and rolling friction (−), and A, α, and β are unknown parameters (−). The AOR and the residual number of particles were considered as the bulk properties. Two prediction equations were obtained from the two bulk properties, as measured using simulations for various coefficients of friction. Through an analysis of variance with a Tukey post-hoc test, a more accurate prediction equation was confirmed. Furthermore, the applications of a single particle and cluster particles to realize non-spherical garlic shapes were compared. Using the most suitable prediction equation, the coefficients of static and rolling friction were suggested for representing the actual garlic cloves.

Results and Discussion

Garlic Properties

The size, mass, moisture content, and standard deviation of the 150 garlic cloves are listed in Table 2. The table shows the morphological distribution of the garlic cloves. Despite the small average thickness, the distribution of thickness was relatively wide compared to the distribution of length and width. Table 3 lists the morphological characteristics of the garlic particle model for the three cases. Normal, thin, and thick models are necessary to represent the broad distribution of the garlic clove thickness. Fig. 7 shows the distribution of the thickness of 150 garlic cloves as a histogram. Thus, the number of particles in each case can be determined. The standard deviation is the average of the standard deviations measured for the length and width. The integrated standard deviation of the three cases is close to the measured value of 3.14 mm, which can also be confirmed based on the solid and dotted lines in Fig. 7. The particle distribution follows a standard normal distribution. The same standard deviation is applied in cases 1, 2, and 3; however, the distributions are different, as the average thicknesses and numbers are different. As three cases are collected to form a pile of 150 particles, the overall distribution is the same as the sum of the distributions of the three cases. The distribution has an average of 20.18 mm and a standard deviation of 3.14 mm. The sizes of the 150 garlic cloves as measured for thickness are presented as a histogram and compared with the distribution of the particles.

Table 2 Measured garlic characteristics
Full size table
Table 3 List of size parameters varied between particle model cases
Full size table
Fig. 7
figure 7

Garlic cloves and particle model size distributions

Full size image

Data represented as mean ± standard deviation.

Using the 150 garlic cloves with the morphological characteristics mentioned above, heap formation was performed using the swing-arm method. As the first bulk property of the garlic cloves, the AOR was measured to be 27.07° ± 11.15°. In addition, the number of garlic cloves remaining as a heap on the bottom plate was 95 ± 4.39.

In the garlic property results, Table 3 for the particle model in the simulation differed from Table 2, which measured the size of actual garlic. In the EDEM software, only the isotropic distribution is applied. This is the reason for the development of multiple models of garlic particles to represent actual garlic cloves. As shown in Fig. 7, the particle model appropriately represented the actual garlic distribution in terms of the overall distribution. In some thickness sections, the number was higher or insufficient, and there were a few thick garlic cloves. However, the approximate shapes of the distributions were similar. Therefore, a simulation analysis can be performed using particles based on the dimensions and standard deviations of these three cases.

Simulation of Heap Formation

The results of the heap formation simulation for confirming the relationship between the coefficients of friction and AOR are shown in Fig. 8. The coefficient of static friction is fixed at 0.2, and the AOR is statistically analyzed based on how different it is according to the coefficient of rolling friction. Although the heap formation is performed with the simulation, the deviation of the manually measured AOR is large. Only two groups show significant differences. The determination of the coefficients of friction between the particles is inappropriate, based on the AOR measured with actual garlic cloves. In the case of the heap formation simulation with the swing-arm method, it is necessary to analyze the residual number of particles potentially involved with the coefficients of friction. Whether it is possible to simulate heap formation using simple spherical particles for garlic cloves should also be confirmed.

Fig. 8
figure 8

Simulated AOR versus the coefficient of rolling friction with a coefficient of static friction of 0.2 and non-spherical particle cases. Same symbol (*, **) means that there is no significant difference by Tukey’s test.

Full size image

The AOR indicates a large difference between the sphericity and uniformity of the particles (Miller & Byrne 1966). The shape of a garlic clove is considerably different from a sphere, and their size distribution is also wide. Consequently, the AORs of garlic cloves have slightly large deviations. It might be difficult to predict the coefficients of friction using the AOR. In the simulations, the friction between the particles affected the heap formation. As can be seen in Fig. 8, the AOR was large at large coefficient of rolling friction. The simulation is analyzed for three particle types with size deviations and thicknesses. When simulating non-spherical particles such as gravel, the standard deviation of the AOR is wide, and there may be some differences from the results for spherical particles. However, suitable results can be obtained using an adjustment algorithm (Elskamp et al., 2017).

The number of garlic particles forming a heap can be conveniently measured in the simulation. After performing the heap formation, the number of particles remaining on the bottom plate is referred to as the residual number of particles. The relationship between the residual number of and the coefficients of friction is shown in Fig. 9. The coefficient of static friction is fixed at 0.2, as before. The residual number of particles is statistically divided into three groups based on the coefficient of rolling friction. The coefficient of determination is 0.4639, which is higher than the result obtained using the AOR.

Fig. 9
figure 9

Simulated residual number of particles versus the coefficient of rolling friction with a coefficient of static friction of 0.2 and non-spherical particle cases. Same symbol (*, **, ***) means that there is no significant difference by Tukey’s test.

Full size image

In the case of garlic cloves, which have a large particle size and are convenient to count, the residual number of particles was more appropriate for classifying the bulk properties in the simulation. For example, the AOR could vary substantially owing to one or two particles on the surface of the heap. In fact, the residual number of particles was divided more clearly than the AOR using the coefficient of rolling friction in the above results. When the particle size is large, such as with garlic cloves, the residual number of particles can be conveniently counted. Furthermore, the residual number of particles can be replaced by the residual mass of the particles on the bottom plate. Clearly, as the AOR of the heap increases, the residual number of particles increases. The residual number of particles can be applied to Eq. 7 like the AOR.

A spherical particle provided by the DEM is applied to confirm whether it can simulate the behavior of garlic cloves. The diameter of the sphere is determined as 22.79 ± 3.55, so as to have the same volume and deviation as the garlic clove particle model. Heap formation simulations are performed for the non-spherical particle model and spherical particle model as illustrated in Fig. 10, and the bulk properties are compared. Differences are identified in the bulk properties between the two models, even though the morphological properties of one particle are matched. When the 150 particles are initially contained in each cylinder, the height is discordant, and the void volume appears to be larger in the spherical particle model. The numerical comparison is based on the residual number of particles. By comparing Fig. 11 and Fig. 12, we can see the difference in the residual number of particles within an equal range of the coefficients of friction. The simulated results are obtained and calculated based on ten repetitions. In the case of the non-spherical particle model, the residual number of particles reaches 110 with a high coefficient of rolling friction. In contrast, the residual number of particles in the spherical particle model does not exceed 90.

Fig. 10
figure 10

Snapshot of the heap formation: a non-spherical particle model and b spherical particle model

Full size image
Fig. 11
figure 11

Simulated residual number of particles versus the coefficient of static friction for various coefficients of rolling friction (0.001–0.2) with non-spherical particles

Full size image
Fig. 12
figure 12

Simulated residual number of particles versus the coefficient of static friction for various coefficients of rolling friction (0.001–0.2) with spherical particles

Full size image

For spherical particle simulations, the residual number of particles converging as the coefficient of static friction increases can be observed in Fig. 12. These results were consistent with those of Li et al. (2017), who determined a predictive equation for iron ore particles. However, the trends of the non-spherical garlic differed with a coefficient of static friction over 0.4. It might be assumed that the biased form of the garlic clove, dissimilar to the iron ore, reduces the residual number of particles at a high coefficient of static friction. The prediction equation could be applied within the range of increase for the residual number of non-spherical particles. Although the trend was different, non-spherical particles had a larger residual number of particles than spherical particles in the entire range. In the DEM simulation, non-spherical particles had to be applied to show the bulk properties of actual garlic cloves.

Validation of Predictive Equation

After verifying that the residual number of particles should be applied to determine the coefficients of friction between garlic clove particles, the unknown parameters of the prediction equation for the residual number of particles are derived using curve fitting. The prediction equation is constructed as shown in Eq. 8 for the range of 0.4 and below, i.e., where the coefficient of static friction and residual number of particles are proportional.

$$ {N}_{res}=123.26\times {\mu}_s^{0.0981}\times {\mu}_r^{0.0264},\kern0.75em {\mathrm{R}}^2=0.7189 $$
(8)

In the above equation, Nres is the residual number of particles (−). Fig. 13 shows the simulation results and prediction curves for the residual number of particles versus the coefficient of static friction with various coefficients of rolling friction. Through the residual number of particles measured in the heap formation simulation, the prediction equation is obtained; this equation can be used to predict the appropriate coefficients of friction. The practical data obtained by repeating the process ten times can be used to predict values within 5% of the error using the prediction equation. Eq. 8 showed an accurate prediction using the residual number of particles. According to Eq. 8, the effect of the coefficient of static friction was significant as the index of the coefficient of static friction is higher than that of the coefficient of rolling friction. This effect was also confirmed in the experiments of Zhou et al. (2002) who studied the AOR of spherical particles. One limitation of our implementation is that the residual numbers of particles can only be compared with each other under the same conditions in terms of the experimental apparatus and the same initial number of particles.

Fig. 13
figure 13

Simulated data and prediction equation as a function of the coefficients of static and rolling friction for the residual number of particles using the non-spherical particle model

Full size image

The coefficients of friction for the garlic clove particles can be estimated using the prediction equation, as the residual number of particles of garlic cloves is measured at 95. As listed in Table 4, we propose five sets of coefficients of friction, and the residual number of particles is calculated as 95 to validate the accuracy of the prediction equation. Fig. 14a shows the results for the residual number of particles obtained by simulation with the five validation sets and the results for the actual garlic cloves. The AOR, which was verified to have low precision in predicting the coefficients of friction, was also compared, as shown in Fig. 14b. The overall results of the validation sets indicate adequate results, without significant differences from the actual results.

Table 4 List of the coefficients of friction of validation sets for the residual number of particles of actual garlic cloves
Full size table
Fig. 14
figure 14

Comparison of bulk properties between actual measurement data and calculated validation sets: a residual number of particles and b AOR.

Full size image

The actual coefficients of static and rolling friction between particles are difficult to measure in practice. In the DEM, the particles are analyzed based on spherical particles and are formed in complex shapes representing the actual garlic cloves in this study. Therefore, the input values of the coefficients of friction may also be slightly different from reality. When researching crops using the DEM, it is important to consider the shape of the crops. After determining the shape of the particles, the approximate coefficients of friction can be derived using the prediction equation for the residual number of particles. In the case of non-spherical corn, to obtain the results within the allowable range of the angle of repose of the material, the corn can be expressed as a multi-sphere like the garlic particles in this study. Moreover, the angle of repose results was matched by changing the friction coefficient several times (Wang et al., 2017). Additional analyses such as shear tests should be performed to determine the correct and typical values of the coefficients of friction. Moreover, minor errors in these procedures can be improved and optimized through additional simulations for describing the actual behavior of the target. The clearly validated garlic clove particles will be used for sowing simulations to plant garlic cloves individually in future work. The behavior in the hopper of a garlic planter containing a bulk of garlic cloves could be accurately analyzed through appropriate inter-particle contact parameters of the particle model. Additionally, the predictive equation would be used for other crops to speed up parameter setting.

Conclusions

In this study, three particle models were created by applying deviations based on actual measured sizes to analyze garlic cloves in the DEM. As garlic cloves are not spherical, particle models for garlic clove shapes were constructed based on clustering. The deviations of the garlic clove particles with three different thickness particle models were confirmed to be similar to the actual garlic size distribution. In addition, the AOR and residual number of particles were measured through an experiment using the swing-arm method to derive the coefficients of friction between the particles. The residual number of particles was more appropriate for the analysis than the AOR, and the equation for predicting the residual number of particles was determined based on simulations of heap formation performed with the garlic clove particles for various coefficients of friction. Realistic simulation results were obtained by applying the coefficients of friction corresponding to the residual number of particles in the garlic cloves. In general, the accurate determination of the coefficients of friction for the particles and realization of their behaviors in the DEM requires a complex process of various comparisons and corrections to the actual behavior. Approximate coefficients of friction can be derived, and initial values for calibration can be effectively selected with the heap formation simulation using the swing-arm method and prediction equation. The findings also facilitate the rapid determination of the bulk properties of non-spherical particles. Nonetheless, further experiments for analyzing the behaviors of particles might be necessary to obtain more accurate contact parameters for garlic clove particles. This work was an experiment on garlic clove particles; for other shapes of non-spherical particles, another experiment should be performed, so as to construct a new prediction equation.