A Nine-Level Switched-Capacitor Step-Up Inverter with Low Voltage Stress

Abstract

This paper proposes a nine-level switched-capacitor step-up inverter (9LSUI) which can achieve a quadruple voltage gain with single dc source. Differing from other switched-capacitor inverters, the voltage stress of switches is effectively reduced due to the elimination of H-bridge, and the peak inverse voltage of all switches is kept within 2V_dc. In addition, the proposed inverter is able to integrate inductive load, and the capacitor voltage self-balancing can be achieved without any auxiliary circuits. Moreover, the topology structure can be flexibly extended to raise the output levels, and the peak inverse voltage of switches can remain constant with the increase of sub-modules in the extended structure. Comprehensive comparisons are performed to verify the outstanding advantages of the proposed inverter. Finally, the steady-state and dynamic performance of the proposed inverter is validated through an experimental prototype, and the experimental results are provided to prove the theoretical analysis.

1 Introduction

Nowadays, multilevel inverters (MLIs) have been widely applied in many areas, such as electric vehicles (EVs), flexible ac transmission systems and motor drives [1,2,3]. Comparing with the conventional two-level inverter, MLIs work better in: reducing the dv/dt on switches; improving output power quality; reducing electromagnetic interference; requiring smaller filters [4].

In general, traditional MLIs are classified into three categories: neutral-point-clamped (NPC) [5, 6]; flying capacitor (FC) [7, 8]; cascaded H-bridge (CHB) [9, 10]. NPC and FC inverters can obtain the desired output voltage by using clamping diodes and floating capacitors. However, the challenge of balancing the capacitor voltage complicates the control strategy along with the increase of the output levels. The CHB inverters consist of H-bridge units, which have the advantages of modular, scalable design and simple control. However, these topologies require multiple dc sources and have no voltage gain, which can limit the applications [11].

Furthermore, the dc sources such as photovoltaic panels, fuel cells and batteries of electric vehicles have low voltage [12], and conventional multilevel inverters suffer from the lack of voltage gain and the unbalance of capacitor voltage. In order to overcome these problems, a dc-dc boost converter is inserted into the front end of the inverter [13]. However, the cascade device will raise power losses and reduce the efficiency of the inverter [14]. To improve the boosting capability, the Z-source techniques have been used in MLIs. However, the extra inductors can increase the volume and cost of inverters. Moreover, the number of output levels has been limited [15,16,17].

Another solution is the switched-capacitor multilevel inverters (SCMLIs) which have no requirement for magnetic components such as inductors and transformers. SCMLIs are able to achieve multilevel output and boost voltage through a switched-capacitor circuit. In addition, the capacitor voltage can be self-balanced without any auxiliary circuits. The step-up switched-capacitor inverter proposed in [18] can output five-level voltage with single dc source. The other single input SC inverter proposed in [19] for high-frequency application employs two capacitors to generate nine-level output voltage. However, the maximum output voltage is only twice the input voltage. The nine-level SC inverter proposed in [20] also has a twice voltage gain.

In order to promote the voltage gain, a generalized inverter has been proposed in [21] to obtain a higher output voltage. Similarly, to increase the flexibility of SCMLIs regarding the output levels and voltage gain, two extendable SCMLIs have been proposed in [22] and [23]. The step-up inverter in [22] reduces the number of power switches, but the ability to integrate inductive loads is lost. For the SC inverter proposed in [23], the capacitors can be charged by a binary asymmetrical pattern, which can significantly raise the number of output levels. However, one of the common shortcomings of the above inverters is that the use of a back-end H-bridge increases the total voltage stress of devices.

The high peak inverse voltage (PIV) of switches can limit the applications of inverters. The accumulation of voltage stress can be avoided by cascading multiple SC inverters [24]. However, multiple isolated dc sources and numerous power components are needed. In addition, the SCMLIs proposed in [25] and [26] eliminate the back-end H-bridge to reduce the PIV. However, both inverters employ numerous switches, which is not conducive to simplify the control strategy, and will lead to an increase of power losses. In [27], a nine-level quadruple-boost inverter with an inherent ability to reverse the polarity of the output voltage has been presented. However, there are two switches that need to withstand the peak value of the output voltage. The step-up SC inverter proposed in [28] reduces the total standing voltage (TSV) of switches. However, numerous capacitors will lead to an increase of system volume and weight.

Considering the aforementioned challenges, this paper proposes a nine-level switched-capacitor inverter (9LSUI) with low voltage stress. The eminent characteristics of the proposed 9LSUI are as follows:

• (1) Nine-level output voltage can be achieved with only two capacitors and single dc source.

• (2) The proposed inverter has a quadruple voltage gain with low voltage stress.

• (3) The PIV of each switch is kept within 2V_dc, which can significantly reduce the TSV of inverter.

• (4) An extendable structure in which the PIV of all switches can be kept within 3V_dc.

• (5) Capacitor voltage can be self-balanced without involving additional controls.

Next section introduces the circuit design and modulation strategy of the proposed inverter. Section 3 presents the comparison between the proposed topology and other inverters. Section 4 demonstrates the steady-state and dynamic experimental results, and conclusion is obtained in Sect. 5.

2 Proposed 9LSUI

2.1 Circuit Design

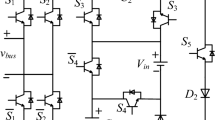
Figure 1 depicts the proposed 9LSUI, in which ten power switches S₁ ~ S₁₀ and two capacitors C₁ and C₂ constitute the SC unit to achieve a multilevel output and voltage boost. Additionally, the complementary switch pairs (S_L, $\overline{S} _{{\text{L}}}$) and (S_R, $\overline{S} _{{\text{R}}}$) constitute two half-bridges to reverse the polarity of the output voltage. The proposed inverter employs single dc source which is set as V_dc. All switches are equipped with an anti-parallel diode except for S₁₀. Capacitors C₁ and C₂ can be charged to V_dc and 2V_dc, respectively. The inverter can output nine levels: 0, ± V_dc, ± 2V_dc, ± 3V_dc, ± 4V_dc. Hence, the proposed topology achieves a quadruple voltage gain.

Fig. 1

Topology of proposed 9LSUI

The proposed inverter has an excellent characteristic of low voltage stress. As shown in Fig. 1, X is the ratio of PIV to V_dc, which can visually indicate the maximum stress of each switch. It can be seen that the PIV of most switches is V_dc, only switches S₈ ~ S₁₀, S_R and $\overline{S} _{{\text{R}}}$ withstand the voltage 2V_dc which is half of the peak output voltage. Therefore, it is worth noting that the features of high boosting factor and low voltage stress make the topology fit for medium and high-power applications with low input voltage.

2.2 Operating Principle

The operating principle of switches and capacitors are shown in Table 1. Where “0” and “1” indicate the off and on states of switches, “C”, “D” and “–” denote the charging, discharging and idle states of capacitors.

Table 1 Switches and capacitors states

Detailed nine operating states and current paths of the proposed inverter are demonstrated in Fig. 2, where the blue highlight and purple highlight lines are the charging current paths of capacitors and the reverse current paths. It can be seen that capacitor C₁ can be charged to V_dc in parallel with dc source when the output voltages are 0, V_dc and ± 3V_dc. Capacitor C₂ can be charged to 2V_dc in parallel with dc source and capacitor C₁ when the output voltages are 2V_dc and –V_dc. The connections of the dc source and capacitors can be changed through the ON/OFF states of switches, so as to achieve nine-level output voltage and quadruple voltage gain.

Fig. 2

Current paths for nine output levels. a + 4V_dc; b + 3V_dc; c + 2V_dc; d + V_dc; e 0; f −V_dc; g −2V_dc; h −3V_dc; i −4V_dc

2.3 Modulation Strategy

Various modulation techniques have been applied to multilevel inverters. In this paper, the phase disposition pulse width modulation (PD-PWM) is selected for the proposed 9LSUI due to its simplicity and low total harmonic distortion (THD) [28].

As shown in Fig. 3, eight carrier signals e₁ ~ e₈ are compared with a sinusoidal reference signal e_s to generate eight pulse signals u₁ ~ u₈. The gate drive signals v_GS1 ~ v_GSR of the switches can be obtained through the logical combination of u₁ ~ u₈. The logical combination can be expressed as

$$v_{{{\text{GS1}}}} = v_{{{\text{GS4}}}} = u_{{6}} + \overline{u}_{{7}} \cdot u_{{8}} ,$$

(1)

$$v_{{{\text{GS2}}}} = (u_{1} + \overline{u}_{2} ) \cdot u_{3} + \overline{u}_{5} \cdot (u_{7} + \overline{u}_{8} ),$$

(2)

$$v_{{{\text{GS3}}}} = v_{{{\text{GS5}}}} = (\overline{u}_{1} \cdot u_{2} + \overline{u}_{3} ) \cdot (u_{5} + \overline{u}_{6} ),$$

(3)

$$v_{{{\text{GS8}}}} = \overline{v}_{{{\text{GS9}}}} = \overline{u}_{2} \cdot (u_{6} + \overline{u}_{7} ),$$

(4)

$$v_{{{\text{GS6}}}} = \overline{v}_{{{\text{GS7}}}} = u_{{6}} ,$$

(5)

$$v_{{{\text{GS10}}}} = \overline{u}_{2} \cdot u_{{6}} ,$$

(6)

$$v_{{{\text{GSL}}}} = \overline{v}_{{{\text{G}}\overline{{{\text{SL}}}} }} = \overline{u}_{4} ,$$

(7)

$$v_{{{\text{GSR}}}} = \overline{v}_{{{\text{G}}\overline{{{\text{SR}}}} }} = u_{5} ,$$

(8)

Fig. 3

PD-PWM method schematic

The modulation index M for the 9LSUI is defined as

$$M = \frac{{A_{{\text{s}}} }}{{4A_{{\text{c}}} }},$$

(9)

where A_s and A_c are the amplitudes of the reference signal and carrier signals. The range of M is 0 < M ≤ 1. The inverter can output different levels with the change of M between 0 and 1.

3 Capacitance and Power Losses

3.1 Design of Capacitor

The voltage fluctuation range of capacitors should be maintained within an acceptable range to improve voltage quality. The capacitor voltage ripple is related to the maximum continuous discharge of the capacitor. Therefore, the effect of the capacitor voltage ripple on the output voltage can be reduced effectively when the proper value of the capacitance is selected.

It can be seen from Fig. 2 and Table 1, C₁ will be in discharging state when output voltages are -V_dc and -2V_dc in the negative half cycle, and C₂ will be in discharging state when the proposed 9LSUI outputs -3V_dc and -4V_dc. As shown in Fig. 3, the maximum continuous discharging intervals of C₁ and C₂ are [t₇, t₁₀] and [t₉, t₁₂]. In fact, C₁ and C₂ are in alternate charging and discharging for part of the time in these two intervals, such as C₁ in the interval [t₇, t₈]. The most extreme case that ignores the charging time of capacitors is considered in the following analysis. The time t₇, t₉, t₁₀ and t₁₂ in Fig. 3 are calculated as follows

$$t_{7} = \frac{1}{{2f_{{\text{s}}} }},$$

(10)

$$t_{9} = \frac{{\pi + \arcsin \left( \frac{1}{2M} \right)}}{{2\pi f_{{\text{s}}} }},$$

(11)

$$t_{10} = \frac{{\pi + \arcsin \left( \frac{3}{4M} \right)}}{{2\pi f_{{\text{s}}} }},$$

(12)

$$t_{{1{2}}} = \frac{{2\pi - \arcsin \left( {\frac{{1}}{{{2}M}}} \right)}}{{2\pi f_{{\text{s}}} }},$$

(13)

where f_s is the frequency of the sinusoidal reference wave. Assuming the load is pure resistive. Therefore, the maximum continuous discharging amount ΔQ_C1 of C₁ within [t₇, t₁₀] can be calculated as

$$\Delta Q_{C1} = \int_{{t_{7} }}^{{t_{10} }} {I_{{{\text{load}}}} \sin (2\pi f_{s} t)} dt.$$

(14)

The maximum continuous discharging amount ΔQ_C2 of C₂ within [t₉, t₁₂] is calculated as

$$\Delta Q_{C2} = \int_{{t_{9} }}^{{t_{12} }} {I_{load} \sin (2\pi f_{s} t)} dt,$$

(15)

where I_load is the amplitude of the load current. Assuming k% is the constant describes the maximum acceptable voltage ripple, the capacitances of C₁ and C₂ can be determined as

$$C_{1} \ge \frac{{\Delta Q_{C1} }}{{k\% \cdot V_{{{\text{dc}}}} }},$$

(16)

$$C_{2} \ge \frac{{\Delta Q_{C2} }}{{k\% \cdot 2V_{{{\text{dc}}}} }}.$$

(17)

3.2 Calculation of Losses

3.2.1 Switching Losses

The switching losses of MLIs occur during the turn-on and turn-off period of power switches due to the inherent switching delay [23]. It is known that the voltage and current of switches exhibit a linear approximation during the switching period. Therefore, the turn-on losses (P_sw,on,i) and the turn-off losses (P_sw,off,i) of the i-th involved power switch can be calculated by

$$\begin{aligned} P_{{{\text{sw,on,}}i}} &{ = }f_{{{\text{sw}}}} \int_{0}^{{t_{{{\text{on}}}} }} {v_{{\text{s}}} (t)i_{{\text{s}}} (t)dt} \\ &{ = }f_{{{\text{sw}}}} \int_{0}^{{t_{{{\text{on}}}} }} {\left( {\frac{{V_{on,i} }}{{t_{{{\text{on}}}} }}t} \right)\left( { - \frac{{I_{{{\text{on,}}i}} }}{{t_{{{\text{on}}}} }}(t - t_{{{\text{on}}}} )} \right)dt} , \\ &= \frac{1}{6}f_{{{\text{sw}}}} V_{on,i} I_{{{\text{on,}}i}} t_{{{\text{on}}}} \\ \end{aligned}$$

(18)

$$\begin{aligned} P_{{{\text{sw,off,}}i}} & = f_{{{\text{sw}}}} \int_{0}^{{t_{{{\text{off}}}} }} {v_{{\text{s}}} (t)i_{{\text{s}}} (t)dt} \\ & = f_{{{\text{sw}}}} \int_{0}^{{t_{{{\text{off}}}} }} {\left( {\frac{{V_{{off,i}} }}{{t_{{{\text{off}}}} }}t} \right)\left( { - \frac{{I_{{off,i}} }}{{t_{{{\text{off}}}} }}(t - t_{{{\text{off}}}} )} \right)dt} , \\ & = \frac{1}{6}f_{{{\text{sw}}}} V_{{off,i}} I_{{off,i}} t_{{{\text{off}}}} \\ \end{aligned}$$

(19)

where f_sw is the switching frequency, v_s and i_s present the voltage and current of switch when the switching state changes, V_on,i and V_off,i are the on-state and off-state voltage of the i-th switch, I_on,i and I_off,i are the on-state and off-state current that across the i-th switch, t_on and t_off are the time of turn-on and turn-off. Therefore, the total switching losses P_sw of the proposed inverter can be obtained as

$$P_{{{\text{sw}}}} { = }\sum\limits_{i = 1}^{14} {\left( {P_{{{\text{sw,on,}}i}} + P_{{{\text{sw,off,}}i}} } \right)} .$$

(20)

3.2.2 Conduction Losses

The conduction losses are related to the parasitic resistance of power devices in current paths, including the conduction resistance R_on of switches, the internal resistance R_D of anti-parallel diodes and the equivalent series resistance R_ESR of the capacitors.

The equivalent resistance for each level is listed in Table 2. According to Fig. 3 and Table 2, in the interval [0, t₁], the load current flows through three switches and three diodes (four switches and two diodes) when the output voltage is 0 (V_dc). Therefore, the energy loss E_loss1 during the interval [0, t₁] can be calculated as

$$\begin{gathered} E_{{{\text{loss1}}}} = \int_{0}^{{t_{1} }} {i_{{{\text{load}}}}^{2} } \left[ {(3R_{{{\text{on}}}} + 3R_{{\text{D}}} )\frac{{A_{{\text{s}}} \sin (2\pi f_{s} t)}}{{A_{{\text{c}}} }} + } \right. \\ \left. {(4R_{{{\text{on}}}} + {2}R_{{\text{D}}} )\left( {{1 - }\frac{{A_{{{\text{ref}}}} \sin (2\pi f_{ref} t)}}{{A_{{\text{c}}} }}} \right)} \right]dt, \\ \end{gathered}$$

(21)

where i_load is the load current, R_on is the conduction resistance of switches and R_D is the internal resistance of anti-parallel diodes.

Table 2 Equivalent resistance for each level

Similarly, the conduction losses in other inverters ([t₁, t₂]-[t₁₃, t₁₄]) are also can be calculated according to Eq. (21). The total conduction losses P_cond as the proposed 9LSUI can be calculated as

$$P_{{{\text{cond}}}} = \sum\limits_{i = 1}^{14} {E_{{{\text{loss}}i}} } \times f_{s} ,$$

(22)

where f_s is the frequency of the sinusoidal reference wave.

3.2.3 Capacitor Ripple Losses

The ripple loss P_rip is caused by the voltage fluctuation of capacitor. The voltage ripple ΔV_rip,Ci of the capacitor C_i is obtained by

$$\Delta V_{{{\text{rip}},C_{i} }} = \frac{1}{{C_{i} }}\int_{t - }^{t + } {i_{{C_{i} }} (t)dt} ,$$

(23)

where i_Ci(t) is the current across capacitor, the interval [t-, t +] is the discharging period of C_i. For the proposed 9LSUI, [t₈, t₉] and [t₉, t₁₂] are the maximum discharging intervals of C₁ and C₂. The ripple losses P_rip can be calculated as

$$P_{{{\text{rip}}}} = \frac{{f_{{\text{s}}} }}{2}\sum\limits_{i = 1}^{2} {C_{i} \Delta V_{{{\text{rip,}}Ci}}^{{2}} } .$$

(24)

Therefore, the total losses P_loss of the proposed 9LSUI can be calculated as

$$P_{{{\text{rip}}}} = \frac{{f_{{\text{s}}} }}{2}\sum\limits_{i = 1}^{2} {C_{i} \Delta V_{{{\text{rip,}}Ci}}^{{2}} } .$$

(25)

Finally, the efficiency of the nine-level inverter can be expressed as

$$\eta = \frac{{P_{{\text{o}}} }}{{P_{{\text{o}}} + P_{{{\text{loss}}}} }}{ = }\frac{{P_{{\text{o}}} }}{{P_{{\text{o}}} + P_{{{\text{sw}}}} + P_{{{\text{cond}}}} + P_{{{\text{rip}}}} }},$$

(26)

where η and P_o are the efficiency and output power of the proposed inverter.

4 Topology Extension and Comparisons

The proposed 9LSUI can be extended with multiple SC units, which can generate more output levels and achieve higher voltage gain. In order to further evaluate the superiority of the proposed topology, a comprehensive analysis and comparison with other recently SCMLIs have been implemented.

4.1 Extended Structure

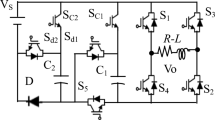
The extended structure of the proposed 9LSUI is shown in Fig. 4. It can be seen that each two SC units are in a back-to-back connection through a power switch pairs P_i1 and P_i2 (i = 1, 2, …, n-1). Notice that these switch pairs have a complementary operation with each other to avoid the short-circuit problem. In the extended topology, n dc sources are used and the voltage is V_dc. Therefore, the number of capacitors (N_Cap) and switches (N_SW) can be expressed as

$$N_{{{\text{Cap}}}} { = 2}n,$$

(27)

$$N_{{{\text{SW}}}} { = 12}n{ + 2}{\text{.}}$$

(28)

Fig. 4

Extended structure of the proposed 9LSUI

In this configuration, the voltage of the capacitor C_i1 remains as V_dc and the capacitor C_i2 is charged to 2V_dc. The PIV of P_i1 and P_i2 is kept within 3V_dc in the extended structure. Therefore, the number of output levels (N_L), the peak value of the output voltage (V_{o, max}) and the TSV for the switches can be obtained as:

$$N_{{\text{L}}} { = 8}n{ + 1,}$$

(29)

$$V_{{{\text{o}},\max }} = 4n \cdot V_{{{\text{dc}}}} ,$$

(30)

$${\text{TSV = (19}}n{ - 2)} \cdot V_{{{\text{dc}}}} .$$

(31)

4.2 Comparison of Nine-level Inverters

In this section, to evaluate the performance of the proposed 9LSUI, a comprehensive comparison with other topologies is made in Table 3. The comparison focuses on the numbers of dc sources (N_Source), capacitors (N_Capacitor), switches (N_Switches) and diodes (N_Diodes). Furthermore, the PIV of semiconductors (switches and diodes), the TSV_pu of semiconductors, the voltage gain and the use of H-bridge are also considered. The terms related to TSV_pu and voltage gain are defined as

$${\text{TSV}}_{{{\text{pu}}}} = \frac{{{\text{TSV}}}}{{V_{o\_\max } }},$$

(32)

$${\text{Voltage Gain}} = \frac{{V_{{o{\text{\_max}}}} }}{{V_{{{\text{dc}}}} }}.$$

(33)

where V_{o_max} and V_dc are the maximum output peak voltage and the dc input voltage.

Table 3 Comparison of single-phase nine-level inverters

According to Table 3, the proposed inverter requires minimum capacitors, which helps to reduce the volume and weight of the inverter. Moreover, compared with other inverters, the proposed topology employs single dc source and two capacitors to achieve quadruple voltage gain, while the boosting factor in [19] and [20] is 2. Although the inverters in [22] and [23] use fewer switches, they all require H-bridge to shift output voltage polarity. Moreover, the large number of diodes used in [22] may limit its capacity of integrating inductive loads.

The PIV of the switches is important role to evaluate the performance of MLIs. The comparison shows that the PIV of the switches is only 2V_dc. Although the inverter in [25] has lower PIV, the use of numerous switches will lead to a high cost. A significant feature of the proposed inverter is low TSV_pu, which also credits to the low PIV of switches. The inverter in [28] has the lowest TSV, but the use of four capacitors increases the volume and cost.

The comparison between the suggested extended structure and other inverters is performed at the output levels of (2 m + 1) or m. Table 4 and Fig. 5. show the comparison results, the proposed extended structure employs less components (capacitors, switches and diodes). Moreover, the proposed structure does not need extra diodes and has the minimum TSV_pu. In a word, the proposed topology has obvious advantages in promoting voltage gain, reducing the number of components and voltage stress of the switches.

Table 4 Comparison of the proposed extended topologies with other inverters when output (2 m + 1) levels

Fig. 5

Comparison of different SCMLIs. a number of sources; b number of capacitors; c number of switches and diodes; d TSV_pu

5 Simulation and Experiment Analysis

5.1 Simulation Results

In order to examine the performance of the proposed inverter, a simulation model of nine-level switched-capacitor inverter is established in MATLAB/Simulink. The simulation parameters are shown in Table 5.

Table 5 Simulation Parameters

The simulation results are shown in Fig. 6. It can be seen that the proposed inverter can output nine-level voltage and achieve a quadruple voltage gain. The capacitor voltages are self-balanced with low voltage ripple.

Fig. 6

Simulation results of output voltage, load current, and capacitor voltage

When the modulation index is 0.9, the Fast Fourier Transform (FFT) of the output voltage is shown in Fig. 7. It can be seen that the THD is 15.18%, and the 40th harmonic component is larger than the others because the carrier frequency is 2 kHz. The low THD can also simplify the design of the filter.

Fig. 7

THD of the output voltage

5.2 Experimental Results

To verify the practicability and effectiveness of the proposed 9LSUI, an experimental prototype has been built as shown in Fig. 8. The components and parameters of the model are shown in Table 6. The experiments examine the steady-state performance and dynamic responses of the proposed topology under several different conditions.

Fig. 8

Picture of the experimental prototype

Table 6 Experimental parameters

Figure 9 shows the steady-state experiment results and efficiency curve. The output voltage and load current are shown in Fig. 9a. It can be seen that the amplitude of output voltage is 120 V, which verifies that the proposed inverter can achieve a voltage gain of 4. Figure 9b presents the output voltage and load current when the inductive load is integrated. The load current appears as a sinusoidal waveform due to low THD. The voltages of C₁ and C₂ under the R & L load are shown in Fig. 9c. It can be observed that C₁ and C₂ are charged to 28.66 V and 57.65 V. Moreover, the capacitor voltage fluctuates periodically within 5 V, which verifies the self-balancing ability of the proposed inverter. Figure 9d shows the theoretical efficiency and experimental efficiency of the proposed inverter under different output power. It can be seen that the 9LSUI has a great performance.

Fig. 9

Steady-state experimental results and efficiency curve. a output voltage and current with a pure resistive load; b output voltage and current with a resistive-inductive load; c capacitor voltages; d efficiency curve of the proposed topology

Figure 10 shows the voltage stress of different switches. The peak inverse voltages of the switches S₁ ~ S₇, S_L, and $\overline{S} _{{\text{L}}}$ are V_dc, and the peak inverse voltages of the switches S₈ ~ S₁₀, S_R, and $\overline{S} _{{\text{R}}}$ are 2V_dc. Table 7 presents the steady-state experimental results. The experimental results are in good agreement with the previous theoretical analysis, which proves that the proposed inverter has the characteristics of low voltage stress across switches.

Fig. 10

Experimental results of stress voltages. a switches S₁-S₄; b switches S₅-S₈; c switches S₉-S_R

Table 7 Steady-state experimental results

Figure 11 and Table 8 present the dynamic experimental results with the change of M. Figure 11a–c show the dynamic responses when the modulation ratio M varies from 0.9 to 0.7, 0.7 to 0.4 and then 0.4 to 0.2. It can be seen that the number of output levels will reduce with the decrease of M. Meanwhile, the amplitude of the load current also decreases accordingly. The waveforms quickly reach new steady-states after these changes, which is in good agreement with the theoretical analysis and design requirements.

Fig. 11

Dynamic experimental results with change of a M from 0.9 to 0.7, b M from 0.7 to 0.4 and c M from 0.4 to 0.2

Table 8 Dynamic experimental results with change of M

Figures 12a, b are the dynamic responses when the dc source varies from 10 to 30 V and from 30 to 10 V. In Fig. 12, the amplitude of the output voltage gradually rises from 40 to 120 V when the input voltage increases. Meanwhile, the voltage of C₁ rises from 10 to 30 V, and the voltage of C₂ rises from 20 to 60 V. It can be seen from Fig. 12b that the variations of load current and voltage are opposite to the ones in Fig. 12a when the input voltage decreases. Figures 12c, d are the dynamic responses when the load varies from no-load to resistive load (50 Ω), and then to resistive-inductive load (50 Ω-15 mH). The output voltage remains constant, and the load current varies instantaneously with the change of load, and then reaches a new steady-state.

Fig. 12

Dynamic experimental results. a dc input voltage V_dc changes from V_in = 10 V to V_in = 30 V. b dc input voltage V_dc changes from V_in = 30 V to V_in = 10 V. c the load changes from no-load to R = 50 Ω. d the load changes from R = 50 Ω to R-L = 25 Ω-15 mH

In summary, the experimental results of the proposed 9LSUI validate the previous theoretical analysis. The capacitor voltage self-balancing can be achieved under steady-state and dynamic conditions, which verifies the practicability and effectiveness of proposed inverter.

6 Conclusion

The paper presents a switched-capacitor step-up inverter, which can generate nine output levels and achieve quadruple voltage gain without H-bridge. In addition, the proposed 9LSUI has voltage-self-balance ability without any auxiliary circuits, and the peak inverse voltage of all switches is kept within 2V_dc. Moreover, the extended structure of the proposed inverter can generate more output levels, while the PIV of all switches is kept within 3V_dc. The comparison results with other inverters show that the proposed inverter has the advantages of reducing the components, raise the voltage gain, and lowering the TSV of devices. An experimental prototype is implemented to verify the effectiveness and feasibility of proposed 9LSUI. The experimental results indicate that the proposed topology performs well in different conditions.