1 Introduction

Carbon fibers are usually made from cellulose, polyacrylonitrile (PAN), or mesophase pitch. Fibers with the precursor cellulose have low thermal and electrical conductivity due to the lattice defects in the carbon structure. Therefore, they are mainly used as insulating materials [1]. Fibers made from PAN or pitch play a more important role economically and are used in aircraft, wind turbine blades, and vehicles.

High temperature treatment of PAN precursors leads to dehydrogenation, cyclization reactions, N2-elimination, and carbonization. Overall, these reactions lead to the high thermal stability and good mechanical properties of the resulting carbon fibers, especially if the fibers were aligned during the stabilization process. Microscopically, the high temperature processing leads to semicrystallinity due to the formation of graphitic domains. The fibers made from polyacrylonitrile have a circumferentially orthotropic structure, i.e., their properties depend on the direction in which they are measured. Heat transport takes place mainly within the graphitic basal planes, which are held together by covalent bonds. Only weak Van der Waals forces act between the basal planes, which reduces transversal heat transport [2, 3].

The anisotropic fiber morphology has a considerable influence on the fiber properties. The anisotropic behavior was extensively studied and compared to micromechanical models in other publications of the author [4,5,6]. The anisotropy affects tensile strength and Young’s modulus, thermal expansion, and electrical and thermal conductivity [7,8,9,10]. Morgan [10] showed that the property profile can be adjusted by the temperature during the production of the fibers. The higher the oven temperature, the more the layers orient themselves in the longitudinal direction of the fibers. This results in a more aligned structure, which significantly increases the anisotropy. As expected, this has an effect on the respective morphology of the carbon fiber.

In the PAN-based carbon fibers, there is mostly a random distribution of the individual layers, while more ordered structures result in the pitch-based ones. Qin et al. [11] investigated the effect of temperature treatment on the morphology of PAN-based carbon fibers and the effects on elemental composition, porosity and mechanical properties, tensile strength, and tensile modulus. In their work, the fibers were high-temperature treated over a range of 1300 °C to 2700 °C. They showed that the carbon content of the fibers increases with increasing processing temperature, while the remaining elements such as nitrogen and hydrogen are split off. In particular, the step from 1300 °C to 2000 °C stands out, where the nitrogen content is reduced from \({4.96}\%\) to \({0.12}\%\), resulting in a carbon yield of \({99.4}\%\). This results in an increased porosity of the fiber, since the elimination of nitrogen leads to the formation of pores and voids in the fiber. These are only eliminated with a further increase in temperature by rearrangements in the lattice structure. With the increase in temperature, an increasing orientation of the crystalline domains becomes apparent. In the case of the PAN-based carbon fibers, a largely unordered structure can be seen for the temperature treatment up to 1300 °C (see Fig. 1). When treated up to 2700 °C , a clear orientation and growth of the graphitic lamellae can be seen.

Fig. 1
figure 1

Scheme of fiber microstructure based on PAN with increasing production temperature

Full size image

The different fiber morphologies also affect the mechanical and thermal properties, as shown by Qin et al. [11] Their findings show that especially the tensile modulus increases with increasing temperature as a result of the increased alignment and growth of the crystallites. However, when the tensile strength is considered, it shows a decrease with increasing high-temperature treatment. The reason for this is the orientation of the graphene layers. With increasing temperature, the amount of entanglement and covalent cross-linking decreases, resulting in a decreased shear modulus. In addition, there is an increase in the microporosity within the fiber, mainly due to cleavage of the chemically bound nitrogen and consequent formation of defects in the crystal structure [8, 10, 11].

Due to the morphology induced anisotropy of the fibers, there are significant differences between the thermal conductivity longitudinal (\({0}^{\circ }\)) and transversal (\({90}^{\circ }\)) to the main fiber axis. In this regard, Zhang [3] suggests that the transverse thermal conductivity is generally equivalent to about \({1}\%\) of the longitudinal thermal conductivity. Our findings in other publications show that this can only be seen as a rough estimation [5]. The literature review summarized in Table 1 shows that the relation between thermal conductivity in fiber direction, \(\kappa _{\parallel }\), and in transverse direction, \(\kappa _{\perp }\), (the anisotropy factor) varies between different fibers.

Table 1 Overview of thermal conductivities for PAN and pitch-based carbon fibers parallel and perpendicular to the longitudinal fiber axis
Full size table

From the literature, it is well-known that the conditions during production of the fiber (mainly the temperature) lead to different morphology and different mechanical properties. So far, the effect on thermal conductivity in fiber and transverse direction has not been studied. The aim of this work is to investigate the influence of the morphology of carbon fibers with varying tensile modulus on the thermal conductivity of composites with a resin matrix made thereof.

2 Materials and methods

2.1 Materials

The resin tetraglycidylmethylenedianiline (TGMDA, Epikote™ RESIN 496, Hexion Inc., Columbus, OH, USA) is four-functional with an epoxy equivalent of \({115}\hbox {g eq}^{-1}\). The used hardener was diethyltoluenediamine (DETDA, XB3473™, hydrogen equivalent weight \({43}\hbox {g eq}^{-1}\)).

The used carbon fibers were HTS40 (Toho Tenax, Chiyoda, Japan), A49 (Dowaksa, Tucson, AZ, USA), IMS65 (Toho Tenax, Chiyoda, Tokyo, Japan), and HR40 (Mitsubishi, Tokyo, Japan). Further properties can be found in Table 2.

Table 2 Manufacturer data of fibers used in the underlying research
Full size table

2.2 Resin preparation and curing

TGMDA and DETDA were mixed stoichiometrically (72:28 m/m). Degassing followed at 10–20 mbar. The samples were cured in a laboratory oven at 120, 160, and 200 °C at each temperature for 1 h with a heating rate of 10 K min−1. A postcuring at 220 °C for 2 h followed.

2.3 Prepreg production and consolidation

The department of Polymer Engineering owns a industry-like processing line to produce prepregs (pre-impregnated fibers). The procedure is as follows: 12 K unidirectional carbon fiber rovings were pre-spread with rollers. A carrier paper was coated with a resin film at room temperature. In the last step, the fibers were compressed with the resin film to the final prepreg with calander rolls (25 °C). The prepregs were stored in a fridge at (–20 °C) before further processing. By hand lay-up the prepregs were stacked and air was removed. It followed a sealing in vacuum bags and curing under atmospheric pressure of 5 bar in a laboratory press at 120, 160, and 200 °C, at each temperature for 1 h with a heating rate of 10 K min−1 . Post-curing at 220° C for 2 h before cooling at a rate of 5 K min−1 followed.

2.4 Determination of fiber volume content

Thermogravimetric analysis (TGA) was conducted with the TG 209 F1 Libra (Netzsch-Gerätebau GmbH, Selb, Germany).

The fiber volume content was determined by TGA according to DIN 16459:2019-12 [16]. In the suggested routine, fibers were dried for 2 h at 120 °C in the TGA. Then, the fibers were heated in the TGA from 20 °C to 800 °C, with a heating rate of 2 K min−1 under a nitrogen flux of 85 mL min−1. Samples cut from the laminates and samples cut from neat resin plates were dried for 2 h in the TGA, then heated up to 450 °C with a heating ramp of \({10}\, \hbox {K\, min}^{-1}\). Finally, an isothermal step for \({170}\, \hbox {min}\) at \({450}\,^{\circ }\hbox {C}\) was performed. All samples were handled with gloves to prevent possible contamination.

In the TGA, the fibers showed only a slight weight loss of \(({1.0}\,{\pm }\,{1.1})\,\%\), which could be attributed to the oxidation of the sizing. During the drying step, no significant weight loss could be detected.

The fiber volume content, \(\Phi\), could then be calculated as

$$\Phi = \frac{{m_{{\text{f}}} }}{{\rho _{{\text{f}}} \left( {\frac{{m_{{\text{f}}} }}{{\rho _{{\text{f}}} }} + \frac{{1 - m_{{\text{r}}} }}{{\rho _{{\text{r}}} }}} \right)}}{\text{, }}$$
(1)

where \(m_\text {f}\) is the mass of the fibers, \(\rho _\text {f}\) is their density, and \(\rho _\text {r}\) represents the density of the resin. The mass of the fibers was calculated by

$$\begin{aligned} m_\text {f} = \frac{m_\text {l} - m_\text {r}}{1 - m_\text {r}}\text {,} \end{aligned}$$
(2)

where \(m_\text {l}\) is the remaining mass of the laminate after the cycle, and \(m_\text {r}\) is the remaining mass of the resin.

The method was successfully verified and tested in comparison to the determination of the fiber volume content via density measurements [5].

2.5 Thermal conductivity measurements of composites

The thermal conductivity was measured by the laser flash method (LFA) with LFA447 (Netzsch GmbH, Selb, Germany). Five shots were used with a duration of \({30}\,\hbox {ms}\) each, the signal was fitted with the Proteus Analysis Software (Netzsch GmbH, Selb, Germany) by the Cape–Lehman algorithm. The tested samples had a diameter of \({12.7}\,\hbox {mm}\).

The density was measured with the AG245 (Mettler-Toledo International Inc., Columbus, Ohio, USA) using Archimedes’ principle. The thermal heat capacity was measured with the DSC 1 (Mettler-Toledo International Inc., Columbus, OH, USA), according to ASTM E1269-11, with a heating rate of \({20}\,\hbox {K\, min}^{-1}\) [17].

2.6 Nanostructural analysis of PAN fibers

For volume-averaged nanostructural analysis, small-angle (SAXS) and wide-angle X-ray (WAXS) scattering were performed on a bundle of parallelly aligned fibers using a Double Ganesha AIR system (SAXSLAB/Xenocs), equipped with a rotating copper anode (Micro-MAx 007HF, Rigaku Corporation, wavelength of \(\lambda = {0.154}\,\hbox {nm}\)). Data were recorded with a position-sensitive detector (Pilatus 100 K for WAXS, PILATUS 300K for SAXS; Dectris). Two-dimensional scattering patterns were converted into one-dimensional intensity profiles of I(q) vs q, where q is given as

$$\begin{aligned} q = \frac{4 \pi }{\lambda } \sin \frac{\theta }{2}, \end{aligned}$$
(3)

with the scattering angle \(\theta\). X-ray diffractograms (XRD) of the carbon fiber bundles were recorded in Bragg–Brentano geometry as coupled \(\theta\)–\(2\theta\) scans using an Empyrean system (PANalytical, Almelo, Netherlands) equipped with a sealed X-ray tube (Cu-\(\hbox {K}_{\alpha }\)), a PIXEL solid state detector, and a spinning stage.

2.7 Thermal conductivity measurements of single fibers

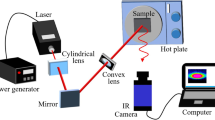
Thermal diffusivity of single fibers was determined via lock-in thermography in accordance with our previous publication [18]. All measurements were done in a vacuum (\(p<{5}\times \hbox {10}^{-2}\, \hbox {mbar}\)). A laser beam (Genesis MX 532-1000 SLM OPS, Coherent, Dieburg, Germany, \(\lambda ={532}\,\hbox {nm}\)) periodically heated the sample with a frequency, f, of \({2}\,\hbox {Hz}\) for HTS40, A49, and IMS65 fibers and \({20}\,\hbox {Hz}\) for HR40 fibers. A higher frequency was chosen for HR40 fibers to decrease the thermal diffusion length and thus ensure the assumption of an infinite sample dimension. The laser power was set to \({0.1}\,\hbox {mW}\) to heat the samples as little as possible while maintaining a suitable signal-to-noise ratio. An infrared (IR) camera (Image IR 9430, InfraTec GmbH, Dresden, Germany) equipped with an 8\(\times\) microscope lens monitored the sample temperature for \({60}\,\hbox {s}\) at \(200\, \hbox {fps}\). The pixel resolution of this setup is \({1.3}\,\mu \hbox {m}\). Measurements were performed using Infratec’s IRBIS active online software. The slope of the logarithm of the amplitude vs the distance from the excitation, \(m_{\text {A}}\), and the phase vs the distance, \(m_{\Psi }\), were evaluated between 0.2 and \({0.8}\,\hbox {mm}\). The thermal diffusivity, \(\alpha\), was calculated utilizing the slope method [19], i.e.,

$$\begin{aligned} \alpha = \frac{\pi f}{m_{\Psi } m_{\text {A}}}. \end{aligned}$$
(4)

For each fiber type, 3 fibers were measured 3 times each.

The volume of at least \({400}\,\hbox {mg}\) of fibers was measured with a pycnometer (Ultrapyc 1200 e, Anton Paar QuantaTec Inc., Boynton, Florida, USA) by analyzing 100 runs. The weight of the samples was determined with an analytical balance (CP324S, Sartorius Lab Instruments GmbH & Co. KG, Göttingen, Germany). Heat capacity was measured via differential scanning calorimetry (Discovery DSC 2500, TA instruments, New Castle, USA) of 3 samples for each fiber type following the ASTM E1269-11 standard [17].

3 Results and discussion

3.1 Morphology of fibers

The amount and spatial distribution of non-graphitizing and graphitizing carbons highly depends on the processing temperature. With increasing temperature, the graphitic domains grow and the layers orient parallel and equidistant to each other. While atoms are connected by strong covalent bonds inside a layer, only Van der Waals forces act perpendicular to the layers. As a result, physical properties such as the tensile modulus and thermal conductivity depend on the measurement direction. In pyrolytic graphite, the thermal conductivity parallel to the graphitic layers is about \({2000}\, {\hbox {W m}}^{-1}\,\hbox {K}^{-1}\), while it is only \({5}\, \hbox {W m}^{-1}\,\hbox {K}^{-1}\) perpendicular to the layers [20]. In general, both tensile modulus and thermal conductivity are expected to increase with increasing processing temperature. Tensile moduli for the investigated fibers are provided by the manufacturers (Table 2), but neither thermal conductivity nor processing conditions are given.

Fig. 2
figure 2

Comparison of the fiber nanostructure. a–d SEM images of the cross sections of a high and low tensile modulus fiber with different magnifications. e, f WAXS and g, h SAXS scattering patterns of corresponding fiber bundles

Full size image

To investigate the fiber morphology, we performed nanostructural analysis using scanning electron microscopy (SEM), small (SAXS) and wide (WAXS) angle X-ray scattering, as well as X-ray diffraction (XRD). SEM images (Fig. 2a−d and Figure S1a, b) of the fiber cross sections reveal a coarse grained pattern suggesting a porous structure. The structure is most dense for HTS40 and IMS65. A49 and HR40 have a less dense, more granular appearance. The increase in roughness seems to be unrelated to the increase in tensile modulus. The 2D-SAXS patterns (Fig. 2e, f, Figure S1c, d) of all fibers exhibit a comparable, barbell form. We attribute this pattern mainly to a preferential orientation of nano- and microvoids along the fiber axes. Assuming a Gaussian distribution, azimuthal averaging shows an orientation with a standard deviation of \({15}^{\circ }\) to \({19}^{\circ }\) (Figure S2). The radially averaged data (Figure S3) reveals a power law behavior of \(q^{-1}\) at an intermediate q-range with q being the scattering vector. This is characteristic for one-dimensional objects and suggests spindle-like voids. At lower values of q, a behavior of \(q^{-4}\) is visible. The crossing point between the two regimes, corresponds to a correlation length, \(l_p\). Assuming

$$\begin{aligned} q \cdot l_p = 2\pi \text {,} \end{aligned}$$
(5)

the correlation length is approximately \({25}\,\hbox {nm}\) for HTS40 and IMS65, \({30}\,\hbox {nm}\) for A49 and \({45}\,\hbox {nm}\) for HR40. The second change of the power law behavior at \(q \approx {0.14}\)Å−1 hints to a feature size of about \({4.5}\,\hbox {nm}\). Assignment to pores or crystallites is inconclusive.

The WAXS data (Fig. 2g–h and Figure S1e–f) show that voids seen in SAXS coexist with an ordered arrangement of graphitic domains. As a simple model, we can imagine the fibers consisting of graphitic bands and voids (Fig. 1). The fibrilar graphitic bands align parallel to the fiber orientation and are separated by the voids. Thus, we attribute the sharp, anisotropic Bragg spot at around 1.8 Å−1 to the average thickness of the crystalline bands. The reflex at about 3.0 Å−1 is isotropic and hints to a turbostratic orientation of the individual layers inside the crystalline bands. XRD measurements (Figure S4) confirm these values and give additional insights into the graphitic structure. The (002) reflex position shifts with increasing tensile modulus from \({25.2}^{\circ }\) (HTS40) to \({26.1}^{\circ }\) (HR40). This indicates that the interlayer distance decreases sligthly from 0.35 nm (HTS40) to 0.34 nm (HR40). At the same time, the ratio of the reflex area to its height changes considerably. While HTS40, A49, and IMS65 have a ratio of about \({2.8}^{\circ }\), it is \({5.6}^{\circ }\) for HR40. This indicates that there are bigger crystalline domains in the HR40 fibers. The area ratio of the (002) and (10) reflexes changes from roughly 36 (HTS40, A49, IMS65) to 57 (HR40), suggesting different shapes of the graphitic domains. A precise determination of the crystal size is not possible, because the anisotropy constant in the Debye–Scherrer equation is unknown for our samples. We roughly estimate the crystalline domain size to be \({4}\,\hbox {nm}\) (HTS40, A49, IMS65) and \({8}\,\hbox {nm}\) (HR40). Despite the absolute value being only a rough estimation, we can definitely say that HR40 has larger crystalline domains.

3.2 Thermal conductivity of laminates

The thermal conductivity, \(\kappa\), can be calculated from the heat capacity, \(c_p\), density, \(\rho\), and thermal diffusivity, \(\alpha\), by the following equation:

$$\begin{aligned} \kappa = \rho \cdot c_p \cdot \alpha \text {.} \end{aligned}$$
(6)

Fig. 3a shows the transverse thermal conductivity of the fiber composites as a function of fiber type and fiber volume content. The fiber HR40 with a tensile modulus of \({390}\,\hbox {GPa}\) also exhibits the highest transverse thermal conductivity, followed by IMS65 with a tensile modulus of \({290}\,\hbox {GPa}\). The two fiber types A49 and HTS40 with tensile moduli of 239 and \({250}\,\hbox {GPa}\), respectively, show only minor differences in tensile modulus and thermal conductivity. The overall trend is that the increasing tensile modulus of the fibers is accompanied by an increase in transverse thermal conductivity. This matches our expectations and can be described by the equation of Lewis and Nielsen [21] (Fig. 3a). An increased tensile modulus indicates higher processing temperatures. As shown in Fig. 1, this correlates with larger crystalline domains in the through-plane cross sections facilitating better heat flow.

Fig. 3
figure 3

Thermal conductivity in a transverse and b fiber direction vs fiber volume content depending on tensile modulus In transverse direction, the thermal conductivity follows the model proposed by Lewis and Nielsen [21]. In longitudinal direction, the thermal conductivity follows a linear mixing model [22]

Full size image

At the same time, we expect a greater thermal conductivity parallel to the fiber direction. In addition to their increased size, the crystallites orient along the fiber. Therefore, the thermal conductivity is much higher in the longitudinal direction than in the transverse direction. This becomes clearly visible in Fig. 3b. The thermal conductivity in the fiber direction of the high-modulus carbon fiber is \({46}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) at a fiber volume content of \({65}\%\), while in the transverse direction it is only \({1.8}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\). In addition, a clear correlation of the tensile modulus and the thermal conductivity is evident here. The higher the tensile modulus, which likely occurs due to higher production temperatures, the greater the thermal conductivity in the fiber direction. As expected from our structural analysis of the fibers, the largest difference is visible between HR40 and the remaining fiber types.

An anisotropy factor can be calculated from the ratio of thermal conductivity in the fiber direction and in the transverse direction. This value is \({4.8}\pm {0.6}\) for the fiber with a tensile modulus of \({239}\,\,\hbox {GPa}\) and then increases to \({8.3}\pm {0.2}\) (\({250}\,\,\hbox {GPa}\)), \({8.5}\pm {0.2}\) (\({290}\,\hbox {GPa}\)), and \({29.4}\pm {2.6}\) (390 GPa). Thus, the higher the tensile modulus, the better the thermal conductivity in the fiber direction compared to the transverse thermal conductivity. The increase in the anisotropy factor with increasing tensile modulus is likely caused by the crystalline domains.

3.3 Thermal conductivity of single fiber measurements

Parallel to the fabrication and analysis of the fiber reinforced composites, the thermal conductivity of neat fibers was measured in fiber direction.

We measured the thermal diffusivity of fibers by lock-in thermography as described in literature [18, 19]. Details about the measurement conditions and principle are given in the Materials and methods section. For the fibers with the lowest tensile modulus, HTS40, we obtained a thermal conductivity of \(({8.8}\pm {0.7})\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\). With increasing tensile modulus, the thermal conductivity along the fiber direction increases steadily up to a value of \(({65.2}\pm {2.6})\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) for HR40 fibers (Fig. 4).

To compare the measurements to the fiber composites, a linear fit for the measured values of the composites was performed. Extrapolating the fiber volume content to \({100}\,\%\) should equal the values for the isolated fibers (Fig. 4). Within the experimental uncertainties, the directly measured values of the fibers and the extrapolated values of the composites match very well.

Overall, an increasing trend of the thermal conductivity in respect to the tensile modulus is visible. This shows that the fiber nanomorphology, mainly determined by the interplay between voids and graphitic domains, correlates with both the tensile modulus and the thermal conductivity.

Fig. 4
figure 4

Comparison of direct measurements of the thermal conductivities of fibers and the values derived from linear fitting of the laminates

Full size image

4 Conclusions

The aim of this work was to investigate the relationship between the morphology of carbon fibers, their tensile modulus, and their thermal conductivity in C-fiber composites with a resin matrix. The most important findings on the influence of the morphology of the carbon fibers under investigation on the thermal conductivity and morphology of the C-fiber can be summarized as follows:

  • The investigation of the carbon fibers by SAXS, WAXS and XRD showed differences in the microstructure of the carbon fiber from different producers. We could link differences in the crystalline domains with the tensile modulus provided by the manufacturer.

  • The microstructure of the fibers controls the composite thermal conductivity. The effect is particularly pronounced in the direction of the fibers, where the thermal conductivity with a fiber volume content of \({65}\,\%\) was \({46}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) when using the high-modulus fibers and \({7}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) when using the fibers with the lowest tensile modulus. In the transverse direction, the thermal conductivity of the composites with \({65}\,\hbox {vol}\%\) fibers was \({1.77}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) and \({0.96}\,\hbox {W m}^{-1}\,\hbox {K}^{-1}\) for the high- and low-modulus fibers, respectively.

  • The anisotropy of the carbon fibers is retained in fiber-epoxy composites. The transverse thermal conductivity increases disproportionately with increasing fiber volume content. It ranges below \({2}\,\hbox {W m}^{-1}\, \hbox{K}^{-1}\) and can be described by the equation of Lewis and Nielsen. In the in-plane direction parallel to the fibers, a linear relationship with regard to volume content was observed. We find a maximum anisotropy between parallel and transversal thermal conductivity for the HR40 fibers.

  • The direct measurements of the thermal conductivity of individual carbon fibers are in good agreement with the extrapolated values from the composite analysis. This proves that a simple linear mixing model can be used to predict the thermal conductivity along the fiber direction.