Abstract
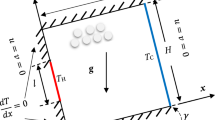
This article presents a comprehensive analysis of time dependent condensation model embedded in a porous medium with variations in liquid–vapour densities. Both similarity and asymptotic solutions for the unsteady liquid–vapour phase change front are obtained with the manifestation of various pertinent parameters. The obtained results are compared which congregate well as depicted clearly in graphs. Results indicate that with different diffusivity and contrast ratios, the similarity front parameter is found to be gradually declining with variation in a density ratio. We have shown for the condensation process, the ratio of sensible to latent heat is independent of time and is equal to the half of the Stefan number of the liquid phase.
Similar content being viewed by others
Change history
05 February 2022
A Correction to this paper has been published: https://doi.org/10.1007/s42757-022-0132-z
References
Bear, J., Buchlin, J.-M. 1981. Modelling and Applications of Transport Phenomena in Porous Media. Kluwer Academic Publishers.
Beckett, G., MacKenzie, J. A., Robertson, M. L. 2001. A moving mesh finite element method for the solution of two-dimensional Stefan problems. J Comput Phys, 168: 500–518.
Bernoff, A. J., Witelski, T. P. 2010. Stability and dynamics of self-similarity in evolution equations. J Eng Math, 66: 11–31.
Bodvarsson, G., Pruess, K., Lippmann, M. 1986. Modeling of geothermal systems. J Petrol Technol, 38: 1007–1021.
Bonacina, C., Comini, G., Fasano, A., Primicerio, M. 1973. Numerical solution of phase-change problems. Int J Heat Mass Tran, 16: 1825–1832.
Carey, V. P. 2007. Liquid-Vapor Phase-Change Phenomena. Taylor & Francis, Inc.
Carslaw, H. S., Jaeger, J. C. 1959. Conduction of Heat in Solids. Clarendon Press.
Chiareli, A. O. P., Huppert, H. E., Worster, M. G. 1994. Segregation and flow during the solidification of alloys. J Cryst Growth, 139: 134–146.
Date, A. W. 1991. A strong enthalpy formulation for the Stefan problem. Int J Heat Mass Tran, 34: 2231–2235.
Douglas, J. 1957. A uniqueness theorem for the solution of a Stefan problem. Proc Am Math Soc, 8: 402–408.
Dutil, Y., Rousse, D. R., Salah, N. B., Lassue, S., Zalewski, L. 2011. A review on phase-change materials: Mathematical modeling and simulations. Renew Sust Energ Rev, 15: 112–130.
Evans, G. W. 1951. A note on the existence of a solution to a problem of Stefan. Q Appl Math, 9: 185–193.
Gupta, S. C. 2003. The Classical Stefan Problem: Basic Concepts, Modelling and Analysis. Elsevier.
Hager, J., Whitaker, S. 2000. Vapor–liquid jump conditions within a porous medium: Results for mass and energy. Transport Porous Med, 40: 73–111.
Harris, K. T., Haji-Sheikh, A., Agwu Nnanna, A. G. 2001. Phase-change phenomena in porous media—a non-local thermal equilibrium model. Int J Heat Mass Tran, 44: 1619–1625.
Khan, Z. H. 2014. Transition to instability of liquid–vapour front in a porous medium cooled from above. Int J Heat Mass Tran, 70: 610–620.
Khan, Z. H., Pritchard, D. 2013. Liquid–vapour fronts in porous media: Multiplicity and stability of front positions. Int J Heat Mass Tran, 61: 1–17.
Khan, Z. H., Pritchard, D. 2015. Anomaly of spontaneous transition to instability of liquid–vapour front in a porous medium. Int J Heat Mass Tran, 84: 448–455.
Lunardini, V. J. 1981. Heat Transfer in Cold Climates. Van Nostrand Reinhold Company.
Masur, L. J., Mortensen, A., Cornie, J. A., Flemings, M. C. 1989. Infiltration of fibrous preforms by a pure metal: Part II. Experiment. Metall Trans A, 20: 2549–2557.
Mattheij, R. M. M., Rienstra, S. W., ten Thije Boonkkamp, J. H. M. 2005. Partial Differential Equations: Modeling, Analysis, Computation. SIAM.
Mortensen, A., Masur, L. J., Cornie, J. A., Flemings, M. C. 1989. Infiltration of fibrous preforms by a pure metal: Part I. Theory. Metall Trans A, 20: 2535–2547.
Ochoa-Tapia, J. A., Whitaker, S. 1997. Heat transfer at the boundary between a porous medium and a homogeneous fluid. Int J Heat Mass Tran, 40: 2691–2707.
Rubin, A., Schweitzer, S. 1972. Heat transfer in porous media with phase change. Int J Heat Mass Tran, 15: 43–60.
Solomon, A. 1981. A note on the Stefan number in slab melting and solidification. Lett Heat Mass Trans, 8: 229–235.
Torranc, K. E. 1986. Phase-change heat transfer in porous media. Heat Transfer, 1: 181–188.
Acknowledgements
The corresponding author is profoundly grateful to the financial support of the National Natural Science Foundation of China (Grant Nos. 51709191, 51706149, and 51606130), Key Laboratory of Advanced Reactor Engineering and Safety, Ministry of Education (Grant No. ARES-2018-10), and State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University (Grant No. Skhl1803).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Khan, Z.H., Ahmad, R. & Sun, L. Effect of instantaneous change of surface temperature and density on an unsteady liquid–vapour front in a porous medium. Exp. Comput. Multiph. Flow 2, 115–121 (2020). https://doi.org/10.1007/s42757-019-0027-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42757-019-0027-9