1 Introduction

Aortic dissection is an acute disease of the aorta and it starts with a tear in the intimal layer [14, 18, 42], which can grow into the medial layer and lead to delamination of the aortic wall. This delamination can result in a false lumen into which the blood can flow, which can result in death due to excessive bleeding [10, 31, 35, 40]. Aortic dissections can be characterized by medial degeneration with loss of elastic fibers, loss of functional smooth muscle cells (SMCs) and an accumulation of glycosaminoglycans/proteoglycans (GAGs/PGs) [6, 7, 65]. This structural weakening of the arterial wall contributes to the initiation and propagation of the aortic dissection. An essential part of the aortic dissection is the delamination of the medial layer, which consists of multiple medial lamellar units (MLUs) [41, 63, 64]. Each MLU consists of different material components, as shown in Fig. 1a–c, [12, 41]. The units are separated by elastic laminae that are closely connected by collagen fibers. Between the elastic laminae there is a mixture of GAGs/PGs and SMCs, with ‘radially oriented’ elastic fibers connecting adjacent elastic laminae. In addition, individual collagen fibers and thin bundles covering the SMCs and the entire interlamellar space are observed.

Fig. 1
figure 1

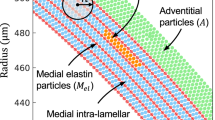
Microstructure of the media: (a) Medial aortic microstructure. Medial layer consists of multiple medial lamellar units, which are separated by elastic laminae (EL) and connected by interlamellar elastin fibers (black arrows) and elastin struts (ES), as indicated in [41]. In the interlamellar space, there are reinforced elastin pores (EP) and smooth muscle cells (SMCs) characterized by elliptical nuclei (N). Collagen fibers (white arrows) adjoin lamellar surfaces and are predominantly oriented circumferentially; (b) Schematic representation of two SMCs and two ELs with their interconnections. Thick collagen fibers (Coll) are closely related to the EL. The left SMC is connected to both ELs via thin elastin protrusions, while the right SMC is connected to the lower EL via oxytalan fiber (Ox). In addition to the basal lamina-like layers, deposits (D) with type IV collagen and heparan sulfate PG are found especially at indentations of the cell surface [12]; (c) Schematic drawing of a normal aortic medial lamellar unit. Medial lamellar unit, bounded by two ELs with interlamellar materials consisting of ‘radially oriented’ elastic fibers (i.e. elastin and related microfibrils, predominately fibrillin-I), SMCs, collagen fibers, adhesion molecules (e.g., fibronectin), and GAGs (not to scale). Elastic fibers provide the mechanical connections between the ELs [26]; (d) Schematic drawing of the initiation mechanism for medial delamination. On the right side of the medial lamellar units there is a local accumulation of GAGs that carry a large amount of negatively charged ions. These ions attract adjacent positive ions and water molecules into the GAG area and lead to a Donnan swelling pressure, which contributes to the separation of the ELs, and can lead to medial delamination [26]

Full size image

It has long been known that aortic dissections mainly occur within the medial layer [6, 33] and that a large number of elastic fibers are ruptured in the dissected area [8, 38, 43, 51]. In experimental studies [33, 52] it is observed that the radially oriented elastic fibers are torn from their connections with elastic laminae during tensile and peeling tests. Humphrey [26] linked the accumulation of GAGs/PGs with medial delamination and hypothesized that the deposition of GAGs/PGs leads to a rather high Donnan swelling pressure, loss of tensile stiffness and the development of stress concentrations that render the region vulnerable to dissection, see Fig. 1c, d. The studies [7, 9, 30, 34, 36] have found extensive accumulations of GAGs/PGs in thoracic aortic aneurysms. As GAGs/PGs carry negative charges along their chains, they attract positively charged ions and water molecules from the surrounding interstitial fluid, causing local swelling of the interlamellar space within the medial layer of an aorta [4, 5, 25, 66]. When the interstitial fluid enters the GAGs/PGs concentrated area, the Donnan pressure increases and the distance between two elastic laminae becomes larger, so that the media tends to delaminate. To maintain the integrity of the tissue, the stress level in the interlamellar tissue increases. Aortic dissections tend to propagate more easily within the elastic laminae than across the laminae [52, 60].

Numerical studies of aortic dissection related to the accumulation of GAGs/PGs are rare. Roccabianca et al. [48, 49] analyzed the influence of GAGs/PGs with semi-analytical and finite element-based methods to show the stress concentration around GAGs/PGs due to swelling pressure. In addition, the initiation and development of medial delamination under the influence of GAGs/PGs were investigated in particle-based studies [2, 3]. A recently published paper by Rolf-Pissarczyk et al. [50] recorded the degradation of interlamellar elastic fibers during aortic dissection with a discrete fiber dispersion model. To the best of our knowledge, there are no other numerical studies investigating the initiation of aortic dissection due to GAGs/PGs accumulation. So far, no study has coupled the swelling behavior of GAGs/PGs and the anisotropic mechanical response of arterial tissues to perform stress analysis during aortic dissection on the mesoscale. Therefore, in the present study, we will propose an improved constitutive model that couples tissue swelling and anisotropic behavior through different fractions of the medial constituents. A stress analysis will be carried out with the finite element (FE) software Abaqus. We will also compare the numerical results with observed failure stresses from experiments and identify high stress locations where delamination can initiate.

The mobility of positively charged ions and water molecules in the media is similar to that of swelling polymers [28, 53] and the mechanism of the swelling behavior of polymers was here transferred to soft tissues [2, 53, 65]. Inspired by previous work, we adopt the theory from swelling polymers in order to simulate GAGs/PGs swelling, which leads to increased stresses in the struts of elastic fibers. To realize different fractions of each constituent of the medial layer [27, 61], we propose a weighted constitutive model that can describe the swelling activity in the medial layer due to the presence of GAGs/PGs and the mechanical response of other vascular materials. More importantly, the weighted constitutive model offers high flexibility to adapt to different cases of material fractions, e.g., to capture the random distribution of GAGs/PGs.

This paper is structured as follows: In Section 2 we introduce a weighted constitutive model to describe the swelling and the mechanical behavior of each material constituent. A few practical numerical aspects will also be presented in this section. Section 3 contains three numerical simulations using Abaqus with an in-house UMAT code. The numerical simulations first demonstrate the application of the proposed model at the macroscopic scale and phenomenologically study the influence of the reference fixed charge density on the mechanical response. In addition, we present the results of a swelling-induced fracture of elastic fibers with more complex boundary conditions on the mesoscale, in which we can observe high Donnan pressures and stresses in the struts of elastic fibers. The third example deals with a comparison between numerical results with and without pre-stretches and pressurization. Finally, in Section 4 we give a summary of the present study and discuss the merits and limitations.

2 Constitutive model and numerical aspects

2.1 Constitutive model

As mentioned in Section 1, medial layers consist of MLUs embedded in collagen fibers. Between the elastic laminae there are SMCs, GAGs/PGs, fibronectin, elastic and collagen fibers. In order to realize the different quantities of each component, we propose a weighted strain-energy function Ψ, which contains the individual components and their weight fractions, i.e.

$${\Psi} = w_{\text{SMCs}}{\Psi}_{\text{SMCs}} + w_{\mathrm{e}}{\Psi}_{\mathrm{e}} + w_{\mathrm{c}}{\Psi}_{\mathrm{c}} + \delta(w_{\text{GAGs}}){\Psi}_{\text{vol}} + w_{\text{GAGs}}({\Psi}_{\text{GAGs}} + {\Psi}_{\text{{pres}}}),$$
(1)

where

$$w_{\text{SMCs}} + w_{\mathrm{e}} + w_{\mathrm{c}} + w_{\text{GAGs}} = 1,$$
(2)

and

$$\delta(w_{\text{GAGs}}) = \begin{cases} 1 & \text{if}\ w_{\text{GAGs}} = 0,\\ 0 & \text{if}\ w_{\text{GAGs}} \neq 0. \end{cases}$$
(3)

The weight of each component is referred to as w and the subscripts SMCs, e, c and GAGs represent the smooth muscle cells, elastic fibers, collagen fibers and GAGs/PGs, respectively. The indicator function δ(wGAGs) is used to ensure the incompressibility of the arterial tissue if no GAGs/PGs are present.

For the SMCs, the elastic fibers and the network of the GAGs/PGs, we use the following neo-Hookean types of strain-energy functions

$$\begin{array}{@{}rcl@{}} {\Psi}_{\text{SMCs}} & =& \mu_{\text{SMCs}}(I_{1} - 3 - 2\ln J), \end{array}$$
(4)
$$\begin{array}{@{}rcl@{}} {\Psi}_{\mathrm{e}} & =& \mu_{\mathrm{e}}(I_{1} - 3 - 2\ln J), \end{array}$$
(5)
$$\begin{array}{@{}rcl@{}} {\Psi}_{\text{GAGs}} & =& \mu_{\text{GAGs}}(I_{1} - 3 - 2\ln J), \end{array}$$
(6)

where μSMCs, μe and μGAGs are respective shear moduli, while I1 is the first invariant of the right Cauchy-Green tensor C = FTF, with the deformation gradient F, and J = det F > 0 denotes the volume ratio, [20]. The volumetric strain-energy function Ψvol characterizes a penalty function used to satisfy the incompressibility of the tissue and is written as

$${\Psi}_{\text{vol}} = \frac{1}{D_{1}}\left(\frac{J^{2}-1}{2}-\ln J \right),$$
(7)

where D1 is a parameter. To calculate the Donnan swelling pressure, the strain-energy function Ψpres is introduced and briefly presented below.

As is known and often described, the collagen fibers are distributed as two symmetrical fiber families with some degree of dispersion both in-plane and out-of-plane. The material properties of these two families are assumed to be the same. We use the model documented in [22] and modify it based on [19] to describe the behavior of collagen fibers, i.e.

$$\begin{array}{@{}rcl@{}} {\Psi}_{\mathrm{c}} = \displaystyle\frac{k_{1}}{2k_{2}}\displaystyle\sum\limits_{i=4,6}\left[ \exp\left(k_{2}{E_{i}^{2}} \right) -1 \right], \quad E_{i} = A{I_{1}}+B{I_{i}}+(1-3A-B){I_{n}}-1, \end{array}$$
(8)
$$\begin{array}{@{}rcl@{}} I_{i} = \textbf{C} : \textbf{M}_{i} \otimes \textbf{M}_{i}, \quad i = 4, 6, \qquad I_{\mathrm{n}} = \textbf{C} : \textbf{M}_{\mathrm{n}} \otimes \textbf{M}_{\mathrm{n}}, \end{array}$$
(9)

where k1, k2 are positive material parameters. The constants A and B are given by 2κopκip and 2κop(1 − 2κip), where κop and κip are measures of the out-of-plane and in-plane dispersion of collagen fibers, respectively. The two symmetric fiber families have mean fiber directions M4 and M6 (two unit vectors) in the reference configuration, while Mn is a vector perpendicular to the plane defined by M4 and M6. We also introduce mi = FMi, i = 4,6, and mn = FMn, which describe the spatial counterparts of the vectors Mi and Mn, respectively.

Motivated by earlier works on the thermodynamic swelling theory and the related numerical implementation, see, e.g., [13, 28, 46, 56], in addition to an isotropic contribution from the GAGs/PGs solid skeleton ΨGAGs we include an osmotic contribution Ψpres, which is responsible for the swelling pressure of the GAGs/PGs.

We then have the Cauchy stress tensor σ, i.e.

$$\begin{array}{@{}rcl@{}} J^{-1}{\boldsymbol{\sigma}} & = & 2 w_{\text{SMCs}} \mu_{\text{SMCs}} (\textbf{b} - \textbf{I}) + 2 w_{\mathrm{e}} \mu_{\mathrm{e}}(\textbf{b} - \textbf{I}) + w_{\mathrm{c}} \displaystyle\sum\limits_{i=4,6}{\boldsymbol{\sigma}}_{i} \\ & & + \displaystyle\frac{\delta(w_{\text{GAGs}})}{D_{1}} (J^{2} - 1)\textbf{I} + 2 w_{\text{GAGs}}\mu_{\text{GAGs}}(\textbf{b} - \textbf{I}) - \pi\textbf{I}, \end{array}$$
(10)

where I denotes the second-order unit tensor while b = FFT is the left Cauchy-Green tensor. The Cauchy stress tensors σi are given by

$${\boldsymbol{\sigma}}_{i} = 2 k_{1} E_{i}\exp (k_{2}{E_{i}^{2}}) [A \textbf{b} + B (\textbf{m}_{i} \otimes \textbf{m}_{i}) + (1 - 3A - B)(\textbf{m}_{\mathrm{n}} \otimes \textbf{m}_{\mathrm{n}})],$$
(11)

where the tensor product of the vectors mi and mi is denoted by mi ⊗ mi.

The expression of the scaled Donnan pressure π [13, 15, 53, 62] is given as

$$\begin{array}{@{}rcl@{}} \pi & =& - \displaystyle\frac{\partial{{\Psi}_{\text{pres}}}}{\partial J} = w_{\text{GAGs}} R T \left(\sqrt{{c_{F}^{2}} + 4c_{\text{ext}}^{2}} - 2c_{\text{ext}}\right), \end{array}$$
(12)
$$\begin{array}{@{}rcl@{}} c_{F} & =& c_{F}^{\text{ref}} \displaystyle\frac{1 - \psi_{s}^{\text{ref}}}{J - \psi_{s}^{\text{ref}}}, \end{array}$$
(13)

where R and T denote the gas constant and the absolute temperature, respectively. The parameter cext represents the concentration of the ions in the external solution, e.g., the interstitial fluid, which in the considered case is present through the arterial wall. The parameters \(c_{F}^{\text {ref}}\) and cF are the reference and current fixed charge density, which represent the concentration of negative ions that are fixed on the GAGs/PGs chains, respectively [53]. It is assumed that the external ion concentration cext is constant, and to balance the negative charges on the GAGs/PGs chains, positively charged ions and water molecules in the interstitial fluid migrate into the GAGs/PGs region, and therefore the tissue shows swelling effects. By varying the fixed reference charge density \(c_{F}^{\text {ref}}\) one obtains a series of equilibrium states with different negatively charged initial states, which allow conclusions to be drawn about the swelling progress due to GAG/PG accumulation.

In studies like [4, 53], \(1 - \psi _{s}^{\text {ref}}\) is given as the fluid volume fraction in the reference configuration based on the theory of porous media. However, the present work does not address the theory of porous media, and we assume that GAGs/PGs are the only constituents that are hydrated with a volume fraction equal to its mass fraction, i.e. \(1 - \psi _{s}^{\text {ref}} = w_{\text {GAGs}}\). Such an assumption is based on material parameters measured under dehydrated conditions [39], and the swelling effect due to the accumulation of GAGs/PGs relates to regions with high GAG/PG concentration. The assumption can be interpreted as a local effect of the swelling of GAGs/PGs, where the molar amount of ions before and after the swelling is given by Eq. (13). The stress analysis in a subsequent section will show that the use of dehydrated material parameters can agree well with experimental results when \(c_{F}^{\text {ref}}\) reaches an average value, as reported in [4, 45].

2.2 Numerical aspects

Numerical simulations with an implicit FE solver require an elasticity tensor to derive from the stress tensor; for details see, e.g., [20, 29]. However, this often involves complex mathematical derivations and algebraic manipulations. Sun et al. [54] proposed an efficient numerical approximation of the elasticity tensor by incrementally perturbing the deformation gradient. We obtained the numerical elasticity tensor using this method, which offers a precise mathematical formulation and good accuracy and is also applicable to different material models. The key to this method is the selection of the perturbation parameter. A poor choice of the perturbation parameter leads to slow convergence rates or numerical errors. We use a perturbation parameter of 10− 8. The accuracy of the numerical elasticity tensor has been validated with examples for swelling hydrogels and for incompressible fiber-reinforced arterial walls, and the simulations show good convergence. The user subroutine UMAT was used within Abaqus [1] to implement the described models, which were then called during the numerical simulations.

3 Representative numerical examples

To demonstrate the ability of the proposed constitutive model to predict arterial swelling due to the presence of GAGs/PGs, albeit in a rather phenomenological way, a first example of a cylindrical segment of an artery at the macroscopic scale is described in Section 3.1. This example aims to show the influence of the reference fixed charge density \(c_{F}^{\text {ref}}\) on tissue swelling from a purely continuum mechanical point of view. In a second example, Section 3.2, the potential of interlamellar fiber damage by swelling of GAGs/PGs is examined. As previously mentioned, the accumulation of GAGs/PGs attracts ions and water molecules from the interstitial fluid and results in a high Donnan swelling pressure. The swelling of the interlamellar space will then initiate medial delamination. The example of MLUs is designed with pre-stretches to study the pathology of medial delamination in a more realistic setting. An estimate of the local failure stress is given to compare numerical and experimental results. Finally, in Section 3.3 we provide a comparison between numerical results with and without preconditioning to see the effects of pre-stretches and pressurization. The comparison should help to select better boundary conditions that can lead to the most realistic results possible.

3.1 Swelling of a cylindrical arterial segment

In this example, a healthy and young arterial segment is modeled as a thick-walled cylindrical tube with two layers (media and adventitia, the solid mechanically relevant layers in healthy arteries). The geometry is created on the basis of [17, 27]. The wall thickness is 1.5 mm, the thickness of the media 1.2 mm (80% of the wall thickness), the inner radius is 3.0 mm, while the arterial length is 10 mm. The mean fiber angle is designated as α and is measured in relation to the circumferential direction of the segment.

3.1.1 Reduced constitutive model, material and structural parameters

The adventitia is treated as a fiber-reinforced tissue with non-symmetric collagen fiber dispersion [22] with no GAGs/PGs (wGAGs = 0). For the media we use the model according to Eq. (1) with δ(wGAGs) = 0, since we consider here the deposition of GAGs/PGs in the medial layer (wGAGs≠ 0). Since this (academic) example is intended to illustrate the application of the proposed swelling model, no distinction is made here between SMCs and elastic fibers. The strain energy is then simplified as

$${\Psi} = w_{\mathrm{m}}{\Psi}_{\mathrm{m}} + w_{\mathrm{c}}{\Psi}_{\mathrm{c}} + w_{\text{GAGs}} ({\Psi}_{\text{GAGs}} + {\Psi}_{\text{pres}}), \qquad {\Psi}_{\mathrm{m}} = \mu_{\mathrm{m}}(I_{1} - 3 - 2 \ln J),$$
(14)

where wmΨm denotes a combined contribution of SMCs and elastic fibers in the media, while μm is the related shear modulus. Note that wm + wc + wGAGs = 1.

The healthy medial layer consists of about 43% SMCs, 23% elastic fibers, 30% collagen and 4% GAGs/PGs by dry weight [27, 48]. As already mentioned, in this example we do not differentiate between SMCs and elastic fibers. Hence, we use wm = wSMCs + we = 0.66, wc = 0.30 and wGAGs = 0.04. The material properties for the media and the adventitia are taken from [39], with additional consideration of GAGs/PGs deposition for the media. The shear modulus μGAGs for the GAGs/PGs originate from [2], where a similar swelling problem was investigated. The material parameters for the Donnan swelling pressure are obtained from [53], where porous media and swelling polymer theories were used to study the volume change of soft tissues. For the analysis, the reference fixed charge density \(c_{F}^{\text {ref}}\) of the media increases linearly from 0 to 5 mol m− 3. The material and structural properties used are summarized in Table 1.

Table 1 Material and structural parameters of the medial and adventitial layers
Full size table

3.1.2 Numerical results

To reduce computational cost and boundary effects on the biomechanical tissue response we use the submodeling technique available in Abaqus. According to the Saint-Venant principle, the boundary conditions of the global model, the cylindrical tube, do not have a noticeable effect in the middle part of the model. The geometry of the submodel used is illustrated in Fig. 2 (𝜃, r and z refer to the circumferential, radial and axial directions, respectively).

Fig. 2
figure 2

Geometry of the submodel used in the middle part of the global model, i.e. the cylindrical tube (see Fig. 3): inner radius Ris, outer radius Ros, and length Ls

Full size image
Fig. 3
figure 3

Global model (cylindrical tube) with a coarse mesh (left), submodel (right) with a finer mesh cut out from the middle part of the tube (red dashed curves). Figure 5 shows results for the element marked as El

Full size image

As a result, we run a simulation with a coarse mesh on the global model (thick-walled cylindrical tube), then cut a slice from the middle part of the tube and proceed with a submodel simulation with a (much) finer mesh, see Fig. 3; the red dashed curves indicate the submodel of the medial layer. In the global model, the deformation of the cylinder is constrained in the axial direction at the two ends. As far as the submodel is concerned, we extract the boundary condition from the Abaqus results of the global model and apply them to the submodel. The global model runs with a coarse mesh of 1200 elements, while the submodel has a refined mesh of 3872 elements; the element type is C3D8HT (8-node thermally coupled brick, trilinear displacement and temperature, hybrid, constant pressure), where the temperature field is used to imitate the change in the reference fixed charge density \(c_{F}^{\text {ref}}\) [28].

The normalized thickness tn is defined as the ratio between the current thickness and the initial thickness of the wall, and is plotted in Fig. 4 against the reference fixed charge density \(c_{F}^{\text {ref}}\). As \(c_{F}^{\text {ref}}\) increases from 0 to 5 mol m− 3, tn increases by over 50% during the swelling process.

The current fixed charge density cF and the Donnan swelling pressure π increase during swelling. Figure 5 shows the results for element El marked in Fig. 3. From Eq. (13) we see that the current fixed charge density cF is inversely proportional to the volume ratio J and proportional to the reference fixed charge density \(c_{F}^{\text {ref}}\). Figure 5a illustrates that cF increases with respect to \(c_{F}^{\text {ref}}\), and Fig. 5c indicates that cF presents an increasing behavior with increasing J, which seems to contradict the inverse correlation between cF and J. Similar rising curves of π with respect to \(c_{F}^{\text {ref}}\) and J can be seen in Fig. 5b and d, respectively. We conclude that \(c_{F}^{\text {ref}}\) has a more significant influence on cF than J. If π increases with \(c_{F}^{\text {ref}}\) to balance for the high pressure, the tissue swells and causes an increased stretch of the solid skeleton. As shown in Eq. (13), the increasing volume would reduce the swelling. However, a high concentration of negative charges in the GAGs/PGs will continue to drive the expansion of the tissue until equilibrium is reached.

Fig. 4
figure 4

Normalized thickness tn vs reference fixed charge density \(c_{F}^{\text {ref}}\). Swelling due to GAGs/PGs causes the arterial wall to thicken by more than 50% at \(c_{F}^{\text {ref}} = 5\) mol m− 3

Full size image

3.2 Swelling of separated medial lamellar units

In this example, we take a closer look at how the swelling of GAGs/PGs affects the stresses in the interlamellar struts of elastic fibers modeled as interlamellar connection elements. A block with the size 150.0 × 108.0 × 63.0μm is considered as a global model to separate different tissue components from one another, see Fig. 6a. As discussed previously, the medial layer is composed of MLUs. The present geometry contains seven MLUs, whereby in Fig. 6b a central unit with the size 50.0 × 18.0 × 3.0μm is illustrated, i.e. the submodel that will be the focus of this analysis. Two struts of elastic fibers are included within the length of 50.0μm. One strut is 3.0μ m thick and indented 10.0μm from the edge. In general, the elastic fibers are inclined by an angle as, e.g., shown in Fig. 1a,c. For the sake of simplicity, however, we assume that the fiber struts are orthogonal to the elastic laminae. Figure 6a also explains how the block is located within the medial thickness (inner radius Ri = 3.0 mm, outer radius Ro = 4.2 mm), starting at R1 = 3.7885 mm and ending at R2 = 3.8965 mm. The geometrical information is modified on the basis of [37, 41, 48, 57,58,59, 63, 64].

Fig. 5
figure 5

Current fixed charge density cF and swelling pressure π with respect to reference fixed charge density \(c_{F}^{\text {ref}}\) and volume ratio J: (a) cF vs \(c_{F}^{\text {ref}}\); (b) π vs \(c_{F}^{\text {ref}}\); (c) cF vs J; (d) π vs J

Full size image
Fig. 6
figure 6

(a) Global model with size 150.0 × 108.0 × 63.0μm, where 7 medial lamellar units in the radial direction are used for the analysis. Elastic laminae and struts made of elastic fibers marked in light blue, while GAGs (PGs and SMCs) are in light gray. Collagen fibers are assumed to be embedded in the elastic laminae. The mean angle of collagen fibers is α and measured with respect to the circumferential direction; location of the block within the medial thickness (inner radius Ri = 3.0 mm, outer radius Ro = 4.2 mm), starting at R1 = 3.7885 mm and ending at R2 = 3.8965 mm; (b) central unit with size 50.0 × 18.0 × 3.0μm between the (dotted) cutting planes 1 and 2, i.e. the submodel, the focus of this analysis. Interlamellar material is assumed to be a mixture of GAGs (PGs and SMCs). Units of numbers are given in μm

Full size image

3.2.1 Constitutive model

The collagen fibers (thick solid lines in Fig. 6a) are embedded in the elastic laminae [12], see light blue areas in Fig. 6. Based on Eq. (1) we then use a model for the elastic laminae according to

$${\Psi} = w_{\mathrm{e}}{\Psi}_{\mathrm{e}} + w_{\mathrm{c}}{\Psi}_{\mathrm{c}} + {\Psi}_{\text{vol}},$$
(15)

with δ(wGAGs) = 1, and we + wc = 1. Since there are no GAGs/PGs and SMCs present in the elastic laminae, the weights wSMCs and wGAGs are zero.

In between the elastic laminae, GAGs/PGs and SMCs (light gray) as well as struts of elastic fibers (light blue) are present. The interlamellar elastic fibers are treated as an isotropic hyperelastic material, for which a neo-Hookean model predefined in Abaqus [1] is adopted. The mixture of GAGs/PGs and SMCs is modeled by a strain-energy function of the form

$${\Psi} = w_{\text{SMCs}}{\Psi}_{\text{SMCs}} + w_{\text{GAGs}}({\Psi}_{\text{GAGs}} + {\Psi}_{\text{pres}}),$$
(16)

where we have we = wc = 0 and wSMCs + wGAGs = 1.

Fig. 7
figure 7

Boundary conditions for the swelling of separated medial lamellar units, global model: (a) global model subjected to pre-strains upre,𝜃 and upre,z in the circumferential and axial directions, respectively. Radial stress σr = 3.28 kPa determined according to Eq. (17), while the geometry is shown in Fig. 6a. Dashed red lines indicate the submodel; (b) during the swelling step the reference fixed charge density \(c_{F}^{\text {ref}}\) is applied linearly to the central unit from 0 to 20 mol m− 3

Full size image

3.2.2 Boundary conditions

In order to observe how the swelling of GAGs/PGs increases the stress in the struts of elastic fibers, we define a boundary-value problem according to Fig. 7. The simulation involves two steps, a pre-straining and pressurization step, i.e. t ∈ [0,1], as well as a GAGs/PGs pool swelling step, i.e. t ∈ (1,2]. The displacement of the block (Figs. 6a and 7a) is constrained in the axial direction (z-direction) on its back (uz = 0). The centerline on the back marked as a square in the (r,z) plane is constrained in the radial direction (r-direction) to avoid a rigid body motion (ur = 0). The front is subjected to an axial pre-strain upre,z of 10% of the axial length [11, 24], i.e. 6.3μm. The right face of the block (Fig. 7a) is constrained in the circumferential direction (𝜃-direction), i.e. (u𝜃 = 0), and on the left face an approximate circumferential pre-strain, say upre,𝜃, is applied which corresponds to 15.0μm [23]. The Young’s modulus of collagen fibers is of the order of 1 GPa [44] and causes negligible deformation in the circumferential direction due to the blood pressure p. The top and bottom of the block are loaded uniformly by a radial stress σr, which is calculated according to (thick-walled cylindrical)

$$\sigma_{r} = \frac{(R_{\mathrm{i}}/R_{\mathrm{o}})^{2} - (R_{\mathrm{i}}/R)^{2}} {1 - (R_{\mathrm{i}}/R_{\mathrm{o}})^{2}} p,$$
(17)

where p is at the systolic level of 120 mmHg (16.0 kPa), R denotes any radius in the media, and Ri, Ro are radii according to Fig. 6a. Since the pressure difference on the two surfaces at R1 and R2 is only 7% we apply a mean radial stress σr of 3.28 kPa to both surfaces.

Azeloglu et al. [4] reports an average fixed charge density of 42 ± 19 mEq/L for the rat aorta. It was estimated that the fixed charge density varied from twice this value in the intima to almost zero in the adventitia. Based on this, the reference fixed charge density \(c_{F}^{\text {ref}}\) is applied linearly in the numerical simulation to the central unit from 0 to 20 mol m− 3, a value in the typical range for arterial tissues. Since the central unit is of interest and the surrounding tissue is mainly involved to avoid false boundary conditions, we do not allow the surrounding tissue to swell.

3.2.3 Material parameters

A complete set of material parameters derived from experiments based on the introduced constitutive model is not yet available. We have therefore adopted parameters from various established research studies. The material properties for the elastic laminae according to Eq. (15) are taken from [39] with a change in the shear modulus μe of the matrix material to the shear modulus of pure elastin [16] (Table 7.2:1 therein). The parameter D1 = 1/(50μe) is used to satisfy the incompressibility condition. The struts of interlamellar elastic fibers treated as a neo-Hookean model are modeled with a shear modulus μef = 200.0 kPa (Young’s moduli in the range of 0.3-1.5 MPa were determined for single elastic fibers [32]). In the study [47] the SMCs were separated and the overall elastic stiffness of young male monkeys was assessed in vitro. The remaining parameters come from [2, 53].

Table 2 Constitutive parameters for the medial lamellar units
Full size table

According to the dry weights provided in Section 3.1.1 we have determined the weights for each component in the elastic laminae as

$$w_{\mathrm{e}} = \frac{23\%}{23\% + 30\%} = 0.43, \qquad w_{\mathrm{c}} = \frac{30\%}{23\% + 30\%} = 0.57,$$
(18)

and in the interlamellar space as

$$w_{\text{SMCs}} = \frac{43\%}{43\% + 4\%} = 0.91, \qquad w_{\text{GAGs}} = \frac{4\%}{43\% + 4\%} = 0.09.$$
(19)

The constitutive parameters are summarized in Table 2.

Fig. 8
figure 8

The top row shows the deformation of the global model, the bottom row of the submodel. Black lines clarify the reference configuration and the color indicates the radial displacement ur of the elements (in μm). Reference configuration t = 0, after pre-straining and pressurization t = 1 and after the GAGs/PGs pool swelling step t = 2

Full size image
Fig. 9
figure 9

Donnan swelling pressure π plotted in the finite elements related to GAGs/PGs areas (in kPa). Plots show the results at the end of the swelling step: (a) diseased condition; (b) healthy condition

Full size image

3.2.4 Numerical results

The simulation starts with a stress-free configuration on which pre-strains and pressure are applied to the global model, see Fig. 7. The boundary constraints are then applied on the submodel of the medial layer from the surrounding tissue, i.e. the central unit between cutting plane 1 and 2 in Fig. 6b. The global model has 62 832 elements of different types (C3D8, C3D8H and C3D8T) while the submodel consists of 14 200 elements (C3D8H and C3D8T).

Figure 8 shows the reference (initial) and the current configurations for the global model and the submodel at the end of each step (reference configuration t = 0, after pre-straining and pressurization t = 1 and after the GAGs/PGs pool swelling step t = 2), while the legend shows the displacement ur in the radial direction. The various materials are shown at t = 0 with the same color as in Fig. 6. During t ∈ (0,1], the pre-strains in the z and 𝜃-directions as well as the pressure in the r-direction are applied on the global model. During t ∈ (1,2], a reference fixed charge density \(c_{F}^{\text {ref}}\) is applied linearly to the central unit from 0 to 20 mol m− 3.

As this example aims to somehow identify the dissection mechanism due to swelling of GAGs/PGs we focus on the submodel, which consists of a (more) detailed microstructure and higher accuracy due to the finer mesh. Figure 9a shows the distribution of the Donnan swelling pressure π in the finite elements related to the GAGs/PGs areas. The minus sign in the result is because of the Donnan pressure defined as − π in 10. The prevailing pressure values in Fig. 9a vary from − 20.0 to − 56.0 kPa. Tam et al. [55] observed that the propagation pressure required to dissect the wall of a porcine thoracic aorta under static condition is in the range of − 26.0 to − 60.0 kPa, which is the same range in terms of our numerical results. In other words, if \(c_{F}^{\text {ref}}\) increases from 0 to 20 mol m− 3, we get a pressure level that can lead to tissue failure. In comparison, Fig. 9b shows the swelling pressure distribution for a healthy condition with low GAG concentration (1%, which corresponds to wGAGs = 0.02 and wSMCs = 0.98, see Eq. (19), and \(c_{F}^{\text {ref}}\) increases from 0 to 10 mol m− 3. The Donnan swelling pressure π is only one third of the diseased condition, the swelling is rather small, and the interlamellar fibers are only slightly elongated.

Fig. 10
figure 10

Maximum principal logarithmic stretch \(\ln \lambda _{1}\) and logarithmic stretches in radial direction \(\ln \lambda _{r}\), circumferential \(\ln \lambda _{\theta }\) and axial direction \(\ln \lambda _{z}\). The plots show the results at the end of the swelling step

Full size image
Fig. 11
figure 11

Maximum principal Cauchy stress σ1 and stresses in radial direction σr, circumferential σ𝜃 and axial direction σz (in kPa). The plots show the results at the end of the swelling step

Full size image

Figure 10 shows the logarithmic stretch distribution in the central unit. The stretches in the circumferential and axial directions are larger than in the radial direction. This may be because the elastic fibers have a higher stiffness than the GAGs/PGs and SMCs and tend to hold the adjacent elastic laminae together. Consequently, the struts of the elastic fibers limit the expansion of the GAGs/PGs in the radial direction. For the circumferential and axial directions, however, the main resistance to swelling comes from the surrounding (rather) soft interlamellar material such as the GAGs/PGs and the SMCs. The lower stiffness of these interlamellar materials enables larger stretches in the 𝜃 and z-directions. In addition, we observe a stress concentration along the boundaries between the different materials, regardless of the accuracy of the stress concentration values, see Fig. 11. The stress in the tissue is larger in the circumferential and axial directions than in the GAGs/PGs and SMCs, which corresponds to the fact that the tissue is the main load bearer in the media.

Fig. 12
figure 12

Illustration of the numerical model used for comparison with experimental data documented in [52]: (a) geometry of a coin-shaped specimen with cross-section Acoin in the reference configuration and force F = 1.25 N, where damage softening and micro-defects occur [52]; (b) force F results in a nominal stress P = F/Acoin over the specimen cross-section Acoin; (c) central unit with area Aunit, whereby the lower surface is fixed in all directions (ur = u𝜃 = uz = 0) and on the upper surface with u𝜃 = uz = 0 a displacement ur = 10.0μm in the radial direction is applied to achieve a similar deformation as in the experiments; (d) for the increase of ur the radial stress generates a resultant force Funit = PAunit on the upper surface, where P is assumed to be the same as in the experiment

Full size image

3.2.5 Estimation of the local failure stress

Sommer et al. [52] investigated the failure behavior of the media of human abdominal aortas with direct tension tests on a coin-shaped specimen. A simplified illustration also capturing the geometry is shown in Fig. 12a. A resultant force F is exerted on the coin-shaped specimen, where Acoin is the cross-section of the specimen in the reference configuration. The results in [52] show that the ‘elastic limit’ is reached at a force F of about 1.25 N, where damage softening and micro-defects occur. As the load progresses, damage continues to develop with the ultimate (limit) force at failure of 1.76 ± 0.20 N. Due to the complexity of the medial microstructure and the simplifications in the construction of the numerical model, it is difficult to perform a direct comparison between the experimental results documented in [52] and the numerical results from Section 3.2.4. In order to get a reasonable approximation of the stress level at which struts of elastic fibers start to damage, we create an alternative numerical simulation based on these experimental tests to gain access to the radial stress component.

The measured force F = 1.25 N results in a nominal stress P over the specimen cross-section of P = F/Acoin = 44.2 kPa (Fig. 12b). In the numerical simulations, the same central unit with the area Aunit as described above is used, see Fig. 12c. The lower surface of the unit is fixed in all directions (ur = u𝜃 = uz = 0) and, on the upper surface, with u𝜃 = uz = 0, a displacement ur is applied in the radial direction to achieve a similar deformation as in the experiments. When ur increases, the radial stress in the material increases and creates a resultant force, say Funit, on the upper surface, see Fig. 12d. The resultant force Funit is an output quantity from Abaqus. We now assume that if this resultant force on the central unit results in a nominal stress P of approximately the same value as the nominal stress from the experiment, i.e. Funit = PAunit, the numerical and experimental results are similar, and the stress in the struts of the elastic fibers obtained from the numerical simulation is regarded as an approximation of the stress occurring in the experiment. The FE results show that when the radial displacement ur reaches 10.0μ m, the force Funit in the central unit is about 6.0 ⋅ 10− 6 N.

The radial stress σr in the central unit for the direct tension test and after swelling is shown in Fig. 13a and b, respectively (enlarged views are displayed in the boxes on the right). There exist stress concentrations at the connections of the elastic laminae and the struts of elastic fibers, which correspond to the observation made based on experiments [33]. In that study, it appears that the elastic fibers become torn from their connections with the elastic laminae. At these locations with stress concentrations, delaminations can also be initiated during aortic dissection. In the direct tension test, the radial stress in the middle of the elastic fiber struts, apart from the high stress concentration at the connection corners, is about 430 kPa, and the stress distribution appears rather homogeneous.

Fig. 13
figure 13

Numerical results for the radial stress σr after (a) the direct tension test, (b) swelling and (c) for the von Mises stress σMises after swelling (in kPa). Enlarged views are displayed in the boxes 1, 2 and 3

Full size image

After swelling, the radial stress distribution is more heterogeneous due to the swelling-induced compression, and the stress state is much more complex, see Fig. 13b. The radial stress σr in the struts after swelling varies between 130.0 kPa in the central area of the strut and 250.0 kPa at the edge. With a more engineering approach we plot the von Mises stress, say σMises, after swelling, see Fig. 13c. The distribution indicates that σMises varies throughout the strut with a value of about 250.0 kPa in the central region. It is important to note that the stress levels obtained from the experiments [52] and from the numerical swelling analysis are of the same order of magnitude for both σMises and σr. We therefore consider that the swelling behavior of GAGs/PGs during the numerical simulation can induce increasing stresses in the elastic fibers until failure.

The swelling behavior due to the existence of GAGs/PGs is a combined result of the accumulation of GAGs/PGs and an increase in the fixed charge density. To show the influence of GAGs/PGs accumulation on the swelling, we increased the GAGs/PGs content in Eq. (19)2 from 4% to 8%, which corresponds to wSMCs = 0.83 and wGAGs = 0.17. By re-running the simulation, we found that with a higher GAGs/PGs content with the same reference fixed charge density \(c_{F}^{\text {ref}}\), e.g., 4.8 mol m− 3, the von Mises stress σMises is about 150.0 kPa for a higher GAGs/PGs content, which is roughly 2.3 times the Mises stress level for a lower GAGs/PGs content. It is therefore to be expected that with a higher GAGs/PGs proportion, the failure stress level can be more easily reached with a lower fixed charge density.

3.3 Comparison of numerical results with/without preconditioning and pressurization

Here we compare simulation results with and without preconditioning (pre-stretches) and pressurization in order to show the sensitivity of the proposed model in regard to these quantities. The Donnan swelling pressure π is shown in Fig. 14, noting that both simulations give similar results for π. Since π depends on the volume of the element that contributes to the change in the current fixed charge density cF 13, there is a slight difference in the pressure distribution between the two cases due to the difference in the element volumes at the beginning of the swelling step. The reference fixed charge density \(c_{F}^{\text {ref}}\) varies in both cases from 0 to 15 mol m− 3. Therefore, it is expected that the Donnan swelling pressure will not vary significantly with preconditioning.

Fig. 14
figure 14

Comparison of the Donnan swelling pressure π in the FEs related to GAGs/PGs (in kPa). Numerical results at the end of the swelling step

Full size image
Fig. 15
figure 15

Cauchy stress distributions in the central unit without preconditioning (top row) and with preconditioning (bottom row): (a) circumferential stress σ𝜃 and axial stress σz; (b) von Mises stress σMises and radial stress σr. Units are given in kPa

Full size image

Stresses in the circumferential direction σ𝜃 and in the axial direction σz are plotted in Fig. 15a. These stresses are higher in the elastic laminae for the preconditioned case due to the pre-stretches in the 𝜃 and z-directions. Figure 15b shows the von Mises stress σMises and the radial stress σr, where the stress transition between the elastic laminae and the struts of elastic fibers is characterized by the different colors. The von Mises stress σMises of the simulation, taking preconditioning into account, is relatively continuous throughout the elastic laminae and struts of elastic fibers, and the value is about 200.0 kPa. In the simulation without preconditioning, however, σMises is much higher in the struts of the elastic fibers than in the remaining materials (factor of 1.5 to 2.0). If one considers the radial stress σr, the simulation without preconditioning results in a much higher σr in the struts (factor from 2.0 to 3.0). The discontinuity in σr due to the elastic laminae and struts of elastic fibers for the simulation without preconditioning is also relatively significant compared to the simulations with preconditioning.

As was analyzed in [21], the radial stress σr is continuous and almost constant through the medial and adventitial layers, and the amount of σr is much smaller than that of the tangential stresses. From the present numerical results, preconditioning gives responses that correspond to the observation in [21] for both σMises and σr. The preconditioning relaxes stresses to a certain extent. This is in line with the fact that residual stresses in arteries have a clearly positive influence on the load-bearing capacity of the material, which also reflects the self-adaption to the varying environment of arterial tissues.

4 Discussion

The present study aimed to propose an advanced weighted constitutive model that can be used to predict and better understand the onset of an aortic dissection by analyzing the swelling behavior of accumulated GAGs/PGs in the medial layer (based on the swelling polymer theory) coupled with the anisotropic response of the arterial material. The user subroutine UMAT was used within Abaqus to implement the proposed constitutive model. To illustrate this, we performed several numerical simulations to predict the stress distribution and swelling mechanism within a medial lamellar unit. Using parameters from various established research studies, we were able to predict failure stresses of the same order of magnitude as obtained from experimental tests. In addition, stress concentrations occurred at the connection of the elastic laminae and the interlamellar struts composed of elastic fibers, which can be considered as hotspots where dissections may start. The present modeling approach provides a foundation for more accurate prediction of aortic dissection and for future modeling work.

The numerical results are based on the weighted constitutive model, which accounts for the different material fractions and provides a basis for investigating the different material contributions. The numerical results show that as the reference fixed charge density \(c_{F}^{\text {ref}}\) increases, the GAGs/PGs pool swells to reach an equilibrium state. During swelling, the solid skeleton, like the interlamellar elastic fibers, is exposed to higher radial stress. A comparison between experimentally-based data [52] and the numerical results has shown that the proposed model is able to predict the effect of the GAGs/PGs swelling behavior, which increases the von Mises stress σMises and the radial stress σr in the elastic fibers up to a failure value that is observed experimentally. A comparison of the numerical results with and without preconditioning and pressurization has shown that residual stresses in the arterial tissue help to increase the load-bearing capability during aortic dissection.

More work is needed to fully understand dissection initiation. In Section 3.2 we restricted the swelling behavior within a central lamellar unit to mimic a concentrated GAGs/PGs pool. In vivo we would expect a more modest transition between the swelling and non-swelling regions. Previous studies have shown that in addition to highly concentrated GAGs/PGs pools, small GAGs/PGs pools are also distributed relatively randomly across the medial layer, see, e.g., [7, 12, 34]. Therefore, it would be interesting to model a random distribution of GAGs/PGs across the medial layer to get more realistic results. Furthermore, in the numerical simulations we used 4% GAGs/PGs by dry weight, which is a relatively low GAGs/PGs concentration compared to diseased arteries [3]. In more severe pathological cases, where massive GAGs/PGs pools accumulate, it is easier to damage and rupture the elastic fibers and develop a detachment of the MLUs, initiating aortic dissection. Further work on a realistic reduction of the SMC portion with increasing weight wGAGs could be of interest. This allows the swelling behavior to be increased even further since GAGs/PGs are softer than SMCs.

Experiments have shown that throughout the interlamellar space there are also single collagen fibers covering the surface of SMCs and thin elastic fiber bundles [41] that we did not include in the numerical simulations. It would be expected that these individual collagen fibers would increase the overall stiffness of the interlamellar material, potentially helping to limit the swelling behavior. It is also worth noting that the geometry used is based on a simplified representation of the spatial organization of some components of the aortic media according to [12], without detailed experimental data on the inclination angle of the elastic fibers and geometry. This implies that more detailed and reliable geometrical data are required to obtain more accurate numerical results. And, of course, more and improved material properties are necessary in order to be able to ultimately compare the modeling results with clinical observations.