A simple phenomenological approach for myocardial contraction: formulation, parameter sensitivity study and applications in organ level simulations

Abstract

Contraction in myocardial tissue is the result of a complex process through which chemical energy on the cellular level is converted into the mechanical energy needed to circulate blood throughout the body. Due to its vital role for the organism, myocardial contractility is one of the most intensively investigated subjects in medical research. In this contribution, we suggest a novel phenomenological approach for myocardial contraction that is capable of producing realistic intracellular calcium concentration (ICC) and myocyte shortening graphs, can be easily calibrated to capture different ICC and contraction characteristics and, at the same time, is straightforward to implement and ensures efficient computer simulations. This study is inspired by the fact that existing models for myocardial contractility either contain a number of complex equations and material parameters, which reduce their feasibility, or are very simple and cannot accurately mimic reality, which eventually influences the realm of computer simulations. The proposed model in this manuscript considers first the evolution of the ICC through a logarithmic-type ordinary differential equation (ODE) having the normalized transmembrane potential as the argument. The ICC is further put into an exponential-type ODE which determines the shortening of the myocyte (active stretch). The developed approach can be incorporated with phenomenological or biophysically based models of cardiac electrophysiology. Through examples on the material level, we demonstrate that the shape of the ICC and myocardial shortening curves can be easily modified and accurately fitted to experimental data obtained from rat and mouse hearts. Moreover, the performance of the model in organ level simulations is illustrated through several multi-field initial-boundary value problems in which we show variations in volume-time relations, heterogeneous characteristics of myocardial contraction and application of a drug in a virtual left ventricle model.

1 Introduction

The ultimate function of the heart is to generate sufficient mechanical energy to enable blood to flow throughout the entire body and return back to the heart. This vital task is achieved through a series of sophisticated activities, whose end production is myocardial contraction. Any kind of heart disease will inevitably have an influence on myocardial contraction, which in turn may lead to heart failure. Revealing the complex mechanisms behind the myocardial contraction in health and disease is one of the most studied aspects of the heart. In this regard, a big number of experimental and clinical studies have been conducted for both humans and animals. Apart from that, the last decades have witnessed extensive utilization of numerical modelling approaches inquiring into myocardial contraction on the cellular and organ level. Undoubtedly, numerical modelling can be considered a powerful tool for investigating myocardial contraction and its implications on heart function in health and disease. In this paper, we contribute to the literature by elaborating novel phenomenological equations for intracellular calcium concentration (ICC) and myocardial shortening which are simple and straightforward to implement and, at the same time, enable us to mimic reality in an accurate way and perform efficient computer simulations of the virtual heart models. It should be noted that the equations for the ICC and myocardial contraction were first used by Cansız et al. [5] and further adopted by Cansız et al. [6, 7] in order to describe myocardial contraction. However, a detailed investigation of the equations at the material and organ level will be carried out for the first time in this manuscript.

1.1 Myocardial contraction

Myocardial contraction stems from the tensile force generated by sarcomeres after a series of events. Essentially, the coupling between the electrophysiology and mechanical activity in the myocytes is linked through the ICC. When a myocyte becomes depolarized, Ca²⁺ in the extracellular space enters the cell through voltage gated channels, where it further causes the release of Ca²⁺ from the sarcoplasmic reticulum (SR). This release results in a sharp increase of the ICC available to bind to a multi-protein structure known as the troponin complex. This process causes the troponin complex to detach and no longer block the binding sites on a long protein strand called the actin filament. These unblocked binding sites allow for cross-bridge elements belonging to the protein strand known as the myosin filament to attach. The cross-bridges can change their configuration through the use of adenosine triphosphate forcing the actin and myosin filaments to slide past each other. The actin filaments are attached to transverse structures called Z-discs placed at longitudinal intervals. A chain-like grouping of these systems is in place so that, when the filaments slide past each other, myocyte shortening occurs and tension is generated in this chain. After a myocyte reaches its full tension, the relaxation process begins, in which Ca²⁺ travels back to the extracellular space and SR. The ICC decays to its resting value slower than the initial sharp release and the filaments return to their initial configuration thereby the myocyte elongates and the tension is released. Figure 1 illustrates typical behaviour of the ICC and the corresponding muscle contraction-relaxation in mice myocytes [34] for different stimulating frequencies. Note that the experimental data are normalized so that the peak value of the ICC with 2 Hz stimulating frequency, $\bar c$, is 1 [-] and the muscle shortening is given in terms of stretch $\lambda ^{a}_{\text {f}}$.

Fig. 1

Experimental data by Lim et al. [34] in mice myocytes. In the diagrams, a the calcium transients and b the corresponding cell shortenings are shown for different pacing frequencies (2 Hz, 4 Hz and 7 Hz) which increase along the arrow direction

Moreover, the ICC transient exhibits regional variations in the ventricles and, naturally, the characteristics of the myocardial contraction vary nonuniformly throughout the ventricles. The mechanical activation of the ventricles occurs in tens of milliseconds upon the local electrical depolarization, namely, a delay between electrical and mechanical activation exists that is often called electromechanical delay (EMD). In a healthy heart, the EMD is shorter at the endocardium compared to the delay at the epicardium and longer near the base than at the apex. Besides, a notable myocardial prestretch is observed at late-depolarized regions due to the contraction of early-depolarized regions, which detains the beginning of myofiber shortening and leads to a longer EMD [23]. Furthermore, the myocardial contraction and fibre strain have longer duration and larger magnitude in the endocardium compared to the epicardium [3, 4]. In addition, it has been reported that timing of muscle relaxation onset and its propagation direction differ at the inner and outer layers of the ventricle [46]. Such variations have been observed in many species and are likely to exist in order to provide an efficient pumping function of the ventricles.

1.2 Modelling approaches for myocardial contraction

Among heart related modelling research studies, myocardial contraction is perhaps one of the most investigated topics. In this context, Hill’s study underlies most of the modelling attempts for skeletal and myocardial muscles [25]. He experimentally studied the energy liberation of isolated skeletal muscles in terms of heat. Based on these observations, he described the tension-velocity relation through an empirical equation. Moreover, he suggested a rheological setting in which the passive response is represented by a purely elastic spring in parallel connected to a branch having a contractile element and an elastic spring that imitates the active response (contraction) of the muscle. Since then, this rheological setting has been referred to as Hill’s three-element model in the literature. Tezören [51] proposed a generalized Hill model for isometric and isotonic phases of the contraction in which the muscle tension is formulated as a function of muscle length, strain rate and activation degree. In a similar way, Pinto [43] suggested an exponential-type equation that relates the muscle force to active contraction and identified the material parameters based on experiments performed on papillary muscles. Apart from empirical modelling attempts, more biophysically based models have been suggested. In this context, the work of Huxley [29] is one of the significant studies motivated by the sliding filament theory (interaction of myosin and actin filaments) of muscle contraction [28]. Inspired by the sliding filament theory, Fung [20] proposed a sinusoidal formulation and adopted it into the three-element Hill model to study the active response of the cardiac muscle. In a similar way, Wong [56, 57] furnished the three-element Hill structure with the Huxley model [29], where the role of calcium binding was additionally taken into account. Consideration of intracellular calcium dynamics is another way of modelling the relation between the force generation and sarcomere shortening, which is employed by many authors [22, 27, 35, 44, 49]. The biophysically based models have also been utilized for organ scale simulations in various studies [19, 30, 32, 33, 45]. For a wide review of biophysically based myocardial contraction studies, the reader is referred to Trayanova et al. [52]. Although such models can to some extent mimic the cellular events during contraction, their application in organ scale simulations is not straightforward. These models consist of a large number of ordinary differential equations (ODEs), which are not straightforward to implement and might cause stability issues [37], and possess many material parameters, which might be difficult to adjust for different simulation conditions. Moreover, large computation requirements can limit the resolution or range of application with current computing capabilities.

Alternatively, numerical frameworks employing purely phenomenological approaches for myocardial contraction can provide efficient computer simulations without having any direct physical interpretation of the events occurring on the cellular and tissue level. In that sense, Pelce et al. [42] proposed a practical contraction model which relates the transmembrane potential to the shortening of myocytes. The model comprises a simple evolution equation for the ICC which is governed by the transmembrane potential. The ICC is used as an input to a phenomenological equation to compute the myocyte contraction. Cherubini et al. [9] performed finite element (FE) simulations of the myocardium with a rheological model having an elastic spring and a contractile element connected in serial, where the deformation of the contractile element is described by the model of Pelce et al. Göktepe et al. [21] generalized Hill’s classical three-element rheology in a three-dimensional setting and utilized the same simple model for the contractile unit in the rheology. Moreover, Nobile et al. [38] modified the Pelce et al. contraction model with an additional term that considers the direct influence of the transmembrane potential on the contraction. Although the equations of Pelce et al. are adequate to represent general characteristics of an excitation-contraction problem, they cannot produce very realistic ICC and myocardial contraction curves. We refer to the work of Göktepe et al. [21] for a detailed parameter sensitivity analysis of the Pelce et al. model.

1.3 Aim of the manuscript

In this study, we propose two ODEs that (i) can precisely mimic the general characteristics of experimentally observed ICC and myocardial shortening behaviour, (ii) can be swiftly adjusted to capture different contraction characteristics on the cellular and organ level and (iii) are straightforward to be implemented within a numerical framework providing efficient computer simulations. To this end, one ODE is developed for the ICC having a logarithmic-type evolution and another ODE is related to the myocardial shortening (active stretch) having an exponential-type evolution in a phenomenological sense. Firstly, we calculate the ICC whose argument is specified as the normalized transmembrane potential. Then, the ICC gives rise to the evolution of the active stretch which causes a muscle shortening on the global scale. The model has only seven material parameters in total and both the ICC and active stretch are treated as internal variables and computed in a local sense.

In order to show the applicability of the proposed equations, we perform a detailed material parameter sensitivity analysis and investigate their fitting capacity to different experimental data of the myocardium obtained from already published works in the literature. The equations are further embedded into our fully implicit staggered solution algorithm for cardiac electromechanics [5] in which the modified Hill model is used to describe the electro-visco-active characteristics of the myocardium. Furthermore, several FE simulations in a personalized left ventricle (LV) model are performed pointing out the usability of the new contraction model. In the first part of the numerical examples, we simulate volume-time (v-t) relations of the LV model having different characteristics with respect to the same electrical activity by simply modifying the material parameters in the active stretch equation. We show that the descending and ascending slope and duration at the peak of the v-t curve can be easily altered. In the second part of the numerical examples, we try to mimic the mechanical activation sequence in the light of clinical studies. For this purpose, we consider the heterogeneous characteristics of the contraction throughout the LV by interpolating some of the material parameters related to the active stretch from the endocardium to the epicardium and from the base to the apex. In the simulations on both the material and organ level mentioned above, the phenomenological Aliev-Panfilov model [2] is used for the description of the cardiac electrophysiology. In the last part of the numerical examples, however, we demonstrate that the proposed contraction model can be coupled to biophysically based models of cardiac electrophysiology, e.g. the model of ten Tusscher et al. [50] which will be referred to as the TNNP (abbreviated based on the names of the authors: ten Tusscher-Noble-Noble-Panfilov) model in the rest of the manuscript. To this end, we keep the active stretch equation unchanged and the ICC, which governs the active stretch, is not calculated through the proposed ICC equation, instead, it is generated by the TNNP model. In this setting, we apply a drug called verapamil, which has effects on the electrophysiology and contractility, to the LV model and study its implications in terms of v-t relations and electrocardiograms (ECGs) and compare them to the control (normal) case.

This paper is organized as follows. In Section 2, we introduce the phenomenological equations of the ICC and active stretch and discuss their performance through a detailed parameter sensitivity analysis. The kinematical setting and governing equations of the electromechanical coupling in the myocardial tissue in a monodomain setting are given in Section 3. The constitutive relations are outlined in Section 4. Section 5 demonstrates the applicability of the proposed model through numerical examples which consist of the fitting to experimental data and several initial-boundary value simulations in a personalized LV model are carried out. Finally, we provide concluding remarks in Section 6.

2 Phenomenological formulation of myocardial contraction

In this section, we introduce our novel phenomenological equations that mimic the myocardial contraction and evolution of its driving ion concentration, i.e. the ICC. Moreover, a detailed parameter sensitivity analysis demonstrating the capacity of the proposed equations is given, where the Aliev-Panfilov model [2], later introduced in Section 4.3.1, is utilized in order to generate the myocyte transmembrane potential with the parameters α = 0.01 [-], b = 0.15 [-], c = 8 [-], γ = 0.002 [-], μ₁ = 0.2 [-] and μ₂ = 0.3 [-].

2.1 Intracellular calcium concentration

Motivated by the resemblance of the negative of the logarithmic function to the descending slope of the ICC observed in experiments, we propose the following logarithm-type evolution equation for the normalized ICC, $\bar c$,

$$ \dot{\bar c} = g(\phi) - \bar c k_1 \qquad \text{with} \qquad g(\phi) = \zeta |\ln(1-\phi)|^{p_1}, $$

(1)

where ϕ is the normalized transmembrane potential value and k₁, ζ, p₁ are the material parameters. Before starting with the parameter sensitivity analysis, it is worth mentioning that all the parameters intrinsically affect the magnitude of the ICC in Eq. (1). Therefore, to be able to clearly demonstrate features other than adjusting the maximum, the magnitudes of the ICC curves, except in Fig. 2b, are equalized through the parameter ζ. By equalized, it is meant that the magnitude of the peak is normalized to the same value via parameter ζ.

Firstly, shifting the peak point of the ICC curve in time without changing the magnitude is illustrated (see Fig. 2a), where k₁ is varied. It is worth noting that the subtracting term $\bar {c}k_{1}$ in Eq (1) is the cause for the descending slope of the ICC. Thus, when k₁ is zero, the ICC reaches its peak and stays there as a plateau (not shown). This is the reason why a decrease in k₁ causes the ICC curves to have a wider nature. Moreover, the magnitude of the ICC is changed independently through the parameter ζ, where an increase in ζ moves the magnitude of the peak up without altering the timing of the peak point (see Fig. 2b). Finally, the effects of the parameter p₁ are investigated. Figure 2c demonstrates that decreasing p₁ values lead to a shift of the location of the peak point in time. At first sight, it seems that the parameter p₁ has a similar effect as k₁. However, the behaviour in the change of the descending limb slope is different when the parameter p₁ is altered. As p₁ is decreased, we observe only a slight flattening of the descending limb and further reductions do not cause the descending limb to form a plateau as k₁ does. Moreover, for p₁ < 0.5 [-], unrealistic ICC curves are produced that almost resemble to the action potential curve (not shown). A summary of the ICC parameters is given in the following.

• Parameter k₁ changes the magnitude and location of the peak in time. This in turn influences the descending and ascending slope.

• Parameter ζ changes the magnitude without changing the location of the peak point in time. The descending and ascending slopes are naturally affected due to the change in magnitude of the peak point.

• Parameter p₁ changes the magnitude and timing of the peak point with a slighter change in the descending slope compared to the change when parameter k₁ is varied.

Fig. 2

Parameter sensitivity analysis for the ICC. Varying a the peak point in time with k₁ = 0.5,0.05,0.02,0.01,0.005 [-], ζ = 1.55 10^− 3,2.22 10^− 4, 1.215 10^− 4,8.37 10^− 5,6.23 10^− 5 [-], p₁ = 3 [-], b the magnitude with ζ = 1.0 10^− 4,1.5 10^− 4, 1.9 10^− 4,2.2 10^− 4,2.5 10^− 4 [-], k₁ = 0.05 [-], p₁ = 3 [-], c the peak point in time with p₁ = 7,4,3,2,1 [-], ζ = 7.64 10^− 8,1.97 10^− 5, 1.22 10^− 4,7.28 10^− 4,4.15 10^− 3 [-], k₁ = 0.02 [-] and d the descending slope with k₁ = 0.05,0.0375,0.03,0.024,0.0195 [-], p₁ = 1,2,3,4,5 [-], ζ = 8.7 10^− 3,1.13 10^− 3,1.56 10^− 4, 2.175 10^− 5,3.09 10^− 6 [-] against the same normalized transmembrane potential. The changing parameters are sequentially varied in the arrow direction. Note that the magnitudes of the ICC curves are kept the same in a, c and d by adjusting ζ accordingly

Furthermore, the combination of the parameters k₁ and p₁ gives us the chance to alter the descending slope of the ICC curve while keeping the ascending slope and peak point unchanged (see Fig. 2d). It should be further noted that apart from the material parameters controlling the ICC transient, the way the transmembrane potential curve evolves is closely related to the shape of the ICC curve, since the transmembrane potential is considered as the argument of the ICC equation. For instance, a prolongation of the action potential duration without changing the upstroke slope (by increasing the parameter γ) results in an elevation in the magnitude of the ICC peak (see Fig. 3a), although none of the parameters in the ICC equation are changed. Likewise, a decrease in the upstroke slope of the transmembrane potential curve (by decreasing the parameter b) leads to a shift of the peak point in time and reduction in the magnitude of the ICC curve (see Fig. 3b).

Fig. 3

Demonstration of variation in the ICC and active stretch curves with respect to different transmembrane potential behaviour. The parameter set is identical with the third curve (from left) in Fig. 4a except for γ = 0.002,0.004,0.006 [-] in a and b = 8,5,3 [-] in b. The parameters are sequentially varied in the arrow direction

2.2 Active stretch

Evolution of $\bar c$ further gives rise to myocardial contraction represented by the active stretch $\lambda ^{a}_{\text {f}}$ that has an exponential-type evolution equation

$$ \dot\lambda^a_{\text{f}} = f(\bar c) - (\lambda^a_{\text{f}} - 1) k_2 \qquad \text{with} \qquad f(\bar c) = \xi[{\exp}(-q {\bar c}^{p_2}) - 1] $$

(2)

in terms of the material parameters k₂, ξ, q and p₂. Before proceeding with the material parameter sensitivity analysis, we note that as with the parameters for the ICC, all parameters in Eq. (2) naturally influence the magnitude of the active stretch. For that reason, the minimum values of the active stretches, except in Fig. 4b, are brought to the same value through the parameter ξ for a clear illustration of the features other than magnitude adjustability. The parameters for the ICC are determined as k₁ = 0.05 [-], p₁ = 3 [-] and ζ = 0.000222 [-].

Fig. 4

Parameter sensitivity analysis for the active stretch. Varying a the peak point in time with k₂ = 0.3,0.05,0.025, 0.015,0.01 [-], ξ = 1.301, 0.245,0.1445,0.1039,0.0823 [-], q = 0.1 [-], p₂ = 1.0 [-], b the magnitude with ξ = 0.06,0.1,0.14,0.19,0.23 [-], k₂ = 0.025 [-], q = 0.1 [-], p₂ = 1.0 [-], c the timing of the peak point together with the duration with q = 1.0, 5.0,10.0,20.0,30.0 [-], ξ = 0.02,0.011,0.0104,0.01015,0.0101 [-], k₂ = 0.025 [-], p₂ = 1.0 [-] and d the slope of the ascending limb with p₂ = 3.0,2.0,1.5,1.0,0.5 [-], ξ = 0.024,0.0223,0.0213, 0.0202,0.0187 [-], k₂ = 0.025, q = 1.0 [-] against the same ICC and transmembrane potential curves. The changing parameters are sequentially varied in the arrow direction. Note that the magnitudes of the active stretch curves are kept the same in a, c and d by adjusting ξ accordingly

Variations in the timing of the minimum value are performed by changing k₂ (see Fig. 4a). For a small k₂ value, the timing of the minimum is delayed and small variations in k₂ can cause a large change in the timing of the minimum. Whereas, when k₂ is large, the timing of the minimum is early in time and k₂ must be largely increased to generate movements towards earlier timings. Another important feature is the ability to independently change the magnitude of the contraction by changing only ξ. This is extremely practical, since it allows ξ to be treated as a parameter that is exclusively tied to the magnitude of the myocardial contraction. Figure 4b displays the movement of the active stretch minimum in magnitude without changing the location in time by a simple adjustment of ξ. In addition, the ascending and descending slopes of the active stretch can be adjusted through q. Figure 4c displays an increase in the slope of both branches of the active stretch along with a shift in time as the parameter q increases. This behaviour can also be interpreted as a prolongation in the duration of the peak contraction. Moreover, the parameter p₂ has a slightly similar effect as the parameter q. As p₂ is decreased in Fig. 4d the slope of ascending limb is reduced and the peak point is shifted in time without a significant alteration in the descending limb slope. Hence, the duration of the active stretch remains almost unchanged in contrast to the effect of the parameter q. A summary of the active stretch parameters is given in the following.

• Parameter k₂ changes the magnitude and location of the minimum in time. This in turn influences the descending and ascending slope.

• Parameter ξ changes the magnitude without changing the location of the minimum in time. The descending and ascending slopes are naturally affected due to the change in magnitude of the minimum.

• Parameter q changes the magnitude and the ascending and descending slope resulting in a change in the duration and time location of the peak point.

• Parameter p₂ predominantly changes the magnitude and the ascending slope while causing a slight change in the the descending slope and the location of the peak point in time.

Furthermore, by a combination of the parameters k₂ and p₂ one can keep the descending slope constant and vary only the ascending slope as demonstrated in Fig. 5a. Another important combination of the parameters k₂ and q is illustrated in Fig. 5b, where a certain amount of increase in the parameters alters the duration of the contraction without changing the location of the peak point.

Fig. 5

Parameter sensitivity analysis for the active stretch. Varying a the slope of the ascending limb with k₂ = 0.009,0.007,0.0042,0.0028, 0.0017 [-], p₂ = 0.8,1.0,1.5,2.0,2.5 [-], ξ = 0.01,0.00935,0.0088,0.0089,0.009 [-], q = 1.0 [-] and b the duration of the minimum with k₂ = 0.007,0.05,0.065,0.08,0.12, q = 1.0,5.0,7.0,10.0,15.0 [-], ξ = 0.0094,0.0206,0.0262,0.032,0.048 [-], p₂ = 2.0 [-] against the same ICC and transmembrane potential curves. The changing parameters are sequentially varied in the arrow direction. Note that the magnitudes of the active stretch curves are kept the same by adjusting ξ accordingly

Moreover, the shape of the ICC (explicitly) and transmembrane potential (implicitly) affects the active stretch evolution. For instance, an increase in the magnitude of the ICC will naturally elevate the magnitude of the active stretch curve (see Fig. 3a). A flattening of the descending limb of the ICC will result in a flattened ascending limb of the active stretch (see Fig. 3b).

3 Excitation-contraction coupling in myocardial tissue

In this section, we introduce the fundamental variables and kinematics that are utilized to characterize the electro-visco-active response of the myocardium. Moreover, the coupled field equations governing the deformation and electrophysiology of the myocardium in a monodomain setting are outlined.

3.1 Primary field variables and kinematics

The electromechanical state in the myocardial tissue is described by four independent sets of field variables

$$ \text{State}(\boldsymbol{\mathnormal{X}},t) := \left \{\boldsymbol{\varphi}(\boldsymbol{\mathnormal{X}},t),{\Phi}(\boldsymbol{\mathnormal{X}},t); \boldsymbol{\mathcal{I}}_{va}(\boldsymbol{\mathnormal{X}},t),\boldsymbol{\mathcal{I}}_e(\boldsymbol{\mathnormal{X}},t) \right\}. $$

(3)

Among the global field variables, the deformation map φ(X,t) and the transmembrane potential Φ(X,t) represent the macroscopic motion and the electrical state of the myocardium, respectively. In addition, the micro-motion emerging from the visco-active deformation $\boldsymbol {\mathcal {I}}_{va}(\boldsymbol {\mathnormal {X}},t)=\{\epsilon ^{v}_{\text {f}},~\epsilon ^{v}_{\text {s}},~\epsilon ^{v}_{\text {n}},~\lambda ^{a}_{\text {f}}\}$ and the micro-diffusion $\boldsymbol {\mathcal {I}}_{e}(\boldsymbol {\mathnormal {X}},t)$ arising from ion concentration differences (e.g. [K]⁺, [Na]⁺, [Ca]²⁺) across the cell membrane are considered as local fields (see Fig. 6). In the numerical framework, the global field variables are discretized spatially whereas the quantities controlling the micro-motion and micro-diffusion are treated in a local sense. The myocardial tissue is assumed to be a continuum body ${{\mathscr{B}}}\in {\mathcal {R}}^{3}$ and ${{\mathscr{B}}}_{t}\in {\mathcal {R}}^{3}$ at initial time $t_{0}\in {\mathcal {R}}$ and current time $t\in {\mathcal {R}}$, respectively, in which excitation-contraction coupling occurs. The hyperelastic nature of the myocardium is formulated through the nonlinear deformation map

$$ \boldsymbol{\varphi}:\left\{ \begin{array}{r@{~}c@{~}l} {\mathcal{B}}\times\mathcal{T} &\rightarrow& \mathcal{B}_t \subset \mathcal{R}^3, \\ (\boldsymbol{\mathnormal{X}},t) &\mapsto& \boldsymbol{\mathnormal{x}} =\boldsymbol{\varphi}_t(\boldsymbol{\mathnormal{X}}) \end{array}\right. $$

(4)

that associates material points $\boldsymbol {\mathnormal {X}}\in {\mathscr{B}}$ to spatial points x = φ_t(X) at time $t\in {\mathcal {R}}$ thereby constituting the current state of the body ${\mathscr{B}}_{t}$. The deformation gradient F := ∇_Xφ_t(X) maps the unit tangent of the reference or the Lagrangian point onto its counterpart in the current or the Eulerian configuration. The non-penetrable deformations are ensured by the constraint J > 0, $J:=\det \boldsymbol {\mathnormal {F}}$. Moreover, the symmetric right Cauchy-Green tensor and left Cauchy-Green tensor are utilized as a strain measure

$$ \boldsymbol{C} := \boldsymbol{\mathnormal{F}}^T \boldsymbol{\mathnormal{g}} \boldsymbol{\mathnormal{F}} \quad \text{and} \quad \boldsymbol{\mathnormal{b}} := \boldsymbol{\mathnormal{F}}\boldsymbol{\mathnormal{G}}^{-1}\boldsymbol{\mathnormal{F}}^T, $$

(5)

respectively, in terms of the covariant Eulerian metric tensor g_ab = δ_ab and contravariant Lagrangian metric tensor G_AB = δ_AB that are used for index raising and lowering purposes in the Cartesian framework. The contractile nature of the myocardium is embodied in the active part of the deformation gradient F^a that emerges from the multiplicative decomposition of the total deformation gradient F

$$ \boldsymbol{\mathnormal{F}}=\boldsymbol{\mathnormal{F}}^m\boldsymbol{\mathnormal{F}}^a \quad \text{with} \quad \boldsymbol{\mathnormal{F}}^m=\boldsymbol{\mathnormal{F}}^e\boldsymbol{\mathnormal{F}}^v. $$

(6)

Furthermore, the mechanical part F^m is multiplicatively split into an elastic part F^e and a viscous part F^v to be able to consider rate-dependent effects arising from the tissue viscosity. The active and viscous deformations of the orthotropic myocardial tissue, which constitute the inelastic part of the deformation gradient, are devised along fibre, sheet and normal directions that are presumed to be orthogonal to each other in the reference configuration. In light of this, the active part of the deformation gradient is prescribed along the fibre direction

$$ \boldsymbol{\mathnormal{F}}^a := \boldsymbol{1} + (\lambda^{a}_{\text{f}} - 1 ) \boldsymbol{\mathnormal{f}}_0 \otimes \boldsymbol{\mathnormal{f}}_0. $$

(7)

Moreover, the viscous part of the deformation gradient is prescribed in the following orthotropic structure

$$ \boldsymbol{\mathnormal{F}}^v := \boldsymbol{1} \displaystyle+ (\lambda^{v}_{\text{f}} - 1 ) \boldsymbol{\mathnormal{f}}_0 \otimes \boldsymbol{\mathnormal{f}}_0+ (\lambda^{v}_{\text{s}} - 1 ) \boldsymbol{\mathnormal{s}}_0 \otimes \boldsymbol{\mathnormal{s}}_0 + (\lambda^{v}_{\text{n}} - 1 ) \boldsymbol{n}_0 \otimes \boldsymbol{n}_0 \\[2ex] $$

(8)

in terms of viscous stretches $\lambda ^{v}_{\text {f}}$, $\lambda ^{v}_{\text {s}}$ and $\lambda ^{v}_{\text {n}}$ corresponding to three mutually orthogonal orientations f₀, s₀ and n₀, respectively. Finally, the prescribed forms of the active and viscous part of the deformation gradient let us attain the explicit expression of the elastic part of the deformation gradient as

$$ \boldsymbol{\mathnormal{F}}^e = \boldsymbol{\mathnormal{F}}^m \displaystyle+ \left( \frac{1}{\lambda^{v}_{\text{f}}} - 1\right) \boldsymbol{\mathnormal{F}}^m \boldsymbol{\mathnormal{f}}_0 \otimes \boldsymbol{\mathnormal{f}}_0 + \left( \frac{1}{\lambda^{v}_{\text{s}}} - 1\right) \boldsymbol{\mathnormal{F}}^m \boldsymbol{\mathnormal{s}}_0 \otimes \boldsymbol{\mathnormal{s}}_0 + \left( \frac{1}{\lambda^{v}_{\text{n}}} - 1\right) \boldsymbol{\mathnormal{F}}^m \boldsymbol{n}_0 \otimes \boldsymbol{n}_{0} $$

(9)

with the mechanical part of the deformation gradient

$$ \boldsymbol{\mathnormal{F}}^m = \boldsymbol{\mathnormal{F}} + \left( \frac{1}{\lambda^{a}_{\text{f}}} - 1\right) \boldsymbol{\mathnormal{F}} \boldsymbol{\mathnormal{f}}_0 \otimes \boldsymbol{\mathnormal{f}}_0. $$

(10)

Note that a fictitious intermediate state between the reference and current configuration is constituted by the rotation free viscous and active part of the deformation gradient in the sense of Cherubini et al. [9] and their orthogonal prescription makes F^e insensitive to the order of F^v and F^a in Eq (6). The stretches along the mutually orthogonal orientations are calculated via the push-forward operation of the Lagrangian unit direction vectors

$$ \boldsymbol{\mathnormal{f}}=\boldsymbol{\mathnormal{F}}\boldsymbol{\mathnormal{f}}_0~\rightarrow~ \lambda_{\text{f}}:=|\boldsymbol{\mathnormal{f}}|, \quad \boldsymbol{\mathnormal{s}}=\boldsymbol{\mathnormal{F}}\boldsymbol{\mathnormal{s}}_0~\rightarrow~ \lambda_{\text{s}}:=|\boldsymbol{\mathnormal{s}}| \quad \text{and} \quad \boldsymbol{n}=\boldsymbol{\mathnormal{F}}\boldsymbol{n}_0~\rightarrow~ \lambda_{\text{n}}:=|\boldsymbol{n}|. $$

(11)

As a result of the orthogonality of the viscous and active part of the deformation gradient, we further multiplicatively split the stretches

$$ \lambda_{\text{f}}=\lambda^e_{\text{f}}\lambda^v_{\text{f}}\lambda^a_{\text{f}}, \quad \lambda_{\text{s}}=\lambda^e_{\text{s}} \lambda^v_{\text{s}} \quad \text{and} \quad \lambda_{\text{n}}=\lambda^e_{\text{n}} \lambda^v_{\text{n}} $$

(12)

into active, viscous and elastic parts in the fibre direction and into viscous and elastic parts in the sheet and normal directions, respectively. The rheology for the electro-visco-elastic response of the myocardium and the multiplicative split of the stretches in three mutually orthogonal directions are demonstrated in Fig. 7. Further simplification can be made by transforming the multiplicative decomposition of the stretches to an additive format in the logarithmic strain space as follows

$$ \epsilon_{\text{f}}=\epsilon^e_{\text{f}}+\epsilon^v_{\text{f}}+\epsilon^a_{\text{f}}, \quad \epsilon_{\text{s}}=\epsilon^e_{\text{s}}+ \epsilon^v_{\text{s}} \quad \text{\normalsize and} \quad \epsilon_{\text{n}}=\epsilon^e_{\text{n}}+ \epsilon^v_{\text{n}} $$

(13)

with

$$ \epsilon_{\text{f}} := \ln\lambda_{\text{f}}, \quad \epsilon_{\text{s}} := \ln\lambda_{\text{s}} \quad \text{and} \quad \epsilon_{\text{n}} := \ln\lambda_{\text{n}}. $$

(14)

This simplified expression of the stretches allows us to construct uncoupled one-dimensional evolution equations for the internal variables, which can be easily updated in a time-discrete setting.

Fig. 6

The multi-field problem: a, b mechanical deformation and c, d electrophysiology of the myocardium. a The macro-motion field φ is constrained by essential $\boldsymbol {\varphi } = \boldsymbol {\bar {\varphi }}$ and natural boundary conditions $\boldsymbol {t} = J^{-1}\boldsymbol {\hat {\tau }}\!\cdot \!\boldsymbol {n}$, c the electrical conductance of the action potential Φ is constrained by essential ${\Phi }=\bar {\Phi }$ and natural boundary conditions $q=J^{-1}{\boldsymbol {\hat {q}}}\cdot \boldsymbol {n}$, b micro-motion field $\boldsymbol {\mathcal {I}}_{va}$ and d micro-diffusion field $\boldsymbol {\mathcal {I}}_{e}$ are locally defined and do not possess any boundary constraints

Fig. 7

Rheology for the electro-visco-elastic response of the myocardium: The upper hyperelastic spring represents the passive response of the myocardium while a the electro-visco-elastic response is formulated through the elastic spring+ dashpot +contractile element in the lower branch for the fibre direction f₀ and b the elastic spring + dashpot for the sheet s₀ and the normal n₀ directions

3.2 Fundamental equations

In the rest of the manuscript, ∇[∙] = d[∙]/dx, div[∙] = ∇[∙] : 1 and $\dot {[\bullet ]} = \text {d}[\bullet ]/\text {dt}$ denote, respectively, the gradient and the divergence with respect to spatial coordinates x and the material time derivative of a quantity. Furthermore, the hat sign $\hat {[\bullet ]}$ is employed to point out the variables that depend on the primary fields.

Cardiac mechanics

The quasi-static stress equilibrium is expressed by the balance of linear momentum in its local spatial form

$$ J~\text{div}\left [J^{-1}\boldsymbol{\hat{\tau}}\right]+ \boldsymbol{\mathnormal{b}} = \boldsymbol{0}\quad \text{in}~ {\mathcal{B}}, $$

(15)

in terms of the Kirchhoff stress tensor $\boldsymbol {\hat {\tau }}$ and the volume-specific body forces b in the reference configuration. The transient electrical state in the myocardial tissue leads to a mechanical deformation (i.e. contraction), therefore, the Kirchhoff stress tensor is formulated not only by means of the deformation field but also by taking the electrical field into account

$$ \boldsymbol{\tau}= \boldsymbol{\hat{\tau}}(\boldsymbol{\varphi},{\Phi} {;\boldsymbol{\mathcal{I}}_{va},\boldsymbol{\mathcal{I}}_{e}}). $$

(16)

The balance of linear momentum (Eq. (15)) is subjected to the prescribed essential boundary condition

$$ \boldsymbol{\varphi} =\boldsymbol{\bar{\varphi}} \quad \text{on} ~ \mathcal{S}_\varphi. $$

(17)

Additionally, the following natural boundary conditions are introduced

$$ \boldsymbol{t}= \boldsymbol{\bar{t}}\quad \text{on} ~ \mathcal{S}_t \quad \text{and} \quad \boldsymbol{t}= {-}\boldsymbol{\hat{\mathnormal{p}}}_{\text{v}}(\boldsymbol{\varphi})=-\hat{p}_{\text{v}}\boldsymbol{n}\quad \text{on} ~ \mathcal{S}_{{\text{v}t}} $$

(18)

with the surface stress traction vector t that is expressed through the Cauchy stress theorem as $\boldsymbol {t}:= J^{-1}\boldsymbol {\hat {\tau }}\cdot \boldsymbol {n}$. The former traction term is prescribed while the latter one is a function of the deformation field and represents the load on the ventricular endocardial surface $\mathcal {S}_{{\text {v}}}$ ($\mathcal {S}_{{\text {v}}}\subset \mathcal {S}$) emerging from ever-changing blood pressure in the ventricular cavity during the cardiac cycle. Note that the expressions $\mathcal {S} = \mathcal {S}_{\varphi } \cup \mathcal {S}_{t}$ and $\mathcal {S}_{\varphi } \cap \mathcal {S}_{t} = \emptyset$ have to be satisfied by the surface subdomains.

Cardiac electrophysiology

Furthermore, the principal equation of the cardiac electrophysiology in a monodomain setting is expressed as

$$ \dot{\Phi} = J \text{div}[J^{-1} \boldsymbol{\hat{q}}] + \hat{F}^{\phi} \quad \text{in}~ {\mathcal{B}} $$

(19)

in terms of the flux vector $\boldsymbol {\hat {q}}$ describing the propagating electrical waves and the nonlinear source term $\hat {F}^{\phi }$ governing the evolution of the transmembrane potential in time. As in the Kirchhoff stress tensor (Eq. (16)), the flux vector and source term depend on both the electrical and mechanical fields

$$ \boldsymbol{\mathnormal{q}} = \boldsymbol{\hat{q}}(\boldsymbol{\varphi},{\Phi}) \quad \text{and} \quad F^{\phi} = \hat{F}^{\phi}(\boldsymbol{\varphi},{\Phi} {;\boldsymbol{\mathcal{I}}_{e}}). $$

(20)

The governing equation of the cardiac electrophysiology (Eq. (19)) is then exposed to the following essential and natural boundary conditions

$$ {\Phi} = \bar{\Phi} \quad \text{on}~{\mathcal{S}}_{\phi} \quad \text{and} \quad q = \bar q \quad \text{on}~ {\mathcal{S}}_{q}, $$

(21)

respectively, along with complementary $\mathcal {S} = \mathcal {S}_{\phi } \cup \mathcal {S}_{q}$ and disjoint characteristics $\mathcal {S}_{\phi } \cap \mathcal {S}_{q} = \emptyset$ of the subdomains. The relation between the electrical surface flux term q and the spatial flux vector $\boldsymbol {\hat {q}}$ can be written through the Cauchy-type formula $q :=J^{-1}\boldsymbol {\hat {q}}\cdot \boldsymbol {n}$. Moreover, a specified transmembrane potential value of the material points at an initial state t = t₀ is needed for the solution of the ODE in Eq. (19)

$$ {\Phi}_0 = {\Phi}(\boldsymbol{\mathnormal{X}},t_0) \quad \text{in}~ {\mathcal{B}}. $$

(22)

4 Constitutive equations

This section briefly presents the constitutive equations characterizing the stress response $\boldsymbol {\hat {\tau }}$, the ventricular blood pressure $\boldsymbol {\hat {p}}_{\text {v}}$, the current source $\hat {F}^{\phi }$ and the conductivity tensor D that is necessary to obtain the flux vector $\boldsymbol {\hat {q}}$. In order to formulate the mutual interaction of the mechanical and electrical fields, we equipped the constitutive equations, except $\boldsymbol {\hat {p}}_{\text {v}}$, with additional terms that enable a mechanical deformation resulting from the tissue depolarization, i.e. contraction, and vice versa, a change in the electrical state upon a mechanical stretch, i.e. mechano-electric feedback. All evolution equations are integrated via an implicit Euler backward integration scheme which allows us to use larger time steps compared to frameworks where an explicit or a semi-implicit time integration scheme is used. The reader is referred to Cansız et al. [5] and Wong et al. [58] for a more comprehensive description the constitutive equations, the evolution equations and their update algorithms.

4.1 Stress response

The stress response of the living myocardial tissue is formulated through the modified Hill model that incorporates the rheologies proposed by Cansız et al. [8] and Göktepe et al. [21] (see Fig. 7). The significant aspect of the resulting rheological model is the multiplicative split of the deformation gradient into electrical, elastic and viscous parts, while the free energy function is additively decomposed into passive and visco-active parts

$$ \psi (\boldsymbol{\mathnormal{g}}, \boldsymbol{\mathfrak{s}};\boldsymbol{\mathnormal{F}},\boldsymbol{\mathnormal{F}}^e)= \hat{\psi}^{p}(\boldsymbol{\mathnormal{g}},\boldsymbol{\mathfrak{s}};\boldsymbol{\mathnormal{F}}) + \hat{\psi}^{va}(\boldsymbol{\mathnormal{g}}, \boldsymbol{\mathfrak{s}};\boldsymbol{\mathnormal{F}}^e). $$

(23)

In the three-dimensional framework, the passive part $\hat {\psi }^{p}(\boldsymbol {\mathnormal {g}},\boldsymbol {\mathfrak {s}};\boldsymbol {\mathnormal {F}})$ is a function of the total deformation gradient and the visco-active part $\hat {\psi }^{va}(\boldsymbol {\mathnormal {g}}, \boldsymbol {\mathfrak {s}};\boldsymbol {\mathnormal {F}}^{e})$ has a strict dependency on the elastic part of the deformation gradient F^e = F(F^vF^a)^− 1. Moreover, $\boldsymbol {\mathfrak {s}}$ denotes the set of structural tensors describing the orthotropic material microstructure

$$ \boldsymbol{\mathfrak{s}} = \{\boldsymbol{\mathnormal{f}}_0\otimes\boldsymbol{\mathnormal{f}}_0,\boldsymbol{\mathnormal{s}}_0\otimes\boldsymbol{\mathnormal{s}}_0,\boldsymbol{n}_0\otimes\boldsymbol{n}_0, {\boldsymbol{\mathnormal{f}}_0\otimes\boldsymbol{\mathnormal{s}}_0}\}. $$

(24)

By making use of the Coleman and Noll method and the Doyle-Ericksen formula, the Kirchhoff stress tensor is written in an additive format

$$ \boldsymbol{\hat{\tau}}= \boldsymbol{\hat{\tau}}^{p} + \boldsymbol{\hat{\tau}}^{va} \quad \rightarrow \quad \boldsymbol{\hat{\tau}}^{p} := 2\partial_{\boldsymbol{\mathnormal{g}}}\hat{\psi}^{p}(\boldsymbol{\mathnormal{g}},\boldsymbol{\mathfrak{s}};\boldsymbol{\mathnormal{F}}) \quad \text{and} \quad \boldsymbol{\hat{\tau}}^{va}:=2\partial_{\boldsymbol{\mathnormal{g}}}\hat{\psi}^{va}(\boldsymbol{\mathnormal{g}}, \boldsymbol{\mathfrak{s}};\boldsymbol{\mathnormal{F}}^e) $$

(25)

with the passive $\boldsymbol {\hat {\tau }}^{p}$ and visco-active $\boldsymbol {\hat {\tau }}^{va}$ stress contributions.

The well-known orthotropic hyperelastic material model of Holzapfel and Ogden [26] is adopted for the passive part of the free energy function and, accordingly, the passive part of the Kirchhoff stress tensor reads

$$ \begin{array}{ll} \hat{\boldsymbol{\tau}}^{p}:= 2\partial_{\boldsymbol{\mathnormal{g}}}\hat\psi^p = {\varPsi}_1~\boldsymbol{\mathnormal{b}} + {\varPsi}_{4\text{f}}~\boldsymbol{\mathnormal{f}} \otimes \boldsymbol{\mathnormal{f}} + {\varPsi}_{4\text{s}}~\boldsymbol{\mathnormal{s}} \otimes \boldsymbol{\mathnormal{s}} + {\varPsi}_{8\text{fs}}~\text{sym}(\boldsymbol{\mathnormal{f}} \otimes \boldsymbol{\mathnormal{s}})+ \hat{p}~\boldsymbol{\mathnormal{g}}^{-1} \end{array} $$

(26)

by means of the deformation dependent scalar coefficients

$$ \begin{array}{r@{~}l@{~}l@{~=~}l} {\varPsi}_1 &:= & 2\partial_{I_{1}} \bar\psi^p & a \exp[b(I_1-3)], \\[2ex] {\varPsi}_{4\text{f}} &:= & 2\partial_{I_{4\text{f}}} \bar\psi^p & 2a_{\text{f}}\langle I_{4\text{f}}-1\rangle \exp[b_{\text{f}}\langle I_{4\text{f}}-1\rangle^2], \\[2ex] {\varPsi}_{4\text{s}} &:= & 2\partial_{I_{4\text{s}}} \bar\psi^p & 2a_{\text{s}}\langle I_{4\text{s}}-1\rangle \exp[b_{\text{s}}\langle I_{4\text{s}}-1 \rangle^2], \\[2ex] {\varPsi}_{8\text{fs}} &:= & 2\partial_{I_{8\text{fs}}} \bar\psi^p & 2a_{\text{fs}}I_{8\text{fs}} \exp[b_{\text{fs}}I_{8\text{fs}}^2], \\[2ex] \hat p &:= & J\partial_{J}U & \displaystyle\frac{\kappa}{2}(J^2 - 1) {-a}, \\[2ex] \end{array} $$

(27)

where a, b, a_f, b_f, a_s, b_s, a_fs, b_fs are material constants describing the deformation state of the isotropic and orthotropic microstructure of the myocardium. For the visco-active part, however, we adopt the simple quadratic free energy function as we previously proposed [5], which leads to the following visco-active part of the Kirchhoff stresses

$$ \hat{\boldsymbol{\tau}}^{va} = \tau_{\text{f}} ~ \boldsymbol{\mathnormal{f}} \otimes \boldsymbol{\mathnormal{f}} + \tau_{\text{s}} ~ \boldsymbol{\mathnormal{s}} \otimes \boldsymbol{\mathnormal{s}} + \tau_{\text{n}} ~ \boldsymbol{n}\otimes \boldsymbol{n} $$

(28)

in terms of the nonlinear visco-active Kirchhoff stress coefficients

$$ \tau_{\text{i}} : = 2\partial_{I_{4{\text{i}}}} \hat\psi^{va} = \frac{\sigma_{\text{i}}}{I_{4{\text{i}}}} \quad \text{with} \quad \sigma_{\text{i}} = \mu_{\text{i}}~\epsilon_{\text{i}}^e \quad \text{for} \quad \text{i}=\{\text{f},\text{s},\text{n}\}, $$

(29)

where μ_i represents the shear moduli. Moreover, the invariants describing the isotropic and orthotropic deformation state are defined as

$$ I_{1}:= \text{tr}\boldsymbol{C}, \quad I_{4\text{f}}:= \boldsymbol{\mathnormal{f}}_0 \cdot \boldsymbol{C} \boldsymbol{\mathnormal{f}}_0, \quad I_{4\text{s}}:= \boldsymbol{\mathnormal{s}}_0 \cdot \boldsymbol{C} \boldsymbol{\mathnormal{s}}_0, \quad I_{4\text{n}}:= \boldsymbol{n}_0 \cdot \boldsymbol{C} \boldsymbol{n}_0, \quad I_{8\text{fs}}:= \boldsymbol{\mathnormal{f}}_0 \cdot \boldsymbol{C} \boldsymbol{\mathnormal{s}}_0. $$

(30)

Evolution equations for internal variables

In this part, we briefly refer to the evolution equations that are required to compute the visco-active part of the stress tensor (Eq. (28)). The deformation driven viscous stretches are evolved according to the equation

$$ \dot\epsilon^v_{\text{i}} = \frac{1}{\eta_{\text{i}}}\left|\frac{\beta_{\text{i}}}{\bar\beta_{\text{i}}}\right|^{m_{\text{i}}} \beta_{\text{i}} \quad \text{with} \quad \beta_{\text{i}}:=\sigma_{\text{i}}:=-\partial_{\epsilon^v} \hat{\psi}^{va}_{\text{i}}(\epsilon^e_{\text{i}}), $$

(31)

which is based on the Biot equation, in terms of the material parameters m_i, η_i and $\bar \beta _{\text {i}}$ in the fibre, sheet and normal directions. Parameter m_i controls the transition from purely linear viscoelastic-to-nonlinear viscoplastic flow. Parameter η_i is the viscosity parameter and $\bar \beta _{\text {i}}$ indicates the activation stress, which is taken as unity to ensure the consistent units. Note that a closed form solution exists for $\epsilon ^{v}_{\text {i}}$ with m_i = 0, whereas for m_i > 0, $\epsilon ^{v}_{\text {i}}$ turns into a nonlinear function of the thermodynamical force β_i necessitating the update of the internal variables $\epsilon ^{v}_{\text {i}}$ through local Newton-Raphson iterations in a time-discrete setting. Note that the evolution equations for $\bar c$ and $\lambda _{\text {f}}^{a}$ are already given in Eqs. (1) and (2), respectively.

4.2 Ventricular blood pressure

Since a quasi-linear relation exists between the ventricular pressure and ventricle cavity volume $\mathcal {V}$ during isovolumetric phases and filling, the pressure development in those phases is expressed through a linear evolution law

$$ \dot{\hat p}_{\text{v}} = \bar\kappa(\tilde\theta-\theta) \quad \text{with} \quad \tilde\theta := \frac{\tilde{\mathcal{V}}}{{\mathcal{V}}_0} \quad \text{and} \quad \theta := \frac{\mathcal{V}}{{\mathcal{V}}_0}, $$

(32)

where $\bar \kappa$ is a material parameter having distinct values for different phases and imposes the condition $\dot {\mathcal {V}}\approx 0$ during isovolumetric phases and $\dot {\hat {p}}_{\text {v}}\approx 0$ during filling. Moreover, $\tilde \theta$, 𝜃, $\tilde {\mathcal {V}}$ and $\mathcal {V}_{0}$ stand for the dilatation at the end of the previous phase, the current dilation, the volume at the end of the previous phase and the initial volume of the ventricle cavity, respectively. For instance, $\tilde \theta$ and $\tilde {\mathcal {V}}$ values are measured at the end point of the ejection phase during the isovolumetric relaxation. Furthermore, the pressure development during the ejection phase is described through the three-element Windkessel model

$$ \dot{\hat p}_{\text{v}} =\frac{1}{C_{ap}}\left( 1+\frac{R_c}{R_p}\right)q + R_c \dot{q} - \frac{ {\hat p_{\text{v}}}}{C_{ap}R_p} \quad \text{with} \quad q := -\dot{\mathcal{V}}, $$

(33)

where the material parameters C_ap, R_c and R_p determine the resistance and compliance properties of the blood flow and q represents the outflow from the ventricle.

4.3 Current source

When we look at the source of the excitation process of the myocardium, it is possible to consider two distinct parts: a purely electrical part $\hat {F}^{\phi }_{e}$ and a mechanical part $\hat {F}^{\phi }_{m}$

$$ \hat{F}^{\phi} = \hat F^{\phi}_e({\Phi},\mathcal{I}_e) + \hat F^{\phi}_m(\boldsymbol{\mathnormal{g}}; \boldsymbol{\mathnormal{F}}, {\Phi}), $$

(34)

where $\mathcal {I}_{e}$ is the set of internal variables. The ion exchange between the intracellular and extracellular media, which is exclusively induced by the excitation of nearby cells above a threshold potential value, is described by the purely electrical part, whereas the mechanical part describes the ion exchange through the cell membrane resulting from the stretch of the tissue and is often labelled as the mechano-electric feedback. In the literature, the characterization of the mechanical part is commonly made through the following simple equation

$$ \hat F^{\phi}_m = G_s \langle\lambda_{\text{f}}-1\rangle({\Phi}_s - {\Phi}), $$

(35)

where λ_f is the stretch along the fibre direction, G_s is the maximum conductance and Φ_s is the resting potential [41]. Nevertheless, this contribution is only activated if the myocardium is under tension, i.e. λ_f > 1. For the purely electrical part, however, two distinct approaches exist: phenomenological and biophysically based models. The former approach requires relatively low computational cost and is capable of reproducing the main features of the transmembrane potential in a myocardial tissue without physical interpretation. In contrast, the latter is based on experimental observations and considers the local evolution of individual ion species at the cost of a demanding computational treatment. In the following, we give a brief introduction of two frequently employed approaches in the context of phenomenological and ionic models.

4.3.1 Phenomenological description: Aliev-Panfilov model

For the phenomenological description of the cardiac electrophysiology, a dimensionless representation is often preferred in the literature by deriving the unitless transmembrane potential ϕ and unitless time τ as

$$ \phi = \frac{\Phi + \delta_{\phi}}{\beta_{\phi}} \quad \text{and} \quad \tau = \frac{t}{\beta_t} $$

(36)

in terms of the scaling factors β_ϕ, β_t and the potential difference δ_ϕ. In the Aliev-Panfilov model [2], the source term is expressed as

$$ \begin{array}{rrl} \hat f^{\phi}_e =& \partial_{\tau} \phi &= c\phi(\phi - \alpha)(1-\phi) - r\phi + I, \\[2ex] & \partial_{\tau}r &= \displaystyle\left[\gamma + \frac{\mu_1r}{\mu_2 + \phi}\right][-r - c\phi(\phi - b - 1)] \end{array} $$

(37)

in terms of the material parameters c, α, γ, μ₁, μ₂, b and the externally applied stimulus I. The fast depolarization behaviour of the transmembrane potential is formulated through Eq. (37)₁ while the slow repolarization process is described by Eq. (37)₂ in a local sense. Therefore, the so-called recovery variable r is treated as an internal variable in the FE implementation. After the necessary calculations, the physical counterpart of the normalized source term (Eq. (37)₁) can be obtained as

$$ \hat{F}^{\phi}_e({\Phi},\mathcal{I}_e) = \frac{\beta_\phi}{\beta_f} \hat f^\phi(\phi,\mathcal{I}_e) \quad \text{with} \quad \mathcal{I}_e=\{r\}. $$

(38)

4.3.2 Ionic description: Ten Tusscher-Noble-Noble-Panfilov model

The biophysical approach to model the current source considers the dynamics of the main channels, pumps, exchangers and concentrations that influence the flow of ions across the myocyte cell and SR membranes. The flow of ions through the cell membrane leads to the change in the transmembrane potential. One such ionic model for the human ventricular cell was developed by ten Tusscher et al. [50]. The model consists of seventeen ordinary differential equations. One set of the ODEs deals with the gating variables g_gate, which are related to how the currents are activated or inactivated. Another set of the ODEs represents the evolution of the concentrations c_ion. Therefore, the set of internal variables in the FE implementation is $\mathcal {I}_{e}= \{ g_{gate}, c_{ion} \}$. The evolution and set of the gating variables are expressed as

$$ \begin{array}{rcl@{\hskip 5Ex}rcl@{\hskip 5Ex}rcl} \dot{g}_{gate} & = & f_{gate}^{g}\left( {\Phi}, \mathcal{I}_e \right) = \frac{1}{\tau_{gate}({\Phi})}\left[g_{gate}^{\infty}({\Phi},c_{ion}) - g_{gate} \right] , \\ g_{gate} & = & \{ g_m,g_h,g_j,g_{xr1},g_{xr2},g_{xs},g_r,g_s,g_d,g_f,g_{K1}^{\infty},g_{fCa},g_g \}. \\ \end{array} $$

(39)

Here, the functions $g_{gate}^{\infty }$ represent the steady state of the gating variables, while the variables τ_gate are related to the time required to reach the steady state [58]. Moreover, the concentration variables c_ion change based on the movement of ions across the membranes and the ODEs for the concentrations along with the set of concentration variables are given by

$$ \dot{c}_{ion} = f_{ion}^c\left( {\Phi}, \mathcal{I}_e\right) \quad \text{with} \quad c_{ion} = \{ c_{Na},c_K,c_{Ca},c_{Ca}^{sr} \}. $$

(40)

The four concentrations are the free intracellular ion concentrations of sodium (Na⁺) c_Na, potassium (K⁺) c_K and calcium (Ca²⁺) c_Ca and the free ion concentration of calcium in the SR (Ca$_{sr}^{2+}$) $c_{Ca}^{sr}$. Further, the ionic currents I_crt are functions of the transmembrane potential Φ, the gating variables g_gate, the concentration variables c_ion and the internal variables $\mathcal {I}_{e}$. The ionic current functions along with the set of ionic currents are

$$ \begin{array}{rl} I_{crt} = &I_{crt}\left( {\Phi},\mathcal{I}_e\right) \quad \text{with}\\[2Ex] I_{crt} = &\{ I_{Na},I_{bNa},I_{NaK},I_{NaCa},I_{K1},I_{Kr},I_{Ks},I_{pK},I_{t0},I_{CaL},\\[2Ex] & ~~I_{bCa},I_{pCa},I_{leak},I_{up},I_{rel} \}. \end{array} $$

(41)

The currents I_crt are defined as the fast sodium current I_Na, background sodium current I_bNa, sodium potassium pump current I_NaK, sodium calcium exchanger current I_NaCa, inward rectifier current I_K1, rapid delayed rectifier current I_Kr, slow delayed rectifier current I_Ks, plateau potassium current I_pK, transient outward current I_t0, L-type calcium current I_CaL, background calcium current I_bCa, plateau calcium current I_pCa, leakage current I_leak, SR uptake current I_up, and the SR release current I_rel. Additionally, a stimulus current I can be applied to initiate depolarization. Note that the currents I_leak, I_up and I_rel occur across the SR membrane and not the cell membrane. These currents deal with the storing and release of calcium in the myocyte. Finally, the purely electrical current source $\hat {F}^{\phi }_{e}$ can be obtained as the negative of the sum of all the currents that flow across the cell membrane

$$ \begin{array}{rcl@{\hskip 5Ex}rcl@{\hskip 5Ex}rcl} \hat{F}^{\phi}_e(I_{crt}\left( {\Phi},\mathcal{I}_e\right)) = - (I_{Na} + I_{bNa} + I_{NaK} + I_{NaCa} + I_{K1} + I_{Kr} + I_{Ks}\\[2EX] + I_{pK} + I_{t0} + I_{CaL} + I_{bCa} + I_{pCa} + I ). \end{array} $$

(42)

For the sake of brevity, the reader is referred to the work of ten Tusscher et al. [50] and Wong et al. [58] for a more comprehensive discussion of the TNNP model.

4.4 Electrical flux

A potential difference between two points in a conductive medium induces an ion flow between those points that is often denoted as electric flux $\boldsymbol {\hat {q}}$ and can be expressed as

$$ \boldsymbol{\hat{q}}=\boldsymbol{D}\cdot\nabla {\Phi} \quad \text{with} \quad \boldsymbol{\mathnormal{D}}:=d_{iso}~\boldsymbol{\mathnormal{g}}^{-1} + d_{ani}~\boldsymbol{\mathnormal{f}} \otimes \boldsymbol{\mathnormal{f}}, $$

(43)

where d_iso and d_ani are isotropic and anisotropic scalar conductivity parameters, respectively.

5 Numerical examples

5.1 Fitting capacity of the proposed model

In order to demonstrate the adequacy and versatility of the proposed equations, we attempt to reproduce several ICC and corresponding cardiomyocyte shortening curves that were obtained from experiments performed on rats [48] and mice [34].

The data concerning the action potential of the cardiomyocytes is not provided in those papers. Therefore, we do not consider real transmembrane potential evolutions which give rise to the ICC and myocardial shortening data in the experiments. Instead, we use reasonable action potential curves that are approximately in line with the duration of the shortening in the experiments. In each of the fittings, the Aliev-Panfilov model is used for the action potential and the excitation is initiated at t = 100 ms by applying a stimulus for 4 ms with I = 1 [-]. The time step is specified as Δt = 0.5 ms. The ICC data that are extracted from the experiments are shifted in time so that the onset of the ICC in the simulations coincides with the experimental data. For the sake of consistency, the same amount of adjustment in time is applied to the corresponding cardiomyocyte shortening data. The material parameters presented in Table 1 are identified manually without using any optimization procedure. In fact, those parameters can be smoothly determined thanks to the knowledge acquired through the parameter sensitivity analysis in Section 2. The experimental data of Smail et al. [48] obtained from a rat heart and our fits are presented in Fig. 8 for (a) the ICC and (b) the cardiomyocyte shortening. The material parameters of the Aliev-Panfilov model are the same as the ones utilized in Section 2 except for b = 0.2 [-]. The graphs demonstrate a quite accurate fit of the proposed phenomenological equations to the experimental data. The whole ICC data is captured and only slight deviations are observed at the beginning and ending of the myocyte shortening.

Table 1 Utilized parameters for the ICC and active stretch curves in Figs. 8, 9, 10, 11 and 12

Fig. 8

Fitting of the proposed phenomenological equations to the experimental data by Smail et al. [48]. The ICC and cardiomyocyte shortening are shown in a and b, respectively. The ICC data is presented as a normalization to the peak concentration and the cell shortening as the ratio of the cell length to the initial cell length. The initial cell length was assumed to be the mean of the control epicardial myocyte cell length, reported as approximately 130 μm

Moreover, Lim et al. [34] performed experiments on freshly dissected LV myocytes from young adult mouse hearts with different stimulation frequencies 2, 4, 7 and 9 Hz and measured the ICC along with the corresponding cell shortening. The experimental data and our fits are presented in Fig. 9 with 2 Hz, in Fig. 10 with 4 Hz, in Fig. 11 with 7 Hz and in Fig. 12 with 9 Hz for (a) the ICC and (b) the cardiomyocyte shortening. We do not consider different stimulation frequencies and the material parameters of the Aliev-Panfilov model are the same as the ones utilized in Section 2 except for b = 0.9 [-]. As seen in the figures, we can almost reproduce the entire ICC and muscle shortening data for different frequencies. In some of the fits, a minor inaccuracy appears when the myocyte gets closer to its fully relaxed state. For instance, the slow relaxation in Fig. 9 and rapid relaxation in Fig. 12 cannot be entirely captured by the proposed equations.

Fig. 9

Fitting of the proposed phenomenological equations to the experimental data at 2 Hz by Lim et al. [34]. The ICC and cardiomyocyte shortening are shown in a and b, respectively. The data for the ICC is normalized to the maximum value of the 2 Hz graph and shifted downward so that the diastolic ICC is 0. The cell shortening, presented in the form of active stretch, is shown as the ratio of the cell length to the diastolic length

Fig. 10

Fitting of the proposed phenomenological equations to the experimental data at 4 Hz by Lim et al. [34]. The ICC and cardiomyocyte shortening are shown in a and b, respectively. The data for the ICC is normalized to the maximum value of the 2 Hz graph and shifted downward so that the diastolic ICC is 0. The cell shortening, presented in the form of active stretch, is shown as the ratio of the cell length to the diastolic length

Fig. 11

Fitting of the proposed phenomenological equations to the experimental data at 7 Hz by Lim et al. [34]. The ICC and cardiomyocyte shortening are shown in a and b, respectively. The data for the ICC is normalized to the maximum value of the 2 Hz graph and shifted downward so that the diastolic ICC is 0. The cell shortening, presented in the form of active stretch, is shown as the ratio of the cell length to the diastolic length

Fig. 12

Fitting of the proposed phenomenological equations to the experimental data at 9 Hz by Lim et al. [34]. The ICC and cardiomyocyte shortening are shown in a and b, respectively. The data for the ICC is normalized to the maximum value of the 2 Hz graph and shifted downward so that the diastolic ICC is 0. The cell shortening, presented in the form of active stretch, is shown as the ratio of the cell length to the diastolic length

5.2 Finite element simulations in a personalized LV model

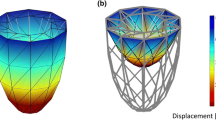
In this subsection, the performance of the proposed contraction model is demonstrated through several FE simulations in a personalized LV geometry that was generated from 4D echocardiography data [7]. The LV geometry is created at end-diastole and discretized by 18,809 four-node tetrahedral elements over 4116 nodes. The discretization corresponds to an average element size of 4.5 mm. Unless differently specified, a constant time step Δt = 2 ms is used in the simulations. The same spatial and temporal resolution are used for both the electrophysiology and mechanical problem. The fibre angle is assigned to material points changing linearly from 70^∘ on the endocardium to − 70^∘ on the epicardium as described by Cansız et al. [6]. Regarding the boundary constraints, linear springs, which impose directional constraints, are attached to the nodes on the basal and epicardial surfaces. The stiffness values of the springs are adopted from our previous work [7] with a slight change in the k_z value at the basal surface. Those stiffness values are applied to mimic physiological LV deformation patterns such as rotation, twist and longitudinal shortening. The discretized geometry, fibre orientation and applied boundary constrains are depicted in Fig. 13. Similar to our previous works [5,6,7], before the final results are obtained, subsequent cycles are carried out until the value of the primary field variables becomes almost constant over the subsequent cycles. In all the simulations, the influence of the mechanical deformation on the source term is neglected with $\hat {F}^{\phi }_{m}=0$ mV/ms for the sake of simplicity.

Fig. 13

Virtualized LV geometry. From left to right: the discretized geometry along with the dimensions (the lengths are in millimetres.), two different views of the fibre orientation and its angle 𝜃 distribution and the springs with different stiffness values (in N/mm) attached to the basal and epicardial surface as boundary constraints

5.2.1 Variations in volume-time relations

The v-t relation is a widely used measure by cardiologists, especially because it can be easily obtained through imaging techniques (e.g. echocardiography) in a non-invasive way. These curves indicate valuable data such as the stroke volume (SV) and ejection fraction (EF) that can be used to evaluate cardiac function at first sight. Additionally, the shapes of the curves, namely, magnitudes of the ascending and descending slopes provide important information such as systolic acceleration and filling rate that can be used for a detailed LV function assessment [15].

A study performed by Zeidan et al. [59] presents several v-t curves for both healthy subjects and patients with coronary and hypertensive heart disease. For ill patients, the study found a loss of symmetry in the v-t curves, a lower early filling rate during diastole and a lack of clear distinction between the early filling period from mid-diastolic diastasis when compared to the healthy subjects. Additionally, the researchers observed that the peak filling rates were lower and the time to peak filling rate was significantly prolonged in the patients with coronary and hypertensive heart disease. Moreover, a study by Duvall et al. [15] showed that the values of systolic emptying rates and diastolic filling rates appear to decrease with age.

In the following, we present various v-t relations with respect to the same electrical activity by only modifying the parameters of the active stretch equation in a similar manner as the examples performed at the material level in Section 2.2. Basically, the aim is to demonstrate how the proposed phenomenological model can be utilized to alter the contraction-relaxation (systole-diastole) characteristics on the organ level.

In order to describe the cardiac electrophysiology, the Aliev-Panfilov model is employed. At time t = 0 ms, the myocardial tissue is assumed to be in a resting state with Φ₀ = − 80 mV and the depolarization wave is initiated by applying a small amount of stimulus, I = 3 [-] for 16 ms, to the upper part of the septum corresponding to the atrioventricular node. Moreover, the scaling factor β_t in the Aliev-Panfilov model is formulated in terms of the activation time t^act whereby early excited regions have a longer action potential duration compared to later activated regions [31]. The activation time t^act is specified as the elapsed time from the excitation of the atrioventricular node until the transmembrane potential of a particular material point reaches − 40 mV. The cycle length is determined as 800 ms. For simplicity, ventricular blood pressure is not taken into account. The necessary material parameters, other than those related to the active stretch, are given in Table 2. The v-t relations with different parameter sets are presented in Fig. 14 along with the electrical activity which is the same in all examples and illustrated through the ECG graph (most upper diagram). The parameters of the active stretch model are manually calibrated. It is worth noting that the descending and ascending slope and duration at peak point of the v-t curves are mainly determined by the parameters k₂, q and p₂, while the parameter ξ is calibrated simply to obtain the same EF value in all curves.

Table 2 Utilized parameters in the simulations

Using a set of parameters which shifts the peak point of the myocardial contraction in time (similar to Fig. 4a), the v-t curves display a comparable movement of the minimum, as seen in Fig. 14 with material set 1. The shifts of the minimum value in time also affect the rate of the ejection (contraction) and filling (relaxation), where a further shift forward in time results in a flatter shape in both the descending and ascending limb of the v-t curve. The same pattern is observed in the myocardial contraction curves in Fig. 4a. Accordingly, the simulations with the parameter set 2 in Fig. 14 demonstrate a similar pattern as that observed in Fig. 5a, where the slope of the myocardial relaxation (filling) is flattened while keeping the rate of the shortening almost the same, thereby the symmetry of the v-t relation is significantly distorted. Moreover, in Fig. 14, the parameter set 3 achieves a notable increase in the duration of the maximum contraction similar to that observed in Fig. 5b, where the duration of the minimum of the myocardial contraction is stretched in time. It is worth noting that the curves generated with material parameter set 4 and 5 do not exhibit a horizontal line at peak value as in Fig. 5b. Observe that the rate of contraction is much steeper for those curves which accordingly results in large viscous stretches. When the peak point is reached, the viscous stretchtes immediately tend to go back their initial state while the active stretch stays as a plateau for a while (similar as in Fig. 5b). Therefore, the LV volume does not stay constant and starts to increase although the active stretch value remains the same for a while. Lastly, we note that the magnitude of the v-t curve can be altered simply with the parameter ξ (not shown) analogously in Fig. 4b.

Fig. 14

Demonstration of various v-t relations with different material sets versus the same electrical activity. The most upper curve illustrates the ECG, which is the same for all simulations, and the first, second and third v-t diagram (from up to down) are obtained with the material set 1, 2 and 3, respectively. The curve numbering starts from the most left in the first and second diagram while in the third one the curve numbering starts in the middle and the material parameters are changed in the arrow direction

The changes in the parameters are easily able to capture differences in the v-t relation characteristics, such as the descending and ascending slope, duration and magnitude of the peak, which are related to systolic and diastolic function. The application of this capacity can be quite broad. One benefit would be gained in fitting a v-t relation obtained from an echocardiography or magneto resonance imaging. Once the v-t data is fitted, one can further perform simulations in order to predict, for instance, the pressure-volume (PV) relation, which is measured invasively in reality, or active and passive contributions to the wall stress, which is not possible to acquire in clinical routine. Moreover, the easily adjustable features of the active stretch equation might be useful when one needs to investigate how the characteristics of v-t relation are interrelated with other aspects of the heart, e.g. mechano-electric feedback, phases in the PV relation, boundary conditions etc.

5.2.2 Regional variations in contraction

Experimental and clinical studies show that there is an elegant electrical and mechanical activation sequence in the heart that achieves an efficient pumping function. In a healthy heart, the depolarization wave coming from the atria enters the ventricles through the atrioventricular node and is then rapidly transmitted to the myocardium by the fast conduction system (the His bundle consisting of the left and right bundle branches and the Purkinje fibres) and the whole ventricles are depolarized in a specific order. In general, elapsed time to the electrical activation is shorter on the subendocardial layers and increases towards the epicardium [14].

Upon ventricular depolarization, the myocytes start to contract with distinct regional variations in terms of timing, magnitude and duration of the contraction [46, 47]. Experimental observations have revealed that the LV contraction starts with a brief myocyte shortening in the subendocardium, which coincides with a rapid pressure increase during the isovolumetric contraction phase. Since the LV cavity volume remains almost constant in this phase, the subendocardial shortening results in an elongation of the subepicardial fibres. The subepicardial contraction starts with the onset of systolic ejection and the time gap between the beginning of subendocardial and subepicardial activation is related to the duration of isovolumetric contraction. In the ejection phase, however, all parts of the ventricle shorten together. The magnitude of shortening is larger in the apical segments than in the basal segments, which creates an observable wave of shortening travelling from the apex towards the base. On the other hand, during diastole, ventricular relaxation does not follow exactly the same pattern. Firstly, a relaxation wave occurs before the closure of the aortic valve in the subendocardial region that travels from the apex to the base. The subepicardium, however, starts to relax after aortic valve closure and travels in the opposite direction, namely from the base towards the apex. During the isovolumetric contraction, shortening of the subendocardial layers leads to a small amount of clockwise apical rotation and anti-clockwise basal rotation. In the course of ejection, however, the subepicardial layers dominate the rotation because of their longer moment arm and the direction of the rotation is reversed due to the opponent fibre orientation on the layers closer to the epicardium.

In the following, we aim to mimic the aforementioned regional variations of myocardial contraction throughout the virtual LV model with the proposed equations. The Aliev-Panfilov model is used for the cardiac electrophysiology and, in order to simplify the simulation, a simultaneous electrical activation is considered in the LV model by applying I = 0.1 [-] for 20 ms to all elements. Thereby, we neglect the influence of the electrical activation sequence on the ventricular contraction and focus only on the parameters related to the active stretch. The LV wall is divided into two equal segments along its thickness: an inner layer (from the endocardial surface to the middle of the LV wall) and an outer layer (from the middle of the LV wall to the epicardial surface). For each segment a different parameter set is assigned for the active stretch equation to be able to illustrate varying contraction characteristics. The material parameters k₂ and ξ for each layer and q for the outer layer are linearly interpolated from the base to the apex (see Fig. 15). Moreover, constant values q = 0.015 [-] and p₂ = 3 [-] for the inner layer and p₂ = 7.5 [-] for the outer layer are specified. With this setting, we could capture heterogeneous characteristics of the contraction. The rest of the necessary material parameters are adopted from Table 2, except for μ_f which is increased by a factor of 3.0. Note that in this simulation the blood pressure in the LV cavity is taken into account. The details of additional considerations regarding the applications of blood pressure in the simulation such as passive inflation and switch conditions between phases of PV relation can be found in our previous works [5, 7]. As in the previous example, we consider a cycle length of 800 ms. In the forthcoming results, the cycle, whose results are presented in the following, starts at time t = 100 ms.

Fig. 15

Distribution of interpolated parameters throughout the LV model

In Fig. 16, the PV relation and rotation of the basal and the apical regions along with twist are depicted. The characterization of LV rotation and twist is performed as described by Cansız et al. [7]. Figure 17 illustrates the snapshots of the active stretch $\lambda ^{a}_{\text {f}}$ distribution and mechanical activation distribution that is obtained according to $\lambda ^{a}_{\text {f}}$ while the values in Fig. 18 are based on the total stretch along the fibre direction λ_f. At this point, it is worth mentioning that for the calculation of the current λ_f value, the reference state is not taken as the undeformed LV geometry, instead, the deformation state at the end of previous cardiac cycle is considered as the reference configuration for the current cycle since a considerable amount of residual deformation exists at end-diastole upon subsequent cycles. This residual deformation has two sources as observed in our previous works [5, 7]. One source is the viscous effects that are considered in the material model. The other one arises from the fact that the value of the active stretch $\lambda ^{a}_{\text {f}}$ at some of the regions in the LV does not totally return to its resting value at the end of the cardiac cycle due to the interpolated parameters in the active stretch equation. Moreover, an element is considered to be mechanically activated when the shortening reaches 10% of its maximum [23]. Bear in mind that EMD and elapsed time to mechanical activation are identical since all elements are instantly stimulated at the same time.

Fig. 16

a Pressure-volume diagram furnished with some important data: stroke volume (SV), EF, end-diastolic volume (EDV), end-systolic volume (ESV) and switch pressures p₁ and p₂. b Rotation of the basal and apical regions along with twist

Fig. 17

Demonstration of a $\lambda ^{a}_{\text {f}}$ distributions at different times in the cycle and b mechanical activation distribution calculated according to $\lambda ^{a}_{\text {f}}$. In the simulation, LV blood pressure is taken into account

Fig. 18

Demonstration of a λ_f distributions at different times in the cycle and b mechanical activation distribution calculated according to λ_f. In the simulation, LV blood pressure is taken into account

In the simulation, physiologically realistic LV contraction with 61% EF and rotation of the basal and apical segments are obtained. Besides, the magnitude of the myocardial shortening ($\lambda _{\text {f}}^{a}$) is mostly larger than 70% throughout the LV model. As a result of the applied material parameters in the active stretch equation, which vary throughout the LV geometry, we could reproduce some important characteristics of the ventricular contraction that are mentioned above. The snapshots of $\lambda ^{a}_{\text {f}}$ and the corresponding mechanical activation distribution presented in Fig. 17 clearly show that the contraction starts first at the inner (subendocardial) layers at the apex and propagates towards the basal segments. A significant outcome of the earlier subendocardial contraction is the manifestation of a moderate positive and negative rotation of the basal and apical regions, respectively, as depicted in Fig. 16b. In addition, the beginning of subendocardial activation coincides with the sudden pressure upstroke in the isovolumetric contraction phase. Afterwards, a similar contraction wave, from the apex to the base, is perceived at the outer (subepicardial) layers. Moreover, higher contractility (smaller $\lambda ^{a}_{\text {f}}$ values) is present in the regions close to the apex. However, the direction of the basal and apical rotations is reversed as the subepicardial layers start to contract and the magnitude of the rotation is considerably increased. This is undoubtedly a result of the longer moment arm of the subepicardial layers which then dominates the behaviour of the rotation during the ejection. On the other hand, the snapshots of $\lambda ^{a}_{\text {f}}$ in Fig. 17 designate that myocardial relaxation first starts at the apex and propagates towards the base at the inner layers, while the outer layers experience the relaxation wave travelling in the opposite direction, from the base to the apex. These results comply well with the observations stated by Sengupta et al. [46].

Nevertheless, if we examine the contraction behaviour based on the total stretch along the fibre direction λ_f (see Fig. 18), the results differ from the evaluation based on $\lambda ^{a}_{\text {f}}$. At first glance, the shortening wave propagates with a similar pattern at the inner layers as in Fig. 17. However, as the contraction wave further expands, smaller total stretch (larger shortening) values are measured at the outer basal region although $\lambda ^{a}_{\text {f}}$ is larger (less contraction) at these regions, see the snapshots at time t = 230 ms and t = 260 ms in Fig. 18. Accordingly, the mechanical activation distribution differs from the one in Fig. 17 as we move from the apex to the base.

Furthermore, the same simulation is performed by neglecting the blood pressure in the LV model to investigate whether the consideration of blood pressure influences the above discussed aspects of the LV contraction. The used parameters are identical except for ξ which is reduced by a factor of 0.78 at every point in the LV model. This is because we would obtain a very high EF in the absence of blood pressure since there would not be any resisting force acting on the endocardium. In the case without blood pressure, the EF is measured as 57%.

As one could expect, the characteristics of the mechanical activation based on $\lambda ^{a}_{\text {f}}$ are the same (not shown) since the evolution of $\lambda ^{a}_{\text {f}}$ is merely governed by the electrical activity. Besides, we observe similar rotation and twist curves with a slight reduction in magnitude (not shown). The essential difference is noticed in the evolution of λ_f and corresponding mechanical activation (see Fig. 19). In the absence of the blood pressure, λ_f follows almost the same pattern as $\lambda ^{a}_{\text {f}}$ and, accordingly, a similar mechanical activation distribution is observed. This difference with respect to the case where the blood pressure is considered can be explained as follows. The presence of blood pressure on the endocardial surface forces myocardial fibres to elongate, particularly, at the inner layers close to the base, which eventually delays the shortening. Therefore, a quite different distribution of λ_f and mechanical activation is observed when the pressure in the LV model is taken into account. However, the sequence of the relaxation has similar characteristics in both cases.

Fig. 19

Demonstration of a λ_f distributions at different times in the cycle and b mechanical activation distribution calculated according to λ_f. In the simulation, LV blood pressure is not taken into account

On the other hand, the simulation results have discrepancies with some of the previously mentioned clinical findings. In contrast to the observation that the subendocardium has smaller stretch values, i.e. higher contractility, than the subepicardium, we had to specify the parameters related to $\lambda ^{a}_{\text {f}}$ so that the outer layers have slightly larger contractility than the inner layers. Such a parameter setting is necessary to be able to obtain mild rotation humps at the beginning of the cycle, which are created by early activation of the subendocardial layers, followed by inverted rotation directions of the inner and outer layers with higher amplitudes (see Fig. 16b). In the simulations where higher contractility is considered for the inner layers, we observe a quite big positive and negative rotation of the basal and apical regions at the onset of the early endocardial contraction, which were far from physiological observations (not shown). Another disagreement was the absence of a significant elongation of the outer layers in the LV model during the isovolumetric contraction phase.

5.2.3 Compatibility to ionic model: drug application

The numerical examples presented here are concerned with the compatibility of the active stretch equation with the TNNP model. For this purpose, we apply a drug called verapamil to the LV model and observe its effects on the cardiac electromechanical behaviour. Verapamil is a calcium channel blocker, which dilates blood vessels, acts as a cardiac depressant and is often used to treat hypertension and chest pain [16, 53]. Furthermore, verapamil can suppress arrhythmias which travel through the atrioventricular node. As observed in some in vitro studies, verapamil can abbreviate the action potential duration [1, 39]. Regarding the contraction behaviour, calcium channel blockers (such as verapamil) are known to reduce the ICC and muscle contractility [53].

We imitate the effects of drugs on the LV physiology using the approach presented in the work of Costabal et al. [11], where the following expression is employed to block specific ion channels

$$ I_{crt}^{drug} = (1 - \beta)I_{crt}. $$

(44)

The fractional block β is a fit of a Hill-type equation

$$ \beta = \frac{C^h}{{IC_{50}}^h + C^h}, $$

(45)

where C is the concentration of the drug, h is an exponent and IC₅₀ is the concentration at which 50% of the current is blocked [12]. These parameters can be obtained via a manual patch clamp technique as performed by Crumb et al. [13]. From the same study, we adopt the parameters blocking the rapid delayed rectifier current I_Kr as IC₅₀ = 499 nM, h = 1.1 [-] and the L-type calcium current I_CaL as IC₅₀ = 202 nM, h = 1.1 [-].

To better accommodate the ionic model with the active stretch equation presented in this paper, we modify the original calcium concentration c_Ca curve of the TNNP model. We alter the time to peak of the c_Ca through a modification in the gate g_g (Equation (39) in the publication [58]) by assigning the time variable τ_g as 300 ms in the case where $g_{g}^{\infty } > g_{g} ~ \text {and} ~ {\Phi } \geq -60 ~ \text {mV}$ do not apply

$$ \begin{array}{rcl@{\hskip 5Ex}rcl@{\hskip 5Ex}rcl} \tau_{g} & = & \begin{cases} \infty ~~~~~~~~~ \text{if} ~ g_{g}^{\infty} > g_{g} ~ \text{and} ~ {\Phi} \geq -60 ~ \text{mV} \\ 300 ~ \text{ms} ~~~~~ \text{otherwise}. \end{cases} \end{array} $$

(46)

Furthermore, the maximal I_up parameter is increased to $I_{up}^{\max \limits } = 0.00085$ mM/ms and the maximal I_rel parameter is decreased to $I_{rel}^{\max \limits } = 0.001399$ mM/ms. All in all, the peak of c_Ca is shifted further in time and the descending slope becomes steeper as compared to the original evolution of c_Ca. Next, regarding the excitation-contraction coupling, the calcium concentration is modified so that it becomes unitless and starts from zero. For this purpose, we subtract the diastolic concentration c_Ca,diastolic from the calcium concentration c_Ca and divide the value by 1 μM

$$ \begin{array}{rcl@{\hskip 5Ex}rcl@{\hskip 5Ex}rcl} \overline{c} & = & \left( c_{Ca}-c_{Ca,diastolic} \right) \frac{1}{1~\upmu \mathrm{M}}. \end{array} $$

(47)

At this point, it is worth mentioning that the ICC, $\overline {c}$, that is obtained out of c_Ca in the TNNP model will be governing the active stretch $\lambda _{\text {f}}^{a}$ in the following examples. Unless differently specified, the necessary material parameters are given in Table 2 for the stress response, in Table 3 for the TNNP model, specified for human myocytes [54], and its initial conditions are given in Table 4. Here, we note that the LV wall is segmented in three equal parts along the radial direction. The inner, middle and outer segments are used to assign endocardial, M cell and epicardial specific parameters, respectively. Moreover, the parameters related to the conductivity are specified as d_iso = 0.05 mm²/ms, d_ani = 1.0 mm²/ms. The diastolic calcium concentration is taken as c_Ca,diastolic = 0.03 μM.

Table 3 Parameters used for the TNNP model. Note the use of the abbreviations half-saturation constant (HSC) and maximal (Max.)

Table 4 Initial conditions utilized for the TNNP model

Before proceeding with the FE simulations of the LV model, we first investigate the effect of verapamil on a single epicardial cell at the material point level (see Fig. 20). A time step Δt = 0.1 ms is used for the entire duration of the presented action potential graphs. The parameters of the active stretch are assigned as k₂ = 0.03 [-], ξ = 0.027 [-], q = 0.4 [-] and p₂ = 1.0 [-]. Note that the action potential in Fig. 20 has a different form compared to the original TNNP epicardial myocyte action potential due to the modified c_Ca evolution by the time variable τ_g in Eq. (46). Higher concentrations of verapamil result in a reduction in the peak and duration of the action potential along with a decrease in the magnitude and time to peak of the ICC $\overline {c}$. Accordingly, the active stretch $\lambda ^{a}_{\text {f}}$ decreases in magnitude and its minimum occurs earlier in time. Moreover, the relaxation is slowed down as manifested by the milder slope of the active stretch for higher concentrations of verapamil.

Fig. 20

Evolution of the transmembrane potential Φ in a and the ICC $\bar {c}$ and the active stretch $\lambda ^{a}_{\text {f}}$ in b for a cycle in the cases of control (c_verap = 0 nM) and two concentrations of verapamil (c_verap = 150 and 1000 nM). The graphs are obtained by using the TNNP model for an epicardial myocyte. Note that $\overline {c}$ is scaled down by a factor of 1.75 for demonstration purposes

For organ scale simulations, we make adjustments in a few maximal current conductances to obtain a meaningful ECG. Due to the discretization used in the simulations, the value of the maximal I_Na conductance is decreased to $C_{Na}^{\max \limits } = 3.56$ nS/pF so that the upstroke velocity is proper enough for a satisfactory conduction velocity. Also, to obtain a positive T wave, it is important to take into account that earlier activated tissue has a longer action potential duration compared to later activated tissue [18]. Motivated by the work of Kotikanyadanam et al. [31], we interpolate the maximal I_Kr and I_Ks conductances ($C_{Kr}^{\max \limits }$ and $C_{Ks}^{\max \limits }$, respectively) with respect to the electrical activation time t^act, which is defined as in Section 5.2.1, through

$$ C_{crt}^{\max} \leftarrow C_{crt}^{\max} \left( m_{\text{int}} t^{\text{act}} + b_{\text{int}} \right), $$

(48)

in terms of the maximal current conductance $C_{crt}^{\max \limits }$ and the interpolation factors m_int = 0.0217 ms^− 1 and b_int = 0.1 [-]. These parameters are interpolated based on the activation time to obtain a heterogeneous distribution of the action potential durations resulting in a positive T wave in the ECG. In each of the FE simulations, we use a smaller time step Δt = 0.1 ms for the first 90 ms of the cycles to ensure stability during the sharp myocyte depolarization. For the rest of the simulation, a larger time step Δt = 2 ms is used since the slope of the action potential in time is less steep. For the chosen time steps, we obtain a quadratic convergence behaviour of the global residual norm through Newton-Raphson iterations and do not encounter any stability problems. A cycle length of 900 ms is considered. The parameters used for the active stretch were k₂ = 0.0072 [-], ξ = 0.00728 [-], q = 0.36 and p₂ = 1.0 [-]. Regarding the initiation of the LV depolarization at the atrioventricular node, a larger stimulus is required for higher concentrations of verapamil. Therefore, we applied a stimulus of I = − 100 pA/pF, I = − 150 pA/pF and I = − 300 pA/pF for the cases of control, c_verap. = 150 nM and c_verap. = 1000 nM, respectively. Furthermore, to reduce the computational load, the blood pressure in the LV is not considered.

The simulations presented in Fig. 21 show the electromechanical behaviour in the control case and in the cases, where two different concentrations of verapamil are applied. The control simulation has a normal ECG with a satisfactory duration of the QRS and QT intervals. Additionally, an EF of 66% is measured. These markers indicate that the LV behaviour is within a physiological range for the electrophysiology and the mechanics. On the other hand, when a verapamil concentration of 150 nM is applied, repolarization occurred earlier and more uniformly, which leads to a smaller QT interval and a reduction in the magnitude of the T wave. Besides, verapamil suppresses the contractility, i.e. the active stretch, resulting in a reduced EF (54%) and a decrease in the duration of systole.

Fig. 21

Illustration of the application of two concentrations of verapamil (c_verap = 150 and 1000 nM) and its comparison to the control case (c_verap = 0 nM). In the snapshots, the transmembrane potential distribution is shown. The graph presents the ECG with normalized voltage (upper curves) and the v-t diagram (lower curves). The timings of the snapshots are shown with triangles in the graph

Moreover, the largest concentration of verapamil with 1000 nM makes the repolarization and end systole occur much earlier. The QT interval decreases severely and the T wave is inverted. The T wave inversion agrees with the snapshot at time t = 210 ms, where the repolarization wave propagates in a similar direction to the depolarization wave. In addition, a low EF of 28% is obtained along with a much reduced systole duration. Furthermore, the duration of the QRS complex remains constant, while its magnitude decreases for higher concentrations of verapamil. The tendency observed in the ECGs and v-t relations can be explained by the action potential and active stretch behaviour seen in Fig. 20. The action potential duration is reduced at higher concentrations of verapamil. This causes an abbreviated QT interval and also affects the action potential duration dispersion leading to a smaller and inverted T wave. Additionally, verapamil lowers the magnitude of the active stretch resulting in a smaller EF.

The results from the single cell and organ scale simulations show a qualitative agreement with observations from other studies. Action potential durations and QT intervals have been reported to either decrease [1, 17, 39] or stay the same [24, 55] when verapamil is applied. In a recent in silico study which used the O’Hara-Rudy action potential model [40], Costabal et al. [10] found no significant change in the QT interval when verapamil was applied. However, a decrease in both action potential magnitude and duration were also observed in another study [60] which used a more recent version of the TNNP model [54]. Therefore, when verapamil is applied, the changes in the QT interval and action potential are linked with the action potential model. Regarding the contraction behaviour, calcium channel blockers are known to reduce the ICC and muscle contractility [53]. Also, a decrease in the magnitude of the peak tension and the time to peak when verapamil is applied to dog trabecular muscles has been observed [36].

6 Concluding remarks

In this work, we have proposed a phenomenologically based myocardial contraction model that comprises only two simple ODEs and seven material parameters in total. The main goal was to accurately reproduce the myocardial contraction behaviour on both cell and organ scale simulations with as little effort as possible. The model primarily constitutes the normalized ICC through a logarithmic-type relation governed by the normalized transmembrane potential. Then, the active stretch that represents the myocardial shortening is computed by an exponential-type relation having the ICC as argument. The developed contraction model was further integrated into our fully implicit staggered solution scheme [7] for cardiac electromechanics, where the ICC and active stretch are treated as internal variables. In the framework, the myocardium was considered as an orthotropic electro-visco-elastic material through the modified Hill model. For the description of cardiac electrophysiology, however, either the phenomenological Aliev-Panfilov model or the biophysically based TNNP model was employed depending on the nature of the problem.

The foremost attractive aspect of the proposed model is its easy calibration to represent different curve characteristics. This aspect of the model was demonstrated through a comprehensive material sensitivity analysis at the material level in which we could easily alter the upstroke and descending slope and magnitude of the ICC curve and the ascending and descending slope, magnitude and duration of the active stretch curve. These abilities further enabled us to fit the model to various experimental data with an excellent accuracy. However, we did not consider real action potential data recorded in the experiments [34, 48] because it was not provided. Instead, when fitting the ICC and active stretch curves, we employed a reasonable action potential evolution and neglected different stimulation frequencies, which can be addressed as a limitation. Moreover, we discussed the dependency of the ICC and active stretch curves on different action potential behaviour.

Furthermore, the capacity of the myocardial contraction model was illustrated through several initial-boundary value problems in a virtual LV model that was generated from 4D echocardiography data. Firstly, a set of simulations similar to the material parameter sensitivity analysis at the material level was performed and the ability to produce different contraction characteristics at the organ scale was demonstrated by means of the v-t relation of the virtual LV model. In addition, the heterogeneous nature of the myocardial contraction, such as variations in the onset of mechanical activation, relaxation sequence and magnitude, throughout the LV was mimicked in a different set of simulations. For this purpose, some of the parameters related to the active stretch equation were simply interpolated from the base to the apex and from the endocardium to the epicardium. Incorporation of regional myocardial contraction variations in the LV model eventually lead to realistic rotation graphs of the basal and apical segments. In the last set of examples, the ionic model of ten Tusscher et al. [50], in contrast to the phenomenological description [2] of cardiac electrophysiology in the previous examples, was employed to demonstrate the feasibility of the active stretch equation with a biophysically based model of cardiac electrophysiology. In the example, we imitated a drug application (verapamil) and studied its implications on contractility as well as on the electrophysiology of the LV model. It was shown that the incorporation of the ICC that is produced by the TNNP model, i.e. c_Ca, into the proposed active stretch equation enables realistic numerical analysis of the excitation-contraction problem without any numerical issue.

One important drawback in our LV model was the absence of the fast conduction system, i.e. the bundle of His and Purkinje fibres. First of all, this limited the ability to obtain a realistic electrical wave propagation and activation sequence and, thus, for instance, the Q and S waves were not detectable in the ECG in Fig. 14. Besides, heterogeneities in the electrical activity are closely linked to different ICC evolutions and, accordingly, to variations in the myocardial contraction throughout the LV. However, we omitted the effect of heterogeneities in the electrical activity on myocardial contraction. Particularly, in Section 5.2.2, we considered the same electrical activation and action potential duration all over the LV model and captured the heterogeneities in the myocardial contraction through the calibration of the material parameters in the active stretch equation.

Some further limitations need to be addressed. First, the phenomenological description is not intended to reproduce some fundamental experimental observations, such as the Frank-Starling law, the force-frequency relationship or Hill’s force-velocity relation. These experimental observations could be considered by adding further dependencies and relationships in the definition of the excitation-contraction coupling. Second, the predictive capabilities of the proposed approach might be reduced without a direct connection to the underlying microstructural mechanisms controlling excitation-contraction coupling. Third, a diminished accuracy of the organ level simulations might be present, since a relatively coarse discretization in space and time was used.

All in all, the proposed contraction model has a huge application potential in computer simulations due to its easy adjustability to different conditions, ability to accurately capture reality, straightforward implementation and compatibility to frameworks having a phenomenological or ionic description of cardiac electrophysiology.