Numerical investigation on epi-off crosslinking effects on porcine corneas

Abstract

Experimental inflation tests, conducted on 90 pig corneas before and after corneal collagen crosslinking (CXL) treatment, are simulated with the finite element method. The experimental sample consists of five groups of corneas treated with different UV-A irradiation times (2.5, 5, 10, 15, and 20 min) at constant irradiance 9 mW/cm². The linear elastic shell theory is used to estimate the equivalent material stiffness of the corneas, revealing that it increases with the exposure time in CXL corneas. In the view of numerical simulations, a simple mechanical model assuming piecewise constant elastic modulus across the corneal thickness is introduced, to estimate the effective increment of the material stiffness in the anterior stroma and the effective depth of the stiffness increment. The two effective quantities are used in the finite element models to simulate the post-CXL tests. Numerical models are able to describe the mechanical effects of CXL in the cornea. The increment of equivalent material stiffness has to be ascribed to a localized increment of the material stiffness in the anterior layers of the cornea, while the posterior layers preserve the original material stiffness. According to the simplified model, the increment of the material stiffness of the anterior cornea increases with the irradiation dose, while the effective reinforcement depth decreases with the irradiation dose. This trend, predicted by a simple mechanical model by imposing equilibrium and compatibility, has been verified by the numerical calculations that captured the global mechanical response of the corneas in untreated and post-CXL conditions.

1 Introduction

The cornea is organized into five principal layers: the epithelium, the Bowman lamina, the stroma, the Descemet lamina, and the endothelium, in order from anterior to posterior surfaces [1]. The stroma, the carrying structure of the cornea, is composed of a matrix of elastin and proteoglycans embedding collagen fibrils, organized into a highly specialized hierarchical architecture enabled by chemical bonds (crosslink) able to provide the necessary mechanical stiffness and to shape the curvature of the lens [2]. In contrast with the prevalent isotropic distribution of the collagen fibrils observed within the anterior third of the thickness, in the deepest layers of the stroma, the collagen fibrils show preferential directions along the nasal-temporal (NT) and superior-inferior (SI) meridians [3, 4].

The cornea is a biological structure, whose behavior depends on geometry and material constituents. From the geometrical point of view, the topography and the pointwise thickness are the most relevant parameters; from the material point of view, fundamental are the composition, the microstructure, and the mechanical properties (material stiffness, material strength, time dependence) of the single constituents [5]. The quasi-spherical shape of the cornea is the optimal mechanical response of the structure to the action of the uniform intraocular pressure (IOP) exerted by the aqueous humor [2, 6]. The spherical shape may be lost as a consequence of the alteration of the corneal tissues. Typical diseases of the cornea are keratoconus and post-laser assisted in situ keratomileusis (LASIK) ectasia.

Keratoconus is a genetic progressive non-inflammatory disease characterized by localized corneal thinning and by the decrease of the crosslink density between collagen fibrils, with the consequent reduction of mechanical stiffness [7]. The localized, paracentral, compliant material region is responsible of the change of the cornea shape from spherical to conical, affecting the refractive properties of the cornea in terms of irregular astigmatism, high myopia, and light sensitivity. Post-surgical corneal ectasia is a rare complication of LASIK. It is in general associated with risk factors, i.e., excessively small corneal thickness, very high myopia, irregularities, or steepening, which are diagnosed with a corneal topography [8].

The modern leading treatment for keratoectasia, which surged as one of the standard treatments for keratoconus, is the corneal collagen crosslinking (CXL) [5], an early intervention carried out to slow down the evolution of the pathology and to avoid invasive and risky perforating keratoplasty [7]. CXL consists of a collagen reinforcement performed on the cornea, activated through the administration of riboflavin (B₂ vitamin) followed by UV-A irradiation at a wavelength of 370 nm [9]. The deposition of riboflavin induces a chemical reaction, which releases oxygen radicals. Photopolymerization caused by UV-A irradiation creates new bonds (crosslinks) between the collagen fibrils located in the anterior stroma. The formation of new crosslinks modifies the microstructure of the anterior cornea. After CXL, collagen fibrils are thicker and stiffer and the global stiffness of the cornea increases, reducing the tendency to further deform [5].

Stemming from the original Dresden protocol [9], various CXL protocols have been proposed. In particular, the epithelium hinders the spreading of riboflavin and causes a larger consumption of oxygen [10]. The epi-off CXL is carried out directly on the stroma after the removal of the epithelium, resulting in a most effective treatment [11,12,13]. The total amount of irradiated energy (i.e., the irradiance dose) has been identified as the most relevant parameter in terms of stiffening effects [14]. Previous studies showed that very short or too prolonged duration of the irradiation does not improve the outcomes of the CXL treatment [15].

The quantification of the mechanical efficacy of the CXL procedures is still an open question, which becomes relevant in the view of personalized treatments. The correct description of the mechanical changes occurring in the cornea during CXL and the quantitative estimation of the corneal stiffening related to the parameters of the procedure (in particular the irradiation dose) opens the possibility of defining personalized protocols.

The recent literature reports a few interesting in vitro studies on animal corneas [9, 15,16,17]. The observed discrepancy between in vitro and in vivo study results suggests using cautiously in vitro tests for quantitative measurements of any mechanical parameters. However, in vitro tests are fundamental in order to understand the mechanical behavior, since by using well-established experimental procedures it is possible to explore a wide range of actions, well outside the physiological ranges. Furthermore, the first attempts of mechanical quantification of CXL outcomes are also not comparable because the measurements as well as the interpretation of the results are very much study dependent. In particular, among studies, there is lack of agreement on the terminology concerning the stiffness parameters, and quantities with different mechanical meaning (elastic modulus, Young's modulus, shear modulus, stiffness) are often mixed up in reporting clinical or experimental data.

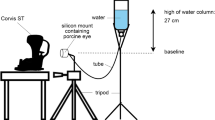
The present study is the companion of an experimental investigation carried out on 90 porcine corneas treated with epi-off CXL at five different exposure times (2.5, 5, 10, 15, and 20 min) and constant irradiance of 9 mW/cm² [18]. The experiments consisted in inflation tests carried out with the goal of evaluating quantitatively the effects of the irradiance dose on the stromal stiffening. In contrast with previous studies that used a different group of corneas for control, the inflation tests were performed on the same corneas before and after CXL. The equivalent stiffness of the cornea before and after CXL, in terms of secant elastic modulus of the stroma, was estimated at different IOP levels using the linearized theory of shells applied to the average experimental results for each group [18]. Results confirmed that the longer the irradiation time, the stiffer the CXL cornea. Short irradiation times provided very similar results, with a slightly growing trend, while longer irradiation times showed an evident increase of the stiffness. The experimental procedure consisted in the de-epithelization and the preconditioning of each specimen, the inflation test under a growing pressure from 1.85 to 30 mmHg, and the depressurization to 1.85 mmHg. After the CXL treatment, timed according to each specific protocol, a second inflation test has been conducted up to 30 mmHg. Images taken during the two tests were elaborated with a graphics software (ImageJ) to reconstruct the geometry of the inflated cornea. Interestingly, the CXL procedure was conducted over a relaxed configuration of the cornea, where the collagen fibrils were not completely uncrimped, introducing a difference from the actual CXL procedures on the human eyes, treated at the physiological IOP. Another difference from clinical experience consists in the healthy conditions of the treated porcine corneas, while in humans CXL is applied only on ectatic corneas.

In the present study, a numerical model of the porcine cornea has been constructed on the basis of the geometry acquired during the tests. The cornea is modeled by considering a nonuniform distribution of the material stiffness across the thickness. Tests conducted on the untreated corneas are used to calibrate the material properties of the natural corneas and to provide a mechanical significance to the secant elastic modulus estimated through the shell theory. Tests conducted on the CXL corneas are used to calibrate the material properties of the treated corneas, by making an assumption on the depth of the penetration across the thickness of the stiffening. The depth is estimated by means of a simple mechanical model of the reinforced cornea.

2 Materials and methods

A sample of 90 eyes of 9-month-old pigs was obtained from a local abattoir (Fumagalli Industria Alimentari S.p.A., Via Briantea, 18, 22038 Tavernerio CO). Specimens were de-epithelized, mounted on the experimental support, pre-conditioned, and tested within 2 days post-mortem. The details of the experimental campaign can be found in [18].

Briefly, during the inflation tests, specimens were subjected to a growing pressure (1.8 to 30 mmHg) in steps of 2.5 mmHg. At each step, images including the entire nasal-temporal (NT) and superior-inferior (SI) profiles of the anterior surface of the cornea were acquired. Subsequently, digital images were segmented with a specific software to recover all the fundamental geometrical parameters, together with the anterior cornea displacements along both NT and SI meridians as a function of the pressure. After the depressurization, a CXL procedure was applied to all the corneas using five different UV-A irradiation times. Each cornea was soaked with riboflavin for 10 min, dosing 2 drops every 3 min. Riboflavin was activated by UV-A using a constant irradiance of 9 mW/cm² at 370 nm wavelength over a circular area of 7.5 mm diameter. During the irradiation, one drop of riboflavin was dosed every 2.5 min. Twenty-two corneas were treated with the accelerated protocol (A-CXL), with 10 min of exposure to UV-A for total energy dose 5.4 J/cm². Seventeen corneas received 2.5 min of UV-A exposure (1.35 J/cm²), sixteen corneas 5 min (2.7 J/cm²), eighteen corneas 15 min (8.1 J/cm²), and seventeen corneas 20 min (10.8 J/cm²). After the CXL treatment and a second inflation test conducted with the same loading and recording procedures, the corneas were sectioned in strips to measure the average thickness.

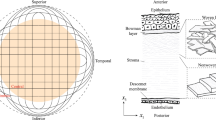
The sets of geometrical data obtained from image are along the NT meridian, the in-plane anterior (${D}_{NT}^A$) and posterior (${D}_{NT}^P$) diameters, and the anterior (${R}_{NT}^A$) and posterior (${R}_{NT}^P$) curvatures; along the SI meridian, the anterior (${D}_{SI}^A$) and posterior (${D}_{SI}^P$) diameters, and the anterior (${R}_{SI}^A$) and posterior (${R}_{SI}^P$) curvatures; from both meridians, the apex elevation (H); from the excised strips, the limbus (t_l), and apex (t_a) thicknesses. Experimental images of the measurements can be found in [18]. Figure 1a shows schematically the in-plane projection of the pig cornea, characterized by different NT and SI diameters, while Fig. 1b illustrates, on the NT meridian section, the meaning of each parameter.

Fig. 1

(a) In-plane view of the elliptical shape of the pig cornea. (b) Geometrical meaning of the parameters used in the construction of the solid model of the cornea

The experimental values, measured on all the specimens, were taken at the image corresponding to the minimum value of pressure applied in the experiments (1.839 mmHg), representative of the unstressed configuration, and analyzed statistically. The average values of each group, listed in Table 1, were used to construct the computational model by using a parametrized cornea generator [19,20,21].

Table 1 Geometrical parameters of the pig corneas

Displacements measured during the tests were elaborated by means of the linearized shell theory to obtain estimates on the average mechanical behavior of the cornea [18, 22]. In particular, the experimental apex displacement w at the physiological IOP p (15 mmHg in each cornea) was used to compute the average equivalent secant elastic modulus E as:

$$E=\frac{p{R}^2}{w\ 2t}\left(1-\nu \right)\left(1-{e}^{-\lambda \psi}\cos \lambda \psi \right)$$

(1)

where R is the NT curvature radius, t the corneal thickness at the apex, ν (here set to 0.5) the Poisson coefficient of the stroma, and the constant λ and the angle ψ, related to the elevation angle φ of a spherical coordinate reference system and to the in-plane corneal radius S=D/2, are defined as:

$$\lambda ={\left[3\left(1-{\nu}^2\right)\right]}^{1/4}\frac{R^{1/2}}{t^{1/2}},\kern0.5em \psi ={\sin}^{-1}\frac{S}{R}-\varphi .$$

(2)

The pre-CXL average and uniform elastic modulus at the physiological IOP, obtained from Eq. (1) using the method illustrated in [22], is denoted with E_b. The post-CXL average and uniform equivalent elastic modulus at the physiological IOP, computed from Eq. (1) for each group of corneas, is denoted with E_a.

Equation 1 holds for a linear elastic material, isotropic and homogeneous, and for a perfectly spherical shell cap of uniform thickness t, mid-surface radius R, in-plane radius S, subtended by the angle 2α, and constrained at the boundaries with pins. The linearized shell theory assumptions are violated by the corneal specimen under exam; thus, the significance of the resulting modulus is very limited and must be regarded only from the qualitative point of view as an indicator of the global corneal stiffness. Furthermore, the estimation refers to a uniform stiffness, which is not corresponding to the actual condition of the CXL corneas. In this sense, it should not be thought nor referred to as the elastic modulus of the cornea.

From clinical and laboratory investigations, it is known that CXL reinforces the anterior portion of the cornea, while the posterior portion remains unchanged [23]. The actual distribution of the reinforcement increment is unknown: accurate measurements on buttons of the cornea taken from different depths, as it was done in [24] for healthy corneas, are missing. An estimate of the depth of the treatment, together with a better estimate of the stiffness of the treated layer, can be obtained from structural mechanics, specifically from an application of the linearized theory of beams.

For the derivation, the material is assumed to be linear elastic isotropic; t is the depth of the cross section at the apex (see Fig. 2a). The inhomogeneity of the post-CXL stiffness across the thickness leads to a nonuniform distribution of the stresses. To describe the cornea after CXL, a two-layer beam model is considered, characterized by two different values of the elastic modulus (posterior E_b and anterior E_c = cE_b). The anterior modulus extends to a depth (1 − d)t. The beam theory delivers a system of two equations for the two constants c and d, in the ranges c > 1 and 0 < d < 1, respectively (see Appendix A for the derivation). Equations 16 and 18 admit the closed form solution:

$$c=\frac{\eta \left(1+\eta \right)}{3-\eta },\kern0.5em d=\frac{2\eta }{3+\eta },\kern0.5em 3>\eta =\frac{E_a}{E_b}>1$$

(3)

with restriction on the value of η to range between 1 and 3.

Fig. 2

(a) Apex cross section of the cornea before CXL treatment, assumed to have a uniform elastic modulus and uniform strain and stress distribution due to the normal force. Bending forces are assumed to be negligible. (b) Idealized distributions of normal strain and stresses across the apex section of the cornea due to normal force (ε_n, σ_n) and bending moment (ε_b, σ_b) after CXL treatment. The elastic modulus is assumed to be piecewise uniform across the thickness. Below the depth (1 − d)t, with 0 < d < 1, the elastic modulus preserves the original value E_b, while above the depth (1 − d)t, it assumes the value E_c = cE_b, with c > 1. The resulting stress distribution across the thickness is piecewise constant (for uniform elongation), and piecewise linear, null at the static barycenter of the section z_c (for change of curvature). The equivalent elastic modulus E_a is the weighted average of E_c and E_b over the two thicknesses (1 − d)t and dt

Relation 3 is obtained without accounting for the curvature of the cornea. A nonuniform distribution of the stresses across the section originates a bending moment which is associated with a variation of the geometric curvature of the cornea. In the case of incremented elastic modulus on the anterior layers, the resulting bending moment extends the anterior fibers of the cornea and increases the geometric curvature, enhancing the corneal forward displacement. In the case of incremented elastic modulus on the posterior layers, the resulting bending moment leads to a reduction of the corneal forward displacement. According to this observation, to counterbalance the increased compliance of the cornea due to the actual curvatures of the cornea, the coefficient c must be increased (almost doubled) with respect to the estimate of Eq. 3.

A more accurate characterization of the material properties of the cornea can be obtained by using finite element simulations. Unlike analytical theories, numerical approaches are able to adopt realistic and biologically meaningful material models and accurate geometrical approximations. In this study, the geometry of the pig cornea is obtained from the parametric solid model generator developed in [19,20,21]. Following [25], the updated parametric model has been adapted to account for the ellipsoidal shape of the pig eye.

The material model considered in this study, presented in previous works [26,27,28], is an advanced hyperelastic material model developed explicitly for the human cornea, which accounts the anisotropy of the material and the quasi-incompressibility of the tissue, neglecting viscosity, porosity, and other time-dependent behaviors. Anisotropy is modeled by statistically distributed (according to a von Mises distribution) collagen fibrils immersed into an isotropic elastin and proteoglycan matrix. The specific form of strain energy density, expressed in finite kinematics, accounts for three contributions, one concerning the volumetric behavior, the second dealing with the isotropic portion of the material (elastin and proteoglycan matrix and 40% of the randomly dispersed collagen fibrils), and the third contribution dealing with the anisotropic portion of the material (60% of the fibrils that albeit dispersed are arranged around a specific average orientation):

$$\psi ={\psi}_{\mathrm{vol}}(J)+{\psi}_{\mathrm{iso}}\left({\overline{I}}_1,{\overline{I}}_2\right)+{\sum}_{M=1,2}{\psi}_{\mathrm{aniso}}\left({\overline{I}^{\ast }}_{4M},{\sigma}_{4M}^2\right).$$

(4)

In turn, the volumetric strain energy density, function of the Jacobian J = det F, with F = ∂x/∂X the deformation gradient, has the form:

$${\psi}_{\mathrm{vol}}(J)=\frac{1}{4}\ K\left({J}^2-1-2\log J\right),$$

(5)

where K is a volumetric stiffness that in linear elasticity would correspond to the bulk modulus. The isotropic strain energy density is of the Mooney-Rivlin form:

$${\psi}_{\mathrm{iso}}\left({\overline{I}}_1,{\overline{I}}_2\right)=\frac{1}{2}\ {\mu}_1\left({\overline{I}}_1-3\right)+\frac{1}{2}\ {\mu}_2\left({\overline{I}}_2-3\right),\kern0.5em {\mu}_1+{\mu}_2=\mu,$$

(6)

where μ is the shear modulus of the material and ${\overline{I}}_1,\kern0.5em {\overline{I}}_2$ are the first and second invariants of the isochoric (modified) Cauchy-Green deformation tensor $\overline{\mathbf{C}}={J}^{-2/3}{\mathbf{F}}^T\mathbf{F}$. The anisotropic strain energy density addresses the contributions of two statistically distributed families of collagen fibrils, with mean orientation a_M. The strain energy density of the M family is characterized by the expression

$${\psi}_{\mathrm{aniso}}\left({\overline{I}}_{4M}^{*},{\sigma}_M^2\right)=\frac{k_{1M}}{2{k}_{2M}}\ \exp \left[{k}_{2M}{\left({\overline{I}}_{4M}^{\ast }-1\right)}^2\right]\left(1+{K}_M^{\ast }\ {\sigma}_M^2\right),$$

(7)

where k_1M is defined as the fibril stiffness (characterizing the smaller strains) and k_2M as the fibril rigidity (characterizing the larger strains). The average pseudo-invariant ${\overline{I}}_{4M}^{\ast }$ is defined as:

$${\overline{I}}_{4M}^{*}=\left[{\kappa}_M\mathbf{I}+\left(1-3{\kappa}_M\right){\mathbf{a}}_M\bigotimes {\mathbf{a}}_M\right]:\overline{\mathbf{C}},$$

(8)

where κ_M is a dispersion parameter that depends on the actual fibril spatial distribution. The coefficient ${K}_M^{\ast }$ is given by:

$${K}_M^{\ast }={k}_{2M}+2{k}_{2M}^2{\left({\overline{I}}_{4M}^{\ast }-1\right)}^2,$$

(9)

and the pseudo-invariant variance is defined as:

$${\sigma}_M^2=\overline{\mathbf{C}}:{\mathbf{a}}_M\bigotimes {\mathbf{a}}_M\otimes {\mathbf{a}}_M\bigotimes {\mathbf{a}}_M:{\overline{\mathbf{C}}}_{2M}-{{\overline{I}}_{4M}^{*}}^2.$$

(10)

More details of the model can be found in the original works [25, 28]. The adopted material model has the known drawback not to be able to account for anisotropic behaviors under volumetric deformations [29]. Despite this limitation, the application to the stromal tissue behavior is appropriate, since the dominant deformation in the cornea is deviatoric.

Besides the orientation of the main direction of each fibril family in each location of the cornea, the model is characterized by seven parameters: K, μ₁, μ₂, k₁₁, k₁₂, k₂₁, k₂₂.

The material model has been derived for applications in the human corneas, where the orientation of the fibrils is switching from an orthogonal NT-SI architecture at the center to a circumferential-radial organization at the limbus (see Fig. 3).

Fig. 3

Schematic visualization of the average orientation of the stromal fibrils assumed in the finite element models of the pig corneas

The actual distribution of the fibrils in pig corneas has been found to be different from humans, with a predominant circumferential orientation [30]. The attempt to adopt an orientation closer to the experimental observations for pigs was not successful, since the resulting shapes of the inflated corneas differed markedly from the experimental ones. As already mentioned in [27], the information provided in [30] is insufficient to build an accurate model of the pig cornea fibril architecture; therefore, in the present study, the human organization was considered [19, 21]. The distribution of the fibrils has been kept constant in all the models.

A solid model of the pig cornea was constructed for each group of corneas, using the average geometrical measurements of the cornea samples as input parameters to define the shape of both anterior and posterior surfaces (see Table 1) [19, 22]. According to the assigned mesh size, the code automatically discretizes the solid model into eight-node brick finite elements with linear shape functions. For the present calculations, 10 elements were inserted across the thickness. Figure 4 shows three views of one of the used finite element meshes (6875 nodes and 5760 brick elements with linear interpolation).

Fig. 4

Finite element mesh of one of the five cases, comprising 6875 nodes and 5760 brick elements with linear interpolation. Unstressed configuration. (a) Posterior view, (b) anterior view, and (c) NT section

The pre-CXL cornea was modeled assuming a uniform stiffness across the thickness. The design of the numerical model of post-CXL corneas requires the introduction of an “equivalent reinforcing depth” in the thickness, above which an increment of the corneal stiffness can be assigned. The reinforcing depth, for this particular model, has only a mechanical meaning and should not be confused with the well-acknowledged demarcation line that marks the region where biochemical phenomena are clinically observable within 2 weeks after the intervention. The reinforcing depth is the ideal mechanical distance that allows to define, in terms of equilibrium and compatibility, the thickness of the uniformly reinforced stroma. The simplified analytic formulas reported in Eq. 5 were used to compute the thickness. From these formulas, it was possible to define a proper subdivision of the thickness in layers (10) to obtain a good approximation for all the cases.

3 Results

Pressure versus apex displacement curves were obtained from the inflation tests conducted on untreated and treated corneas. Average and standard deviation values of the apex displacement as a function of the pressure for untreated and treated corneas of different groups are visualized in Fig. 5a, b, c, d, and e. Figure 5f collects the pressure versus apex displacement curves for all the treated corneas. Figure 5 shows that the effect of CXL is to increase the stiffness of the cornea and to reduce the dispersion around the average value, with a marked decrease of the variance.

Fig. 5

Experimental results for inflation tests for the five cornea groups, irradiated 2.5, 5, 10, 15, and 20 min, respectively. IOP versus apex displacement. (a–e) Comparison between the untreated corneas and the treated corneas of each group. (f) Comparison of the average response of the five groups of treated corneas

Figure 6a shows the average secant elastic modulus, obtained by averaging the values of all the experimental curves and grouped in untreated and post-CXL tests for each protocol. Figure 6b shows the analytical curves of the parameters c and d of Eq. 3 and the corresponding values for the five groups. The estimated pre- and post-CXL secant moduli and the parameters c and d are listed in Table 2.

Fig. 6

(a) Average untreated E_b and post-CXL E_a cornea equivalent secant elastic moduli as obtained from the experiments. (b) Dependence of the constants c and d from the ratio between the post-CXL cornea equivalent elastic modulus E_a and the untreated cornea equivalent modulus E_b. Circles visualize the values of the d and c parameters for the five protocols. Both parameters grow with the ratio E_a/E_b

Table 2 Equivalent secant elastic moduli for untreated and post-CXL corneas, for each protocol, and coefficients for the estimate of reinforced moduli and treatment depth according to Eq. 3

The finite element models of the five groups of the corneas have been used to tune the material parameters of the untreated corneas by best-fitting of the experimental IOP-apical displacement curves. The parameters are listed in Table 3 (first row of each group). Table 3 also reports the parameters to be assigned at the anterior layers to best fit the post-CXL experimental IOP-apical displacement curves (third row of each group). The post-CXL values of the stiffness parameters have been initially estimated by amplifying the best-fitted values obtained for untreated corneas by the coefficient c in Table 2 (second row of each group). For all cases, the formula underestimates the experimental stiffness. The best-fitting calibration procedure applied to the post-CXL cases has provided higher values for the k₁₁ and k₁₂ stiffness. The increment of the stiffness coefficients is, for the five cases, about double the increment predicted by the theoretical formula based on the beam model. Note that the volumetric compressibility and rigidity coefficients have not been modified. For reference, the very first line of Table 3 contains the values of the analyses documented in [27].

Table 3 Modeling parameters for each group of corneas. First line, literature comparison. First line of each group, preoperative parameters; second line, best-fitted post-CXL values from analytical simplified formula; third line, best-fitted calibrated post-CXL values

Figure 7a, b, c, d, and e compare the numerical results with the experimental data, for the five groups of corneas, in terms of pressure versus apex displacement. In each figure, the black symbols denote the experimental data and the white symbols the numerical results. The gray symbols denote the numerical results for the treated corneas as obtained using the prediction of the two-material beam formula. Figure 7f collects the numerical results for the five groups, by comparing untreated and treated corneas.

Fig. 7

Comparison between the experimental and numerical results for inflation tests for the five cornea groups, irradiated 2.5, 5, 10, 15, and 20 min, respectively. IOP versus apex displacement curves. Stiffness parameters have been calibrated for each group for the untreated cases. The stiffnesses for the treated cases have been evaluated using the formulas in Eq. 3 (gray circles) and subsequently doubled to obtain a good correspondence: (a) 2.5 min, (b) 5 min, (c) 10 min, (d) 15 min, (e) 20 min, (f) all

Figure 8 shows the maps of the stress distribution in the NT meridional section at the physiological IOP (assumed to be 15 mmHg). The figures compare one of the untreated cases with the 2.5-min and 20-min irradiation CXL cases.

Fig. 8

Numerical results. NT stress component (MPa) distribution for (a) untreated cornea; (b) 2.5-min irradiated cornea; (c) 20-min irradiated cornea

Figure 9 compares the numerically computed NT profiles before and after CXL treatment for the five groups. Images show a retraction of the CXL profile with respect to the untreated cases.

Fig. 9

Numerical results. Comparison between the NT profiles of treated (red contours) and untreated (blue contours) corneas for the five groups: (a) 2.5 min, (b) 5 min, (c) 10 min, (d) 15 min, (e) 20 min

4 Discussion

The CXL is an ophthalmological procedure used to increase the stiffness of the anterior layers of the stroma. Acknowledged outcomes of CXL are the stabilization of ectasia and the halting of the keratoconus evolution. CXL can be performed according to several protocols. Both riboflavin dose and time interval between sequential imbibition are important during the intervention, but, according to the clinical observations, the most relevant parameter for the cornea stiffening is the irradiation dose, i.e., the total amount of energy irradiated during the entire procedure. Clearly, the same amount of energy can be delivered by combining different powers and irradiation times. Under the assumption of the Bunsen-Roscoe law, it is believed that the corneal stiffening is proportional to the dose [23]. Under the assumption that, using the same irradiation dose, the same increment of stiffening is obtained on the cornea, several protocols have been proposed as an alternative to the original Dresden protocol. From the clinical point of view, alternative higher dose/shorter time protocols are more appealing since they increase the tolerability for the patient, by reducing the irradiation time and potential damage to the corneal tissues [31, 32]. Although the current clinical trend is the preservation of the epithelium, to facilitate the formation of chemical bonds in deeper layers of the cornea, the epithelium is often removed (epi-off) before riboflavin soaking and irradiation.

Although the mechanical action of CXL is well known, the open issue for CXL procedures is the quantitative estimate of the corneal stiffness increment as a function of the irradiation time, at fixed irradiation power or at fixed dose. A qualitative assessment might not be sufficient for the definition of the parameters of the optimal patient-specific procedure. The establishment of a relation between dose, irradiation times, and level of corneal stiffening will contribute to the definition of customized CXL.

By using experimental results on porcine corneas [18], the present study focuses on the mechanical interpretation of the CXL outcomes, trying to quantify the stiffening effects of the intervention, i.e., geometrical flattening of distorted corneas and halting of the keratoconus progression. Experiments conducted at constant irradiation power and different times on five groups of corneas have revealed that a larger dose, i.e., a longer exposure time, leads to a greater stiffening. The linearized shell theory provides an estimate of the average (intended as a value that refers to the entire cornea shell) secant material stiffness of the cornea, before and after CXL. The values E_b and E_a are estimated using a theory that accounts for uniform material across the thickness and over the cornea surface and thus are intrinsically related to its shape and layered structure, and somewhat limited by the simplifying assumptions. However, they can be used to feed more sophisticated models of the cornea that can deliver more accurate estimates of the actual modifications induced by CXL. Advanced models are characterized by several geometrical and material parameters; to be able to reproduce the reality, the parameters must be calibrated on a specific patient. With the surge of advanced diagnostic machines based on imaging, nowadays the geometry of the human cornea is easily acquired and it is possible to reconstruct with a high level of fidelity the solid model of a patient-specific cornea. On the contrary, the characterization of the material properties is not an easy task. The simplest models require the estimation of five to seven parameters. Clearly, a single test on a cornea cannot be able to provide all of them, but, with the aid of an approximated guess of the global corneal stiffness, it would be possible to quantify the mechanical effects of CXL. The present study is setting a first step toward the possibility to refine the information provided by a single test in terms of a quantitative estimation of the increment of the corneal stiffness.

By averaging the geometrical data acquired from the images with a specific software, for each group counting 15 to 22 porcine corneas, it was possible to construct the average solid model; a few of the outlier geometries have been excluded from each group. Table 1 lists the average geometrical parameters of the five groups; differences can be attributed to the biological variability of the specimens and to distinct deliveries from the abattoir. The corresponding average finite element models have been constructed using a parametric solid model generator able to describe the ellipsoidal shape of porcine corneas [27]. The subdivision of the model into ten layers across the thickness has been chosen to maintain the same discretization in the five groups, for the untreated and treated cases. Untreated corneas have been considered homogeneous across the thickness, while it was necessary to modify the material properties of the anterior elements of the treated corneas, characterized by a reinforced anterior layer.

The definition of the equivalent reinforcing depth, where an increment of the corneal stiffness is assigned, is based on a simple bi-material beam model. By equating the resulting axial force and bending moment of the bi-material beam and of the homogeneous equivalent beam, it is possible to obtain an estimate of the ratio between the elastic moduli of the two materials and an estimate of the relative thickness of the two layers. The two equivalent moduli E_b and E_a obtained from the shell theory are used to compute, for each group of corneas, the effective depth of the treatment and the increment of the stiffness of the treated layer (Table 2). Note that the reinforcing depth must not be confused with the well-acknowledged demarcation line, which marks the region where biochemical phenomena are clinically observable until two weeks after the intervention. The reinforcing depth is an ideal mechanical distance that defines, in terms of equilibrium and compatibility, the thickness of the treated reinforced stroma.

For each group of corneas, the homogeneous case has been used to calibrate the parameters of the material model of the cornea through an identification procedure. The material model accounts for a compressibility coefficient, whose significance is moderate, since it is used to enforce the incompressibility, and it has been set according to previous studies [19, 21]. The two rigidity coefficients, which model the behavior of fully extended fibrils, have also a moderate importance, since the tests do not involve large deformations. Four parameters (μ₁, μ₂, k₁₁, k₂₁) instead are related to the behavior of the collagen fibrils. Crosslinking causes the formation of new bonds between adjacent fibrils, which stiffen and thicken. The first two parameters (μ₁, μ₂) describe the isotropic behavior of the matrix, given by elastin, proteoglycans, and about 40% of the collagen fibrils, disposed randomly. The k₁₁ and k₂₁ parameters describe the behavior of 60% of the fibrils that are oriented in specific directions, providing anisotropy to the tissues. In consideration of the specific action of the CXL, it is likely that the increment of stiffness should be assigned only to the collagen stiffness parameters.

The best-fitting parameters for the five groups of untreated corneas are listed in Table 3, first line of each group. The identification procedure consisted in a sequence of numerical analyses, in each of which the parameters were modified to reduce progressively the difference on the anterior NT and SI profiles between experimental images and numerical results. Interestingly, the calibrated values of the stiffness do not agree with the values obtained in previous studies [27], showing a smaller value for the isotropic stiffness (0.01 MPa versus 0.08 MPa for μ₁ and -0.009 MPa versus -0.07 MPa for μ₂, resulting in a shear modulus 10 times smaller) and a larger value for anisotropic stiffness (0.23 MPa to 0.45 MPa versus 0.09 for k₁₁ and k₁₂, resulting in a value 3 to 5 times larger). These differences may be related to the use of different experimental protocols, and to the accurate preservation of the eye specimens before the execution of the test, that avoided the leaking of storage fluids in the specimens in the present campaign.

The subsequent analyses for CXL corneas have been conducted by exploiting the information obtained from the bi-material beam model. The stiffness coefficients of the untreated cases have been amplified by the coefficient c in Table 2, and these values have been applied to the anterior layers according to the estimate given by the coefficient d in Table 2. The predictions obtained using the suggestions of the beam model (gray circles in Fig. 7) underestimated the experimental results. The best-fitting calibration procedure applied to the treated eyes revealed that only the collagen fibril stiffness parameters were underestimated. Interestingly, for each group of corneas, the increment of the stiffness to be applied to best fit the experimental post-treatment data was about double of what the two-material beam model was suggesting.

The present study differs from previous published works because it describes the increment of the corneal stiffness in the anterior layer of the stroma. The study documented in [17] on rabbit corneas used a different experimental protocol, by including a non-treated control group, and the effects of the supplied CXL irradiance were analyzed by means of finite element simulations by considering a unique hyperelastic Ogden model for the entire thickness. The equivalent tangent (as opposite to the secant) elastic modulus ranged from 0.6 MPa for untreated corneas to 1.2 MPa for the ones with the most intense treatment, but the stiffness values cannot be compared to the present results because they refer to different animal species.

We must observe that, given the complexity of the cornea microstructure, the present results are approximated, since the model disregards the presence of posterior layers that show a different stiffness. Thus, the equivalent secant modulus has to be intended as a homogenized value. Furthermore, the presence of several material parameters in the model leads to the attainment of one of the multiple set of parameters that are achievable through a numerical calibration based on a single test. Many sets of parameters may lead to the same anterior shape, at least for the untreated case. In the present study, the experience acquired in previous works helped in selecting an acceptable set of material values for starting the calibration.

The simplified bi-material beam model used in this study is a very rough approximation of the behavior of a post-treated cornea. Despite its simplicity, though, the model accounts for equilibrium and compatibility, conditions to be satisfied by any system in physiological conditions. The bi-material beam model suggests that, for an assigned increment of equivalent stiffness of the cornea, the increment of stiffness of the anterior layer must be compensated by a reduction of the depth of the anterior layer itself. If the same concept is applied to a curved beam, things become more complex because of the curvature; thus, the effect will be different if the increment of stiffness is assigned to the anterior layer (with a larger curvature radius) or to the posterior layer (with a smaller curvature radius). In the former case, the reinforcing effect is reduced because of the larger radius; in the latter case, the effect is increased because of the smaller radius. Thus, the prediction of the model has to be intended as a lower bound for the case of the cornea.

The reduction of the effective depth of the treatment with the increase of the dose is in agreement with clinical observations. Furthermore, clinical investigation revealed that the increment of stiffness in the shallow layers of the cornea shows a logarithmic decrement with the increase of the depth [32].

The change of stiffness modifies the stress distribution across the corneal thickness. The knowledge of the stress distribution is of relevance for the short-term and for the long-term follow-up. Figures 8b and c) show that, as a consequence of the stiffness, the stress level in the anterior layers of the cornea increases noticeably, up to 3 times the original value. This aspect calls for further investigations, to assess the long-term performance of the treatment using in vivo testing on animals.

The increase of stiffness in the anterior layers modifies also the global response of the cornea to the action of the IOP. Figure 9 shows that, under the same IOP, the CXL corneas move backward with an evident reduction of the curvature, confirming a beneficial effect of the treatment also from the refractive point of view.

The present numerical study is affected by simplifying assumptions that limit the applicability of the model to human cases. Improvements can be obtained by using a more realistic distribution of the stromal stiffness across the cornea thickness. Additionally, it would be also interesting to describe the variability of the stiffness over the corneal surface, which can be acquired in vivo using modern techniques based on ultrasound spectroscopy [33], scanning acoustic microscopy [34], supersonic shear wave propagation [35], or confocal Brillouin microscopy [36]. Finally, a more realistic finite element model may consider an increment of the corneal stiffness limited to the 7.5 mm diameter central part of the cornea, where the irradiation is actually applied.

The estimation of the corneal elastic modulus has been done using the linearized shell theory, which provides one single value for each level of pressure. The pre-CXL average and uniform elastic modulus at the physiological IOP is denoted with E_b. The post-CXL average and uniform equivalent elastic modulus at the physiological IOP is denoted with E_a. Under the assumption of small strains and linear isotropic elasticity, an estimate of the magnitude of the reinforced elastic modulus E_c = cE_b and of the efficient depth t_c = (1 − d)t can be obtained from the beam theory. A portion of the cornea of thickness t is taken in proximity of the apex. For a linear elastic material, the uniaxial constitutive relation reads:

$$\sigma (z)=\mathrm{E}\left(\mathrm{z}\right)\upvarepsilon\ (z)$$

(11)

For a case of uniform extension $\overline{\varepsilon}$, compatibility requires:

$$\varepsilon (z)=\overline{\varepsilon}$$

(12)

For the case of pure deflection with curvature $\overline{\chi}$, compatibility requires:

$$\upvarepsilon =\overline{\chi}\left(z-{z}_c\right)$$

(13)

where z is a cross-thickness abscissa measured from the posterior surface and z_c is the coordinate of the mechanical barycenter of the cornea, given by:

$${z}_c=\frac{c\left(1-{d}^2\right)+{d}^2}{2\left[c\left(1-d\right)+d\right]}\ t.$$

(14)

Before CXL, the elastic modulus of the stroma is assumed to be constant across the thickness. The distribution of the stresses across the thickness is therefore continuus and follows the distribution of the strains. By way of simplification, it is assumed that CXL increases uniformly the elastic modulus of the stroma to the value E_c = cE_b, with c > 1, up to the depth t_c; thus, d t is the thickness of the untreated stroma (Fig. 2b). The inhomogeneity of the post-CXL stiffness across the thickness leads to the modification of the stress distribution, which becomes piecewise linear. The linear momentum balance imposes:

$${\int}_0^t\mathrm{E}\left(\mathrm{z}\right)\overline{\varepsilon}\ dz=\left[{E}_c\left(1-d\right)+{\mathrm{E}}_bd\right]\ t\ \overline{\varepsilon}={E}_a\ t\ \overline{\varepsilon}$$

(15)

which gives:

$${E}_a={E}_b\left[c\left(1-d\right)+d\right]$$

(16)

The angular momentum balance imposes:

$${\int}_0^t\mathrm{E}\left(\mathrm{z}\right)\overline{\chi}\left(z-{z}_c\right) dz=\frac{d^4-2 cd\left({d}^3-2{d}^2+3d-2\right)+{c}^2{\left(1-d\right)}^4}{c\left(1-d\right)+d}\overline{\chi}{E}_b\frac{t^3}{12}=\overline{\chi}{E}_a\frac{t^3}{12}$$

(17)

which, accounting for Eq. 16, gives:

$${E_b}^2\left[{d}^4-2 cd\left({d}^3-2{d}^2+3d-2\right)+{c}^2{\left(1-d\right)}^4\right]={E_a}^2$$

(18)

The solution of Eqs. 16 and 18 is given in Eq. 3.

Appendix A

The estimation of the corneal elastic modulus has been done using the linearized shell theory, which provides one single value for each level of pressure. The pre-CXL average and uniform elastic modulus at the physiological IOP is denoted with E_b. The post-CXL average and uniform equivalent elastic modulus at the physiological IOP is denoted with E_a. Under the assumption of small strains and linear isotropic elasticity, an estimate of the magnitude of the reinforced elastic modulus E_c = cE_b and of the efficient depth t_c = (1 − d)t can be obtained from the beam theory. A portion of the cornea of thickness t is taken in proximity of the apex. For a linear elastic material, the uniaxial constitutive relation reads

$$ \sigma (z)=\mathrm{E}\left(\mathrm{z}\right)\upvarepsilon \left(\mathrm{z}\right) $$

(A1)

For a case of uniform extension $\overline{\varepsilon}$, compatibility requires

$$ \varepsilon (z)=\overline{\varepsilon} $$

(A2)

For the case of pure deflection with curvature $\overline{\chi}$, compatibility requires

$$ \varepsilon =\overline{\chi}\left(z-{z}_c\right) $$

(A3)

where z is a cross-thickness abscissa measured from the posterior surface and z_c is the coordinate of the mechanical barycenter of the cornea, given by

$$ {z}_c=\frac{2\left(1-{d}^2\right)+{d}^2}{2\left[c\left(1-d\right)+d\right]}t. $$

(A4)

Before CXL, the elastic modulus of the stroma is assumed to be constant across the thickness. The distribution of the stresses across the thickness is therefore continuum and follows the distribution of the strains. By the way of simplification, it is assumed that CXL increases uniformly the elastic modulus of the stroma to the value E_c = cE_b , with c > 1, up to the depth t_c; thus dt is the thickness of the untreated stroma, Fig. 2(b). The inhomogeneity of the post-CLX stiffness across the thickness leads to the modification of the stress distribution, which becomes piecewise linear. The linear momentum balance imposes

$$ {\int}_0^tE(z)\overline{\varepsilon} dz=\left[{E}_c\left(1-d\right)+{E}_bd\right]t\overline{\varepsilon}={E}_at\overline{\varepsilon} $$

(A5)

which gives

$$ {E}_a={E}_b\left[c\left(1-d\right)+d\right] $$

(A6)

The angular momentum balance imposes

$$ {\int}_0^tE(z)\overline{\chi}\left(z-{z}_c\right) dz=\frac{d^4-2 cd\left({d}^3-2{d}^2+3d-2\right)+{c}^2{\left(1-d\right)}^4}{c\left(1-d\right)+d}\overline{\chi}{E}_b\frac{t^3}{12}=\overline{\chi}{E}_a\frac{t^3}{12} $$

(A7)

which, accounting for Eq. (A6) gives

$$ {E}_b^2\left[{d}^4-2 cd\left({d}^3-2{d}^2+3d-2\right)+{c}^2{\left(1-d\right)}^4\right]={E}_a^2 $$

(A8)

The solution of Eqs. (A6) and (A8) is given in Eqs. (5).